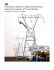vcvc2
Transcription
vcvc2
Electrostatic Potential & Capacitance
ES – 02 – 01 of 21
Electrostatic potential at a point :
It is the work per unit charge that is done to bring a small charge in from infinity to that point
along any path.
1 q
The electrostatic potential V at a distance r from a point charge q is V =
4π ε 0 r
#. Electrostatic potential is a scalar quantity. SI unit of electrostatic potential is volt (V).
#. Electrostatic potential is considered to vanish at infinity.
#. In a conductor, electrostatic potential at the surface is always constant whatever the shape of it is.
Definition of 1 volt :
If 1 joule of work has to be done to move 1 coulomb of charge from infinity to the given
point, then the potential at that given point is 1 volt.
r
#. The electric field around a charged body can be described not only by the electric field strength E
but also by the electrostatic potential V.
Properties of electrostatic potential :
i) It vanishes at points in space infinitely far away from all sources,
ii) it decreases along the electric line of force.
r
#. Electric potential decreases along the line of force (in the direction of the electric field E ).
#. An electron in an electric field moves towards the higher potential whereas a proton moves
towards the lower potential.
#. If a dielectric of dielectric constant K is placed in the medium, the electrostatic potential decreases
V
F
E
as V ′ =
F′ =
also E ′ =
K
K
K
Q. Why the earth is considered to be at zero potential?
Earth has a very large size. Potential of earth does not change with the addition or subtraction
of small charge; therefore, earth is considered to be at zero potential.
1 q
[V =
: as radius of the earth r is very large, V is practically zero,
4π ε 0 r
whatever the amount of charge given to the earth.]
Q. Why electric potential in the field of a negative charge is lower at near points and higher at distant
points?
1 (− q )
For a negative charge, the electric potential is V =
4π ε 0 r
For near points, r is less and V is more negative (lower);
for distant points, r is more and V is less negative (higher).
Difference between electric field and electric potential :
Electric field
Electric potential
i) A vector
i) A scalar
ii) Tells us what force a test charge would ii) Tells us how much work has to be done
feel if it was placed there
to move a test charge there from very
far away
iii) As we move away from the source,
iii) As we move away from the source,
electric field decreases as the inverse
electric potential decreases as the
2
inverse of the distance ( 1/r )
square of the distance ( 1/r )
iv) Decreases or increases more rapidly
iv) Decreases or increases less rapidly
than electric field.
POTENTIAL DIFFERENCE
ES – 02 – 02 of 21
Potential difference :
The potential difference between two points in space in an electric field is defined as the
amount of work done in bringing a unit positive charge from one point to the other against
the electric field.
How to compute the potential difference?
To compute the electric potential difference between two points A and B placed in an
electric field, we move a test charge q 0 from B to A. The amount of work done, per unit charge,
in moving this charge from B to A is the electric potential difference between points A and B.
V A − VB =
WB A
q0
WA
q0
Thus, the electrostatic potential at a point in the electric field is the work in bringing a unit positive
charge from infinity to that point.
If we imagine that the point B to be gradually taken away to infinity, then VB = 0 and V A =
#. Potential increases steadily as we move against the electric field; it decreases steadily as we move
along the field.
Potential due to a point charge :
We want to calculate the electrostatic potential at A at a distance r0 from a point charge q.
The electrostatic potential is the work W A done per unit charge to bring the test charge q 0 from
infinity to A, radially. To calculate this work done, we break the path from infinity to A into many
small segments δ r , find out how much work is to be done for each segment and ultimately add them
up.
We consider two points P and P′ at a distance r and r + δ r from q, with PP′ = δ r
1
q
The electric field at P is E =
4π ε 0 r 2
r
The test charge q 0 , placed at P, experiences a force q0 E . The test charge q 0 can be moved against
r
r
this force, without acceleration, by applying an external force F = − q0 E
Work done to move the test charge q 0 over the segment P′P is
r r
r
r
δ W = F ⋅ ∂ r = − q0 E ⋅ ∂ r = − q0 E ∂ r cos180° = q0 E ∂ r
(
)
q0 q
(δ r ) = q 0 q δ 2r
2
4π ε 0 r
4π ε 0 r
δ r (r + δ r ) − r
1
1
=
−
As δ r is very small, we approximate 2 =
(r + δ r ) r
r r +δ r
r
=
1
∴ δ W (P′ to P) =
q0 q
4π ε 0
1
1
−
r r +δ r
……….(1)
ES – 02 – 03 of 21
Now we consider a series of closely separated points P1, P2, P3, …… radially outwards all the way
to infinity at distances r1 , r2 , r3 ,....... from q.
We now use equation (1) repeatedly and add them up to get the work W A done in bringing a test
charge q 0 from infinity to A along any path as
W A = δ W (P1 to A ) + δ W (P2 to P1 ) + δ W (P3 to P2 ) + ...............
=
q0 q 1
1 1
1 1
1
− + − + − + .....
4π ε 0 r0
r1 r1 r2 r2
r3
or, W A =
q0 q 1
WA
q 1
or,
=
4π ε 0 r0
q0
4π ε 0 r0
Thus, for a point A at a distance r from a point charge q ,the electrostatic potential is V A =
q
4π ε 0
V A is positive if q is positive; V A is negative if q is negative.
Potential at a point due to a dipole :
PQ → dipole, q → charge strength,
2a → dipole length.
Let r be the vector from the dipole
center to a general
point A. We want to calculate the
potential at A.
We consider r >> 2a.
Let r1 and r2 be the distances from
+ q and − q respectively from A.
Potential at
1
VA =
4π ε 0
A is
(+ q ) (− q )
+
r2
r1
Now, r1 = r 2 + a 2 − 2 a r cos θ
2
and
r2 = r 2 + a 2 + 2 a r cos θ
2
As a 2 is very small (r >> a ) , it can be neglected and we write
2a
2a
2
2
r1 = r 2 − 2 a r cos θ ≈ r 2 1 −
cos θ and r2 = r 2 + 2 a r cos θ ≈ r 2 1 +
cos θ
r
r
1
r
Taking square root and reciprocating,
2a
1 1
= 1 −
cos θ
r1 r
r
−1 / 2
≈
a
1
a
1
1 + cos θ = + 2 cos θ
r
r
r r
ES – 02 – 04 of 21
and
−1 / 2
2a
a
1 1
1
a
1
= 1 +
cos θ
≈ 1 − cos θ = − 2 cos θ
r2 r
r
r
r
r r
q 1
1
q 1
a
1
a
∴ VA =
+ 2 cos θ − + 2 cos θ
_ =
4π ε 0 r1 r2 4π ε 0 r r
r r
2a q 1
p cos θ
q 2a
1
=
cos θ =
cos θ =
2
2
4π ε 0 r
4π ε 0 r
4π ε 0
r2
p cos θ
1
∴ VA =
4π ε 0
r2
(Q p = 2 a q )
This tells us that the potential due to a dipole depends not only on the distance r but also on the
r
r
angle θ between the position vector r and the dipole moment vector p . Besides, the potential
falls off as 1 / r 2 , not as 1/ r (in case of potential due to a single charge).
r
r
We get the potential at A with position vector r due to the dipole moment p at the origin as
r r
p⋅r
1
VA =
(r >> a )
(Q pr ⋅ rr = p r cosθ )
3
4π ε 0 r
Case 1 :
If θ = 90°, cos θ = cos 90° = 0 and VA = 0.
This tells us that no work is done in bringing a charge from infinity towards a dipole along
the perpendicular bisector of the dipole. That is, the potential is zero anywhere on the
equatorial plane.
Case 2 :
If θ = 0°, cos θ = cos 0° = 1 and VA is maximum.
r
Hence, potential is maximum on the axis of the dipole and in a direction of p . It takes the
p cos θ
1
form V A = +
4π ε 0
r2
Case 3 :
If θ = 180°, cos θ = cos180° = − 1 and VA is minimum.
r
Hence, potential is minimum on the axis of the dipole and in a direction opposite to p .
1
p cos θ
It takes the form VA = −
4π ε 0
r2
#. The electric field is zero at a point exactly midway between two equal charges of same sign, but
the potential at this point is twice that due to a single charge.
#. Electric potential at any point on the axial line of a dipole has a maximum positive or negative
value as well as the electric field is also not zero.
#. Electric potential at any point on the equatorial line of a dipole is zero while the electric field is
not zero (V = 0 but E ≠ 0).
#. Electric field at any point on the equatorial line of two charges of same magnitude and sign is zero
but the electric potential is twice that due to a single charge (V ≠ 0 but E = 0).
#. The dipole potential is cylindrically symmetric.
Comparison : potential due to a point charge and a dipole :
ES – 02 – 05 of 21
1)
For a point charge, the potential varies as 1/r,
For a dipole, in a fixed direction, the potential varies as 1/ r 2
2)
For a point charge, potential is independent of direction;
For a dipole, there is a dependence on direction.
Expression for the Electric Potential due to a distribution of n point charges (System of
charges) (in terms of their position vectors) :
We consider a system of n point charges
q1 , q 2 , q3 , ......., q n placed in vacuum at
points whose position vectors w.r.t. a point P
r r r
r
are r1 , r2 , r3 , .........rn respectively w.r.t. some
origin. We want to find out the electrostatic
potential V at the point P.
The potential V1 at P due to the charge q1 is V1 =
q1
4π ε 0
1
r1 P
( r1P = distance between q1 and P)
Similarly, the potential V2 at P due to q 2 and V3 due to q3 are V2 =
q2
4π ε 0
q3
1
1
and V3 =
r2 P
4π ε 0 r3 P
where r2 P and r3 P are the distances of P from the charges q 2 and q3 , respectively, and so on for
the potential due to other charges.
By the principle of superposition, the potential V at P due to the total charge configuration is the
algebraic sum of potentials due to the individual charges.
Hence, total potential V = V1 + V2 + V3 + ............ + Vn =
1
4π ε 0
q1
q
q
q
+ 2 + 2 + ............. + n
r
r2 P
r3 P
rn P
1P
If we have a continuous charge distribution characterized by a charge density ρ , we divide it
into small volume elements each of size ∆V and carrying charge ρ ∆V . We then determine the
potential due to each volume element and sum over all such contributions, and thus determine the
potential due to the entire distribution.
EQUIPOTENTIAL SURFACE
Equipotential surface :
Any surface that has the same electric potential at every point is called an equipotential
surface.
r
#. Direction of the electric field E is a normal to the equipotential surface.
#. An equipotential surface can be drawn throughout the region where an electric field exists.
Shape of equipotential surfaces for different charge configurations :
ES – 02 – 06 of 21
1) Point charge - the equipotential
surfaces are surfaces of spheres of
varying radii centered on the point
charge; electric fields are radial,
starting from the charge.
Same is true for a negative point charge.
2) Two equal and opposite
charges
3) Two equal and
positive charges
4) Uniform field - the
equipotential surfaces are
planes perpendicular to the
direction of the electric field.
Properties of equipotential surfaces :
ES – 02 – 07 of 21
1)
No work is required to be done in moving a charge over an equipotential surface,
2)
equipotential surfaces do not intersect each other,
3)
equipotential surfaces indicate regions of strong (crowded) and weak (more spaced)
electric fields.
Q. No two equipotential surfaces can intersect each other : comment.
An equipotential surface is normal to the electric field intensity. If two equipotential surfaces
intersect then at the point of intersection there will be two directions of electric field intensity
which is impossible.
#. Earth is a conductor; its surface is regarded as a equipotential.
Importance of equipotential surfaces :
These give us a visual picture as regard to both the direction and magnitude of the electric
r
field in a region of space. At each point, E is perpendicular to the equipotential surface. Crowded
surfaces indicate stronger fields where as more spaced surfaces indicate weaker fields.
Electric field from electric potential :
A – a point on an equipotential surface having a potential V
B – a point on an equipotential surface having a potential V + ∂V
∂ l – separation between these two equipotential surfaces.
We move a unit test charge from B to A, in the direction of
r
E , over the perpendicular distance ∂ l .
r
Work done = E ∂ l
This work equals the potential difference V A − VB . Thus,
r
r
∂V
E ∂ l = V − (V + ∂ V ) = − ∂V , i.e., E = −
∂l
r
As E is positive, ∂V is negative.
Thus, the direction of electric field is in the direction of
decreasing potential. Further, the field is in the direction where
this decrease is the steepest.
We also can write
r
∂V
.
E =−
∂l
We thus conclude that (i) electric field is
in the direction where the potential decreases steepest and (ii) its magnitude is given by the change in
the magnitude of potential per unit displacement normal to the equipotential surface at that point.
The negative sign also indicates that as we move in the direction of the electric field, the potential
decreases.
∂V
Electric field at any point is equal to the negative of potential gradient at that point, i.e., E = −
∂l
#. Unit of potential gradient is V/m.
ELECTROSTATIC POTENTIAL ENERGY ES – 02 – 08 of 21
Electric potential energy :
The electric potential energy of a system of point charges is defined as the work required to
be done to bring the charges constituting the system to their respective locations from
infinity.
Potential Energy stored in a system of two charges :
Two point charges q1 and q 2 located at A and B with position
r
r
vectors r1 and r2 are considered. In this configuration, the two
charges possess electric potential energy, which we calculate as :
a) we remove two charges to positions such that they are infinitely apart;
r
b) we then move the charge q1 and bring it to location r1 . No work is being done as there is no
other charge in the neighbourhood;
r
c) now we move q 2 to its location r2 . This time q 2 is moved in the field of charge q1 lying at A
r
( position vector r1 ). The work done in moving q 2 from infinity to point B in the electric
field of charge q1 is
W = (work done in moving a unit charge from infinity to point B) x q 2
= (Electric potential due to charge q1 at B) × q 2
=
1
4π ε 0
q1
q1 q 2
1
1 q1 q 2
r r × q2 =
r r =
r2 − r1
4π ε 0 r2 − r1
4π ε 0 r12
where r12 is the distance between the points A and B.
This work done gets stored in the system of charges as electric potential energy and we write
1 q1 q 2
U =
4π ε 0 r12
Potential energy belongs to the system of charges as a whole − it does not belong to any particular
charge or other. We can not locate this energy at any precise place.
If q1 q2 > 0, the two charges repel one another. We will have to do work to bring the charges closer
to one another. This work gets stored in the system as potential energy which can be recovered by
allowing the two charges to move from one another - their potential energy gets converted into
kinetic energy.
If q1 q2 < 0, the two charges attract one another. We extract work from the two charge system by
allowing them to come close together from apart on account of attraction.
Expression for the Electric Potential energy due to a distribution
of 3 point charges (in terms of their position vectors) :
ES – 02 – 09 of 21
We consider three charges q1 , q 2 and q3 with position vectors r1 , r2 and r3 respectively. We want
to calculate the potential energy of the system.
First, to bring q1 from infinity to r1 , no work is done.
Next, we bring q 2 from infinity to r2 . This time work is
done as q 2 is being brought in the field created by q1 .
r
Work done in this step is q 2 V1 (r2 ) =
1
4π ε 0
q1 q 2
r1 2
The charges q1 and q 2 together create a potential all around, which, at any point P is given by
V 12 =
1
4π ε 0
q1
q
+ 2
r
r2 P
1P
Work done in bringing q3 from infinity to the point r3 is q3 times V 1 2 at r3 which is given by
r
q 3 V 1 2 (r3 ) =
1
4π ε 0
q1 q 3 q 2 q3
+
r
r
1
3
2
3
The total work done in assembling the three charges at the given locations is obtained by adding the
works done in different steps and is given by
q q
q q
1 q1 q 2
U =
+ 1 3 + 2 3
4π ε 0 r1 2
r13
r2 3
The potential V is independent of the manner in which the configuration was assembled. The
potential energy is characteristic of the present state of configuration, not on how that state was
achieved.
Potential energy of a charge in a field :
Let some system of sources create a certain field with a potential V. If we now bring in a
r
charge q from infinity to a point A with position vector r , the work we do gets stored as potential
r
energy of this charge. Potential energy of charge q at position r in a given field = q V (r )
If q is positive and moved from a lower to a higher potential, we do some work and this work gets
stored as potential energy of the charge q.
If q is negative and moved from a higher to a lower potential, the PE of the charge increases.
A charge of 1C is moved through a potential of 1V. The PE of the charge increases by 1 J.
Electron-volt :
It is the PE gained or lost by an electron in moving through a potential difference of 1V.
Since the charge on an electron is 1.6 × 10−19 C, 1 eV = 1.6 × 10−19 J
Potential energy of two point charges in an external electric field :
ES – 02 – 10 of 21
We consider two charges q1 and q 2 with position vectors r1 and r2 respectively in a given field. In
this situation, the total potential energy of the
system is the algebraic sum of three parts :
a. PE of q1 due to its interaction with
the source,
b. PE of q 2 due to its interaction with the
source and
c. PE due to the interaction between q1 and q 2 .
Hence, potential energy of two point charges q1 and q 2 in a given electric field is
q1 q 2
1
V r1 q1 + V r2 q 2 +
r r
4π ε 0 r1 − r2
Work done in rotating a dipole in a uniform electric field : AND
Potential energy of a dipole in a uniform external electric field :
AB → dipole, q → charge strength, 2a → dipole length,
p = 2 a q = dipole moment
r
Let the axis of the dipole makes an angle θ with the direction of the electric field E .
r
r
Two equal and opposite forces + q E and − q E act on the two ends of the dipole and forms a
couple. The dipole experiences a torque τ , given by τ = p E sin θ
If the dipole is rotated through a small angle dθ against this torque, the small amount of work
( d W ) done is d W = τ dθ = p E sin θ dθ
When the dipole is rotated from an angle θ 1 to some other angle θ 2 , the total work done is
θ
W =
2
∫ p E sin θ
θ
dθ = p E [− cos θ ] θ 12 = − p E (cos θ 2 − cos θ 1
θ
1
This work, done in rotating the dipole, gets stored as potential energy.
)
……….(1)
ES – 02 – 11 of 21
Special Cases :
a) θ 1 = 0°, θ 2 = 90°
(
)
W = − p E (cos θ 2 − cos θ 1 ) = − p E cos 90 o − cos 0 o = − p E (0 − 1) = p E
b)
θ 1 = 90° , θ 2 = 180°
c)
θ 1 = 0°, θ 2 = 180°
(
)
W = − p E (cos θ 2 − cos θ 1 ) = − p E cos 180 o − cos 90 o = − p E ( − 1 − 0) = p E
(
)
W = − p E (cos θ 2 − cos θ 1 ) = − p E cos 180 o − cos 0 o = − p E ( − 1 − 1) = 2 p E
Thus, an amount of work 2 p E is required to reverse an electric dipole from the direction of the
electric field.
While calculating the potential energy stored in a dipole, the initial angle θ 1 is taken to be 90°. The
reason for this that if we hold the dipole perpendicular to the electric field and bring it from infinity
to some position in the field, the work done by the external agent on charge + q is equal and
opposite to the work done on charge – q. The net work done on the dipole is zero and hence its
potential energy is also zero. Thus, we take θ 1 = 90°, θ 2 = θ and carry out as
U = − p E (cos θ − cos 90° ) = − p E cos θ
r r
In vector notation, U = − p ⋅ E
Electrostatics of Conductors :
Electrostatic field inside a conductor is zero –
Under the influence of the external electric field
r
E 0 , the free electrons inside the conductor begin to move
r
in a direction opposite to E 0 . Negative charges are
induced on the left end of the conductor and positive
charges on the right. This charge separation process
r
continues until the electric field Ep set up by the induced
charges becomes equal and opposite to the external field
r
E 0 . The net electric field inside the conductor is
r
r
E = E 0 − Ep = 0
……….(2)
ES – 02 – 12 of 21
Electric field just outside a charged conductor is perpendicular to the surface of the conductor
(Electric line of force emanate (start) normally from the surface of a charged conductor)
Had it not been so, there would be a component of the electric field along the surface of the
conductor. This would cause movement of the free electrons in the conductor and a current would
flow (surface current) along the direction of that component. This is never observed. Hence there can
be no component of the electric field parallel to the surface of the charged conductor. Thus we
conclude that the electric field, as well as the lines of force, is perpendicular to the surface of the
charged conductor.
Charge resides on the surface of conductor –
We consider a conductor carrying
an excess charge q with no currents
flowing in it. We select a Gaussian surface
inside the conductor just near its boundary.
r
As the electric field E ′ is zero at all points
inside the conductor, the flux φ E through
the Gaussian surface must be zero.
According to Gauss’ theorem,
r r
q
φ E = ∫ E ′ ⋅ ds =
ε0
As φ E = 0 , we write q = 0.
Hence there can be no charge in the
interior of the conductor because the
Gaussian surface lies just near the outside boundary. The entire excess charge q must reside at the
surface of the conductor.
Electrostatic potential is constant for the entire conductor –
We know that the electric field is equal to the negative of the potential gradient, i.e.,
dV
E=−
dr
But, inside the conductor, E = 0 and, moreover, it has no tangential component on the surface of the
conductor. This gives,
dV
=0
or, V = constant.
dr
Hence the electrostatic potential is constant throughout the volume of a conductor and has the same
value (as inside) on its surface. Thus the surface of a conductor is an equipotential surface.
Surface charge distribution may be different at different points of a conductor –
We know,
surface charge density σ =
Electric ch arg e
.
Area
A smaller surface area, say conical or pointed portions of the surface, will have higher surface charge
density. This is used in the construction of lightning arrestor.
ES – 02 – 13 of 21
Electric field at the surface of a charged conductor is proportional to surface charge density –
We consider a charged conductor of
irregular shape. Let σ be the surface
charge density at any point of its surface.
r
To determine E at this point, we consider a
cylindrical Gaussian surface (pill box)
about this point. The pill box lies partly
inside and partly outside of the conductor. It
has negligible height and has a crosssectional area ∆S . We know that the
electric field E is zero inside the conductor
and just outside the surface, it is normal.
The contribution to the total flux through
the pill box comes only from its outer cross
section.
We write,
φ E = E ∆S
Charge enclosed by the pill box q = σ ∆S
q
By Gauss’ theorem, φ E =
∴ E ∆S =
σ ∆S
ε0
ε0
or, E =
σ
ε0
or, E ∞ σ
Electrostatic shielding –
(Electric field is zero in the cavity of a hollow charged conductor ) –
We consider a conductor with a cavity, with no
charge inside the cavity. If the conductor is charged, we
know that the entire excess charge resides on the surface
of the conductor and the electric field inside the
conductor (cavity) is zero. If the conductor is placed in
an external electric field, the induced charges reside on
the surface of the conductor only and the net electric
field inside the conductor (cavity) is zero again. This is
utilized in protecting sensitive instruments from the
effects of unwanted electric field. The instruments are
placed inside such a cavity.
When a conductor is placed in an electric field :
1.
Inside the conductor, both the electric field and the charge is zero;
2.
charges reside only at the surface of the conductor;
3.
Immediately outside the surface of the conductor, the electric field is perpendicular to
the surface;
4.
the entire body of the conductor (including its surface) is at a constant potential.
DIELECTRICS
ES – 02 – 14 of 21
Dielectrics are insulators which do not allow net flow of electric charge but permits the passage of
electrical effects through it. These can be polarized under the influence of an external electric field.
Only displacement of charge takes place; free movement of charges is not possible
Examples : glass, wax, water, etc.
There are two types of dielectrics : polar and non-polar.
Polar dielectrics :
A molecule in which the center of mass of positive charges does not coincide with that of the
negative charges is called a polar dielectric.
Such molecules have unsymmetrical shapes and have permanent dipole moment.
Examples : HCl, H2O, etc.
Non-polar dielectrics :
A molecule in which the center of mass of positive charges coincides exactly with that of the
negative charges is called a non-polar dielectric.
Such molecules have symmetrical shapes and have no net dipole moment.
Examples : H2, O2, etc.
Permittivity of vacuum ε 0 , dielectric constant K of a substance and its permittivity ε are related as
ε = Kε 0
Effect of electric field :
On polar dielectrics :
When a polar dielectric is exposed to an electric field, the existing dipoles tend to align
themselves along the direction of the electric field. This alignment increases if the strength of the
field is increased or the temperature is decreased.
On non-polar dielectrics :
When a non-polar dielectric is exposed to an electric field, within each atom the protons as a
whole are pulled in the direction of the field while the electrons are pushed the opposite way. Thus,
each atom gets distorted. Two new centers of charge, separated by a short distance (proportional to
the strength of the applied field) get created. In effect, each atom becomes a tiny electric dipole, with
a moment parallel to the external electric field and proportional to it.
In general :
When a dielectric, polar or non-polar, is placed in an
electric field, the electron cloud of atoms within the dielectric
gets displaced towards the positive end of the field and the
protons are pushed towards the negative end. The atoms now
have poles and are said to have become polarized
(polarization of a dielectric). A dielectric slab has many
layers of atoms. In two consecutive layers inside the slab,
opposite poles of atoms face each other and neutralize each
other's effect. Only atoms in the outermost layer are left unneutralized. The surface layer near the positive plate has unneutralized negative poles whereas that near the negative
plate has un-neutralized positive poles. Due to this
polarization the dielectric is equivalent to two charged
surfaces with induced surface charge densities, say + σ p and
r
− σ p . Due to this, an electric field of intensity E P is set up inside the dielectric slab in a direction
opposite to the direction of the external field E 0 . This reduces the effective (resultant) electric field
as E = E 0 − E P
ES – 02 – 15 of 21
r
The dipole moment per unit volume of a substance is called polarization and is denoted by P . It can
r
r
be shown that P = χ C E where χ C is called the electric susceptibility of the dielectric medium.
Dielectric constant :
1.
The ratio E 0 / E = K gives the dielectric constant of the dielectric substance. Since E0 is
always greater than E, K is always greater than 1.
2.
If V0 be the potential difference in the absence of the dielectric and V be the potential
difference in the presence of the dielectric then dielectric constant K = V0 / V
3.
Dielectric constant of a medium is defined as the ratio of the electrostatic force between two
charges when kept in vacuum (F) to the force when they are kept in that medium (F ′) .
It is also called relative permittivity. Dielectric constant K = F / F ′ .
When the temperature of a dielectric is increased, the field within the dielectric decreases and hence
the dielectric constant K decreases.
Q. Dielectric constant of a conductor is infinity – explain.
This is because the electric field inside a conductor is zero so that the dielectric constant,
which is the ratio of the applied electric field to the reduced electric field, will be infinite for
a capacitor.
Dielectric strength :
If the external electric field intensity is very large, the negative charges from a molecule can
be knocked off from the positive charges and these free charges make the dielectric conducting. This
is called the breakdown of the dielectric.
The maximum electric field that a dielectric material can withstand, beyond which it loses its
insulating property and starts conducting electricity, is called its dielectric strength.
#. The unit of dielectric strength is kV/mm.
CAPACITOR
Capacitor :
Any isolated system of two conducting bodies, of any shape and size, separated by a distance
in space, is called a capacitor.
#. It is an arrangement by which the capacitance of a conductor (to store charge) is increased.
#. It is used to store charge and hence to store electrical energy. It is used either to absorb or to
release large amounts of charge without developing high potential difference.
#. It consists of two conductors, of any shape and size, carrying different potentials and charges. The
conductors are placed close together in some definite positions in space relative to one another.
#. Symbol of capacitor : fixed : ||
variable :
Capacitance :
The capacitance or the capacity of a capacitor is defined as the charge required to be
supplied to one of the conductors of the capacitor to increase the potential difference between
the two conductors by unit amount.
The ratio of the charge Q to the potential difference V (= φ 2 − φ 1 ) is called
ES – 02 – 16 of 21
the capacitance C of the capacitor. Thus,
Q
Q
C=
or, C =
(φ 2 − φ 1 )
V
Q
V is proportional to Q but the ratio , the capacitance, is a constant. It is independent of V or Q.
V
The capacitance is determined solely geometrically - by shape, size, relative positions of the two
conductors and the medium between the conductors.
#. SI unit of capacitance is Coulomb/Volt (C/V) or farad (F) .
#. Smaller units of capacitance : micro-farad (µF), nano-farad (nF) and pico-farad (pF).
#. Net charge on a capacitor is zero because the two plates have equal and opposite charges.
1 Farad –
Capacitance of a capacitor is said to be one farad when a charge of 1 coulomb raises its potential
through 1 volt. 1 F = 1 C V −1
[
Dimension of capacitance :
]
[M]−1 [L]−2 [T]4 [A]2
{ C = Q/V ⇒ Q = AT, V = J/C }
Capacitance of a parallel plate capacitor :
Two parallel conducting plates G
and H, of area A, separated by a distance d
forms a parallel plate capacitor.
Let + σ is the surface charge density of the
plate G and that of plate H is − σ .
To avoid edge effects, A >> d 2 is considered.
The electric field E = σ / ε 0 between the
plates is uniform and directed from G to H.
If V is the potential difference between the
plates G and H, then
σ
V
E=
or, V = E d =
d
d
ε0
Total charge on each plate = Q = σ A
By definition, Capacitance C =
charge
Q
=
potential difference V
or, C =
σ A
A
=ε0
σ
d
d
ε0
Thus, C ∞ A and C ∞ 1 / d ; we say that the capacitance of a capacitor is determined pure
geometrically.
r
The electric field E between the plates of a capacitor is uniform ( σ / ε 0 ) and the field in the region
outside the plates is zero.
Unit of ε0 : F m−1
A
C = ε 0
d
or , ε 0 = C
d
A
ES – 02 – 17 of 21
Capacitance of a parallel plate capacitor when a dielectric slab is inserted between its plates
Let a dielectric slab (of thickness t) is inserted
between the plates (of separation d) of a parallel plate
capacitor. Under the effect of the applied external electric
field E 0 , opposite charges are developed on the outer
surfaces of the dielectric due to polarization. The polarized
r
charges develop a reverse electric field E P .
Let
K = dielectric constant of the dielectric,
A = area of the capacitor plates and
σ
Q
=
Charge on the capacitor plates Q = Aσ , E0 =
ε 0 Aε 0
The capacitance C 0 of the capacitor without any dielectric in between (vacuum between the
A
capacitor plates) is C 0 = ε 0
d
E
The resultant electric field E inside the dielectric slab reduces to E = E 0 − E P = 0
K
The potential difference V between the plates is
E
t
Q
t
V = E 0 (d − t ) + E t = E0 (d − t ) + 0 t = E 0 d − t + =
d − t +
K
K Aε 0
K
∴ Capacitance (with the dielectric slab in between) is C =
ε0
Again,
C
=
C0
Q
=
V
Q
Q
t
d − t +
Aε 0
K
=ε0
A
d−t +
t
K
A
d−t +
t
K =
d
which gives C > C 0
A
t
ε0
d−t +
d
K
Thus, a dielectric slab of thickness t and dielectric constant K increases the capacitance by a factor
d
t
d−t +
K
Special case :
When the dielectric slab fills up the space between the plates of the capacitor completely :
A
A
A
C =ε0
=ε0
=ε0
K = K C0
(Q t = d )
t
d
d
d−t +
d− d +
K
K
∴ C = K C 0 That is, the capacitance increases by a factor K.
A
A
=ε
d
d
Here, ε = Kε 0 = permittivity of the dielectric.
Again, C = K C 0 = Kε 0
When K = 1, ε = ε 0 = permittivity of free space (vacuum).
Dielectric constant :
ES – 02 – 18 of 21
The ratio of the capacitance with the dielectric as the medium within (C) to its capacitance
when the conductors are in vacuum ( C 0 ) is called the dielectric constant or relative
permittivity of the dielectric substance. ∴ Dielectric constant K = C/ C 0
Combination of capacitors :
Series combination :
Let 2 capacitors of capacitances C1 and C 2
are connected in series. When a potential difference V
is applied across A and D, a charge, say Q, is
transferred from D to A, a charge − Q is left on D.
This − Q induces a charge + Q on C and so on.
Q
Q
and V2 =
respectively.
C1
C2
As the capacitors are connected in series, the sum of the potential differences must be equal to V.
The potential drops across C1 and C 2 are V1 =
Thus, V = V1 + V1 =
1
Q
Q
1
+
= Q
+
C1 C 2
C1 C 2
∴The resulting capacitance is C =
Q
V
Reciprocating,
1
1
Q
+
C1 C 2
1
∴
=
C
Q
If there are N number of capacitors in series,
1 1
1
=
+
C C1 C 2
or,
1
=
C
N
V
1
=
C
Q
1
∑C
n =1
n
Parallel combination :
Let 2 capacitors capacitances C1 and C 2 are
connected in parallel. When a potential difference V
is applied across A and D, all the capacitors will
have a common potential difference V but different
charges given by Q1 = C1 V and Q2 = C 2 V
Total charge stored in the system is
Q = Q1 + Q2 = Q (say) = C1 V + C 2 V = V (C1 + C 2 )
The resultant capacitance of the combination is C =
Q V (C1 + C 2 )
=
V
V
If there are N number of capacitors in parallel, C =
N
∑C
n =1
n
or, C = C1 + C 2
Q. What is the utility of less capacitance of series combination of capacitors?
ES – 02 – 19 of 21
It is used to increase the potential of a charge as V ∞ 1/C. The charge can easily flow and be
consumed.
Q. What is the utility of more capacitance of parallel combination of capacitors?
It is used to decrease the potential of a charge as V ∞ 1/C. The charge can easily be
stored at low potential.
Energy stored in a capacitor :
We take a parallel plate capacitor of capacitance C. We charge the capacitor in a series of
small steps. In each step we transfer a small amount of charge, say ∂ Q ′ , from the negative plate to
the positive plate of the capacitor. In doing so, we do a small amount of work, say ∂ W , which gets
stored in the capacitor as electrostatic potential energy.
When the charges on the plates have reached, say ± Q ′ , the potential difference between the plates
Q′
is V ′ =
C
Next we add additional charge ∂ Q′ , i.e., the charge becomes Q ′ + ∂ Q ′ .
Thus, ∂ W = work done in increasing the charge from Q ′ to Q ′ + ∂ Q ′
To get the total energy stored in the capacitor, we add up these small ∂ W s, to get W.
Since ∂ Q ′ is very small, we may write
1
1
∂ W ( Q ′ to Q ′ + ∂ Q ′ ) =
Q′ ⋅ ∂ Q′ ≈
(Q ′ + ∂ Q ′)2 − (Q ′)2
C
2C
∴ Total work done W(Q) = work done in putting charges from 0 to ± Q on the capacitor plate
= ∑ ∂ W(Q′ to Q ′ + ∂ Q ′ )
{
}
many small
steps
[{(∂ Q′)
1
2C
=
1
Q2
Q2 =
2C
2C
2
} {(2 ∂ Q′)
− (0 ) +
=
2
2
− (∂ Q ′)
2
} + {(3 ∂ Q′)
2
− (2 ∂ Q ′)
2
} + ........... + {(Q )
2
− (Q − ∂ Q ′)
(C V ) = C 2 V 2 = 1 C V 2
Q2
=
(Q Q = C V )
2C
2C
2C
2
This total work gets stored in the capacitor an electrostatic energy.
1 Q2
1
∴ Energy E =
Also, E = C V 2
2 C
2
E ∞ C . Thus for a given voltage, the larger the capacitance, the greater the energy stored.
2
Also, W =
[ Aliter :
∂ W ( Q ′ to Q ′ + ∂ Q ′ ) =
Q
1
Q′ ⋅ ∂ Q′
C
1
1
Integrating, W = ∫ Q ′ ⋅ ∂ Q ′ =
C
C
0
]
Q
∫
0
1
Q′ ⋅ ∂ Q′ =
C
Q
Q′2
1 Q2
1 Q2
− 0 =
=
C 2
2 0
2 C
2
}]
Energy stored in a capacitor (in terms of electric field) :
ES – 02 – 20 of 21
We consider a parallel plate capacitor with :
A – Area of the plates, d – separation between the plates and
σ – surface charge density on the plates.
Electric field E =
σ
ε0
or, σ = E ε 0
Capacitance C = ε 0
A
d
Total charge Q = σ A
We know that electrical energy stored in the capacitor is
2
2
2
Q2
1
1
1
d
1 E ε0 A d
1
2
2
=
= (σ A) ⋅
= (E ε 0 A) ⋅
=
= ε 0 E2 × Ad
A 2
2C 2
2
ε0 A 2
ε0 A
ε0
d
1
= ε 0 E 2 × volume between the capacitor plates
2
∴ Electrical energy density = Electrical energy per unit volume =
ε0
E 2 (Unit : J m−3 )
2
Thus we see that whenever there is a non-zero electric field of strength E, there is an electrical
energy density of amount
ε0
2
E2
Van de Graff generator
ES – 02 – 21 of 21
It is a machine capable of generating
potential difference of a few million volts
and electric field close to the breakdown field
of air (∼ 3 x 106 V/m). It is used to accelerate
charged particles (electrons, ions) to high
speeds and energies for various experiments.
The moving insulating belt carries
positive charge continuously to the inner
sphere, sprayed on it by a spray comb
connected to a battery. This charge is
transferred to the outer large shell by a
collector comb.
Principle :
Let Q = charge on the large shell at any instant,
q = charge on the inner sphere at any instant,
R and r be the radii of the outer and inner spheres respectively.
1 Q q
The potential on the outer shell is VR =
+
4π ε 0 R R
1 Q q
The potential on the inner sphere is Vr =
+
4π ε 0 R r
∴ The potential difference V = Vr − VR =
q 1 1
Q q Q q
− =
+ −
−
R R 4π ε 0 r R
4π ε 0 R r
1
So, if q is positive, the potential difference of the inner sphere is always higher than that of
the outer shell. If the two spheres are connected by a conducting wire (collector comb), the charge q
will flow entirely to the outer shell, irrespective of the charge Q already present on the outer shell.
Q. Why should be the radius of outer sphere of a van de Graff generator be sufficiently large?
1 Q
Potential on spherical shell is given by V =
4π ε 0 R
Larger the radius R of the spherical shell, the more charge it can collect without
being raised to a high potential.
Similar documents
Elektrostatika: Hukum Coulomb
 • charge of a capacitor = q,
• q net charge on the capacitor,
which is zero
• all points on a plate are at the same
electric potential.
• there is a potential difference be
tween the two plates
• T...
• charge of a capacitor = q,
• q net charge on the capacitor,
which is zero
• all points on a plate are at the same
electric potential.
• there is a potential difference be
tween the two plates
• T...