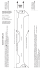Tugas Analisa Numerik
Transcription
Tugas Analisa Numerik
Tugas Analisa Numerik Tugas dikumpulkan dalam format pdf dengan penamaan file : tugas_anum_NRP.pdf Batas akhir pengumpulan tugas : 1 Juni 2015 jam 15:00 WIB Dikirim ke alamat email : [email protected] 1. If the velocity distribution of a fluid flowing through a pipe is known (Fig. 1), the flow rate Q (that ´ is, the volume of water passing through the pipe per unit time) can be computed by Q = vdA. where v is the velocity and A is the pipe’s crosssectional area. (To grasp the meaning of this relationship physically, recall the close connection between summation and integration.) For a circular pipe, A = πr2 and dA = 2πr dr. Therefore ˆ r v (2πr) dr Q= 0 where r is the radial distance measured outward from the center of the pipe. If the velocity distribution is given by 1 r 6 v = 2 1− r0 where r0 is the total radius, If the total radius is based on your last number of NRP in cm (10 for the case last number is 0) compute Q using the multiple-application trapezoidal rule. Discuss the results. Figure 1: 2. The basic differential equation of the elastic curve for a cantilever beam (Fig. 2) is given as d2y = −P (L − x) dt 2 where E is the modulus of elasticity and I is the moment of inertia. Solve for the deflection of the beam using Heun’s method and Third-Order Runge-Kutta method. The following parameter values apply: E = 30000 ksi, I = 800 in4 , P = 1 kip, L = 10 f t. Compare your numerical results to the analytical solution, PLx2 Px3 + y=− 2EI 6EI EI Figure 2: 1