Integralregning for A-niveau i stx, udgave 3

Transcription

Integralregning
for A-niveau i stx, udgave 3
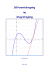
2015 Karsten Juul
Stamfunktion (ubestemt integral)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Hvad er en stamfunktion? .............................................................1
Unders€g om g(x) er stamfunktion til f (x) ................................1
G€r rede for at g(x) er stamfunktion til f (x) ..............................1
En funktion har mange stamfunktioner.........................................2
Symbol for stamfunktion (ubestemt integral). ..............................2
Bestem stamfunktion med Nspire. ................................................2
Bestem stamfunktion uden hj•lpemidler......................................3
Bestem f (x) dx...........................................................................3
Integral af sammensat funktion.....................................................4
Find en bestemt af stamfunktionerne. ...........................................5

Bestemt integral
11. Hvad er det bestemte integral........................................................6
12. Udregn  ab f ( x)dx med Nspire. .....................................................6
13. Udregn
b
a f ( x)dx uden hj•lpemidler...........................................6
Areal og bestemt interal
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
Areal og bestemt integral. .............................................................7
Kvadrant........................................................................................7
Areal mellem graf og x-akse. Uden hj•lpemidler. ......................8
Areal mellem graf og x-akse. Med hj•lpemidler.........................8
Areal mellem grafer. Eksempel 1. .............................................10
Areal mellem grafer. Eksempel 2. .............................................10
Areal i tilf•lde der ikke er standard............................................11
Opgave hvor integral og areal er givet........................................11
Opdelt omr‚de.............................................................................12
Fortolk integral. Eksempel 1......................................................12
Bestem k s‚ areal er lig et oplyst tal............................................13
Rumfang af omdrejningslegeme
27. Rumfang af omdrejningslegeme. ................................................14
28. Rumfang af sk‚l. .........................................................................14
29. Rumfang af ring. .........................................................................15
Andre anvendelser
30. Andre anvendelser. .....................................................................15
Beviser
31.
32.
33.
34.
35.
36.
37.
Formler for bestemt integral. ......................................................16
Hvad er en arealfunktion? ...........................................................17
Vigtig regel om arealfunktioner..................................................17
Bevis for at A' (x) = f (x) ............................................................18
Areal n‚r graf ligger over x-akse.................................................19
Areal mellem grafer. ...................................................................20
Areal n‚r graf ligger under x-akse...............................................21
Tidligere versioner af dette h•fte har skiftet adresse til
http://mat1.dk/integralregning_for_a_niveau_i_stx_udgave_1.pdf
http://mat1.dk/integralregning_for_a_niveau_i_stx_udgave_2.pdf
Integralregning for A-niveau i stx, udgave 3, Ä 2015 Karsten Juul
5/8-2015
Nyeste version af dette h•fte kan downloades fra http://mat1.dk/noter.htm. H•ftet m‚ benyttes i
undervisningen hvis l•reren med det samme sender en e-mail til [email protected] som oplyser at dette h•fte
benyttes, og oplyser hold, niveau, l•rer og skole.
Stamfunktion (ubestemt integral)
1. Hvad er en stamfunktion?
g (x) er en stamfunktion til f (x)
hvis
g (x) differentieret giver f (x)
dvs. hvis
g ( x)  f ( x)
2. Unders€g om g(x) er stamfunktion til f (x) .
Opgave
Unders€g om g ( x)  13 x3  4 x er en stamfunktion til f ( x)  x 2 .
Besvarelse
For at unders€ge om g (x) er stamfunktion til f (x) ,
vil vi differentiere g (x) :
g ( x) 
 13 x3  4 x    13 x3  4 x   13  x3  4 
1
3
 3 x 2  4  x 2  4  f ( x)
Da g (x) differentieret ikke giver f (x) , g•lder:
g ( x) er ikke en stamfunktion til f ( x)
3. G€r rede for at g(x) er stamfunktion til f (x) .
Opgave
G€r rede for at g ( x)  13 x3  4 er en stamfunktion til f ( x)  x 2 .
Besvarelse
For at g€re rede for at g (x) er stamfunktion til f (x) ,
vil vi differentiere g (x) :
g ( x) 
 13 x3  4   13 x3  4  13  x3  0 
1
3
 3 x 2  x 2  f ( x)
Da g (x) differentieret giver f (x) , g•lder:
g ( x) er en stamfunktion til f ( x)
1
2015 Karsten Juul
4. En funktion har mange stamfunktioner.
 32 x  14 x 2 
3
2
 12 x

 5 

3
2
 x

3
2
 12 x
3
2
1
4
x x
2
 32 x  14 x 2
3
2
x  14 x 2  c
 8 
1
2
er stamfunktion til
3
2
3
2
x  14 x 2  4,75
3
2
x  14 x 2  2,75
3
2
x  14 x 2  ( 0,25)
3
2
x  14 x 2  ( 4,25)
 12 x
uanset hvilket tal vi skriver i stedet for c .
I koordinatsystemet har vi tegnet graferne for
nogle af stamfunktionerne til 32  12 x .
4.1 Regel
Hvis h(x) er en af stamfunktionerne til f (x) ,
s‚ er funktionerne h( x)  k samtlige stamfunktioner til f (x) .
4.2 Regel
Hvis h(x) er en stamfunktion til f (x) , s‚ vil stamfunktionerne til f (x) v•re de
funktioner hvis graf vi kan f‚ ved at rykke h(x)-grafen op eller ned.
5. Symbol for stamfunktion (ubestemt integral).
Symbolet
 f ( x) dx
betyder:
og l•ses:
stamfunktionerne til f (x)
det ubestemte integral af f (x)
N‚r vi finder ud af hvad
Eksempel:
 (2 x  1)dx
 f ( x) dx
er lig, s‚ siger vi at vi integrerer f (x)
 x2  x  c
6. Bestem stamfunktion med Nspire.
P‚ skabelon-paletten v•lger vi integralskabelonen
Vi m‚ selv tilf€je  c :
Nspire skriver kun ƒn af stamfunktionerne:
For at finde stamfunktion til
2
f ( x)  3x  ,
x
skal vi efter integraltegnet angive at x  0 :
2
x0
Husk at trykke p‚ h€jrepilen inden du taster den
lodrette streg!
skal st‚ uden for
2015 Karsten Juul
7. Bestem stamfunktion uden hj•lpemidler.
k
har stamfunktionen
k x
x
har stamfunktionerne
1
2
xa
har stamfunktionen
nÄr k er en konstant
1
a 1
 x a 1
ln( x)  c
i intervallet
x0
1
x
ln( x)  c
i intervallet
x0
ex
ex  c
Hvis:
s‚:
f (x)
k  f (x)
har stamfunktionen
f.eks.
12x3
har stamfunktionerne 12  14 x 4  c
Hvis:
f (x)
g (x)
har stamfunktionen
har stamfunktionen
f.eks.
6  ex
x  1x
f.eks.
6x  c
f.eks.
x3
1
4
MEN
4x
har IKKE stamfunktionen
1
 4 x 1
x 1
MEN
1
har IKKE stamfunktionen ln(2  x)
2 x
F (x)
G (x)
dvs.
3x 4  c
og
F ( x)  G ( x)
har stamfunktionen F ( x)  G ( x)
har stamfunktionen
6x  ex  c
1
2
x 2  ln( x)  c
i intervallet
 f ( g (x))  g'(x) dx  F ( g (x))  c , hvor F (t )  f (t ) . Se ramme 9.
3
3
4
f.eks.
da
 ( x 2  1)  2 x dx   ( x 2  1)  ( x 2  1) dx  14 ( x 2  1)  c
Advarsel:
x4  c
F (x)
k  F (x)
har stamfunktionen
f ( x)  g ( x)
f ( x)  g ( x)
6
x2  c
x 1
s‚:
f.eks.
x0
 t   t
1 4
4
3
Man kan IKKE integrere et udtryk ved at integrere hver del af udtrykket
(bortset fra visse specielle tilf•lde ), f.eks.
x3  e x
x3
1 4
x
4
1
4
ex
5  ex
 ex
x4
ex
5x  e x
1
8. Bestem
 f (x) dx .
Opgave
Bestem  6 x 2dx .
Besvarelse
 6 x 2dx
 6  211 x 2 1  c  6  13 x3  c 
2 x3  c .
3
2015 Karsten Juul
9. Integral af sammensat funktion.
Regel for stamfunktion til sammensat funktion:
9.1
 f ( g (x))  g'(x) dx
hvor F (t )  f (t ) .
 F ( g (x))  c ,
Bevis for reglen ved hj•lp af metoden fra ramme 2:
Vi bruger reglen for at differentiere sammensat funktion:
F ( g (x))  c 
 F ( g (x))  g '(x)  0  f ( g (x))  g'(x)
Da F ( g (x))  c differentieret giver f ( g (x))  g '(x) , er F ( g (x))  c en stamfunktion til f ( g (x))  g '(x) .
Eksempler pÅ brug af denne regel:
9.2
 ( x 2  1)
3
 ( x 2  1)
 2 x dx 
3
 ( x 2  1) dx 
Kontrol for regnefejl (se ramme 2):
9.3
1
(x2
4
 1) 4  c
,
da
 t   t
1 4
4
3
.
14 ( x2  1)4   14  4( x2  1)41  ( x2  1)  ( x2  1)3  2 x
I f€lgende eksempel tilf€jer vi tallet 2 foran x for at opn‚ at det der st‚r, er differentialkvotienten af
den indre funktion x 2  1 . For at lighedstegnet skal g•lde, ganger vi samtidig integralet med 12 .
 ( x 2  1)
3
 x dx 
1 1
 ( x 2  1) 4
2 4
1 3 x
9.4
 3e
9.5
x  1 :
da
dx 
1
2
c 
1 3 x
e
3x 2
 x3  1 dx
ln(t )  1t ,
  ( x 2  1)3  2 x dx 
1 2
( x  1) 4
8
c ,
1
2
da
  ( x 2  1)3  ( x 2  1) dx 
 t   t
1 4
4
1
 x3  1  3x 2dx

.

da et  et .

 (13 x) dx  e1 3 x  c ,

3
1
 x3  1  ( x3  1)dx
 ln( x3  1)  c
,
t 0 .
4
2015 Karsten Juul
10. Find en bestemt af stamfunktionerne.
10.1 Opgave (Vi kender et punkt p‚ stamfunktionens graf)
F er en stamfunktion til f ( x)  2 x  3 .
Det er oplyst at
grafen for F g‚r gennem punktet (1, 6) .
I nogle opgaver er denne oplysning formuleret s‚dan:
F (1)  6 .
Find F .
Besvarelse
Da F er en stamfunktion til f ( x)  2 x  3 , findes en konstant c s‚
F ( x)  x 2  3 x  c
Da grafen for F g‚r gennem punktet (1, 6) , m‚
N‚r vi inds•tter et grafpunkts x-koordinat i forskriften og regner ud, s‚ f‚r vi
grafpunktets y-koordinat.
(1)2  3(1)  c  6
s‚ c   4 , dvs.
F ( x)  x 2  3 x  4 ,
  x  
10.2 Opgave (Vi kender en linje der er tangent til stamfunktionens graf)
F er en stamfunktion til f ( x)  2 x  3 .
Det er oplyst at
Linjen med ligningen y  x  5 er tangent til grafen for F .
Find F .
Besvarelse
Da F er en stamfunktion til f ( x)  2 x  3 , findes en konstant c s‚
F ( x)  x 2  3 x  c
F€rst udregner vi et punkt der ligger p‚ grafen for F ,
nemlig det punkt ( x0 , y0 ) hvori tangenten r€rer grafen.
Af tangentens ligningen y  x  5 ser vi at tangenth•ldningen er 1 :
F ( x0 )  1
2 x0  3  1
x0  1
N‚r vi inds•tter et grafpunkts x-koordinat i
forskriften for differentialkvotienten og regner ud,
s‚ f‚r vi grafpunktets tangenth•ldning.
Da x0  1 og ( x0 , y0 ) ligger p‚ linjen med ligningen
y  x5
f‚r vi
y0  (1)  5
y0  6
At en linjes ligning er y  ax  b betyder at for et punkt p‚
linjen kan vi udregne y-koordinaten ved at gange xkoordinaten med a og l•gge b til resultatet.
Nu kender vi et punkt p‚ grafen for F . S‚ kan vi bruge metoden fra opgave 10.1.
5
2015 Karsten Juul
Bestemt integral
11. Hvad er det bestemte integral.
Det bestemte integral fra a til b af f (x) er tallet
b
 a f ( x) dx
 F (b )  F ( a )
hvor F (x) er en stamfunktion til f (x) .
Det bestemte integral er et tal.
 ba f (x) dx
12. Udregn
Det ubestemte integral er funktioner.
med Nspire.
P‚ skabelon-paletten v•lger vi integralskabelonen
Eksempel:
13. Udregn  ab f (x) dx uden hj•lpemidler.
13.1 N‚r vi udregner bestemte integraler uden hj•lpemidler, er det praktisk at bruge
symbolet
F ( x) ba
F (b)  F (a )
som betyder
Fordelen er at vi kan skrive stamfunktionen inden vi inds•tter gr•nserne a og b for x .
13.2 Simpel opgave
Udregn
4
 1(6 x
2
Her skal du skrive en stamfunktion til det der stÄr
efter integraltegnet. Du skal ikke skrive +c .
 5) dx .
Svar
4
 1(6 x
2

 5) dx  2 x3  5 x

4
1

 

 243  54  2(1)3  5(1)  105
13.3 Opgave med sammensat funktion
Udregn
1
 12 (2 x  1)
3
dx .
Svar (FÄrst finder vi stamfunktionen ved hjÅlp af metoden fra ramme 9)
 (2 x  1)
1
3
dx 
 12 (2 x  1)
3
dx 
1
2
 (2 x  1)

3
2 dx 
1
1
(2 x  1) 4 0
8


1
2
 (2 x  1)
4
1
8 ( 2  1  1)
6
3
( 2 x  1) dx 
 18 (2  12  1) 4 
1 1
 (2 x  1) 4
2 4
1
8
1
(2 x  1) 4
8
c 
 14  18  04 
c
1
8
2015 Karsten Juul
Areal og bestemt interal
14. Areal og bestemt integral.
14.1 Regel
Areal nÇr graf er over x-aksen
A er arealet mellem f-graf og x-akse
i intervallet a  x  b .
Hvis
er
14.2 Regel
f ( x)  0
f
a xb
for
A
b
A   f ( x) dx
a
Areal nÇr graf er under x-aksen
Hvis
f ( x)  0
er
A  
14.3 Regel
b
a
A
a xb
for
f
BemÇrk: ”minus integral”
er et positivt tal.
f ( x) dx
Areal mellem grafer
A er arealet mellem f-graf og g-graf
Hvis
er
f ( x)  g ( x)
A
b
a
for
f
a xb
A
 f ( x)  g ( x) dx
g
15. Kvadrant.
y
I opgaver hvor vi skal bestemme arealer,
kan der st‚ ordet kvadrant.
Koordinatakserne deler planen op i fire kvadranter.
2. kvadrant
1. kvadrant
Figuren viser hvad de fire kvadranter hedder.
x
3. kvadrant
7
4. kvadrant
2015 Karsten Juul
16. Areal mellem graf og x-akse. Uden hj•lpemidler.
Opgave Oplysninger du bruger, skal med i besvarelsen. I nogle opgaver i dette hÅfte er opgaveteksten en del af besvarelsen.
Figuren viser grafen for funktionen f ( x)  4  x 2 og linjen med
ligningen x  1 . Grafen for f sk•rer x-aksen i punkterne
x  1
(– 2 , 0) og (2 , 0) . Bestem arealet af det gr‚ omr‚de.
Her skal du skrive en stamfunktion
til det der stÄr efter integraltegnet.
Du skal ikke skrive +c .
Besvarelse
Det gr‚ omr‚de er
f
omr‚det mellem grafen for f og x-aksen i intervallet  1  x  2 .
Da f ( x)  0 i dette interval, er arealet
2
1(4  x
2
) dx
4 x  x 
Se 13.2
4  2   2   4  (1)   (1) 
1 3 2
3
1
=
3
1
3
=
Venstre grÅnse
skal stÄ nederst.
Se 14.1

= 8  83   4  13
8
3
= 8  4
3
1
3

Çvre grÅnse fÉrst, sÄ nedre.
Disse klammer skal du kun bruge hvis
opgaven er uden hjÅlpemidler. Med
hjÅlpemidler skal du kun taste
integralet og trykke pÄ enter.
1
3
= 9
Arealet af det gr‚ omr‚de er 9 .
17. Areal mellem graf og x-akse. Med hj•lpemidler.
Opgave
f ( x)   x3  4,5 x 2  6 x  2 . Bestem areal af omr‚det der i f€rste kvadrant
afgr•nses af f-graf og koordinatakser.
BemÇrkning
Nspire tegner f-graf, og vi markerer det s€gte areal.
N‚r vi g‚r fra venstre mod h€jre, s‚ starter omr‚det ved y-aksen,
dvs. der hvor x er 0, s‚ integralets nedre gr•nse er 0.
Omr‚det slutter ved det ene f•llespunkt for f-graf og x-akse, s‚ dette punkts
x-koordinat er integralets €vre gr•nse. Vi skal l€se ligningen f (x) = 0 for at
finde x-koordinater til f•llespunkter for f-graf og x-akse. P‚ figur ser vi at vi
skal bruge den af l€sningerne der ligger mellem 0 og 1.
areal  
0 ,5
0
f ( x) dx  
0, 5
0
( x 3  4,5 x 2  6 x  2) dx
Se 14.1
Opgave
f ( x)   x3  4,5 x 2  6 x  2 . Bestem areal af omr‚det der i fjerde kvadrant
afgr•nses af f-graf og f€rsteakse.
BemÇrkning
Nspire tegner f-graf, og vi markerer det s€gte areal.
N‚r vi g‚r fra venstre mod h€jre, s‚ starter omr‚det ved et f•llespunkt for
f-graf og x-akse, s‚ dette punkts x-koordinat er integralets nedre gr•nse.
Omr‚det slutter ved et f•llespunkt for f-graf og x-akse, s‚ dette punkts
x-koordinat er integralets €vre gr•nse. Vi skal l€se ligningen f (x) = 0 for at
finde x-koordinater til f•llespunkter for f-graf og x-akse.
areal   
2
0, 5
2
f ( x) dx    ( x3  4,5 x 2  6 x  2) dx
0 ,5
Se 14.2
Ramme 17 fortsÅtter pÄ nÅste side.
8
2015 Karsten Juul
Opgave
f ( x)   x3  4,5 x 2  6 x  2 . Bestem areal af omr‚det der i f€rste kvadrant
afgr•nses af f-graf og koordinatakser.
Besvarelse 1 Skal kunnes.
P‚ figur har Nspire tegnet graf for f ( x)   x3  4,5 x 2  6 x  2 , og vi har vist
omr‚det der i f€rste kvadrant er afgr•nset af f-graf og koordinatakser. Vi ser at
dette omr‚de starter ved y-aksen, dvs. ved x = 0, s‚ integralets nedre gr•nse er 0.
Omr‚det slutter ved et f•llespunkt for f-graf og x-akse, s‚ dette punkts
x-koordinat er integralets €vre gr•nse.
Nspire l€ser ligningen f (x) = 0 dvs. ligningen  x3  4,5 x 2  6 x  2  0
mht. x og f‚r at f•llespunkternes x-koordinater er x  0,5 og x  2 .
Det s€gte areal er alts‚ areal mellem f-graf og x-akse i intervallet 0  x  0,5 .
Da f (x)  0 i dette interval, er
areal =
udregnet af Nspire
Areal af omr‚de der i f€rste kvadrant afgr•nses af f-graf og akser, er 0,422 .
Besvarelse 2 Skal ikke kunnes, men er nyttig for nogen.
Se 14.1
Venstre grÅnse
skal stÄ nederst.
Samme figur som i besvarelse 1.
Besvarelse 3 Skal ikke kunnes, men er god kontrol.
Vi taster f ( x)   x3  4,5 x 2  6 x  2 og f‚r Nspire til at tegne graf (se figur).
For denne f‚r vi Nspire til at udregne integral fra x = 0 til f€rste f•llespunkt for
f-graf og x-akse. N‚r der sp€rges om nedre gr•nse, taster vi 0 enter. N‚r der
sp€rges om €vre gr•nse, f€rer vi mark€r til sk•ringspunkt s‚ der st‚r
sk•ringspunkt, og klikker.
areal = 0,421875  0,422
OvenstÄende er ikke grundigt nok til at vÅre en brugsanvisning til Nspire.
Det er et eksempel pÄ hvordan en besvarelse kan se ud.
9
2015 Karsten Juul
18. Areal mellem grafer. Eksempel 1.
Opgave
Bestem arealet af det omr‚de der afgr•nses af graferne for funktionerne
f ( x)  x 2  1
og
g ( x)  32  x
Besvarelse 1 Skal kunnes.
Nspire tegner grafer for f ( x)  x 2  1 og g ( x)  32  x . P‚ figur ser vi at
integralets gr•nser er x-koordinater til grafers sk•ringspunkter.
Nspire l€ser ligningen f (x) = g(x) , dvs. x 2  1  32  x mht. x og f‚r at
x-koordinaterne til grafernes sk•ringspunkter er  12 og 2 .
ADVARSEL: Det er ikke altid at du
skal lÉse denne ligning. Se ramme 19.
Da g ( x)  f ( x) for  12  x  2 , er det s€gte areal lig
Venstre grÅnse
skal stÄ nederst.
Besvarelse 3 Skal ikke kunnes, men er god kontrol.
Vi taster
f (x)=x2–1 og g(x)= 32 x
Besvarelse 2 Skal ikke kunnes, men er nyttig for nogen.
og f‚r Nspire til at tegne grafer (se figur).
For disse f‚r vi Nspire til at udregne areal
mellem grafer mellem sk•ringspunkterne.
N‚r der sp€rges om nedre og €vre gr•nse,
f€rer vi mark€r til sk•ringspunkt s‚ der st‚r
sk•ringspunkt og klikker.
areal = 2,60417  2,60
Hvis grÅnserne ikke er skÅringspunkter, men givne
tal, kan vi bruge en formulering som:
udregne areal mellem grafer fra x=2 til
x=5 . N‚r der sp€rges om nedre og €vre
gr•nse taster vi tallene 2 og 5.
OvenstÄende er ikke grundigt nok til at vÅre en
brugsanvisning til Nspire. Det er et eksempel pÄ
hvordan en besvarelse kan se ud.
19. Areal mellem grafer. Eksempel 2.
8
5
areal   ( f ( x)  g ( x)) dx
areal   ( f ( x)  g ( x)) dx
Her er integralets gr•nser l€sninger
til ligningen f (x) = g(x) .
Her er integralets gr•nser IKKE l€sninger
til ligningen f (x) = g(x) .
1
2
10
2015 Karsten Juul
20. Areal i tilf•lde der ikke er standard.
20.1 Opgave Figuren viser grafen for funktionen f ( x)  x 2 og linjen
l: y  2 x  1 . l er tangent til grafen for f i punktet (1, 1) .
I f€rste kvadrant afgr•nser grafen for f sammen med
linjen l og f€rsteaksen en punktm•ngde M der har et areal.
Bestem arealet af M.
Besvarelse Ligningen 2 x  1  0 har l€sningen x 
1
2
, s‚ l sk•rer
f
l
( 12 , 0) .
x-aksen i punktet
Areal af M
=
(areal mellem f-graf og x-akse i intervallet 0  x  1 ) –
(areal mellem l og x-akse i intervallet 12  x  1 )
=
0 x 2dx
=
( 13 13  13
1
1
1 3 1
3
0
 x   x
0 )  (1  1)  (( )  )  =
 12 (2 x  1) dx

3
2
=
1 2
2
1
2
2
x
1
3

1
1
2
 14 =
1
12
20.2 Opgave Funktionen g er en stamfunktion til funktionen f .
Ligningen f (x) = g(x) har netop 2 l€sninger.
x
f (x)
–6
0
–2
0
0
–3
g(x)
0
8
3
0
Bestem arealet af det bl‚ omr‚de.
Besvarelse Da f (–6) = 0 og f (–2) = 0 , m‚ –6 og –2 v•re de to l€sninger til ligningen f (x) = g(x) , s‚
–6 og –2 er x-koordinater til f-grafens sk•ringspunkter med x-aksen. Det bl‚ areal er alts‚
arealet mellem f-graf og x-akse i intervallet –2  x  0 .
Da f (x)  0 i dette interval, er arealet lig minus integralet:
areal =  
0
2
f ( x) dx
=  g ( x) 0 2
da g er stamfunktion til f
=  ( g (0)  g (2))
=  (0  83 )
=
if€lge tabel
8
3
21. Opgave hvor integral og areal er givet.
Opgave Figuren viser to omr‚der med arealer 10
og A . Bestem A n‚r det er oplyst at
3
(1)
5
0
f ( x) dx  34
3
(2)
0
(3)
3
5
x5
f
Besvarelse
f ( x) dx  10
3
da f ( x)  0 for 0  x  3
f ( x) dx   A
da f ( x)  0 for 3  x  5
10
3
A
If€lge indskudss•tningen (se 30.1) er
5
0
f ( x) dx 
3
0
f ( x) dx 
5
3
f ( x) dx
Heraf og af (1), (2) og (3) f‚r vi
4  10  ( A)
3
3
s‚
A2
11
2015 Karsten Juul
22. Opdelt omr‚de.
Arealet fra a til b er summen af arealerne:
4 + 6 + 3 = 13
Integralet fra a til b er summen af integralerne:
(–4) + 6 + (–3) = – 1
Areal mellem f-graf og x-akse i intervallet a  x  b er 13 .
b
a
f ( x) dx   1
23. Fortolk integral. Eksempel 1.
0
) dx  76 .
Giv en geometrisk fortolkning af dette.
Det er oplyst at
Opgave
 1 (3x  x
2
f ( x )  3 x  x 2 .
Besvarelse Vi skitserer grafen for funktionen
Da f ( x)  0 for 1  x  0 , g•lder:
0
 1 f ( x) dx
f
er arealet mellem f-grafen og x-aksen
i intervallet 1  x  0
s‚
7 er arealet mellem f-graf og x-akse i intervallet 1  x  0
6
dvs.
7 er arealet af det gr‚ omr‚de .
6
Opgave
Det er oplyst at n‚r
f ( x)  3x 2  32
er
1
0
f ( x) dx   12 .
Giv en geometrisk fortolkning af dette.
f
Besvarelse Vi tegner grafen for f .
A = gr‚t areal under x-akse
Da
er
B = gr‚t areal over x-akse
og
(integral fra 0 til 1) = (–A) + B
 12 = (–A) + B
og dermed
Det gr‚ areal under x-aksen er
1
2
A = B + 12
enhed st€rre end det gr‚ areal over.
Opgave
P‚ figuren ses graferne for to line•re funktioner f og g
som sk•rer hinanden i et punkt A hvis x-koordinat er 2 .
Det oplyses at
2
7
0 f ( x) dx  2 g ( x) dx  10,5
.
Fortolk tallet 10,5 .
Besvarelse
Venstre integral er areal mellem f-graf og x-akse i intervallet 0  x  2 .
H€jre integral er areal mellem g-graf og x-akse i intervallet 2  x  7 .
I alt: 10,5 er arealet af trekant ABO .
12
2015 Karsten Juul
26. Bestem k s‚ areal er lig et oplyst tal.
Eksempel hvor k er en grÇnse.
Figuren viser grafen for f ( x)  x 2  1 og linjen med ligningen x  k .
Vi vil bestemme et positivt tal k s‚
det gr‚ areal = 3
2
f
dvs.
k
0 ( x 2 1) dx
 3
2
Nspire l€ser denne ligning mht. k for k  0 og f‚r
k  1,08004  1,080
Eksempel hvor k er i forskriften.
Figuren viser grafen for f ( x)  2  k x 2 hvor 0  k  2 .
Vi vil bestemme k s‚
det gr‚ areal = 7
2
dvs.
1
Husk at taste gangetegn
7
2
 1(2  k x ) dx  2
mellem k og x .
f
Nspire l€ser denne ligning mht. k for 0  k  2 og f‚r
k  3
4
Eksempel hvor k bÅde er en grÇnse og er i forskriften.
Figuren viser graferne for
f ( x)  1  x 2
og
g ( x)  k  x
hvor
5
k .
4
Vi vil bestemme k s‚ det gr‚ areal er 4 .
3
P‚ figuren ser vi at vi har brug for at kende de to viste sk•ringspunkter mellem x-aksen og graferne:
g
f
Vi l€ser 1  x 2  0 og f‚r x  1
Vi l€ser k  x  0 og f‚r x  k
For at finde gr•nser for integralerne l€ste
vi ligningerne f ( x)  0 og g ( x)  0 .
Heraf og af figuren f‚r vi, da
Ofte skal du ikke l€se disse ligninger.
4
3
det gr‚ areal =
I stedet skal du m‚ske l€se f ( x)  g ( x) .
at
k
1
2
0 (k  x) dx  0 (1 x ) dx
Eller m‚ske fremg‚r integralets gr•nser
af tekst og figur.
 4
3
Nspire l€ser denne mht. k for k 
5
og f‚r
4
k2
13
2015 Karsten Juul
Rumfang af omdrejningslegeme
27. Rumfang af omdrejningslegeme.
Punktm•ngden M p‚ venstre figur drejer vi 360 om x-aksen.
S‚ f‚r vi omdrejningslegemet p‚ h€jre figur.
27.1 Formel for rumfang V af omdrejningslegeme:
V  π
f
b
a
 f ( x)2 dx
.
f
M
27.2 Opgave
Venstre figur ovenfor viser grafen for funktionen
f ( x) 
4
5
x ,
1
2
 x3 .
Omr‚det M mellem f-grafen og x-aksen drejer vi 360 om x-aksen. S‚ f‚r vi omdrejningslegemet
som vi har tegnet ovenfor til h€jre.
Bestem rumfanget V af dette omdrejningslegeme.
Besvarelse
Husk !
Husk !
Venstre grÅnse skal stÄ nederst.
28. Rumfang af sk‚l.
Opgave
To funktioner f og g er givet ved
f ( x )  x 0 ,8  2 ,
f
0 x3
g ( x)  2,5  ( x  1)0,5 , 1  x  3
g
Det gr‚ omr‚de p‚ figuren drejer vi 360 om x-aksen.
S‚ f‚r vi en glassk‚l.
Bestem rumfanget af glasset.
Besvarelse
Omr‚det mellem f-grafen og x-aksen drejer vi 360 om x-aksen.
S‚ f‚r vi et omdrejningslegeme der ikke er en sk‚l. For at g€re det til en sk‚l skal vi fjerne noget. Det
vi fjerner, er omdrejningslegemet som vi f‚r ved at dreje omr‚det mellem g-grafen og x-aksen 360
om x-aksen. Rumfanget af glasset er
3
3
2
2
π   ( x 0,8  2) dx  π   ( 2,5  ( x  1)0,5 ) dx  69,8898  69,9
0
1
14
udregnet af Nspire
2015 Karsten Juul
29. Rumfang af ring.
Opgave To funktioner f og g har forskrifterne f ( x)  2 x 3  3 x 2  92
og g ( x)  3 .
Det gr‚ omr‚de p‚ 1. figur drejer vi 360 om x-aksen. S‚ f‚r vi det ringformede
omdrejningslegeme p‚ 2. figur. Bestem rumfanget af denne ring.
f
f
f
g
f
g
g
Besvarelse Det gr‚ omr‚de p‚ 3. figur drejer vi 360 om x-aksen. S‚ f‚r vi en skive hvis rumfang er
π
1
0
 f ( x) 2 dx
2257
140

π
udregnet af Nspire
Herfra skal vi tr•kke hullets rumfang. Hullet er den skive vi f‚r ved at dreje
det gr‚ omr‚de p‚ 4. figur 360 om x-aksen. Hullets rumfang er alts‚
π
1
0
 g ( x) 2 dx
 9π
Alts‚ er ringens rumfang
Advarsel
udregnet af Nspire
2257
140
π  9π 
997
140
π
Hullets rumfang kunne
vi have udregnet ved at
bruge formlen for
rumfang af cylinder.
Vi kan IKKE sl‚ udregningerne sammen i ƒt integral som vi kan med areal.
π
1
0
2
 f ( x)  g ( x) 
dx 
157
140
π
h
er IKKE ringens rumfang!
Det vi har udregnet her, er rumfanget af det omdrejningslegeme vi
f‚r n‚r det gr‚ omr‚de p‚ figuren til h€jre drejes 360 om x-aksen.
h( x )  f ( x )  g ( x )
Andre anvendelser
30. Andre anvendelser.
Hvis I i en eksamensopgave skal bruge integral til at udregne andet end graf-afgr•nset areal og rumfang af
omdrejningslegeme, s‚ vil der i opgaven st‚ den integralformel I skal bruge. I skal s‚ finde ud af at s•tte tal
ind i integralformlen. M‚ske skal I f€rst udregne disse tal. Det I skal udregne med et integral kan b‚de v•re
geometriske st€rrelser og st€rrelser fra f.eks. naturvidenskab.
Opgave: Figuren viser en gavl. Langs den buede kant er et r€dt lysstofr€r der har form
som en del af grafen for f (x) = –x2 + 8x – 12 . Gavlens bredde er 2 m. Det oplyses at
b
buel•ngden af grafen for en funktion f i et interval a  x  b er  f ( x) 2  1 dx .
a
Bestem l•ngden af lysstofr€ret.
Overvejelser: f (x) = 0 har l€sningerne 2 og 6 s‚ a = 2 . Hertil l•gger vi gavlens
bredde og f‚r b = 4 . Da f '(x) = –2x + 8 , skal der under rodtegnet st‚ (–2x + 8)2 + 1 .
15
2015 Karsten Juul
Beviser
31. Formler for bestemt integral.
31.1 SÇtning (Indskudss•tningen for integraler)
N‚r f har en stamfunktion i et interval, og a , b og c er tal i dette interval, s‚ er
b
a
f ( x) dx 
c
f ( x) dx 
a
b
f ( x) dx
c
31.2 SÇtning (Regneregler for bestemt integral)
N‚r f og g har stamfunktioner i et interval, og a og b er tal i dette interval, og k er et tal, s‚ er
b
 a  f ( x)  g ( x) dx
a

a
b
 a  f ( x)  g ( x) dx
b
a
b

k  f ( x) dx  k 
b
b
a
b
f ( x) dx 
a
f ( x) dx 
a
b
g ( x) dx
g ( x) dx
f ( x) dx
31.3 Bevis (Indskudss•tningen for integraler)
Lad F v•re en stamfunktion til f .
c
a
f ( x) dx

b
c
f ( x) dx

F (c)  F (a )  F (b)  F (c)

F (b)  F (a )

a
b
If€lge definitionen p‚ bestemt integral.
f ( x) dx
Hermed er s•tningen bevist.
31.4 Bevis (Regneregler for bestemt integral)
De tre formler kan bevises p‚ n•sten samme m‚de. Vi beviser nummer to.
f (x) har en stamfunktion F (x) , og g (x) har en stamfunktion G (x) .
Funktionen H ( x)  F ( x)  G ( x) er en stamfunktion til h( x)  f ( x)  g ( x) da
H ( x)   F ( x)  G ( x)   F ( x)  G( x)  f ( x)  g ( x)  h( x)
hvor reglen for at differentiere en differens er begrundelsen for andet lighedstegn. Nu er
b
 a  f ( x)  g ( x) dx

b
 H (b)  H (a )   F (b) G (b)    F (a) G (a )  
 a h( x) dx
F (b)  F (a )  (G (b) G (a )) 
b
a
f ( x) dx 
b
a
g ( x) dx
Hermed er formlen bevist.
16
2015 Karsten Juul
32. Hvad er en arealfunktion?
f (x)
A(x)
x
Den viste graf er p‚ en sk•rm.
N‚r vi tr•kker x-prikken mod h€jre, bliver det gr‚ omr‚de st€rre.
A(x) er arealet af det gr‚ omr‚de.
A(x) kaldes arealfunktionen for f .
P‚ billedet ser vi at A(9)  36 og A(11)  53 .
33. Vigtig regel om arealfunktioner.
33.1 SÇtning
Betyder at grafen ligger pÄ eller over x-aksen.
N‚r
A(x) er arealfunktionen for en ikke-negativ funktion f (x) , a  x  b
s‚ g•lder at
A(x) er en stamfunktion til f (x)
dvs.
A( x)  f ( x)
17
2015 Karsten Juul
34. Bevis for at A' (x) = f (x) .
SÇtning (Se ramme 32 og 33)
N‚r A(x) er arealfunktionen for en ikke-negativ funktion f (x) , a  x  b
er
A( x)  f ( x)
Bevis
F
E
D
G
f
H
x1 b
C
x0
a
f (x) er ikke-negativ og voksende i intervallet a  x  b .
x0 og x1 er to tal i intervallet a  x  b , og x0  x1 .
Vi beviser kun p‚standen for voksende
funktioner, men den g•lder ogs‚ for
funktioner der ikke er voksende.
Af figuren ser vi at
areal af rektangel CDGH
<
areal af gr‚ omr‚de
<
areal af rektangel CEFH
Dette kan vi ogs‚ skrive s‚dan:
f ( x0 )  ( x1  x0 )

A( x1 )  A( x0 )

f ( x1 )  ( x1  x0 )
Ulighedstegnene g•lder stadig n‚r vi dividerer de tre udtryk med x1  x0
da x1  x0 er positiv:
A( x1 )  A( x0 )
(1)
f ( x0 )


f ( x1 )
x1  x0
P‚ tilsvarende m‚de kan vi vise at (1) ogs‚ g•lder n‚r x1  x0 .
Vi giver x1 v•rdier der ligger t•ttere og t•ttere p‚ x0
s‚ f ( x1) kommer vilk‚rlig t•t p‚ f ( x0 ) .
S‚ kommer br€ken i (1) vilk‚rlig t•t p‚ f ( x0 )
(da den if€lge (1) er t•ttere p‚ f ( x0 )
end f ( x1) er ).
Med symboler kan vi skrive dette s‚dan:
(2)
f ( x0 ) 
lim
x1  x0
A( x1 )  A( x0 )
x1  x0
Fra differentialregningen ved vi at differentialkvotienten kan udregnes som en gr•nsev•rdi p‚ f€lgende
m‚de:
(3)
A( x0 ) 
lim
x1  x0
A( x1 )  A( x0 )
x1  x0
Af (2) og (3) f€lger at A( x0 )  f ( x0 ) ,
og dette er det vi ville bevise.
18
2015 Karsten Juul
35. Areal n‚r graf ligger over x-akse.
35.1 SÇtning om areal mellem f-graf og x-akse n‚r f (x)  0
Hvis
f ( x)  0 for a  x  b og
M er omr‚det mellem f-grafen og x-aksen
i intervallet a  x  b
f
s‚ g•lder
b
 a f ( x) dx
M
 arealet af M
Bevis
A(x) er arealfunktionen for f (x) .
F (x) er en stamfunktion til f (x) .
If€lge s•tning 33.1 er A(x) en stamfunktion til f (x) .
Da A(x) og F (x) er stamfunktion til samme funktion, findes en konstant c s‚
A( x)  F ( x)  c .
(*)
Nu f‚s
areal af M
 A(b)
If€lge definitionen p‚ arealfunktion.
 A(b)  A(a )
Da A(a )  0 .
  F (b)  c    F (a)  c 
If€lge (*) .
 F (b)  F (a )

b
 a f ( x) dx
Hermed er s•tning 35.1 bevist.
19
2015 Karsten Juul
36. Areal mellem grafer.
36.1 SÇtning om areal mellem grafer
Hvis der i et interval a  x  b g•lder om to funktioner f og g at
f ( x)  g ( x)
og M er omr‚det mellem f-grafen og g-grafen i dette interval (se venstre figur), s‚ er
areal af M 
b
 a  f ( x)  g ( x) dx
f ( x)  k
M1
f (x )
M
g ( x)  k
g (x )
Bevis
Vi v•lger et tal k s‚ graferne for f ( x)  k og g ( x)  k ligger over x-aksen. Se h€jre figur.
Nu f‚r vi
Areal af M
 areal af M1
 areal mellem x -akse 
 areal mellem x -akse 
 
  

og
graf
for
f
(
x
)

k


 og graf for g ( x)  k 
b
b

 a  f ( x)  k  dx

 a  f ( x)  k    g ( x)  k  dx

 a  f ( x)  g ( x) dx

 a  g ( x)  k  dx
b
if€lge s•tning om areal mellem
f-graf og x-akse n‚r f (x)  0 .
if€lge formel for
integral af differens.
b
20
2015 Karsten Juul
37. Areal n‚r graf ligger under x-akse.
37.1 SÇtning om areal mellem f-graf og x-akse n‚r f (x)  0
Hvis
f ( x)  0
for
a xb
s‚ er
b
a
f ( x) dx   A
f
Bevis
Grafen for funktionen g ( x)  0 er sammenfaldende med x-aksen,
s‚ A er arealet mellem f-graf og g-graf i intervallet a  x  b .
A 

b
 a  g ( x)  f ( x) dx
if€lge s•tning om areal mellem grafer
b
 a 0  f ( x)  dx
 
b
a
f ( x) dx
k  1 i regel om integral af k  f (x)
21
2015 Karsten Juul
Stikordsregister
A
Andre anvendelser ..............................................15
areal ..........................................7, 8, 10, 11, 12, 13
areal mellem graf og x-akse, med hj•lpemidler...8
areal mellem graf og x-akse, uden hj•lpemidler ..8
areal mellem grafer.........................................7, 10
areal mellem grafer, bevis ..................................20
areal over x-akse ...................................................7
areal under x-akse .................................................7
areal under x-akse, bevis ....................................21
areal, bestem k ....................................................13
areal, bevis..........................................................19
arealfunktion.................................................17, 19
arealfunktion, bevis ............................................18
B
bestemt integral ....................................................6
bestemt integral af sammensat funktion ...............6
bestemt integral med Nspire .................................6
bestemt integral uden hj•lpemidler......................6
buel•ngde...........................................................15
F
fortolk integral ....................................................12
I
indskudss•tningen for integraler........................16
integral, indskudss•tning ...................................16
integral, regneregler............................................16
integrere ............................................................... 2
K
kvadrant ............................................................... 7
N
Nspire..........................................2, 6, 9, 10, 13, 14
O
omdrejningslegeme.......................................14, 15
opdelt omr‚de .................................................... 12
R
regneregler for integraler ................................... 16
rumfang.............................................................. 14
rumfang af omdrejningslegeme ......................... 14
rumfang af ring .................................................. 15
rumfang af sk‚l .................................................. 14
S
stamfunktion .......................................1, 2, 3, 5, 17
stamfunktion med Nspire..................................... 2
stamfunktion til sammensat funktion................... 4
stamfunktion uden hj•lpemidler ......................... 3
stamfunktion, grafpunkt givet.............................. 5
stamfunktion, tangent givet.................................. 5
U
ubestemt integral...........................................2, 4, 6
ubestemt integral af sammensat funktion ............ 4
ubestemt integral uden hj•lpemidler................... 3

Integralregning for A-niveau i stx, udgave 3

Transcription

Similar documents

Integralregning - Sct. Knuds Gymnasium

Anvendelser af andengradspolynomier

besvarelse 1

Affaldsguide

Snit i kvist forfra

Vejledning til Roll-up printfiler

Klik her for at læse artiklen

Projektdokumentation (pdf)