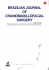Fulltext - ETH E

Transcription

Fulltext - ETH E

DISS. ETH NO. 23183
SIMULATION TECHNIQUES FOR
MECHANO-CHEMICAL INTERACTIONS IN
MORPHOGENESIS
A thesis submitted to attain the degree of
DOCTOR OF SCIENCES of ETH Zurich
(Dr. sc. ETH Zurich)
presented by:
Simon Tanaka
Master of Science ETH in Mechanical Engineering
born on May 27th 1985
citizen of Adligenswil LU
accepted on the recommendation of:
Prof. Dr. Dr. Dagmar Iber, examiner
Prof. Dr. Bastien Chopard, co-examiner
Prof. Dr. Edoardo Mazza, co-examiner
2016
Ever tried. Ever failed.
No matter. Try Again.
Fail again. Fail better.
— Samuel Beckett
Abstract
Morphogenetic research aims at understanding the fundamental principles and mechanisms by which organs and organisms obtain their shape and size. Complementary
to experimental research, computational morphogenesis offers a modern approach to
investigate existing and generate novel hypotheses in perfectly controlled and transparent
conditions. Although many morphogenetic mechanisms require the tight inter-coupling
of both the signalling network and the underlying dynamically growing tissue model, this
has only been considered in a handful of studies due to the complexity or lack of tools.
The presented thesis is concerned with the advancement and application of modelling
and simulation techniques for computational morphogenesis.
The first part of the thesis focuses on the continuous formulation of a model for embryonic
long bone development. This application serves as a representative system to study
symmetry breaking, which is a central problem for many morphogenetic processes. The
simulations start from a homogeneous tissue structure, and it is proposed that the
symmetry is broken by a Turing-type signalling mechanism leading to the characteristic
central-lateral organization of differentiated cell types. The viscous properties of the
growing tissue are modelled by a Newtonian fluid with local mass sources to represent
proliferation and hypertrophic cell volume increase. The mechanical tissue model and
the signalling model are fully coupled, and it is shown that the behaviour is thereby
significantly affected.
In the second part of the thesis, the two-dimensional cell-based simulation framework
LBIBCell is introduced and numerically validated. The cells are arbitrarily deformable
and consist of elastic structures, namely the membranes and cell-cell junctions, which are
immersed in a fluid. Since the membranes are impermeable to the fluid, fluid-structure
interaction occurs. The software natively offers the possibility to closely couple reactionadvection-diffusion-based signalling models to the tissue, and is thus ideally suited for
morphogenetic applications.
The last part investigates the behaviour of Turing-like receptor-ligand signalling systems
on growing cellular tissue. It is demonstrated that the results are qualitatively altered as
compared to the solution on continuous domains. Specifically, it leads to the emergence of
novel phenomena such as salt-and-pepper pattern formation and cell clustering. In order
to recover tissue-wide pattern formation similar to continuous domains, a three-component
Turing-like system is proposed and studied on growing cellular tissue.
Using different modelling approaches, it is demonstrated that mechano-chemical interi
actions, as well as the cellular nature of the tissue, can lead to altered behaviour and
emerging phenomena. In the future, the increasing quantity and quality of experimental data, e.g. sub-cellular resolution live imaging, will lead to an increasing need for
appropriate mathematical models and computational tools.
ii
Zusammenfassung
Das Forschungsgebiet der Morphogenese beschäftigt sich mit der Erforschung von grundlegenden Mechanismen, welche für die Formgebung von Organismen und deren Organen
verantwortlich sind. Ergänzend zu Experimenten bieten rechnergestützte Simulationen
eine moderne Alternative, um existierende Hypothesen unter kontrollierten Bedingungen
zu testen, und um auf einfache Art und Weise neue Modelle zu entwickeln. Obwohl
viele morphogenetische Modelle intrinsisch aus zwei gekoppelten Systemen bestehen,
nämlich dem wachsenden Gewebe und einem das Verhalten der Zellen steuernde signaltransduktorischen Netzwerk, wurden bisher aufgrund der Komplexität und der fehlenden
Software-Implementierungen oft nur Teilaspekte studiert. Die vorgelegte Dissertation
beschäftigt sich mit der Weiterentwicklung und Anwendung von Modellierungs- und
Simulationstechniken im Bereich der morphogenetischen Forschung.
Im ersten Teil der Arbeit wird ein kontinuierliches Modell entwickelt um Teilaspekte
der embryonalen Entwicklung von Röhrenknochen zu verstehen. Diese Anwendung dient
stellvertretend dazu, das grundlegende Problem der Symmetriebrechung zu studieren.
Es wird ein Turing-Mechanismus vorgeschlagen, welcher die zu Beginn der Simulation
vorhandene Symmetrie zu brechen imstande ist, und welcher die typische Gewebestruktur
des Vorläufers des späteren Röhrenknochens erklären kann. Die viskosen Eigenschaften
des wachsenden Gewebes werden durch ein Fluid beschrieben, und Zellproliferation
und hypertrophe Zellvergrösserung werden dabei durch Massenquellen repräsentiert. Es
wird gezeigt, dass sich das Verhalten des signaltransduktorischen Modells durch die
vollständige Kopplung an das Gewebemodell signifikant verändert.
Im zweiten Teil der Arbeit wird die zweidimensionale, zellbasierte Simulationsumgebung
LBIBCell vorgestellt und numerisch validiert. Die beliebig deformierbaren Zellen bestehen aus elastischen Zellmembranen und Zellverbindungen, welche sich in einem Fluid
befinden, und deren Impermeabilität zu einem Fluid-Struktur-Kopplungsproblem führt.
Die Software ermöglicht es, reaktions-advektions-diffusionsbasierte signaltransduktorische
Modelle einzukoppeln, und ist deshalb massgeschneidert um morphogenetische Probleme
zu studieren.
Im letzten Teil wird aufgezeigt, dass sich Turing-ähnliche Systeme, welche auf RezeptorLigandeninteraktion basieren, auf wachsenden, zellaufgelösten Geweben anders verhalten
als auf kontinuierlichen Domänen. Insbesondere treten neuartige Phänomene, wie beispielsweise gesprenkelte Muster und Clusterbildung, auf. Ausserdem wird ein modifizierter Drei-Komponenten-Turing-Mechanismus auf wachsenden, zellaufgelösten Geweben
iii
studiert, welcher sich ähnlich verhält wie der klassische Turing-Mechanismus auf kontinuierlichen Domänen.
Mithilfe verschiedenartiger Modellierungsansätzen wird in dieser Dissertation gezeigt, dass
sich mechanochemische Mechanismen auf dynamischen, zellaufgelösten Domänen anders
verhalten und dass unter Umständen neuartige Phänomene entstehen können. Hand
in Hand mit der verstärkten Verfügbarkeit von neuartigen experimentellen Daten, wie
beispielsweise Live-Cell-Imaging mit subzellulärer Auflösung, wird in Zukunft der Bedarf
an entsprechenden mathematischen Modellen und deren Software-Implementierungen
zunehmen.
iv
Contents
Abstract (English/Deutsch)
1 Introduction
1.1 Modelling and Simulation for Morphogenetic Problems
1.2 Continuum Tissue Models . . . . . . . . . . . . . . . .
1.3 Spheroid Models . . . . . . . . . . . . . . . . . . . . .
1.4 Vertex Models . . . . . . . . . . . . . . . . . . . . . .
1.5 Cellular Potts Models . . . . . . . . . . . . . . . . . .
1.6 Immersed Boundary Cell Models . . . . . . . . . . . .
1.7 Subcellular Element Models . . . . . . . . . . . . . . .
1.8 Software Frameworks and Standards . . . . . . . . . .
1.8.1 Chaste . . . . . . . . . . . . . . . . . . . . . . .
1.8.2 CompuCell3D . . . . . . . . . . . . . . . . . . .
1.8.3 CellSys . . . . . . . . . . . . . . . . . . . . . .
1.8.4 EPISIM . . . . . . . . . . . . . . . . . . . . . .
1.8.5 Other Frameworks . . . . . . . . . . . . . . . .
1.8.6 Mark-up Languages, Standards and Guidelines
1.9 Scope and Organization of the Thesis . . . . . . . . .
i
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
2
3
6
7
9
11
13
14
14
15
16
17
17
18
19
2 Continuous Approach: Application to Early Long Bone Development
2.1 Continuous Model of Early Long Bone Development . . . . . . . . . . . .
2.1.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.2 Model Description . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.3 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.4 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Modelling Multiple Cell Types with Partial Differential Equations . . . .
2.2.1 Model Formulation . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2.2 Differentiation Delay . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2.3 Cell Volume Increase upon Differentiation . . . . . . . . . . . . . .
2.2.4 Multiple Cell Types . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2.5 Numerical Validation . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
22
22
25
35
46
49
49
50
51
52
53
55
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
v
Contents
3 Cell-based Approach: The Software Framework LBIBCell
3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.1 Cell Representation . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2 Fluid and Fluid-Structure Interaction . . . . . . . . . . . . . . .
3.2.3 Signalling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Numerical Methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.1 Lattice Boltzmann Method . . . . . . . . . . . . . . . . . . . . .
3.3.2 Immersed Boundary Method . . . . . . . . . . . . . . . . . . . .
3.4 Software . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.1 Cell Representation . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.2 User-provided Solvers . . . . . . . . . . . . . . . . . . . . . . . .
3.4.3 Input and Output . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.4 Physical Processes . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.5 Biological Processes . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.6 Performance . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.7 Tools, Dependencies and Documentation . . . . . . . . . . . . . .
3.4.8 Availability . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5 Mechanical Validations . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.1 Error Norms . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.2 Validation of the Fluid Solver, Immersed Boundary Method and
Mass Sources . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.3 Comparison to Farhadifar et al., 2007 . . . . . . . . . . . . . . .
3.6 Reaction-Advection-Diffusion Solver Validation . . . . . . . . . . . . . .
3.6.1 Diffusion of a Dirac Delta Peak . . . . . . . . . . . . . . . . . . .
3.6.2 Nonlinear Reaction and Diffusion . . . . . . . . . . . . . . . . . .
3.7 Application Example: Cell Division, Differentiation and Signalling . . .
3.8 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 Turing Patterns on Cellular Tissue
4.1 Introduction to Receptor-Ligand Interaction in Developmental Biology
4.2 Receptor-Ligand-Interaction-based Turing Systems . . . . . . . . . . .
4.3 Two-Component Turing System . . . . . . . . . . . . . . . . . . . . . .
4.3.1 Numerical Validation on Continuous Domain . . . . . . . . . .
4.3.2 Numerical Validation on Regular Cellular Domain . . . . . . .
4.3.3 Analysis on Irregular Cellular Domain . . . . . . . . . . . . . .
4.4 Three-Component Turing System . . . . . . . . . . . . . . . . . . . . .
4.4.1 Numerical Validation on Continuous Domain . . . . . . . . . .
4.4.2 Numerical Validation on Regular Cellular Domain . . . . . . .
4.4.3 Analysis on Irregular Cellular Domain . . . . . . . . . . . . . .
4.5 Activated Growth . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.6 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
vi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
57
58
59
59
59
61
61
61
64
65
65
66
67
68
69
73
73
74
74
74
.
.
.
.
.
.
.
74
82
85
85
88
92
94
.
.
.
.
.
.
.
.
.
.
.
.
95
96
98
100
100
101
106
110
110
110
112
115
116
Contents
5 Conclusion
117
Acknowledgements
121
A Appendix: Other Projects
123
A.1 Design and Optimization of a Microfluidic Gradient Generator . . . . . . 123
A.2 Quantification of Gradients in Gel-based Release Systems . . . . . . . . . 123
A.3 Simulation of the Growth Plate Dynamics in Embryonic Long Bone Development . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
Bibliography
148
vii
1 Introduction
Morphogenetic modelling and simulation help to understand the processes by which
form and shapes of organs (organogenesis) and organisms (embryogenesis) emerge. This
requires two mutually coupled entities: the biomolecular signalling network and the tissue.
Whereas the modelling of the signalling has been discussed and used in a multitude of
works, the realistic modelling of the tissue has only onset in the last decade on a larger
scale.
In this chapter, common tissue modelling techniques are reviewed. Besides the continuum
approach, the principles and main applications of the spheroid, vertex, cellular Potts,
immersed boundary and subcellular element models are discussed in detail. In recent
years, many software frameworks, implementing the aforementioned methods, have been
developed. The most widely used frameworks and modelling markup languages and
standards are presented.
This chapter has been published as:
Tanaka S, Simulation Frameworks for Morphogenetic Problems, MDPI Computation,
Special Issue: Multiscale Modeling and Simulation in Computational Biology, 2015, 3(2),
197-221
1
Chapter 1. Introduction
1.1
Modelling and Simulation for Morphogenetic Problems
Morphogenesis is the carefully orchestrated process by which the shapes and structures of
organs and organisms form, such that they can reliably fulfil their function. Research in
developmental biology cumulated myriads of genetic, molecular biological and biophysical
experiments in various model organisms over the last decades. However, many important
core mechanisms, which may be based on self-organization, are still not understood.
Complementary to experimental approaches, mathematical modelling and computer
simulations can be used to answer morphogenetic questions on a systems biology level.
Simulations allow researchers to study a beforehand formulated hypothesis of a governing
core mechanism in a very controlled way. Rather than just describing and characterizing
the existing knowledge using phenomenological models, mechanistic modelling aims at
creating explanatory models to gain confidence into the underlying mechanisms [Craver,
2006]. The emerging phenomena on the tissue or organ level, which are accessible to
validation, act as strong indications for the validity or falsity of the hypothesis.
At the coarsest level, the tissue is described by a macroscopic continuous material. For
instance, the tissue might be described by an incompressible viscous fluid [Dillon and
Othmer, 1999]. However, many cellular processes such as cell migration and adhesion,
cell polarity, directed division, monolayer structures and differentiation cannot be cast
into a continuous formulation in a straightforward way. Although it has been shown
for particular cases, e.g. anisotropic cell division [Bittig et al., 2008], this exercise is
not always possible without incisive simplifications and assumptions. For instance, the
authors of [Osborne et al., 2010] compared two cell-based models (spheroid and vertex
model) to a continuous model of healthy and cancerous crypt renewal. Although all
models recover the fundamental behaviour, specific differences exist. The cell-based
models require averaging over many simulation runs to account for stochasticity. On the
other hand, stochasticity leads to phenomena (such as the monoclonality hypothesis in
crypts) which cannot be predicted by deterministic continuous models. Cell-based models
usually suffer from a larger number of parameters as compared to continuous models.
Therefore, the authors of [Murray et al., 2011] derived a one-dimensional continuous
model from cell-based models, and found good agreement. Instead of either using cellbased or continuous approaches, they vote for the derivation of continuous formulations
based on discrete models to understand a problem on different scales.
In this chapter, a selection of frequently and increasingly used tissue modelling approaches
(illustrated in Figure 1.1), as well as software frameworks, is presented and discussed. In
Figure 1.2, the discussed modelling techniques are related to the biological scales which
they are able to represent, as well as to the computational complexity.
2
1.2. Continuum Tissue Models
Figure 1.1 – Tissue and cell models. A Continuous tissue model of a single cell layer to simulate
tip growth and branching, where the surface is displaced in normal direction according to the local
signal concentration, reprinted with permission from [Menshykau et al., 2014]; B Spheroid model of a
liver lobule, reprinted with permission from [Hoehme et al., 2010]; C Vertex model to study epithelial
dynamics, reprinted from [Farhadifar et al., 2007] with permission from Elsevier; D Cellular Potts model
of blood vessel growth, reprinted with permission from [Merks et al., 2008]; E Immersed boundary cell
model of a proliferating tissue; F Subcellular element model of a single cell subject to a stretching force,
c
reproduced by permission of IOP Publishing from [Sandersius et al., 2011]. All rights reserved IOP
Publishing.
1.2
Continuum Tissue Models
At the highest level of abstraction, the tissue is modelled as a continuous material. The
tissue can, amongst others, be described as a (visco-) elastic material, a viscous fluid, or
reaction-diffusion processes. In the following, these approaches are discussed in the light
of morphogenetic tissue modelling.
A continuum theory for soft incompressible hyperelastic tissue, similar to the description
of nonlinear elastic materials, has been developed [Rodriguez et al., 1994], extended
[Taber, 2001] and applied to various morphogenetic problems. To account for finite
volumetric (anisotropic) tissue growth and remodelling, the total deformation gradient
tensor F = F ? · G is split into two tensors, namely the (passive) elastic deformation
gradient tensor F ? , and the (active) growth tensor G. In order to generalize the theory
of finite volumetric growth, it is necessary to find a growth tensor G to model the
tissue properties. The dependency of the growth tensor G on the stress tensor σ is
called ’morphogenetic law’ and is a constitutive law depending on the tissue of interest
[Taber, 2009b]. One possible hypothesis is Beloussov’s hyper-restoration hypothesis,
which assumes that cells respond (and overshoot) to local stress changes [Taber, 2009a].
To solve the equations, finite element methods are used.
The finite volumetric growth theory has been used to study many morphogenetic processes
- reviewed in [Wyczalkowski et al., 2012] - including stress-dependent bone growth
3
Figure 1.2 – Scales and modelling approaches of signalling (grey) and tissue modelling
approaches (red). On the horizontal axis, typical length scales are given. The vertical axis indicates
increasing computational complexity. At the highest level of detailism, molecules and their interactions
can be simulated using molecular dynamics. The accessible length and time scales, however, are small due
to the computational complexity. Continuous signalling models (such as deterministic reaction-diffusion
equations and stochastic partial differential equations) allow to simulate large biochemical interaction
networks. Both single cells and entire tissues can be modelled using continuous formulations. Resolving
cells, and possibly subcellular structures explicitly, requires complex meshing and moving boundaries, thus
leading to relatively high computational complexity. To simulate entire organs, however, the continuous
approach has the lowest computational complexity. Currently, the vertex and spheroid models use the cell
as the smallest resolved unit. In contrast to the vertex model, the spheroid model does not resolve the cell
geometry explicitly and is therefore the most efficient cell-based approach among the presented models.
The cellular Potts, subcellular element and immersed boundary models are capable to explicitly represent
subcellular structures (e.g. the nucleus), and they resolve arbitrarily deformable cell shapes explicitly.
The high computational complexity limits these approaches to smaller tissues. These methods allow for
coarse-graining, i.e. not every individual cells, but multiple cells are associated with a computational
entity. In the case of the immersed boundary method, an entire tissue/organ can be represented by an
immersed boundary ’cell’ [Dillon and Othmer, 1999], thus closing the loop to the continuous approach.
[Rodriguez et al., 1994], the gastrulation process in sea urchin embryos [Taber, 2009b],
Drosophila ventral furrow formation [Muñoz et al., 2007, Munoz et al., 2010], avian head
fold formation [Varner et al., 2010], brain morphology development [Filas et al., 2012],
initialization of budding processes in branching morphogenesis [Kim et al., 2013], and
bending morphogenesis of the primitive heart tube [Shi et al., 2014].
To study mechanical cell-substrate interactions, the Oster-Murray-Harris model assumes
that cells, which are described by a scalar cell concentration, exert active forces generated
by the actomyosin and move within an extracellular matrix (ECM). The latter is modelled
as a linear viscoelastic medium. By modelling the motion of the cells being biased into
the direction of the highest strain, the cells’ forces deform the substrate, and cells many
cell diameters away are influenced. This mechanism has the capability to form patterns
in a self-organizing fashion, thus being an interesting biomechanical mechanisms for
morphogenesis, e.g. mesenchymal cells embedded in an ECM [Murray et al., 1983].
4
1.2. Continuum Tissue Models
Oftentimes, embryonic tissue can be modelled as a viscous fluid when being interested in
the long timescale behaviour [Foty et al., 1994, Forgacs et al., 1998]. Furthermore, it has
been shown that high proliferative activity leads to a fluidization of the tissue [Ranft
et al., 2010]. The authors of [Dillon and Othmer, 1999] used the Navier-Stokes equation
to describe the embryonic limb as fluidic tissue:
1
ρ (∂t u + (∇ · u) u) = −∇p + µ ∆u + ∇ (∇ · u) + f
3
ρ∇ · u = S,
(1.1a)
(1.1b)
where u denotes the velocity field, p the pressure field, and f an external force field.
The local mass source S can be used to model proliferation, which may be controlled
by biomolecular signalling. Usually, the Reynolds number Re = UνL , with U being a
characteristic velocity, L a characteristic length scale, and ν the kinematic viscosity, is very
small. Assuming L = 10−3 [m], U = 10−8 [m/s] and ν = 101 . . . 102 m2 /s [Forgacs
et al., 1998], then Re = 10−13 . . . 10−12 can be estimated. By non-dimensionalizing
Equation (1.1), and assuming Re → 0, the Stokes equations can be written as:
1
0 = −∇p + ∆u + ∇ (∇ · u)
3
∇ · u = S,
(1.2a)
(1.2b)
where all variables (and differential operators) now denote dimensionless quantities.
Instead of computing the velocity field based on a tissue model, it can be acquired from
experimental data. To this end, tissue shapes are taken at regular developmental stages
using microscopy and subsequent image processing. Morphing and interpolation are
needed for the continuity of the velocity fields [Karimaddini et al., 2014, Iber et al., 2015].
The movement of chemotactic cells of the slime mold (Acrasidae, e.g. Dictyostelium)
in a chemical gradient has been described by the authors of [Keller and Segel, 1970].
In their original work, they derived a system of reaction-diffusion partial differential
equations for two chemical species, their complex, and a mass density of the amoebae.
The interplay between diffusion, complex formation and chemotaxis leads to complex
pattern formation, as observed in nature.
If cell mechanics is ignored, tissue growth can be achieved by formulating laws how to
move the tissue boundaries as a function of the biomolecular signalling. This approach
has been used to study the ability of a Turing-type signalling mechanism to control the
branching of embryonic lungs [Menshykau et al., 2014]; an example is given in Figure
1.1A.
5
1.3
Spheroid Models
A wide range of models have been developed which model cells as particle-like (colloidal)
objects (cf. Figure 1.1B). The cells are assumed to have spherical, isotropic shape,
which is represented by soft sphere interaction potentials. It has been shown that the
Johnson-Kendall-Roberts (JKR) theory for adhesive spheres can be applied to cells [Chu
et al., 2005]. The JKR model features a hysteresis effect, i.e. the distance at which
cells lose contact when being pulled apart is larger than the distance at which they
formed contact when having approached each other earlier [Drasdo and Hoehme, 2005].
Alternatively, Hertz contact models [Drasdo et al., 2007], harmonic interaction potentials
[Drasdo et al., 1995] and dashpot-spring elements [Palsson, 2001] have been applied.
Because the used interaction potentials are very diverse and purely phenomenological, the
interested reader may find details elsewhere [Drasdo et al., 1995, Palsson, 2001, Drasdo
et al., 2007, Drasdo, 2007].
To move the cells, the over-damped (i.e. acceleration and thus inertial effects are ignored)
equations of motion can be solved deterministically [Palsson and Othmer, 2000]. The
authors of [Drasdo et al., 1995, Drasdo et al., 2007] used a Metropolis algorithm to solve
the friction dominated stochastic (Langevin) equations since cells perform random walks
when being isolated. The Langevin equation for a cell i with velocity ui at position xi is
given as [Drasdo et al., 2007]:
γ + Γfis ui +
X
j6=i
Γfij ui − uj =
N
X
F ij + η i (t) ,
(1.3)
j=0
where γ is an effective friction coefficient.
(iy)
(iy)
The tensor Γfiy = γk niy ⊗ niy + γ⊥ E − niy ⊗ niy (with y = s for substrate- and
y = j for cell-cell interactions) is composed of a parallel and perpendicular contribution
(ij)
(ij)
x −x
with friction coefficients γk and γ⊥ , respectively. niy = |xyy −xii | is the unit vector from
cell i to entity y. The repulsive and attractive forces F ij are derived from the interaction
potentials, and η i (t) is a noise term.
Various implementations for cell cycle, cell growth, division, migration and signalling
have been developed, e.g. [Drasdo and Hoehme, 2003, Galle et al., 2005, Drasdo et al.,
2007, Macklin et al., 2012]. In order to introduce geometrical anisotropy and cell polarity,
the cells can be represented by ellipsoids (or ellipses in two dimensions). Dallon, Othmer
and Palsson [Palsson and Othmer, 2000, Dallon and Othmer, 2004] applied an ellipsoid
cell model to study the chemotactic behaviour of Dictyostelium discoideum (slime mold)
cells.
The spheroid model origins from a spheroid model variant where each cell is represented
by a computational particle, but explicit cell boundaries are represented by Voronoi
tesselation (also known as Dirichlet domains) [Honda, 1978]. It has been used to study
6
1.4. Vertex Models
pattern formation of the epidermis in butterfly [Honda et al., 2000], and intestinal crypt
dynamics [Meineke et al., 2001]. The authors of [Gevertz and Torquato, 2006] used a
spheroid-Voronoi model in combination with a reaction-diffusion based signalling model to
study the interplay between VEGF signalling, blood vessel formation and tumorogenesis.
The epithelial renewal mechanisms in intestinal crypts have been studied with a spheroid
model, where the cells are interconnected by springs, but the cell shape represented by
Voronoi tesselation [van Leeuwen et al., 2009]. Finally, hybrid (multi-scale) models, which
combine the cell representation of the spheroid model and the efficiency of continuous
tissue description have been proposed [Kim et al., 2007, Kim and Othmer, 2013]. The
authors of [Pathmanathan et al., 2009] show how the mechanical properties relate to the
model parameters both in the spheroid and vertex model.
Due to the simple geometric representation, spheroid models are predestined for problems
with large numbers of cells where cellular and subcellular details (such as arbitrarily
deformable shapes) can be omitted or modelled into the interaction potentials. More
detailed tissue modelling approaches are discussed in the following.
1.4
Vertex Models
In two dimensions, the vertex model approximates each cell by a polygon. The interface
between each pair of neighbouring cells is represented by a common edge, and the points
of intersection by vertices. Since two neighbouring cells share a common edge which
means that gaps (interstitial space) cannot be natively represented. On the other hand,
undesired overlaps are avoided. Hence the vertex model is most appropriate to represent
densely packed epithelial tissue. The vertex model originates from the work introduced
by Honda and co-workers [Honda and Eguchi, 1980]. They use Voronoi tesselation to
construct polyhedral geometries around cell centers. Extensive reviews can be found in
[Fletcher et al., 2013, Fletcher et al., 2014]. Different approaches have been developed
to move the vertices; however, they have in common that the forces solely act on the
vertices itself. The force F i acting on a vertex i can be formulated explicitly [Weliky and
Oster, 1990, Weliky et al., 1991], or by using an energy potential E [Nagai and Honda,
2001, Farhadifar et al., 2007]:
Fi =
∂E
,
∂Ri
(1.4)
with Ri being a junctional direction of vertex i. A typical energy function includes area
elasticity, line tension and contractility of the cell perimeter [Farhadifar et al., 2007]:
E (Ri ) =
X Kα α
2
Aα − A0α
2
+
X
<i,j>
Λij lij +
X Γα
L2α .
α
2
(1.5)
7
The first term on the right hand side describes the area elasticity, with Kα being the
area elasticity coefficient, Aα the current area and A0α the resting area. The second term
denotes line tension, which, for vertex i, considers all neighbouring vertices j. Λij is the
line tension coefficient, and lij the edge length, and < i, j > denotes the summation over
all edges. The last term represents the perimeter contractility, with Γα being the cell
perimeter contractility coefficient and Lα the cell’s perimeter.
Once the forces are defined, different approaches have been used to move the vertices.
Either, at each time step, the entire morphology is relaxed to its local steady state, e.g.
using a conjugate gradient method [Farhadifar et al., 2007]. In this case, the vertex model
describes stable and stationary topologies, because force balance is assumed, and the
local minimum of the energy function is computed. Or, in the simplest deterministic way,
the cells are moved according to the overdamped Newtonian mechanics, where inertia
can be neglected [Nagai and Honda, 2001]:
η
dxi
= F i,
dt
(1.6)
where xi denotes the position of vertex i, η the mobility coefficient, and F i the force
acting on vertex i. As a third approach, a Monte Carlo algorithm to shorten the cell
boundaries and thus relaxing the tissue (termed ’boundary shortening procedure’ in
[Honda, 1978]) can be applied.
More related models can be found for plant biology. Brodland and co-workers [Chen
and Brodland, 2000, Brodland and Chen, 2000] used a finite element formulation.
Alternatively, an explicit spring network can be relaxed to equilibrium at each time step
[Rudge and Haseloff, 2005]. A similar formulation is used in the open source platform
VirtualLeaf [Merks et al., 2011], but there a Monte Carlo energy minimization approach,
similar to the Potts models [Graner and Glazier, 1992], is used for relaxation.
Different biologically motivated processes can alter the connectivity of the topology. An
number of basic mesh restructuring processes have been identified (nicely summarized in
[Fletcher et al., 2013]): cells can change neighbours (T1 transition), delaminate or die
(element removal, T2 transition), or clot together (element intersection, T3 transition).
Furthermore, node switching has to be applied to prevent self-intersection. Cell division
is modelled by splitting the mother cell and introducing a new edge.
Several vertex models have been combined with biomolecular signalling. The authors of
[Schilling et al., 2011] used the cell polygons to solve the partial differential equations,
representing reaction-diffusion systems, in a Finite Volume framework. However, the
chemical species can only diffuse freely across the entire tissue, or are bound to cells
without diffusion (ordinary differential equations). Advection has been ignored. A similar
approach has been taken by the authors of [Smith et al., 2011], where the polygonal
elements serve as a mesh for a finite element method.
8
1.5. Cellular Potts Models
Although the vast majority of models have been formulated in two spatial dimensions,
three-dimensional versions have been proposed. In the simplest case, the vertices are
allowed to move in all spatial dimensions. This approach has been used to study buckling
behaviour of an infinitely thin single layer tissue [Osterfield et al., 2013]. Honda and
co-workers [Honda et al., 2004, Honda et al., 2008] used Voronoi tesselation to represent
polyhedra, the three-dimensional counterpart of the vertex model’s polygons. In recent
work, viscosity has been added to the model to study epithelial vesicle growth in three
dimensions [Okuda et al., 2014].
The vertex model has been used to study numerous morphogenetic problems, such as to
explore the hypothesis of a mechano-sensing mechanism on Drosophila wing disc growth
control [Hufnagel et al., 2007]. Brodland and co-workers [Brodland et al., 2007] developed
a model variant and achieved realistic cell rearrangement and sorting behaviour as
observed in embryonic epithelia. However, they find that cells are artifactually stiffening
when cell edges shorten towards zero length. Also in the wing disc, Schilling and
co-workers [Schilling et al., 2011] studied the effect of signalling on the mechanical
tension between compartments of different cells, namely cell sorting. The authors of
[Farhadifar et al., 2007] analyzed the topological transition of the irregular polygons
of the Drosophila wing disc into regular, largely hexagonal patterns (cf. Figure 1.1C).
They compare simulated network morphologies to experimental data, and they found
parametric spaces which lead to good agreement. Furthermore, they estimated the
parameter values from laser ablation experiments.
In general, for many vertex model variants, it is unclear how they can be extended to
include the mechanical effects of the cytoskeleton (e.g. the viscous behaviour). The
finite element formulation of Brodland and co-workers [Brodland et al., 2007] is an
interesting approach to combine cell-based vertex models with a continuous description
of the viscoelastic material.
1.5
Cellular Potts Models
The cellular Potts model (CPM), first introduced by Graner and Glazier [Graner and
Glazier, 1992, Glazier and Graner, 1993], originates from the Ising model [Ising, 1925] and
on its later generalization, the Potts model [Potts, 1952], which show phase transition
phenomena in ferromagnetic materials. The CPM is also known - according to its
founders and main contributors - as the Glazier-Graner-Hogeweg (GGH) model [Glazier
et al., 2007]. The key element of the CPM is the lattice. Each lattice site x carries a
spin σ (x) ∈ Z+,0 , where each spin value represents a cell identity (with the exception
of σ = 0, which usually denotes extracellular space). The central element of the CPM,
similar to the Ising model, is the Metropolis algorithm [Metropolis et al., 1953]. The
update algorithm seeks to minimize a Hamiltonian energy function H that is defined over
the entire domain. In the original form [Graner and Glazier, 1992, Glazier and Graner,
9
1993], the Hamiltonian H is composed of two contributions, a volume constriction term
Hv and a cell-cell adhesion term Ha :
H = Hv +Ha =
X
λv Vσ − VσT
σ
2
+
X
J τ (σ (x)) , τ σ x0
· 1 − δ σ (x) , σ x0
,
(x,x0 )
(1.7)
where Vσ and VσT are the actual and target volume of cell σ, respectively. The coefficient
λv controls the energy penalization. The term J (τ, τ 0 ) is the surface energy between
two cell types τ and τ 0 . Here, τ (σ (x)) denotes the cell type of the cell σ at position
x. The inverse Kronecker delta 1 − δ (·, ·) equals one if σ 6= σ 0 , which is true if the two
P
neighbouring lattice sites are of different cell type. The summation (x,x0 ) runs over all
lattice sites x and its neighbouring lattice sites x0 . To summarize, the cell-cell adhesion
contribution is only non-zero across cell-cell interfaces, and only if the two cells are of
different cell types. The modified Metropolis algorithm is implemented as follows: a
lattice site x and a neighbouring lattice site x0 are chosen randomly. The probability of
converting the spin σ (x0 ) of the lattice site x0 into the spin value σ (x) is set to be:
0
p σ (x) → x =

1
if ∆H (σ (x) → x0 ) < 0
exp (−∆H (σ (x) → x0 ) /T )
otherwise
.
(1.8)
Thus a lattice site conversion is accepted if it decreases the global Hamiltonian. An
increased Hamiltonian is accepted with a Boltzmann-distributed probability, which
exponentially decreases with an increasing energy jump. If the lattice consists of N
lattice sites, then a series of N spin-copy attempts is called a Monte Carlo step (MCS).
The factor T corresponds to the ’temperature’ in the antecedent Ising model. Similar to
the Ising model, the CPM may show phase transition behaviour as a result of changing
temperature. Thus, restrictions on the temperature have been proposed [Glazier et al.,
2007] to guarantee domain connectivity. In general, it is difficult to interpret the
biophysical meaning of the ’temperature’ [Glazier et al., 2007, Marée et al., 2007].
Since the entire computational domain has to be finely resolved by the lattice (and not
only the cells of interest), the memory requirements and computational costs may be
high. However, as for many lattice-based algorithms, high performance computing and
parallelization techniques can be applied efficiently [Swat et al., 2012]. As it is the case
for every inherently stochastic approach, multiple repetitions are required for statistical
reasons, thus increasing the computing time.
The CPM has been coupled to reaction-diffusion equations by applying finite difference
discretization and explicit time integration [Hogeweg, 2000, Hogeweg, 2002, Hogeweg and
Takeuchi, 2003], and has been applied to study blood vessel formation, where it was found
that cell elongation is required to explain the vascular network formation [Merks et al.,
2006], and where a vessel branching mechanism was shown to reproduce experimental
10
1.6. Immersed Boundary Cell Models
observations [Merks et al., 2008] (cf. Figure 1.1D). The authors of [Szabó and Czirók,
2010] studied the tip growth of blood vessel sprouts, and Bauer and co-workers [Bauer
et al., 2007] the inducing effect of tumors on angiogenesis. Furthermore, the CPM was
used to simulate cell sorting [Graner and Glazier, 1992, Glazier and Graner, 1993], kidney
branching [Hirashima et al., 2009], somitogenesis [Hester et al., 2011] and chicken limb
morphogenesis [Poplawski et al., 2007].
1.6
Immersed Boundary Cell Models
In the two-dimensional IBCell (immersed boundary cell) model, the shapes (i.e. the
membranes) of the cells are approximated by finely resolved polygons [Rejniak et al.,
2004, Rejniak, 2007, Dillon et al., 2008]. However, in contrast to the vertex model, cells
do not share edges, but each cell rather owns its own edge in the IBCell model. An
illustration is given in Figure 1.1E. These polygons are immersed in a fluid, and, in a
first step, the vertices are passively advected by the fluid velocity field u. Hence, the
membrane is impermeable to the fluid. In other words, the curvilinear coordinates of
the boundary points (q, r, s) are attached to a material fluid particle, and the Eulerian
coordinates of that particle at time t are denoted as X (q, r, s, t). The material derivative
Du
∂2X
Dt (x, t) = ∂t2 (q, r, s, t) is the acceleration of whatever material point is at position x
at time t. On the cell boundary, various force generating processes F can be modeled,
including membrane tension, cell-cell and cell-substrate junctions, and forces exerted by
the cytoskeleton. For example, membrane tension can be modelled as a set of Hookean
springs connecting each pair of vertices of the polygon. The cellular geometries thus
represent the elastic material properties of the tissue. The fluid, in which the polygons
describing the cell shapes are immersed in, is divided into compartments: the fluid
inside the cells represents the viscous properties of the cytoplasm, whereas the fluid
in the inter-cellular space represents the viscous properties of the extracellular matrix
and interstitial fluid. The fluid is, as already given in Equation (1.1), described by the
Navier-Stokes equation. The local mass source S may be used to model cell growth. In
contrast to the Lagrangian polygons, the fluid equations are solved on an Eulerian mesh.
To solve the mechanical interaction between the elastic structures and the fluid, the
immersed boundary method is used [Peskin, 2003]. The conversion from Lagrangian
variables (e.g. force density F (q, r, s, t)) to their Eulerian counterparts is executed by
integrating over the material coordinates:
Z
f (x, t) =
F (q, r, s, t) δ (x − X (q, r, s, t)) dqdrds ,
(1.9)
where δ (·) denotes the delta Dirac function. For the numerical implementation, the
delta Dirac function is approximated by a kernel function in such a way that it covers
11
multiple grid points on which the conversions in Equation (1.9) and (1.10) are evaluated.
Examples of widely used kernel functions can be found in [Mittal and Iaccarino, 2005].
The equation of motion of the Lagrangian particles reads:
∂X
(q, r, s, t) = u (X (q, r, s, t) , t) =
∂t
Z
u (x, t) δ (x − X (q, r, s, t)) dx ,
(1.10)
where the same kernel function is used for the interpolation of the velocity field to the
Lagrangian vertices of the polygon. By iteratively solving the fluid equations, interpolating
the velocity field to the cell geometries, moving the cells, recomputing the forces acting on
the cell geometries, distributing the forces to the local fluid neighbourhood and restarting
the process, fully coupled fluid-structure interaction is achieved and fluid-structure
interaction, an inherently difficult problem, can be handled.
The IBCell model has been independently developed by Rejniak [Rejniak, 2007] and
Dillon [Dillon et al., 2008]. While the model of Rejniak uses a single membrane with
a single mass source in the middle of the cell and compensating mass sinks distributed
in the interstitial neighbourhood of the membrane, the model of Dillon et al. has two
interconnected closed polygons to represent membrane of finite thickness and thus nonzero bending stiffness, and cell growth is mimicked by water channels along the membrane.
The different versions of the model have been applied to ductal tumorogenesis, and no
fundamental difference of the results was found [Rejniak and Dillon, 2007].
As compared to the subcellular element model and the vertex model, the mechanical
processes (elasticity and viscosity) are explicitly represented and can be directly associated
with experimental measurements. Although the membrane and cell-cell junction forces
are phenomenological (like the potentials in the spheroid and subcellular element model),
the IBCell model’s explicit representation of the cell membranes, the interstitial space
and the cell-cell junctions allows to study cell intercalations and topological changes in a
much more intuitive way than in the vertex model, and cytoskeletal viscosity is natively
included. Additionally, the polygonal shapes of cells in a densely packed tissue is an
emergent property rather than a model assumption (vertex model).
A drawback of the IBCell model is, however, its inherent computational complexity. Even
for two-dimensional models, the need for Navier-Stokes solvers, the finely discretized cell
shape and the iterative immersed boundary method currently limit the number of cells to
a few thousand. In contrast to the subcellular element model and the the vertex model,
the generalization of the IBCell model into three dimensions is an expensive exercise,
requiring complex triangulation of the cell surface. Three-dimensional simulations similar
to the IBCell model to study the membrane of red blood cells in blood flow are limited
to a few cells [Le et al., 2009].
On the other hand, the IBCell model could be used to represent clusters of cells or even
entire tissues instead of individual cells, thus closing the gap to the continuous approach
12
1.7. Subcellular Element Models
to model tissue as fluid (cf. Section 1.2). Dillon and co-workers [Dillon and Othmer,
1999] modeled the limb bud tissue as a viscous fluid, and used the immersed Boundary
method to model the tissue boundary.
1.7
Subcellular Element Models
The subcellular element model (SEM), first presented by Newman [Newman, 2005],
assumes that the cytoskeleton of a cell is divided into a number of subcellular elements.
Each element is mathematically and computationally represented by a point particle,
and biophysically, they interact via forces derived from interaction potentials. In the
simplest version, two potentials have to be specified: an intracellular interaction potential
Vintra for the interaction of elements within an individual cell, and an intercellular
interaction potential Vextra for the interaction of elements between different cells. Besides
representing the cytoskeleton, dedicated elements can represent the extracellular matrix,
the cell membrane, the nucleus, or other organelles or cellular structures. To that end, the
modeller has to model the interaction potentials between the element types accordingly.
Since the Lagrangian elements move freely in space, there is no need for an underlying
grid. Neglecting inertia effects, the equation of motion for the position yαi of a subcellular
element αi of cell i reads [Newman, 2005]:
η
XX
X
∂y αi
Vinter y αi − y βi , (1.11)
Vintra y αi − y βi − ∇αi
= ζ αi − ∇ αi
∂t
j6=i β
β 6=α
i
i
j
where ζαi is Gaussian noise, and η the viscous damping coefficient. The first term
represents intra-cellular interactions, and the summation runs over all remaining elements
βi of cell i. The inter-cellular interaction described by the second term takes all pairinteractions between the elements βj of other cells j and the elements αi of cell i into
account. Numerically, the forward Euler and a two-step Runge-Kutta scheme have been
used to integrate Equation (1.11) [Christley et al., 2010].
Similar to the inter-atomic interaction potentials in molecular dynamics simulations, the
phenomenological potentials Vintra , Vinter are chosen such that the subcellular elements
prefer to be in an equilibrium distance to their neighbouring elements, i.e. that the
subcellular elements repel each other when the distance between two cells is low, and
attract each other when the distance is large. However, the attractive force rapidly
decreases to zero at large distances. The authors of [Newman, 2005] used a Morse
potential for both the inter- and intracellular potentials Vintra , Vinter :
V (r) = U0 exp (−r/ξ1 ) − V0 exp (−r/ξ2 ) ,
(1.12)
where r denotes the distance between two subcellular elements. The energy scale
parameters U0 , V0 and the length scale parameters ξ1 , ξ2 control the magnitude and
13
shape of the potential, as well as the location of the equilibrium distance.
It has been shown that the simplest implementations of the SEM successfully recover
biophysical cell behaviour on intermediate time scales and for low strains. An illustration
of a stretching simulation is given in Figure 1.1F. The high-frequency response of the
cytoskeleton, as well as the long time and high strain behaviour could not be recovered.
An extension has been proposed to capture active cytoskeleton restructuring (active
cytoskeleton polymerization and depolimerization of actin filaments and microtubules)
[Milde et al., 2014]. This is realized by adding and removing subcellular elements in a
smooth way in order to polarize the cell. In this way, cell polarization and migration
could be realized.
Using mean field theory, it has been shown that the coarse-grained mechanical behaviour
can be written as an analytically derived partial differential equation [Newman, 2005], and
that the macroscopic properties do not depend on the number of discretizing elements
[Sandersius and Newman, 2008]. Indeed, it has been found that macroscopic tissue
viscosity is an emerging property of cellular processes [Sandersius et al., 2011].
Due to the explicit representation of arbitrary cell shapes, the SEM requires a high number
of computational particles to represent a cell, making it a computationally expensive
method as compared to the three-dimensional vertex model or the three-dimensional
spheroid model. However, due to its algorithmic simplicity borrowed from molecular
dynamics, efficient library implementations can be used [Christley et al., 2010, Milde
et al., 2014]. It has been reported that the SEM is suitable to study problems with up to
10,000 cells [Newman, 2005].
To date, the SEM has not been widely used to study morphogenetic or related problems. To study the dynamics of layers of epidermal cells, the SEM has been efficiently
implemented for GPU’s and coupled to an ordinary-differential-equation-based model of
Notch signalling [Christley et al., 2010]. The authors of [Milde et al., 2014] improved the
cytoskeleton remodelling algorithms, and studied cell migration, growth and proliferation,
and coupled the model to simplified juxtacrine signalling models. Cell motility and invasion of tissue, which are for instance important processes in primitive streak formation,
have been demonstrated by Sandersius and co-workers [Sandersius et al., 2011].
1.8
1.8.1
Software Frameworks and Standards
Chaste
The original aim of Chaste1 [Pitt-Francis et al., 2009, Mirams et al., 2013] was to
create a comprehensive simulation environment for physiological simulations (cardio
1
14
http://www.cs.ox.ac.uk/chaste/
1.8. Software Frameworks and Standards
electrophysiology), and later for a wider range of computational biology. Chaste, which
is developed by a large team from the University of Oxford, makes extensive use of
modern software engineering methods such as agile and test-driven software development.
The framework offers core functionality for meshing, solving ODE’s, PDE’s and I/O.
Furthermore, it makes use of highly parallelized libraries such as PETSc2 to provide
parallelized data structures and (FEM) solvers.
Cell-based Chaste denotes a collection of cell-based tissue model implementations. This
includes cellular automata models (as reviewed in [Moreira and Deutsch, 2002]), cellular
Potts models (cf. Section 1.5), spheroid models (cf. Section 1.3) and vertex models
(cf. Section 1.4) [Fletcher et al., 2013]. Currently, cell-based Chaste does not offer
the possibility to use the markup languages CellML [Cuellar et al., 2003] or SBML (cf.
Subsection 1.8.6).
In recent years, cell-based Chaste has been used to study several biological problems,
most notably the renewal dynamics of intestinal crypts in the gut. Van Leeuwen and
co-workers [van Leeuwen et al., 2009] developed a spheroid-Voronoi model [Meineke
et al., 2001] (cf. Section 1.3) in combination with a signalling and cell cycle model.
They perform virtual experiments to predict the mechanisms and conditions of clonal
expansion and niche succession. Furthermore, the vertex model has been used to simulate
healthy and mutageneous crypt dynamics. Fletcher and co-workers [Fletcher et al.,
2012] use a vertex model to study different hypotheses on monoclonal conversion, and
find that the stem cell niche hypothesis is more favourable than the immortal stem cell
hypothesis. To take mechanical properties, such as cell adhesion, into account to simulate
the behaviour of mutageneous cells in the crypt, particle-Voronoi models [Mirams et al.,
2012] and spheroid models [Dunn et al., 2013] have been used. The authors of [Dunn
et al., 2012b, Dunn et al., 2012a] study the mechanical interplay between the basement
membrane and an epithelial monolayer using a particle-Voronoi cell model. In particular,
they study the homeostasis between cell migration and death. Figueredo and co-workers
[Figueredo et al., 2013] developed an on-lattice agent-based model which incorporates a
multitude of cell behaviour such as proliferation, cell death and motility. Furthermore,
they coupled it to cell-cycle and reaction-diffusion-signalling models.
1.8.2
CompuCell3D
The open-source modelling framework CompuCell3D3 , whose development is mainly
driven by researchers from the Indiana University and led by James Glazier, implements
the cellular Potts (Glazier-Graner-Hogeweg) model [Swat et al., 2012]. The framework
is highly modular, and customized modules - written either in C++ or Python - can
be developed and added as plugins. This way, the user can add, for instance, own
2
3
www.mcs.anl.gov/petsc/
http://www.compucell3d.org/
15
Hamiltonian energy functions as given in Equation (1.7). The core is parallelized using
the shared-memory paradigm, thus limiting the software to desktop computers and
servers. CompuCell3D uses its own XML-based format to store and load models. To
solve PDE-based signalling models, a built-in facility is offered. Most noteworthy,
CompuCell3D offers a mature user interfacing infrastructure: a model editor, a graphical
tool to draw and configure cells, import and segment experimental microscopy images,
and for visualizing and analysing the simulation results. A thorough collection of manuals
and tutorials are supplementing the framework.
CompuCell3D has been deployed to study a broad range of developmental and biological
problems, and a few of them shall be highlighted here. To explain the regular pattern
formation in somitogenesis, Glazier and co-workers [Glazier et al., 2008] studied a clock
based mechanism. A clock- and wavefront-free mechanisms for somitogenesis has been
proposed [Dias et al., 2014]. They propose a self-organizing patterning mechanism based
on cell-cell interaction and polarization. Computer simulations using CompuCell3D
were indeed successful in achieving self-organizing patterns. Many authors studied
angiogenesis and vasculogenesis [Guidolin et al., 2009, Kleinstreuer et al., 2013], lumen
formation during blood vessel formation [Boas and Merks, 2014], and the interplay
between angiogenesis and tumorogenesis [Shirinifard et al., 2009]. CompuCell3D has
also been used to study tumor and cancer growth [Shirinifard et al., 2009, Poplawski
et al., 2010, Li and Lowengrub, 2014]. Also classical morphogenetic problems have been
explored, including primitive streak formation in chick embryos [Vasiev et al., 2010] and
salivary gland branching morphogenesis [Ray et al., 2013]. The authors of [Poplawski
et al., 2007] studied the influence of the AER on limb bud shape formation.
1.8.3
CellSys
The freely available, but closed-source three-dimensional framework CellSys4 [Hoehme
and Drasdo, 2010], mainly developed by Stefan Hoehme, Dirk Drasdo and co-workers,
is built around the spheroid model (as described in Section 1.3). The software, written
in C++, offers graphical user interfaces and real-time rendering of the results. CellSys
offers already parametrized cell models, cell migration, cell-cycle and signalling models.
The authors of CellSys developed the software in the context of liver regeneration.
They studied the influence of parameters and mechanisms on liver regeneration when
hepatocytes were damaged by drugs [Hoehme et al., 2007], and found that, besides
hepatocyte proliferation, cell polarization plays a crucial role. The model has been
compared with experimental data [Hoehme et al., 2010] to obtain a so-called virtual liver
that may help to understand the mechanisms of liver regeneration and diseases [Drasdo
et al., 2014, Schliess et al., 2014].
4
16
http://msysbio.com/
1.8. Software Frameworks and Standards
1.8.4
EPISIM
The modelling platform EPISIM5 [Sütterlin et al., 2013], available as free closed-source
software, is developed by researchers from the Heidelberg University and is an attempt to
standardize models in systems biology, in particular multi-scale agent-based tissue models,
cell behaviour and signalling models. To this end, it is inherently using the Systems
Biology Markup Language SBML (cf. Section 1.8.6). The platform, offering graphical
user interfaces (SBML model importer, signalling and cell behaviour model editor), aims
to be easy and intuitive to operate, such that it may be used by biologists without
computer and computational science background. The compilation into executable
code, and the multi-scale time step algorithms are hidden from the user. However,
the simple and entirely graphical usability comes at the price of less flexibility and
extensibility. Currently, an ellipsoid (agent-based) and a lattice-based tissue model are
implemented. Although EPISIM exploits multicore processors by using multithreading,
it is not distributed-memory parallelized, but it offers the possibility to run parameter
screens by launching independent instances on cluster computers [Sütterlin et al., 2013].
EPISIM has been used by the authors to model epidermal homeostasis in two and three
dimensions [Sütterlin and Grabe, 2014] and wound healing [Safferling et al., 2013]. A
range of functionalities, such as cell behavioural, cell-cycle, differentiation, signalling and
mitosis, have been implemented.
1.8.5
Other Frameworks
The open-source framework VirtualLeaf6 [Merks et al., 2011] implements a vertex model
[Nagai and Honda, 2001], which is appropriate for plant tissue modelling since it restricts
relative cell movements. The Hamiltonian energy function is minimized by a Monte
Carlo algorithm. The framework allows for solving ordinary-differential-equation-based
signalling models for each cell, as well as partial-differential-equation-based reactiondiffusion signalling models.
The aim of the freely available, but closed-source software Biocellion7 [Kang et al., 2014]
is to allow for high-performance computing on (massively parallelized super-) computers
with millions to billions of cells. To that end, a parallelized data structures, domain
decomposition, load balancing and PDE solvers are implemented, but hidden from the
user. Biocellion offers an agent-based (spheroid) cell model. The authors used the
software to reproduce cell sorting and microbial pattern formation.
The free two- and three-dimensional software Morpheus8 [Starruß et al., 2014] offers
5
http://tigacenter.bioquant.uni-heidelberg.de/episim.html
https://code.google.com/p/virtualleaf/
7
http://biocellion.com
8
http://imc.zih.tu-dresden.de/wiki/morpheus
6
17
a cellular Potts tissue model, coupled ODE lattices (for intracellular processes) and
deterministic and stochastic reaction-diffusion finite difference solvers. Signalling models
can be loaded in SBML format. Morpheus has been applied to pancreatic [de Back
et al., 2013a, de Back et al., 2013b] and vascular pattern formation [Köhn-Luque et al.,
2011, Köhn-Luque et al., 2013].
The open-source software OpenCMISS9 [Bradley et al., 2011] focuses on organ-level
modelling by means of continuum tissue models.
1.8.6
Mark-up Languages, Standards and Guidelines
In order to efficiently and unambiguously describe and store systems biology models (as
for example in the database BioModels [Li et al., 2010]), multiple standards have been
developed recently. MIRIAM [Le Novère et al., 2005] and MIASE [Waltemath et al.,
2011a] are guidelines to describe biological models and their simulation execution. The
exchange format SED-ML [Waltemath et al., 2011b] uses MIASE to define simulation
experiments. The Systems Biology Markup Language SBML10 [Hucka et al., 2003] is
a machine-readable standard to describe biological reactions. The standard supports
the description of, amongst others, mathematical functions, species, kinetic parameters,
reactions and compartments. To date, more than 260 software packages, including
CompuCell3D, make use of SBML. Similarly to SBML, CellML [Cuellar et al., 2003] is
an XML-based exchange format, but aims at the general description of the structure and
mathematics of cells. Apart from compartment (lumped-parameter) models, CellML
does currently not support spatial processes. The Cell Behaviour Ontology11 [Sluka
et al., 2014] describes (spatial) physical and biological processes of cells and tissues. It is,
however, not yet realised in SBML. The standard language (ontology) BioPAX [Demir
et al., 2010] focuses more on reaction network visualization and qualitative analysis.
Conversion tools, such as from BioPAX to SBML, are available [Büchel et al., 2012].
FieldML [Christie et al., 2009] is a general format for spatial models including partial
differential equations.
9
http://physiomeproject.org/software/opencmiss
http://www.sbml.org
11
http://cbo.biocomplexity.indiana.edu/
10
18
1.9. Scope and Organization of the Thesis
1.9
Scope and Organization of the Thesis
The presented thesis seeks to contribute to the advancement of modelling and simulation
methods to answer questions from developmental biology. This is achieved by studying
a specific biological system, namely the development of early long bone structures in
mice, and by developing, implementing and applying a computational tool. The topic
and scope of these studies is discussed in the following paragraphs.
In Chapter 2, a continuous tissue modelling approach has been chosen to describe a model
aiming at explaining the symmetry breaking mechanisms in early long bone development.
The initially symmetric, longitudinal and homogeneous bone primordia in the hand
plate of the developing limb undergo multiple stages of differentiation to finally form
the characteristic long bone architecture. This process comprises a symmetry-breaking
pre-patterning and the control of differentiation by a signalling network. A minimal
mechano-chemical signalling mechanism is proposed and studied on a growing domain.
Due to the massive elongation, tissue growth cannot be ignored. Since the long-term
properties of embryonic tissue resembles behaviour of fluids with high viscosity [Phillips
and Steinberg, 1978, Forgacs et al., 1998], an isotropic Newtonian fluid description is used.
Proliferation and hypertrophic cell volume increase is represented by signalling-controlled
mass sources, and rigid walls enforce longitudinal tissue growth. This simple tissue model
is sufficient to study the behaviour of the signalling model under growth conditions.
However, the development of more sophisticated, visco-elastic and anisotropic tissue
models is not within the scope of this thesis. A formulation to study multiple cell types
based on binary scalar index fields is proposed and numerically validated.
As a response to the limitations of continuous tissue models, a cell-based tissue model is
presented in Chapter 3. The objective of this part is to formulate, implement and make
publicly available one of the currently most detailed tissue models as a well-documented
and user-friendly open-source software framework. The software, called LBIBCell, natively
offers closely coupled reaction-advection-diffusion solvers, and is therefore tailored to
the needs of computational morphogenesis. Thorough numerical validations of the
mechanical and signalling aspects are required to demonstrate convergence and correct
implementation. Biophysical validations of the dynamic properties, however, are left for
future studies because specific biological questions and experimental data are needed. A
simulation example illustrates the main elements and capabilities of LBIBCell. Massive
parallelization for supercomputers and three-dimensional extensions are not within the
scope of this thesis.
In Chapter 4, the software LBIBCell is subsequently used to study the behaviour of
Turing-like receptor-ligand signalling mechanisms on growing cellular tissue. These
mechanisms are recurring motifs and relevant for a wider range of developmental systems.
The interpretation and translation of these findings to specific biological questions is left
for future research.
19
2 Continuous Approach: Application to Early Long Bone Development
In this chapter, continuous modelling techniques will be used to study their capability to
model early long bone development. The formation of embryonic long bone structures
requires a sophisticated spatial organization of cellular signalling, proliferation, and differentiation programs. Based on the reported biochemical interactions, a regulatory model
for the core signalling factors Indian Hedgehog (IHH), its receptor Patched (PTCH1),
and the extracellular protein PTHrP is developed. Two cell types, proliferating/resting chondrocytes and (pre-)hypertrophic chondrocytes, are included and represented
by scalar concentration fields. It is shown that the reported IHH-PTCH1 interaction
gives rise to a Turing mechanism, and that inclusion of PTHrP is important to achieve
robust patterning when coupling patterning and tissue dynamics. The model reproduces
relevant spatio-temporal gene expression patterns, as well as a number of relevant mutant
phenotypes. In summary, it is proposed that a ligand-receptor based Turing mechanism
may control the emergence of patterns during long bone development, with PTHrP as
an important mediator to confer patterning robustness when the sensitive Turing system
is coupled to the dynamics of a growing and differentiating tissue. In order to resolve
the disadvantages associated with the scalar cell concentration representation, an index
field-based multi-cell model is introduced.
The first section of this chapter has been published as:
Tanaka S and Iber D, Inter-dependent tissue growth and Turing patterning in a model
for long bone development, Physical Biology (2013) 10:056009
21
Chapter 2. Continuous Approach: Application to Early Long Bone
Development
2.1
2.1.1
Continuous Model of Early Long Bone Development
Introduction
Long bones develop by endochondral ossification [Kronenberg, 2003, Provot and Schipani,
2005, Wuelling and Vortkamp, 2011]. As part of the process, mesenchymal stem cells
(which are the multipotent precursors of cells involved in bone formation) aggregate in
condensations and differentiate into chondrocytes (Figure 2.1). As the bone develops,
different types of chondrocytes emerge in different parts of the condensation and express
different sets of genes. Most prominently proliferating and resting chondrocytes are found
at the ends of the bone primordium within well-defined domains, while hypertrophic
chondrocytes emerge in the center of the domain. How this spatial pattern emerges from
the regulatory interactions is so far unresolved.
Figure 2.1 – Signalling in long bone development. Hypertrophic chondrocytes secret the protein
IHH (arrow (A)1), and proliferating chondrocytes express the IHH receptor PTCH1 (gene Ptch1 ) (A2),
as well as the diffusible, extracellular protein PTHrP (gene Pthrp) (A3). IHH signalling, which results
from the binding of IHH to its receptor PTCH1, enhances PTHrP synthesis (A4). PTHrP production is
also stimulated by BMP signalling (A5). PTHrP inhibits the differentiation of proliferating chondrocytes
into hypertrophic chondrocytes (A6). The proliferation rate of the proliferating chondrocytes is enhanced
by IHH signalling (A7).
The patterning process occurs on a growing domain. Growth of the bone domain is
a consequence of both proliferation and differentiation into larger cells [Cooper et al.,
2013]. Cell differentiation into hypertrophic chondrocytes, and, at later stages, apoptosis
of hypertrophic chondrocytes and replacement by invading osteoblasts all start in the
center of the domain [Wuelling and Vortkamp, 2010, Wuelling and Vortkamp, 2011].
The core regulatory network has been defined to comprise Parathyroid hormone-related
protein (PTHrP), Indian Hedgehog (IHH), and its receptor PTCH1 [Lanske et al.,
1996, Vortkamp et al., 1996, Kronenberg, 2003]. In what follows, we use the following
convention: protein names are written all-capitalized (e.g. IHH for the protein Indian
Hedgehog), and their gene names are italicized (e.g. Ihh). Furthermore, the expression
of a gene is defined as the production rate of the protein (e.g. Ihh expression is the
production rate of IHH). IHH signalling is the event of binding of a IHH protein to its
22
2.1. Continuous Model of Early Long Bone Development
receptor (and thus triggering downstream regulatory processes) and therefore corresponds
to the concentration of the ligand-receptor complex. The abbreviated gene and protein
names are summarized in Table 2.1.
Table 2.1 – Terminology of the proteins and the associated genes.
IHH
Ihh
Ihh expression
IHH signalling
PTHrP
Pthrp
Pthrp expression
PTCH1
Ptch1
Ptch1 expression
the
the
the
the
the
the
the
the
the
the
protein Indian Hedgehog
gene encoding Indian Hedgehog
production of the protein IHH
signal PTCH12 IHH
protein parathyroid hormone-related protein
gene encoding PTHrP
production of the protein PTHrP
receptor for IHH
gene encoding PTCH1
production of the receptor PTCH1
The gene Ihh is expressed mainly by hypertrophic chondrocytes in the center of the
domain (Figure 2.1, arrow 1; abbreviated as A1 going forward), but expression of Ihh can
be detected already around embryonic day (E)10.5 (days post coitum) in the forelimb
before hypertrophic chondrocytes emerge. The gene Ptch1, which encodes the IHH
receptor PTCH1, is expressed mainly by proliferating and resting chondrocytes [Hilton
et al., 2005] (Figure 2.1, A2). The gene Pthrp is expressed by resting periarticular
chondrocytes that reside at the ends of the domain [Karp et al., 2000] (Figure 2.1,
A3). The expression of Pthrp is controlled by IHH (Figure 2.1, A4) [Vortkamp et al.,
1996, Kobayashi et al., 2005] and BMP signalling [Pateder et al., 2001, Pateder et al.,
2000, Zhang et al., 2003, Zou et al., 1997] Figure 2.1, A5). PTHrP is a diffusible,
extracellular protein that increases the pool of mitotically active (i.e. proliferating)
chondrocytes by preventing their differentiation into hypertrophic chondrocytes (Figure
2.1, A6) [Karaplis et al., 1994, Weir et al., 1996], but, unlike Hedgehog signalling, PTHrP
does not enhance their proliferation rate (Figure 2.1, A7) [Karp et al., 2000].
While the core regulatory network has been resolved, it has remained unclear how the
patterns and the spatio-temporal control of the process emerge from these interactions.
A number of mathematical models have been developed to explain the distribution of the
signalling proteins IHH and PTHrP and their impact on bone growth and development
[Bougherara et al., 2010, van Donkelaar and Huiskes, 2007, Brouwers et al., 2006, Isaksson
et al., 2008, Garzon-Alvarado et al., 2009, Garzon-Alvarado et al., 2010]. Garzon-Alvarado
and colleagues suggest a Schnakenberg-type Turing patterning mechanism based on
regulatory interactions between IHH and PTHrP [Garzon-Alvarado et al., 2009]. In
particular, they postulate that the rate of PTHrP production and IHH removal are
both proportional to the concentration of PTHrP squared times the IHH concentration
([PTHrP]2 [Ihh]). While IHH signalling indeed enhances Pthrp expression [Karsenty
et al., 2009], PTHrP signalling negatively impacts on its own expression [Kobayashi
23
Development
et al., 2005], which contradicts a key assumption of the model. Moreover, there is no
experimental evidence that PTHrP would enhance the removal of IHH; PTHrP rather
blocks Ihh production by preventing hypertrophic differentiation [Vortkamp et al., 1996]
and downregulates the action of IHH [Kobayashi et al., 2005]. The reaction kinetics in
that model are thus unlikely to reflect the physiological situation.
A Turing mechanism based on alternative molecular interactions might, however, well
underlay patterning during long bone development. To that end it was recently shown
that the interaction of the Hedgehog protein with its receptor PTCH1 together with the
signalling-dependent upregulation of Ptch1 expression can result in a Schnakenberg-type
Turing mechanism [Menshykau et al., 2012]. It was demonstrated that this mechanism
can explain the observed branching pattern in wildtype and mutant mice, and the
question arises whether a Turing mechanism based on the Hedgehog-receptor interaction
could also explain the emergence of the central-lateral organization in the early bone
primordium. Here the situation is somewhat different from the lung in that patterning
occurs on a rapidly expanding domain (the growth speed differs greatly between species
and bones [Cooper et al., 2013]), but the pattern remains stable and no further spots
(apart from the secondary growth plate) emerge on the growing domain. This is rather
unusual for a Turing pattern, and can be achieved only if feedbacks alter the Turing
parameters accordingly without losing the patterning capacity altogether. This is by no
means simple, in particular, if considering how small Turing spaces usually are.
In the bone, it is well known how growth and differentiation are controlled by the core
regulatory network, i.e. production of the signalling proteins depends on the local density
of the particular cell types which changes during long bone development as proliferating
chondrocytes concentrate at the ends of the domain and hypertrophic chondrocytes in
the center and the entire structure expands. This allowed us to study a fully coupled
growth-signalling model, while in the lung we studied only a one-way coupled model,
i.e. the growth of the domain was prescribed and impacted the signalling, but not vice
versa. The parameter space for which Turing mechanisms yield patterns is typically very
small. We therefore wondered whether a model that couples the IHH-PTCH1-based
Schnakenberg-type Turing mechanism with the underlying tissue dynamics could still
generate the observed patterns on a growing and differentiating tissue domain, i.e. the
emergence of hypertrophic chondrocytes and Ihh expression in the center of the domain,
the predominance of proliferating chondrocytes towards the sides of the domain, and the
emergence of a differentiation zone towards the center of the domain).
In addition to purely biochemical interactions, mechano-biological cues have been shown
to impact chondrocyte proliferation and differentiation, directionality of growth, and
tissue deformation of bone development [Henderson and Carter, 2002]. Furthermore,
also the mechanical properties of the surrounding perichondrium impact bone growth by
generating tension [Foolen et al., 2008]. It was shown though that the direct mechanical
impact hypothesis is not sufficient to explain growth regulation [Foolen et al., 2009].
24
Rather, signalling in periochondrial cells is regulated by tension, which in turn indirectly
impacts on bone growth [Foolen et al., 2011]. Since these mechanisms do not explain the
emergence of the central-lateral organization, and because they seem to have an external
(not coupled) impact, they are not part of our model.
In summary, based on the reported biochemical interactions we developed a regulatory
model for the core signalling factors IHH, PTCH1, and PTHrP and included two cell types,
maturing (proliferating & resting) chondrocytes as well as pre-hypertrophic chondrocytes.
We show that the IHH-PTCH1 module gives rise to a Schnakenberg-type Turing kinetics,
and that inclusion of PTHrP is important to achieve robust patterning when coupling
patterning and growth. The model reproduces all relevant spatiotemporal gene expression
patterns, as well as a number of relevant mutant phenotypes. We thus find that a ligandreceptor based Turing mechanism can control the emergence of patterns during long bone
development, and that in such a regulatory framework PTHrP is important to confer
patterning robustness.
2.1.2
Model Description
Given the central role of the IHH/PTHrP feedback loop in the regulation of endochondral
ossification we develop a minimal model that focuses on this IHH-PTHrP feedback loop
and the growth of the bone tissue by local proliferation and differentiation (Fig. 1A).
We include three signalling proteins, IHH (symbol for the dimensional concentration
[I], units mol/m3 ), its receptor PTCH1 (symbol for the dimensional concentration
[R], units mol/m3 ), and PTHrP (symbol for the dimensional concentration [P], units
mol/m3 ) and two cell types, proliferating chondrocytes (symbol for the dimensional
cell concentration [C], units mol/m3 ) and hypertrophic chondrocytes (symbol for the
dimensional cell concentration [H], units mol/m3 ). We describe the dynamics of the
regulatory signalling proteins and the two cell types, Xi , with a set of coupled partial
differential equations (PDE) of isotropic advection-reaction-dispersion type, i.e.
∂t [Xi ]
| {z }
time derivative
+
∇ · ([Xi ]u)
|
{z
}
dilution & advection
= DXi ∆[Xi ] + R ([Xj ]) ,
|
{z
diffusion
}
|
{z
(2.1)
}
reaction
where [Xi ] denotes the concentration of Xi , ∂t the time derivative, u denotes the external
velocity field (units [m/s]), DXi represents the diffusion coefficient of component Xi
(units m2 /s ), ∆ denotes the Laplace operator, and R([Xj ]) represents the reaction
terms (units mol/ s · m3 ) that will be derived. The term ∇ · ([Xi ]u) models the effects
of dilution and advection as the tissue grows. The square brackets and overscores denote
dimensional variables and operators. We model tissue as an incompressible fluid and
describe tissue growth with a Navier-Stokes equation where the source term depends on
the proliferation and differentiation signals. In the following we describe the details of
the model.
25
Development
Figure 2.2 – Modeled long bone development. Proliferating chondrocytes C, (shown in red)
proliferate or differentiate into hypertrophic chondrocytes H (shown in blue). H express the secreted
protein Indian Hedgehog IHH (symbol I), and C its receptor PTCH (R). PTCH and IHH form a complex
(symbol R2 I) and trigger processes controlling differentiation (C → H). Panel (A) and (B) illustrate
two different regulatory hypotheses: in (A), the inhibitory effect of IHH signalling is directly affecting
differentiation (The Directly Coupled Model), whereas in (B) the IHH signalling leads to production
of a hypothetical paracrine factor P that prevents differentiation (The Indirectly Coupled Model). (C )
Deforming tissue growth. Proliferating chondrocytes C (shown in red) divide, which is modeled as a local
mass source Sprol (left path). As a result of hypertrophic differentiation, the cells increase in volume and
lead to a local mass source Sdiff (right path). Both mechanisms induce a velocity field u in the fluid,
whose internal boundary is passively advected.
Tissue dynamics. The developing bone structure grows as a result of cell proliferation
and differentiation. Proliferating chondrocytes are small in size but expand rapidly while
the cell volume of hypertrophic chondrocytes is 4-fold larger than that of resting or
proliferating chondrocytes. The cell density for the two populations is thus different.
Any expansion of these populations in number must thus translate into an expansion of
the domain.
The mechanical response of embryonic tissue corresponds to an elastic solid for high
frequency perturbations. On a long time scale, on the other hand, the tissue behaves
26
like a viscous fluid, or shows active behavior [Phillips and Steinberg, 1978]. One possible
explanation might be that even when assuming an elastic material, active reorganization
of the tissue (proliferation, apoptosis, local cellular rearrangements) leads to a fluidization
of the tissue [Ranft et al., 2010]. As a result, a wide range of vertebrate (early) embryonic
tissue has previously been shown to be well described by an immiscible viscous fluid on a
long time scale [Forgacs et al., 1998]. We therefore model the mechanical behaviour of the
tissue by introducing an incompressible Newtonian fluid with density ρ (units kg/m3 ),
dynamic viscosity µ (units [kg/ (s · m)]) and local molar source S (units mol/ s · m3 ).
The tissue growth model is summarized in Figure 2.2. This model has been applied to
early vertebrate limb development simulations [Dillon et al., 2003] and, in an extended
anisotropic formulation, to Drosophila imaginal disc development [Bittig et al., 2008].
The Navier-Stokes equation is given as:
1 ρ∂t u = −∇p + µ ∆u + ∇ ∇ · u
3
ρ ∇·u
(2.2)
= ωS ,
(2.3)
where p denotes the scalar fluid pressure field (units kg/ m · s2 ), and ωS = ω(S prol +
S diff ) denotes the local mass production rate, which is composed of contributions from
proliferation and increase in cell volume (hypertrophic differentiation). Assuming dominance of viscous dissipation, we ignored inertial heffects
i (creeping flow). ω is the cellular
kg
mass of proliferating chondrocytes, measured in mol . For simplicity we did not include
Hedghog regulation of chondrocyte proliferation explicitly because its inclusion did not
affect the wildtype patterning process in the model. Proliferating chondrocytes thus
proliferate at a constant rate ϕ, i.e.
S prol = ϕ[C] .
(2.4)
Tissue growth by differentiation into hypertrophic chondrocytes is described by:
S diff = (Φ − 1) Rdiff [C] ,
(2.5)
where Φ reflects the Φ-fold higher volume of hypertrophic chondrocytes compared to
proliferating chondrocytes and Rdiff , as defined in Equation (2.15), is the rate of cell
differentiation.
The interface between the chondrogenic and surrounding tissue is modeled as a passively
advected boundary. Its position, together with the velocity field u, is coupled to the
morphogen dynamics as described in Equation (2.1).
The perichondrial bone collar embraces the central anlage, mainly next to the hypertrophic
chondrocytes [Kronenberg, 2003, Horton and Degnin, 2009]. The ’Directed Dilation’
27
Development
hypothesis [Wolpert, 1981, Wolpert, 1982] states that the perichondrial collar exerts
tension and pressure in such a way that radial growth is restricted and the primordium
is forced to grow in longitudinal direction. Therefore, we mimicked the circumferential
perichondrium as a tube with rigid walls, which forces the tissue to grow in longitudinal
direction. The length of the tube is chosen so as to permit an about sixfold increase in
length as observed in nature [Schipani and Provot, 2003]. When reaching the ends of the
bone collar tube, the tissue forms the characteristic rounded epiphyseal cartilage. Since
the bone collar tube is fixed, it is a non-coupled feature in the model.
The reaction kinetics. The ligand IHH binds to at least two PTCH1 receptors and
forms a multimer [Goetz et al., 2006]. We therefore use as rate of complex formation
kon [I][R]2 (kon having units m6 / mol2 · s ) and koff [R2 I] (koff having units [1/s]) as
rate of dissociation. Ihh is expressed by pre-hypertrophic chondrocytes [H] [Bitgood and
McMahon, 1995, Vortkamp et al., 1996], and we therefore write for the production rate
ρI [H] (ρI measured in [1/s]). Moreover, we expect that as for other ligands receptorindependent decay of IHH is negligible and we therefore do not include an explicit decay
reaction. We then have for the reaction term:
R([I]) =
ρI [H]
− k on [R]2 [I] + k off [R2 I] .
| {z }
|
production
{z
complex formation
(2.6)
}
The expression of the gene Ptch1 is enhanced by IHH signalling [St-Jacques et al., 1999],
and the rate of Ptch1 expression must therefore be a function of the concentration of
the complex, i.e. f ([R2 I]). We will use a linear approximation as the simplest possible
relation for the receptor production rate f ([R2 I]), and write f ([R2 I]) = ρR [C] + v[R2 I],
where ρR [C] and v are zero and first order rate constants, respectively. Both ρR and
v are measured in [1/s]. This linear approximation implies that we assume that the
concentration of the IHH-PTCH1 complex is much lower than the signalling threshold
(Hill constant K) of a potential cooperative Hill-type regulation of the upregulation
2 I]
of Ptch1 expression, i.e. [R[R
∼ [R2 I]. Unbound PTCH1 is removed by complex
2 I]+K
formation and restored by its dissociation. In the absence of contrary experimental
evidence we will further assume linear decay of PTCH1 at rate δ R [R]. Moreover, since
Ptch1 is expressed only on the resting and proliferating, but not on the hypertrophic
chondrocytes, PTCH1 will also be lost as a result of cell differentiation at rate Rdiff
(having units [1/s]), which will be defined later in Equation (2.15). The spatio-temporal
dynamics of free PTCH1 can then be described by
R([R]) = ρR [C] + ν[R2 I] −(δ R + Rdiff )[R] −2 kon [R]2 [I] + k off [R2 I] .
|
28
{z
production
}|
{z
loss
}|
{z
complex formation
}
(2.7)
The dynamics of the complex [R2 I] is then described by
R([R2 I]) = kon [R]2 [I] − k off [R2 I] −δ R2 I [R2 I] ,
|
{z
complex formation
}|
{z
(2.8)
}
degradation
where the complex is assumed to be degraded at rate δ R2 I [R2 I].
This set of equation corresponds to the classical Schnakenberg Turing model if we make
a quasi-steady state approximation for the binding of IHH and PTCH1, while assuming
that the diffusion of the membrane-bound IHH-PTCH1 complex is slow compared to its
binding and turn-over kinetics. The quasi-steady state concentration of bound receptor,
[R2 I], is then proportional to [R]2 [I], i.e.
[R2 I]SS =
k on
[R]2 [I] = Γ[R]2 [I]
k off + δ R2 I
with
Γ=
k on
.
k off + δ R2 I
Consequently, the following equations for the ligand IHH and for the receptor PTCH1
are obtained:
R([I]) = ρI [H] + (k off Γ − k on )[R]2 [I]
R([R]) = ρR [C] − (δ R + Rdiff )[R] + ((k off + ν) Γ − 2 k on )[R]2 [I] .
(2.9)
The gene Pthrp is expressed by non-hypertrophic resting or proliferating chondrocytes
[C] in response to signalling of the IHH-PTCH1 complex R2 I [Karsenty et al., 2009].
For simplicity, we use a Heaviside function, H (·), to implement the threshold response
of Pthrp expression to IHH signalling. [P ] is produced when the complex concentration
[R]2 [I] drops below the threshold θP . The reaction term for the protein PTHrP [P] then
reads:
R([P]) = ρP H [R]2 [I] − θP [C] − δ P [P]
with
H (x) =

0
if x < 0
1
if x ≥ 1
.
(2.10)
Cell dynamics. Both proliferating chondrocytes [C] and pre-hypertrophic chondrocytes
[H] are represented as cell number densities and obey Equation
(2.1). The dilution term
for a component X in Equation (2.1) is given by [X] ∇ · u . The divergence of the
velocity field is composed of the contributions of proliferation and differentiation:
∇·u=
ω
ω
S prol + S diff =
ϕ + (Φ − 1) Rdiff [C] ,
ρ
ρ
(2.11)
29
Development
where ϕ, measured in [1/s], represents the constant proliferation rate (c.f. Equation (2.4)).
Proliferating chondrocytes differentiate at rate Rdiff into hypertrophic chondrocytes.
Upon proliferation, the cell density of the proliferative chondrocytes [C] increases with
the rate ω/ρS prol . The equations then read:
R ([C]) = −Rdiff [C] +
ω
S prol [C]
ρ
(2.12)
R ([H]) = ΦRdiff [C] .
(2.13)
The diffusion constants of the cells are small and equal, i.e. DC = DH = Dcell . With
Equation (2.4), the following partial differential equations are obtained:
∂t [C] + ∇ · ([C]u) = Dcell ∆[C] − Rdiff [C] +
ω
ϕ[C]2
ρ
∂t [H] + ∇ · ([H]u) = Dcell ∆[H] + ΦRdiff [C] .
(2.14)
Here, two different models of cell differentiation are studied. In the simpler model there
is a direct coupling between IHH signalling and cell differentiation. In the second model
cell differentiation is controlled by the protein PTHrP which in turn is regulated by
IHH signalling (i.e. by [R]2 [I]). For the directly coupled model (index d), the local
differentiation sets in when the local IHH signalling R2 I deceeds the threshold θd . The
indirectly coupled model (index i), on the other hand, leads to differentiation once
PTHrP, P, falls below the threshold θi :
d
i
Rdiff
Rdiff = δ H θd − [R]2 [I]
= δ H θi − [P] .
(2.15a)
(2.15b)
Here δ̄ denotes the differentiation rate; H (·) denotes the Heaviside function.
Boundary conditions. Indian Hedgehog [I] can diffuse freely into the tissue that
surrounds the nascent bone domain, e.g. the limb. The surrounding tissue is of finite
size Ldomain , and zero-flux boundary conditions are applied for [I] at the edge of the
surrounding domain. PTCH1 [R], PTHrP [P], and the cells [C] and [H], are restricted to
the chondrogenic tissue of length Lbone , i.e. zero-flux boundary conditions n · ∇[X] = 0
are applied to [R], [P], [C] and [H]. In case of the receptor PTCH1 this reflects its
membrane-bound state. In case of PTHrP this is a good approximation given its low
diffusion coefficient.
30
Parameter values. The measurement of the parameter values (i.e. diffusion coefficients,
production and degradation rates) in vivo is complicated and has only been carried
out in few model systems, but not in the developing bone [Kicheva et al., 2007, Yu
et al., 2009, Ries et al., 2009]. However, our conclusions do not depend on the exact
values of parameters, but mainly depend on their relative values as can be seen by
non-dimensionalizing the model. To non-dimensionalize the model we need to choose
characteristic length and time scales, as well as characteristic concentrations. As characteristic time scale we use T . Accordingly we have to rescale our dimensional time t
into its non-dimensional counterpart t, i.e. t = T t. As characteristic length scale we
use L. Accordingly we have to rescale our dimensional spatial coordinates xi into their
non-dimensional counterparts xi , i.e. xi = Lxi , and similar for the velocity field u = u TL .
We non-dimensionalize the Ihh, Ptch1, and PTHrP concentrations with respect to their
characteristic concentrations, i.e. I = [I]/I0 , R = [R]/R0 , and P = [P]/P0 . Similarly for
the cells we use the characteristic densities, i.e. C = [C]/C0 , H = [H]/H0 .
The non-dimensional parameters are obtained by non-dimensionalizing with the respective
scales, i.e. δ = T δ. The equations can be further simplified by choosing appropriate
scales and by combining parameter combinations into new composite parameters. Thus
2
we write for the characteristic time scale T = DL . This choice of time scale leads to the
R
classic Schnakenberg equations with the diffusion coefficient of the
q slowly diffusing factor
being equal to 1. The characteristic length scale is set to L = γDR /δ R with the nondimensional scaling factor γ = T δ R =
L2 δ R
.
DR
The fluid pressure p is non-dimensionalized
2
µ
T p.
as p =
The dimensionless Reynolds-number Re = ρL
µT is a measure for the relative
importance
rof inertia over viscous effects. For the characteristic protein concentrations we
use R0 =
δR
,I
kon −koff Γ 0
=
cell densities we set C0 =
δR
1
R0 2 kon −(koff +ν) Γ ,
H0 = ωρ .
and P0 =
ρP
.
δR
Finally for the characteristic
DI
DP
, DP = D
,
DR
R
ϕ
Dcell = DDcell , the differentiation rate δ = δδ , the proliferation rate ϕ = δ , and the
R
R
R
ρI H0
ρR
θd
θP
production rates ρI = δ I0 , ρR = δ̄ R , and the thresholds θP = R2 I , θd = R2 I , θi = Pθi0
R 0
R
0 0
0 0
As composite parameters, the non-dimensional diffusion constants DI =
are obtained. The non-dimensional model reads:
∂t I + ∇ · (Iu) = DI ∆I + γ ρI H − R2 I
∂t R + ∇ · (Ru) = ∆R + γ ρR C − (1 + Rdiff ) R + R2 I
∂t P + ∇ · (Pu) = DP ∆P + γ H R2 I − θP C − δP P
∂t C + ∇ · (Cu) = Dcell ∆C − γ Rdiff C + γϕC2
∂t H + ∇ · (Hu) = Dcell ∆H + γΦRdiff C
(2.16)
31
Development
d
Rdiff
= δH θd − R2 I
(2.17a)
i
Rdiff
= δH (θi − P)
(2.17b)
1
Re∂t u = −∇p + ∆u + ∇ (∇ · u)
3
∇ · u = γ((Φ − 1) Rdiff + ϕ)C .
(2.18a)
(2.18b)
The dimensionless model contains seven parameters less than the dimensional one and the
patterning mechanism no longer depends on absolute diffusion and decay constants, but
only on the relative diffusion coefficients and the relative decay rates. Similarly, the absolute protein concentrations do not matter but only the relative concentrations (as a result
from the relative expression and decay rates) relative to the threshold concentrations.
The non-dimensional parameter values are given in Table 2.2 and lie within the Turing
space. Here a 10-fold higher diffusion rate for the ligand I than for its receptor R is used,
which is in good agreement with experimental observations [Kumar et al., 2010, Hebert
et al., 2005, Kicheva and González-Gaitán, 2008, Swaminathan et al., 1997, Yu et al.,
2009]. Moreover, the proliferation and differentiation rate are set equal in the model and
are likely to be of similar order of magnitude in reality. The production rates are difficult
to compare, given the different normalizations, and depend on the signalling thresholds
θ.
Initial values. The initial values of all components are summarized in Table 2.2. Zero
concentration for I is used, though also non-zero concentrations could be used without
affecting the pattern. The initial P concentration is chosen such that differentiation is
blocked initially. P is degraded and diluted due to the expansion of the primordium,
such that differentiation begins at later times when the P concentration has dropped
below the critical concentration at which it prevents a cell from differentiating. Additionally to the initial P concentration, the influx of maternal P may support the initial
inhibition of differentiation. PTCH1 is internalized constitutively and can be visualized
at the cell surface only by blocking or significantly delaying its internalization [Incardona
et al., 2000]. Although PTCH1 is not detected at significant levels on the cell surface at
steady state, even these low levels rapidly remove IHH from the cell surface [Incardona
et al., 2000], presumably through rapid cycling at rate. Therefore, a non-dimensional
concentration of one as initial condition is used.
Initially there are mainly proliferating chondrocytes in the digit primordia, and therefore
nondimensional cell densities C0 = 0.9 and H0 = 0.1 for proliferating and hypertrophic
chondrocytes are used, respectively.
32
Table 2.2 – Parameter values used for the model. The indices d and i refer to the directly and indirectly
coupled model, respectively. All the other parameters are the same for all three models.
Ldomain
γ
DI
DP
Dcell
ϕ
δ
Φ
ρI
ρR
δP
θP
θd
θi
I0
R0
P0
C0
H0
Lbone (t = 0)
Wbone (t = 0)
20
100
10
0.01
0.001
0.0005
0.05
4
10
0.1
0.001
1
0.02
30
0
1
1000
0.9
0.1
1
2/5
size of bounding box
scaling factor
diffusion coefficients
proliferation rate
differentiation rate
volume ratio H/C
production rates
decay rate
threshold for P production
threshold for differentiation
uniform initial values
initial bone domain length
initial bone domain width
The chondrogenic tissue of initial non-dimensional length Lbone (t = 0) = 1 and width 0.4
is placed in the center of a square of non-dimensional size Ldomain = 20, representing the
surrounding tissue.
Comparison of model parameter values to measured values. The parameter
values can in part be compared to experimental values by converting these to their
dimensional counterparts based on the established length and developmental time scales.
Concentration ranges, on the other hand, have not been determined experimentally.
The growth speed differs between bones. Murine embryonic tibia bones measure about 1
mm at embryonic day 14 and grow by about 250 µm between embryonic day 14 and 15,
and faster thereafter [Blakley, 1979]. Chicken femurs measure about 5 mm at embryonic
day 10 and grow by about 1 mm until day 11 and take about 2.5 days to double in
length[Kanczler et al., 2012]. Thus in both embryos the growth accelerates, but this
acceleration appears to be mainly driven by ossification in the center, and would thus
not apply to our model which focuses on an earlier process. Since we did not find any
data for this earlier growth process we will use the earliest known growth rates. In
the simulation, the tissue grows about two-fold in the interval t = [0, 20] which would
33
Development
correspond to about 4 days in case of the murine measurements and 5 days in case of the
chicken. t = 1 thus corresponds to t = 5 [days] = 18000 [s] and the characteristic time
scale is thus T ≈ 18000 [s]. We then have δ R = γ/T ≈ 5.6 × 10−3 s−1 which is some
100-fold higher than the typical ligand-independent receptor turn-over rates that have
been measured for other receptor systems (in the order of 5 × 10−5 s−1 ) [Eden et al.,
2011, Lloyd and Ascoli, 1983, Valley et al., 2008, Woods et al., 1989, Ginsburg et al.,
1998, Singh et al., 2001] and almost 10-fold higher than the ligand-induced Dpp receptor
turn-over rate (5 × 10−4 s−1 ) [Mizutani et al., 2005]. While this may appear high, Ptch
is well known to be internalized constitutively at a rather high rate such that blockage
of internalization greatly increases its membrane concentration [Incardona et al., 2000].
Besides the embryonic growth rate may well be lower initially which would correspond
to a lower value for δ R .
q
The characteristic length is L = T DR . The diffusion coefficient for membrane receptors
is in the range D = 0.001 . . . 0.1 µm2 s−1 [Kumar et al., 2010, Hebert et al., 2005].
Using the upper value of DR = 0.1 µm2 s−1 we obtain as characteristic length scale
L = 42 [µm]. The initial non-dimensional length of the simulated bone structure is
Lbone (t = 0) = 1 which then corresponds to 42 [µm] and may well reflect the initial
size of the mesenchymal condensations from which the bone forms by endochondral
ossification. Again if the embryonic growth rate was lower initially this would correspond
to larger size of the initial mesenchymal condensations. For the other diffusion coefficients
we would have DI = 10 × DR = 1 µm2 s−1 which is well within the physiological range
for soluble proteins such as Dpp and Wg in the wing disc, if somewhat on the high end
[Kicheva and González-Gaitán, 2008, Swaminathan et al., 1997, Yu et al., 2009]. Finally,
for PTHrP we have DP = 0.01 × DR = 0.001 µm2 s−1 which implies that PTHrP has
to diffuse rather poorly for the patterning mechanism to work. This restriction could be
removed by introducing the PTH/PTHrP receptor as a further variable. For the sake of
parsimony we refrain from doing this.
The dynamic viscosity of tissue is known to be approximately µ ≈ 104 [P a · s] [Forgacs
et al., 1998], some 107 -fold higher than for water, and the mass density of the tissue is
2
−14 and is virtually
ρ ≈ 1000 kg/m3 . The Reynolds number computes as Re = ρL
µT ≈ 10
zero. As expected, the inertial effects are neglectably small (Stokes regime) and the
terms on the left hand side of Equation (2.18) can therefore be omitted.
Simulation. The PDE’s are solved with finite element methods as implemented in COMSOL Multiphysics 4.3a. COMSOL Multiphysics is a well-established software package
and several studies confirm that COMSOL provides accurate solutions to reactiondiffusion equations both on constant[Cutress et al., 2010] and growing two-dimensional
domains[Carin, 2006, Thummler and Weddemann, 2007, Weddemann and Thummler,
2008, Germann et al., 2011, Menshykau and Iber, 2012]. The mesh and the time step
were refined until further refinement no longer resulted in noticeable improvements as
judged by eye.
34
For Equations (2.16), the Coefficient Form PDE module with Zero Flux boundary
conditions have been used both for the moving boundary and the boundary of the
outer domain. The dilution Xi (∇ · u) term is taken as a right hand side contribution
f = −Xi S.
To solve Equations (2.18), namely Equation (2.18b), a local mass source is added to the
weak expressions of the Creeping Flow module. The inertia terms in Equation (2.2) are
omitted, as well as µ/3∇ (∇ · u), since these terms are negligible for sets of parameters
used in this study.
The Moving Mesh ALE module is applied to the mesh. The moving boundary’s mesh
velocity is set to the local fluid velocity, and Prescribed Mesh Displacement was used
for the bone collar. The Heaviside function H (·) is smoothed sigmoidally in the interval
[−0.05, 0.05].
2.1.3
Results
In a first step, the signalling network is solved on a constantly growing domain, where only
proliferation is considered (referred to as the prescribed growth model). It is demonstrated
that the Turing pattern has the potential to control the central-lateral organization on
a growing domain. In a second model, differentiation is directly regulated by the level
of IHH signalling (referred to as the directly coupled model, see Figure 2.2 (A)). It is
found that the direct impact of the Turing system on differentiation leads to volatility in
the patterning. In a final model, differentiation is indirectly controlled via the level of
a paracrine factor that inhibits cell differentiation, and which in turn is controlled by
the level of IHH signalling (referred to as the indirectly coupled model, see Figure 2.2
(B)). This factor can be interpreted as PTHrP. By introducing this additional integrator
stability is retrieved and all experimentally observed patterns under wildtype and mutant
conditions are reproduced.
Patterning on a Bone Tissue that expands according to a Prescribed Overall
Growth Rate
The first question is whether the signalling mechanism could at all result in the experimentally observed patterning. To avoid the complication of the feedbacks between
patterning and tissue growth the signalling system is first solved on a constantly growing
domain, i.e. without IHH signalling affecting growth and differentiation (and thus the
local mass source S). There is thus no spatially varying feedback on the production
as would arise from the (here ignored) cell differentiation; the pattern thus evolves for
constant (Turing) parameter values. Growth is prescribed by a function. In a first study
linear growth is analysed, and the local proliferation rate must therefore decreases as the
35
Development
total area A (t) of the tissue increases, i.e.
Sprol (t) = γϕ
A (t = 0)
C.
A (t)
(2.19)
The overall growth rate of the domain is then constant, corresponding to an approximately
constant growth speed of the long bone. This is equivalent to a growth rate proportional
to a passively advected and diluted compound. To capture the experimental growth
pattern [Schipani and Provot, 2003] we adjusted the length of the bone collar tube such
that the domain would grow about fourfold longitudinally before growing radially to
form the epiphysis. Growth in width is minor and can be controlled by the distance of
the bone collar to the chondrogenic tissue.
Figure 2.3 (A) shows the initial domain at t = 0. The other panels in Figure 2.3 (B-E)
show how the patterns of various components evolve over time (until t = 40) along the
midline that is indicated in Figure 2.3 (A). Focus has been laid on the pattern in the
middle of the domain because most pattern changes occur along the length of the domain,
while the pattern is relatively stable and uniform along the width of the domain.
Thus Figure 2.3 (B) shows the concentration of the signalling complex R2 I on the
midline. The Turing patterning mechanism, based on the interaction between I and
R, results in spatial patterns as the domain reaches a critical size at t ≈ 17.7, and R2 I
concentrates at the edges of the domain (Figure 2.3 (B)). This is consistent with the
experimental observation that IHH signalling induces Pthrp expression in that part of
the domain. IHH signalling (R2 I) is present throughout the domain, though at a much
lower concentration. This would explain the observed impact of IHH signalling on the
proliferation of chondrocytes.
The Turing pattern emerges at time t ≈ 19.7 and stays stable until t ≈ 23.1, when a
pattern inversion occurs (Figure 2.3 (B)) and high IHH signalling also emerges in the
centre of the domain. However, at that stage many additional processes have already
started (most importantly the invasion of osteoblasts and ossification) that affect the
patterning and that are not part of our model which focuses on the initial patterning
events. At later times t ≈ 35.2 the high IHH signalling reappears at the ends. Whenever
IHH signalling is absent or low for long times, the initially nonzero PTHrP concentration
decreases and finally drops below the threshold where proliferating chondrocytes start
to differentiate. This occurs at time t ≈ 22.9 − 23.1 (central differentiation) and
t ≈ 34.7 − 36.3 (lateral differentiation; c.f. Figure 2.3 (E)). As a result proliferation (and
resting) chondrocytes (pC) are reduced in the center of the domain (Figure 2.3 (C ))
and hypertrophic chondrocytes emerge (Figure 2.3 (D)). The transition between the two
populations are sharper in the embryo, but overall the signalling mechanism appears to
produce realistic patterns with the linear prescribed domain growth.
36
Figure 2.3 – The prescribed growth model. (A) The initial geometry of the chondrogenic tissue
together with the growth restricting walls. (B-E) The local growth rate is spatially uniform and decreases
reciprocally proportional to the area of the chondrogenic tissue, leading to linear elongation of the domain.
(B) The concentration levels of R2 I at the ends emerge at t ≈ 19.7 and stay stable until t ≈ 23.1. Then
IHH signalling increases in the middle, where Ihh expressing hypertrophic chondrocytes accumulate.
Upon epiphyseal differentiation at time t ≈ 35.2, high IHH signalling reappears at the ends. (C-D) The
concentrations of proliferative and hypertrophic chondrocytes are close to complementary. (E) The
differentiation rate leads to high hypertrophic differentiation in the center of the domain at time t ≈ 22.9,
and at the ends at time t ≈ 34.7. (F-J ) The local growth rate is spatially uniform and constant, leading
to exponential elongation. (F ) The complex concentration at t = 40. The midline concentration is also
depicted in (G). (G) Additional modes appear at time t ≈ 34.1 in the complex concentration. (H-J )
The additional modes in the complex concentration are reflected in the cell concentrations (H-I ) and
the differentiation rate (J ). The initial values are uniformly zero for R2 I and the differentiation rate,
uniformly 0.9 for C, and uniformly 0.1 for H (c.f. Table 2.2).
37
Development
We also analysed pattern formation on an exponentially growing domain, i.e.
Sprol (t) = γϕC.
(2.20)
An example of the geometry at a later time point (t = 40) is shown in Figure 2.3 (F ). In
the initial phase we observe similar patterning dynamics as with linear growth because
the growth rate is small and in the same range. At later stages the growth speed increases
significantly, leading to different dynamics of the Turing system. It is known from the
analysis of Turing models on exponentially growing domains that the number of spots
correlates with the size of the domain [Crampin et al., 1999]. This property is also
found on our dynamically growing domain (Figure 2.3(F-G)). Interestingly, the emerging
patterns are not evenly spaced.
Direct Coupling of Turing Patterns and Growth result in Pattern Instability
We next solved a model in which growth and patterning are directly coupled via signalling
d
of the IHH-receptor complex. The differentiation rate Rdiff
is now directly controlled by
2
R I (Equation (2.17a)).
Since the signal R2 I is zero at the beginning, differentiation occurs immediately and
leads to a spatially homogeneous loss of the proliferating chondrocytes and an accumulation of hypertrophic chondrocytes, respectively (Figure 2.4 (C-E)). The hypertrophic
chondrocytes start to express Ihh, which, in turn, activates its signalling pathway. The
Turing pattern emerges at t ≈ 0.4, but cannot rescue a spatial organization any more
due to the high levels of Ihh expression. Due to the uniformly inhibited differentiation,
the hypertrophic chondrocyte population is only diluted as a result of proliferation. At
time t ≈ 22.8, the radial symmetry is lost and the Turing system does not lead to the
correct cellular organization any more.
The high sensitivity on initial values of this model is another feature arguing against its
biological relevance. Figure 2.4 (F-J ) show the same simulation as shown in Figure 2.4
(A-E), but with slightly disturbed initial cell concentrations (uniform distribution with
mean 1 and range 0.05). Although the initial system dynamics is stable, the perturbations
of the initial conditions lead to different solutions at later stages as shown in Figure 2.4
(A) and (F ). This behaviour is a strong indication for implausibility of the model.
As expected for a Turing pattern, the length of the bone primordium determines the
number of spots (or modes) (Figure 2.4), i.e. the distance between each two spots cannot
exceed a certain length, otherwise a new spot emerges in between. The patterning
dynamics are very fast because diffusion and reactive turnover dominate over advective
transport for our choice of parameters. This pattern transition behaviour conforms to
the well studied Turing system behaviour on domains with prescribed growth [Crampin
et al., 1999].
38
Figure 2.4 – The directly coupled model. (A-E) and (F-J ) show the same simulations with noisy
initial cell concentrations. (B) The domain grows exponentially. The radial symmetry of IHH signalling
is lost at t ≈ 22.8. (C-D) The proliferative chondrocytes differentiate into hypertrophic chondrocytes at
the beginning; the domain is subsequently expanded by proliferation. (E) Differentiation is high at t = 0
and zero otherwise. (G-J ) The results are similar for different noisy initial conditions, but the Turing
system cannot deterministically pattern the chondrogenic domain. The initial values are uniformly zero
for R2 I and the differentiation rate, uniformly 0.9 for C, and uniformly 0.1 for H (c.f. Table 2.2).
39
Development
Stable Patterning with an Indirect Coupling of Patterning and Growth
Instead of the IHH-PTCH1 complex R2 I, controlling differentiation directly, we now
introduce PTHrP production by proliferative chondrocytes P, as an intermediator. The
IHH-PTCH1 complex R2 I, induces expression of this intermediator P, which can diffuse
i
and prevents differentiation into hypertrophic chondrocytes as described by Rdiff
in
Equation (2.17b).
The IHH-PTCH1 complex R2 I, emerges at time t ≈ 17.7 and stays stable until t ≈ 24.9
(Figure 2.5 (A)). The complex accumulates at the ends of the domain, which triggers
expression of Pthrp (Figure 2.5 (B)). As the pattern changes at time t ≈ 24.9, Pthrp
expression moves slightly towards the center of the domain as indeed observed in the
embryo. While PTHrP accumulates at the ends, where it prevents differentiation into
hypertrophic chondrocytes, it is further degraded in the centre of the domain, and finally
drops below the threshold of differentiation inhibition (Figure 2.5 (C )). Differentiation
starts at time t ≈ 24.9 (Figure 2.5 (D)) and leads to fast transition of proliferating into
hypertrophic chondrocytes (Figure 2.5 E-F) and therefore to high growth rates. The
high Ihh expression by (pre-)hypertrophic chondrocytes in the centre (cf. Figure 2.5
(G)) subsequently leads to high IHH signalling (2.5 (A)), since the residual proliferating
chondrocytes are still able to express Ptch1 at high levels.
Experiments also reveal the IHH-dependent expression of Ptch1 adjacent to the Ihhexpressing domain in the center [St-Jacques et al., 1999]. This pattern has so far been
counterintuitive given that IHH signalling induces Pthrp expression at the very ends of
the domain. In the model the rate of Ptch1 expression is given by ρR [C] + ν[R2 I] where
the first term captures the constitutive expression and the second term the effect of the
signalling-dependent positive feedback. If the signal-induced Ptch1 production is much
smaller than the generation of PTCH1 by ligand-unbinding and recycling (i.e. ν k off )
then we indeed observe Ptch1 expression adjacent to the Ihh expressing domain (Figure
2.5 (H )). There is indeed good experimental evidence for strong PTCH1 recycling which
would correspond to the large k off [Incardona et al., 2000].
In order to avoid very high IHH signalling at places where the proliferative chondrocyte density is very low, we introduced a threshold on IHH signalling-induced
Ptch1 expression by proliferating chondrocytes (Figure 2.6). The expression term
reads γ ρR C + R2 IH (C − 0.05) , where the threshold value 0.05 is chosen such that the
Ptch1 expression is largely removed from the center of the domain. As a result, the
IHH signalling is restricted to the transition zone between proliferative and hypertrophic
chondrocytes (Figure 2.6 (A)), and so is the Ptch1 expression (Figure 2.6 (H )). The
Pthrp expression (Figure 2.6 B), differentiation pattern (Figure 2.6 (D)), cell organization
(Figure 2.6 (E-F )) and Ihh epxression (Figure 2.6 (G)) are only marginally affected.
With the domain growing further, the IHH signalling decreases at the ends and differenti40
Figure 2.5 – The indirectly coupled model. (A) The complex accumulates at the ends between
time t ≈ 17.7 and t ≈ 24.9. The IHH signalling upregulates significantly upon differentiation in the center
at time t ≈ 24.9 and at the ends at time t ≈ 37.7. (E) Proliferating chondrocytes express Pthrp at high
levels of IHH signalling. (C ) Pthrp expression leads to local accumulation of PTHrP, which inhibits cell
differentiation. (D) At locations where PTHrP concentration is low, proliferative chondrocytes (shown
in (E)) differentiate into hypertrophic chondrocytes (shown in (F )). The increase of cell volume causes
accelerated longitudinal growth. Although the conditions in the center always allow differentiation for
t > 24.9, the majority of proliferative chondrocytes differentiate in a short time span. (G) Hypertrophic
chondrocytes express Ihh, which leads to high levels of IHH signalling (cf. (A)) (H ) Ptch expression is
positively upregulated at locations of high IHH signalling. The initial values are uniformly zero for R2 I,
P expression and the differentiation rate, uniformly 1000 for P, uniformly 0.9 for C, uniformly 0.1 for H,
uniformly γρI H0 and γρR C0 for I and R expression, respectively (c.f. Table 2.2).
ation - analogously to the central differentiation - begins at time t ≈ 37.7. Again, the high
differentiation rate leads to a high growth speed, resulting in bulged structures mimicking
the epiphyses. The accumulation of hypertrophic chondrocytes can be interpreted as
the secondary ossification centers. The hypertrophic chondrocytes at the tips produce
Ihh, leading to a significant upregulation of IHH signalling (Figure 2.6 (A)) and Ptch1
expression (Figure 2.6 (H )). We note, however, that this model may not be adequate to
describe the processes in the epiphysis. The here described patterning corresponds to a
first phase during endochondral ossification. In a second phase apoptosis of hypertrophic
41
Development
Figure 2.6 – The indirectly coupled model with a threshold on Ptch production. Ptch is
not expressed any more when the concentration of proliferating chondrocytes is negligible. (A) IHH
signalling is only high in transition zones, although Ihh is expressed at high levels in the center. (B-G) The
introduced threshold does not significantly affect Pthrp and Ihh expression, PTHrP and cell differentiation.
(H ) Ptch expression is only upregulated at locations of high IHH signalling (cf. (A)) The initial values are
uniformly zero for R2 I, P expression and the differentiation rate, uniformly 1000 for P, uniformly 0.9 for
C, uniformly 0.1 for H, uniformly γρI H0 and γρR C0 for I and R expression, respectively (c.f. Table 2.2).
chondrocytes and invasion of osteoblasts from the perichondrium drive bone growth
[Schipani and Provot, 2003]. Proliferation and differentiation of chondrocytes continues
in the two separated domains. This part of the process is not included in this model
as we were interested in the mechanism by how symmetry is broken and by which the
differentiation pattern is first generated.
Mutants
An important test for the suitability of a mathematical model is its consistency with
a wide range of independent experimental observations. Knock-out mice exist for all
proteins included in the model. In the Ihh null mouse (Ihh −/− ) only a reduced number
of hypertrophic chondrocytes accumulate in the center of the domain, but premature
chondrocytes no longer vanish from the center and no functional bone forms [St-Jacques
42
Figure 2.7 – Mutants. Parts of the network of the indirectly coupled model were altered to assess
the effect on the phenotype. (A) Ihh expression is shut off. The complex fails to form a pattern, and
so the downstream processes. The tissue grows due to it’s intrinsic proliferation. When the initial
PTHrP concentration falls below the differentiation threshold θi , the entire primordium differentiates
instantaneously, leading to highly accelerated growth. (B-C ) Pthrp expression is shut off. The complex
pattern is formed normally at time t ≈ 17.7, but the downstream Pthrp expression pattern cannot
form. The initial PTHrP is diluted and degraded, leading to spatially homogeneous, instantaneous
differentiation at time t ≈ 24.9. (D-F ) Pthrp is overexpressed tenfold. (D) The complex pattern forms
normally at time t ≈ 17.7 and stays stable until the end of the observed period of time at t = 40. (E)
The Pthrp expression is regulated by the complex, thus entopic. (F ) The PTHrP concentration is high,
leading to global inhibition of differentiation. Therefore, no spatial organization of the cells can be
observed. The initial values are uniformly zero for R2 I and P expression, uniformly 1000 for P, and
uniformly γρR C0 for R expression for all mutants (c.f. Table 2.2).
et al., 1999]. The gene expression pattern in the Ihh null mouse (Ihh −/− ) are greatly
disturbed: Ptch and Pthrp expression are absent, and the PTHrP receptor is misexpressed
[St-Jacques et al., 1999]. In our model, IHH signalling is indeed completely absent, and
the complex is homogeneously zero (Figure 2.7 (A)). Consequently, the distribution
of premature chondrocytes remains spatially homogenous. However, the degradation
and dilution of PTHrP leads to uniform differentiation at time t ≈ 23.3 and thus to
instantaneous growth. This is not observed in the embryo, presumably because of the
differentiation blocking effects, that are not included in this simple model.
Bones in mice lacking Parathyroid hormone (PTH) and PTHrP are much smaller than in
the wildtype, and the zones of proliferating chondrocytes and bone formation are shrunk
[Miao et al., 2002]. Hypertrophic chondrocytes, however, still emerge in the center of the
domain, perhaps because of the effects of maternal PTHrP given the much more severe
phenotype in Pth/Pthrp receptor (−/−) mutant mice [Lanske et al., 1996]. Most Pth/Pthrp
43
Development
receptor (−/−) mutant mice die and those that survive exhibit accelerated differentiation
of chondrocytes in bone, and their bones, grown in explant culture, are resistant to the
effects of PTHrP and Sonic hedgehog [Lanske et al., 1996]. In our model, the spatial
distribution of IHH signalling emerges correctly in the beginning (cf. Figure 2.7 (B-C )),
but spatially organized cell organization is absent. Similar to the Ihh −/− simulation, the
uniform differentiation due to degradation and dilution of the initially available PTHrP
concentration of maternal origin, leads to high growth rates.
Overexpression of Pthrp leads to blocking of hypertrophic differentiation and to delayed
endochondral processes [Weir et al., 1996]. Indeed, differentiation is completely absent
in our simulation, although the IHH signalling and the downstream Pthrp expression
pattern form correctly (cf. Figure 2.7 (D-E)). The PTHrP concentration levels are
consistently high (Figure 2.7 (F )).
Sensitivity and Robustness
When probing the robustness of the model by varying the setpoint parameters we notice
large differences in the impacts of the parameter values (Figure 2.8). Those parameters
that define the Turing space have the largest impact on the patterning process. Most
importantly, these are the initial proliferative and hypertrophic cell densities C0 and H0 ,
and the expression rates of I, ρI , and R, ρR , as these together define the initial total Ihh
and Ptch expression rates ρI H0 and ρR C0 , respectively (cf. Equation (2.16)). Accordingly,
the system is highly sensitive to these parameters. Furthermore, the Schnakenberg system
depends on the ratio of the diffusion coefficients DI and DR , as well as on the scaling
factor γ. While DR = 1 is kept constant, the diffusion coefficient of IHH, DI , can
only be modestly varied. Similar considerations apply to the scaling factor γ. The
diffusion coefficient of PTHrP and the cells can be varied massively without affecting the
qualitative emergence of the central-lateral organization. The threshold parameters θP
(controlling the Pthrp expression) and θi (controlling the differentiation) can be varied
by almost one order of magnitude. This is a consequence of the high ratio of minimal
and maximal values in the complex pattern, which is one of the characteristic features
of Turing patterns. The initial PTHrP concentration P0 affects the time point when
differentiation starts. Is it too low, differentiation may set in when the complex pattern is
not yet formed. Higher values, on the other hand, lead to delayed differentiation, but still
lead to qualitatively correct phenotypes. Besides dilution, the initial decrease of PTHrP
is governed by the protein degradation δP , whose value can be changed moderately. The
system is relatively sensitive to changes in the proliferation rate ϕ. This is due to the
resulting exponential longitudinal growth in the beginning. With insufficient proliferation,
the primordium is not able to reach the critical length where the pattern appears. Too
high proliferation, on the other hand, prevents the pattern to form. Here also the initial
length of the bone, Lbone (t = 0), is important, and in particular shorter initial lengths
are not tolerated very well. For a shortened initial geometry, the constant proliferation
of the proliferating chondrocytes leads to an initial lengthening until the critical aspect
44
Figure 2.8 – Local parameter sensitivity for the indirectly coupled model. The set point
parameters from Table 2.2 were changed as long as the central-lateral organization still appeared. The
values were normalized to the set point parameters, and the factor by which the basal parameter value
can be changed is shown. The values were changed with 1% accuracy if less than 10%, and with 10%
accuracy if less than 100%, and with 100% accuracy otherwise. The volume ratio Φ and the differentiation
rate δ are not shown since they only affect the differentiative growth rate, but not the emergence of
the central-lateral organization. The diffusion coefficients of PTHrP, DP , and the cells, Dcells , as well
as the initial concentration of PTHrP, P0 , can be increased massively without affecting the qualitative
emergence of the central-lateral organization.
ratio is reached, at which the Turing pattern emerges. However, if the initial geometry is
too short, proliferation cannot reach the critical length any more within the period under
consideration. The size of the outer domain, Ldomain , mimicking the limb bud ectoderm,
can be changed moderately.
Patterning is much less sensitive to the choice of parameters for PTHrP than for those
affecting the Turing module directly. It can be concluded that the Turing system is
relatively sensitive to changes in parameters, whereas, in particular, the differentiation
process is highly robust to perturbations.
45
Development
2.1.4
Discussion
We developed a model for long bone development based on the known regulatory
interactions. In line with our previous work [Menshykau et al., 2012] we find that
the IHH-PTCH1 interaction can result in a Schnakenberg-type Turing system. We
further show that this patterning module results in the experimentally observed cell
distributions as well as gene expression and signalling patterns if the equations are
solved on a bone-shaped domain that expands at the embryonic growth speed. Thus
hypertrophic chondrocytes accumulated in the center of the domain and expressed Ihh
while proliferating chondrocytes accumulated to the sides and expressed Ptch. In the
embryo patterning and growth are linked and we therefore also coupled our Turing model
with a tissue mechanics model in a next step. Here the IHH-PTCH complex inhibited
differentiation to hypertrophic chondrocytes and thus promoted expansion of proliferating
chondrocytes. Since hypertrophic chondrocytes expressed Ihh, the tissue dynamics affects
the expression of the Turing components. Given the small size of the parameter space
for which Turing patterns can be observed we were concerned that the coupling would
destroy the pattern. Indeed when we coupled the patterning module directly to the tissue
mechanics module the pattern became highly unstable, and we were no longer able to
find parameter sets that would give realistic patterns.
In a next step we introduced a further component, PTHrP. IHH binding to PTCH1 induces
the expression of Pthrp, and PTHrP in turn inhibits the differentiation to hypertrophic
chondrocytes. With this intermediate step added we could now obtain realistic patterns
also when the Turing system was coupled to the tissue mechanics module. We reproduced
all experimentally observed cell distributions as well as gene expression and signalling
patterns while the bone domain was growing at the experimentally observed growth speed.
In addition, Pthrp expression was restricted to the edges of the domain as observed in
the embryo [Hilton et al., 2005].
The model was non-dimensionalized before analysis to reduce the number of parameters.
As far as quantitative measurements are available (growth speed, domain size, diffusion
coefficients) we find that the model parameter values are consistent with measured
values when transformed back to their dimensional counterparts. Moreover, the model
reproduces the observed gene expression patterns as well as key mutant phenotypes.
Further quantitative comparisons and data-based parameter estimation procedures as
are common for ordinary differential equation-based models [Geier et al., 2012, Raol
et al., 2004], however, are not yet possible, given the available data.
While the good match of model and experimental observations supports a central role
of IHH signalling in the early patterning during long bone formation we note that the
Ihh −/− Gli3 −/− double knock-out exhibits normal early patterning (with some later
defects), and Pthrp expression remains restricted to the ends of the domain [Hilton
et al., 2005, Koziel et al., 2005]. This observation is at odds with our current model, as
46
GLI3 is a key downstream transcription factor of IHH signalling. In the absence of IHH,
the receptor PTCH1 remains unbound and in its unbound form PTCH1 enhances the
expression of the Gli3 gene [Butterfield et al., 2009] and the proteolytic processing of the
GLI3 protein into the GLI3R repressor form, which prevents expression of downstream
target genes such as PthrP [Hilton et al., 2005, Koziel et al., 2005]. As a result, Ihh null
mice cannot express Pthrp, and the mesenchymal condensations differentiate uniformly
into hypertrophic chondrocytes [St-Jacques et al., 1999, Hilton et al., 2005, Koziel et al.,
2005]. In the absence of Ihh and Gli3, we would expect spatially uniform expression of
PthrP. The spatial restriction of PthrP expression in Ihh −/− Gli3 −/− double knock-out
mice therefore points to an alternative patterning process that restricts Pthrp expression
to the sides and thereby restricts the emergence of hypertrophic chondrocytes to the
center.
One possible mechanism by which Pthrp expression may be restricted to the ends of
the domain are factors that are secreted by the joints. Various ligands from the TGF-β
family are all present in the joints and SMAD3-dependent signalling and signals of
BMPR-IA (ALK3) have previously been shown to stimulate Pthrp expression [Pateder
et al., 2001, Pateder et al., 2000, Zhang et al., 2003, Zou et al., 1997]. Conditional
removal of Smad4 with Hoxa13-cre prevents cartilage formation and ossification [Bénazet
et al., 2012]. Inclusion of such a IHH-independent cue of Pthrp expression on the distal
boundaries would trivially result in the observed distal restriction of the Pthrp expression
patterns. Future modelling efforts is proposed to be focused on understanding the selforganized emergence of BMP signalling that marks the joints. Moreover, it is suggested
to evaluate the contribution of the BMP-dependent expression of Pthrp to the wildtype
patterning process based on published mutant phenotypes.
In summary, the model reproduces experimental data very well and provides an explanation for the formation of the counterintuitive pattern that requires long-distance
signalling of the morphogen IHH. The ligand-receptor based Turing mechanism can
yield such pattern using physiological parameter values. PTHrP had to be introduced
in the model as a mediator between the Turing system and the tissue growth module
to ensure the stability of the pattern on the expanding domain. Further experimental
studies are required to define the redundant or parallel mechanisms that ensure the
correct expression of Pthrp in Ihh −/− Gli3 −/− double knock-out mice and to quantify
their relative contributions in the wildtype. BMP-receptor signalling provides a good
candidate mechanism. Interestingly, we have previously shown that also BMP-receptor
interactions can give rise to Schnakenberg-type Turing patterns [Badugu et al., 2012].
Turing mechanisms have been proposed for many patterning phenomena. Yet, the Turing
components have been difficult to define. The example of long bone patterning adds
another example, where a ligand-receptor based Turing mechanisms can describe both
the wildtype and mutant conditions very well, even when embedded in a feedback that
47
Development
controls the expansion of a rapidly growing tissue. This supports the notion that Turing
mechanisms in nature may be more generally implemented based on a receptor-ligand
interaction. For receptor-ligand interactions to give rise to Turing patterns, ligand and
receptors need to interact cooperatively (non-linearly), the receptor-ligand interaction
must increases the receptor concentration on the membrane, and ligands need to diffuse
faster than receptors. These three conditions are met by many receptor-ligand systems,
such that this mechanism could be widely used in nature.
48
2.2. Modelling Multiple Cell Types with Partial Differential Equations
2.2
Modelling Multiple Cell Types with Partial Differential Equations
Partial differential equations are a convenient way to describe reaction-advection-diffusion
processes of signalling models. If only one cell type is present, and tissue dynamics can
be neglected, the equations can be solved directly. However, in case of multiple cell
types it is not always straightforward to integrate a continuous description of the tissue
dynamics. Here, (delayed) differentiation of cells into different cell types and hypertrophic
cell volume change upon differentiation are discussed.
2.2.1
Model Formulation
Partial differential equations have been widely used to describe spatial signalling models
in morphogenesis [Murray, 1993]. Oftentimes, only one cell type is assumed, and therefore
the governing equations apply to the entire domain. However, if the equations shall be
dependent on multiple cell types, the latter have to be represented explicitly. A possible
approach would be to model cell types as cell densities or cell concentrations, i.e. a scalar
field for each cell type. This approach has been chosen for example to model early bone
development as presented in Section 2.1. However, there are a few drawbacks associated
with that approach. Having cell mixtures might not be desired, and instead sharply
defined domains with homogeneous cell populations are required. It is also unnecessary to
have two scalar fields to describe two cell types if they are complementary. Assuming that
a cell type C1 differentiates into cell type C2 , then the negation C1¬ ) should by definition
be C2 , and they are supposed to sum up to C1 + C2 = 1 at any time and everywhere.
Alternatively, the cell types C1 and C2 can be defined by means of an index scalar field
D = D (x, t):
C1 := 1 · (D > θD )
C2 := 1 · (D ≤ θD ) ,
(2.21)
where θD is an arbitrary threshold value which may be set to θD = 1/2. For later
purposes, also negations are defined:
C1¬ := 1 · (D ≤ θD )
C2¬ := 1 · (D > θD ) .
(2.22)
Obviously, the cell types can only take values ∈ {0, 1} such that the scalar variables C
and C ¬ can be used in a simple way in signalling model equations. For example, assuming
that only C1 expresses the protein P, and only C2 can degrade it, the governing equation
49
Development
would read:
∂t P + ∇ · (Pu) = DP ∆P + ρP · C1 − δP · P · C2 ,
(2.23)
where DP denotes the diffusion coefficient, u the velocity field in case of a growing or
moving tissue, ρP the production rate and δP the degradation rate.
The index field D is governed by the following equation:
∂t D + u · ∇D = DD ∆D − δD · D · Ξ · C1 − δD · D · C1¬ .
(2.24)
In the following, all terms are discussed. The equation is of reaction-diffusion type with
advection, but without dilution. It has to be noted that there is no such thing as cell
diffusion in this model at the time; the diffusion is only for numerical purposes and shall
be chosen as small as possible. Further development of the model would be needed to
include chemotaxis, cell migration, and further processes. The condition function Ξ is
controlling the degradation of D, and it depends on the specific model. It is potentially
a Boolean operator, i.e. once certain conditions are fulfilled, differentiation takes place.
For example, it is assumed that differentiation occurs whenever the concentration of a
hypothetical morphogen M drops below a certain threshold θM . The condition function
would read:
Ξ (M) =

1,
if (M < θM )
0,
otherwise
.
(2.25)
The decay rate δD controls how fast C1 is converted into C2 , which will be discussed
in Section 2.2.2 in more detail. The rightmost term in Equation (2.24) is there for
numerical reasons: the decay of D ceases right upon reaching the threshold θM as defined
in Equation (2.21). It is therefore desirable to diverge from the critical threshold θM ,
which is achieved by an arbitrary decay δD controlled by C1¬ .
The model can be extended by adding differentiation delay, growth (proliferation and
volume increase upon differentiation) and differentiation cascades with multiple cell types,
which will be discussed in the following sections.
2.2.2
Differentiation Delay
Due to the exponential decay of D in Equation (2.24), the time to reach the critical value
(in this case θD = 1/2) can be easily computed:
τ diff =
50
ln (2)
.
δD
(2.26)
This is the time span from reaching the differentiation triggering condition Ξ to the
actual cell type conversion. The higher δD , the more instantaneous the differentiation.
To be more precise, it is a time integrator: The differentiation triggering condition has
to be fulfilled for an accumulated time τ diff before the actual cell type conversion takes
place. If an approximately instantaneous differentiation is desired, a large value of δD
is chosen such that τ diff is negligibly small. However, if the model requires a temporal
delay, Equation (2.26) can be used to do so.
2.2.3
Cell Volume Increase upon Differentiation
One way of describing the mechanical properties of embryonic tissue is by assuming that
it behaves similar to a viscous fluid on longer time scales. This approach has been used
to model limb bud [Dillon and Othmer, 1999] and embryonic long bone development as
presented in Section 2.1. The incompressible Navier-Stokes equations, which describe
the mechanical properties of all cell types, are previously described in Equation (2.2).
Here, the viscous tissue model and the index-field-based cell type model are combined.
In two dimensions, it is for example assumed that the cells C1 are growing Φ-fold in
area when differentiating into C2 . This process might represent hypertrophic cell volume
increase upon differentiation (cf. Section 2.1). The naive attempt would be to simply
write for the mass source:
S diff = (Φ − 1)
δD
· Ξ · C1 .
ln (2)
(2.27)
That is, a net mass gain of (Φ − 1) units (gaining +Φ and losing −1) is obtained. The
rate δD /ln (2) is the inverse from Equation (2.26), i.e. this mass gain has to take place
within the differentiation time τ diff . The same conditions hold as for the index field decay:
the differentiation condition Ξ has to be fulfilled and cells C1 must be available.
However, this leads to spurious results because the mass source leads to an expansion of
the differentiation zone and thus to a systematic exceeding of the added mass. Changing
the dynamics of D is undesired because the differentiation time τ diff shall still be controlled
via δD . The only solution is to correct the mass source such that the total mass increase
is linear and not exponential. However, it is also undesirable to integrate the domain
areas or introduce an additional diluted factor (and make S diff proportional it). But the
(accumulated) time τ̃ a certain location is already differentiating can be estimated by
taking the local value of D:
τ̃ (x, t) = −
1
ln (D (x, t)) .
δD
(2.28)
Next, the evolution of a small area A with a scaled uniform mass source S̃ = Sdiff ·A0 /A(t)
51
Development
is considered:
∂t A = ASdiff
A0
= Sdiff A0 ,
A
(2.29)
which can be integrated over the differentiation time τ̃ :
A = A0 + Sdiff A0 τ̃ ,
(2.30)
such that the true scaled mass source S̃ is found:
S̃ (τ̃ ) =
Sdiff
.
1 + Sdiff τ̃
(2.31)
A drawback of this formulation of the mass source S̃ might be that it is spatially nonuniform in the differentiating zone. Furthermore, the dependency of the source on the
differentiation time τ̃ represents an additional complexity and source of numerical errors.
Therefore, a constant, effective source S̃ c is derived. Integration of the scaled source,
given in Equation (2.31), leads to:
Z τ̃ = ln(2)
δ
D
τ̃ =0
S diff
ln(2)
dτ̃ = ln 1 + S diff
diff
1+S τ
δD
,
(2.32)
and the average, constant, uniform mass source S̃ c is determined as:
S̃ c =
2.2.4
δD
ln(2)
ln 1 + S diff
ln(2)
δD
.
(2.33)
Multiple Cell Types
Supposing that a model requires the differentiation cascade C1 → C2 → C3 → C4 , three
index fields D1,2,3 are needed to define the cell types:
C1
C2
C3
C4
52
:=
:=
:=
:=
1 · (D1
1 · (D1
1 · (D1
1 · (D1
> θD )
≤ θD ) · (D2 > θD )
≤ θD ) · (D2 ≤ θD ) · (D3 > θD )
≤ θD ) · (D2 ≤ θD ) · (D3 ≤ θD ) ,
(2.34)
and the negations read:
C1¬
C2¬
C3¬
C3¬
:=
:=
:=
:=
1 · (D1
1 · (D2
1 · (D3
1 · (D3
≤ θD )
≤ θD )
≤ θD )
> θD ) .
(2.35)
Of course, by exploiting the idea of the binary system, the four cell types could also be
represented by only two index fields. This exercise is left for future applications. The
index fields obey equations similar to Equation (2.24). The differentiation is one-way,
i.e. the reversion is not possible, and e.g. differentiation into C4 is only possible iff C3
exists and the differentiation condition is fulfilled. The model will have to be extended
to enable de-differentiation.
2.2.5
Numerical Validation
To validate the scaled source given in Section 2.2.3, a differentiation front sweeps across
an initially circular disc, and the cells increase Φ-fold in area upon differentiation, such
that the analytical solution of the final disc area is known to be ΦAinit . An illustration
is given in Figure 2.9A. The numerical analysis is carried out with the commercial finite
element software COMSOL for different mesh sizes (cf. Figure 2.9B). For the simulations,
the parameter values given in Table 2.3 are used.
For both the initial and final disc area, an approximately first order convergence w.r.t.
the number of elements is found (cf. Figure 2.9CD).
Table 2.3 – Parameters used for the numerical validation.
initial radius
simulation time
fluid density
fluid viscosity
diffusion coefficient index variable
differentiation threshold
decay of index variable
speed of differentiation front
volume expansion upon differentiation
r(t = 0) = 1/2
T = 200
ρ=1
µ = 10
D = 1e − 6
θ = 5.5
δ = 0.05
u = 0.006
Φ=4
53
Development
3.5
3
2.5
N=106
N=366
N=1616
N=6546
2
1.5
1
0.5
0
50
100
150
200
−2
10
−1
10
−3
10
−2
10
−4
10
2
10
3
10
2
10
3
10
Figure 2.9 – Numerical validation. A A circular disc with radius r(t = 0) = 1/2 consists homogeneously of a red cell type. A differentiation front sweeps across the disc from left to right. The red
cells increase their area four-fold when undergoing differentiation into the blue cell type. Once the
differentiation terminated, the final circular disc is expected to have a radius r(t = ∞) = 1. B The
analytical solution for the total area is A(t = 0) = π/4 and A(∞) = π. Using finite element methods, the
numerical solution is subject to numerical errors. Here, results for different numbers of mesh elements
(N = {106, 366, 1616, 6546}) are shown. Finer meshes consistently lead to more accurate results. C
Convergence analysis at t = 0. Using linear mesh elements, a first order convergence is achieved w.r.t.
number of mesh elements. The fitted slope is -0.9983. A slope of -1 (red) is shown. D Convergence
analysis at t = 200. The order of convergence is less than first order w.r.t. number of mesh elements.
The fitted slope is -0.8591. A slope of -1 (red) is shown.
54
2.3. Discussion
2.3
Discussion
Whenever multiple cell types shall be represented, and cell type mixtures are undesired,
the presented formulation based on binary scalar index fields is a practicable way to extend
a partial-differential-equation-based signalling model. The binary cell type variables
can be used in the signalling equations in an intuitive and straightforward way. Cell
differentiation and differentiation delays can be made dependent on signalling conditions,
and differentiation cascades are easily implemented. The formulation needs an externally
calculated or prescribed velocity field. It does not necessarily need to be divergence-free,
such that cell volume changes upon differentiation and proliferation can be included
when combined with a tissue model as presented in Section 2.1.
Sharp cell type boundaries and an ideally inexistent diffusion of the binary index field
might be numerically undesirable, but the numerical artefacts can be reduced by refining
the mesh and setting a small diffusion coefficient which is chosen to be small enough not
to significantly alter the results.
The presented model might be used to study the differentiation cascades as presented in
the long bone development model in Section 2.1. Figure 2.10 shows an example of the
growth plate architecture (cf. Appendix A.3).
Figure 2.10 – Multiple cell types in a model for long bone development. The growth plate
is defined by the differentiation cascade from resting and proliferating, to prehypertrophic and finally
to hypertrophic chondrocytes. Sharp boundaries define uniform regions. Credits to Sami Ben Said (cf.
Appendix A.3).
55
3 Cell-based Approach: The Software Framework LBIBCell
The simulation of morphogenetic problems requires the simultaneous and coupled simulation of signalling and tissue dynamics. A cellular resolution of the tissue domain is
important to adequately describe the impact of cell-based events, such as cell division,
cell-cell interactions, and spatially restricted signalling events. A tightly coupled cellbased mechano-regulatory simulation tool is therefore required. This chapter presents an
open-source software framework for morphogenetic problems. The cell model, numerical
methods and the software structure are discussed, and numerical validations demonstrate
the accuracy and convergence of the implementation. An application example illustrates
the software framework’s capabilities to simulate signalling-dependent tissue dynamics.
This chapter has been published as:
Tanaka S, Sichau D, Iber D, LBIBCell: A Cell-Based Simulation Environment for
Morphogenetic Problems, Bioinformatics, 2015 Jul 15;31(14):2340-7
57
Chapter 3. Cell-based Approach: The Software Framework LBIBCell
3.1
Introduction
During morphogenesis, tissue grows and self-organises into complex functional units
such as organs. The process is tightly controlled, both by signalling and by mechanical
interactions. Long-range signalling interactions in the tissues can be mediated by
diffusible substances, called morphogens, and by long-range cell processes [Restrepo et al.,
2014]. The dynamics of the diffusible factors can typically be well described by systems
of continuous reaction-advection-diffusion partial differential equations (PDE’s). The
appropriate tissue representation depends on the relevant time scale. For a homogeneous
isotropic embryonic tissue, experiments show that the tissue is well approximated by
a viscous fluid on long time scales (equilibration after 30 minutes to several hours)
and by an elastic material on short time scales (seconds to minutes) [Forgacs et al.,
1998]. However, biological control typically happens on a shorter time scale, and many
cellular processes such as cell migration and adhesion, cell polarity, directed division,
monolayer structures and differentiation cannot be cast into a continuous formulation in
a straight-forward way. A number of cell based simulation techniques at different scales
and different level of detail have been developed to study these processes; a thorough
overview can be found in Chapter 1.
For many morphogenetic phenomena, which arise from a tight interaction between the
biomolecular signalling and the tissue physics, an explicit computational representation
of the cell shapes is required. Here, the flexible software framework LBIBCell is presented.
It is based on the immersed boundary method [Peskin, 2003], which has previously been
used to model deformable cells [Rejniak et al., 2004, Rejniak, 2007]. LBIBCell represents
the individually deformable cells as highly resolved, massless elastic polygons being
immersed in fluid. The cytoplasm and the extracellular matrix and fluid are represented
by an incompressible Newtonian fluid, which accounts for the viscous properties of the
tissue.
In the model and software implementation presented in this chapter, a vast amount
of biological processes such as cell growth, cell division, apoptosis and polarization
has been realized. As a novelty, the software permits to tightly couple biomolecular
reaction-advection-diffusion-based signalling models to a cell-resolved, physical tissue
model. In addition, the software offers great flexibility to add custom extensions and
biologically motivated processes. The fluid and signalling processes are solved using the
lattice Boltzmann method. Due to the very high level of detail, the viscoelastic cell model
is computationally expensive and has not yet been implemented in three dimensions. The
core components and the general approach of the model are described in the following
sections.
58
3.2. Approach
3.2
Approach
The approach used for the presented model permits the coupled simulation of tissue and
signalling dynamics. To describe the tissue dynamics, the visco-elastic cell model needs
to represent both the cellular structures and their elastic properties, as well as the viscous
behaviour of the cytoplasm and of the extracellular space surrounding the cells. The
model therefore rests on three core parts: the representation of cells, the representation
of the fluid and the fluid-structure interaction, and the coupling of the tissue part to the
signalling model. To describe the interaction between the viscous fluid and the elastic
structures, which are immersed in the fluid, we use the immersed boundary (IB) method
[Peskin, 2003] as previously implemented in the visco-elastic cell model, also called IBcell
model [Rejniak et al., 2004, Rejniak, 2007]. To solve the viscous fluid behaviour, we
use the lattice Boltzmann method, which is an efficient mesoscopic numerical scheme,
originally developed to solve fluid dynamics problems [Chen and Doolen, 1998]. The
method has previously been successfully applied to reaction-diffusion equations such as
Turing systems ([Ponce Dawson et al., 1993]), as well as to coupled scalar fields such
as temperature [Guo et al., 2002]. The method was for the first time combined with
the immersed boundary method [Peskin, 2003] by [Feng and Michaelides, 2004], and has
later been used to study red blood cells in flow by [Zhang et al., 2007]. In the following,
an overview of the implemented methods is provided; the implementation details are
given in section 3.4.
3.2.1
Cell Representation
Cells are represented as massless, purely elastic structures, which are described by sets
of geometry points forming polygons. The geometry points are connected via forces. In
a first approximation, the elastic structures can be identified to represent the elastic cell
membranes. However, more elastic structures can be added to the intra-/extracellular
volume to mimic the visco-elastic properties of the cytoskeleton or the extracellular matrix.
The user can implement biological mechanisms which operate on the cell representations.
For example, a new junction to a neighbouring cell might be created when the distance
between two neighbouring cell boundaries falls below a threshold distance. Similarly, a
junction might be removed when overly stretched.
3.2.2
Fluid and Fluid-Structure Interaction
The visco-elastic cell model represents the content of cells (the cytoplasm) as well as
the extracellular space (the interstitial fluid and the extracellular matrix) as a viscous,
Newtonian fluid. The intra- and extracellular fluids interact with the elastic membrane,
i.e. the fluids exert force on the membrane, and the membrane exerts force on the fluids.
Furthermore, the velocity field of the fluid, which is induced by the forces, moves and
59
Figure 3.1 – Algorithm overview. The algorithm consists of three coupled layers. The geometry
X (l, t) (top part, discussed in more detail in Figure 3.2) is used to compute the forces F (l, t) acting
on each of the geometry nodes. These forces, which do not necessarily coincide with a lattice point,
are scattered to the fluid lattice (middle part) using the immersed boundary method kernel function,
F (l, t) → f (t). After advancing the fluid solver by one time step, the velocity is interpolated to the
geometry node position using the same kernel function, u (x, t) → U (l, t). The geometry nodes are
moved according to their velocity U (l, t) and the iteration is restarted. The velocity u (x, t) of the
fluid lattice is also copied to the reaction-advection-diffusion solvers (PDE), together with the position
X (l, t) → x (t) of the geometry. The state of the reaction-advection-diffusion solvers, which are used to
model signalling, may be used to compute mass sources S (x, t) for the fluid solver.
deforms the elastic structures. This interaction, well-known as fluid-structure interaction,
lies at the heart of the tissue model. Forces (e.g. membrane tension or cell-cell forces)
acting on these points are exerted on the fluid by distributing the force to the surrounding
fluid. Due to the local forcing, the fluid moves. At this step, the membrane point are
advected passively by the fluid. As a result the forces need to be re-evaluated on the
points. By repeating the forcing-advection steps, the interaction is realized iteratively.
60
3.3. Numerical Methods
As a result of this iterative process, the (elastic) structures are coupled to the (viscous)
fluid. Depending on the parametrisation, this model allows to describe both elastic, or
viscous, or visco-elastic material behaviour. The upper part of Figure 3.1 illustrates the
immersed boundary interaction. The implemented IB kernel function has bounded
support, i.e. each geometry point influences and is influenced only its immediate
neighborhood. Here, the dimension of the kernel function is four by four (cf. Figure 3.1).
The fluid equations are solved using the lattice Boltzmann method [Chen and Doolen,
1998], which is described in detail in Section 3.3.1. The Reynolds number is typically
≪ 1, hence the regime is described by Stokes flow1 .
3.2.3
Signalling
The signalling network is represented as a system of reaction-advection-diffusion processes.
The elastic membranes may act as no-flux boundaries for compounds which only exist in
the extra- or intracellular volume, respectively. The reaction-advection-diffusion solvers
can be equipped with potentially coupled reaction terms in order to model signalling
interactions of diffusing factors. Depending on the model, the signalling may impact
the tissue dynamics. This can be done, for instance, by making the mass source of the
fluid dependent on the values of the reaction-advection-diffusion solvers such that the
tissue expands locally (cf. Figure 3.1). Furthermore, the diffusing compounds can be
individually configured to diffuse freely across the entire domain, or only inside or outside
the cells (e.g. using no-flux boundary conditions for the cell membranes).
3.3
3.3.1
Numerical Methods
Lattice Boltzmann Method
For the fluid, the standard lattice Boltzmann scheme (with the single-relaxation-time
Bhatnagar-Gross-Krook collision operator) is used [Chen and Doolen, 1998]. It has
been shown, that the incompressible Navier-Stokes equations can be recovered in the
hydrodynamic limit [Chen and Doolen, 1998]. The Boltzmann equation is discretized on
a D2Q92 lattice and reads:
1
wi ρ
fi (x + v i , t + 1) − fi (x, t) = − (fi (x, t) − fieq (x, t)) + ∆t 2 (v i · f ) , (3.1)
τ
cs
1
The Reynolds number reads Re = UνL , with U being a characteristic velocity, L a characteristic length
scale, and ν the kinematic viscosity. Assuming L = 10−3 [m], U = 10−8 [m/s] and ν = 101 . . . 102 [m2 /s],
then Re = 10−13 . . . 10−12 can be estimated [Forgacs et al., 1998].
2
the
nine-velocity lattice
in
two
dimensions is
defined
as
v0
=
[0, 0],
v
=
[cos
(π
(i
−
1)
/2)
,
sin
(π
(i
−
1)
/2)]
for
i
=
{1,
2,
3,
4},
and
v
=
i
i
√
2 [cos (π (i − 1) /2) + π/4, sin (π (i − 1) /2 + π/4)] for i = {5, 6, 7, 8}
61
where fi denotes the particle distribution function in the direction i, and can be interpreted
as the probability density of finding particles with velocity v i at time t at position x.
The relaxation time τ is related to the kinematic viscosity ν = c2s τ − 12 . For isothermal
√
flows, the speed of sound cs is defined as cs = c/ 3 using the lattice speed c = ∆x/∆t.
The lattice spacing and the time step are chosen as ∆x = ∆t = 1 to guarantee consistency
with the lattice. The last term of Equation (3.1) represents the external body force [He
et al., 1997].
Equation (3.1) implies a two step algorithm: firstly, the distribution functions fi perform
a free flight to the next lattice point (left hand side). Secondly, on each lattice point, the
incoming distribution functions collide and relax towards a local equilibrium distribution
fieq , which is controlled by the relaxation time τ (right hand side). The equilibrium
distribution is taken as:
"
fieq
#
v i v i − v 2 : uu
vi · u
= ωi ρ 1 + 2 +
,
cs
2c2s
(3.2)
with the fluid velocity u and the fluid density ρ. The operator : denotes the dyadic
tensor scalar product. For the D2Q9 lattice, the population weights ωi can be found as
ω0 = 4/9, ω1−4 = 1/9, and ω5−8 = 1/36.
Finally, the macroscopic quantities (density ρ and momentum density ρu) can be
computed using the zeroth and first order moments:
ρ=
8
X
i=0
fi
ρu =
8
X
fi v i .
(3.3)
i=0
The fluid pressure p is related to the mass density ρ as p = ρc2s .
For solving the reaction-advection-diffusion equation of a compound φ, a multi-distribution
function approach is chosen [Bartoloni et al., 1993, Guo et al., 2002], i.e. an additional
lattice Boltzmann solver is coupled to the fluid solver. We implemented different schemes
(D2Q4,D2Q5), which exhibit slightly different stability and accuracy [Li et al., 2001].
For the D2Q5 3 scheme, we follow [Huber et al., 2008] and [Parmigiani et al., 2009] and
write for the lattice Boltzmann equation:
gi (x + v i , t + 1) − gi (x, t) = −
3
1
(gi (x, t) − gieq (x, t)) .
τD
the five-velocity lattice in two dimensions is defined as v 0
[cos (π (i − 1) /2) , sin (π (i − 1) /2)] for i = {1, 2, 3, 4}
62
(3.4)
=
[0, 0] and v i
=
3.3. Numerical Methods
The equilibrium distribution functions is taken as:
gieq
1
= φwi 1 + 2 (v i · u) .
cs
(3.5)
Instead of the local first moment, the velocity field u from the fluid is transferred. The
weights wi are chosen as w0 = 1/3 and w1−4
= 1/6.
The relaxation parameter τD is
1
2
related to the diffusion coefficient as D = cs τD − 2 , and the local compound density
φ reads:
φ=
4
X
gi .
(3.6)
i=0
All variables are expressed in lattice Boltzmann units δx, δt and have to be converted to
physical units.
No-flux Boundary Condition for Reaction-Advection-Diffusion Equations
The missing incoming distribution functions are approximated by equilibrium distributions. The momentum is spatially first order interpolated between the fluid in direction
of the missing population, and the known zero momentum at the wall. The density is
spatially first order extrapolated from the fluid.
Pressure Boundary Condition for the Fluid Equations
Within the computational domain, lattice points can act as internal pressure boundaries,
i.e. points with prescribed fluid pressure, which may be needed to implement mass sinks
in case of growing cells/tissues. All distribution functions are rescaled such that the
prescribed pressure is obtained. The velocity field is not affected, since the rescaling
factor γ cancels:
P
γv i fi (x, t)
u (x, t) = Pi
.
i γfi (x, t)
(3.7)
Unit Conversion and Lattice Boltzmann Variables
The domain is discretized with ∆x and ∆t (LB to non-dimensional units ND). For
example, the diffusion coefficient (and similarly the kinematic viscosity) can be converted
63
as follows:
DLB
∆x2
= DND .
∆t
(3.8)
The diffusion coefficient DLB (in LB units) and the relaxation time τ LB are related as:
D
3.3.2
LB
1 LB 1
=
τ −
3
2
.
(3.9)
Immersed Boundary Method
The PDE’s are prefentially solved on a Eulerian grid, whereas cells are naturally represented in a Lagrangian manner. The two frames can be bridged using the immersed
boundary method, which was introduced in [Peskin, 1977]. This technique is appropriate
for complex and moving boundaries and fluid-structure interactions. The material equations are solved on a Eulerian grid, whereas the boundary equations are expressed in
a Lagrangian way. An introduction can be found in [Mittal and Iaccarino, 2005], and
detailed discussions in [Peskin, 2003].
The curvlinear (boundary) coordinates (q, r, s) are attached to a material point. At time
t, the coordinates in the Eulerian framework read X (q, r, s, t). The material derivative
Du
∂2X
Dt (x, t) = ∂t2 (q, r, s, t) is the acceleration of whatever material point is at position x
at time t. The conversion from Lagrangian variables (e.g. mass density M (q, r, s, t) or
force density F (q, r, s, t)) to their Eulerian counterparts is executed by integrating over
the material coordinates:
Z
ρ (x, t) =
Z
f (x, t) =
M (q, r, s, t) δ (x − X (q, r, s, t)) dqdrds
(3.10)
F (q, r, s, t) δ (x − X (q, r, s, t)) dqdrds ,
(3.11)
where δ (·) denotes the delta Dirac function. For the numerical implementation, the
Delta Dirac function is approximated in such a way that it covers multiple grid points,
on which the conversions in Equation (3.10) and (3.12) are evaluated. The equation of
motion of the Lagrangian particles reads:
∂X
(q, r, s, t) = u (X (q, r, s, t) , t) =
∂t
64
Z
u (x, t) δ (x − X (q, r, s, t)) dx .
(3.12)
3.4. Software
Using the Hodge decomposition4 , the material is described by
ρ
∂u
+ (u · ∇) u = −∇p + µ∆u + f
∂t
∇ · u = 0.
(3.13)
(3.14)
To couple the immersed boundary method to the lattice Boltzmann method, the LB
forcing term f has to be obtained from the Lagrangian force F following a similar way
as [Feng and Michaelides, 2004]. The Lagrangian force F i of the geometry point i is
composed of membrane forces (cf. Equation (3.19)) and cell junction forces (cf. Equation
(3.19)):
cj
Fi = Fm
i + Fi .
(3.15)
F i is distributed to the local fluid neighborhood according to Equation (3.11), and the
Eulerian force f on the lattice point x is then used in the LB collision term in Equation
(3.1).
The discretized delta Dirac function for one spatial dimension is defined as:
  1 1 + cos πkrk
2
δ 1D (r) = 4
0
if krk ≤ 2
if krk > 2
,
(3.16)
and the two-dimensional discretized delta Dirac function is a multiplication of Equation
(3.16):
δ (r) = δ 1D (r) δ 1D (r) .
(3.17)
This implies that the Lagrangian force F i of a membrane point i is distributed to the
4 × 4 = 16 nearest fluid lattice points. By discretizing the membrane into mebrane points
i, the discretized delta Dirac functions overlap.
3.4
3.4.1
Software
Cell Representation
The cell geometries consist of two elements, the GeometryNodes, which act as the IB
points, and the Connections, connecting pairs of GeometryNodes. A simplified cell is
visualized in Figure 3.2. The Connections are attributed with a domainID flag, which is
an identifier for the surrounded domain (respecting the counter-clockwise directionality
4
any vector field u can be written as ρ Du
− f = −∇p + w, where ∇ · w = 0
Dt
65
Figure 3.2 – Elements of the geometry representation. The cells are closed polygons, consisting
of geometry nodes (discs in the top part) and connections (shaded boxes in the top part) between each
two geometry nodes. Each connection stores two references to its preceding and successive geometry
nodes, and vice versa each geometry node stores two references to its preceding and successive connection
(visualized by aggregation arrows in the top part). Directionality of the polygon is counter clockwise by
convention. Each geometry node has a unique, immutable nodeID attribute, which is allocated internally
upon creation of a new geometry node. Each connection features a domainID attribute, which denotes the
domain identifier of the domain on the left hand side. The domain identifier on the right hand side is by
definition zero, representing the extracellular space. Using the domainID of the connections, the domainID
of the lattice nodes is automatically set (lower part). Additionally, each domainID is associated with a
cellType. The behaviour of the MassSolverXX, BioSolverXX and CDESolverXX can be made dependent
on the domainID and/or cellType attributes by the user.
convention). The domain identifier on the other side (on the right hand side) is zero by
convention, representing the interstitial space. The domainID of the Connections are
copied to the fluid and reaction-advection-diffusion solvers. Moreover, the domainID’s
are associated with a cell type flag, cellType. By applying custom differentiation rules,
the cellType of individual cells may be changed according to custom criteria; otherwise
the all cells default to cellType=1 (with cellType=0 being the interstitial space, again).
In this way, the reaction terms and the mass sources may be made dependent on specific
cells, or specific cell types.
3.4.2
User-provided Solvers
The user can add the following routines: MassSolverXX, CDESolverXX, and BioSolverXX
(XX being a name to be chosen). The MassSolverXX - as described above - adds or
substracts mass from/to the fluid solver. The CDESolverXX is used to implement the
reaction terms of the signalling models. Finally, the BioSolverXX can be used to execute
biologically motivated operations on the geometry and the forces. Such an operation
might be cell division, which is discussed in more detail in Section 3.4.5. Figure 3.3A
summarizes the most important classes and their interactions. The classes which are
subject to customization are shaded. In order to add a new customized routine (e.g. a
66
3.4. Software
Figure 3.3 – Simplified UML diagram of important classes. The classes which have to be provided
by the user are shaded. XX refers to an arbitrary solver name. A The SimulationRunner controls the
execution of the simulation. The GeometryHandler has a collection of PhysicalNodes, representing the
lattice, a collection of BoundaryNodes which are woven into the lattice, and a Geometry object. The
latter contains the cell’s geometric information, namely the GeometryNodes and the Connections. The
GeometryNodes and the Connections each have two references of the preceding and successive elements,
as also explained in Figure 3.2. BioSolverXX obtains references from the GeometryHandler and the
ForceSolver to alters states accordingly. Similarly, the MassSolverXX obtains a reference to the lattice
and adds mass sources to the fluid. B To implement new custom routines, the user must inherit from
provided base classes (from BioBaseSolver for biologically motivated routines, from BaseCDESolver for
reaction-advection-diffusion processes, and from BaseMassSolver for mass modifying routines)
mass modifying solver MassSolverXX, a reaction-advection-diffusion solver CDESolverXX,
or a biologically motivated solver BioSolverXX), the user needs to inherit from their
respective virtual base classes (cf. Figure 3.3B). Figure 3.4 visualizes the routines, which
are called iteratively by the SimulationRunner (cf. Figure 3.3A).
3.4.3
Input and Output
The communication to the user is achieved via the loading and dumping of configuration
files. A general configuration file contains the global simulation parameters, such as the
simulation time, the domain size, the fluid viscosity, and the diffusion coefficients for
the reaction-advection-diffusion solvers. The geometry points and the corresponding
geometrical connections are stored in a geometry file. A third file contains the forces,
67
Figure 3.4 – Iterative processing in the solver At initiation, the library loads the user-provided
configuration files (containing global simulation parameters, initial geometry, initial forces). During
each iteration, the library’s class SimulationRunner (cf. Figure 3.3A) successively calls the physical
routines (the lattice Boltzmann method to solve the fluid and reaction-advection-diffusion processes,
and the immersed boundary method to solve the fluid-structure interaction) and the biological routines
(biologically motivated re-arrangement of the geometry, modifications of the forces, etc.). The current
configuration and optionally the entire solver states can be saved at a chosen frequency.
including forces between a pair of geometry points, freely defined forces or spatially
anchored points. The fluid and reaction-advection-diffusion solver states may be written
either to .txt files or in .vtk format and can be post-processed with third-party software
(e.g. Matlab or ParaView). Optionally, the solver states can be saved in a loadable
format to resume the simulation.
3.4.4
Physical Processes
Viscous and Elastic Behaviour
The viscous behaviour is implemented using a representation of an incompressible fluid
(solved using the lattice Boltzmann method, cf. Section 3.3.1), which converges to the
Navier-Stokes equation in the hydrodynamic limit. The fluid is solved on a regular
Cartesian and Eulerian grid. The membranes are represented by sets of points, which
are connected to form closed polygons. A variety of forces may act on the membrane
nodes, such as e.g. membrane tensions (cf. Section 3.4.4). The interaction between the
fluid and the elastic structures is formulated using the immersed boundary method (cf.
Section 3.3.2). The membrane points move according to the local fluid velocity field in a
Lagrangian manner.
68
3.4. Software
Reaction-Diffusion of Biochemical Compounds
The biochemical signalling can be described by sets of coupled reaction-diffusion partial
differential equations. Similar to the fluid equations, these equations are solved on a
regular Cartesian and Eulerian grid (solved using the lattice Boltzmann method, cf.
Section 3.3.1). The concentrations of the compounds can be accessed by other solvers,
for example to make other processes such as cell division dependent on signalling factors.
The cell boundaries can be chosen to be either invisible to the diffusing compounds, or
to be no-flux boundaries. To account for advection, the fluid velocity field is directly
transferred from the fluid solver since the fluid and the reaction-diffusion lattices coincide
spatially. The coupling of the solvers is visualized in Figure 3.1.
Forces
Forces are an integral part of the simulation environment. A force is always connected to
a membrane point. Any type of conservative force (which can be derived from a potential)
can easily be implemented. Currently, the following types of forces are implemented:
• spring force between two geometrical nodes
• spring force between a geometrical node and a spatial anchor point
• free force acting on a geometrical node
• horizontally or vertically sliding force (thus enforcing only the y or x coordinate,
respectively)
• constant force between two geometrical nodes
Application examples include constant forces between two geometrical nodes that can be
used to model constant membrane tension, which leads to the minimization of a cells
perimeter (discussed in Section 3.4.5). Moreover, a geometrical point can dynamically
explore its local neighbourhood and establish a force to another geometrical point from
another cell, thus mimicking cell-cell junctions (discussed in Section 3.4.5).
3.4.5
Biological Processes
The biological solvers (BioSolver) accommodate the functionalities that are related to
biological processes. These processes may be mostly related to modifications of the
forces and the geometry. The BioSolver has full access to the compound concentrations.
Furthermore, it is aware of the cells, whose geometries are stored individually. This enables
the BioSolver to compute cell areas and averaged or integrated compound concentrations.
Since all cells are individually tagged, cell behaviour can be made dependent on cell
69
identity. Additionally to the cell identity, cells also carry a cell type tag, which can be
changed depending on run-time conditions. This latter functionality can be used to
model cell differentiation.
Consider a cell division event as an example. Here, a division plane has to be chosen. The
choice of its position and direction is subject to the user’s model: the cell division plane
might be set perpendicular to the cell’s axis of strongest elongation. Next, the cell has
to be divided, which requires the removal of the corresponding geometrical connections,
and the insertion of new geometrical nodes and connections to close the divided cells.
Note that the concentration fields of the compounds, as well as the velocity- and pressure
fields of the fluid solver are not directly altered in the biological module.
Control of Cell Area
Depending on the biological model of the user, the cell area has to be controlled. By
assuming that a cell might change its spatial extent in the third dimension, the area might
shrink or expand as a response to forces exerted by its neighbouring cells, which can
effectively be modelled as an ’area elasticity’. In the limiting case, the cell resists external
forces, maintains its area and only reacts with changes of the hydrostatic pressure. In
general, to control the area of cells, the reference area for each cell needs to be adapted.
The reference area acts as a set point for a simple proportional controller, i.e. the local
mass source Sk in the cell k is proportional to the area difference between the current
cell area Ak (t), and the set point area A0k :
Sk = α A0k − Ak (t) ,
(3.18)
where α is a proportional constant. More advanced control methods, such as e.g.
proportional-integral control methods, can be realized easily.
This approach of controlling the cell area can also be used to let
a controlled way, i.e. a cell differentiating into an hypertrophic
volume. Implementing this process would be as simple as setting
set point area. The area controller will bring the cell close to its
cells grow or shrink in
cell type may grow in
the new target area as
new area.
Membrane Tension
The definition of forces acting between pairs of membrane points allows for simulating
the cell’s membrane tension. By default, a constant contracting force Fi with magnitude
ϕm is applied to every pair of neighbouring membrane points. Hence the resulting force
on membrane point i is composed of a force pointing to its preceding membrane point
70
3.4. Software
i − 1, and a force pointing to its successive membrane point i + 1:
Fim
=ϕ
m
xi−1 − xi
xi+1 − xi
+
|xi−1 − xi | |xi+1 − xi |
.
(3.19)
This approach can be interpreted as an actively remodelled membrane: when stretched,
new membrane is synthesized in order to not increase the membrane tension on longer
time scales (hours). On the other hand, excessive membrane is degraded to abide the
membrane tension. Therefore, the membrane tension minimizes the cell’s perimeter.
Since the intracellular fluid (and thus the cell area) is conserved in the absence of
neighbouring cells and active mechanisms, the cell assumes a circular shape. On short
time scales (seconds), the passive (non-remodelled) elastic membranes can be modelled
by using Hookean spring potentials. The membrane tension will then be proportional to
deviation from the resting membrane perimeter. In both cases, the membrane is flexible
(i.e. has no bending stiffness); if bending stiffness should be required by the user, this
can be easily realised in a custom BioSolver.
The implementation of membrane tension needs to consider the geometry remeshing.
Whenever a new membrane point is inserted, it needs to get connected to its neighbours
instantly, because the cell will be overly stretched in the absence of membrane tensions.
A membrane point’s forces need to be removed upon its removal. Algorithmically, this
is realized by removing and reconstructing all membrane forces at every time step. At
this point, the magnitude of the membrane tension can be made dependent on signalling
factors.
BioSolverMembraneTension is an example of a class managing the membrane tensions
with immediate remodelling, and BioSolverHookeanMembraneTension implements simple Hookean springs.
Cell Junctions
A cell can create cell junctions to neighbouring cells. In the simplest case, each membrane
point i uses the function getGeometryNodesWithinRadiusWithAvoidanceClosest to
get the closest membrane point j of another cell, which is within a predefined cut-off
radius lmax , or zero if there is no such membrane point. Once a candidate membrane
point fulfils the criteria, a new Hookean force Fi with a spring constant k j and resting
length l0 is created:
Ficj

k j xj −xi (|xj − xi | − l0 )
|xj −xi |
=
0
if |xj − xi | < lmax
.
(3.20)
else
71
The cell junction forces are regularly (potentially not at every time step) deleted and
renewed, where the frequency of cell junction renewal might reflect the cell junction
synthesis rate.
The function getGeometryNodesWithinRadiusWithAvoidance returns all membrane
points of another cell, which are within a predefined cut-off radius; the returned list
might be empty. This opens up the possibility to introduce randomness by choosing the
membrane point randomly from the candidate list. The probability to create a junction
might depend on the junction length: the shorter, the higher the probability to form
a new junction. Also the removal of membrane points might be randomized, and the
probability made dependent on the junction length, i.e. overly stretched junctions are
removed with higher probability. Even the membrane point whose junctions shall be
updated might be chosen randomly. Again, the number of updated membrane nodes per
time reflects the cell’s limited cell junction synthesis activity.
The membrane points are internally stored in an fast neighbor list data structure, which
is well suited for spatial range queries. BioSolverCellJunction is an example of a class
responsible for cell junctions.
Cell Division
The cell division functionality requires several steps. First, criteria will have to be
defined which cells shall be divided. Criteria might be maximal cell area, maximal
spatial expansion, or biochemical signals. Once a cell committed for division, the cell
division plane will have to be chosen. Again, how to chose the plane is subject to
biological modelling. A frequently used rule is to use a plane defined by a random
direction vector and the center of mass of the cell. However, different rules can be readily
implemented, such as random directions drawn from non-uniform probability distributions
(which, in turn, can be controlled e.g. by signalling factor gradients) or division planes
perpendicular to the longest axis ([Minc et al., 2011]). In a next step, the two membrane
segments are determined which intersect with the division plane; this is implemented in
getTwoConnectionsRandomDirection or getTwoConnectionsLongestAxis. These two
membrane segments are subsequently removed, and two new membrane segments across
the cell are introduced, leading to a cut through the mother cell. Finally, a new domain
identity number has to be given to one of the daughter cells; the other daughter cell
inherits the domain identity number from the mother cell. The new domain identity
number is set to the largest domain identity number plus one, and it is automatically
copied to the physical grid. Both daughter cells by default inherit the cell type flag from
the mother cell, which is also automatically copied to the physical grid.
The basic cell division functionality is implemented in the class BioSolverCellDivision.
72
3.4. Software
Differentiation
Differentiation changes the cell type flag of the cells according to user-defined, biologically motivated rules. These rules might be based on the cell area, or on a signalling
factor concentration, possibly integrated over the cell area. Once being committed for
differentiation, the cell changes its cell type flag according to the rule. The new cell type
flag will be automatically copied to the physical grid. The cell type flag can be used to
make signalling dynamics, but also other biologically motivated processes dependent on
the cell type.
The association between the domain identifier flags and the cell type flags is stored in the
cellTypeTrackerMap_, which is a member of the GeometryHandler. This makes sure
that all BioSolverXX classes have easy access to this information. A basic implementation
of the differentiation control can be found in BioSolverDifferentiation.
3.4.6
Performance
The internal data structure uses a fast neighbor list (cell list) implementation to optimize
for range queries (e.g. searching for other cells in the local neighborhood), which
exhibits a search complexity of O (N ), with N being the number of membrane points to
represent the cells. Many iterative computations (LB and IB routines such as particle
streaming and collision, gathering of velocity and scattering of force) are parallelized
using the shared memory paradigm. However, a few computational steps cannot be
parallelized. This is typically the case when write-operations occur on shared data
structures, such as the data structures storing the geometry nodes and the force structs
(e.g. in ForceSolver::deleteForceType() and GeometryHandler::computeAreas()).
Moreover, the geometry remeshing (refining and coarsening) functions as well as the data
I/O are not parellelized, but are assumed to occur much less frequently than the actual
fluid and reaction-advection-diffusion solvers. Therefore, since the fraction of sequential
code is not negligible, the software should best be run on fast multi-core processors.
3.4.7
Tools, Dependencies and Documentation
A compiler with C++0x support (such as GCC 4.7 or higher) is required. The software
depends on Boost (http://www.boost.org; 1.54.0 or higher), OpenMP, CMake (http:
//www.cmake.org) and vtk (http://www.vtk.org/; 5.8 or higher). The source code is
extensively documented using Doxygen (http://www.stack.nl/~dimitri/doxygen). Git
(http://git-scm.com) is used for version control. The software has only been tested on
linux operating systems.
73
3.4.8
Availability
The documentation and source code are available on
http://tanakas.bitbucket.org/lbibcell/index.html
3.5
Mechanical Validations
This section is concerned with the numerical validation of the fluid solver and the
immersed boundary method. On a tissue scale, the cell topologies are compared to an
alternative cell model, as well as to experimental data.
3.5.1
Error Norms
For the numerical validations, the error norms given in Table 3.1 have been used.
u = u (x, t) denotes the numerical solution at point x and time t, and ue the according
exact solution. Summation is taken over all grid points N .
Table 3.1 – Error norm definitions.
relative L1
L1rel
3.5.2
PN
|u−ue |
i=1
= P
N
e
|u |
i=1
relative L2
sP
N
L2rel =
i=1
P
N
(u−ue )2
(ue )2
i=1
relative L∞
L∞
rel =
maxi (|u−ue |)
maxi (|ue |)
Validation of the Fluid Solver, Immersed Boundary Method and
Mass Sources
To validate the implementation of the fluid solver, the reaction-advection-diffusion
solver and the immersed boundary method, validation tests using problems with known
analytical solutions are executed.
The dimensionless problem is as follows: a circular cell (diameter 1) is placed in the
middle of a square domain of size 10x10. The end simulation time is T = 1. Inside the
cell, a diffusing species is defined, where the cell membrane acts as a no-flux boundary
condition. No production and degradation of the species occurs. The initial condition of
the species is set to be uniformly 1. The diffusion coefficient as well as the kinematic
viscosity of the fluid are set to 1. No membrane forces are applied; iso-pressure outflow
boundary conditions are applied to the domain boundaries.
Three different scenarios are considered:
• Case I: a constant point mass source is placed in the middle of the cell (dimensionless
strength is 1); see Figure 3.5A
74
3.5. Mechanical Validations
2
1.5
1
0
0.5
1
1
0.8
0.8
0.6
0.6
1
0
0.5
1
1
1
1
0.8
0.8
0.6
0.6
1.5
2
1.8
1.6
1.4
1.2
1
0
0.5
0
1
0.5
1
1
1
1
0.8
0.8
0.6
0.6
1.5
2
1.5
1
0
0.5
1
0
0.5
1
1
1.5
2
Figure 3.5 – Validation cases: evolution of area and concentration. T is the non-dimensional
normalized time, A the non-dimensional normalized area, C the non-dimensionalized normalized concentration. The column X1 shows area A vs. time T ; column X2 shows concentration C vs. time T ; and
column X3 shows concentration C vs. area A. A Case I: constant point-like mass source; B Case II:
constant uniform mass source; C Case III: uniform mass source proportional to the concentration C.
• Case II: a constant uniform mass source inside the cell (dimensionless strength is
log(2)/A0 , where A0 = 0.52 π is the initial cell area; this leads to a doubling of the
cell area in time T ), see Figure 3.5B
• Case III: a uniform mass source inside the cell, where the strength is scaled linear
proportional to the species concentration (= 1·C(t), where C(t) is the concentration
of the species; this leads to a linear mass/area increase in time), see Figure 3.5C
For all three cases, the circular cell starts to grow, and the species is diluted, i.e. the species
concentration drops as the area increased. Ideally, the integrated species concentration is
conserved. The relative L1 errors of the simulations w.r.t. the analytical solutions are
computed for both the area and concentration evolution.
The simulations are executed at different levels of space and time discretization. As a
measure, we take the diameter resolution of the circular cell, which is set to {10, 20, 40, 80}.
As a result, the discretized values (LB denotes lattice Boltzmann units, and ND denotes
75
non-dimensional) for all cases can be found in Table 3.2.
Table 3.2 – Lattice Boltzmann discretization of Cases I-III. ND and LB denote non-dimensional and
lattice Boltzmann units, respectively
circle diameter
domain size
τ fluid
ν LB fluid
τ diff
ν LB diff
δx
T LB
δt
S LB = S ND · δδ2t
x
10
100x100
1
1/6
1
1/6
0.1
1e4
1e-4
1e-2
20
200x200
1
1/6
1
1/6
0.05
4e4
25e-6
1e-2
40
400x400
1
1/6
1
1/6
0.025
1.6e5
625e-8
1e-2
80
800x800
1
1/6
1
1/6
0.0125
6.4e5
15625e-10
1e-2
The validation results for Case I are given in Figure 3.6. Figure 3.6A shows the relative
error temporal evolution of the cell area for the different resolutions, and 3.6B the relative
error temporal evolution of the integrated concentration. The concentration error is
much more noisy because it is only evaluated on lattice points. When the cell grows,
the membrane sweeps across the lattice, and whenever a new lattice site enters the
intracellular domain, the integrated concentration increases abruptly. To compute the
convergence w.r.t. to spatial and temporal resolution, the relative errors at T N D = 1 are
evaluated for the area, but the temporal mean is taken for the concentration convergence
analysis. Figure 3.6C shows the convergence analysis for the area. For the finer grids,
the convergence order is approximately 1. Figure 3.6D depicts the convergence analysis
for the integrated concentration, where the fitted order of convergence is ≈ 1.2.
The validation results for Case II are given in Figure 3.7. Figure 3.7A shows the relative
much more noisy because the it is only evaluated on lattice points. When the cell grows,
convergence w.r.t. to spatial and temporal resolution, the relative errors at T ND = 1 are
The validation results for Case III are given in Figure 3.8. Figure 3.8A shows the relative
much more noisy because the it is only evaluated on lattice points. When the cell grows,
76
−3
x 10
2.5
0.05
DIA=10
DIA=20
DIA=40
DIA=80
2
DIA=10
DIA=20
DIA=40
DIA=80
0.045
0.04
0.035
1.5
0.03
0.025
1
0.02
0.015
0.5
0.01
0.005
0
0
0.2
0.4
0.6
0.8
1
0
−6
−4
−7
−4.5
−8
−5
−9
−5.5
−10
−6
−11
−6.5
−12
2
2.5
3
3.5
4
4.5
−7
0
0.2
0.4
0.6
0.8
1
2
2.5
3
3.5
4
4.5
Figure 3.6 – Case I validation: point source. An initially circular cell is growing through addition
of mass. The mass is added by using a point source in the middle of the domain. Four different spatial
resolutions have been computed, corresponding to a resolution of DIA = {10, 20, 40, 80} lattice points
for the diameter of the initial circular cell. A The time evolution of the relative error of the cell area
for 4 different lattice resolutions. B The time evolution of the relative error of the spatially integrated
concentration (mass conservation) for 4 different lattice resolutions. C Convergence plot of the relative
error of the cell area as a function of the lattice resolution. The fitted slope is -1.80. The dashed line
denotes a slope of -2. D Convergence plot of the relative error of the integrated concentration (mass
conservation) as a function of the lattice resolution. The fitted slope is -1.22. The dashed line denotes a
slope of -1.
convergence w.r.t. to spatial and temporal resolution, the relative errors at T ND = 1 are
Finally, the immersed boundary force distribution is validated (Case IV). The initial
setup is similar to the Cases I-III, but a constant membrane force is applied, and there is
no mass source. Due to numerical leakage, the cell starts to shrink and looses mass/area.
77
0.08
0.05
DIA=10
DIA=20
DIA=40
DIA=80
0.07
0.06
DIA=10
DIA=20
DIA=40
DIA=80
0.045
0.04
0.035
0.05
0.03
0.04
0.025
0.02
0.03
0.015
0.02
0.01
0.01
0.005
0
0
0.2
0.4
0.6
0.8
1
−2.5
0
0
0.2
0.4
0.6
0.8
1
2
2.5
3
3.5
4
4.5
−3
−4
−3
−5
−3.5
−6
−4
−7
−4.5
−5
−8
2
2.5
3
3.5
4
4.5
−9
Figure 3.7 – Case II validation: uniformly distributed source. An initially circular cell is growing
through addition of mass. The mass is added by applying a constant uniform mass source on the entire
cellular domain. Four different spatial resolutions have been computed, corresponding to a resolution of
DIA = {10, 20, 40, 80} lattice points for the diameter of the initial circular cell. A The time evolution of
the relative error of the cell area for 4 different lattice resolutions. B The time evolution of the relative
error of the spatially integrated concentration (mass conservation) for 4 different lattice resolutions. C
Convergence plot of the relative error of the cell area as a function of the lattice resolution. The fitted
slope is -0.99. The dashed line denotes a slope of -1. D Convergence plot of the relative error of the
integrated concentration (mass conservation) as a function of the lattice resolution. The fitted slope is
-1.43. The dashed lines denote slopes of -1 and -2, respectively.
The dimensionless force is chosen to be F ND = 1e3, and the dimension conversion is
described in Table 3.3. The discretization of the validation setup can be found in Table
3.4.
Besides the spatial and temporal discretization of the lattice, also the discretization of
the immersed boundary is studied in Case IV. The distance between any two neighboring
boundary points is shorter than the parameter MAXLENGTH, which is always a factor
of the lattice discretization δx . If MAXLENGTH is set to 0.5, then the distance between
two boundary points does not exceed half of the lattice spacing. MAXLENGTH=0.5 is a
frequently used constant [Peskin and Printz, 1993]; however, here, we also tested smaller
(0.1) and larger (2.5) values.
78
0.07
0.05
DIA=10
DIA=20
DIA=40
DIA=80
0.06
0.05
0.04
0.035
0.03
0.04
0.025
0.03
0.02
0.015
0.02
0.01
0.01
0.005
0
0
0.2
0.4
0.6
0.8
0
1
−2.5
−3
−3
−4
−3.5
−5
−4
−6
−4.5
−7
−5
−8
−5.5
DIA=10
DIA=20
DIA=40
DIA=80
0.045
2
2.5
3
3.5
4
4.5
−9
2
0
0.2
2.5
0.4
3
0.6
3.5
0.8
4
1
4.5
Figure 3.8 – Case III validation: fully coupled system. An initially circular cell is growing
through addition of mass. The mass is added by applying a mass source on the entire cellular domain,
but the mass source strength is proportional to the concentration of the intracellular concentration.
Therefore, the cellular area should increase linearly in time. Four different spatial resolutions have been
computed, corresponding to a resolution of DIA = {10, 20, 40, 80} lattice points for the diameter of the
initial circular cell. A The time evolution of the relative error of the cell area for 4 different lattice
resolutions. B The time evolution of the relative error of the spatially integrated concentrations (mass
conservation) for 4 different lattice resolutions. C Convergence plot of the relative error of the cell area as
a function of the lattice resolution. The fitted lattices is -1.01. The dashed line denotes a slope of -1. D
Convergence plot of the relative error of the integrated concentration (mass conservation) as a function of
the lattice resolution. The fitted slope is 1.50. The dashed lines denote slopes of -1 and -2, respectively.
The validation results of Case IV are showed in Figure 3.9. In Figure 3.9A, the evolution
of the relative errors of the area are shown for different lattice resolutions. Figure 3.9B
shows the convergence as a function of MAXLENGTH. The MAXLENGTH= {0.1, 0.5} values
lead to almost similar results, thus confirming that MAXLENGTH=0.5 is indeed sufficient.
The convergence as a function of the lattice resolution is shown in Figure 3.9C. The fitted
order of convergence is approximately 1. MAXLENGTH= {0.1, 0.5} lead to indistinguishable
results; however, even MAXLENGTH=2.5 still leads to converging results.
Here, for the convergence analyses, the fluid, mass sources, fluid outlet boundary conditions, the advection and diffusion of a species, its no-flux boundary condition, the
79
Table 3.3 – Lattice Boltzmann discretization of mass and force. ND and LB denote non-dimensional
and lattice Boltzmann units, respectively.
mass density
mass units [M ]
ND
LB
ρN D
ρLB
LB→ ND ]
[1]
mass density units 2D
[M/L2 ]
[δm
LB→ ND
δm
LB→
ND )2
(δx
LB
F
[1]
F ND
force
force units
[M L/T 2 ]
[1]
LB→
δm
(
ND δ LB→ ND
x
LB→
ND 2
δt
)
Table 3.4 – Lattice Boltzmann discretization of the convergence analysis of Case IV. ND and LB denote
non-dimensional and lattice Boltzmann units, respectively.
circle diameter
domain size
τ fluid
ν LB fluid
τ diff
ν LB diff
δx
T LB
δt
mass density ρND = 1
ND
δm = ρρLB (δx )2
δ2
F LB = F ND δmtδx
80
100x100
1
1/6
1
1/6
0.1
1e4
1e-4
1
1e-2
160
200x200
1
1/6
1
1/6
0.05
4e4
2.5e-5
1
2.5e-3
320
400x400
1
1/6
1
1/6
0.025
1.6e5
6.25e-6
1
6.25e-4
640
800x800
1
1/6
1
1/6
0.0125
6.4e5
1.5625e-06
1
1.5625e-4
1e-3
5e-4
2.5e-4
1.25e-4
immersed boundary and membrane forces are considered. We showed that all aspects are
converging and conclude that the net order of convergence of the fully coupled system is 1.
Depending on the aspect under consideration, it can be higher. It is well known that the
standard immersed boundary method suffers from fluid leakage, because the discretized
kernel function is not divergence-free. Several improvements have been proposed (e.g.
[Peskin and Printz, 1993, Niu et al., 2006]).
80
0.2
0.15
MAXLENGTH = 0.1
0.2
0.4
0.6
0.02
0.8
1
0.05
0
−1.9
MAXLENGTH = 2.5
0
0.2
0.4
0.6
0.8
1
−2
−4
−2
0
2
−2
0
2
−2
0
2
−2
0
2
0.02
0.04
−2.3
0.015
0.03
MAXLENGTH = 0.02
MAXLENGTH = 0.5
0
0.2
0.4
0.6
0.8
1
0
−2.4
MAXLENGTH = 0.1
MAXLENGTH = 0.5
0.005
MAXLENGTH = 2.5
0.01
MAXLENGTH = 0.02
0.01
MAXLENGTH = 0.1
0.02
0
−1.8
MAXLENGTH = 0.1
MAXLENGTH = 0.5
MAXLENGTH = 2.5
0
MAXLENGTH = 0.02
0.04
MAXLENGTH = 0.5
0.05
−1.7
0.06
MAXLENGTH = 0.02
0.1
0
−1.6
0.1
0.08
MAXLENGTH = 2.5
0
0.2
0.4
0.6
0.8
−2.5
1
−2.6
−4
−1.5
MAXLENGTH = 0.02
MAXLENGTH = 0.1
MAXLENGTH = 0.5
MAXLENGTH = 2.5
−2
−3
−3.1
−2.5
−3.2
−3.3
−4
−3
−3.92
−3.5
−3.94
−4
−4.5
−3.96
2
2.5
3
3.5
4
4.5
−3.98
−4
Figure 3.9 – Case IV validation: mass conservation. A constant membrane tension is applied to
an initially circular cell. The contractile force will lead to a shrinking cell due to mass leaking of the
immersed boundary. Here, the influence of the immersed boundary discretization is investigated. Four
different spatial resolutions have been computed, corresponding to a resolution of DIA = {10, 20, 40, 80}
lattice points for the diameter of the initial circular cell. MAXLENGTH denotes the maximally tolerated
distance between each two immersed boundary points (measured in space discretization units). A The
time evolution of the relative error of the cell area for 4 different lattice resolutions, and for 3 values of
MAXLENGTH. B The relative error of the cell area as a function of MAXLENGTH for different lattice resolutions.
C Convergence plot of the relative error of the cell area as a function of the lattice resolution, plotted for
3 values of MAXLENGTH. The fitted slope of the two finest lattices is 0.9891.
81
3.5.3
Comparison to Farhadifar et al., 2007
The cell topologies are compared to results of the cell vertex model as presented in
[Farhadifar et al., 2007]. Starting from a single cell, a tissue with more than 1000 cells is
grown with a constant mass source of 0.004 (in LB units). A cell is divided in a random
direction if it exceeds an area of 380 (in LB units). The membrane tension is varied
(F LB = {0.001, 0.01, 0.02} in LB units).
The snapshots in Figure 3.10 show the topology for different values of membrane tension
(A very low membrane tension; B medium membrane tension; C high membrane tension).
The higher the membrane tension, the higher the rearrangement activity because cell-cell
junctions are broken more easily, and the cells can more easily assume a preferential
shape (hexagonal in the domain, circular at the boundary). In Figure 3.10D, the tissue
shown in figure 3.10B is relaxed, i.e. cell division is stopped, and only rearrangement is
occurring towards an equilibrium configuration.
For these cases, the number of vertices are counted. The result is shown in Figure 3.11,
together with the experimental and model results of [Farhadifar et al., 2007]. Although
the topologies for different membrane tensions differ significantly, the distribution of the
number of vertices (equivalent to the number of neighbors) is not significantly affected.
The relaxed topology, however, is shifted towards higher occurrence of hexagons. Overall,
our results are in agreement with the experimental and simulation results obtained by
[Farhadifar et al., 2007].
82
Figure 3.10 – Cell topologies for different membrane forces. A The membrane force constant
is small (F LB = 0.001), such that the cells cannot rearrange adequately. B The membrane force constant
is relatively high (F LB = 0.01), such that the rearrangement activity alters the topology significantly. C
The membrane force constant is even higher (F LB = 0.02). D The tissue shown in B is relaxed towards
equilibrium. The color code denotes the domain identifier value (red = young cells, blue = old cells)
83
low tension
medium tension
high tension
Farhadifar experiment
Farhadifar case I
medium tension
medium tension relaxed
Figure 3.11 – Comparison of the cell topologies to literature results. Pn denotes the occurrence
fraction of an n-sided polygon. Polygons with n > 9 are lumped into n = 9. A ’Low/medium/high
tension’ correspond to different membrane tensions (F LB = {0.001, 0.01, 0.02} in LB units). ’high tension’
has a slightly higher occurrence of penta- and hexagons. B ’Farhadifar experiment’ is the polygon
distribution in a third instar Drosophila wing disc. ’Farhadifar case I’ and ’Farhadifar case II’ denote
simulations with low and high relative contractility, respectively. ’Medium tension relaxed’ corresponds
to an equilibrated simulation with F LB = 0.01 after proliferation has stopped.
84
3.6. Reaction-Advection-Diffusion Solver Validation
3.6
Reaction-Advection-Diffusion Solver Validation
In this section, the reaction, advection and diffusion processes are systematically (individually and in combination) validated against known analytical solutions.
3.6.1
Diffusion of a Dirac Delta Peak
Since the solution of the diffusion of a Dirac delta peak is analytically known, it serves
as a widely-used benchmark problem. The dimensionless governing equation for the
concentration C = C (x, y, t) reads:
∂t C = D∇2 C ,
(3.21)
with D being the diffusion coefficient. The analytical solution is:
M
x2 + y 2
exp −
C=
Lz 4πtD
4Dt
!
,
(3.22)
where Lz = 1 for the two-dimensional problem. The unit of C is M/L2 , and the initial
condition is:
C (t = 0) = M δ (x) δ (y) .
(3.23)
The problem is chosen (domain size, time) such that the peak does not reach the domain
boundary. Hence, the choice of domain boundary conditions is irrelevant - periodic
boundary conditions are used here.
Only Diffusion with DND = 1e-4
The square domain has the size 1x1, start time is T = 0.5, end time at T = 1.0, and the
diffusion coefficient is DND = 1e-4 (all in non-dimensional units). The discretizations
and simulation results are summarized in Table 3.5. Figure 3.12 shows the convergence
plots; the order of convergence using diffusive scaling is ≈ 2.
Table 3.5 – Parameters and results for the diffusion of a Dirac delta peak with DND = 1e-4.
grid size
∆x
τ LB
DLB
∆t
#ts
L1rel
L2rel
L∞
rel
100x100
200x200
400x400
800x800
0.01
0.05
0.025
0.0125
0.55
0.55
0.55
0.55
1/60
1/60
1/60
1/60
1/60
1/240
1/960
1/3840
30
120
480
1920
0.091007891
0.0207633065
0.0051907356
0.00129597891
0.0822064867
0.0210007355
0.0052734649
0.00131972334
0.116583712
0.0308902078
0.00782753363
0.00196335032
85
−2
−2
−2
−2.5
−2.5
−2.5
−3
−3
−3
−3.5
−3.5
−3.5
−4
−4
−4
−4.5
−4.5
−4.5
−5
−5
−5
−5.5
−5.5
−5.5
−6
−6
−6
−6.5
−6.5
−6.5
−7
−7
−6.5
−6
−5.5
−5
−4.5
−7
−7
−6.5
−6
−5.5
−5
−4.5
−7
−7
−6.5
−6
−5.5
−5
−4.5
Figure 3.12 – Convergence analysis for the diffusion of a Dirac delta peak with DND = 1e-4.
The fitted slopes are {2.0402, 1.9876, 1.9656}.
diffusion coefficient is DND = 1e − 3 (all in non-dimensional units). The discretizations
plots; the order of convergence using diffusive scaling is ≈ 2.
Table 3.6 – Diffusion of a Dirac delta peak with DND = 1e-3.
grid size
∆x
τ LB
DLB
∆t
#ts
L1rel
L2rel
L∞
rel
100x100
200x200
400x400
800x800
0.01
0.05
0.025
0.0125
1.0
1.0
1.0
1.0
1/6
1/6
1/6
1/6
1/60
1/240
1/960
1/3840
30
120
480
1920
0.00364984052
0.000904295513
0.000225521866
5.63450996e-05
0.00367077689
0.000910758759
0.00022726156
5.6788714e-05
0.00546352404
0.00135707576
0.000338723179
8.46467564e-05
−5
−5
−5
−5.5
−5.5
−5.5
−6
−6
−6
−6.5
−6.5
−6.5
−7
−7
−7
−7.5
−7.5
−7.5
−8
−8
−8
−8.5
−8.5
−8.5
−9
−9
−9
−9.5
−9.5
−9.5
−10
−7
−6.5
−6
−5.5
−5
−4.5
−10
−7
−6.5
−6
−5.5
−5
−4.5
−10
−7
−6.5
−6
−5.5
−5
−4.5
Figure 3.13 – Convergence analysis for the diffusion of a Dirac delta peak with DND = 1e-3
86
plots; the order of convergence using diffusive scaling is ≈ 1.7.
Table 3.7 – Diffusion of a Dirac delta peak with DND = 1e-2.
grid size
∆x
τ LB
DLB
∆t
#ts
L1rel
L2rel
L∞
rel
100x100
200x200
400x400
800x800
0.01
0.05
0.025
0.0125
5.5
5.5
5.5
5.5
10/6
10/6
10/6
10/6
1/60
1/240
1/960
1/3840
30
120
480
1920
0.0608197161
0.0178214139
0.00504715889
0.0018380263
0.058218662
0.0157994717
0.00411674488
0.00148601208
0.0848366695
0.0218396233
0.00533725918
0.0019917119
−2
−2
−2
−2.5
−2.5
−2.5
−3
−3
−3
−3.5
−3.5
−3.5
−4
−4
−4
−4.5
−4.5
−4.5
−5
−5
−5
−5.5
−5.5
−5.5
−6
−6
−6
−6.5
−6.5
−6.5
−7
−7
−6.5
−6
−5.5
−5
−4.5
−7
−7
−6.5
−6
−5.5
−5
−4.5
−7
−7
−6.5
−6
−5.5
−5
−4.5
Figure 3.14 – Convergence analysis for the diffusion of a Dirac delta peak with DND = 1e-2.
Advection and Diffusion with DND = 1e-3
plots; the order of convergence using diffusive scaling is ≈ 2. The advection is chosen
such that it is not aligned with any lattice direction (VxND = 0.1 and VyND = 0.05).
Table 3.8 – Advection and diffusion of a Dirac delta peak with DND = 1e-3.
grid size
∆x
τ LB
DLB
∆t
#ts
L1rel
L2rel
L∞
rel
100x100
200x200
400x400
800x800
0.01
0.05
0.025
0.0125
1.0
1.0
1.0
1.0
1/6
1/6
1/6
1/6
1/60
1/240
1/960
1/3840
30
120
480
1920
0.0375505604
0.00925002034
0.00230382095
0.000575413373
0.0339101271
0.00829929163
0.00206350525
0.00051516695
0.0309315123
0.00749238573
0.00186178655
0.000464870467
87
−3
−3
−3
−3.5
−3.5
−3.5
−4
−4
−4
−4.5
−4.5
−4.5
−5
−5
−5
−5.5
−5.5
−5.5
−6
−6
−6
−6.5
−6.5
−6.5
−7
−7
−7
−7.5
−7.5
−7.5
−8
−7
−6.5
−6
−5.5
−5
−4.5
−8
−7
−6.5
−6
−5.5
−5
−4.5
−8
−7
−6.5
−6
−5.5
−5
−4.5
Figure 3.15 – Convergence analysis for the advection and diffusion of a Dirac delta peak
with DND = 1e-3. The fitted slopes are {2.0090, 2.0129, 2.0177}.
3.6.2
Nonlinear Reaction and Diffusion
In order to assess the forward Euler time integration of the reaction terms, the solver
is validated with a nonlinear advection-reaction-diffusion problem. The dimensionless
governing equation for C = C (x, y, t) reads [Hundsdorfer, 2000]:
∂t C + α∇C = D∇2 C = γC 2 (1 − C) ,
(3.24)
on the domain Ω = [0, 1]2 and t ∈ [0, 1]. The corresponding analytical solution is:
C (x, y, t) = (1 + exp (a (x + y − bt) + c))−1 ,
(3.25)
p
√
with a = γ/4D, b = 2α + γD and c = a(b − 1). The parameters for this validation
are chosen to be α = 0 (no advection), γ = 1 and DND = 1/10 unless stated otherwise.
The simulation start time is at T = 0 until T = 1. The initial condition and the nonautonomous boundary condition are taken from the analytical solution. For the Dirichlet
boundary condition, we implemented an extrapolation method [Guo et al., 2002].
Nonlinear Reaction and Diffusion with τ LB = 1.0
The discretizations and simulation results are summarized in Table 3.9. Figure 3.16
shows the convergence plots; the order of convergence using diffusive scaling is ≈ 2.
Table 3.9 – Nonlinear reaction and diffusion with τ LB = 1.0.
88
grid size
∆x
τ LB
DLB
#ts
L1rel
L2rel
L∞
rel
100x100
200x200
400x400
800x800
0.01
0.05
0.025
0.0125
1.0
1.0
1.0
1.0
1/6
1/6
1/6
1/6
6000
24000
96000
384000
4.03921232e-05
9.99054571e-06
2.48426722e-06
6.19399311e-07
4.09998098e-05
1.01834612e-05
2.53770679e-06
6.33416366e-07
4.95703838e-05
1.23982366e-05
3.10016918e-06
7.75125961e-07
−10
−10
−10.5
−10.5
−11
−11
−11.5
−11.5
−12
−12
−12.5
−12.5
−13
−13
−13.5
−13.5
−14
−14
−14.5
−14.5
−15
−7
−6.5
−6
−5.5
−5
−4.5
−15
−7
−9
−10
−11
−12
−13
−14
−6.5
−6
−5.5
−5
−4.5
−15
−7
−6.5
−6
−5.5
−5
−4.5
Figure 3.16 – Convergence analysis of nonlinear reaction and diffusion with τ LB = 1.0. The
fitted slopes are {2.0089, 2.0054, 1.9996}.
Nonlinear Reaction and Diffusion with τ LB = 5.5
The discretizations and simulation results are summarized in Table 3.10. Figure 3.17
shows the convergence plots; the order of convergence using diffusive scaling is ≈ 2.
Table 3.10 – Nonlinear reaction and diffusion with τ LB = 5.5.
grid size
∆x
τ LB
DLB
#ts
L1rel
L2rel
L∞
rel
100x100
200x200
400x400
800x800
0.01
0.05
0.025
0.0125
5.5
5.5
5.5
5.5
5/3
5/3
5/3
5/3
600
2400
9600
38400
0.00363336447
0.000888798547
0.000220605829
5.50155182e-05
0.0040673309
0.0009952117
0.0002471255
6.1650796e-05
0.00600994916
0.00148037657
0.00036855964
9.20537154e-05
−5
−5
−5
−5.5
−5.5
−5.5
−6
−6
−6
−6.5
−6.5
−6.5
−7
−7
−7
−7.5
−7.5
−7.5
−8
−8
−8
−8.5
−8.5
−8.5
−9
−9
−9
−9.5
−9.5
−9.5
−10
−7
−6.5
−6
−5.5
−5
−4.5
−10
−7
−6.5
−6
−5.5
−5
−4.5
−10
−7
−6.5
−6
−5.5
−5
−4.5
Figure 3.17 – Convergence analysis of nonlinear reaction and diffusion with τ LB = 5.5. The
fitted slopes are {2.0146, 2.0141, 2.0092}.
Nonlinear Reaction, Advection and Diffusion with τ LB = 1.0
The following parameter values have been used: α = −1, γ = 100 and = 0.01. The
discretizations and simulation results are summarized in Table 3.11. Figure 3.18 shows
the convergence plots; the order of convergence using diffusive scaling is ≈ 2.
89
Table 3.11 – Nonlinear reaction, advection and diffusion with τ LB = 1.0.
grid size
∆x
τ LB
DLB
#ts
L1rel
L2rel
L∞
rel
100x100
200x200
400x400
800x800
0.01
0.05
0.025
0.0125
1.0
1.0
1.0
1.0
1/6
1/6
1/6
1/6
600
2400
9600
38400
0.00972180917
0.00231511028
0.000570188653
0.00014183038
0.0243634067
0.00576189117
0.00141800649
0.000352862116
0.122253471
0.0287694742
0.0070933502
0.00176767032
−4
−3
−2
−4.5
−3.5
−2.5
−5
−4
−3
−5.5
−4.5
−3.5
−6
−5
−4
−6.5
−5.5
−4.5
−7
−6
−5
−7.5
−6.5
−5.5
−8
−7
−6
−8.5
−7.5
−6.5
−9
−7
−6.5
−6
−5.5
−5
−4.5
−8
−7
−6.5
−6
−5.5
−5
−4.5
−7
−7
−6.5
−6
−5.5
−5
−4.5
Figure 3.18 – Convergence analysis of nonlinear reaction, advection and diffusion with
τ LB = 1.0. The fitted slopes are {2.0319, 2.0351, 2.0356}.
Nonlinear Reaction, Advection and Diffusion with τ LB = 0.55
The following parameter values have been used: α = −1, γ = 100 and = 0.001. The
discretizations and simulation results are summarized in Table 3.12. Figure 3.19 shows
the convergence plots; the order of convergence using diffusive scaling is ≈ 2.4.
Table 3.12 – Nonlinear reaction, advection and diffusion with τ LB = 0.55.
90
grid size
∆x
τ LB
DLB
#ts
L1rel
L2rel
L∞
rel
100x100
200x200
400x400
800x800
0.01
0.05
0.025
0.0125
0.55
0.55
0.55
0.55
1/60
1/60
1/60
1/60
600
2400
9600
38400
0.0409224861
0.00551244929
0.00102394912
0.000240977833
0.141186927
0.0223036505
0.00412699029
0.000969345222
0.832616598
0.153020257
0.0271154949
0.00657281291
−3
−1
0
−4
−2
−1
−5
−3
−2
−6
−4
−3
−7
−5
−4
−8
−6
−5
−9
−7
−6.5
−6
−5.5
−5
−4.5
−7
−7
−6.5
−6
−5.5
−5
−4.5
−6
−7
−6.5
−6
−5.5
−5
−4.5
Figure 3.19 – Convergence analysis of nonlinear reaction, advection and diffusion with
τ LB = 0.55. The fitted slopes are 2.4652, 2.3993, 2.3452.
91
3.7
Application Example: Cell Division, Differentiation
and Signalling
To demonstrate the capabilities of the software we first consider a tissue model with
cell-type specific cell division and signalling-dependent differentiation (Figure 3.20). In
the beginning, a circular cell with radius R = 10 is placed in the middle of a quadratic
400 by 400 domain (Figure 3.20A). Iso-pressure boundary conditions are set at the border
of the domain. The initial cell is of red cell type, which is proliferating at a high rate.
When considering a single layer epithelium, mass uptake, which is needed for modelling
cell growth and finally proliferation, is assumed to occur from the apical cavity through
the apical membrane. Additionally, the initial cell secretes a signalling factor I which
inhibits differentiation of the red cell type into the green cell type. Once the cell area
doubled, the cell is divided in a random direction (cf. Figure 3.20B). The daughter
cells inherit the cell type, but only the mother cell continues to express the signalling
molecule I. All cells of red type integrate the concentration of I over their area. For low
signalling levels, the red cell type differentiates into the green cell type. The green cell
type does not grow and only divides if external forces stretch the cell. In Figure 3.20C,
the daughter cell’s signalling level dropped after cell division, and differentiation occurred.
The cells close to the secreting initial cell remain protected from differentiation, whereas
more distant cells differentiate irreversibly. Due to the randomly chosen cell division
axis, it might happen that the proliferating red cells get trapped (cf. Figure 3.20D). The
expression of I is switched off at time t=5000, thus leading to complete differentiation
shortly after (cf. Figure 3.20E). After proliferation stopped, the cells slowly rearrange
because cell-cell junctions are broken if overly stretched, and new junctions are formed
(according to Equation (3.20) ). At the boundary of the tissue, the cells try to reach a
spherical shape, while in the middle mainly characteristic penta- and hexagonal shapes
emerge (cf. Figure 3.20E and Section 3.5.3).
92
3.7. Application Example: Cell Division, Differentiation and Signalling
Figure 3.20 – Cell Division, Differentiation and Signalling. A The initial configuration consists
of a single, circular cell of type red. The red cell type proliferates at a high rate. The initial cell is tagged
and expresses a signalling molecule I which inhibits differentiation. B The first cell division occurs. The
division axis is chosen randomly. The daughter cell inherits the cell type from the mother cell, but only
the mother cell keeps expressing the signalling molecule I. C The signalling level (the spatially integrated
concentration of the signalling molecule) drops in cells far away from the initial cell and differentiation
into the green cell type occurs. The green cell type does not grow intrinsically, and only divides if overly
stretched by external forces. D The highly proliferating red cells are trapped in the forming tissue due
to the randomly chosen cell division axis. At t = 5000, the expression of the differentiation inhibiting
molecule I is switched off, which leads to the differentiation of the remaining red cells. E In the absence
of high proliferation, the cells rearrange to maximize the perimeter/area ratio. Characteristic penta- and
hexagonal cell shapes emerge (cf. Supp. 3.5.3). Cells close to the boundary try to take a circular shape.
93
3.8
Discussion
The extendible and open-source cell-based simulation environment LBIBCell is tailored to
study morphogenetic problems. The novel framework permits the coupled simulation of a
physically motivated visco-elastic cell model with regulatory signalling models. Processes
such as viscous dissipation, elasticity, advection, diffusion, local reactions, local mass
sources and sinks, cell division and cell differentiation are implemented.
The presented framework permits to study a variety of mechano-regulatory mechanisms.
By making the cell division orientation dependent on signalling cues, the effect on
the macroscopic tissue geometry may be studied. Cell migration can be modelled
by introducing gradient-dependent forces on specific cell types. Cell sorting may be
achieved by specifying multiple cell types with differential cell-cell junction strengths.
The framework is specifically designed to study the mutual effects of signalling and
biophysical cell properties.
The visco-elastic cell model represents cell shapes at very high resolution and is thus, unlike
the vertex model, not restricted to densely packed tissues. Furthermore, hydrodynamic
interaction, membrane tension and hydrostatic pressure are integral components of the
model. The fact that a velocity field is available on the entire domain is a critical
advantage to account for advection of the signalling components, thus allowing for a
spatial description of intracellular concentrations.
Thorough numerical validations of different aspects (fluid solver, mass solver, immersed
boundary method, nonlinear reaction, advection, dilution and diffusion) demonstrated
accurate implementation and consistent convergence of at least first order using diffusive
scaling.
The model is, however, not easily extendable to the third dimension. Since a meshing of
the surface will be required, the algorithmic and computational complexity are expected
to be significant and subject to future work. The presented framework is, however, ideal
to study intrinsically two-dimensional morphogenetic problems, such as apical surface
dynamics of epithelia as studied previously also by [Farhadifar et al., 2007] and [Ishihara
and Sugimura, 2012] in two dimensions.
94
4 Turing Patterns on Cellular Tissue
The multimeric binding of freely diffusing ligands to receptors on the cell surfaces is capable
to form patterns, which has been extensively studied in the context of computational
developmental biology. On continuous computational domains it can be shown that this
interaction can lead to Turing-type instability mechanisms, which exhibit, depending on
the parametrization, characteristic regular spot and stripe patterns. In this chapter, after
an overview of the relevance of receptor-ligand interactions in developmental biology, the
behaviour on cellular and growing domains is investigated computationally using the
cell-based simulation tool LBIBCell as previously described in Chapter 3. As compared
to the continuous domain counterparts, qualitatively novel behaviour, including semirandom salt-and-pepper patterns and cluster formation, is found. A three-component
model, consisting of a ligand, a receptor and a diffusing activator, is studied on cellular
and growing domains. In contrast to the simple ligand-receptor system, the patterns of
the three-component system span over multiple cell scales and are potential candidates
for morphogenetic problems where tissue-wide coordination is required.
This chapter has been prepared for submission as:
Tanaka S, Menshykau D, Iber D, Receptor-Ligand Patterning on Growing Cellular
Domains
95
Chapter 4. Turing Patterns on Cellular Tissue
4.1
Introduction to Receptor-Ligand Interaction in Developmental Biology
Symmetry breaking mechanisms are of fundamental importance in developmental biology
[Li and Bowerman, 2010]. Starting from a fertilized vertebrate egg, several rounds
of cleavage lead to a symmetric ball, the morula, and later to the blastula. What
mechanism causes a set of cells being in a genetically identical state to order into complex
patterns in a reliable, deterministic and robust way? In 1952, Alan Turing proposed
that the interaction between two diffusible chemical species are capable to create regular
spatial patterns [Turing, 1952], and proposed that this mechanism might be the basis for
symmetry breaking in morphogenesis. Later, Alfred Gierer and Hans Meinhardt [Gierer
and Meinhardt, 1972] defined specific requirements for a Turing mechanism: instability
only occurs if and only if one diffusible chemical compound acts as a local (short-range)
auto-catalytic activator, and the other diffusible compound as a long-range inhibitor;
the latter has to diffuse faster in order to antagonize the self-enhancing properties of
the activator. Initial perturbations will be amplified, leading to deterministic patterns.
Although the macroscopic patterns may reach a steady state, the Turing mechanisms
are constantly out-of-equilibrium, i.e. both compounds are unceasingly produced and
degraded.
The intrinsic symmetry breaking properties and the rich variety of patterns and behaviour
have been analysed in the context of many biological problems. Because of the stunning
similarity, the Turing patterns have been extensively compared to the sea shell [Meinhardt,
2009] and animal skin patterns [Sanderson et al., 2006]. Many regular structures, such as
the mammalian palate [Economou et al., 2012], alligator teeth patterning [Kulesa et al.,
1996], murine digit formation [Miura et al., 2006], feather primordia development [Jiang
et al., 1999] and hair follicle pre-patterning [Sick et al., 2006] have been studied in the
light of Turing mechanism variants.
Despite the appealing properties, a number of questions arise with regard to the realisticity
of Turing mechanisms in developmental biology. Besides the identification of the core
players, the requirement for a large difference of the diffusion coefficients raises questions
about the direct applicability of Turing mechanisms. For example, the secreted proteins
Nodal and Lefty, members of the transforming growth factor β family, are a well-conserved
system in many organisms. In agreement with the definition of the Turing mechanism,
Nodal acts as an auto-catalytic short-range activator, and Lefty as a long-range inhibitor,
and it was shown that the diffusivities are significantly different [Muller et al., 2012]. In
general, however, contemplable molecules diffuse at a similar rate (assuming that the
diffusion coefficient in aqueous solutions can be approximated by D ∼ M −0.37 with M
being the molecular weight) [Sober, 1969], which is contradictory to the requirements for
Turing instability. Furthermore, the rather small parametric space of Turing instabilities
is criticised to be unlikely that evolution repeatedly succeeded to find a combination of
96
4.1. Introduction to Receptor-Ligand Interaction in Developmental Biology
working parameters [Murray, 1982].
A recent approach interprets the short-range activator to be a membrane-bound receptor
or an intracellular pathway, respectively, and the long-range inhibitor to be a diffusing
ligand. As we will show in Subsection 4.2, the receptor-ligand interaction mechanisms
can lead to a Schnakenberg-type mechanisms [Schnakenberg, 1979], for which a number
of systems are qualified for: the interaction between the intercellular molecule Hedgehog
and its receptor Patched was suggested to be the dominating mechanisms to control
branching morphogenesis in murine mice [Menshykau et al., 2012, Cellière et al., 2012]; a
similar module consisting of the ligand GDNF and its receptor RET controls branching
of the developing kidney [Menshykau and Iber, 2013]; the secreted protein BMP and its
receptor BMPR may give rise to a Turing instability leading to digit pre-patterning in
the hand plates of mice [Newman and Frisch, 1979, Badugu et al., 2012]. By adding
additional feedbacks, coupling multiple Turing modules, or by restricting the receptor
to the membrane of cellular structures, it was shown that the parameter space where
instability occurs can be significantly enlarged [Kurics et al., 2014].
In a very generalized definition, mechanisms with ’locally acting positive feedback loops
and globally acting negative regulators’ [Sohrmann and Peter, 2003], but with spatial
transport mechanisms being different from free diffusion, may be defined to be Turinglike as opposed to the original Turing mechanism consisting of two diffusible chemical
compounds. For example, mechano-chemical models are based on the interaction of
one diffusing signal and one cell type which migrates up a chemical gradient [Oster and
Murray, 1989, Maini et al., 1991]. The first mechanism of this kind has been developed
to explain the self-organizing properties of Dictyostelium discoideum. By expressing
the chemotactic flux of the continuous cell density to be proportional to the gradient
of the chemo-attractant, a set of differential equations resembling the one of a Turing
mechanisms can be obtained [Keller and Segel, 1970].
Variants of the Turing mechanism make use of the discrete nature of biological tissue, i.e.
compartmentalization into intra- and extracellular domains, as well as a representation
of the cell membrane. Starting from the standard Turing model, patterning can be
achieved if the reaction is restricted to the surface of a two dimensional manifold, even
if the bulk diffusion rates of the activator and inhibitor are equal [Levine and Rappel,
2005]. Alternatively, one compound may be identified as a membrane-bound receptor
or as an intracellular signalling factor. Because of the multimeric clustering of many
receptor-ligand systems [Bray et al., 1998], the derived equations may lead to the
reactive non-linearities which are typical for Turing mechanisms. Using two non-diffusible
intracellular compounds and two diffusing messenger molecules, a possible symmetry
breaking mechanism was studied using computer simulations [Rauch and Millonas, 2004].
The extracellular morphogens may diffuse at a similar rate, thus avoiding the criticism
of unrealistic differences in diffusion rates of the involved species.
97
Although intrinsically different from Turing systems, it is worth mentioning mechanisms
based on cell-cell communication. For example, the lateral binding of the membranebound ligand Delta to the receptor Notch is increasing Notch production, but decreasing
Delta production. Solved on discrete cellular domains, salt-and-pepper patterns emerge
by amplifying initial perturbations [Collier et al., 1996]. Communication through direct
cell-cell contact has been studied - both theoretically and experimentally - in connection
with the stripe pattern formation in zebrafish [Kondo and Asai, 1995, Nakamasu et al.,
2009]. It was shown that two pigment cell types interact with Turing-like short-range
activation and long-range inhibition, but, against the expectation, the hypothetical
diffusible factors have not been identified yet. However, it was shown that one pigment
cell type induces repulsive motion in the other cell type by direct contact via pseudopodia
[Yamanaka and Kondo, 2014]. The identification of the core mechanisms, and the
question of which interactions can still be regarded as Turing or Turing-like mechanisms,
is still subject to an ongoing debate [Mahalwar et al., 2014, Watanabe and Kondo, 2015].
Cytonemes, which are long and thin cellular projections which deliver or receive signalling
molecules upon direct cell contact, can span several hundred micrometers across a tissue
[Ramírez-Weber and Kornberg, 1999, Kornberg, 2013]. Recently, cytonemes have been
found in an increasing number of systems, and the pre-dominating current perception of
morphogen dispersion via diffusion might have to be revised in specific cases [Kornberg,
2014]. This might have consequences on the applicability and interpretation of Turing
mechanisms in the future.
4.2
Receptor-Ligand-Interaction-based Turing Systems
Assuming that one ligand molecule V binds to two receptor molecules U , a complex C
is formed. Furthermore, it is assumed that both the receptor U and complex C diffuse
at a slow and equal rate DU,C on the membrane surface, and that the ligand V diffuses
at a higher rate DV in the entire domain. The receptor U and ligand V are produced
at a constant rate ρU,V , and the receptor U and complex C are degraded at a rate δU,C .
The degradation of the ligand V is assumed to be negligible. The corresponding partial
differential equations read [Kurics et al., 2014]:
∂τ U = DU ∆U + ρU + νC − δU U − 2kon U 2 V + 2koff C
(4.1a)
∂τ V = DV ∆V + ρV − kon U 2 V + koff C
(4.1b)
2
∂τ C = DC ∆C − δC C + kon U V − koff C .
(4.1c)
By assuming that the binding process and turnover of the receptor-ligand complex C are
fast compared to the diffusing processes, a steady-state assumption for Equation (4.1c)
98
4.2. Receptor-Ligand-Interaction-based Turing Systems
can be made:
CSS =
kon
U 2 V = ΓU 2 V
koff + δC
with
Γ=
kon
,
koff + δC
and substitution into Equation (4.1a,4.1b) yields:
∂τ U = DU ∆U + ρU − δU U + (2koff Γ − 2kon + νΓ)U 2 V
∂τ V = DV ∆V + ρV − (kon − koff Γ)U 2 V .
In the following, the non-dimensional quantities u = U/U0 , v = V /V0 , x = X/L, t = DLU2 τ ,
V
d= D
DU are defined using the reference concentrations U0 , V0 and the reference length
scale L. Substitution yields:
ρU
U0 V0 2
L2 δU
− u + (2koff Γ − 2kon +νΓ)
u v
∂t u = ∆u +
DU
δU U0
δU
L2 δU
ρV
∂t v = d∆v +
− (kon − koff Γ) u2 v .
DU
δU V0
Upon re-definition of the constant parameters, and assuming ν > 2δC , we arrive at the
dimensionless Schnakenberg-type system [Schnakenberg, 1979]:
∂t u = ∆u + γ a − u + u2 v
(4.2a)
∂t v = d∆v + γ b − u2 v .
(4.2b)
The receptor u is limited to the membrane surface, i.e. the membrane acts as a zero-flux
boundary condition on a two-dimensional tissue representation. As a result, the reactions
only take place on the membrane surface, but not in the interstitial space.
Furthermore, a modified three-component variant of the standard Schnakenberg system
is analysed. A second compound w is produced upon high u2 v signalling activity, and it
promotes production of the receptor u. Like the ligand v, w diffuses freely, and acts as
an activator. A similar derivation and non-dimensionalization yields:
∂t u = ∆u + γ a − u + u2 v + kw
∂t v = d∆v + γ b − u2 v
(4.3a)
(4.3b)
∂t w = d∆w = γ ρH u2 v − δw ,
(4.3c)
where k, ρ are production constants and δ the activator degradation constant. Notably,
v, w may share the same diffusion coefficient ratio d. The signal u2 v activates the
2
production of w via the Hill equation H (x) = x2x+κ with the Hill constant κ.
Throughout this chapter, similar parameter sets based on the ones given in Table 4.1
have been used for the two- and three-component system. The receptor production rate
a is set to zero for the three-component system because the activator w regulates the
99
receptor production via the term kw in Equation (4.3a).
Table 4.1 – Parameter values for the two- and three-component Turing systems.
4.3
two-component system
three-component system
d = {20, 100}
a = 0.1
b = 0.9
γ = {40, 100}
d = {20, 100}
a=0
b = 0.5
γ = {40, 100}
k = 0.7
ρ = 25
δ = 3.8
κ = 1.0
Two-Component Turing System
In this section, the two-component system is studied under various conditions. First, the
numerical solutions of the software LBIBCell, previously introduced in Chapter 3, are
compared to the solutions of a commercial finite element solver both on continuous and
cellular domains consisting of square cells. Next, the behaviour is studied on cellular
domains with realistic cell shapes, and finally under growth conditions.
4.3.1
Numerical Validation on Continuous Domain
The standard Schnakenberg system, given in Equation 4.2) with the parameters given
in Table 4.1 and d = 100, γ = {70, 100} is solved on a continuous domain until steady
state is reached. The domain is an equilateral triangle with leg length L = 10. The
triangular shape facilitates convergences towards the same pattern arrangement due
to the hexagonal steady state pattern on infinitely large domains. Dirichlet boundary
conditions with uBC = v BC = 0 apply at the boundary. The LBIBCell simulations are
quantitatively (maximal values) and qualitatively compared to results obtained using
the commercial finite element solver COMSOL Multiphysics 5.0.
For the LBIBCell simulations, the same lattice Boltzmann relaxation times τuLB = 0.53
and τvLB = 3.5, corresponding to DuLB = 0.01 and DvLB = 1, are used for all lattice sizes.
The non-dimensional simulation time is T = 10. Table 4.2 gives the parameter values
and the results for the maximal concentrations in the domain, and Figure 4.1 shows the
concentration of the receptor u.
100
4.3. Two-Component Turing System
Table 4.3 – COMSOL parameter values and results for the maximal receptor concentration u.
COMSOL mesh setting
number of elements
umax for γ = 70
umax for γ = 100
normal
fine
finer
extrafine
extremelyfine
265
417
817
2744
10832
6.71
6.83
6.91
6.86
6.85
6.58
6.69
6.99
6.93
6.95
Table 4.2 – LBIBCell parameter values and results for the maximal receptor concentration u.
lattice size
∆x
∆t
#ts
umax for γ = 70
umax for γ = 100
100x100
200x200
400x400
800x800
0.1
0.05
0.025
0.0125
1e-4
2.5e-5
6.25e-6
1.5625e-06
1e5
4e5
1.6e6
6.4e6
4.473
5.76
6.10
6.365
4.141
5.577
6.438
6.796
Using the commercial finite element solver COMSOL, the system is implemented using
the module Coefficient Form PDE and standard settings. The mesh size has been set to
{normal, fine, finer, extrafine, extremelyfine}. The maximal concentrations in the domain
for γ = {70, 100} are given in Table 4.3, and the concentration patterns for the receptor u
are shown in Figure 4.1. There is no clear convergence upon grid refinement; restricting
the time step has no impact on the solution. For γ = 70, steady-state is reached at
≈ T = 2.0, and for γ = 100 at ≈ T = 6.0.
The patterns of both solvers are qualitatively in good agreement. The maximal concentration values in the domain obtained with LBIBCell converge, but the COMSOL
solutions do not show monotonous convergence. Overall, however, the difference between
the two solvers converge upon lattice/mesh refinement.
Next, the standard Schnakenberg system is solved with both LBIBCell and COMSOL
for different parameter sets on a square domain of dimensionless size 10x10. Periodic
boundary conditions apply to the ligand v. The results for the receptor concentration u,
shown in Figure 4.2, are qualitatively consistent.
4.3.2
Numerical Validation on Regular Cellular Domain
The standard Schnakenberg system is solved for different parameter sets using LBIBCell
and the commercial finite element solver COMSOL. The parameter sets given in Table
4.1 are used on a domain of dimensionless size 10x10, and periodic boundary conditions
apply to the ligand v. A very thin interstitial space of dimensionless width 0.00625
surrounds the tissue due to LBIBCell meshing reasons. Zero-flux boundary conditions
101
Figure 4.1 – Comparison between LBIBCell and COMSOL. Two-component Turing system
on a triangular domain with dimensionless leg length L = 10 for the reaction scaling factors γ = {70, 100}
and different lattice and mesh sizes, respectively. A COMSOL solutions for γ = 70 and different number
of mesh elements. B LBIBCell solutions for γ = 70 and different lattice sizes. C COMSOL solutions for
γ = 100 and different number of mesh elements. D LBIBCell solutions for γ = 100 and different lattice
sizes.
apply to the receptor u at the cell boundaries; the ligand v, however, is diffusing freely.
The reactions take only place inside cells. Two different cell sizes are used: a coarse
tissue consisting of 20x20 cells, and a fine tissue consisting of 40x40 cells.
The results are shown in Figure 4.3, and the patterns are, in contrast to the continuous
domain (cf. Figure 4.2), not smooth and regular. Only a few cells have a high level of
signalling, while their neighbour cells have virtually zero activity. Unlike the continuous
behaviour, the pattern is not deterministic since it depends on the random initial
conditions. However, the distance between activated cells is, similar to the continuous
domain, controlled by the parameters d and γ. Smaller cells lead, in general, to more
activated cells and smaller distances between activated cells. Both solvers lead to
qualitatively consistent results, but the LBIBCell results show distinct boundary effects.
102
Figure 4.2 – Two-component Turing system on static periodic domain. Qualitative comparison
of COMSOL and LBIBCell simulations of the standard Schnakenberg Turing instability for d = {20, 100}
and γ = {40, 100}.
In order relate these effects to the domain boundary condition or the very thin surrounding
extracellular space, Dirchlet boundary conditions are applied in a next step.
The non-dimensional domain size is 12x12 with zero-flux Dirichlet boundary conditions
for the ligand v. The tissue domain size is 10x10, with 20x20 and 40x40 cells, and
simulation setup is otherwise unchanged. Figure 4.4 shows the comparison between the
results obtained with LBIBCell and COMSOL. The qualitative behaviour is similar, and
both softwares show a distinct boundary effect, which is more pronounced as compared to
Figure 4.3. The LBIBCell solver tends to show a more regular, aligned border of activated
cells which may be rooted in the fact that LBIBCell uses a regular Cartesian grid, whereas
COMSOL generates a less regular triangulated mesh. It can be concluded that both
the choice of the domain boundary condition, as well has the very thin surrounding
extracellular space, have a more pronounced impact on the appearance of boundary
effects using LBIBCell. In the interior of the domain, however, both solvers lead to
qualitatively similar results.
103
Figure 4.3 – Two-component Turing system with periodic boundary conditions. Qualitative
comparison of COMSOL and LBIBCell simulations of the standard Schnakenberg Turing instability for
d = {20, 100} and γ = {40, 100} and two different cell sizes. A COMSOL results on 20x20 cells. B
LBIBCell results on 20x20 cells. C COMSOL results on 40x40 cells. D LBIBCell results on 40x40 cells.
104
Figure 4.4 – Two-component Turing system with zero-flux Dirichlet boundary conditions.
Qualitative comparison of COMSOL and LBIBCell simulations of the standard Schnakenberg Turing
instability for d = {20, 100} and γ = {40, 100}. A COMSOL results on 20x20 cells. B LBIBCell results
on 20x20 cells. C COMSOL results on 40x40 cells. D LBIBCell results on 40x40 cells.
105
4.3.3
Analysis on Irregular Cellular Domain
The Schnakenberg system, previously introduced in the Section 4.2, is solved on a static
cellular domain consisting of irregularly shaped cells. The dimensionless domain size is
10x10 with periodic boundary conditions for the ligand v. A very thin interstitial space
of dimensionless width 0.00625 surrounds the tissue due to LBIBCell meshing reasons.
The ligand v is freely diffusing, whereas the receptor u is limited to the cell surface, and
zero-flux boundary conditions apply to the cell membranes.
The stationary results for different diffusion coefficients d = {20, 100}, reaction scaling
factors γ = {40, 100}, and dimensionless cell areas A = {0.0625, 0.25} are shown in
Figure 4.5. As in the setup with regular quadratic cells (cf. Figure 4.3), the patterns are
not smooth and regular.
Because some combinations of parameter values lead to distinct boundary effects originating from the intracellular margin between tissue and domain boundary, the solution is
compared to larger domain sizes as shown in Figure 4.6. The boundary effect is limited
to a finite width and does not impact the interior of the tissue.
Furthermore, the two-component Schnakenberg system as described in Section 4.2 is
studied on different lattice resolutions 400x400 (∆x = 0.025, ∆t = 1e − 5) and 800x800
(∆x = 0.0125, ∆t = 2.5e − 6) for the parameter values d = 100, γ = 100, and cell area
Acell = {0.0625, 0.25}. The results, shown in Figure 4.7, are qualitatively consistent, and
numerical discretization artefacts can be excluded.
Figure 4.5 – Two-component Turing system on static tissue. The ligand v diffuses freely, and
the receptor u is restricted to the cells. Different parameter combinations for the diffusion coefficient ratio
d = {20, 100} and the reaction scaling factor γ = {40, 100} are analysed. The receptor concentration u is
shown. A The tissue consists of large cells with a dimensionless area of A ≈ 0.25. B The tissue consists
of small cells with a dimensionless area of A ≈ 0.0625.
106
Figure 4.6 – Two-component Turing system on large static tissue. The parameter values
d = 100, γ = 100 have been chosen, and the dimensionless domain size is 25x25 with approximately 1e4
cells.
Figure 4.7 – Lattice refinement study of a two-component Turing system on static cellular
tissue. The dimensionless domain size is 10x10 with periodic boundary conditions for the ligand v. A
The tissue consists of large cells with a dimensionless area of A ≈ 0.25. The lattice size is 400x400. B
The tissue consists of small cells with a dimensionless area of A ≈ 0.0625. The lattice size is 400x400. C
The tissue consists of large cells with a dimensionless area of A ≈ 0.25. The lattice size is 800x800. D
The tissue consists of small cells with a dimensionless area of A ≈ 0.0625. The lattice size is 800x800.
In a next step, the behaviour of the Schnakenberg system is analysed on growing tissue.
All cells proliferate uniformly, i.e. a constant uniform mass source with dimensionless
source strength S = 10 is applied and the cells divide when reaching a threshold value.
The results are given in Figure 4.8. Unlike to stationary patterns on static tissue, the
activated cells form compact clusters. They emerge whenever an activated cell divides
107
Figure 4.8 – Two-component Turing system on proliferating tissue. Different parameter
combinations for the diffusion coefficient ratio d = {20, 100} and the reaction scaling factor γ = {40, 100}
are analysed. The receptor concentration u is shown. A The tissue consists of large cells with a
dimensionless area of A ≈ 0.25. B The tissue consists of small cells with a dimensionless area of
A ≈ 0.0625.
since both daughter cells inherit the activation. If the growth rate is high compared to
the reaction turnover rate, the patterns will rearrange into the static patterns as shown
in Figure 4.5. On smaller cells, the clusters assume radially oriented elongated shapes.
In order to quantify the clustering phenomenon, the pair correlation (radial distribution)
function has been computed for the growing scenarios. Figure 4.9AC show the pair
correlation functions for large and small cells, respectively. The first peak reflects the
average cluster size, and qualitatively matches the observations shown in Figure 4.8. The
relative order of the cluster sizes is conserved on different cell sizes. The magnifications
shown in Figure 4.9BD show the secondary peaks which indicate the average distance
between clusters. It can be concluded consistently that the larger a cluster, the larger
the distance to neighbouring clusters, and vice versa. Smaller cells, in general, lead
to smaller clusters and smaller distances between clusters. For comparison, the pair
correlation function is computed for the pattern on static tissue with parameters d = 100
and γ = 100 (magenta line in Figure 4.9CD). The primary peak is missing due to the
absence of clustering, and the secondary peak indicates that the average distance between
activated cells is significantly smaller than the average distance between clusters in case
of tissue growth.
108
Figure 4.9 – Pair correlation function ρ (r) for clusters on growing cellular domains. The
pair correlation function ρ (r) describes the relative average density of active cells in the neighbourhood
r. Different parameter combinations for the diffusion coefficient ratio d = {20, 100} and the reaction
scaling factor γ = {40, 100} are analysed. A The pair correlation function for different parameter sets
on a tissue consisting of large cells with a non-dimensional area of A ≈ 0.25. The arrowheads denote
the maxima, which are a measure for the average cluster size. B Magnification of A around ρ (r) = 1
reveals secondary peaks (arrowheads), which are a measure for the average distance between clusters.
C The pair correlation function for different parameter sets on a tissue consisting of small cells with a
non-dimensional area of A ≈ 0.0625. The arrow heads denote the maxima, which are a measure for the
average cluster size. The pair correlation of the static case is given in magenta. D Magnification of C
around ρ (r) = 1 reveals secondary peaks (arrowheads), which are a measure for the average distance
between clusters.
109
4.4
Three-Component Turing System
In this section, the three-component system is studied under various conditions. First,
the numerical solutions of the software LBIBCell, previously introduced in Chapter 3,
are compared to the solutions of the commercial finite element solver COMSOL both on
continuous and cellular domains consisting of square cells. Next, the behaviour is studied
on cellular domains with realistic cell shapes, and finally under growth conditions.
4.4.1
Numerical Validation on Continuous Domain
Using LBIBCell and COMSOL, the three-component Turing system, previously described
in Section 4.2, is solved for the parameter sets given in Table 4.1 on continuous domains
until steady state is reached. The dimensionless domain size is 10x10, and periodic
boundary conditions apply to both v and w.
The results, as shown in Figure 4.10, are qualitatively consistent, although the pattern
wavelength differs for d = 100 and γ = 100 due to the stripe orientation. For both solvers,
no pattern emerges for the diffusion coefficient ratio d = 20.
Figure 4.10 – Three-component Turing system on continuous static domain. Qualitative
comparison of COMSOL and LBIBCell simulations of the three-component Turing instability for d =
{20, 100} and γ = {40, 100}. For d = 20, both solvers predict absence of Turing instability.
4.4.2
Numerical Validation on Regular Cellular Domain
The three-component Turing system, as described in Section 4.2, is solved for different
parameter sets using LBIBCell and COMSOL. The parameter sets given in Table 4.1 are
used on a domain of dimensionless size 10x10, and periodic boundary conditions apply
to the ligand v. A very thin interstitial space of dimensionless width 0.00625 surrounds
the tissue due to LBIBCell meshing reasons. Zero-flux boundary conditions apply to
110
4.4. Three-Component Turing System
Figure 4.11 – Three-component Turing system with periodic boundary conditions. Qualitative comparison of COMSOL and LBIBCell simulations of the standard Schnakenberg Turing instability
for d = {20, 100} and γ = {40, 100} and two different cell sizes. A COMSOL results on 20x20 cells. B
LBIBCell results on 20x20 cells. C COMSOL results on 40x40 cells. D LBIBCell results on 40x40 cells.
the receptor u at the cell boundaries; the ligand v and the transmitter w, however, are
diffusing freely. The reactions take only place inside cells. Two different cell sizes are
used: a coarse tissue consisting of 20x20 cells, and a fine tissue consisting of 40x40 cells.
The results are shown Figure 4.11. Interestingly, the volatile transition from spots to
stripes, and vice versa, appears to be dependent on the solver implementation and the cell
size. Although the appearance of spots and stripes is not always identical, the average
111
wavelength is qualitatively consistent. Most notably, patterns emerge for the diffusion
coefficient ratio d = 20 (recalling that, on the continuous domain, no pattern appears for
the diffusion coefficient ratio d = 20, cf. Figure 4.10), indicating that the cellular domain
increases the parametric Turing space. The behaviour of the three-component system on
cellular domains is intrinsically different to the two-component system (cf. Figure 4.3):
patterns spanning multiple cells, resembling the ones on continuous domains, appear.
Therefore, the presented receptor-ligand system might form a fundamental mechanism
by which tissue-wide pattern coordination occurs. Boundary effects are less pronounced
as compared to the two-component Turing system.
4.4.3
Analysis on Irregular Cellular Domain
The three-component system, as described in Section 4.2, consists of two freely diffusing
ligands v, w. Periodic boundary conditions apply to the diffusing compounds. In a first
step, the system is solved on static cellular tissue as shown in Figure 4.12 for different
parameters values d = {20, 100}, γ = {40, 100}, and cell areas A = {0.0625, 0.25}.
In contrast to the salt-and-pepper pattern of the two-component system, smooth and
coordinated patterns are recovered on a tissue scale. The patterns resemble the ones on
continuous domains (cf. Figure 4.2). Like the continuous Schnakenberg counterpart, the
pattern is very sensitive to small variations of the parameter values, but the mode and
wavelength are qualitatively consistent when changing the cell size.
Figure 4.12 – Three-component Turing system on static tissue. The ligand v diffuses freely,
and the receptor u is restricted to the cells. Different parameter combinations for the diffusion coefficient
ratio d = {20, 100} and the reaction scaling factor γ = {40, 100} are analysed. The receptor concentration
u is shown. A The tissue consists of large cells with a dimensionless area of A ≈ 0.25. B The tissue
consists of small cells with a dimensionless area of A ≈ 0.0625.
112
4.4. Three-Component Turing System
Figure 4.13 – Three-component Turing system on proliferating tissue. Different parameter
combinations for the diffusion coefficient ratio d = {20, 100} and the reaction scaling factor γ = {40, 100}
are analysed. The receptor concentration u is shown. A The tissue consists of large cells with a
non-dimensional area of A ≈ 0.25. B The tissue consists of large cells with a non-dimensional area of
A ≈ 0.0625.
The pattern might also be affected by tissue growth. Figure 4.13 shows the same scenarios
as in Figure 4.12 on an uniformly proliferating tissue. The lower the reaction scaling
factor γ, the higher the impact of tissue growth, and vice versa. The appearance of regular
patterns is largely disturbed, and no clear influence of the cell size can be estimated.
The three-component Schnakenberg system is studied on different lattice resolutions
400x400 (∆x = 0.025, ∆t = 1e − 5) and 800x800 (∆x = 0.0125, ∆t = 2.5e − 6) for the
parameter values d = 100, γ = 100, and cell area Acell = {0.0625, 0.25}. The results,
shown in Figure 4.14, are qualitatively consistent, and numerical discretization artefacts
can be excluded.
113
Figure 4.14 – Lattice refinement study of a three-component Turing system on static
cellular tissue. The dimensionless domain size is 10x10 with periodic boundary conditions for the
ligand v. A The tissue consists of large cells with a dimensionless area of A ≈ 0.25. The lattice size is
400x400. B The tissue consists of small cells with a dimensionless area of A ≈ 0.0625. The lattice size is
400x400. C The tissue consists of large cells with a dimensionless area of A ≈ 0.25. The lattice size is
800x800. D The tissue consists of small cells with a dimensionless area of A ≈ 0.0625. The lattice size is
800x800.
114
4.5. Activated Growth
4.5
Activated Growth
Instead of applying a constant, uniform mass source as previously done in Section 4.3.3
and 4.4.3, the latter can be made dependent on the signalling levels of the Turing systems.
Figure 4.15AB shows the two-component Schnakenberg system with d = 100 and γ = 100
on a differentially growing tissue consisting of large and small cells, respectively. The
mass source is proportional to the signalling level of the cell, i.e. only activated cells
proliferate at a high rate. Additionally to the signalling patterns, characteristic cell
morphology patterns emerge because the non-activating cells are displaced and squeezed
by the activated ones. Alternatively, the signalling might influence growth indirectly via
differentiation. For example, using the three-component Turing system with d = 100
and γ = 100, differentiation from the highly proliferating phenotype into a quiescent
phenotype occurs whenever the signalling content of a cell drops below a threshold value.
Interesting tissue topologies might emerge (cf. Figure 4.15CD).
Figure 4.15 – Turing systems on differentially proliferating tissue. For all simulations, a
diffusion ratio d = 100 and a reaction scaling factor γ = 100 have been used. The local proliferation rate
is controlled by the signalling. A The two-component system is solved on a tissue consisting of large
cells with A ≈ 0.25. The proliferation rate is proportional to the receptor concentration u. B The same
system as in A is solved on a tissue consisting of small cells with A ≈ 0.0625. C The three-component
system is solved on a tissue consisting of large cells with A ≈ 0.25. Whenever the average receptor
concentration u of cell drops below a threshold value θ = 0.6, the cell irreversibly differentiates from the
highly proliferating black phenotype into a quiescent red phenotype. D The same system as in C is
solved on a tissue consisting of small cells with A ≈ 0.0625.
115
4.6
Discussion
Here, the behaviour of Turing mechanisms has been studied on cellular domains, and,
compared to the continuous domain, it has been found that several phenomena emerge.
The slowly diffusing compound is interpreted as a membrane-bound receptor, and the
quickly diffusing compound as a freely diffusing ligand. Assuming multimeric complex
formation, a Schnakenberg-type Turing system can be derived [Schnakenberg, 1979].
Semi-random salt-and-pepper patterns are found when solved on static cellular domains,
and cluster formation emerges on uniformly growing tissue. To retrieve tissue-wide
coordination of the patterns, and to meet the critics that differential diffusivity is unlikely
to be met by many biological systems, a modified three-component Turing system is
proposed where the two extracellular compounds are allowed to diffuse at a similar rate.
In contrast to the two-component Schnakenberg system, tissue growth does not impact
the patterns qualitatively.
Many theoretical and computational morphogenetic studies assume a continuous domain,
and oftentimes growth is assumed to be negligible. The emerging phenomena of Turing
patterns on cellular domains, however, prove that care has to be taken in making
a continuous assumption, and many models would benefit from a thorough analysis
on cellular domains. Furthermore, cell-based tissue models enable to represent many
cellular processes such as (directed) cell division, signalling-controlled proliferation and
differentiation.
Computational studies allow to quickly investigate the combination of signalling models
and cell-based tissue representations to generate novel, emerging behaviour. However,
the relevance of these hypotheses still needs to be investigated in the light of specific
biological applications, i.e. the molecular players need to be identified.
116
5 Conclusion
The focus of this thesis was to advance modelling and simulation methods to study
complex mechano-chemical interactions in morphogenetic problems. Computational
studies formulated both on the meso- and macroscopic level revealed their respective
chances and limitations.
On the macroscopic level, a continuous model for early long bone development has been
developed. The model is based on a continuous description of a viscous fluid to represent
the mechanical long-term behaviour of growing embryonic tissue. Furthermore, it is
fully coupled to a signalling model based on a Turing mechanism, i.e. the signalling
molecules are advected as a result of tissue growth and movement, and the signalling
network controls cell proliferation and differentiation. It was shown that growth impacts
the behaviour of the signalling patterns and hence cannot be neglected.
A simple signalling model, which leads to correct pattern predictions on a static domain,
is not able to reproduce stable patterning any longer when tissue growth is enabled.
After modifying the signalling model by introducing an additional intermediate signalling
level which acts as a signal integrator, stable patterning could be recovered.
The mechanical tissue properties have been represented by a Newtonian fluid, and the
different cell types by passively advected cell density concentrations. This approach
suffers from the inability to represent sharp boundaries between different cell types.
Further, it results in cell type mixtures instead of subdomains with homogeneous cell
populations. In order to remedy these shortcomings, a framework to describe multiple
cell types has been developed and numerically validated. The approach is based on binary
index fields and takes into account cell volume change upon differentiation. However,
the macroscopic approach will still have to be extended in the future to represent further
cellular mechanisms: directed cell division, intercalation and migration, and active
cytoskeleton remodelling to name just a few.
Alternatively to continuous models, the resolution of the dominating mesoscopic unit,
the cell, offers new perspectives to model cellular behaviour. The strength of cell-based
117
Chapter 5. Conclusion
modelling techniques is that biological behaviour can be modelled and implemented
intuitively, and the effect on the macroscopic scale (tissue) can be studies as an emerging
property [Rauzi et al., 2008, Ranft et al., 2010]. In the context of this thesis, a twodimensional model based on the immersed boundary method has been developed and
implemented as the open-source software library LBIBCell. Focus has been laid on clean
software architecture, extendibility, extensive code documentation, version control and,
to a lesser extent, on high-performance parallel computing aspects. LBIBCell represents
the viscous behaviour of the cytoskeleton and the interstitial fluid and extracellular
matrix. Cell-cell junctions are explicitly resolved and their dynamics can be studied in
great detail. Due to its flexibility and the possibility to represent detailed user-specified
cellular mechanisms, and thanks to its inherent coupling to advection-reaction-diffusion
processes, it serves as a versatile tool to study fundamental developmental mechanisms.
By studying the behaviour of the seminal Turing mechanism on cellular, dynamically
growing tissues, it was shown that emerging, unexpected phenomena might come to light.
Therefore, besides the great flexibility to model cellular processes, it is recommended to
use cell-based simulation approaches to ensure that the results are independent of the
chosen modelling paradigm.
In the future, besides the careful numerical validation of the methods, there is a need
to demonstrate that the relevant biophysical material properties are well represented.
In particular, it has to be shown that the macroscopic visco-elastic properties of tissues
[Foty et al., 1994, Delarue et al., 2014], but also the microscopic behaviour, such as cell
division and migration, can be recovered [Staple et al., 2010, Guillot and Lecuit, 2013].
Even though cell-based modelling opens new opportunities and advantages as compared
to continuous tissue models, they currently suffer from certain restraints regarding their
descriptional and computational complexity. An infinite variety of behaviour and rules
with large numbers of parameters can be formulated, and potentially misguide modellers
to unnecessarily inflate the model’s complexity. Uncertainty quantification for spatiotemporal models, an emerging research topic, will be a valuable approach for model
discrimination and to avoid inadequate model complexity [Tauriello et al., 2015].
If the number of cells is very large, the computational costs of cell-based models is
significantly higher as compared to continuous tissue models. In particular, arbitrarily
deformable cell models, such as the immersed boundary cell model, realize their very
high mechanical accuracy and structural complexity with very high computational costs.
Therefore, they are effectively limited to small numbers of cells and/or two spatial dimensions. This might be an issue for a certain class of morphogenetic problems: whenever
the modeller aims at explaining phenomena which intrinsically rely on three-dimensional
effects, a three-dimensional model formulation might be required when two-dimensional
simplifications or attempts to compensate for the missing third dimension turn out to be
too incisive. For example, the mechanics of branching morphogenesis cannot be studied
in two-dimensional cross-sectional models without compensation of the circumferential
forces which are pivotal for budding and bud lengthening processes.
118
Continuous tissue models and simple cell-based models can readily be studied in three dimensions, but three-dimensional versions of geometrically complex arbitrarily deformable
cell models, such as the vertex model and the immersed boundary model, are not yet
implemented in software frameworks. The implementation of highly detailed threedimensional cell models requires high performance computing considerations in order
to be able to study large numbers of cells. Currently, no computational framework for
arbitrarily deformable cells is capable of exploiting large supercomputers with hundreds
to thousands of cores.
If the modeller succeeds in deriving continuous equations of the cellular processes, then
the problem of interest is ideally analysed both on a cellular or subcellular scale and on
the macroscopic scale. Unfortunately, this exercise may be difficult, and it has to be
decided in each case whether the cellular mechanisms do manifest on the macroscopic
scale, or if they can be neglected. Studies, where it has been shown how certain cell-based
models can be described by means of macroscopic continuous description, may be helpful
for modellers to choose an appropriate modelling approach [Newman, 2005].
In the future, cell-based modelling aiming at the realistic and accurate representation
of the tissue, goes hand in hand with the increasing availability of spatially highly
resolved experimental data, e.g. from advances in live imaging techniques; both fields are
currently undergoing massive progression. Therefore, it is to be expected that the need
for spatio-temporal modelling will increase in the future - both in academia and industry.
119
Acknowledgements
First I would like to give thanks to my supervisor, Prof. Dagmar Iber. She gave me the
opportunity to learn about spatio-temporal modelling in biology, and supported me for
years in finding a way to contribute to the group’s field of research. Furthermore, I would
like to thank Prof. Bastien Chopard, Prof. Edoardo Mazza and Prof. Niko Beerenwinkel
for accepting to be part of my thesis committee.
I acknowledge the Swiss Confederation, the Swiss National Science Foundation SNF, the
Swiss Institute of Bioinformatics SIB and the National Institute for Mathematical and
Biological Synthesis NIMBioS for funding, training and the conference invitation.
A special thanks goes to the members of the CoBi group in its current composition Anna, Diana, Harold, Jannik, Lada, Marcelo, Marco, Odyssé, Patrick, Roberto, Zahra for the excellent working environment, as well as to the alumni, in particular Dr. Dzianis
Menshykau, Dr. Federico Felizzi and Dr. Georgios Fengos.
I would like to thank my external collaborators, Amarendra Badugu, Lucas Ahrens and
Prof. Prasad Shastri.
It was a pleasure to work with the Master students I supervised, and therefore I would
like to take the opportunity to thank David Sichau, Roger Rossé, Joelle Barido-Sottani,
Sami Ben Said and Chao Feng.
Finally, I would like to thank my family - my mother, my deceased father, my brother
and Edgar the Dog - for their lifelong unconditional support.
121
A Appendix: Other Projects
A.1
Design and Optimization of a Microfluidic Gradient
Generator
This project has been executed within the SNF Sinergia grant ’Developmental engineering
of endochondral ossification from mesenchymal stem cells’. The goal of the project was
to develop a microfluidic device which allows cell culturing in morphogen gradients a central interest of in-vitro morphogenetic research. A Master student was jointly
supervised between the group of Prof. Savas Tay on the experimental microfluidic side,
the group of Prof. Dagmar Iber on the design and computational side. The Tay group
published the experimental findings as:
T. Frank, S. Tay. Flow-switching allows independently programmable, extremely stable,
high-throughput diffusion-based gradients. Lab on a Chip, 13:1273–81 (2013),
and the Iber group the computational studies as:
Tanaka S and Iber D, Simulation of a Microfluidic Gradient Generator using Lattice
Boltzmann Methods. Current Synthetic and Systems Biology (2013) 1, 102.
A.2
Quantification of Gradients in Gel-based Release Systems
The following project is a collaboration with Lucas Ahrens, PhD student in the group of
Prof. Prasad Shastri, Institute for Macromolecular Chemistry, University of Freiburg,
Germany, within the SNF Sinergia grant ’Developmental engineering of endochondral
ossification from mesenchymal stem cells’. The group’s goal is the development, characterization and optimization of polymer-gel-based delivery systems. Disc-shaped delivery
devices made from gelatin are loaded with soluble signals and used to establish signal
123
Appendix A. Appendix: Other Projects
gradients in in vitro three-dimensional cell culture experiments.
The Iber group provides consulting based on computer simulations, which in turn are
validated by experimental data by the Shastri group. A quantitative understanding of the
gradient generation process allows to optimize cell culturing experiments to demonstrate
differential cellular response in morphogen gradients.
The following publication is in preparation:
Ahrens L, Tanaka S, Iber D, Shastri P, Quantification of Gradients in Gel-Based Release
Systems.
A.3
Simulation of the Growth Plate Dynamics in Embryonic Long Bone Development
The following project has been realized in the context of a Master thesis by Sami Ben
Said, supervised by the Iber group. Based on the findings presented in Section 2.1 and
2.2, the signalling network has been extended by a module containing transcription
factor Gli3 dynamics in order to be able to explain more mutants. The model does
not explain symmetry breaking, which was the focus of Section 2.1, but rather assumes
GDF5 signalling centers at the ends of the primary bone structures. Due to the high
level of details and the use of the multiple cell type model presented in Section 2.2, the
growth plate of growing bone could be finely resolved and explained.
The following publication is in preparation:
Ben Said S, Tanaka S and Iber D, Robustness of Long Bone Development to a large
evolutionary difference in growth speeds.
124
Bibliography
[Badugu et al., 2012] Badugu, A., Kraemer, C., Germann, P., Menshykau, D., and Iber,
D. (2012). Digit patterning during limb development as a result of the BMP-receptor
interaction. Scientific reports, 2:991.
[Bartoloni et al., 1993] Bartoloni, A., Battista, C., Cabasino, S., Paolucci, P. S., Pech,
J., Sarno, R., Todesco, G. M., Torelli, M., Tross, W., Vicini, P., Benzi, R., Cabibbo,
N., Massaioli, F., and Tripiccione, R. (1993). LBE Simulations of Rayleigh-Benard
Convection on the APE100 Parallel Processor. International Journal of Modern Physics
C, 04(05):993–1006.
[Bauer et al., 2007] Bauer, A. L., Jackson, T. L., and Jiang, Y. (2007). A cell-based model
exhibiting branching and anastomosis during tumor-induced angiogenesis. Biophysical
journal, 92(9):3105–21.
[Bénazet et al., 2012] Bénazet, J.-D., Pignatti, E., Nugent, A., Unal, E., Laurent, F.,
and Zeller, R. (2012). Smad4 is required to induce digit ray primordia and to initiate
the aggregation and differentiation of chondrogenic progenitors in mouse limb buds.
Development (Cambridge, England), 139(22):4250–4260.
[Bitgood and McMahon, 1995] Bitgood, M. J. and McMahon, A. P. (1995). Hedgehog
and Bmp genes are coexpressed at many diverse sites of cell-cell interaction in the
mouse embryo. Developmental Biology, 172(1):126–138.
[Bittig et al., 2008] Bittig, T., Wartlick, O., Kicheva, A., González-Gaitán, M., and
Jülicher, F. (2008). Dynamics of anisotropic tissue growth. New Journal of Physics,
10(6):063001.
[Blakley, 1979] Blakley, A. (1979). Embryonic bone growth in lines of mice selected for
large and small body size. Genetical research, 34(2):77–85.
[Boas and Merks, 2014] Boas, S. E. M. and Merks, R. M. H. (2014). Synergy of cell-cell
repulsion and vacuolation in a computational model of lumen formation. Journal of
the Royal Society, Interface / the Royal Society, 11(92):20131049.
125
Bibliography
[Bougherara et al., 2010] Bougherara, H., Klika, V., Marsik, F., Marik, I. A., and Yahia,
L. (2010). New predictive model for monitoring bone remodeling. Journal Of Biomedical
Materials Research Part A, 95(1):9–24.
[Bradley et al., 2011] Bradley, C. P., Bowery, A., Britten, R., Budelmann, V., Camara,
O., Christie, R. G., Cookson, A., Frangi, A. F., Gamage, T. B., Heidlauf, T., Krittian,
S., Ladd, D., Little, C., Mithraratne, K., Nash, M., Nickerson, D. P., Nielsen, P.
M. F., Nordbø, O., Omholt, S., Pashaei, A., Paterson, D., Rajagopal, V., Reeve,
A., Röhrle, O., Safaei, S., Sebastián, R., Steghöfer, M., Wu, T., Yu, T., Zhang, H.,
and Hunter, P. J. (2011). OpenCMISS: a multi-physics & multi-scale computational
infrastructure for the VPH/Physiome project. Progress in biophysics and molecular
biology, 107(1):32–47.
[Bray et al., 1998] Bray, D., Levin, M. D., and Morton-Firth, C. J. (1998). Receptorclusteringasa cellularmechanism to controlsensitivity. Nature, 393(6680):85–88.
[Brodland and Chen, 2000] Brodland, W. G. and Chen, H. H. (2000). The Mechanics
of Heterotypic Cell Aggregates: Insights From Computer Simulations. Journal of
Biomechanical Engineering, 122(4):402.
[Brodland et al., 2007] Brodland, W. G., Viens, D., and Veldhuis, J. H. (2007). A new
cell-based FE model for the mechanics of embryonic epithelia. Computer methods in
biomechanics and biomedical engineering, 10(2):121–8.
[Brouwers et al., 2006] Brouwers, J. E. M., van Donkelaar, C. C., Sengers, B. G., and
Huiskes, R. (2006). Can the growth factors PTHrP, Ihh and VEGF, together regulate
the development of a long bone? Journal of biomechanics, 39(15):2774–2782.
[Büchel et al., 2012] Büchel, F., Wrzodek, C., Mittag, F., Dräger, A., Eichner, J., Rodriguez, N., Le Novère, N., and Zell, A. (2012). Qualitative translation of relations
from BioPAX to SBML qual. Bioinformatics (Oxford, England), 28(20):2648–53.
[Butterfield et al., 2009] Butterfield, N. C., Metzis, V., McGlinn, E., Bruce, S. J., Wainwright, B. J., and Wicking, C. (2009). Patched 1 is a crucial determinant of asymmetry and digit number in the vertebrate limb. Development (Cambridge, England),
136(20):3515–3524.
[Carin, 2006] Carin, M. (2006). Numerical Simulation of Moving Boundary Problems
with the ALE Method: Validation in the Case of a Free Surface and a Moving
Solidification Front. Excert from the Proceedings of the COMSOL Conference.
[Cellière et al., 2012] Cellière, G., Menshykau, D., and Iber, D. (2012). Simulations
demonstrate a simple network to be sufficient to control branch point selection, smooth
muscle and vasculature formation during lung branching morphogenesis. Biology open,
1(8):775–88.
126
Bibliography
[Chen and Brodland, 2000] Chen, H. H. and Brodland, W. G. (2000). Cell-level finite element studies of viscous cells in planar aggregates. Journal of biomechanical engineering,
122(4):394–401.
[Chen and Doolen, 1998] Chen, S. and Doolen, G. D. (1998). Lattice Boltzmann Methods
for Fluid Flows. Annual Review of Fluid Mechanics, 30(1):329–364.
[Christie et al., 2009] Christie, R. G., Nielsen, P. M. F., Blackett, S. A., Bradley, C. P.,
and Hunter, P. J. (2009). FieldML: concepts and implementation. Philosophical transactions. Series A, Mathematical, physical, and engineering sciences, 367(1895):1869–84.
[Christley et al., 2010] Christley, S., Lee, B., Dai, X., and Nie, Q. (2010). Integrative
multicellular biological modeling: a case study of 3D epidermal development using
GPU algorithms. BMC systems biology, 4:107.
[Chu et al., 2005] Chu, Y.-S., Dufour, S., Thiery, J. P., Perez, E., and Pincet, F.
(2005). Johnson-Kendall-Roberts theory applied to living cells. Physical review
letters, 94(2):028102.
[Collier et al., 1996] Collier, J. R., Monk, N. a., Maini, P. K., and Lewis, J. H. (1996).
Pattern formation by lateral inhibition with feedback: a mathematical model of
delta-notch intercellular signalling. Journal of theoretical biology, 183(4):429–446.
[Cooper et al., 2013] Cooper, K. L., Oh, S., Sung, Y., Dasari, R. R., Kirschner, M. W.,
and Tabin, C. J. (2013). Multiple phases of chondrocyte enlargement underlie differences
in skeletal proportions. Nature, 495(7441):375–378.
[Crampin et al., 1999] Crampin, E. J., Gaffney, E. A., and Maini, P. K. (1999). Reaction
and diffusion on growing domains: scenarios for robust pattern formation. Bulletin of
mathematical biology, 61(6):1093–1120.
[Craver, 2006] Craver, C. F. (2006). When mechanistic models explain. Synthese,
153(3):355–376.
[Cuellar et al., 2003] Cuellar, A. A., Lloyd, C. M., Nielsen, P. M. F., Bullivant, D. P.,
Nickerson, D. P., and Hunter, P. J. (2003). An Overview of CellML 1.1, a Biological
Model Description Language. Simulation, 79(12):740–747.
[Cutress et al., 2010] Cutress, I. J., Dickinson, E. J. F., and Compton, R. G. (2010).
Analysis of commercial general engineering finite element software in electrochemical
simulations. J Electroanal Chem, 638(1):76–83.
[Dallon and Othmer, 2004] Dallon, J. C. and Othmer, H. G. (2004). How cellular movement determines the collective force generated by the Dictyostelium discoideum slug.
Journal of theoretical biology, 231(2):203–22.
127
Bibliography
[de Back et al., 2013a] de Back, W., Zhou, J. X., and Brusch, L. (2013a). On the role
of lateral stabilization during early patterning in the pancreas. Journal of the Royal
Society, Interface / the Royal Society, 10(79):20120766.
[de Back et al., 2013b] de Back, W., Zimm, R., and Brusch, L. (2013b). Transdifferentiation of pancreatic cells by loss of contact-mediated signaling. BMC systems biology,
7(1):77.
[Delarue et al., 2014] Delarue, M., Joanny, J.-F., Julicher, F., and Prost, J. (2014). Stress
distributions and cell flows in a growing cell aggregate. Interface Focus, 4:20140033–
20140033.
[Demir et al., 2010] Demir, E., Cary, M. P., Paley, S., Fukuda, K., Lemer, C., Vastrik, I.,
Wu, G., D’Eustachio, P., Schaefer, C., Luciano, J., Schacherer, F., Martinez-Flores, I.,
Hu, Z., Jimenez-Jacinto, V., Joshi-Tope, G., Kandasamy, K., Lopez-Fuentes, A. C., Mi,
H., Pichler, E., Rodchenkov, I., Splendiani, A., Tkachev, S., Zucker, J., Gopinath, G.,
Rajasimha, H., Ramakrishnan, R., Shah, I., Syed, M., Anwar, N., Babur, O., Blinov,
M., Brauner, E., Corwin, D., Donaldson, S., Gibbons, F., Goldberg, R., Hornbeck, P.,
Luna, A., Murray-Rust, P., Neumann, E., Ruebenacker, O., Reubenacker, O., Samwald,
M., van Iersel, M., Wimalaratne, S., Allen, K., Braun, B., Whirl-Carrillo, M., Cheung,
K.-H., Dahlquist, K., Finney, A., Gillespie, M., Glass, E., Gong, L., Haw, R., Honig,
M., Hubaut, O., Kane, D., Krupa, S., Kutmon, M., Leonard, J., Marks, D., Merberg,
D., Petri, V., Pico, A., Ravenscroft, D., Ren, L., Shah, N., Sunshine, M., Tang, R.,
Whaley, R., Letovksy, S., Buetow, K. H., Rzhetsky, A., Schachter, V., Sobral, B. S.,
Dogrusoz, U., McWeeney, S. K., Aladjem, M., Birney, E., Collado-Vides, J., Goto, S.,
Hucka, M., Le Novère, N., Maltsev, N., Pandey, A., Thomas, P., Wingender, E., Karp,
P. D., Sander, C., and Bader, G. D. (2010). The BioPAX community standard for
pathway data sharing. Nature biotechnology, 28(9):935–42.
[Dias et al., 2014] Dias, A. S., de Almeida, I., Belmonte, J. M., Glazier, J. A., and Stern,
C. D. (2014). Somites without a clock. Science (New York, N.Y.), 343(6172):791–5.
[Dillon et al., 2003] Dillon, R., Gadgil, C., and Othmer, H. G. (2003). Short- and longrange effects of Sonic hedgehog in limb development. Proc. Natl. Acad. Sci USA,
100(18):10152–10157.
[Dillon and Othmer, 1999] Dillon, R. H. and Othmer, H. G. (1999). A mathematical
model for outgrowth and spatial patterning of the vertebrate limb bud. Journal of
theoretical biology, 197(3):295–330.
[Dillon et al., 2008] Dillon, R. H., Owen, M. R., and Painter, K. (2008). A single-cellbased model of multicellular growth using the immersed boundary method. Contemporary Mathematics, pages 1–15.
[Drasdo, 2007] Drasdo, D. (2007). Single-Cell-Based Models in Biology and Medicine.
Mathematics and Biosciences in Interaction. Birkhäuser Basel, Basel.
128
Bibliography
[Drasdo and Hoehme, 2003] Drasdo, D. and Hoehme, S. (2003). Individual-based approaches to birth and death in avascu1ar tumors. Mathematical and Computer
Modelling, 37(11):1163–1175.
[Drasdo and Hoehme, 2005] Drasdo, D. and Hoehme, S. (2005). A single-cell-based
model of tumor growth in vitro: monolayers and spheroids. Physical biology, 2(3):133–
47.
[Drasdo et al., 2007] Drasdo, D., Hoehme, S., and Block, M. (2007). On the Role of
Physics in the Growth and Pattern Formation of Multi-Cellular Systems: What
can we Learn from Individual-Cell Based Models? Journal of Statistical Physics,
128(1-2):287–345.
[Drasdo et al., 2014] Drasdo, D., Hoehme, S., and Hengstler, J. G. (2014). How predictive
quantitative modelling of tissue organisation can inform liver disease pathogenesis.
Journal of hepatology, 61(4):951–956.
[Drasdo et al., 1995] Drasdo, D., Kree, R., and McCaskill, J. S. (1995). Monte Carlo
approach to tissue-cell populations. Physical Review E, 52(6):6635–6657.
[Dunn et al., 2012a] Dunn, S.-J., Appleton, P. L., Nelson, S. A., Näthke, I. S., Gavaghan,
D. J., and Osborne, J. M. (2012a). A two-dimensional model of the colonic crypt
accounting for the role of the basement membrane and pericryptal fibroblast sheath.
PLoS computational biology, 8(5):e1002515.
[Dunn et al., 2012b] Dunn, S.-J., Fletcher, A. G., Chapman, J. S., Gavaghan, D. J., and
Osborne, J. M. (2012b). Modelling the role of the basement membrane beneath a
growing epithelial monolayer. Journal of theoretical biology, 298:82–91.
[Dunn et al., 2013] Dunn, S.-J., Näthke, I. S., and Osborne, J. M. (2013). Computational models reveal a passive mechanism for cell migration in the crypt. PloS one,
8(11):e80516.
[Economou et al., 2012] Economou, A. D., Ohazama, A., Porntaveetus, T., Sharpe, P. T.,
Kondo, S., Basson, M. A., Gritli-Linde, A., Cobourne, M. T., and Green, J. B. a.
(2012). Periodic stripe formation by a Turing mechanism operating at growth zones in
the mammalian palate. Nature genetics, 44(3):348–51.
[Eden et al., 2011] Eden, E., Geva-Zatorsky, N., Issaeva, I., Cohen, A., Dekel, E., Danon,
T., Cohen, L., Mayo, A., and Alon, U. (2011). Proteome half-life dynamics in living
human cells. Science (New York, N.Y.), 331(6018):764–8.
[Farhadifar et al., 2007] Farhadifar, R., Röper, J.-C., Aigouy, B., Eaton, S., and Jülicher,
F. (2007). The influence of cell mechanics, cell-cell interactions, and proliferation on
epithelial packing. Current biology : CB, 17(24):2095–104.
129
Bibliography
[Feng and Michaelides, 2004] Feng, Z.-G. and Michaelides, E. E. (2004). The immersed
boundary-lattice Boltzmann method for solving fluid–particles interaction problems.
Journal of Computational Physics, 195(2):602–628.
[Figueredo et al., 2013] Figueredo, G. P., Joshi, T. V., Osborne, J. M., Byrne, H. M.,
and Owen, M. R. (2013). On-lattice agent-based simulation of populations of cells
within the open-source Chaste framework. Interface focus, 3(2):20120081.
[Filas et al., 2012] Filas, B. A., Oltean, A., Beebe, D. C., Okamoto, R. J., Bayly, P. V.,
and Taber, L. A. (2012). A potential role for differential contractility in early brain
development and evolution. Biomechanics and Modeling in Mechanobiology, 11(8):1251–
1262.
[Fletcher et al., 2012] Fletcher, A. G., Breward, C. J. W., and Chapman, J. S. (2012).
Mathematical modeling of monoclonal conversion in the colonic crypt. Journal of
theoretical biology, 300:118–33.
[Fletcher et al., 2013] Fletcher, A. G., Osborne, J. M., Maini, P. K., and Gavaghan, D. J.
(2013). Implementing vertex dynamics models of cell populations in biology within
a consistent computational framework. Progress in biophysics and molecular biology,
113(2):299–326.
[Fletcher et al., 2014] Fletcher, A. G., Osterfield, M., Baker, R. E., and Shvartsman, S. Y.
(2014). Vertex models of epithelial morphogenesis. Biophysical journal, 106(11):2291–
304.
[Foolen et al., 2008] Foolen, J., van Donkelaar, C., Nowlan, N., Murphy, P., Huiskes, R.,
and Ito, K. (2008). Collagen orientation in periosteum and perichondrium is aligned
with preferential directions of tissue growth. Journal of orthopaedic research : official
publication of the Orthopaedic Research Society, 26(9):1263–8.
[Foolen et al., 2011] Foolen, J., van Donkelaar, C. C., and Ito, K. (2011). Intracellular
tension in periosteum/perichondrium cells regulates long bone growth. Journal of
orthopaedic research : official publication of the Orthopaedic Research Society, 29(1):84–
91.
[Foolen et al., 2009] Foolen, J., van Donkelaar, C. C., Murphy, P., Huiskes, R., and Ito,
K. (2009). Residual periosteum tension is insufficient to directly modulate bone growth.
Journal of biomechanics, 42(2):152–7.
[Forgacs et al., 1998] Forgacs, G., Foty, R. A., Shafrir, Y., and Steinberg, M. S. (1998).
Viscoelastic properties of living embryonic tissues: a quantitative study. Biophysical
journal, 74(5):2227–34.
[Foty et al., 1994] Foty, R. A., Forgacs, G., Pfleger, C. M., and Steinberg, M. S. (1994).
Liquid properties of embryonic tissues: Measurement of interfacial tensions. Physical
Review Letters, 72(14):2298–2301.
130
Bibliography
[Galle et al., 2005] Galle, J., Loeffler, M., and Drasdo, D. (2005). Modeling the effect
of deregulated proliferation and apoptosis on the growth dynamics of epithelial cell
populations in vitro. Biophysical journal, 88(1):62–75.
[Garzon-Alvarado et al., 2009] Garzon-Alvarado, D. A., Garcia-Aznar, J. M., and
Doblare, M. (2009). A reaction-diffusion model for long bones growth. Biomechanics
And Modeling In Mechanobiology, 8(5):381–395.
[Garzon-Alvarado et al., 2010] Garzon-Alvarado, D. A., Peinado Cortes, L. M., and
Cardenas Sandoval, R. P. (2010). A mathematical model of epiphyseal development:
hypothesis of growth pattern of the secondary ossification centre. Computer methods
in biomechanics and biomedical engineering, page 1.
[Geier et al., 2012] Geier, F., Fengos, G., Felizzi, F., and Iber, D. (2012). Analyzing
and constraining signaling networks: parameter estimation for the user. Methods in
molecular biology (Clifton, NJ), 880:23–39.
[Germann et al., 2011] Germann, P., Menshykau, D., Tanaka, S., and Iber, D. (2011).
Simulating Organogensis in COMSOL. In Proceedings of COMSOL Conference 2011.
[Gevertz and Torquato, 2006] Gevertz, J. L. and Torquato, S. (2006). Modeling the
effects of vasculature evolution on early brain tumor growth. Journal of theoretical
biology, 243(4):517–31.
[Gierer and Meinhardt, 1972] Gierer, A. and Meinhardt, H. (1972). A theory of biological
pattern formation. Kybernetik, 12(1):30–39.
[Ginsburg et al., 1998] Ginsburg, E. S., Gao, X., Shea, B. F., and Barbieri, R. L. (1998).
Half-life of estradiol in postmenopausal women. Gynecologic and obstetric investigation,
45(1):45–48.
[Glazier et al., 2007] Glazier, J. A., Balter, A., and Popławski, N. J. (2007). Magnetization to Morphogenesis: A Brief History of the Glazier-Graner-Hogeweg Model. In
Single-Cell-Based Models in Biology and Medicine, volume 2, pages 79–106. Birkhäuser
Basel, Basel.
[Glazier and Graner, 1993] Glazier, J. A. and Graner, F. (1993). Simulation of the
differential adhesion driven rearrangement of biological cells. Physical Review E,
47(3):2128–2154.
[Glazier et al., 2008] Glazier, J. A., Zhang, Y., Swat, M. H., Zaitlen, B. L., and Schnell,
S. (2008). Coordinated action of N-CAM, N-cadherin, EphA4, and ephrinB2 translates
genetic prepatterns into structure during somitogenesis in chick. Current topics in
developmental biology, 81(07):205–47.
[Goetz et al., 2006] Goetz, J. A., Singh, S., Suber, L. M., Kull, F. J., and Robbins, D. J.
(2006). A highly conserved amino-terminal region of sonic hedgehog is required for the
131
Bibliography
formation of its freely diffusible multimeric form. The Journal of biological chemistry,
281(7):4087–4093.
[Graner and Glazier, 1992] Graner, F. and Glazier, J. A. (1992). Simulation of biological
cell sorting using a two-dimensional extended Potts model. Physical Review Letters,
69(13):2013–2016.
[Guidolin et al., 2009] Guidolin, D., Albertin, G., Sorato, E., Oselladore, B., Mascarin,
A., and Ribatti, D. (2009). Mathematical modeling of the capillary-like pattern
generated by adrenomedullin-treated human vascular endothelial cells in vitro. Developmental dynamics : an official publication of the American Association of Anatomists,
238(8):1951–63.
[Guillot and Lecuit, 2013] Guillot, C. and Lecuit, T. (2013). Mechanics of epithelial
tissue homeostasis and morphogenesis. Science (New York, N.Y.), 340:1185–9.
[Guo et al., 2002] Guo, Z., Shi, B., and Zheng, C. (2002). A coupled lattice BGK model
for the Boussinesq equations. International Journal for Numerical Methods in Fluids,
39(4):325–342.
[He et al., 1997] He, X., Zou, Q., Luo, L.-s., and Dembo, M. (1997). Analytic solutions
of simple flows and analysis of nonslip boundary conditions for the lattice Boltzmann
BGK model. Journal of Statistical Physics, 87(1-2):115–136.
[Hebert et al., 2005] Hebert, B., Costantino, S., and Wiseman, P. (2005). Spatiotemporal
image correlation Spectroscopy (STICS) theory, verification, and application to protein
velocity mapping in living CHO cells. Biophysical journal, 88(5):3601–3614.
[Henderson and Carter, 2002] Henderson, J. H. and Carter, D. R. (2002). Mechanical
induction in limb morphogenesis: the role of growth-generated strains and pressures.
Bone, 31(6):645–53.
[Hester et al., 2011] Hester, S. D., Belmonte, J. M., Gens, S. J., Clendenon, S. G., and
Glazier, J. A. (2011). A multi-cell, multi-scale model of vertebrate segmentation and
somite formation. PLoS computational biology, 7(10):e1002155.
[Hilton et al., 2005] Hilton, M. J., Tu, X., Cook, J., Hu, H., and Long, F. (2005). Ihh
controls cartilage development by antagonizing Gli3, but requires additional effectors
to regulate osteoblast and vascular development. Development (Cambridge, England),
132(19):4339–4351.
[Hirashima et al., 2009] Hirashima, T., Iwasa, Y., and Morishita, Y. (2009). Dynamic
modeling of branching morphogenesis of ureteric bud in early kidney development.
[Hoehme et al., 2010] Hoehme, S., Brulport, M., Bauer, A., Bedawy, E., Schormann,
W., Hermes, M., Puppe, V., Gebhardt, R., Zellmer, S., Schwarz, M., Bockamp, E.,
132
Bibliography
Timmel, T., Hengstler, J. G., and Drasdo, D. (2010). Prediction and validation of cell
alignment along microvessels as order principle to restore tissue architecture in liver
regeneration. Proceedings of the National Academy of Sciences of the United States of
America, 107(23):10371–6.
[Hoehme and Drasdo, 2010] Hoehme, S. and Drasdo, D. (2010). A cell-based simulation
software for multi-cellular systems. Bioinformatics (Oxford, England), 26(20):2641–2.
[Hoehme et al., 2007] Hoehme, S., Hengstler, J. G., Brulport, M., Schäfer, M., Bauer,
A., Gebhardt, R., and Drasdo, D. (2007). Mathematical modelling of liver regeneration
after intoxication with CCl(4). Chemico-biological interactions, 168(1):74–93.
[Hogeweg, 2000] Hogeweg, P. (2000). Evolving mechanisms of morphogenesis: on the
interplay between differential adhesion and cell differentiation. Journal of theoretical
biology, 203(4):317–33.
[Hogeweg, 2002] Hogeweg, P. (2002). Computing an organism: on the interface between
informatic and dynamic processes. Bio Systems, 64(1-3):97–109.
[Hogeweg and Takeuchi, 2003] Hogeweg, P. and Takeuchi, N. (2003). Multilevel selection
in models of prebiotic evolution: compartments and spatial self-organization. Origins
of life and evolution of the biosphere : the journal of the International Society for the
Study of the Origin of Life, 33(4-5):375–403.
[Honda, 1978] Honda, H. (1978). Description of cellular patterns by Dirichlet domains:
the two-dimensional case. Journal of theoretical biology, 72(3):523–43.
[Honda and Eguchi, 1980] Honda, H. and Eguchi, G. (1980). How much does the cell
boundary contract in a monolayered cell sheet? Journal of Theoretical Biology,
84(3):575–588.
[Honda et al., 2008] Honda, H., Motosugi, N., Nagai, T., Tanemura, M., and Hiiragi,
T. (2008). Computer simulation of emerging asymmetry in the mouse blastocyst.
[Honda et al., 2004] Honda, H., Tanemura, M., and Nagai, T. (2004). A threedimensional vertex dynamics cell model of space-filling polyhedra simulating cell
behavior in a cell aggregate. Journal of theoretical biology, 226(4):439–53.
[Honda et al., 2000] Honda, H., Tanemura, M., and Yoshida, A. (2000). Differentiation of
wing epidermal scale cells in a butterfly under the lateral inhibition model–appearance
of large cells in a polygonal pattern. Acta biotheoretica, 48(2):121–36.
[Horton and Degnin, 2009] Horton, W. A. and Degnin, C. R. (2009). FGFs in endochondral skeletal development. Trends in endocrinology and metabolism: TEM,
20(7):341–348.
133
Bibliography
[Huber et al., 2008] Huber, C., Parmigiani, A., Chopard, B., Manga, M., and Bachmann,
O. (2008). Lattice Boltzmann model for melting with natural convection. International
Journal of Heat and Fluid Flow, 29(5):1469–1480.
[Hucka et al., 2003] Hucka, M., Finney, A., Sauro, H. M., Bolouri, H., Doyle, J. C.,
Kitano, H., Arkin, A. P., Bornstein, B. J., Bray, D., Cornish-Bowden, A., Cuellar,
A. A., Dronov, S., Gilles, E. D., Ginkel, M., Gor, V., Goryanin, I. I., Hedley, W. J.,
Hodgman, T. C., Hofmeyr, J.-H., Hunter, P. J., Juty, N. S., Kasberger, J. L., Kremling,
A., Kummer, U., Le Novère, N., Loew, L. M., Lucio, D., Mendes, P., Minch, E.,
Mjolsness, E. D., Nakayama, Y., Nelson, M. R., Nielsen, P. M. F., Sakurada, T.,
Schaff, J. C., Shapiro, B., Shimizu, T. S., Spence, H. D., Stelling, J., Takahashi, K.,
Tomita, M., Wagner, J., and Wang, J. (2003). The systems biology markup language
(SBML): a medium for representation and exchange of biochemical network models.
Bioinformatics, 19(4):524–531.
[Hufnagel et al., 2007] Hufnagel, L., Teleman, A. A., Rouault, H., Cohen, S. M., and
Shraiman, B. I. (2007). On the mechanism of wing size determination in fly development.
Proceedings of the National Academy of Sciences of the United States of America,
104(10):3835–40.
[Hundsdorfer, 2000] Hundsdorfer, W. (2000). Lecture Notes: Numerical Solution of
Advection-Diffusion-Reaction Equations. Technical report.
[Iber et al., 2015] Iber, D., Tanaka, S., Fried, P., Germann, P., and Menshykau, D.
(2015). Simulating tissue morphogenesis and signaling. Methods in molecular biology
(Clifton, N.J.), 1189(1):323–38.
[Incardona et al., 2000] Incardona, J. P., Lee, J. H., Robertson, C. P., Enga, K., Kapur,
R. P., and Roelink, H. (2000). Receptor-mediated endocytosis of soluble and membranetethered Sonic hedgehog by Patched-1. Proc. Natl. Acad. Sci USA, 97(22):12044–12049.
[Isaksson et al., 2008] Isaksson, H., van Donkelaar, C. C., Huiskes, R., and Ito, K. (2008).
A mechano-regulatory bone-healing model incorporating cell-phenotype specific activity.
[Ishihara and Sugimura, 2012] Ishihara, S. and Sugimura, K. (2012). Bayesian inference
of force dynamics during morphogenesis. Journal of theoretical biology, 313:201–11.
[Ising, 1925] Ising, E. (1925). Beitrag zur Theorie des Ferromagnetismus. Zeitschrift für
Physik, 31(1):253–258.
[Jiang et al., 1999] Jiang, T. X., Jung, H. S., Widelitz, R. B., and Chuong, C. M. (1999).
Self-organization of periodic patterns by dissociated feather mesenchymal cells and
the regulation of size, number and spacing of primordia. Development (Cambridge,
England), 126(22):4997–5009.
134
Bibliography
[Kanczler et al., 2012] Kanczler, J. M., Smith, E. L., Roberts, C. A., and Oreffo, R. O. C.
(2012). A novel approach for studying the temporal modulation of embryonic skeletal
development using organotypic bone cultures and microcomputed tomography. Tissue
engineering Part C, Methods, 18(10):747–760.
[Kang et al., 2014] Kang, S., Kahan, S., McDermott, J., Flann, N., and Shmulevich, I.
(2014). Biocellion: accelerating computer simulation of multicellular biological system
models. Bioinformatics (Oxford, England), pages 1–9.
[Karaplis et al., 1994] Karaplis, A. C., Luz, A., Glowacki, J., Bronson, R. T., Tybulewicz,
V. L., Kronenberg, H. M., and Mulligan, R. C. (1994). Lethal skeletal dysplasia from
targeted disruption of the parathyroid hormone-related peptide gene. Genes Dev,
8(3):277–289.
[Karimaddini et al., 2014] Karimaddini, Z., Ünal, E., Menshykau, D., and Iber, D. (2014).
Simulating Organogenesis in COMSOL : Image-based Modeling. In Proceedings of
COMSOL Conference 2014, Cambridge.
[Karp et al., 2000] Karp, S. J., Schipani, E., St-Jacques, B., Hunzelman, J., Kronenberg,
H., and McMahon, A. P. (2000). Indian hedgehog coordinates endochondral bone
growth and morphogenesis via parathyroid hormone related-protein-dependent and
-independent pathways. Development (Cambridge, England), 127(3):543–548.
[Karsenty et al., 2009] Karsenty, G., Kronenberg, H. M., and Settembre, C. (2009).
Genetic control of bone formation. Annu Rev Cell Dev Biol, 25:629–648.
[Keller and Segel, 1970] Keller, E. F. and Segel, L. A. (1970). Initiation of slime mold
aggregation viewed as an instability. Journal of theoretical biology, 26(3):399–415.
[Kicheva and González-Gaitán, 2008] Kicheva, A. and González-Gaitán, M. (2008). The
Decapentaplegic morphogen gradient: a precise definition. Curr Opin Cell Biol,
20(2):137–143.
[Kicheva et al., 2007] Kicheva, A., Pantazis, P., Bollenbach, T., Kalaidzidis, Y., Bittig,
T., Juelicher, F., and Gonzalez-Gaitan, M. (2007). Kinetics of morphogen gradient
formation. Science, 315(5811):521–525.
[Kim et al., 2013] Kim, H. Y., Varner, V. D., and Nelson, C. M. (2013). Apical constriction initiates new bud formation during monopodial branching of the embryonic
chicken lung. Development (Cambridge, England), 140(15):3146–55.
[Kim and Othmer, 2013] Kim, Y. and Othmer, H. G. (2013). A hybrid model of tumorstromal interactions in breast cancer. Bulletin of mathematical biology, 75(8):1304–50.
[Kim et al., 2007] Kim, Y., Stolarska, M. A., and Othmer, H. G. (2007). A Hybrid Model
for Tumor Spheroid Growth In Vitro I: Theoretical Development and Early Results.
Mathematical Models and Methods in Applied Sciences, 17(supp01):1773–1798.
135
Bibliography
[Kleinstreuer et al., 2013] Kleinstreuer, N., Dix, D., Rountree, M., Baker, N., Sipes, N.,
Reif, D., Spencer, R., and Knudsen, T. (2013). A computational model predicting
disruption of blood vessel development. PLoS computational biology, 9(4):e1002996.
[Kobayashi et al., 2005] Kobayashi, T., Soegiarto, D. W., Yang, Y., Lanske, B., Schipani,
E., McMahon, A. P., and Kronenberg, H. M. (2005). Indian hedgehog stimulates
periarticular chondrocyte differentiation to regulate growth plate length independently
of PTHrP. The Journal of clinical investigation, 115(7):1734–1742.
[Köhn-Luque et al., 2011] Köhn-Luque, A., de Back, W., Starruss, J., Mattiotti, A.,
Deutsch, A., Pérez-Pomares, J. M., and Herrero, M. (2011). Early embryonic vascular
patterning by matrix-mediated paracrine signalling: a mathematical model study. PloS
one, 6(9):e24175.
[Köhn-Luque et al., 2013] Köhn-Luque, A., de Back, W., Yamaguchi, Y., Yoshimura, K.,
Herrero, M., and Miura, T. (2013). Dynamics of VEGF matrix-retention in vascular
network patterning. Physical biology, 10(6):066007.
[Kondo and Asai, 1995] Kondo, S. and Asai, R. (1995). A reaction diffusion wave on the
skin of the marine angelfish Pomacanthus. Nature, 376(6543):765–768.
[Kornberg, 2013] Kornberg, T. B. (2013). Cytonemes extend their reach. The EMBO
journal, pages 1–2.
[Kornberg, 2014] Kornberg, T. B. (2014). Cytonemes and the dispersion of morphogens.
Wiley Interdiscip Rev Dev Biol, 3(6):445–463.
[Koziel et al., 2005] Koziel, L., Wuelling, M., Schneider, S., and Vortkamp, A. (2005).
Gli3 acts as a repressor downstream of Ihh in regulating two distinct steps of chondrocyte differentiation. Development (Cambridge, England), 132(23):5249–5260.
[Kronenberg, 2003] Kronenberg, H. M. (2003). Developmental regulation of the growth
plate. Nature, 423(6937):332–336.
[Kulesa et al., 1996] Kulesa, P. M., Cruywagen, G. C., Lubkin, S. R., Maini, P. K.,
Sneyd, J., Ferguson, M. W. J., and Murray, J. D. (1996). On a model mechanism for
the spatial patterning of teeth primordia in alligator. J. Theor. Biol., 180(4):287–296.
[Kumar et al., 2010] Kumar, M., Mommer, M. S., and Sourjik, V. (2010). Mobility of
Cytoplasmic, Membrane, and DNA-Binding Proteins in Escherichia coli. Biophysical
journal, 98(4):552–559.
[Kurics et al., 2014] Kurics, T., Menshykau, D., and Iber, D. (2014). Feedback, receptor
clustering, and receptor restriction to single cells yield large Turing spaces for ligandreceptor-based Turing models. Physical Review E, 90(2):022716.
136
Bibliography
[Lanske et al., 1996] Lanske, B., Karaplis, A. C., Lee, K., Luz, A., Vortkamp, A., Pirro,
A., Karperien, M., Defize, L. H., Ho, C., Mulligan, R. C., Abou-Samra, A. B., Jüppner,
H., Segre, G. V., and Kronenberg, H. M. (1996). PTH/PTHrP receptor in early
development and Indian hedgehog-regulated bone growth. Science, 273(5275):663–666.
[Le et al., 2009] Le, D.-V., White, J., Peraire, J., Lim, K. M., and Khoo, B. C. (2009). An
implicit immersed boundary method for three-dimensional fluid-membrane interactions.
Journal of Computational Physics, 228(22):8427–8445.
[Le Novère et al., 2005] Le Novère, N., Finney, A., Hucka, M., Bhalla, U. S., Campagne,
F., Collado-Vides, J., Crampin, E. J., Halstead, M., Klipp, E., Mendes, P., Nielsen,
P. M. F., Sauro, H. M., Shapiro, B., Snoep, J. L., Spence, H. D., and Wanner, B. L.
(2005). Minimum information requested in the annotation of biochemical models
(MIRIAM). Nature biotechnology, 23(12):1509–15.
[Levine and Rappel, 2005] Levine, H. and Rappel, W.-J. (2005). Membrane-bound
Turing patterns. Physical Review E, 72(6):061912.
[Li et al., 2010] Li, C., Donizelli, M., Rodriguez, N., Dharuri, H., Endler, L., Chelliah,
V., Li, L., He, E., Henry, A., Stefan, M. I., Snoep, J. L., Hucka, M., Le Novère, N.,
and Laibe, C. (2010). BioModels Database: An enhanced, curated and annotated
resource for published quantitative kinetic models. BMC systems biology, 4:92.
[Li and Lowengrub, 2014] Li, J. F. and Lowengrub, J. (2014). The effects of cell compressibility, motility and contact inhibition on the growth of tumor cell clusters using
the Cellular Potts Model. Journal of theoretical biology, 343:79–91.
[Li et al., 2001] Li, Q., Zheng, C., Wang, N., and Shi, B. (2001). LBGK simulations of
Turing patterns in CIMA model. Journal of scientific computing, 16(2):121–134.
[Li and Bowerman, 2010] Li, R. and Bowerman, B. (2010). Symmetry breaking in biology.
Cold Spring Harbor perspectives in biology, 2(3):a003475.
[Lloyd and Ascoli, 1983] Lloyd, C. E. and Ascoli, M. (1983). On the mechanisms involved
in the regulation of the cell-surface receptors for human choriogonadotropin and mouse
epidermal growth factor in cultured Leydig tumor cells. J Cell Biol, 96(2):521–526.
[Macklin et al., 2012] Macklin, P., Edgerton, M. E., Thompson, A. M., and Cristini, V.
(2012). Patient-calibrated agent-based modelling of ductal carcinoma in situ (DCIS):
from microscopic measurements to macroscopic predictions of clinical progression.
Journal of theoretical biology, 301:122–40.
[Mahalwar et al., 2014] Mahalwar, P., Walderich, B., Singh, A. P., and Nüsslein-Volhard,
C. (2014). Local reorganization of xanthophores fine-tunes and colors the striped
pattern of zebrafish. Science (New York, N.Y.), 345(6202):1362–4.
137
Bibliography
[Maini et al., 1991] Maini, P. K., Myerscough, M. R., Winters, K. H., and Murray, J. D.
(1991). Bifurcating Spatially Heterogeneous Solutions in a Chemotaxis Model for
Biological Pattern Generation. Bulletin Of Mathematical Biology, 53(5):701–719.
[Marée et al., 2007] Marée, A. F. M., Grieneisen, V. A., and Hogeweg, P. (2007). The
Cellular Potts Model and Biophysical Properties of Cells, Tissues and Morphogenesis.
In Single Cell Based Models in Biology and Medicine, volume 2.
[Meineke et al., 2001] Meineke, F. A., Potten, C. S., and Loeffler, M. (2001). Cell
migration and organization in the intestinal crypt using a lattice-free model. Cell
proliferation, 34(4):253–66.
[Meinhardt, 2009] Meinhardt, H. (2009). The Algorithmic Beauty of Sea Shells, volume
XXXIII of The Virtual Laboratory. Springer Berlin Heidelberg, Berlin, Heidelberg.
[Menshykau et al., 2014] Menshykau, D., Blanc, P., Ünal, E., Sapin, V., and Iber, D.
(2014). An interplay of geometry and signaling enables robust lung branching morphogenesis. Development, 141:4526–4536.
[Menshykau and Iber, 2012] Menshykau, D. and Iber, D. (2012). Simulating Organogenesis with Comsol: Interacting and Deforming Domains . Proceedings of COMSOL
Conference 2012.
[Menshykau and Iber, 2013] Menshykau, D. and Iber, D. (2013). Kidney branching
morphogenesis under the control of a ligand-receptor-based Turing mechanism. Physical
biology, 10:46003.
[Menshykau et al., 2012] Menshykau, D., Kraemer, C., and Iber, D. (2012). Branch Mode
Selection during Early Lung Development. PLoS computational biology, 8(2):e1002377.
[Merks et al., 2006] Merks, R. M. H., Brodsky, S. V., Goligorksy, M. S., Newman, S. A.,
and Glazier, J. A. (2006). Cell elongation is key to in silico replication of in vitro
vasculogenesis and subsequent remodeling. Developmental biology, 289(1):44–54.
[Merks et al., 2011] Merks, R. M. H., Guravage, M., Inzé, D., and Beemster, G. T. S.
(2011). VirtualLeaf: an open-source framework for cell-based modeling of plant tissue
growth and development. Plant physiology, 155(2):656–66.
[Merks et al., 2008] Merks, R. M. H., Perryn, E. D., Shirinifard, A., and Glazier, J. A.
(2008). Contact-inhibited chemotaxis in de novo and sprouting blood-vessel growth.
PLoS computational biology, 4(9):e1000163.
[Metropolis et al., 1953] Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller,
A. H., and Teller, E. (1953). Equation of State Calculations by Fast Computing
Machines. The Journal of Chemical Physics, 21(6):1087.
138
Bibliography
[Miao et al., 2002] Miao, D., He, B., Karaplis, A. C., and Goltzman, D. (2002). Parathyroid hormone is essential for normal fetal bone formation. The Journal of clinical
investigation, 109(9):1173–1182.
[Milde et al., 2014] Milde, F., Tauriello, G., Haberkern, H., and Koumoutsakos, P. (2014).
SEM++: A particle model of cellular growth, signaling and migration. Computational
Particle Mechanics.
[Minc et al., 2011] Minc, N., Burgess, D., and Chang, F. (2011). Influence of cell geometry
on division-plane positioning. Cell, 144(3):414–26.
[Mirams et al., 2013] Mirams, G. R., Arthurs, C. J., Bernabeu, M. O., Bordas, R.,
Cooper, J., Corrias, A., Davit, Y., Dunn, S.-J., Fletcher, A. G., Harvey, D. G., Marsh,
M. E., Osborne, J. M., Pathmanathan, P., Pitt-Francis, J., Southern, J., Zemzemi, N.,
and Gavaghan, D. J. (2013). Chaste: an open source C++ library for computational
physiology and biology. PLoS computational biology, 9(3):e1002970.
[Mirams et al., 2012] Mirams, G. R., Fletcher, A. G., Maini, P. K., and Byrne, H. M.
(2012). A theoretical investigation of the effect of proliferation and adhesion on
monoclonal conversion in the colonic crypt. Journal of theoretical biology, 312:143–56.
[Mittal and Iaccarino, 2005] Mittal, R. and Iaccarino, G. (2005). Immersed Boundary
Methods. Annual Review of Fluid Mechanics, 37(1):239–261.
[Miura et al., 2006] Miura, T., Shiota, K., Morriss-Kay, G., and Maini, P. K. (2006).
Mixed-mode pattern in Doublefoot mutant mouse limb-Turing reaction-diffusion model
on a growing domain during limb development. Journal of Theoretical Biology, 240:562–
573.
[Mizutani et al., 2005] Mizutani, C., Nie, Q., Wan, F., Zhang, Y., Vilmos, P., SousaNeves, R., Bier, E., Marsh, J., and Lander, A. (2005). Formation of the BMP activity
gradient in the Drosophila embryo. Dev Cell, 8(6):915–924.
[Moreira and Deutsch, 2002] Moreira, J. and Deutsch, A. (2002). Cellular Automation
Models of Tumor Development: A Critical Review. Advances in Complex Systems,
05(02n03):247–267.
[Muller et al., 2012] Muller, P., Rogers, K. W., Jordan, B. M., Lee, J. S., Robson, D.,
Ramanathan, S., and Schier, a. F. (2012). Differential Diffusivity of Nodal and Lefty
Underlies a Reaction-Diffusion Patterning System. Science, 336(6082):721–724.
[Muñoz et al., 2007] Muñoz, J. J., Barrett, K., and Miodownik, M. (2007). A deformation
gradient decomposition method for the analysis of the mechanics of morphogenesis.
Journal of Biomechanics, 40(6):1372–1380.
[Munoz et al., 2010] Munoz, J. J., Conte, V., and Miodownik, M. (2010). Stressdependent morphogenesis: Continuum mechanics and truss systems. Biomechanics
and Modeling in Mechanobiology, 9(4):451–467.
139
Bibliography
[Murray, 1982] Murray, J. (1982). Parameter space for turing instability in reaction
diffusion mechanisms: A comparison of models. Journal of Theoretical Biology,
98(1):143–163.
[Murray, 1993] Murray, J. D. (1993). Mathematical Biology, volume 18 of Interdisciplinary
Applied Mathematics. Springer-Verlag, New York.
[Murray et al., 1983] Murray, J. D., Oster, G., and Harris, A. K. (1983). A mechanical
model for mesenchymal morphogenesis. Journal of mathematical biology, 17(1):125–129.
[Murray et al., 2011] Murray, P. J., Walter, A., Fletcher, A. G., Edwards, C. M., Tindall,
M. J., and Maini, P. K. (2011). Comparing a discrete and continuum model of the
intestinal crypt. Physical biology, 8(2):026011.
[Nagai and Honda, 2001] Nagai, T. and Honda, H. (2001). A dynamic cell model for the
formation of epithelial tissues. Philosophical Magazine Part B, 81(7):699–719.
[Nakamasu et al., 2009] Nakamasu, A., Takahashi, G., Kanbe, A., and Kondo, S. (2009).
Interactions between zebrafish pigment cells responsible for the generation of Turing
patterns. Proceedings of the National Academy of Sciences of the United States of
America, 106(21):8429–8434.
[Newman and Frisch, 1979] Newman, S. A. and Frisch, H. L. (1979). Dynamics of skeletal
pattern formation in developing chick limb. Science (New York, N.Y.), 205(4407):662–8.
[Newman, 2005] Newman, T. J. (2005). Modeling Multicellular Systems Using Subcellular Elements. Mathematical Biosciences and Engineering, 2(3):613–624.
[Niu et al., 2006] Niu, X., Shu, C., Chew, Y., and Peng, Y. (2006). A momentum
exchange-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows. Physics Letters A, 354(3):173–182.
[Okuda et al., 2014] Okuda, S., Inoue, Y., Eiraku, M., Adachi, T., and Sasai, Y. (2014).
Vertex dynamics simulations of viscosity-dependent deformation during tissue morphogenesis. Biomechanics and modeling in mechanobiology.
[Osborne et al., 2010] Osborne, J. M., Walter, A., Kershaw, S. K., Mirams, G. R.,
Fletcher, A. G., Pathmanathan, P., Gavaghan, D. J., Jensen, O. E., Maini, P. K.,
and Byrne, H. M. (2010). A hybrid approach to multi-scale modelling of cancer.
Philosophical transactions. Series A, Mathematical, physical, and engineering sciences,
368(1930):5013–28.
[Oster and Murray, 1989] Oster, G. F. and Murray, J. D. (1989). Pattern formation
models and developmental constraints. Journal of Experimental Zoology, 251(2):186–
202.
140
Bibliography
[Osterfield et al., 2013] Osterfield, M., Du, X., Schüpbach, T., Wieschaus, E. F., and
Shvartsman, S. Y. (2013). Three-dimensional epithelial morphogenesis in the developing
Drosophila egg. Developmental cell, 24(4):400–10.
[Palsson, 2001] Palsson, E. (2001). A three-dimensional model of cell movement in
multicellular systems. Future Generation Computer Systems, 17:835–852.
[Palsson and Othmer, 2000] Palsson, E. and Othmer, H. G. (2000). A model for individual and collective cell movement in Dictyostelium discoideum. Proceedings of the
National Academy of Sciences of the United States of America, 97(19):10448–53.
[Parmigiani et al., 2009] Parmigiani, a., Huber, C., Chopard, B., Latt, J., and Bachmann,
O. (2009). Application of the multi distribution function lattice Boltzmann approach
to thermal flows. The European Physical Journal Special Topics, 171(1):37–43.
[Pateder et al., 2001] Pateder, D. B., Ferguson, C. M., Ionescu, A. M., Schwarz, E. M.,
Rosier, R. N., Puzas, J. E., and O’Keefe, R. J. (2001). PTHrP expression in chick
sternal chondrocytes is regulated by TGF-beta through Smad-mediated signaling.
Journal of cellular physiology, 188(3):343–351.
[Pateder et al., 2000] Pateder, D. B., Rosier, R. N., Schwarz, E. M., Reynolds, P. R.,
Puzas, J. E., D’Souza, M., and O’Keefe, R. J. (2000). PTHrP expression in chondrocytes, regulation by TGF-beta, and interactions between epiphyseal and growth plate
chondrocytes. Experimental cell research, 256(2):555–562.
[Pathmanathan et al., 2009] Pathmanathan, P., Cooper, J., Fletcher, A. G., Mirams,
G. R., Murray, P. J., Osborne, J. M., Pitt-Francis, J., Walter, A., and Chapman, J. S.
(2009). A computational study of discrete mechanical tissue models. Physical biology,
6(3):036001.
[Peskin, 1977] Peskin, C. S. (1977). Numerical analysis of blood flow in the heart. Journal
of Computational Physics, 25(3):220–252.
[Peskin, 2003] Peskin, C. S. (2003). The immersed boundary method. Acta Numerica,
11.
[Peskin and Printz, 1993] Peskin, C. S. and Printz, B. F. (1993). Improved Volume
Conservation in the Computation of Flows with Immersed Elastic Boundaries. Journal
of Computational Physics, 105(1):33–46.
[Phillips and Steinberg, 1978] Phillips, H. M. and Steinberg, M. S. (1978). Embryonic
tissues as elasticoviscous liquids. I. Rapid and slow shape changes in centrifuged cell
aggregates. Journal of cell science, 30:1–20.
[Pitt-Francis et al., 2009] Pitt-Francis, J., Pathmanathan, P., Bernabeu, M. O., Bordas,
R., Cooper, J., Fletcher, A. G., Mirams, G. R., Murray, P. J., Osborne, J. M., and
Walter, A. (2009). Chaste: A test-driven approach to software development for
biological modelling. Computer Physics Communications, 180(12):2452–2471.
141
Bibliography
[Ponce Dawson et al., 1993] Ponce Dawson, S., Chen, S., and Doolen, G. D. (1993).
Lattice Boltzmann computations for reaction-diffusion equations. The Journal of
Chemical Physics, 98(2):1514.
[Poplawski et al., 2010] Poplawski, N. J., Shirinifard, A., Agero, U., Gens, S. J., Swat,
M. H., and Glazier, J. A. (2010). Front instabilities and invasiveness of simulated 3D
avascular tumors. PloS one, 5(5):e10641.
[Poplawski et al., 2007] Poplawski, N. J., Swat, M. H., Gens, S. J., and Glazier, J. A.
(2007). Adhesion between cells, diffusion of growth factors, and elasticity of the AER
produce the paddle shape of the chick limb. Physica A, 373:521–532.
[Potts, 1952] Potts, R. B. (1952). Some generalized order-disorder transformations.
Mathematical Proceedings of the Cambridge Philosophical Society, 48(01):106–109.
[Provot and Schipani, 2005] Provot, S. and Schipani, E. (2005). Molecular mechanisms of
endochondral bone development. Biochemical and biophysical research communications,
328(3):658–665.
[Ramírez-Weber and Kornberg, 1999] Ramírez-Weber, F. a. and Kornberg, T. B. (1999).
Cytonemes: Cellular processes that project to the principal signaling center in
Drosophila imaginal discs. Cell, 97(5):599–607.
[Ranft et al., 2010] Ranft, J., Basan, M., Elgeti, J., Joanny, J.-F., Prost, J., and Jülicher,
F. (2010). Fluidization of tissues by cell division and apoptosis. Proceedings of the
National Academy of Sciences of the United States of America, 107(49):20863–8.
[Raol et al., 2004] Raol, J., Girija, G., and Singh, J. (2004). Modelling and Parameter
Estimation of Dynamical Systems.
[Rauch and Millonas, 2004] Rauch, E. M. and Millonas, M. M. (2004). The role of
trans-membrane signal transduction in turing-type cellular pattern formation. Journal
of Theoretical Biology, 226(4):401–407.
[Rauzi et al., 2008] Rauzi, M., Verant, P., Lecuit, T., and Lenne, P.-F. (2008). Nature
and anisotropy of cortical forces orienting Drosophila tissue morphogenesis. Nature
cell biology, 10(12):1401–1410.
[Ray et al., 2013] Ray, S., Yuan, D., Dhulekar, N., Oztan, B., Yener, B., and Larsen, M.
(2013). Cell-based multi-parametric model of cleft progression during submandibular
salivary gland branching morphogenesis. PLoS computational biology, 9(11):e1003319.
[Rejniak, 2007] Rejniak, K. A. (2007). An immersed boundary framework for modelling
the growth of individual cells: an application to the early tumour development. Journal
of theoretical biology, 247(1):186–204.
142
Bibliography
[Rejniak and Dillon, 2007] Rejniak, K. A. and Dillon, R. H. (2007). A Single Cell-Based
Model of the Ductal Tumour Microarchitecture. Computational and Mathematical
Methods in Medicine, 8(1):51–69.
[Rejniak et al., 2004] Rejniak, K. A., Kliman, H. J., and Fauci, L. J. (2004). A computational model of the mechanics of growth of the villous trophoblast bilayer. Bulletin
of mathematical biology, 66(2):199–232.
[Restrepo et al., 2014] Restrepo, S., Zartman, J. J., and Basler, K. (2014). Coordination
of patterning and growth by the morphogen DPP. Current Biology, 24(6):R245—-R255.
[Ries et al., 2009] Ries, J., Yu, S. R., Burkhardt, M., Brand, M., and Schwille, P. (2009).
Modular scanning fcs quantifies receptor-ligand interactions in living multicellular
organisms. Nat Methods, 6(9):643–U31.
[Rodriguez et al., 1994] Rodriguez, E. K., Hoger, A., and McCulloch, A. D. (1994). Stressdependent finite growth in soft elastic tissues. Journal of Biomechanics, 27(4):455–467.
[Rudge and Haseloff, 2005] Rudge, T. and Haseloff, J. (2005). A Computational Model
of Cellular Morphogenesis in Plants. In Capcarrère, M. S., Freitas, A. A., Bentley,
P. J., Johnson, C. G., and Timmis, J., editors, Advances in Artificial Life, volume
3630 of Lecture Notes in Computer Science, pages 78–87. Springer Berlin Heidelberg,
Berlin, Heidelberg.
[Safferling et al., 2013] Safferling, K., Sütterlin, T., Westphal, K., Ernst, C., Breuhahn,
K., James, M., Jäger, D., Halama, N., and Grabe, N. (2013). Wound healing revised:
A novel reepithelialization mechanism revealed by in vitro and in silico models. Journal
of Cell Biology, 203(4):691–709.
[Sandersius and Newman, 2008] Sandersius, S. A. and Newman, T. J. (2008). Modeling
cell rheology with the Subcellular Element Model. Physical biology, 5(1):015002.
[Sandersius et al., 2011] Sandersius, S. A., Weijer, C. J., and Newman, T. J. (2011).
Emergent cell and tissue dynamics from subcellular modeling of active biomechanical
processes. Physical biology, 8(4):045007.
[Sanderson et al., 2006] Sanderson, A. R., Kirby, R. M., Johnson, C. R., and Yang,
L. (2006). Advanced Reaction-Diffusion Models for Texture Synthesis. Journal of
Graphics, GPU, and Game Tools, 11(3):47–71.
[Schilling et al., 2011] Schilling, S., Willecke, M., Aegerter-Wilmsen, T., Cirpka, O. A.,
Basler, K., and von Mering, C. (2011). Cell-sorting at the A/P boundary in the
Drosophila wing primordium: a computational model to consolidate observed non-local
effects of Hh signaling. PLoS computational biology, 7(4):e1002025.
[Schipani and Provot, 2003] Schipani, E. and Provot, S. (2003). PTHrP, PTH, and the
PTH/PTHrP receptor in endochondral bone development. Birth defects research Part
C, Embryo today : reviews, 69(4):352–362.
143
Bibliography
[Schliess et al., 2014] Schliess, F., Hoehme, S., Henkel, S. G., Ghallab, A., Driesch, D.,
Böttger, J., Guthke, R., Pfaff, M., Hengstler, J. G., Gebhardt, R., Häussinger, D.,
Drasdo, D., and Zellmer, S. (2014). Integrated metabolic spatial-temporal model
for the prediction of ammonia detoxification during liver damage and regeneration.
Hepatology (Baltimore, Md.), pages 1–12.
[Schnakenberg, 1979] Schnakenberg, J. (1979). Simple chemical reaction systems with
limit cycle behaviour. Journal of Theoretical Biology, 81(3):389–400.
[Shi et al., 2014] Shi, Y., Yao, J., Xu, G., and Taber, L. A. (2014). Bending of the
looping heart: differential growth revisited. Journal of biomechanical engineering,
136(8):1–15.
[Shirinifard et al., 2009] Shirinifard, A., Gens, S. J., Zaitlen, B. L., Poplawski, N. J.,
Swat, M. H., and Glazier, J. A. (2009). 3D multi-cell simulation of tumor growth and
angiogenesis. PloS one, 4(10):e7190.
[Sick et al., 2006] Sick, S., Reinker, S., Timmer, J., and Schlake, T. (2006). WNT
and DKK Determine Hair Follicle Spacing Through a Reaction-Diffusion Mechanism.
Science, 314(5804):1447–1450.
[Singh et al., 2001] Singh, A. B., Norris, K., Modi, N., Sinha-Hikim, I., Shen, R., Davidson, T., and Bhasin, S. (2001). Pharmacokinetics of a transdermal testosterone
system in men with end stage renal disease receiving maintenance hemodialysis and
healthy hypogonadal men. The Journal of clinical endocrinology and metabolism,
86(6):2437–2445.
[Sluka et al., 2014] Sluka, J. P., Shirinifard, A., Swat, M. H., Cosmanescu, A., Heiland,
R. W., and Glazier, J. A. (2014). The cell behavior ontology: describing the intrinsic
biological behaviors of real and model cells seen as active agents. Bioinformatics
(Oxford, England), 30(16):2367–2374.
[Smith et al., 2011] Smith, A. M., Baker, R. E., Kay, D., and Maini, P. K. (2011).
Incorporating chemical signalling factors into cell-based models of growing epithelial
tissues. Journal of mathematical biology.
[Sober, 1969] Sober, H. A. (1969). Handbook of Biochemistry. Selected Data for Molecular
Biology. Annals of Internal Medicine, 70(1):239.
[Sohrmann and Peter, 2003] Sohrmann, M. and Peter, M. (2003). Polarizing without a
c(l)ue. Trends Cell Biol, 13(10):526–533.
[St-Jacques et al., 1999] St-Jacques, B., Hammerschmidt, M., and McMahon, A. P.
(1999). Indian hedgehog signaling regulates proliferation and differentiation of chondrocytes and is essential for bone formation. Genes Dev, 13(16):2072–2086.
144
Bibliography
[Staple et al., 2010] Staple, D. B., Farhadifar, R., Röper, J.-C., Aigouy, B., Eaton, S.,
and Jülicher, F. (2010). Mechanics and remodelling of cell packings in epithelia. The
European physical journal. E, Soft matter, 33(2):117–27.
[Starruß et al., 2014] Starruß, J., de Back, W., Brusch, L., and Deutsch, A. (2014).
Morpheus: a user-friendly modeling environment for multiscale and multicellular
systems biology. Bioinformatics (Oxford, England), 30(9):1331–2.
[Sütterlin and Grabe, 2014] Sütterlin, T. and Grabe, N. (2014). Graphical Multi-Scale
Modeling of Epidermal Homeostasis with EPISIM. In Computational Biophysics of
the Skin, volume 3, pages 421–460. Pan Stanford Publishing.
[Sütterlin et al., 2013] Sütterlin, T., Kolb, C., Dickhaus, H., Jäger, D., and Grabe, N.
(2013). Bridging the scales: semantic integration of quantitative SBML in graphical
multi-cellular models and simulations with EPISIM and COPASI. Bioinformatics
(Oxford, England), 29(2):223–9.
[Swaminathan et al., 1997] Swaminathan, R., Hoang, C. P., and Verkman, A. S. (1997).
Photobleaching recovery and anisotropy decay of green fluorescent protein GFPS65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein
translational and rotational diffusion. Biophysical journal, 72(4):1900–1907.
[Swat et al., 2012] Swat, M. H., Thomas, G. L., Belmonte, J. M., Shirinifard, A., Hmeljak,
D., and Glazier, J. A. (2012). Multi-scale modeling of tissues using CompuCell3D.,
volume 110. Elsevier Inc.
[Szabó and Czirók, 2010] Szabó, A. and Czirók, A. (2010). The Role of Cell-Cell Adhesion in the Formation of Multicellular Sprouts. Mathematical modelling of natural
phenomena, 5(1):106.
[Taber, 2001] Taber, L. A. (2001). Iomechanics of Cardiovascular Development. Annual
review of biomedical engineering, 3:1–25.
[Taber, 2009a] Taber, L. A. (2009a). Theoretical Study of Beloussov’s Hyper-Restoration
Hypothesis for Mechanical Regulation of Morphogenesis. Biomech Model Mechanobiol.,
7(6):427–441.
[Taber, 2009b] Taber, L. A. (2009b). Towards a unified theory for morphomechanics.
Philosophical transactions. Series A, Mathematical, physical, and engineering sciences,
367(1902):3555–3583.
[Tauriello et al., 2015] Tauriello, G., Economides, E. A., Hadjidoukas, P., Angelikopoulos,
P., Kulakova, L., and Koumoutsakos, P. (2015). Approximate Bayesian Computation
for in Silico Cells. In 8th GRACM International Congress on Computational Mechanics,
number July.
145
Bibliography
[Thummler and Weddemann, 2007] Thummler, V. and Weddemann, A. (2007). Computation of Space-Time Patterns via ALE Methods. Excert from the Proceedings of the
COMSOL Conference.
[Turing, 1952] Turing, A. M. (1952). The Chemical Basis of Morphogenesis. Philosophical
Transactions of the Royal Society B: Biological Sciences, 237(641):37–72.
[Valley et al., 2008] Valley, C. C., Solodin, N. M., Powers, G. L., Ellison, S. J., and
Alarid, E. T. (2008). Temporal variation in estrogen receptor-alpha protein turnover
in the presence of estrogen. Journal of molecular endocrinology, 40(1):23–34.
[van Donkelaar and Huiskes, 2007] van Donkelaar, C. C. and Huiskes, R. (2007). The
PTHrP-Ihh feedback loop in the embryonic growth plate allows PTHrP to control hypertrophy and Ihh to regulate proliferation. Biomechanics And Modeling In Mechanobiology, 6(1-2):55–62.
[van Leeuwen et al., 2009] van Leeuwen, I. M. M., Mirams, G. R., Walter, A., Fletcher,
A. G., Murray, P. J., Osborne, J. M., Varma, S., Young, S. J., Cooper, J., Doyle, B.,
Pitt-Francis, J., Momtahan, L., Pathmanathan, P., Whiteley, J. P., Chapman, J. S.,
Gavaghan, D. J., Jensen, O. E., King, J. R., Maini, P. K., Waters, S. L., and Byrne,
H. M. (2009). An integrative computational model for intestinal tissue renewal. Cell
proliferation, 42(5):617–36.
[Varner et al., 2010] Varner, V. D., Voronov, D. A., and Taber, L. A. (2010). Mechanics
of head fold formation: investigating tissue-level forces during early development.
[Vasiev et al., 2010] Vasiev, B., Balter, A., Chaplain, M. A. J., Glazier, J. A., and Weijer,
C. J. (2010). Modeling gastrulation in the chick embryo: formation of the primitive
streak. PloS one, 5(5):e10571.
[Vortkamp et al., 1996] Vortkamp, A., Lee, K., Lanske, B., Segre, G. V., Kronenberg,
H. M., and Tabin, C. J. (1996). Regulation of rate of cartilage differentiation by Indian
hedgehog and PTH-related protein. Science, 273(5275):613–622.
[Waltemath et al., 2011a] Waltemath, D., Adams, R., Beard, D. A., Bergmann, F. T.,
Bhalla, U. S., Britten, R., Chelliah, V., Cooling, M. T., Cooper, J., Crampin, E. J.,
Garny, A., Hoops, S., Hucka, M., Hunter, P. J., Klipp, E., Laibe, C., Miller, A. K.,
Moraru, I. I., Nickerson, D. P., Nielsen, P. M. F., Nikolski, M., Sahle, S., Sauro, H. M.,
Schmidt, H., Snoep, J. L., Tolle, D., Wolkenhauer, O., and Le Novère, N. (2011a).
Minimum Information About a Simulation Experiment (MIASE). PLoS computational
biology, 7(4):e1001122.
[Waltemath et al., 2011b] Waltemath, D., Adams, R., Bergmann, F. T., Hucka, M.,
Kolpakov, F., Miller, A. K., Moraru, I. I., Nickerson, D. P., Sahle, S., Snoep, J. L.,
and Le Novère, N. (2011b). Reproducible computational biology experiments with
146
Bibliography
SED-ML–the Simulation Experiment Description Markup Language. BMC systems
biology, 5(1):198.
[Watanabe and Kondo, 2015] Watanabe, M. and Kondo, S. (2015). Comment on "Local
reorganization of xanthophores fine-tunes and colors the striped pattern of zebrafish".
Science, 348(6232):297–297.
[Weddemann and Thummler, 2008] Weddemann, A. and Thummler, V. (2008). Stability Analysis of ALE-Methods for Advection-Diffusion Problems. Excert from the
Proceedings of the COMSOL Conference.
[Weir et al., 1996] Weir, E. C., Philbrick, W. M., Amling, M., Neff, L. a., Baron, R., and
Broadus, a. E. (1996). Targeted overexpression of parathyroid hormone-related peptide
in chondrocytes causes chondrodysplasia and delayed endochondral bone formation.
Proceedings of the National Academy of Sciences of the United States of America,
93(19):10240–5.
[Weliky et al., 1991] Weliky, M., Minsuk, S., Keller, R., and Oster, G. (1991). Notochord morphogenesis in Xenopus laevis: simulation of cell behavior underlying tissue
convergence and extension. Development (Cambridge, England), 113(4):1231–44.
[Weliky and Oster, 1990] Weliky, M. and Oster, G. (1990). The mechanical basis of cell
rearrangement. I. Epithelial morphogenesis during Fundulus epiboly. Development
(Cambridge, England), 109(2):373–86.
[Wolpert, 1981] Wolpert, L. (1981). Cellular basis of skeletal growth during development.
British medical bulletin, 37(3):215–9.
[Wolpert, 1982] Wolpert, L. (1982). Cartilage Morphogenesis in the limb. In Cell
Behaviour: A Tribute to Michael Abercrombie. New York: Cambridge University.
[Woods et al., 1989] Woods, M. N., Gorbach, S. L., Longcope, C., Goldin, B. R., Dwyer,
J. T., and Morrill-LaBrode, A. (1989). Low-fat, high-fiber diet and serum estrone sulfate
in premenopausal women. The American journal of clinical nutrition, 49(6):1179–1183.
[Wuelling and Vortkamp, 2010] Wuelling, M. and Vortkamp, A. (2010). Transcriptional
networks controlling chondrocyte proliferation and differentiation during endochondral
ossification. Pediatric nephrology (Berlin, Germany), 25(4):625–631.
[Wuelling and Vortkamp, 2011] Wuelling, M. and Vortkamp, A. (2011). Chondrocyte
proliferation and differentiation. Endocrine development, 21:1–11.
[Wyczalkowski et al., 2012] Wyczalkowski, M. A., Chen, Z., Filas, B. A., Varner, V. D.,
and Taber, L. A. (2012). Computational models for mechanics of morphogenesis. Birth
Defects Research Part C - Embryo Today: Reviews, 96(2):132–152.
147
Bibliography
[Yamanaka and Kondo, 2014] Yamanaka, H. and Kondo, S. (2014). In vitro analysis
suggests that difference in cell movement during direct interaction can generate various
pigment patterns in vivo. Proceedings of the National Academy of Sciences of the
United States of America, 111(5).
[Yu et al., 2009] Yu, S. R., Burkhardt, M., Nowak, M., Ries, J., Petrášek, Z., Scholpp, S.,
Schwille, P., and Brand, M. (2009). Fgf8 morphogen gradient forms by a source-sink
mechanism with freely diffusing molecules. Nature, 461(7263):533–536.
[Zhang et al., 2003] Zhang, D., Schwarz, E. M., Rosier, R. N., Zuscik, M. J., Puzas, J. E.,
and O’Keefe, R. J. (2003). ALK2 functions as a BMP type I receptor and induces
Indian hedgehog in chondrocytes during skeletal development. Journal of bone and
mineral research : the official journal of the American Society for Bone and Mineral
Research, 18(9):1593–1604.
[Zhang et al., 2007] Zhang, J., Johnson, P. C., and Popel, A. S. (2007). An immersed
boundary lattice Boltzmann approach to simulate deformable liquid capsules and its
application to microscopic blood flows. Physical biology, 4(4):285–95.
[Zou et al., 1997] Zou, H., Wieser, R., Massagué, J., and Niswander, L. (1997). Distinct
roles of type I bone morphogenetic protein receptors in the formation and differentiation
of cartilage. Genes Dev, 11(17):2191–2203.
148

Fulltext - ETH E

Transcription

Similar documents

Bioteck Training Course

Linear Growth Retardation (Stunting) and Nutrition Ricardo Uauy

Spectrum of imaging features of SAPHO/ CRMO syndrome

Cell signalling responses to dietary components Dissertação para a

Juvenile osteopetrosis - Archives of Disease in Childhood

The evolution of the morphology and structure of the mandible and

PDF

A Survey on the Achievements of the Oracle Bone Digitization

Case studies Mozaik

Retaining the articular cartilage in finger joint amputations.

brazilian journal of craniomaxillofacial surgery