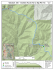
Verkaik et al.

Transcription

Verkaik et al.

KNMI-HYDRA project
Phase report 9
Wind Climate Assessment of the Netherlands 2003:
Extreme value analysis and spatial interpolation methods
for the determination of extreme return levels of wind speed
KNMI, May 2003
Wind climate assessment of the Netherlands 2003
Extreme value analysis and spatial interpolation methods for the
determination of extreme return levels of wind speed
J.W. Verkaik (Job)*, A. Smits (Ilja) and J. Ettema (Janneke)
Royal Netherlands Meteorological Institute (KNMI)
Section Observation and Modelling, Department Climatological Services (WM/KD)
Date: April 24, 2003
*Corresponding author
*Tel: +31 30 2206864
*Fax: +31 30 2210407
*E-mail: [email protected]
*P.O. Box 201, 3730 AE De Bilt, the Netherlands
J.W. Verkaik, A. Smits and J. Ettema
Contents:
1
Introduction ...................................................................................................... 5
2
Data description ............................................................................................... 7
2.1
2.2
2.3
2.4
2.5
3
Development of the Dutch measuring network.........................................................7
Recording practice....................................................................................................8
Data selection...........................................................................................................8
Quality of wind data ..................................................................................................9
Homogeneity of time series ....................................................................................10
Extreme value analysis of wind speed......................................................... 13
3.1
Basic model ............................................................................................................15
3.1.1
3.1.2
3.2
Storm maxima selection .........................................................................................18
3.2.1
3.2.2
3.3
3.4
3.5
Selection of independent maxima ............................................................................... 18
Imposing thresholds .................................................................................................... 20
Probability distribution ............................................................................................26
Transformation of wind speed ................................................................................27
Split up and/or combining of seasons and wind directions .....................................29
3.5.1
3.5.2
3.5.3
3.5.4
3.5.5
3.5.6
4
Approach 1: analysis of all hourly values .................................................................... 15
Approach 2: analysis of peak-over-threshold maxima. ............................................... 17
Splitting annual return levels into seasonal return levels ............................................ 29
Harmonising directional return levels .......................................................................... 32
Calibrating directional return levels to omni-directional return levels.......................... 35
Combining directional return levels to omni-directional return levels`......................... 41
Combining seasonal return levels to annual return levels` ......................................... 42
Methods of combining and splitting seasons and wind direction classes ................... 43
Validation and results of the extreme value analysis ................................. 47
4.1
4.2
4.3
4.4
Validation by comparing with observations.............................................................47
Validation by comparing choices ............................................................................48
Threshold range .....................................................................................................52
Definitions of wind direction classes and seasons..................................................53
4.4.1
4.4.2
4.5
4.6
4.7
5
Wind direction.............................................................................................................. 53
Season ........................................................................................................................ 54
Climate variations ...................................................................................................55
Results....................................................................................................................56
Conclusions ............................................................................................................58
Alternative extreme value analyses.............................................................. 61
5.1
5.2
Analysis on yearly maxima .....................................................................................61
Bayesian analysis ...................................................................................................64
5.2.1
5.2.2
5.2.3
5.3
Other alternative extreme value analyses ..............................................................68
5.3.1
5.3.2
5.4
6
Peak-over-threshold values......................................................................................... 65
Yearly maxima............................................................................................................. 66
Conclusions ................................................................................................................. 67
One-step Markov chain model .................................................................................... 68
Combined GEV model................................................................................................. 69
Conclusions ............................................................................................................69
Interpolation of surface wind ........................................................................ 73
6.1
6.2
The planetary boundary-layer.................................................................................73
Transformation model.............................................................................................74
6.2.1
Surface layer ............................................................................................................... 75
1
6.2.2
6.2.3
6.2.4
6.2.5
6.3
7
Interpolation algorithm................................................................................................. 80
Impact of radius of influence and number of iterations ............................................... 81
Roughness map .....................................................................................................82
6.4.1
6.4.2
6.4.3
6.4.4
6.4.5
6.4.6
6.4.7
6.5
Potential wind speed ................................................................................................... 76
Ekman Layer ............................................................................................................... 76
Impact of blending height on macro wind.................................................................... 77
IBL development in the two-layer model ..................................................................... 78
Barnes’ interpolation method ..................................................................................79
6.3.1
6.3.2
6.4
Spatial data on land-use.............................................................................................. 83
Surface elevation......................................................................................................... 84
Area-averaged surface roughness .............................................................................. 84
Footprint approximation............................................................................................... 85
Drag relation for water ................................................................................................. 86
Comparison of gustiness analysis with roughness maps............................................ 87
Local roughness analysis of the Dutch wind measuring locations.............................. 89
Comparison of the two-layer model to models currently in use ..............................90
Validation of interpolation method ............................................................... 91
7.1
Test datasets ..........................................................................................................92
7.1.1
7.1.2
7.2
Validation of Barnes’ interpolation method .............................................................94
7.2.1
7.2.2
7.3
8
Performance of simulating dataset I............................................................................ 95
Performance of simulating dataset II......................................................................... 100
Validation of the footprint approximation ..............................................................102
7.3.1
7.3.2
7.3.3
7.4
Dataset I: 5 successive years...................................................................................... 93
Dataset II: storm events selected ................................................................................ 93
Mesoscale footprint length ........................................................................................ 103
Local footprint length ................................................................................................. 105
Assignment of surface roughness lengths ................................................................ 105
Conclusions ..........................................................................................................106
Integration of statistics and interpolation.................................................. 107
8.1
First interpolation, then statistics ..........................................................................108
8.1.1
8.1.2
8.1.3
8.2
Fist statistics, then interpolation............................................................................110
8.2.1
8.2.2
8.2.3
8.3
8.4
8.5
9
Test data set.............................................................................................................. 110
Results....................................................................................................................... 111
Discussion ................................................................................................................. 111
Patterns in the potential and macro wind..............................................................112
Comparison with Wieringa and Rijkoort’s results .................................................114
Possible model artefacts ......................................................................................115
8.5.1
8.5.2
8.6
Results....................................................................................................................... 108
Validation................................................................................................................... 109
Conclusions ............................................................................................................... 110
Fixed gustiness roughness for potential wind speed over sea ................................. 115
Alternative roughness length averaging algorithm .................................................... 117
Conclusions ..........................................................................................................118
Evaluation and recommendations.............................................................. 121
9.1
9.2
Evaluation.............................................................................................................121
Recommendations................................................................................................123
References ............................................................................................................ 125
List of symbols ..................................................................................................... 129
Symbols corresponding with Section 3, 4 and 5. ..............................................................129
Symbols corresponding with Section 6, 7 and 8. ..............................................................130
Appendices ........................................................................................................... 133
A
Figures corresponding with Section 2 ......................................................................133
2
B
C
D
E
F
G
3
4
1 Introduction
This report gives a detailed overview of results corresponding with phase 9 of the KNMIHYDRA project, wind climate assessment of the Netherlands 2003. In phase 9 the research
done earlier in the KNMI-HYDRA project is reviewed and the validation regarding the
statistical method, the interpolation method and the integration of these two methods will be
discussed.
So far, several phase reports have been written within the framework of the HYDRA project,
most of them with main subject the statistical method of modelling extreme values of wind
speed (phase 2, 4, 5, 6 and 7) or the method of interpolating surface wind speed values
(phase 3, 10, 11 and 12). The statistical method produces return levels corresponding with
return periods of 0.5 year up to 10,000 years at station locations, not only for the whole year
and omni-directional but also per season and per wind direction class. The interpolation
method makes it possible to obtain wind speed and direction information at non-station
locations taking into account the effects of surface roughness.
Both methods have been improved in time and the modifications that are made are
described in the mentioned phase reports. This report gives a detailed overview of the
developments and validations of the two methods, and their integration. The integration of
the statistical method and interpolation method can be done in two ways, after validation of
the methods separately. One way is to apply the interpolation method on station time series
first, followed by applying the statistical method on the simulated time series. The other way
is to apply the statistical method on the station time series first, followed by applying the
interpolation method on the obtained return levels. Figure 1.1 gives a schematic view of the
possible ways that can be followed. Both ways have their advantages and disadvantages in
consistency (biased or unbiased return levels) and efficiency (robust or non-robust return
levels). In this report both ways are discussed and validated. The choice for a certain method
is not only based on the validation of both ways, but also the results of research done by
HKVconsultants (Kalk and Van Noortwijk, 2003) and Van den Brink et al. (2003) are taken into
account. Ettema, (2003, phase 8) showed that no physical boundary on the wind speed has
to be taken into account.
5
Station time series
Interpolation
Statistics
Consistency and
efficiency
Statistics
A
B
Interpolation
C
DD
…
HKV
Phys. H. vd
bound Brink
Evaluating outcomes and choice for method,
resulting in written report
Final statistics
Figure 1.1: Scheme of possible ways of integration of the statistical method with the interpolation
method.
In this report, Section 2 describes the available wind data that are used for analyses and
validation. The statistical method of modelling extreme values of wind speed is described in
Section 3 while Section 4 discusses the validation and results of this statistical method.
Section 5 discusses some alternative statistical methods. The method of interpolating
surface wind is described in Section 6 while Section 7 discusses the validation and results of
this interpolation method. Section 8 describes the integration of the statistical method and the
interpolation method. Finally, Section 9 evaluates the results of this study and gives
recommendations for application of the results and future research.
6
2 Data description
For the assessment of the Dutch wind climate well described wind data of high quality are
essential. Therefore a close examination of all available wind data from the measuring
stations of the Netherlands is necessary. In this section we will discuss the development of
the observational network, the length of time series (Section 2.1), the recording practice
(Section 2.2), the selection of time series for this assessment (Section 2.3), the availability
and the quality of wind data (Section 2.4), the homogeneity of the time series (Section 2.5)
and other information that is of concern for a correct interpretation of the measurements of
wind speed and direction.
2.1
Development of the Dutch measuring network
Wind speed measurements in the Netherlands started around 1890. Before that time the
wind speed at sea was mostly estimated with use of the scale of Beaufort, which has a large
inaccuracy when translating this scale to m/s. Till 1940 the wind speed was only recorded the
last 10 minutes of the hour instead of continuously. In general for extreme storms the 10minute averaged values are higher than the hourly averaged data, and the difference can be
rather large. Because before 1940 no continuous data are recorded, it is not possible to
detect the difference between 10-min and hourly averages to correct the data. In Figure A.1
an overview is given of the length of the time series of all stations once operational in the
Netherlands. Stations with data of bad quality or with short time series are not plotted in
Figure A.1 and these are also left out of further analyses.
Since 1950 hourly averaged wind speeds are recorded. But in the period 1950 to 1960 many
time series contain systematically gaps without measurements during the weekends and at
night-time. These stations are listed as well in Figure A.1. In Figure A.2a it is seen that in
1965 the wind stations were mainly concentrated in the western part of the Netherlands.
Large regions in the east were not covered at all.
Until 1971 there were two measurement networks operational at KNMI, a climatological
network with only hourly averaged wind speeds, and a synoptic network with hourly and 10minutes averages. In 1971 the two networks merged. With regard to the former climatological
network some stations are added and some are removed because of this. The observational
sites are distributed all over the country and for all regions measurements became available.
Around 1981 a revision of the observation network took place. Some stations are displaced
which caused such inhomogeneities that it is impossible to couple the times series of the old
and new stations. In Figure A.2b the observation network in the year 1985 is shown. In
comparison to the network in 1965, there are more stations in 1985 and they are more
uniformly distributed over the country. From 1985 until now the density of the observation
network increased, especially in the western part of the Netherlands. The present operational
network is shown in Figure A.2c. Recently more stations are placed in Zeeland along the
7
south-west coast (see also Figure A.1). In this region the density of the network is the
highest. It is clear that the mutual distance between stations is not uniform over the country.
2.2
Recording practice
For climatological purposes the hourly averaged wind speed (FH) is usually used. For
synoptical analyses 10-minutes averages (FF) that are commonly used instead. The major
part of the data that will be used in this project is also hourly averaged wind speed. However,
Wieringa and Rijkoort (1983) deduced “hourly averages” by interpolation of synoptic data.
Until 1996 the wind speed is recorded in knots (= nautical miles per hour). Since July 1996
the wind speed is measured in m/s. In the data base the wind speed is recorded with a
resolution of 0.1 m/s. The old records in knots are rounded off at 0.1 m/s with a
transformation factor of 0.5144 m/s per knot. Therefore, for the period before July 1996 the
only values that are found in the data base, are 0.0, 0.5, 1.0, 1.5, 2.0, 2.6, etc. A form of
clustering may appear when at manned stations the anemometer was out of order. Then the
wind speed was sometimes estimated by hand. These estimates were accurate for the
average wind speed. However, a human observer has a preference for even numbers and
multiples of 5. This may result in some distortion in the frequency distributions (Verkaik,
2001).
The wind direction is reported in units of 10 degrees, starting from 10 to 360. There are two
special codes: 0 and 990. Code 0 applies to calms. However, records exist with non-zero
wind speed and direction 0, because the wind direction is averaged only over the last ten
minutes preceding the full hour. If the wind speed in that period (FF) is zero, then the wind
direction will be zero as well. The hourly averaged wind, however, is not necessarily zero.
Code 990 applies to variable wind direction. This means that the standard deviation is larger
than 30 degrees.
2.3
Data selection
For the 1983-assessment (Wieringa and Rijkoort, 1983) wind speed records with a length of
almost 20 years or longer were available from about 17 sites in the Netherlands. The stations
used for determination of the statistical parameters by Rijkoort (1983) are marked red in
Figure A.1. He used the other available stations for validation of his model.
For the statistical analysis in this report, 31 stations (Figure 3.1 and Figure 3.2) with time
series longer than 20 years form the basis. The other stations are used to validate the
interpolation and statistical methods and to add information about regions that are not
covered well with those 31 stations. For the validation of the interpolation method all
available data is used in different sub-sets.
8
2.4
Quality of wind data
For climatological research information on the quality of the data is of great importance.
Therefore every measurement in the data base gets a quality code. This code indicates
whether data is valid, questionable, suspected, added or corrected by hand. Only the data
with qualification “valid data” is used in this assessment. For the interpretation of wind
measurements it is important to know how the measurements and recording are done. Also
the exact location and height of the mast and the land cover in its vicinity must be known, for
instance, to be able to apply exposure corrections. Not only the present conditions are of
interest, also the history of a station is needed to interpret the climatological data correctly.
Changes in the stations surrounding may have influence the measurements and require
different corrections.
From the earliest measurements it is difficult to retrieve information about the exact location
of the mast, the measurement and recording equipment, and other information that is
required for determination of the quality of the data. Too much of this information is lost to
correct for inhomogeneities or other inconsistencies. Wieringa and Rijkoort (1983) made a
selection of the 57 wind stations that were operational in the period 1951-1980. Quality
requirements that a data set has to comply were: completeness of the time series, open
terrain in the vicinity of the mast, and availability of information about the history of the
station. Wieringa and Rijkoort (1983) used stations that meet the requirements only partly for
validation of the results, and for interpolation between “good” stations if their mutual distance
was large. We adopted their selection of stations and extended it with stations that started
measurements after 1980. In Verkaik (2001) all available information about the Dutch wind
stations for the last 50 years is summarized.
The wind is not always measured under the same circumstances with regard to obstacles,
neither is it always measured at the same height. A correction for the roughness of the
surrounding can be applied to the measurements if the roughness is known. For this purpose
a description that the wind is measured above grass surrounded by crops is not enough. The
roughness at a meteorological site can be deduced from turbulent wind speed fluctuations.
The gustiness is the only parameter that has been measured routinely at meteorological
stations that carries turbulence information. From 1971 onwards gusts have been measured
besides hourly averaged wind speed. Changes in the measured gustiness reflect
environmental changes of the vicinity of the station. The gustiness analysis itself is described
in Wieringa (1976) and Verkaik (2000). The gustiness analysis results in local roughness
lengths, z0, that depend on wind direction because the surrounding is not uniform in all
directions. The z0’s may change in time due to changes in the vicinity. With these z0’s,
exposure corrections can be made on the wind speed measurements. The corrected wind
speed is the potential wind speed that is a reference wind speed at 10-meters height and
free of local roughness effects. The calculation method of potential wind speed from
measured wind speed will be described in section 6.2.2.
9
2.5
Homogeneity of time series
The time series of wind speed may reveal inhomogeneities due to station relocations or
changing surroundings of the stations. The exposure correction will reduce these
inhomogeneities only partly. Since these inhomogeneities may influence the statistical
analysis of the data, it is important to check these time series of potential wind speed on
inhomogeneities. This check is done with use of two statistical tests: the von Neumann ratio
(von Neumann, 1941) and the Buishand range test (Buishand, 1982). Both tests are
performed on the times series of measured wind speed and on the exposure corrected
potential wind speed. The time series of 31 stations are analysed that have data for the
period of 1983 up till 2002.
Based on the value of the test quantity in comparison with the 95% and 99% percentile, it is
determined whether the time series are homogeneous or not.
Station
nr
210
225
229
235
240
252
260
265
269
270
275
277
279
280
285
290
308
310
312
316
320
321
330
331
343
344
350
356
370
375
380
Measured wind speed
Von Neumann Buishand Total
¸¸
¸¸
¸¸
¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸
¸¸
¸¸
¸¸
¸
¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸¸¸
¸¸¸¸
¸¸¸¸
¸¸
¸¸
¸¸
¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸
¸¸
¸¸
¸¸
¸¸¸¸
¸¸¸¸
¸¸¸¸
¸¸
¸¸¸¸
¸¸¸¸
¸¸¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
Potential wind speed
Von Neumann Buishand
Total
¸¸¸¸
¸¸¸¸
¸¸
¸¸¸
¸¸¸¸
¸¸¸¸
¸¸¸¸
¸¸
¸¸
¸¸
¸¸¸¸
¸¸¸
¸¸¸¸
¸¸¸
¸¸¸
¸¸
¸¸¸¸
¸¸¸¸
¸¸¸¸
¸¸¸¸
¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸¸¸
¸¸
¸¸¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸¸¸
¸
¸¸¸¸
¸¸¸¸
¸¸
¸¸
¸¸
¸
¸¸
¸¸
¸¸
¸¸
¸
¸¸
¸¸¸¸
¸¸¸¸
¸
¸¸¸
¸¸¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸¸
¸
¸
¸
¸¸
¸
¸¸
¸¸
¸¸
¸¸
¸¸¸
¸¸¸
¸¸¸
¸¸¸¸
¸¸¸
¸¸¸¸
¸¸¸¸
¸¸¸¸
¸¸¸¸
Station
+/+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
nr
210
225
229
235
240
252
260
265
269
270
275
277
279
280
285
290
308
310
312
316
320
321
330
331
343
344
350
356
370
375
380
Table 2.1: Results of inhomogeneity tests von Neumann (1941) and Buishand (1982). The number of
stars indicate the measure of inhomogeneity. The last column (+/-) contains the evaluation of the
comparison between measured and potential wind speed time series of homogeneity based on
absolute values of test quantity.
10
In Table 2.1 the results of the tests are summarized. The number of stars (*) indicates the
measure of inhomogeneity. This means that homogeneous time series have no stars, while
inhomogeneous time series may get at most 4 stars. In Table 2.1 it is seen that the time
series of measured wind speed contain more inhomogeneities than of potential wind speed.
This confirms the expectation that the exposure correction removes local effects from the
measured wind speed time series. Besides comparing the number of stars in the table, also
the absolute differences in the test quantities of both tests can be compared for the potential
with of measured wind speed. From this comparison it appears that for 9 out of 31 stations
the measured time series are more homogeneous than those of potential wind speed. Those
stations are mostly sea stations or stations that contain several changes in location, which
are not always well documented. This shows that the exposure correction factors may be not
fully accurate. For 3 stations the results are more or less comparable. This means that for 19
stations the time series of potential wind speed are more homogeneous than those of
measured wind speed.
11
12
3 Extreme value analysis of wind speed
Aim of the KNMI-HYDRA project is to determine wind speed values that correspond with
return periods of 0.5 year up to 10,000 years. These wind speeds are called return levels and
concern not only annual and omni-directional data, but also they concern different seasons
(Table 3.1) and wind direction classes (Table 3.2) since this is a requirement of RIKZ and
RIZA. Instead of using the well-known four astronomical seasons, six seasons of two months
each are used, because of the climatological inhomogeneities of the astronomical seasons in
the Netherlands, particularly in spring and autumn. The definitions of the seasons and wind
direction classes are in agreement with those in Rijkoort (1983).
1
2
3
4
5
6
Season
Midwinter
Spring
Presummer
Midsummer
Autumn
Prewinter
Months
January, February
March, April
May, June
July, August
September, October
November, December
Table 3.1: Subdivision of a year into seasons.
01
02
03
04
05
06
030°
060°
090°
120°
150°
180°
Wind direction
015°-044°
07
045°-074°
08
075°-104°
09
105°-134°
10
135°-164°
11
165°-194°
12
210°
240°
270°
300°
330°
360°
195°-224°
225°-254°
255°-284°
285°-314°
315°-344°
345°-014°
Table 3.2: Subdivision into wind direction classes, where 90° represents east, 180° south, 270° west
and 360° north.
The return period of 10,000 year is far more lengthy than time series of measured data at
stations throughout the Netherlands (Section 2). For this reason probability distributions are
used to model the data and to extrapolate them to return periods of 0.5 year up to 10,000
years. This section describes the method of modelling extreme wind speed values using
these probability distributions.
Aim of the method of modelling is to obtain return levels that are consistent and efficient as
well. Consistent in this context means that the results are not biased to levels that are
systematic too low or too high. Return levels that are systematically too low are called
negatively inconsistent and return levels that are systematically too high are called positively
inconsistent. Inconsistent return levels may be caused by analyses that are based too much
on relative low wind speeds or by inhomogeneity properties of data. Efficient in this context
means that the results are robust or stable with small uncertainty margins. Non-robust or
unstable return levels with large uncertainty margins are called inefficient. A possible cause
of inefficient return levels is the lack of sufficient data.
13
Section 3.1 describes two main approaches of modelling extreme wind values that have
been evaluated within the framework of the KNMI-HYDRA project. These approaches
concern the analysis of all hourly values, which elaborates the original Rijkoort-Weibull model
(Rijkoort, 1983) and the analysis of peak-over-threshold values. The peak-over-threshold
values are local storm maxima that exceed a given wind speed satisfying an independence
condition. The selection of these local storm maxima is described in Section 3.2. The
modelling of storm maxima is done by fitting a probability distribution to the storm maxima.
Two generally used distributions in modelling peak-over-threshold values are described in
Section 3.3. These concern the conditional Weibull distribution and the generalised Pareto
distribution. For some applications, a mathematical power transformation of wind speed
values is performed before a probability distribution is fitted. Section 3.4 explores if such a
transformation is useful to model storm maxima properly. Section 3.5 describes what
methods can be used to split up or combine results to obtain seasonal, annual, directional
and omni-directional return levels to guarantee that the return levels are in agreement with
each other. The aim for receiving seasonal and directional return levels makes the analysis
rather complex. Section 3.5 is therefore an extensive part of this report.
All available wind speed data that have been used in this study, are described in Section 2.
For the extreme value analysis data is used from 31 stations (Figure 3.1) that all have a
measurement length of at least 19 years (Figure 3.2).
Figure 3.1: Spatial distribution of stations. This concerns 31 stations with at least 19 years of data.
14
Figure 3.2: Time series of the 31 stations that are used in the statistical analysis.
3.1
Basic model
Within the framework of the KNMI-HYDRA project, two main approaches for extreme value
statistics are elaborated.
The first approach concerns a method developed by Rijkoort (1983), the so-called RijkoortWeibull model (RW-model) and the modified RW-model (Smits, 2001b) in which
improvements of a number of shortcomings of the original RW-model are implemented. The
modified RW-model has been developed after an extensive analysis of the original RWmodel with recommendations to improve the model (Smits, 2001a). In both the original and
the modified RW-model, all hourly wind speed values are used without imposing a high
threshold and without the condition of independence between the values.
The second approach analyses hourly wind speed values that are filtered by imposing a
threshold and an independence condition. The filtering algorithm results in the analysis of
peak-over-threshold (POT) storm maxima. This approach has been described in Smits
(2001c). These two approaches will be worked out in detail in this report and advantages and
disadvantages will be discussed.
3.1.1
Approach 1: analysis of all hourly values
The original RW-model (Rijkoort, 1983) is based on the analysis of all hourly values without
threshold restrictions or independence conditions. The probability distribution that has been
used to model daytime hours is the Weibull distribution:
15
  u κ 
Fd (u ) = 1 − exp −    ,
  α  
(3.1)
where α is the scale parameter in m/s and κ the shape parameter. Fd (u ) gives the
probability that for an arbitrary hour during daytime the average wind speed in m/s is less
than u.
For nighttime hours a modification of the Weibull distribution has been used:
 
u
Fn (u ) = 1 − exp− 
 α


 u  
1 + γ stab exp −  
 5  

κ

,


(3.2)
where γ stab is an additional parameter in the nighttime distribution and also called the
stability parameter since it models the effect of the stable nocturnal boundary layer
stratification. Fn (u ) gives the probability that for an arbitrary hour during nighttime the
average wind speed is less than u. The factor 5 in (3.2) has been derived empirically.
The next step in the RW-model concerns a subdivision of the data into seasons and wind
direction classes (Table 3.1 and Table 3.2) in order to fit the Weibull distribution to high levels
of wind speed more properly. The idea behind this subdivision is that seasonal and
directional data are more homogeneous than annual and omni-directional data. This
theoretical argument fulfils also the practical need required by RIKZ and RIZA for statistical
results per season and wind direction class. To obtain omni-directional and/or annual
frequency distributions, the seasonal and directional frequency distribution are combined.
The method described above results in a scale parameter, a shape parameter, a stability
parameter, a number of daytime hours and a number of nighttime hours per season and wind
direction class. Because of this large number (5 parameters x 6 seasons x 12 wind direction
classes = 360 per station) of parameters and the rather noisy pattern of directional results,
the directional Weibull parameters are subjected to harmonic analysis. Because a wind rose
is often bimodal the harmonisation is performed by making use of a bimodal sine function.
This results in a reduction of the number of parameters to a number of 150 per station.
Additional smoothing and simplification algorithms are applied to reduce the number of
parameters even more.
Because successive hourly wind speed values are strongly autocorrelated, a persistence
correction (correction for low return levels of wind speed) has been applied by making use of
annual maxima. Without such a persistence correction, levels of wind speed corresponding
with low return periods would be too high. It turned out that this correction also functions as a
tail correction, which is a correction for high return levels of wind speed.
Smits (2001a) concluded that the persistence/tail correction is a very weak point of the RWmodel and causes unstable results. For this reason the modified RW-model (Smits, 2001b)
replaces the persistence and tail correction of the original RW-model by a correction factor
16
that only corrects for persistence between successive hourly values and that does not correct
for deviations in the tail of the distribution. In contrast with the correction in the original RWmodel, this persistence correction has a physical meaning as it is related to the length of a
storm. The modified RW-model also applies a threshold at 2 m/s to prevent low wind speed
values influencing the results for wind speed values concerning high return periods.
Furthermore it excludes the additional smoothing and simplification algorithms on the
parameters.
These modifications result in a rather efficient model with realistic geographical patterns in
the return levels of wind speed. However, the exclusion of the tail correction causes
considerable negatively inconsistent return levels, especially concerning stations inland.
These inconsistent return levels are especially manifested by the 10,000-year return levels of
375 Volkel and 290 Twenthe that equal 24.6 and 23.5 m/s respectively. These values are
lower than the highest wind speeds that are measured at these stations which are equal to
26.9 and 23.7 m/s respectively. Therefore, the results of the modified RW-model are not
suitable to use directly, but they can form a basis for further analysis. However, the tail
correction that has to be developed to make the modified RW-model suitable can be seen as
an extreme value analysis on its own (because the tail correction has to be station
dependent) which makes the basis (the modified RW-model) redundant. This makes the
approach described in this section less preferable.
3.1.2
Approach 2: analysis of peak-over-threshold maxima.
An alternative to the approach in de preceding section where all hourly values are analysed,
is the analysis of partial duration series, time series that are filtered by imposing a threshold
and an independence condition. As a result of this filter, only peak-over-threshold maxima
(POT) are analysed. Like the first approach, a split up of the data into seasons and wind
direction classes is necessary to fulfil the practical need. Because the selected peaks are not
autocorrelated, a persistence correction as used in approach 1 will not be necessary.
In approach 1, the analysis of all hourly value forms the main frame of the model, in
approach 2 this main frame concerns the analysis of the POT values. This method consists
of a number of steps that will be worked out more in detail.
The first step concerns the way of filtering all hourly values. An independence condition and
a threshold have to be imposed to ensure that the selected maxima are independent of each
other and high enough. The independence condition and the value of the threshold level are
not trivial. This together with the storm maxima selection procedure will be discussed in
Section 3.2.
After the selection of storm maxima one has to deal with the choice for the statistical
probability distribution to model the storm maxima. The most appropriate distributions for the
analysis of peak-over-threshold values of wind speed are the conditional Weibull distribution
17
(CWD) and the asymptotic generalised Pareto distribution (GPD). Both distributions will be
discussed more in detail in Section 3.3.
Section 3.4 discusses the transformation of peak-over-threshold values with a certain power.
In the literature this transformation is often proposed to achieve more rapidly convergence
when annual maxima are modelled with the asymptotic generalised extreme value (GEV)
distribution.
Last but not least methods are presented to obtain “in between” results (directional and
seasonal) and “final” results (omni-directional and annual). These methods concern splitting
up of annual results into season results, splitting up of omni-directional results into directional
results, combining seasonal results to annual results and the combining of directional results
to omni-directional results. This rather complicated subject will be discussed in Section 3.5.
3.2
Storm maxima selection
This section describes the method of storm maxima selection out of all hourly wind speed
values. The procedure of selecting independent maxima is explained in Section 3.2.1.
Selected maxima above a certain threshold, storm maxima, are used to estimate extreme
return levels of wind speed. The determination of an appropriate threshold is discussed in
Section 3.2.2.
3.2.1
Selection of independent maxima
The method that analyses peak-over-threshold maxima does not make use of all hourly wind
data. Only hours are selected with at least 48 hours between them to ensure independence
between the selected extremes (Palutikov et al., 1999). As a result, no correction is needed
to deal with the persistence of successive hourly wind speed values. This is in contrast with
the modified RW-model discussed in Smits (2001b).
The selection of independent maxima is as follows:
A moving 97-hours window is constructed. If the wind speed during the middle hour (nr. 49)
of the window equals the maximum wind speed of the whole window, this hour and the
corresponding wind speed are selected. An equivalent procedure has been applied in
Waterloopkundig Laboratorium (1993) where discharges are filtered for the Rhine (15 days is
used as span) and the Meuse (8 days is used as span). An advantage of this storm selection
is that it is equally moving forward and moving backward. Another advantage is the threshold
independence. This means that when a threshold is imposed in a later stadium of the
analysis (after the selection of independent maxima), the set of selected hours will not be
influenced (except for those hours with wind speeds below the threshold). When a threshold
is imposed in an earlier stadium of the analysis (before the selection of independent
maxima), other hours can be selected with another set of selected hours and corresponding
wind speeds as a result.
18
After applying the selection procedure, not all selected hours make part of real storm events.
Also hours during calm periods can be selected. These low values will be filtered out though
after imposing a threshold (Section 3.2.2).
To analyse storm maxima per wind direction class, one could divide the selected storm
maxima according to the procedure described above among the wind direction classes
(Method I). A disadvantage of Method I is that some wind direction classes, especially
classes with relatively low wind speeds, do not get much data which makes analyses for
these classes more difficult. For this reason, the directional storm selection procedure has
been changed. When analysing a certain wind direction class, wind speed values
corresponding with hours from other wind direction classes are disregarded by setting them
to zero (Method II). Especially for wind direction classes with relatively low wind speed
values, Method II results in more selected storm maxima than Method I.
Figure 3.3 shows an example of both storm maxima selection procedures. This figure shows
that with the procedure according to Method I, three storm maxima are selected. Method I
divides these three storm maxima between the wind direction classes A, B and C. For the
example this means that each wind direction class gets only one storm maximum. However,
with Method II each wind direction class gets three storm maxima instead of only one. This
larger number of observations reduces the statistical noise when modelling the selected
storm maxima.
Figure 3.3: Example of the result of two storm maxima selection procedures. Method I selects 3 omnidirectional storm maxima which are equally divided between the wind direction classes A, B and C.
Method II selects the same 3 omni-directional storm maxima, but selects in total 9 directional storm
maxima.
An additional consequence of the directional method of storm maxima selection according
Method II is the introduction of persistence between wind directions. Because during a storm
more than one wind speed corresponding with different wind directions can be selected, the
total number of directional storm maxima will always be the same or higher than the total
19
number of omni-directional storm maxima. The procedures discussed in Section 3.5 that
concern the calibration of directional return levels (Section 3.5.3) and the combination of
directional return levels (Section 3.5.4) have to take this property into account.
3.2.2
Imposing thresholds
Peak-over-threshold maxima are usually analysed after imposing a threshold on the selected
maxima to prevent relatively low values of influencing the results for return periods of
interest. Sometimes this threshold is imposed in the storm selection procedure, but it can
also be done after the storm selection procedure (like described in Section 3.2.1). Figure 3.4
shows an example of the dependence of the threshold on the return levels for station 265
Soesterberg. Visible in this figure is that low thresholds result in low return levels and that
high thresholds result in a rather noisy pattern in the return levels. A notable point is the
decrease of the return level with approximately 4 m/s by increasing the threshold from 11.5
to 12.0 m/s. Also for other stations, seasons and wind direction classes these properties
often exist. The most likely reason for the low return levels for low thresholds is the different
behaviour of relatively low wind speeds compared with wind speeds that are relatively high.
The reason for the noisy pattern in Figure 3.4 for higher thresholds is the increasing lack of
data for higher thresholds. This makes clear that a threshold that is too low, results in
negatively inconsistent return levels and that a threshold that is too high, results in inefficient
return levels. In other words, a balance has to be found between consistency and efficiency.
Determining thresholds with an appropriate balance between consistency and efficiency can
be done visually and numerically. Both ways will be described and discussed in this section.
Figure 3.4: Example of a threshold plot, showing 10,000-year return levels that are estimated with the
conditional Weibull distribution (Section 3.3) for thresholds between 0 and 21 m/s, concerning omnidirectional data derived from station 265 Soesterberg.
Figure 3.4 also makes clear that the usage of a single threshold does not result in very
efficient return levels because of the sometimes large differences between return levels that
20
correspond with successive thresholds. For more efficient results, it’s therefore sensible to
use a threshold range instead of one single threshold. Chosen is to separate the thresholds
0.5 m/s from each other within the threshold range (Section 3.3), also visible in the example
of Figure 3.4.
Below, the visual and numerical method of threshold determination are described and
differences between the methods are discussed. At the end of this section is described how
to deal with the threshold range.
Visual threshold determination
One way to obtain appropriate minimal values of the threshold range is to use conditional
mean excess (CME) graphs (Davison, 1984). A CME-graph plots the mean excess E (ω ) in
m/s of all selected storm maxima above a certain threshold ω against that threshold:
∑ (u i − ω )
E (ω ) =
i ∈ Ad
Aω
,
(3.3)
where Aω = { j : u j > ω } and u i represent the selected maxima in m/s above threshold ω in
m/s.
When using the generalised Pareto distribution (Section 3.3) to model storm maxima the
lowest value of the CME-graph above which the graph is approximately linear can be seen
as an appropriate minimal value of the threshold range. Figure 3.5 shows an example of a
CME-graph. An appropriate minimal value of the threshold range for the storm maxima in the
example would be about 8 m/s.
Figure 3.5: Example of a conditional mean excess (CME) graph, concerning annual and omnidirectional data at station 265 Soesterberg. Above the threshold of 8 m/s the graph is quite linear,
indicating that this value is an appropriate minimal value of the threshold range.
21
Another way to determine appropriate minimal values of the threshold range is a visual look
at threshold plots like Figure 3.4 to search for stabilisation of the return levels. The threshold
value that corresponds with the position of the beginning of such a stabilisation can then be
used as the minimal value of the threshold range. For the example in Figure 3.4, again the
value of 8 m/s seems to be appropriate.
In Smits (2001c), both CME-graphs and threshold plots for all stations have been analysed.
Based on this study, minimal values of the threshold range have been chosen that
correspond with an exceedance frequency of 10 times per season with respect to seasonal
analysis and 43 times per year with respect to annual analysis.
Numerical threshold determination
A numerical method to determine minimal values of the threshold range has been described
by Waarts et al. (2002). This method makes distinction between consistency and efficiency
and has been applied on traffic loads in The Netherlands.
The procedure of this method applied on wind speeds is set out below:
1) Choose threshold value ω equal to 0 m/s.
2) Formulate hypotheses:
• Null hypothesis (H0): differences between the return level estimated with threshold ω
and those that are estimated with higher thresholds ω` > ω, are caused by inefficiency
(less data for higher thresholds).
• Alternative hypothesis (HA): differences between the return level estimated with
threshold ω and those that are estimated with higher thresholds ω` > ω, are caused
by inconsistency (systematic under- or overestimating of return levels for lower
thresholds).
3) Test H0 (described below).
4) If H0 is not rejected (equal to rejection of HA) go to 6.
5) Increase ω with a certain step (in this study this step equals 0.5 m/s). Go to 2.
6) Minimal value of the threshold range is set on ω.
The procedure of testing H0 is set out below:
1) Estimate conditional distribution parameters at threshold ω.
2) Simulate a large number (in this study this number equals 1000) of samples with a
random number generator based on the estimated conditional distribution parameters.
The size of each sample equals the number of wind speeds higher than ω in the original
dataset.
3) Estimate for each of the samples the conditional distribution parameters and the
corresponding 10,000-year return level as function of thresholds ω` ≥ ω.
4) Determine the 95% confidence interval of the 10,000-year return level at each threshold
ω` ≥ ω by taking the 2.5% percentile and the 97.5% percentile of the samples.
22
5) H0 is not rejected if the 10,000-year return levels (based on measured wind speed
values) fall within the simulated 95% confidence interval for each threshold ω` ≥ ω.
Figure 3.6 shows an example of this procedure where the conditional Weibull distribution
(Section 3.3) has been used to estimate the distribution parameters. For this example, the
numerical method produces a threshold of 8.0 m/s as equilibrium between consistency and
efficiency.
Figure 3.6: Numerical threshold selection for station 265 Soesterberg. At a threshold of 0.0 m/s (upper
left graph) most estimated values do not fall within the 95% confidence intervals of the 10,000-year
return levels. At a threshold of 7.5 m/s (upper right graph) this number is strongly reduced and at a
threshold of 8.0 m/s (lower graph) all estimated values fall within the 95% confidence intervals.
Comparison between visual and numerical threshold determination
For the annual omni-directional dataset, the results of the visual and numerical method of
threshold determination are listed in Table 3.3. Four stations (229 Texelhors, 252 K13, 270
Leeuwarden and 277 Lauwersoog) show a rather high threshold that is determined by the
numerical method. These stations have in common that their threshold plots have an
increase in return levels as function of threshold even for higher thresholds, so without
stabilisation of the return levels from a certain threshold. For this reason, it is difficult to
determine a threshold with the help of the visual threshold selection method.
Averaged over all stations, the values for the visual method correspond with an exceedance
frequency of approximately 43 times per year, while the values obtained with the numerical
23
method correspond with an exceedance frequency of approximately 45 times per year. So in
general, the visual and numerical methods of selecting thresholds result in quite similar
results.
For seasons, the visual and the numerical method produce different thresholds. Due to the
strong reduction in the available data compared with the annual data set (by a factor of 6),
the balance between consistency and efficiency moves to lower thresholds for seasonal data
sets. This results in threshold levels that are usually not much higher than zero (0-2 m/s)
regarding the numerical method, while the thresholds obtained with the visual method
become only marginal lower in the case of the January/February season compared with the
annual dataset.
Station
210 Valkenburg
225 IJmuiden
229 Texelhors
235 De Kooy
240 Schiphol
252 K13
260 De Bilt
265 Soesterberg
269 Lelystad
270 Leeuwarden
275 Deelen
277 Lauwersoog
279 Hoogeveen
280 Eelde
285 Huibertgat
290 Twenthe
308 Cadzand
310 Vlissingen
312 Oosterschelde
316 Schaar
320 Goeree
321 Europlatform
330 Hoek van Holland
331 Tholen
343 Rotterdam Geulhaven
344 Zestienhoven
350 Gilze-Rijen
356 Herwijnen
370 Eindhoven
375 Volkel
380 Beek
Mean
Method
Visual
Numerical
9.0
8.5
8.5
10.0
15.0
9.5
8.5
10.5
8.0
10.0
17.0
10.0
7.0
9.5
8.0
8.0
8.5
10.5
14.5
10.0
8.5
9.0
16.5
12.5
8.0
8.0
8.5
9.0
9.5
10.0
8.0
9.5
9.0
11.5
7.5
10.5
10.0
11.0
8.0
9.5
9.5
9.0
8.0
9.0
8.0
10.0
9.0
10.0
9.5
10.0
8.5
9.0
8.0
9.0
8.0
9.0
7.0
8.0
9.5
9.0
7.5
8.5
9.6
9.4
Table 3.3: Minimal values of the threshold range in m/s obtained with a visual and a numerical method
applied on omni-directional annual data. Averaged over the stations, the values obtained with the
visual method correspond with an exceedance frequency of approximately 43 times per year and the
values obtained with the numerical method correspond with an exceedance frequency of
approximately 45 times per year.
24
Based on the discussion above, there are no indications that the minimal values of the
threshold range that are obtained with the visual method of determination are too low. This
means also that there are no indications that the resulting return levels are inconsistent.
However, both the visual and the numerical method are applied on each station separately.
As a result of this some possible inconsistency can be covered by the inefficiency that is
inherent in separate station analyses. When using a method where all station results are
gathered into one single graph, this inconsistency possibly can be revealed. Therefore,
graphs have been constructed where all station dependent threshold plots have been
summarized into one single threshold plot. Because of the geographical differences in the
wind climate, this can only be done appropriately by a normalisation of the axes (x-axis:
threshold and y-axis: return level) of the station dependent threshold plots. After this, graphs
can be generated by showing the mean or median values as function of the normalised
threshold.
For the season January/February and for the whole year these graphs with median values
are presented in the lower graph of Figure B.1a and the lower graph of Figure B.1b for two
probability distributions (CWD and GPD, see Section 3.3). These two graphs, together with
not shown graphs for other seasons, make clear that still some inconsistency exists when
using threshold levels that are obtained with the visual method. Thresholds chosen too low,
result in too low return levels. Therefore, the thresholds that are obtained with the visual
method, have been increased to prevent that the analysis results in inconsistent return
levels. The thresholds have been set on values that correspond with an exceedance
frequency of 7 times per season (instead of 10 times) concerning seasonal analysis and 10
times per year (instead of 43 times) concerning annual analysis as minimal values of the
threshold range.
Maximum values of the threshold range are set to values that correspond with an
exceedance frequency of 2 times per year, because this frequency is the highest frequency
aimed in the KNMI-HYDRA project. Another reason for choosing these maximum values is
that higher thresholds will result in rather inefficient return levels.
Average over threshold range
When using a threshold range, return levels can be obtained by two methods. The first
method is to average the distribution parameters over the threshold range. These averaged
distribution parameters can be used to calculate corresponding return levels. The other
method is to calculate return levels by averaging the threshold dependent return levels over
the threshold range.
The latter method is preferred, because the parameters of a probability distribution are
related to each other. Averaging these parameters independently of each other can result in
a disturbed relation between the parameters causing unreliable return levels. Following the
25
latter method, return levels are calculated for a fixed set of return periods or exceedance
frequencies. An overview of these return periods is given in Table 3.4.
Return periods
0.5
0 .7
1.0
1.5
2.0
3 .0
5
7
10
15
20
30
M
M
M
M
M
M
500,000
700,000
1,000,000 1,500,000 2,000,000 3,000,000
5,000,000 7,000,000 10,000,000
Table 3.4: List of fixed return periods in years that are used to calculate corresponding return levels.
Table 3.4 also shows return periods that are higher than 10,000 years and therefore also
higher than for aim in the KNMI-HYDRA project. The reason that corresponding return levels
are calculated is that these return periods or exceedance frequencies are needed in a
number of procedures discussed in Section 3.5 (respectively the procedures in Section 3.5.3,
Section 3.5.4 and Section 3.5.5). Other return periods or exceedance frequencies and
corresponding return levels than the ones in Table 3.4 are obtained by linearly interpolating
of the fixed return periods.
3.3
Probability distribution
Selected peak-over-threshold values (storm maxima) can be analysed with several
probability distributions. Often used distributions for modelling storm maxima are the
conditional Weibull distribution (CWD) and the generalised Pareto distribution (GPD). The
cumulative distribution function of the CWD (FCWD ) is defined as follows:
 ω κ  u κ 
FCWD (u ) = 1 − exp  −    ,
α
 α  
 
with u ≥ ω ,
(3.4)
where u represents the wind speed in m/s, α the scale parameter in m/s, κ the shape
parameter and ω the threshold value in m/s.
For κ = 1 , the CWD equals the exponential distribution:
ω − u 
FCWD (u ) = 1 − exp 
,
 α 
with u ≥ ω .
(3.5)
The cumulative distribution function of the GPD (FGPD ) is defined as follows:
γ


FGPD (u ) = 1 − 1 − (u − ω )
σ


1/ γ
,
with u ≥ ω ,
(3.6)
where σ represents the scale parameter in m/s and γ the shape parameter. The GPD is an
asymptotic distribution for excesses over high thresholds and the maxima of samples of
26
events from the GPD are GEV (generalized extreme value, see also Section 3.4) distributed
with the same shape parameter γ. If γ has a positive value, the distribution is bounded at the
upper end (ω + σ / γ ) .
For γ = 0 , also the GPD equals the exponential distribution:
ω − u 
FGPD (u ) = 1 − exp 
,
 σ 
with u ≥ ω .
(3.7)
The parameters α and κ of the CWD and the parameters σ and γ of the GPD can be
estimated with the maximum likelihood estimation (MLE) procedure. As described in Section
2 there is a clustering in the measured wind speed data of every 0.5 m/s. Although the
potential wind speed is calculated from the measured wind speed using different factors
which reduces the effect of clustering, the clustering effect is still visible in histograms of
potential wind speed. Therefore it is justified to apply the maximum likelihood procedure on
wind speed classes of 0.5 m/s: [0.0-0.4], [0.5-0.9], etc.
The CWD and the GPD both are applied on the selected peak-over-threshold values.
Comparison between the results of these distributions are described in Smits (2001c). The
main conclusions of this analysis are that the GPD results in inefficient return levels
compared with the CWD, the CWD results in a stabilisation in return levels as function of
threshold and the CWD generates generally higher return levels compared with the CWD.
For the season January/February (Figure B.1a) and for the whole year (Figure B.1b) results
are presented. This figure includes plots where all station results are presented. The values
on the axes are divided by the 10-year return level based on the empirical distribution
function. Doing this, the differences in the values on the axes between the stations are
reduced which makes it possible to create a total view of all the stations in one single plot.
The lower graphs of Figure B.1a and Figure B.1b are also discussed in Section 3.2.2. It is
clear that the CWD models the peak-over-threshold values more appropriately than the GPD
and therefore the CWD is to be preferred.
3.4
Mathematical transformation of wind speed
Besides the two main approaches of modelling extreme events of wind speed values
discussed in Section 3.1 (the analysis of all hourly wind speed values and the analysis of
peak-over-threshold values), another main approach exists to model extreme events of wind
speed values. This approach concerns the analysis of yearly maxima of hourly wind speed
values. The analysis of yearly maxima with respect to the dataset used in this section is
discussed in Section 5.1 and Section 5.2.2. Yearly maxima are often modelled with the
asymptotic GEV (generalised extreme value) distribution.
27
The cumulative distribution function (FGEV ) is defined as follows:
1

FGEV ( y ) = exp− (1 − θy ) θ  ,




if θ ≠ 0
(3.8)
FGEV ( y ) = exp[− exp( − y )] ,
if θ = 0
(3.9)
where θ represents the shape parameter and y, known as the Gumbel reduced variate, is
given by
u−λ
y=
(3.10)
β
where β represents the scale parameter in m/s and λ the location parameter in m/s.
The shape parameter θ determines the type of distribution. The GEV distribution with θ = 0
(3.9) represents the Fisher-Tippett Type I distribution, known as the Gumbel distribution.
(3.8) with a negative value of θ represents the Fisher-Tippett Type II, known as the Frechet
distribution. (3.8) with a positive value of θ represents the Fisher-Tippett Type III, known as
the Reverse Weibull distribution.
The Gumbel distribution and the Frechet distribution are both unbounded at the upper end of
the distribution, but the Frechet distribution has a heavier tail than the Gumbel distribution
and is bounded at the lower end (u > λ + β / θ ) of the distribution. Furthermore, the Reverse
Weibull distribution is bounded at the upper end (u < λ + β / θ ) of the distribution.
The classical extreme value theory describes how the maxima of samples of size N from
sufficiently long sequences of independent and identically distributed random variables can
be fitted asymptotically (for large N) to the Fisher-Tippett Type I, II or III distribution (Fisher
and Tippett, 1928). These distributions were combined into the GEV distribution (Von Mises
(1936; Jenkinson, 1955).
If the above property of large N is not met, the rate of convergence to the GEV distribution is
slow (Cook, 1982). This can result in false indications of the choice of the asymptote. For
example, a Gumbel plot can be curved (suggesting a Fisher-Tippett Type III distribution)
while the real reason for the curvature is slow convergence. To achieve a more rapidly rate
of convergence, a number of authors (e.g. Cook, 1982; Harris, 1996) use a power of the wind
speed instead of the wind speed itself. For a proper value of the power, the shape parameter
of the parent Weibull distribution is often used (equals ±2 in many cases).
From this the question rises if such a mathematical transformation has also to be applied on
wind speed when analysing peak-over-threshold wind speed values instead of analysing
yearly maxima. When the peak-over-threshold values are fitted with the CWD, this question
is not of any importance. It is easy to show that when wind speed values are CWD
distributed, the power of the wind speed values are also CWD distributed with scale
parameter equal to the power of the original scale parameter and shape parameter equal to
28
the original shape parameter divided by the power. Therefore a mathematical transformation
of the wind speed for the CWD in the form of the usage of a power does not result in different
return levels. For the GPD, no examples in the literature are found where a mathematical
transformation has been applied. For these reasons, no mathematical transformation is
performed on the wind speed values.
3.5
Split up and/or combining of seasons and wind directions
Results are needed for the whole year without regard to wind direction and also for each
season and for every wind direction class. Four methods to obtain these results have been
analysed. All methods have the property that the annual and seasonal results are linked to
each other in a way that the annual return levels are always higher than the seasonal return
levels. The same can be stated about the wind direction classes. The omni-directional and
directional return levels are linked to each other in a way that the omni-directional return
levels are always higher than the directional return levels.
The four methods make use of a number of procedures. These procedures are discussed in
the Sections 3.5.1-3.5.5. They concern the splitting of annual return levels into seasonal
return levels (Section 3.5.1), the harmonisation of directional return levels (Section 3.5.2), the
calibration of directional return levels to omni-directional return levels (Section 3.5.3), the
combination of directional return levels to omni-directional return levels (Section 3.5.4) and
the combination of seasonal return levels to annual return levels (Section 3.5.5). Finally, all
four methods are discussed in Section 3.5.6.
3.5.1
Splitting annual return levels into seasonal return levels
A whole year contains six times as much data than a single season. For this reason, directly
estimated annual return levels are more efficient than directly estimated seasonal return
levels. One way to make use of this property for the determination of seasonal return levels
is to determine seasonal return levels by using a season dependent multiplication factor
applied on the annual return levels. This factor is obtained by spatially smoothening of the
station dependent seasonal multiplication factors. As result the seasonal return levels will be
more efficient than the directly estimated seasonal return levels. If no smoothing method is
used, the obtained seasonal return levels are equal to the directly estimated seasonal return
levels what means that making use of the factor does not improve the results. One method to
smooth the factors is to calculate the mean of the several station dependent factors. The
several factors can be obtained by calculating the quotient of the directly estimated seasonal
return levels and the directly estimated annual return levels per station. When these factors
are averaged, one gets:
U j ,s (T )
1
,
ysf j (T ) =
(3.11)
S s U s (T )
∑
29
where ysf j represents the averaged year-to-season factor per season j, U s the annual
return level in m/s for station s and U j ,s the return level in m/s for season j and station s, all
as function of the return period T in years. S represents the total number of stations used.
Then the ysf can be used as multiplication factor for all the stations:
Uˆ j ,s (T ) = U s (T )ysf j (T ) ,
(3.12)
where Uˆ j ,s (T ) represents the corrected return level in m/s for season j and for station s as
function of the return period T in years.
(3.11) and (3.12) concern only omni-directional results, but the factor can also be used for
directional results:
Uˆ ij ,s (T ) = U i ,s (T )ysfij (T ) ,
(3.13)
where
ysfij (T ) =
1
S
U ij ,s (T )
∑ U i ,s (T ) .
(3.14)
s
To prevent a systematic geographical under- or overestimation (inconsistency) of the
corrected seasonal return levels, the station dependent multiplication factor must not have a
geographical pattern. This can be examined by determining the factor per season for several
return periods. For the return periods 0.5 year and 10,000 year these values are numerically
presented in Table 3.5 and geographically in Figure B.2a (0.5 year) and Figure B.2b (10,000
year).
All geographic figures concerning Section 3, 4 and 5 are interpolated with the minimumcurvature Spline method (Franke, 1982) with the options: 1) type: Tension, 2) weight: 0.3 and
3) number of points: 12. Although this interpolation method does not account for any change
in surface roughness, this method of interpolation gives a rather good image of possible
geographic patterns.
30
Station
210 Valkenburg
225 IJmuiden
229 Texelhors
235 De Kooy
240 Schiphol
252 K13
260 De Bilt
265 Soesterberg
269 Lelystad
270 Leeuwarden
275 Deelen
277 Lauwersoog
279 Hoogeveen
280 Eelde
285 Huibertgat
290 Twenthe
308 Cadzand
310 Vlissingen
312 Oosterschelde
316 Schaar
320 Goeree
321 Europlatform
331 Tholen
344 Zestienhoven
350 Gilze-Rijen
356 Herwijnen
370 Eindhoven
375 Volkel
380 Beek
Mean
1
0.89
0.87
0.87
0.88
0.87
0.92
0.84
0.84
0.87
0.87
0.83
0.90
0.86
0.87
0.91
0.85
0.87
0.85
0.90
0.89
0.87
0.91
0.85
0.90
0.87
0.87
0.85
0.84
0.83
0.85
0.85
0.87
Return period = 0.5 year
2
3
4
5
0.78 0.67 0.67 0.77
0.75 0.68 0.72 0.82
0.79 0.67 0.69 0.81
0.74 0.63 0.64 0.77
0.79 0.66 0.65 0.72
0.78 0.66 0.67 0.82
0.79 0.67 0.64 0.70
0.78 0.69 0.67 0.71
0.76 0.63 0.60 0.72
0.81 0.66 0.64 0.73
0.80 0.68 0.64 0.72
0.84 0.70 0.68 0.79
0.77 0.65 0.63 0.73
0.80 0.66 0.65 0.74
0.80 0.68 0.69 0.81
0.80 0.65 0.65 0.71
0.81 0.69 0.68 0.78
0.77 0.66 0.68 0.77
0.79 0.72 0.75 0.84
0.80 0.71 0.72 0.82
0.74 0.68 0.72 0.82
0.77 0.67 0.70 0.82
0.78 0.70 0.72 0.80
0.81 0.67 0.67 0.77
0.79 0.69 0.67 0.76
0.81 0.69 0.67 0.76
0.79 0.67 0.65 0.72
0.78 0.63 0.62 0.70
0.80 0.69 0.66 0.72
0.79 0.66 0.63 0.73
0.77 0.65 0.64 0.74
0.79 0.67 0.67 0.76
6
0.83
0.89
0.89
0.88
0.84
0.89
0.85
0.81
0.78
0.85
0.83
0.88
0.79
0.84
0.87
0.83
0.85
0.87
0.87
0.86
0.90
0.89
0.88
0.83
0.80
0.87
0.84
0.84
0.85
0.86
0.85
0.85
Return period = 10,000 year
1
2
3
4
5
6
0.89 0.96 0.78 0.59 0.89 0.94
0.98 0.95 0.83 0.79 0.90 0.85
0.93 0.84 0.63 0.60 0.73 0.83
0.88 0.98 0.59 0.62 0.78 0.79
0.96 0.90 0.81 0.68 0.80 0.83
0.89 0.70 0.52 0.65 0.92 0.74
0.99 0.89 0.67 0.73 0.70 0.88
1.03 0.85 0.71 0.68 0.83 0.87
1.04 0.75 0.63 0.46 0.68 0.94
0.93 0.70 0.60 0.56 0.61 0.76
0.95 0.88 0.77 0.67 0.87 0.87
0.94 0.66 0.70 0.65 0.63 0.76
1.17 0.98 0.87 0.74 1.09 1.06
0.95 0.77 0.61 0.51 0.68 0.78
1.02 0.78 0.74 0.75 0.81 0.80
0.92 0.62 0.54 0.50 0.62 0.83
0.99 0.89 0.97 0.77 0.80 1.05
0.99 0.94 0.92 0.72 0.82 0.92
0.97 0.85 0.90 0.73 0.89 0.99
0.99 0.91 1.08 0.83 0.88 0.99
0.96 0.95 0.97 0.80 0.91 1.01
0.97 0.94 0.87 0.75 0.96 0.83
1.01 0.97 0.93 0.82 0.95 0.99
0.97 0.80 0.95 0.73 0.94 0.98
1.00 0.83 0.73 0.61 0.85 0.99
0.86 0.88 0.70 0.61 0.72 0.84
0.97 0.83 0.79 0.80 0.88 0.91
0.98 0.90 0.76 0.60 0.77 0.85
0.99 0.74 0.75 0.73 0.76 0.91
0.90 0.91 0.62 0.48 0.57 0.70
0.97 0.86 0.77 0.78 0.83 1.00
0.97 0.85 0.76 0.68 0.81 0.89
Table 3.5: Year-to-season factors (quotient of omni-directional seasonal return levels and omnidirectional annual return levels) for the return periods 0.5 and 10,000 year. 1-6 represents the season
(see Table 3.1).
Not surprisingly, the values of ysf are the highest in the winter and the lowest in the summer.
More important is that there is no clear geographical pattern visible, especially not for the
10,000-year return period. Therefore, a station independent multiplication factor (obtained by
averaging over the stations) can be used to calculate the 10,000-year seasonal return levels
out of the 10,000-year annual return levels. For the 0.5-year return levels, the station
dependent multiplication factor is used (the same as making use of directly estimated
seasonal return levels), since 0.5 year is within the measuring range and because of the
(small) geographical pattern. For return periods between 0.5 and 10,000 year, a logarithmic
function is used to make a gradual change from station dependent multiplication factors to
station independent multiplication factors:
f (T ) = 1 − 0.74
log(
T
)
0.5 ,
(3.15)
where T represents the return period in years and f the fraction of the station independent
factor to be used
31
Figure 3.7: Fraction f of the station independent multiplication factor as function of return period to be
used in calculating seasonal return levels out of annual return levels. For low return periods the
fraction is small what means that the individual station seasonal return levels have a large weight and
the individual station annual return levels a small weight. For high return periods the fraction is large
what means that the individual station seasonal return levels have a small weight and the individual
station annual return levels a large weight.
In Figure 3.7, f is plotted as function of the return period. For low return periods the fraction is
small what means that the individual station seasonal return levels have a large weight and
the individual station annual return levels a small weight. For high return periods the fraction
is large what means that the individual station seasonal return levels have a small weight and
the individual station annual return levels a large weight. For example, the fraction is 0 for a
return period of 0.5 year and 0.95 for a return period of 10,000 year.
3.5.2
Harmonising directional return levels
Each directional analysis uses only data from that wind direction class. Therefore resulting
return levels are rather independent of each other because only few information of other wind
direction classes is included. The few information that has been included is caused by the
persistence property of neighbouring wind direction classes. As a result, directly estimated
directional return levels often show a rather noisy pattern over the wind direction classes.
‘Directly’ means in this context that the results are obtained without making use of smoothing
functions, splitting procedures or combination procedures. Often though, behind this noisy
pattern also a pattern becomes visible that can be identified by a bimodal function. An
example of the noisy pattern and the bimodal behaviour can be seen in Figure 3.8.
32
Figure 3.8: Directional return levels corresponding with station 280 Eelde, season May/June and a
return period of 10,000 year. Visible are the rather noisy pattern and the bimodal behaviour.
A bimodal function is used to subject the directional return levels to harmonic analysis. The
purpose of such a harmonisation is to reduce the noise in the directional return levels. The
function that is used for harmonisation, is a mixed function of two sine functions with each an
amplitude and phase shift that are both estimated. Furthermore these sine functions have
period lengths, which are set equal to 360 and 180 degrees. The harmonisation function is
equivalent to the harmonisation function used in the RW-model and also discussed in
Section 3.1.1. However, the function in the RW-model performs harmonisation on the
distribution parameters instead of the return levels. Chosen is to perform harmonisation on
the return levels for the same reason as discussed in Section 3.2.2 to prevent a disturbed
relation between the parameters.
The harmonisation results in:
U i (T ) = Uˆ i (T ) + ε ,
(3.16)
Uˆ i (T ) = a0 (T ) + a1(T ) sin(30i + a2 (T )) + a3 (T ) sin( 60i + a4 (T )) .
(3.17)
where
U i (T ) represents the directly estimated return level in m/s per wind direction class i as
function of the return period T in years, Uˆ i (T ) represents the harmonised return level in m/s
per wind direction class i as function of the return period T and the term ε represents a
random disturbance. a1 and a3 represent the amplitudes concerning the period lengths of
respectively 360 and 180 degrees, a2 and a4 represent the phase shifts concerning again
the period lengths of respectively 360 and 180 degrees and a0 represents the offset.
33
The parameters a0 , a1 , a2 , a3 and a4 in (3.17) can be estimated by transforming Uˆ i (T )
into:
Uˆ i (T ) = a0 (T ) + b1(T ) sin 30i + b2 (T ) cos 30i + b3 (T ) sin 60i + b4 (T ) cos 60i ,
(3.18)
where
b1(T ) = a1(T ) cos a2 (T ) ,
(3.19)
b2 (T ) = a1(T ) sin a2 (T ) ,
(3.20)
b3 (T ) = a3 (T ) cos a4 (T ) ,
(3.21)
b4 (T ) = a3 (T ) sin a4 (T ) .
(3.22)
(3.18) can be fitted with linear regression using the method of multiple least squares.
Because the several wind direction classes do not include the same number of observations,
the corresponding directional return levels have different confidence intervals. For this
reason one could opt for the more complicated method of weighted least squares (WLS)
instead of the method of ordinary least squares (OLS) to take into account the different
number of observations per wind direction class. Because the differences in the number of
observations between the wind direction classes are relatively small, WLS would only slightly
improve the results. Therefore OLS is used to harmonise the directional return levels.
After applying linear regression the estimates of b1(T ), b2 (T ), b3 (T ) and b4 (T ) can be used
to calculate the estimates of a1(T ), a2 (T ), a3 (T ) and a4 (T ) :

 b2 (T ) 

if b1(T ) > 0
arctan
b1(T ) 


a2 (T ) = 
,
arctan b2 (T )  + 180 if b (T ) < 0
1
 b (T ) 

 1


b1(T )
a1(T ) =
,
cos(a2 (T ))

 b4 (T ) 

if b3 (T ) > 0
arctan
b3 (T ) 


a4 (T ) = 
,
arctan b4 (T )  + 180 if b (T ) < 0
3
 b (T ) 

 3


b3 (T )
a3 (T ) =
.
cos(a4 (T ))
(3.23)
(3.24)
(3.25)
(3.26)
The estimates of the parameters a0 (T ), a1(T ), a2 (T ), a3 (T ) and a4 (T ) are used to calculate
the harmonised directional return levels Uˆ i (T ) .
(3.23)-(3.26) concern only annual results, but the harmonisation procedure can also be
applied on seasonal results.
An example of the harmonisation procedure is presented in Figure 3.9.
34
Figure 3.9: Harmonisation example of directional return levels corresponding with station 280 Eelde,
season May/June and a return period of 10,000 year.
Figure 3.9 shows the same directly estimated directional return levels like Figure 3.8, as well
as the harmonised return levels obtained with the method described above. The reduction of
noise is clearly visible.
3.5.3
Calibrating directional return levels to omni-directional return levels
The extreme value model described so far in Section 3 is able to calculate directly estimated
directional and omni-directional return levels. Because the estimation of the directional return
levels takes place independently of the estimation of the omni-directional return levels, the
directional and the omni-directional results are not linked to each other. For example this
could be manifested by omni-directional return levels that are lower than certain directional
return levels.
One way to correct for the property described above is to calibrate the directional return
levels to the omni-directional return levels. This means that the directional return levels are
corrected with the help of the omni-directional return levels using a correction factor that is
modelled by comparing the omni-directional exceedance frequencies with the combined
directional exceedance frequencies. This method is similar to the method applied by RIKZ in
modelling direction dependent extreme levels of high water, wave height and wave periods
(Roskam et al, 2000). However, the omni-directional and combined directional exceedance
frequencies are at this stage not comparable, because the selected omni-directional peakover-threshold maxima (storm maxima) are not divided between the azimuth sectors for
directional analysis. Instead, a storm maxima selection takes place for each wind direction
class separately (as described in Section 3.2.1). As a result, the total number of directional
storm maxima is always higher than or equal to the total number of omni-directional storm
35
maxima. For this reason, one has to correct for persistence between wind direction classes
before the calibration of the directional results to the omni-directional results can be
performed. This will be done using a persistence correction factor.
The persistence correction factor pcf has been set up by modelling the ratio between the
observed combined directional exceedance frequencies and the observed omni-directional
exceedance frequencies of the selected storm maxima:
12
pcf (u ) =
∑Gi (u )
i =1
G(u )
,
(3.27)
where Gi represents the observed exceedance frequency per year for wind direction class i
and G the observed omni-directional exceedance frequency per year, both at wind speed
level u in m/s.
(3.27) concerns only annual results, but the pcf can also be calculated for seasonal results
(expressed by the index j):
12
pcf j (u ) =
∑Gij (u )
i =1
G j (u )
.
(3.28)
Because the total number of directional storm maxima is higher than the total number of
omni-directional storm maxima, the pcf is always higher than or equal to 1. The pcf can be
interpreted as the total number of wind direction classes during a storm. Figure 3.10 shows
an example of the pcf. This figure shows an obvious decline in the pcf with the wind speed,
which means a decrease in the number of wind direction classes for more severe storms.
Figure 3.10: Example of the persistence correction factor, concerning omni-directional data obtained
from station 225 IJmuiden for the season January/February. Visible is the decline for higher wind
speed levels.
36
The pcf as function of wind speed can be modelled with a linear regression model as
described by Smits (2001b). The transformed persistence correction factor pcft can be
expressed as:
pcft (u ) = a + bpt (u ) + ε (u ) ,
(3.29)
with
and
pcft (u ) = ln( pcf (u ) − 1) ,
(3.30)
pt (u ) = ln[− ln(1 − p(u ))] ,
(3.31)
where a represents the offset and b the slope in the regression equation. Furthermore
represents ε a random disturbance, p the observed percentile of the omni-directional storm
maxima and pt the transformed observed percentile of the omni-directional storm maxima,
all at wind speed level u in m/s.
With (3.29), the modelled persistence correction factor pcˆf can be calculated:
pcˆf (u ) = exp(a + b{ln[− ln(1 − pˆ (u ))]}) + 1 ,
(3.32)
where pˆ (u ) represents the modelled percentile of the omni-directional storm maxima at wind
speed level u in m/s calculated from the directly estimated omni-directional return levels. The
parameters a and b are calculated for each station, for each season and for the whole year.
For the example in Figure 3.10, the modelled persistence correction factor is plotted as blue
line in Figure 3.11 (without restriction). In contrast with the observed values, the modelled
values are calculated, plotted and used only for wind speed values above a certain level
( x ≥ 0 or p(u ) ≥ 0.632 ) because this method is not suitable for relatively low wind speeds.
For the example in Figure 3.10 this means that only values equal to or higher than 14 m/s
are plotted. For wind speeds lower than 14 m/s, the observed persistence correction factor is
used.
The modelled persistence correction factor that corresponds with a return period of 10,000
year does have a noisy geographical pattern. To avoid this pattern that is mainly caused by
statistical uncertainties, the persistence correction factor that corresponds with a return
period of 10,000 year has been set at fixed values for each season and for the whole year
that are the same for all stations (Table 3.6).
Season
January, February
March, April
May, June
July, August
September, October
November, December
Year
pcf
1.20
1.25
1.25
1.20
1.15
1.15
1.20
Table 3.6: Fixed persistence correction factors for all stations corresponding with a return period of
10,000 year.
37
For the example in Figure 3.10, the modelled persistence correction with fixed persistence
correction factor for the 10,000-year return period results in the red line in Figure 3.11 (with
restriction). Again, the modelled values are calculated and plotted only for wind speed values
above a certain level.
Figure 3.11: Example of modelling the ratio between combined and omni-directional exceedance
frequencies (persistence correction factor), concerning omni-directional data obtained from station 225
IJmuiden for the season January/February. The modelling without restriction concerns regression
output where no fixed ratio values corresponding with a return period of 10,000 year have been used.
The modelling with restriction uses the fixed ratio values from Table 3.6.
After applying the persistence correction factor on the combined directional exceedance
frequencies by dividing the combined directional exceedance frequencies by the persistence
correction factor, the omni-directional exceedance frequencies and the corrected combined
directional exceedance frequencies can be compared objectively. The ratio between those
two frequencies at fixed levels can be seen as a tail correction factor (tcf). This tcf is used to
correct the directional exceedance frequencies by multiplying the directional exceedance
frequencies with the tcf:
Gˆ i (u ) = Gi (u )tcf (u ) = Gi (u )
G(u )
12
∑Gi (u ) / pcˆf (u )
i =1
=
Gi (u )G(u )pcˆf (u )
12
∑Gi (u )
,
(3.33)
i =1
where Ĝi represents the corrected exceedance frequency per year for wind direction class i,
G j the non-corrected exceedance frequency per year for wind direction class i, and G the
exceedance frequency per year, all at wind speed level u in m/s. When the exceedance
frequencies G j and G are less than 2 times per year, the modelled exceedance frequencies
are used, otherwise the observed exceedance frequencies are used.
38
(3.33) concerns only annual results, but the tcf can also be used for seasonal results:
Gˆ ij (u ) = Gij (u )tcf j (u ) = Gij (u )
G j (u )
12
∑Gij (u ) / pcˆf j (u )
i =1
=
Gij (u )G j (u )pcˆf j (u )
12
∑Gij (u )
,
(3.34)
i =1
where Ĝij represents the corrected exceedance frequency per year for wind direction class i
in season j, Gij the non-corrected exceedance frequency per year for wind direction class i in
season j, G j the exceedance frequency per year in season j, pcˆf j the modelled persistence
correction factor in season j and tcf j the tail correction factor in season j, all at wind speed
level u in m/s.
If tcf is obtained without making use of the pcf ( pcf = 1) it is guaranteed that the directional
exceedance frequencies are linked to the omni-directional exceedance frequencies. This
means that the omni-directional return levels are always higher than the directional return
levels. In theory, by making use of the persistence correction factor the linking property is not
guaranteed anymore. In practice however, the consequences are negligible and the omnidirectional return levels and directional return levels are still linked.
Figure 3.12 shows an example of a wind speed level dependent tcf. This figure shows that
the tail correction factor declines for higher wind speed levels, resulting in lower directional
return levels.
Figure 3.12: Example of modelling the ratio between omni-directional frequencies and corrected
combined frequencies (tail correction factor), concerning data obtained from station 225 IJmuiden for
the season January/February. This ratio can be used as factor to correct the directional frequencies.
For the example in Figure 3.12, the precise effect of the tcf on the directional return levels is
presented in Table 3.7. The non-corrected values are obtained by harmonising the directional
return levels. The corrected values are obtained by correcting the harmonised directional
39
return levels by making use of the tcf. This table shows that the effect is minimal for wind
direction classes with relative low return levels (3, 4 and 5) while the effect is somewhat
stronger for wind direction classes with high return levels (8, 9 and 10).
Wind direction
class
1
2
3
4
5
6
7
8
9
10
11
12
Noncorrected
24.33
21.57
18.85
17.82
19.56
23.52
27.71
30.20
30.42
29.22
27.74
26.29
Corrected
24.15
21.45
18.80
17.79
19.49
23.38
27.48
29.89
30.08
28.91
27.45
26.04
Table 3.7: 10,000-year directional return levels in m/s, concerning station 225 IJmuiden for the season
January/February. The non-corrected values are obtained by harmonising the directional return levels.
The corrected values are obtained by correcting the harmonised directional return levels by making
use of the tail correction factor.
The extreme value model described in Section 3 does not provide distribution parameters,
but only return levels at fixed exceedance frequencies (Table 3.4) Therefore, the modelled
exceedance frequencies G(u ) , G j (u ) , G j (u ) and Gij (u ) are determined by linearly
interpolating of the fixed exceedance frequencies. Figure 3.13 shows an example of this
interpolation method. This figure presents dots that correspond with return levels at fixed
exceedance frequencies. Other exceedance frequencies are obtained by making use of the
straight lines that connect the dots with each other.
Figure 3.13: Example of linear interpolation of exceedance frequencies, concerning omni-directional
data obtained from station 225 IJmuiden for the season January/February.
40
3.5.4
Combining directional return levels to omni-directional return levels
Instead of correcting directional exceedance frequencies with the help of omni-directional
exceedance frequencies (Section 3.5.3), also omni-directional exceedance frequencies can
be corrected with the help of directional exceedance frequencies. This method calculates
omni-directional exceedance frequencies by combining the exceedance frequencies
concerning the several wind direction classes. The way of combining guarantees that the
omni-directional return levels will not be lower than the directional return levels. Because of
the method of determining the directional storm maxima (Section 3.2.1), some persistence
between wind direction classes exists. When performing the combination, one has to take
this property into account by using the persistence correction factor as discussed in Section
3.5.3:
12
Gˆ (u ) =
∑Gi (u )
i =1
pcˆf (u )
,
(3.35)
where Gi represents the exceedance frequency per year per wind direction class i, pcˆf the
modelled persistence correction and Gˆ the resulting exceedance frequency per year, all at
wind speed level u in m/s. Again, when the exceedance frequencies Gi are less than 2 times
per year, the modelled exceedance frequencies are used, otherwise the observed
exceedance frequencies are used.
(3.35) concerns the combination of directional annual return levels to omni-directional annual
return levels, but this method of combination can also be used to combine directional
seasonal return levels to omni-directional seasonal return levels:
12
Gˆ j (u ) =
∑Gij (u )
i =1
pcˆf j (u )
,
(3.36)
where Gij represents the exceedance frequency per year in season j for wind direction class
i, pcˆf j the persistence correction factor in season j and Gˆ j the resulting exceedance
frequency per year in season j, all at wind speed level u in m/s. Again, when the exceedance
frequencies Gij are less than 2 times per year, the modelled exceedance frequencies are
used, otherwise the observed exceedance frequencies are used.
To determine the modelled exceedance frequencies Gi (u ) and Gij (u ) , again the
interpolation method as discussed in Section 3.5.3 is used.
41
3.5.5
Combining seasonal return levels to annual return levels
In the same way omni-directional exceedance frequencies can be obtained by combining
directional exceedance frequencies (Section 3.5.4), it is possible to obtain annual
exceedance frequencies by combining the exceedance frequencies concerning the several
seasons. This guarantees that the annual return levels will not be lower than the seasonal
return levels. Because persistence between seasons is negligible, no persistence correction
is needed:
Gˆ (u ) =
6
∑G j (u ) ,
(3.37)
j =1
where G j represents the exceedance frequency per year in season j and Gˆ the resulting
exceedance frequency per year, both at wind speed level u in m/s. Again, when the
exceedance frequencies G j are less than 2 times per year, the modelled exceedance
frequencies are used, otherwise the observed exceedance frequencies are used.
(3.37) concerns the combination of seasonal omni-directional return levels to annual omnidirectional return levels, but this method of combination can also be used to combine
seasonal directional return levels to annual directional return levels:
Gˆ i (u ) =
6
∑Gij (u ) ,
(3.38)
j =1
where Gij represents the exceedance frequency per year in season j for wind direction class
i and Gˆ i the resulting exceedance frequency per year for wind direction class i, all at wind
speed level u in m/s. Again, when the exceedance frequencies Gij are less than 2 times per
year, the modelled exceedance frequencies are used, otherwise the observed exceedance
frequencies are used.
To determine the modelled exceedance frequencies G j (u ) and Gij (u ) , again the
interpolation method as discussed in Section 3.5.3 is used.
42
3.5.6
Methods of combining and splitting seasons and wind direction classes
There is more than one way to link seasonal to annual return levels and directional to omnidirectional return levels in a way that the omni-directional return levels are always higher
than the directional return levels and that the annual return levels are always higher than the
seasonal return levels.
In schematic form the methods are listed in Figure 3.14 where Method A corresponds to the
method described in Smits (2001c). In the figure, 1 corresponds with the procedure described in
Section 3.5.1, 2 with the one in Section 3.5.2, 3 with the one in Section 3.5.3, 4 with the one in Section
3.5.4 and 5 corresponds with the procedure described in Section 3.5.5.
Method A:
Method B:
1
Method C:
Method D:
1
2
3
5
2
3
5
2
4
5
2
4
5
1
= Splitting annual return levels into seasonal return levels
2
= Harmonising directional return levels
3
= Calibrating directional return levels to omni-directional return levels
4
= Combining directional return levels to omni-directional return levels
5
= Combining seasonal return levels to annual return levels
Figure 3.14: Methods of obtaining seasonal and directional return levels and annual and omnidirectional return levels. 1 corresponds with the procedure discussed in Section 3.5.1, 2 with the one
discussed in Section 3.5.2, etc.
More in detail the methods are described as follows:
43
•
Method A
Estimating seasonal directional return levels U ij (T ) and seasonal omni-directional
return levels U j (T ) .
(2) Harmonising seasonal directional return levels U ij (T ) . Results in Uˆ ij (T ) .
(3) Calibrating seasonal directional return levels Uˆ ij (T ) to seasonal omni-directional
return levels U j (T ) . Results in Uˆ ij (T ) .
(5) Combining seasonal directional return levels Uˆ ij (T ) and seasonal omni-directional
return levels U j (T ) to annual directional return levels Uˆ i (T ) and annual omnidirectional return levels Uˆ (T ) .
•
Method B
Estimating annual directional return levels U i (T ) and annual omni-directional return
levels U (T ) .
(1) Splitting annual directional return levels U i (T ) and annual omni-directional return
levels U (T ) into seasonal directional return levels Uˆ ij (T ) and seasonal omnidirectional return levels Uˆ j (T ) using multiplication factors.
(2) Harmonising seasonal directional return levels Uˆ ij (T ) . This results in Uˆ ij (T ) .
(3) Calibrating seasonal directional return levels Uˆ ij (T ) to seasonal omni-directional
return levels Uˆ j (T ) . This results in Uˆˆ ij (T ) .
(5) Combining seasonal directional return levels Uˆˆ ij (T ) and seasonal omni-directional
return levels Uˆ j (T ) to annual directional return levels Uˆ i (T ) and annual omnidirectional return levels Uˆ (T ) .
•
Method C
Estimating seasonal directional return levels U ij (T ) .
(2) Harmonising seasonal directional return levels U ij (T ) . This results in Uˆ ij (T ) .
(4) Combining seasonal directional return levels Uˆ ij (T ) to seasonal omni-directional
return levels Uˆ j (T ) .
(5) Combining seasonal directional return levels Uˆ ij (T ) and seasonal omni-directional
•
Method D
Estimating annual directional return levels U i (T ) .
(1) Splitting annual directional return levels U i (T ) into seasonal directional return
levels Uˆ ij (T ) using multiplication factors.
(2) Harmonising seasonal directional return levels Uˆ ij (T ) . This results in Uˆ ij (T ) .
(4) Combining seasonal directional return levels Uˆ ij (T ) to seasonal omni-directional
return levels Uˆ j (T ) .
(5) Combining seasonal directional return levels Uˆ (T ) and seasonal omni-directional
ij
44
In short (cryptical manner) the methods are described as follows:
• Method A: omni-directional ⇒ directional, seasonal ⇒ annual.
• Method B: omni-directional ⇒ directional, annual ⇒ seasonal ⇒ annual.
• Method C: directional ⇒ omni-directional, seasonal ⇒ annual.
• Method D: directional ⇒ omni-directional, annual ⇒ seasonal ⇒ annual.
From analyses it appeared that directly estimated seasonal return levels are very inefficient
in comparison to directly estimated annual return levels. Because for seasonal analysis a 1/6
part of the year data is used, the seasonal return levels are less efficient (so with higher
uncertainty margins) than the annual return levels. The annual return level that is calculated
by combining the seasonal return levels is always higher than the highest seasonal return
level. Together with the relatively high uncertainty margins of seasonal results, the annual
return level calculated by combining the seasonal return levels is positively biased. In Figure
3.15 an example of this property is shown. Possible seasonal 10,000-year return levels are
plotted with its uncertainties. The resulting annual return level with these uncertainties
included (blue dotted line) is higher than without these uncertainties (black solid line).
Figure 3.15: Example of possible seasonal 10,000-year return levels and annual 10,000-year return
levels. The annual return levels (dotted and solid line) are calculated by combining the seasonal return
levels with and without uncertainty margins (brackets). The annual return level calculated from the
seasonal return levels with uncertainty margins is positively biased.
Due to this positive bias, it is not preferable to calculate annual return levels by combining
the directly estimated seasonal return levels like in Method A and C. On the other side, return
levels obtained by the analysis of annual data may be inconsistent (biased). This is due to
the seasonal pattern that is commonly known for wind speed in the Netherlands. Severe
storms mostly occur in the winter half year (October till March) and occasionally in the
summer half year (April till September). This seasonality implies that the requirement of
extreme value analysis for an identically distributed variable will not be met (see for example
Davison and Smits, 1990). Therefore, annual data can be seen as a mix of several
populations, also called heterogeneity.
45
Method B and D that both make use of the homogeneity property of seasonal data and the
efficiency of annual data, includes the determination of multiplication factors (Section 3.5.1).
These multiplication factors can be used to estimate seasonal return levels out of annual
return levels followed by the combination of seasonal return levels to annual return levels
(Section 3.5.5).
For wind direction classes the same idea of multiplication factors can be used to estimate
directional return levels out of omni-directional return levels. To prevent that the factors are
location dependent, it is preferable to use harmonisation (Section 3.5.2) on the directional
return levels to reduce the noise in directional return levels instead of the use of multiplication
factors. Omni-directional return levels could then be calculated by combining the directional
return levels (Section 3.5.4), like in Method C and D. Because each wind direction class
yields uncertainties, even after harmonisation, the omni-directional return levels calculated by
combining the directional return levels are rather inefficient. For this reason the calibration of
the directional return levels to the directly estimated omni-directional return levels (Section
3.5.3) is preferred, like in Method A and B. This is a valid way because of the homogeneity
properties of the omni-directional data.
In Section 4 the validation of the different methods will be discussed in which the mutual
differences will be explained.
46
4
Validation and results of the extreme value analysis
This section discusses the validation of the choices made in the statistical model as
described in Section 3. These concern the probability distribution that is used to model the
peak-over-threshold values in Section 3.3 (CWD or GPD) and the linking of directional and
seasonal return levels to omni-directional and annual return levels in Section 3.5 (Method A,
B, C or D). For making the validation easier, a fifth method to link results to each other is
introduced in addition to the Methods A, B, C and D. This Method 0 concerns the directly
estimation of directional, omni-directional, seasonal and annual return levels. In this context
directly means without splitting up, calibrating and/or combining results. This method is not
an option in choosing a final method, because the results are not linked to each other. This
method is useful however for validation.
Furthermore, the effect of different threshold ranges is examined as well as the impact of the
definition of wind direction classes and seasons as used in Section 3 and the impact of
climate variations.
Validation takes place by comparing the results with observations (Section 4.1) and by
comparing the choices in probability distribution and methods between each other (Section
4.2). The effect of different threshold ranges on the return levels is discussed in Section 4.3
The impact of the definition of wind direction classes and seasons is discussed in Section 4.4
and Section 4.5 discusses the impact of climate variations. Finally, results are presented in
Section 4.6.
4.1
Validation by comparing with observations
One way of validation is to compare return levels obtained by the statistical method that
correspond with high exceedance frequencies with return levels that are obtained by the
empirical distribution function. The percentiles of the observations in this empirical
distribution function are calculated with the plotting formula of Gringorten (1963):
m − 0.44  N

Fp (u m ) = 1 −
⋅ ,
N + 0.12  Y

(4.1)
where M represents the total number of selected storm maxima, Y the number of years and
u m the ranked storm maximum observation (from the smallest u1 to the highest u N ).
In Figure C.1a and Figure C.1b the deviation of the omni-directional annual return levels
averaged over the set of 31 stations are plotted for the CWD and GPD, respectively. In the
figures also the corresponding 95%-confidence interval of the deviation and the one of the
mean deviation are shown. For both distributions all methods are performed and shown. The
figures show the same pattern for the several choices in distribution and in method, but all
possible model choices seem to underestimate the observations for higher return periods
(from about T = 5 to 30 years). For the highest return period in the figures (T = 30 years)
47
however, a stabilisation or even a less underestimation seems to exist. It is important to find
out, if the increasing behaviour in the mean deviation extends for even higher return periods.
This has been examined by making a selection of 13 stations that have all a measuring
length of at least 40 years. Doing so, the comparison period has been lengthened from 30 to
70 years. The results of the comparison are presented in Figure C.1c for the CWD and
Figure C.1d for the GPD. These figures show that for the CWD the underestimation
disappears, but that the underestimation remains for the GPD, except for Method 0. Based
on these figures, the CWD is preferable to use. A choice between the methods however is
difficult to make, because of the small differences between the figures.
4.2
Validation by comparing choices
Another way to validate the choices in the model described in Section 3 is to compare the
return levels from the model for the different methods (A, B, C and D) with those resulting
from Method 0. These comparisons can then mutually be compared to quantify the effect of
the heterogeneity properties of directly estimated annual results, the effect of combining
directly estimated seasonal results to annual results and the effect of combining directly
estimated directional results to omni-directional results. Figure C.2a (CWD) and Figure C.2b
(GPD) show the results of this comparison with omni-directional annual return levels. Again
the shown results are averaged over the set of 31 stations. First the results for the CWD will
be discussed for all methods. Afterwards the results for the GPD in comparison with the
CWD are discussed.
Method B uses homogeneous seasonal return levels that are corrected for statistical noise
by using year-to-season multiplication factors (see Section 3.5.1). Combining these seasonal
return levels to annual results and comparing these annual return levels with the directly
estimated annual return levels of Method 0 gives an indication of the heterogeneity error
made when annual return levels are directly estimated. The upper right panel of Figure C.2a
shows that this error equals about –1.0 m/s for a return period of 10,000 years. Thus directly
estimated annual return levels yields negatively biased return levels in comparison with the
annual return levels resulting from combining corrected seasonal return levels.
Method A also uses homogeneous seasonal return levels but these are not corrected for
statistical noise, since they are directly estimated and not obtained by using year-to-season
multiplication factors. Therefore, the difference between Method A and Method B gives an
indication of the error made when combining directly estimated seasonal return levels to
annual return levels. The upper left panel of Figure C.2a shows that the difference between
omni-directional annual return levels obtained by Method A and 0 equals about –0.3 m/s for
a return period of 10,000 years. The difference between the upper left and upper right panel
gives the difference between Method A and B. For a return period of 10,000 years this yields
a difference of –0.3 m/s (Method A – Method 0) minus –1.0 m/s (Method B – Method 0) =
about +0.7 m/s (Method A – Method B). This means that combining directly estimated
seasonal return levels to annual return levels (Method A) yields positively biased return
48
levels in comparison with the annual return levels resulting from combining corrected
seasonal return levels (Method B).
Method C and D combine directional results to omni-directional results instead of calibrating
directional return levels to omni-directional return levels, like Method A and B do. Method D
uses year-to-season factors like Method B, which means that the difference in omnidirectional annual return levels between Method D and Method B gives an indication of the
difference between when omni-directional annual return levels are obtained by combining
directional return levels and when omni-directional annual return levels are obtained by using
directly estimated annual omni-directional return levels. The lower right panel of Figure C.2a
shows that the difference between Method D and 0 equals about –0.5 m/s for a return period
of 10,000 years, which yields a difference between method D and B of about +0.5 m/s (–0.5
m/s minus –1.0 m/s).
Method C does not use year-to-season factors, but combines directly estimated seasonal
return levels to annual return levels, like Method A. This means that the difference between
Method C and Method A gives an indication of the difference between when combining
seasonal directional return levels to seasonal omni-directional return levels and when directly
estimated omni-directional return levels are used. The lower left panel of Figure C.2a shows
that the difference between Method C and 0 equals a value of about –0.3 m/s for a return
period of 10,000 years. The difference between Method C and A yields therefore in an value
of about 0.0 m/s (–0.3 m/s minus –0.3 m/s). Apparently, averaged over the stations,
combining seasonal directional return levels to seasonal omni-directional return levels yield
the same return levels as when directly estimated seasonal omni-directional return levels are
used.
For wind direction classes, one can obtain omni-directional return levels by combining
directional return levels or by using the directly estimated omni-directional return levels. As
described above, the lower left and right panel of Figure C.2a indicate the differences in
annual return levels between these two methods. However, exact differences also can be
calculated for each month and for the whole year, separately. First directly estimated
directional and omni-directional return levels per season and for the whole year are derived
(Method 0). To correct for the noisy pattern in these directional return levels, the
harmonisation procedure as discussed in Section 3.5.2 is applied on the directly estimated
directional return levels. Then the corrected directional return levels can be combined using
the procedure as discussed in Section 3.5.4. The resulting combined directional return levels
can be compared with the directly estimated omni-directional return levels to learn more
about the effect of these two different methods of obtaining omni-directional return levels.
Differences between the combined directional return levels and the directly estimated omnidirectional return levels obtained with the CWD are given in Table 4.1 for each season and
for the whole year.
49
Station
210 Valkenburg
225 IJmuiden
229 Texelhors
235 De Kooy
240 Schiphol
252 K13
260 De Bilt
265 Soesterberg
269 Lelystad
270 Leeuwarden
275 Deelen
277 Lauwersoog
279 Hoogeveen
280 Eelde
285 Huibertgat
290 Twenthe
308 Cadzand
310 Vlissingen
312 Oosterschelde
316 Schaar
320 Goeree
321 Europlatform
331 Tholen
344 Zestienhoven
350 Gilze-Rijen
356 Herwijnen
370 Eindhoven
375 Volkel
380 Beek
Mean (CWD)
Mean (GPD)
1
1.5
0.3
1.4
2.8
1.0
1.4
-0.3
0.3
0.8
0.0
-0.5
-0.8
-1.8
-1.3
1.0
-0.7
-0.8
-1.9
-0.4
-0.8
0.6
1.4
1.0
-1.4
-0.9
0.0
2.1
-0.8
-1.3
-0.8
0.7
0.0
-1.5
2
-0.2
-1.8
-2.5
-5.9
-2.5
1.6
-0.1
-1.1
-0.3
-0.8
-0.7
1.4
-0.1
-1.3
2.5
0.3
2.5
-1.6
1.3
2.5
-1.2
1.3
1.3
1.7
-0.4
-0.9
2.0
-0.2
2.3
-3.9
-0.1
-0.2
-1.4
Season
3
4
-1.7
1.4
0.3
0.6
1.3
1.4
0.3
0.2
-1.5
0.7
1.3
3.6
-0.3
-2.6
-0.3
-0.5
-0.4
0.2
-0.4
-1.1
-1.0
-0.1
-1.4
-1.8
-1.3
-0.5
0.0
0.9
2.1
0.5
-2.6
-1.6
-5.5
1.3
-3.2
1.1
0.6
0.9
-1.5
0.0
-0.1
1.8
3.5
1.6
-2.0
-0.5
-3.4
-0.6
-1.1
1.1
-0.7
0.4
-1.8
-1.7
-2.5
-0.4
0.8
0.2
-1.6
-1.0
-1.1
-1.3
-0.8
0.1
-1.9
-0.8
5
-2.0
0.0
2.1
-0.5
-1.1
-1.4
-0.1
-2.5
-0.5
2.1
-3.9
1.3
-2.2
0.3
2.2
-2.2
1.7
0.3
-0.3
1.3
1.4
-0.3
0.6
-1.9
-1.8
0.9
-2.0
-0.8
0.1
-0.2
0.0
-0.3
-1.5
6
0.2
1.1
0.3
0.7
1.4
2.7
2.0
1.0
0.2
0.2
1.6
-0.7
-1.1
-0.5
0.6
-0.7
-0.2
1.2
-2.9
-1.0
3.8
2.3
0.2
0.1
-1.1
2.2
0.5
2.3
0.2
0.0
0.0
0.5
-1.0
Year
1.8
-0.2
-2.7
-2.8
1.0
-2.3
2.8
2.6
6.9
-3.3
1.6
-3.0
1.7
-1.8
1.2
-1.6
1.4
-0.1
0.2
0.6
1.8
0.5
1.6
-0.9
2.3
1.4
2.1
1.7
-0.9
1.2
2.4
0.6
-0.2
Table 4.1: Differences between combined directional 10,000-year return levels and directly estimated
omni-directional 10,000-year return levels in m/s obtained with the CWD. The directional return levels
are harmonised by the procedure described in Section 3.5.2. The average over the stations is
calculated for both the CWD and the GPD.
Averaged over the stations, the differences concerning the CWD are rather small. For the
seasons May-June (-0.8) and November-December (+0.5) the differences are just significant.
However, because of the non-existing structural pattern over the seasons (the mean
differences seem to be randomly positive as well as negative), the resulting differences can
be seen as statistical noise and not as systematic differences between the methods.
Because omni-directional return levels are more efficient than directional return levels (omnidirectional analysis includes more data than directional analysis), the method where
directional return levels are calibrated to the omni-directional return levels (Method A and B)
is preferred to the method where the directional return levels are combined to omnidirectional return levels (Method C and D).
Some more can be noticed when looking at Figure C.2a. It is clear that the confidence
intervals corresponding with Method B for high return periods are much smaller than the
ones corresponding with the Methods A, C and D. Explanation for this behaviour is that
Method B is the only method that is based on the directly estimated omni-directional annual
return levels like Method 0. This is especially the case for the highest return period (10,000
50
year) and not for the lowest return period (0,5 year), because for the high return periods a
fixed year-to-season factor is used, while for low return periods a station dependent factor is
applied (see Section 3.5.1). The other methods are not based on omni-directional annual
return levels. Method A is based on directly estimated omni-directional seasonal return
levels, Method C is based on directly estimated directional seasonal return levels and
Method D is based on directional annual return levels. Therefore, deviations with the directly
estimated omni-directional annual return levels (Method 0) for these methods are quite large.
Based on the above, in the case of the CWD Method B is the method that has the best
properties concerning efficiency and consistency by making use of annual data (efficiency),
seasonal data (consistency) and omni-directional data (efficiency). Therefore, Method B is
preferred to the Methods A, C and D.
When comparing Figure C.2b for the GPD with Figure C.2a for the CWD it becomes clear
that there is a discrepancy between the CWD and the GPD for all four methods in
comparison with Method 0. The large mean deviations of the methods from Method 0 for the
GPD are caused by the fact that the Methods A, B, C and D make use of split up analysis
with regard to seasons and wind direction classes instead of making use of only omnidirectional annual analysis like Method 0. Because of the splitting into smaller datasets lower
threshold values have to be used. The discussion of Figure B.1a and Figure B.1b (see
Section 3.2.2) made clear that for the GPD lower threshold values result in lower return
levels than for the CWD. Due to these two reasons, the splitting up and lower return levels
for lower threshold for the GPD, all four methods produce return levels that are low
compared with the return levels obtained by Method 0. In Table 4.1 the underestimation of
the return levels for the GPD is clearly seen. All differences are significant smaller than zero
except for the whole year. This means that when omni-directional seasonal return levels are
obtained by combining the directional seasonal return levels, the resulting omni-directional
seasonal return levels are lower then the directly estimated omni-directional seasonal return
levels. The negative values are the consequence of splitting up into wind directions classes
as described above.
Based on the results in Table 4.1, Figure C.2a and Figure C.2b, it is preferable to use the
CWD in combination with Method B.
51
4.3
Threshold range
In Section 3.2.2 it is argued to use a threshold range instead of one single threshold to
reduce statistical uncertainty. Lower and upper limits of the range are chosen with the use of
visual and numerical determination of a balance between consistency and efficiency. Based
on analyses of this balance the lower limits of the threshold range are fixed on wind speeds
that correspond with an exceedance frequency of 10 times per year concerning annual
analysis and 7 times per season concerning seasonal analysis. The upper limits are fixed on
values that correspond with an exceedance frequency of 2 times per year concerning annual
analysis and 2 times per season concerning seasonal analysis.
This section studies the effect of two other threshold ranges on the return levels. These
ranges include lower threshold values than the one mentioned above. To compare the three
threshold ranges, directly estimated omni-directional 10,000-year return levels are obtained
for each season and for the whole year (like Method 0). Both the CWD and GPD are used as
probability distributions. The resulting return levels are averaged over the same set of 31
stations as used in Section 3. For the season January, February and for the whole year
these mean return levels are listed in Table 4.2.
Year
Exceedance
frequency (#/year)
10 – 2
40 – 10
> 40
January, February
Return level
Range
(m/s)
(m/s)
CWD GPD
14.6 – 17.9 33.2 32.4
10.4 – 14.2 32.5 29.9
0.0 – 10.0 21.5 24.0
Exceedance
Range
frequency (#/season)
(m/s)
7–2
11.0 – 15.5
11 – 7
7.5 – 10.6
> 11
0.0 – 7.1
Return level
(m/s)
CWD GPD
32.0 29.2
30.9 26.7
21.5 23.8
Table 4.2: 10,000-year return levels obtained by three different threshold ranges. The return levels are
directly estimated and concern omni-directional data for the whole year and the season January,
February. The ranges and return levels are averaged over 31 stations. Both the CWD and GPD are
used as probability distributions.
Table 4.2 makes clear that the range with the lowest threshold values result in return levels
that are substantially lower than the return levels obtained with the other threshold ranges for
both the CWD and the GPD. For the CWD however, the differences between the return
levels that are obtained by using the range with the highest threshold values and the return
levels that are obtained by using the middle threshold range are rather small (0.7 and 1.1 m/s
respectively). For the GPD, the differences are larger (2.5 and 2.5 m/s respectively). The
results concerning the other seasons (not shown) are similar.
The above indicates that very low threshold values result in very inconsistent return levels,
but also that the effect of the threshold on the return levels is rather small above a certain
threshold concerning the CWD. This corresponds to the conclusions drawn in Section 3.2.2
and in Section 3.3.
52
4.4
Definitions of wind direction classes and seasons
In Section 3, definitions of wind direction classes and seasons are given together with an
explanation about why these definitions are used. This section discusses the influence of a
different classification of a year into 6 seasons and of a wind rose into 12 sectors. So the
number of wind direction classes or seasons remains the same, which means that only a
shift takes place over wind direction or in time. For this analysis data of the same 31 stations
as described in Section 3 is used. The effects of different directional definitions are described
in Section 4.4.1 and the effects of different seasonal definitions in Section 4.4.2.
4.4.1
Wind direction
For wind direction classes, the influence of a shift of 10 degrees to the left and to the right in
the compass on the return levels is analysed. This means that for example the first wind
direction class changes from 015°-034° to 005°-034° (Shift left) and 025°-054° (Shift right).
To analyse the effects of these shifts on the return levels, annual and seasonal directly
estimated directional return levels are obtained for return periods of 0.5 year and 10,000
years according to the default wind direction class definition and the modified wind direction
class definitions. For each definition the return levels for 0.5 and 10,000 years are averaged
over the stations per season and per wind direction class. The highest directional return
levels per season are selected for each wind direction class definition. This procedure is
applied with both probability distributions, the CWD and the GPD. Table 4.3 lists the
differences between the modified and default definitions for the return periods 0.5 and 10,000
years.
Season
1
2
3
4
5
6
Year
Shift left
T=0.5 year
T=10,000 year
CWD GPD
CWD GPD
0.1
-0.1
0.0
0.4
-0.1
0.0
-0.1
-0.3
0.0
-0.4
0.0
-0.7
-0.1
0.0
0.0
0.0
0.1
0.1
0.1
-0.1
0.1
0.0
0.1
0.5
-0.1
0.1
-0.1
0.0
Shift right
T=0.5 year
T=10,000 year
CWD GPD
CWD GPD
-0.2
0.2
-0.1
0.0
-0.1
-0.1
-0.2
-0.4
-0.2
-0.2
-0.2
0.0
-0.1
0.2
-0.1
0.2
-0.1
-0.1
-0.1
0.1
-0.1
0.4
-0.1
-0.4
-0.1
-0.5
-0.1
-0.4
Table 4.3: Differences between return levels following modified wind direction class definitions (Shift
left with as first class 005°-034° and Shift right with as first class 025°-054°) and those following the
default wind direction class definition (first class 015°-044°). The return levels correspond with return
periods 0.5 year and 10,000 years and are obtained using the CWD and GPD as probability
distributions.
Table 4.3 shows that the differences in return level regarding the modified wind directions
classes are rather small in the case of the CWD (between -0.2 m/s and +0.1 m/s). For the
GPD, the differences are somewhat larger, but are still not very large (between -0.7 m/s and
+0.5 m/s). These larger differences are consequences of the inefficiency property of the GPD
compared with the CWD as stated in Section 3.3. It appears that the definition of wind
53
direction classes is of minor importance with respect to the return levels for low and high
return periods as well, especially for the CWD.
4.4.2
Season
For seasons, a shift in time with one month is studied. This means that the first season
changes from January-February, the default season definition, to December-January, the
modified season definition. To analyse the effects of this shift on the return levels, an
equivalent procedure like the one concerning the shift in wind direction is used. Per wind
direction class directly estimated seasonal return levels are obtained that correspond to
return periods of 0.5 year and 10,000 years according to the default season definition and
the modified season definition. The return levels are determined with both the CWD and the
GPD. These return levels are averaged over the stations. The highest seasonal return levels
per wind direction class are selected for both season definitions. Table 4.4 lists the
differences in return levels between the modified definition (first season is DecemberJanuary) and the default definition (first season is January-February).
Wind direction
class
1
2
3
4
5
6
7
8
9
10
11
12
Omni
T=0.5 year
CWD
GPD
0.1
0.2
-0.1
0.2
0.4
0.0
-0.4
0.1
-0.8
0.2
-1.1
0.2
-0.5
0.3
-1.0
0.2
-1.4
0.1
-0.4
0.0
-1.4
-0.4
0.4
0.0
0.1
-1.4
T=10,000 year
CWD
GPD
-0.2
0.2
-0.2
0.3
-0.1
0.0
-0.1
0.2
-0.3
0.1
-1.1
0.2
-0.2
0.3
-0.1
0.2
-0.8
0.1
-0.1
0.0
0.1
-0.4
-0.8
0.0
0.1
1.0
Table 4.4: Differences between return levels following a modified season definition (first season
December-January) and those following the default season definition (first season January-February).
The return levels correspond with return periods of 0.5 year and 10,000 years and are obtained using
the CWD and GPD as probability distributions.
Table 4.4 shows that the effect of the shift in season is somewhat stronger than the effect of
the shift in wind direction class. The differences concerning the CWD are still small (between
-0.4 m/s and +0.3 m/s), but the differences concerning the GPD are quite large (between -1.4
m/s and 1.0 m/s). Also this behaviour is a consequence of the inefficiency property of the
GPD compared with the CWD. It appears that the definition of seasons is not of major
importance with respect to the return levels when using the CWD.
54
4.5
Climate variations
Climate variations in the wind climate need to be considered when present. Climate
variations can be studied by analysing the effect of lengthening the times series. As
described in Section 2 the length of the times series is very variable and range from a few
years to more than 50 years. The extreme value analysis described in Section 3 is applied on
time series with at least 20 years of measurements. A consequence of only using a lower
limit for the numbers of years, is that the length of the time series is not equal for the stations.
The length varies from 20 years (several stations) to 52 years (Schiphol).
Because of the intrinsic variation in the wind climate, the variable time series length could
have some effect on the return levels. To examine this effect, 13 stations are selected that
are complete for the time period 1962-2001. This time period is subdivided into the time
periods 1962-1981 and 1982-2001. For both the time periods, the extreme value analysis is
performed following Method 0, so direct estimation of return levels. The return levels are
obtained by making use of the CWD and the GPD as probability distributions. In Figure C.3
the return levels for both time periods are presented geographically with in Figure C.3a the
0.5-year return levels and in Figure C.3b the 10,000-years return levels. In Table 4.4 the
absolute differences in return levels between the two time periods (1982-2001 minus 19621981) corresponding with return periods of 0.5 year and 10,000 years are listed for the 13
stations. Also percentages are given to indicate the relative differences between the period
1982-2001 with respect to the period 1962-1981.
Station
225 IJmuiden
240 Schiphol
260 De Bilt
265 Soesterberg
270 Leeuwarden
275 Deelen
280 Eelde
310 Vlissingen
344 Zestienhoven
350 Gilze-Rijen
370 Eindhoven
380 Beek
Mean
T=0.5 year
CWD
GPD
0.2 (-1.0%)
0.2 (-1.0%)
-0.4 (-2.2%)
-0.4 (-2.2%)
-1.0 (-6.6%)
-1.0 (-6.6%)
-0.5 (-3.2%)
-0.5 (-3.2%)
-0.4 (-2.2%)
-0.3 (-1.7%)
-1.6 (-9.3%)
-1.6 (-9.3%)
0.4 (-2.5%)
0.4 (-2.5%)
0.1 (-0.6%)
0.1 (-0.6%)
-0.7 (-3.6%)
-0.6 (-3.1%)
-0.3 (-1.7%)
-0.3 (-1.7%)
-1.0 (-6.1%)
-1.0 (-6.1%)
-1.6 (-9.5%)
-1.6 (-9.5%)
0.7 (-4.5%)
0.7 (-4.5%)
-0.5 (-2.7%)
-0.5 (-2.8%)
T=10,000 year
CWD
GPD
-2.3 (1-7.1%) -2.6 (1-8.3%)
0.7 (-12.1%) 4.0 (-13.7%)
-5.0 (-15.7%) -5.2 (-16.9%)
2.5 (1-8.2%) 4.8 (-16.7%)
-2.7 (1-6.6%) -5.4 (-12.5%)
-4.1 (-11.6%) -4.1 (-12.3%)
2.1 (1-6.4%) 0.2 (-10.6%)
-0.5 (1-1.6%) -1.2 (1-3.9%)
-1.0 (1-3.5%) 0.7 (-12.7%)
-4.1 (-11.9%) -7.2 (-19.7%)
-3.3 (-10.1%) -5.3 (-16.6%)
-6.0 (-18.1%) -4.7 (-15.1%)
1.6 (-15.8%) 1.1 (-14.3%)
-1.7 (1-4.9%) -1.9 (1-5.2%)
Table 4.5: Differences in return levels between the time periods 1962-1981 and 1982-2001 (19822001 minus 1962-1981) in m/s and in percentages (between brackets). The return levels correspond
with return periods of 0.5 year and 10,000 years and are obtained using the CWD and GPD as
probability distributions.
Both Table 4.4 and Figure C.3 make clear that the time period used has a large effect on the
return levels, especially on the 10,000-year return levels. The differences vary from –6.0 m/s
(-18.1%) to +2.5 m/s (8.2%) concerning the CWD and from –7.2 m/s (-19.7%) to +4.8 m/s
55
(16.7%) concerning the GPD. In contrast with the geographical pattern in the 0.5-year return
levels (Figure C.3a), the pattern in the 10,000-year return levels differs severely when
comparing the two time periods (Figure C.3b). The differences are quite large, but because
they are both positive and negative, the differences averaged over the stations could be near
to zero. However, the mean difference equals -1.7 m/s (-4.9%) concerning the CWD and -1.9
m/s (-5.2%) concerning the GPD that are both just significant. These values and the
agreement between the CWD and the GPD indicate a systematic difference between the
time periods due to climate variations.
Based on the above, two important things can be concluded concerning the length of time
series. The first conclusion is that stations with time series including only the two last
decades produce relatively low return levels in comparison with stations with longer time
series. The second conclusion is that the geographical pattern in return levels for higher
return periods is strongly dependent of the time period and can be seen as a result of
statistical uncertainty. For lower return periods, also the effect of the climate variation is
visible, but the geographical pattern does only change marginal.
4.6
Results
From Section 4.1 and Section 4.2 it appeared that it is preferable to use the CWD in
combination with Method B. Section 4.4 and Section 4.5 both give no reason to reconsider
the choice of the probability distribution or the method to link the return levels to each other.
In Table 4.6 annual omni-directional return levels that are based on the CWD for Method A
and Method B are numerically presented for several return periods. The return levels of
Method A are listed, because this method corresponds with the method of Smits (2001c). In
the table the results are listed for the 31 stations summarized in Figure 3.2 that have a
measurement length of at least 19 years. Of these stations all available data is used for the
statistical analysis, so the size of the dataset used vary from station to station.
56
Station
210 Valkenburg
225 IJmuiden
229 Texelhors
235 De Kooy
240 Schiphol
252 K13
260 De Bilt
265 Soesterberg
269 Lelystad
270 Leeuwarden
275 Deelen
277 Lauwersoog
279 Hoogeveen
280 Eelde
285 Huibertgat
290 Twenthe
308 Cadzand
310 Vlissingen
312 Oosterschelde
316 Schaar
320 Goeree
321 Europlatform
331 Tholen
344 Zestienhoven
350 Gilze-Rijen
356 Herwijnen
370 Eindhoven
375 Volkel
380 Beek
Mean
Minimum
Maximum
Method A
T=100 T=101 T=102 T=103 T=104
20.1
23.8
26.8
29.7
32.5
20.4
23.5
26.3
28.8
31.1
21.8
26.0
29.8
33.4
36.7
21.0
25.0
28.4
32.0
36.1
20.3
24.4
27.9
31.0
33.8
23.4
27.3
30.9
34.2
37.5
16.1
19.8
23.1
26.1
28.8
16.8
21.1
25.0
28.6
32.1
19.1
24.7
30.0
35.0
39.8
19.3
24.0
28.4
32.6
36.5
18.1
22.2
25.8
29.0
32.1
20.3
24.5
28.5
32.1
35.4
17.0
20.7
23.8
26.7
29.3
17.8
21.9
25.7
29.1
32.1
22.1
26.1
30.0
33.5
36.7
15.8
20.4
25.0
29.3
33.5
20.6
24.2
27.3
30.1
32.8
19.2
22.7
25.6
28.2
30.6
21.1
24.4
27.3
29.9
32.5
20.2
23.2
25.7
28.3
31.6
21.9
25.2
27.8
30.0
32.1
22.6
26.0
28.9
31.5
33.8
20.1
23.1
25.5
27.4
29.0
19.2
22.7
25.6
28.1
30.5
19.8
24.2
28.1
31.7
35.1
18.7
22.1
24.9
27.3
29.6
17.2
21.0
24.2
26.9
29.4
18.8
22.9
26.6
29.9
33.0
17.7
21.8
25.5
28.8
31.9
16.4
20.7
25.0
29.3
33.6
17.3
20.9
23.9
26.5
28.9
19.4
23.2
26.7
29.8
32.9
15.8
19.8
23.1
26.1
28.8
23.4
27.3
30.9
35.0
39.8
Method B
T=100 T=101 T=102 T=103 T=104
20.0
23.7
26.7
29.4
32.1
20.2
23.4
26.0
28.4
30.3
21.8
26.1
30.2
34.2
38.2
21.0
25.1
28.7
32.2
36.0
20.3
24.4
27.9
31.1
34.0
23.4
27.4
31.3
35.3
39.3
16.1
19.9
23.0
25.7
28.0
16.9
21.1
24.7
27.8
30.4
19.3
24.8
29.5
33.6
37.0
19.4
24.2
28.9
33.7
38.4
18.2
22.4
26.0
29.3
32.4
20.4
24.5
28.6
32.6
36.7
16.9
20.1
22.3
23.5
24.2
17.9
22.1
25.9
29.5
33.1
22.0
25.9
29.4
32.4
34.9
16.0
20.9
25.7
30.7
35.6
20.5
23.9
26.4
28.3
30.0
19.1
22.5
25.2
27.5
29.5
20.9
24.1
26.8
29.1
31.2
20.0
22.8
25.0
26.8
28.3
21.7
24.7
26.9
28.7
30.3
22.4
25.6
28.4
30.8
33.0
19.9
22.7
24.7
26.2
27.4
19.2
22.4
25.0
27.1
29.1
19.8
24.1
27.7
30.6
33.2
18.7
22.2
25.4
28.7
32.1
17.3
21.0
24.1
26.8
29.1
18.8
23.0
26.5
29.8
32.6
17.7
21.8
25.3
28.4
31.1
16.6
21.1
25.6
30.4
35.2
17.3
20.8
23.5
25.7
27.7
19.3
23.2
26.5
29.5
32.3
16.0
19.9
22.3
23.5
24.2
23.4
27.4
31.3
35.3
39.3
Table 4.6: Annual omni-directional return levels based on the CWD for Method A and B corresponding
with return periods (T) of 1, 10, 100, 1,000 and 10,000 year.
In Figure C.4 for all stations the exceedance frequencies are plotted as function of wind
speed using the plotting position Fp to plot the storm maxima (4.1). Again the CWD is used
as distribution function and Method A and B to link the results to each other.
Furthermore, Figure C.5 presents geographically annual omni-directional return levels that
are again based on the CWD for Method A and Method B. In this figure the differences in
surface roughness are not included, because a mathematical interpolation procedure is
applied. Both methods produce for low return periods a rather clear geographical pattern in
their return levels. Stations offshore and near the coast produce clearly higher return levels
than stations more inland. For high return periods this pattern disappears and a rather noisy
pattern remains. This pattern is not very likely and is probably the result of the inevitable
statistical uncertainty when analysing stations independently of each other. The described
methods have reduced this uncertainty somewhat by imposing a threshold range instead of a
single threshold, but a stronger reduction needs to be performed. This reduction can possibly
be achieved by making use of the interpolation method that is described in Section 6 and
57
validated in Section 7. Integration of the extreme value analysis and the interpolation is
discussed in Section 8.
In Figure C.6 per station 10,000-year return levels based on the CWD for Method B are
plotted as function of the wind direction with different graphs for the seasonal and annual
results. Well seen in the graphs of this figure is the linking property between the directional
and the omni-directional return levels and between the seasonal and annual return levels.
The annual return level is always higher than seasonal return levels. Also the omnidirectional return level is higher than the directional return levels. This means that the omnidirectional annual return level is for every station the highest return level.
4.7
Discussion
This section discusses the statistical model and validation results in the context of the theory
of Section 3. Section 3.1 described two main approaches of extreme value modelling of wind
speed values. Approach 1 concerns a model that is based on all hourly wind speed values,
while Approach 2 concerns a model that analyses peak-over-threshold values. Approach 2
has been worked out in detail in Sections 3.2-3.5. Roughly can be said that a choice has to
be made between a model that is efficient but severely underestimates the return levels of
wind speed (Approach 1) and a model that is somewhat less efficient but produces
consistent results when applying the right choices for a number of options (Approach 2).
Approach 1 can only be used when a proper tail correction is imposed. The development of
such a correction though forms a complete extreme value study on itself and makes the
basis of the model superfluous. As result the main advantage (efficiency) of Approach 1 is
undone. Approach 2 does not need a tail correction, which is a big advantage. A
disadvantage of this approach is that because of using only peak-over-threshold values a
relatively small number of wind speed values is used, which results in a somewhat less
efficient model (compared with Approach 1) with less realistic geographical patterns.
However, appropriate choices of the options within Approach 2 reduce the inefficiency while
the consistency property remains. Therefore it is preferable to use Approach 2 instead of
Approach 1.
Combination of the two approaches is not to prefer, because Approach 2 would then serve
as a station dependent tail correction for Approach 1. Doing that the efficiency advantage of
Approach 1 would disappear. This means that the results of the combination has the same
disadvantages and advantages as Approach 2. However, the combination of the two
approaches yields a more complex model than Approach 2.
The options in Approach 2 concern the threshold value (Section 3.2), the probability
distribution (Section 3.3) and the way of linking return levels to each other (Section 3.5).
The threshold value has been chosen at that level where a balance exists between
consistency and efficiency. Furthermore, a threshold range is used with more efficient results
compared when using a single threshold value.
58
Two probability distributions are discussed for the modelling of peak-over-threshold values,
the conditional Weibull distribution (CWD) and the generalised Pareto distribution (GPD).
The CWD is preferred because of its more efficient return levels and its stabilisation in return
levels as function of threshold compared with the GPD.
Four methods of linking return level to each other are described and these are validated in
Section 4.1 and 4.2. Splitting annual into seasonal return levels is preferred, because it
makes use of the homogeneity property of seasonal data (consistency) and the efficiency
property of annual data as well. Furthermore, calibrating directional to omni-directional return
levels is preferred, because omni-directional analysis results in more efficient return levels
than directional analysis while the consistency property is the same as when combining
directional to omni-directional results. Method B follows both ways of linking return levels to
each other and is therefore to prefer.
It appeared that a change in the definitions of seasons and wind direction classes does not
have considerable influence on the return levels resulting from the statistical model (Section
4.4). With respect to climate variations it needs to be considered that the time period
analysed is of importance and that observed geographical patterns corresponding with high
return periods are mainly the result of statistical uncertainties (Section 4.5). Both sections
give no reason though to reconsider the threshold range, the choice of the probability
distribution (CWD) or the method to link the return levels to each other (Method B).
The inefficiency of Approach 2 with the threshold range, the CWD as probability distribution
and Method B as the way of linking results to each other can be reduced even more by
applying the interpolation method that will be discussed in Section 6, 7 and 8.
59
60
5
Alternative extreme value analyses
Besides the statistical model described in Section 3 and validated in Section 4, the literature
suggests some alternative extreme value analyses. A number of these alternatives is
described in this section. Section 5.1 describes the analysis of yearly maxima, Section 5.2
describes Bayesian analysis and some other analysing methods are described in Section
5.3. In these sections the results of the analyses are presented. In Section 5.4 the return
levels resulting from these alternative extreme value analyses are compared with the model
suggested in Section 4.
5.1
Analysis on yearly maxima
Besides peak-over-threshold analysis also an analysis is performed on yearly maxima.
Advantage of the analysis on yearly maxima is that no threshold has to be applied compared
with the statistical model suggested in Section 3 and 4. Two well-known and accepted
probability distributions are applied, concerning the GEV distribution (see Section 3.4, Eq.
(3.8)) and the Gumbel distribution (see Section 3.4, Eq. (3.9)). The parameters of the GEV
distribution are estimated with the maximum likelihood estimation (MLE) procedure and the
parameters of the Gumbel distribution are estimated using linear regression. For these
calculations, the same stations and time series as described in Section 3 are used. Resulting
10,000-year return levels concerning omni-directional data for the seasons 1 (January,
February), 4 (July, August) and 6 (November, December) and for the whole year are listed in
Table 5.1. Also the mean return level, the median and the standard deviation are included in
the table.
Looking at Table 5.1, a number of remarks can be made. The standard deviations
concerning the GEV analysis are higher than the ones concerning the Gumbel analysis. This
is not surprising, because the missing shape parameter θ in the Gumbel distribution results
in less degrees of freedom. But for the season 1 (January, February) and especially the
whole year, the standard deviation concerning the GEV analysis is very high. These high
standard deviations are the result of a number of extremely high 10,000-year return levels
that are not realistic. Most obvious is the value of 182.6 m/s concerning station 343
Rotterdam Geulhaven, but also the value of 117.8 m/s concerning station 285 Huibertgat,
both for the whole year. These too high return levels result in a mean return level that is
rather high compared to the other seasons and to the Gumbel analysis. When looking at the
difference between the mean and the median the same conclusion can be drawn. Due to the
non-realistic high return levels in a number of cases, it can be stated that the GEV
distribution is not appropriate in analysing yearly maxima of hourly averaged wind speed in
the Netherlands.
61
Station
210 Valkenburg
225 IJmuiden
229 Texelhors
235 De Kooy
240 Schiphol
252 K13
260 De Bilt
265 Soesterberg
269 Lelystad
270 Leeuwarden
275 Deelen
277 Lauwersoog
279 Hoogeveen
280 Eelde
285 Huibertgat
290 Twenthe
308 Cadzand
310 Vlissingen
312 Oosterschelde
316 Schaar
320 Goeree
321 Europlatform
331 Tholen
344 Zestienhoven
350 Gilze-Rijen
356 Herwijnen
370 Eindhoven
375 Volkel
380 Beek
Mean
Median
Standard deviation
1
25.9
28.8
31.7
28.9
33.7
39.5
29.7
33.7
62.9
37.2
33.1
38.1
24.6
30.6
35.7
44.8
33.3
29.6
30.7
31.0
27.9
36.3
26.9
28.7
57.3
29.4
37.4
34.1
66.7
55.9
24.2
35.8
33.1
10.9
GEV
4
17.5
25.0
21.0
18.7
26.3
21.6
23.8
23.3
16.5
24.9
22.2
29.6
19.4
15.0
21.7
18.8
27.7
18.8
24.5
21.7
22.8
22.5
23.5
21.4
16.3
18.7
20.1
19.8
24.8
14.1
34.0
21.8
21.7
4.3
6
30.9
29.5
24.3
31.1
26.3
25.3
24.8
23.6
27.0
31.0
26.1
28.8
18.6
25.4
28.2
29.0
24.8
25.8
24.2
24.8
26.8
27.2
25.0
27.8
33.5
32.2
25.4
23.5
26.9
21.9
27.9
26.7
26.3
3.1
Year
29.8
34.5
47.6
35.2
32.0
50.9
27.6
36.8
77.0
76.4
30.4
46.2
21.6
54.6
117.8
48.7
33.8
34.1
32.6
40.4
26.8
62.5
25.3
36.9
182.6
32.9
36.5
38.5
67.8
36.7
25.4
47.7
36.7
32.0
1
39.1
39.2
37.7
40.7
42.8
41.2
34.8
37.6
45.4
43.2
37.0
42.4
34.2
38.8
43.0
38.3
38.1
38.0
36.8
36.4
38.1
44.3
36.9
36.9
44.8
37.0
35.8
41.3
37.0
35.7
34.1
38.9
38.1
3.2
Gumbel
4
6
25.5
39.0
30.7
32.3
27.1
33.7
28.0
36.4
28.3
36.3
34.0
36.1
24.5
32.5
24.4
32.9
20.9
38.8
25.7
35.4
25.7
34.9
27.4
35.0
22.2
29.8
20.0
32.7
28.5
34.7
20.3
34.0
28.9
36.2
27.1
34.8
29.7
34.5
31.2
35.7
33.0
39.8
34.5
33.8
28.2
35.6
25.2
35.9
25.3
39.4
24.9
34.8
25.9
32.2
25.0
36.6
26.4
36.1
19.9
30.2
24.2
34.6
26.5
35.0
25.9
34.9
3.8
2.4
Year
38.9
34.5
38.2
39.3
38.8
36.4
33.5
34.8
40.6
39.9
38.2
38.5
30.2
34.8
37.8
37.1
35.7
34.0
35.0
32.7
36.7
38.2
33.4
34.7
38.8
35.9
34.9
38.4
35.5
36.7
32.9
36.3
36.4
2.5
Table 5.1: 10,000-year return levels obtained by GEV and Gumbel analysis on yearly maxima. It
concerns omni-directional data and the seasons 1 (January, February), 4 (July, August) and 6
(November, December) and the whole year.
From Table 5.1 it can also be noticed that the Gumbel analysis results in more realistic
10,000-year return levels. Furthermore, the geographical pattern that usually exists for low
exceedance frequencies does not fully disappear concerning the 10,000-year return levels
for the seasons 1, 4 and 6 (Figure D.1). This is in contrast with the statistical analysis
discussed in Section 3 and 4 where the pattern disappears for high return periods (Figure
C.3). Possible cause for this property of the Gumbel analysis is the lower statistical
uncertainty, as the Gumbel distribution does not include a shape parameter. As a result,
possible patterns are not veiled by a high statistical uncertainty, with as consequence that
patterns can stay visible even for high return periods. A cause for the noisy geographical
pattern of the high return levels resulting from the suggested statistical model is a possible
different behaviour of the shape parameter at offshore and coastal stations compared with
inland stations. This property concerning the CWD is discussed in more detail in Section 8.
As stated earlier, the Gumbel analysis generates rather realistic 10,000-year return levels
compared with the GEV analysis with no extremely high return levels. Also this is the result
of not including the shape parameter θ. The value of θ determines if there is an upward curve
62
in the tail (θ < 0) or a downward curve in the tail (θ > 0) . The upward curve is expressed by
a lower limit in the return levels and the downward curve by an upper limit. For the Gumbel
analysis the curve is straight and the value of θ equals zero. If there are indications that an
upward or downward curve exist, neglecting the shape parameter will result in inconsistent
(negatively or positively biased) return levels. For this reason, it is analysed how often the
GEV analysis produces an upper limit in return levels (θ > 0) for all wind direction classes
and seasons. Table 5.2 shows the percentage of the 31 stations with an upper limit per wind
direction class and season.
In Table 5.2 it is clearly seen that in a number of cases a percentage of 100% is reached
which means that for all stations an upper limit exists for the corresponding wind direction
class and season. In general, the percentages are considerably higher than 50%, which is an
evident indication that a downward curve is present. This means also that the straight curve
of the Gumbel analysis is not justified, resulting in too high return levels (positively
inconsistent).
Wind direction
class
01
02
03
04
05
06
07
08
09
10
11
12
Omni
1
094
100
100
100
097
097
090
090
087
090
100
100
081
2
087
100
097
097
090
097
094
094
090
097
090
100
094
Season
3
4
094 097
100 094
100 097
090 090
084 094
084 081
058 081
061 094
035 074
074 077
090 087
094 097
039 094
5
094
097
094
100
097
077
097
094
077
097
090
097
068
6
097
100
097
094
097
100
100
090
100
094
097
100
100
Year
084
090
090
077
094
077
084
065
061
068
065
087
042
Table 5.2: Percentage of stations (%) with a positive value for the shape parameter of the GEV
distribution (upper limit) per wind direction class and season.
From Table 5.2 it can also be noticed that the percentages of the wind direction classes for
the whole year and of the seasons for the omni-directional class are in general considerably
lower than the percentages per wind direction class and season. This indicates nonhomogeneity of the whole year and omni-directional data (mixed distributions) or lack of data
concerning the several seasons and wind direction classes. Both features are not justified
according to the conditions required for the classical extreme value theory (Section 3.4). This
theory describes how the maxima of samples of size N from sufficiently long sequences of
independent and identically distributed random variables can be fitted asymptotically (for
large N) to the Fisher-Tippett Type I, II or III distribution. Because the GEV distribution
includes the Fisher-Tippett Type II and III distributions and the Gumbel distribution
corresponds with the Fisher-Tippett Type I distribution, the classical extreme value theory
also applies to the GEV and Gumbel distribution. Because of the non-homogeneity of the
whole year and omni-directional data, the condition of identically distributed random variables
63
is not met. Because of the lack of data concerning seasons and wind direction classes the
condition of large N is also not met. Both indicate that the GEV and Gumbel are not justified
to analyse the yearly maxima.
5.2
Bayesian analysis
Recently, a study has been performed by HKVconsultants (Kalk en van Noortwijk, 2003). This
study evaluates Bayesian analysis of extreme wind speeds in the Netherlands. The results of
the HKV study will be outlined in this section..
Bayesian analysis is based on the theorem of Bayes (Bayes, 1763). Most important
differences of the Bayesian analysis with the ones described in Section 3, 4 and 5.1 is that
parameter uncertainty and distribution type uncertainty are taken into account. The
parameter uncertainty is taken into account by not using the maximum likelihood estimates,
but by integrating the likelihood function. The distribution type uncertainty is taken into
account by using more then one probability distribution and to give weights to the several
distributions.
The analysis has been applied on a set of 10 stations in the Netherlands. These stations are
selected in corporation with HKV, RIKZ and KNMI. They are well scattered over the
Netherlands (Figure 5.1) and the length of their time series is at least 28 years (Figure 5.2).
Figure 5.1: Spatial distribution of stations used in the Bayesian analysis performed by HKVconsultants.
This concerns 10 stations with at least 28 years of data.
64
Figure 5.2: Time series of the 10 stations that are used in the Bayesian analysis performed by
HKVconsultants.
The data of the stations concern omni-directional data and the winter half year (October till
April). Two methods to select data are applied on this dataset. Peak-over-threshold (POT)
values are analysed in Section 5.2.1 and yearly maxima are analysed in Section 5.2.2. The
POT-analysis includes three probability distributions: the CWD, the GPD and the exponential
distribution. The yearly maxima analysis includes nine probability distributions: the
exponential, Rayleigh, normal, lognormal, gamma, Weibull, Gumbel, generalised gamma and
the GEV distribution. The main conclusions from this study are outlined in Section 5.2.3.
5.2.1
Peak-over-threshold values
The first kind of data that has been analysed concerns POT-values. These values have been
selected by making use of the independent maxima selection procedure as discussed in
Section 3.2.1. For the resulting POT-values thresholds are selected above which the data
are fitted to a probability distribution. The threshold selection has been performed with the
help of threshold plots as discussed in Section 3.2.2 and with the help of a subjective
balance between consistency and efficiency. In Table 5.3 it is shown that for the 10 selected
stations the resulting thresholds correspond with exceedance frequencies of about three to
four times per year. In contrast with the method discussed in Section 3, no threshold range is
used.
Station
235 De Kooy
240 Schiphol
250 Terschelling
260 De Bilt
280 Eelde
290 Twenthe
310 Vlissingen
375 Volkel
380 Beek
Threshold
18.0
17.5
18.5
13.5
15.5
13.5
17.0
18.0
13.5
15.0
Exceedance
frequency
3.6
3.0
3.8
3.2
2.7
3.0
3.0
2.8
3.8
2.9
Table 5.3: Chosen thresholds (m/s) and corresponding exceedance frequencies (# per year) in the
analysis of peak-over-threshold values by HKVconsultants
65
Table 5.4 shows return levels for several return periods that are obtained by applying the
Bayesian analysis on the POT-values together with return levels that are obtained by using
the MLE-procedure. The MLE-results are obtained by not taking into account parameter
uncertainty.
Station
235 De Kooy
240 Schiphol
250 Terschelling
260 De Bilt
280 Eelde
290 Twenthe
310 Vlissingen
375 Volkel
380 Beek
Mean
Minimum
Maximum
Maximum likelihood estimation
2
3
4
T=2 T=10 T=10 T=10 T=10
21.9
24.7
28.5
31.9
35.2
21.3
24.3
28.1
31.7
34.9
22.2
24.5
27.1
29.4
31.3
17.0
19.5
22.6
25.2
27.6
19.1
21.9
25.5
28.6
31.4
17.0
20.7
26.9
34.2
42.8
20.2
22.4
25.0
27.2
29.1
21.0
22.7
24.5
25.8
26.9
17.5
20.2
23.5
26.4
29.1
18.2
20.6
23.4
25.9
28.0
19.5
22.1
25.5
28.6
31.6
17.0
19.5
22.6
25.2
26.9
22.2
24.7
28.5
34.2
42.8
T=2
21.9
21.3
22.3
17.1
19.1
17.2
20.2
21.0
17.5
18.3
19.6
17.1
22.3
Bayesian analysis
T=10 T=102 T=103 T=104
24.7
28.6
32.7
37.2
24.3
28.3
32.5
37.0
24.7
27.8
31.2
35.1
19.6
23.0
26.6
30.5
22.0
25.9
30.1
34.9
20.5
25.4
31.0
37.6
22.6
25.5
28.6
32.1
23.0
25.4
27.6
30.0
20.2
23.9
27.9
32.6
20.7
23.9
27.3
31.1
22.2
25.8
29.5
33.8
19.6
23.0
26.6
30.0
24.7
28.6
32.7
37.6
Table 5.4: Return levels obtained by HKVconsultants by analysing peak-over-threshold values with the
MLE-procedure and with the method of Bayes for a number of return periods. The CWD is used as
probability distribution.
Table 5.4 concerns only analysis with the CWD, because the exponential distribution and the
GPD are discarded for different reasons. The exponential distribution is discarded because
of its large weight related to its bad fit, the GPD because of its undesirable behaviour with
large thresholds.
In Section 5.4 the results of Table 5.4 will be discussed and compared with the return levels
obtained from the method described in Section 3.
5.2.2
Yearly maxima
HKV also performed analysis applied on yearly maxima. Nine probability distributions are
considered: the exponential, Rayleigh, normal, lognormal, gamma, Weibull, Gumbel,
generalised gamma and the GEV distribution. For the same reasons as for the GPD, the
GEV distribution is discarded. Return levels based on eight distributions obtained by applying
the Bayesian analysis together with the results of the MLE-procedure are shown in Table 5.5.
The MLE-results are obtained by not taking into account parameter uncertainty and by giving
equals weights to the several probability distributions.
66
Station
235 De Kooy
240 Schiphol
250 Terschelling
260 De Bilt
280 Eelde
290 Twenthe
310 Vlissingen
375 Volkel
380 Beek
Mean
Minimum
Maximum
Maximum likelihood estimation
2
3
4
T=2 T=10 T=10 T=10 T=10
22.0
25.1
28.8
32.5
36.9
21.2
24.5
28.4
32.6
37.6
22.3
24.7
27.4
30.4
34.4
16.6
19.6
23.2
27.3
32.3
19.1
22.1
25.9
30.1
34.8
16.8
26.8
19.9
22.5
25.8
29.5
33.7
20.6
22.8
25.4
27.9
31.0
17.1
20.0
23.4
26.7
30.6
18.0
20.7
23.7
27.0
31.1
19.4
22.9
16.6
19.6
23.2
26.7
30.6
22.3
26.8
28.8
32.6
37.6
T=2
22.1
21.3
22.2
16.7
19.1
16.9
20.0
20.6
17.2
18.0
19.4
16.7
22.2
Bayesian analysis
T=10 T=102 T=103 T=104
25.3
29.3
33.7
39.1
24.6
28.7
33.3
38.7
24.6
27.7
31.2
35.8
19.8
23.7
28.3
33.7
22.2
26.2
30.9
36.2
21.0
26.6
32.9
40.8
22.6
26.0
30.1
34.7
23.0
25.7
28.5
32.0
20.2
23.9
27.9
32.8
20.8
24.1
27.8
32.4
22.4
26.2
30.5
35.6
19.8
23.7
27.8
32.0
25.3
29.3
33.7
40.8
Table 5.5: Return levels obtained by HKVconsultants by analysing yearly maxima with the MLEprocedure and with the method of Bayes for a number of return periods. Eight probability distributions
are used.
In Section 5.4 the results of Table 5.5 will be discussed and compared with the return levels
obtained from the method described in Section 3.
5.2.3
Conclusions
Main conclusions of the study performed by HKVconsultants (Kalk en van Noortwijk, 2003) are
set out below.
In general the following conclusions are drawn:
• With a Bayesian analysis it is possible to take account of statistical uncertainties.
• A Bayesian analysis can be done on the basis of peak-over-threshold values as well as
yearly maxima.
• Return levels increase when statistical uncertainties are taken into account.
• Using Bayes weights, it is possible to discriminate between different probability models
and to quantify how well a distribution fits to the data.
With regard to the peak-over-threshold values the following conclusions are drawn:
• The choice of a threshold is not straightforward, while its value influences the results. As
far as the authors are aware, a widely accepted statistical method for determining a
proper threshold is not yet known in the literature.
• For higher thresholds the GPD shows an undesirable behaviour in the sense that the
return levels increase as a function of the threshold. In fact, the estimated return levels
are too large from a physical point of view.
• The CWD is more robust than the GPD when high thresholds are chosen.
With regard to the yearly maxima the following conclusions are drawn:
• When the number of annual maxima is small, the GEV distribution shows an undesirable
behaviour in the sense that the return levels are too high from a physical point of view.
67
•
Basis on the investigated stations, it is not possible to indicate a probability distribution,
which performs best for all the stations. For different stations different probability
distributions receive a high Bayes weight.
5.3
Other alternative extreme value analyses
In Smits (2001a), other alternative extreme value analyses are discussed. In this section two
analyses are shortly summarized and discussed, while more detailed information is found in
Smits (2001a). These concern the one-step Markov chain model and the combined GEV
model. Section 5.3.1 outlines the one-step Markov chain model and Section 5.3.2 outlines
the combined GEV model.
5.3.1
One-step Markov chain model
The one-step Markov chain model simulates a number of synthetic time series of hourly
mean wind speed values basis on measured time series. The length of each synthetic time
series equals the return period of interest in years. From each time series the maximum is
determined. The average of these maxima of all synthetic times series is the estimate of the
return level with the return period of interest. The simulation is performed by using a
transitional and probability matrix (TPM) that is based on the measurements. This TPM gives
the probabilities of changing from a certain wind speed class at a certain moment to another
wind speed class at the next hour. The width of the wind speed classes is set on 1 m/s. To
transform the wind speed classes into wind speed values a uniform random generator is
used, but for the lowest (width 2 m/s) and highest wind speed classes a shifted exponential
distribution random generator is used. The shifted exponential distribution is a special case
of the CWD and GPD as described in Section 3.3.
Some disadvantages exist about using the one-step Markov chain model as described
above:
• The highest wind speed class is fitted by the shifted exponential distribution. It is
questionable whether this is the most appropriate distribution to use.
• The model includes a highest wind speed class, which contains all wind speeds above a
certain wind speed. This limit can be seen as the threshold like the one in the analysis of
peak-over-threshold values as discussed in Section 3.2.2. The value of the limit is chosen
to be the nearest integer of the 99.5% percentile of all hourly values. The appropriateness
of the height of the 99.5% percentile has not been examined for the wind speed time
series that are used. For this reason, it is not clear if there is some inconsistency
(threshold too low) or some inefficiency (threshold too high) in the return levels.
Furthermore, the usage of only one threshold instead of a threshold range implies rather
inefficient return levels as discussed in Section 3.2.2.
• Besides the wind speed, also information with respect to season and wind direction is
needed. For this purpose, TPM’s for each season have to be constructed what is easily
done. However, besides wind speed also wind directions has to be simulated. This
68
extension makes the model much more complex, while only a few procedures are given
in literature about this complexity.
The first disadvantage mentioned is equivalent to the choice of the probability distribution as
discussed in Section 3.3, while the second disadvantage is equivalent to the choice of
threshold as discussed in Section 3.2. Both disadvantages possibly can be compensated
when they are treated in the same way as in Approach 2. The third disadvantage, however,
is not easy to compensate. For this reason has been decided not to elaborate the one-step
Markov chain model.
5.3.2
Combined GEV model
The alterative models discussed in Section 5.1, 5.2 and 5.3.1 did not produce return levels
per season or wind direction class. However, the model discussed in Section 5.1 with the
GEV as probability distribution has also been applied on separate seasons and wind
direction classes. These return levels are combined to annual and omni-directional return
levels to keep the linking properties between the return levels. The combination has been
done by using the procedures described in Section 3.5.5 (combining seasonal return levels
to annual return levels) and Section 3.5.4 (combining directional return levels to omnidirectional return levels). This so called combined GEV model results in very high, nonrealistic 10,000-year return levels (up to 226.3 m/s). Because the way of combining seasonal
and directional results is performed without smoothing algorithms, the resulting annual and
omni-directional return levels are positively biased, as discussed in Section 3.5.6. Together
with the very inefficient return levels obtained with the GEV distribution (Section 5.1), the
resulting annual and omni-directional return levels are severely positively biased. Even when
Method B (Section 3.5.6) is followed to keep the linking properties between the return levels,
the resulting return levels are not satisfactory because of the very inefficient return levels that
are obtained when the GEV distribution is used. For these reasons has been decided also
not to elaborate the combined GEV model.
5.4
Conclusions
Section 3 and Section 4 discussed the analysis of all hourly wind speed values (Approach 1)
and the analysis of peak-over-threshold wind speed values (Approach 2). It was stated that
Approach 2 is preferable with the conditional Weibull distribution (CWD) as probability
distribution and with Method B as the method of linking return levels to each other.
Alternative extreme value analyses are described in Section 5. From these alternative
models the one-step Markov chain (Section 5.3.1) and the combined GEV model (Section
5.3.2) are already discussed in Smits (2001a). The one-step Markov chain model is not
preferable to use, because of the complexity concerning including wind direction classes and
the few information about this subject in the literature. The combined GEV model is also not
preferable, because of the highly inefficient return levels that are obtained with the GEV
69
distribution together with the inconsistency property (positively biased) when combining
directional and seasonal return levels to omni-directional annual return levels.
A summary of the alternative extreme value models discussed in Section 5.1 (analysis on
yearly maxima) and Section 5.2 (Bayesian analysis by HKV) together with the proposed
POT-model discussed in Section 3 and 4 (with the CWD and Method B) is given in Table 5.6.
In this table the 10,000-year return levels are averaged over the stations that are analysed by
HKV (Figure 5.2) without station 250 Terschelling. For “HKV, Yearly maxima, MLE” also
station 290 Twenthe is omitted.
Method
POT, Method B, CWD
Yearly maxima, GEV
Yearly maxima, Gumbel
HKV, POT, MLE
HKV, POT, Bayes
HKV, Yearly maxima, MLE
HKV, Yearly maxima, Bayes
10,000 year
return level
31.8
35.5
35.6
31.7
33.7
33.5
35.6
Table 5.6: 10,000-year return levels in m/s averaged over a number of stations following several
models of extreme value analysis. The stations concern the same set of stations as used by HKV with
omitting of 250 Terschelling. For “HKV, Yearly maxima, MLE” also 290 Twenthe is omitted.
Table 5.6 shows that the 10,000-year return levels of both analyses of yearly maxima
(“Yearly maxima, GEV” and “Yearly maxima, Gumbel”) are rather high. Section 5.1
discussed these analyses and concluded that the GEV analysis produces very inefficient
return levels. The Gumbel analysis produces positively biased return levels because of
omitting the shape parameter. Therefore, the GEV and Gumbel analysis of yearly maxima
are not to prefer. Furthermore, it is stated in Section 5.1 that following the classical extreme
value theory, the GEV distribution and the Gumbel distribution are not justified to analyse the
yearly maxima when seasons and wind direction classes are taken into account.
In Table 5.6 also 10,000-year return levels obtained with the suggested method in Section 3
can be compared with the results of HKV.
The difference between “POT, Method B, CWD” and “HKV, POT, MLE” is marginal, because
both analyses are based on the conditional Weibull distribution and the maximum likelihood
estimation procedure. The marginal difference is caused by a different set of data used
(whole year against winter half year), different thresholds (threshold range against a single
threshold) and different methods of linking the results to each other (Method B against
Method 0). These differences weigh less severe than the similarities between the analyses.
The difference between the “HKV, POT, MLE”-method and the “HKV, POT, Bayes”-method
is caused by the fact that in the second method the statistical parameter uncertainty is taken
into account. For this reason, the 10,000-year return level averaged over the stations
increases with 2 m/s.
The “HKV, Yearly maxima, MLE”-method is based on yearly maxima instead of peak-overthreshold values. Again, the maximum likelihood estimate procedure is used, so no statistical
70
uncertainties are taken into account. Furthermore, eight probability distributions are used
instead of only one in the analysis of peak-over-threshold values. This analysis results in a
10,000-year return level averaged over the stations that is about 2 m/s higher than the same
analysis based on peak-over-threshold values (“HKV, POT, MLE”).
The “HKV, Yearly maxima, Bayes”-method includes besides statistical parameter
uncertainties also statistical distribution uncertainties (because of the multiple probability
distributions). This analysis results in a 10,000-year return level averaged over the stations
that is again about 2 m/s higher than the same analysis based on peak-over-threshold values
(HKV, POT, Bayes”).
The analyses performed by HKV are only applied on data concerning the winter half year
and without regarding wind direction. Condition of the extreme value analysis within the
KNMI-HYDRA project is, however, to generate also return levels or exceedance frequencies
per season and per wind direction class. It is unclear how this splitting affects seasonal and
directional analyses by HKV.
Besides statistical analysis, also a study is performed about the existing of a possible
physical upper limit in the wind speed (Ettema, 2003). If such an upper limit exists, the
statistical method should consider this property by forcing the extreme return levels of wind
speed to be lower than the upper limit. The study concluded that even when an upper limit
exists, its level lies substantially higher than the values obtained by the statistical method
described in Section 3. Therefore, the statistical method does not need to be modified
considering a possible physical upper limit in the wind speed.
Furthermore, recently an extreme value analysis concerning surge levels is performed by
Van den Brink et al. (2003). Ensemble simulations were generated with the KNMI General
Circulation Model ECBilt and these were analysed with the GEV distribution. Also this study
did not give any indications for modifying the statistical method of extreme value analysis
described in Section 3.
71
72
6 Interpolation of surface wind
In the Netherlands wind speed and direction are measured at several locations as described
in Section 2. These locations often do not correspond to the locations where the wind
climatology is required for the calculation of the hydraulic conditions by RIKZ and RIZA.
Therefore a model is needed that interpolates wind in a physically correct way. The
interpolation model presented here comprises a transformation model, interpolation method
and a roughness footprint method. In Section 6.1 the physical processes in the atmosphere
that determine the wind speed profiles are described. In Section 6.2 the transformation from
one place to another with use of a two-layer model is described. In Section 6.3 an
interpolation method, Barnes’ technique, applied to the wind speed is discussed. The
footprint method to assess roughness lengths is described in Section 6.4. The validation of
the interpolation method as entirety will be discussed in Section 7.
6.1
The planetary boundary-layer
Wind in the atmosphere is the result of large-scale temperature and pressure differences.
Synoptic weather systems generate high wind speeds over the whole depth of the
atmosphere. For the major part these winds are not directly influenced by the presence of a
lower boundary to the atmosphere, the surface. Only in the lowest layer of the atmosphere
the presence of the surface in noticeable by a diurnal cycle in temperature and friction
induced by the surface. The depth of this layer may be in the order of 102–103 m. This layer
is called the planetary boundary layer (PBL). In the PBL the wind turns and retards with
decreasing height. Surface friction will always slow down the wind. The rougher the surface,
the stronger the wind is decelerated.
Vertical temperature differences in the PBL will determine the magnitude of the vertical
momentum exchange. Strong convection, caused by surface heating, will enhance the
exchange, while surface cooling will result in a stable stratification where vertical fluxes are
depressed. With strong convection the vertical momentum exchange is large. This results in
relatively high wind speeds at the surface and relative low wind speeds at higher altitudes.
Under these unstable conditions vertical wind speed gradients are small. In stable
stratification the influence of surface friction is confined to a small region near the surface.
This results in a shallow layer of low wind speed near the surface above which the wind
speed increases strongly with height.
The influence of vertical temperature differences in the PBL on the wind speed and direction
is illustrated in Figure E.1 en Figure E.2. Here the average wind speed and direction for
different heights in the surface layer are plotted as a function of the time of day during the
month May. Data are taken at the Cabauw research tower of KNMI, located in the
Netherlands near the village Schoonhoven (Van Ulden & Wieringa, 1996). Among other
parameters, wind speed and direction are measured at this tower at several heights up to
200 m. Figure E.1 shows the diurnal cycle of the average wind speed. As explained above
73
the wind speed close to the surface has its maximum at mid day during convective
conditions. This is accompanied by a minimum in wind speed at higher levels. During night
time the surface wind is lower due to stable stratification, however, at higher levels the wind
speed is higher.
In high wind speed conditions turbulence in the PBL is mainly caused by friction related to
surface roughness. Convection plays a minor role. The wind speed profile called “neutral” in
this case.
Figure E.2 shows the associated wind direction variations ( DD200 m − DDz ) with z for different
heights ( z = 10, 20, 40, 80 and 140 m). During daytime, with strong vertical mixing, there is
no change in wind direction with height. During night time, however, the wind backs strongly
with decreasing height.
6.2
Transformation model
The surrounding of a station location influences directly the wind measurements. The surface
area that influences the measurements at a certain location and height is called the source
area or footprint area. The dimensions of this area are determined by the height of the
measurement and the stability of the atmosphere. The lower the measuring level, the
smaller footprint. So the surface wind is strongly influenced by the local roughness. Because
of that, large differences in wind speed can be found over short horizontal distances.
However, the source area of the roughness increases in magnitude with height. Over
heterogeneous terrain the average roughness will converge to a spatially averaged value.
This implies that even over regions with heterogeneous roughness the large-scale wind
speed, the wind at the top of the PBL, will still be rather uniform. This forms the backbone of
the interpolation used in this project. The wind measured at one location can be transformed
to that at another location by assuming the wind at the top of the PBL is nearly the same. If
the roughness of the two sites is known there are models to link the surface wind speed to
the wind speed at the PBL-height and vice versa.
This transformation is an example of “regionalisation”. For wind speed, examples can be
found in Wieringa (1986, henceforth W86) and Bergström et al. (1988). Examples of
regionalisation of other meteorological parameters in non-neutral conditions can be found in
De Rooy (1995) and Hutjes (1996).
In this project we will adopt the transformation model from Wieringa (1986, W86). The model
of W86 comprises two layers. In the lower layer, the surface layer, Monin-Obukhov theory is
used. In this layer a local roughness parameter with a small footprint area is used. In the
second layer, the Ekman layer, geostrophic resistance laws apply. The footprint area of the
roughness parameters in this layer is much larger, representing a large-scale average. The
interface of the layers is called the ‘blending height’ ( zbh ). Local roughness variations have
blended into the large-scale (meso-scale) roughness.
74
The wind speed profile in the surface layer is described in Section 6.2.1. Section 6.2.2
explains the concept of potential wind speed. The wind in the Ekman layer is described in
Section 6.2.3. The influence of the height of the blending height on the wind on top of the
Ekman layer is discussed in Section 6.2.4.
To simulate the wind correctly it is important to handle multiple roughness transitions
accurately. In Section 6.2.5 different models are compared with the two-layer model with
regard to the adjustment of the wind speed to a new surface roughness.
6.2.1
Surface layer
The surface layer is defined as a thin layer close to the surface where there no storage or
generation of momentum, or any other entity. This implies that fluxes in the surface layer are
constant with height. The rotation of the Earth and hence the Coriolis force does not play a
role in this layer. This implies that the wind does not turn with height in the surface layer.
According to Monin-Obukhov theory the average wind speed under neutral conditions is a
logarithmic function of height (Obukhov, 1971; Businger et al. 1971, Tennekes, 1973):
U=
u*  z
ln
κ  z0

 .

(6.1)
Here U is the wind speed [m/s]; u * is the friction velocity [m/s], related to the momentum flux
2
( u * = −u ' w ' , u ' and w ' are turbulent fluctuations of the horizontal and vertical wind speed,
respectively); κ is the von Kármán constant ( κ = 0.4 , Frenzen et al, 1995); z is the height
[m]; and z0 is the local roughness length [m]. In surface layers over homogeneous terrain z0
is well defined and u * is constant with height.
Plotting the neutral wind speed profile versus the logarithm of height gives a straight line. The
roughness length is the height where the downwards extrapolated wind speed would become
zero. However, the logarithmic wind speed profile is not valid that close to the surface. The
lower application limit of (6.1) is 20 ⋅ z0 . The assumption of constant flux imposes an upper
limit on the applicability of (6.1). In high wind speed conditions and in case of strong
convection the constant flux layer can be up to 100–200 m thick. During stable night time
conditions it may be less than 50 m thick.
75
6.2.2
Potential wind speed
In the KNMI-HYDRA project wind data is corrected for wind direction- and time-dependent
variations in exposure of the anemometer. The followed procedure is illustrated in Figure E.3.
From the measured wind speed the wind speed at the blending height is computed. From
(6.1) the ratio of the wind speed at two heights, z1 and z2, in the surface layer can be
expressed as:
U (z2 ) ln(z2 z0 )
=
.
(6.2)
U (z1 ) ln(z1 z0 )
The wind at the blending height will be called the mesowind (U meso ). We will consider a
hypothetical site meeting the WMO requirements: measuring height = 10 m; roughness
length = 0.03 m in all directions. From the mesowind the wind over this hypothetical site can
be computed using (6.2) as well. This wind speed is by definition the potential wind speed
(U p ). With the blending height at 60 m the relation between the potential wind and the
mesowind becomes:
ln(60 0.03 )
U meso =
⋅ U p = 1.31 ⋅ U p .
(6.3)
ln(10 0.03 )
The potential wind speed can be computed from the measured wind speed U (z ) at height z
over the local roughness z0 :
Up =
ln(zbh z0 ) 1
⋅
⋅ U (z ) .
ln(z z0 ) 1.31
(6.4)
The local roughness length is direction dependent and can evolve in time. It can be derived
from gustiness analysis (Wieringa, 1976; Verkaik, 2000).
6.2.3
Ekman layer
In the Ekman layer the Coriolis force becomes important. As result the wind direction backs
with height in this layer. This results in a component of the wind speed that is perpendicular
to the surface wind speed. For the parallel and perpendicular component the geostrophic
drag relations apply (Wieringa, 1983):
κ
 zf
U − U macro
= ln
u* m
 u* m
κ
Vmacro
= −B .
u* m

 + A ,

(6.5)
(6.6)
Here u * m [m/s] is the friction velocity at blending height, A en B [-] are stability dependent
parameters ( A = 1.9 and B = 4.5 in neutral conditions). The Coriolis parameter f [Hz]
equals 2Ω sin ϕ = 1.1 ⋅ 10 −4 Hz, where Ω is the angular velocity of the Earth's rotation and ϕ is
76
the latitude. U macro and Vmacro [m/s] are the components of the macrowind. U macro is
parallel to the surface wind, Vmacro is perpendicular to U macro . With U macro in east direction,
Vmacro points north on the Northern Hemisphere.
Matching the surface and Ekman layer at the blending height one can deduce:
U macro =
  u* m 

 − A ,
ln
  fz0 

u
= −B * m .
κ
u* m
κ
Vmacro
(6.7)
(6.8)
In the Ekman layer a large-scale, meso-roughness ( z0m ) is used, having a large footprint
area. Using these relations it is possible to estimate the macrowind from the surface wind if
the roughness length is known. When potential wind speed is used as input, the mesowind is
computed using (6.3). Inversion of (6.1) yields
u* m =
κU meso
ln(zbh z0 m )
(6.9)
for the friction velocity at the blending height. From this friction velocity and z0m the
macrowind follows from (6.7) and (6.8).
In Figure E.4 the relation between wind speed and direction at surface and at macro level is
plotted as function of the roughness length. Here the planetary boundary layer is
homogeneous in roughness: the roughness lengths and friction velocity in the surface layer
and Ekman are equal. When the roughness length increases the macrowind speed increases
and the wind direction at macro level veers more with regard to the surface wind direction.
The rate of the wind speed increase is increases with roughness length. So changes in
roughness lengths do not have much impact on the wind speed at the top of the Ekman layer
if the roughness is small ( < 0.1 m). These changes have only influence on the macrowind
direction.
6.2.4
Impact of blending height on macrowind
The blending height is a function of the horizontal extent of the surface heterogeneities.
When changes in roughness occur over short distances the blending height will be small. As
rule of thumb the horizontal length scale of the roughness heterogeneity is seven times as
large as the blending height (Claussen, 1989). Wieringa (1986) set the blending height at 60
m. This corresponds to a length scale of ~400 m, which seem reasonable for the landscape
of the Netherlands.
When the local and meso-roughness lengths are not equal, the macrowind speed depends
on the blending height. The blending height divides the PBL into the surface layer with the
local roughness length, and the Ekman layer with a meso-roughness length. In the
77
transformation of the surface wind to the macrowind, more weight can be given to the local
roughness length by increasing the blending height. This may be an important feature when
modelling the wind speed downwind of large-scale roughness change, like the coastal zone
(see also section 6.2.5).
In Figure E.5 the macrowind is plotted as function of the blending height. The 10-m wind
speed is fixed at 10 m/s and the local roughness length at 0.1 m. A number of curves are
given for a range of meso-roughness lengths (z0m = 0.0001 - 0.5 m). Figure E.5 shows that if
the local roughness is larger than the meso-roughness the macrowind increases with the
blending height as explained above. If the meso-roughness is larger than the local roughness
length, the effect of the blending is reversed and an increase of the blending height leads to
a decrease in macrowind. However, from Figure E.5 it is clear that the macrowind is not very
sensitive to the blending height.
6.2.5
IBL development in the two-layer model
After a roughness transition an internal boundary layer (IBL) will develop. The change in
roughness will affect the layer close to the surface at first. Then the change in flow properties
will diffuse upwards through the surface. This is a slow process, driven by the flow itself. The
growth rate of IBLs is one tenth of the wind speed, as rule of thumb. Complete adjustment to
the new surface will be confined to a layer that comprises only the lowest 10% of the IBL.
The structure of the IBL and the new equilibrium layer is depicted in Figure E.6. Growth rate
formulae from Panofsky and Dutton (1984) are used here (see also Walmsley, 1989).
At some distance downwind the roughness change the wind speed profile may look like that
in Figure E.7. Here a simplified profile after a smooth-to-rough transition is plotted. Above the
IBL-height the profile remains undisturbed. Below the IBL-height the profile is adapted to the
new surface. For both profiles applies that when the profiles are extrapolated downward to
the height at which the wind speed is zero, this height equals the roughness length of the
corresponding source area. For the upper profile this is the roughness length upstream of the
transition, and the roughness downstream the transition for the lower profile. The knee in the
profile climbs with growing fetch.
IBL-models require well-defined roughness transitions, one upstream value and one
downstream value. In many parts of the world multiple transitions occur at short fetches.
Therefore, the validation of IBL-models has mainly been restricted to short fetches.
Experiments with multiple IBLs are rare (Deaves, 1981). Some models indicate that the
second IBL grows faster in case the surface roughness is returning to its initial value (Duijm,
1983). Eventually multiple IBLs will diffuse by turbulent mixing. This process is not described
in most IBL-models. In these models the number of IBLs can increase only. Modelling the
wind speed profile over large area then leads to a huge number of IBLs. As a result major
simplifications to the roughness map are necessary when using IBL-models.
78
The two-layer model does not include an IBL-model. However, after a roughness transition
the local- and the meso-roughness used will be different as a result of the different source
area for their roughness. This way the two-layer model reproduces the typical IBL wind
speed profile as in Figure E.7. However, the knee in the profile is fixed at the mesolevel,
while the roughness lengths associated with the two parts of the profile are constantly
changing with fetch. In the simple IBL-model of Figure E.7 the knee in the profile, the IBLheight, climbs with fetch, while the roughness length remains constant.
Now we will compare the development of the 10-m wind from the two-layer model with that of
IBL-models. We consider the sea–land transition where the land roughness length is 0.1 m.
We compare W86 with several IBL-models: K2000 (Kudryavtsev et al., 2000), WAsP (Troen
et al, 1989), Coast (Van Wijk et al., 1990), and a small-scale model by Townsend (1965). For
W86 and Townsend's model the roughness length of the sea is fixed at 0.001 m, the others
models compute the drag of the sea from the wind speed. K2000 and Coast are used in
near-neutral mode, the other models are neutral by themselves. The wind at 10 m over sea
is fixed at 10 m/s. The results are plotted in Figure E.8 and Figure E.9. Figure E.8shows the
sea–land transition, Figure E.9 the land–sea transition where the wind speed over land is
fixed at 7 m/s. Coast is developed for onshore flow only.
Apart from Townsend's model, all models show a similar adjustment of the 10-m wind to the
new surface roughness. The rate of adjustment, both at small and large fetches, in the twolayer model depends on the length scales chosen in the footprint approximation for the localand meso-roughness and the mesolevel. Details about this approximation are given in
Section 6.4.4. The footprint length scale for the meso-roughness used here is 10 km and for
the local roughness it is 600 m. With these length scales the two-layer adjusts more slowly
than the other models. From the other models Wasp adjusts fastest and the Coast model
adjust slowest. A close resemblance with the Coast model can be obtained when the
footprint is set at 8 km. In the land–sea transition the two-layer model adjust slower than the
other models.
The footprint length scales could be tuned such that the two-layer model matches closely
with some of the IBL-models. However, we will see that this will lead to reduced accuracy of
the interpolation method in the simulations.
6.3
Barnes’ interpolation method
In this section we will introduce the interpolation method by Barnes as described in Barnes
(1964) and Krishnamurti & Bounoua (1996). Barnes’ technique consists of multiple scans
using a weighted linear sum of the observations within a defined region of influence. As
observations we will use the eastwards ( u ) and northwards ( v ) component of the
macrowind speed, respectively, and interpolate these components separately.
79
The wind speed components are computed from the macrowind estimates at the station
locations accordingly:
u = U macro ⋅ cos(270 − DDmacro ) ,
(6.10)
v = U macro ⋅ sin(270 − DDmacro ) .
(6.11)
Here DDmacro is the meteorological wind direction at macro level [degrees]. It ranges from
zero for northern wind to 180° for southern wind clockwise, and so on.
The macrowind, computed from the potential wind at the stations and the two-layer model, is
used as input. In Figure E.10 an example of an input field is given. It represents the
macrowind at May 28, 2000, 15:00 GMT.
The interpolation algorithm used is described in Section 6.3.1. The parameters in this
algorithm influence the resulting wind field. The impact on the results of two parameters, the
radius of influence and number of iterations, are described in the Sections 6.3.2.
6.3.1
Interpolation algorithm
The interpolation algorithm is described in Barnes (1964) and Krishnamurti and Bounoua
(1996). It yields field values at a regular grid from input observations that can be irregularly
distributed. It comprises a convergent weighted-averaging interpolation scheme which can
be used to obtain any desired amount of detail in the analysis of a set of randomly spaced
data.
In the present application the input field is the north- or eastward component of the wind
speed at the station locations. The regular output field is defined on a rectangular grid in local
coordinates. It is defined within the domain of the roughness map, starting with an offset from
the lower left corner. The distance between grid points is set at 10 km and the offset is set at
half this distance: 5 km.
The first guess of the wind field, U ij e1 , at the grid point (i , j ) is computed from:
N
U ij e1 =
∑W (d s ,R ) ⋅ U so
s =1
N
∑W (d s ,R )
.
(6.12)
s =1
Here N [-] is the number of stations; d [m] is the distance between the observation point s
and the grid point; R [m] is the radius of influence; U so [m/s] is the observed wind speed at
station s ; W is the weighting function defined as:
 − 4d 2 
,
W (d , R ) = exp
 R2 


80
(6.13)
As it is clear from (6.13), the weighting function will give the strongest weight to the
observations that are nearby the grid point and it decreases quickly with distance. For
distances larger than R , the weighting function W is less than 0.02. The weight function is
explicitly related to the density of the observations, which determines the ultimate resolution
obtainable in the analysis.
Next the field values at the observation locations, U seν , are computed from the grid values,
U ijν , on the ν -th iteration. These values are computed as the weighted sum of the nearest 5
grid point values ( N po int =5):
N po int
U seν =
∑ W (d s ,R ) ⋅ U ijν
s =1
N po int
.
(6.14)
∑W (d s ,R )
s =1
From these estimates and the observed values a discrepancy field can be computed:
∆νs = U so − U seν .
(6.15)
This field is used as a new input field and added to the first guess:
N
U ije (ν +1) = U ijeν +
∑W (d s ,R ) ⋅ ∆νs
s =1
N
∑W (d s ,R )
.
(6.16)
s =1
The maximum number of iterations is specified ( ν max = N pass = 5).
6.3.2
Impact of radius of influence and number of iterations
From (6.13) it is seen that the smaller the radius of influence R , the strongest weight is given
to the stations nearby and the faster the scheme converges to show the smaller structures in
the macrowind. The effect of R on the fitted wind field will be illustrated using the wind field
in a storm situation: May 28, 2000; 15:00 hour GMT. The macro wind field, estimated at the
station location serves as input field (Figure E.11). When a small value for R is chosen (20
km), the fitted field at the grid points is mainly determined by the macro wind at the nearest
station. The irregularities in the input field will also be present in the output field (Figure
E.11). With increasing R the fitted output field becomes smoother and smoother (Figure E.
12 and Figure E.13).
81
6.4
Roughness map
For the calculation of the wind speed and direction at the top of the surface and Ekman layer
the roughness length of that layer is needed. Roughness information can be assessed from a
land-use map, because every land-use class has its typical roughness length. Besides
roughness elements on the surface also surface elevation has influence on the roughness.
The main part of the Netherlands is rather flat, but in some parts orography may be of
influence. Therefore from the land-use map and the information of the surface elevation, two
roughness lengths are computed that are combined to one roughness length. This is done by
summing the corresponding drag coefficients.
As mentioned before the footprint area is the surface area that influences the measurements.
With use of a simple footprint method roughness lengths experienced at a certain height and
location can be computed from the land-use map. The presence of water in the footprint
leads to a complication since the roughness of water is a function of the wind speed.
Therefore a different procedure of averaging roughness length is used when a part of the
footprint area covers water.
In the footprint approximation a choice has to be made with regard to length scales for local
and large-scale roughness, z0 ,map and z0 m ,map respectively. Therefore the local roughness
derived from gustiness measurements, z0 ,gust , is compared to the local roughness length
from the land-use map. For the mesoscale roughness lengths no comparison with
measurements is possible due to the lack of wind profile measurements at high altitudes. For
validation we use the results of the two-layer model at the station locations with different
settings for the large-scale length scale (see Section 7.3).
Here the production of the roughness map used in this project will be described. In Section
6.4.1 the available land-use data is described and in Section 6.4.2 the available information
on surface elevation. In Section 6.4.3 a method to average roughness lengths is described.
In Section 6.4.4 a simple footprint approximation is described to compute the area-averaged
roughness length for both layers for a certain location. In Section 6.4.5 the calculation of the
drag coefficient for water surfaces is described. In Section 6.4.6 the comparison between
local roughness lengths from the gustiness analysis and the land-use map is made, which
result in an optimal choice for the local length scale in the footprint approximation. In Section
6.4.7 the local roughness from the land-use map is compared with the gustiness roughness
length at the station locations.
82
6.4.1
Spatial data on land-use
The surface roughness is assessed from a land-use map of the Alterra1 (LGN3+, De Wit et
al., 1999; Thunnissen and De Wit, 2000). This is a raster file covering the whole of the
Netherlands with a resolution of 25 m. To each pixel a land-use class is assigned. A number
of 40 classes are used in LGN3+. We assigned a roughness length to each class (Wieringa,
1993).
ID
0
1
2
3
4
5
6
7
8
9
10
11
12
16
17
18
19
20
21
22
23
24
z0 (m) Class name
0.03
0.03
0.17
0.07
0.07
0.16
0.07
0.15
0.1
0.39
0.07
0.75
0.75
0.001
0.001
1.6
0.5
1.1
1.1
2.0
0.03
0.001
no data
Grass
Maize
potatoes
Beets
Cereals
other agricultural crops
foreign land
greenhouses
orchards
bulb cultivation
deciduous forest
coniferous forest
fresh water
salt water
continuous urban area
built-up in rural area
deciduous forest in urban area
coniferous forest in urban area
built-up area with dense forest
Grass in built-up area
bare soil in built-up area
ID z0 (m) Class name
25
26
27
28
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
0.1
0.5
0.0003
0.1
0.0002
0.0003
0.02
0.06
0.04
0.0003
0.03
0.04
0.06
0.06
0.75
0.03
0.1
0.75
0.07
0.03
0.001
main roads and railways
buildings in rural area
Runways
parking lots
salt marshes
beaches and dunes
sparsely vegetated dunes
vegetated dunes
heath lands in dune areas
shifting sands
heath lands
heath lands with minor grass influence
heath lands with major grass influence
raised bogs
forest in raised bogs
miscellaneous swamp vegetation
reed swamp
forest in swamp areas
swampy pastures in peat areas
herbaceous vegetation
bare soil in natural areas
Table 6.1: Land use classes and roughness lengths in LGN3+.
In Table 6.1 the land-use classes and the assigned roughness lengths are listed. Outside the
Netherlands a uniform roughness of 0.15 m is adopted. No distinction in winter and summer
roughness length for agricultural land is made. Two classes were added to LGN3+: runways
and parking lots. This was done because in LGN3+ the concrete runways were added to the
class built-up area, resulting in erroneous and way too high roughness values in airport
areas, especially close to many anemometer locations. The runways were identified by hand
and added to the new class with low roughness. The same applies to large parking lots in the
Amsterdam Airport Schiphol area. After this correction the roughness map of the Schiphol
area must still be regarded as unreliable however, the large-scale roughness is still strongly
overestimated.
1
http://cgi.girs.wageningen-ur.nl/cgi/projects/lgn/
83
6.4.2
Surface elevation
Surface elevation is assessed from the GTOPO302 database. In this database the surface
elevation is given at a resolution of (1/120)° (≅ 1 km). This grid has been interpolated using
spline and exported into new grid on a 500-m resolution in local (X,Y)-coordinates. Height
differences are assessed by comparing the height at point (X,Y) with the neighbouring points
on the 500-m grid.
The roughness length due to orography z0H is computed from
z 0 H = 0.2 ⋅
∆H 2
,
L
(6.17)
where ∆H is the height difference over distance L (Agterberg & Wieringa, 1989). The
resolution of GTOPO30 is not enough to resolve small hills, dikes, etc. In the coming years a
high-resolution elevation map of the Netherlands will become available. Then this part of the
roughness map asks for revision.
It should also be noted that although orography adds to the roughness on large scales, on
small scales orography may induce acceleration of wind and complex circulation patterns
around hills (Jackson & Hunt, 1975; Jacobs, 1984). In the two-layer model these effects are
not incorporated. This may lead to very local errors in the wind field in the vicinity of dikes
and hills. So measurements from locations where these phenomena can be expected need
to be interpreted with care (for example station 380 Beek).
6.4.3
Area-averaged surface roughness
Roughness lengths can not be averaged directly. The logarithm of the roughness length can
be averaged, however. From the physical point of view this corresponds to averaging the
wind speed gradient or friction velocity u * . In this project the effective roughness is computed
from the average drag coefficient at the blending height (Claussen, 1990). This method was
also used by W86. In comparison to the log-averaging this method gives stronger weight to
the larger roughness in the averaging domain. From the physical point of view this
corresponds to averaging the momentum flux u *2 .
The drag coefficient, Cd , is defined as
2
u 
Cd ≡  *  ,
U 
and using (6.1) it can be expressed as
 κ 
Cd = 

 ln(z z0 ) 
2
http://edcdaac.usgs.gov/gtopo30/gtopo30.html
84
(6.18)
2
(6.19)
The roughness due to orography can also be expressed as a drag coefficient by this
equation and this drag can be added to the ‘skin drag'. (6.19) can be inverted the compute
the roughness length from the total drag.
6.4.4
Footprint approximation
The footprint is the surface area contributing to the flux or concentration of an atmospheric
entity at a certain point. The footprint depends on the entity under consideration, the
atmospheric stability and of measuring height (Schmid, 1994; Horst & Weil, 1992; Horst,
1999). In Figure E.14 an example is given. The terrain here consists of water on the east and
land on the west. At some distance inland we imagine a measuring tower with sensors at two
heights. The wind is onshore. The footprint of the lower sensor is small and is close to the
tower. This is indicated by the ellipsoids at the surface, partially over land and partially over
water. The inner ellipsoid could represent the area which determines 50% of the measured
entity by this sensor, the outer ellipsoid represents 90% area. All numbers and scale ratios in
this example are fictitious.
Here we will make a simple approximation to the footprint using the following procedure. The
area surrounding the evaluation point is split into 72 sectors of 5° wide. For each pixel i in
sector j the drag coefficient at the blending height is determined from the equation.
2
Cd ,i


κ
=
 .
 ln (zbh z0 ,i )
(6.20)
The roughness length is determined from Table 6.1. The drag coefficient of water is wind
speed dependent and will not be added to the total drag at this stage.
A weighted average of Cd, i is computed using the weight function
W (x i , D ) = e − xi
D
,
(6.21)
where x i is the distance from the source area to evaluation point i . In Figure E.15 a plot is
given of the weighting function with D = 3 km. The length scale D determines the extent of
the footprint. So the footprint has the shape of a wedge. To the pixels in the area that are
nearest to the evaluation point (6.21) gives the largest weight. However, the wedge is also
very narrow at short distances. The most significant contribution is given by the pixels at a
distance where the weighted surface reaches a maximum. The weighted surface, S , can be
expressed as:
(
dS ∝ d x ⋅ e − x D
It reaches a maximum where
[
)
(6.22)
]
dS
d
=
x ⋅ e− x D = 0 ⇒
dx dx
x  −x D

=0⇒
1 −  ⋅ e
D

x=D
85
(6.23)
So the major contribution to the footprint comes from the roughness at a distance D . Studies
on internal boundary layer growth indicate that flow properties like roughness at height z
response to surface features up to 10 or 100 times their own height, so up to 100 ⋅ z (Bradley,
1968; Rao et al., 1974; Duijm, 1983). For the wind speed measurements at 10-m height this
implies that D is in the order of 1 km. As reference for the local roughness lengths derived
from the map, the roughness lengths derived from gustiness analysis of the measuring
stations of KNMI are available. A maximum correlation between the roughness lengths was
found with D = 600 m (see section 6.4.6).
For the large scale roughness for the Ekman layer D may be several kilometres, but there is
hardly any reference for this length scale. It will be part of the investigations in this project.
Agterberg & Wieringa (1989) averaged the meso-roughness over blocks of (5 km)2.
The average drag of sector j coefficient, C' d ,i , is given by:
Cd′ , j
∑ W (x i , D ) ⋅ C d , i
= i
∑ W (x i , D )
(6.24)
i
Also the surface fraction covered by water, ( fw′ ,i ) is determined. Only the source area up to a
distance of 3 × D is considered.
′ j and fw,
′ i are smoothed using a weighted moving
Now the wind direction dependent Cd,
average:
Cd , j =
k =2
∑ w k ⋅ Cd′ , j + k , and
(6.25)
∑ w k ⋅ fw′ , j + k ,
(6.26)
k = −2
k =2
fw , j =
k = −2
where w {− 2,−1,0,1,2} = {0.08,0.13,0.18,0.22,0.18,0.13,0.08} are the weighting coefficients (see
Figure E.16).
6.4.5
Drag relation for water
The total drag at the evaluation point for wind directions in sector j is computed from the sum
of the above described drag coefficient and the drag coefficient of water, Cd ,water :
Cd = Cd , j + fw , j ⋅ Cd ,water (U ) ,
(6.27)
where the drag of water can be expressed using (6.18) and the Charnock relation
z0 =
α ⋅ u *2
,
g
86
(6.28)
where g is the acceleration of gravity [9.82 m s −2 ] and α is the Charnock constant for which
the value 0.017 is used that applies to the open ocean (Charnock, 1955; Garratt, 1977). For
shallow waters, however, values as large as 0.032 have been reported for α (Benschop,
1996). Basically, α is determined by the wave conditions which in turn are a function of wind
speed, water depth and wave age. Often a lower limit is set to z0,min = 1.5 ⋅ 10 −5 m. As we
mainly deal with shallow waters in this project we choose the higher value of 0.032 for α.
If the depth of the water limits the wave growth there may also be an upper limit. Recently De
Waal (2002) reported extensively on the subject of wind drag over water with special
attention for the relevant issues for the Dutch water management.
For the wave growth and water rise the drag relation for water is crucial. However, the wind
is only a weak function of this relation. The reason for this is the fact that the wind speed
always depends on z0 in a logarithmic way: U ∝ ln(z z0 ) . From this the following sensitivity
relation can be derived:
dz0
dU
1
=−
.
(6.29)
U
ln(z z0 ) z
With z = 10 m and z0 = 0.001 m the first factor on the right-hand-side of (6.29) is about 0.1.
This means that a 100% error in z0 yields only a 10% error in U . In this paper we will
validate the model on the wind speed, not on wave growth or water rise. Because of the
weak sensitivity of U on z0,water it will be hard to monitor errors in the choice for the drag
relation for water. It is probably better to test for this when validating the wave growth and
water rise directly.
6.4.6
Comparison of gustiness analysis with roughness maps
From the resulting drag coefficients the corresponding roughness lengths can be computed
with (1.19). The estimates of the local roughness length derived from the land-use map and
footprint approximation ( z0, map ) can be compared to that from gustiness analysis ( z0,gust ).
The gustiness model used is that of Verkaik (2000). Here, the roughness length is computed
from the ratio between the gust wind speeds to the average wind speeds. From this ratio and
the inertia of the measuring chain the roughness length can be computed.
In contrast with the footprint approximation the gustiness analysis does not define a source
area with a certain diameter. Another difference between the methods is that the gustiness
analysis feels the obstacles in the surrounding of the station, also when these obstacles are
not included in the roughness map. So the gustiness analysis is entirely independent from
the land-use footprint analysis. This makes it well suited for comparison purposes. Close
examination of differences between the two methods reveals that often the land-use map is
in error, partially due to its finite resolution. Isolated obstacles may not be resolved with a
pixel size of 25 m2, while these can have a large impact on the observed gustiness and wind
speed.
87
Figure E.17 shows a plot of z0,gust versus z0, map for 46 stations. Offshore stations,
surrounded by water, are excluded from this figure. Coastal stations are included, however.
For each station the gustiness analysis is done for a 20° wide sector. The results of the
gustiness analysis for the period of 2001-2002 are used for each station. The footprint length
scale for z0,map used here is D = 600 m. The blue dots in Figure E.17 are the sector
roughness lengths for all stations. For three stations, De Bilt, Schiphol and Terschelling, the
results are highlighted for reasons given later. The discretisation in z0,gust is the result of the
coarse resolution at which the wind speed is logged (1 m/s). This figure shows that there is
quite some scatter. Especially, z0, map seems to underestimate the roughness where z0,gust
is small as well.
Figure E.17 also shows a lower limit to z0, map . This is the result of the use of the Charnock
relation for the water drag with a fixed wind speed, which is set here at 8 m s −1 . This wind
speed corresponds to values data selection on which the gustiness analysis is applied for
these stations (Verkaik, 2000). The lowest z0, map -values have footprints comprising water
only and the roughness length is given by the Charnock relation. The z0,gust -values for these
sectors are higher, in the order of 10-3 m. Wind speeds in the order of 15–20 m/s are
necessary to achieve such roughness lengths from the Charnock relation. So the difference
between z0,gust and z0, map cannot be explained from a difference in applied wind speeds.
Another explanation could be that there is some roughness that is felt by the gustiness, but
that is not represented in roughness map or is lying out of the footprint domain. The latter
argument can be supported by examination of the roughness lengths at station 315
Hansweert. This station is the station with the largest fraction of water in the footprint in our
selection. A map of the land-use in the stations surrounding is given in Figure E.19. In Figure
E.20 the roughness lengths as resulting from the gustiness and land-use analysis as function
of the wind direction are given.
In the direction interval 150°–300° the footprint comprises water only, and this is reflected by
the small z0, map . The z0,gust is larger over this range. There are two directions where z0,gust
has local minima, however: 135° and 215°. From the map in Figure E.19 it is clear that these
are the directions where the water extends to more than 5 km upstream. That z0,gust is
higher in other directions indicates that the gustiness signals roughness over such distances.
We might conclude that the footprint length scale for the local roughness should be larger
than 600 m, or that the fetch should be extended beyond three times this length scale.
Overall results would not improve, however. The extremely large footprint found at station
Hansweert is probably a result of the lack of roughness elements nearby. Over land distant
roughness elements are usually overcome by nearby roughness elements.
The scatter in Figure E.17 is considerable. However, it is of more importance how errors in
the roughness length propagate through our calculations. Using the potential wind speed as
input for our calculations means transforming the surface wind speed to the blending height
using z0,gust . Downscaling the estimated mesowind at an arbitrary location to the surface
wind z0, map is used. The mismatch between the roughness lengths can therefore best
88
expressed as an error factor, which is the ratio between the upward and downward
transformation:
ln 60 z0 ,gust ln 10 z0 ,map
E z0 =
⋅
(6.30)
ln 10 z0 ,gust ln 60 z0 ,map
(
(
) (
) (
)
)
This error factor, E z0 , is plotted in Figure E.18. The lower limit to z0, map is reflected in this
figure as upper limit , increasing with z0,gust .
From this figure it is clear that although the errors in the smooth sectors may seem large in
Figure E.17, the errors in rough sectors have a lot more impact. Station 260 De Bilt has been
highlighted since correspondence between z0, map and z0,gust is the worst at this station of
all. It combines the most sheltered station location in the Netherlands with inaccurate landuse information. This station is maintained for just one reason: it is the residence of KNMI.
For the same reason the time series covers a large number of years. However, it should be
seriously considered to exclude this station from our selection.
From statistics on E z0 station 260 De Bilt turns out to have the highest average value
(+15%) and one the highest standard deviations as well (variation over wind direction 13%).
The most important station this moment to RIZA is station 240 Schiphol. This station scores
in the middle group with average error +1% and standard deviation 4%. The station with the
smallest standard deviation (1%) and a small average error as well (-2%) is station 250
Terschelling.
6.4.7
Local roughness analysis of the Dutch wind measuring locations
The footprint length for the local roughness can be validated with the roughness lengths
resulting from the gustiness analysis, which is done at the locations of the stations with use
of the wind measurements. In Figure E.21a Figure E.21g the local roughness lengths from
the gustiness analysis and the footprint method are plotted for every station. The vertical
scale of the roughness length is not the same for all figures. The figures show that the
differences between the gustiness and the footprint roughness may be quite large at some
places (e.g. 225, 260 and 330). But for several stations (stations 235, 248, 269, 275 and 370)
it is clear that the gustiness and the local roughness length are rather similar even if there is
a change in roughness (land-sea or wood-grass). The roughness from the gustiness analysis
shows a more smooth roughness pattern over the wind direction where the footprint method
gives an undulated pattern (e.g. station 391). Influence of a greater footprint length for most
of the stations the roughness more bad in comparison to the gustiness analysis. Only for a
few stations the results with a footprint length of 1000 m are better than with one of 600 m.
Also the results of the interpolation method for different footprint lengths show that the
footprint length of 600 m gives better results for the average wind vector than a footprint
length of 1000 m. The differences between the simulated wind speeds are small, but in
comparison with the measured values the optimal footprint length for the local roughness is
600 m. So the validation with the interpolation method and the gustiness analysis reveals
both the same optimal footprint length.
89
6.5
Comparison of the two-layer model to models currently in use
In the models currently in use at RIZA and RIKZ the interpolation is done at meso level or no
transformation is done at all. In the transformation from land station statistics to large water
bodies the effect of the roughness change on the wind speed profile in the Ekman layer is
neglected this way.
When transforming the wind speed over land to water, it will increase. As in the current
model the wind speed at mesolevel is assumed constant, the estimated increase is the result
of the adjustment of the wind speed profile in the surface layer only.
In the two-layer model the wind speed is interpolated at macro level. This implies that that, in
contrast to the current models, the wind speed at meso level is adjusted by large scale
roughness changes. The mesowind will be larger over large water bodies compared to the
mesowind over land. Consequently the estimated increase of the surface wind speed over
water will be larger. This is illustrated in Figure E.22. Here the increase in estimated wind
speed at 10-m over water in comparison to the 10-m wind speed over land is plotted as
function of the wind speed over land. The dashed curves indicate the increase with
mesowind assumed constant. The roughness over land is set at 0.2 m. The roughness of
water is given by the Charnock relation (Eq. (6.28)). Two values for the Charnock parameter
are used. With the smaller Charnock parameter the difference in roughness between water
and land is larger and the wind speed increase is larger as well. For very high wind speeds
the roughness of water increases strongly according to (6.28), and the increase becomes
smaller. The solid lines indicate the estimated increase in surface with the macro wind
assumed constant. It is clear that the increase is significantly larger.
This implies that wind speed estimates from the two-layer model for the inland water bodies
will be larger than those from the current model when wind speed statistics from land stations
are used for input.
If the statistics of offshore stations is directly applied as the wind speed in the delta estuaries,
the effect will be reversed. The presence of land upstream of the point of interest will reduce
the surface wind speed and mesowind speed all together. In case coastal stations are used
as input, the roughness of the upstream surface compared to the roughness of water will
determine whether an increase or decrease of the mesowind can be expected. This depend
strongly on the wind direction considered for coastal stations.
90
7 Validation of interpolation method
In this section the performance of the interpolation method as described in Section 6 is
assessed, which encloses the two-layer model and the interpolation scheme of Barnes
(1964). Especially its performance during extreme wind speed events is important to the
HYDRA-project. The principle of the two-layer model is adopted from Wieringa (1986). The
interpolation scheme for the macro wind and the derivation of the roughness lengths are
different, however. The data set of wind speed and direction used in this study is extended
with more stations and longer time series in comparison to the data used by Wieringa and
Rijkoort (1983).
Two-layer model
The two-layer model uses the wind measurements as input data. For every station the local
roughness lengths are computed per wind direction sector with use of the gustiness analysis,
which is performed on the wind measurements. With use of these local roughness lengths
the potential wind speed is computed from the wind speed measurements. The potential
wind speed is the wind speed that would be measured at 10-meter height if the site had a
local roughness length of 0.03 m (short-cut grass). So the local roughness effects of the
siting of the station are removed. From potential wind speed the wind speed at blending
height, meso wind, is computed. This meso wind is transferred further upwards to the top of
the boundary layer, macro level, with use of the mesoscale roughness length. At macro level
the macro wind as ‘measured’ at all measurement sites is interpolated to a regular grid
according to the Barnes’ interpolation method. With this interpolated macro field it is possible
to calculate the wind speed at 10 meters height at any desired location in the Netherlands.
The transformation downwards to the blending height is done with use of the mesoscale
roughness length for the chosen site. For the computation of the wind speed at 10 meters
height the local roughness length is needed. The local roughness length of the gustiness
analysis is only available at the measurement sites and not at any location. Therefore the
local and the mesoscale roughness lengths are derived from the land-use map with the
footprint method. More detailed information about the two-layer model, used formulae and
land-use map is given in chapter 6.
Validation method regarding execution of model
The two-layer model and the techniques applied to get a 10-meter wind speed and direction
at any location in the Netherlands needs to be validated and optimised. For validation we
mimic the interpolation method, as it will be used in the end: the wind is simulated at a
location where no measurements are available. The validation method comprises the
execution of the interpolation method using wind data available at all stations available
except one. For this excluded station location the wind speed and direction is simulated with
the two-layer model, as if it is a location without any measurements. With the data of the
other stations the macro wind field is constructed and interpolated. Using the gridded macro
wind field, the macro wind at the excluded station is simulated. Then this macro wind is
transformed downwards to the 10-meter wind with use of the local and mesoscale roughness
91
from the land-use map. For every hour data this validation procedure is repeated for every
station.
The difference between simulated and measured wind gives information about the quality of
the two-layer model. Information is gained about the difficulties of simulating wind data at
different locations that has no measurements. The difference between macro wind fields
before and after the interpolation is a measure for the effect of the Barnes’ interpolation
method. Therefore the two-layer model is run with different settings for the parameters of the
interpolation scheme. At least the validation of the interpolation method contributes to the
validation of the local and mesoscale roughness lengths determined with use of the footprint
approximation. By comparing the simulated with measured values for the 10-meter wind and
the potential wind, it is possible to judge the accuracy of the roughness lengths at local and
mesoscale. The comparison of the local roughness length from the land-use map with the
results of the gustiness analysis is performed in Section 6.3.6.
From 1962 onwards the observation network is sufficiently dense to run the interpolation
method. For the optimal validation the simulation would enclose this whole period on hourly
basis. But the computational time for this simulation is too large for validation purposes.
Therefore we limit our datasets when evaluating the interpolation method. The characteristics
of these datasets are specified in Section 7.1. The interpolation method can be split up into
two parts: the interpolation scheme applied at macro level and the roughness lengths used
for transformation up- and downwards. In Section 7.2 the validation of parameters for the
Barnes’ interpolation scheme is discussed. In Section 7.3 the validation of the roughness
lengths at local and mesoscale is discussed.
7.1
Test datasets
The HYDRA-project has to result in wind statistics at any location in the Netherlands. A main
part of the statistical methods consists of extrapolating wind speeds to low return
frequencies. The method is formulated such high wind speed events have a large influence
on the result of the extrapolation. Therefore the emphasis of the validation should lie on the
performance of the interpolation during extreme wind speed events. Events occurred in the
past are associated with strong winds mainly from westerly directions. However before we
can focus on high wind speed events, it is necessary to know its performance during
moderate wind speed conditions. Running several simulations of 40 years hourly data take
too much computational time. Instead we took 5 successive years to validate on average,
dataset I. This dataset comprises too few events to apply extreme statistics on. Therefore we
selected the most extreme events over the period of 40 years, which form together dataset II.
These two datasets and their characteristics are discussed in Sections 7.1.1 (dataset I) and
7.1.2 (dataset I).
92
7.1.1
Dataset I: 5 successive years
Dataset I consists of hourly data for 5 successive years, for the period 1997-2001. This
means that in total 43824 hours are simulated. In the dataset all stations are included, also if
its time series does not cover the whole period, but only e.g. one year. The frequency
distributions of the potential wind speed and measured wind direction over this period show
that this contains all kinds of situations concerning the wind speed and direction (see Figure
F.1). To construct these graphs all available data of all stations are combined so the graphs
present an average over the Netherlands. The distributions per station can be slightly
different depending on its location and environment. For determining the distribution of the
wind direction, bins of 30 degrees are used, which means that the bin of 30° contains wind
directions in the range of 15-44°. Wind direction class 0 contains all hours on which the wind
direction was variable and not detectable because of calm weather. It is seen that all
directions are well represented in this data set. Westerly winds are slightly in the majority.
For the potential wind speed distribution bins of 1 m/s are used. The wind speeds in this
dataset are mainly in the range of 2 to 7 m/s. Dataset I comprises too few extreme events to
apply extreme statistics on. However this dataset is very suitable for the evaluation of the
average performance of the method as a function of the wind direction and wind speed and
for the validation of the local and mesoscale roughness lengths derived with the footprint
analysis.
7.1.2
Dataset II: storm events selected
For the validation of the interpolation method during extreme wind speed events only data of
storm periods need to be selected, these form dataset II. The method to select storm events
is largely the same as the selection of storm maxima in Section 3.2. For the 13 stations that
have a dataset containing minimal 40 years, the hours with extreme wind speeds are
selected in the period of 1962 to 2001. The used stations are described in Section 2. The
storm selection is done with a storm filter applied on the data record of each station
separately. The storm filter itself is described in chapter 3.2. In the storm filter an
independency of 48 hours is enforced, so per station only one hour per event is selected.
The wind speeds at these hours are ranked to their exceedance frequency. Per year the top
20 of independent events are selected per station. This means that per station 20x40
years=800 hours are selected. After combining the hours of all 13 stations together to one
dataset some hours will be doubled. Successive hours of one storm can be selected, since
the summit of the storm occurs at subsequent hours for different stations. In total 7071 hours
are selected at which at least at one station a high wind speed has occurred.
The frequency distribution of wind direction and potential wind speed in dataset II are
constructed in the same way as for dataset I (see Figure F.2). The frequency distribution of
the wind direction shows that the direction southwest to west dominates (sector 210-270°
contains about 50% of the data). The other directions are underrepresented in comparison to
the distribution of dataset I. An important difference between dataset I and II is that dataset I
93
consists of continuous data only, where dataset II contains hours with high wind speed. In
the wind speed distribution this difference is expressed in a shift towards higher wind speeds
in dataset II. For the interpolation method the hours of dataset II of all available stations are
used, not only the data of the 13 stations on which the storm selection is applied. This
dataset is very suitable to evaluate the performance of the interpolation method under high
wind speed conditions and how it deals with large differences in wind speed, which occur
during storms. The dataset covers the period from 1962 to 2001, so it encloses the increase
in the network density. This makes the dataset also appropriate to evaluate the influence of
operational network evolution on the results of the interpolation method.
7.2
Validation of Barnes’ interpolation method
The Barnes’ interpolation method itself is described in Section 6.2. It is described as an
interpolation technique that is able to regain details that are present in the data. The choice
for the radius of influence and for the number of iterations seems to be of large influence on
the results. Therefore, this validation is mainly concentrated on these parameters. For large
R the number of iterations is of minor importance. So we first concentrate on the choice for
R and then we will look for the optimal number of iterations.
To study the effect of R the range of 50 to 500 km is chosen to examine, because that is the
range in which the simulated wind speed depends largely on the choice of the radius of
influence (see Figure E.10). In Table 7.1 the settings for the different runs performed are
summarized.
Run number
1
2
3
4
5
Radius of influence
(km)
050
100
200
300
500
Table 7.1: Settings of radius of influence for validation of the Barnes’ interpolation method.
These runs are done with both datasets described, dataset I with 5 years of data and dataset
II with events selected. The results of the simulations with dataset I as input are described in
Section 7.2.1 with as main purpose to evaluate the average performance of the interpolation
method. The representation of several storm events in dataset II by the model is analysed in
Section 7.2.2. In this section statistical analysis is performed on the results and some storms
are studied in more detail.
94
7.2.1
Performance of simulating dataset I
Dataset I is made of the continuous data of 5 successive years in the period 1997-2001. The
main characteristic of this dataset is that the dataset includes all kinds of situations regarding
wind speed and direction. For validation it is impossible to evaluate every single simulated
hour. Therefore we chose verification procedures to validate the wind speed, wind direction
and wind vector. First these procedures are described and then the results for the different
runs.
Verification procedures to evaluate the average performance
For the verification of the model the validation procedure is applied that consists of excluding
one station and simulating the wind for that location. From the interpolation method the wind
speed and direction results at different levels in the atmosphere are written to one data file
per station together with the measured data. With measured data we refer to the data that is
measured or derived from the measurements, like the potential and macro wind. So the
measured macro wind is the wind at the top of the boundary layer computed with use of the
potential wind and the mesoscale z0 . Estimated or measured data comprises the wind data
after applying the interpolation scheme and the transformation downwards. So the estimated
macro wind is the macro wind above the location after the applying the interpolation scheme.
The estimated potential wind speed is the potential wind speed that is computed with the
two-layer model when the measured data of the station itself is left out of the simulation.
Two validation procedures are applied on output data for the different runs. The first
procedure consists of the calculation of the average wind speed. To gain more information
about the performance per wind direction the hours are selected on basis of bins of 10
degrees in wind direction. For the selection the estimated wind direction is used for the
computation of the averaged estimated wind speed and the measured direction for the
measured wind speed. The calculation of the averaged wind speed per wind direction sector,
d, is as follows:
nd
ud =
∑ u d ,t
t =1
nd
.
(7.1)
The directional average wind speed ud is equal to the summation of the instantaneous wind
speed, u d,t , over the number of observations in the corresponding wind direction sector, nd ,
divided by this number. This equation is applied for every wind direction sector separately.
95
The corresponding standard deviation per wind direction , σud , is given by
nd
σud =
1
nd
nd
∑ (ud,t − ud )
2
t =1
=
∑ (ud,t )
2
t =1
nd
 nd
 u
 t =1 d , t
−
 nd


∑
2



 =



nd
∑ (ud,t )2
t =1
nd
− (u d ) .
2
(7.2)
When no measurements of wind speed or direction are available the computation is not
performed. These formulas, (7.1) and (7.2), can be applied on wind speeds at the different
levels (10-meter, meso and macro level) in the atmosphere. The effect of the interpolation
method becomes clear when comparing the average wind speed before and after
interpolation at macro or surface level. The difference per wind direction sector between the
estimated u d ,e and measured u d , m averaged wind speed is defined as:
∆u d = (u d ,e − u d , m )
(7.3)
This means that negative values for ∆ud correspond with an underestimation of wind speed
by the simulation and positive values indicate at an overestimation.
The second procedure is calculating the difference between the measured and estimated
wind vector at station locations, so information about the performance on wind speed and
direction is combined. The vector difference at time t, (∆u)t , is defined as:
(∆u)t
=
[ue ⋅ cos(d e ) − u m ⋅ cos(d m )]t
−
(7.4)
[ue ⋅ sin(d e ) − u m ⋅ sin(d m )]t
where d e and d m represent the estimated and measured wind direction, respectively.
Averaging the vector difference over time is conform to formula (7.1) with ∆u instead u :
n
∆u =
∑ (∆u)t
t =1
(7.5)
n
Equations (7.4) to (7.5) are applied on the data of each separate run and yield one score per
station. From these validations it may return that for a station it is difficult to simulate the
measurements. Then we have to find out what the cause is of this dissimilarity, the
measurements, the interpolation method, incorrectness in the land-use map or other
reasons.
To evaluate differences between the runs, it is preferable to have one score for every run to
compare. As stated above the major differences are expected for the range in the radius of
influence in the interpolation method of Barnes’. Since its influence is most clear directly after
96
interpolating the macro wind, a score per run is defined by averaging the difference between
the macro wind vector before and after the interpolation. The average macro wind vector
difference per station is determined according to (7.4) and (7.5) and then averaged over the
total number of stations, m = 51:
m
∆umacro =
∑ (∆umacro )x
(7.6)
x =1
m
The standard deviation of the score per station is defined as:
m
σ ∆umacro =
1 m
(∆umacro )x − ∆umacro
m x =1
∑(
)
2
=
∑ (∆umacro )x 2
x =1
m
−
∆umacro
m
2
.
(7.7)
These equations together give a score per run, which indicated the average difference
between the macro wind vector before and after the interpolation. They give no information
about the performance on interpolating extreme situations.
Average 10-meter wind speed
The 10-meter wind speed is derived from the measurements with use of the locale
roughness information. Dataset I is used to compute the time-averaged wind per station,
according to (7.1). Figure F.3 shows the spatial distribution of the averaged wind speed per
station interpolated with use of a simplified method. This means local areas with maxima
values like at sea before station 225 IJmuiden and besides station 340 Woensdrecht are not
realistic, but result of the applied interpolation procedure. This interpolation procedure is
purely mathematic, so no roughness lengths are taken into account, which will be done later
when the output is generated at a regular grid. The average measured 10-meter wind speed
distribution shows a clear gradient over the country with high values above sea ( u pot = 8 m/s
at station 252 K13) and low values inland ( u pot = 3.7 m/s at station 260 De Bilt). This is in
agreement with the roughness map. The highest averaged wind speed occurs where the
roughness length is lowest and visa versa.
The averaged estimated wind speed is rather similar to the measured distribution (see Figure
F.4). For all runs a sea-inland gradient exists. The amplitude of this gradient diminishes with
the radius of influence, but the pattern stays similar. The wind speed is the result of the last
step in the interpolation method, including the downward transformation from macro level
towards mesoscale. In this downward transformation the mesoscale roughness length is of
influence on the resulting wind speed. To evaluate only the effect of the interpolation method
of Barnes’, the performance of the method at macro level has to be analysed.
97
Average macro wind speed
The macro wind speed before applying the interpolation is averaged per station over the
period of 5 years (1997-2001) according to (7.1). So the wind direction is not taken into
account. Since synoptic variations in geostrophic wind speed have horizontal scales of
hundreds of kilometres, the macro wind speed is not expected to show strong variationsover
such distances. The spatial distribution of the macro wind speed before the interpolation
method is shown in Figure F.5. The contours are plotted with use of a standard interpolation
procedure (v4 in Matlab). There is a gradient visible in macro wind speed over the country.
Along the coast the average macro wind speed is about 11 m/s and higher, while inland
values of 8 to 10 m/s are common. The maximum macro wind speed of 12.8 m/s is attained
at station 285 Huibertgat and the minimum value of 8.1 m/s at station 260 De Bilt. Besides
the existence of a general gradient coast-inland, there exist some very local gradients.
Between the stations 331 Tholen and 340 Woensdrecht the difference in average macro
wind is 2.1 m/s over 15 km. A local gradient of the same magnitude is seen between the
stations 260 De Bilt and 265 Soesterberg of about 1.7 m/s over 10 km. These local gradients
are not in correspondence with the theory. They reflect differences in exposure at the
measuring sites that are not represented accurately in the roughness map.
After interpolation with the Barnes’ technique, the pattern of the macro wind speed differs per
run (Figure F.6a. to Figure F.6e.). For small values of the radius (50 and 100 km) the pattern
over the country is rather similar to that of the measured macro wind speed, so before
interpolation (f5). High values for the macro wind speed are found along the coast and lower
values inland, the values themselves differ from run to run. In comparison with the measured
values the values from the simulations are in general lower. The averaged macro wind speed
over all stations before the interpolation comes to 9.6 m/s and after the interpolation to 9.5
m/s for run1 up to 9.1 m/s for run 5. The larger the radius is set the smoother and more
homogeneous the gradient in macro wind speed appears to be. The distribution of the
average macro wind speed of run 3 and 4 agree to the findings of Wieringa and Rijkoort
(1983, WR83) for the period of 1961-1980. In Figure F.7 the results regarding the macro
wind speed of Wieringa and Rijkoort is shown. Their average macro wind speed before
interpolation is given at 16 station locations and the corresponding macro wind speed after
interpolation is indicated with isolines. WR83 found a stronger gradient as well in the macro
wind speed before as after interpolation. In general, they found higher values for the
measured macro wind speed along the coast (of about 12 m/s) and of the same magnitude
inland (of about 9.5 m/s) than we did. The comparison of macro wind speeds after
interpolation reveals that run 3 and 4 result in the same distribution of the wind speeds as
WR83, but with significant lower values due to the larger smoothing effect of a larger R .
Average differences in macro wind vector
The above validation of the interpolation method does not include the performance on the
wind direction. Therefore differences in wind vector are computed on hourly basis and then
averaged over time per station with use of (7.6) and (7.7). The resulting wind vector per
station is mainly a measure for the smoothing effect of the interpolation method. All stations
98
result in an average macro wind vector difference in the range of 2 m/s to 6 m/s. In general
the stations at the edge of the map give the highest values, like K13 in the North Sea (station
252) and Beek (station 380) (see Figure F.8a. to Figure F.8e.). The stations with data
available are marked with a black cross in a square. For these figures a simple interpolation
procedure is applied to draw contours in between the station locations, so locale patterns
among stations are not the result of the interpolation method of Barnes’. For the different
runs the pattern over the country is in general the same. But run 3 and 4 show larger blue
areas ( (∆umacro ) < 3 m/s) that mean that for these runs, the average wind vector differences
are smaller. In all runs, stations 225 IJmuiden and 275 Deelen stand out through their higher
values in comparison to their environment. Later on we will see if this is the same when using
other validation procedures.
The macro wind vector difference is averaged over all stations. The results of ∆umacro
runs 1 to 5 ( R = 50 – 500km) are summarized in Table 7.2.
Run number
Difference in macro wind vector (m/s)
for
Standard deviation (m/s)
1.
3.126
0.706
2.
2.948
0.607
3.
2.906
0.527
4.
3.034
0.506
5.
3.316
0.521
Table 7.2: Results of dataset I concerning the average macro wind vector difference before and after
interpolation and its standard deviation.
It shows that run 3 (radius = 200 km) has the lowest value for the averaged macro wind
vector difference followed by run 4 with a slightly higher value. There the score is determined
on basis of the difference between the macro wind vector before and after the interpolation,
the lower the score is the better the interpolation method performs. Since run 3 and 4 have
the lowest scores they do better than the other runs. Runs 1 and 5 have the lowest and
highest value for the radius of influence and show the highest values for the macro wind
vector difference. But the differences between the runs are very small. The standard
deviation of this wind vector shows the smallest value for run 4 ( R = 300 km). The value of
the standard deviation of 0.506 m/s is smaller than the average itself, which means that all
stations show a deviation of the same magnitude for the macro wind vector difference. On
basis of the average performances of the different runs, it can be concluded that a radius in
the order of 200-300 km is the best. But this gives no information about the performances
during extreme wind events that are included in dataset II.
99
7.2.2
Performance of simulating dataset II
Dataset II is made in order to validate the performance of the interpolation method under
high wind speeds, because statistical extrapolation is mainly based on high wind speeds.
Therefore the performance of the interpolation method to simulate extremely high wind
speeds is of major importance. The same settings of the interpolation method are applied.
Therefore the same numbering is used for the runs with dataset II as mentioned in Table 7.1.
To validate the simulation of high wind speed some events are studied in detail, especially
those for which the estimated wind speed differs strongly from the measurements.
October 17, 1967
The storm of October 17, 1967 is a storm with strong western winds. This storm has the
highest listed potential wind speeds for the station 275 Deelen of the period 1961-2001. In
Figure F.11 the potential wind fields are plotted and in Figure F.12 the wind field at macro
level. The contours display the wind speed and the arrows represent the wind vector when
available at the station location. Plotting the contours is done with use of a simple standard
interpolation method, because the output of the model is only produced at station locations
and not at grid. In both figures the upper left picture displays the input wind fields at surface
and macro level, respectively. The other plots display the wind fields resulting from the
interpolation method at surface and macro level for the different runs (see Table 7.1). These
plots are produced according to the validation procedure, so excluding one station each time
and simulating the wind at that station. Figure F.11 shows that the potential wind speed at
station 275 Deelen is the highest measured at 12:00 hour GMT.
In the transformation of this value upwards to the macro level, the large meso roughness
length of Deelen causes an exceptionally high macro wind speed (see upper left plot of
Figure F.12). There is a strong gradient in macro wind speed between the stations 260 De
Bilt and 265 Soesterberg. Also, the wind vectors at these two stations show differences in
direction. In 1967 there were no stations located east of 275 Deelen. To reproduce the
gradient and the high wind speed at Deelen the grid point east of Deelen are given very high
values. Because of this, estimated wind speeds east of Deelen, for instance at station 290
Twenthe, become extremely large. In Figure F.10 the estimated wind speed at Twenthe for
this event is given as function of Barnes’ radius of influence and for different numbers of
iterations. It shows that Barnes’ scheme is unstable for small radii. The numbers of iterations
expresses the confidence in the measurements. If the measured wind speed at Deelen is
given large confidence and should be reproduced by the interpolation this number should be
large. Figure F.10 shows that for a stable and realistic interpolation Barnes’ radius should be
large (> 200–300 km). Then the number of iterations becomes less important.
February 14, 1979
A totally different storm is the one that occurred at February 14, 1979. For the station 270
Leeuwarden this storm is the fifth in the list of extreme wind speeds. This event is selected,
100
because it is one of the few storms with eastern winds. At 18 UTC station 270 is the only
station that has measured a high wind speed of 25 m/s. The potential wind speeds measured
at stations in the neighbourhood are in general 10 m/s lower. Nevertheless the wind speed at
station 270 is not a mistake or error, because in the weather report is written “a cutting
snowstorm rushed from the northeast over the north of the Netherlands. On the Frisian
countryside wind gusts of about 90 km/h were measured”. This snowstorm was a small-scale
feature that is only visible in the measurements of station 270. We will show that such events
cannot be simulated adequately.
In Figure F.13 and Figure F.14 the potential and macro wind fields measured and simulated
according to the validation procedure are plotted. For the macro wind derived from the
measurements it is seen that the wind speed at station 270 Leeuwarden is much higher than
the surrounding stations. In the measured macro wind a second large maximum is found at
station 235 Schiphol. In the validation procedure one station at the time is excluded and for
that station the value is estimated on basis of the other available stations, like in case no
measurements were done at this location. At February 14, the only northern station with a
high measured potential wind speed is station 270 Leeuwarden. Therefore the validation
results in an underestimation of 13 m/s for station 270 at 18 UTC. For simulation of the
surrounding stations, the high wind speed at station 270 is included, which results in values
of the potential and macro wind speed higher than estimated for station 270. It seems that
two local maxima are simulated with a local minimum in between (see Figure F.13 and
Figure F.14). This pattern is not realistic.
Therefore the simulation is repeated, but then not according to the validation procedure, but
with the interpolation method, so with all available data included. In Figure F.15 the results
for the wind fields at macro level are plotted. In this figure the maximum in wind peed
corresponds in place with the measurements, situated over the northern part of the country.
The smaller R , the higher the maximum macro wind speed is. With a radius of 50 km, the
individual measurements at the stations influence directly the fitted macro field (compare
Figure F.14a with Figure F.15a). In comparison with the fitted macro fields of Figure F.14 and
Figure F.15, the most differences occur in the vicinity of station 270 Leeuwarden. The
influence of excluding Leeuwarden from the analysis is smaller with larger R , which is
expected on basis of the definition of R . The larger R , the further the method “looks” to
compose the fitted macro field. For R ≥ 500 km, it seems to be of minor importance if a
station is excluded or not (Figure F.14f and Figure F.15e). The pattern is almost the same
without any indication of a maximum wind speed in the north. For this case the interpolation
method is clearly not able to reproduce the extreme wind speed if station 270 Leeuwarden is
not used in the simulation. We conclude that some extreme wind speeds are caused by
atmospheric circulation patterns that are too small to be resolved by the observational
network. This implies that such events ill not appear in the simulation either.
101
7.3
Validation of roughness lengths
For the two-layer model roughness lengths are necessary for the calculation of the wind
speed at top of the surface and Ekman layer. These roughness lengths are derived from a
land-use map, LGN3+, with use of the footprint approximation. This footprint model is
described in more detail in Section 6.3.4. In that section the performance in comparison with
IBL-models shows that the method deals well with the development of IBL’s. The influence of
different settings for the footprint approximation on the simulated potential and macro wind
speed will be analysed in this section.
The footprint approximation has three main parameters that may influence the local and
mesoscale roughness for a specific site. The first parameter is the footprint length for the
local roughness derived from the land-use map. The optimal value for this parameter can be
obtained by computing the average performance of the wind for different settings of this
parameter. The comparison with the results of the gustiness analysis per station is described
in Section 6.3.6. The second parameter is the footprint length for the mesoscale roughness
length. The roughness experienced at the top of the boundary is not measured and therefore
not direct comparable to measurements. Evaluation of the results from the interpolation
method with different mesoscale footprint lengths has to result in the optimal setting. The
third parameter is the surface roughness length that corresponds to a certain land-use class.
Literature gives mostly a range for surface roughness length assigned to a land-use
category, so variation within a certain range is possible.
The validation of the roughness can be done with use of the measured and estimated wind
speed and direction. For this purpose both wind directions, estimated and measured, are
split into sectors of 10 degrees. Per wind direction the difference in averaged wind speed is
calculated with use of (7.1) and (7.3). Comparing the averaged simulated and measured
potential wind speed gives information about from which wind direction the wind speed is
mostly over- or underestimated. The environment and location of the 51 stations are
completely different from each other that may result in dissimilar performances of the
interpolation method. Therefore all 51 stations are evaluated. Differences in the averaged
wind speed reveal information about the correctness of the local roughness and about
present roughness elements in the direct neighbourhood.
A similar validation procedure is constructed to gain information about the difference in wind
direction between the simulations, d e , and the measurements, d m , at every time step t:
(∆d )t = (d e − d m )t .
(7.8)
This difference is corrected so the difference has to be equal or smaller than 180°. The
average and standard deviation of the wind direction difference are computed on similar way
as for wind speed:
102
n
∆d = (d e − d m ) =
∑ (d e − d m )t
t =1
n
.
(7.9)
n
σ ∆d =
∑ 2(∆d )t
t =1
n
−
2∆d
.
n
(7.10)
The difference in wind direction is plotted against the measured wind direction, which is split
into bins of 10°. This results in a more detailed view about the correctness of the local
roughness length that belongs to that wind direction sector. At macro level the perpendicular
component of the wind speed is dependent on the magnitude of the mesoscale wind speed.
As consequences the wind direction at macro level changes with wind speed at the blending
height. Therefore the difference between the simulated and measured wind direction at 10
meter may vary with wind speed. Also, in case of low wind speed the wind direction may not
be well defined. For these reasons thresholds of wind speeds ( u m = 2, 3, 4, 6, 8 m/s) are
introduced to verify this effect on the estimated wind directions. Both validation procedures
give information on one of the components of the wind, the direction or the speed at different
levels in the atmosphere. The effect of the footprint length for the mesoscale roughness is
studied in Section 7.3.1 and the local footprint length in Section 7.3.2. The influence of
changing the surface roughness length assigned to a certain land-use class is discussed in
Section 7.3.3.
7.3.1
Mesoscale footprint length
For validation of the mesoscale roughness, no direct validation is possible as for the local
roughness. Only the mesoscale roughness is needed in the upward transformation from
potential wind to macro wind and backwards to potential wind again. Therefore, differences
between the measured and simulated potential wind speed and direction give information
about the quality of the mesoscale roughness. From analysis with the average wind vector
difference (see (7.3) and (7.4)) it appears that different footprint length for the mesoscale
roughness has on average small impact on the average wind vector over all stations
together. But per station the influence of the footprint length scale may be different. Biases in
the average wind direction and in wind speed as function of the measured wind direction may
be directly related to the accuracy of the roughness surrounding the station. The measured
wind speed is divided into bins of 10 degrees and forms the basis for the further
computations. The average wind speeds estimated and measured are computed with (7.1)
and the difference between them with (7.3). For the difference in wind direction (7.9) is
applied with a threshold of 4 m/s. From this equation, negative values for the difference in
wind direction mean that in the transformation downward the wind direction backs too much
in comparison to the measured direction due to too high roughness lengths. The results
shown in this section are from the interpolation method with a radius of influence of 300 km.
103
In Figure F.16 the results of the potential wind for 8 stations are plotted. These stations are
selected on basis of the performance of the model. In the plots the difference in wind speed
and in wind direction are plotted as function of bins in measured wind direction. Station 240
Schiphol shows also an underestimation of wind speed in all direction. The largest difference
occurs with wind from southeast, over the transition from runway to building area. This
suggests that the mesoscale z0 is overestimated in directions where in the land-use map
built-up areas are situated. Mainly this is due to the incorrect representation of the platforms
and the buildings situated at the airport area on the land-use map. For station 225 IJmuiden
the wind speed is underestimated in all directions. In the northeast sector the
underestimations in wind speed and wind direction are largest. This coincides with the
IJmuiden city area, which means that the roughness corresponding to that area is too high.
Another station that has a bad representation of the measurements is station 330 Hoek van
Holland. In all direction the differences in wind speed and direction are strongly negative.
Especially, the northeast to the south the error in wind direction is more than 20°. In this
sector the river with the docks are situated. Station 315 Hansweert is situated at a land-water
transition. Its results show that this transition is difficult to catch correctly.
Generally, an overestimation of wind speed goes along with a positive difference in wind
direction. It can be explained as follows. In the surface layer there is no change in wind
direction with height. Going upward towards the top of the boundary layer the wind directions
veers with height. Going down the wind directions backs. The angle of veering or backing
increases with roughness. So in case the mesoscale z0 is too high (too low) for a location
the wind backs too little (too much), which results in a positive (negative) difference.
Meanwhile the wind speed decreases too little (too much) resulting in a too high (too low)
potential wind speed.
Besides stations that show large deviates between the measurements and simulations, there
are also stations for which the interpolation method performs very well. For example stations
269 Lelystad, 279 Hoogeveen, 280 Eelde and 323 Wilhelminadorp show small differences
between measured and simulated wind speed and direction. The environment of the stations
270 and 280 are relative homogeneous, but station 323 is situated at the coast.
For some stations the influence of the mesoscale footprint length on the mesoscale z0 and on
the performance of the interpolation method can be large. For a station situated in
inhomogeneous terrain the mesoscale z0 changes with the chosen footprint length.
Especially when a transition in roughness is located at a distance within the footprint length.
It appears that a footprint length of 10 km give the smallest averaged wind vector differences
according to (7.6). For individual stations the optimal footprint length may differ from the
overall optimal.
104
7.3.2
Local footprint length
In Section 6.3.6 the comparison of the z0 of footprint approximation with the gustiness
analysis is made. That analysis showed that for some stations the local z0 deviates strongly
from the gustiness, while for other stations they correspond very well. A footprint length of
600 m correlates optimal with roughness length from the gustiness analysis. In the two-layer
model the local z0 from the footprint approximation is used for the downward transformation
of the meso or potential wind speed to the 10-meter wind speed. It appeared that the effect
of different local footprint lengths on the estimated wind speed is very small. Other
parameters seem to have more influence on the simulated surface wind speed.
7.3.3
Assignment of surface roughness lengths
In Section 6.3 the assignment of surface roughness length to land-use categories is
explained. Not all categories of the land-use map are described in literature. For most of the
categories described in literature a range for the surface roughness length is given
depending on the density of the obstacles. The roughness lengths of crops may change
during the growing season, but we set them to a constant value throughout the year. The z0
for built-up area may vary from 0.7 m for low buildings to 1.6 m for regular built towns
(Wieringa, 1993). Since high z0 gain more weight in the calculation of the directional z0, small
changes in low values for surface z0 will have no large influence on the z0 resulting from the
footprint approximation. Nevertheless it is plausible that a change in the z0 for continuous
urban area may have direct influence on the directional z0 for several measurement sites
and on the results of the interpolation method.
In the land-use map different classes with different z0 are assigned to rural area with
buildings and for continuous urban area. But in the land-use map itself almost all buildings,
villages and cities are appointed as continuous urban area with a relative high value for z0 .
In some cases the roughness in the direction of a built-up area seems to be overestimated.
Therefore we chose to set the surface z0 for built-up area to 1.1 m instead of 1.6 m. For the
roughness length at the stations it appears that a lower surface roughness for urban area
has no large influence. For station 343 Rotterdam Geulhaven and 344 Zestienhoven the
impact is largest. In Figure F.17 the effect of z0 = 1.1 m and 1.6 m for continuous urban area
on the mesoscale and local roughness for both stations is shown. Both stations are situated
in vicinity of large urban areas, where deviations between local z0 of the gustiness and of
the footprint analysis were large. Comparing to the impact of the local and mesoscale
footprint length of the roughness the effect of a lower surface z0 is very small.
Since the influence on the directional roughness at station location is very small, it is
plausible that a change in the surface z0 of one class has not much influence on the results
of the interpolation method. A run with dataset I is done with the adapted surface z0 for
urban areas. The averaged vector difference on macro level reveals that adaptation of the
surface z0 gives slightly worse results. At the stations itself small differences are observed,
105
some stations give better results, some worse. The influence of changing the surface z0 with
0.5 m on the results of the interpolation method is so small that the surface z0 of other landuse classes are not validated in more detail.
7.4
Conclusions
The interpolation method comprises the two-layer model, the roughness maps, and Barnes’s
interpolation technique. The performance has been tested with regard to averages on at
dataset of 5 years. The differences between the estimated and measured wind speed and
direction at both surface and macro level are used as indicators.
Average macro wind speed is generally equal or larger than 11 m/s, while inland values from
8 to 10 m/s are found. The average values of the macro wind of nearby stations can deviate
up to 2 m/s. This indicates the sum of the uncertainties in model and roughness maps in the
local wind climate assessment. Compared Wieringa and Rijkoort’s results, a weaker coast–
land gradient is found here.
The Barnes interpolation technique fits a smooth field through the macro wind field. The
average difference between the fitted field and the macro wind at the station location
depends weakly on the radius of influence in the Barnes algorithm. R The smallest
differences are found for R = 200–300 km. The average difference per station is about
2.9 ± 0.5 m/s.
Case studies of storm situations show that very localized extremes can occur in fields during
storms. The interpolation algorithm is not able to simulate these extremes. For these extreme
situations R and also the number of iterations in the Barnes algorithm becomes important.
The stability of the algorithm requires R ≥ 200 km.
The average differences in estimated and measured wind speed and direction are used to
validate the mesoscale footprint length used to derive roughness maps from the land use
maps. The average performance is only a very weak function of this length scale. Best
performance is achieved with a length scale of 10 km.
Adjustment of the roughness length assigned to specific land use classes has hardly any
noticeable influence on the performance of the interpolation method.
We conclude that the interpolation method is a very robust model for averages. However, for
extremes the model becomes sensitive for parameters like R or the number of iterations.
This is mainly a consequence of the extremes being recorded at only a single station.
106
8 Integration of statistics and interpolation
With the statistical method described in Section 3 extreme return levels of wind speed
corresponding with return periods up to 10,000 years can be obtained for the station
locations. However, these locations are not always the most interesting locations. Surely for
water management wind speed statistics over water and at water-land transitions are more
relevant.
Changes in surface roughness both on small and large scales have a strong impact on the
wind speed. These changes can be modelled by the method described in Section 6. To
obtain extreme return levels of wind speed the extreme value analysis and the spatial
interpolation of surface wind need to be integrated.
The statistical method itself analyses time series mainly independently of each other. Large
differences in return levels between stations are found from this analysis. These differences
will partially be the result of statistical noise and the effects of insufficient sampling. The
statistical noise may exceed the effects of changes in roughness, especially concerning high
return periods. An integration of the statistics and the interpolation may reduce the noise and
may result in spatially coherent return levels.
An approach to integrate the statistics and the interpolation is to interpolate the hourly wind
speed as it is observed simultaneously at all stations and to derive time series of wind speed
on a grid synthetically. These time series can then be analysed statistically the same way as
the series from the station locations. This approach is the most straightforward and plausible
application of the interpolation method from a physical point of view. However, it is
computationally very demanding. Furthermore, it can be expected that the impact of the
limited observational network density and of the noisy pattern in observed wind fields is large
on the interpolated wind speed extremes.
Another approach is to derive the extreme return levels of wind speed doing the statistical
analysis first, followed by the interpolation method applied on these extreme return levels of
wind speed. Underestimation due to insufficient sampling or limited network density will be
avoided this way. Moreover, this approach is less demanding computationally. Before the
statistically extrapolated wind speed can be used as input for the interpolation method,
however, some assumptions need to be made. The input for the interpolation method
comprises the wind speed at different stations with a fixed return period. It is implicitly
assumed that this wind speed occurs simultaneously at all stations. In reality this is rarely the
case. Second, the wind direction is assumed to be the same over all stations. Neither this is
usually the case. For the omni-directional statistics a fixed wind direction for all stations must
be chosen.
In Section 8.1 the results will be presented of the statistical analysis applied to the
interpolated time series. In Section 8.2 the results of the statistical analysis on the measured
107
time series are used as input for the interpolation method. In Section 8.3 the resulting
patterns in the potential and macro wind are discussed. In Section 8.4 the results are
compared with those of Wieringa and Rijkoort. In Section 8.5 possible model artefacts are
discussed, which may influence the results. Finally, in Section 8.6 the conclusions are
summarized.
To make an objective comparison between both ways of integration, a fixed set of 19 stations
is used for statistical modelling. The stations concern 210 IJmuiden, 229 Texelhors, 235 De
Kooy, 240 Schiphol, 260 De Bilt, 265 Soesterberg, 270 Leeuwarden, 275 Deelen, 277
Lauwersoog, 280 Eelde, 290 Twenthe, 308 Cadzand, 310 Vlissingen, 330 Hoek van Holland,
344 Zestienhoven, 350 Gilze-Rijen, 370 Eindhoven, 375 Volkel and 380 Beek. Each of these
stations data comprises 30 years of data in the time period of 1972-2001.
Many geographical distributions of wind speed will be shown in this section. Note that in
these figure the coloured contours are the result of a mathematical procedure (spline).
Results of the interpolation method, and with that the effects of roughness, are only given at
the locations where numbers are plotted.
8.1
First interpolation, then statistics
The extreme events of 51 stations that are selected in dataset II (Section 7) are used again
in this section as input for the interpolation. For the validation procedure, the interpolation
results are not performed on a regular grid, but only at the station locations. For this purpose
the input value of the station under consideration is excluded from the input and simulated
with use of the data of the other stations (as described in Section 7). Of the 19 stations
mentioned the simulated time series are subjected to the statistical analysis to obtain return
levels that correspond to return periods of 0.5 year up to 10,000 years. In Section 8.1.1 the
results of this approach are described. In Section 8.1.2 the results are validated. In Section
8.1.3 the conclusions are summarized.
8.1.1
Results
In Figure G.1 the resulting 10,000-year return levels are plotted for the 19 stations. Note that
the spatial interpolation in the plot is constructed with a mathematical procedure. The
roughness map can be seen in the pattern, with lower values in the middle of the country
where the highest roughness lengths are, due to the woods. Along the coast the values are
higher due to the lower roughness lengths. In Figure G.1 the Barnes’ radius of influence R is
set to 300 km, the optimal value according to the validation of the interpolation technique
(Section 7.2). This radius implies a rather strong smoothing effect of the storm events,
especially when the extreme event is recorded only at one station. Therefore the 10,000-year
return levels based in simulated time series are underestimated. At some stations the highest
measurements are about 3 m/s higher then the return levels in Figure G.1. Higher return
levels are obtained when the simulated station itself is not excluded from the input data, but
108
still the smoothening effect of the interpolation method will be large (Section 7.2.2). It turns
out that many extreme events cannot be interpolated accurately. In the next section this
problem will be discussed with use of a simplified statistical method applied on the simulated
time series.
8.1.2
Validation
To evaluate the effect of smoothening storm events on the statistics in more detail a
simplified version of the statistical model is used without extrapolation. First, the storm filter is
applied to select independent storm maxima (Section 3.2). The corresponding hours are
ranked according to the exceedance frequencies of the maxima. In Figure G.2 the results of
this statistical analysis are shown for those stations that have remarkable results. The
plotting function used is described in Section 4.1. In the upper panel of Figure G.2 the storm
filter and ranking are applied on the measured and estimated wind speed, separately.
However, most extreme events in the simulated dataset do not have to occur simultaneous
with the measured events. This is illustrated in the lower panel of Figure G.2. Here the
measured wind speed is ranked and plotted according to the plot function together with the
estimated wind speed at the corresponding hours. The latter have not been ranked.
For most of the stations the exceedance frequencies of the simulated potential wind speed
with R = 300 km are lower than those of the measured wind speed, especially for higher
wind speeds. The differences between the wind speeds with a frequency of 0.01 per year
vary from − 1 to + 6 m/s. The chosen R clearly clearly has impact on the results of the
statistical analysis. For smaller radii ( R < 300 km) the simulated wind speed with an
exceedance frequency of 0.1 per year and higher, is scattered around the measured wind
speed. For a radius of 300 km and larger, the simulated wind speed is in general lower than
the measured wind speed. The underestimation becomes larger with larger radii. For the
stations with small differences shown in the upper panel of Figure G.2, in the lower panel the
simulated wind speed is scattered around the measured wind speed. The differences
between the simultaneously measured and simulated data can reach more than 10 m/s.
These large differences occur mainly during periods that either the measuring network was
less dense or a storm event was only observed at one station.
Apparently R has a large impact on the results of the statistical model, even without
extrapolation to high return levels. The larger R the stronger is the underestimation of
extreme events.
109
8.1.3
Conclusions
It is clear that the network density is insufficient to capture the small events, especially in the
earlier periods. This was already observed in some special cases (section 7.2.2). Even
nowadays too many storm events are only measured at one station, which makes simulation
of such a storm event impossible. Therefore most of the extreme wind speeds that occur
during storm events are smoothened by the interpolation technique. For this reason, the
simulated wind speed series at the station locations are generally lower than the measured
time series. This has large consequences for the statistical analysis. It is shown that when
first interpolation is applied it leads indeed to a severe underestimation of the wind speed
extremes for low return periods as well as for high return periods.
8.2
First statistics, then interpolation
We noticed that small-scale events causing high wind speeds are not always recorded, while
these events have a large impact on the estimated return levels. Apparently the chance that
a wind speed extreme is actually recorded by the observational network is not very large.
Therefore, the wind field can be considered “under-sampled in space”. Doing first the
statistical extrapolation may reduce or solve this problem. However, the extrapolating
enlarges statistical noise. This causes a high degree of variability between the analyses of
different stations, even when their mutual distance is small.
In this section we will examine whether it is possible to derive accurate estimates of the wind
speed for extreme return periods at a station location by interpolating the statistical
extrapolations from nearby stations. The simulated wind speed can then be compared to the
statistically derived extreme. Various values for the Barnes parameter R can again be used
as well as averaging the wind speed at macro level. We will focus our attention, however, to
averaging the macro wind. The test dataset is different from the that used in the interpolation
method and will described in Section 8.2.1. In Section 8.2.2 the results of this approach are
described. In Section 8.2.3 these results are discussed.
8.2.1
Test dataset
The dataset we use for input comprises the return levels that are obtained with the model
described in Section 3.The conditional Weibull distribution is used as probability distribution
and Method B is used to link the results to each other with regard to seasons and wind
directions. This statistical method is applied on the hourly measured data of 19 stations for
the time period 1972-2001. These stations are the same as used in Section 8.1. The
statistical model yields return levels for seasons and wind direction classes that form the
input for the interpolation method. The interpolation method needs a wind direction besides a
wind speed. For the marginal statistics per wind direction sector the wind direction of that
sector is imposed. For the omni-directional statistics the wind direction is set to southwest,
110
from which the most extreme wind speeds are likely to come. This assumption seems to be
justified for most of the stations.
8.2.2
Results
Figure G.3 shows the spatial pattern of the 10,000-year omni-directional annual return level
resulting from the statistical method (Section 3), which is used as input data for the
interpolation method. Figure G.4 shows the results after interpolation with the wind speed
averaged at macro level. In this figure the results of the interpolation are plotted on a larger
set than only the 19 stations. This is done for presentation purposes, while the analysis itself
is done on the 19 stations mentioned. As the wind speed is averaged at macro level, all
patterns found in Figure G.4 are the result of differences in roughness only. Contours are
drawn by the mathematical spline interpolation. Therefore the stations become more
consistent with each other. This contrasts with Figure G.3 where implausible patterns are
found. For instance, Figure G.3 shows larger extremes at some inland stations than along
the coast. As a result, the patterns in Figure G.4 may seem physical plausible, the
differences with Figure G.3 are rather large, however. Not only the values are different, but
also the pattern over the country is different.
8.2.3
Discussion
The implausible patterns in the input fields are primarily observed for return periods. The
patterns result from the parameters of the conditional Weibull distribution (CWD). These
concern the scale parameter α cwd and the shape parameter κ cwd . The shape parameter
becomes increasingly important for higher return periods. For relatively low return periods the
scale parameter dominates the estimates. Because the location and the scale parameter are
higher over sea and onshore than inland, return levels corresponding with low return periods
are higher onshore than inland.
For high return periods κ cwd becomes the dominating parameter. The κ cwd is higher over
sea and onshore than inland. This has as consequence that the difference in return levels
between coastal and inland stations becomes smaller with higher return periods. It can even
happen that above a certain return period the return level inland becomes higher than the
return level over sea and onshore. For a number of stations this happens within the range of
return periods of interest in this project. The differences in scale and shape parameter
between sea and onshore stations and inland are so large, that for the highest return periods
of interest non-realistic geographically patterns are generated.
The difference in shape parameters between onshore and inland is illustrated in Figure G.5
and Figure G.6. The κ cwd ’s are averaged over the inland stations 260, 265, 275, 290, 370,
375 and 380. The mean κ cwd is plotted in Figure G.5 as function of the wind direction for
different seasons. Direction 13 refers to the omni-directional distribution. In Figure G.6 the
same is done for the coastal stations 312, 316, 320, 321 and 331. It is seen that the mean
111
shape parameters scatters more for the coastal stations than for the inland stations. For
inland stations, κ cwd is in the range 1.5 to 3.0, while onshore it is in the range 2.0 to 4.0.
Both plots also indicate that there is no consistent pattern in a way that a certain season
gives higher or lower values for κ cwd over the directions compared with other seasons.
Inland κ cwd seems to be smaller for western wind than for eastern wind. Especially the
yearly statistics shows low shape parameter values for western wind. Such a pattern is not
found for the coastal stations.
In Figure G.7 the spatial distribution of the median of κ cwd over the seasons and thresholds
is plotted for western winds (wind direction classes 9, 10 and 11). The difference in shape
parameter shows up as a gradient from the coastal regions to inland regions. It could be
suggested that the wind speed distribution at macro level still has the same shape parameter
inland and along the coast. Then the difference in shape parameters at surface level would
result from the difference in surface roughness. In section 8.5 the impact of surface
roughness on κ cwd will be explored. This hypothesis implies that for eastern wind inland
values for κ cwd would extend up to the coast. In Figure G.8 the median of κ cwd for eastern
wind (wind direction classes 3, 4 and 5) is plotted. Indeed the pattern in shape parameter has
vanished. Surprisingly, however, the values in Figure G.8 are close to the coastal values for
western wind (Figure G.7), while one would expect that they would be close to the inland
values for western wind. This can only be explained by a different value for κ cwd for western
and eastern wind at macro level.
The κ cwd is an important parameter to the return levels with very low frequency of
exceedance. Patterns in κ cwd will result in patterns in the return levels for high return
periods. In the concept of the interpolation method, the wind at macro level has weak
patterns that can be interpolated easily. In the next section the patterns in the wind both at
surface and macro level are examined in detail.
8.3
Patterns in the potential and macro wind
The basic assumption of the interpolation method is that spatial differences in surface wind
speed are caused by differences in surface roughness and that these differences will
diminish at higher level in the planetary boundary layer. Examining the strength of the
patterns in the potential and macro wind can test this assumption. We will do this by fitting a
simple sloping plane to the data points. The wind speed, U in [m/s], is fitted to the following
model:
U = U offset + r x ⋅ (x − x offset ) + r y ⋅ (y − y offset )
(8.1)
For the offset coordinates the location (x offset , y offset ) = (150,450 ) are chosen (Amersfoortse
coordinates in km). The magnitude of the slope in [m/s /100km] is given by r = r x2 + r y2 ,
and the direction of increasing wind speed in [degrees] is given by β where tan β = r y r x .
112
The slope itself, SL in [%/100 km], is expressed as:
SL = 100% × r U offset
(8.2)
The results for the patterns in the slope and in the direction of increase as function of return
period for the potential wind and for the macro wind are plotted in Figure G.9 and Figure
G.10. Both figures contain the slope (filled circles) and angle in wind direction (open
triangles) for two different wind directions, west (blue) and east (red).
For potential wind from the west (Figure G.9, in blue) it is seen that for low return periods the
wind speed decreases going onshore, ~20% per 100 km, and direction increases ~310°. For
higher return periods the sea-inland pattern, the slope of the plane, becomes weaker. So the
difference in extreme wind speed between sea and inland becomes relatively smaller. The
direction of increase turns going from low to high return levels from northwest to north. For
potential wind from the east (Figure G.9, in red) the pattern is relatively stronger than for
western winds, although the absolute values of the wind speed will be smaller. The relative
strength of the pattern decreases only slightly with increasing return period. For all return
periods the eastern wind increases in northwest direction.
At macro level the slopes of the plane over the country for the two wind directions have
become weaker. Especially for eastern wind (Figure G.10, in red) the pattern is weak over all
return periods and its direction is therefore irrelevant. For western wind (Figure G.10, in blue)
there is hardly any pattern for small return periods. However, for higher return periods the
pattern becomes stronger, even stronger than at surface level (for 10,000-year return level:
potential wind ~12 %/100 km and macro wind ~16 %/100 km). The direction of increase turns
to east for all return periods.
The weak patterns for eastern and western wind for low return periods confirm the
assumption that the macro wind speed is suitable for interpolation. However, for large return
periods and western wind the pattern at macro level becomes very strong. Its direction of
increase, with higher values in the east, cannot be understood from a physical point of view.
Synoptic depressions gain depth over sea and fill up over land, mainly because of increased
roughness. Therefore the macro wind is expected to become smaller over land than over
sea.
113
8.4
Comparison with Wieringa and Rijkoort’s results
Apart from the region of Zeeland the pattern in the 10,000-year return level (Figure G.4)
agrees rather well with the pattern in the 1,000-year return levels of Wieringa and Rijkoort
(1983, Figure 5.21). The input values from Figure G.3 are far more irregular than those of
Wieringa and Rijkoort. It is important to notice, however, that Wieringa and Rijkoort were
forced to apply ad hoc adjustments to their results to come to a plausible geographical
pattern. For their figure 12 stations were used as input of which 3 stations have been
adjusted. The other data points in their figure are derived by interpolation of the distribution
parameters of the surface wind. Therefore these additional stations will fit in the pattern by
definition. Station 310 Vlissingen is the only “coastal” station used in the input dataset, the
other coastal stations are interpolated.
Using the values of Wieringa and Rijkoort’s Figure 5.21 as input for the computation of the
macro wind we observe that the inland values (∼30 m/s) and offshore values (∼40 m/s)
nearly yield the same macro wind speed. However, the values at some coastal stations (e.g.
32.5 m/s at station 330 Hoek van Holland, 33.6 m/s at station 225 IJmuiden) are expected to
be nearly the same to the offshore values as for western wind these stations experience no
roughness induced wind reduction.
The differences that can be seen in Figure G.4 between coastal and offshore stations may
be the result of the different definition of potential wind speed at sea stations compared with
coastal stations. For offshore stations a roughness length of 2 mm is used while for coastal
(and inland) stations a roughness length of 0.03 meter is used (Section 2). For the 10,000year return levels this difference in roughness yields a difference of about 3.5 m/s (see
Figure G.4). In the results of Wieringa and Rijkoort the difference between coastal and
offshore stations is clearly higher (about 7 m/s). This means that in Wieringa and Rijkoort’s
analysis the macro wind field along the coast is not consistent with the field offshore and
inland.
In absolute way the values of Wieringa and Rijkoort are generally higher than the ones
obtained by us, because about 3 m/s can be added to the 1,000-year return levels of
Wieringa and Rijkoort to obtain 10,000-year return levels. This yields a relative difference of
about 10% concerning the 10,000-year return levels.
Wieringa and Rijkoort (1983) also found a distinctive difference in shape parameter over sea
and land. They did not attempt to do any physical interpolation and so they did not encounter
the problem we face with currently. Wieringa and Rijkoort interpolated the parameters of the
statistical distribution instead, although they did not provide a procedure for this.
114
8.5
Possible model artefacts
The difference in shape parameter between land and sea is too large from a physical point of
view. This poses a serious problem to the interpolation of statistical extremes. In this section
we will examine various assumptions made in the interpolation method, the roughness maps,
and the derivation of the potential wind speed that may influence the estimated shape
parameter. In Section 8.5.1 the assumption of a fixed roughness length for sea is regarded.
In Section 8.5.2 an alternative algorithm for averaging the roughness length is explored.
8.5.1
Fixed gustiness roughness for potential wind speed over sea
In the method applied, the potential wind speed for offshore and coastal stations is derived
by computing the wind speed at meso level from the measured wind speed with a gustiness
derived roughness length (Section 6.1.2). This roughness length is not wind speed
dependent whereas the roughness of water is. The exposure correction that is computed
from the roughness length has a fixed value that is also not wind speed dependent. Scaling
the measured wind speed with a constant factor will not influence κ cwd ; only the scale
parameter α cwd will be modified.
For offshore stations it would have been possible to estimate the wind speed at meso level
using a roughness length derived from the Charnock relation instead of a fixed roughness
length. In that case the ratio between the wind speed at measuring level and meso level
would increase with wind speed. As a result there will be a change in shape parameter in the
meso and potential wind and consequently also in the macro wind. Next we will assess the
magnitude of this effect.
When doing a gustiness analysis the ratio between the maximum gust in one hour and the
average wind speed in the corresponding hour is determined (Verkaik, 2000). To prevent
convective turbulence dominating mechanical turbulence, only cases above a minimal wind
speed U thr are selected. Applying a higher U thr will increase the average wind speed of the
selected data. So, for offshore stations an increase in the gustiness derived roughness
length z0,gust as function of U thr may be visible.
For the direction 225°–245° z0,gust is plotted as function of the average wind speed in the
selected data for the stations 320 Lichteiland Goeree (LEG, Figure G.11) and station 321
Europlatform (EPF, Figure G.12). Values for U thr are applied in the range 6 − 20 m/s . The
average wind has been computed from the wind speed at sensor height, which is 38.3 m for
LEG and 29.1 m for EPF. The roughness lengths according to the Charnock relation are
plotted as well, using two different values for the Charnock parameter α ( α = 0.017 m and
α = 0.032 m). The increase of z0,gust with U thr is clear for both stations. For LEG the values
of z0,gust are smaller than those derived from the Charnock relation regardless the value of
α , except for the lowest threshold wind speeds. For EPF, z0,gust lies in between the two
values of α .
115
When determining the exposure corrections for the measured wind speed, the gustiness
analysis has been carried out using a rather low threshold wind speed to ensure a large
dataset in all direction bins. From the Figure G.11 and Figure G.12 it can be seen that the
roughness length approximates 0.3 mm in that case. Consequently, the meso wind speed
will be computed using this, rather low, value. Instead of using this fixed roughness length,
the Charnock relation could have been used as well. Figure G.11 and Figure G.12 show that
the Charnock relation with α = 0.017 can reasonably describe the roughness of the sea.
Then the ratio between the measured wind speed and the meso wind speed becomes wind
speed dependent.
In Figure G.13 the difference dU is plotted between the meso wind speed computed using a
fixed roughness length of 0.3 mm and the meso wind speed computed using the roughness
length that follows from the Charnock relation, z0 ,charnock . The differences are computed for
two values for the Charnock constants. In this example the sensor height has been fixed at
30 m. The difference is computed as:
dU =
U meso (z0,charnock )
U meso (z0 = 0.3 mm )
−1
(8.3)
The two different meso wind speeds, from fixed z0 and with a Charnock constant, can both
be transformed to macro level. Going from meso level to macro level in the two-layer model,
the roughness length over water is always computed from the Charnock relation. So for both
wind speeds the same roughness length will be used in this transformation. However, the
transformation to macro level is not linear in wind speed. This implies that the relative
difference between the meso wind speeds will be enhanced by the transformation. This
effect is illustrated in Figure G.13 as well.
Figure G.13 shows that the difference between the gustiness derived meso wind speed and
the one that follows from the Charnock relation, increases from about zero for low wind
speeds to about 2–3% for very high wind speeds. With the measured wind speeds, U sensor =
30 m/s, the difference in meso wind speed is in the range 1.4 to 2.1%, while for the macro
wind the range in dU is 1.5 to 2.2%. In the example of Figure G.13 a station with measuring
height 30 m has been chosen. For stations that have lower measuring height, the effect is
stronger since the height interval, over which the new roughness length is applied, from
measuring height to the blending height, is larger. For a station like station 312
Oosterschelde the effect is twice as strong.
The increasing correction with wind speed due to a different roughness length for sea can
deform the frequency distribution for high wind speeds at meso and macro level. For
example for station LEG the meso wind speed needs a correction increasing from 0% for 10
m/s to 3% for 40 m/s. The effect of the deformation has been assessed by applying a simple
linear transformation to the wind speed:
116

 U − 10 
U ' = U 1 + 0.03 ⋅ 

 30 

(8.4)
This deformation leads to an increase of the 10,000-year return level of 1 m/s (~3%). For
other stations this value will slightly differ.
8.5.2
Alternative roughness length averaging algorithm
When a land roughness is too high it will lead to an overestimation of the macro wind over
land. Averaging roughness lengths is done by averaging drag coefficients at the blending
height (Section 6.3.3). This method gives more weight to the largest roughness lengths in the
domain. In comparison to other algorithms published in literature this method yields the
largest roughness lengths over heterogeneous terrain (e.g. Claussen, 1990). So an
alternative algorithm will influence the sea–land pattern at macro level. The question rises to
what extent the chosen averaging algorithm explains the macro wind over land to be larger
than that over sea. We will examine this possibility by considering an alternative averaging
algorithm. Note that for homogeneous terrain all algorithms will yield the same roughness
length.
For any algorithm to average drag coefficients at the blending height, an effective roughness
length ( z0,eff ) can be computed. This is a value intended to represent a spatial average in
heterogeneous terrain such that by use of boundary layer similarity theory a correct average
of surface stress is found. The effective roughness length is expressed as:
2




1
1

 = 


 ln(z z

bh
0,eff ) 
 ln(zbh z0 ) 

Here zbh is the blending height. The brackets
2
(8.5)
indicate a spatial average.
As alternative algorithm we will average the logarithms of the roughness length. Claussen
(1990) showed that this method yields the smallest effective roughness lengths. The effective
roughness length is then calculated from:
ln z0,eff = ln z0
(8.6)
In Table 8.1 some examples of typical differences are given. We consider a domain
comprising two different roughness lengths with equal area fraction, z01 and z02 .
Furthermore we use zbh = 60 m, and for the computation of the effect on macro wind G we
use wind speed U = 30 m/s at height z = 10 m.
117
z01 [m]
z02 [m]
Type heterogeneity
z0,eff [m]
Cd
ln z0
G [m/s]
Cd
ln z0
Coastal area
0.001
0.1
0.024
0.010
61.9
57.0
Coastal area
0.001
0.3
0.070
0.017
70.3
59.9
Inland
0.100
1.0
0.460
0.320
100.6
91.9
Inland
0.300
1.0
0.610
0.550
109.4
105.7
Table 8.1: Effect of two different roughness lengths averaging algorithms on the effective roughness
length and on the macro wind speed with two different roughness lengths.
Table 8.1 shows that the differences in z0,eff and G are largest when the roughness lengths
in the domain are very different (second row). Wind speeds at macro level are always
smaller using the log-averaging ln z0 instead of the drag-averaging Cd . The largest
differences between the approaches can be expected in the coastal area, where the largest
differences in roughness lengths are observed. Going onshore the log-averaging adjust
slower to the high roughness over land, leading to a smaller macro wind just after the
coastline.
As the roughness will not change over the homogeneous sea surface, only the roughness
transformation to land may influence the pattern in the macro wind. The last row of the table
can be considered typical for a landscape comprising open farmland and urban or forested
areas both with a surface cover of 50%. The effect of a different averaging algorithm in this
example is about 5%. In a landscape where only 20% of the surface is rough ( z0 = 1 m ) and
80% is smooth ( z0 = 0.3 m ), the difference becomes smaller (2%) as the landscape
becomes more homogeneous.
Most of the stations are located in open land, so the difference will usually be smaller than
5%. Compared to the patterns found in the western macro wind at high return periods this
difference is insignificant.
8.6
Conclusions
The interpolation method applied to the present dataset is does not lead to acceptable
results to estimate extreme wind speeds at non-station locations. Frequently an extreme is
recorded at one station, while the wind speed at other stations is considerably lower. This
problem prohibits the interpolation of hourly measurements.
The interpolation of statistically extrapolated extremes reveals a remarkable difference in
behaviour of the statistical extrapolations between the coastal/offshore stations and the
inland stations. For high exceedance frequencies the gradient in the wind speed found at
surface level can be explained by differences in roughness between sea and land. For lower
exceedance frequencies the difference in surface wind speed becomes smaller than can be
expected from differences in roughness between sea and land.
118
The changing roughness of water as function of wind speed and the possible overestimation
of the average roughness over land do not fully explain the change in gradient at surface
level. This change results in awkward gradients in the macro wind: it becomes larger over
land than over sea. This gradient contradicts with the fact that synoptic depressions loose
strength when moving onshore as the result of increased roughness.
The return levels for high return periods of the coastal stations are low compared to those of
the land stations. This difference cannot be explained by the interpolation method. The most
extreme wind speeds are associated solely to wind from sea. Then the extremes of coastal
stations are expected to be much higher than those of land stations. This discrepancy
between statistical extrapolations and the concept of the interpolation method implies a major
adjustment of the extremes at the coast when the interpolation method is applied. Therefore,
the application of the interpolation method is not recommended at this stage.
119
120
9 Evaluation and recommendations
9.1
Evaluation
To model extreme values of wind speed a new statistical method has been developed to
replace the existing Rijkoort-Weibull model (RW-model). The RW-model could not be
reproduced. Moreover, some severe weaknesses of the RW-model have become clear,
concerning the persistence, tail correction, and the effect of low wind speeds on the extreme
return levels. The main difference of the developed statistical method with the RW-model is
the analysis of peak-over-threshold values (POT-values) instead of analysing of all hourly
wind speeds. This POT-model excludes the non-interesting, low wind speeds from the
analysis. The POT-values are modelled with the conditional Weibull distribution, which
performs better than, for instance, the generalized Pareto distribution. A threshold range is
used to reduce statistical uncertainties by averaging return levels over the threshold range. A
new method is developed to ensure correspondence between marginal statistics of separate
seasons and wind direction classes and the omni-directional annual statistics. This method
exploits the low statistical uncertainty of the annual statistics in combination with the
homogeneity of the separate seasons.
The station by station results of the model show reasonable patterns in wind speed over the
Netherlands for high exceedance frequencies. However, for low exceedance frequencies
irregular, noisy patterns in return level exist. These results may seem to be worse than the
results from the RW-model. However, Rijkoort applied ad hoc, irreproducible corrections to
their results in order to obtain a regular geographic pattern.
The return levels obtained with the present model can be compared to those of the original
RW-model. It shows that, averaged over the Netherlands, the 10,000-year return levels of
the POT-model are about 10% lower (≈32 m/s) than those of the RW-model (≈35 m/s). A
comparative analysis performed by HKVconsultants for nearly the same dataset and model
confirms these lower results of the POT-model.
The RW-model is tuned to yield the correct yearly maxima of wind speed. An analysis of the
yearly maxima based on the present dataset yields 10,000-year return levels that are about
12% higher than obtained from the POT-model. However, the results from the yearly maxima
analysis are very unreliable since it yields extremely large return level for some stations.
HKVconsultants also came to higher return levels analysing the yearly maxima compared to the
POT-model (about 6%). HKVconsultants also performed a Bayesian analysis of 10 stations,
including statistical uncertainties, on the peak-over-threshold values and the yearly maxima.
This yielded 6% higher return levels concerning the peak-over-threshold values and 12%
higher return levels concerning the yearly maxima compared with the POT-model. It should
be noted that the differences given here are averages over the stations. There are large
differences between the analyses of individual stations.
121
Comparing the time periods 1962-1981 and 1982-2001 it appeared that the corresponding
return levels differ systematically. For the latter period the return levels with a return period of
10,000 years are on average almost 2 m/s lower. This difference is just significant and
reflects climate variations. Furthermore, the observed geographical patterns corresponding
with high return periods are different for the two time periods and are therefore mainly the
result of statistical uncertainties.
The geographical interpolation method developed in this project is well suited to replace the
spatial interpolation methods developed by RWS. The major difference between the current
methods and the presently proposed method is the height at which the wind speed is
interpolated or assumed constant. In the methods of RWS this height is the top of the surface
layer for the inland waters. For the coast and the estuaries the statistics of a coastal station,
representative for wind over water, is used directly without any transformation. The impact of
large-scale roughness changes, occurring over the inland water and the estuaries, on the
wind profile in the Ekman layer, the layer above the surface layer, is missing. In the method
developed here the wind is interpolated at the top of the Ekman layer so the impact of the
large-scale roughness on the wind profile in the Ekman layer is present. Consequently, the
estimated surface wind speed over water resulting from the present method is larger than the
current methods of RWS. This increase can be larger than tens of percents. Its magnitude
depends strongly on the difference in roughness between land and water, however.
A consistent spatial pattern in return levels over the complete domain, including the
Netherlands and the coastal waters, is not achieved, however, with the currently developed
statistical model and interpolation method. On the one hand, the limited spatial density of the
measuring network and the irregular patterns in wind fields during storm events inhibits the
interpolation of hourly averaged wind speeds. On the other hand, the interpolation of
statistically extrapolated extremes is hampered by a systematic and partially unexplained
difference in curvature of the statistical extremes. This difference in curvature is most
obvious seen in the comparison of the return levels for coastal stations and inland stations.
The return levels at the coast are relatively lower than those inland. Due to the difference in
roughness, the macro wind will become larger inland than at the coast. This result can be
considered physically unrealistic.
A prototype application is developed transforming statistics from one station to its direct
surrounding, including the effects of changing roughness. The user made choice for a
particular input station is crucial. Using different stations as input may lead to considerably
different estimates.
122
9.2
Recommendations
A complete update of the RW-model has not been achieved. To achieve this a successful
integration of the statistical method and the interpolation method is required. This will reduce
the uncertainties of and the differences between the individual analyses of the station
statistics. Simulations can then be used to determine the ranges of uncertainty in the return
levels. The large uncertainties associated with the spatial patterns and interpolation make
such simulation superfluous at this point.
In the line of the KNMI-HYDRA project, a better understanding and interpretation of the
physical nature of the extremes present in the dataset is needed. The failure to interpolate
the wind speed with regard to extremes indicates a mismatch between the physical events
selected and the physical model employed. The irregularity of the return levels at the stations
indicates that an alternative definition of storms and selection of extreme events may lead to
a spatially more homogeneous analysis.
The observed difference in the curvature of the statistical analysis between sea and land, if
still present then, may be explained by applying a more sophisticated physical model of the
atmospheric boundary layer. This model may also reveal the exact influence of atmospheric
stability, which is assumed to be negligible in this study. Applying the model on hourly data
may lead to restrictions on the shape parameter of the statistical distributions. Doing so, the
specific sampling effect of using hourly averaged wind speed needs to be considered.
Alternatively, analysing simultaneously measured wind speeds, as coherent wind fields, may
be a way to circumvent the limitations imposed by the density of the observation network.
Using a (simple) re-analyses tool more meteorological data can be used.
The present statistical analysis shows that the results of the RW-model for the stations are
not biased. The proposed interpolation method, however, leads to significantly higher wind
speed estimates over the inland water bodies. The large impact this may have on the models
in use by RWS justifies an elaborate validation of this effect. To begin the present dataset
can be used for further analysis. However, many KNMI measuring stations at strategic
locations have been removed the last decennia. Therefore, a dedicated measuring campaign
may be required.
The statistical results for station locations will be made available in phase report 14. These
tables should be used with caution: on average the return levels presented are lower than
those from alternative analyses. Moreover, there are large differences in the exceedance
frequencies between stations.
Within the limits of its accuracy the interpolation method can be used for moderate wind
speeds. The method can also be used to transform the statistics from a station to its
surrounding taking into account the surface roughness.
123
124
References
Agterberg, R. and Wieringa, J., 1989. Mesoscale terrain roughness mapping of the
Netherlands. Technical Report, TR-115, Royal Netherlands Meteorological Institute
(KNMI), the Netherlands.
Barnes, S.L., 1964. A technique for maximizing details in numerical weather maps analysis.
Journal of Applied Meteorology, 3, 396−409.
Bayes, T., 1763. An essay towards solving a problem in the doctrine of chances.
Philosophical transactions of the Royal Society of London, 53, 370−418.
Benschop, H., 1996. Windsnelheidsmetingen op zeestations en kust stations: herleiding
waarden windsnelheid naar 10-meter niveau (Dutch). Technical Report, TR-188, Royal
Netherlands Meteorological Institute (KNMI), the Netherlands.
Bergström, H., Johansson, P.-E. and Smedman, A.-S., 1988. A study of wind speed
modification and internal boundary-layer heights in a coastal region. Boundary-Layer
Meteorology, 42, 313−335.
Bradley, E.F., 1968. A micrometeorological study of velocity profiles and surface drag in the
region modified by a change in surface roughness. Quarterly Journal of the Royal
Meteorological Society, 94, 361−379.
Buishand, T.A., 1982. Some methods for testing the homogeneity of rainfall records. Journal
of Hydrology, 58, 11-27.
Charnock, H., 1955. Wind stress on a water surface. Quarterly Journal of the Royal
Meteorological Society, 81, 639.
Claussen, M., 1989. Subgrid-scale fluxes and flux divergences in a neutrally stratified,
horizontally inhomogeneous surface-layer. Contributions to atmospheric physics, 62,
236−245.
Claussen, M., 1990. Area-Averaging of Surface Fluxes in a Neutrally Stratified, Horizontally
Inhomogeneous Atmospheric Boundary Layer. Atmospheric Environment, 24A,
1349−1360.
Cook, N.J., 1982. Towards better estimation of wind speeds. Journal of Wind Engineering
and Industrial Aerodynamics, 9, 295−323.
Davison, A.C., 1984. Modelling excesses over high thresholds, with an application. Statistical
Extremes and Applications (J. Tiago de Oliveira, ed.), 461−482, Reidel, Dordrecht.
Davison, A.C. and Smith, R.L., 1990. Models for exceedances over high thresholds. Journal
of the Royal Statistical Society: Series B, 3, 393−442.
Deaves, D.M., 1981. Computations of wind flow over changes in surface roughness. Journal
of Wind Engineering and Industrial Aerodynamics, 7, 65−94.
De Rooy, W.C., 1995. Regionalisation of meteorological parameters. Scientific Report,
WR95-06, Royal Netherlands Meteorological Institute (KNMI), the Netherlands.
De Waal, J.P., 2002. Windmodellering voor bepaling waterstanden en golven. Report in
progress, RIZA, Lelystad, the Netherlands.
De Wit, A.J.W., van der Heijden, Th.G.C. and Thunnissen, H.A.M., 1999. Vervaardiging en
nauwkeurigheid van het LGN grondgebruiksbestand (Dutch). Report, 663, DLO-Staring
Centrum, Wageningen, the Netherlands.
125
Duijm, N.J., 1983. Model voor de stroming in een neutrale oppervlakte laag na een
verandering in oppervlakte ruwheid (Dutch). Scientific Report, WR83-3, Royal
Ettema, J., 2003. Analysis of wind fields for wind climate assessment of the Netherlands, a
literature study. Royal Netherlands Meteorological Institute (KNMI), Climatological
Services, the Netherlands.
Fisher, R.A. and Tippett, L.H.C., 1928. Limiting forms of the frequency distribution of the
largest or smallest members of a sample. Mathematical Proceedings of the Cambridge
Philosophical Society, 24, 180−190.
Franke, R., 1982. Smooth interpolation of scattered data by local thin plate splines. Comp. &
Maths. with Applls, 8-4, 237−281.
Garratt, J.R., 1977. Review of drag coefficients over oceans and continents. Monthly
Weather Review, 105, 915−929.
Gringorten, I.I., 1963. A plotting rule for extreme probability paper. Journal of Geophysical
Research, 68, 813−814.
Harris, R.I., 1996. Gumbel re-visited - a new look at extreme value statistics applied to wind
speeds. Journal of Wind Engineering and Industrial Aerodynamics, 59, 1−22.
Horst, T.W., and Weil, J.C., 1992. Footprint estimation for scalar flux measurements in the
atmospheric surface layer. Boundary-Layer Meteorology, 59, 279−299.
Horst, T.W., 1999. The footprint for estimation of atmosphere-surface exchange fluxes by
profile techniques. Boundary-Layer Meteorology, 90, 171−188.
Hutjes, R.W.A., 1996. Transformation of near-surface meteorology in a small-scale
landscape with forests and arable land. PhD thesis, Rijksuniversiteit Groningen, the
Netherlands.
Jackson, P.S., and Hunt, J.C.R., 1975. Turbulent wind flow over a low hill. Quarterly Journal
of the Royal Meteorological Society, 101, 929−955.
Jacobs, A.F.G., 1984. The flow around a thin closed fence. Boundary-Layer Meteorology, 28,
317−328.
Jenkinson, A.F., 1955. The frequency distribution of the annual maximum (or minimum)
values of meteorological elements. Quarterly Journal of the Royal Meteorological
Society, 81, 158−171.
Kalk, H. and Van Noortwijk, J., 2003. Bayesian estimation of wind velocity return periods.
HKVconsultants, The Netherlands.
Krishnamurti, T.N., and Bounoua, L., 1996. An introduction to numerical weather prediction
techniques. CRC Press, Boca Raton, Florida, 293 pp.
Kudryavtsev, V.N., Makin, V.K., Klein Tank, A.M.G. and Verkaik, J.W., 2000. A model of wind
transformation over water-land surfaces. Scientific Report, WR-2000-01, Royal
Palutikof, J.P., Brabson, B.B., Lister, D.H. and Adcock, S.T., 1999. A review of methods to
calculate extreme wind speeds. Meteorological Applications, 6, 119−132.
Panofsky, H.A. and Dutton, J.A., 1984. Atmospheric Turbulence. Models and Methods for
Engineering Applications. Jon Wiley & Sons, New York, 397 pp.
126
Rao, K.S., Wyngaard, J.C. and Coté, O.R., 1974. The structure of the Two-Dimensional
Internal Boundary Layer over a Sudden Change of Surface Roughness. Journal of the
Atmospheric Sciences, 31, 738−746.
Rijkoort, P.J., 1983. A compound Weibull model for the description of surface wind velocity
distributions. Scientific Report, WR 83-13, Royal Netherlands Meteorological Institute
(KNMI), the Netherlands.
Roskam, A.P., Hoekema, J. and Seijffert, J.J.W., 2000. Richtingsafhankelijke extreme
waarden voor HW-standen, golfhoogte en golfperioden. National Institute for Coastal
and Marine Management (RIKZ), the Netherlands.
Schmid, H.P., 1994. Source areas for scalars and scalar fluxes. Boundary-Layer
Meteorology, 67, 293−318.
Smits, A., 2001a. Analysis of the Rijkoort-Weibull model. Technical Report, TR-232, Royal
Smits, A., 2001b. Estimation of extreme return levels of wind speed: a modification of the
Rijkoort-Weibull model. Royal Netherlands Meteorological Institute (KNMI),
Climatological Services, the Netherlands.
Smits, A., 2001c. Estimation of extreme return levels of wind speed: an analysis of storm
maxima. Royal Netherlands Meteorological Institute (KNMI), Climatological Services, the
Netherlands.
Townsend, A.A., 1965. The response of a turbulent boundary layer to abrupt changes in
surface conditions. Journal of Fluid Mechanics, 22, 799−822.
Troen, I. and Petersen, E.L., 1989. European Wind Atlas. Risø National Laboratory.
Roskilde, Denmark.
Thunnissen, H.A.M. and De Wit, A.J.W. The national land cover database of the
Netherlands. In K.J. Beek & M. Molenaar (eds.), Geoinformation for all. XIX congress of
the International Society for Photogrammetry and Remote Sensing (ISPRS). [Lemmer],
GITC, 2000. Int. Arch. Photogramm. Remote Sens. Vol. 33, Part B7/3, 223−230 (cd-rom)
Van den Brink, H.W., Können, G.P. and Opsteegh, J.D., 2002. The reliability of extreme
surge levels, estimated from observational records of order hundred years. Journal of
Coastal Research.
Van Ulden, A.P. and Wieringa, J., 1996. Atmospheric boundary layer research at Cabauw.
Boundary-Layer Meteorology, 78, 39−69.
Van Wijk, A.J.M., Beljaars, A.C.M., Holtslag, A.A.M. and Turkenburg, W.C., 1990. Diabatic
wind speed profiles in coastal regions: comparison of an internal boundary layer (IBL)
model with observations. Boundary-Layer Meteorology, 51, 49−74.
Verkaik, J.W., 2000. Evaluation of two gustiness models for exposure correction calculations.
Journal of Applied Meteorology, 39, 1613−1626.
Verkaik, J.W., 2001. Documentatie windmetingen in Nederland (Dutch). Royal Netherlands
Meteorological Institute (KNMI), Climatological Services, the Netherlands.
Von Mises, R., 1936. La Distribution de la Plus Grande de n Valeurs. Reprinted in Selected
Papers, II, Amer. Math. Soc., Providence, RI (1954), 271-294.
Von Neumann, J., 1941. Distribution of the ratio of the mean square successive difference to the
variance. Ann. Math. Statist., 13, 367-395.
127
Waarts, P.H., de Wit, M.S. and Vrouwenvelder, A.C.W.M., 2002. Traffic loads in The
Netherlands: from measured data to design values. TNO Building and Construction
Research and Delft University of Technology, the Netherlands.
Walmsley, J.L., 1989. Internal boundary-layer height formulae — a comparison with
atmospheric data. Boundary-Layer Meteorology, 47, 251−262.
Waterloopkundig Laboratorium (WL), EAC/RAND, 1993. Toetsing uitgangspunten
rivierdijkversterkingen: deelrapport 2: Maatgevende belastingen.
Wieringa, J., 1976. An objective exposure correction method for average wind speeds
measured at a sheltered location. Quarterly Journal of the Royal Meteorological Society,
102, 241−253.
Wieringa, J. 1986. Roughness-dependent geographical interpolation of surface wind speed
averages. Quarterly Journal of the Royal Meteorological Society, 112, 867−889.
Wieringa, J., 1993. Representative roughness parameters for homogeneous terrain.
Boundary Layer Meteorology, 63, 323−363.
Wieringa, J., and Rijkoort, P.J., 1983: Windklimaat van Nederland. (Dutch). Staatsuitgeverij,
Den Haag, the Netherlands, 263 pp.
128
List of symbols
Symbols corresponding with Section 3, 4 and 5.
a0 , a1,..., a4
b1, b2 ,..., b4
f
i
j
m
p
pt
pcf
pcf t
s
tcf
u
y
ysf
Aω
E
F
Fd
Fn
Fp
G
H0
HA
M
N
S
T
U
Y
α
β
γ
γ stab
ε
ϑ
κ
λ
σ
harmonisation terms [-]
harmonisation terms [-]
fraction of station independent multiplication factor [-]
wind direction class [-]
season [-]
index of ranked value [-]
percentile of storm maxima [-]
transformed percentile of storm maxima [-]
persistence correction factor [-]
transformed persistence correction factor [-]
station number [-]
tail correction factor [-]
wind speed [m/s]
Gumbel reduced variate [-]
year-to-season factor [-]
set including hours with corresponding wind speed higher than ω [-]
mean excess [m/s]
cumulative distribution function [-]
cumulative distribution function during daytime [-]
cumulative distribution function during nighttime [-]
plotting position [-]
exceedance frequency per year [-]
null hypothesis [-]
alternative hypothesis [-]
total number of storm maxima [-]
sample size [-]
total number of stations [-]
return period [years]
return level [m/s]
number of years [-]
(conditional) Weibull scale parameter [m/s]
GEV scale parameter [m/s]
GPD shape parameter [-]
stability parameter [-]
random disturbance [-]
GEV shape parameter [-]
(conditional) Weibull shape parameter [-]
GEV location parameter [m/s]
GPD scale parameter [m/s]
129
ω
CWD
GEV
GPD
threshold [m/s]
conditional Weibull distribution
generalised extreme value
generalised Pareto distribution
Symbols corresponding with Section 6, 7 and 8.
d
dU
f
fw
g
r
s
u
u*
u* m
u'
v
wk
w'
xi
x
y
z
zbh
z0
z0 h
z0 m
z0,charnock
z0,eff
z0, gust
z0, map
z0m,map
z1
z2
A
B
Cd
D
DD
DDmacro
E z0
distance from grid point to observation point in interpolation algorithm [m]
difference in wind speed [m/s]
Coriolis parameter (f = 1.1 ⋅ 10 −4 ) [Hz]
fraction surface covered with water [-]
acceleration of gravity (g = 9.82) [m/s2]
magnitude of the slope of a plane [m/s /100km]
station number
eastwards component of the wind speed [m/s]
friction velocity [m/s]
friction velocity at blending height [m/s]
turbulent fluctuation of horizontal wind speed [m/s]
northward component of wind speed [m/s]
weighted moving average
turbulent fluctuation of vertical wind speed [m/s]
distance from source area to evaluation point i [m]
Amersfoortse x-coordinate [km]
Amersfoortse y-coordinate [km]
height [m]
blending height, interface between surface layer and Ekman layer [m]
local roughness length [m]
roughness length due to orography [m]
meso roughness length [m]
local roughness length from Charnock relation [m]
effective local roughness length [m]
local roughness length from gustiness analysis [m]
local roughness length from land-use map [m]
meso roughness length from land-use map [m]
height 1 [m]
height 2 [m]
stability dependent parameter ( A = 1.9 in neutral conditions)
stability dependent parameter (B = 4.5 in neutral conditions)
drag coefficient
length scale of footprint approximation [m]
wind direction [degrees]
wind direction at macro level [degrees]
error ratio between z0,map and z0,gust [-]
130
G
N
N po int
N pass
PBL
R
S
SL
U
Ue
Uo
U macro
U meso
Up
U sensor
U thr
Vmacro
W
α
α cwd
β
∆H
Ω
κ
κ cwd
ϕ
ν
macro wind [m/s]
total number of stations [-]
number of nearest grid points in interpolation algorithm (N po int = 5 ) [-]
maximum of ν in interpolation algorithm (N pass = 5) [-]
planetary boundary layer
radius of influence in interpolation algorithm [m]
weighted surface in footprint approximation [m2]
slope of a plane in macro wind [%/100 km]
wind speed [m s-1]
estimated wind speed [m/s]
observed wind speed [m/s]
macro wind component parallel to surface wind [m/s]
meso wind speed [m/s]
potential wind speed [m/s]
wind speed at sensor height [m/s]
threshold [m/s]
macro wind component perpendicular to U macro [m/s]
weight function
Charnock constant [-]
conditional Weibull scale parameter [-]
direction of increasing wind speed [degrees]
surface height difference over distance [m]
angular velocity of the Earth’s rotation
von Kármán constant (κ = 0.4) [-]
conditional Weibull shape parameter [-]
latitude
ν -iteration in interpolation algorithm [-]
131
132
Appendices
A Figures corresponding with Section 2
Figure A.1: Times series of 51 stations used for validation of interpolation method
133
a.
b.
c.
Figure A.2: Spatial distribution of operational measurement stations in a) 1965; b) 1985, and c) 2001.
134
B Figures corresponding with Section 3
Figure B.1a: Threshold plots for the season January/February. The upper left graph corresponds with
100 year return levels, the upper right graph with 10,000-year return levels. The lower graph
summarizes these values by showing median values. The denominator on the axes (10 year return
level) is obtained by making use of the empirical distribution function.
135
Figure B.1b: Threshold plots for the whole year. The upper left graph corresponds with 100 year
return levels, the upper right graph with 10,000-year return levels. The lower graph summarizes these
values by showing median values. The denominator on the axes (10 year return level) is obtained by
making use of the empirical distribution function.
136
Figure B.2a: Year-to-season factors corresponding with a return period of 0.5 year.
137
Figure B.2b: Year-to-season factors corresponding with a return period of 10,000 year.
138
C Figures corresponding with Section 4
Figure C.1a: Validation of model results (model minus observations). The results correspond to the
CWD applied on stations presented in Figure 3.1 (31 stations).
139
Figure C.1b: Validation of model results (model minus observations). The results correspond to the
GPD applied on stations presented in Figure 3.1 (31 stations).
140
Figure C.1c: Validation of model results (model minus observations). The results correspond to the
CWD applied on stations with at least 40 years data (13 stations).
141
Figure C.1d: Validation of model results (model minus observations). The results correspond to the
GPD applied on stations with at least 40 years data (13 stations).
142
Figure C.2a: Comparison of model results. The results correspond to the CWD applied on stations
presented in Figure 3.1 (31 stations).
143
Figure C.2b: Comparison of model results. The results correspond to the GPD applied on stations
presented in Figure 3.1 (31 stations).
144
Figure C.3a: 0.5 year return levels in m/s following Method 0. Two time periods have been evaluated:
1962-1981 and 1982-2001. For both time periods the CWD and GPD are used.
145
Figure C.3b: 10,000-year return levels in m/s following Method 0. Two time periods have been
evaluated: 1962-1981 and 1982-2001. For both time periods the CWD and GPD are used.
146
Figure C.4a: Comparison plots between annual omni-directional storm maxima on the one side and
Method A and B (based on the CWD) on the other side.
147
Figure C.4b: Continuation of Figure C.4a.
148
Figure C.4c: Continuation of Figure C.4b.
149
Figure C.4d: Continuation of Figure C.4c.
150
Figure C.4e: Continuation of Figure C.4d.
151
Figure C.4f: Continuation of Figure C.4e.
152
Figure C.5a: Annual omni-directional return levels based on Method A and the CWD.
153
Figure C.5b: Annual omni-directional return levels based on Method B and the CWD.
154
Figure C.6a: 10,000-year annual and omni-directional return levels and 10,000-year return levels per
season and wind direction class based on Method B and the CWD.
155
Figure C.6b: Continuation of Figure C.6a.
156
Figure C.6c: Continuation of Figure C.6b.
157
Figure C.6d: Continuation of Figure C.6c.
158
Figure C.6e: Continuation of Figure C.6d.
159
Figure C.6f: Continuation of Figure C.6e.
160
D Figures corresponding with Section 5
Figure D.1: 10,000-year return levels based on the Gumbel distribution for the seasons 1 (January,
February), 4 (July, August) and 6 (November, December) and for the whole year.
161
162
E Figures corresponding with Section 6
Wind speed (m s-1)
8
6
4
200 m
140 m
80 m
40 m
20 m
10 m
2
0
2
4
6
8
10 12 14 16 18 20 22 24
Time of Day (GMT)
DDz - DD200 m (degrees)
Figure E.1: Diurnal cycle of the average wind speed in May at the Cabauw tower.
0
-10
140 m
80 m
40 m
20 m
10 m
-20
-30
2
4
6
8
10 12 14 16 18 20 22 24
Time of Day (GMT)
Figure E.2: Diurnal cycle of the average wind direction in May at the Cabauw tower.
163
102
Blending Height
Reference Height
101
Height (m)
Meso Wind
100
Potential Wind
Local z0
Measured Wind
-1
10
Reference z0
10-2
0
2
4
6
-1
8
10
Wind Speed (m s )
Macro wind - 10-m wind
35
Wind Direction Veer
Wind Speed Increase Factor
6
30
5
4
25
3
20
2
1
10-3
10-2
10-1
100
15
Wind Direction Veer (degrees)
Wind Speed Increase Factor
Figure E.3: Definition of the potential wind speed. The measured wind speed is transformed upwards
to the blending height using the local roughness length. Then it is transformed downwards to
reference height using the reference roughness length.
Roughness length (m)
Figure E.4: Relation between the surface wind and the macrowind and the wind veer as function of
roughness length.
164
40
Macro Wind Speed (m s-1)
Meso roughness length (m):
35
30
0.0001
0.001
0.01
0.05
0.1
0.5
25
20
15
50
75
100
125
150
175
200
Blending Height (m)
Figure E.5.: Influence of the choice for the blending height on the macrowind speed for different
values of the meso-roughness. The local roughness used here is 0.1 m and the wind speed at 10-m
height is 10 m/s.
60
Equilibrium boundary layer
Internal boundary layer
Height (m)
Undisturbed upstream profile
40
20
0
Transition region
0
100
200
300
New equilibrium
400
500
Fetch (m)
Figure E.6: Growth of the internal boundary layer after a change in surface roughness.
165
2
Height (m)
102
Undisturbed upstream profile
4
3
2
IBL-height
101
4
3
2
New equilibrium profile
100
2
3
4
5
6
Wind Speed (m s-1)
Figure E.7: Typical wind speed profile at some distance after a smooth-to-rough change in surface
roughness.
Wind speed (m s-1)
z0 = 0.001 m → z0 = 0.1 m
Hydra
Townsend
WAsP
Kudryavtsev & Makin
Coast
10
9
8
7
0
1
2
3
4
5
6
7
8
9
10
Distance (km)
Figure E.8: Adjustment of the 10-m wind after a smooth-to-rough change in roughness according to a
number of models.
166
Wind speed (m s-1)
z0 = 0.1 m → z0 = 0.001 m
10
9
Hydra
Townsend
WAsP
Kudryavtsev & Makin
8
7
0
1
2
3
4
5
6
7
8
9
10
Distance (km)
Figure E.9: Adjustment of the 10-m wind after a rough-to-smooth change in roughness
according to a number of models.
10 m s-1
Figure E.10: Macrowind field on the station location (May 28, 2000; 15:00 hour GMT).
167
10 m s-1
Figure E.11: Macrowind field on the station location in black, in grey the wind field fitted with Barnes’
R = 20 km (May 28, 2000; 15:00 hour GMT).
10 m s-1
Figure E. 12: As Figure E.11 with Barnes’ R = 70 km.
168
10 m s-1
Figure E.13: As Figure E.11 with Barnes’ R = 140 km.
Figure E.14: Schematic representation of the footprint. The lower (white) footprint, corresponding to
the surface layer, mainly comprises land. The larger (red) footprint, corresponding to the Ekman layer,
entirely comprises water surface.
169
1.0
Weight
0.8
0.6
0.4
0.2
0.0
0
1
2
3
4
5
6
7
8
9
10
Distance (km)
Figure E.15: Footprint weighting function for distance exp(− x D ) , with D = 3 km.
0.25
Weight
0.20
0.15
0.10
0.05
0.00
k-3
k-2
k-1
k
k+1 k+2 k+3
Bin
Figure E.16: Directional smoothing function for the footprint. Each bin is 5° wide.
170
Land-use Roughness (m)
100
All stations
260 De Bilt
240 Schiphol
250 Terschelling
3
2
10-1
3
2
10-2
3
2
10-3
3
2
10-4 -4
10
2
3 4
10-3
2
3 4
10-2
2
3 4
10-1
2
3 4
100
Gustiness Roughness (m)
Figure E.17: Scatter plot of the gustiness derived roughness length versus the roughness length
resulting from the land-use map and footprint model. The footprint length scale used here is 600 m.
1.4
All stations
260 De Bilt
240 Schiphol
250 Terschelling
Error Factor
1.3
1.2
1.1
1.0
0.9
0.8
10-4
2
3 4
10-3
2
3 4
10-2
2
3 4
10-1
2
3 4
100
Gustiness Roughness (m)
Figure E.18: Error factor (see text for definition) as function of the gustiness derived local
roughness length.
171
Figure E.19: Land-use map of station 315 Hansweert and its surroundings. The location of the wind
mast is indicated by the intersection point of the white lines in the centre of the map. The area plotted
here is (20 km)2.
Roughness length (m)
100
Land-use
Gustiness analysis
3
2
10-1
3
2
10-2
3
2
10-3
3
2
10-4
0
45
90
135
180
225
270
315
360
Wind direction (degrees)
Figure E.20: Roughness length from the land-use map and the gustiness analysis as function of wind
direction at the location 315 Hansweert.
172
station 210 Valkenburg
2
0.01
0.001
0.0001
0
30
60
90
station 229 Texelhors
roughness length (m)
0.01
90
120 150 180 210 240 270 300 330 360
wind direction (degrees)
station 235 De Kooy
z0 local
z0 meso
z0 gustiness
0.1
0.01
0.001
30
60
90
0.0001
0
120 150 180 210 240 270 300 330 360
station 240 Schiphol
2
30
60
90
0.01
z0 local
z0 meso
z0 gustiness
1
0.1
120 150 180 210 240 270 300 330 360
station 252 K13
2
z0 local
z0 meso
z0 gustiness
1
60
1
0.001
0.001
0.1
0.01
0.001
30
60
90
0.0001
0
120 150 180 210 240 270 300 330 360
station 260 De Bilt
2
30
60
90
0.01
z0 local
z0 meso
z0 gustiness
1
0.1
120 150 180 210 240 270 300 330 360
station 265 Soesterberg
2
z0 local
z0 meso
z0 gustiness
1
30
2
z0 local
z0 meso
z0 gustiness
0.1
0.1
0.01
0.001
0.001
0.0001
0
0.01
0.0001
0
120 150 180 210 240 270 300 330 360
1
0.0001
0
0.1
0.001
2
0.0001
0
z0 local
z0 meso
z0 gustiness
1
0.1
station 225 IJmuiden
2
z0 local
z0 meso
z0 gustiness
1
30
60
90
0.0001
0
120 150 180 210 240 270 300 330 360
30
60
90
120 150 180 210 240 270 300 330 360
Figure E.21: Roughness lengths (m) derived with gustiness analysis (blue), and with footprint
approximation for local (length = 600 m) and meso-scale (length = 10 km) for stations 210, 225, 229,
235, 240, 252, 260 and 265.
173
station 269 Lelystad
2
0.01
0.001
30
60
90
station 275 Deelen
0.01
90
120 150 180 210 240 270 300 330 360
station 277 Lauwersoog
z0 local
z0 meso
z0 gustiness
0.1
0.01
0.001
30
60
90
0.0001
0
120 150 180 210 240 270 300 330 360
station 279 Hoogeveen
2
30
60
90
0.01
z0 local
z0 meso
z0 gustiness
1
0.1
120 150 180 210 240 270 300 330 360
station 280 Eelde
2
z0 local
z0 meso
z0 gustiness
1
60
1
0.001
0.001
0.1
0.01
0.001
30
60
90
0.0001
0
120 150 180 210 240 270 300 330 360
station 285 Huibertgat
2
30
60
90
0.01
0.001
z0 local
z0 meso
z0 gustiness
1
0.1
120 150 180 210 240 270 300 330 360
station 290 Twenthe
2
z0 local
z0 meso
z0 gustiness
1
30
2
z0 local
z0 meso
z0 gustiness
0.1
0.0001
0
0.01
0.0001
0
120 150 180 210 240 270 300 330 360
1
0.0001
0
0.1
0.001
2
0.0001
0
z0 local
z0 meso
z0 gustiness
1
0.1
0.0001
0
station 270 Leeuwarden
2
z0 local
z0 meso
z0 gustiness
1
0.1
0.01
0.001
30
60
90
120 150 180 210 240 270 300 330 360
0.0001
0
30
60
90
120 150 180 210 240 270 300 330 360
Figure E.21b: Same as Figure E.21a for stations 269, 270, 275, 277, 279, 280, 285 and 290.
174
station 308 Cadzand
2
0.01
0.001
30
60
90
station 312 Oosterschelde
0.01
90
120 150 180 210 240 270 300 330 360
station 316 Schaar
z0 local
z0 meso
z0 gustiness
0.1
0.01
0.001
30
60
90
0.0001
0
120 150 180 210 240 270 300 330 360
station 320 L.E. Goeree
2
30
60
90
0.01
z0 local
z0 meso
z0 gustiness
1
0.1
120 150 180 210 240 270 300 330 360
station 321 Europlatform
2
z0 local
z0 meso
z0 gustiness
1
60
1
0.001
0.001
0.1
0.01
0.001
30
60
90
0.0001
0
120 150 180 210 240 270 300 330 360
station 330 Hoek van Holland
2
30
60
90
0.01
0.001
z0 local
z0 meso
z0 gustiness
1
0.1
120 150 180 210 240 270 300 330 360
station 331 Tholen
2
z0 local
z0 meso
z0 gustiness
1
30
2
z0 local
z0 meso
z0 gustiness
0.1
0.0001
0
0.01
0.0001
0
120 150 180 210 240 270 300 330 360
1
0.0001
0
0.1
0.001
2
0.0001
0
z0 local
z0 meso
z0 gustiness
1
0.1
0.0001
0
station 310 Vlissingen
2
z0 local
z0 meso
z0 gustiness
1
0.1
0.01
0.001
30
60
90
120 150 180 210 240 270 300 330 360
0.0001
0
30
60
90
120 150 180 210 240 270 300 330 360
Figure E.21c: Same as Figure E.21a for stations 308, 310, 312, 316, 320, 321, 330 and 331.
175
station 343 R'dam Geulhaven
2
0.01
0.001
30
60
90
station 350 Gilze-Rijen
60
90
0.01
120 150 180 210 240 270 300 330 360
station 356 Herwijnen
z0 local
z0 meso
z0 gustiness
1
0.1
0.1
0.01
0.001
30
60
90
0.0001
0
120 150 180 210 240 270 300 330 360
station 370 Eindhoven
2
30
60
90
0.01
0.001
z0 local
z0 meso
z0 gustiness
1
0.1
120 150 180 210 240 270 300 330 360
station 375 Volkel
2
z0 local
z0 meso
z0 gustiness
1
30
2
z0 local
z0 meso
z0 gustiness
0.001
0.1
0.01
0.001
30
60
90
120 150 180 210 240 270 300 330 360
0.0001
0
30
60
90
120 150 180 210 240 270 300 330 360
station 380 Beek
2
z0 local
z0 meso
z0 gustiness
1
0.01
0.0001
0
120 150 180 210 240 270 300 330 360
1
0.0001
0
0.1
0.001
2
0.0001
0
z0 local
z0 meso
z0 gustiness
1
0.1
0.0001
0
station 344 Zestienhoven
2
z0 local
z0 meso
z0 gustiness
1
0.1
0.01
0.001
0.0001
0
30
60
90
120 150 180 210 240 270 300 330 360
Figure E.21d: Same as Figure E.21a for stations 343, 344, 350, 356, 370, 375 and 380.
176
∆U (m s-1)
15
Macro level transformation; α = 0.017
Macro level transformation; α = 0.032
Meso level transformation; α = 0.017
Meso level transformation; α = 0.032
10
5
0
10
20
30
U10 over land (m s-1)
40
Figure E.22: Increment of the 10-m wind over water in comparison to the 10-m wind over
land. The transformation is applied at meso and at macro level. The roughness of water is
given by the Charnock relation. Two constants for the Charnock parameter are considered.
The roughness of the land in this example is 0.2 m.
177
178
F
Figures corresponding with Section 7
18
14
16
12
10
12
Percentage (%)
Percentage (%)
14
10
8
6
8
6
4
4
2
2
0
0
30
60
0
90 120 150 180 210 240 270 300 330 360
Wind Direction (degrees)
a.
0
5
10
15
20
Potential Wind Speed (m/s)
25
30
b.
Figure F.1: Frequency distributions concerning dataset I of a. measured wind direction (degrees); b.
potential wind speed (m/s).
35
12
30
10
Percentage (%)
Percentage (%)
25
20
15
10
6
4
2
5
0
8
0
30
60
0
90 120 150 180 210 240 270 300 330 360
Wind Direction (degrees)
a.
0
5
10
15
20
Potential Wind Speed (m/s)
25
30
b.
Figure F.2: Frequency distributions concerning dataset II of a. measured wind direction (degrees); b.
potential wind speed (m/s).
179
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
Figure F.3: Spatial distribution of potential wind speed (m/s) averaged over 5-year period (1997-2001)
as derived from measurements (dataset I) before interpolation method applied.
180
9
9
8.5
8.5
8
8
7.5
7.5
7
7
6.5
6.5
6
6
5.5
5.5
5
5
4.5
4.5
4
4
3.5
3.5
3
3
a.
b.
9
9
8.5
8.5
8
8
7.5
7.5
7
7
6.5
6.5
6
6
5.5
5.5
5
5
4.5
4.5
4
4
3.5
3.5
3
3
c.
d.
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
e.
Figure F.4: Spatial distribution of wind speed (m/s) after interpolation method applied and averaged
over 5-year period (1997-2001) per station for a. run 1; b. run 2; c. run 3; d. run 4; e. run 5.
181
13
12.5
12
11.5
11
10.5
10
9.5
9
8.5
8
Figure F.5: Spatial distribution of macro wind speed (m/s) averaged over 5-year period (1997-2001)
as derived from measurements (dataset I) before interpolation method applied.
182
13
13
12.5
12.5
12
12
11.5
11.5
11
11
10.5
10.5
10
10
9.5
9.5
9
9
8.5
8.5
8
8
7.5
7.5
a.
b.
13
13
12.5
12.5
12
12
11.5
11.5
11
11
10.5
10.5
10
10
9.5
9.5
9
9
8.5
8.5
8
8
7.5
7.5
c.
d.
13
12.5
12
11.5
11
10.5
10
9.5
9
8.5
8
7.5
e.
Figure F.6: Spatial distribution of macro wind speed (m/s) after interpolation method applied and
averaged over 5-year period (1997-2001) per station for a. run 1; b. run 2; c. run 3; d. run 4; e. run 5.
183
Figure F.7: Yearly average of macro wind speed at 16 stations together with isolines of the wind
speed field fitted by Wieringa and Rijkoort (1983, figure 4.7; page 83).
184
5
5
4.75
4.75
4.5
4.5
4.25
4.25
4
4
3.75
3.75
3.5
3.5
3.25
3.25
3
3
2.75
2.75
2.5
2.5
2.25
2.25
2
2
a.
b.
5
5
4.75
4.75
4.5
4.5
4.25
4.25
4
4
3.75
3.75
3.5
3.5
3.25
3.25
3
3
2.75
2.75
2.5
2.5
2.25
2.25
2
2
c.
d.
5
4.75
4.5
4.25
4
3.75
3.5
3.25
3
2.75
2.5
2.25
2
e.
Figure F.8: Spatial distribution of difference (estimated – measured) in macro wind vector averaged
over time per station for a. run 1; b. run 2; c. run 3; d. run 4; e. run 5.
185
Figure F.9: Bias in the potential wind speed for run 1 (estimated – measured) for station 310
Vlissingen as function of time.
Wind speed (m s-1)
40
Number of iterations
1
3
5
8
11
15
35
30
25
20
15
3
4
5
6
7 8 9105
2
3
4
5
6
7 8 9106
Barnes Radius (m)
Figure F.10: Estimated wind speed at station 290 Twenthe as function of the radius of influence for
different numbers of iterations. Case October 17, 1967; 12:00 hour GMT.
186
30
30
25
25
20
20
15
15
10
10
5
5
0
0
30
30
25
25
20
20
15
15
10
10
5
5
0
0
30
30
25
25
20
20
15
15
10
10
5
5
0
0
Figure F.11: Potential wind fields (m/s) at macro level of October 17, 1967 at 12 UTC. a. before
interpolation; b. after interpolation for run 1; c. for run 2; d. for run 3; e. for run 4; f. for run 5.
187
80
80
70
70
60
60
50
50
40
40
30
30
20
20
80
80
70
70
60
60
50
50
40
40
30
30
20
20
80
80
70
70
60
60
50
50
40
40
30
30
20
20
Figure F.12: Wind fields (m/s) at macro level of October 17, 1967 at 12 UTC. a. before
188
30
30
25
25
20
20
15
15
10
10
5
5
0
0
30
30
25
25
20
20
15
15
10
10
5
5
0
0
30
30
25
25
20
20
15
15
10
10
5
5
0
0
Figure F.13: Potential wind fields (m/s) at macro level of February 14, 1979 at 18 UTC. a. before
189
50
50
45
45
40
40
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
50
50
45
45
40
40
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
50
50
45
45
40
40
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
Figure F.14: Wind fields (m/s) at macro level of February 14, 1979 at 18 UTC. a. before interpolation;
b. after interpolation for run 1; c. for run 2; d. for run 3; e. for run 4; f. for run 5.
190
50
50
45
45
40
40
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
50
50
45
45
40
40
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
50
45
40
35
30
25
20
15
10
5
0
Figure F.15: Wind fields (m/s) at macro level of February 14, 1979 at 18 UTC without excluding
stations. a. after interpolation for run 1; b. for run 2; c. for run 3; d. for run 4; e. for run 5.
191
-5
-1
-10
-2
-15
-20
120 150 180 210 240 270 300 330 360
station 269 Lelystad
20
2
10
1
5
0
0
-5
-1
-10
-2
-3
0
-15
30
60
90
2
15
10
1
5
0
0
-5
-1
-10
-2
-3
0
-15
30
60
90
2
15
10
1
5
0
0
-5
-1
-10
-2
-3
0
-15
30
60
90
30
60
90
-20
120 150 180 210 240 270 300 330 360
station 279 Hoogeveen
20
2
5
0
0
-5
-1
-10
-2
-15
30
60
90
-20
120 150 180 210 240 270 300 330 360
station 315 Hansweert
20
2
15
10
1
5
0
0
-5
-1
-10
-2
-3
0
-15
30
60
90
-20
120 150 180 210 240 270 300 330 360
station 330 Hoek van Holland
3
20
wind speed
wind direction
2
15
10
1
5
0
0
-5
-1
-10
-2
-3
0
-20
120 150 180 210 240 270 300 330 360
15
10
1
wind speed
wind direction
20
wind speed
wind direction
-15
3
-20
120 150 180 210 240 270 300 330 360
station 323 Wilhelminadorp
3
-10
-2
-3
0
20
wind speed
wind direction
-5
-1
wind speed
wind direction
-20
120 150 180 210 240 270 300 330 360
station 280 Eelde
3
estimated - measured wind speed (m/s)
15
0
3
wind speed
wind direction
3
5
0
-3
0
90
estimated - measured wind direction (degrees)
60
30
10
1
-15
30
60
90
0
15
2
0
20
wind speed
wind direction
5
10
1
-3
0
15
2
station 240 Schiphol
3
20
wind speed
wind direction
station 225 IJmuiden
3
-20
120 150 180 210 240 270 300 330 360
Figure F.16: Difference in average potential wind speed and direction (estimated – measured) (m/s)
per wind direction sector for stations 225, 240, 269, 279, 280, 315, 323 and 330.
192
station 343 R'dam Geulhaven
2
station 344 Zestienhoven
2
1
1
0.1
0.1
0.01
0.001
0.01
0.001
meso z0stad=1.6
meso z0stad=1.1
lok z0stad=1.6
lok z0stad=1.1
0.0001
0
30
60
90
120 150 180 210 240 270 300 330 360
meso z0stad=1.6
meso z0stad=1.1
lok z0stad=1.6
lok z0stad=1.1
0.0001
0
30
60
90
120 150 180 210 240 270 300 330 360
Figure F.17: Directional local and mesoscale roughness length (m) from footprint approximation
( Dmeso = 10 km, Dlocal = 600 m) with z0 = 1.1 m and z0 = 1.6 m for continuous urban area for
stations 343 and 344.
193
194
G Figures corresponding with Section 8
Figure G.1: 10,000 year omni-directional annual return levels [m/s] obtained by first interpolation with
R = 300 km on dataset II, followed by the statistical method.
195
Figure G.2: Exceedance frequencies for potential wind speeds measured and estimated (run 4) from
dataset II for stations 225, 240, 260, 275, 310 and 344. For explanation of the upper and lower panels
see text.
196
Figure G.3: Input data for the interpolation on statistical extremes concerning onmi-directional and
yearly 10,000-year return levels.
Figure G.4: First statistics, then interpolation with macro wind speed averaging concerning onmidirectional and yearly 10,000-year return levels.
197
Figure G.5: Mean shape parameter of the land stations 260, 265, 275, 290, 370, 375 and 380 as
function of wind direction for different seasons. Direction 13 refers to the omni-directional distribution.
Figure G.6: Mean shape parameter of the offshore stations 312, 316, 320, 321 and 331 as function of
wind direction for different seasons. Direction 13 refers to the omni-directional distribution.
198
Figure G.7: Median (over seasons, thresholds) shape parameter distribution for western wind.
Figure G.8: Median (over seasons, thresholds) shape parameter distribution for eastern wind.
199
Potential Wind Speed Patterns
Season Jan-Feb; CWD
360
Slope (% / 100 km)
350
20
340
330
10
320
angle; 255°-285°
slope; 255°-285°
angle; 75°-105°
slope; 75°-105°
5.
0
10
.0
20
.0
50
.0
10
0.
0
20
0.
0
50
0.
10 0
00
.
20 0
00
.
50 0
00
10 .0
00
0.
0
2.
0
1.
0
300
0.
5
0
310
Direction of increase (degrees)
30
Return Period (years)
Figure G.9: Slope and direction of increase in the potential wind for two wind directions (east and
west) as function of return period for the season January-February.
Macro Wind Speed Patterns
30
110
Slope (% / 100 km)
90
angle; 255°-285°
slope; 255°-285°
angle; 75°-105°
slope; 75°-105°
20
70
50
30
10
10
-10
Direction of increase (degrees)
Season Jan-Feb; CWD
-30
5.
0
10
.0
20
.0
50
.0
10
0.
0
20
0.
0
50
0.
10 0
00
.
20 0
00
.
50 0
00
10 .0
00
0.
0
2.
0
1.
0
0.
5
0
Return Period (years)
Figure G.10: Slope and direction of increase in the macro wind for two wind directions (east and west)
as function of return period for the season January-February.
200
Charnock: α = 0.017
Gustiness LEG, southwest
3
2
z0 (m)
10-3
7
6
5
4
3
2
10-4
10
12
14
16
18
20
22
Usensor (m s-1)
Figure G.11: Gustiness derived roughness length for station 320 Lichteiland Goeree (LEG) in
direction 225°–244° as function of the average wind speed in the selected data. Also plotted is the
roughness length according to the Charnock relation for two values of the Charnock parameter α.
Gustiness EPF, southwest
3
2
z0 (m)
10-3
7
6
5
4
3
2
10-4
10
12
14
16
18
Usensor (m s-1)
Figure G.12: As figure 6, for station 321 Europlatform (EPF).
201
20
22
3.5
α = 0.032: meso wind
α = 0.032: macro wind
α = 0.017: meso wind
α = 0.017: macro wind
3.0
2.5
dU (%)
2.0
1.5
1.0
0.5
0.0
-0.5
10
15
20
25
30
35
40
Usensor (m s-1)
Figure G.13: The relative effect of using Charnock relation for the roughness length in the surface
layer in stead of a fixed gustiness derived roughness length on the meso- and macro wind as function
of wind speed; assumed sensor height 30 m.
202

Verkaik et al.

Transcription

Similar documents

Sony CDX

What does it measure? The Visioscan® VC 98 USB is a special UVA

Rapping up Safety!

2016 TheWeatherChannel

Stylolite formation process: Surface Roughness Measurements and

Surface Finish Analysis

Factsheet Insurance

Swallow Rocks to Big Mountain

Dia 1

EM27/SUN