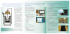Course: Brachiation Mechanics And Robotics: Analysis, Simulation

 Course: Brachiation
Mechanics And Robotics: Analysis, Simulation, And Construction
IWR Robotics Lab, 26 – 30/03, 2012 Instructor: Prof. Michael J. Coleman (a) (c) (b) Continuous-­‐contact Magnetic “Hands” Passive-­‐Dynamic Tinkertoy 3D Brachiator: (a) Front and side views of the brachiating toy made from modified TInkertoys for the body, permanent magnets for the hand-­‐holding, and rubber balloon covering for anti-­‐slip hands. One hand is balloon covered while the other is uncovered to reveal the magnets, (b) brachiator in motion, and (c) CAD model for computing the center of mass and moment of inertia matrix. • Overview: This course will be a brief introduction to brachiation mechanics and robotics. The course will involve studying simple mechanical/ mathematical models, simulating the models on the computer, and building physical models using construction toys and very basic construction materials. The course is open to undergraduate students and graduate students (Master’s and Ph.D.’s). • What is brachiation? Brachiation means ‘swinging from branch to branch’ using alternating hands. Some examples of brachiating creatures are gibbons and siamangs. Despite its intermittent nature, brachiation is a very smooth motion overall that requires minimal effort to maintain forward momentum and directional stability as well as to change direction or alter flight path. There are two fundamental brachiating gaits over a variety of speeds, handhold spacings, and gait frequencies: (1) continuous-­‐contact gait (one hand is on a handhold ata time with smooth pendular motions interrupted by hand exchanges) and (2) ricochetal gait (ballistic vaulting between handholds combined with pendular motions at the handholds). Continuous-­‐
contact gait and ricochetal gait are analogous to walking and running on two legs, respectively. • Mechanical/Mathematical Models: We will study an evolution of existing complete mechanical models of brachiation of increasing complexity and create new ones. The models will compose the smooth swinging motions between hand-­‐holds with collision models for the impulsive hand-­‐hold events. We will use both particle and single/mutli-­‐rigid body models with one or more degrees of freedom. This course needs some geometry (kinematics), of course, but the emphasis here is on complete mechanics analyses [ ‘F=ma’ (linear momentum balance), ‘MC=dHC/dt’ (angular momentum balance), ‘Pin = dEK/dt’ (power balance), and dynamical systems]. • Computer simulation: We will write simple MATLAB (or similar) routines to study the dynamics and stability of the simple models of brachiation, including animation. We will also use Working Model 2D dynamics simulation package. Various bits of existing code will be provided. • Building physical models : We will use classic plastic Tinkertoys (or the like) , the newer Tinkertoy Superstructs to build brachiation robots of various sorts, and the simplest construction materials (tapes, glues, magnets, suction cups, fasteners, etc.). • What will happen in lectures? Relevant reviews of mechanics, general introductions, and videos. Detailed explanations and calculations concerning mechanics, energetics, stability, etc. Some programming tips. Group work on modeling, computer simulation, and construction. • How will you spend your time when doing homework? You will read papers and do mechanics calculations, by hand and on the computer, related to brachiation. See attached paper with bibliography for readings. • Final Project/Competition A main outcome of the course is the the capstone project of creating a simple brachiation model; simulating it on the computer; analyzing its effectiveness, stability and energetics; and, building a physical version of it. We may have individual projects for one or more individuals in a team or a project competition between teams or individuals. The projects may involve modifying the passive-­‐dynamic models built by the instructor to include some of the following: adding degrees of freedom and bodies to more closely mimic gibbons and siamangs, using different hand-­‐hold techniques, permitting richochetal gaits, adding power, or adding sensors and control. • Prerequisites: Introductory dynamics and system dynamics, elementary linear algebra including linear equation solution and eigenvalues/eigenvectors, elementary ordinary differential equations, basic MATLAB skills including ODE simulation, linear equation solving, eigenvalue-­‐eigenvector calculation, basic graphics.