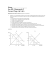Physics 1408-002 Principles of Physics

Physics 1408-002
Principles of Physics
Lecture 19
– Chapter 12 –
March 26, 2009
Sung-Won Lee
[email protected]
Chapter 12
Static Equilibrium;
Elasticity and Fracture
•!The Conditions for Equilibrium
•!Solving Statics Problems
•!Stability and Balance
•!Elasticity; Stress and Strain
•!Fracture
•!Trusses and Bridges / Arches and Domes
Announcement I
Lecture note is on the web
Handout (6 slides/page)
http://highenergy.phys.ttu.edu/~slee/1408/
*** Class attendance is strongly encouraged and will be
taken randomly. Also it will be used for extra credits.
HW Assignment #8 will be placed on
MateringPHYSICS today, and is due by
11:59pm on Wendseday, 4/1
Approach to Statics
•! In general, we can use the two equations!
!
F
! =0
!
!
" =0
to solve any statics problem.!
When choosing axes about which to calculate
torque, the choice can make the problem
easy....!
Torque due to Gravity
12-2 Solving Statics Problems
A board of mass M = 2.0 kg serves as a seesaw for two children.
Child A has a mass of 30 kg and sits 2.5 m from the pivot point,
P (his center of gravity is 2.5 m from the pivot).
Consider total external torque on a system of
masses in a uniform gravitational field.
At what distance x from the pivot must child B, of mass 25 kg,
place herself to balance the seesaw? Assume the board is
uniform and centered over the pivot.
m4
m1
x4
m3
m2
12-2 Solving Statics Problems
Hanging Lamp
At what distance x from the pivot must child B, of mass 25 kg,
place herself to balance the seesaw? Assume the board is
uniform and centered over the pivot.
•! A lamp of mass M hangs from the end of plank of mass m and
length L. One end of the plank is held to a wall by a hinge, and
the other end is supported by a massless string that makes an
angle with the plank. (The hinge supplies a force to hold the
end of the plank in place.)
–!What is the tension in the string?
–!What are the forces supplied by the
hinge on the plank?
m
!"
hinge
L
M
Hanging Lamp...
•! First use the fact that
!!
!
!F = 0
in both x and y directions:
x:
T cos ! + Fx = 0
y:
T sin ! + Fy - Mg - mg = 0
"
Hanging Lamp...
y
x
!
LMg +
y
L
mg - LT sin ! = 0
2
x
which we can solve to find:
Now use ! = 0 in the z direction.
"!If we choose the rotation axis to
be through the hinge then the
hinge forces Fx and Fy will not
enter into the torque equation:
L
LMg + mg - LT sin ! = 0
2
•! So we have three equations and three unknowns:"
! T cos ! + Fx = 0
T sin ! + Fy - Mg - mg = 0
m
!"
L/2
M
Mg
Fy
L/2
mg
Fx
m%
"
m$
!
!$ M + ' g
#" M + &% g
#
2& ˆ
2
Fx =
i
T =
tan (
sin '
1
Fy = mg ĵ
2
m
L/2
M
Mg
Fy
!"
L/2
mg
Fx
12-3 Stability and Balance
If the forces on an object are such that they tend
to return it to its equilibrium position, it is said
to be in stable equilibrium.
12-3 Stability and Balance
An object in stable equilibrium may become
unstable if it is tipped so that its center of
gravity is outside the pivot point. Of course, it
will be stable again once it lands!
12-3 Stability and Balance
If, however, the forces tend to move it away from
its equilibrium point, it is said to be in unstable
equilibrium.
12-3 Stability and Balance
People carrying heavy loads automatically
adjust their posture so their center of mass is
over their feet. This can lead to injury if the
contortion is too great.
Humans adjust their posture
to achieve stability when
carrying loads.
12-4 Elasticity; Stress and Strain
Hooke’s law: the change in
length (#l) is proportional to
the applied force (F).
12-4 Elasticity; Stress and Strain
The change in length of a stretched object depends not
only on the applied force, but also on its length, crosssectional area and the material from which it is made.
The material factor, E, is called the elastic modulus or
Young’s modulus, and it has been measured for many
materials.
Elastic modulus=
stress
strain
Young’s Modulus: Elasticity in Length
•! Tensile stress is the ratio of the
external force (F) to cross-sectional
area (A)
–! For both tension and compression
•! The elastic modulus is called
Young’s modulus
•! SI units of stress: Pascals, [Pa]
–! 1 Pa = 1 N/m2
•! The tensile strain is the ratio of
F
the change in length to
tensile stress
F Lo
Y=
= A =
the original length
!L
tensile strain
A !L
Lo
12-4 Elasticity; Stress and Strain
•! All objects are deformable,
i.e. it is possible to change the shape or size (or both) of an object
through the application of external forces
–! Sometimes when the forces are removed, the object tends to its original
shape, called elastic behavior
–! Large enough forces will break the bonds between molecules
and also the object
12-4 Elasticity; Stress and Strain
Stress is defined as the force per unit area. (F/A)
Strain is defined as the ratio of the change in length to
the original length. (#l/l0)
Therefore, the elastic modulus (E) is equal to the
stress divided by the strain: