New Routines for Gridding of Temperature and

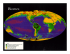
New Routines for Gridding of Temperature
and Precipitation Observations
for “seNorge.no”
Matthias Mohr
(P.O. Box 43, N-0313 OSLO, NORWAY)
ABSTRACT
Daily maps of temperature and precipitation with 1 km horizontal resolution for the
whole of Norway are produced for seNorge.no. In order to produce these maps, daily
observations of 24-hour mean temperature as well as 24-hour accumulated
precipitation are used.
Maps for the current day are produced at 08:00 UTC on every day of the week,
whereas maps for the preceding 18 days are produced on every Tuesday of the week at
09:00 UTC. The weekly runs should take manual observations into account that are
submitted on a weekly or monthly basis.
The spatial interpolation of temperature and precipitation observations was previously
done in ArcInfo. However, since ArcInfo is not an operational platform at met.no, new
routines had to be developed to create an operational Linux application.
This report describes the new routines that were developed in Fortran for this purpose.
The new routines are both faster and more flexible than the ArcInfo programs that
were used until now.
________________________________________________________________________________________
No. 08/2008
Oslo, 02.07.2008
1
Introduction
Daily mean temperature measurements as well as 24-hour accumulated daily precipitation
observations are used to produce maps of temperature and precipitation with 1 km horizontal
resolution for the whole of Norway. These maps are updated on a daily basis and published on
the website “seNorge.no”. The process of spatially interpolating temperature and precipitation
observations shall hereinafter simply be called “gridding”.
Gridding of temperature and precipitation measurements was previously done using ArcInfo
routines that were developed by Ole-Einar Tveito (e.g. Jansson et al., 2007, page 13-15).
However, since ArcInfo is not an operational platform at met.no, it was decided that new
routines should be developed for the gridding of temperature and precipitation observations.
Fortran90/95 was used in combination with Perl and Shell scripts to create an operational
Linux application that is started daily as a Crontab job on “skypumpe.oslo.dnmi.no”. Daily
gridding is performed at 08:00 UTC on every day of the week, whereas gridding for the
preceding 18 days (= weekly gridding) is carried out every Tuesday of the week at 09:00
UTC. The latter gridding is done to take into account manual observations that are not
submitted on a daily basis, but on a weekly or monthly basis. Furthermore, observations that
were subsequently corrected in accordance with in-house quality control procedures are taken
into account by the weekly gridding.
Measured 24-hour mean temperatures are first “de-trended” or “reduced” to sea level, to a
common latitude and to a common longitude (Tveito et al., 2000). Furthermore, the average
and the lowest altitude in a circle of 20 km radius surrounding each station are used in order
to determine whether a particular station is situated in a valley or on a mountain top. All five
dependencies are treated as linear expressions. For the daily de-trending, regression
coefficients based upon monthly mean temperature data were used. These were calculated
from monthly mean temperature data for Norway, Sweden, Denmark and Finland using stepwise linear regression (Tveito et al., 2000).
For the spatial interpolation of “de-trended” temperatures, Kriging is used in conjunction with
the semi-variogram parameters for the de-trended monthly mean temperatures of the
respective month (Tveito et al., 2000). The method is also called residual kriging or detrended kriging. A different method was used in ArcInfo that is called “Topogrid”. Topogrid
uses ANUDEM version 4.5. for ArcInfo 7.2.1 and later versions (e.g. Hutchinson, 1989).
For the spatial interpolation of precipitation, the method of triangulation is used. Moreover,
gridded precipitation values are corrected for the altitude of the respective seNorge grid point,
using a vertical precipitation gradient of 10% per 100 m height difference below an altitude of
1000 m above sea level as well as a gradient of 5% per 100 m height difference above an
altitude of 1000 m above sea level (Tveito et al., 2000).
This report describes the new routines that were developed for this purpose. The new routines
are both faster and more flexible than the ArcInfo programs that were used until now. The
gridding algorithms described herein are going to be further developed in the near future,
including for instance weather types, geostrophic wind directions or other types of
geostatistical information.
Description of “seNorge” Web Site
The website ”seNorge.no” shows snow, weather, water and climate maps for Norway that are
updated on a daily basis (Fig. 1). In this report, the programs are described that are used to
produce daily temperature and precipitation maps for this website with 1 km horizontal
resolution for the whole of Norway. All the other maps are produced by the Norwegian Water
Resources and Energy Directorate (NVE).
Figure 1. seNorge.no web site with 24-hour accumulated gridded precipitation map for the 24
hours preceding 06 UTC on 08 April 2008.
On www.seNorge.no, daily, monthly and annual values are shown as well as mean values for
climatological periods and climate scenarios. The maps go as far back in time as the 1960s
and include forecasts for the two following days as well. Different themes are presented and
in total the web site includes several hundreds of thousands of maps. In addition, time series
from met.no weather stations as well as from NVE river flow stations can be displayed by
clicking on the icon.
1
The seNorge web site is useful for hazard mitigation especially in conjunction with floods,
droughts, energy supply shortages, avalanches and landslides. The web site should also be
useful for commercial businesses as well as outdoor enthusiasts.
Daily and Weekly Crontab Jobs
Two new Crontab jobs were added on “skypumpe.oslo.dnmi.no”. The two Crontab jobs
consist of Perl scripts that are located at /klimaprod/applikasjon/gridding/seNorge/snoakk/.
The Perl scripts are called
•
”snokart_day.pl” (for the daily runs) and
•
”snokart_week.pl” (for the weekly runs).
The Perl scripts are executed on every day of the week at 08:00 UTC (“snokart_day.pl”) as
well as on every Tuesday of the week at 09:00 UTC (“snokart_week.pl”).
Main Fortran Programs
The two Perl scripts “snokart_day.pl” and “snokart_week.pl” call the two Fortran executables
•
“snokart_day” (for the daily runs) and
•
“snokart_week” (for the weekly runs)
in the folder /klimaprod/applikasjon/gridding/seNorge/snoakk for the daily and weekly runs,
respectively. Flow diagrams for these two Fortran programs can be found in Appendix A and
B.
In the unlikely event that the Fortran program should crash for whatever reason, an email is
automatically sent out to [email protected]. More information on the program
status can be found in the log files “snokart_day.log”, “snokart_week.log” and
“lag_status.log” in the folder /klimaprod/applikasjon/gridding/seNorge/snoakk. Also, it is
worth checking the mail box for automatically generated e-mail messages from Crontab.
The log file “lag_status.log” summarises the status of all the runs carried out until present, i.e.
from 31 March 2008 until the present date. Normally, the programs have been completed
successfully if “STATUS OF SYSTEM CALL = 0” is shown in the log files or in the e-mail
messages.
Scripts for Generating Figures and FTP Transfer
After completing the Fortran programs for the daily and weekly runs, a Perl script is executed
that produces the figures that are published at seNorge.no. Moreover, the Perl script transfers
the gridded temperature and precipitation data by FTP to the Norwegian Water Resources and
2
Energy Directorate (NVE) for further processing. Different Perl scripts are executed for the
daily and weekly runs.
The scripts for the daily and weekly runs are located at /klimaprod/applikasjon/gridding/bin
and are called
•
“mk_daygrid_today.pl” (for the daily runs) and
•
“mk_daygrid_week.pl” (for the weekly runs).
While the first script is run directly after “snokart_day.pl”, the second script is run directly
after “snokart_week.pl”. The Perl scripts in this folder were slightly modified in order to work
with the new routines. A documentation of all scripts can be found at
/klimaprod/applikasjon/gridding/doc. The Perl scripts were originally developed by Eli Alfnes
in 2006.
The Perl scripts in the folder /klimaprod/applikasjon/gridding/bin contain commands to
produce the daily PNG-figures, to mask and swap the BIL-files (byte swapping is not needed
anymore with the new routines), as well as to transfer the daily and weekly output files via
FTP to the NVE. Moreover, the snow and water related gridded products that are produced at
NVE are transferred back to met.no by these scripts.
Main Fortran Programs for Daily, Weekly and Batch Runs
The Fortran source code has to be compiled with the Intel Fortran Compiler (“ifort”) on Linux
or the Compaq Visual Fortran Compiler on Windows. To my best knowledge, these are the
only compilers currently available that include routines to write directly to (“unblocked”)
binary output files (such as BIL-files). The writing to binary files is accomplished using the
option FORM='BINARY' in the open statement. (It is unclear whether the same format can be
produced using the FORM='UNFORMATTED' and ACCESS='STREAM' option in other compilers.)
The programs were almost entirely written in Fortran90/95 (with the exception of some
subroutines that are still in Fortran77). The main Fortran programs are called
•
“snokart_day.f90” (for the daily runs)
•
“snokart_week.f90” (for the weekly runs)
•
“snokart_batch.f90” (for user-specified time period)
The Fortran programs are stored at /klimaprod/applikasjon/gridding/seNorge/snoakk/. Both
programs “snokart_day.f90” and “snokart_week.f90” read the actual date and time from the
system clock of the computer they are running on. The programs call the gridding routines for
temperature and precipitation for the current day and for the preceding 18 days (including the
current day), respectively.
The program “snokart_batch.f90” runs the gridding routines for a user-specified time period
with two command line arguments, the starting date and the finishing date. The dates have to
3
be specified as strings with 10 characters (i.e. as character strings of the form “dd.mm.yyyy”).
Here, “dd” stands for the day of the month (in 2 digit form), “mm” for the month of the year
(in 2 digit form) as well as “yyyy” for the year (in 4 digit form). Note that both gridding
routines “snokart_week.f90” and “snokart_batch.f90” are run backwards in time.
Fortran Programs for Gridding of Temperature and
Precipitation
The Fortran programs that perform the actual gridding of temperature and precipitation are
called
•
“tam_read_and_process.f90” (for temperature gridding) and
•
“precip.f90” (for precipitation gridding).
In these programs, the date is automatically read from a command line argument that has to be
a character string of the form “dd.mm.yyyy”. Hence, these programs can also be run
separately from the main Fortran programs by typing
•
“tam_read_and_process dd.mm.yyyy” or
•
“precip dd.mm.yyyy”
This ensures a flexible system that can be run for several days or months in the past.
Note that running “precip dd.mm.yyyy” reads the ArcASCII grid file with de-trended air
temperatures for the same day (a file called “tm0_okb2d_yyyy_mm_dd.asc” which is stored
at /klimagrid/daily/tam/ascii/ on skypumpe.oslo.dnmi.no). Since “precip.f90” requires the
ArcASCII grid file with de-trended air temperatures for the same day, it is advisable to always
run both programs after each other for one and the same day, i.e. to run
“tam_read_and_process.f90” first and “precip.f90” thereafter for one and the same day.
Therefore, it is strongly recommended to run “snokart_batch.f90” instead of running the two
programs “tam_read_and_process.f90” and “precip.f90”, independently.
Directory Structure
The Fortran programs use relative directories to each other as well as directories for the output
files in BIL and ASCII format. The relative directories should never be changed! The absolute
directories for the output files, however, can be changed in the variable definition statements
in the Fortran programs. In this case the programs have to be re-compiled using the shellscript “make_all.sh” at /klimaprod/applikasjon/gridding/seNorge/snoakk/. (The absolute
directories are only given in the two main Fortran programs “tam_read_and_process.f90” and
and “precip.f90”, as well as in the subroutine “tm2rrst.f90”.)
4
In order for the relative paths to work, all Fortran programs have to be stored in one and the
same main directory as well as in the three sub-folders “temperatur”, “snoakk” and “precip”.
Using relative directories in most places (rather than absolute directories) the programs can be
moved to other locations or other computers very easily. The output directories can be
changed very easily and the program can be moved from Linux to Windows without too much
effort.
Database Servers
A new Oracle/SQL database server was installed in April 2008. This required some small
changes in the SQL scripts. The new server is called “dvh” instead of “dvh10”. However,
changing the server to “dvh10” sometimes also changed the output format of one and the
same SQL query! Hence, the SQL database calls were slightly modified in order to work with
the new SQL database server.
The database that is used is essentially the same as the one that is used within eKlima (see
http://eklima.met.no). It is called data warehouse or “datavarehuset” (=“dvh”) in Norwegian.
However, with the new SQL database server, “dvh10” should always be used in place of
“dvh”.
Database Queries
Our intention was to retrieve as much information as possible from the SQL database, in order
to avoid static files that have to be updated manually, whenever some information on station
data (e.g. station coordinates) is changed or updated.
The SQL database calls are performed using shell scripts in Linux or batch files in Windows.
The SQL Plus software is used for this purpose.
In Linux, the SQL shell scripts (with extensions “.sh”) call SQL scripts (with extensions
“.sql”). In total, four shell/SQL scripts are run, namely two for obtaining daily temperature
and precipitation data as well as two for obtaining station meta data (such as station
coordinates, station latitude and longitude, station altitude and station type). The scripts are
summarised in Table 1.
Table 1. Name and location of shell and SQL scripts, as well as action carried out by SQL
scripts. Note that in Windows a batch file is used instead of the shell script. The batch file in
Windows does not require an SQL script, but produces a temporary SQL script.
Name of shell and
SQL script
“tamrr.sh”
“tamrr.sql”
“stasjonskart.sh”
“stasjonskart.sql”
“rr.sh”
“rr.sql”
Location of shell and SQL script
Action carried out by SQL script
/klimaprod/applikasjon/gridding/seNorge/temperatur
obtains 24-hour average daily temperature
observations (valid from 06 UTC on the
previous day to 06 UTC on the current day)
obtains station coordinates in the UTM Zone
33 coordinate system as well as station
altitudes
obtains 24-hour accumulated daily recipitation
observations (valid from 06 UTC on the
previous day to 06 UTC on the current day)
/klimaprod/applikasjon/gridding/seNorge/temperature
/klimaprod/applikasjon/gridding/seNorge/precip
5
“stasjonskart3.sh”
“stasjonskart3.sql”
/klimaprod/applikasjon/gridding/seNorge/precip
obtains station coordinates in UTM Zone 33
coordinate system as well as longitudes,
latitudes, station altitudes and station types
The database tables that are used in these queries are called “t_diurnal“, “t_diurnal_flag“,
“st_info” and “st_type”.
Gridding of Temperature Observations
Description of Input Data
Daily mean temperature is output from the Oracle database using the SQL database queries
described above. The temperature data is written to a file called “utfil2.lst”, whereas the
station meta data (coordinates, altitudes, station types…) is written to a file called “stkart.lst”.
Note that a station with one and the same station number can occur several times in
“stkart.lst”, since the meta data is updated every time the status of a station has changed. For
simplicity, only the most recent meta data record with the most recent station type is used in
the programs described herein.
The database shell scripts, SQL queries and database output files that are used from within the
Fortran programs are summarised in Table 2.
Table 2. Names of output files as well as SQL database queries and shell scripts that are used
to retrieve the data for temperature gridding.
Name of file
utfil2.lst
stkart.lst
Name of Program/SQL query
tamrr.sh/tamrr.sql
stasjonskart.sh/stasjonskart.sql
Data in File
Station number, mean temperature (TAM)
Station number, UTM coordinates, station
altitude, station type, etc.
De-Trending of Temperatures (“The De-Trending Equation”)
Firstly, observed daily 24-hour mean temperatures from all stations are de-trended. This
means that the temperatures are “reduced” to sea level, to a common latitude and longitude as
well as to a common exposure with respect to the local terrain.
Using the station coordinates in latitude and longitude as well as the station altitudes, the
temperatures are “reduced” to sea level, to a common latitude and longitude. Moreover, the
local terrain in the vicinity of each station is taken into account by using the mean and the
minimum elevation within a circle of 20 km radius surrounding each station.
The de-trending method is based on the principle that temperature can be described as a sum
of deterministic and stochastic processes (Tveito et al. 2000). In this study, five independent
variables were chosen to describe the large-scale spatial climate trends, based on the results
obtained by Tveito and Førland (1999). Three of these are based on topography, the two last
ones are longitude and latitude, which in combination describe both distance to sea and
latitudinal variability.
6
The vertical temperature decrease is the most dominating trend component. Even though it is
often defined as the standard lapse rate of -6.5°C/km, the real lapse rate varies with the
season. Moreover, the real lapse rate depends on the local terrain characteristics. Hence,
station altitude does not provide sufficient explanation of the spatial variability of
temperature, especially during the winter season (Tveito et al. 2000). Therefore two other
topographical parameters were defined: The mean altitude within a circle of 20 km radius
surrounding a station as well as the minimum altitude within the same circle. Both parameters
give an indirect measure of the local terrain at the station relative to the mesoscale terrain. The
idea is that stations at high elevations compared to the surroundings (e.g. hill tops) behave
differently temperature-wise than stations located at lower elevations compared to the
surroundings (e.g. valleys or basins). Hence, these parameters identify in conjunction with the
station altitude whether a station is situated in a valley or on a mountain top. If a station is
situated in flat terrain, the effects of the mean and the minimum elevation within a circle of 20
km radius surrounding a station will compensate for each other.
Within the de-trending equation linear expressions are used. Any linear combinations of the
five features described above are accounted for. Consequently, de-trended temperatures are
calculated from observed station temperatures as:
Tde−trended = Tstation − v1 ⋅ z station − v2 ⋅ z mean, 40 km − v3 ⋅ z min, 40 km − v4 ⋅ lat station − v5 ⋅ lonstation − const
where Tstation is the measured 24-hour mean temperature at the station and Tde-trended is the detrended 24-hour mean temperature at the same station. Moreover, zstation is the altitude of the
station, zmean,40km the mean altitude within a circle of 40km diameter surrounding the station,
zmin,40km the lowest altitude within a circle of 40km diameter surrounding the station, latstation
the latitude of the station, and lonstation the longitude of the station.
The monthly stepwise linear regression coefficients v1 to v5 as well as the monthly constants
const were obtained from trend analysis by Tveito et al. (2000). The authors used step-wise
linear regression in order to estimate deterministic trends in long-term average monthly mean
temperatures. Data from 1152 stations in Norway, Denmark, Sweden and Finland has been
used in the analysis.
The monthly values for these coefficients from Tveito et al. (2000) are given in Table 3. The
method has proven to be robust and reliable, and can also be applied to daily values (Tveito et
al., 2005). Hence, the monthly stepwise linear regression coefficients from Table 3 are used
for the daily interpolation of 24-hour mean temperature within the scope of seNorge.
Table 3. Monthly stepwise linear regression coefficients and constants used for calculating
de-trended 24-hour mean temperatures. Regression coefficients and constants are chosen
depending only upon the month of the observations.
Month
v1 (coefficient for
z_station)
v2 (coefficient for
z_mean,40km)
v3 (coefficient for
z_min,40km)
v4 (coefficient for
lat_station)
v5 (coefficient for
lon_station)
const
Jan
-0.0012
Feb
-0.0019
Mar
-0.0046
Apr
-0.0061
May
-0.0063
Jun
-0.0063
Jul
-0.0061
Aug
-0.0057
Sep
-0.0055
Oct
-0.0046
Nov
-0.0032
Dec
-0.0016
-0.0051
-0.0043
-0.0021
-0.0006
0.0007
0.0011
0.0009
0.0
-0.0011
-0.0016
-0.0031
-0.0041
-0.0083
-0.0062
-0.0033
-0.0008
0.0
0.0021
0.0016
0.0005
0.0
-0.0017
-0.0054
-0.0089
-0.2694
-0.1918
-0.2579
-0.3288
-0.4166
-0.4460
-0.3700
-0.3763
-0.3764
-0.3349
-0.3491
-0.2459
-0.4395
-0.4282
-0.3044
-0.1505
-0.0363
0.0914
0.1290
0.0370
-0.0543
-0.1581
-0.2194
-0.3470
19.4879
14.7045
19.8752
26.0346
35.1963
39.4180
35.9240
36.8990
34.4318
29.1849
25.9764
18.0301
7
The GTOPO 30 digital elevation model (USGS, 1996) was used as a terrain model for
seNorge. The terrain from GTOPO30 was re-projected to UTM Zone 33 (WGS84) and
interpolated to a resolution of 1 x 1 km2. From the resulting terrain model, zmin,40km and
zmean,40km were calculated for each 1 x 1 km2 cell for the whole of Norway, Denmark, Sweden
and Finland (Tveito et al. 2000).1 The fields are shown in Fig. 2. It is planned to use a more
accurate digital elevation model from the Norwegian Mapping Authority in the near future.
Figure 2. Variation of parameters used as independent variables in de-trending 24-hour mean
temperatures. Figures are taken from Tveito at el. (2000).
Values from the 1 km resolution fields that are shown in Fig. 2 were interpolated to the exact
location of all stations. Hence, for each station, the station coordinates in UTM Zone 33
(WGS84) are used to compute values of latstation, lonstation, zmin,40km and zmean,40km from the ArcASCII grid files with the corresponding fields. Bi-linear interpolation is used for this purpose.
1
The result is stored in ArcASCII grid files named “fenno_dem_u33.asc”, “fenno_lat.asc”, “fenno_long.asc”,
“fenno_min40.asc” and “fenno_mean40.asc” for the altitudes, latitudes and longitudes of each grid cell, as well
as for the minimum altitudes within a circle of 40 km diameter around each grid cell and the mean altitudes
within a circle of 40 km diameter around each grid cell, respectively.
8
The de-trended 24-hour mean temperatures from all available stations (Tde-trended in equation
above) were finally interpolated to the whole of Norway. For this spatial interpolation two
new methods were tested, namely a thin-plate spline technique called ANUSPLIN as well as
ordinary 2-dimensional Kriging.
The number of stations with daily 24-hour mean temperature records is usually between 190
and 205. However, for the daily runs, the number can be as low as 150 or even lower in some
cases. This is usually connected to a problem or delay with entering the data into the database.
Hence, re-running the same day(s) at a later stage (such as in the weekly runs) usually solves
this problem.
Description of ArcInfo routine TOPOGRID/ANUDEM
Gridding of de-trended temperature observations was previously done using the ArcInfo
routine “TOPOGRID”. TOPOGRID is an interpolation method specifically designed for the
creation of hydrologically correct digital elevation models (DEMs) from comparatively small,
but well selected elevation and stream coverages. TOPOGRID is based upon the ANUDEM
Fortran program (see http://www.geo.u-szeged.hu/~papesz/ddm/arc-topogrid-command.pdf
for more information on Topogrid).
The interpolation procedure ANUDEM has been designed to take advantage of the types of
input data commonly available and the known characteristics of elevation surfaces. The
method uses an iterative finite difference interpolation technique. It is optimized to have the
computational efficiency of ‘local’ interpolation methods such as inverse distance weighted
interpolation, without losing the surface continuity of global interpolation methods such as
kriging and splines. It is essentially a discretised thin plate spline technique, where the
roughness penalty has been modified to allow the fitted DEM to follow abrupt changes in
terrain, such as streams and ridges (for more information on ANUDEM, see
http://fennerschool.anu.edu.au/publications/software/).
Description of Fortran routine ANUSPLIN
Since TOPOGRID and ANUDEM are mainly thought for interpolating topographical data, we
were recommended to use ANUSPLIN instead (Hutchinson, personal communication).
The ANUSPLIN package contains Fortran programs for fitting surfaces to noisy data as a
function of one or more independent variables. ANUSPLIN is a program that fits an arbitrary
number of (partial) thin plate smoothing spline functions of one or more independent
variables. It is suitable for data sets with up to 2000 points. The degree of smoothing is
normally determined by minimising the generalised cross validation (GCV) or the
generalised maximum likelihood (GML) of the fitted surface (see Hutchinson, 2006).
Both ANUDEM and ANUSPLIN are avaible as licensed executables from The Fenner
School of Environment and Society, Australian National University, Canberra, Australia (for
more information see http://fennerschool.anu.edu.au/publications/software/). The source code
of these programs could, unfortunately, not be made available.
9
Problems with ANUSPLIN
Unfortunately, the results of the ArcInfo routine TOPOGRID, which is based upon
ANUDEM, could not be reproduced by ANUSPLIN.
Several smoothing configurations were tested for the spatial interpolation of de-trended
temperatures in conjunction with ANUSPLIN. The default smoothing in ANUSPLIN that is
determined by minimising the generalised cross validation (GCV) produced temperature
maps that looked far too smooth. Smoothing determined by minimising the generalised
maximum likelihood (GML) of the fitted surface led to even smoother output fields.
It was tested to use the smoothing by “minimising the true mean square error” (see
Hutchinson, 2006) using a supplied error standard deviation estimate. This led to more
promising results. However, the difficulty with this option was that the standard deviation
estimate had to be estimated in advance. Usually a value of 0.4 performed quite well, with a
slightly lower value leading to the crash of ANUSPLIN and a slightly higher value leading to
smoother fields (Fig. 3).
A comparison of an interpolated de-trended temperature field over Norway using both
ANUSPLIN and TOPOGRID is shown in Fig. 3. Here, the recommended (default)
smoothing of minimising the generalised cross validation (GCV) was used for ANUSPLIN.
In general, ANUSPLIN shows much smoother fields than TOPOGRID. The agreement,
however, was much better when “minimising the true mean square error using a supplied
error standard deviation estimate” was used as a smoothing option. Nevertheless,
ANUSPLIN fields were still much smoother than the corresponding fields that were
produced by TOPOGRID.
Hence, ANUSPLIN did not meet our requirements of an exact interpolation method, i.e. an
interpolation method that produces a surface that passes exactly through all of the data points
(e.g. Deutsch and Journel 1992; Ali 2004). An exact interpolation method should be able to
exactly reproduce the values at the locations of the input data. In other words, the
interpolation method should be able to exactly reproduce the observed temperature values at
the locations of the weather stations. Kriging, triangulation as well as some spline methods
are examples of exact interpolation methods. The exactness (also sometimes called
exactitude) of the interpolation methods presented herein is investigated in Fig. 4 for
temperature and Fig. 10 for precipitation; although this is not strictly true, since the closest
seNorge grid points are used in the comparison presented herein and not the locations of the
weather stations.
It is planned to discuss the excessive smoothing issue with the author of ANUSPLIN, and a
solution to this problem might perhaps be found in the future. In the meantime, however, it
was decided to use Ordinary Kriging from the open source Geostatistical Software Library
(Deutsch and Journel, 1992) instead. Ordinary Kriging might indeed be a better choice for
the interpolation of de-trended temperatures, if the semi-variogram can be calculated
automatically for every day. Also, different semi-variograms might be used for different
regions of Norway and semi-variograms might be obtained from weather prediction model
data rather than from observations (Tveito, personal communication).
10
Figure 3. Comparison of spatially interpolated de-trended temperatures from 21 April 2008.
ANUSPLIN with default smoothing (“minimise generalised cross validation”) results in
much smoother fields than TOPOGRID and 2D Ordinary Kriging. Using ANUSPLIN with
customised smoothing (“minimise true mean square error”) with a value of 0.4 results in
much better results. Same legend applies for all figures.
11
Description of 2D Ordinary Kriging and GSLIB
Kriging is a geostatistical technique to interpolate values of a random field (in our case, the
surface temperature) as a function of the geographic location. The value at an “unobserved
location” is obtained from observations of its value at nearby locations.
Kriging relies on the spatial auto-correlation structure of the data, which determines the
weighting values. This is a more rigorous approach to modelling, as correlation between data
points determines the estimated value at an unsampled point. Ordinary Kriging, which is
used herein, assumes an unknown constant trend. For more information on ordinary kriging
see, for instance, Deutsch and Journel (1992).
To utilize ordinary kriging, a spatial correlation model for the quantity of interest must be
established. This is usually specified in the form of a semi-variogram or a covariance
function. The semi-variogram is a function describing the expected difference in value
between pairs of samples with a given relative orientation.
For a stationary random function, there is a very simple relationship between the semivariogram (“Y”) and the covariance function (“C”), namely
Y(distance) = sill - C(distance).
Here, distance denotes the distance between two points and sill the maximum semi-variance
value of the semi-variogram model. Consequently, the covariance function and, hence,
correlation reaches its maximum, when distance goes to zero. On the other hand, the
covariance function as well as correlation go to approximately zero, when distance goes to
infinity. In this case, no further variance can be explained by the semi-variogram or
covariance model.
Hence, the semi-variogram quantifies the assumption that things nearby tend to be more
similar than things that are farther apart. Moreover, a neighbourhood must be defined for
which observations are taken into account at a certain distance from the point of interest. This
is called the “maximum search radius” in the Geostatistical Software Library. The resulting
(spatially interpolated) values are then computed by a linear combination of the observed
values with weights between 0 and 1.
Hence, observations of the quantity at nearby locations are weighted together to result in a
value of the quantity at the “unobserved location”. In the case presented herein, the quanity is
the de-trended 24-hour mean air temperature. Hence, the de-trended 24-hour mean
temperature at an “unobserved location” is calculated as the linear combination of the detrended 24-hour mean temperature from nearby stations as
n
Tunobserved −location = ∑ Tobserved −location (i ) ⋅ ε (i )
i =1
where Tobserved-location(i) are the de-trended 24-hour mean temperature values from the
surrounding stations, ε(i) the weighting coefficients (also called the “kriging weights”) and
Tunobserved-location the value of the de-trended 24-hour mean temperature at the “unobserved
location”. In every case, the sum of all weighting coefficients is equal to 1. The maximum
search radius determines which surrounding stations are used for the linear combination in
the above equation. In the study presented herein, a maximum search radius of 100 km is
used.
12
The Ordinary 2-dimensional Kriging routine from the Geostatistical Software Library
(GSLIB) with the file name “okb2d.f90” was used (Deutsch and Journel, 1992). A newer
version is available at http://www.gslib.com/ and it is planned to use the newer version in the
near future.
Interpolation of De-Trended Temperatures using Ordinary Kriging
Spatial interpolation of de-trended temperatures is done in “tamread_and_krige.f90”. The
GSLIB routine “okb2d.f90” is used. Output temperatures are stored in an ArcASCII grid file
called “okb2d.asc”.
Variograms were selected depending only upon the month when the data was measured. The
monthly variograms from Tveito et al. (2000) were used (Table 4). In contrast to Tveito et al.
(2000), however, the nugget values of the semivariograms were chosen to be zero for all
months.
In the study from Tveito et al. (2000), monthly standard normal temperatures from 1247
stations in Denmark, Norway, Sweden and Finland were used to compute semi-variograms
for monthly mean temperatures as a function of distance only. According to the report, the
station cover was good in southern parts of Sweden and Finland and south-eastern Norway,
whereas the station network was sparse in the mountains and northern parts of Sweden,
Finland and Norway as well as in western Jutland (Denmark).
Table 4. Semi-variogram parameters used in the Kriging of daily de-trended temperatures for
seNorge. The semi-variograms were established from long-term average monthly mean
temperature data of 1247 stations in Denmark, Norway, Sweden and Finland (Tveito et al.,
2000). Note that the nugget values of the semi-variograms were set to zero in the study
presented herein.
Month
Jan
Feb
Mar
Apr
May
Jun
Jul
Aug
Sep
Oct
Nov
Dec
*) Exponential
Nugget
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
0.0
model applied
**) Spherical
Sill
7.0
5.0
1.3
0.33
0.7
1.0
0.6
0.19
0.3
1.3
3.5
7.0
model applied
13
Range (km)
250 *
250 *
200 *
100 *
75 *
150 *
500**
100 *
75 *
175 *
200 *
250 *
From time to time, the ordinary Kriging routine from GSLIB that is used herein seems to
“crash”, which results in completely unrealistic values. For this reason, a check is performed
that
1. the variance of the resulting field averaged over all data grid points is smaller than 50,
2. the resulting spatially interpolated temperatures are between -60˚C and +50˚C at all
grid points.
If one of the above conditions is not fulfilled, the ordinary Kriging routine is run once again,
until the problem is solved and realistic values are returned. No other problems were
encountered with this GSLIB routine.
Comparison of Results from Ordinary Kriging, Topogrid and
ANUSPLIN
A simple test of the quality of an interpolation routine is whether the routine succeeds in
preserving the values at the locations of the input data. If there is too much smoothing, for
instance, the interpolated values at the locations of the input data points are going to be
different to the values of the input data itself.
In the ideal case, the values are exactly the same and the correlation coefficient is equal to 1.
However, because we use the interpolated values on a 1 x 1 km grid in our case, the
correlation coefficient is not going to be equal to 1 even in the ideal case, but slightly smaller.
Such a test is presented here. All three routines were used for the interpolation of de-trended
temperature values and exactly the same de-trended temperature values were used as input to
all three routines. The output values at those pixels were chosen that are closest to the
locations of the data points that have been used as input to the interpolation routine. Data from
April 2008 consisting of 30 days in total was chosen.
Indeed Ordinary Kriging performs very well, perhaps even slightly better than Topogrid in
conjunction with ArcInfo. ANUSPLIN, however, performs generally less well (Fig. 4). In
fact, if the default smoothing option is used in ANUSPLIN (“minimise generalised cross
validation”), ANUSPLIN performs very poorly.
When the option “minimise true mean square error using supplied error standard deviation
estimate” is used in ANUSPLIN together with a value of 0.4 for the error standard deviation
estimate, ANUSPLIN performs almost as good as Ordinary Kriging (Fig. 4). In this case, the
correlation between spatially interpolated de-trended temperatures at 1 km horizontal
resolution and observed de-trended temperatures is almost as good as with Ordinary Kriging
or Topogrid (Fig. 4).
Another comparison between Ordinary Kriging and Topogrid is presented in Fig. 5. Here, a
histogram is shown of the differences in interpolated “de-trended” temperature from Ordinary
Kriging (routine OKB2D in Fortran) and Topogrid (ArcInfo). All seNorge grid points from all
30 days of April 2008 (altogether approximately 14.5 million data points) were used. It can be
seen that the majority of the points reveals only very small differences. Indeed about 95% of
the grid points have differences within the range of ±0.5˚C.
14
Figure 4. Comparison of daily results from Topogrid (ArcInfo), Ordinary Kriging and
ANUSPLIN for April 2008. The figures reveal the ability of the interpolation routines to
reproduce the temperatures at the locations of the temperature observations. Observed
temperatures are compared to interpolated temperatures at the seNorge grid points closest to
the locations of the temperature observing stations. Note that this is not a cross validation.
15
Figure 5. Histogram of differences in interpolated “de-trended” temperature from Ordinary
Kriging (GSLIB routine in Fortran) and Topogrid (ArcInfo). All seNorge grid points from all
30 days of April 2008 were used. Exactly the same de-trended temperature values were used
as input to both interpolation routines.
16
Calculation of Final seNorge Temperature Maps
The interpolated de-trended temperatures from above were used to produce a temperature
map with 1 x 1 km horizontal resolution for the whole of Norway. For this purpose, the same
equation is used that is used for de-trending observed station temperatures. However, the
opposite sign is used for the six different terms.
Hence, daily seNorge temperature maps are calculated as:
TseNorge (i, j ) = Tde−trended (i, j ) + v1 ⋅ z DEM , Norge (i, j ) + v2 ⋅ z mean , 40 km (i, j ) + v3 ⋅ z min, 40 km (i, j )
+ v4 ⋅ lat grid −cell (i, j ) + v5 ⋅ lon grid −cell (i, j ) + const
where Tde-trended(i, j) are the daily interpolated de-trended station temperatures on a 1 x 1 km
grid that are obtained by either Ordinary Kriging. TseNorge(i, j) are the final seNorge daily
temperature maps on a 1 x 1 km grid that are published on seNorge.
Moreover, zDEM,Norge are the altitudes above sea level on a 1 x 1 km grid obtained from a
digital elevation model of Norway. zmean,40km are the mean altitudes within a circle of 40km
diameter surrounding each 1 x 1 km grid cell, obtained from the same digital elevation model.
and zmin,40km are the lowest altitudes within a circle of 40km diameter surrounding each 1 x 1
km grid cell. The final two parameters latgrid-cell and longrid-cell are the latitudes and longitudes
of the grid cells, respectively.
An example of a seNorge daily temperature map is shown in Fig. 6. In the western parts of
Norway (“Vestlandet”) the influence of zmin,40km and zmean,40km on the gridded temperature
maps can clearly be seen.
17
Figure 6. Example of daily temperature map from seNorge. The map was produced with the
new routines described herein.
18
Gridding of Precipitation Observations
The Norwegian climate is characterised by extremely large variations in precipitation, mostly
owing to the complex topography of Norway. Mean annual precipitation can vary between
300 and more than 3000 mm over a distance of a few tens of kilometres only. However, in
general, precipitation increases with height above sea level. Furthermore, precipitation
decreases from the western to the eastern parts of the country, due to a combination of the
topography of Norway as well as the prevailing westerly winds.
In this study, the only factor that is taken into account is the increase of precipitation with
height. It is planned, however, to include wind-direction dependent lee effects in the statistical
model in the future.
Description of Input Data
Daily 24-hour accumulated precipitation is output from the Oracle database using the SQL
database queries described on page 6. The data is written to a file called “utfil_test2.lst”,
whereas the station meta data (with coordinates, altitude, station type, etc.) is written to a file
called “stkart3.lst”.
Note that a station with one and the same station number can occur several times in
“stkart3.lst”, since new meta data is added every time the status of a station has changed. For
simplicity, only the meta data record in which the station main type is “A”, “I”, ”N” or “V” is
used in the programs described herein.
Consequently, only stations with main types “A”, “I”, ”N” and “V” from any of the meta data
records in file “stkart3.lst“ are used. However, stations with main type “N” and under-type “I”
as well as stations with main type “N” and under-type “O” are not used. Also, stations with
main type “N” and under-type “T” are not used. For simplicity, it was decided to exclude a
station from the analysis, if these three main types and under types (“NI”, “NO” and “NT”)
occur in one or more meta data record(s) for a particular station.
The database shell scripts, SQL queries and database output files that are used within the
Fortran programs are summarised in Table 5.
Table 5. Names of output files as well as SQL database queries and shell scripts that are used
to retrieve the data.
Name of file Name of Program/SQL query
utfil_test2.lst rr.sh/rr.sql
stkart3.lst
Data in File
Station number, 24-hour accumulated
precipitation (RR), quality flags for RR
stasjonskart3.sh/stasjonskart3.sql Station number, UTM coordinates,
altitude, latitude, longitude, station type,
etc.
19
“Exposure Correction” of Precipitation Observations
Observed daily 24-hour accumulated precipitation observations from all stations are corrected
for measurement losses due to mainly aerodynamic effects near the rim of the gauges and
blowing/drifting snow as well as for measurement losses due to evaporation and wetting. The
method of Førland et al. (1996) is used. In this analysis, a distinction between liquid and solid
precipitation was made and an operational correction of precipitation measured at various
types of stations was developed. The model for correcting solid precipitation (i.e. snow) is
entirely based upon data collected at the Jokioinen meteorological observatory in Finland.
The losses in precipitation amount can be particularly large during snowfall and high wind
speeds. For the daily precipitation maps on seNorge, the Recommended Model 2: “SIMPLE
CORRECTION MODEL” (Monthly values) from Førland et al. (1996) was used. Even
though this model is recommended for monthly values only, it was used for the production of
the daily precipitation maps.
In this model, every station is assigned an exposure class (Table 6). For all approximately
1800 stations that are included in the data file with exposure class values, about 164 stations
have been assigned an exposure class of “1”, 187 stations have been assigned an exposure
class of “2”, 553 stations an exposure class of “3”, 518 stations an exposure class of “4” and
409 stations an exposure class of “5”. Most very exposed stations can be found in costal
regions within the western parts of Norway or on mountain locations within the interior parts
of Norway. Extremely sheltered stations can be found mostly within parts surrounding Oslo,
whereas all intermediate values can be found in parts in between (Fig. 7).
For extremely exposed stations and solid precipitation (i.e. snow), the correction factor is as
high as 1.80 (Table 6), meaning that 80% more precipitation is added to the observed value.
In the same case, the correction factor for extremely sheltered stations is as low as 1.05. The
correction factors are recommended for the Nordic gauges with wind shields. For unshielded
gauges, the correction factors are even higher than the values presented in Table 6 (Førland et
al. 1996).
Table 6. Exposure correction factors used for production of daily precipitation maps.
Observed precipitation is multiplied with respective correction factor. “Standard correction
factors for monthly precipitation” from Førland et al. (1996) were used for correcting daily
precipitation observations.
Class
Exposure
1
2
Extremely sheltered small glade in forest
Intermediate position between forest and
plain
Relatively unsheltered location on a plain
Relatively unsheltered location in coastal or
mountain region
Extremely unsheltered location in coastal or
mountain region
3
4
5
Correction factor k
Liquid (kl)
1.02
1.05
Solid (k )
1.05
1.10
1.08
1.11
1.20
1.40
1.14
1.80
20
Hence, observed precipitation sums are corrected for exposure and other losses using the
following simple equation:
RRcorrected = k s ⋅ ( RRobserved + pe + 0.035)
for
TseNorge(station) < 0˚C
RRcorrected = (k s + kl ) / 2 ⋅ ( RRobserved + pe + 0.095)
for
0˚C ≤ TseNorge(station) < 2˚C
RRcorrected = kl ⋅ ( RRobserved + pe + 0.11)
for
TseNorge(station) ≥ 2˚C
where RRobserved is the 24-hour accumulated precipitation from the SQL database, RRcorrected is
the exposure-corrected 24-hour accumulated precipitation that is used for the production of
daily precipitation maps for seNorge, ks and kl the correction factors from Table 6 and pe is
the mean daily evaporation loss for Nordic manual gauges from Table 7.
For pe the average value between the Swedish and the Norwegian gauges from Førland et al.
(1996) is used (last column in Table 7). This value depends only upon the month of the year.
The last value in the equation above accounts for the wetting loss, which again is specified as
the average value between the Swedish and the Norwegian rain gauges from Førland et al.
(1996). The recommended values for wetting have been used here. These are 0.035 mm/day
for snow, 0.095 mm/day for mixed precipitation and 0.11 mm/day for liquid precipitation.
All the three corrections described above shall hereinafter be simply summarised with the
term “exposure correction”.
21
Figure 7. Exposure classes for precipitation stations. These are used to correct precipitation
values according to the Simple Correction Model for monthly values from Førland et al.
(1996). This model is applied for the correction of the daily values that are used for seNorge.
22
Table 7. Recommended value of mean daily evaporation loss (mm/day) for Nordic manual
gauges from Førland et al. (1996). The values from the last column were used for seNorge.
Month
January
February
March
April
May
June
July
August
September
October
November
December
Daily
evaporation
loss for Swedish
manual gauges
0.02
0.03
0.04
0.12
0.10
0.15
0.15
0.10
0.05
0.03
0.03
0.02
Daily
evaporation
loss for Norwegian
manual gauges
0.02
0.02
0.03
0.16
0.04
0.06
0.06
0.05
0.03
0.02
0.02
0.02
Average
value
between Swedish and
Norwegian gauges
0.02
0.025
0.035
0.14
0.07
0.105
0.105
0.075
0.04
0.025
0.025
0.02
The exposure classes for most stations are stored in a static file called “eksposisjon_2008.txt”
at /klimaprod/applikasjon/gridding/seNorge/precip/. If for some reason, an exposure class is
missing for an observing station, an email is automatically sent to [email protected] and
[email protected]. In this case, the exposure class for the respective station has to be
estimated manually and added to the file “eksposisjon_2008.txt” as an additional row. It is
planned to include the exposure class values in the SQL database in the near future.
Triangulation of Precipitation Observations
For interpolating precipitation observations in between the locations of observing stations
triangulation is used. Triangulation is a method developed to model surfaces in a twodimensional plane. Triangulation represents a fairly quick method and creates a set of
adjacent, non-overlapping triangles between observation points.
In our case, triangulation of precipitation involves the solution of large meshes of triangles,
with hundreds of observations (Fig. 7). One disadvantage of triangulation, however, is that it
is limited to cover the area between observation points. Areas outside defined triangles will be
cut off. Hence, the technique is purely an interpolation technique and does not allow for
extrapolation.
The methodology described herein was also used in Jansson et al. (2007).
23
Description of Delaunay triangulation from Geompack (DTRIS2)
Gridding of exposure-corrected precipitation observations was previously done using the
ArcInfo routines “Createtin” and “Tinlattice”. To perform the triangulation in Fortran, the
routines from Barry Joe's Geompack and Mesh Generation Research website in Fortran 77
were used (see http://members.shaw.ca/bjoe/).
The newer C++ version of Geompack, Geompack++, is a comprehensive object-oriented
software package for finite element mesh generation (triangular, quadrilateral, surface,
tetrahedral, hexahedral-dominant). The routines are available for Windows and Linux and the
source code can easily be included in any software.
Geompack90, the Fortran 90 predecessor of Geompack++ and successor of GEOMPACK, is
no longer available since July 2003. However, Barry Joe points out that Geompack90 has
been superseded by the much better and faster Geompack++. GEOMPACK, the original
Fortran 77 package is no longer supported, but can be downloaded from the above website.
In the programs described herein, the DTRIS2 subroutine from the original GEOMPACK
Fortran 77 package was used. The routine constructs the Delaunay triangulation of a set of
2D vertices using an incremental approach and diagonal edge swaps. Vertices are first sorted
in lexicographically increasing (X,Y) order, and then are inserted one at a time from outside
the convex hull.
An example of this Delaunay triangulation is shown in Figure 8 for the 20 May 2008. It can
be seen that the triangles are very large over areas along the Norwegian border in the east, as
well as over coastal parts in the west. Over the northernmost parts of Norway, no triangles
could be constructed due to the absence of any stations.
24
Figure 8. Example of Delaunay triangulation of Norwegian precipitation observations. The
example shows the stations used for the interpolation of 24-hour accumulated precipitation
observations for 20 May 2008.
The “Point in Triangle Test”
The triangle nodes from the DTRIS2 subroutine of GEOMPACK are used in conjunction with
the precipitation observations for the respective day (files “triangle_nodes.dat“ and “rr.par”,
respectively). The latter file also includes the UTM Zone 33 coordinates of the stations as
well as their altitudes. Note that the most recent set of coordinates is used for a station number
that has several different sets of coordinates for different time periods.
In order to find out whether a grid point is situated in a triangle or not, the "Point in triangle
test" according to the Barycentric Technique is carried out (for more information on this
technique see http://www.blackpawn.com/texts/pointinpoly/default.html). Barycentric
coordinates are the coordinates defined by the common center of mass of two or more bodies.
In the context of a triangle, barycentric coordinates are also known as areal coordinates.
25
If the point of interest (the respective grid point of seNorge) is denoted P and the three points
of the respective triangle to be investigated are denoted A, B and C, the three vectors (AB),
(AC) and (AP) can be calculated from the x- and y-coordinates of these points. Thereafter, the
barycentric coordinates can be computed using scalar products of different combinations of
these vectors as:
u=
{( AB) ⋅ ( AB)}⋅ {( AC ) ⋅ ( AP)} − {( AC ) ⋅ ( AB)}⋅ {( AB) ⋅ ( AP)}
{( AC ) ⋅ ( AC )}⋅ {( AB) ⋅ ( AB)} − {( AC ) ⋅ ( AB)}2
v=
{( AC ) ⋅ ( AC )}⋅ {( AB) ⋅ ( AP)} − {( AC ) ⋅ ( AB)}⋅ {( AC ) ⋅ ( AP)}
{( AC ) ⋅ ( AC )}⋅ {( AB) ⋅ ( AB)} − {( AC ) ⋅ ( AB)}2
where u and v are the barycentric coordinates of the point P with respect to the triangle
consisting of the three points A, B and C.
The point P is situated in the triangle ABC if all three conditions
u ≥ 0,
v ≥ 0 and
u+v≤1
are fulfilled. In this case, the triangle ABC is used for obtaining a precipitation value at the
seNorge grid point P through linear interpolation.
In the same way, station heights from the three points A, B and C are linearly interpolated to
the point P, in order to get a fictitious station height at the point P. These two values are then
used in conjunction with the real altitude of the grid point P to estimate the daily 24-hour
accumulated precipitation at point P (see below).
Interpolation of Exposure-Corrected Precipitation Observations
The linear interpolation of exposure-corrected precipitation values within each triangle is
carried out as:
∂rr ( y2 - y1 ) * (rr3 - rr1 ) - ( y3 - y1 ) * (rr2 - rr1 )
=
∂x
( x3 - x1 ) ⋅ ( y2 - y1 ) - ( x2 - x1 ) ⋅ ( y3 - y1 )
∂rr ( x3 - x1 ) * (rr2 - rr1 ) - ( x2 - x1 ) * (rr3 - rr1 )
=
∂y
( x3 - x1 ) ⋅ ( y2 - y1 ) - ( x2 - x1 ) ⋅ ( y3 - y1 )
rr (i, j ) = rr1 + ( x(i ) − x1 )
∂rr
∂rr
+ ( y ( j ) − y1 )
∂y
∂x
where x1, x2, and x3 are the x coordinates of the three points A, B and C, respectively.
Similarly, y1, y2, and y3 are the y coordinates of the three points A, B and C, respectively, and
rr1, rr2, and rr3 are the exposure corrected precipitation observations from the three points A,
26
B and C (RRcorrected in the equation above). The three quantities x(i), y(j) and rr(i,j) are the xand y-coordinates of the respective seNorge grid point as well as the interpolated exposure
corrected precipitation value at the respective seNorge grid point, respectively.
The above expressions can be derived from the equations of a linear surface located in
between the three points. The complete derivation of these expressions is described in, for
instance, Nilsson (1997). In Nilsson (1997), the same expressions are used for calculating
horizontal pressure gradients.
An example of triangulated precipitation observations is shown in Fig. 9 (upper figures). It
can be seen that the differences between ArcInfo and the new Fortran routines are very small.
Triangulation of Station Altitudes
In the same way as described above, station altitudes are triangulated. Hence, station altitudes
above sea level are used in place of observed 24-hour accumulated precipitation values. It has
to be pointed out that exactly the same triangles have to be used.
The same linear interpolation is performed within each triangle; however, using station
altitudes in place of exposure corrected precipitation values. The resulting field shall
hereinafter be called zstation,triangulated(i, j).
Again, interpolated values are only calculated in between observation points. Areas outside of
the defined triangles will be cut off and assigned “no-data” values. An example of
triangulated station altitudes is shown in Fig. 9 (lower figures). It can be seen that the
differences between ArcInfo and the new Fortran routines are very small.
27
Figure 9. Triangulated precipitation and station altitude values (upper and lower figures). The
results from ArcInfo and Fortran are compared (left and right hand side). Date is 30 March
2008. The same legend applies to left and right hand side figures.
28
Comparison of Interpolated Values with Observations
A simple test of the quality of an interpolation routine is whether the routine succeeds in
preserving the values at the locations of the input data. If there is too much smoothing in the
interpolation routines, for instance, the interpolated values at the locations of the input data
points are going to be different to the values of the input data itself. One of the advantages of
triangulation, however, is that there is virtually no smoothing at all.
In the ideal case, the values would be exactly the same and the correlation coefficient would
be equal to 1. However, in our case we use the interpolated values on a 1 x 1 km grid and
even in the ideal case the correlation coefficient is not going to be equal to 1, but slightly less
than 1.
Such a test is presented here. The output values at those pixels are chosen that are closest to
the locations of the data points that have been used as input to the interpolation routine. It can
be seen that the triangulation of the new Fortran routines (using DTRIS2 from Geompack)
performs exactly as well as the triangulation of ArcInfo (Fig. 10). Indeed, no difference in
performance could be found. The results are approximately the same for both precipitation
and station altitude (Fig. 10, upper and lower figures).
Another comparison between ArcInfo and the new Fortran routines is presented in Fig. 11.
Here, a histogram is shown of the differences in interpolated daily precipitation from Fortran
routines (using DTRIS2 from Geompack) and ArcInfo. All seNorge grid points from all 30
days of April 2008 (altogether approximately 14.5 million points) were used. Exactly the
same daily precipitation values were used as input data to both routines. It can be seen that the
majority of the points reveals only very small differences. Indeed more than 99% of the grid
points have differences within the range of ±0.5mm.
29
Figure 10. Comparison of daily precipitation values and station heights with interpolated
values for April 2008. The figures reveal the ability of the interpolation routines to reproduce
the values at the locations of the precipitation observing stations. Observed precipitation
values are compared to interpolated values at the seNorge grid points closest to the locations
of the precipitation observing stations. Note that this is not a cross validation.
30
Figure 11. Histogram of differences in triangulated precipitation from Fortran (DTRIS2
routine from Geompack) and ArcInfo (Createtin/Tinlattice). All seNorge grid points from all
30 days of April 2008 were used. Exactly the same precipitation observations were used as
input to both interpolation routines.
31
Calculation of Final seNorge Precipitation Maps
The interpolated exposure-corrected precipitation values from above were used in conjunction
with the interpolated station altitude values to produce a daily precipitation map with 1 km
horizontal resolution for the whole of Norway. For this purpose, the triangulated values from
above are used together with a digital elevation model for Norway.
Precipitation is expected to increase by 10% for each 100 m increase in altitude. However,
above 1000 m height above sea level, precipitation increases less rapidly with height.
Therefore, an increase of 5% for each 100 m increase in altitude is used above this height. The
difference between the real terrain and the triangulated station altitudes (zDEM,Norge(i, j) and
zstation-triangulatede(i, j), respectively) is used to parameterise this increase in precipitation.
This leads to the following equations, where daily seNorge precipitation values are calculated
from a), b), c) or d) as:
a) If zstation,triangulated(i, j) < 1000 m and zDEM,Norge(i, j) < 1000 m:
⎧ (z DEM , Norge (i, j ) − z station ,triangulated (i, j )) ⎫
rrseNorge (i, j ) = rrstation ,triangulated (i, j ) ⋅ ⎨1 +
⎬
1000
⎩
⎭
b) If zstation,triangulated(i, j) < 1000 m and zDEM,Norge(i, j) > 1000 m:
⎧ (1000 − z station ,triangulated (i, j )) (z DEM , Norge (i, j ) − 1000) ⎫
rrseNorge (i, j ) = rrstation ,triangulated (i, j ) ⋅ ⎨1 +
+
⎬
1000
2000
⎭
⎩
c) If zstation,triangulated(i, j) > 1000 m and zDEM,Norge(i, j) > 1000 m:
⎧ (z DEM , Norge (i, j ) − z station ,triangulated (i, j )) ⎫
rrseNorge (i, j ) = rrstation ,triangulated (i, j ) ⋅ ⎨1 +
⎬
2000
⎭
⎩
d) If zstation,triangulated(i, j) > 1000 m and zDEM,Norge(i, j) < 1000 m:
⎧ (z station ,triangulated (i, j ) − 1000) (1000 − z DEM , Norge (i, j )) ⎫
rrseNorge (i, j ) = rrstation ,triangulated (i, j ) ⋅ ⎨1 −
−
⎬
2000
1000
⎭
⎩
where zDEM,Norge(i, j) and zstation,triangulatede(i, j) are the altitudes of the real terrain and the
triangulated station heights, respectively. rrseNorge(i, j) are the final gridded values of daily
precipitation that are published on seNorge.no.
An example of a daily precipitation map is shown in Fig. 12. The influence of the triangles on
the gridded precipitation maps can clearly be seen.
32
Figure 12. Example of daily precipitation map from seNorge. The map was produced with
the new routines described herein.
33
Summary & Conclusions
New routines have been developed for the spatial interpolation of 24-hour mean temperature
and 24-hour accumulated precipitation from weather observations collected by the Norwegian
Meteorological Institute (met.no).
The spatially interpolated maps cover the whole of Norway with 1 km horizontal resolution.
The only exception are the northernmost parts of the country, where no precipitation maps are
available at present. However, complete coverage of Norway is going to be achieved in the
very near future.
The temperature and precipitation maps are updated daily at 08:00 UTC. The maps are
published daily on the Internet at seNorge.no. Moreover, the maps are used by the Norwegian
Water Resources and Energy Directorate (NVE) to produce maps of hydrological and snowcover related properties.
The “old” routines were programmed in ArcInfo/AML. However, since ArcInfo is not an
operational platform at met.no new routines were developed in Fortran. A technical
description of the new programs is given in this report. In contrast to the “old” routines in
ArcInfo, where a static station cover was used, it was tried to keep the “new” routines as
flexible as possible. Hence, all station meta data, with the exception of the station exposure
class for precipitation, is retrieved daily from the climate database. The remaining parameters
that are needed are calculated within the program.
The new interpolation routines in Fortran were compared to the old routines in ArcInfo. In
general, the results of the interpolations are very similar for both temperature and
precipitation. Indeed, 95% of the seNorge grid points show differences in interpolated
temperature of less than ±0.5˚C. Furthermore, more than 99.9% of the grid points show
differences in precipitation of less than ±0.1mm.
A simple test of the quality of the interpolation routines was carried out. For that purpose, it
was investigated whether the routine succeeds in preserving the values at the locations of the
input data. If there is too much smoothing in the interpolation routine, for instance, the
interpolated values at the locations of the input data are going to be different to the values of
the input data itself.
For the interpolation of 24-hour mean temperature, it is shown that Kriging performs very
well (perhaps slightly better than Topogrid in ArcInfo). The thin-plate spline ANUSPLIN
interpolation package in Fortran performs generally less well, with the problem that the
interpolation routine applies to much smoothing to the output data. In fact, if the default
smoothing option (“minimise generalised cross validation”) is used, ANUSPLIN performs
very poorly.
For the interpolation of 24-hour accumulated precipitation, the triangulation routines that
were developed in Fortran, perform exactly as well as the ArcInfo routines (“Createtin” and
“Tinlattice”) that were originally used. No difference in performance could be found.
34
References
Ali, T. A., 2004: “On the selection of an interpolation method for creating a terrain model
(TM) from LIDAR data”, Proceedings of the American Congress on Surveying and Mapping
(ACSM) Conference 2004, Nashville TN, U.S.A.
Deutsch, C. V., and A. G. Journel, 1992: “GSLIB Geostatistical Software Library and User’s
Guide”, Oxford University Press, New York/Oxford, 340 pages.
Førland, E. J., P. Allerup, B. Dahlström, E. Elomaa, T. Jónsson, H. Madsen, J. Perälä, P.
Rissanen, H. Vedin and F. Vejen, 1996: “Manual for operational correction of Nordic
precipitation data”, DNMI report nr. 24/96 (available from www.met.no).
Hutchinson, M. F., 1989: “A new method for gridding elevation and streamline data with
automatic removal of pits”. Journal of Hydrology 106: 211-232.
Hutchinson, M., 2006: “ANUSPLIN VERSION 4.36 – USER GUIDE”, Centre for Resource
and Environmental Studies, The Australian National University, Canberra.
Jansson, A., O. E. Tveito, P. Pirinen and M. Scharling, 2007: “NORDGRID – a preliminary
investigation on the potential for creation of a joint Nordic gridded climate dataset”, met.no
report no. 03/2007, Climate (available from www.met.no)
Nilsson, L., 1997: “Tids- och rumsvariationer av geostrofisk vind på olika platser i Sverige,
Danmark, Norge och Finland”, Master thesis, Department of Meteorology, Uppsala
University, Uppsala, Sweden.
Tveito, O.E. and E.J.Førland, 1999: “Mapping temperatures in Norway applying terrain
Information, geostatistics and GIS”, Norsk geografisk tidsskrift 53 (4), pp. 202-212
Tveito, O. E., E. Førland, R. heino, I. Hansen-Bauer, H. Alexandersson, B. Dahlström, A.
Drebs, C. Kern-Hansen, T. Jónsson, E. Vaarby Laursen and Y. Westman, 2000: “Nordic
temperature maps”, DNMI Report no. 09/00 (available from www.met.no)
Tveito, O. E., I. Bjørdal, A. O. Skjelvåg and B. Aune, 2005: ”A GIS-based agro-ecological
decision system based on gridded climatology, Met. Apps., Vol. 12: 1, p. 57-68.
35
Appendix A. Flow Chart of “snokart_day.f90”
For the production of the daily maps, the Perl script “snokart_day.pl” is executed on
skypumpe.oslo.dnmi.no from Crontab every morning at 08:00 UTC. The Perl script is stored
at /klimaprod/applikasjon/gridding/seNorge/snoakk. Note that “snokart_day.f90” is called
from this Perl script.
Below a flow chart is shown describing the processes that are executed within the Fortran
program “snokart_day.f90”. Note that another Perl script (“mk_daygrid_today.pl” at
/klimaprod/applikasjon/gridding/bin) is called from the above Perl script after the completion
of this Fortran program.
Call subroutine “date_and_time” (to obtains today’s date from system clock)
Run program “tam_read_and_process.f90” with date as input argument (for temperature gridding)
Run program “precip.f90” with date as input argument (for precipitation gridding)
Call subroutine “lag_status.f90” (check if “tam_read_and_process.f90”
and “precip.f90” executed successfully, otherwise send email)
Produce “metdata_day.zip” (for FTP transfer to NVE)
Run program “bil2png” (optionally) to produce PNG-figures of
tam and rr (this is now done in “mk_daygrid_today.pl”)
Figure A1. Flow chart of main Fortran program ”snokart_day.f90” for the daily runs.
36
Appendix B. Flow Chart of “snokart_week.f90”
For the production of the weekly maps, the Perl script “snokart_week.pl” is executed on
skypumpe.oslo.dnmi.no from Crontab every Tuesday morning at 09:00 UTC. The Perl script
is stored at /klimaprod/applikasjon/gridding/seNorge/snoakk. Note that “snokart_week.f90” is
called from this Perl script.
Below a flow chart is shown describing the processes that are executed within the Fortran
program “snokart_week.f90”. Note that another Perl script (“mk_daygrid_week.pl” at
/klimaprod/applikasjon/gridding/bin) is called from the above Perl script after the completion
of this Fortran program.
Call subroutine “date_and_time” (to obtains today’s date from system clock)
Start loop for processing last 18 days
Run program “tam_read_and_process.f90” with date as input argument (for temperature gridding)
Call subroutine “lag_status.f90” (check if “tam_read_and_process.f90” executed successfully
(in this case returning status = 0), otherwise send email)
Run program “precip.f90” with date as input argument (for precipitation gridding)
Call subroutine “lag_status.f90” (check if “precip.f90” executed successfully
(in this case returning status = 0), otherwise send email)
Finish loop for processing last 18 days
Produce “metdata_week.zip” in “binzip” directory (for FTP transfer of BIL files to NVE)
Run another loop over the last 18 days to produce PNG-figures (optional) of tam and rr (this is now
done in “make_daygrid_week.pl”)
Figure B1. Flow chart of main Fortran program ”snokart_week.f90” for the weekly runs.
37
Appendix C. Flow Chart of “tam_read_and_process.f90”
Delete files from previous run (okb2d.asc, utfil2.lst, tmaxa.sur, tmaxa.cov, tmaxagrd.asc, tam.par)
Read command line argument (= date) to determine day of run
Set monthly regression coefficients (from Tveito et al., 2000)
Read files fenno_dem_u33.asc, fennomean.asc, fenno_min40.asc, fenno_lat.asc and
fenno long.asc (files are covering whole of Norway)
Run SQL database query “tamrr.sh” and check if output file “utfil2.lst” complete
Run subroutine “lst2par.f90” (delete stations with missing temperature observations
in “utfil2.lst”)
Run subroutine “lagfil.f90” (executes SQL database query “stasjonskart.sh” to obtain station
coordinates and altitudes and combines those with temperature observation records from “utfil2.lst”;
creates new file “st_tmp2.dat”)
Calculate ”fennomean”, “fenno_min40”, “fenno_lat” and “fenno_long” from ArcASCII grid files at
station locations using bilinear interpolation
Calculate ”de-trended” temperatures at station locations using ”fennomean”, “fenno_min40”,
“fenno_lat” and “fenno_long” as well as station altitude (see de-trending equation)
Run subroutine ”tamread_and_krige.f90” to perform ordinary kriging of a 2-D rectangular grid from
"Geostatistical Software Library" (Deutsch and Journel, 1992). If Kriging not successful (happens
occasionally), run Kriging once again. Result is interpolated de-trended temperature field.
Calculate gridded temperature fields for whole of Norway by adding trend components from
ArcASCII grid files ”fennomean”, “fenno_min40”, “fenno_lat” and “fenno_long” (see page 18)
Produce BIL files, move BIL files to “/klimagrid/daily/tam” directory; zip daily log file as well as
daily “value0”-file and append to zipped archives “tam_read_and_process_log.zip“ and “value0.zip”
Figure C1. Flow chart of program ”tam_read_and_process.f90” for temperature gridding.
38
Appendix D. Flow Chart of “precip.f90”
Delete files from previous run (“utfil_test2.lst”, “precip.txt”, “rr.par”)
Read command line argument (= date) to determine day of run
Run SQL database query “stasjonskart3.sh” (to obtain station coordinates, station meta data, etc.)
Run SQL database query “rr.sh”, writes output into file “utfil_test2.lst”
(to obtain daily 24-hour accumulated precipitation data from Climate Data Warehouse)
Run subroutine “lst2par2.f90” (delete stations with missing precipitation
observations in “utfil_test2.lst”)
Combine precipitation observations with station coordinates and station types
(use most recent record from “t_st_info”, “t_st_type” tables in SQL database)
Run subroutine “tm2rrst.f90” to calculate daily mean air temperature at precipitation stations (Use
“de-trended” temperatures from “tamread_and_krige.f90” together with station coordinates, station
altitudes as well as ”fennomean” and “fenno_min40” values at station locations)
Run subroutine “read_exposure_class_values.f90” (reads exposure classes for precipitation stations
from file “eksposisjon_2008.txt”; sends e-mail if station is not in file “eksposisjon_2008.txt”)
Calculate exposure corrected precipitation values (use Recommended model 2: “Simple Correction
Model (“Monthly values“) from “Manual for operational correction of Nordic precipitation data”)
Check station types (use only main types “A”, “I”, “N” and “V”; discard station if main type “N”
occurs together with under-type “I”, “O” or “T”). Write data into file “rr.par”.
Call subroutine “test_temp_stations.f90” (Perform spatial interpolation using data from “rr.par” file
and Geompack package “DTRIS2”)
Call subroutine “DTRIS2” from Geompack (stored in “geompack.f90”) in order to construct a
Delaunay triangulation of 2D vertices (triangle nodes are written to file “triangle_nodes.dat”)
39
Continued from previous page:
Return from subroutine “DTRIS2” and from subroutine “test_temp_stations.f90” to main
program
Call subroutine “point_in_triangle.f90” (Read data from files “triangle_nodes.dat” and “rr.par”;
perform “point-in-triangle” test for each triangle and each seNorge grid point)
Compute precipitation values at each seNorge grid point (use horizontal linear interpolation within
each triangle)
Compute interpolated station height values at each seNorge grid point (use horizontal
linear interpolation within every triangle)
Read 1km horizontal resolution “Digital Elevation Model” (DEM) for Norway and calculate
difference in elevation between DEM and triangulated station heights
Compute gridded precipitation values using 10% difference in precipitation per 100m difference in
elevation between DEM and triangulated station heights (use 5% for share of elevation difference
that is situated above an altitude of 1000m above sea level)
Mask output fields with “Digital Elevation Model” that is used (only values for grid points with
elevations of more than 0 meters above sea level are output)
Produce BIL files, move BIL files to “/klimagrid/daily/rr” directory; zip daily log file as well as daily
“rr.par”-file and append to zipped archives “precip_log.zip “ and “rr_par.zip”
Figure D1. Flow chart of Fortran program ”precip.f90” for precipitation gridding.
40