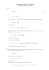Erwartungswert(16.09.2004)

Kapitel 2
Erwartungswert
2.1 Erwartungswert einer Zufallsvariablen
Definition 2.1 Der Erwartungswert EX einer diskreten Zufallsvariablen X mit Wahrscheinlichkeitsfunktion PX ist definiert als
EX =
X
x
xPX (x) :
Für spätere Notationen sei angemerkt, dass der Erwartungswert einer Zufallsvariablen häufig
einfach mit bezeichnet wird.
Beispiel 2.1 (Anzahl der ,,Köpfe” beim zweifachen Münzwurf)
1.0
P(x)
0.8
0.6
0.4
0.2
0.0
-1
0
1
2
3
Abbildung 2.1: Wahrscheinlichkeitsfunktion
In Beispiel 1.1a hatten wir die folgende Wahrscheinlichkeitsfunktion für die Anzahl der ,,Köpfe”
beim zweifachen Werfen einer Münze bestimmt,
12
2.1. ERWARTUNGSWERT EINER ZUFALLSVARIABLEN
8
>
>
>
<
X (x) = >
P
>
>
:
1
4
1
2
1
4
0
13
für x = 0
für x = 1
für x = 2
sonst :
Damit erhält man als Erwartungswert
EX
=
2
X
x=0
X (x) = 0(1=4) + 1(1=2) + 2(1=4) = 1 :
xP
Wir werden jetzt zwei mögliche Interpretationen des Erwartungswertes kennenlernen.
a) EX ist die x-Koordinate des Schwerpunktes der Wahrscheinlichkeitsfunktion von X .
Die Wahrscheinlichkeitsfunktion ist in Abbildung 2.1 graphisch dargestellt. Stellen Sie sich die drei
Balken in Abbildung 2.1 als Metallstäbe vor, die an die x-Achse geklebt sind. Versuchen Sie dann,
die Wahrscheinlichkeitsfunktion auf eine scharfe Kante zu legen und dort auszubalancieren.
Wenn Sie die Wahrscheinlichkeitsfunktion so, wie in Abbildung 2.2 dargestellt, auf die Kante legten,
fiele die Funktion nach rechts, in Abbildung 2.3 würde sie nach links fallen.
1.0
P(x)
0.8
0.6
0.4
0.2
0.0
-1
0
1
2
3
Abbildung 2.2: Kippt nach rechts
Wenn die Kante exakt unter dem Erwartungswert wäre, wie in Abbildung 2.4, würde die Funktion die
Balance halten.
In diesem Beispiel ist der Erwartungwert gerade 1.
Der Erwartungswert ist also der Schwerpunkt von PX .
b) Der Erwartungswert EX kann als Mittelwert sehr vieler Realisationen von X aufgefasst werden.
14
KAPITEL 2. ERWARTUNGSWERT
1.0
P(x)
0.8
0.6
0.4
0.2
0.0
-1
0
1
2
3
Abbildung 2.3: Kippt nach links
1.0
P(x)
0.8
0.6
0.4
0.2
0.0
-1
0
1
2
3
Abbildung 2.4: Gleichgewicht: Erwartungswert als Schwerpunkt
Stellen Sie sich dazu vor, dass Sie die zwei Münzen sehr oft werfen.
Eine typische Folge von Ergebnissen könnte so aussehen:
Wurfspiel
Ergebnis x
Summe
Mittelwert
1
0
0
0/1
2
1
1
1/2
3
1
2
2/3
4
0
2
2/4
5
2
4
4/5
:::
10 000
:::
0
:::
10 068
:::
1:0068
Abbildung 2.5 zeigt die ersten fünf Mittelwerte.
Abbildung 2.6 zeigt den Pfad der Mittelwerte bei 10 000 simulierten Wurfspielen. In jedem Wurfspiel
wird die Münze zweimal geworfen und die Anzahl der ,,Köpfe” bestimmt. Nach jedem Wurfspiel wird
der Mittelwert der bisher erzeugten Realisationen von X berechnet. Abbildung 2.6 zeigt, dass der Pfad
der Mittelwerte sich mit wachsender Anzahl der Realisationen stabilisiert, gegen einen endgültigen
Wert konvergiert. Um zu zeigen, dass dies kein einmaliges Ergebnis war, sind in Abbildung 2.7 drei
solcher Mittelwertpfade dargestellt.
Wir folgern aus diesen Bildern, dass der Mittelwert mit zunehmender Anzahl von Spielen gegen den
Erwartungswert EX = 1 konvergiert. Diese Tatsache lässt sich natürlich auch exakt beweisen.
2.1. ERWARTUNGSWERT EINER ZUFALLSVARIABLEN
15
Mittlere Kopfzahl
2.0
1.5
1.0
*
*
* *
0.5
0.0
0
*
1
2
3
4
5
6
7
8
9
10
Anzahl der Spiele
Abbildung 2.5: Pfad der ersten fünf Mittelwerte
Mittlere Kopfzahl
2.0
1.5
*
*
1.0 *
*
**
** * *
* ************************** *************************************************************************************************************
**************
****
0.5
0.0
1
10
100
1000
10000
Anzahl der Spiele
Abbildung 2.6: Pfad der Mittelwerte bei 10 000 Würfen
Diese beiden Interpretationen lassen sich genauso auf stetige Zufallsvariablen anwenden.
Definition 2.2 Der Erwartungswert X einer stetigen Zufallsvariablen X mit der Dichtefunktion fX ist definiert als
EX
1
Z
=
1
xfX (x)dx :
Beispiel 2.2 Die Dichtefunktion einer Zufallsvariablen X sei gegeben durch
(
X (x) =
f
2x
0
für 0 x 1
sonst :
16
KAPITEL 2. ERWARTUNGSWERT
Mittlere Kopfzahl
2.0 *
*
1.5
*
1.0 *
* *
**
*
**
***************
* ********
**
** ** ***
***
** *** ******************************************************************************************************************************************************************************************************************************************
0.5
**************
* ** *
* ***
*
*
* *
*
****
0.0
1
10
100
1000
10000
Anzahl der Spiele
Abbildung 2.7: Drei Mittelwertpfade in je 10 000 Spielen
Der Erwartungswert berechnet sich dann als
1
Z
E (X )
=
xf
1
Z1
=
X (x)dx =
2
2x
0
dx
=
Z0
x
1
1
2 3
x 3 0
1
Z1
=
0 dx +
x
0
2
3
Z
2x dx +
x
0 dx
1
:
a) Der Erwartungswert ist die x-Koordinate des Schwerpunktes der Dichtefunktion.
2.0
f(x)
1.5
1.0
0.5
0.0
-1
0
E(X) 1
2
Abbildung 2.8: Erwartungswert als Schwerpunkt der Dichtefunktion
Stellen Sie sich die Dichtefunktion aus einer Metallplatte gemacht vor. Wenn wir die Dichtefunktion auf eine Kante legten, die genau unter E (X ) wäre, würde die Dichtefunktion die
Balance halten.
b) Um die zweite Interpretation des Erwartungswertes anzuwenden, betrachten wir X als wöchentliche Auslastung einer Maschine, gemessen als Anteil der möglichen Auslastung. Dann bedeutet also X = 1, dass die Maschine zu 100% ausgelastet und X = 0:5, dass die Maschine zu
50% ausgelastet ist usw..
2.2. ERWARTUNGSWERT EINER FUNKTION EINER ZUFALLSVARIABLEN
17
Typische Beobachtungen über mehrere Wochen könnten so aussehen:
Werte:
Summe:
Mittelwert:
0.80
0.80
0.80
0.59
1.39
0.70
0.39
1.78
0.59
0.65
2.43
0.61
0.37
2.80
0.56
usw.
usw.
usw.
Abbildung 2.9 zeigt eine graphische Darstellung der ersten fünf Mittelwerte.
Mittlere Auslastung
1.0
**
0.5
***
0.0
0
1
2
3
4
5
6
7
8
9
10
Anzahl der Wochen
Abbildung 2.9: Pfad der ersten fünf Mittelwerte
Abbildung 2.10 zeigt uns, dass der Pfad der Mittelwerte, jeweils berechnet als Durchschnitt
der bisher vorliegenden Realisationen, mit zunehmender Anzahl der Realisationen gegen den
Erwartungswert von X konvergiert.
Mittlere Auslastung
1.0
0.8
* ****
* ** ******* ************** ********* ************************************************************************
* * *
******* *****
*****
0.6
0.4 *
0.2
0.0
1
10
100
1000
10000
Anzahl der Wochen
Abbildung 2.10: Konvergenz der Mittelwerte gegen den Erwartungswert
2.2 Erwartungswert einer Funktion einer Zufallsvariablen
Gelegentlich braucht man nicht nur den Erwartungswert der Zufallsvariablen X selbst, sondern auch den Erwartungswert EH (X ), wobei H (X ) eine Funktion der Zufallsvariablen X
ist, z.B. H (X ) = X 3 oder H (X ) = (X 6)2 .
18
KAPITEL 2. ERWARTUNGSWERT
Beispiel 2.3 Betrachten Sie folgendes Spiel. Ich werfe zwei faire Münzen.
X
sei die Anzahl der
,,Köpfe”.
Die Spielregeln sind die folgenden:
Sie zahlen 3 DM, um zu spielen.
Wenn
X
= 0,
verlieren Sie die 3 DM.
X
= 1,
bekommen Sie 5 DM (3+2).
X
= 2,
bekommen Sie 4 DM (3+1).
Ihr Gewinn ist eine Funktion von X , die in der folgenden Tabelle aufgelistet ist:
:
X
H (X )
0
-3
:
1
+2
2
+1
Wenn Sie vor der Entscheidung stehen, ob Sie dieses Spielangebot annehmen oder nicht, ist es für Sie
wichtig, den Erwartungswert von H (X ) zu kennen. Bevor wir dieses Beispiel fortsetzen können, ist
der Erwartungswert einer Funktion H (X ) einer Zufallsvariablen X zu definieren.
Definition 2.3 Sei H (X ) eine Funktion der Zufallsvariablen X . Der Erwartungswert
EH (X ) ist definiert durch:
EH (X ) =
X
x
1
Z
EH (X ) =
1
H (x)PX (x) ; falls X diskret ist,
H (x)fX (x)dx ; falls X stetig ist.
Für das obige Beispiel hatten wir die Wahrscheinlichkeitsfunktion schon in Beispiel 1.1a berechnet.
Damit ist der Erwartungswert:
E H (X )
=
=
2
X
x=0
(
X (x) = H (0)PX (0) + H (1)PX (1) + H (2)PX (2)
H (x)P
3)(1=4) + (2)(1=2) + (1)(1=4) = 1=2
DM
(= 50Pf
pro Spiel)
Im Mittel gewinnen Sie also 50 Pf pro Spiel. Auf lange Sicht lohnt sich also das Spiel für Sie. Wenn
Sie dagegen nur ein einziges Mal spielen, ist die Wahrscheinlichkeit 1=4, dass Sie Ihre 3 DM verlieren
werden.
Beispiel 2.4 Die stetige Zufallsvariable X besitze die Dichtefunktion aus Beispiel 2.2, d.h.
(
X (x) =
f
1
2x
0
0
sonst :
x
2.3. MOMENTE
19
Die Funktion H (X ) sei gegeben durch
H (X )
=
X
2
:
Dann ist der Erwartungswert von H (X )
Z1
EH (X )
=
x
2
Z1
2x dx =
0
2x
3
dx
0
2 4 1
1
= x =
4
2
0
:
Nützlich sind die folgenden Rechenregeln für Erwartungswerte, die sich aus den entsprechenden Regeln für Summen bzw. Integrale ergeben.
Satz 2.1 (Rechenregeln für Erwartungswerte)
a) E = ,
wenn eine Konstante ist.
b) EH (X ) = EH (X ),
insb. EX
=
EX .
c) E (H (X ) + G(X )) = EH (X ) + EG(X ),
von X ist, insb. E (X + ) = EX + .
Beweis:
H (X ) = ; E =
wenn G(X ) eine weitere Funktion
Z1
1
f (x)dx = f (x)dx = .
1
1 {z }
|
R
1
Auf die weiteren Beweise verzichten wir hier.
2.3 Momente
Wichtige Funktionen einer Zufallsvariablen X sind die Potenzen X k , d.h.
H (X ) = X k :
Definition 2.4 0k
=
EX k heißt das k-te Moment von X .
Es gilt:
1. Moment:
01 = EX
: : : 01 }
20
KAPITEL 2. ERWARTUNGSWERT
2. Moment
02 = EX 2
3. Moment
03 = EX 3
Sind alle Momente einer Zufallsvariablen bekannt, so ist dadurch die Verteilung dieser Zufallsvariablen eindeutig bestimmt. Es ist
0k = EX k =
X
x
xk PX (x);
falls X diskret ist,
Z 1
k
xk fX (x)dx;
k = EX =
0
falls X stetig ist.
1
(2.1)
(2.2)
Eine weitere wichtige Funktion einer Zufallsvariablen ist
)k :
H (X ) = (X
Definition 2.5 k = E (X )k heißt das k-te zentrale Moment von X , auch zentriertes Moment oder Moment um den Erwartungswert.
Erstes zentrales Moment:
1 = E (X
) = EX
E = =0:
Zweites zentrales Moment:
2 = E (X
)2 Var X
2 :
Das zweite zentrale Moment stimmt also mit der Varianz überein, die wir abkürzend auch
mit 2 bezeichnen.
Drittes zentrales Moment:
3 = E (X
)3 :
2.4 Die Varianz einer Zufallsvariablen
Besonders wichtig ist das zweite zentrale Moment 2
von X ist:
2 = X2
=
E (X
=
E (X )2 , da es gleich der Varianz
EX )2 = V arX :
Nützlich zur Berechnung von Varianzen ist die folgende Regel:
Satz 2.2
2 = V arX = EX 2
(EX )
2
2.4. DIE VARIANZ EINER ZUFALLSVARIABLEN
21
Beweis:
2
=
=
E (X
EX 2
)2 = E (X 2 2X + 2 ) = EX 2 E (2X ) + E2
2
2
2
2
2
2
2EX + = EX
2(EX ) + (EX ) = EX
(EX )
}
Beispiel 2.5 In den Beispielen 2.2 und 2.4 hatten wir den Erwartungswert
EX
bzw.
EX
2
einer
stetigen Zufallsvariablen mit der Dichtefunktion
(
1
X (x) =
2x
0
0
sonst
= 2=3
und
EX
f
x
berechnet. Es war
EX
2
= 1=2
:
2
(2=3) = 1=18
:
Damit ist nach der Regel aus Satz 2.2
V arX
= 1=2
Dies ist i.allg. einfacher als
Z1
(x
2
2=3) 2xdx =
:::
= 1=18
:
0
Wichtig sind die folgenden Rechenregeln für Varianzen, die aus den Rechenregeln für Erwartungwerte folgen.
Satz 2.3 (Rechenregeln für Varianzen)
Sei c eine Konstante. Dann gilt:
a) V ar () = 0
b) V ar (X ) = 2 V arX
c) V ar (X
Beweis:
a) Es ist
und
d.h.
+ ) =
V arX
E = E2 = 2 ;
V ar() = 2
2 = 0 :
22
KAPITEL 2. ERWARTUNGSWERT
b)
V ar(X )
=
=
E (X )2
2 (EX 2
(E (X )) =
E (2 X 2 )
2
2
(EX ) ) = V arX
2 (EX )2
E (X + E (X + ))2 = E (X + E (X EX )2 = V arX
EX
2
c)
V ar(X + )
=
=
)2
}
Diese Formeln kann man sich auch auf anschauliche Weise merken. Die Quadratwurzel aus
der Varianz ist die Standardabweichung einer Zufallsvariablen und misst die Breite einer
Verteilung oder die Streuung einer Zufallsvariablen. Die Varianz ist also das Quadrat eines
Streuungsmaßes. Es ist doch nur vernünftig, dass
a) die Streuung einer Konstanten, d.h. einer Zufallsvariablen, die nur einen einzigen Wert
annehmen kann, Null ist,
b) ein Streuungsmaß mit dem Faktor , also das Quadrat eines Streuungsmaßes mit dem
Faktor 2 zu multiplizieren ist, wenn ich jeden möglichen Wert dieser Zufallsvariablen
mit einem Faktor multipliziere,
c) sich ein Streuungsmaß nicht ändert, wenn ich den Wertebereich einer Zufallsvariablen
um eine Konstante verschiebe.