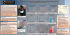Focus on Food Engineering Research and Developments

Transcription

FOCUS ON FOOD ENGINEERING
RESEARCH AND DEVELOPMENTS
FOCUS ON FOOD ENGINEERING
RESEARCH AND DEVELOPMENTS
VIVIAN N. PLETNEY
EDITOR
Nova Science Publishers, Inc.
New York
Copyright © 2007 by Nova Science Publishers, Inc.
All rights reserved. No part of this book may be reproduced, stored in a retrieval system or
transmitted in any form or by any means: electronic, electrostatic, magnetic, tape, mechanical
photocopying, recording or otherwise without the written permission of the Publisher.
For permission to use material from this book please contact us:
Telephone 631-231-7269; Fax 631-231-8175
Web Site: http://www.novapublishers.com
NOTICE TO THE READER
The Publisher has taken reasonable care in the preparation of this book, but makes no expressed or
implied warranty of any kind and assumes no responsibility for any errors or omissions. No
liability is assumed for incidental or consequential damages in connection with or arising out of
information contained in this book. The Publisher shall not be liable for any special,
consequential, or exemplary damages resulting, in whole or in part, from the readers’ use of, or
reliance upon, this material.
Independent verification should be sought for any data, advice or recommendations contained in
this book. In addition, no responsibility is assumed by the publisher for any injury and/or damage
to persons or property arising from any methods, products, instructions, ideas or otherwise
contained in this publication.
This publication is designed to provide accurate and authoritative information with regard to the
subject matter covered herein. It is sold with the clear understanding that the Publisher is not
engaged in rendering legal or any other professional services. If legal or any other expert
assistance is required, the services of a competent person should be sought. FROM A
DECLARATION OF PARTICIPANTS JOINTLY ADOPTED BY A COMMITTEE OF THE
AMERICAN BAR ASSOCIATION AND A COMMITTEE OF PUBLISHERS.
LIBRARY OF CONGRESS CATALOGING-IN-PUBLICATION DATA
Focus on food engineering research and developments / Vivian N. Pletney (editor).
p. cm.
Includes index.
ISBN-13: 978-1-60692-567-6
1. Food industry and trade--Research. I. Pletney, Vivian N.
TP370.8.F63 2006
664--dc22
2007028557
Published by Nova Science Publishers, Inc.
New York
CONTENTS
Preface
Expert Commentary
vii
Computer-Vision Based Analysis of Color as a
Tool for Food Process Control
Vural Gökmen and İdris Süğüt
Chapter 1
Transport Phenomena During Drying of Food Materials
Kamil Kahveci and Ahmet Cihan
Chapter 2
The Influence of Interactions Occurring Between
Micro-Organisms on Predicting the Safety of
Lactic Acid Cheese
Izabela Steinka
Chapter 3
Chapter 4
Chapter 5
Chapter 6
1
13
165
The Development of Engineering Technology to
Improve the Quality of Production of Tropical Fruit in
Developing Countries
B. Jarimopas, P. Sirisomboon, R. Sothornwit and
A. Terdwongworakul
239
Development of Gel Products Containing Fruit Pieces
Using Osmotic Treatments without byProduct Generation
N. Martínez-Navarrete, M.M. Camacho,
E. García-Martínez and M.E. Martín-Esparza
307
Quality Aspects of Dehydrated and Rehydrated Fruit
in Relation to Drying Method
C. Contreras, M.E. Martín-Esparza, A. Chiralt and
N. Martínez-Navarrete
Pest Control Using High Pressure Carbon Dioxide as
an Advanced Technology
Mustafa Bayram
339
361
vi
Chapter 7
Chapter 8
Chapter 9
Contents
Effects of Permeation on Mass Transfer Coefficient for
Laminar Non-Newtonian Fluid Flow in
Membrane Modules During Clarification/
Concentration of Fruit Juice
Sirshendu De, Sunando DasGupta and S. Ranjith Kumar
397
Effect of Smooth Roll Grinding Conditions on
Reduction of Sizings in the Wheat Flour Milling Process
Aleksandar Fistes and Gavrilo Tanovic
453
An Effect of Relative Air Humidity on the Content of
Volatile Compounds in Roasting Cocoa Beans
Wieslawa Krysiak, Teresa Majda and Ewa Nebesny
467
Chapter 10
Bulguration: Combined Cooking and Drying Operation
Mustafa Bayram
Chapter 11
Water Sorption on Foodstuffs - Alternative Models
497
Sylwester Furmaniak, Artur P. Terzyk, Leszek Czepirski, Ewa
Komorowska-Czepirska, Joanna Szymońska and Piotr A. Gauden
Chapter 12
A Forecast Analysis on Food Nutrition Supply and
Demand Worldwide
Wenjun Zhang, Wengang Zhou, Xiyan Zhang, Yongkai Xia
and Wei He
Index
483
517
531
PREFACE
Food engineering refers to the engineering aspects of food production and processing.
Food engineering includes, but is not limited to, the application of agricultural engineering
and chemical engineering principles to food materials. Genetic engineering of plants and
animals is not normally the work of a food engineer.
Food engineering is a very wide field of activities. Among its domain of knowledge and
action are:
•
•
•
•
•
Design of machinery and processes to produce foods.
Design and implementation of food safety and preservation measures in the
production of foods.
Biotechnological processes of food production.
Choice and design of food packaging materials.
Quality control of food production.
Chapter 1 - Drying has been one of the most important techniques used in food
preservation for long years. The drying process has to be performed considering energy
economy and the quality standards for the product. Therefore, it is of great importance to
understand the physical phenomena taking place in the drying processes. Various mass
transfer mechanisms such as molecular diffusion, capillary flow and hydrodynamic flow may
take place during the drying process of food materials. Drying is generally composed of a
series, parallel and/or series-parallel combination of these mechanisms. In addition to the
complexity because of these various transport mechanisms in the drying processes, the
structures of materials are also too complex. These constitute the main reasons that make the
understanding and modeling the drying process difficult. There are three basic approaches
used in modeling as empirical, semi-empirical, and theoretical. Empirical and semi-empirical
approaches consider only external resistance to mass transfer between product and air while
the theoretical approaches consider only internal resistance to mass transfer. At the theoretical
modeling two kinds of approaches are used. These are discrete approach and continuum
approach. In discrete approach, transport is examined in a network structure representing the
material structure and generally the purpose of use of this approach is to determine transport
parameters as an alternative to the experimental measurements. On the other hand, continuum
approach is commonly used for describing the transport taking place at macroscopic level. In
continuum approach, the food material is considered as a fictitious continuum and the effects
viii
Vivian N. Pletney
of the physical phenomena taken into consideration are lumped into effective transport
coefficients. There are many models suggested based on continuum approach. The main
difficulty in using a model based on a continuum approach arises from determination of these
effective transport parameters. Most of the transport parameters are strongly dependent on
concentration, temperature and material structure. Various models have been suggested to
clarify the effect of temperature and concentration on transport parameters. However,
relatively little is known on the effect of structure on transport parameters.
In conclusion, it may be stated that drying of food materials is a complex unit operation
and main problem to overcome on the way to better understand and describe drying processes
is to reveal the effect of structure on transport.
Chapter 2 - This paper discusses numerous problems occurring in relation to
microbiological quality of lactic acid cheese. Lactic acid cheese constitutes the source of
various nutritive substances, what results in a possibility of allochthonous micro-flora to grow
despite the presence of starter micro-flora. One of the issues discussed herein comprised the
results of microbiological research depending on tvarog packing system. The influence of
packing system on surface micro-flora population was assessed. Moreover, the problem of
growth of enterococci and LAB (Lactic Acid Bacteria) populations depending on stage of
tvarog production as well as packing system was also raised. The issue of interactions
occurring among micro-organisms that re-infect tvarogs and the influence of these
interactions on the growth of individual micro-organisms was also discussed. The author also
presented the possibility to apply JMTPH computer program for assessment of the dynamics
of changes of tvarog micro-organisms during product storage. Another chapter includes
assessment of the influence of lactic acid bacteria on the behaviour of individual groups of
micro-organisms occupying tvarog surface, depending on packaging hermetic properties. It
was also very important to assess the safety of tvarogs in the context of a possibility of
enterotoxin synthesis in conditions of various packing systems. Finally, the models of
optimising lactic acid cheese quality were presented, what included application of plant
additives of biostatic character, modification of used packaging as well as employing the
probabilistic mathematical model helpful in evaluation of enterotoxin synthesis, depending on
the level of staphylococci and yeast populations.
Chapter 3 - Many developing countries are rich in agricultural and food resources but are
unable to maximize the export income they earn from them because they lack value-adding
technology. In other words, developing countries typically must sell their products in cheap
unfinished form to nations which possess the technology that adds profitability to these
goods. Accordingly, if developing countries wish to earn more revenue for the improvement
of their people’s employment and education, they must develop food engineering technology
alongside other food science technologies. These efforts at technological self-improvement
should be supported by the developed countries as the reduction of the knowledge and income
gaps between the industrialized and developing worlds will do much to further global peace
and happiness.
The desired trend for food engineering research is to focus on developing engineering
technology that will help to improve tropical fresh produce quality. This chapter discusses
three facets of this trend. The first aspect concerns the physical properties of tropical fruit and
vegetables, which consist of post-harvest loss, physical characteristics, mechanical properties,
firmness, friction, and non-destructive quality grading techniques relating to mangoes,
mangosteen, durian, sweet tamarind, guava, tangerines, snake egg plants, white long radish
Preface
ix
and lime. The second aspect concerns innovations in machinery and devices used with
mangosteen, durian, young coconut, dry over-mature coconut and baby corn. State of the art
design, operating principles and key performance tests of tropical fruit machinery and
inventions will be reviewed. The third aspect concerns packaging technology, particularly
that which is directed towards the extension of the shelf life of the aforementioned tropical
fresh produce.
There are three current realities which inform this book. They are as follows: that there is
a high incidence of post-harvest loss and a corresponding magnitude of shortage in research
and development work on tropical fresh produce; that the global flow of information is
increasing while agricultural labor is becoming scarcer and more expensive; and that tropical
produce engineering technology must be thoroughly understood. Accordingly, we make two
recommendations: for producer countries to instigate a dramatic increase in the research and
development that they conduct into tropical fresh produce, and in the support that they
provide for this research; and that the research trend should cover all economic tropical fruit
and vegetable goods grown in the producer countries and all aspects of engineering
technology that they use, with a particular emphasis on developing computerized nondestructive techniques for quality assurance.
Chapter 4 - Fruits are products of a very important nutritional interest. Nevertheless, and
mainly due to their relatively short shelf-life and modern-day eating habits, the level of
consumption is below that recommended by the World Health Organization. In this sense, the
development of foods with a high fresh or processed fruit content, that maintain the
nutritional and sensorial properties of the fresh fruit, may contribute to stimulating the interest
of the consumer, thus increasing the product consumption. Osmotic dehydration (OD)
techniques have been widely applied in fruit processing, since they require little energy and
allow us to obtain high quality products. However, its industrial use may be limited by the
management of the osmotic solution (OS). To solve this problem, the re-use of the OS in
more than one OD cycle, with or without a previous re-concentration stage, may be
considered. When there is no re-concentration, the re-use will be limited by the possible
microbiological contamination and by the progressive dilution that takes place after each OD
cycle, which may affect the kinetics of the osmotic process. On the other hand, as some native
hydrosoluble compounds, such as volatiles, acids, minerals, vitamins and phytochemicals,
will be released together with water into the OS during OD, its management as an ingredient
in some product formulation seems to be an interesting alternative. To this end, this work
analyses the viability of formulating a fruit-gel product with the osmodehydrated fruit
(strawberry, kiwi or grapefruit) and the re-used OS obtained from the dehydration step, in
order to diminish the loss of flavour, aroma and functional components of the fruit and avoid
the generation of by-products in the process. In this study, the number of OS re-use cycles has
been optimized, on the basis of its microbial recounts, the dilution level, the solution
enrichment in fruit bioactive compounds, the fruit-solution ratio used during the dehydration
step and the fruit-gel ratio in the final product. The kind and concentration of gelling agents,
which best favour the properties of aspect (transparency) and texture of the gels, taking the
peculiar composition of the re-used OS used as gelling medium into account, have been
identified. The conditions in which the fruit pieces are mixed with the gelling solution have
also been studied and defined. Finally, the fruit-gel product formulation conditions have been
optimized, on the basis of its sensory acceptance and its compositional stability during
storage, ensuring the thermodynamic equilibrium between the fruit and the gel when mixed.
x
Vivian N. Pletney
The microbiological stability of the product was of at least 15 days in refrigerated storage.
During this time, the evolution of some properties such as phytochemicals, vitamins, acids,
volatile compounds, colour and texture was studied.
Chapter 5 - The development of new attractive dehydrated fruit-based products, to be
consumed as dried or rehydrated, with high quality and reasonable shelf-life, will increase
and diversify its availability in the market. In this sense, it is necessary to optimize the
dehydration operation conditions to achieve not only the maximum process efficiency and
control, but also various characteristics in the final product in relation to colour, texture, water
activity, nutritive value, etc. Air drying has been the most frequently selected process for
industrial food dehydration, due to its efficiency, versatility and easy management. However,
it is known that it provokes considerable changes in sensory and nutritional quality. Some
research works refer to the advantages of applying microwaves to convective drying
associated with the fast volumetric heating of the product due to its high penetration power.
On the other hand, the application of certain pre-treatments before drying operation, such as
vacuum impregnation or vacuum pulsed osmotic dehydration, could help to enhance the
stability and quality attributes, as high temperatures are not employed and specific solutes can
be incorporated into the porous structure. In this chapter the advantages of microwave
application to convective drying of apple and strawberry are pointed out. These are related to
the great reduction in process time and to the fact that they allow obtaining a dehydrated
product with a greater resistance to deformation and fracture and a greater stability during
commercialization. Nevertheless, its use is not recommendable when the product has to be
used or eaten after its rehydration, as the structural damage caused by microwaves decreases
the mechanical resistance and the retention capacity of the incorporated liquid phase. The
colour of dehydrated or rehydrated product is more affected by microwave treatments when
the fruit pigment content is relevant, as occurs with strawberry anthocyanins. Application of a
previous vacuum impregnation/osmotic dehydration step with sugared solutions is always
recommended.
Chapter 6 - Food products are always under the risk of infestation by pests. In view of the
competitive markets, there has been increasing demand for quality in foods in terms of
freedom from pest and pesticide contaminants. Also, it is very important for trade purpose
suffer economic and quality losses. Zero tolerance of insect pest in foods has been adopted in
some of countries and there is a tendency to achieve this goal in overall the world.
The governments, the food industries and exporters are dependent on fumigation as a
quick and effective tool for insect pest control in food commodities. Fumigants are widely
used for pest elimination in these commodities. Toxic substances have therefore been used to
destroy for example pests, as well as their eggs, larvae, cocoons and adults. Currently used
substances, such as methyl bromide, hydrogen phosphide, ethylene dioxide, malathion etc.,
are characterized by more or less serious problems. In recent years, that fumigation
technology based on the chemical control of products has been facing threats/constraints
because of regulatory concerns, the development of resistance, handling hazards, residues,
food safety, cost, carcinogenicity, involvement in ozone depletion, resurgence, environmental
pollution and other factors. Reliance upon fumigation as an overall solution to infestation
problems in food products has become questionable. The chemical action of fumigants upon
commodities and the environment has necessitated the withdrawal of many fumigants from
the market. Also, some of them are being phase out their uses at the international level.
Preface
xi
Due to becoming the target of increasing criticism of toxic substances, such concerns
have led to the development of non-chemical methods for the control of insect pests that
infest food commodities. One such method is the high pressure carbon dioxide application,
which mainly involves the use of CO2 at high pressure (10-40 bar) for food fumigation. It is a
new effective, non-chemical, non-residual, safe, fast and environmentally friendly method for
the food industry. It has been generated and developed within last 20 years. Carbon dioxide
is a fumigant and being used to control pests in the food industry. After extensive testing,
high pressure carbon dioxide fumigation can be accepted as the advanced pest control
technology for the future. Nowadays, it is particularly indispensable for the gentle, safe,
natural and organic food products. If operation time for the fumigation is constraint and nonchemical treatments are required, this technique is suitable for conventional products.
Chapter 7 - Membrane based clarification and concentration of fruit juice has become a
popular unit operation in modern fruit juice processing industries. The well known membrane
modules used for this purpose are tubular and spiral wound modules. Therefore, design of
these modules is of utmost industrial importance. The key parameter for design of membrane
modules is mass transfer coefficient. Most of the fruit juices have non-Newtonian rheology,
e.g., power law, ellis fluid, etc. Till today, the mass transfer coefficient for such systems used
is approximated from the corresponding relations developed for Newtonian fluids. Hence, a
detailed fluid flow modeling with non-Newtonian rheology is urgently warranted. In the
present work, this aspect is attempted. The expressions of the mass transfer coefficients are
derived from the first principles for laminar, non-Newtonian fluid flow in a porous conduit.
The effects of the permeation are incorporated quantitatively in the mass transfer coefficient
from a theoretical basis. The analysis is carried out for various non-Newtonian rheologies.
Effects of the operating conditions, i.e., Reynolds number, permeate flux, etc. on mass
transfer coefficient are also investigated. Two flow geometries are considered. Flow through a
tube and that through a rectangular thin channel, which are useful for the design of the tubular
and spiral wound cross flow membrane modules. The developed relations of mass transfer
coefficients would be of tremendous help to the design engineers.
Chapter 8 - A laboratory roll stand Variostuhl, equipped with smooth rolls (250 mm
diameter, 100 mm length), was used to examine, under simulated commercial conditions, the
effect of roll speed and roll differential on the reduction of sizings and coarse middlings from
the primary break passages of the wheat flour milling process. The samples were obtained
from the industrial mill, intercepting the sizings and coarse middlings from the 1st, 2nd and 3rd
break stage that normally would have gone to the purification system, as well as intercepting
the purified sizings (cleaned middlings) that normally would have gone to the reduction
system of the wheat flour milling process. As roll velocity increases flour release was
increased, milling energy consumption rose while flour quality (as determined by ash content)
was not affected. By increasing roll velocity it is possible to increase feed rate to the rolls and,
therefore, the disposable roll surface is used more efficiently. Flour release rose when
differential was increased from 1.1 up to 1.25 but decreased when differential increased from
1.25 up to 5.0. Increasing roll differential led to an increase in milling energy consumption.
These effects can be explained by the relative contribution of compressive and shearing
forces acting on the particles passing through the grinding zone of the smooth rolls.
Considering the results obtained in this study (flour release, flour quality and milling energy
xii
Vivian N. Pletney
consumption) a differential of 1.25, relative to a fast roll speed of 5 m/s could be designated
as optimal.
Chapter 9 - The Ivory Coast cocoa beans were convectively roasted at 135°C, at the air
flow rate of 1.0 m/s and relative air humidity (RH) of 0.4%, 2.0% and 5.0%. Volatile
components of raw and roasted beans were analyzed by SPME/GC/GCMS and identified by
comparing their retention indices with that of standards included in a database and their mass
spectra with standard spectra included in NIST computer library. Almost 100 different
volatile compounds were identified in examined samples of roasted cocoa. They ranked
among aldehydes, ketones, alcohols, esters, monoterpenes, pyrazines, acids, lactones, furan
derivatives, and sulfur-containing compounds. It was found that a rise in the relative air
humidity from 0.4% to 2.0 and 5.0% increased the contents of pyrazines, volatile acids,
esters, furan derivatives, and sulfur-containing compounds in a headspace of roasted cocoa. In
contrast, the contents of alcohols and aldehydes in the headspace were considerably lower
when the cocoa beans were roasted at the relative air humidity of 5.0% as compared to that
when less humid air was used for convective heating.
Chapter 10 - Cooking and drying are two main unit operations used widely in food
processing. Consecutive cooking and drying operations supplies perfect properties to gain to
food products and called as bulguration. Individually, the former method is used nearly for all
food products before consumption. Cooking is a well-known way to destruct microorganisms,
insect, insect eggs and larvaes for food safety. Also, it increases the digestive property of food
with starch gelatinization, protein gelation and textural softening. However, it is very difficult
to store this product without drying due to its high moisture content after cooking. Therefore,
food products should be dried. Drying is required to prolong storage time of food products.
Bulguration is the gaining of the some functional characteristics on the finished product such
as the resistance to mold contamination, insect attacks and radiation, inactivation of enzymes
and microorganisms, encapsulation of numerous nutritional components in food products,
easy preparation after bulguration due to semi and ready-to-eat form, obtaining long shelf-life
having economical products with safety, decreasing undesired components e.g. phytic acid in
contrast to increasing desired one e.g. folate/folic acid. As raw materials, cereals, pulses,
seeds, vegetables, fruits etc. can be used.
Recently, the use of bulguration in the food industry dramatically increases as an optimal
method due to above situations. Bulguration is an ancient technique; however, the modern
technology re-discovered it. In this chapter, the techniques of bulguration are explained with
examples. Also, the results of the recent researches are given.
Chapter 11 - It is well known that sorption isotherms of foodstuffs are very important for
design, modeling and optimization of important processes for example drying, aeration,
predicting of stability and quality during packaging and storage of food. Many literature
reviews conclude that the BET (and its modifications) and the GAB sorption isotherm
equations are the most popular and applicable for description of isotherms of foodstuffs. The
authors showed recently the applicability of the GDW model for description of water sorption
on different foodstuffs. Moreover, it was also shown that the GAB model (also widely
applied in food science) is the special case of the GDW equation. In this review the authors
present the current state of art and also an attempt of application of different models of water
sorption, namely CMMS, DD and modified CDS for description of water sorption data on
different starch samples and other foodstuffs.
Preface
xiii
Chapter 12 - This paper aimed to make a longer-term forecast analysis on global food
nutrition supply and demand. The forecasts of supplies of food calories and proteins for the
world and various regions over the period 2010-2030 were given, and food nutrition supply
and demand balance in the forecast period was discussed.
If the past pattern continues, the global total food calorie supply would grow at the annual
rate of 13.43±0.71 kcal/cap/day and reach 3210.4±67.3 kcal/cap/day in 2030. Total food
calorie supplies for all of the regions would grow during the forecast period and, in most
regions they are forecast to be greater than 3000 kcal/cap/day from 2015-2020. Total food
protein supply for all regions but not Oceania, is forecast to grow during the forecast period.
The proportion of animal sourced protein in total food protein supply is in 2030 forecast to
increase and reach 35.5%, 61.6%, 56.8%, and 21.7% for Asia, Europe, South America, and
Africa.
Food calorie supply in the world is expected to exceed the adequate energy intake after
around 2015. Strong focus should be worldwide put on the over-intake of food calorie in the
near future. Global food protein supply is not expected to be greater than the adequate range
during the period 2010-2030. Food protein supply in Africa and Caribbean would be just a
little greater than the basic demand in the forecast period. Food protein intake in these regions
should be improved in the coming years.
In: Focus on Food Engineering Research and Developments ISBN: 978-1-60021-898-9
Editor: Vivian N. Pletney, pp. 1-12
© 2007 Nova Science Publishers, Inc.
Expert Commentary
COMPUTER-VISION BASED ANALYSIS OF COLOR
AS A TOOL FOR FOOD PROCESS CONTROL
Department of Food Engineering, Hacettepe University,
06800 Beytepe, Ankara, Turkey
ABSTRACT
The color is the first sensation that the consumer perceives and uses as a tool to
accept or reject, because the color observation allows the detection of certain anomalies
or defects of a product. Commercial color-measuring devices are designed to contact the
materials to perform the color measurements. The main drawback of using these devices
is the limitations in size and geometry of the area that subjected to color measurement,
because they measure a small area with a fixed geometry making the measurement quite
unrepresentative for heterogeneous materials like many processed foods. With a digital
imaging system, it is possible to register the color of foods using three-color sensors. In
this case, surface color of the food is detected online in a non-contact manner and
monitored throughout the process. By using appropriately developed computer
algorithms, highly accurate and reliable information can be obtained about the color
changes in a food during processing. This kind of algorithm can be used as a process
control tool for automatic visual inspection in an industrial production process and can
improve the overall quality of the product. The advantage of computerized visual
inspection over inspection by humans is that machines can evaluate color continuously
and objectively. This chapter describes novel approaches for a non-contact computer
vision based color measurement system and its potential applications in food processing.
1. INTRODUCTION
The overall appearance of any object is a combination of its chromatic and geometric
attributes. Both of these attributes should be accounted for when making visual or
instrumental assessments of appearance. The color is the first sensation that the consumer
2
perceives and uses as a tool to accept or reject, because the color observation allows detecting
certain anomalies or defects of a product.
The human eye has receptors for short (S), middle (M), and long (L) wavelengths, also
known as blue, green, and red receptors. This means, in principle, three parameters are
required to describe a color sensation. A specific method for associating three parameters (or
tristimulus values) is called a color space which specifies how color information is
represented. A color component is also referred to as a color channel. The XYZ is the first
color space that mathematically defined by the Commission Internationale d'Eclairage (CIE)
in 1931. The L*a*b* color space is perceptually uniform and the most complete model
defined by the CIE in 1976 to serve as a device-independent, absolute model to be used as a
reference. It is based on the XYZ color space as an attempt to linearize the perceptibility of
color differences, using the color difference metric described by the Macadam ellipse. The
non-linear relations for L*, a* and b* are intended to mimic the logarithmic response of the
human eye. Here, L* is the luminance or lightness component, which ranges from 0 to 100,
and parameters a* (from green to red) and b* (from blue to yellow) are the two chromatic
components, which range from –120 to 120 [1-3].
2. INSTRUMENTAL MEASUREMENT OF COLOR
A lot of color-measuring instruments are available in the market for several applications.
Most of them are designed to contact the materials to perform the color measurements. These
instruments are successfully used for color measurement of homogenous materials. However,
the main drawback of using a color-measuring instrument is the limitations in size and
geometry of the area that subjected to measurement. A commercial instrument usually
measures a small area with a fixed geometry. This makes the measurement quite
unrepresentative for heterogeneous materials like many food items [4]. Repetitive
measurements are therefore required to increase the accuracy. In most cases, increasing the
repetitions is not a viable approach for irregularly shaped objects. Instead, an approach taking
the overall surface into account is required to obtain meaningful information about the color.
This is especially important for industrial applications in which the color homogeneity is an
important feature of the material. In such a case, commercial color measuring instruments are
not fit for purpose as a process control and/or product quality control tool.
3. COMPUTER VISION BASED MEASUREMENT OF COLOR
A typical image captured by a digital camera consists of an array of vectors called pixels.
Each pixel has red, green and blue color values:
⎡ x r ( n, m ) ⎤
⎢
⎥
x[n, m] = ⎢ x g (n, m)⎥
⎢ x (n, m ) ⎥
⎣ b
⎦
Computer-Vision Based Analysis of Color as a Tool for Food Process Control
3
where, Xr, Xg and Xb are values of the red, green and blue components of the (m,n)th pixel,
respectively. In digital images, Xr, Xg and Xb color components are represented in 8 bits, i.e.,
they are allowed to take integer values between 0 and 255 (=28-1) [5].
RGB values of an image captured by a digital camera can be converted into
device-independent L*a*b* units. Computational approaches that convert RGB values into
L*a*b* units have been previously reported using the standard equations [2,6,7]. However,
usefulness of a computer vision system as a tool for color measurement depends on the
accuracy of color transformation. Digital cameras have built-in white-balancing systems
modifying actual color values, therefore pixel values in an image captured by a camera of a
machine vision system or a consumer camera may not correspond to true colors of imaged
objects.
Therefore, it is better to build calibrated models by using the charts which reflect the
variations in color space. The necessity of a calibration process to obtain device-independent
L*a*b* color units have been previously underlined [8]. However, the information is lacking
on how the accuracy of color measurement could be improved by calibration process in these
reports.
3.1. Description of the Technique
Following section describes a computer-vision based technique calibrated with ANN
modeling to measure color in foods. The model allows a user to determine a polygonal region
of interest. This feature increases the accuracy in color measurement when compared to
commercial color-measuring devices. To perform the color measurement, digital images of
food samples are taken using a color digital camera under well controlled conditions
(illumination, lamp angle and distance).
The calibration of computer vision based color measurement system was performed by
using an Agfa 5x7 inch reflective color chart (figure 1) which is an internationally accepted
IT8 standard (IT8.7/2-1993) with device-independent color definitions. The chart consists of
288 colored squares, and has been designed to represent the color space from full saturation to
near neutrals at highlight, mid-tone and shadows.
Figure 2 shows the algorithm used to convert camera RGB values to spectrophotometric
CIE L*a*b* values. Based on this algorithm, the first step is the conversion of color values
from RGB to L*a*b* using the standard conversion equations, and the second step is the
correction of L*a*b* values through an ANN model.
4
Figure 1. Agfa 5x7 inch color chart (IT8.7/2-1993) used to build a calibrated ANN model for the correction
of monitor L*a*b* values.
= 2.4
RGB values by
digital camera
RGB to XYZ
//Observer:2o ; Illuminant: D50
var_R = ( R / 255 )
var_G = ( G / 255 )
var_B = ( B / 255 )
Conversion of color values
RGB
CIE L*a*b*
by using equations
//Where R = 0 ÷ 255
//Where G = 0 ÷ 255
//Where B = 0 ÷ 255
if ( var_R > 0.04045 ) var_R = ( ( var_R + 0.055 ) / 1.055 ) ^ 2.4
else
var_R = var_R / 12.92
if ( var_G > 0.04045 ) var_G = ( ( var_G + 0.055 ) / 1.055 ) ^ 2.4
else
var_G = var_G / 12.92
if ( var_B > 0.04045 ) var_B = ( ( var_B + 0.055 ) / 1.055 ) ^ 2.4
else
var_B = var_B / 12.92
var_R = var_R * 100
var_G = var_G * 100
var_B = var_B * 100
Correction of color values
CIE L*a*b*
CIE L*a*b*
by using an ANN model
CIE L*a*b* values
by ANN
X = var_R * 0.4360 + var_G * 0.3851 + var_B * 0.1431
Y = var_R * 0.2225 + var_G * 0.7169 + var_B * 0.0606
Z = var_R * 0.0139 + var_G * 0.0971 + var_B * 0.7142
XYZ to L*a*b*
var_X = X / ref_X // ref_X = 96.422
var_Y = Y / ref_Y // ref_Y = 100.000
var_Z = Z / ref_Z // ref_Z = 82.521
if ( var_X > 0.008856 ) var_X = var_X ^ ( 1/3 )
else
var_X = ( 7.787 * var_X ) + ( 16 / 116 )
if ( var_Y > 0.008856 ) var_Y = var_Y ^ ( 1/3 )
else
var_Y = ( 7.787 * var_Y ) + ( 16 / 116 )
if ( var_Z > 0.008856 ) var_Z = var_Z ^ ( 1/3 )
else
var_Z = ( 7.787 * var_Z ) + ( 16 / 116 )
CIE-L* = ( 116 * var_Y ) - 16
CIE-a* = 500 * ( var_X - var_Y )
CIE-b* = 200 * ( var_Y - var_Z )
Figure 2. Algorithm used to convert camera RGB values to spectrophotometric CIE L*a*b* values.
5
An ANN is a nonlinear mathematical model that learns from the examples through
iterations. ANNs are made of a large number of nodes or artificial neurons, which are
disposed in a parallel structure. Each ANN has one input layer containing one node for each
independent variable, one or more hidden layers, where the data are processed, and one
output layer, containing one node for each dependent variable. The data from the input layer
are propagated through the hidden layer and then to all network, which are associated with a
scalar weight. Neurons in the hidden and output layers calculate their inputs by performing a
weighted summation of all the outputs they receive from the layer before. Their outputs, on
the other hand, are calculated by transforming their inputs using a non-linear transfer
function. Then, the network output is compared with the actual output provided by the user.
The difference is used by the optimization technique to train the network. Thus, the training
process requires a forward pass to calculate an output and a backward pass to update the
weights in feed-forward back-propagation networks [9,10]. A great advantage of ANN
models is that, they do not require prior knowledge of the relationship between the input and
output variables, and instead of that, they figure out these relationships through training.
Therefore, complex processes can be optimized to produce the desired outputs using
successfully trained ANN models.
A feedforward backpropagation network was used for the conversion of monitor color
values to spectrophotometric color values in CIE L*a*b* units. Sigmoid function (Eq.1) was
used in the hidden layers as the transfer function which gave outputs in the range [-1,1].
f ( x) =
1
1 + exp(− x)
Eq. (1)
In the output layer, the training function was purelin (Eq. 2) which gave outputs in the
range [-∞,+∞].
f ( x) = x
Eq.(2)
Representative examples, obtained by experimental data sets, were presented to the
network so that it could integrate this knowledge within its structure. The learning function
was the gradient descent with momentum and Bayesian regularization was used as the
training algorithm. Several ANN topologies were trained using the experimental data sets.
The data set consisting of 288 data points were divided into two parts for training (252 data
points) and testing (36 data points). Input and output layers consisted of three neurons which
corresponded to monitor color values and spectrophotometric color values in CIE L*a*b*
units, respectively. After each training session, train and test data sets were simulated by
ANN. The error measures used for comparing the performance of various ANN
configurations were estimated using Eq. (3);
n
SSE = ∑ (VD − VP ) 2
i =1
Eq. (3)
6
where, n is the number of data points, VD and VP are the measured and the predicted color
values.
3.2. Accuracy of Color Measurement
Among the different network architectures, the 3-6-6-3 network topology appeared as the
best performing one which exhibited a great capability for calibrating the monitor color
values to the spectrophotometric color values in CIE L*a*b* units (figure 3).
Monitor Color
Spectrophotometric
Color values
L*
L*
a*
a*
b*
b*
Figure 3. Topology of the ANN model used to correct monitor L*a*b* values.
The accuracy in color measurement is usually determined as the Euclidian distance (Eq.
4) between two colors (ΔE). ΔE of less than 1.0 is usually desired for accuracy of a color
measurement system.
ΔE = ( L1 − L2 ) 2 + (a1 − a2 ) 2 + (b1 − b2 ) 2
Eq. (4)
ΔE of less than 1.0 is usually considered as an indication of high accuracy for a color
measuring instrument. The ΔE values for the estimated values and the real
spectrophotometric values of 288 colored squares in the IT8 chart used for training and
testing is shown in figure 4. The maximum ΔE value was determined to be 0.45 in the
computer vision based color measurement system described above.
7
a.
b.
Figure 4. Change of ΔE value for the patches on IT8 color chart (a) the color patches used for training, (b) the
color patches used for testing.
8
The commercial colorimeters measure color in a small area with fixed geometry (usually
circle in a few square centimeters). This is the major drawback of the commercial instruments
which makes the color measurement problematic especially for heterogeneous materials. It is
the usual way to make repetitive measurements over the surface in order to obtain meaningful
information about the color. From the industrial point of view, it is unattractive to make
several measurements and averaging the results for a single product to get useful information
about the color. In practice, a system which has the capability of measuring color in the
overall area of a material is advantageous and of commercial interest. In this respect,
averaging the values of all pixels in a digital image of a material using a non-contact
computer vision technique is absolutely better than averaging the values of repetitive
measurements using a contact colorimeter in terms of accuracy and analysis time. For
example, after the frying process, different kinds of image pixels appear in a typical fried
potato image (figure 5a). The color of this potato crisp can be measured by marking a
polygonal area over the image which represents the whole surface as shown in figure 5b.
Color measurements were also performed by a color spectrophotometer (Minolta model CM3600d spectrophotometer) or a portable colorimeter (ColorSavy model CM2C colorimeter)
for the same potato crisp sample making a dozen of measurements from different regions.
a.
b.
Figure 5. (a) Digital image of a potato crisp sample, (b) polygonal area marked on the image of potato crisp
which subjected to color measurement by computer vision based analysis.
Figure 6 shows the results of pixel by pixel analysis of color performed by the computer
vision based color measurement system and the results of 12 repetitive measurements
performed by the spectrophotometer and the portable colorimeter. In order to emphasize the
capability of computer vision based color measurement system, data points are represented in
colors as the monitor RGB counterparts of each data points in CIE L*a*b* units determined
by the appropriate technique. It is clear from the results that the color values determined by
the spectrophotometer and by the portable colorimeter are perceptually not accurate. This
9
case exemplifies that commercial instruments have certain limitations when dealing with the
color of rough and heterogeneous materials like potato crisps.
In addition to the advantage of averaging color values of all pixels, the measurement of
color in a region of interest over a material’s surface may be of greater importance under
certain circumstances. In that case, measuring the color in a user defined polygonal area may
be useful to get appropriate information about the color of different regions over the surface
of a single material. A commercial device is not capable of extracting color information for a
specific region of a heterogeneous material. Figure 7 shows a cookie sample composed of two
regions with and without cocoa. Two regions with different shapes in this image can be
processed pixel by pixel to determine average L*, a* and b* values separately by defining
polygonal area of interest.
Figure 6. The results of color measurements by means of computer vision technique (pixel by pixel
measurements), color spectrophotometer and portable color mouse (12 repetitive measurements).
10
a.
b.
Figure 7. (a) Digital image of a cookie sample composed of two regions, (b) polygonal areas marked on the
image of cookie sample which subjected to color measurement by computer vision based analysis.
4. CONCLUSION
The computer vision based image analysis system described here offers some advantages
over the commercial color-measuring instruments namely the possibility of performing noncontact color measurement without sample preparation, and extracting meaningful
information in a specific region of interest over a material surface. This kind of system can be
used as a tool for automatic visual inspection of colors in an industrial production process and
can improve the overall quality of the product. The advantage of computerized visual
inspection over inspection by humans is that machines can evaluate color continuously and
objectively.
REFERENCES
[1]
[2]
[3]
[4]
Papadakis, S.E.; Abdul-Malek, S.; Kamdem, R.E.; Yam, K.L. (2000). A versatile and
inexpensive technique for measuring color of foods. Food Technology 54(12), 48-51.
Segnini, S.; Dejmek, P.; Öste, R. (1999). A low cost video technique for colour
measurement of potato chips. Lebensmittel-Wissenschaft and Technologie. 32(4),
216-222.
Yam, K.L.; Papadakis, S. (2004). A simple digital imaging method for measuring and
analyzing color of food surfaces. Journal of Food Engineering. 61, 137-142.
Antonelli, A.; Cocchi,M.; Fava, P.; Foca, G.; Franchini, G.C.; Manzini, D.; Ulrici, A.
(2004). Automated evaluation of food colour by means of multivariate image analysis
coupled to a wavelet-based classification algorithm. Analytica Chimica Acta. 515, 313.
[5]
[6]
[7]
[8]
[9]
[10]
11
Gonzales, R. C.; Woods, R. E. (2002). Digital Image Processing, Prentice Hall, New
Jersey.
Paschos, G. (2001). Perceptually uniform color spaces for color texture analysis: An
empirical evaluation. IEEE Transactions on Image Processing. 10(6), 932-937.
Mendoza, F.; Aguilera, J.M. (2004). Application of image analysis for classification
of ripening bananas. Journal of Food Science. 69, 471-477.
León K.; Mery, D.; Pedreschi, F.; León, J. (2006). Color Measurement in L*a*b*
units from RGB digital images. Food Research International. 39, 1084-1091.
Gonçalves, E.C.; Minim, L.A.; Coimbra, J.S.R.; Minim, V.P.R. (2005). Modeling
sterilization process of canned foods using artificial neural networks. Chemical
Engineering Process. 44, 1269-1276.
Bishop, M.C., (1994). Neural network and their applications, Review in Scientific
Instruments. 65(6), 1803–1832.
APPENDIX 1. MATLAB CODE FOR EXTRACTING THE COLOR
INFORMATION OF A POLYGONAL MARKED REGION IN AN IMAGE
RGB=imread(‘image.extension’);
RGB=im2double(RGB);
Z=roipoly(RGB);
[d1,d2]=size(Z);
c=0;
L=[ ];
for a=1:d1
for b=1:d2
if Z(a,b)==1
n=1;
c=c+1;
L(n,c)=a;
n=2;
L(n,c)=b;
end
end
end
P=[ ];
for n=1:c
P(n,:)=impixel(RGB2,L(2*n),L(2*n-1));
end
roired=[ ];roigreen=[ ];roiblue=[ ];
sum_red=0;sum_green=0;sum_blue=0;
for n=1:c
sum_red=sum_red + P(n,1);
12
sum_green=sum_green + P(n,2);
sum_blue=sum_blue + P(n,3);
end
roired=sum_red/c;
roigreen=sum_green/c;
roiblue=sum_blue/c;
RGB__value=[roired roigreen roiblue]
Chapter 1
TRANSPORT PHENOMENA DURING
DRYING OF FOOD MATERIALS
Mechanical Engineering Department, Trakya University,
22180 Edirne, TURKEY
ABSTRACT
Drying has been one of the most important techniques used in food preservation for
long years. The drying process has to be performed considering energy economy and the
quality standards for the product. Therefore, it is of great importance to understand the
physical phenomena taking place in the drying processes. Various mass transfer
mechanisms such as molecular diffusion, capillary flow and hydrodynamic flow may take
place during the drying process of food materials. Drying is generally composed of a
series, parallel and/or series-parallel combination of these mechanisms. In addition to the
complexity because of these various transport mechanisms in the drying processes, the
structures of materials are also too complex. These constitute the main reasons that make
the understanding and modeling the drying process difficult. There are three basic
approaches used in modeling as empirical, semi-empirical, and theoretical. Empirical and
semi-empirical approaches consider only external resistance to mass transfer between
product and air while the theoretical approaches consider only internal resistance to mass
transfer. At the theoretical modeling two kinds of approaches are used. These are discrete
approach and continuum approach. In discrete approach, transport is examined in a
network structure representing the material structure and generally the purpose of use of
this approach is to determine transport parameters as an alternative to the experimental
measurements. On the other hand, continuum approach is commonly used for describing
the transport taking place at macroscopic level. In continuum approach, the food material
is considered as a fictitious continuum and the effects of the physical phenomena taken
into consideration are lumped into effective transport coefficients. There are many
models suggested based on continuum approach. The main difficulty in using a model
based on a continuum approach arises from determination of these effective transport
parameters. Most of the transport parameters are strongly dependent on concentration,
temperature and material structure. Various models have been suggested to clarify the
14
effect of temperature and concentration on transport parameters. However, relatively little
is known on the effect of structure on transport parameters.
In conclusion, it may be stated that drying of food materials is a complex unit
operation and main problem to overcome on the way to better understand and describe
drying processes is to reveal the effect of structure on transport.
1. INTRODUCTION
Drying of food materials is used as a preservation technique. Microorganisms that cause
spoilage and decay can not grow and multiply in the absence of water [1]. In addition,
enzymes that cause chemical changes can not function in an environment lacking water. It is
therefore necessary to expose food materials to a proper drying process to reduce their water
content.
It is possible to classify drying processes in several ways. For example, drying processes
can be classified as batch and continuous [1]. In batch drying process, food material is
inserted into the drying equipment and drying proceeds for a given period of time. In the
continuous drying process, however, food materials are continuously added to the dryer and
dried material continuously removed. Drying processes can also be categorized depending on
the physical conditions used to add heat and remove water vapor. The most common type of
process under this categorization is the process in which heat is added by direct contact with
heated air at atmospheric pressure and the resulting water vapor is removed by the air. In
addition, there are other processes, in which heat is added indirectly through a metal wall or
by radiation.
Types of driers used in the food industry display a considerable diversity particularly
depending on the type of process used in drying. Schematic views of some common driers are
shown in figure 1. Brief information on various types of driers is also given below.
Sun Drying and Solar Dryers
Drying of food materials by spreading them on an appropriate ground is called sun
drying. In this case, part or all of the heat required for drying is supplied by direct radiation
from the sun. Solar drying means the processes where solar collectors are used for heating the air.
Tray Dryers
In tray dryers, food materials are usually laid on trays as a very thin layer. The required
heat is supplied by the air sweeping over the trays or by conduction or radiation from heated trays.
15
Tunnel Dryers
In tunnel dryers, trays or trolleys containing food materials move through a tunnel, in
which heat is supplied and water vapor is removed. Food material generally moves along the
tunnel parallel or opposite to the direction of air flow.
Roller or Drum Dryers
In this type of driers, food material is spread on the surface of a heated drum and the
drum is rotated. The food remains on the drum surface for the greater part of the rotation
during the time that drying takes place.
Fluidized Bed Dryers
In fluidized bed dryers, food material is held suspended during the drying process with
the help of the upward flow of the drying air. The air flow may be horizontal to help the food
material to convey in the dryer. In this type of dryers a major part of the heat is transferred by
convection.
Spray Dryers
In this type of driers, liquid or fine solid material is sprayed into a heated air flow as fine
droplet dispersion form. Drying speed is extremely high in this type of drying process. For
this reason, this process is generally used in drying of food materials which damage due to
prolonged exposure to hot air stream.
Pneumatic Dryers
In pneumatic dryers, solid food particles are conveyed rapidly with an air stream. The
heat necessary for drying is supplied by the air. Generally, a classifier is used in this type of
driers. Dried particles are separated in this classifier. The remaining humid part is recirculated for additional drying.
Rotary Dryers
In rotary dryers, food material is taken into a horizontal inclined cylinder. The necessary
heat for drying is provided by an air stream moving along the cylinder or by the transfer of
the heat from the walls of the cylinder by conduction. The cylinder rotates in certain types
and in other types the cylinder is stationary and the material is conveyed by a paddle or screw
rotating in the cylinder.
16
Trough Dryers
In this type of dryers, food material is loaded on a trough-shaped conveyor belt made of
mesh. Drying air is blown through the bed of material. The movement of the conveyor
continually turns over the material and hence exposes wet surfaces to hot air.
Bin Dryers
In bin dryers, food material is contained in a perforated bottom bin. Drying process is
performed by vertically upward conveyance of hot air along the bin.
Belt Dryers
In this type of dryers, food material is laid on a horizontal mesh or a solid belt and hot air
is passed over the material. Mostly, the belt is mobile. In some cases, the belt is stationary and
material is conveyed by scrappers.
Vacuum Dryers
In vacuum drying, material is inserted in an evacuated cabinet and the drying process is
performed in this cabinet. The required heat is mainly transferred by conduction or radiation.
This process which allows drying at lower temperatures is generally used for food materials
that are damaged by exposure to high temperatures.
Freeze Dryers
In freeze dryers, food material is loaded on shelves or belts in a chamber under vacuum.
Material is generally frozen before loading into the dryer. The heat is transferred to food by
conduction or radiation. The resulting vapor is removed by a vacuum pump and is condensed.
In certain cases, sheets of expanded metals and heated plates are inserted between food
materials to enhance heat transfer and moisture removal.
Microwave Dryers
Drying process in microwave dryers is performed using polarization occurring at
molecular and atomic level. The heat developed in a material by an alternating
electromagnetic field results from the polarization process within the product when molecules
within the material rotate and move laterally millions of times per second in an attempt to
align with the changing field. Microwave heating provides a uniform heat flux throughout the
material.
17
Radio Frequency Dryers
In a radio frequency drying system, a RF generator creates an alternating electric field
between electrodes. The material is conveyed between the electrodes. In this case, alternating
energy causes polar molecules in the water to continuously reorient themselves to face
opposite poles. This frictional movement causes the water content of food material to heat up
rapidly and leave the medium by vaporization.
Infrared Dryers
In the infrared dryers, the electromagnetic energy of infrared rays is used for drying. The
depth of penetration of infrared is a function of its wavelength. Generally, the shorter the
wavelength, the greater is its penetration power. The most important advantage of this type of
drying is economy. For biological materials, however, infrared heater temperatures greater
than 830°C should be avoided as this can char the product and cause surface damage [3].
Heat Pump Dryers
Heat pump dryer consists of a drying chamber equipped with a circulation system and the
components of an air-conditioning refrigeration system. The drying air is dehumidified by the
evaporator and reheated by the condenser of the heat pump. The maximum drying
temperature is determined by the condensing temperature of the refrigerant used. Heat pump
drying is essentially a low-temperature process which can be controlled from -20°C to 70°C
by selecting an appropriate refrigerant and regulating the compressor capacity and air flows
within the system [4].
Superheated Steam Dryers
In the superheated dryer, wet solids are fed into the flow of pressurized superheated
transport steam by means of a pressure tight rotary valve, plug screw or similar. The transport
steam is superheated indirectly via a tubular heat exchanger, by a heating media such as
medium pressure steam, flue gases or thermal oil [5]. Also, electrical heating can be applied.
In the subsequent drying ducts, moisture is vaporized from the product, forming excess
transport steam and lowering its degree of superheat. Normally the residence time in the
system is 5-60 seconds only. For some materials, a second superheater is necessary to achieve
the required dryness. The dry material is separated in a high efficiency cyclone and the
material is discharged from the dryer by means of another pressure tight rotary valve. From
the cyclone, the transport steam is recycled by a centrifugal fan to the inlet of the first heat
exchanger. The excess steam generated is continuously bled off.
18
Hybrid Dryers
Particularly, dryers manufactured using latest technology consist of a combination of
different types of drying processes. They are preferred mostly because the combination
allows utilization of the most advantageous aspect of each process for food material and
drying process. Common hybrid dryers used in drying are listed below.
•
•
•
Microwave-Convective Dryers, Microwave-Infrared Dryers, Microwave-Vacuum
Dryers, Microwave-Superheated Steam Dryers,
Infrared-Convective Dryers, Infrared-Vacuum Dryer, Infrared-Heat Pump Dryers,
Radio Frequency-Heat-Pump Dryers, Radio Frequency-Vacuum Dryers.
centrifugal
fan
heater
feed
product
steam
product
ROLLER DRYER
TRAY DRYER
vapour
vapour
feed
feed
heater
product
hot air
FLUIDISED DRYER
Figure 1. continued on the next page.
air
product
PNEUMATIC DRYER
19
feed
feed
steam
atomiser
product
hot air
condensate
ROTARY DRYER
SPRAY
DRYER
product
steam
heated plates
vapour
steam jet
vacuum pump
steam
food
steam jet
vacuum pump
compression
mechanism
FREEZE DRYER
feed
infrared heater
condenser
water
INFRARED DRYER
heating
media
aspirator
excess
steam
infrared heater
feed
product
product
SUPERHEATED STEAM DRYER
vacuum pressure controller
cooler
INFRARED-VACUUM DRYER
Figure 1. Schematic view of various types of dryers used in food industry [2].
product
20
2. STRUCTURE OF FOOD MATERIALS
Food materials are porous and hygroscopic materials and their structure has a strong
effect on transport and transport parameters. Structure has a strong effect particularly on mass
diffusivity, permeability and thermal conductivity. On the other hand, its effect on thermal
diffusivity is relatively weak [6].
Porous Materials
A porous medium is a multi-phase system consisting of a solid phase and one or more
fluid phases that occupy the pore space. The pore space of the porous medium consists of
pores (nodes) and throats (bond) as connections between pores. The pores and throats are
distributed randomly inside the porous medium. They have irregular shapes and therefore the
structure of porous medium is very complex (see figure 2). Porous materials are divided into
two groups as porous and capillary porous materials. This distinction is based on pore size.
Materials with pore diameter equal to or higher than 10-7m are called porous materials, and
smaller than 10-7m are called capillary porous materials [8]. The majority of food materials
are capillary-porous materials [9].
Figure 2. Examples of porous media (10 x magnified): a) beach sand, b) sandstone; c) limestone; d) rye
bread; e) wood; f) human lung (adapted from[7]). with permission.
21
Pores in porous materials may be classified in three groups: (a) interconnected pores, (b)
isolated or closed pores and (c) dead-end or blind pores (see figure 3). The interconnected
pores are usually accessible from many directions. Blind or dead end pores are accessible
from one direction only. Isolated pores are inaccessible and behave as part of the solid.
Isolated pores decrease the diffusivity characteristics of the porous medium.
Blind Pore
Closed Pore
Interconnected Pore
Figure 3. Different types of pores in a porous medium.
Hygroscopic and Non-Hygroscopic Materials
In non-hygroscopic materials, pore spaces are filled with liquid if the material is fully
saturated, and with air if it is completely dry (see figure 4). In non-hygroscopic materials
bound water content is quite low and vapor pressure is the function of temperature only [8].
Non-hygroscopic materials do not shrink during drying process. However, hygroscopic
materials contain large amounts of physically bound water and therefore these materials
usually shrink during the drying process. Food materials are in the hygroscopic material class
where the modeling of drying process is more complex due to shrinkage.
Solid Phase
Bound
Gas
Hygroscopic
Figure 4. continued on next page.
22
Liquid Water
Gas Phase
Solid Phase
Non-Hygroscopic
Figure 4. Hygroscopic and non-hygroscopic materials (adapted from [10]).
3. TRANSPORT PARAMETERS
Dimensionless Numbers
Various dimensionless numbers are encountered when dealing with the transport
phenomena during the drying process. Most of these numbers are given in table 1 together
with their physical meanings.
Table 1. Dimensionless numbers and heir physical meanings
D.less Number
Equation
Physical Meaning
Biot
h L
Bi m = m
D
mass transfer across the boundary/mass transfer within the solid
Biot
Bi q =
Fourier
Fo =
Dt
L2
dimensionless time in the unsteady state regime
Grashof
Gr =
gL3β v ρ 2 ΔT
ν
buoyancy forces/viscous forces
Lewis
Le =
α
D
thermal diffusivity/mass diffusivity
Nusselt
Nu =
hqL
Peclet
Pe =
vL
ν
convection/diffusion
Prandtl
Pr =
ν
α
momentum diffusivity/mass diffusivity
Reynolds
Re =
vL
ν
inertial force/viscous force
Schmidt
Sc =
ν
D
momentum diffusivity/mass diffusivity
Sherwood
Sh =
h mL
D
mass transfer/mass diffusivity
hqL
λ
λ
heat transfer across the boundary/heat transfer within the solid
convective heat transfer/conductive heat transfer
23
Table 1. Continued
D.less Number
Stanton
Equation
h
St m = m
v
St q =
Stanton
Physical Meaning
wall mass transfer/mass transfer by convection
h q / ρC p
v
heat transferred to fluid/heat transported by fluid
where L is the characteristic dimension of a solid body (m).
Relative Humidity
Relative humidity is the ratio of the mole fraction of water vapor in a given moist air
sample to the mole fraction in a saturated air sample at the same temperature and pressure. By
using the perfect gas law, it can be expressed as the ratio of the actual vapor pressure Pv (Pa)
to the vapor pressure of the saturated air at the same temperature Pv,sat (Pa).
ϕ = Pv / Pv,sat (T)
(1)
Humidity Ratio
The humidity ratio of moist air is defined as the ratio of the mass of water vapor Mv (kg)
to the mass of dry air contained in the moist air Ma (kg).
ω = Mv / Ma
(2)
Saturation Humidity Ratio
The saturation humidity ratio ωsat is the humidity ratio of moist air saturated with respect
to water at the same temperature and pressure.
Specific Humidity
The specific humidity ωs is the ratio of the mass of water vapor to the total mass of air in
a particular volume of air.
ωsp =
Mv
Mv + Ma
The specific humidity is related to the humidity ratio by the following way:
(3)
24
ωsp =
ω
1+ ω
(4)
Dry-Bulb Temperature
The dry bulb temperature Tdb (°C) is the temperature measured by a (dry) thermometer
immersed in a vapor-gas mixture.
Wet-Bulb Temperature
The psychrometric wet -bulb temperature Twb (°C) is measured by placing a thermometer
having a water-moistened wick covered bulb into a fast moving stream of ambient air. If the
air surrounding the wet-bulb thermometer is not saturated, evaporation of water from the wick
will occur. This will cause the bulb to cool. The amount of cooling is proportional to the
evaporation rate. Having waited long enough, a steady-state is reached. This final equilibrium
temperature is called the wet-bulb temperature of the moist air. The psychrometric wet-bulb
temperature is not the same as the adiabatic temperature which is the temperature reached by
moist air and water if the air is adiabatically saturated by the evaporating water. However, the
adiabatic and psychrometric wet-bulb temperatures are nearly equal for moist air.
Dew-Point Temperature
The dew-point temperature Tdp (°C) is the temperature at which a given unsaturated airvapor mixture becomes saturated.
Vapor Pressure
The vapor pressure Pv (Pa) is the partial pressure exerted by the water vapor molecules in
moist air. When air is fully saturated with water vapor, its vapor pressure is called the
saturated vapor pressure Pv,sat (Pa).
Gas Pressure
The total gas pressure Pg (Pa) is the sum of partial pressures of air and vapor.
Pg = Pv + Pa
(5)
If it is assumed that gas phase obeys ideal gas law:
Pi M̂ i = ρ i R̂T
(6)
25
where M̂ i is the molecular mass (kg/mol) R̂ is the universal gas constant (8.314 J/(mol K)
and T is the temperature (K).
An average molar mass can also be written as:
M̂ g = (M̂ a + M̂ v − M̂ a )Pv / Pg
(7)
where M̂ g , M̂ a and M̂ v are the molar mass of gas, air and vapor (kg/mol), respectively.
Capillary Pressure
Capillarity can be explained by considering the effects of two opposing forces: adhesion,
the attractive force between the molecules of two dissimilar substances, and cohesion, the
attractive force between the molecules of a single substance. The magnitude of attraction
between gas molecules is smaller when compared to liquids due to greater distance. This
results in higher attraction of liquid molecules in a liquid gas interface towards the interior
liquid compared to the surrounding gas and a surface tension takes place at the interface.
Surface tension values between water and air at different temperatures under atmospheric
pressure are given in table 2 together with other physical properties of the water.
Table 2. Surface tension between water and air and other
properties of water (adapted from [11])
T(°C)
0
10
20
30
40
50
60
70
80
90
100
σx103(N/m)
75.64
74.23
72.75
71.20
69.60
67.94
66.24
64.47
62.67
60.82
58.91
ρ(g/cm3)
0.99984
0.99970
0.99821
0.99565
0.99222
0.98803
0.98320
0.97778
0.97182
0.96535
0.95840
Cp(J/gK)
4.2176
4.1921
4.1818
4.1784
4.1785
4.1806
4.1843
4.1895
4.1963
4.2050
4.2159
Pv(kPa)
0.6113
1.2281
2.3388
4.2455
7.3814
12.344
19.932
31.176
47.373
70.117
101.325
η(Pa s)
1793
1307
1002
797.7
653.2
547.0
466.5
404.0
354.4
2314.5
281.8
λx103(W/mK)
561.0
580.0
598.4
615.4
630.5
643.5
654.3
663.1
670.0
675.3
679.1
Surface tension will also occur in a similar way at the solid material/liquid interface, and
at the solid material/gas interface. The angle between the edge of the meniscus and the solid
material is called contact angle (see figure 5 and figure 6). The contact angle acquires a value
in compliance with the balance of surface tensions at the interface between gas, liquid and
solid. Thus, the contact angle is a function of the characteristics of the liquid, the gas and the
solid material. The forces are balanced if
σ sg = σ sl + σ lg cos θ
(8)
26
where σ is the surface tension (N/m) and the indices sg, sl and lg denote the solid-gas, solidliquid and liquid-gas interfaces, respectively. The contact angle θ (rad) can then be given as:
cos θ =
σ sg − σ sl
(9)
σ lg
If the contact angle is between 0<θ<90° the surface is called hydrophile (water-loving) and
σsl is smaller than σsg. If the contact angle equals to zero, the liquid wets the solid surface
fully and σsg = σlg which in turn means that no work (energy) is needed to create the solidliquid interface. If the contact angle is bigger than 90°, the surface is called hydrophobic
(water-hating). In the special case when θ= 180°, no work is needed to create the solid-gas
interface. In this case, σsg will be equal to zero. This means that a drop of liquid on the
surface of the solid remains separated by a thin film of vapor [12, 13].
θ
a)
θ
b)
Figure 5. A liquid drop on a a) hydrophobic and b) hydrophile surface (adapted from [13]).
σsg
θ
σlg
σsl
Figure 6. The balance of forces that results in a contact angle θ (adapted from [13]).
The combination of surface tension and meniscus due to the capillaries causes the two
phases to experience different pressures. If the surface of the tube is hydrophile (as in pore
surfaces in a solid food material), there will be an under-pressure in the liquid and the liquid
27
will penetrate the tube. The magnitude of the pressure difference over a meniscus (Pg - Pl) is
calculated from the force acting on the water. This force for a circular tube can be written as
follows:
F = 2πro σ cos θ
(10)
where σ is the surface tension between liquid and gas (N/m); θ is the contact angle (rad), ro is
the tube radius (m). By dividing the driving force by the sectional area of circular tube, the
underpressure, or capillary pressure Pc (Pa) is determined as:
Pc =
2σ cos θ
ro
(11)
For a pore cross section that is not circular, a more general expression for the capillary
pressure can be obtained from the equilibrium of forces as:
⎛1 1⎞
Pc = σ cos θ⎜⎜ + ⎟⎟
⎝ r1 r2 ⎠
(12)
where r1 and r2 are the principal radii of the meniscus in two orthogonal directions. Equation
(12) is known as the Laplace formula for capillary pressure.
In describing the capillary flow in a porous material, the capillary pressure head h (m) is
usually used instead of capillary pressure Pc (Pa). Capillary pressure head h (m) for the case
that the air pressure is constant and equals to the atmospheric pressure is defined as:
h = Pc /(ρg )
Capillary pressure (head )
(13)
Drying
Wettin
mirr
(Sirr)
Liquid content
Saturation
Figure 7. Capillary pressure head as a function of liquid content and saturation.
msat
(Ssat)
28
where ρ is the density (kg/m3) and g is the gravitational acceleration (m/s2). The capillary
pressure (head) is a function of the liquid content or the saturation degree and it usually has
the shape as shown in figure 7.
Viscosity
Viscosity is one of the most important transport properties of liquids and gases. The
dynamic viscosity (η) is defined by the following equation for a Newtonian fluid:
τ = ηγ
(14)
where τ is the shear stress (Pa), γ is the shear rate (1/s) and η is the dynamic viscosity (Pa s).
Viscosity is usually determined by measuring the shear stress via capillary or rotational
viscometer at various shear rates.
Chemical Potential
Chemical potential, μ̂ (J/mol), is a term introduced by Willard Gibbs. He defined it as
follows: If to any homogeneous mass in a state of hydrostatic stress we suppose an
infinitesimal quantity of any substance to be added, the mass remaining homogeneous and its
entropy and volume remaining unchanged, the increase of the energy of the mass divided by
the quantity of the substance added is the potential for that substance in the mass considered.
The chemical potential of a system is the amount by which the energy of the system
would change on condition that an additional particle were added. If a system has more than
one species of particle, there is a separate chemical potential associated with each species.
If a thermodynamic system containing n constituent species is considered, its total
internal energy U (J) can be written to be a function of the entropy S (J/K), the volume V
(m3), and the number of moles of each species N1,..., Nn:
U = U (S, V, N1 ;..., N n )
(15)
It is emphasized by referring U as the internal energy that the energy contributions resulting
from the interactions between the system and external objects are excluded. The chemical
potential of the ith species is defined as the partial derivative of the internal energy [14].
⎛ ∂U
μˆ i = ⎜⎜
⎝ ∂N i
⎞
⎟⎟
⎠ S, V , N j ≠ i
(16)
In real systems, it is usually difficult to hold the entropy fixed since this requires complete
thermal insulation. It is therefore more convenient to define the Helmholtz free energy A (J),
which is a function of the temperature, volume, and number of moles:
A = A(S, V, N1 ;..., N n )
29
(17)
In terms of the Helmholtz free energy, the chemical potential is
⎛ ∂A
μˆ i = ⎜⎜
⎝ ∂N i
⎞
⎟⎟
⎠S,V , N j≠i
(18)
If the pressure and temperature are assumed to be constant, the chemical potential can be
expressed as the partial derivative of the Gibbs free energy G (J) with respect to mole number
of the species.
⎛ ∂G
μˆ i = ⎜⎜
⎝ ∂N i
⎞
⎟⎟
⎠S,V , N j≠i
(19)
The chemical potential of water vapor μ̂ (J/mol)is related to water activity aw by:
μˆ = μˆ o + R̂T ln a w
(20)
where μ̂ o is the chemical potential for pure water (J/mol), R̂ is the ideal gas law constant
(8.314 J/(mol K)) and T is the temperature (K).
Concentration
Concentration of a mixture and its components may be expressed in terms of mass and
mol. In terms of mass, concentration of a mixture and component i are given by:
C = M/V
Ci = M i / V
or
ρ = M/V
ρi = M i / V
(21)
where M (kg) and Mi (kg) are the mass of the mixture and component i and V is the total
volume (m3). A related quantity, the mass fraction of component i is defined as:
)
m i = M i / M = Ci / C
or
)
m i = M i / M = ρi / ρ
(22)
Molar concentration of a mixture and component i and the mole fraction of component i
are defined as:
Ĉ = N / V
)
n i = N i / N = Ĉ i / Ĉ
Ĉ i = N i / V
(23)
(24)
30
where N and Ni are the mol of the mixture and component i, respectively.
It can easily be shown that:
M = ∑ Mi
C = ∑ Ci
i
N = ∑ Ni
i
Ĉ = ∑ Ĉi
i
i
ρ = ∑ ρi
i
)
)
n = ∑ ni
)
)
m = ∑ mi
(25)
i
(26)
i
The mass concentration and molar concentration are related through the molar mass of
component i as:
C i = M̂ i Ĉ i
(27)
Using the ideal gas law for a mixture of gases, the following equation can be written for gas I
Pi V = N i R̂T
(28)
where Pi (Pa) is the partial pressure of gas i for which there is Ni moles, and R̂ is the
universal gas constant (8.314 J/(mol K)). Therefore, concentration of any gas in a mixture can be
written in terms of its partial pressure as:
Ĉ i =
Ni
P
= i
V R̂T
(29)
The total concentration is related to the total pressure. Using the equation PV = NR̂T , total
concentration can be written as:
Ĉ =
P
R̂T
(30)
r
r
The gradient of concentration ( ∇C or ∇Ĉ ) is assumed to be the driving force for
molecular diffusion, although it does not have the dimensions of force. Fick’s law relating
diffusion to a concentration gradient is derived by analogy with heat conduction.
Moisture Content
Moisture content of a wet material is defined as the ratio between the total mass of water
Mw (kg) and the mass of dry solid Md (kg).
m=
Mw
Md
(31)
31
Sometimes a wet basis moisture content mwb (kg water/kg wet substance), which is the
moisture ratio based on the total mass of wet material, is used.
mw =
Mw
Mt
(32)
The two moisture contents are related by the following expression:
m=
mw
1 − mw
(33)
Moisture Ratio
Moisture ratio is dimensionless moisture content and is defined as:
mr =
m − me
mo − me
(34)
where m, mo, me are the instantaneous, initial and equilibrium moisture contents respectively.
In certain drying processes, materials are not continuously exposed to uniform relative
humidity and temperature conditions. In such cases, the following equation not incorporating
the equilibrium moisture content is used instead of the equation defined in Eq. (34).
mrr =
m
mo
(35)
Saturation
Saturation degree (or pore saturation) is defined as the volume fraction of void space
filled by moisture in a substance.
S=
Vw
Vvoid
(36)
Saturation takes values from 0 (when the medium is completely dry) to 1 (when the
medium is completely saturated). There is a relationship between saturation and moisture
content as:
m=
ψρ w
S
(1 − ψ)ρ ds
(37)
32
where ρw and ρds are the densities of water and dry solid (kg/m3) and ψ is the porosity of
material.
Mass Capacity
Mass capacity is a potential for mass transfer and is defined by analogy with that of
temperature. The heat capacity of a body is given as:
⎛ ∂H ⎞
CP = ⎜
⎟
⎝ ∂T ⎠ P
(38)
where H is the enthalpy (J), T is the temperature (K) and P is the pressure (Pa). Similarly,
mass capacity of a body is given as [15]:
⎛ ∂m ⎞
Cm = ⎜
⎟
⎝ ∂W ⎠ T
(39)
where W is called moistness (°M). If a mean mass capacity is assumed over a range of
moistness, then the quantity of moisture passing from one place at W2 to another at W1
(W2>W1) is given by C m ( W2 − W1 ) [15].
A scale of moistness has been constructed by Luikov [16]. The scale is chosen so the
moistness at the maximum hygroscopic moisture content (ϕ=1) is 100°M, and the mass
capacity C om of the standard body is taken as one hundredth of the maximum sorptional
moisture content m omax . The moistness of the standard body W (°M) at any moisture content
mo then becomes:
W=
mo
mo
= o 100
o
C m m max
(40)
If the standard body is in contact with another material at hygrothermal equilibrium, the
degree of moistness is everywhere the same and the mass capacity of the second material can
be obtained from its moisture content.
Cm =
m
W
The value of Cm (kg/(kg°M)) is usually determined experimentally based on Eq.( 41).
(41)
33
Water Activity
Water activity is one of the most important parameters of food processing. Many physical
and chemical factors are affected by water activity significantly. Water activity is defined as
the ratio of the vapor pressure of water in a material (Pv) to the vapor pressure of pure water
(Pvo) at the same temperature.
aw =
Pv
Pvo
(42)
When the vapor pressure and temperature equilibrium are obtained, the water activity of a
material is equal to the relative humidity of surrounding air.
Some Microorganisms and
Their Growth Minima
Water
Activity
1.0
Fresh vegetables,Fruits, Meats
Poultry, Fish, Mik
Cured Meats, such as Ham
0.9
Salami, Some Dry Cheeses
Cl. Botulinum
Salmonella
Most Bacteria
Most Yeasts
Staphylococcus
Some Foods and Their
Water Activity Ranges
Flour, Cakes, Rice, Beans, Cereals
Most Molds
0.8
Intermediate Moisture Foods
Salt, Preserved Foods, Jams
Holophilic Bacteria
0.7
Extremely Osmophilic
Microorganisms
(Some Molds and Yeasts)
Rolled Oats
Dried Fruits, Caramels
0.6
Dehydrated Foods
0.5
Figure 8. Water activity levels of some foods and growth minima’s of micro-organisms (adapted from [17]).
Water activity levels of some foods and growth minima’s of micro-organisms are given
in figure 8. Chemical effects increasing with water activity are enzymatic and nonenzymatic
browning reactions (Maillard reactions) and microbial damage. Since enzymes in many food
materials are not inactivated during heating process, enzymatic reactions occur also in low
moisture contents. Nonenzymatic browning reactions, too, are affected by water activity. In
the presence of water, carboxyl and amino compounds are involved as reactants, products, or
catalysts in the browning process [17]. In low water activities, enzymatic and browning
reaction rates are low due to substrate solubility and mobility. And for high water activity
34
values, water dilutes the reactants and the rate of browning falls. Bacterial growth occurs at
extremely high water activity levels and is dormant for a water activity below 0.90 [17]. Most
yeast and moulds, however, can proliferate at water activity levels as low as 0.80. Physical
changes such as texture and aroma can depend greatly on water activity. Textural changes are
most often seen in freeze drying and subsequent storing of foods, particularly for meats and
fish. The water activity in dried foods can also affect the retention of aroma [17].
Equilibrium Moisture Content
One of the most important parameters in drying is the humidity of the air in contact with
the solid material. Let us assume that a wet material is exposed to an air stream with constant
humidity and temperature and there is no change in conditions of air. If it is waited long
enough, the solid material will have a definite moisture content. This moisture content is
known as the equilibrium moisture content of the material under the specified humidity and
temperature of the air. The moisture content is usually expressed on the dry basis as kg
water/kg dry solid. If the material contains more moisture than its equilibrium value in
contact with air of a given humidity and temperature, it will dry until it reaches equilibrium
value. If the material contains less moisture than its equilibrium value, it will adsorb water
until it reaches equilibrium value. For air having 0% humidity, the equilibrium value of all
materials is zero. In general, at low relative humidities, the equilibrium moisture content is
greater for food materials high in protein, starch and lower for food materials high in soluble
solids [1].
Equilibrium moisture content is generally determined experimentally. There are two
different approaches called gravimetric and hygrometric [18]. In gravimetric method, air
temperature and water activity is kept constant until the moisture content of the sample
achieves a constant equilibrium value. The air may be circulated or stagnant. In hygrometric
method, the moisture content of the sample is maintained at a constant value until the
surrounding air reaches to equilibrium value.
Numerous mathematical models also exist to predict the equilibrium moisture content
(see table 3). Some of these models are theoretical (such as Modified BET and GAB), some
are semi-empirical (such as Henderson and Halsey) and some are empirical (such as Smith
and Oswin) (for more details see Ref. [19]). Of these models, Halsey model yields better
results for many food materials compared to Henderson model [20]. The BET and Harkins
and Jura equations provide acceptable predictions only for ϕ<0.3 and Modified Chung and
Pfost equation is suitable for cereal grains [21]. Oswin model provides satisfactory results for
protenaceous foods, starchy foods, meats and vegetables [22].
35
Table 3. Theoretical and empirical sorption models
Name
Model Equation
Freundlich
m e = a (a w )1 / b
BET
m e = m ml c a w /[(1 − a w )(1 − a w + ca w )]
Harkins and Jura
ln a w = b − (a / m e2 )
Oswin
m e = a (a w /(1 − a w )) b
Smith
m e = a − b ln(1 − a w )
Halsey
m e = [a / ln a w ]
Henderson
m e = [ln(1 − a w ) /(−a )]
Chung-Pfost
m e = −[ln(− ln a w / a )] / b
Kuhn
m e = a / ln a w + b
Iglesias and Chirife
ln m e + (m e2 + m 0.5 ) 0.5 = ba w + a
GAB
m e = (m ml cka w ) / [(1 − ka w )(1 − ka w + cka w )]
Anderson
m e = (abca w ) / 1 + (b − 2)ca w + (1 − b)c 2 a w
Peleg
m e = aa + ba
1/ b
1/ b
[
]
[
c
w
]
d
w
Caurie
m e = exp[a w ln a − 1 /(0.045b)]
Modified BET
m e = m m ca w /[(1 − a w )(1 − c ln(1 − a w ))]
Modified Oswin
m e = (a + bT)(a w /(1 − a w )) c
Modified Halsey
m e = [exp(a + bT ) / ln a w ]
Modified Henderson
m e = {− ln(1 − a w ) / [a (T + b)]}
Modified Chung-Pfost
m e = −{ln[(−(T + b) ln a w ) / a ] / c)}
1/ c
1/ c
where
a, b, c, k
constants
aw
T
me
mml
m0.5
water activity
temperature (°C),
equilibrium moisture content ( kg water/kg dry solid)
monolayer moisture content ( kg water/kg dry solid)
moisture content at aw=0.5 ( kg water/kg dry solid)
Sorption Isotherms
A sorption isotherm is the graphic representation of the sorption behavior of a substance.
It represents the relationship between the equilibrium moisture content of a product and the
water activity of the material at a particular temperature. As shown in figure 9, there are three
basic shapes for sorption isotherms. There is a closed loop hysterisis between desorption and
adsorption isotherms as shown in figure 10. The desorption isotherm always has the larger
equilibrium moisture content.
36
Moisture Content, m
1
2
3
Water Activity, aw
Moisture Content, m
Figure 9. Basic shapes of sorption isotherms. 1. Highly hygroscopic, 2. Medium hygroscopic, 3. Low
hygroscopic, sensitive to high air humidity (adapted from [23]).
Strongly
bound
monolayer
Less strongly
bound
water layers and
capillary adsorbed
water
Solvent and
free water
Desorption
Adsorption
A
0.0
C
B
0.2
0.4
0.6
0.8
1.0
Water Activity, aw
Figure 10. Sorption isotherms.
Bound and Unbound Water
If the equilibrium moisture content of a material is continued to its intersection with the
100% humidity line, the moisture is called bound water (see figure 11). This water in the
material exerts a vapor pressure less than that of liquid water at the same temperature. If such
a material contains more water than indicated by intersection with the 100% humidity line, it
exerts vapor pressure equal to that of pure liquid at the same temperature. This excess
moisture content is called unbound water. The unbound water is held primarily in the voids of
the solid.
37
Free Moisture
Free moisture is the moisture above the equilibrium moisture content (see figure 11). Free
moisture is the moisture that can be removed by drying under a given relative humidity.
bound moisture
unbound moisture
Relative Humidity, φ
1.0
free moisture
0.5
0.0
me
mc
Moisture Content, m
Figure 11. Types of moisture involved in the drying.
Thermophysical Properties
Thermophysical properties of a material are those which control the thermal energy
transport and/or storage within it, as well as the transformations undergone by the material
under the action of heat [24]. The density, specific heat, thermal conductivity and thermal
diffusivity are regarded as thermophysical properties. These properties are dependent on the
temperature, the material chemical composition and the physical structure.
Density
There are various density definitions for a porous material. The most important ones are
apparent density and substance density. Their values are generally determined by
experimental measurements. Volumetric displacement method, dimension method,
stereopycnometer method and buoyant force method are the commonly used methods to
determine apparent density [25]. Apparent volume of the sample is measured by these
methods. Subsequently, density is calculated by dividing the measured sample weight by this
determined volume. In volumetric displacement method, the apparent volume is determined
by placing the sample in a container of known liquid volume and measuring the volume
displacement. In dimension method, the apparent volume is determined by averaging a
number of dimension measurements with micrometers. In stereopycnometer method, the
sample is covered with silicone grease to make it impervious to gases and its apparent volume
38
is measured by a stereopycnometer. In buoyant force method, the apparent volume is
determined by measuring the buoyant force applied on the sample when coated sample is
immersed in a known liquid. Substance density is mostly determined using a gas (helium)
stereopycnometer. Density of a wide variety of foods at different moisture content can be
found in Refs. [19], [25] and [26].
The density is dependent on moisture content of the material. It is difficult to measure the
density as a function of moisture content and hence empirical correlations are often used for
this purpose. The correlations are generally in the following forms:
ρ = a + bm w
ρ = a + bmw + cm2w
ρ = a + bm w + cm 2w + dm 3w
(43a)
ρ = a + b exp(cm w )
ρ = a + b exp(cm 2w )
ρ = a + b ln m w
(43b)
ρ = a + b ln(m w + c)
ρ = a + b / mw + c / m2w
ρ = a + b / mw + clnmw
(43c)
where ρ is the density (kg/m3) and mw is the moisture content in wet basis (kg water/kg wet
substance) and a, b, c and d are empirical constants.
Alternatively, densities of food materials can be determined using the densities of
components constituting the material [27]:
ρ=
1
)
m
∑ i / ρi
(44)
i
)
where m i is the mass fraction of component i and ρi is the corresponding density. The
mass fractions of components of food materials can be obtained from USDA Handbook 8
[28]. The densities for basic components can be estimated using the equations given in
table 4.
Table 4. Densities of food components as a function of temperature. (adapted from [27])
Component
ρ (kg/m3)
Carbohydrate
ρ = 1.5991x10 3 − 0.31046T
Protein
ρ = 1.3299 x10 3 − 0.51840T
Fat
ρ = 9.2559x10 2 − 0.41757T
Ash
ρ = 2.4238x10 3 − 0.28063T
Fiber
ρ = 1.5991x10 3 − 0.31046T
Water
ρ = 997.18 + 3.1439 x10 −3 − 3.7574 x10 −3 T 2
Ice
ρ = 916.89 − 0.13071T
39
Apparent or Bulk Density
Apparent or bulk density is defined as the ratio between the current weight of the material
and its overall volume.
ρ app =
Ms + M w
Vs + Vw + Va
(45)
where Ms (kg) and Mw (kg) are the masses of dry solid and water, respectively; and Vs (m3),
Vw (m3) and Va (m3) are the volumes of dry solid, water and air respectively.
Substance Density
Substance density is defined as the ratio between the total mass of the material and its
overall volume excluding all pores.
ρs =
Ms + M w
Vs + Vw
(46)
Particle Density
Particle density is defined as the ratio between the total mass of the material and its
overall volume excluding only externally connected pores.
ρp =
Ms + M w
Vs + Vw + Vcp
(47)
Dry Solid Density
Dry solids density is defined as the ratio between the mass of solid in the material and the
volume occupied by the solid.
ρ ds =
Ms
Vs
(48)
The dry solid density is related with the apparent density as follows:
ρ app = ρ ds (1 − ψ) + ψSρ w
where ψ is the porosity and S is the saturation degree.
(49)
40
Equilibrium Density
Equilibrium density is defined as the ratio between the mass of the material at the
equilibrium with environmental air and its overall volume.
ρe =
Me
Ve
(50)
True Density
The density of a pure component substance i of a material is calculated using its mass and
volume as follows.
ρi =
Mi
Vi
(51)
Specific Heat
Specific heat C P (J/(kg K)) is defined as the amount of energy Q (J) needed to increase
the temperature of one kilogram of matter by one degree Celcius.
CP =
Q
M (T2 − T1 )
(52)
Specific heat of food materials are generally determined experimentally by the following
methods: mixture method, comparison method, adiabatic method and differential scanning
calorimeter method (see Ref. [19] for details). Specific heat for a wide variety of foods at
different moisture content can be found in Refs. [19] and [26]. Specific heat is dependent on
composition and temperature. These dependences are generally expressed using the
correlations in the following forms:
C P = a + bm w
CP = a +
C P = a + bm w + cm 2w
b
b
c
+ c ln m w
+ 2 CP = a +
mw
mw mw
C P = a + bm w + cT
C P = a + bm w + cm 2w + dm 3w
(53a)
C P = a + bm w /(1 + m w )
(53b)
C P = a + bm w + cm 2w + dT C P =
am w
b
+
1 + mw 1 + mw
(53c)
41
where mw is the moisture content in wet basis (kg water/kg wet substance), T is the
temperature (°C) and a, b, c, and d are empirical constants.
Specific heat of food materials may also be obtained using specific heats of components
constituting the material. In the context of such approach, Leninger and Baverloo [29] have
suggested the following correlation:
)
)
)
C p = (0.5m f + 0.3m s + m w )4.18
(54)
)
)
)
where m f , m s and m w are the mass fraction of fat, solid and water respectively. This
equation references the specific heat of water (4.18 kJ/kg) at 20°C. Charm [30] has proposed
another correlation in the form of Equation (54) as follows:
)
)
)
C p = 2.094m f + 1.256m s + 4.187m w
(55)
This equation references the values of specific heat at 75°C. Heldman and Singh [31] have
proposed the following correlation for 20°C or lower temperature:
)
)
)
)
)
C p = 1.424m c + 1.549m p + 1.675m f + 0.837m a + 4.187m w
(56)
where the coefficients represent the specific heats of carbohydrate, protein, fat, ash and water.
A more general equation in the form of Eqs. (54)-(56) can be expressed as follows:
)
C P = ∑ m i C pi
(57)
i
)
where m i is the mass fraction of component i and Cpi is the corresponding specific heat. The
mass fractions of components of food materials can be obtained from USDA Handbook 8 [28].
Table 5. Specific heat capacities of food components as a
function of temperature. (adapted from [27])
Component
CP [kJ/(kg°C)]
Carbohydrate
C P = 1.5488 + 1.9625x10 −3 T − 5.9399 x10 −6 T 2
Protein
C P = 2.0082 + 1.2089 x10 −3 T − 1.3129 x10 −6 T 2
Fat
C P = 1.9842 + 1.4733x10 −3 T − 4.8008x10 −6 T 2
Ash
C P = 1.0926 + 1.8896x10 −3 T − 3.6817 x10 −6 T 2
Fiber
C P = 1.8459 + 1.8306 x10 −3 T − 4.6509 x10 −6 T 2
Water
Ice
C P = 4.0817 − 5.3062 x10 −3 T + 9.9516 x10 −4 T 2 (-40<T<0°C)
C P = 4.1762 − 9.0864 x10 −5 T + 5.4731x10 −6 T 2 (0<T<150°C)
C P = 2.0623 + 6.0769 x10 −3 T
The specific heats for basic components can be estimated using the equations given in table 5.
42
Thermal Conductivity
Thermal conductivity expresses the efficiency of a material as a heat conductor and it is
defined by the Fourier equation:
r
r
J q = − λ ∇T
(58)
r
where J q is the heat flux vector (W/m2), λ is the thermal conductivity (W/(m K)) and T is the
temperature (°C).
Thermal conductivity of food materials depends on its composition and temperature and
it is generally determined experimentally. For measurement of thermal conductivity, there are
steady state techniques such as guarded hot plate and radial heat flow method, quasi-steady
techniques such as Cenco-Fitch and Rahman-Fitch method and transient techniques such as
line source method. The details on thermal conductivity measurement methods can be
obtained from Ref. [19]. In addition, thermal conductivity values of a wide variety of foods at
different moisture content can be found in Refs. [19] and [26].
Measurement of thermal conductivity as a function of composition and temperature is
difficult. Hence, generally empirical correlations are used. Thermal conductivity of food
materials decreases with a decrease in moisture content. Therefore, it is usually found a linear
relation between thermal conductivity and moisture content [19]. However, the linear
correlation of thermal conductivity with moisture content is limited to small changes in
moisture. Hence, nonlinear correlations are also needed to cover the whole range of moisture
content.
λ = a + b exp(cm w )
(59a)
λ = a + b / m w + c / m 2w λ = a + b / m w + c ln m w λ = a + bm w + cT
(59b)
λ = a + bm w + c / T
(59c)
λ = a + bm w
λ = a + bm w + cm 2w
λ = (a + bT + cT 2 )(d + em w )
where mw is the moisture content in wet basis (kg water/kg wet substance) and a, b, c, and d
are empirical constants.
Thermal conductivity correlations given above are limited to specific materials and
varieties. However, there are also correlations that can be used for various types of foods.
Sweat [32] has proposed the following linear model for predicting the thermal conductivity of
fresh fruits and vegetables giving predictions within 15% of most experimental values.
λ = 0.148 + 0.439m w
(60)
The above model is limited to water content above 60% (wet basis). Another correlation in
the form of Eq. (60) has been suggested by Sweat [33] for thermal conductivity prediction of
the meat.
λ = 0.08 + 0.52m w
43
(61)
This correlation is limited to water content from 5% to 88% (wet basis) and temperature from
0°C to 60°C. The correlation developed by Sweat [32] (Eq. (60)) shows that thermal
conductivity is strongly dependent on the water content for all fruits and vegetables except
apple. This is probably because of the fact that apple is a highly porous fruit. Therefore, it will
be suitable to use more general correlations containing the porosity term [19]. One of this
type of correlations has been suggested by Rahman [34] for thermal conductivity prediction
of apple, beef, pear, potato and squid as follows:
m
λ 1
= 1.82 − 1.66 exp(−0.85 w )
λ o 1 − εa
m wo
(62)
where ε a is the volume fraction of air. This correlation is limited to water content between
5% to 88% (wet basis), porosity from 0 to 0.5 and temperature from 20 to 25°C.
Another frequently used approach for thermal conductivity prediction involves the use of
thermal conductivities of components constituting the material. Sweat [26] has proposed the
following correlation for solid and liquid foods.
)
)
)
)
)
λ = 0.25m c + 0.155m p + 0.16m f + 0.135m a + 0.58m w
(63)
The following equation has been suggested by Choi and Okos [27] for liquid foods.
)
)
)
)
)
λ = 0.2051m c + 0.2m p + 0.175m f + 0.135m a + 0.61m w
(64)
Riedel [35] has proposed the following equation for fruit juices, sugar solutions and milk over
a temperature range from 0°C to180°C.
λ = (326.58 + 1.0412T + 0.00337T 2 )(0.46 + 0.54m w )(1.73x10 −3 )
(65)
A more general model for thermal conductivity prediction can be written as follows [27]:
λ = ∑ λi εi
(66)
i
where εi is the volume fraction of component i and λi is the corresponding thermal
conductivity. The volume fraction is used in Eq. (66) since the thermal conductivity is
dependent on the spatial structure of the material. The volume fraction can be defined as
follows.
εi =
)
m i / ρi
)
∑ m i / ρi
i
(67)
44
)
where m i is the mass fraction of component i. The mass fractions of components of food
materials can be obtained from USDA Handbook 8 [28]. The thermal conductivities for basic
components can be estimated with the equations given in table 6.
Table 6.Thermal conductivities of food components as a
Component
λ [W/(m°C)]
Carbohydrate
λ = 0.20141 + 1.3874x10 −3 T − 4.3312x10 −6 T 2
Protein
λ = 0.17881 + 1.1958x10 −3 T − 2.7178x10 −6 T 2
Fat
λ = 0.18071 + 2.7604x10 −4 T − 1.7749x10 −7 T 2
Ash
λ = 0.32962 + 1.4011x10 −3 T − 2.9069x10 −6 T 2
Fiber
λ = 0.18331 + 1.2497 x10 −3 T − 3.1683x10 −6 T 2
Water
λ = 0.5710 + 1.7625x10 −3 T − 6.7036x10 −6 T 2
Ice
λ = 2.2196 − 6.2489x10 −3 T + 1.0154x10 −4 T 2
There are also more different models proposed for thermal conductivity prediction. The
following equation has been developed by Marinos-Kouris and Maroulis [18] using thermal
conductivity data for more than 100 food materials in 11 different categories:
λ=
⎡ E ⎛1
⎡ E ⎛1
1
1 ⎞⎤
m
1 ⎞⎤
⎟⎟⎥ +
⎟⎟⎥
λ o exp ⎢− ao ⎜⎜ −
λ i exp ⎢− ai ⎜⎜ −
1+ m
⎣⎢ R̂ ⎝ T TR ⎠⎦⎥ 1 + m
⎣⎢ R̂ ⎝ T TR ⎠⎦⎥
(68)
where E ao (J/mol) is the activation energy for heat conduction in dry material at m=0, Eai
(J/mol) is the activation energy at m=∞, R̂ is the ideal gas constant (8.3143 (J/(mol K)), T is
the material temperature (°C) and TR is a reference temperature (°C). The reference
temperature has been chosen as 60 °C by Marinos-Kouris and Maroulis [18].
In determining thermal conductivity for heterogeneous materials, structural models must
be used and the effect of geometry must be taken into consideration. Some structural models
available in the literature are given in table 7. In series model, layers of components are
placed normal to the heat flow. On the other hand, in parallel model, layers of components are
placed in the direction of the heat flow. In mixed model, heat conduction occurs by parallel
and vertical heat flow. The random model assumes that both phases are dispersed randomly.
Maxwell model is for the case where one phase in continuous and the other phase is dispersed
as uniform spheres [18].
45
Table 7. Structural models for thermal conductivity in
heterogeneous materials (adapted from [18])
Model
Equation
Perpendicular (series)
1 / λ = (1 − ε) / λ1 + ε / λ 2
Parallel
λ = (1 − ε)λ1 + ε λ 2
Mixed
1/ λ =
Random
λ = λ(11−ε ) λε2
Effective medium theory
Maxwell
⎛1− ε
1− F
ε ⎞
⎟
+ F ⎜⎜
+
⎟
(1 − ε) λ1 + ε λ 2
λ
λ
2 ⎠
⎝ 1
[
λ = λ1 b + (b 2 + 2(λ1 / λ 2 ) /( Z − 2)1 / 2
]
b = [Z(1 − ε) / 2 − 1 + (λ 2 / λ1 )(εZ / 2 − 1)]/( Z − 2)
λ=
λ 2 [λ 1 + 2λ 2 − 2(1 − ε)(λ 2 − λ 1 )]
λ 1 + 2λ 2 + (1 − ε)(λ 2 − λ 1 )
where λ is the effective thermal conductivity, λi is the thermal conductivity of phase i, ε is the volume
fraction of phase 2, and F and Z are the parameters.
Thermal Diffusivity
Thermal diffusivity α (m2/s) indicates how heat will be diffused in a material when it is
heated and is defined by the Fourier equation.
∂T
= α∇ 2 T
∂t
(69)
Thermal diffusivity is related to the thermal conductivity as:
α = λ / ρC P
(70)
Thermal diffusivities of food materials are affected considerably by the composition of
the material. In addition, temperature also affects the thermal diffusivity. Pressure, too, may
have a considerable effect. The effect of moisture content is generally linear for moisture
higher than 10% and is non-linear for lower levels of moisture. Thermal diffusivity can be
measured experimentally or may be obtained indirectly from the specific heat and density
data. Typical thermal diffusivity value for most food is 1.0-2.0x10-7 m2/s [6].
For the prediction of thermal diffusivity as a function of moisture content and
temperature, empirical correlations are generally used. Empirical correlations are mostly in
the following forms.
α = a + bm w
α = a + bm w + cm 2w
α = a + b exp(cm w )
α = a + b / m w + c / m 2w α = a + b / m w + c ln m w α = a + bm w + cT
(71a)
(71b)
46
where α is the thermal diffusivity (m2/s), mw is the moisture content in wet basis (kg water/kg
wet substance), T is the temperature (°C) and a, b and c are the empirical constants.
Thermal diffusivities of food materials can also be calculated using the thermal
diffusivities of the components of food material as follows [27]:
)
α = ∑ αi mi
(72)
i
)
where m i is the mass fraction of component i and αi is the corresponding thermal diffusivity.
The mass fractions of components of food materials can be obtained from USDA Handbook 8
[28]. The thermal diffusivities for basic components can be predicted by the equations given in
table 7.
Table 8.Thermal diffusivities of food components
as a function of temperature. (adapted from [27])
Component
α (m2/s)x106
Carbohydrate
α = 8.0842x10 −2 + 5.3052x10 −4 T − 2.3218x10 −6 T 2
Protein
α = 6.8714 x10 −2 + 4.7578x10 −4 T − 1.4646x10 −6 T 2
Fat
α = 9.8777 x10 −2 + 1.2569 x10 −4 T − 3.8286x10 −8 T 2
Ash
α = 1.2461x10 −1 + 3.7321x10 −4 T − 1.2244x10 −6 T 2
Fiber
α = 7.3976x10 −2 + 5.1902 x10 −4 T − 2.2202x10 −6 T 2
Water
α = 0.1317 + 6.2477 x10 −4 T − 2.4022x10 −6 T 2
Ice
α = 1.1756 − 6.0833x10 −3 T + 9.5037 x10 −5 T 2
Inverse Approaches for the Prediction of Thermophysical Properties
Inverse modeling is a general mathematical method to determine unknown causes on the
basis of observation of their effects, as opposed to modeling of direct problems whose
solution involves finding effects on the basis of a description of their causes [36]. Inverse
approaches for the prediction of the thermophysical properties become widely used in the last
few decades. Inverse approaches can also be used to obtain other physical properties such as
heat and mass transfer coefficients. To use this approach, first the governing equations and
boundary conditions are defined. If physical properties are known, the problem is a direct
one. The objective of the direct problem is to determine the temperature and moisture content
fields in the drying material. On the other hand, for the inverse problems, physical properties
are unknown parameters. Assumed values for these properties are used to solve the model
equations. Desired parameters are determined by systematically minimizing the differences
between observed and simulated state variables.
47
Enthalpy
The enthalpy is defined as the heat content per unit mass. Enthalpy is relative, that is, the
actual heat content is dependent on the datum or zero point chosen. The enthalpy of moist air
per unit mass is defined as the sum of the enthalpies of dry air and superheated water vapor
per unit mass.
h ma = h a + ωh v
(73)
where ω is the humidity ratio of air (kg water/ kg dry air). hma (J/kg), ha (J/kg) and hv (J/kg)
are the enthalpies of the moist air, dry air and superheated water vapor per unit mass,
respectively.
The enthalpy of dry air per unit mass is defined as:
h a = C Pa (T − TR )
(74)
where CPa (J/(kg K)) is the specific heat of dry air at constant pressure and TR (°C) is the
reference temperature.
The enthalpy of the superheated water vapor per unit mass can be expressed as follows:
h v = C Pv (T − Tdp ) + Δh vap + C Pw (Tdp − TR )
(75)
where Tdp is the dew point temperature (°C) and Δh vap is the enthalpy of vaporization (J/kg).
Sensible Heat
The sensible heat Q (J) is the heat energy absorbed or released when a body changes
temperature.
Q = mC P (T1 − T2 )
(76)
where m is the mass (kg), CP is the specific heat at constant pressure (J/kg K)) and T is the
temperature (°C).
Enthalpy of Vaporization
Enthalpy of vaporization Δĥ vap (J/mol) is the quantity of heat required to transform a
substance from a liquid phase to vapor phase at a constant temperature. Slightly higher energy
is required to evaporate water from solid material than that required to evaporate free water
because water is partially bound in materials. The enthalpy of vaporization is a function of the
temperature at which the vaporization occurs and the moisture content of material. It
48
decreases as the temperature increases and increases as the moisture content decreases.
Enthalpy of evaporation of free water at various temperatures is given in table 9.
Table 9. Enthalpy of vaporization of water as a
T (°C)
0
25
40
60
80
100
Δĥ vap (kJ/mol)
45.054
43.990
43.350
42.482
41.585
40.657
Heat Transfer Coefficients
The surface heat transfer coefficient hq (W/(m2K)) and overall heat transfer coefficient Uq
(W/(m2K)) are defined as:
J q = h q ΔT
J q = U q (ΔT) LM
(77)
where Jq is the heat flux (W/m2), T is the temperature (°C) and LM is the log-mean
temperature difference between the two media. Surface heat transfer coefficient is not a
property of the material, but rather a property of convective heat transfer system between
solid surface and fluid. The surface heat transfer coefficient is dependent on the
thermophysical properties of fluid and solid (density, specific heat and thermal conductivity),
characteristics of the solid (shape, dimensions, surface temperature, surface roughness,
outgoing fluxes), and the characteristics of fluid flow (velocity, turbulence intensity) and the
systems (heat transfer equipment) [19]. The surface heat transfer coefficient can be
determined experimentally or calculated from empirical correlations. Empirical correlations
generally involve the following dimensionless numbers: Nusselt, Reynolds and Prandtl.
Luikov [37] states that empirical correlations should also include the Gukhman number
defined as:
Gu = (Ta − Tm ) / Ta
(78)
where Ta is the temperature of drying air (K) and Tm is the temperature of moist surface (K).
The Gukhman number is a generalized variable determining the peculiarities of simultaneous
heat and mass transfer with evaporation.
Mass Transfer Coefficients
The mass flux density Jm (kg/(m2s)) is defined by the following equation in which the
driving force can be the partial pressure difference, the concentration difference or the mol
fraction difference [6]:
J m = h m ΔC
J m = h P ΔP
J m = h n Δn f
(79)
49
where hm (m/s), hP (kg/(m2s Pa)), hn (-) are the mass transfer coefficients. The mass transfer
coefficients can be determined experimentally or calculated from empirical correlations.
Empirical correlations generally involve the following dimensionless numbers: Sherwood,
Schmidt and Reynolds. Luikov [37] states that these correlations should also include the
Gukhman number, which defines the capacity of a mobile gas to evaporate the liquid for
capillary porous bodies. Under certain simplifications, mass transfer coefficient hm may also
be calculated through the following Lewis equation:
h q / h m = ρC P
(80)
Mass Diffusivity
Mass diffusivity D (m2/s) is defined by the following diffusion equation:
∂C
= D∇ 2 C
∂t
(81)
Mass diffusivity is generally determined using experimental techniques. There are also
empirical correlations for mass diffusivity prediction. Marinos-Kouris and Maroulis [18] have
developed the following correlation using the diffusivity data for more than 100 food
materials in 11 different categories:
D=
⎡ E ⎛1
1
1
D o exp ⎢− ao ⎜⎜ −
1+ m
⎢⎣ R̂ ⎝ T TR
⎡ E ⎛1
⎞⎤
m
1
⎟⎟⎥ +
D i exp ⎢− ai ⎜⎜ −
⎢⎣ R̂ ⎝ T TR
⎠⎥⎦ 1 + m
⎞⎤
⎟⎟⎥
⎠⎥⎦
(82)
where E ao (J/mol) is the activation energy for diffusion in dry material at m=0, Eai (J/mol) is
the activation energy for diffusion in wet material at m=∞, R̂ is the ideal gas constant
(8.3143 (J/(mol K)), T is the material temperature (°C) and TR is a reference temperature (°C).
The reference temperature has been selected as 60 °C by Marinos-Kouris and Maroulis [18].
Diffusibility
The diffusion coefficient in a porous material (Deff) is lower than the diffusion coefficient
in the absence of a porous material (D). The ratio of these diffusion coefficients is called the
diffusibility of porous material.
Q dif = D eff / D
(83)
50
Phase Change Criterion
The phase change criterion εpc is defined as the ratio of the vapor diffusion coefficient Dv
to the coefficient of total moisture diffusion Deff and it has a value between 0 and 1.
ε pc = D v / D eff
(84)
If the diffusion is mainly in the liquid phase inside the material, phase change criterion has a
value around εpc ≈ 0. If the controlling mechanism of diffusion is mainly by water vapor
diffusion, phase change criterion has a value around εpc ≈ 1. Phase change criterion varies
with moisture content, but it is usually taken constant.
Porosity
The porosity of a porous material is defined as the ratio of the total void or pore volume
to the total volume of the material
ψ=
Vvoid
Vtotal
(85)
Porosity
Porosity
Porosity
b
a
Moisture content
Porosity
Porosity is the most important geometrical properties of a porous material and has a direct
effect on the physical properties. Porosity of food materials is within a broad range
(0≤ψ≤0.99). Porosity data for numerous food materials can be obtained from Ref. [25].
Usually, porosity is not measured directly. Instead, it is calculated by Eq. (86) through
measured apparent and substance density. Methods for direct measurement of porosity are
also available such as direct method, gas expansion method and optical method [25]. For
hygroscopic materials, porosity shows a change during the drying process. In many cases,
variation of porosity with moisture content is expressed by empirical correlations. Linear,
exponential and power law equations are most often used equations for this purpose.
The formation of pores in drying has been grouped into two generic types by Rahman
[38]. These types are: pore formation with an inversion point and that without an inversion
point (see figure 12). These models have been suggested based on experimental data available
in the literature. Porosities of most food materials decrease with the increase of moisture content
as in the case shown in figure 12 c.
Moisture content
c
Moisture content
Figure 12. Change of porosity with moisture content (adapted from [38]).
d
Moisture content
51
Apparent Porosity
Apparent porosity is the ratio of total enclosed void volume to the total volume of the
material and is given by:
ψ app = 1 −
ρ app
ρs
(86)
where ρ app is the apparent density (kg/m3) and ρs is the substance density (kg/m3).
Open Pore Porosity
Open pore porosity is the ratio of the volume of pores connected to the outside to the total
volume:
ψ op = 1 −
ρ app
ρp
(87)
where ρ p is the particle density (kg/m3).
Closed Pore Porosity
Closed pore porosity is the difference between apparent porosity and open pore porosity:
ψ cp = ψ app − ψ op
(88)
Permeability
Permeability refers to the resistance of a solid food matrix against the pressure driven
flow (see figure 13) and it is one of the most important physical properties of a porous
medium. If a porous medium is considered as a bundle of tubes of varying diameter
embedded in the solid matrix (see figure 14), permeability can be defined as follows [8]:
K=
1
∑ Δε pi ri2
8τ i
(89)
where τ is the tortuosity, Δε pi is the volume fraction of pores in the ith class with radius ri.
Permeability is related to the hydraulic conductivity KH (m/s) as follows:
52
KH =
ρl g
K
ηl
(90)
where ρl is the density of the liquid water (kg/m3), g is the gravitational acceleration (m/s2)
and ηl is the viscosity of the liquid water (Pa s).
Permeability is a transport parameter depending on material structure and is independent
of fluids flowing along the material. However, in case of a fluid consisting of a liquid and a
gas phase, the permeability will depend on the saturation degree of the porous medium, since
the voids available for each of the fluids change. The liquid, for example, will block pores for
gas transport and, consequently, changes the gas permeability. In order to express models for
the permeabilities for two-phase flow in a porous medium, the overall permeability is divided
into two parts as intrinsic and relative permeability.
Porous, impermeable
Porous, permeable
bili
bili
High porosity, low permeability
Low porosity, high permeability
Figure 13. Permeability and porosity (adapted from [39]).
Figure 14. Idealized porous permeable media as bundle of tubes of varying diameters (adapted from [40]).
~ ~ ~
K = Ki ⋅ kr
(91)
53
where Ki is the intrinsic permeability (m2), which only depends on the geometrical porous
structure; kr is the relative permeability, which depends on the saturation degree of the liquid
used. Permeabilities are generally obtained from experiments in which the flow of a given
fluid is measured as a function of the pressure difference over the relevant sample. In this
way, it is possible to determine intrinsic permeability using dry samples. It is more difficult to
determine relative permeability requiring partially saturated samples [41]. For example, if a
partially saturated sample is exposed to liquid moisture, the sample may be fully saturated.
For determining relative permeabilities of gases drying of the sample must be minimized by
applying highly saturated gas phase. In addition, the strength of the material is equally
important. Since cracks may be formed in a material of low strength, the obtained
permeability values will be useless.
The saturation S takes values in the range 0≤S≤1. In this case, limit values for relative
permeability may be given as follows [41]:
~
~
~
lim k r = 0
~
lim k r = I
S→0
(92)
S→1
Below a certain critical saturation degree, the liquid phase in the pores breaks up into
isolated islands and continuous liquid pathways across the sample no longer exist. This means
that below this critical saturation degree, which is called irreducible saturation degree Sir, the
relative permeability for liquid moisture drops to zero. Thus:
~
~
k rl = 0
for
S ≤ Sir
(93)
Different forms of relations have been suggested for relative permeabilities depending on
the degree of saturation. Among these relations, the following are widely used which assumes
that porous structure is isotropic [41, 42].
⎛ S − Sir
k rl = ⎜⎜
⎝ 1 − Sir
⎞
⎟⎟
⎠
a
⎛ 1− S
k rg = ⎜⎜
⎝ 1 − Sir
⎞
⎟⎟
⎠
b
(94)
where a and b are constants. In some cases Sir is taken equal to zero. Widely used relations in
the form of Eq. (94) for relative permeabilities are as follows [8]:
⎧⎛ S − S ir
⎪⎜
k rl = ⎨⎜⎝ 1 − S ir
⎪
⎩0
⎧1 − 1.1S
k rg = ⎨
⎩0
⎞
⎟⎟
⎠w
⎫
S > S ir ⎪
⎬
⎪
S < S ir ⎭
S < 1 / 1.1⎫
⎬
S > 1 / 1.1⎭
(95)
(96)
These relations are not based on a firm physical basis. Thus, they do not always yield
consistent results with experimental observations.
54
Tortuosity
Tortuosity factor is defined as the ratio between the actual path traveled by a fluid
element between two points divided by the straight line path between the same two points.
τ = L eff / L
(97)
where Leff is the traveled distance through the porous medium and L is the simple orthogonal
distance across the medium. Some prefer to use (L eff / L) 2 and refer to this quantity as
tortuosity.
Tortuosity of porous materials is generally determined experimentally by using different
techniques, such as conductivity and diffusion techniques, the ions transit-time technique and
the pore-distribution technique by using the capillary-pressure curve. It can also be obtained
theoretically by mathematical models.
Using Fick’s first law to describe fluid diffusion through cylindrical paths the following
empirical expression can be obtained [43] for tortuosity factor:
τ = 2.23 − 1.13Vvoid ρ(0.92γ p )1+ n
(98)
where γ is a pore shape factor, ρ is the bulk density of the solid and n is the pore shape factor
exponent. Pore shape factor is defined as
γp =
4Vvoid A p
=
A
Ad
(99)
where A is the total surface area by BET adsorption (m2), d is the average pore diameter (m)
and Ap is the total pore area (m2).
In porous materials, effective diffusivity differs from the theoretical diffusivity by a
factor related to the structure of the solid as follows:
D eff = D the ψ / τ
(100)
where ψ is the porosity and τ is the tortuosity factor. The tortuosity factor lumps all
deviations from straight diffusion paths into a single dimensionless parameter.
Flux and Driving Force
A system not in equilibrium thermodynamically heads towards maximum entropy
irreversibly and tries to achieve equilibrium. Dissipation of driving forces occurs with the flux
toward equilibrium. In mass transport, this is the flux of matter. The flux Ji of a component i
is defined as the mass or the number of moles of i crossing a unit surface area in sec. The flux
55
is obviously related to the velocity of transport. If a mass of concentration Ci is moving with a
velocity vi in a direction perpendicular to a surface, the flux Ji and velocity vi are related by [44]:
J i = v i Ci
(101)
In irreversible processes, a force driving the system to equilibrium is the negative of the
gradient of a potential energy. Driving forces dissipate energy irreversibly and cause fluxes.
Potentials for various types of transport are seen in table 10. When the potentials become
uniform throughout the system, no force exists, and all net fluxes go to zero. The general
equation for the movement of a substance through a medium where there is no absolute
barrier is given by [44]:
J = LΦ
(102)
where J is amount/unit time = flux, (kg or moles)/( sec) per m2 surface area, Φ driving force
and L conductance =1/ resistance = conductance per unit area.
Table 10. Potentials for various types of transport
Process
Heat conduction
Diffusion
Convection
Potential
Temperature
Concentration or Partial Pressure
Total Pressure
Current
Heat
Molecules
Fluid Flow
Dissipation Function
The dissipation function φ is the rate at which internal heat energy is produced. It is equal
to the sum of the products of the fluxes Ji and the driving forces Φi [44]:
φ = ∑ ΦiJi
(103)
i
Velocity and Mass Average Velocity
The velocity of a bulk mixture and of its components due to the diffusion in z direction
can be illustrated as in figure 15.
56
vB
vB-v
v=mAvA+ mBvB
vA
vA-v
z
Figure 15. Velocities due to diffusion (adapted from [45]).
In this figure, v is the mass average velocity, vA-v and vB-v are the diffusional velocities
of components A and B.
In the case of a mixture, the mass and molar bulk velocity can be written as follows:
n )
n C
v = ∑ mi vi = ∑ i vi
i =1
i =1 C
,
n )
n Ĉ
v̂ = ∑ n i v i = ∑ i v i
i =1
i =1 Ĉ
(104)
)
)
where m i and n i are the mass and molar fractions of component i.
Shrinkage
Shrinkage DR (Sb) expresses a relative or reduced dimensional change of volume, area or
thickness and it is often represented by the following way [46]:
Sb = V / Vo
(105)
where V is the volume of the material (m3) and Vo is the initial volume (m3).
Isotropic Shrinkage
Isotropic shrinkage is the uniform shrinkage in all dimensions of the material.
Anisotropic Shrinkage
Anisotropic shrinkage is the nonuniform shrinkage in different dimensions of the
material.
57
4. THERMODYNAMIC EQUILIBRIUM RELATIONSHIPS
For a mixture of n components, the equilibrium between a liquid (l) and its vapor (v) can
be expressed using the chemical potential as:
μˆ li = μˆ vi
i=1,2,..n
(106)
The chemical potential for a pure substance is equal to molar Gibbs function of a phase
ĝ (J/mol). The equilibrium can then be expressed as follows [47]:
ĝ l = ĝ v
(107)
The differential of a chemical potential for a single phase of a pure substance can be written
as [47]:
)
dĝ = −ŝdT + υˆ dP + μˆ dn − dw σ
(108)
)
where ŝ is the molar entropy (J/(mol K)), υ̂ is the molar volume (m3/mol), n is the molar
fraction and dw σ is the amount of work made by the surface tension to extend the phase
separation surface (J/mol). If the phase interface is assumed to have a constant area and the
molar fraction to be constant, Eq. (108) becomes as follows:
dĝ = −ŝdT + υˆ dP
(109)
Since dμˆ l = dμˆ v and thermodynamic equilibrium requires thermal equilibrium:
− ŝ l dT + υˆ l dPl = −ŝ v dT + υˆ v dPv
(110)
Clapeyron-Clasius Equation
The Clapeyron–Clausius equation can be obtained from Eqs. (106-110) if at equilibrium
on a flat interface the pressures are equal ( Pv = Pl = P ) and the system has only one degree of
freedom (Gibbs rule applied to a phase change) [47].
dP ŝ v − ŝ l
=
dT υˆ v − υˆ l
The enthalpy of evaporation Δĥ vap (J/mol) is equal to T(ŝ v − ŝ l ) . Therefore:
(111)
58
Δĥ vap
dP
=
dT T(υˆ v − υˆ l )
(112)
This equation is known as Clapeyron-Clasius equation that can be applied to a phase change
of a pure vapor at a constant temperature and pressure. If the specific volume of the liquid
water is negligible with respect to that of the vapor and the specific volume of vapor can be
expressed by the ideal gas law, Eq. (112) becomes as follows [47]:
dP Δĥ vap PΔĥ vap
≈
=
dT Tυˆ v
R̂T 2
or
d ln P Δĥ vap
=
dT
R̂T 2
(113)
Kelvin Equation
From the definition of capillary pressure, the following equation can be written:
dPc = dPv − dPl
(114)
Liquid and the vapor phase are both governed by a Gibbs-Duhem equation [47]:
ŝ l dT − υˆ l dPl + dμˆ l = 0
ŝ v dT − υˆ v dPv + dμˆ v = 0
(115)
If the temperature is assumed to be constant and we use Eq. (106), Eq. (115) becomes:
υˆ l dPl = υˆ v dPv
(116)
If Eq. (116) is substituted into Eq. (114):
dPc =
υˆ l − υˆ v
dPv
υˆ l
(117)
Assuming that the vapor obeys to the ideal gas law:
dPc = dPv −
R̂T dPv
υˆ l Pv
(118)
If Eq. (118) is integrated from Pc=0 and Pv=Pvo to Pc, Pv and we assume that the molar volume
for the liquid water is constant:
Pc = (Pv − Pvo ) −
R̂T ⎛ Pv
ln⎜
υˆ l ⎜⎝ Pvo
⎞
⎟⎟
⎠
(119)
59
If the molar volume of the liquid is negligible with respect to that of the vapor (i.e., the vapor
pressure is not too high), the first term on the right hand side of Eq. (119) can be omitted [47].
Therefore:
Pc = −
R̂T ⎛ Pv ⎞
⎟
ln⎜
υˆ l ⎜⎝ Pvo ⎟⎠
(120)
Equation (120) is known as Kelvin’s equation.
Equilibrium between Water and Moist Air
Both the Clapeyron-Clasius and Kelvin equations are valid only for pure water. For the
case of a liquid in equilibrium with a mixture of ideal gases with a total pressure Pg, the
following relation can be written instead of Eq. (119):
Pc = (Pg − Pgo ) −
R̂T ⎛ Pv ⎞
⎟
ln⎜
(121)
Because of the equilibrium between water and moist air, the total gas pressure can be
considered to be constant. Therefore:
Pc = −
R̂T ⎛ Pv ⎞
⎟
ln⎜
(122)
Furthermore, since the molar volume of the liquid phase is much smaller than that of the
vapor, the influence of the gas pressure on the vapor tension of the liquid Pvo can be
neglected. In this case, Pv has the meaning of the partial pressure in the gas mixture and Pvo of
the vapor tension of the liquid for a flat surface when Pc=0 [47].
5. DRYING KINETICS OF FOOD MATERIALS
The drying process of food materials has a typical character (see figure 16 ). Drying rate
displays differences at certain periods during drying. In the beginning, the temperature adjusts
itself until reaching a steady state. This period is usually quite short and it is generally ignored
in the drying models. After this period, it is entered a period in which the drying rate remains
constant. This period is called constant rate period. In this period, the temperature of wet solid
surface is the same as the wet bulb temperature of the drying air. The moisture level at the
end of constant rate period is called the critical moisture content. If the material has lower
moisture content than the critical moisture content, a decrease is observed in the moisture
transfer from the material. This period is called falling rate period. In the falling rate period,
60
the surface temperature rises. In many food materials the falling rate period has several
stages. These stages are called first falling rate period, second falling rate period and so on.
m A
mc
dm
dt
B
C
B
A
dm
dt
C
T
C B
A
D
D
E
D
B C
D
E
m
E
E
t
t
mc
m
A
t
Figure 16. Characteristic drying, drying rate and temperature curves for hygroscopic materials.
In figure 16; A-B is the heating period, B-C is the constant rate period of drying, C is the
critical moisture content, C-D is the first falling rate period, D-E is the second falling rate
period.
Drying in the Constant-Rate Period
In the constant rate drying period, the surface of the solid is very wet and a continuous
film of water exists on the drying surface. This water is entirely unbound water and acts as if
the solid are not present. The rate of evaporation under the given air condition is independent
of the solid and is essentially the same as the rate from a free liquid surface. Increased
roughness of the solid surface, however, may lead to higher rates than from a flat surface. The
drying rate in the constant rate period is determined by conditions external to the material
being dried including temperature, air humidity, flow, area of material surface, and pressure.
The water evaporated in the constant-rate period is supplied from the interior of the material.
This period continues as long as the water is supplied to the surface as fast as it is evaporated.
Evaporation during this period is similar to that in determining the wet bulb temperature, and
in the absence of heat transfer by radiation or conduction, the surface temperature is
approximately that of the wet bulb temperature [1].
If it is assumed that the heat transfer to the material surface is only by convection and the
mass transfer from the surface to the drying medium, the mass and heat transfer for the
constant-rate period can be expressed as:
J m = h m (ωS − ω)
(123)
J q = h q (T − Twb )
(124)
where Jm is the total mass flux (kg/(m2s)), Jq is the total heat flux (J/(m2s)), hm is the mass
transfer coefficient (kg/(m2s)) and hq is the heat transfer coefficient (W/(m2K)). ωS is the
moisture content of the air in equilibrium with the surface of the product (kg moisture/kg dry
61
air), ω is the moisture content of the bulk air (kg moisture/kg dry air), T is the drying
temperature (°C) and Twb is the wet bulb temperature (°C).
Drying in the Falling-Rate Period
Constant rate period is followed by the falling rate period. Critical moisture content is
between these two drying rates. The critical moisture content is the minimum moisture
content that will sustain a rate of flow of free water to the surface of the solid equal to the
maximum rate of removal of water vapor from the solid under the drying conditions [1]. Point
C in figure 16 is at the critical free moisture content. At this point, there is insufficient water
on the surface to maintain a continuous film of water. The entire surface is no longer wetted,
and the wetted area continually decreases in this first falling period rate until the surface is
completely dry at point D in figure 16. In the falling rate period, the rate of internal mass
transfer to the material surface controls the drying process.
Controlling Resistance
The drying process may be divided in three different categories, namely, externally
controlled drying, internally and externally controlled drying and internally controlled drying.
The category in which a considered drying process is included is estimated by the Biot
number for the mass transfer, which is the ratio of external mass transfer to internal mass
transfer. The drying process of food materials can be classified as externally controlled when
Bi<0.1, the process is both internally and externally controlled when 1<Bi<100 and the
drying process is purely internally controlled when Bi>100. In externally controlled drying
processes, the mass transfer inside the material is neglected, and it is assumed that the water
content inside the material is uniform. In the case that the drying process is partly or fully
internally controlled the profiles of water content is nonuniform inside the material. The
moisture content gradients are higher when Bi is larger or the evaporation rate from the
surface is greater. In food materials, the constant rate period is very rarely observed due to the
high critical moisture content of most of the foods.
Similar to the Biot number for mass transfer, the Biot number for heat transfer can be
used for predicting which resistance, convection or conduction, dominates the heat transfer. A
large Biot number (Bi>100) indicates that the conductive resistance controls the heat transfer.
In this case, it is easier for heat to leave the surface by convection than to reach it by
conduction. Under this condition, large temperature gradients within the solid exist. A small
Biot number (Bi<0.1) represents the case where conduction resistance is negligible and the
temperature gradient within the solid is quite small. For values between 0.1 and 100, both
internal and external resistance to heat transfer should be taken into account.
62
6. TRANSPORT PHENOMENA
In porous materials, mass and heat transfer may occur in quite a number of varying
mechanisms (see table 11 and figure 17). Drying is generally composed of a series, parallel
and/or series-parallel combination of these mechanisms. Dominant mass transfer mechanism
is capillary flow for materials with large water content. On the other hand for materials with
low moisture content diffusion in the vapor phase is dominant mechanism. In some cases, a
considerable amount of evaporation and a consequential pressure rise may occur. In this case,
the dominant mass transport mechanism may be hydrodynamic flow.
Poiseuille Flow
Knudsen Diffusion
T2
T1
T1<T2
Condensation-Evaporation
Molecular Diffusion
h
Stefan Diffusion
Surface Diffusion
Capillary Flow
Figure 17. Various mass transport mechanisms in a porous material (adapted from [9]).
Table 11.The heat and mass transport mechanisms in a porous material
Gas Transport
Transport Mechanism
Cause and Potential of Transport
Knudsen Diffusion
concentration or pressure
Slip Flow
total pressure
Poiseuille Flow
total pressure, gravity
Molecular Diffusion
concentration or partial pressure
63
Table 11. (continued)
Liquid Transport
Heat Transport
Transport Mechanism
Cause and Potential of Transport
Stefan Diffusion
partial pressure
temperature, …
Molecular Diffusion
concentration
Capillary Flow
capillary force
Surface Diffusion
concentration
Hydrodynamic Flow
total pressure, gravity
Heat Conduction
temperature
Heat Radiation
temperature in 4th power
Air Flow
total pressure, density differentials
Enthalpy Flow
moisture movement
GAS TRANSPORT MECHANISMS
Molecular mass transfer processes in which molecules move under a concentration
gradient or a partial pressure gradient are called diffusion processes. If the molecules move
under a total pressure gradient, transfer is called bulk mass transfer. Mass transfer mechanism
in gas phase varies depending on the nature of momentum transfer occurring due to molecular
collisions, which generally are of two types. Collisions between molecules are referred to as
intermolecular collisions and collisions between molecules and pore walls are referred to as
molecule wall collisions. The type of collision depends on the length of the mean free path
relative to the diameter of the tube. The mean free path length λ is the average distance
traveled by a molecule between two successive collisions. The mean free path length λ
depends on the gas type, the temperature and the mean pressure and is determined with the
following equation [48, 49]:
λ=
ηg
Pg
πR̂T
2
(125)
where ηg is the dynamic viscosity of gas (Pa s), Pg is the mean gas pressure (Pa), R̂ is the
ideal gas constant (J/(mol K)), T is the temperature (K). For vapor and air at atmospheric
pressure and room temperature, the mean free path length is of the order magnitude of 5x10-8
m [50]. The ratio between the mean free path and the pore diameter is called the Knudsen
number.
Kn =
λm
d
(126)
Mass transfer mechanisms according to the value of Knudsen number are given in table 12.
When the value of Knudsen number is much less than unity, the probability of intermolecular
64
collisions is much greater that that of molecule-wall collisions. In this case, if a total pressure
gradient exists, there will be a viscous flux. If a partial pressure gradient exists, then the
collisions between the molecules in the mixture will result in molecular diffusion. When
Knudsen number is much larger than unity, molecule-wall collisions reach to much more
significant levels. In this case, mass transfer occurs with Knudsen diffusion. Since Knudsen
diffusion is not affected by the existence of any other gas, both total pressure gradient in a
single phase system and partial pressure gradient in a multicomponent system result in
Knudsen diffusion. When the Knudsen number has the value around 1, intermolecular
collisions and molecule-wall collisions are at comparable levels. In this case, two different
flow regimes are available, which are not new mechanisms but transitions between the
mechanism described above. The transition between Knudsen diffusion and viscous flux is
called slip flux. And the transition between Knudsen diffusion and molecular diffusion is
called transition diffusion.
Table 12. Various gas transport mechanisms based
on the Knudsen number (adapted from [50])
Knudsen Number
Kn<<1
Kn ≅ 1
Kn>>1
Total Pressure Gradient
Viscous Flux
Slip Flux
Knudsen Diffusion
Partial Pressure Gradient
Molecular Diffusion
Transition Diffusion
Knudsen Diffusion
Knudsen or Free Molecule Diffusion
Since porous materials have irregularly shaped pores, it is difficult to describe mass
transfer from them. A single capillary tube is generally considered to obtain a basic model.
The Knudsen diffusion between two points in a capillary tube is defined as:
Ĵ mz = w p v z (Ĉ g 2 − Ĉ g1 )
(127)
where Ĵ m is the molecular flux (mol/(m2s)), wp is a dimensionless probability factor, v z is
the mean molecular speed (m/s) and Ĉ g is the molar concentration (mol/m3). The mean
molecular speed can be calculated from the kinetic theory of gases as:
vz =
8R̂T
πM̂ g
(128)
where R̂ is the gas constant (8.3143 J/(mol K)), T is the temperature (K) and M̂ g is the
molecular mass of gas (kg/mol). Calculation of probability factor wp is much more complex.
The value of the probability factor is known for some simple geometries. For a long straight
circular tube of radius r and length L, wp is 2r/(3L). In this case, Eq. (127) may be expressed
as follows:
Ĵ mz =
2rp
3L
8R̂T
(Ĉ g 2 − Ĉ g1 )
πM̂ g
65
(129)
Eq. (129) can be written in differential form as:
Ĵ mz = −
2rp
3
8R̂T dĈ g
πM̂ g dz
or
Ĵ mz = D k ,sp
dĈ g
dz
(130)
where D k ,sp is the Knudsen diffusion coefficient for a single pore and is proportional to the
pore radius and the mean molecular velocity.
The Equation (130) is valid for a circular tube. For different geometries, an equation in
the same form can be obtained but with different geometrical parameters. For this reason a
general equation is defined using a Knudsen coefficient Ko (m). Knudsen diffusion coefficient
Dk,sp (m2/s) is related to Knudsen coefficient Ko as.
D k ,sp =
4
K o vz
3
(131)
Considering transfer in all directions, Knudsen diffusion in a porous material may be
expressed as follows:
r
r
Ĵ m = D k ∇Ĉ g
or
r
r
J m = D k ∇C g
(132)
Knudsen diffusion coefficient for porous materials is generally determined
experimentally. It can also be determined by the following equation by means of the diffusion
coefficient of the single pore:
Dk =
ψ
D k ,sp
τ
(133)
where ψ and τ are the porosity and tortuosity factor.
Slip Flux
Slip flux is a transition regime between viscous flux and Knudsen diffusion. In this
regime, there exists a partial interaction among molecules. Momentum loss resulting from
molecule-wall collision is not fully transferred to the rest of the fluid. For this reason, the
velocity of gas stream does not approach to zero when it approaches to the wall. In other
words, the Hagen-Poiseuille equation, which assumes a zero wall velocity, is no longer valid.
Gas flows like it is slipping at the wall, so there appears a positive velocity along the wall.
66
To simplify the derivation of transport equations for slip flux, the following assumptions
can be made. Flow is isothermal and is at steady regime, bulk viscosity effects are negligible,
there is not external force except the gravitational force and the change of convected
momentum is negligible. In addition, it can be assumed that the axial velocity is more
strongly dependent to radial coordinate compared to axial coordinate. Therefore, the NavierStokes equation takes the following form for a long cylindrical capillary [51]:
−
dPg
dz
+
dΨg
dz
+ ηg
1 d ⎛ dv z ⎞
⎜r
⎟=0
r dr ⎝ dr ⎠
(134)
where Pg is the gas pressure (Pa), ηg is the dynamic viscosity of gas (Pa s), Ψg is the gravity
potential of gas (m2/s2), vz is the axial velocity (m/s) and r and z are the radial and axial
coordinates, respectively. Integrating Eq. (137) yields:
vz = −
1
ηg
⎛ dPg dΨg ⎞ r 2
⎟
⎜
⎜ dz − dz ⎟ 4 + c 2
⎠
⎝
(135)
When the Maxwell slip boundary condition given below is applied.
r = rp
v z = −G
dv z
dr
(136)
Equation (135) becomes:
vz = −
1
4η g
⎛ dPg dΨg
⎜⎜
−
dz
⎝ dz
⎞ 2
⎟⎟(rp − r 2 + 2Grp )
⎠
(137)
where rp is the radius of capillary (m). The total volumetric flow rate Q vol (m3/s) can then be
written as:
rp
Q vol = 2π ∫ v z rdr = −
0
πrp2 ⎛ dPg dΨg ⎞ 2
⎟ rp + 4Grp
⎜
−
8ηg ⎜⎝ dz
dz ⎟⎠
(
)
(138)
The average velocity over the cross section can be expressed as:
rp2
Q vol
vz = 2 = −
8ηg
πrp
⎛ dPg dΨg ⎞⎛
4G ⎞⎟
⎜⎜
⎟⎟⎜1 +
−
dz ⎠⎜⎝
rp ⎟⎠
⎝ dz
where G is the slip modulus defined as:
(139)
1/ 2
ηg ⎛ 8R̂T ⎞⎟
G ≈ 1.19 ⎜
Pg ⎜⎝ πM̂ g ⎟⎠
=
2ηg
Pg rp
Ko
67
(140)
where Ko is the Knudsen coefficient (m) and can be defined as:
Ko=0.89Dk
(141)
where Dk is the Knudsen diffusion coefficient (m2/s). The factor 0.89 comes fitting to the
experimental data [51]. If Eq. (140) is substituted into Eq. (139), one can find:
⎛ rp2
K ⎞⎛ dPg dΨg
−
v z = −⎜
+ o ⎟⎜⎜
⎜ 8ηg Pg ⎟⎝ dz
dz
⎠
⎝
⎞
⎟⎟
⎠
(142)
A general form of Eq. (142) can be written as:
⎛B
K ⎞⎛ dPg dΨg ⎞
⎟
−
v z = −⎜ k + o ⎟⎜⎜
⎜ ηg
Pg ⎟⎠⎝ dz
dz ⎟⎠
⎝
(143)
where Bk (m2) is a viscous flow parameter evaluated for the mean pore radius of the porous
medium. Bk is more commonly known as permeability (Kg) and is generally obtained from
experiments. Equation (143) can be written in vectorial form as:
r
⎛ Kg Ko ⎞ r
r
⎟( ∇Pg − ∇Ψg )
v z = −⎜
+
⎜ ηg
Pg ⎟⎠
⎝
(144)
Molar flux Ĵ m (mol/(m2s)) can then be expressed as follows:
r
r
⎞ r
Pg
r
1 ⎛⎜ K g
Ĵ m = v g Ĉ g = v g
Pg + K o ⎟( ∇Pg − ∇Ψg )
=−
⎟
R̂T
R̂T ⎜⎝ ηg
⎠
(145)
Multiplication by the molecular weight of gas gives the result in (kg/(m2s)).
r
r
⎞ r
M̂ g ⎛ K g
⎜
Jm = −
Pg + K o ⎟( ∇Pg − ∇Ψg )
⎟
⎜
R̂T ⎝ ηg
⎠
(146)
Flux equation may alternatively be defined as follows:
r
r
r
Pg M̂ g
Jm = −
K g 1 + b K / Pg ( ∇Pg − ∇Ψg )
R̂Tηg
(
)
(147)
68
r
r
r
Pg M̂ g
Jm = −
K app ( ∇Pg − ∇Ψg )
R̂Tηg
(148)
where Kapp is the apparent gas permeability K app = K g (1 + b K / Pg ) , and bK is the Klinkenberg
parameter (Pa), which depends on the geometry of the pore spaces. By plotting Kapp as a
function of 1 / Pg , bK and the Kg can be determined from the slope and the intercept,
respectively.
Viscous Flux
Collision of molecules with the wall causes gas molecules to lose momentum. The loss of
momentum in gas molecules adjacent to the wall is transferred to other molecules through
intermolecular collisions. This leads to a decrease in molecule flow rates from the wall
towards the tube center. If the gas flow is laminar, the momentum exchange results in a
smooth velocity profile. This flow regime is called viscous flow regime.
The viscous flow is described by the Navier-Stokes equation. The derivation of the
transport equation is quite similar to that of slip flux. The only difference is due to boundary
condition. Similar to those for the slip flux, it can be assumed that the flow is isothermal and
is at steady regime, bulk viscosity effects are negligible, there is no external force except the
gravitational force, change of convected momentum is negligible and axial velocity is more
strongly dependent on radial coordinate compared to the axial coordinate. In this case, the
Navier-Stokes equation takes the following form for a long cylindrical capillary:
−
dPg
dz
+
dΨg
dz
+ ηg
1 d ⎛ dv z ⎞
⎜r
⎟=0
r dr ⎝ dr ⎠
(149)
where Pg is the gas pressure (Pa), ηg is the dynamic viscosity of gas (Pa s), Ψg is the gravity
potential of gas (m2/s2), vz is the axial velocity (m/s) and r and z are the radial and axial
coordinates, respectively. Integration of Eq. (149) yields:
vz = −
1
ηg
⎛ dPg dΨg ⎞ r 2
⎟ + c2
⎜⎜
−
dz ⎟⎠ 4
⎝ dz
(150)
No-slip condition is valid on the surface for viscous flow:
r = rp
vz = 0
where rp is the radius of capillary (m). Therefore Eq. (150) becomes as follows:
(151)
vz = −
1
4η g
⎛ dPg dΨg ⎞ 2
⎜⎜
⎟⎟(rp − r 2 )
−
dz
dz
⎝
⎠
69
(152)
The total volumetric flow rate Q vol (m3/s) can then be written as:
Q vol =
π rp4 ⎛ dPg dΨg ⎞
⎜
⎟
−
8ηg ⎜⎝ dz
dz ⎟⎠
(153)
where Qvol is the volumetric flow rate (m3/s), rp is the capillary radius (m), ηg is the dynamic
viscosity (Pa s) Pg is the pressure (Pa). This equation is known as Hagen-Poiseuille equation.
The average velocity over the cross section can be defined as:
vz =
rp2
Q vol
=
−
8ηg
πrp2
⎛ dPg dΨg
⎜⎜
−
dz
⎝ dz
⎞
⎟⎟
⎠
(154)
A general form of Eq. (154) can be expressed as:
vz = −
Bk
ηg
⎛ dPg dΨg
⎜⎜
−
dz
⎝ dz
⎞
⎟⎟
⎠
(155)
where Bk (m2) is a viscous flow parameter evaluated for the mean pore radius of the porous
medium. Bk is generally determined experimentally and is more commonly known as the
permeability Kg.
vz = −
K g ⎛ dPg dΨg ⎞
⎟
⎜
−
ηg ⎜⎝ dz
dz ⎟⎠
(156)
Equation (156) can be written in vectorial form as:
r
Kg r
r
vz = −
( ∇Pg − ∇Ψg )
ηg
or
r
K i k rg r
r
vz = −
( ∇Pg − ∇Ψg )
ηg
(157)
This equation is known as Darcy equation. Molar and mass flux equations may then be
expressed as follows:
r
r
Pg
K i k rg Pg r
Ĵ m = v g Ĉ g = v g
=−
( ∇Pg − ∇Ψg )
ηg R̂T
R̂T
(158)
70
r
r
K i k rg M̂ g Pg r
J m == −
( ∇Pg − ∇Ψg )
ηg
R̂T
(159)
Molecular Diffusion
Molecular diffusion means the relative motion of different species of a mixture according
to each other under concentration gradient. For a binary mixture, the diffusive fluxes of
species can be written according to the Fick’s first law as:
r
r
J mA = −D gAB∇C gA
r
r
J mB = −D gAB∇C gB
(160)
r
where J m is the mass flux vector (kg/(m2s)) and Cg is the concentration of diffusing
substance (kg/m3). Dg is the gas diffusion coefficient (m2/s) and it describes the transfer rate
of diffused gas with random molecular motion. In a two component system, satisfying the
condition of zero volume change on mixing, the diffusion coefficient of each component is
equal, i.e. DgAB=DgAB. Therefore the behavior of the system can be described in terms of a
single diffusion coefficient Dg.
The free gas diffusion coefficient Dg,free in a binary gas mixture at low to moderate
pressures can be accurately predicted using the kinetic theory. The following semi-empirical
equation has been proposed by Gilliland [52]:
D g ,free = 4.3x10 −3
T3/ 2
1
1 1/ 2
(
+
)
Pg (υˆ + υˆ 1gB/ 3 ) 2 M̂ gA M̂ gB
1/ 3
gA
(161)
where D g ,free is the diffusion coefficient (cm2/s), T is the temperature (K), Pg is the pressure
of the gas mixture (bar), M̂ gi is the molecular mass of gas i (g/mol), and υ̂gi is the molar
volume of gas i (cm3/(g mol)). As it can be seen from Eq. (161) that the gas diffusion
coefficient in a binary mixture is inversely proportional to the pressure of the gas mixture.
Another equation predicting the diffusion coefficient more accurately has been proposed
by Fuller et. al. [53] as follows:
D g ,free = 1.01x10 −3
[
Pg (∑ ϑ
T1.75
)
1/ 3
a gA
+ (∑ ϑ
)
]
1/ 3 2
a gB
(
1
1 1/ 2
+
)
M̂ gA M̂ gB
(162)
where D g ,free is the diffusion coefficient (cm2/s), T is the temperature (K), Pg is the pressure
(bar) and M̂ g is the molecular mass (g/mol). The diffusion volume ∑ ϑ a is the sum of the
atomic volumes for all the atoms in each molecule. These atomic parameters are determined
by a regression analysis of many experimental data. Equation (162) usually gives results
within four percent of experimental data when water is the solvent [54].
71
Another way to predict the diffusion coefficient for gases is to take into account the
forces acting between molecules. Hirschfelder et al. [55] derived the following equation for
diffusivity for non-polar gases using the Lennard-Jones potential, which describes the
attractive and repulsive forces between atoms.
D g ,free = 1.88x10 −3
T3/ 2
1
1 1/ 2
(
+
)
Pg L2 Ω D M̂ gA M̂ gB
(163)
where D g ,free is the diffusion coefficient (cm2/s), Pg is the pressure (bar), M̂ g is the molecular
o
mass (g/mol) and L is the characteristic length ( A ) and ΩD is the diffusion collision integral,
which is dimensionless. The characteristic length in Eq. (163) may be estimated as:
L=
L1 + L 2
2
(164)
where L1 and L2 are the characteristic lengths of gas species in the mixture. The diffusion
collision integral can be determined approximately by the following equation [56, 57]:
Ω D = (1.06036T ′) −0.1561 + 0.193 exp(−0.47635T ′) +
1.03587 exp(−1.52996T ′) + 1.76474 exp(−3.89411T ′)
(165)
where
T′ =
σbT
E
1/ 2
⎛E
E ⎞
E = ⎜⎜ c1 + c 2 ⎟⎟
⎝ σB σB ⎠
(166)
where σ b is the Boltzmann constant (1.3805x10-23 J/K), T is the temperature (K), Ec1 and Ec2
are the characteristic energies of gas species (J).
The gas diffusion coefficient through the porous medium is usually related to the free gas
diffusion coefficient in an open space as follows:
Dg =
ψ
D g ,free
τ
(167)
where ψ and τ are the porosity and the tortuosity factor.
Stefan Diffusion
Diffusion of water vapor through a layer of stagnant air is called Stefan diffusion. This
type of diffusion is encountered during evaporation of water from a wet surface to bulk air.
Water and water vapor are present at the same time in a system. The quantity of vapor
72
increases in time due to water evaporating in the vicinity of water and gas interface. This
results in an increase in the absolute pressure in the vicinity of gas and liquid phase interface.
The absolute pressure gradient causes water vapor to move away from the interface. The real
flux of water vapor is then higher than it would correspond to the gradient of its partial
pressure [58]. Since the process is relatively slow, the physical situation may be simplified
assuming that absolute pressure remains constant ( P = Pv + Pa =constant). In this case, total
air flux in the vicinity of liquid surface must be equal to zero. Otherwise, there would be an
increase in total pressure due to the increase in the quantity of air in the vicinity of the
interface. While water vapor moves away from the interface, the air flows towards the
interface according to its concentration gradient. Since the pressure is constant, this should
lead to the flow of water vapor and air mixture from the interface with convection.
Flux for vapor and air can be expressed as [58]:
r
r
r
J mv = − D va ∇ρ v + ρ v v
(168)
r
r
r
J ma = −D av ∇ρ a + ρ a v
(169)
where D is the diffusion coefficient (m2/s), ρ is the concentration (kg/m3), and v is the
velocity (m/s). In Equations (168) and (169), the first terms represent the flux arising from
diffusion and the second terms represent the flux due to convection. Under assumptions
P=constant and T=constant, it follows from the ideal gas law that
ρg =
M̂ g Pg
R̂T
=constant
(170)
where M̂ g is the molar mass of the vapor air mixture (kg/mol), R̂ is the gas constant (8.314
J/(kg K)) and T is the temperature (K). Therefore:
ρ v + ρ a = ρ g =constant
(171)
r
r
∇ ρ v = −∇ ρ a
(172)
and
For the diffusion coefficients, we can write Dva=Dav. The velocity of the mixture can then
be written from Eq. (169) as:
vg =
D av r
D va r
∇ρ a =
∇ρ v
ρa
ρg − ρ v
If Eq. (173) is substituted into Eq. (168), we have
(173)
r
r
J mv = − D va ∇ρ v − D va
r
r
J mv = −D va ∇ρ v (1 +
ρv r
∇ρ v
ρg − ρ v
ρg r
ρv
) = −D va
∇ρ v
ρg − ρv
ρg − ρ v
73
(174)
(175)
Using ideal gas law, the following relations can be written for water vapor and water vaporair mixture:
ρv =
M̂ v Pv
ρg =
M̂ g Pg
R̂T
R̂T
for water vapor
(176)
for water vapor-air mixture
(177)
Assuming M̂ v ≈ M̂ g yields:
r
Pg r
M̂
J mv = − D va v
∇ρ v
R̂T Pg − Pv
(178)
Equation (178) is valid for diffusion of water vapor in the air. To express diffusion in porous
materials, Krischer [59] proposed introduction of a factor called resistance factor.
r
Pg r
D M̂
J mv = − va v
∇Pv
ζ R̂T Pg − Pv
(179)
where ζ (>1) is the diffusion resistance factor and describes the decrease of the vapor flow in
the solid in comparison with that in stagnant gas.
Diffusive transport of water vapor can be obstructed by the presence of liquid islands in
the pore throats. However, under a thermal gradient, a vapor pressure gradient develops in the
gas phase and causes water to evaporate from one side of the liquid island, and diffuse in the
gas phase to a liquid island of lower temperature where it condenses. The evaporationcondensation process repeats itself on the other side of the liquid island.
Heat and mass balance equations for this kind of transport was first expressed by Henry
[60] assumed that moisture migrates entirely in the gaseous phase and that the continuous
network of spaces included in the solid, the amount of vapor in the solid varies linearly with
74
the concentration of vapor and temperature, and the diffusion coefficient is constant. In this
case, the balance equations can be written as follows:
Mass Balance
The net amount of water entering an element by diffusion equals to the increase in
moisture in the air and the increase in moisture in the solid.
∂C v
∂m
+ (1 − ε a )ρ s
(180)
∂t
∂t
where εa is the volume fraction of air in pores, b is a factor taking into account the tortuosity
of the diffusion path, Dv is the vapor diffusion coefficient (m2/s), Cv is the vapor
concentration (kg/m3), ρs is the solid concentration (kg/m3) and m is the moisture content in
dry basis ( kg water/kg dry solid).
ε a bD v ∇ 2 C v = ε a
Energy Balance
The increase in the heat content of the solid equals to the amount of heat entering by
conduction and the heat involved in the desorption (or absorption) of water by solid:
ε a ρs C P
∂T
∂m
= λ∇ 2 T − q vol
∂t
∂t
(181)
where CP is the specific heat capacity (J/(kg K)), λ is the heat conductivity (W/(m K), qvol is
heat involved in the desorption (or absorption) of water by solid (J/m3).
The mass and energy balance equations can be written in more compact form as follows [21]:
γ
∂C
∂m
= D1v ∇ 2 C v − v
∂t
∂t
δ
∂m
∂T
2
= D11
v∇ T−
∂t
∂t
(182)
where
γ=
λ
1 − εa
q vol
, D11
ρ s , D1v = bD v , δ =
v =
ε a ρs C P
ε a ρs C P
εa
LIQUID TRANSPORT MECHANISMS
Molecular Diffusion
Molecular diffusion of fluids is defined by Fick’s first law as in gases.
(183)
r
r
J ml = − D l ∇C l
75
(184)
r
where J ml is mass flux vector (kg/(m2s)), Cl is concentration of diffusing substance (kg/m3)
and Dl is the liquid diffusion coefficient (m2/s). Liquids have strong intermolecular forces.
However, they are not ordered as atoms and molecules in a solid. Therefore, describing the
liquid state quantitatively is more difficult. Three different approaches are available for the
prediction of diffusion coefficient in fluids. These are: hydrodynamical theory, quasicrystalline theory, and fluctuation theory. The most commonly used one is the hydrodynamical theory, which relates diffusion to the viscosity of liquid movement. Stokes
described the force acting on an atom and Einstein proposed the following equation relating
the diffusion coefficient to the mobility of the atom [54]:
D lAB =
σbT
6π r ηlB
(185)
where σb is the Boltzmann’s constant (1.3805x10-23 J/K), r is the radius of the spherical solute
(m) and ηl is the viscosity of the solvent (Pa s). This model has many drawbacks because of
its simplifications of molecular interaction, but it does predict diffusion coefficients within an
order of magnitude [61, 62].
Another correlation, which is widely used for diffusion coefficient is the Wilke-Chang
equation, which is, in essence, an empirical modification of the Stokes-Einstein relation given
in Eq. (185):
D lAB =
7.4x10 −8 (ξ B M̂ lB )1/ 2 T
ηlB υˆ 0lA.6
(186)
where DlAB (cm2/s) is the diffusion coefficient of solute A at very low concentrations in
solvent B, M̂ lB is the molecular mass of solvent B (g/mol), T is the temperature (K), ηlB is
the viscosity of solvent B (cP) and υ̂lA is the molar volume of solute A at its normal boiling
temperature, (cm3/g mol) and ξB is the association factor of solvent B, dimensionless. The
association factor takes values in the range from 1.0 to 2.6 and accounts for interactions of the
solvent. The factor is 1.0 for non-polar solvents, 1.5 for ethanol, and 2.6 for water [62]. This
correlation usually gives results within ten percent of experimental data when water is the
solvent. The error increases slightly when using organic solvents and is not suited for
predicting diffusivity when water is the solute [62, 63].
The Wilke-Chang equation does not give accurate results for concentrated solutions.
Vignes [64] states that this is because of the fact that most concentrated solutions are nonideal. Therefore, Leffler and Cullinan [65] included the changes in viscosity at different
concentrations resulting in Eq. (187):
) ⎛
∂ ln γ lA ⎞
⎟
D lABηlm = (D olABηlm )(D olABηlA ) n A ⎜⎜1 +
∂ ln x A ⎟⎠
⎝
(187)
76
where D oAB (cm2/s) is the diffusion coefficient, independent of concentration, ηlm is the
)
viscosity of the mixture (cP), n A is the mole fraction, γ is the activity coefficient. If viscosity
data are known for the mixtures and the individual components, the Lefler and Cullinan
equation gives accurate predictions for the diffusion coefficients in concentrated solutions.
Capillary Flow
Capillarity refers to the flow of a liquid through the voids and over the surface of a solid
due to molecular attraction between the liquid and solid. This form of transport was first
analyzed by Buckinghan [66], who suggested capillary potential ΨH (m) as driving force for
unsaturated capillary flow. Depending on capillary potential, mass flux is expressed as:
r
r
J m,vol = −K H ∇ΨH
(188)
r
where J m,vol is the volumetric flux (or specific charge) (m3/(m2s)) and KH is the hydraulic
conductivity (m/s). Under isothermal conditions, capillary potential is usually assumed to be
proportional to the gradient of moisture concentration. In this case, mass flux may be defined
as follows:
r
r
J m = − K l ρ s ∇m
(189)
where Kl is the liquid conductivity (m2/s) and it is defined as:
Kl =
σ cos θ r1 2
∫ r f (r )dr
4ηl r 2 f (r ) ro
(190)
where σ is the surface tension (N/m), f(r) is the differential curve for distribution of pore sizes
by radius r, ro and r1 are the minimum and maximum values of radii of capillaries (m), ηl is
the dynamic viscosity of liquid water (Pa s).
Surface Diffusion
Hill [67] regarded the surface diffusion phenomenon as a random walk process of the
molecules on a solid surface. When a molecule adsorbs onto a surface, it tends to sit at the
bottom of the potential well of the underlying solid. These minima correspond to potential
adsorption sites. The possible adsorption sites vary from one adsorption system to another.
The case EA> ES>ET can be chosen as the basis for the surface diffusion phenomenon, where
EA (J/mol), ES (J/mol) and ET (J/mol) are the potential barrier among adsorption sites, the
differential heat of adsorption, and the thermal motion of molecules, respectively. When
EA< ES surface flow does not take place. When an adsorbed molecule gains energy E between
EA and ES, this molecule hops from site to site in the adsorbed states. After several hopping
77
have occurred, the molecules may finally detach (desorb) from the surface. An adsorbed
molecule, however, remains on the adsorption site when E<ES and is desorbed when E>EA.
Various types of hopping possible are shown in figure 18. Molecules randomly hop to a
neighboring site after various holding times. It is generally assumed that when a molecule hit
a site occupied by another molecule it would immediately bounce off and continue until
finding an unoccupied site.
hopping
molecule
adsorbed
molecule
Figure 18. Modes of jumping (adapted from [68]).
The surface diffusion flux is defined as:
r
r
J m = − D lS∇C lS
(191)
where DlS is the surface diffusion coefficient (m2/s).
Surface diffusion is not taken directly into account by any of the existing drying models.
Philip and De Vries [69] state that it seems unlikely that diffusion in the adsorbed phase will
affect the total heat and mass transfer process in significant amount. Their reasoning is that
part of the water that evaporates from or condenses on the surfaces may recirculate in a single
air filled pore through the surface migration process [21].
Hydrodynamic Flow
Hydrodynamic flow of liquid water is defined by Darcy law similar to that for gases.
r
r
K r
v w = − l (∇Pl − ∇Ψw )
ηl
(192)
r
where v w is the mass average velocities (m/s), K i is the permeability of liquid (m2), and Ψw
is the gravity potential of liquid water (m2/s2).
The range of validity of the Darcy equation is expressed in terms of the Reynolds
number. The upper limit of the validity of the Darcy equation is at a value of Re between 1
and 10 [70]. The importance of Darcy flow compared to diffusion is decided taking the Peclet
number into consideration. If Peclet number is small enough Darcy flow may be omitted.
78
ENERGY TRANSPORT MECHANISMS
Heat transfer in drying process of food materials may take place by different mechanisms
such as conduction, convection and radiation. In general, the main mechanism for heat
transfer is heat conduction. Heat transfer by conduction is defined by the Fourier’s law:
r
r
J q = −λ∇T
(193)
r
where λ is the thermal conductivity (W/(m K)), ∇T is the temperature gradient. In addition
to the conduction, heat transfer will also be accomplished by convection due to the movement
of the three phases: solid, liquid and gas. The evaporation may also have significant thermal
effects.
DRYING MODELS
Mathematical modeling of drying behavior of food materials is important because it
enables scientific process design, minimization of energy cost and minimization of cost due to
the quality constraints. However, it is very hard to describe the drying process with a single
and simple model due to the complexity of the drying process. The difficulties arise from the
following reasons:
There is a mixture of various transport mechanisms and the contribution of different mechanisms to the total
transport varies from place to place and as drying proceeds,
The most of transport properties are strongly affected by concentration, temperature and physical structure,
The modeling of structural parameters like porosity, tortuosity and permeability is complicated,
Structure of the material may be heterogeneous showing regions of different permeability to the transport of
moisture,
Material may have complex shape, which are difficult to describe mathematically,
Material may shrink significantly in the process,
Drying temperature, humidity etc. may change during the drying process.
Drying models for porous materials may be categorized into three distinct groups,
theoretical, empirical, and semi-empirical. The theoretical models consider only internal
resistance to moisture transfer while the empirical and semi-empirical models consider only
external resistance.
Theoretical Models
Theoretical models can be classified into two categories: the continuum approach and
discrete approach. In discrete approach, transport from porous medium is considered at pore
level. Porous materials have a quite complex structure. The difficulty in modeling due to
complex structure is overcome by describing a pore network which takes account only the
basic features of geometry and topology of the porous structure (see figure 19). Transport
process is considered in this network structure representing the porous medium. The most
79
important advantage of this type of modeling is to facilitate the understanding of the
macroscopically observed mass transfer phenomena. Modeling based on discrete approach is
used for two different objectives. One is the computation of the effective parameters at the
scale of a representative volume of the microstructure. The other is to describe transport
process at the scale of the product. However, approach that is generally used in defining
transport at macroscopic level is continuum approach. In continuum approach, there is no
need to define the structure of the medium at microscopic level. Therefore, the purpose of use
is only to analyze the drying process at product level. Continuum modeling is a classical
approach used for media having complex microstructure. Continuum modeling is also a
phenomenological approach because it requires determination of transport coefficients
experimentally. In this type of approach, transition from microscopic level to macroscopic
level may be considered as an operation of smoothing out the microscopic heterogeneity of
the relevant properties. In other words, porous media is assumed to be a fictitious continuum.
The effects of the physical phenomena taken into consideration are lumped into effective
transport coefficients. The greatest difficulty in using a model based on a continuum approach
arises from determination of these transport parameters which are dependent moisture
content, temperature and material structure. Many models have been suggested based on
continuum approach. The most important ones are molecular diffusion model, receding front
model, Philip and de Vries model, Luikov model, Krischer model and Berger and Pei model.
The continuum approach has gained a firmer basis through the Whitaker model [71, 72] by a
volume averaging technique. The most important feature of the volume averaging technique
is the possibility of determining the effective parameters through the solution of closure
problems defined over regions representative of the pore microstructure. In this way, a
fundamental aspect of the problem which is the disordered nature of the porous
microstructure could be analyzed [73]. In this chapter, the models only based on continuum
approach will be considered.
Solid Phase
Pore (Site)
Solid Phase
Figure 19. Conversion from the porous medium to the pore network (adapted from [73]).
Molecular Diffusion Model
Fick's first law does not consider the fact that the gradient and local concentration of a
diffusing substance in a material decreases with an increase in time. In such cases, Fick’s
second law is used for expressing diffusion. The Fick's second law states that the change in
concentration of a diffusing substance in a material over time is equal to the change in local
diffusion flux.
80
Let us consider the control volume seen in figure 20 to derive the Fick’s second law. Let
us assume that there are mass fluxes towards the inside and outside of this control volume.
The mass fluxes into the control volume can be written as follows:
jm , x = − D
∂C
∂x
jm , y = − D
∂C
∂y
jm , z = − D
∂C
∂z
(194)
where D is the diffusion coefficient (m2/s) and C is the concentration (kg/m3). Mass
conservation can be expressed as:
Mass in-Mass out+Mass generated=mass stored
(195)
Quantities of mass entering and exiting control volume at Δt time can be defined as follows:
jm ,x ΔyΔzΔt
jm,x + Δx ΔyΔzΔt
jm, y ΔxΔzΔt
jm ,z ΔxΔyΔt
jm,y+ Δy ΔxΔzΔt
jm,z+ Δz ΔxΔyΔt
(196)
(197)
Generated or depleted mass and stored mass in control volume at Δt time may be expressed as:
IΔxΔyΔzΔt (generated amount)
CΔxΔyΔz (stored amount)
(198)
where I is the rate of mass generation or depletion per unit volume (kg/(m3s)). Substituting all
the terms into Eq. (195) gives the following differential equation called Fick’s second law:
∂c ∂ ⎛ ∂c ⎞ ∂ ⎛ ∂c ⎞ ∂ ⎛ ∂c ⎞
= ⎜D ⎟ + ⎜D ⎟ + ⎜D ⎟ + I
∂t ∂x ⎝ ∂x ⎠ ∂y ⎝ ∂z ⎠ ∂z ⎝ ∂z ⎠
(199)
In cylindrical and spherical coordinate, the diffusion equation is as follows [74]:
∂c 1 ⎧ ∂ ⎛ ∂c ⎞ ∂ ⎛ D ∂c ⎞ ∂ ⎛ ∂c ⎞⎫
= ⎨ ⎜ rD ⎟ + ⎜
⎟ + ⎜ rD ⎟⎬ + I
∂t r ⎩ ∂r ⎝ ∂r ⎠ ∂θ ⎝ r ∂θ ⎠ ∂z ⎝ ∂z ⎠⎭
(200)
∂c ⎞
1 ∂ ⎛ ∂c ⎞⎫
1 ∂ ⎛
∂c 1 ⎧ ∂ ⎛ 2 ∂c ⎞
⎜ D ⎟⎬ + I
= 2 ⎨ ⎜r D ⎟ +
⎜ D sin θ ⎟ +
∂θ ⎠ sin 2 θ ∂φ ⎜⎝ ∂φ ⎟⎠⎭
∂r ⎠ sin θ ∂θ ⎝
∂t r ⎩ ∂r ⎝
(201)
All these diffusion equations can be expressed in vectorial form as:
∂C r r
= ∇ ⋅ Jm + I
∂t
r
r
J m = − D∇C
(202)
∂C
−D
∂x
Δx
−D
Δz
x
∂C
∂x
81
x + Δx
Δy
Figure 20. Control volume showing inflows and outflows of a substance by diffusion.
This model is based on the assumption that mass transfer occurs only with molecular
diffusion. However, there are also other mass transfer mechanisms. The effects of other
transfer mechanisms can be considered to be lumped into diffusion coefficient. So, the
diffusion coefficient becomes an effective parameter.
r
∂C
= ∇ ⋅ (D eff ∇C) + I
∂t
(203)
Although molecular diffusion model is the most commonly used model to express drying
behavior of food materials, it is also the most criticized model. The reason, of course, is that it
assumes that mass transfer occurs only by molecular diffusion. Fortes and Okos [21]
attributes widely usage of this model to the logarithmic behavior resembling experimental
drying curves. Sherwood [75] states that the success of diffusion equation lies in the fact that
the calculations are made by integration techniques, which compensate for the error caused by
wrong distribution assumption.
Solutions of Diffusion Equation for Some Simple Geometries
It is possible to obtain analytical solution of diffusion equation for some simple
geometries under certain assumptions. Suppose that:
•
•
•
•
•
•
•
the diffusion coefficient is independent of moisture content for a given temperature,
the material is isothermal during drying,
the moisture is initially uniformly distributed throughout the material,
surface moisture content of the samples instantaneously reaches equilibrium with the
conditions of the surrounding air,
the material size and geometry remain constant during drying,
there is no mass generation or depletion inside the material.
Let us use the following dimensionless variables:
82
C − Ce
D
1
t* = 2 t
(204)
∇*2 = 2 ∇ 2
,
,
Co − Ce
L
L
where L is the characteristic dimension (half-lengths for a slab, radius for a cylinder, a sphere
and a spheroid) (m) and t is the time (s). The diffusion equation and initial and boundary
conditions can then be written as follows:
C* =
∂C*
= ∇ 2 C*
*
∂t
C*
t =0
=1
(205)
,
dC *
dt
=0
,
C* = 0
(206)
S
s .a .
In order to predict a drying curve, it is necessary to determine an equation defining the
average moisture content. Therefore, calculated average moisture content can be compared
with the corresponding experimental results. This equation can be expressed as follows:
mr =
m − me
1
= ∫ C*dV
mo − me V V
(207)
where m, mo, me are the instantaneous, initial and equilibrium moisture contents respectively,
and V is the volume of the material.
For the geometries given in figure 21, analytical solutions of diffusion equation subjected
to the initial and boundary conditions defined by Eq. (206) are given below.
Slab
Cardioid
Cylinder
Hexagon
Sphere
Corrugated (loop 1/8)
Figure 21. Some conventional and nonconventional shapes.
Ellipsoid
Epitrochoidal
83
Conventional Shapes
Infinite Slab
mr =
2
⎛
8 ∞
1
2 π D eff t ⎞
⎜
⎟
exp
(
2
n
1
)
−
−
∑
⎜
4L2 ⎟⎠
π 2 n =1 (2n − 1) 2
⎝
[76, 77]
(208)
Semi-Infinite Slab
2
2
⎛
⎞⎤
1
⎛ 8 ⎞ ⎡∞
⎜ − (2n − 1) 2 π D eff t ⎟⎥ ×
mr = ⎜ 2 ⎟ ⎢ ∑
exp
2
2
⎜
⎝ π ⎠ ⎢⎣n =1 (2n − 1)
4L1 ⎟⎠⎥⎦
⎝
2
⎡∞
⎛
⎞⎤
1
⎜ − (2n − 1) 2 π D eff t ⎟⎥
exp
⎢∑
2
2 ⎟
⎜
4L 2 ⎠⎥⎦
⎢⎣n =1 (2n − 1)
⎝
[78 ,79]
(209)
Finite Slab
3
2
⎛
⎞⎤
1
⎛ 8 ⎞ ⎡∞
⎜ − (2n − 1) 2 π D eff t ⎟⎥ ×
exp
mr = ⎜ 2 ⎟ ⎢ ∑
2
2
⎜
⎝ π ⎠ ⎢⎣n =1 (2n − 1)
4L1 ⎟⎠⎥⎦
⎝
2
* ⎞⎤
⎡∞
⎛
1
⎜ − (2n − 1) 2 π D eff t ⎟⎥ × [78 ,79]
exp
⎢∑
2
2
⎜
4L 2 ⎟⎠⎦⎥
⎝
⎣⎢n =1 (2n − 1)
(210)
2
⎡∞
⎛
⎞⎤
1
⎜ − (2n − 1) 2 π D eff t ⎟⎥
exp
⎢∑
2
2
⎜
4L 3 ⎟⎠⎥⎦
⎢⎣n =1 (2n − 1)
⎝
Sphere
mr =
− n 2 π 2 D eff t ⎤
6 ∞⎡1
exp(
)⎥
∑
⎢
L2
π 2 n =1 ⎣ n 2
⎦
[76, 80]
(211)
Hemisphere
∞ ∞
mr = ∑ ∑ b nm exp(−D eff α 2nm t )
n =0m =1
[81, 82]
(212)
84
Here αnm are the roots of Cnth order Bessel function J Cn ( x ) = 0 and coefficients bnm are
defined as:
b nm
1
⎡1
⎤
(24n + 18) ⎢ ∫ P2 n +1 ( x * )dx * ∫ (r * ) 3 / 2 J Cn (α nm r * )dr * ⎥
0
⎣0
⎦
=
J C2 n +1 (α nm )
2
(213)
Here P2n+1 is the (2n-1)th order Legendre function. The eigenvalues Λn are obtained using:
Λ2n = 2(n + 1)(2n + 1)
(214)
The eigenvalues determine the order (Cn) of the Bessel function (JCn) according to:
C n = (Λ2n + 1 / 4)1 / 2
(215)
Infinite Cylinder
∞ ⎡ 4
D t ⎤
mr = ∑ ⎢ 2 exp(−α 2n eff2 )⎥
L ⎦
n =1 ⎣ α n
[76, 83]
(216)
Here α n (n=1,2,.....) are the roots of zeroth order Bessel function J o ( x ) .
Finite Cylinder
mr =
D t ⎤
8 ∞ ∞⎡ 1
exp((−α 2n + β 2m ) eff2 )⎥
*2 ∑ ∑ ⎢ 2 2
L ⎦
l n =1m=1⎣ α n β m
[84, 85]
(217)
where l* is the dimensionless half-length of the cylinder. β m is defined as:
βm =
(2m − 1)π
2l
m = 1, 2,.....
(218)
Prolate and Oblate Spheroid
mr =
(
)
D eff t
1 N
* *
∫ ∑ c n Ω n r , z exp( −Λ n 2 )
V V n =1
L
[86, 87]
(219)
85
Here cn (n=1,2,...) are constants and Λ n and Ω n (n=1,2,...) are the eigenvalues and
eigenfunctions respectively. Eigenvalues Λ n in the Eq. (219) can be obtained by the
following equation:
(
Ω n (r, z ) = ∑ d njf j r * , z*
N
n =1
)
(220)
where fj is an element of a group of base functions and d nj are constants to be determined.
Function f j is called the Galerkin function and it is obtained by the multiplication of function
Ω by an element of a complete set of functions. Function Ω is selected so as to satisfy the
homogeneous boundary condition. Function f j with j varying from 1 to N constitutes a set of
base functions. Using the Galerkin procedure eigenvalues γ n and constants d nj can be
obtained. Thus the constants cn in Eq. (219) can be obtained by the following equation:
*
*
*
*
∫ f i C (r , z )dV = ∫ ∑ f i c n Ω n (r , z )dV
N
(221)
V n =1
V
Nonconventional Shapes
Analytical solution of diffusion equation for some nonconventional shapes seen in figure
21 has been obtained by Rotstein et al. [88] using conformal mapping. Cross sectional areas
of these nonconventional shapes are given in table 13.
Table 13. Cross sectional area for some nonconventional
shapes (L is the characteristic length)
cardioid
corrugated
3 2
πL c
2
129 2
πL r
128
epitrochoid
41π 2
Lc
36
Hexagon
3 3 2
Lh
2
Cardioid
m 4 32 ∞ ∞
1
1
2
=
(1 − 2 ) exp(−Fmc Dt )
∑∑
m o 3 π 2 n =1m=1(2n + 1) 2 α 2m
αm
(222)
where αm (m=1, 2,.....) are the roots of zeroth order Bessel function J o ( x ) and Fm is the
i
shape factor defined as:
86
⎛ (2m + 1)2 ⎞
⎟ + m
(223)
F = ⎜⎜
2
⎟
L2i
⎝ 4l
⎠
where i is the shape index (i=c, cardioid, i=h, hexagon, i=g, corrugated, i=e, epitrochoid), l
is the vertical semi-length (m).
2
i
m
Hexagon
m
32 ∞ ∞
1
1 h
= 0.9060 2 ∑ ∑
Sm exp(−Fmh Dt )
2
2
mo
π n =0m=0 (2n + 1) α m
(224)
where
Shm = a 2 + b 2 f 6 + c 2 f12 + d 2 f18 + e 2 f 24 + f 2 f 30
(225)
where f k is given by the following functional relation:
2
⎛ k! ⎞ −2 j
⎟⎟ α m
f k = ∑ (−1) 2 ⎜⎜
j=0
⎝ (k − j)! ⎠
k
j
2j
(226)
Corrugated (Loop 1/8)
m
32 ∞ ∞
1
1 ⎡
13
⎤
= 0.9524 2 ∑ ∑
1 + ( ) 2 f12 ⎥ exp(−Fmg Dt )
2
2 ⎢
mo
16
π n =0m=0 (2n + 1) α m ⎣
⎦
(227)
Epitrochoid
m
32 ∞ ∞
1
1 ⎡ 25 ⎤
= 0.9119 2 ∑ ∑
1 + f 4 exp(−Fme Dt )
mo
π n =0m=0 (2n + 1) 2 α 2m ⎢⎣ 36 ⎥⎦
(228)
DIFFUSION MODEL FOR SHRINKING MEDIA
Mass balance in a shrinking porous material may be expressed as follows:
∂ρ s r r
+ ∇(ρ s v s ) = 0 for solid phase
∂t
(229)
∂ρ l r r
+ ∇(ρ l v l ) = 0 for liquid phase
∂t
87
(230)
r
where ρs and ρl are the concentrations of the solid and liquid (kg/m3), v s is the solid
r
displacement velocity (m/s) and v l is the liquid velocity (m/s). Also:
r
r
r
ρv = ρ s v s + ρ l v l
(231)
ρ = ρs + ρl
(232)
where ρ is the total concentration (kg/m3). The mass flux can be divided into two separate
terms in terms of diffusion and convection:
r
r
r
ρ k v k = J mk + ρ k v
k=l,s
(233)
The moisture content m is the ratio of the two phase mass concentrations:
m = ρl / ρs
(234)
If the liquid flow is assumed to be diffusive, it can be expressed with respect to the solid
phase frame reference. Using Eqs. (231), (233), and (234) yields:
r
r r
ρ
ρl (v l − vs ) = −
D eff ∇m
1+ m
(235)
If this relation is combined with the two mass balance equations (Eqs. (229) and (230)), the
liquid transport takes the following form:
ρs
r ρ
r
r r
∂m
+ ρs v s ⋅ ∇m = ∇(
D eff ∇m)
∂t
1+ m
(236)
Relation Between Solid Displacement and Water Loss
The solid and liquid phase concentrations depend on the dry solid concentration and can
be given as follows [89]:
ρs =
ρso
1 + βm
ρl =
mρ so
1 + βm
(237)
where ρso is the initial solid concentration (kg solid/m3 total volume) and β is the volumetric
shrinkage coefficient. Using Eq. (237), we obtain:
88
ρ (1 + βm) − ρsoβm
ρ m
ρso
= ρso − β so
= so
1 + βm
1 + βm
1 + βm
Therefore:
ρs =
(238)
ρs = ρso − δρl
(239)
Equations (229) and (239) lead to:
−β
r
∂ρ l r
− ∇ ⋅ ( ρ sv s ) = 0
∂t
(240)
−β
r r
r r
∂ρ l
+ ρ s∇ ⋅ v s + v s ⋅ ∇ ρ s = 0
∂t
(241)
−β
r r
r r
∂ρ l
+ ρ s∇ ⋅ v s − δv s ⋅ ∇ ρ s = 0
∂t
(242)
r r
∂ρ l r r
+ v s ⋅ ∇ ρ s ) + ρs∇ ⋅ v s = 0
∂t
(243)
− β(
From the conservation of the liquid phase, we can write:
r r
r
∂ρ l r r
+ ∇(ρ l v l − ρ l v s ) + ∇(ρ l v s ) = 0
∂t
(244)
If we use the diffusion flux:
r
r
∂ρ l r r
+ ∇ ⋅ J m + ∇ ⋅ (ρ l v s ) = 0
∂t
(245)
r r
r r
∂ρ l r r
+ ∇ ⋅ J m + ρl∇ ⋅ v s + v s∇ ⋅ ρl = 0
∂t
(246)
r r
r r
∂ρ l r r
+ v s ⋅ ∇ρ l = − ∇ ⋅ J m − ρ l ∇ ⋅ v s
∂t
(247)
If we replace Eq. (247) into Eq. (243):
r r
r r
r r
− β(−∇ ⋅J m −ρ l ∇ ⋅ v s ) + ρs ∇ ⋅ v s = 0
(248)
r r
r r
β ∇ ⋅J m +(βρ l + ρ s ) ∇ ⋅ v s = 0
(249)
89
r r
r r
β ∇ ⋅ J m + ρ so ∇ ⋅ v s = 0
(250)
r r
r r
β ∇ ⋅ J m = −ρ so ∇ ⋅ v s
(251)
r
The diffusion flux J m is defined as.
r
ρ D r
J m = − so ∇m
1 + βm
(252)
Therefore Eq. (251) becomes:
r ⎛ ρ D r ⎞
r r
β ∇ ⋅ ⎜⎜ − so ∇m ⎟⎟ = −ρso ∇ ⋅ v s
⎠
⎝ 1 + βm
(253)
which can be simplified in:
r ⎛ D r ⎞
r r
β ∇ ⋅ ⎜⎜
∇m ⎟⎟ = ρso ∇ ⋅ v s
⎠
⎝ 1 + βm
(254)
Rheological Behavior
The deformation of drying material can be partially characterized by the solid-liquid
momentum equation. These deformations define structural displacements and therefore the
solid velocity. The momentum conservation can be defined as follows:
ρ
r
r r ~
r rr
∂v
+ ρv ⋅ ∇v = ρF + ∇ ⋅ σ
∂t
(255)
r
~ is the stress tensor (Pa) and F
where σ
is the external force (N) applied to the sample. If it is
assumed that there are no external forces and the inertial term is negligible, Eq. (255)
becomes as:
r ~ r
∇⋅σ
=0
(256)
with the boundary condition below which implies that the loading to the material surface is absence.
~ ⋅ nr = 0
σ
S
(257)
The solid liquid momentum conservation equation is not sufficient to describe the response of
a specific material to an applied loading. An equation is required which defines rheological
behavior. Mihoubi et al. [90] considered both elastic and viscoelastic cases. They separated
90
strain tensor in two parts for each case. One is directly bound to the material behavior ( ~εM )
and the other is bound to the moisture and temperature variation ( ~ε )
r
~ε = ~ε + ~ε
M
r
(258)
The strain tensor ~εr depends on the moisture migration ~εH and the temperature variation ~εT .
~ε = ~ε + ~ε
r
T
H
(259)
The strain tensors depending on the moisture migration and temperature variation can be
derived from the thermodynamics of linear irreversible process as [90]:
⎧~εT = α T ΔT
⎨~
⎩ εH = β T ΔT
1
ε ij = ( v i , j + v j,i )
2
v i, j =
∂v i
∂x j
(260)
vi =
∂ (ν p s ) i
∂t
(261)
where αT is the thermal expansion coefficient (1/K), βT is the volumic expansion coefficient
(1/K), and νp is the Poisson coefficient.
Elastic Behavior
Stress-strain relation in the classic elasticity is related by the Hooke law generalized in
three dimensions:
~ = λ′(~ε ) T ⋅ ~
σ
1 + 2μ′~εm
m
(262)
~
where 1 is a unit tensor, λ′ and μ′ are the Lame coefficients (Pa). Lame coefficients are
related the Young modulus E (Pa) and the Poisson ratio ν by the following equations [90]:
λ′ =
E yν
(1 + ν)(1 − 2ν)
μ′ =
Ey
2(1 + ν)
where Ey is the Young modulus (Pa).
(263)
91
Viscoelastic Behavior
Strain rate in a viscoelastic material changes in time. The most appropriate approach for
describing the deformation of many real products is the viscoelastic approach. The
application of the principle of correspondence in the space of Laplace space for a viscoelastic
material responding to the deformation solicitations leads to the following generalized law of
Hooke [90]:
2
⎞
⎛
σij (s) = ⎜ P (s) − Q (s) ⎟ ε m ,kk (s)δ ij + 2Q (s) ε m ,ij
3
⎠
⎝
(264)
Returning to actual space, several shapes are derived according to the regime of solicitation.
Among all these shapes, the one bound to a stepwise solicitation represents well because we
have the effect of the deformation and the rate of the deformation [90].
t
t
∂ε m ,ij (τ)
2
⎛
⎞ ∂ε m ,kk (τ)
σ ij ( t ) = ∫ ⎜ K V ( t − τ) − G r ( t − τ) ⎟
δ ijdτ + 2 ∫ G r ( t − τ)
dτ
δτ
3
∂τ
⎠
0⎝
0
(265)
In the matrix form
~
~
~
t
t
~ ( t ) = ⎛⎜ K ( t − τ) − 2 G ( t − τ) ⎞⎟ ∂ εm (τ) : 1 dτ + 2 G ( t − τ) ∂ εm (τ)dτ
σ
∫ V
∫
r
r
δτ
3
∂τ
⎠
0⎝
0
(266)
where t is the time (s), KV is the volume model (Pa) and Gr is the relaxation model (Pa).
Mathematical Transformation
The flux and continuity equations for liquid phase can be written as follows:
r
r
J m = −ρs D∇m
(267)
r
1 r
∂m v r
+ v s ⋅ ∇m = ∇ ⋅ (Dρs ∇m)
∂t
ρs
(268)
The actual position in space of a small mass element of the moving solid can be denoted by a
r
time dependent vector r ( t ) . However, it might be more advantageous to use the Lagrangian
description, in which the initial position of each small mass element is indicated by a vector
r r
rL = r (0) . The partial time derivatives for both coordinate systems are related by [41]:
r r
∂m
∂m
+ v s ⋅ ∇m
=
∂t rrL ∂t rr
(269)
92
The transformations for the gradient and divergence are defined as.
r −T r
r
⎛ ∂r ⎞
∇ rr (*) = ⎜ r ⎟ ⋅ ∇ rrL (*)
⎝ ∂z ⎠
r
r ⎛ 1 ⎛ ∂rr
∇ rr ⋅ (*) = f ∇ rrL ⋅ ⎜ ⎜⎜ r
⎜ f ⎝ ∂ rL
⎝
(270)
−1
⎞
⎞
⎟⎟ ⋅ (*) ⎟
⎟
⎠
⎠
(271)
where
r
⎛ ∂r
1
= Det⎜⎜ r
f
⎝ ∂ rL
⎞ ρso
⎟⎟ =
⎠ ρs
(272)
where f is the shrinkage function, ρs is the solid concentration (kg/m3) and ρso is the dry solid
concentration (kg/m3). Applying these transformation rules to the flux and continuity
equations yields:
r −T r
r
⎛ ∂r ⎞
J m = −ρso f D ⎜⎜ r ⎟⎟ ⋅ ∇ rL m
⎝ ∂ rL ⎠
∂m
∂t
r
rL
r −1
r
r ⎧⎪
⎛ ∂r ⎞ ⎛ ∂r
r
= ∇ rL ⋅ ⎨D eff ⎜⎜ r ⎟⎟ ⋅ ⎜⎜ r
⎝ ∂ rL ⎠ ⎝ ∂ rL
⎪⎩
(273)
⎞
⎟⎟
⎠
−T
⎫⎪
r
⋅ ∇ rrL m ⎬
⎪⎭
(274)
r r
The deformation of a material is described by means of ∂ r / ∂rL . The amount of solid remains
constant during drying. Therefore, the following restriction has to be satisfied [41]:
r
⎛ ∂r
Det⎜⎜ r
⎝ ∂ rL
⎞ 1 ρso
⎟⎟ = =
⎠ f ρs
(275)
The deformation in the case of isotropic shrinkage is mathematically given by [91]:
−1 / 3
r ⎛⎜ f
∂r ⎜
r = 0
∂ rL ⎜
⎜0
⎝
0
f
0
⎞
⎟
0 ⎟
⎟
f −1 / 3 ⎟⎠
0
−1 / 3
Assuming no gradients in the ρso , the continuity equation becomes:
(276)
r
r
∂m
= ∇ rrL ⋅ (D eff f 2 / 3∇ rrL m)
∂t rrL
93
(277)
One-Dimensional Shrinkage
The deformation in one dimensional shrinkage is defined as [41]:
−1
r ⎛f
∂r ⎜
r = ⎜0
∂ rL ⎜
⎜0
⎝
0
1
0
0⎞
⎟
0⎟
⎟
1 ⎟⎠
(278)
The flux and continuity equations can then be written as:
J m,ξ = −ρso f 2 D
∂m
∂ξ
∂
∂m
∂m
)
= (D eff f 2
∂ξ
∂t ξ ∂ξ
(279)
(280)
ANOTHER DIFFUSION MODEL FOR SHRINKING MEDIA
Mass balance equations for solid and liquid phases can be written as follows:
r
∂ρ s r
+ ∇ ⋅ (ρs v s ) = 0 for solid
∂t
(281)
r
∂ρ l r
+ ∇ ⋅ (ρ l v l ) = 0 for liquid
∂t
(282)
If we use the relation ρs = ρ so /(1 + βm) , the mass balance equation for solid phase becomes
as follows:
r r
∇ ⋅ vs =
β ∂m
β r r
v s ⋅ ∇m +
1 + βm
1 + βm ∂t
(283)
The balance equation for liquid phase can be rearranged as:
r r
r
∂ρ l r r
+ ∇(ρ l v l − ρ l v s ) + ∇(ρ l v s ) = 0
∂t
(284)
94
r
Using the diffusion flux J m , we obtain:
r
r
∂ρ l r r
+ ∇ ⋅ J m + ∇ ⋅ (ρ l v s ) = 0
∂t
(285)
r r
r r
∂ρ l r r
+ ∇ ⋅ J m + ρ l ∇ ⋅ v s + v s ⋅ ∇ρ l = 0
∂t
(286)
and from Eq. (252):
r r
r r
∂ρ l r ⎛ ρ so D r ⎞
+ ∇⎜⎜ −
∇m ⎟⎟ + ρ l ∇ ⋅ v s + v s ⋅ ∇ρ l = 0
∂t
⎠
⎝ 1 + βm
(287)
If we use the relation ρ l = mρs and write Eq. (283) into Eq. (287), we find:
(
)
r
⎡ β r r
∂ρs
∂m ∂
β ∂m ⎤
+ ρs
+
− ρso D∇m + ρ l ⎢
v s ⋅ ∇m +
+
∂t
∂t ∂x
1 + βm ∂t ⎥⎦
⎣1 + β m
r
r
r
v s ⋅ m∇ρ s + ρ s ∇m = 0
m
(
)
(288)
Recalling that ρs = ρ so /(1 + βm) and ρs = ρso − δρl :
1 ∂m r ⎛ D r ⎞
1 r r
= ∇ ⋅ ⎜⎜
∇m ⎟⎟ −
v s ⋅ ∇m
1 + βm ∂t
⎝ 1 + βm
⎠ 1 + βm
(289)
Equations (283) and (289) define the mass transfer from a shrinking body and can be solved
for vs, and m.
RECEDING FRONT MODEL
Experimental observations show that during drying of some products evaporation takes
place inside the material at a certain depth which divides the system into two regions as dry
and wet, as shown in figure 22. For a hygroscopic material, the dry zone is called the sorption
zone due to the adsorptive nature of moisture retention. In the dry zone, moisture is in vapor
phase only and, in the wet zone, it is in liquid or mixed form. As drying proceeds the
evaporating front recedes increasing the ratio of dry to wet zones. The simplest case for this
model assumes that the saturation S is 1 in the wet region and 0 in the dry region. Balance
equations related to this case can be defined as follows [92, 93]:
95
Evaporation Front
Drying Surface
Symmetry Plane
Drying Air
Heat Flux
Wet Zone
Dry Zone
Moisture Flux
z=L
z=zF(t)
z=0
Figure 22. Receding front model (adapted from [93]).
Wet Zone (1)
∂m fw
∂ ⎛ ∂m fw ⎞
= ⎜ Dl
⎟
∂z ⎝
∂z ⎠
∂t
ρC pl
∂T1 ∂
∂T
= (λ eff 1 )
∂t ∂z
∂z
(290)
(291)
where Dl is the liquid transfer coefficient (m2/s), CPl is the specific heat of water (J/(kg K)),
mfw is the moisture content of free water (kg water/kg dry solid) and λ eff is the effective
thermal conductivity (W/(m K)). The thermal conductivity is calculated from the following
equation:
λ eff = λ l +
D′v M̂ v ∂Pv,sat (T)
Δh vap
∂T
R̂T
(292)
where λl is the thermal conductivity of liquid (W/(m K)), M̂ v is the molecular mass of the
vapor, Δh vap is the evaporation enthalpy (J/kg), R̂ is the ideal gas constant (8.314 J/(mol
K)), Pv,sat (T ) is the saturation vapor pressure (Pa). D′v is the vapor transfer coefficient (m2/s),
which includes the contribution of both convective and diffusive flows and it is defined as:
96
⎞
⎛
K i k rg Pv / η v
⎟
D′v = D v ⎜1 +
⎜ D v + K i k rg (Pg − Pv ) /(ε av ηv ) ⎟
⎠
⎝
(293)
where Dv is the vapor diffusion coefficient (m2/s), Ki is the intrinsic permeability (m2), k rg is
the relative permeability of gas phase, ηv is the dynamic viscosity (Pa s) and εav is the ratio of
air and vapor diffusion coefficients.
Dry or Sorption Zone (2)
ρ
∂m sorb
∂m sorb
∂
∂ D′ M̂ ∂P
= ρ (D sorb
)+ ( v v v)
∂t
∂z
∂z
∂z R̂T ∂z
ρC Pv
∂T2 ∂
∂T
= (λ v 2 )
∂t
∂z
∂z
(294)
(295)
where CPv is the specific heat capacity of vapor (J/(kg K)), λv is the thermal conductivity of
vapor (W/(m K)), msorb is the adsorbed water content (kg water/kg dry solid) and Dsorb is the
transfer coefficient of adsorbed water (m2/s). For a non-hygroscopic material, msorb is zero
and Dsorb is negligible.
Evaporation Front
The following conditions must be satisfied at the moving boundary:
∂m fw
∂m sorb D′v M̂ v ∂Pv
= ρD sorb
+
∂z
∂z
R̂T ∂z
(296)
D′ M̂ ∂P
∂ (λ eff Tl ) ∂ (λ v T2 )
+ Δh vap v v v
=
∂z
∂z
R̂T ∂z
(297)
T1 = T2 ,
(298)
ρD l
m fw = 0
The most important difficulty in using this model arises from determination of the boundary
for the moving evaporation front [93].
PHILIP AND DE VRIES MODEL
In this model, the moisture content and temperature gradient are assumed to be the
driving force in moisture transport. In addition, mass transport in liquid phase is assumed to
97
occur with the effect of capillarity. The Flux and balance equations for this model can be
defined as follows:
Liquid Water
Darcy law is used in this model to express mass transfer in liquid phase [69].
r
r
Kk r
J ml = −ρ l i rl (∇Pl − ∇Ψl )
ηl
(299)
where ρl is the density of the liquid water (kg/m3), Ki is the intrinsic permeability (m2), krl is
the relative permeability of the liquid water and ηl is the dynamic viscosity of the liquid water
(Pa s). Pl and Ψl are the pressure (Pa) and gravity potential (m2/s2) of the liquid water,
r
respectively. If the term ∇Pl is expressed as a function of moisture content and temperature,
liquid water flux can be written as:
r
r
r
Kk r
J ml = −D lm ∇m − D lT ∇T + ρ l i rl ∇Ψl
ηl
(300)
where T is the temperature (°C) and m is the moisture content (kg water/kg dry solid). Dlm
and DlT are the isothermal and thermal diffusivities of water (m2/s) and are given by
D lm = ρ l
K i k il ∂Pl
ηl ∂m
D lT = ρ w
K i k rl ∂Pl
ηl ∂T
(301)
Water Vapor
The water vapor transport is described by Fick’s first law and by using the assumption of
a steady diffusion in a closed system between an evaporation source and a condensation sink.
The commonly used expression for the vapor flux in terms of moisture and temperature
gradients is as follows [93]:
r
r
r
J mv = − D vm ∇m − D vT ∇T
(302)
where Dvm and DvT are the isothermal and thermal diffusivities of vapor and are defined as [73]:
D vm = f (ψ)D va
M̂ v g ρ v ∂Pl
Pg − Pv R̂T ρ l ∂m
Pg
(303)
98
D vT = f (ψ )D va
r
ρ v (∇T) av 1 dPv,sat
r
Pg − Pv ρ l (∇T) Pv*,sat dT
Pg
(304)
In these equations f (ψ ) is a function of porosity and moisture content, Dva is the diffusion
coefficient of vapor in air (m2/s), g is the gravitational acceleration (m/s2), P v, sat (T) is the
r
saturation vapor pressure (Pa), (∇T) av is the average air temperature gradient, ρv and ρw are
the concentrations of vapor and liquid (kg/m3).
Balance Equations
If the flux equations are taken into consideration, the mass and energy conservation
equations can be written as follows:
r
r
r
r ⎛K k r ⎞
∂m r
= ∇ ⋅ (D T ∇T) + ∇ ⋅ (D m ∇m) + ∇ ⋅ ⎜⎜ i rl ∇Ψl ⎟⎟
∂t
⎠
⎝ ηl
∂ (ρC p T)
∂t
r
r
r
r
= ∇ ⋅ (λ∇T) + Δh vap∇ ⋅ (D vm∇m)
(305)
(306)
where DT=DwT+DvT is the overall thermal diffusivity (m2/s), Dm=Dwm+Dvm is the overall
isothermal mass diffusivity (m2/s), λ is the thermal conductivity (W/(m K)) and ρCP is the
volumetric heat capacity of the porous material (J/(m2K)).
LUIKOV MODEL
This model is one of the most frequently used drying models. In this model, heat and
mass transfer equations are derived by employing the principles of nonequilibrium
thermodynamics theory. As it is well known, if two points of a system are at different
potentials, a potential difference in the system is established which causes the flow of entity
from the point of higher potential towards that of lower potential. The entity may be either of
matter or heat or electricity. When two or more irreversible processes take place
simultaneously in a thermodynamic system, they may interfere with each other and produce a
cross effect. This model is based on taking into consideration such cross effects involved in
heat and mass transport in a porous material.
Potentials for Heat and Mass Transfer
The total entropy increases in an irreversible process, whereas in a reversible process
there is no change in the total entropy. The entropy production in an irreversible process gives
99
a dissipation of energy, i.e. energy is lost. Entropy production can be calculated from the
dissipation function φ (J/(m3s)) as:
φ=T
n
dS
= ∑ JiΦi
dtdV i =1
(307)
where J i and Φ i are the conjugated fluxes ([…]/(m2s)) and forces (J/(kg[…])), respectively,
T is the temperature (K), S is the entropy (J/K)), t is the time (s) and V is the volume (m3).
Although transport processes are irreversible, in nonequilibrium thermodynamic theory,
these processes are assumed to be in local thermodynamic equilibrium. Local equilibrium
means that the Gibbs equation (Eq.(308)) holds for a small region of the space and for
changes in the variables that are actually not infinitely small.
TdS = dU + pdV − ∑ μ i dN i
(308)
i
where U (J) is the internal energy, P (Pa) is the pressure, μ (J/kg) is the chemical potential and
N is the number of moles. The moisture in a porous material may exist in the frozen, liquid or
vapor state; in addition, there will be some air. It is generally assumed that the change in
chemical potential of air is negligibly small. In addition, the frozen moisture is immobile, and
therefore no chemical changes take place. In this case, assuming also that the pressure is
constant, the thermodynamic forces of heat and mass transfer in a porous material can be
derived from Eq. (308) to be:
1
Φ q = − ∇T
T
(309)
Φ l = −T∇(μ l / T)
(310)
Φ v = −T∇(μ v / T)
(311)
The dissipation function can then be expressed as follows:
φ = J q Φ q + J l Φ l + J v Φ v = −J q
1
∇T − J l T∇(μ l / T) − J v T∇(μ v / T)
T
(312)
Transfer Fluxes
The all thermodynamic forces or gradients give rise to fluxes of heat, mass and other
forms of energy. If these gradients are not too large, it is a fundamental postulate of
irreversible thermodynamics that the fluxes are linear, homogeneous function of the
gradients. Thus:
100
n
J i = ∑ L ik Φ k
(313)
k =1
The coefficients Lik ([…]2/s) are called phenomenological because they are determined by the
rate at which the phenomena proceed. According to the Onsager’s fundamental theorem,
cross coefficients are symmetrical if a proper choice for the conjugated fluxes and forces is
made.
L ik = L ki
(314)
These identities are called the Onsager reciprocal relations. They express a connection
between two reciprocal phenomena. These reciprocal relations can be derived from the
principle of microscopic reversibility, using the statistical thermodynamics. Since the entropy
in an irreversible process must increase, Eq. (307) must be positive, which gives the two
additional restrictions to the phenomenological coefficients.
L ii ≥ 0
L ii L kk ≥ L2ik
(i=1,2…n)
(i ≠ k ;
(315)
i,k=1,2,…n)
(316)
In other words, the main coefficients must be positive or zero and the coupling coefficients
are limited in magnitude to the square root of the product between the corresponding main
coefficients. If there is no metastable equilibrium and all the forces and flows are
independent, the inequality sign holds in Eqs. (315) and (316).
The following set of phenomenological equations can be written for the mass and heat
transport in a porous material:
J q = L qq Φ q + L ql Φl + L qv Φ v
(for heat transfer)
(317)
J ml = L lq Φ q + L ll Φ w + L lv Φ v
(for liquid water transfer)
(318)
J mv = L vq Φ q + L vw Φ w + L vv Φ v
(for water vapor transfer)
(319)
In the material, vapor and liquid phases are in equilibrium. Therefore, the chemical potentials
and their gradients are equal:
μl = μ v = μ w
and
r
r
r
∇μ l = ∇μ v = ∇μ w
(320)
Consequently:
J q = L qq Φ q + (L ql + L qv ) Φw
(321)
101
J ml = L lq Φ q + L l Φ w
(322)
J mv = L vq Φ q + L v Φw
(323)
1
Φ q = − ∇T
T
(324)
Φ w = −T∇(μ w / T)
(325)
and
The equations (321-323) expresses that heat transfer depends not only on thermal
conduction but also on the redistribution of mass (Dufour effect) and mass transfer is
determined not only by differences in chemical potential but also by thermal diffusion (Soret
effect). From Onsager reciprocal relations, the cross coefficients are equal.
Lql = Llq
and
Lqv = Lvq
(326)
Since the chemical potential is a function of the intensive and specific state parameters, the
following equation can be written when pressure is constant:
r
∂μ r
∇Tμ w = w ∇T m
∂m
(327)
where m is the moisture content (kg moisture/kg dry solid). Taking all of these into account,
the mass and heat flux equations can be written as follows:
r
∂μ r
1
J ml = −L lw T w ∇ T m − L lq ∇T
∂m
T
(328)
r
∂μ r
1
J mv = −L vw T w ∇ T m − L vq ∇T
∂m
T
(329)
r
∂μ r
1
J q = −L qq ∇T − (L ql + L qv )T w ∇ T m
T
∂m
(330)
In practice, it is quite usual to present Eqs. (328-330) as follows:
r
r
r
J ml = −ρs D l (∇ T m + δ Tl ∇T)
(331)
r
r
r
J mv = −ρs D v (∇ T m + δ Tv ∇T)
(332)
102
r
r
∂μ r
J q = −λ∇T − ρ s (D l δ Tl + D v δ Tv )(T w ∇ T m)
∂m
(333)
where Dl (m2/s) and Dv (m2/s) are the diffusivities of the liquid and of the vapor, δTl (1/°C)
and δTv (1/°C) are the thermal gradient coefficients and λ (W/(m K) is the thermal
conductivity. Any potential gradient can result in moisture transfer. Under certain
circumstances a pressure gradient can arise in a moist body. Then there will be an associated
moisture flow.
r
r
J mP = δ P ∇Pg
(334)
where δP is the moisture filtration coefficient (kgm/(sN)). In drying applications Dufour effect
is generally omitted since it is not at significant levels [16, 94]. In addition, flux for liquid and
vapor phases are expressed in one single equation using effective parameters, instead of
defining separately. In this case, Eqs. (331)-(333) become as follows:
r
r
r
J m = −ρ s D(∇ T m + δ T ∇T)
(335)
r
r
J q = −λ∇T
(336)
Balance Equations
An analytical description of drying in a porous material can be obtained by using the
foregoing equations for the fluxes in mass and energy balances over the material.
Temperature Equation
The energy balance can be written as:
ρs C P
r r
4
∂T
= −∇ ⋅ J q − ∑ h i I i
∂t
i =1
(337)
4
where CP is the specific heat capacity (J/(kg K)) and ∑ h i I i is the heat source or sink. The
i=1
source or sink term is due to the phase change of the water within the porous body and can be
defined as follows [95]:
∑ h i I i = −Δh vap ε pc ∇ ⋅ [ρ s D(∇m + δ T ∇T)] − Δh vap ε pc ∇ ⋅ (δ P ∇Pg )
4
i =1
r
r
r
r
r
(338)
103
where Δh vap is the enthalpy difference for a change between the condensed and vapor states
(J/kg), ε pc is the ratio of vapor diffusion coefficient to the coefficient of total moisture
diffusion. Substituting Eqs. (336) and (338) into Eq. (337), we obtain:
ρs C P
∂T
= Δh vapε pcρs D∇ 2 m + (λ + Δh vapε pc δ T )∇ 2 T + Δh vapε pc δ P ∇ 2 Pg
∂t
(339)
Luikov [16] expresses moisture content in terms of moisture potential (m=CmW). Therefore:
ρs C P
∂T
= Δh vap ε pc ρ s C m D∇ 2 W + (λ + Δh vap ε pc δ T )∇ 2 T + Δh vap ε pc δ P ∇ 2 Pg
∂t
(340)
Moisture Content Equation
The mass balance for each species in the material can be written as:
ρs
r r
∂m i
= −∇ ⋅ J mi + I i
∂t
(341)
where I is the volumetric capacity of the source of the material (kg/(m3s)). The overall mass
can be obtained from Eq. (341) as:
ρs
r r
4
∂m
= −∇ ⋅ J m + ∑ I i
∂t
i =1
(342)
4
Since the moisture is neither lost nor created ( ∑ I i = 0 ). Substituting Eqs. (334) and (335)
i =1
into (342), we have:
ρs
∂m
= ρ s D∇ 2 m + ρ s Dδ T ∇ 2 T + δ P ∇ 2 Pg
∂t
(343)
Expressing moisture content in terms of moisture potential, Eq. (343) becomes:
ρs C m
∂W
= ρs C m D∇ 2 W + ρs Dδ T ∇ 2 T + δ P ∇ 2 Pg
∂t
(344)
Pressure Equation
Assuming that the moisture filtration of liquid is small as compared with that of vapor
and air, the mass flux equation can be written as follows:
104
r
r
r
r
J m = ∑ J mi = J mv + J ma
r
r
J m = −δ P ∇Pg
(345)
i
If the mass transfer equations for liquid and gas are summed, the following equation is
obtained:
ρs
r r
r
∂(u v + u a )
= −∇ ⋅ ( J mv + J ma ) + I v + I a
∂t
(346)
where u is the mass average velocity (m/s). The specific mass content of the vapor and the
gas mixture can be determined by gas equation as follows:
ρs ( u v + u a ) =
Pg M̂ g
R̂T
ψS
(347)
where P is the pressure (Pa), M̂ is the molar mass (kg/mol), R̂ is the ideal gas law constant
(8.314 J/(mol K)), ψ is the bulk porosity of the body, and S is the saturation of the pores and
capillaries in the body. On differentiating and assuming T2>>cP and T>>dS and letting
cP =
ψSM̂ g
(348)
ρ s TR̂
we obtain:
ρs
∂Pg
∂(u v + u a )
= ρs c p
∂t
∂t
(349)
where cp is the air capacity (kg m2/(kg N)). Substituting Eqs. (345) and (349) into Eq. (346)
yields:
ρs c P
∂Pg
∂t
= δ P ∇ 2 Pg − ρs ε pc C m
∂W
∂t
(350)
With the substitution Eq.(342) into Eq. (348), we obtain:
ρs c P
∂Pg
∂t
= −ε pc ρs C m D∇ 2 W − ε pc ρs Dδ T ∇ 2 T + (1 − ε pc )δ P ∇ 2 Pg
(351)
Let us write the balance equations again:
ρs C P
∂T
= Δh vap ε pc ρ s C m D∇ 2 W + (λ + Δh vap ε pc δ T )∇ 2 T + Δh vap ε pc δ P ∇ 2 Pg
∂t
(352)
ρs C m
ρs c P
∂W
= ρs C m D∇ 2 W + ρ s Dδ T ∇ 2 T + δ P ∇ 2 Pg )
∂t
∂Pg
∂t
105
(353)
= −ε pc ρs C m D∇ 2 W − ε pc ρs Dδ T ∇ 2 T + (1 − ε pc )δ P ∇ 2 Pg
(354)
A general set of boundary conditions for this system can be defined as follows [16]:
W = WS
δm
δ δ ∂T
∂W
+ h m ( W − Wa ) = 0
+ Jm + m T
C m ∂n
∂n
T = TS
λ
∂T
+ J q + h q (T − Ta ) + h m Δh vap (1 − ε pc )( W − Wa ) = 0
∂n
Pg = PS
on
Γ1
(355)
on
Γ2
(356)
on
Γ3
(357)
on
Γ4
(358)
on
Γ5
(359)
where hm is the convective mass transfer coefficient (kg/(m2s)) and hq is the convective heat
transfer coefficient (W/(m2K)). Subscripts a and S stand for ambient and surface respectively.
The first term in Eq. (358) is the amount of heat passing into the body, the second term and
the third term are the heat supplied at the surface, and the last term is the amount of heat
expended in the phase change of the fluid. The first term in Eq. (356) is the moisture flux in
the direction normal to the surface, while the last two terms describe the amount of moisture
removed from the surface.
Equations (356) and (358) can be written in a general form as [95]:
k11
∂T
+ J *q* = 0
∂n
k 22
∂W
+ J *m* = 0
∂n
(360)
where
J *q* = a q (T − Ta ) + a ε ( W − Wa ) + J *q J *m* = a δ (T − Ta ) + a m ( W − Wa ) + J *m
aε =
Δh vap h m
λ
(1 − ε pc )K 11
aq =
K11h q
λ
DJ q ⎤
⎡J
J *m = K 22 ⎢ m −
⎥
⎣ h m Cmλ ⎦
δ T Δh vap
K 22 δ T h q
⎡ 1
⎤
a m = K 22 h m ⎢
−
(1 − ε pc )⎥ a δ = −
Cmλ
Cm
⎣hm
⎦
J *q = (
K11
)
λ
(361)
(362)
(363)
106
The partial differential equations for temperature, pressure and moisture potential are not
symmetric; however, by multiplying Eq. (352) by δ T / C m , Eq. (353) by Δh vap ε pc and Eq.
(354) by −Δh vap δ p / δ m .a symmetric set of equations can be obtained.
c′q
∂T
= k11∇ 2 T + k12 ∇ 2 W + k13∇ 2 Pg
∂t
(364)
c′m
∂m
= k 21∇ 2 T + k 22 ∇ 2 W + k 23∇ 2 Pg
∂t
(365)
c′p
∂P
= k 31∇ 2 T + k 32 ∇ 2 W + k 33∇ 2 Pg
∂t
(366)
where
c′q = ρ s C P δ′T
k11 = (λ + Δh vapε pc δ T )δ′T k12 = k 21 = Δh vap ε pc δ m δ′T
(367)
k13 = k 31 = Δh vap ε pc δ P δ′T
(368)
c′m = ρ s Δh vap ε pc C m
c ′P =
−ρ s c P Δh vap δ P
δm
k 22 = Δh vap ε pc δ m
k 33 =
− Δh vap (1 − ε pc )δ 2P
δM
k 23 = k 32 = Δh vap ε pc δ P
(369)
where
δ m = ρs C m D
δ′m = δ m / C m
(370)
Analytical solution of Luikov heat and mass transfer differential equation system are only
obtained for simple geometrical shapes and boundary conditions. For a slab, a cylinder, and a
sphere, Luikov and Mikhailov [96] used the Laplace transform technique to obtain their
solutions. These same problems were also taken into account by Mikhailov and Özisik [97]
using the finite integral transform technique. They obtained the same solutions as those of
Luikov and Mikhailov [96]. However, it was seen subsequently that these solutions ignored
the possible existence of complex eigenvalues. If complex eigenvalues exist, these solutions
can be grossly in error [98]. More satisfactory solutions were also obtained for Luikov’s
differential equation system using different approaches (see Ref. [98, 99]).
KRISCHER MODEL
This model assumes that moisture transfer occurs with the combined effect of capillary
flow of liquid and diffusion of vapor. The main difference between Luikov and this model is
that, in the Luikov model, the total moisture content is assumed as the driving force for both
107
water and water vapor transport, while this model considers liquid water and water vapor
transport separately. In this model, the driving force for water vapor transport is assumed to
be the gradient of its partial pressure in the air and the driving force for liquid water transport
is taken as the gradient of the liquid moisture content. The flux and balance equations for this
model are as follows.
Liquid Phase
r
r
J ml = −ρ l K l ∇u
(371)
r
where J ml is the liquid flux (kg/m2s), ρl is the density of liquid water (kg/m3), Kl is the liquid
diffusivity (m2/s) and u is the liquid content by volume (m3 liquid/m3 solid).
Vapor Phase
r
D
M̂ r
J mv = − v,free v ∇Pv
ζ R̂T
(372)
r
where J mv is the flux of water vapor (kg/m2s), Pv is the partial pressure of water vapor in the
air (Pa), D v,free is the gas diffusion coefficient in open space (m2/s), ζ (>1) is the diffusion
resistance factor, which describes the decrease of the vapor flow in the porous medium in
comparison with that in stagnant gas. R̂ is the gas constant (8.314 J/(mol K)) and T is the
temperature (K).
Balance Equations
Let us look at, before expressing balance equations, what the approach of Krischer was
while constructing flux equations. ρ l u term in liquid mass flux equation can be written as
follows [58].
ρl u =
m l Vl m l
=
= Cl
Vl V V
(373)
If this equation is substituted into the flux equation, we obtain:
r
r
J ml = −K l∇C l
(374)
As can be seen, the equation used by Krischer for liquid transport is analogous to Fick’s law.
108
If the state equation is used, vapor transport equation can be expressed as follows:
r
D 1 r R̂T
J mv = −
∇(
Cv )
ζ R v T M̂ v
(375)
Let us assume that the temperature is constant too. In this case, it is possible to write:
r
r
D
J mv = − v,free ∇C v
ζ
(376)
In addition, if D v = D v,free / ζ is considered as the diffusion coefficient for porous material,
again a relation analogous to Fick’s law is obtained.
Assuming that transport parameters are constant, balance equations may be expressed as
follows.
∂u
= K l∇ 2 u
∂t
(for the liquid water)
(377)
∂ρ v D v,free 2
=
∇ Cv
∂t
ζ
(for the water vapor)
(378)
In order to get the same physical dimensions in both transport equations, the transport
equation for liquid water can be multiplied by ρw and the equation for water vapor transport
by M̂ v /(R̂T) . Therefore:
ρl
∂u
= ρl K l∇ 2 u
∂t
M̂ v ∂Pv M̂ v D v ,free 2
=
∇ Pv
R̂T ζ
R̂T ∂t
(379)
(380)
Krischer introduced two additional corrections in the mass balance equation for water
vapor. The first is the reduction of the accumulation term on the left-hand side by the
multiplication factor (ψ-u), which expresses the fact that water vapor can appear only in that
part of the porous space where water in the liquid state is not present, and its accumulation is
therefore limited to only that space [58]. There is no need for reduction in the term at the right
side of the equation. Because, the reduction for this term has already been made through the
diffusion resistance factor ζ. The second correction contains the inclusion of Stefan diffusion
[58]. Mass flux for Stefan diffusion is defined as follows (see Eq. (178)):
r
Pg r
D
1
J v = − v,free
∇Pv
ζ R v T Pg − Pv
109
(381)
where Stefan diffusion is defined by the multiplication factor Pg/(Pg-Pv). Therefore, mass
balance equation for vapor phase becomes:
(ψ − u )
M̂ v ∂Pv M̂ v D v,free Pg
=
∇ 2 Pv
R̂T ζ Pg − Pv
R̂T ∂t
(382)
The total mass balance of moisture can then be written as follows:
ρl
Pg
M̂ ∂P
M̂ D
∂u
∇ 2 Pv
+ (ψ − u ) v v = ρ l K l ∇ 2 Pv + v v ,free
∂t
R̂T ∂t
R̂T ζ Pg − Pv
(383)
BERGER AND PEI MODEL
In this model, the total internal moisture transfer is assumed to consist of two different
mechanisms. These are capillary flow of liquid due to gradient in liquid content, and the
diffusion of vapor through empty pores due to a gradient in partial vapor pressure. The
internal heat transfer is assumed to be governed by heat conduction and enthalpy of
vaporization. In addition, it is assumed that external heat and mass transfer is proportional to
the temperature and the partial vapor pressure difference between the surface of the drying
solid and the external drying media. The main difference of this model from the Krischer
model is that this model takes sorption isotherms into consideration, as opposed to Krischer
model, by using two coupling equations between the three dependent variables u, ρv and T.
These two equations are: the Clasius-Clapeyron’s equation and the equation of the sorptional
isotherm of the system.
Flux and balance equations for this model where Fick’s law is used to express both
internal mass transfer mechanisms are as follows:
Liquid Phase
r
r
J ml = −K l ρ l ∇u
(384)
where Kl is the liquid conductivity in the solid (m2/s), ρl is the density of the liquid (m3/kg)
and u is the liquid content by volume (m3 liquid/m3 solid).
110
Vapor Phase
r
M̂ r
J mv = −D v (ε void − u ) v ∇Pv
R̂T
(385)
where Dv is the vapor diffusivity (m2/s) and εvoid is the void fraction of solid (m3 air/m3 solid),
R̂ is the gas constant (8.314 J/(mol K)), T is the temperature (K), Pv is the vapor pressure
(Pa). It is assumed that the temperature changes are small. Therefore:
r ⎛ P M̂
M̂ v r
∇Pv = ∇⎜ v v
⎜ R̂T
R̂T
⎝
⎞ r
⎟ = ∇C v
⎟
⎠
(386)
r
r
J mv = −D v (ε void − u )∇C v
(387)
Balance Equations
If the Kl and Dv are assumed to be constant, the mass balance equations for the liquid
and vapor transfer can be written as follows:
ρl
∂u
= K l ρ l ∇ 2 u − I ev
∂t
(388)
[
]
r
r
∂
[(ε void − u )C v ] = D v∇ ⋅ (ε void − u )∇C v + I vap
∂t
(389)
where Ivap is the rate of evaporation (kg/(m3s). Using the two mass balance equations above,
the total moisture transfer equation can be expressed as:
∂C v
= K lρl∇ 2 u +
∂t
r
r
− u )∇ 2 C v − (∇u ) ⋅ (∇C v )
(ρ l − C v ) ∂u + (ε void − u )
∂t
[
D v (ε void
]
(390)
The rate of enthalpy of vaporization can be defined as: q vap = Δh vap I vap , where Δh vap is the
evaporation enthalpy (J/kg). In this case, the energy balance equation can be written as
follows:
r
r
Δh vap ⎧⎪ ⎡
⎤
∂ 2ρ v
∂T
= α∇ 2 T +
−
∇
⋅
∇
(
u
)
(
C v )⎥
⎨D v ⎢(ε void − u )
2
∂t
ρ s C p ⎪⎩ ⎢⎣
∂x
⎥⎦
∂C
∂u ⎫
− (ε void − u ) v + C v
⎬
∂t ⎭
∂t
(391)
111
where α is the thermal diffusivity (m2/s).
In the original model, proposed by Berger and Pei [100] it is considered a one
dimensional system seen in figure 23 and the following boundary conditions at x=0:
K lρl
∂C
∂u
+ D v (ε void − u ) v = h m (C v − C va )
∂x
∂x
h q (Ta − T) = Δh vap K l ρ l
∂u
∂T
−λ
∂x
∂x
(392)
(393)
where hm is the mass transfer coefficient (m/s), hq is the heat transfer coefficient (W/(m2K))
∂u
denotes the amount of
and λ is the thermal conductivity (W/(m K)) the term Δh vap K l ρ l
∂x x =0
heat required to evaporate the liquid flux at the surface.
It is assumed that no mass and heat is transferred across the surface of the drying material
at x=L. Therefore:
K lρl
∂C
∂u
= D v (ε void − u ) v = 0
∂x
∂x
∂T
=0
∂x
(394)
(395)
In the original model, moisture content with respect to volume has been used when
expressing the liquid flux. Today, it is preferred to use moisture content with respect to mass.
Furthermore, in the original model the temperature changes were assumed to be small and
therefore vapor concentration gradient has been used as driving force instead of partial vapor
pressure gradient. The flux and balance equations may be expressed as follows in terms of the
moisture content with respect to mass and vapor pressure:
r
r
J ml = −K l ρ s ∇m
(396)
r
r
r
M̂ ⎛ ε g − ε l ⎞ r
⎟∇Pv
J mv = −D v (ψ − u )∇ρ v J mv = −D v v ⎜⎜
R̂T ⎝ ε s ⎟⎠
(397)
K lρs
Kv
∂ 2m
∂m
− I ev = ρ s
2
∂t
∂x
M̂ ∂ ⎡⎛ ε − ε l ⎞ ⎤
M̂ v r ⎡⎛ ε g − ε l ⎞ r ⎤
⎟⎟∇Pv ⎥ + I ev = v ⎢⎜⎜ g
⎟Pv ⎥
∇ ⋅ ⎢⎜⎜
R̂T
R̂T ∂t ⎢⎣⎝ ε s ⎟⎠ ⎦⎥
⎣⎢⎝ ε s ⎠
⎦⎥
(398)
(399)
112
K l ρs ∇ 2 m + D v
r ⎤
ρ r
M̂ v ⎡⎛ ε g − ε l ⎞ 2
⎟⎟∇ Pv − s ∇m ⋅ ∇Pv ⎥ =
⎢⎜⎜
ρl
R̂T ⎣⎢⎝ ε s ⎠
⎥⎦
⎛
1 M̂ v Pv ⎞⎟ ∂m M̂ v ⎛ ε g − ε l ⎞ ∂Pv
⎜
⎟
ρ s ⎜1 −
+
⎜ ρ R̂T ⎟ ∂t
R̂T ⎜⎝ ε s ⎟⎠ ∂t
l
⎝
⎠
( )( )
λ
∂ 2 T Δh vap M̂ v ⎧⎪ ⎡⎛ ε g − ε l
∇ 2T 2 +
⎨D v ⎢⎜
ρs C p
ρ s C p R̂T ⎪⎩ ⎣⎢⎜⎝ ε s
∂x
⎛ εg − εl
⎜⎜
⎝ εs
(400)
r ⎤
⎞ 2
ρ r
⎟⎟∇ Pv − s ∇m ⋅ ∇Pv ⎥ −
ρl
⎥⎦
⎠
( )( )
(401)
⎞ ∂Pv ρ s ∂m ⎫⎪ ∂T
⎟⎟
+ Pv
⎬=
∂t ⎪⎭ ∂t
⎠ ∂t ρ l
where m is the moisture content by mass (kg moisture/kg dry solid) and εs, εl and εg are the
volume fraction of solid, water and gas, respectively.
External Drying Media
Jm
Jq,ext
x=0
Jmv
Jml
-Jq
q& vap
x
Ivap
Drying Material
x=L
Figure 23. Schematic view for Berger and Pei model (adapted from [100]).
WHITAKER MODEL
This model was proposed by Whitaker [71, 72] to describe the simultaneous heat, mass
and momentum transfer in a porous media. The biggest advantage of this model is that the
physics of the model is better understood, the assumptions are very clear and the parameters
are well defined. In addition, all mechanisms for mass and heat transfer were taken into
consideration: liquid flow due to capillary forces, vapor and gas flow due to convection and
diffusion, internal evaporation of moisture and heat transfer by convection, diffusion and
conduction.
113
Microscopic Equations
In this model a representative volume is considered as shown in figure 24 to express mass
and heat transfer. The figure at the left represents the microscopic scale and the figure at the
right the macroscopic scale. Porous structure is assumed to consist of three phases, namely,
solid, liquid and gas. The solid phase will be represented here by s, the liquid phase by l and
gas by g. The gas phase is assumed to consist of air (denoted by a) and vapor (denoted by v).
Figure 24. Pore and macroscale in a porous body (adapted from [93]).
At microscopic level, mass and heat transport equations can be derived using the
conservation laws as follow:
Mass Conservation
If it is assumed that no chemical reaction exists during the transport process, mass
conservation equation for each phase can be written as follows:
r
∂ρ r
+ ∇ ⋅ (ρv) = 0
∂t
(402)
where ρ is the concentration of phase considered (kg/m3). The mass conservation equation for
each species in the phase may be expressed as follows.
r
∂ρ i r
+ ∇ ⋅ (ρ i v i ) = 0 for i=1,2,..n
∂t
(403)
where ρi is the concentration of species i (kg/m3) and vi is the velocity of species i (m/s). The
following relations can be written for the velocities and concentrations of species:
114
r
ρ r
v = ∑ i vi ,
i ρ
ρ = ∑ ρi
(404)
i
where v is the mass average velocity (m/s) and ρ is the total concentration (kg/m3).
Linear Momentum Principle
For each phase, momentum conservation can be written as:
r
Dv r ~
ρ
=∇⋅σ
Dt
(405)
~ is the stress tensor (Pa). In the above equation, body forces such as gravitational
where σ
force are neglected. The angular momentum principle requires this tensor to be symmetric.
~=σ
~T
σ
(406)
Energy Conservation
Energy conservation for each phase can be written as follows:
r r
r
∂ (ρh ) r
DP ~ r r
+ ∇ ⋅ (ρhv) = −∇ ⋅ J q +
+ τ : ∇v
Dt
∂t
(407)
r
where h is the enthalpy per unit mass (J/kg), J q is conductive heat flux vector (W/m2), ~τ is
rr
the viscous stress tensor (Pa). The term ~τ : ∇v is the viscous dissipation, P is the pressure
(Pa) and DP / Dt is the compression work. In the above equation, the source or sink of
electromagnetic radiation was neglected. The viscous dissipation and the compression work
for the liquid and gas phase can also be neglected. Therefore, the energy equation becomes as
follows:
r r
r
∂ (ρh ) r
+ ∇ ⋅ (ρhv) = −∇ ⋅ J q
∂t
(408)
We can also assume that the enthalpy is independent of pressure. Therefore:
h = C P (T − TR )
(409)
where CP is the specific heat capacity (J/(kgK)) and TR is the reference temperature (°C).
The conservation laws can then be written for each phase as follows:
115
Solid Phase
r
The solid phase is considered to be rigid and fixed in space ( v s = 0 ). In this case, we
must deal only with the conservation of energy.
ρs
r r
∂h s
= −∇ ⋅ J qs
∂t
(410)
If the assumption defined in Eq. (409) is taken account and the conductive heat flux is
r
r
expressed as J q = −λ s ∇Ts according to the Fourier law, the energy equation can be written as:
ρs C Ps
∂Ts
= λ s ∇ 2 Ts
∂t
(411)
where λs is the thermal conductivity of the solid phase (W/(mK)).
Liquid Phase
The mass and energy conservation equation for the liquid phase can be expressed
asllows:
r
∂ρ l r
+ ∇ ⋅ (ρ l v l ) = 0
∂t
ρ l C Pl
(412)
r r
∂Tw
+ ρ l C Pl v ⋅ ∇Tl = λ l ∇ 2 Tl
∂t
(413)
Gas Phase
The gas phase is more complicated than the other phases since it contains two
components: air and vapor. The total mass conservation can be expressed as follows:
∂ρ g
∂t
r
r
+ ∇ ⋅ (ρ g v g ) = 0
v
(414)
v
The species velocity v gi can be written in terms of the mass average velocity v g and the
r
diffusion velocity u i :
r
r
r
v gi = v g + u i
(i=a,v)
Therefore, the mass conservation of air and vapor can be given as follows:
(415)
116
∂ρ gi
∂t
r
r
r
r
+ ∇ ⋅ (ρg i v g ) = −∇ ⋅ (ρ gi u i ) i =a,v
(416)
Moreover, by expressing the diffusive flux as:
r
r
ρ gi u i = −ρ g D va ∇(ρ gi / ρ g )
(417)
where D va is the binary molecular diffusion coefficient for vapor and air (m2/s), we obtain:
∂ρ gi
∂t
[
r
r
r
r
+ ∇ ⋅ (ρg i v g ) = ∇ ⋅ − ρ gi D va ∇(ρgi / ρ g
]
i=a,v
(418)
For a multicomponent phase, the energy conservation equation can be written as:
[
]
r
r r
r
∂
∑ (ρ gi h gi ) + ∇ ⋅ ∑ ρ gi h gi v gi = −∇ ⋅ J q
∂t i
i
(419)
The mass average enthalpy can be defined in a similar manner to the mass average velocity as:
h g = ∑ (ρ gi h gi / ρ g )
(420)
i
Therefore, Eq. (419) becomes as follows:
ρ g C Pg
∂Tg
∂t
r
r r
r
r
+ ρ g C Pg v g ⋅ ∇Tg = λ g ∇ 2 Tg − ∇ ⋅ (ρ a h a u a + ρ v h v u v )
(421)
where
C Pg = (ρ a C Pa + ρ v C Pv ) / ρ g
(422)
For the species of gas phase, ideal gas law can be assumed.
Pi = ρi R̂T / M̂ i
i=a,v
(423)
where R̂ is the ideal gas constant (8.314 J/(mol K)) and M̂ i is the molar mass of species i
(kg/mol). The total gas pressure can be written as:
Pg = Pa + Pv
(424)
117
Boundary Conditions
A general set of the boundary conditions must be defined to complete the set of
equations. Let us assume that Γlg represents the interface between liquid and gas phases, Γsl
the interface between solid and liquid and Γsg the interface between solid and gas. The
following relations are valid for these interfaces:
Γlg=Γgl
Γsl=Γls
Γsg=Γgs
(425)
The boundary conditions for the solid-liquid interface Γsw can be written as:
r
vl = 0
(426a)
r r
r r
J qs ⋅ n ls = J ql ⋅ n ls
(426b)
Ts = Tl
(426c)
r
r
r
where n ls ( n ls = −n sl ) is the unit normal vector directed from the liquid phase toward to the
solid phase. The boundary conditions for the solid-gas interface Γsg can be given as follows:
r
vg = 0
(427a)
r r
r r
J qs ⋅ n sg = J qg ⋅ n sg
(427b)
Ts = Tg
(427c)
The boundary conditions for the liquid-gas interface Γwg can be written as follows:
r
r r
r
r r
ρ v ( v v − w ) ⋅ n gw = ρ w ( v l − w ) ⋅ n gw
(428a)
r
r r
ρ a ( v a − w ) ⋅ n gw = 0
(428b)
r
r r
r
r r
ρ g ( v g − w ) ⋅ n gw = ρ w ( v l − w ) ⋅ n gw
(428c)
r
r
r
r
r r
ρ l (h v − h l )(v l − w ) ⋅ n gl = ( J ql − J qg ) ⋅ n gl
(428d)
Tl = Tg
(428e)
r
where w is the velocity of water-gas interface (m/s).
118
Volume Averaging Method
The equations defined above cannot be solved on a microscopic level since the geometry
of the porous medium and the distribution of the phases are not observable and are too
complex to describe. Whitaker [71, 72, 101] introduced the concept of the averaging
elementary volume to relate the microscopic geometrical and physical properties of the real
porous medium to the macroscopic properties of the continuum model. With this method,
governing equations are spatially smoothed leading to continuum equations defining the
transport process. Although the equations become solvable in this case, the method has its
own drawbacks, especially difficulties in determination of effective parameters that appear in
the macroscopic equations.
In volume averaging method, an averaging volume is associated to each point in porous
material. This volume can be in any shape. In figure 24 averaging volume is represented by a
circle. This representative volume provides upscaling of transport equations from pore scale
to macroscopic scale. There are three types of average used in the study of drying. These are:
spatial average, phase average and intrinsic average and they are defined as:
〈 y〉 =
1
∫ ydV
VV
〈 yi 〉 =
1
∫ y i dV
V Vi
〈 yi 〉 i =
1
∫ y i dV
Vi Vi
spatial average
(429)
phase average
(430)
intrinsic average
(431)
When it is interested in the average of some quantity related with a single phase, the phase
average is employed. However, it should be noted that if yi is constant, the phase average is
not equal to this value. In this situation, the use of intrinsic average is more appropriate.
The phase average and intrinsic average are related as.
〈 yi 〉 = εi 〈 yi 〉 i
(432)
where ε i is the volume fraction of the phase i ( ε i = Vi / V ).
Common expressions used in averaging are given below:
r
r
1 r
1 r
〈 ∇y w 〉 = ∇ 〈 y w 〉 +
n ws y w dΓ +
∫
∫ n wg y w dΓ
V Γws
V Γwg
(433)
r r
r r
1 r r
1 r r
〈 ∇ ⋅ v w 〉 = ∇〈 v w 〉 +
vw ⋅ n ws dΓ +
∫
∫ v w ⋅ n wg dΓ
V Γws
V Γwg
(434)
〈
r r
r r
∂〈 y w 〉 1
∂y w
1
−
y w w ⋅ n wg dΓ −
y w w ⋅ n ws dΓ
〉=
∫
∫
∂t
V Γwg
V Γws
∂t
119
(435)
Macroscopic Equations
The following macroscopic transport equations can be obtained by averaging the pore
scale transport equations over the averaging volume [71, 93]:
Mass Conservation
liquid phase
ρl
r r
∂ε l
+ ρl∇ ⋅ 〈 v l 〉 + 〈 J m 〉 = 0
∂t
(436)
vapor in the gas phase
(
)
(
[
)
r
r
r
r
~
∂
ε g 〈ρ v 〉 g + ∇ ⋅ 〈ρ v 〉 g 〈 v g 〉 − 〈 J m 〉 = ∇ ⋅ 〈ρ g 〉 g D eff ⋅ ∇(〈ρ v 〉 g / 〈ρ g 〉 g
∂t
]
(437)
air in the gas phase
(
)
(
)
[
r
r
r
r
∂
~
ε g 〈ρ a 〉 g + ∇ ⋅ 〈ρ a 〉 g 〈 v g 〉 = ∇ ⋅ 〈ρ g 〉 g D eff ⋅ ∇(〈ρ a 〉 g / 〈ρ g 〉 g
∂t
]
(438)
Energy Conservation
〈ρ〉 C P
[
]
[
r
r
r
~ r
∂〈T〉
+ ρ l C P l 〈 v l 〉 + 〈ρ g 〉 g 〈 C P 〉 g 〈 v g 〉 ⋅ ∇〈T〉 + Δh vap 〈 J m 〉 = ∇ ⋅ λ eff ∇(T〉
∂t
]
(439)
where
〈ρ〉 C P = ε s ρ s C Ps + εl ρl C Pl + ε g 〈ρ v 〉 g C Pv + ε g 〈ρ a 〉 g C Pa
(440)
〈ρ〉 = ε s ρs + εl ρl + ε g 〈ρ v 〉 g + ε g 〈ρ a 〉 g
(441)
with
and Δhvap is the evaporation enthalpy (J/kg). In Eq. (439), local thermal equilibrium is
assumed:
120
〈T〉 = 〈Ts 〉 s = 〈Tl 〉 l = 〈Tg 〉 g
(442)
~
~
The effective diffusivity D eff and effective thermal conductivity λ eff in Eqs. (437)-(438)
are obtained from the process of upscaling from pore scale transport equations to macroscopic
equations [71].
The capillary pressure is defined as the difference between gas pressure and liquid
pressure: 〈 Pc 〉 = 〈 Pg 〉 g − 〈 Pl 〉 l . Vapor pressure is determined from sorption isotherm.
With the analysis of the conservation of linear momentum, the following equations are
obtained for the liquid and gas phase:
~ ~
K i ⋅ k rg r
r
〈vg 〉 = −
.∇〈 Pg 〉 g
ηg
~ ~
r
K ⋅k r
〈 v l 〉 = − i rl .∇〈 Pl 〉 l ,
ηl
(443)
~
~
~
where K i is the intrinsic permeability tensor, k rl and k rg are the relative permeability
tensors.
To apply control volume method, Eqs. (436)-(439) must be reformulated as follows:
∂y r r
−∇⋅J
∂t
(444)
r
where y is a scalar quantity, and J is mass or energy flux vector. To reformulate the system,
a set of main variables must be selected to define the whole drying process. One possible
choice can be average temperature 〈T〉 , volume fraction of the liquid water ε l and intrinsic
phase average of air density in the gas phase 〈ρ a 〉 g . In this case, the system can be written as
follows if additionally the average notation 〈 〉 is dropped for simplicity [93]:
[
r
r
r
r
r
r
∂
ρ l ε l + ε g ρ v + ∇ ⋅ ρl v l + ρ v v g = ∇ ⋅ ρ g D eff ⋅ ∇(ρ v / ρ g
∂t
(
)
(
)
[
r
r
r
r
r
∂
ε g ρ a + ∇ ⋅ ρa v g = ∇ ⋅ ρ g D eff ⋅ ∇(ρ a / ρ g
∂t
(
(ε s ρ s
)
(
)
]
]
∂h s
∂h
∂h
∂h
+ ε lρl l + ε g ρ v v + ε g ρa a ) +
∂t
∂t
∂t
∂t
r r v
r
r r
ρ l C pl v l + (ρ v C Pv + ρ a C Pa ) v g ⋅ ∇T + Δh vap J m = ∇ ⋅ (λ eff ∇T)
[
]
(445)
(446)
(447)
In addition, the following relations can be written:
∂
∂
∂
(ε i ρ i h i ) = ε i ρ i ( h i ) + h i (ε i ρ i )
∂t
∂t
∂t
(448)
∂
(ε s ρ s ) = 0
∂t
hs
121
(449)
∂h s
∂h v
∂h a
∂h l
+ εlρl
+ εgρv
+ εgρa
)=
∂t
∂t
∂t
∂t
(ε s ρ s
∂
(ε s ρ s h s + ε l ρ l h l + ε g ρ v h v + ε g ρ a h a ) −
∂t
∂
∂
⎤
⎡ ∂
⎢h l ∂t (ε l ρ l ) + h v ∂t (ε g ρ v ) + h a ∂t (ε g ρ a )⎥
⎦
⎣
(450)
r
r
r
r r
r
∇ ⋅ (ρhv) = ρ v ⋅ ∇h + h∇ ⋅ (ρ v)
(451)
In this case, the second term on the left hand side of Eq. (447) becomes as follows:
[ρ C
l
]
[
]
r
r
r r
r
r
v l + (ρ v C Pv + ρ a C Pa ) v g ⋅ ∇T = ∇ ⋅ ρ l h l v l + (ρ v h v + ρ a h a ) v g −
r
r
r
r
r
r
h l∇ ⋅ (ρ l v l ) + h v ∇ ⋅ (ρ v v g ) + h a ∇ ⋅ (ρ a v g )
[
Pl
]
(452)
The enthalpy of vaporization can be expressed as: Δh vap = h v − h l at temperature T.
Therefore:
Δh vap J m ,vap = h v J m,vap − h l J m,vap
(453)
The evaporation rate Jm,vap can be computed in two different ways: one from the conservation
equation for liquid water, the other from the conservation equation for water vapor.
J m,vap = −ρ l
J m,vap =
r r
∂
(ε l ) − ρ l ∇ ⋅ ( v l )
∂t
(454)
[
r
r
r
r
r
∂
(ε g ρ v ) + ∇ ⋅ (ρ v v g ) − ∇ ⋅ ρ g D eff ⋅ ∇(ρ v / ρ g )
∂t
]
(455)
With the substitution of the equations given above, the energy equation becomes as follows:
r
r
r
∂
∑ ε i ρi h i + ∇ ⋅ ρl h l v l + ( ρv h v + ρa h a ) v g =
∂t i=s,w ,v,a
r
r
r
r
r
r
r r r
h a ∇ ⋅ ρ g D eff ⋅ ∇(ρ a / ρ g + h v ∇ ⋅ ρ g D eff ⋅ ∇(ρ v / ρ g + ∇ ⋅ λ eff ∇T
(
[
)
]
[
]
(
)
(456)
The energy equation can be further simplified by assuming that, within the averaging volume,
the variation of enthalpy is small compared with its value.
122
r
r
r
∂
∑ ε i ρi h i + ∇ ⋅ ρl h l v l + ( ρv h v + ρa h a ) v g =
∂t i=s,w ,v,a
r
r
r
r
r
r
r r r
∇ ⋅ ρ g h a D eff ⋅ ∇(ρ a / ρ g + ∇ ⋅ ρ g h v D eff ⋅ ∇(ρ v / ρ g + ∇ ⋅ λ eff ∇T
(
[
)
]
[
]
(
)
(457)
CAPILLARY FLOW MODEL
If the capillarity is the primary mode for transport, two different formulations may be
expressed under isothermal conditions. One of these is capillary pressure formulation and the
other capillary diffusivity formulation [8].
Capillary Pressure Formulation
⎞
∂C l r ⎛
Kk r
+ ∇ ⋅ ⎜⎜ − ρ l i rl ∇(P − Pc ) ⎟⎟ = −I vap
∂t
ηl
⎝
⎠
(458)
where C is the concentration (kg/m3), ρ is the density (kg/m3), Ki is the intrinsic permeability
(m2), kr is the relative permeability, η is the viscosity (Pa s), Pc is the capillary pressure (Pa)
and Ivap is the rate of evaporation (kg/(m3s)). If Pc >>P (capillary pressure is large) and Ivap=0
(no significant evaporation):
∂C l r ⎛ K i k rl r ⎞
+ ∇ ⋅ ⎜⎜ ρ l
∇Pc ⎟⎟ = 0
∂t
ηl
⎝
⎠
(459)
In this form of transport equation both water concentration and capillary pressure are
involved. This equation is also known as Richard’s equation. Generally, capillary head h (m)
is used instead of capillary pressure [8]. In this case, Eq. (459) can be written as:
∂C l r ⎛ K i k rl ρ l g r ⎞
+ ∇ ⋅ ⎜⎜ ρ l
∇h ⎟⎟ = 0
∂t
ηl
⎝
⎠
(460)
⎛ ∂C l ⎞ ∂h r ⎛ K i k rl ρ l g r ⎞
+ ∇ ⋅ ⎜⎜ ρ l
∇h ⎟⎟ = 0
⎜
⎟
ηl
⎝ ∂h ⎠ ∂t
⎝
⎠
(461)
or
where g is the gravitational acceleration (m/s2), ∂C l / ∂h is the specific moisture capacity.
123
Capillary Diffusive Formulation
Another formulation equivalent to capillary pressure formulation for capillary flow may
be expressed as follows [8]:
∂C l
= D l∇ 2 Cl
∂t
(462)
This equation is similar to the commonly used diffusion equation. In Eq. (462), Dl is the
capillary diffusivity of liquid water and is defined as:
D l = −ρ l2 g
K i k rl ∂h
ηl ∂C l
(463)
Datta [8] reported that it will be better to use capillary pressure formulation in multi-domain
foods, since the capillary pressure variation with moisture content will be different in
different domains of material.
When a formulation is used in which capillary pressure (head) is the driving force, the
most important problem arises from the determination of the relationship between capillary
head and moisture content. Such a relation can be obtained only using other material
properties data. One of the relations to be used for this purpose is Kelvin’s equation [102].
EMPRICAL AND SEMI-EMPRICAL MODELS
Due to the complexity of transport mechanisms, empirical and semi-empirical models are
often used to describe the thin-layer drying behavior of food materials. Of these models, those
used frequently are given in table 14. The empirical models constitute a direct relationship
between the average moisture content and the drying time. They neglect the fundamentals of
the drying process and therefore their parameters have no physical meaning. The semitheoretical models are generally derived by simplifying general series solutions of Fick's
second law or they are modified forms of simplified models. The empirical and semiempirical models require small time compared to theoretical models and do not need
assumptions of geometry of a typical food, its mass diffusivity and conductivity, et cetera.
[103]. Therefore they are useful for automatic control processes. Empirical and semiempirical models are valid within the temperature, relative humidity, air flow velocity and
moisture content range for which they were developed [104]. Among these drying models,
the Page models, the Henderson and Pabis model, the two-term exponential model and the
Midilli et al. model are widely used models to simulate the thin layer drying behavior of food
materials.
124
Lewis Model
In this model, mass transfer is expressed by analogy to heat flow from a body immersed
in a cool fluid, in other words, to Newton’s law of cooling [105]. The drying rate is assumed
to be proportional to the difference in moisture content between the material being dried and
equilibrium moisture content at the drying air condition. The most important drawback of this
model is that it generally overpredicts the early stages and underpredicts late stages of the
drying process.
Page and Modified Page Models
Page model has been proposed by Page [106] to eliminate the drawback of the Lewis
model. For this purpose, Page [106] introduced an exponent to time term in Levis model.
However, the introduction of the exponent causes the model to become a purely empirical
model. This parameter has an effect of moderating the time and the model in this case gives
better results for the prediction of moisture loss.
Henderson and Pabis Model
Various approximations and variations of the diffusion model have been used to simulate
the drying behavior of food materials. The model proposed by Henderson and Pabis [107] is
of this type and corresponds to the first term of a general series solution of Fick’s second law.
The slope of this model, coefficient k, is related to effective diffusivity when drying process
takes place only in the falling rate period and liquid diffusion controls the process [108].
Two Term Exponential, Diffusion Approach, Verma et al., Logarithmic,
Midilli et al., Jena and Das Models
These models are modified forms of the Henderson and Pabis model, based on
simplification of a general series solution of Fick's second law. Among these models, two
term exponential and Midili et al. model have been used frequently because they produce
better fit to experimental data as compared to other models.
Two Term, Modified Henderson and Pabis Models
It is not possible to express drying behavior of food materials having several
compartments with the first term of a general series solution of Fick’s second law with the
sufficient accuracy due to different drying resistance in each compartment. In such cases,
exponential terms equal to the number of compartments must be used to define drying in each
compartment. Two term and Modified Henderson and Pabis models have been proposed to
simulate the drying process of such type of materials. Sharma et al. [109] used these two- and
125
three-term models to simulate the thin-layer drying behavior of rough rice with three
compartments, the hull, bran and endosperm.
Geometric, Thompson, Wang and Singh, Logistic, Weibull Distribution
Models
All of these models are empirical models and have been proposed for simulating the
drying behavior of various types of food materials. For example, Thompson model has been
suggested to simulate the drying behavior of shelled corn in the temperature range 60–150°C
[110]. Wang and Singh model has been proposed to simulate the drying of medium-grain
rough rice [111].
The coefficient of correlation (r) can be used to determine the suitability of the empirical
and semitheoretical models in describing the experimental drying data. Correlation coefficient
values close to one mean the fit is good. In addition to correlation coefficient; standard
deviation (es) and mean squared deviation (χ2) can be used to determine suitability of the fit.
These parameters are defined as follows [112]:
n obs
n obs
n obs
n obs ∑ mrpre ,i mrexp,i − ∑ mrpre ,i ∑ mrexp,i
r=
i =1
i =1
⎛
⎞
n obs ∑ (mrpre ,i ) 2 − ⎜ ∑ mrpre ,i ⎟
i =1
⎠
⎝ i=1
n obs
n obs
2
i =1
⎛ n obs
⎞
n obs ∑ ( mrexp,i ) 2 − ⎜ ∑ mrexp,i ⎟
i =1
⎝ i=1
⎠
n obs
2
(464)
n obs
∑ (mrpre,i − mrexp,i ) 2
es =
i =1
n obs
(465)
n
χ2 =
∑ (mrpre,i − mrexp,i ) 2
i =1
n obs − n const
(466)
where mrpre,i is the ith predicted moisture ratio, mrexp,i is the ith experimental moisture ratio,
nobs is the number of observations and nconst is the number of constants in the drying model.
126
Table 14. Thin-layer drying models
Name
Lewis
Model equation
mr = exp(− kt )
N.C.
Page
mr = exp(−kt )
2
Modified Page
mr = exp(−(kt ) )
2
Modified Page II
mr = exp(−c( t / L2 ) n )
2
Henderson&Pabis
mr = a exp(− kt )
2
1
n
n
Geometric
mr = at
−n
2
Wang&Singh
mr = 1 + at + bt 2
2
Two term exponential
mr = a exp(− kt ) + (1 − a ) exp(− kat )
2
Thompson
t = a ln mr + b(ln mr ) 2
2
Logarithmic
mr = a 0 + a exp(−kt )
3
Logistic
mr = a 0 /(1 + a exp(kt ))
3
Diffusion approach
mr = a exp(− kt ) + (1 − a ) exp(− kbt )
3
Verma et al.
mr = a exp(−kt ) + (1 − a ) exp(−gt )
3
Two term
mr = a 1 exp(− k 1 t ) + a 2 exp(− k 2 t )
4
Midilli et al.
mr = a exp(− kt ) + bt
4
Jena and Das
mr = a exp(−kt + b t ) + c
4
Weibull distribution
mr = a − b exp(−(kt ))
4
Modified Henderson and Pabis
mr = a exp(− kt ) + b exp(−gt ) + c exp(−ht )
6
n
n
where mr is the moisture ratio, t is the time (s), L is the characteristic length (m) and a, b, c, n, k, g and
h are the empirical constants
8. SHRINKAGE
The drying process causes shrinkage in volumes and heat and mass exchange areas of
food materials. This shrinkage in the drying process particularly affects the diffusion
coefficient of the material significantly. Heat and mass transport and shrinkage are generally
coupled. The following procedure is followed in coupling. Shrinkage is modeled with respect
to moisture content, including sometimes other physical properties, and this predetermined
relationship of dimensional changes is used to modify the geometry with time in the
simulation [8]. Shrinkage models used in the literature are given in the comprehensive review
prepared by Mayor and Sereno [46]. Of these models, those given in tables 15 and 16 are
empirical models. Mayor and Sereno [46] states that linear empirical models are adequate to
describe materials and process conditions leading to negligible porosity development during
the drying process, or to a uniform development of porosity, corresponding to a linear
decrease of volume in the whole range of humidity. If development of porosity increases
sharply during the final stage of drying, linearity is lost and the behavior is best described by
nonlinear models seen in table 16 such as exponential models or a quadratic model [46, 113].
These models usually produce a good fit with the experimental data, but their use is limited
because of their dependence on the drying conditions and on the material and they require
127
extensive experimental testing and should not be extrapolated. For modeling shrinkage, some
fundamental models are also used. They are based on mass balances, density and porosity
definitions and assume in most cases additivity of the volumes of the different phases in the
system [46]. These fundamental methods have been classified by Mayor and Sereno [46] in
three groups: models which show a linear shrinkage behavior throughout the whole drying
process (table 17); models which include deviations of this linear behavior (table 18) and
models which include explicitly variations of the porosity through the drying process (table 19).
The fundamental models allow the prediction of moisture content and/or change in volume to
be obtained without complicated mathematical calculations. Furthermore, it is not usually
necessary to obtain experimental shrinkage values at every process conditions, as in the case
of empirical models.
Table 15. Linear empirical models for shrinkage (adapted from [46])
Model
Geometry and reduced dimension
slab-thickness; cylinder-volume
sphere-radius
ellipsoid-(x,y,z coordinates);
sphere-radius
cylinder-volume
Material
Apple
Soybean
Apricot
Carrot, Amylose starch gel,
Broccoli stem
slab-(thickness,width,length);
sphere-volume;
(cube,cylinder)-volume
sphere-volume
cylinder-(volume, radial, axial)
slab-(thickness, width, length)
sphere-volume
Grape
Green bean
Fish muscle (shark)
Fish muscle (ocean perch)
Cherry
D R = a 1ε w + a 2
Fish muscle (ocean perch)
D R = 1 + βm
cube-volume
slab-thickness
cylinder-volume
Apple, carrot, potato
gelatin gel, carrot
Apple, carrot, banana, potato
E ⎤
⎡
D R = 1 + ⎢a 1 exp(− a )⎥ m
R̂T ⎦
⎣
T (Kelvin)
sphere-volume
Grape
D R = a 1 + (a 2 + a 3 φ + a 4 T)Δm
sphere-bed volume
wheat, canola
D R = (a 1T + a 2 ) + (a 3 T + a 4 ) m
cylinder-volume
Potato
D R = a 1m + a 2
Potato
where ai is the empirical constants, m moisture content (kg water/kg dry solid), εw the volume fraction
of water (volume of water/total volume), β shrinkage coefficient, Ea activation energy (J/mol),
R̂ universal gas constant (8.314 J/(mol K)), T temperature (°C), φ relative humidity.
128
Table 16. Non-linear empirical models for shrinkage (adapted from [46])
Model
D R = 0.16 + 0.816(m / m o ) +
Geom.& Red. dim.
Material
cylinder-volume
Carrot, pear, potato,
sweet potato
slab-volume
Garlic
A v / A vo = a 1 + a 2 m + a 3 m 2 + a 4 m 3
cylinder-surface area to
volume ratio
D R = a1 + a 2 m + a 3m 2 + a 4 m3
cylinder-bed volume
D R = a 1 + a 2 exp(−a 3 t )
slab-surface area
slab-thickness
Potato, squash
Apple
hemispherediameter;
cylinder-length
Cauliflower
D R = a 1 + a 2 m + a 3 m 3 / 2 + a 4 exp(a 5 m)
slab-thickness
Garlic
D R = a 1 + a 2 ( m / m o ) + a 3 (m / m o ) 2
(cylinder, slab)-volume
D R = a 1 exp(a 2 m / m o )
(cylinder, slab)-volume
0.022 exp(
0.018
m
) + b1 (1 −
)
m + 0.025
mo
b1 = 0.209 − b 2
D R = a1 + a 2
b2 =
0.966
m o + 0.796
m
m
+ exp(a 3
)
1+ m
1+ m
Apple,
carrot,
potato, squid
Apple,
carrot,
potato, squid
where ai is the empirical constants, m moisture content (kg water/kg dry solid), Av the surface area to
the volume ratio (1/m).
Table 17. Linear fundamental models for shrinkage (adapted from [46])
Model
Geom.& Red. dim.
V ⎛ m + 0.8 ⎞ A ⎛ V ⎞
⎟
⎟;
=⎜
=⎜
Vo ⎜⎝ m o + 0.8 ⎟⎠ A o ⎜⎝ Vo ⎟⎠
V
m
= b1 + b 2
Vo
mo
b1 =
Material
2/3
m o (ρ s / ρ w )
1
, b2 =
m o (ρ s / ρ w ) + 1
m o (ρ s / ρ w + 1
Vegetables
volume
Sugar beet root
cube-area
Carrot, potato, sweet
potato, radish
cube-area
potato, radish
Uniform drying model
A ⎛ V
=⎜
A o ⎜⎝ Vo
⎞
⎟
⎟
⎠
2/3
a)
m + b1
1
1
V
=
; b1 = m e ( − 1) +
ρe
ρe
Vo
m o + b1
b)
ρo
V
= b1 m + b 2 , b 1 =
, b 2 = 1 + b1 − ρ o
Vo
mo + 1
Core drying model
1 − b2
V
= b1 m + 1 , b1 =
,
Vo
mo − me
(m e + 1)ρ o
A
V
b2 =
,
= ( )2/3
(m o + 1)ρ e A o
Vo
where m is the moisture content (kg water/kg dry solid), A area (m2), V volume (m3), ρ density (kg/m3).
129
Table 18. Non-linear fundamental models for shrinkage (adapted from [46])
Model
Semi-core drying model
V
= b1 m + b 2
Vo
b1 =
Material
cube-area
potato, radish
cylinder-volume
Cassava root
A
V
= ( )2/3
Ao
Vo
1 − b3
m o − m e + b 4 (b 3 m o − m e + b 3 − 1)
b m − m e − b 4 (b 3 m o − m e + b 3 − 1)
b2 = 3 o
m o − m e − b 4 (b 3 m o − m e + b 3 − 1)
b3 =
Geom.& Red. dim.
(m e + 1)ρ o
ρ − (1 − m)ρ e
, b4 = e
ρo
(m o + 1)ρ e
D r = b1 + b 2 (m / m o ) + 0.26b 3 (1 − m / m o ) 3
b1 =
m o (ρ s / ρ w )
1
, b2 =
m o (ρ s / ρ w ) + 1
m o (ρ s / ρ w + 1
b3 =
0.966
m o + 0.796
where m is the moisture content (kg water/kg dry solid), A area (m2), V volume (m3), ρ density (kg/m3).
Table 19 Fundamental models for shrinkage including porosity (adapted from [46])
Model
Geom.&Red.dim.
Material
cylinder-volume
sweet potato
cylinder-volume
sweet potato
Model A (inclusion of initial porosity)
⎛
⎞
m
D R = ⎜⎜ b1
+ b 2 (m) ⎟⎟ b 3
⎝ mo
⎠
−1
(
)
χ sg. + ρ sn (m)b 4 b1
⎛ χ sg. ρ sn ,o
⎞
+
b1 = ⎜⎜1 +
b 4 ⎟⎟ , b 2 =
mo
mo
mo
⎝
⎠
b3 =
χ
χ
1 − ψ (m o )ρ sn (m o )
, b 4 = cw + st
1 − ψ (m)ρ sn (m)
ρ cw ρ st
Model B (without inclusion of initial porosity)
1 (b1 + χ sg / ρ sg + χ / ρ sn )ρ o
DR =
(1 − ψ )
mo + 1
χ
χ
b1 = cw + st
ρ cw ρ st
DR =
1 ⎡ ρ o (m − m o ) ⎤
⎢1 +
⎥
(1 − ψ ) ⎣
ρ w (1 + m o ) ⎦
slab-volume
Beef meat
DR =
ρo 1 + m
(1 − ψ ex − ψ )
, ρ= m
)
ρ 1 + mo
∑ m i /(ρ T ) i
slab-volume
Squid
⎤
1 ⎡ ρ o (m − m o )
− ψo ⎥
⎢1 +
ρ w (1 + m o )
(1 − ψ ) ⎣
⎦
cylinder-volume
Apple,
potato,
carrot, squid
i =1
DR =
)
where m is the moisture content (kg water/kg dry solid), m mass fraction (kg/kg total mass), χ constituent concentration
3
(kg/kg dry solid), ψ porosity, ρ density (kg/m ).
130
9. DIFFUSIVITY
In a porous material, various diffusion coefficient definitions exist depending on the
transport mechanism. Diffusion may in general be divided into two parts as molecular and
capillary diffusion. Molecular diffusion can occur in liquid and gas phase. Molecular
diffusion in the gas phase becomes more important when the water saturation decreases.
Generally, liquid and gas diffusion are expressed in one single equation instead of defining
individually. In this case, diffusivity becomes an effective parameter. This effective
diffusivity value is different from diffusivity value which is only for liquid or for gas.
Capillary diffusivity has two components one due to moisture gradient and the other due to
temperature gradient. Capillary diffusivity due to the temperature gradient is mostly omitted.
Capillary diffusivity data is generally unavailable. However, effective diffusivity data
available in the literature is close to capillary diffusivity when the material is very wet
because the molecular diffusion in that condition is insignificant [102]. For materials with low
moisture content, effective diffusivity is close to molecular diffusivity.
Diffusion coefficient for a porous material is generally determined experimentally.
Commonly used techniques are: sorption kinetics method, permeation method, concentrationdistance curve method and drying method. Among these techniques, drying method is the one
widely used. Although there are alternative approaches to determine diffusivity by drying
method, all approaches are based on diffusion equation. Different approaches based on the
drying method are given below.
Simplified Methods
In these methods, solution of diffusion equation is used to determine diffusion
coefficient. Series solutions of the diffusion equation for some simple geometries are as
follows.
mr =
8
π2
⎡
π 2 D eff t 1
π 2 D eff t
π 2 D eff t
1
−
+
exp(
−
9
)
+
exp(
−
25
)+
exp(
)
⎢
9
25
4L2
4L2
4L2
⎣
⎤
π 2 D eff t
1
exp(−49
) + ..⎥
2
49
4L
⎦
mr =
(467)
π 2 D eff t
π 2 D eff t
π 2 D eff t
1
6 ⎡
1
exp(
9
)+
−
+
exp(
−
4
)
+
−
exp(
)
⎢
9
4
L2
π2 ⎣
L2
L2
⎤
π 2 D eff t
1
exp(−16
) + ..⎥
2
16
L
⎦
(468)
Deff t
D t
) + 0.131 exp(−30.5 eff2 ) +
L
L2
D t
D t
0.0534 exp(−74.9 eff2 ) + 0.029 exp(−139.1 eff2 ) + ..
L
L
(469)
m r = 0.692 exp(−5.78
131
where L is the characteristic length (m). Since the values of the exponential terms of Eq.
(467) (for infinite slab), Eq. (468) (for sphere) and Eq. (469) (for infinite cylinder) except the
first terms contribute little to moisture ratio when the value of D eff t / L2 is greater than 0.2, the
first term can be taken into account for finding the effective moisture diffusivity. If, also,
natural logarithms are taken of these equations, they become as:
ln(m r ) = ln
8 π 2 D eff
−
t
π2
4L2
(470a)
ln(m r ) = ln
6 π 2 D eff
−
t
π2
L2
(470b)
π 2 D eff
(470c)
t
L2
From Eqs. (470), plots of ln(mr) versus drying time t give straight lines with the slopes of
ln(m r ) = ln 0.692 − 5.78
Slope =
π 2 D eff
4L2
Slope =
π 2 D eff
L2
Slope = 5.78
π 2 D eff
L2
(471)
These slopes are used as a measure for the diffusivity (see figure 25).
x
ln(mr)
x
x
x
Slope=f(Deff;L)
x
x
x
x
x
x
t
Figure 25. Experimental drying curve.
This method can not be used when the diffusion coefficient is strongly dependent on
concentration. In this case, the following procedure is followed in determining the diffusivity.
The theoretical moisture ratio is evaluated numerically for a range of the Fourier numbers.
Then, the same ratio is evaluated using experimental data. Subsequently, both theoretical and
experimental moisture ratio curves are plotted versus time and the Fourier number on a
semilogarithmic diagram as shown in figure 26. Moisture diffusivity is determined with the
help of the following equation by comparing the slopes of both curves [114]:
132
⎛ ∂m r ⎞
⎜
⎟
⎝ ∂t ⎠ exp 2
L
D=
⎛ ∂m r ⎞
⎜
⎟
⎝ ∂t ⎠ the
1.0
(472)
x
x
x
mr
x
x
experimental
x
0.1
x
theoretical
x
x
x
x
0.0
0
2
4
6
0.0
0.2
0.4
0.6
8 t (h) 10
0.8 Fo
1.0
Figure 26. Theoretical and experimental drying curves (adapted from [114]).
Regular Regime Method
The regular regime method with which concentration dependent diffusivity can be
calculated is based on the experimental measurement of the regular regime curve. Regular
regime curve is the drying curve when it becomes independent of the initial concentration
profile. The method assumes that material is homogeneous and nonporous, however it can
also be applied to cellular tissue foods such as apples and potatoes [115]. In this method, the
diffusion equation is solved numerically for the regular regime period of an isothermal
diffusion process to obtain diffusivity. Regular regime method is rather complicated and
needs successive interpolations and differentiations of the experimental drying data.
However, a short-cut method has also been proposed to avoid this rigorous procedure [116].
Regression Analysis Method
In this method, first partial differential equations governing drying process are created.
Geometry and particular boundary conditions are taken into consideration. Diffusivity is
mostly expressed as a parametric model of local moisture content, temperature, or any other
property. Following assignment of initial guess for parameters contained in the diffusion
coefficient, the partial differential equation system is solved numerically. The values obtained
are compared with experimental values with non-linear regression analysis. If the criterion of
the least sum of squares is not satisfied, a new guess of the model parameters is fed back to
the numerical calculation. Procedure is continued until a final convergence is obtained.
133
Diffusion coefficient of food materials are mostly obtained by using one of the drying
techniques given above. For various food materials, diffusion coefficients or correlations
obtained using the diffusivity data are given in table 20. Diffusion coefficient is affected by
many physical properties. Brief explanations on these factors are given below.
Temperature
The dependence of the diffusivity on temperature is generally described by the Arrhenius
equation as follows:
D eff = D o exp(−
Ea
R̂T
(473)
)
Potential Energy
Here Do is the diffusion coefficient factor, R̂ is the universal gas constant (8.314 J/(mol K)),
T is the air temperature (K) and Ea is the activation energy (J/mol). Activation energy values
for various food materials are given in table 21. Activation energy is used to describe
temperature dependence of diffusion coefficient. According to the energy levels involved in a
reaction and to the collision theory of reactive molecules, enough energy must be generated to
provide the necessary activation energy to be able to develop the reaction (figure 27) [114,
117]. Activation energy will not itself provide any idea of the reactivity of a given system,
only information on temperature dependence of the reaction. Activation energy is also related
to moisture content. The activation energy for diffusion increases at lower moisture contents
since generally the interaction forces between moisture and solid are higher at lower moisture
contents.
energy level in an activated state
activation energy
for reverse reaction
average energy
of reactants
activation
energy
average energy of reactants
heat of reaction
Figure 27. Potential energy levels during a given endothermic reaction [114, 117].
134
Pressure
Under certain conditions, there may be a significant increase in the gas pressure inside
the material during drying. As it can be seen from Eqs. (161)-(163), gas pressure is inversely
proportional to diffusion coefficient and any increase in the gas pressure causes gas diffusion
coefficient to decrease.
Composition
Moisture diffusivity of most food materials shows a strong dependence on composition.
Diffusivity is generally small for small values of moisture content and shows an increase with
increasing moisture content and approaches to a constant value for values of moisture content
higher than a certain value. Concentration dependence of diffusion coefficient is generally
expressed by relations in linear, polynomial and exponential forms. Also, some studies show
that an increase in the salt content of food materials leads to a decrease in moisture diffusivity
particularly for high temperature and low moisture content. A decrease is also observed in the
diffusion coefficient of some food materials with an increase in fat content. Some other
studies show that with an increase in protein content, moisture diffusion coefficient can take
higher values.
Shrinkage
Diffusion coefficient is highly affected by shrinkage. This effect is due to the decreasing
diffusion path in shrinking media [118]. Some researchers incorporated the volume change into
the diffusion coefficient in order to take account the shrinkage effect on transport properties.
They suggested multiplying the diffusion coefficient by a power of the volume changing
factor, which is the ratio between the actual volume and a reference volume that is either the
basic initial volume or the volume of the totally dried samples [119]:
⎛V⎞
D eff
= ⎜⎜ ⎟⎟
D eff ,R ⎝ Vo ⎠
n
(474)
The power exponent used by Crank [74] was 2 and by Fish [120], 2/3. Another approach used
in the literature is based on calculating first a reference diffusion coefficient by using the
initial thickness of the product. The diffusion coefficient obtained can thereafter be corrected
for the shrinkage by applying:
⎛ L ⎞
D eff
= ⎜⎜ ⎟⎟
D eff ,R ⎝ L o ⎠
n
(475)
The shrinkage during drying is sometimes neither ideally three-dimensional, nor onedimensional. For these cases, the following equation is suggested for the diffusion
135
coefficient [121, 122]:
⎛V⎞
D eff
= ⎜⎜ ⎟⎟
D eff ,R ⎝ Vo ⎠
2/ n
(476)
where the exponent n equals to 1 for one-dimensional shrinkage and equals to 3 for isotropic
three-dimensional shrinkage. This parameter n may be viewed as a measure of the degree of
isotropicity of the deformation and is related to volume shrinkage by [119]:
Sb = Sdn
(477)
where Sb and Sd are defined as
Sb =
V
Vo
Sd =
L
d
or
d o Lo
(478)
Other Factors
In food materials enzymatic and microbiological changes may also have an effect on
diffusion coefficient. Enzymatic reactions may change the internal properties of food
material. Furthermore, the micro-organisms may also influence the surface of the food
material, changing the equilibrium moisture content of food at the surface. Another factor
acting on diffusion coefficient is pretreatment. Food materials may be exposed various types
of pretreatment before drying. Pretreatment generally causes a change in the porosity of food
materials and this leads to a change in diffusion coefficient.
CONCLUSION
A large number of models have been proposed to simulate drying process of food
materials. The basic reason of such an abundance of model propositions is the variety of
transport mechanisms involved in drying process and complexity of material structures.
Models based on continuum approach are preferred generally to simulate drying at
macroscopic level. Among proposed models based on continuum approach, Whitaker model
is one step ahead of other models in that physical basis of this model is stronger. However,
the empirical character of transport coefficients as in other models based on the continuum
approach constitutes the most important drawback of this model. The majority of transport
coefficients show a stronger dependence on concentration, temperature and material structure.
The effect of concentration and temperature on transport parameters is relatively well known
and various models have been proposed to express these effects. However, there is relatively
limited knowledge on the effect of structure on transport. It may be said that determination
the effects of structure on transport will hereafter be one of the basic topics in studies related
drying behavior of food materials.
Table 20. Moisture diffusion coefficients of various food materials
Material
Meth&Geom
Apple
(Red Delicious)
Slope
Cylinder
Apple (organic)
Slope
Slab
Apple pomace
Slope
Slab
Apricot
Slope
Slab
Banana
Regression
Cylinder
Banana
Slope
Slab
Barley
-
Basil leave
Slope
Slab
Bean
Regression
Sl.-Sph.
Drying Conditions
Hot air
m=0.06-8.5, T= 40-70°C
v=3 m/s ,d=0.7cm , L=10d
PT: water bath
Hot air
mw=0.11-0.82, T=40-60°C
v=0.8m/s, L=5-9 mm
PT: 5% lemon solution
Microwave
mw=0.25-0.40
N=150-600W
Hot air
mw=0.16-078, T=50-80°C
v=0.2-1.5m/s
Hot air
m=0.2-3.8, T=60-80°C
v=1.3 m/s
Hot air (Tunnel)
m=0.24-4, T=40-60°C
v=0.3-0.7m/s, L=4mm
Effective Diffusion Coefficient (m2/s) Dmin=4.13x10-12 Dmax=1.041x10-5
D eff = 1.65x10 −6 exp(−
19.34
)
Ref.
123
R̂Tab
Deff= 2.27x10-10 –Deff=4.97x10-10
124
Deff=1.0465x10-8 for N=150W , Deff=2.2130x10-8 for N=30W
Deff=2.7157x10-8 for N=450W , Deff=3.6854x10-8 for N=600W
125
D eff = 1.14x10 −7 + 2.25x10 −9 T + 1.47 x10 −7 v
126
D eff = 1.36 x10 −7 exp(−
13.4
)
127
R̂Tab
Deff =6.61x10-11 for T=40°C, v=0.3 m/s
Deff =1.95x10-10 for T=60°C, v=0.3 m/s
Deff =1.61x10-10 for T=50°C, v=0.5 m/s
Deff =9.80x10-11 for T=40°C, v=0.8 m/s
Deff =2.41x10-10 for T=60°C, v=0.8 m/s
,
,
,
,
Deff =1.57x10-10 for T=50°C, v=0.3 m/s
Deff =7.33x10-11 for T=40°C, v=0.5 m/s
Deff =2.23x10-10 for T=60°C, v=0.5 m/s
Deff =1.74x10-10 for T=50°C, v=0.8 m/s
128
m=0.10-0.27
T=30-70°C
Open sun
mw=0.04-0.87
Te=30-36.5°C
ϕe=0.24-0.28
qs=195-796 W/m2
Deff=1.31x10-11-6.52x10-10
129
Deff =6.44x10-12
130
T=25-40°C
Deff=4.35x10-11-3.79x10-9
131
Table 20. (Continued).
Material
Meth&Geom
Beef Meat
Slope
Slab
Biscuit
-
Black grape
Black tea particle
Broccoli floret
Carrot
Slope
Sphere
Slope
Sphere
Drying Conditions
Hot air
m=0.1-2.8, T=6.6-40.4°C
d=38mm h=10mm
m=0.10-0.60
T=20-100°C
Hot air
mw=0.25-0.79, T=60°C
v=1.1 m/s
PT: Potassium carbonate
solution: 5% K2CO3 +
0.5% olive oil
PT: Ethyl oleate plus
potassium
carbonate
solution
potassium
hydroxide
solution
sodium carbonate solution
Hot air
T=80-120°C
v=0.25-0.65m/s
D eff = 5.09x10 −6 exp(
24.643
)
Ref.
132
R̂Tab
Deff=8.6x10-10-9.4x10-10
133
Deff =3.82x10-10
Deff =1.05x10-9
134
Deff =1.28x10-9
Deff =8.64x10-10
Deff =7.97x10-10
D eff = 1.68x10 −7 exp(−
406.02
)
R̂Tab
135
Regression
Hot air
T=50-75°C
v=1.2-2.25m/s
l=10mm
Deff=3.5780x10-6 for T=50°C, v=1.2m/s , Deff=5.9747x10-6 for T=60°C, v=1.2m/s
Deff=16.6770x10-6 for T=75°C, v=2.25m/s
136
Slope
Sphere
Hot air
mw=0.06-088, T=50-70°C
v=0.5-1.0m/s
Dims: 1x1x1cm
2x2x2cm
Deff=0.776x10-9 - 9.335x10-9
137
Material
Carrot
Meth&Geom
Slope
Slab
Carrot
Slope
Slab
Carrot core
Slope
Cylinder
Carrot cortex
Slope
Cylinder
Celery
Inverse M.
Chelwa
Slope
Cylinder
Cherry
(sweet)
Regression
Sphere
Drying Conditions
Hot air
m=0.2-14, T=55-75°C
v=1.6 m/s, Dims:1x1x1cm
D eff = 3.0x10 −6 exp(−
22.1426
PT: NaCl
D eff = 4.0 x10 −8 exp(−
10.0017
PT: Sucrose
D eff = 2.0 x10 −7 exp(−
14.8729
PT: Sucrose+NaCl
D eff = 3.0x10 −7 exp(−
16.2130
Infrared
mw=0.0-0.9, T=50-80°C
L=1-2mm
Hot air
m=1.17-6.39, T=40-70°C
v=1.5,3m/s, d=0.7cm
PT: water bath
Hot air
m=1.05-5.31, T=40-70°C
v=1.5-3m/s, d=0.7cm
PT: water bath
m=0.09-9.82
T=49.1°C
ρc=461-1428kg/m3
L=3-10mm
Open sun
m=0.1-2.5,Te=32.5-42.5°C
ϕe=0.15-0.32
qs=460-820W/m2
Hot air
m=0.1-2.6, T= 50-80°C
φ=0.05-0.5, v=1-5 m/s
Ref.
)
R̂Tab
)
R̂Tab
138
)
R̂Tab
)
R̂Tab
Deff =7.295x10-11 for T=50°C , Deff =9.309x10-11 for T=60°C
139
Deff =6.42x10-10 -14.7x10-10
140
Deff =6.68x10-10 -13.6x10-10
140
Deff = 7.98x10−4 exp(0.130m −
3217.3 1323.7
+
)
ρc
Tab
141
D eff = 17.57 x10 −11 exp(−1.591m m )
142
143
Material
Meth&Geom
Cherry
(sour)
Slope
Sphere
Chestnut
Slope
Sphere
Drying Conditions
Hot air
mw=0.2-0.82, T=55-65°C
v=1 m/s
Hot air
m=0.04-0.50, T=70-90°C
Ref.
Deff =4.75x10-10 for T=55°C, Deff =5.57x10-10 for T=65°C
144
D eff = 1.2152 x10 −5 exp(−
22.578
D eff = 9.8684 x10 −6 exp(−
21.926
20.458
Chestnut
Slope
Sphere
Hot air
m=0.04-0.40, T=70-90°C
D eff = 6.6979 x10 −6 exp(−
Chickpea
Regression
Sphere
T=15-40°C
9.71x10-11-5.98x10-10
Coconut presscake
Coffe cherry
Corn
Slope
Slab
Regression
Sphere
Slope
Sphere
Vacuum
m=0.02-1.038
P=65 mmHg
T=65-75°C, L=2-4 mm
Hot air
mw=0.11-0.66T=45,60°C
Hot air
mw=0.14-0.3, T=55-75°C
PT: alkali solution
)
for Longal variety
)
for Martainha variety
)
for Viana variety
R̂Tab
145
R̂Tab
R̂Tab
D eff = 0.3753x10 −8 exp(549.8L −
145
129
171.9
)
T
146
Deff =0.1x10-10-1x10-10 for T=45°C , Deff =0.3x10-10-3x10-10 for T=60°C
147
Deff =9.488x10-11 for T=55°C,Deff =1.153x10-10 for T=65°C,Deff =1.768x10-10
for T=75°C
Deff =1.424x10-10 for T=55°C,Deff =1.733x10-10 for T=65°C,Deff =2.716x10-10
or T=75°C
148
Cracker
-
m=0.03-0.14
T=40-90°C
Deff=1.41x10-11-1.81x10-9
129
Date (red soft )
Slope
Sphere
Hot air
m=0.4-1.6, T=50-80°C
v=1.5 m/s
149
Date (tempo 2)
Slope
Sphere
Hot air
m=0.4-1.5, T=50-80°C
v=1.5 m/s
149
Material
Meth&Geom
Drying Conditions
Ref.
Date (tempo 3)
Slope
Sphere
Hot air
m=0.5-1.5, T=50-80°C
v=1.5 m/s
149
Dough
-
M=0.20-0.50
T=15-203°C
Deff=1.30x10-10-1.00x10-9
129
Dill leave
Slope
Slab
Hot air
mw=0.05-0.82, T=50-70°C
v=1.1 m/s
Deff =6.69x10-10 for T=50°C , Deff =9.21x10-10 for T=60°C , Deff =1.43x10-9 for
T=70°C
150
Eggplant
Slope
Slab
Fig
Slope
Sphere
Fig
Slope
Sphere
Vacuum
m=0.0-0.16, T=30-50°C
P=2.5,5,10kPa
Dims: 45x25x20mm
Open sun
mw=0.25-0.74,Te=3547°C
Hot air (conditioned)
m=0.14-1.9, T=55-85°C
ϕ=0.10 , v=0.5-3 m/s
D eff = 2.012x10 −4 exp(−
29.52
)
Tab
151
Deff =2.47x10-10
152
D eff = 4.83x10 −4 exp(−
37.27
D eff = 2.01x10 −2 exp(−
45.81
R̂Tab
) , D eff = 8.77 x10 −5 exp(−
) ,
R̂Tab
D = 5.99 x10 −2 exp(−
30.81
) for v=0.5 and 1 m/s
R̂Tab
48.47
R̂Tab
) eff
for v=2.0 and 3
153
m/s
Garlic
Slope
Slab
Garlic
Regression
Slab
Hot air
m=0.08-1.56, T=40-60°C
v=0.8m/s, L=3-5mm
Hot air
m=0.27-1.35, T=50-80°C
v=2-4m/s
D eff = 1.61x10 −6 exp(−
23.48
)
154
R̂Tab
D eff = 7.490x10 −6 exp(−
27.84
R̂Tab
)
155
Material
Meth&Geom
Grape
Regression
Sphere
Grape (Sultana)
Slope
Slab
Green bean
Slope
Slab
Green pepper
Slope
Slab
Kale
Slope
Slab
Kiwi
Regression
Slab
Lentil
Regression
Slab
Mango
Slope
Slab
Minced meat
-
Milk (skimmed)
Minced meat
Drying Conditions
Hot air
m=0.2-2.4, T=40-70°C
v=1-2.3m/s
PT: alkali solution
(1% of sodium hydroxide)
D eff = 1.6x10 −3 exp(−
Hot air
m=0.18-3 , T=65°C
v=0.45m/s
Hot air
mw=0.14-0.9, T=50-70°C
v=1 m/s , L=4cm (length)
Hot air
mwo=0.94, T= 25-45°C
v=4.1 m/s , l=10mm
Hot air
mw=0.16-0.86, T= 3060°C
v= 1 m/s
L=10-50mm (layer thick)
Hot air
m=0.15-4.65, T=30-90°C
L=6mm
D eff = 0.522 exp(−
Ref.
) exp[− (0.0075Tab + 1.829)m ]
54
R̂Tab
156
49
R̂Tab
) exp[− (0.0012Tab + 0.309)m ]
Deff=6.44 x10-10
157
D eff = 5.53x10 −4 exp(−
35.43
)
R̂Tab
D eff = 1.320x10 −2 exp(−
51.4
)
R̂Tab
Deff =14.8894x10-10 – 55.9451x10-10
D eff = 1.476 x10 −5 exp(−
27
)
R̂Tab
158
159
160
161
T=15-40°C
Deff=3.53x10-10-1.33x10-9
131
Hot air
m=0.08–8, T=55-65°C
L=2.8 mm
Hot air
m=0.3-1.8, T= 30-120°C
T=65°C
162
Deff =5.0x10-11-53.0x10-11
114
-
m=0.3-0.8, T=30-50°C
Deff= 0.24x10-10-2.1x10-10
163
-
Hot air
m=0.3-1.8, T= 30-120°C
-11
Deff =5.0x10 -53.0x10
-11
114
Material
Meth&Geom
Mint leave
Slope
Slab
Mint leave
Slope
Slab
Mulberry
Regression
Slab
Mullet roe
Slope
Slab
Murici
Regression
Slab
Olive cake
Slope
Slab
Olive
extraction
oil
Olive
extraction
oil
Slope
Slab
Regression
Slab
Okra
Slope
Sphere
Onion
-
Drying Conditions
Open sun
mw=0.1-0.86,
Te=30-36.5°C
φe=0.24-0.28
qs=195-796W/m2
Hot air
mw=0.1-0.85, T=35-60°C
v=4.1m/s
Hot air
m=0.1-4.6, T=60-80°C
v=1.2 m/s
Hot air
m=0.3-1, T= 20-40°C
v=1.0 m/s
Dims.20x10x3cm
Hot air
mwo=0.88, T= 50-70°C
v=1.5 m/s
Hot air
mw=0.05-0.45
T=50-110°C, v=1.2m/s
Hot air
m=0.1-2 , T=20-80°C
v=1.0m/s
Hot air
mw=0.05-0.45
T=80-110°C, v=1.2m/s
Hot air
mw=0.15-0.9 , T=50-70°C
v=1m/s
m=0.10-10
T=40-80°C
Ref.
Deff =7.04x10-12
130
Deff =3.067x10-9 for T=35°C , Deff =5.837x10-9 for T=45°C,
164
Deff =2.32x10-10, Deff =2.84x10-10, Deff =3.58x10-10 for T=60,70,80°C (CRP)
Deff =5.03x10-10, Deff =6.68x10-10, Deff =8.43x10-10 for T=60,70,80°C (FFRP)
Deff =2.63x10-9 , Deff =2.30x10-9 , Deff =2.76x10-9 for T=60,70,80°C (SFRP)
165
D eff = 19.8x10 −4 exp(−
37.2
)
R̂Tab
166
D
Deff =1.275x10-9 for T=50°C , Deff =1.975x10-9 for T=60°C, Deff =2.906x10-9 for
T=70°C
D eff = 3.128x10 −6 exp(−
17.97
D eff = 1.615x10 −7 exp(−
15.77
167
)
168
)
169
R̂Tab
R̂Tab
Deff=4.89x10-8 - 9.98x10-8
170
T=50°C
171
Deff=1.38x10-11-6.60x10-9
129
Material
Meth&Geom
Orange skin
Regression
Slab
Regression
Slab
Drying Conditions
Hot air
m=0.25-3.66, T=30-90°C
v=2.5 m/s, L=0.45cm
Hot air
mw=0.3-088, T=40,60°C
v=1.25-3.25m/s
Papaya
PT: osmotical
D = 3.957 x10 −4 exp(−
36.36
m −0.0496 )
172
R̂Tab
Deff =1.72x10-9
v=1.25m/s
Deff =2.21x10-9
v=3.25m/s
Deff =1.03x10-9
v=1.25m/s
Deff =1.11x10-9
v=3.25m/s
Ref.
for T=40°C and v=1.25m/s , Deff =2.71x10-9
for T=60°C and
for T=60°C and
for T=60°C and
for T=60°C and
173
Parsley leave
Slope
Slab
Open sun
mw=0.06-0.84
Te=30-36.5°C
ϕe=0.24-0.28
qs=195-796 W/m2
Parsley leave
Slope
Slab
Hot air
mw=0.05-0.82, T=50-70°C
v=1.1 m/s
T=70°C
150
Pasta
-
mw=0.05-0.27, T=40-74°C
Deff=0.8x10-11-9.3x10-11
163
Pasta (Semolina)
Regression
Slab
Hot air
m=0.14-0.50, T=40-100°C
Dims:100.0x20.0x1.3mm
Deff = 1.2x10−11 exp(−3036.95(
Pea
-
T=30-65°C
Deff=3.1x10-10-6.6x10-10
Slope
Hot air
m=0.16-7.52, T= 55-65°C
v=0.8 m/s, L=3.5mm
PT: 1% KMS
PT: 1% ascorbic acid
Peach
Deff =4.53x10-12
130
1
1
−
) exp(6.46m)
T 293
174
163
175
Material
Meth&Geom
Pear
Regression
Sphere
Pineapple
-
Pistachio nuts
Slope
Sphere
Drying Conditions
mw=0.2-0.8, T=30-50°C
v=0.5-1.5m/s, ϕ=0.4-0.6
L=4mm
Ref.
1 + 1.2987 x10 −2 m
24.3
exp(−
)
1 + 4.5111x10 −1 m s
R̂Tab
176
D eff = 1.1276 x10 −5
m=3.80-5, T=30-50°C
Deff=5.38×10-12-2.64×10-9
Hot air
mw=0.37-0.05
T=25-70°C
ϕ=0.05- 0.2
v=0.5-1.5m/s
Deff=1.37x10-10
Deff =2.26x10-10
Deff =5.24x10-10
Deff =7.01x10-10
Deff =5.42x10-11
Deff =2.29x10-10
Deff =4.91x10-10
Deff =8.82x10-10
Deff =1.70x10-10
Deff =3.26x10-10
Deff =5.25x10-10
Deff =8.07x10-10
Deff =1.36x10-11
Deff =2.98x10-10
Deff =5.82x10-10
Deff =8.40x10-10
Deff =1.80x10-10
Deff =3.48x10-10
Deff =5.75x10-10
Deff =9.29x10-10
Deff =1.81x10-11
Deff =3.25x10-10
Deff =5.90x10-10
Deff =8.90x10-10
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
for
T=25°C, φ=0.05, v=0.5 m/s
T=40°C, φ=0.05, v=0.5 m/s
T=55°C, φ=0.05, v=0.5 m/s
T=70°C, φ=0.05, v=0.5 m/s
T=25°C, φ=0.20, v=0.5 m/s
T=40°C, φ=0.20, v=0.5 m/s
T=55°C, φ=0.20, v=0.5 m/s
T=70°C, φ=0.20, v=0.5 m/s
T=25°C, φ=0.05, v=1.0 m/s
T=40°C, φ=0.05, v=1.0 m/s
T=55°C, φ=0.05, v=1.0 m/s
T=70°C, φ=0.05, v=1.0 m/s
T=25°C, φ=0.20, v=1.0 m/s
T=40°C, φ=0.20, v=1.0 m/s
T=55°C, φ=0.20, v=1.0 m/s
T=70°C, φ=0.20, v=1.0 m/s
T=25°C, φ=0.05, v=1.5 m/s
T=40°C, φ=0.05, v=1.5 m/s
T=55°C, φ=0.05, v=1.5 m/s
T=70°C, φ=0.05, v=1.5 m/s
T=25°C, φ=0.20, v=1.5 m/s
T=40°C, φ=0.20, v=1.5 m/s
T=55°C, φ=0.20, v=1.5 m/s
T=70°C, φ=0.20, v=1.5 m/s
129
177
Material
Meth&Geom
Drying Conditions
Pistachio nuts
Slope
Sphere
mw=0.37-0.05
T=25-70°C
ϕ=0.05- 0.2
v=0.5-1.5m/s
Plantain
(Musa AAB)
-
Plum
Slope
Slab
m=0.12-1.2, T=37-62°C
φ=0.01, v=3.6m/s
L=7.2-20mm
Hot air
m=0.09-9.86, T=55-65°C
L=3.5 mm
Deff=1.37x10-10 for T=25°C, φ=0.05, v=0.5 m/s
Deff =2.26x10-10 for T=40°C, φ=0.05, v=0.5 m/s
Deff =5.24x10-10 for T=55°C, φ=0.05, v=0.5 m/s
Deff =7.01x10-10 for T=70°C, φ=0.05, v=0.5 m/s
Deff =5.42x10-11 for T=25°C, φ=0.20, v=0.5 m/s
Deff =2.29x10-10 for T=40°C, φ=0.20, v=0.5 m/s
Deff =4.91x10-10 for T=55°C, φ=0.20, v=0.5 m/s
Deff =8.82x10-10 for T=70°C, φ=0.20, v=0.5 m/s
Deff =1.70x10-10 for T=25°C, φ=0.05, v=1.0 m/s
Deff =3.26x10-10 for T=40°C, φ=0.05, v=1.0 m/s
Deff =5.25x10-10 for T=55°C, φ=0.05, v=1.0 m/s
Deff =8.07x10-10 for T=70°C, φ=0.05, v=1.0 m/s
Deff =1.36x10-11 for T=25°C, φ=0.20, v=1.0 m/s
Deff =2.98x10-10 for T=40°C, φ=0.20, v=1.0 m/s
Deff =5.82x10-10 for T=55°C, φ=0.20, v=1.0 m/s
Deff =8.40x10-10 for T=70°C, φ=0.20, v=1.0 m/s
Deff =1.80x10-10 for T=25°C, φ=0.05, v=1.5 m/s
Deff =3.48x10-10 for T=40°C, φ=0.05, v=1.5 m/s
Deff =5.75x10-10 for T=55°C, φ=0.05, v=1.5 m/s
Deff =9.29x10-10 for T=70°C, φ=0.05, v=1.5 m/s
Deff =1.81x10-11 for T=25°C, φ=0.20, v=1.5 m/s
Deff =3.25x10-10 for T=40°C, φ=0.20, v=1.5 m/s
Deff =5.90x10-10 for T=55°C, φ=0.20, v=1.5 m/s
Deff =8.90x10-10 for T=70°C, φ=0.20, v=1.5 m/s
Ref.
Deff =2.32x10-10 -18.01x10-10
178
T=65°C
179
177
Material
Plum (Stanley)
Meth&Geom
Slope
Sphere
Pollen
Sphere
Pork lean
-
Potato
Regression
Slab
Potato
Slope
Cylinder
Prawn
Slope
Cylinder
Prune
Regression
Sphere
Pumpkin
Slope
Slab
Drying Conditions
Hot air
T=60-80°C, v=1-3 m/s
-9
Deff =1.179x10 -6.671x10
180
PT: 2% NaOH solution
Deff =1.197x10-7-4.551x10-7
Fluidized bed
m=0.03-0.1, T=40-45°C
D eff = 1.0285x10 −6 exp(−
Hot air
m=0.4-1.0, T= 10-30°C
Hot air
m=0.25- 2, T=40-85°C
v=0.5, 1 m/s,
Dims:45x 20x10 mm
Hot air
m=0.24-3.55, T=40-70°C
v=1.5,3m/s, d=0.7-1.4cm
PT: water bath
Open sun
m=0.1-3, Te=32.5-42.5°C
ϕe=0.15-0.32
qs=460-820W/m2
Hot air (Tunnel)
m=0.02-0.2, T=70-80°C
v=5m/s
Hot air
mw=0.1-0.92, T=50-60°C
v=1 m/s , L=0.7 cm
29.69
)
R̂Tab
Deff =1.1x10-11-2.0x10-11
D eff = 7.18x10 −5 exp(−
Ref.
-9
181
114
31580
R̂Tab
) exp[(−0.0025Tab + 1.22)m ]
182
Deff =4.55x10-10 -10.2x10-10
140
D eff = 18.09 x10 −11 exp(−1.279m m )
142
T=70°C
183
Deff=3.88x10-10 for T=50°C, Deff=6.58x10-10 for T=55°C, Deff=9.38x10-10 for
T=60°C
184
Drying Conditions
Hot air
m=0.04 -0.67, T=40-60°C
v=0.8 m/s
D eff = 1.95x10 −5 exp(−
Open Sun
m=0.05 -0.67,
Te=21.6-39.7°C
ϕe=12.1-51.5
qs=205.1-796.2 W/m2
Deff=1.66 x10-11
Solar Tunnel
m=0.05 -0.67
Deff=1.94 x10-11
Quince
Regression
Slab
m=0.3-4.7, T=35-55°C
v=0.2-0.6m/s, ϕ=0.4-0.7
L=4mm
Deff =0.65x10-10-6.92x10-10
Quinoa seed
Regression
Sphere
Hot air
m=0.09-0.26, T=30-90°C
D eff = − 2.11x10 −7 m o + 7.95x10 −7 exp(−
Raisin
-
M=0.15-2.40, T=60°C
Deff=5.0x10-11-2.5x10-10
133
Red bell pepper
(Lamuyo)
Slope
Slab
Hot air
m=0.02-10.11, T=50-80°C
v=2.5 m/s, Dims:1x1x1cm
Deff=3.2x10-9 for T=50°C , Deff=6.9x10-9 for T=60°C
Deff=10.2x10-9 for T=70°C , Deff=11.2x10-9 for T=80°C
188
Red pepper
Slope
Slab
Red pepper
Slope
Cylinder
Red pepper
Slope
Cylinder
Material
Pumpkin seed
(hull-less)
Meth&Geom
Slope
Slab
Hot air
mwo=0.91, T= 25-45°C
v=4.1 m/s , l=10mm
Hot air
m=3.25-0.11, T=50-65°C
v=0.4 m/s
Rotary dryer
m=1.05-3.3, T=50-65°C
v=0.8 m/s
33.15
Ref.
)
R̂Tab
185
186
(
)
D eff = 0.043x10 −2 exp(−
42.8
37.76
D eff = 1.95x10 −5 exp(−
24.76
187
159
)
189
)
190
R̂Tab
R̂Tab
)
R̂Tab
)
R̂Tab
D eff = 4.92x10 −3 exp(−
37.98
Drying Conditions
Hot air
m=0.06-1.22
T= 110–180°C
v=0.5-3 m/s
-
M=0.50-0.53
T=40-100°C
Deff=2.38x10-11-4.84x10-10
129
Rose hip
Regression
Sphere
Hot air
m=0.07-0.49, T=50-80°C
v=15 m/s
192
Rough rice (long)
-
Hot air
mo=0.13, T=12-50°C
D eff = 8.24 x10 −4 exp(−
49.19
Rough rice
(medium)
-
Hot air
mo=0.22, T=40-70°C
D eff = 5.08x10 −4 exp(−
43.56
Rough rice (short)
-
Hot air
mo=0.32,T=35-54°C
D eff = 9.33x10 −3 exp(−
53.37
Rough rice
Regression
Cylinder
Hot air
m=0.24-1.22
T= 40–60°C
v=1.5-3 m/s
D eff = 1.64v −0.85 exp(−
Rough rice
Regression
Ellipsoid
Hot air
m=0.24-1.22
T= 40–60°C
v=1.5 m/s
Deff= 4.176x10-8
Deff= 4.644x10-8
Deff= 5.508x10-8
Deff= 5.976x10-8
Deff= 7.524x10-8
Salami
-
Soya bean
(Nidera A6381)
Regression
Sphere
Material
Meth&Geom
Rice
(cooked)
Slope
Cylinder
Rice (parboiled)
Hot air
m=0.4-0.45, T= 10-20°C
Hot air
m=0.14-0.27, T=19-75°C
v=0.23m/s
D eff = 2.5x10 −5 exp(−
36.44
)
Ref.
191
R̂Tab
)
193
)
194
)
195
R̂Tab
R̂Tab
R̂Tab
4706
)
v 0.076 Tab
for T=40°C
for T=45°C
for T=50°C
for T=55°C
for T=60°C
84
87
Deff =0.03x10-11-0.37x10-11
114
Deff =1.78x10-11-7.28x10-11
196
Material
Meth&Geom
Soya bean
(Nidera A5409)
Regression
Sphere
Soya bean
SlopeSlab
Soya bean
(Brazilian Doko)
Regression
Sphere
Squid mantle
Regression
Hollow
cylinder
Sugar beet
-
Tomato
Slope
Slab
Drying Conditions
Hot air
m=0.10- 0.30, T=25-70°C
v=0.23m/s
Hot air
m=0.10-0. 3, T=30,50°C
v=0.5-1.5m/s
Hot air
mw=0.11-0.82
T= 31.5–58.5 C
v= 0.33–3.17 m/s
Hot air
m=0.148-2.74, T= 34.3°C
v=1.05 m/s
(
)
D eff = 4.51x10 −7 + 1.9x10 −8 m o exp(−
27
)
196
R̂Tab
Deff =2.38x10-10 for T=30°C and v=0.5m/s
v=0.5m/s
v=1.0m/s
v=1.0m/s
v=1.5m/s
Ref.
, Deff =2.50x10-10
for T=40°C and
, Deff =2.43x10-10
for T=30°C and
, Deff =2.84x10-10
for T=50°C and
, Deff =2.83x10-10
for T=40°C and
197
Deff
4848.5
= 8.64 exp(−
) exp(3.8m)
Tab
R2
198
D eff = 8.23x10 −11 exp(0.0646mr)
199
T=40-84°C
Deff=0.4x10-10-1.3x10-10
163
Hot Air
mw=0.11-0.94, T=55-70°C
v=1.5 m/s
D eff = 6.987 x10 −5 exp(−
32.94
)
R̂Tab
17.40
200
PT: alkaline ethyl oleate
solution
D eff = 3.284x10
Deff =1.31x10-9
201
Deff=7.61×10-12-3.62×10-9
129
Tomato (organic)
Slope
Slab
Solar tunnel
mw=0.12 -0.93
T=22.4-35.6°C
ϕ=14.5-50.9
qs=202.3-767.4W/m2
Turnip
-
m=0.31-7, T=20-100°C
−7
exp(−
)
R̂Tab
Material
Meth&Geom
Wheat (broom)
Regression
Ellipsoid
Wheat
(parboiled)
Slope
Sphere
White mulberry
Slope
Sphere
Yam
(Dioscorea alata)
Yam
(Dioscorea
rotundata)
Yoghurt
Regression
Slab
Regression
Slab
Slope
Slab
Drying Conditions
Hot air
m=0.14-0.29, T=64-75°C
v=0.64m/s
Hot air
mw=0.1-0.45, T=40-50°C
v=3.7 m/min
Hot air
mw=0.17-0.82, T=50°C
v=1 m/s
Hot air
mwo=0.69, T= 50-80°C
v=1.5
m/s,
Dims.=50x20x10mm
PT: water bath
PT: sodium metabisulphite
solution
Hot air
mwo=0.71, T= 50-80°C
v=1.5
m/s
,
Dims.=50x20x10mm
PT: water bath
PT: sodium metabisulphite
solution
Hot air
m=0.09-3.81 ,T=40-50°C
v=2 m/s
[
]
D eff = 3.3x10 −6 + 36 x10 −6 ( m o − 0.222) exp(−
D eff = 2 x10 −4 exp( −
37
32
)
R̂Tab
)
Ref.
202
203
R̂Tab
Deff =2.231x10-10-6.909x10-10
204
Deff =9.21x10-8 for T=50°C
Deff =1.41x10-7 for T=70°C
Deff =1.53x10-8 for T=50°C
Deff =2.54x10-7 for T=70°C
,
,
,
,
Deff =1.23x10-7 for T=60°C
Deff =2.84x10-7 for T=80°C
Deff =2.37x10-7 for T=60°C
Deff =4.01x10-7 for T=80°C
205
Deff =1.386x10-6 for T=50°C
Deff =5.121x10-6 for T=70°C
Deff =3.392x10-6 for T=50°C
Deff =9.008x10-6 for T=70°C
D eff = 2.11x10 −5 exp(
26.07
R̂Tab
,
,
,
,
)
Deff =2.548x10-6 for T=60°C
Deff =1.041x10-5 for T=80°C
Deff =5.449x10-6 for T=60°C
Deff =1.298x10-5 for T=80°C
205
206
where: Deff is the effective diffusion coefficient (m2/s), m moisture content in dry basis (kg moisture/kg dry solid), mw moisture content in wet basis (kg
water/kg wet substance), mm hourly mean moisture content (kg water/kg dry matter), ms sugar concentration (kg sugar/kg dry solids), T temperature (°C), Tab
absolute temperature (K), v velocity (m/s), L thickness (m), l length (m) h height (m), d diameter(m), ϕ relative humidity, P pressure ( mmHg or kPa), R̂
universal gas constant (8.314 J/(molK)), N power (W), qs solar radiation (W/m2), PT pretreatment, CRP constant rate period, FFRP first falling rate period,
SFRP second falling rate period, (Subscripts: e ambient air, o initial)
151
Table 21. Activation energies of various food materials for mass transfer
Ea (kJ/mol)
Ref.
Materials
Apple (red delicious)
19.96-22.62
123
Mullet roe
37.2
166
Avocado
Banana
Banana
Beef meat
Black tea particle
Broccoli
Carrot
Carrot
Carrot core
Carrot cortex
Cauliflower leave
Cherry (sweet)
Chestnut (Longal)
Chestnut (Martainha)
Chestnut (Viena)
Corn
Corn
Date (Red Soft)
Date (Tempo 2)
Date (Tempo 3)
Dill leave
Eggplant
Fig
Garlic
Garlic
Grape (Sultanin)
Grape (Chasselas)
Green bean
Green bean
Green pea
Green pepper
Kale
Kiwi
Lettuce leave
Mango
Mint leave
Mint leave
Mulberry
39.8
13.4
15.5-25.3
-24.64
406.02
26.2
12.7-28.7
22.43
24.78
16.53
19.82
53
22.578
21.926
20.458
29.56-30.56
27.61
35.17
29.50
44.02
35.05
29.52
30.81-48.47
23.48
27.84
54
49
35.43
39.47
24.7-28.40
51.4
36.12
27.00
19.82
22.95-27.68
82.93
62.96
21.2
207
127
208
132
135
209
207
139
140
140
210
143
145
145
145
148
211
149
149
149
150
151
153
154
155
156
156
158
212
213
159
160
161
210
214
215
164
165
Mushroom (Ag. Bisp.)
Mushroom (Pl. florida)
Olive cake
Olive oil extraction
Olive oil extraction
Okra
Orange skin
Parsley leave
Pear
Pistachio nuts
Plantain
Pollen
Potato
Potato
Prune
Pumpkin
Pumpkin seed (hulles)
Quince
Quinoa seed
Red bell pepper
Red pepper
Red pepper
Red pepper
Rice (cooked)
Rose hip
Rough rice (long)
Rough rice (medium)
Rough rice (short)
Soya bean (Nid. A6381)
Soya bean (Nid. A5409)
Sugar beet
Tomato
Wheat (broom)
Wheat (parboiled)
Yam (Dios. alata)
Yam (Dios. rotundata)
Yoghurt
19.79
23.59
17.97
15.77
26.71
51.26
36.36
43.92
24.3
30.79
38.81
29.69
16.3-108
31.5
57.00
78.93
33.15
33.83-41.52
32.50-40.99
39.70
42.80
37.76
24.76
36.44
46.00
49.19
43.56
53.37
28.80
27.00
28.8
32.94
32.00
37.13
41.71-69.45
25.26-46.46
26.07
210
210
168
169
170
171
172
150
176
177
178
181
207
216
183
184
185
186
187
188
159
189
190
191
192
193
194
195
197
197
217
201
203
204
206
206
207
Materials
Ea (kJ/mol)
Ref.
152
NOMENCLATURE
a
aw
A
A
b
bK
Bk
Bim
Biq
c
cp
C
constant
water activity
Helmholtz free energy [J]
area (m2)
constant
Klinkenberg parameter (Pa)
viscous flow parameter [m2]
Biot number for mass transfer
Biot number for heat transfer
constant
air capacity [kgm2/(kgN)]
concentration [kg/m3]
molar concentration [mol/m3]
Ĉ
Cm
CP
d
d
D
DR
d
e
es
Ey
Ea
Ec
f
f
〈f 〉
mass capacity [kg/(kg°M)]
specific heat [J/(kgK)]
diameter [m]
constant
Diffusion coefficient [m2/s]
shrinkage dimension [volume, area, thickness]
constant
constant
standard deviation
Young modulus [Pa]
activation energy [J/mol]
characteristic energy [J]
constant
function
spatial average of function f
〈f s 〉
〈f s 〉
F
Fmi
Fo
g
ĝ
G
G
Gr
Gr
Gu
h
h
hm
hn
hP
hq
H
I
J
Jm
Jm,vol
phase average of a function fs, which represents a property of the s phase
s
intrinsic phase average of a function fs, which represents a property of the s phase
force [N]
shape factor [1/m2]
Fourier number
gravitational acceleration [m2/s]
molar Gibbs function [J/mol]
Gibbs free energy [J]
slip modulus [m]
relaxation model [Pa].
Grashof number
Gukhman number
capillary pressure head [m]
specific enthalpy [J/kg]
mass transfer coefficient [kg/(m2s) or m/s]
mass transfer coefficient
mass transfer coefficient [kg/(m2sPa)]
heat transfer coefficient [W/(m2K)]
enthalpy [J]
the volumetric capacity [kg/(m3s)]
transfer flux [[…]/(m2s)]
moisture flux density [kg/(m2s)]
volumetric flux density [m3/(m2s)]
Ĵ m
Jn(x)
Jq
k
kr
K
Ki
Ko
KH
Kl
Kn
KV
l
L
L
Le
M
M̂
m
mw
)
m
mr
r
n
)
n
N
Nu
P
Pn(x)
Pe
Pr
qvol
q&
Q
Qdif
Qvol
r
r
r
R̂
Re
s
ŝ
S
S
S
Sb
Sc
Sh
Stm
Stq
t
T
u
u
molecular flux density [mol/(m2s)]
Bessel function of the first kind of order n
heat flux density [J/(m2s)]
constant
relative permeability
permeability [m2]
intrinsic permeability [m2]
Knudsen flow parameter [m]
hydraulic conductivity [m/s]
liquid conductivity [kg/(ms)]
Knudsen number
volume model [Pa]
half length [m]
characteristic length (m)
phenomenological transport coefficient [[…]2/s]
Lewis number
mass [kg]
molecular mass [kg/mol]
moisture content in dry basis [kg moisture/kg dry solid]
moisture content in wet basis [kg water/kg wet substance]
mass fraction
moisture ratio
unit normal vector
molar fraction
the number of moles
Nusselt number
pressure [Pa]
Legendre polynomial of the first kind of order n
Peclet number
Prandtl number
heat of desorption or absorption [J/m3]
volumetric heating [W/m3]
heat energy [J]
diffusibility
volumetric flow rate [m3/s]
radius [m]
radial coordinate [m]
correlation coefficient in Eq. (463)
universal gas constant [8.314 J/(molK)]
Reynolds number
Laplace transformation parameter
molar entropy [J/(molK)]
entropy [J/K]
saturation degree
Surface area [m2]
relative volumetric shrinkage [V/Vo]
Schmidt number
Sherwood number
Stanton number for mass transfer
Stanton number for heat transfer
time [s]
temperature [°C or K]
velocity [m/s]
Moisture content by volume [m3 liquid/m3 solid]
153
154
U
Uq
v
V
w
wp
W
x
y
y
z
~
1
internal energy [J]
overall heat transfer coefficient [W/(m2K)]
velocity [m/s]
volume [m3]
velocity [m/s]
dimensionless probability factor
mass-transfer potential or degrees of moistness [°M]
coordinate [m]
coordinate [m]
scalar quantity in Eq. (443)
coordinate [m]
unit tensor
Greek Letters
α
α
αT
β
βn
βv
βT
δ
δm
χ
χ2
δP
δT
Δhvap
Δĥ vap
thermal diffusivity [m2/s]
root of Bessel function in Eqs. (212)-(218)
thermal expansion coefficient [1/K]
shrinkage coefficient
root of cosine function in Eqs. (217) and (218)
thermal expansion coefficient [1/K]
volumic expansion coefficient [1/K]
Kronecker delta in Eqs. (264)-(266)
moisture conductivity coefficient [kg/mh°M]
constituent concentration (kg/kg dry matter)
mean square deviation
moisture filtration coefficient [kgm/(sN)]
thermo-gradient coefficient [1/°C]
evaporation enthalpy [J/kg]
molar evaporation enthalpy [J/mol]
ε
ε
εav
εpc
φ
φ
γ
γ
γp
Γ
η
ϕ
Φ
λ
λ
λ′
volume fraction
strain
ratio of air and vapor diffusion coefficient
phase change criterion
dissipation function [J/(m3s)]
zenith angle [rad] in Eq. (201)
shear rate [1/s] in Eq. (16)
activity coefficient in Eq. (187)
pore shape factor in Eqs. (102) and (103)
Boundary surface [m2]
dynamic viscosity [Pa s]
relative humidity
thermodynamic force [J/(kg[…])]
thermal conductivity [W/(mK)]
mean free path length [m]
Lame coefficient [Pa]
Λ
μ
μ̂
eigenvalue
chemical potential [J/kg]
chemical potential [J/mol]
μ′
Lame coefficient [Pa]
ν
νp
kinematic viscosity [m2/s]
Poisson coefficient
θ
θ
ρ
σ
σ
σb
contact angle [rad]
azimuth angle [rad] in Eq. (200) and (201)
density or concentration [kg/m3]
surface tension [N/m]
stress [Pa]
Boltzmann constant [1.3805x10-23J/K]
υ̂
tortuosity
shear stress [Pa] in Eq. (16)
molar volume [m3/mol]
τ
τ
ω
ΩD
Ω
ξ
ξ
ψ
Ψg
ΨH
ζ
humidity ratio [kg moisture/kg dry air]
diffusion collision integral
eigenfunction in Eqs. (229)-(221)
association factor
solid based coordinate [m]
porosity
gravity potential [m2/s2]
capillary potential [m]
diffusion resistance factor
Subscripts
a
a
ab
app
av
c
c
cp
cw
c
db
dp
ds
e
e
eff
ex
exp
f
fw
F
h
irr
g
g
k
air
ash
absolute
apparent
average
capillary
cardioid
closed pore
cell wall material
carbohydrate
dry bulb
dew point
dry solid
equilibrium
epitrochoide
effective
excess
experimental
fat
free water
moving evaporation front
haxagon
irreducible
gas
corrugated
Knudsen
l
lg
LM
m
max
ml
o
liquid
liquid-gas
log-mean
moist
maximum
monolayer
standard
155
156
Subscripts (Continued)
o
op
p
P
p
pre
R
s
s
sat
s.a.
sg
sg
sl
sn
sp
sp
sorb
st
S
the
v
vap
w
w
wb
*
initial
open pore
protein
particle
pore
predicted
reference
solid
substance
saturated
symmetry axis
solid-gas
sugar
solid-liquid
solution
specific
single pore
adsorbed water
starch
surface
theoretical
vapor
evaporation
water
wet basis
wet bulb
dimensionless
Superscripts
*
o
T
dimensionless
standard
transpose
Overlines
∼
^
average
tensor
molar
fraction
REFERENCES
[1]
[2]
[3]
Geankoplis, C. J. Transport Processes and Unit Operations; 3rd Edition; Prentice –Hall
International Inc.: New Jersey, 1993.
Earle, R. L.; Earle M. D. Unit Operations in Food Processing; 2nd edition; Pergamon
Press: Oxford, 1983.
Sheridan, P.; Shilton, N. J. Food Eng. 1999, 41, 203-208.
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
[30]
157
Wijesinghe, B. (1997). Low temperature drying of food materials using energy-efficient
heat pump dryers [Newsletter]. www.nwfpa.org .
Barr-Rosin Ltd. (2007). Superheated steam drying – environmental and energy saving
drying technology. www.barr-rosin.com.
Saravacos, G. D. In Engineering and Food for the 21st Century; Jorge, W.-C.; Gustavo
V. B.-C.; José, M. A.; CRC Press: New York, 2002.
Dullien, F. A. L. Porous media: Fluid Transport and Pore Structure; Academic Press
Inc.: New York, 1992.
Datta, A. K. J. Food Eng. 2007, 80, 80-95.
Bruin, S.; Luyben, K. Ch. A. M. In Advances in Drying; Mujumdar, A. S.; Hemisphere
Publishing Corporation: New York, 1980; Vol. 1, pp. 155-216.
Yamsaengsung, R.; Moreira, R. G. J. Food Eng. 2002, 53, 1–10.
Weast, R. C.; Lide, D. R.; Astle, M. J.; Beyer, W. H. Handbook of Chemistry and
Physics, 70th Edition; CRC Press Inc.: Boca Raton, FL, 1989.
Atkins, P. W. Physical Chemistry; 5th Edition; Oxford University Press, 1994.
Janz, M. (1997) Methods of Measuring the Moisture Diffusivity at High Moisture
Levels. Lund Institute of Technology, Licentiate Thesis, Sweden.
Baierlein, R. Thermal Physics; Cambridge University Press, 2003.
Keey, R.B. Drying Principles and Practise; Oxford:Pergamon Press, 1972.
Luikov, A. V. Heat and Mass Transfer in Capillary-Porous Bodies; Chapter 6,
Pergamon Pres: Oxford, 1966.
Karel, M. F.; Lund D. B. Physical Preservation of fruits and vegetables by drying.
UNIDO, Paper No: 29, pp. 1-9.
Marinos-Kouris, D.; Maroulis, Z. B. In Handbook of Industrial Drying; Mujumdar, A.;
CRC: New York, 2006; Vol. 1, pp. 82-114.
Rahman, S. Food Properties Handbook; CRC: 1995.
Iglesias, H.A.; Chirife, J. J. Food Sci. 1976, 41, 984-992.
Fortes, M.; Okos, M. R. In Advances in Drying; Mujumdar, A. S.; Taylor&Francis:
1980; Vol.1, pp 119-154.
Boguet, R; Chirife, J.; Iglesias, H. A. J. Food. Tech. 1978, 13, 319-327.
Abdula, M. (1993) Calculation of water sorption isotherms for multicomponent
mixtures of protein-containing products. Ph.D Thesis. Technical University of Lodz.
Lodz. Poland.
Urbicain, M. J.; Lozano, J. E. In Handbook of Food Engineering Practice; Valentas, K.
J.; Rotstein, E.; Singh, R. P.; CRC: New York, 1997, Chapter 11.
Boukouvalas, Ch. J.; Krokida, M. K.; Maroulis, Z. B.; Marinos-Kouris, D. International
J. Food Prop. 2006, 9, 715–746.
Sweat, V. E. In Engineering Properties of Food; Rao, M. A.; Rizvi, S. S. H.; 2nd ed.;
Marcel Dekker: New York, 1995, pp. 99-138.
Choi, Y; Okos, M.R. In Food Engineering and Process Applications; LaMaguer, M;
Jelen, P.; Elsevier: New York, 1986; Vol. 1.
USDA Handbook 8, http://www.ars.usda.gov/2007.
Leninger, H. A.; Baverloo, W. A. Food Process Engineering; 1st ed.; Springer: 1975.
Charm, S. E. The Fundamentals of Food Engineering; 3rd ed. AVI Publishing:
Westport, CT, 1978.
158
[31] Heldman, D. R.; Singh, R. P. Food Process Engineering; 2nd ed.; AVI: New York;
1981.
[32] Sweat, V. E. J. Food Sci. 1974, 39, 1080-1083.
[33] Sweat, V. E. ASAE Trans. 1975, 18(3), 564-568.
[34] Rahman, M. S. J. Food Eng. 1991. 15(4), 261-268.
[35] Riedel, L. Chem. Ing.-Tech. 1949, 21, 340-341.
[36] Hopmans, J. W.; Simunek, J. I.; Romano, N.; Durner, W. In Methods of Soil Analysis,
Dane J. H.; Topp, G. C.; Soil Science Society of America Book Series No. 5, 2002,
963-1008.
[37] Luikov, A. V. In Advances in Heat Transfer; Irvine, T. F.;Hartnett, J. P.; Academic
Press: New York, 1964, Vol. 1, pp. 123-184.
[38] Rahman, M. S. Drying Technology. 2001, 19(1), 1–13.
[39] Alnajım, A. (2004) Modelisation Et Simulation Du Comportement Du Beton Sous
Hautes Temperatures Par Une Approche Thermo-Hygro-Mecanique Couplee.
Application A Des Situations Accidentelles. Ph.D Thesis. Universite De Marne La
Vallee, Annee, France.
[40] Datta, A. K. Biological and Bioenvironmental Heat and Mass Transfer; Marcel Dekker:
New York, 2002.
[41] Kroes, B. (1999) The Influence of Material Properties on Drying Kinetics, Ph.D
dissertation;Technische Universiteit Eindhoven, Holland, 1999.
[42] Whitaker, S.; Chou, W. T. H. Drying Tech. 1983, 1(1), 3-33.
[43] Lowell, S.; Shields,J. E.; Thomas, M. A.; Thommes, M. Characterization of Porous
Solids and Powders: Surface Area, Pore Size and Density; Springer, 2006.
[44] Bassingthwaighte J. B. (2005). Osmosis and filtration: passive solute and water
transport, http://bioeng.washington.edu/Courses/BIOEN589/06/handout/06osm.pdf.
[45] J. Welti-Chanes, H. Mújica-Paz, A. Valdez-Fragoso, and R. León-Cruz. In Transport
Phenomena in Food Processing; Edited by Jorge Welti-Chanes, Jorge F. Vélez-Ruiz,
Gustavo V. Barbosa-Cánovas 2003 by CRC Press.
[46] Mayor, L.; Sereno A. M. J. Food Eng. 2004, 61, 373–386.
[47] Baggio P.; Bonacina C.; Schrefler B. A. Transp. Porous Med.. 1997, 28, 233-251.
[48] Cunningham, R. E.; Williams, R. J. J. Diffusion in Gases and Porous Media; Plenum
Press: New York, 1980.
[49] Carman P. C. Flow of gases through porous media, Butterworths Scientific Publications
1956
[50] Reinecke, S. A. (2000) The effect of Water Content on Knudsen Diffusion in
Unconsolidated Porous Media; MSc Dissertation, Toronto University, Toronto, Canada.
[51] Kerkhof, P. J. A. M.; Geboers, M. A. M. Chem. Eng. Sci. 2005, 60, 3129-3167.
[52] Gilliland, E. R. Indust. and Eng. Chem. 1934, 26(1), 681-685.
[53] Fuller, E. N.; Schettler, P. D.; Giddings, J. C. Indust. And Eng. Chem. 1966, 58(19).
[54] Poling, B. E.; Prausnitz, J. M.; O’Connell, J. P. The Properties of Gases and Liquids;
Fifth Edition; The McGraw-Hill Companies: 2004; All Chapter 11.
[55] Hirschfelder, J. O.; Bird, R. B.; Spotz, E. L. Chemical Reviews. 1949, 44(205).
[56] Gosse, J. In Les Techniques de l'Ingénieur, Constantes Physico-Chimiques, K. 2005,
425.
[57] Sercombe, J.; Vidal, R.; Gallé, C.; Adenot F. Cement and Conc. Res. 2007, 37(4), 579588.
159
[58] Rovnanikova, P.; Cerny, R. Transport Processes in Concrete;Taylor&Francis: 2002.
[59] Krischer, O.; Kast, W. Die Wissenschaftlichen Grundlagen der Trocknungstechnik;
Erster Band, dritte Auflage; Springer: Berlin, 1992.
[60] Henry, P. S. H. Proc. R. Soc. 1939, 171A, 215-241.
[61] Hines, A. L.; Maddox, R. N. Mass Transfer; Upper Saddle River: Prentice-Hall, 1985.
[62] Jacobson, A. (2006) Diffusion of Chemicals into Green Wood. Ph.D Thesis. School of
Chemical and Biomolecular Engineering Georgia Institute of Technology.
[63] Perry, R. H.; Green, D.W. Perry's Chemical Engineers' Handbook; 7th ed.; McGrawHill: 1997; 2581.
[64] Vignes, A. Indust. and Eng. Chem. Funda. 1966, 5(2), 189-199.
[65] Leffler, J.; Cullinan, H. T. Indust. and Eng. Chem. Funda. 1970, 9(1), 84-88.
[66] Buckinghan, E. A. Studies on the Movement of Soil Moisture. U. S. Dept. Agr. Bull.
1907, 38.
[67] Hill, T. L. J. Chem. Phys. 1956, 25:730.
[68] Imakoma, H.; Okazaki, M.; Toei, R. In Advances in Drying; Mujumdar, A. S.;
Hemisphere Publishing Corporation: New York, 1992; Vol. 5, pp. 77-108.
[69] Philip, J. R.; de Vries, D. A. Trans. Am. Geophys. Union. 1957, 38(2), 222-232.
[70] Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Pub. Co.: 1972.
[71] Whitaker, S. Advances in Heat Transfer. 1977, 13, 119-203.
[72] Whitaker, S. In Heat and Mass Transfer in Granular Porous Media: Advances in
Drying 1; Mujumdar, A. S.; Hemisphere Publ. Corp.: Washington DC, 1980; pp 23-61.
[73] Prat, M. Chem. Eng. J. 2002, 86(1-2), 153-164.
[74] Crank, J. The Mathematics of Diffusion; Clarendon Pres: Oxford, 1975; Vol. 49, pp. 4749, 90-91.
[75] Sherwood T. K. Trans. AIChE. 1936, 32, 150-168.
[76] Muthukumarappan, K.; Gunasekaran, S. Tr. ASAE. 1990, 33(5), 1637-1641.
[77] Singh, B.; Gupta, A. K. J. Food Eng. 2007, 79, 459–470.
[78] Fan, C. C.; Liaw, S. P.; Fu, W. R.; Pan, B. S. J. Food Sc. 2003, 68(3), 886-891.
[79] Reyes, A.; Alvarez, P. I.; Marquardt, F. H. Drying Technology. 2002, 20(7), 1463–
1483.
[80] El-Beltagy, A.; Gamea, G. R.; Amer Essa, A. H. J. Food Eng. 2007, 78, 456–464.
[81] Bon, J.; Simal, S.; Rosselld, H.C.; Mulet, A. J. Food Eng. 1997, 34, 109-122.
[82] Mulet, A.; Sanjuán, N.; Bon, J.; Simal, S. Eur Food Res Tech. 1999, 210, 80-83.
[83] Jain, D.; Pathare, P. B. J. Food Eng. 2007, 78, 1315–1319.
[84] Ece, M. C.; Cihan, A. Tr. ASAE. 1993, 36(3), 837-840.
[85] Kahveci, K.; Cihan, A.; Ece, M. C. Intern. J. Energy Res. 2003, 27, 1133-1145.
[86] Lima, A. G. B.; Farias, S. N.; Lima, D. R. Brazilian Journal of Chemical Engineering.
2004, 21(4), 667-680.
[87] Hacıhafızoğlu, O.; Cihan, A.; Kahveci, K.; De Lima, A. G. B. Eur Food Res Tech.
2007, (in Press).
[88] Rotstein, E.; Laura, P. A.; de Cemborain, E. J. Food Science. 1974, 39, 627-631.
[89] Chemkhi, S.; Zagrouba, F.; Bellagi, A. Drying Tech. 2004, 22(5), 1023–1039.
[90] Mihoubi, D.; Zagrouba, F.; Vaxelaire, J.; Bellagi, A.; Roques, M. Drying Tech. 2004,
22(1-2), 91–109.
[91] Ketelaars, A. A. J. (1992) Drying deformable media; kinetics, shrinkage and stresses.
Ph.D Thesis. Eindhoven University of Technology, The Netherlands.
160
[92] Chen, P.; Schmidt, P. S. Drying ’89. 1990, 162-168.
[93] Vu, T. H. (2006) Influence of Pore Size Distribution on Drying Behaviour of Porous
Media by a Continuous Model. Ph.D Thesis. Otto-von-Guericke-Universität
Magdeburg.
[94] Irudayaraj, J.; Haghighi, K.; Stroshine, R. L. J. Agricultural Eng. Res. 1992, 534, 209229.
[95] Lewis, R. W.; Ferguson, W. J. Int. J. Num. Meth. in Eng. 1990, 29, 357-369.
[96] Luikov, A.V.; Mikhailov, Yu. A. Theory of Energy and Mass Transfer; Chaps.1-2;
Pergamon Press: Oxford, 1965.
[97] Mikhailov, M. D.; Ozisik, M. N. Unified Analysis and Solutions of Heat and Mass
Diffusion; Chap.10; John Wiley: New York, 1984.
[98] Liu, J. Y.; Cheng, S. Int. J. Heat Mass Transfer. 1991, 34(7), 1747 1754.
[99] Chang, W. J.; Weng, C. I. J. Heat Mass Transfer. 2000, 43, 3621-3632.
[100] Berger, D.; Pei, D. C. T. J. Heat Mass Transfer. 1973, 16(2), 293-302.
[101] Whitaker, S. The Method of Volume Averaging; Kluwer Academic Publishers:
Dordrecht, The Netherlands, 1999.
[102] Data, A. K. J. Food Eng. 2007, 80, 96–110.
[103] Parry, J. L. J. Agricultural Eng. Res. 1985, 32, 1–29.
[104] Fortes, M.; Okos, M. R. Tr. ASAE. 1981, 22, 761-769.
[105] Lewis, W. K. J. Industrial and Eng. Chem. 1921, 13(5), 427–432.
[106] Page, C. (1949) Factors influencing the maximum rates of air drying of shelled corn in
thin layers. MSc Thesis(unpublished), Purdue University, West Lafayette, IN 47907
USA.
[107] Henderson, S. M.; Pabis, S. J. f Agricultural Eng. Res. 1969, 6(3), 169–174.
[108] Madamba, P. S.; Driscoll, R. H.; Buckle, K. A. J. Food Eng. 1996, 29, 75–97.
[109] Sharma, A. D.; Kunze, O. R.; Tolley, H. D. Tr. ASAE. 1982, 25, 221–224.
[110] Thompson, T. L.; Peartt, R. M.; Foster, G. H. Tr. ASAE. 1968, 11(4), 582–589.
[111] Wang, C. Y.; Singh, R. P. ASAE. 1978, Paper No. 78-6505, St. Joseph, MI, USA.
[112] Chapra S. C.; Canale R. P. Numerical Methods for Engineers; McGraw-Hill Book
Company: New York, 1989; p 337.
[113] Mulet, A.; Tarrazo, J.; Garcia-Reverter, J.; Berna, A. 1997. Shrinkage of cauliflower
florets and stems during drying. In Engineering and Food at ICEF 7; Ed. R. Jowitt;
Sheffield Academic Press: Sheffield, UK, 1997; pp 97–100.
[114] Beringues, J. C. (1999) Sorption isotherms and water diffusivity in Muscles of pork
ham at different NaCl contents. Ph.D Thesis. UPC, Barcelona.
[115] Shoeber, W. J. A. H. (1976) Regular regimes in sorption processes. Ph.D Thesis.
Eindhoven, The Netherlands (Quoted by Luyben et al., 1980).
[116] Schoeber, W. J. A short cut method for the calculation of drying rates in case of a
concentration-dependent diffusion coefficient. Proceeding of First International
Symposium on Drying. Montreal, 1978.
[117] Villota, R.; Hawkes, J. G. In Handbook of Food Engineering; Eds. Heldman, D. R.;
Lund, D. B.; Marcel Dekker, Inc.: New York, USA, 1992; pp 39-144.
[118] Katekawa, M. E.; Silva, M. A. Drying Tech. 2006, 24, 5–20.
[119] Giri, S. K.; Prasad, S. International Journal of Food Properties. 2006, 9(3), 409–419.
[120] Fish, B. P. In Fundamental Aspects of Dehydration of Foodstuffs; Society of Chemical
Industry: London, Macmillan Co, New York, 1958; pp 143–157.
161
[121] Gekas, V. C.; Motarjemi, Y.; Lamberg, I.; Hallström, B. In Preconcentration and
Drying of Food Materials; Ed. Bruin, S.; Elsevier Science Publishers BV: Amsterdam,
The Netherlands, 1988; pp 317-319.
[122] Gekas, V. C.; Lamberg, I. J. Food Eng. 1991, 14, 317–326.
[123] Teixeira, M. B. F.; Tobinaga, S. J. Food Eng. 1998, 36, 169-181.
[124] Sacilik, K.; Elicin, A. K. J. Food Eng. 2006, 73, 281–289.
[125] Wang, Z.; Sun, J.; Chen, F.; Liao, X.; Hu, X. J. Food Eng. 2007, 80, 536–544.
[126] Togrul, I. T.; Pehlivan, D. J. Food Eng. 2003, 58, 23–32.
[127] Baini, R.; Langrish, T. A. G. J. Food Eng. 2007, 79, 330–343.
[128] Karim, Md. A.; Hawlader, M. N. A. J. Food Eng. 2005, 70, 35–45.
[129] Saravacos, G. D.; Maroulis, Z. B. Transport Properties of Foods; 1st edition; CRC:
New York, 2001.
[130] Akpinar, E. K. J. Food Eng. 2006, 77, 864–870.
[131] Gurtas, F. S.; Ak, M. M.; Evranuz, E. Ö. Turk J. Agric. For. 2001, 25, 297-304.
[132] Trujillo, F. J.; Wiangkaew, C.; Pham, Q. T. J. Food Eng. 2007, 78, 74–85.
[133] Mujumdar, A. S.; Devahastin, S. Practical Guide to Industrial Drying; Ed. S.
Devahastin,
(Exergex,
Montreal,
2000).
www.geocities.com/drying_guru/chapter1fundamentals.pdf
[134] Doymaz, I. J. Food Eng. 2006, 76, 212–217.
[135] Panchariya, P. C.; Popovic, D.; Sharma, A. L. J. Food Eng. 2006, 76, 212–217.
[136] Mrkic´, V.; Ukrainczyk, M.; Tripalo, B. J. Food Eng. 2007, 79, 640–646.
[138] Singh, B.; Gupta, A. K. J. Food Eng. 2007, 79, 459–470.
[139] Togrul, H. J. Food Eng. 2006, 77, 610–619.
[140] Srikiatden, J.; Roberts, J. S. J. Food Eng. 2006, 74, 143–152.
[141] Bialobrzewski, I.; Markowski, M. Drying Tech. 2004, 22(7), 1777–1789.
[142] Jain, D.; Pathare, P. B. J. Food Eng. 2007, 78, 1315–1319.
[143] Alejandra Mabellini; Mabel B. Vullioud; Carlos A. Márquez; Antonio De Michelis.
(2005).
http://www.enpromer2005.eq.ufrj.br/nukleo/pdfs/0287_drying_kinetics_of_sweet_cherries.
pdf
[145] Guine´, R. P. F.; Fernandes, R. M. C. J. Food Eng. 2006, 76, 460–467.
[146] Jena, S.; Das, H. J. Food Eng. 2007, 79, 92–99.
[147] Sfredo, M. A.; Finzer, J. R. D.; Limaverde, J. R. J. Food Eng. 2005, 70, 15–25.
[148] Doymaz, I.; Pala, M. J. Food Eng. 2003, 60, 125–130.
[149] Falade, K. O.; Abbo, E. S. J. Food Eng. 2007, 79, 724–730.
[150] Doymaz, I.; Tugrul, N.; Pala, M. J. Food Eng. 2006, 77, 559–565.
[151] Wu, L.; Orikasa, T.; Ogawa, Y.; Tagawa, A. J. Food Eng. 2007 (in press).
[153] Babalis, S. J.; Belessiotis, V. G. J. Food Eng. 2004, 65, 449–458.
[154] Sacilik, K.; Unal, G. Biosystems Eng. 2005, 92(2), 207–215.
[155] Pezzutti, A.; Crapiste, G. H. J. Food Eng. 1997, 31, 113-123.
[156] Azzouz, S.; Guizani, A.; Jomaa, W.; Belghith, A. J. Food Eng. 2002, 55, 323–330.
[157] Margaris, D. P.; Ghiaus, A. G. J. Food Eng. 2007, 79, 1115–1121.
162
[159] Ertekin, F. K. J. Food Sc.. 2002, 67(1), 168-175.
[160] Mwithiga, G.; Olwal, J. O. J. Food Eng. 2005, 71, 373–378.
[161] Simal, S.; Femenia, A.; Garau, M. C.; Rossell, C. J. Food Eng. 2005, 66, 323–328.
[162] Goyal, R. K.; Kingsly, A. R. P.; Manikantan, M. R.; Ilyas, S. M. Biosystems Eng. 2006,
95(1), 43–49.
[163] Doulia, D.; Tzia, K.; Gekas V. (1999). A knowledge Base for the Apparent Mass
Diffusion Coefficient (Deff ) of Foods. Available: www.nelfood.com
[165] Maskan, M.; Gogus, F.; J. Food Eng. 1998, 37, 437-449.
[166] Fan, C. C.; Liaw, S. P.; Fu, W. R.; Pan, B. S. J. Food Sc. 2003, 68(3), 886-891.
[167] Giraldo-Zuniga1, A. D.; Arévalo-Pinedo, A.; Rezende, J. R.; Silva, C. S.; Monteiro, J.
A.; J. Food Proces. Preserv. 2006, 30(6), 699–705.
[168] Akgun, N. A.; Doymaz, I. J. Food Eng. 2005, 68, 455–461.
[169] Celma, A. R.; Rojas, S.; Lo´pez, F.; Montero, I.; Miranda, T. J. Food Eng. 2007, 80,
1261–1271.
[170] Doymaz, I.; Gorel, O.; Akgun, N. A. Biosystems Eng. 2004, 88(2), 213–219.
[172] Garau, M. C.; Simal, S.; Femenia, A.; Rossello, C. J. Food Eng. 2006, 75, 288–295.
[173] El-Aouar, A. A.; Azoubel, P. M.; Murr, F. E. X. J. Food Eng. 2003, 59, 85–91.
[174] De Temmerman, J.; Verboven, P.; Nicolai, B.; Ramon, H. J. Food Eng. 2007, 80, 892–
903.
[175] Kingsly, R. P.; Goyal, R. K.; Manikantan, M. R.; Ilyas, S. M. Int. J. Food Sc. Tech.
2007, 42, 65–69.
[176] Guine´, R. P. F.; Rodrigues, A. E.; Figueiredo, M. M. Ap. Math. Comp. 2007 (in press).
[177] Kashaninejad, M.; Mortazavi, A.; Safekordi, A.; Tabil, L. G. J. Food Eng. 2007, 78,
98–108.
[178] Johnson, P. N. T.; Brennan, J. G.; Addo-Yobo, F. Y. J. Food Eng. 1998, 37(2), 233242.
[179] Goyal, R. K.; Kingsly, A. R. P.; Manikantan, M. R.; Ilyas, S. M. J. Food Eng. 2007, 79,
176–180.
[180] Menges, H. O.; Ertekin, C. Energy Conv. and Manag. 2006, 47, 2337–2348.
[181] Vizcarra-Mendoza, M. G.; Martínez-Vera, C.; Ruiz-Martínez, R. S. 15th International
Drying Symposium (IDS 2006). 2006, pp 504-507, Budapest, Hungary.
[182] Hassini, L.; Azzouz, S.; Peczalski, R.; Belghith, A. J. Food Eng. 2007, 79, 47–56.
[183] Sabarez, H. T.; Price, W. E. J. Food Eng. 1999, 42, 167–172.
[185] Sacilik, K. J. Food Eng. 2007, 79, 23–30.
[186] Kaya, A.; Aydin, O.; Demirtas, C.; Akgün, M. Desalination. 2007, 212, 328–343.
[187] Gely, M. C.; Santalla, E. M. J. Food Eng. 2007, 78, 1029–1033.
[188] Vega, A.; Fito, P.; Andre´s, A.; Lemus, R. J. Food Eng. 2007, 79, 1460–1466.
[189] Kaleemullah, S.; Kailappan, R. J. Food Eng. 2006, 76, 531–537.
[190] Kaleemullah, S.; Kailappan, R. Biosystems Eng. 2005, 92(1), 15–23.
[191] Ramesh, M. N. Lebensm-Wiss u-Technol. 2003, 36, 245–255.
[192] Marquez, C. A.; De Michelis, A.; Giner, S. A. J. Food Eng. 2006, 77, 566–574.
[193] Lu, R.; Siebenmorgen, T. J. Tr. ASAE. 1992, 35(6), 1955–1961.
[194] Aguerre, R.; Suarez, C.; Viollaz, P. E. J. Food Tech. 1982, 17(6), 679–686.
163
[195] Steffe, J. F.; Singh, R. P. J. Agricultural Eng. Res. 1982, 27, 489–493.
[196] Gely, M. C.; Giner, S. A. Biosystems Eng. 2007, 96(2), 213–222.
[197] Akosman, C.; Kalender, M. F. Ü. Fen ve Müh. Bil. D. 2004, 16(2), 243-251.
[198] Barrozoa, M.A.S.; Henriquea, H. M.; Sartorib, D. J. M.; Freireb, J. T. J. Stored
Products Res. 2006, 42, 348–356.
[199] Teixeira, M. B. F.; Tobinaga, S. J. Food Eng. 1998, 36, 169-181.
[201] Sacilik, K.; Keskin, R.; Elicin, A. K. J. Food Eng. 2006, 73, 231–238.
[202] Gaston, A. L.; Abalone, R. M.; Giner, S. A.; Bruce, D. M. Biosystems Eng. 2004,
88(22), 175–185.
[203] Mohapatra, D.; Rao, P. S. J. Food Eng. 2005, 66, 513–518.
[205] Falade, K. O.; Olurin, T. O.; Ike, E. A.; Aworh, O. C. J. Food Eng. 2007, 80, 1002–
1010.
[206] Hayaloglu, A. A.; Karabulut, I.; Alpaslan, M.; Kelbaliyev, G. J. Food Eng. 2007, 78,
109–117.
[207] Zogzas, N. P; Maroulis, Z. B.; Marinos-Kouris, D. Drying Tech. 1996, 14(10), 2225–
2253.
[208] Nogueira, R.; Park, K. J. Drying Parameters to Obtain Bananapassa. In Proceedings of
the 8th International Drying Symposium, Montreal, Canada, Part A, 1992, 874–883.
[209] Simal, S.; Rossello, C.; Berna, A.; Mulet, A. J. Food Eng.1998, 37, 423–435.
[210] Lopez, A.; Iguaz, A.; Esnoz, A.; Virseda, P. Drying Tech. 2000, 18(4–5), 995–1006.
[211] Tolaba, M.; Suarez, C. Lebensmittel-Wissenschaft und-Technologie. 1988, 21, 83–86.
[212] Senadeera, W.; Bhandari, B. R.; Young, G.; Wijesinghe, B. J. Food Eng. 2003, 58,
277–283.
[213] Simal, S.; Mulet, A.; Tarrazo, J.; Rosello, C. Food Chem. 1996, 55, 121–128.
[214] Ruiz-Lopez, I. I.; Garcia-Alvarado, M. A. J. Food Eng. 2007, 79, 208–216.
[215] Park, K. J.; Vohnikova, Z.; Brod, F. P. R. J. Food Eng. 2002, 51, 193–199.
[216] Simal, S.; Rossello , C.; Berna, A.; Mulet, A. Chem. Eng. Sc. 1994, 49(22), 3739–3744.
[217] Vaccarezza, L.M.; Lombardi, J. L.; Chirife, J. J. Food Technol. 1974, 9, 317-327.
Chapter 2
THE INFLUENCE OF INTERACTIONS OCCURRING
BETWEEN MICRO-ORGANISMS ON PREDICTING THE
SAFETY OF LACTIC ACID CHEESE
Izabela Steinka*
Gdynia Maritime University
Department of Commodity and Cargo Sciences
Poland, 81-225 Gdynia, Morska 83
ABSTRACT
This paper discusses numerous problems occurring in relation to microbiological
quality of lactic acid cheese. Lactic acid cheese constitutes the source of various nutritive
substances, what results in a possibility of allochthonous micro-flora to grow despite the
presence of starter micro-flora. One of the issues discussed herein comprised the results
of microbiological research depending on tvarog packing system. The influence of
packing system on surface micro-flora population was assessed. Moreover, the problem
of growth of enterococci and LAB (Lactic Acid Bacteria) populations depending on stage
of tvarog production as well as packing system was also raised. The issue of interactions
occurring among micro-organisms that re-infect tvarogs and the influence of these
interactions on the growth of individual micro-organisms was also discussed. Author
presented also the possibility to apply JMTPH computer program for assessment of the
dynamics of changes of tvarog micro-organisms during product storage. Another chapter
includes assessment of the influence of lactic acid bacteria on the behaviour of individual
groups of micro-organisms occupying tvarog surface, depending on packaging hermetic
properties. It was also very important to assess the safety of tvarogs in the context of a
possibility of enterotoxin synthesis in conditions of various packing systems. Finally, the
models of optimising lactic acid cheese quality were presented, what included application
of plant additives of biostatic character, modification of used packaging as well as
employing the probabilistic mathematical model helpful in evaluation of enterotoxin
synthesis, depending on the level of staphylococci and yeast populations.
*
Izabela Steinka: [email protected]
166
Izabela Steinka
INTRODUCTION
Tvarog is a product formed as a result of dehydration of lactic acid curds after the
processes of reheating and pressing, produced in Europe. Tvarog is manufactured from milk
soured with a starter consisting of the following bacteria cultures: Lactococcus lactis spp.
lactis v. diacetylactis, Lactococcus lactis spp. cremoris, Lactococcus lactis spp. lactis and 4
% Leuconostoc lactis. Hence, the non-regional name – lactic acid cheese – renders the
product characteristics. This product, together with other similar ones, belongs to the group of
unripened cheese. The rennin is not applied during its production. The commonly used names
vary depending on the region where it is produced: in Russia it occurs as domasznij syr, while
in Poland as tvarog. Slightly similar products comprise: Italian mozzarella, German quark,
cottage cheese produced in North America or its form coming from Latin America - Queso
blanco. Apart from these, there are also other products known in the market, however they are
less similar to typical tvarogs. These include: impastata, bakers cheese, cream cheese, petit
susie, gervais, fromage frias ala crème, ymer, lactofil. The above-mentioned cheese differs
significantly from typical unripened lactic acid cheese with regard to production technology
(acid and rennin), the presence of dressing or cream, the fat content and the consistency.
Unripened lactic acid cheese such as cottage cheese, quark or tvarog constitute products
of significant protein content and they are especially susceptible to the influence of microorganisms. In literature, there are numerous data available concerning in particular the
microbiological quality of cottage cheese, however there are hardly any information on lactic
acid cheese.
MICROBIOLOGICAL QUALITY OF TVAROGS AND COTTAGE CHEESE
From the literature, it results that the improperly produced cottage cheese can constitute
the source of mould comprising the following strains: Candida famata, Candida spherica
Candida robusta, Pichia membranofaciens, Saccharomyces exiquus (Westal 1998). The
research of Rosenthal shows that the undesired changes of taste and odour of hermetically
packed cottage cheese result from the growth of mould belonging to species: Penicillium,
Geotrichum, Mucor and Alternaria (Rosenthal et al. 1996).
Our research conducted on cottage cheese showed the various level of mould in these
products (Steinka 2000). In 37 cheese samples, yeast at the level from 0 up to 7.45 log10cfu/g
and mould at the level from 0 up to 3.92 log10cfu/g were observed. Carem cheese was
characterised by much better quality: in no sample yeast count exceeded the level of 3.72
log10cfu/g, and for mould - the count of 3.20 log10cfu/g.
The microbiological quality of cottage cheese products is discussed in publications of
Sims 1989, Ashenafi 1990, Maniar 1994. From data obtained by Asfhenafi, it results that the
quality of majority of these products is influenced not only by the presence of yeast and
enterococci, but also faecal coliforms. The presented results concerning cheese coming from
the market arouse hygienic reservations. Bacillus cereus and Staphylococcus aureus are
observed at the level of 102-103, while 55% of the samples contain faecal coliforms.
It appears that cottage cheese stored in different temperature conditions and devoid of
sorbic acid supports the growth of Pseudomonas fluorescens. Different types of Salmonella
Influence of Interactions Occurring Between Micro-Organisms…
167
show the ability to survive in these products (Sims et al. 1989). The authors observed 100fold increase of Salmonella typhimurium count in tvarogs with pepper and garlic, especially
in those products which were not enriched with sorbic acid. During further laboratory
research conducted by the authors as regards addition of proteins or vegetable ingredients, the
decrease in count of staphylococci was observed at the temperature of 10oC and 20oC.
Whereas in the same conditions, Bacillus cereus and S. typhimurium counts increased in
cottage cheese. The count of Yersinia enterocolitica cells increased only at 10oC, while the
decrease of these bacteria number was observed at the temperature of 20oC. Addition of
sorbic acid to these products resulted in reduction or stabilisation of bacteria count at the
constant level. Pathogenic micro-flora present in cottage cheese some in cases can include:
Listeria monocytogenes and Clostridium sporogenes (Chen et al. 1993, Stañczak et al. 2000).
There exist many controversies concerning the unequivocal assessment of adverse
influence of certain environmental conditions on the survival rate of Listeria monocytogenes
in cottage cheese. Majority of authors (Benkeroum and Sandine 1988, George and Lund
1988, Ryster and Marth 1985) prove the growth of populations or at least the presence of this
pathogen at constant level in the product.
Hicks et al. (1991) and Piccinnin (1995) agree that storage in refrigerating conditions
results in reduction of Listeria count in cottage cheese.
The condition determining survival rate in tested cottage cheese was neither
concentration of H+ ions nor hermetic packaging. Listeria is able to grow in environment of
acidity lower than those occurring in lactic acid cheese (George et al. 1988).
From data presented by Chen et al. 1993, it results that inoculation of cottage cheese with
these species gives the possibility to observe their behaviour during storage in conditions of
atmosphere modified with carbon dioxide. In this research, during two months of storage at
three temperatures, the reduction in count of Clostridium sporogenes was observed. The
decrease in number of Listeria monocytogenes cells was observed in cottage cheese at the
temperature of 4oC, while as soon as at 7o it was possible to determine the growth of these
micro-organisms by one logarithmic cycle. In traditionally packed cottage cheese, the
literature data showed the increase of these bacteria count by 1000 times.
The significant number of conducted research concerned also the problem of survival rate
of pathogenic bacteria in cottage cheese, indicating the possibility of their occurrence in these
products (Piccinin and Shelef 1995, Hicks and Lund 1991 and Farrag et al. 1992).
These data suggest that such products as unripened lactic acid cheese can support the
growth of pathogenic micro-flora, since they do not include special biostatic additives.
This is especially notable, because the composition of products includes significant
number of lactic acid bacteria, what should be sufficient for the absence of pathogenic microflora resulting from the inter-microorganism antagonism.
However, the prolonged refrigerating storage of products can be the reason for the
presence of psychrotrophic micro-flora in lactic acid cheese. This concerns mostly food of
animal origin. While listing the psychrotrophs isolated from dairy products, Champagne et al.
(1994) mentions above all such bacteria as: Listeria monocytogenes, Yersinia enterocolitica
or Bacillus cereus.
As far as psychrotrophic micro-flora is concerned, the strains of Pseudomonas
fluorescens and Enterobacter aglomerans were identified in cottage cheese (Lund et al.
1988). The behaviour of psychrotrophs depending on the level of added carbon dioxide was
investigated by Maniar 1994, Fedio 1994, Moir et al. 1993.
168
Izabela Steinka
Tvarogs have no dressing or cream, what makes their micro-flora differ both qualitatively
and quantitatively from the one being predominant in cottage cheese. Micro-organisms
occurring in cottage cheese comprise such species as: Escherichia coli, Enterobacter sp.,
Bacillus subtilis, Enterococcus faecalis, Enterococcus faecium, Staphylococcus aureus,
Micrococcus sp., Candida quilierimonde, Candida famata, Candida lusitaniae, Geotrichum
candidum, Aspergillus flavus (Steinka et al. 1999, 2001, 2002).
Due to the product instability, tvarogs are stored in refrigerating conditions. There exist
many data on changes of physico-chemical and sensory properties of these products.
However, there are only few micro-biological tests connected with quality of these products
(Cais et al. 1998, Steinka et al. 1998, 1999a,b, 2000, 2001c, 2006b, Steinka 1999c, 2001a,b,d,
2003a, 2004, 2005a,b, 2006b,c, Ziółkowski et al. 2003).
Data obtained by Steinka et al. (2002a) showed the presence of Bacillus sp. bacteria in
lactic acid cheese stored in refrigerating conditions. During refrigerating storage, the intensive
growth of Staphylococcus epidermidis was also observed in hermetically-packed tvarogs. The
number of samples, in which the presence of staphylococci was detected increased by 77.7%
in relation to amount observed on the day of buying the tvarog by the customers (Steinka et
al. 2002a).
Table 1 presents the micro-organisms that could be isolated from stored lactic acid cheese
prior to implementation of HACCP system to their production.
Table 1. Type and count of micro-organisms isolated from
tvarogs during refrigerating storage
Type of micro-flora
Enterococcus
Haemolysing Streptococcus á
Micrococcus
Bacillus
Staphylococcus epidermidis
Candida
Mould
Storage time (days)
0
7
Micro-organism count (cfu/g)
1.82 ·106
9.93·105
6
2.2 ·10
5.6·104
0
4·104
1.22 ·106
9·104
0
9·104
4
9 ·10
4·104
7.45 ·105
3.71·104
14
5.19·105
0
5·101
3.13·105
5.98·105
0
3.2·104
Steinka et al. 2002a.
From our previous research, it results that the psychrotrophic micro-flora present in lactic
acid cheese could also include Micrococcus sp. and Staphylococcus sp.
Prior to implementation of HACCP system into the production of lactic acid cheese, the
count of psychrotrophic micro-organisms in tvarogs coming from the market was equal at the
maximum to 1.4·103 cfu/g.
In tvarogs packed into PA/ PE and stored for the period of 7 days after purchase, the
count of populations of these micro-organisms could reach the level of 3.0•105 cfu/g. In more
than 52% of tvarog samples, and after 14 days of refrigerating storage from the date of
purchase, the count of psychrotrophic micro-flora increased tenfold in relation to the level
observed after one week (Steinka et al. 1999b). Unripened lactic acid cheese is also illustrated
by only a few mathematical descriptions (Steinka 2003, 2005c).
169
With the help of mathematical models, it is possible to predict most of all the
technological details in tvarogs such as: the influence of salt level and the initial level of a
starter on pathogen survival rate (Bozukart 2001). Another subject of prediction can be
evaluation of time of cutting cottage cheese, taking the growth of starter cultures into account
(Crofcheck et al. 1999). In ripening cheese (white cheese), the prediction concerned e.g.
diffusion during long-term brining (Turhan et al. 1992).
Many years of research on lactic acid cheese showed that microbiological quality of
tvarogs was various, depending not only on applied technology, but also on the production
plant as well as layer, from which the sample is taken for tests.
Observations presented in Table 2. confirmed the differences in count of microorganisms populations on the surface and inside the cheese mass (Steinka et al. 2006b).
Table 2. Level of micro-organisms in tvarogs,
depending on place of taking a sample
Type of microflora
Escherichia coli
Mould
Yeast
Place of taking a
sample
from
tvarogs
Surface
Inside
Surface
Inside
Surface
Inside
Average
cfu/g
Standard
deviation
2.48
2.10
0.31
0.13
2.52
2.43
0.2
0.2
0.09
0.07
0.1
0.2
Steinka et al. 2006 b.
Count of mould on the surface was higher by 58.1% than the number observed inside the
cheese mass. In the case of yeast and Escherichia coli these values were equal to 15.0 and
3.6% respectively. Statistic analysis showed that there existed a weak correlation between
count of yeast inside the a/m product mass and on its surface ( r 0.136) ( Steinka et al. 2006b).
Table 3. illustrates the model of changes of micro-organisms count present in several
batches of lactic acid cheese packed into PA/PE, taking surface and inside layers of tvarog
cubes into account.
Table 3. Models illustrating total count of micro-organisms in tvarogs
Type of microflora
Escherichia coli
Mould
Yeast
Model of changes
Z=0.091-0.291x-0.33y-0.006x2 –-0.2xy-0.225y2
Z=3.844-0.897x-0.175y-0.082x2 +0.549xy-0.205y2
Z=-0.151-3.811x+4.993y+0.345x2
+0.125xy2
0.479y
Steinka et al 2006b; x-tvarog surface, y-inside of tvarog mass, z-number of micro-organisms in tvarog.
During his research, Parisi compared the behaviour of chosen bacteria and mould in
dependence on the distance of product surface from the packaging laminates (Steinka and
Parisi 2006). Research was conducted in order to provide knowledge on the differences
170
Izabela Steinka
between cheese produced using citric acid and using lactic acid. Cheese manufactured using
citric acid was packed into cryovac, while lactic acid cheese was packed into PA/PE
laminates. Determination of micro-organisms was performed from the four layers: upper
sample 0-5 mm from the packaging surface, middle sample 5-15 mm and lower sample 15-30
mm from the packaging surface. The averaged sample contained micro-organisms from layers
of 0-30 mm.
In cheese packed into cryovac, the Escherichia coli bacteria grew better in lower and
middle layers. In the surface cheese layer, the reduction in bacteria count was observed.
The growth of fungi (yeast and mould) was observed by Parisi in samples taken from all
cheese layers, however the dynamics of growth were the greatest in a lower layer. The
behaviour of fungi in sample taken from the layers 0-30 mm from the packaging surface was
similar to the one observed in cheese packed into PA/PE laminates (Steinka et al. 2006b).
Test results obtained by other authors show that the intensity of micro-organism
occupation of a certain layer of food product is dependant on type of bacteria and type of
food.
Research conducted by Ingram in meat products showed the growth of staphylococci
count by 0.7 cfu/g inside the ham, whereas on its surface the population size varied by only
0.1 cfu/g (Ingram 1996). The results of both research show a different expansion of many
species of micro-organisms in external and internal lots of food product.
THE DYNAMICS OF CHANGES OF FACULTATIVE ANAEROBIC
MICRO-FLORA IN LACTIC ACID CHEESE
The tables present average values of certain types of bacteria and fungi occurring in lactic
acid cheese prior to implementation of HACCP system. Population sizes were different,
depending on the packaging type.
The microbiological requirements for tvarogs valid during that time (1991-2003)
assumed the absence of coagulase-positive staphylococci in 0.1 g, what was later verified for
the presence of these bacteria in number not greater that 10 cfu in one gram of a product.
Salmonella and Listeria monocytogenes could not occur in 1 g of a product. The limits for
4
yeast assumed the maximum presence equal to 10 cfu/g, whereas mould was not permissible
2
at the level higher than 5•10 cfu/g. The presence of coliforms was accepted at the level not
greater than 0.001 g (the Standard and the Decree of Polish Minister).
Results of testes conducted in individual years, and presented in Table 4., show that the
level of many micro-organisms present in these products was inconsistent with the a/m
requirements.
Table 5. below presents the levels of fungi detected after implementation of HACCP
system, depending on type of packaging. From these data it results that PA/PE packaging is
the best type of packaging, at high level of initial contamination. However, results concerning
the behaviour of populations of other micro-organism species in tvarogs packed with different
systems do not entirely confirm these observations.
171
Table 4. Levels of contamination of tvarogs with allochthonous micro-flora
Type of microorganisms
Type
of
packaging
Staphylococci
E. coli
PA/PE
Staphylococcus
aureus
Yeast
E.coli
PA/PE/
Cryovac
Initial
contamination
cfu/g/ log10cfu/g
1.1 •10-1
1.2•101
Count after 14
days of storage
cfu/g / log10cfu/g
2.3.103
0
2.1•103
1.1•103
1•104
1.6•103/1.6•102
1.4•106
1.7•101/0
Staphylococcus
aureus
Yeast
5.4•102 / 9.1•101
4.6•102/2.1•102
9.1•104 /6.6•103
4.4•106/8.2•105
Enterococci
6.1•103/1.5•105
4.8•105/1•104
2.97
1.6
2.85
1.39
E. coli
PA/PE
Staphylococcus
aureus
Yeast
Enterococci
4.17
Parchment
paper
Staphylococcus
aureus
Yeast
Author
Steinka 1998
Steinka
Stankiewicz Steinka,
Morawska 1999
Steinka
Zukowski,
Hildebrand 2000
Steinka Kukulowicz
2002
5.25
3
3.3•10
3.7•105
6.4•101
4•101
2.9•105
6.3•105
Steinka Mieczkowska
2003
Enterococci
Steinka – collective study conducted in Microbiological Laboratory in years 1998-2003.
Table 5. Level of fungi (yeast and mould) in tvarogs
prior to HACCP implementation
Type
of
fungi
Type of packaging
Market
quality
log10cfu/g
Count of fungi after
storage
log10cfu/g
Yeast
Mould
Yeast
Mould
Yeast
Traditionally- parchment paper
4.46
4.73
6.79
4.0
3.81
7 days
4.95
5.73
6.11
3.86
4.25
14 days
3.79
6.27
6.11
4.11
5.91
1.71
2.2
2.36
Mould
Own Study.
Vacuum system - PA/PE
Atmosphere modified with nitrogen
addition
172
Izabela Steinka
It should be noticed that the kinetics of populations changes is different, depending on
way of conducting the production. These changes are determined together by the state of raw
material, packing system as well as the presence of background micro-flora and re-infecting
micro-flora. Model of changes of populations occurring in lactic acid cheese produced
without taking GHP rules into account was dveloped by Steinka 2002a, Steinka 2003a, 2005a.
However, in order to compare the dynamics of population changes depending on the
production system, the kinetics of growth should be determined.
2
1,8
1,6
y= -1,075x2 + 4,895x- 3,82
R2 = 1
1,4
1,2
1
y= 0,595x- 0,2367
R2 = 0,4789
Log cfu/h
0,8
0,6
0,4
0,2
0
0
7
14
-0,2
Time of population growth (days)
Figure 1. Kinetics of changes of Enterococcus sp. population in tvarogs produced without GHP.
Attempts were made to compare the growth of Enterococcus sp., Staphylococcus aureus
bacteria and yeast during refrigerating storage of tvarogs produced in HACCP system as well
as manufactured by dairy plants without implemented quality system. Significant differences
were noticed in the dynamics of growth of e.g. enterococci count in tvarogs.
Changes in enterococci count during 7 days of storage were equal to 1.67 log10cfu/g up
to the day 7, and 1.19 log10cfu/g between day 7 and 14 (figure 1).
The growth of staphylococci was not as dynamic – the observed change was equal on the
average to 0.26 log10cfu/g in the first week of storage, and yeast was equal to 0.48
log10cfu/g during that period.
The presented figures (figure 1 and figure 2), reflecting the behaviour of enterococci
observed during 14 days of product storage, present the different behaviour of these bacteria
in both production systems.
173
Evaluation of kinetics of changes of tested streptococci populations show that in the case
when GHP rules are not applied, the rate of population growth is ca. 3.7-fold higher (3.68)
than in the case of tvarog production conducted in HACCP system.
From obtained data it results that variability of population count is significantly
diversified, unless critical checkpoints are introduced.
0,0045
0,004
0,0035
0,003
y= 0,0021x- 0,0024
0,0025
R2 = 0,9196
0,002
log cfu/h
y= 0,0011x2 - 0,0022x+ 0,0011
R2 = 1
0,0015
0,001
0,0005
0
0
7
14
-0,0005
-0,001
Time of population growth (days)
Figure 2. . Kinetic changes of Enterococcus population in tvarog produced in HACCP system.
For packing lactic acid cheese, several types of packaging are applied: PA/PE laminates,
foamed polystyrene trays wrapped with a thin PE film – so called: frischaltenfolie, aluminium
foils with parchment paper, the parchment paper and cryovac. The hermetic level of
packaging as well as its barrier properties are responsible for the behaviour of surface microflora behaviour. The rate of micro-flora growth can be inhibited or stimulated by conditions
occurring inside the packaging. A specific ecological niche is created between surfaces of
packaging and the product characterised by conditions dependant on the packaging hermetic
level.
A very significant influence of packaging material of tvarog quality is also observed.
Research conducted on the influence of packaging on cottage cheese and cream cheese
quality showed that both the packaging and the storage of these products in polystyrene
containers also did not meet microbiological expectations. Whereas applying the packaging
made of waxed cardboard significantly favoured maintaining good quality (Steinka 1999c).
Cottage cheese packed into containers with sealed covers provided better protection against
174
Izabela Steinka
contamination than packaging with separate moveable covers. Sealable covers made of
aluminium film allowed additional sterilisation and limiting the presence of surface microflora.
During further research on cottage cheese and cream cheese it was additionally observed
that contamination with yeasts was significantly dependant on technology of cheese
production, while the packaging hermetic properties had no influence on mould level in
products (Steinka et al. 2000).
Majority of research available in literature is devoted to the influence of packing system
on organoleptic properties of the products. Only a few studies raise the issue of interactions
occurring among product micro-flora, depending on the packing system. It has a first-grade
significance for the quality and safety of food.
The packaging hermetic properties accompanied by application of vacuum packing
system constitutes a special hygienic problem.
PACKING AS A FACTOR DETERMINING THE PRODUCT QUALITY
Apart form packaging type and packing system, the time and conditions of product
storage constitute very significant factors responsible for quality of stored cheese.
In figures 3 and 4, the sizes of populations of facultative anaerobic bacteria in tvarogs
coming from the market are presented. Tvarogs were packed into different types of
packaging: parchment paper, PA/PE laminate and cryovac.
6
5
4
Log cfu/g 3
2
1
0
Paper
Cryovac
PA/PE
Packaging type
E.coli
Enterococcus sp.
Staphylococcus aureus
Figure 3. The Influence of packaging type on growth of facultative anaerobic bacteria in tvarogs.
175
7
6
5
4
Log cfu/g
Yeast
3
Mould
2
1
0
Paper
Cryovac
PA/PE
Packaging type
Figure 4. The influence of packaging type on growth of fungi populations in tvarogs.
From conducted research it results that the level of contamination with bacteria and fungi
was significantly dependent on the packaging type. The greatest count of micro-organisms
was detected in cheese packed into parchment paper.
Application of HACCP system and the packaging made of plastics such as Cryovac
showed better protective properties in comparison to PA/PE laminate.
It is probable that in the case of Cryovac application, blowing nitrogen through the
surface of cheese contributed to modification of atmosphere after closing the packaging.
From literature analysis it results that food products hermetically packed into plastic
packaging can pose a hazard connected with production of bacterial toxins (Post et al. 1988,
Adams et al. 2000, Steinka et al. 2001c, 2004, Duffranse 2000).
The safety of hermetically packed products is not always improved by applying modified
gaseous atmosphere into their packing. From numerous reports, it results that selection of
appropriate composition of atmosphere can be adapted to inhibition of certain types of microflora, since every species reacts differently to the presence of CO2. Therefore, for example:
the growth of Staphylococcus aureus is intensively inhibited at 50-100% CO2, however the
0
obligatory condition is temperature of 10 C. From research of Kimura, it appears that
staphylococci are more sensitive to the influence of certain concentrations of carbon dioxide
in comparison to Escherichia coli rods, what stands in contradiction to the previous opinions
on reactions of these bacteria in relation to application of modified atmosphere (Kimura
1999).
176
Izabela Steinka
From literature it results that addition of carbon dioxide causes changes of generation
time in laboratory conditions, depending on its concentration and type of micro-flora (table
6).
Table 6. The influence of carbon dioxide on micro-organisms populations
Type of micro-organisms
Pseudomonas,
Flavobacterium
Achromobacter
Moraxella-Acinetobacter
Carbon dioxide
concentration
Reaction of micro-organisms
10-20 %
Inhibiting
20-70 %
Time prolongation
,
Lactic acid bacteria
Sustaining of growth
Yeast
50%
50-100-fold increase in count
Clostridium botulinum
Clostridium perfringens
Listeria monocytogenes
< 50%
Minimal growth inhibiting
< 50%
50-100%
Depending on the temperature
– inhibiting or sustaining of
growth
Own study on the basis of Nguyen and Carlin 1994, FDA 2001, Zagory 1995, Philips 1996, Adams
2000.
The presence of bacterial toxins in hermetically packed food products is not always
preceded by obvious organoleptic symptoms. From data presented in literature, it results that
at room temperature, 60% of CO2 addition, 25% of oxygen presence and 15% of nitrogen
concentration in packed fish fillets, the organoleptic changes occur at the same time as the
presence of toxins in products. Whereas at the same composition of gaseous atmosphere in
packaging and the temperature of 4.40C, the presence of toxins precedes the indicators of
spoiled fish fillet by 7 days (Tyszkiewicz 1992).
Control of parameters responsible for physico-chemical changes of products is possible
in the case of meat and its products packed with application of modified atmosphere or using
active packaging.
In the case of lactic acid cheese, application of the above-mentioned technologies is much
more difficult due to the delicate product structure. Attempts to pack cottage cheese in
modified atmosphere were made by Dixon, 1988, Honer, 1988, Brody, 1989, Fedio, 1994,
Maniar, 1994. The stability of quality features of mozzarella cheese was described by Alves
et al. (1996) and Elliot et al. Tvarogs packed with MAP system were investigated by PanfilKuncewicz et al. (1997). However, application of modified atmosphere in technology of
tvarog packing revealed that there existed a relationship between concentration of carbon
dioxide and the adverse sensory changes (Fedio 1994). In Poland, there are several systems of
hermetical packing of cheese into plastic packaging, among others: vacuum-packing into
177
PA/PE films and shrink-wrapping with Cryovac laminate. The non-hermetic packing methods
include: packing into aluminium films with parchment paper and into the parchment paper.
Evaluation of physico-chemical changes of tvarogs packed in a traditional way was conducted
by Pieczonka 1993, Kujawski et al. 1994, Chojnowski et al. 1999, Molska et al. 1992,
Œmietana et al. 1997. There are not many data on assessment of quality of lactic acid cheese
hermetically packed with vacuum and non-vacuum systems (Panfil-Kuncewicz 1997a,b,
Steinka et al. 1998, 1999c, 2001b). Technological and technical aspects of packing tvarogs
and soft cheese into various types of packing films were presented by Œmietana et al. 1997
and Marcotte et al. 2001.
Significant information on the influence of modified atmosphere on unripened cheese
quality is presented by Gonzales-Fandos et al. 1999. However, the subject of his study is fresh
cheese Cameron, which acidity differs from acidity of tvarogs and is equal to pH ~6.35. This
products is characterised by the fat content of 54-56% and 7 days of stability period.
Research on the effect of 100% CO2 addition during packing Cameron cheese, as well as
prolonged time of storage result in decrease in number of psychrotrophic bacteria only in the
early period. Whereas, their increase can be detected between day 7 and day 30 of product
storage. In the case of mesophilic micro-flora, this growth is observed between day 12 and
day 30 of cheese storage. From the research of Fandos, it also results that the growth of
Enterobacteriaceae rods is noticeable between day 7 and 15. The research results of Fandos
are similar to data obtained by Moir (1993), who observed the growth of psychrotropic
bacteria in tested products despite the presence of CO2. In tvarogs vacuum-packed into
PA/PE laminates, where atmosphere was not modified, Steinka et al. (1999b) observed the
increase of psychrotrophs count during product storage. However, vacuum-packing did not
favour the growth of Listeria monocytogenes rods in tvarogs. The number of samples
indicating the presence of this rod after 14 days of storage could evidence the change of
atmosphere during product breathing or the metabolism of other micro-organisms. Number of
tvarog samples, where Listeria monocytogenes was present decreased by 24% after 14 days of
storage (Steinka et al. 1999b).
The significant factor determining the growth of micro-organisms in tvarogs is pH value
characterising the products. From data obtained by Moir, it results that when CO2 additive
does not exceed the value of 40%, then the acidity value does not change while packing the
cheese using MAP technology. In tvarogs packed into both types of laminates, the acidity
varied from 4.26 to 5.03 pH. During 14 days of storage, no significant changes were observed
in acidity of vacuum-packed cheese. In tvarogs packed into Cryovac laminates, the decrease
in content of organic acids was observed up to the day 7 of storage, what could result from
the growth of alkalising micro-flora of the mould (Steinka 2003a).
In tvarogs of low count of contaminating micro-organisms, the acidity variations during
storage are insignificant (table 7).
178
Izabela Steinka
Table 7. Acidity of tvarogs of low level of contamination
with allochthonous micro-flora
Storage time of tvarogs in PA/PE packaging (days)
Average
0
2
4
acidity values
pH
4.73±0.06
4.59±0.05
4.63±0.04
7
14
4.56±0.03
4.63±0.08
Own study.
From the research of Steinka (2003a), it results that during the period up to day 7, no
reduction is observed in number of all tested groups of micro-organisms isolated from
tvarogs.
It often happens that the aesthetics and convenience play a decisive role in purchase of a
product by a consumer. The results of study of consumer preferences concerning tvarogs
packaging revealed that among the selection factors connected with packaging, very
significant were such indicators as: tightness (71.8% of respondents), aesthetic appearance
(59.4% of respondents) and information on the packaging that is important for 64% of those
polled (Steinka 2003a). High water content in lactic acid cheese is the reason for their low
stability and the difficulties connected with selection of packaging as well as storage
problems.
Research conducted in recent years concerning the possibility to apply hermetic
packaging for tvarogs still has not solved many problems and has not answered numerous
arousing doubts (Panfil–Kuncewicz et al. 1997 a,b, Panfil–Kuncewicz et al. 1997b, Steinka
1999c, Steinka 2001b, Steinka et al. 2001c). The research of Panfil–Kuncewicz et al. proved
the improvement of microbiological quality of tvarogs stored in modified atmosphere,
however the composition of applied atmosphere that allowed obtaining that effect is
considered to worsen the sensory quality of the products. Microbiological tests concerning
hermetic packing of tvarogs (Steinka et al. 2001c, Steinka 2004) showed a possibility of
staphylococcal enterotoxin to occur in stored products.
In subject literature, there are no such models which would take all parameters into
account at the same time: packaging type, packing system, biological and biogenic factors
dependent on variable conditions of product storage in packaging.
Biological factors should be understood as live organisms belonging to Eucaryota and
Procaryota, constituting autochthonic micro-flora and secondary food contamination. The
notion ‘biogenic factors’ refers to products of basic and secondary metabolism of these
organisms formed as a consequence of transformations resulting from their physiology. The
biogenic factors include fermentation products (organic acids, alcohols), aldehydes, gases,
toxins, bacteriocins, antibiotics as well as products of proteolysis, liopolysis and
decomposition of specific organic substances.
The table below presents few mathematical models that are valid in predictive
microbiology and which concern cheese quality issues. The type of tests conducted in such
cheese and its products are presented in table 8.
There exists only one predictive model concerning tvarog micro-flora, which presence
results from certain contamination and re-infection level (Steinka 2003a). Appropriate
selection of packaging type and packing system determines quality of the product and safety
179
of a consumer. This results from the fact that in hermetically-packed tvarogs, there occur
interactions between product and micro-flora as well as among product, micro-flora and the
packaging. The influence of the above-mentioned biological factors and biogenic factors on
the type of interactions is dependent on packing system and decides about the quality of
products stored in refrigerating conditions. Multidirectional character of interactions
influences also safety of these products. This arouses difficulties in adapting mathematical
description to changes of interaction types having the influence on safety of hermeticallypacked lactic acid cheese.
Table 8. Predictive models of the micro-organisms behaviour in cheese
Authors of
a model
Brouillaud
–Delante
1997
Bolton
1999
Bozukart
2001
Steinka
2003
Tamagnini
2005
Type of described changes
Type
model
Linear
Evaluation of probability of growth of
Behaviour of Yersinia enterocolitica
Type of dairy
product
Micro-organisms
in dairy
products
Mexican
cheese
Feta cheese
Surface micro-flora
Lactic acid cheese
Polynomial
Crottin
Sheep’s milk
cheese
Cheese
Vitalistic,
Churchil,
Gompertz
Neural
network
Poirazi
2006
Streptococcus macedonicus
Yersinia
enterocolitica,
typhimurium
Salmonella
of
Logistic
Gompertz
Own study.
Nevertheless, in recent years, actions aiming at improvement of product safety has been
more and more often observed. These tendencies include taking packaging into account in
predictive models, as well as application of a new generation of packaging or using
bacteriostatic additives. However, taking these factors into account and excluding them
require new research to be conducted as regards evaluation of interactions occurring among
micro-flora both in raw material and with possible re-infections.
ASSESSMENT OF INTERACTIONS OCCURRING AMONG TVAROG
MICRO-FLORA IN MODEL CONDITIONS
The significant element taken into account in predicting the quality and safety of products
should be interactions occurring between micro-organisms.
Among interactions occurring between micro-organisms based on the presence of
numerous nutritive substances, there are such which result from the severe competition for
food. The developed defence mechanisms work in the form of such interactions which ensure
the possibility of using nutrition substances to all types of micro-organisms.
180
Izabela Steinka
Among micro-organisms, the complete dependence of species on reciprocal metabolism
is commonly known. The interactions of syntrophic character cause that in order to inhibit the
growth of one micro-organism, it is enough to limit the growth of another one. In some
fermented dairy products, the syntrophic phenomenon is responsible for proper organoleptic
properties. A very special case of syntrophic character is the dependence between cells of
Streptococcus thermophilus and Lactobacillus delbrueckii bulgaricus in yoghurt.
However, most often the interactions occurring between cells of Procaryota are based on
the phenomena of competition for food, and the interactions are most often of antagonistic
character.
Knowledge on food requirements of certain type of micro-flora is necessary for proper
prediction of direction of micro-organism metabolism in the presence of other species. If only
two micro-organisms species are present in the environment, then their growth is different
than in the situation when there are much more of them. The interactions are also different in
laboratory conditions and in food. In tvarogs, the growth of micro-organisms in a
monoculture also occurs differently than in the presence of many cultures.
The behaviour of micro-organisms in tvarogs is significantly dependent also on other
factors, which include:
•
•
•
•
•
type and count of technical micro-flora (starters) in tvarog,
type and count of other micro-organisms,
type of packaging,
packing system,
production stage, during which penetration of micro-organisms occurs: raw material,
curd, unpacked finished products, packed finished product.
The example of micro-organism behaviour in tvarogs, depending on the moment of
infection, contamination size or the presence of other micro-organisms, can be the behaviour
of Staphylococcus aureus and Enterococcus faecalis, if they are added to milk or to the
produced lactic acid curd.
Tests were conducted in laboratory conditions. Enterococci and staphylococci were
added to milk, which was then soured using a typical starter for production of lactic acid
cheese. The starter composition contained of bacteria of Lactococcus sp. type in amount of
96% and Leuconostoc lactis in amount of 4%.
The table below presents changes in count of micro-flora infecting raw material and the
curd, in the case when inoculum of this bacteria is added to the curd or the milk, then a curd is
produced and such a semi-product is stored in refrigerating conditions (table 9).
In the case of traditional packing of tvarogs into parchment paper, the growth of faecal
streptococci could be observed in the final period of refrigerating storage of products (figure.
5). The behaviour of population can evidence that re-infection with enterococci occurred not
during milk souring, but at further stages of tvarog production.
181
Table 9. Changes of staphylococci and enterococci in model
conditions depending on production stage
Type of microorganism
Time of curd storage (days)
Production
/inoculum
log10cfu/g
Staphylococcus
aureus
Enterococcus
faecalis
stage
Milk
2.30 cfu/mL
Curd 2.75cfu/g
Milk
2.74 cfu/mL
Curd
2.0 cfu/g
2
4
7
14
2.30
0
0
0
2.30
3.33
1
2.90
1
2.25
0
3.74
2.47
3.14
2
3.46
Own study.
4,5
4
3,5
y= 0,0833x3 - 0,7236x2 + 1,9331x+ 2,144
3
R2 = 0,9974
2,5
log cfu/g
2
1,5
1
0,5
0
0
2
4
7
14
Storage time (days)
Figure 5. The influence of refrigerating storage on enterococci population in tvarogs packed into parchment
paper.
Enterococci and yeast constitute predominant micro-flora in tvarogs (Steinka et al.
2001c). The modelling research was conducted, in order to evaluate interactions between
micro-flora most often present in lactic acid cheese.
The behaviour of starter micro-flora, yeast and staphylococci was tested in the presence
of certain inoculum of enterococci present in milk or in semi-products (lactic acid curd).
The influence of enterococci of technical micro-flora (Lactococcus spp. and Leuconostoc
lactis) and their interactions with other micro-organisms occurring depending on inoculum is
presented in the figures.
182
Izabela Steinka
As a result of souring milk with starter consisting of pure dairy cultures, lactic acid curds
were obtained, in which count of lactic acid bacteria after 14 days of souring was equal from
8.22 to 8.51 log10cfu/g. Number of Lactococcus bacteria decreased after 14 days of storage to
7.25-7.9 log10cfu/g on the average.
Inoculation of milk with Entrococcus faecalis cultures resulted in changes of count of
these bacteria after curd formation by 0.67 log10cfu/g. In the moment of curd formation, the
count of faecal enterococci was equal to 3.33 log10cfu/g. During curd storage, the
insignificant changes of enterococci population count occurred up to day 4 of its storage
(figure. 6). However, after 14 days the level of enterococii was different from the initial value
only by 0.11 log10cfu/g.
These changes were described by a polynomial equation of the third order. As much as
99.4% of variability of enterococci population could be explained with the help of this model
(table 10.).
5
4.5
4
3.5
3
Log cfu/g 2.5
2
1.5
1
0.5
0
Curd C
Curd B
Milk
0
2
4
7
14
Tim e (days)
Figure 6. Changes of enterococci count depending on curd production stage and applied inoculum.
Addition of faecal streptococci of initial inoculum 2 log log10cfu/g to the formed curd
resulted in detecting inhibition of growth of these bacteria after 14 days of storage (figure 6).
183
Table 10. Tendency of changes of enterococci depending on
tvarog production stage and the presence of allochthonous micro-flora
Experimental variant
Soured milk with Enterococcus
faecalis ATTC 29241
inoculum 4log cfu/g.
A-produced curd
Equation form
y = -0.0142x3 + 0.1839x2 - 0.6919x + 3.85
r2
0.994
B and C-curds with Enterococcus
faecalis ATTC 29241
inoculum 2 (B) and
4 log cfu/g ( C)
y = 0.0883x3 - 0.8729x2 + 2.4788x + 0.84 (B)
0.844
y = 0.0467x3 - 0.2593x2 + 0.114x + 4.772 (C)
0.954
4
3
2
D-curd with Enterococcus faecalis
ATTC 29241 and Staphylococcus
aureus ATTC 25923 after
milk fermentation
y = 0.1483x - 1.8483x + 8.0267x - 14.057x +10.42
0.999
E-curd with Enterococcus faecalis
ATTC 29241 and Candida sp. after
milk fermentation
y = -0.035x3 + 0.3864x2 - 1.1386x + 4.8
0.951
F–industrially
produced tvarogs
y = -0.005x4 + 0.1383x3 - 1.0775x2 + 2.8392x + 0.84
0.555
y- Enterococcus faecalis count, x-storage time.
The tendency of observed population changes was characterised by polynomial equation
of the third order (table 10). The coefficient of determination of this model showed that only
84.4% of observed variability of enterococci populations could be explained by the influence
of time of exposure to low temperature.
The addition of 4 log cfu/g of enterococci to the curd showed different dynamics of
population changes (figure 6). Equation describing changes of Enterococcus faecalis during
storage of a curd with additive in amount of 4 log cfu/g reflected to a great extent the real
variability of streptococci populations in stored curd (table 10).
Only 5.6% of observed streptococci variability did not result from the influence of curd
storage time of the behaviour of enterococci.
The presence of Staphylococcus aureus population in stored curd caused that count of
enterococci in a curd insignificantly decreased after 14 days of storage. However, the
reduction of size of streptococci population did not exceed the value of 0.28 log10cfu/g (figure
7).
184
Izabela Steinka
10
8
6
Log cfu/g
4
2
0
Lactococcus sp.
Enterococcus sp.
0
2
4
7
14
Time (days)
Figure 7. Changes in count of enterococci in the presence of populations: Lactococcus sp. and
Staphylococcus aureus (variant D).
The addition of yeast of Candida kefyr species to the curd (inoculum 3 log cfu/g) and the
presence of Enterococcus faecalis of inoculum equal to 4 log cfu/g resulted in detecting a
small decrease in count of Candida and a small increase in count of faecal streptococci after
14 days of curd storage. However, the magnitude of changes of Enterococcus population did
not exceed the value of 0.38 log10cfu/g (figure 8).
Changes in count of Enterococcus population in the presence of lactic acid bacteria and
Candida could be expressed with the help of a polynomial equation of the third order
characterised by a high value of coefficient of determination (table 10).
9
8
7
6
5
Lo g cf u/ g
4
3
2
1
Lactococcus sp.
0
Candida kef yr
0
2
4
T i me ( d ays)
Enterococcus sp.
7
14
Figure 8. Changes of enterococci count in the presence of populations: Lactococcus sp. and Candida kefyr
(variant E).
185
3.5
3
2.5
2
log cfu/g
1.5
1
0.5
0
0
2
4
Time (days)
7
14
Figure 9. Changes of enterococci count in vacuum-packed tvarogs.
Observation of enterococci population in vacuum-packed tvarogs showed that during
storage of the products, the increase in count of these bacteria occurred by 0.82 log log10cfu/g
on the average up to the second day of storage. Between day 2 and day 10 of storage, the
reduction in faecal streptococci count by ca. 1 log10cfu/g was detected (figure 9).
Enterococci population in tvarogs showed dynamics of changes similar to the enterococci
population added to the curds before their storage at low temperature (Variant B).
Equation describing changes of bacteria count in hermetically-packed tvarogs is a
polynomial equation of the fourth order characterised by a low coefficient of determination
value. The value of coefficient r2 showed the presence of other, apart from storage time,
factors influencing the population behaviour (table 10).
The polynomial equation determined for describing changes did not describe 44.5% of
variability of faecal streptococci population as time-dependant function.
The behaviour of enterococci population observed in variants B, C, D and E was similar,
no matter if additional type of re-infecting micro-organisms was present in the curd or
enterococci were present there as a monoculture. Another dynamics of changes were
observed in the case when curd subjected to final technological treatment i.e. lactic acid
cheese was closed in hermetic packaging (Variant F).
In this experiment, no significant influence of interactions occurring between
staphylococci and streptococci as well as between yeast and enterococci was observed on the
dynamics of changes of bacteria present in curds in model conditions.
No apparent antagonism was observed between lactic acid bacteria and enterococci. At
ratio 2:1 this phenomenon was expressed as lack of evident reduction in number of faecal
streptococci in a curd.
186
Izabela Steinka
In physiologically optimum conditions of the monoculture growth, the antagonistic
influence of lactic acid bacteria in relation to significant number of pathogenic bacteria is
known (Usajewicz 2000). The author investigated the influence of lactic acid rods on
pathogenic strains of staphylococci and Salmonella. Research on interactions of enterococci
with other bacteria concerned the microflora responsible for defects in ripening rennet cheese
(Usajewicz 1995). The quoted research indicates the significant influence of enterococci on
proteolytic activity of some bacteria of Lactococcus type that can have the influence on
determining the sensory and physico-chemical properties of obtained curds (Usajewicz 1995).
There exist only a few data concerning reciprocal interactions between faecal streptococci and
facultative pathogenic micro-organisms (yeast and staphylococci) in conditions of lactic acid
curd production (Steinka 2003a).
From other research conducted e.g. by Kornacki et al. (2002), it results that the effect of
inhibiting micro-organisms of faecal origin by technical micro-flora is obtained in tvarogs
only in certain technological conditions. However, the observed effect concerned faecal rods
of coli group, and not streptococci of Enterococcus type.
Lack of significant changes of streptococci population count and their apparent
synergistic interactions with yeast and staphylococci, at certain inoculum, causes that
enterococci remain at the constant level for a long time of curd storage.
Obtained results indicate also the low sensitivity of enterococci to the presence of
Lactococcus sp., staphylococci or yeast. In model conditions, regardless of the level of
infection with enterococci within the inoculum range 2-4 log cfu/g, changes of these bacteria
count were not significant after 14 days of curd storage. It was also observed that at low
initial contamination of tvarogs with enterococci, the reduction of these bacteria count after
14 days of storage was insignificant and did not exceed the value of 1 log10cfu/g.
A small change in environmental conditions is able to change the intensity of observed
phenomena or the total effect of interactions detected during production or manufacture of
tvarogs.
For interactions occurring among bacteria cells, the size of population occurring together
in a given environment is of a great significance. The example is interaction between
Staphylococcus aureus and Lactococcus rods presented in figure 10.
187
10
9
8
7
6
Log cfu/g 5
4
3
2
1
0
0
2
4
7
14
Time (days)
inoculum9
inoculum7
inoculum5
inoculum3
Figure 10. The behaviour of Staphylococcus aureus in lactic acid curd during storage.
At constant number of Lactococcus sp. cells in lactic acid curds produced in model
conditions, the dying-out time of staphylococci is dependent on the initial inoculum of
Staphylococcus aureus. Analyses of predictions of staphylococci changes in model
conditions, where only one population occurs (apart from staphylococci), show a completely
different behaviour of these bacteria than the one observed in environment containing several
populations (figure 11).
The reduction time for monoculture in laboratory model conditions is different than for
dicultures in the same conditions (table 11).
Table 11. Inhibition of growth of staphylococci tvarog curd
depending on the inoculum level
Inoculum
Log jtk/g
10
9
8
6
3
Size of reduction of Staphylococcus areus population count
log10cfu number
4
5
6
Reduction time (days)
7
10
11
3
9
12
4
5
6
5
6
7
3 cycles 2 days
-
Own research.
The behaviour of staphylococci investigated in lactic acid curds in the presence of three
other strains of micro-organisms is presented in the figure below.
188
Izabela Steinka
8
7
6
5
Log cfu/g 4
3
2
1
0
0
2
4
7
14
Time (days)
Yeast
Enterococcus sp.
Figure 11. The influence of interactions among staphylococci, enterococci, yeast and lactic acid bacteria in a
curd on population behaviour during storage.
Changes in count of yeast, enterococci and staphylococci populations show rather
synergistic interactions among these cells as well as small inhibiting effect on staphylococci
caused by present populations of Lactococcus, Enterococcus and yeast.
Changes observed in the so-called ‘co-cultures’ could be determined as logit and
described with the help of polynomial equations.
4
3
2
2
Y1 = 0.3771x - 4.7058x + 20.293x - 34.744x + 23.85 r =0.99
3
2
4
3
2
Y2= -0.0783 x + 0.5279 x - 0.4838x + 3.654-yeast r = 0.98
2
2
Y3= -0.1733 x + 1.9933 x - 7.2567 x + 7.6767x + 4.5 r = 0.99
where:
Y1- enterococci count, Y2 - yeast count, Y3 - staphylococci count,
x – time of refrigerating storage
2
r – equation coefficient of determination
(1)
(2)
(3)
189
THE INFLUENCE OF HERMETIC PACKING ON STARTER MICROFLORA AT HIGH CONTAMINATION LEVEL OF TVAROGS
The influence of packing on micro-organism populations in tvarogs has to be considered
in the aspect of the behaviour of both technological and re-infecting micro-flora. Irrespective
of the number of populations infecting raw material or a curd constituting semi-product for
the manufacture of tvarogs, the technical micro-flora occurs in the conditions of hermetic
packing.
The conducted research on the influence of vacuum packing on starter bacteria
populations showed a varied behaviour of these micro-organisms, depending on whether they
occur as the only cultures present in soured raw material or a curd, or whether they are
present in ready products (tvarogs). Tests were performed during 14 days of curd and tvarog
o
storage at the temperature of 6±2 C.
Evaluation of dynamics of changes of lactic acid bacteria populations was conducted
during storage of lactic acid curds and tvarogs manufactured in model conditions, in
dependence on vacuum packing.
It was observed that vacuum packing did not influence changes of allochthonous microflora count up to day 7 of storage of curds manufactured in model conditions. The dynamics
of changes of lactic acid bacteria were varied during storage of model lactic acid curds and
tvarogs manufactured in industrial conditions.
9
8
4
3
2
y = 0,0363x - 0,5158x + 2,4938x - 4,7542x + 11,15
R2 = 1
7
6
4
3
2
y = -0.0742x + 0.7433x - 2.4308x + 3.0217x + 4.54
5
log cfu/g
4
2
R =1
3
2
1
0
0
2
Curd B
4
7
Time of storage (days)
Curd F
polynom.
Figure 12. Changes of Lactic Acid Bacteria in curd B and tvarog (F) during storage.
14
polynom.
190
Izabela Steinka
As a result of souring the milk with pure lactic acid bacteria cultures, the lactic acid curds
were obtained, in which count of lactic acid bacteria after 14 hours of souring was equal from
8.22 to 8.41 log10cfu/g. In tvarogs produced industrially, number of lactic acid bacteria
ranged from 5.44 log10cfu/g to 6.32 log10cfu/g (figure 12).
Statistically significant differences were observed in sizes of Lactococcus sp. population
in tvarogs (C) and curd manufactured in model conditions (B) for á=0.05. The average
differences between count of lactic acid bacteria for C and B were significant and were equal
to t = - 1.9280 and t = –3.9967.
Number of lactic acid bacteria in vacuum–packed tvarog LT could be expressed with the
help of mathematical equation presented below:
2
L T = 31.295-3.05•LSP r -0.706 , r 0.498 , p 0.16
á0.05
(4)
LT – count of lactic acid bacteria
SP – vacuum-packed curd
T – vacuum-packed tvarog
Correlation coefficient between variables indicated high correlation between counts of
lactic acid bacteria in both tested products, however the value of coefficient of determination
2
R showed that only 33% of variability of Lactococcus sp. count in tvarogs (C) could be
explained with changes observed in stored curds produced in model conditions (B).
During storage of curds A and B (Curd A was a control sample and remained without
packaging, while curd B was vacuum-packed and manufactured in model conditions), no
statistically significant differences in the dynamics of changes of Lactococcus sp. count were
observed.
However, from obtained data it results that vacuum packing constitutes factor influencing
the dynamics of growth of technological micro-flora population in lactic acid curd during
final period of storage in refrigerating conditions (figure 13).
Regardless of the presence of packaging, the significant differences were detected in the
dynamics of changes of Lactococcus sp. population between day 7 and 14 of curd storage
(figure 13).
In control curds remaining without packaging (A) the level of lactic acid bacteria after 14
days was the same as before storage (A), while in vacuum-packed curd (B) the decrease in
population count by 1 logharithmic cycle was observed (figure 13).
191
Log cfu/g
8,5
y= -0,0133x4 + 0,1083x3 - 0,2167x2 + 0,0117x+ 8,33
R2 = 1
8,4
8,3
8,2
8,1
8
7,9
y= 0,0363x4 - 0,5158x3 + 2,4938x2 - 4,7542x+ 11,15
R2 = 1
7,8
7,7
7,6
0
2
4
7
14
Time of storage (days)
Curd A
Curd B
polynom.
polynom.
Figure 13. Changes of Lactic Acid Bacteria count in curds A and B during storage.
Polynomial equation of the fourth order describing variations of Lactococcus sp.
population count in curds A and B showed a different direction of observed changes (figure
13).
LSP=0.25951+0.96344LSN
2
r 0.509, r 0.259 , p =0.381
á 0.05
(5)
L- number of lactic acid bacteria,
SP - vacuum-packed curd
SN - non-vacuum packed curd
However, in the case of curds produced in similar technological conditions, the
differences in dynamics of changes of lactic acid bacteria for vacuum-packed curds and curds
remaining without packaging were not as significant as differences between micro-flora of
curds and lactic acid cheese (figures 12 and 13).
In vacuum-packed products of animal origin, changes in lactic acid bacteria population
count and their metabolism are varied and dependant on type of the product, packing system,
time and way of storage as well as secondary micro-flora present in a product (Holly et al.
1992, Jackson et al. 1992, Nicolai et al. 1993).
Confirmation of the importance of vacuum-packing in stabilising the growth of lactic
acid bacteria can also be the model developed for tvarog produced in industrial conditions.
192
Izabela Steinka
From the presented model, it results that in lactic acid cheese manufactured in industrial
conditions, the behaviour of applied autochthonous micro-flora is influenced by other factors
than in the case of non-packed semi-products (curds). Probably, it is dependent not only on
technologies applied in production plants, but also on the presence of micro-flora re-infecting
milk. Determined equation of linear regression for vacuum-packed and unpacked curds show
that only 25.8% of changes of lactic acid bacteria count can be explained by application of
vacuum-packing.
This is consistent with observations of Maniar et al., who detected significant discrepancy
between lactic acid bacteria count in cottage cheese, depending on level of atmosphere
modification of the above-mentioned packaging wherein the product was stored (Maniar et al.
1994).
Whereas, the predictive model of Nicolai describing the dynamics of changes in vacuumpacked meat indicates the significant influence of the environmental pH value on changes of
lactic acid bacteria count during storage of packed products.
The observed behaviour of lactic acid bacteria during refrigerating storage of the curds
without re-infection is not significantly dependent on the presence of packaging up to day 7
of curd storage. Changes in fermentation bacteria population count during storage of vacuumpacked curds produced in model conditions and industrially manufactured curds show
significant differences in relation to the semi-product.
INVESTIGATION OF INTERACTIONS IN TVAROGS OF HIGH
MICRO-FLORA CONTAMINATION LEVEL
From numerous research on lactic acid cheese (Steinka 2003a), it results that time of
tvarog storage is not the only one and the most significant factor determining the population
size in products.
In minor part of available literature, the changes of microbiological quality of cottage
cheese and tvarogs packed using vacuum or in modified atmosphere are described Maniar
1994, Fedio 1994, Panfil –Kuncewicz 1997a,b, Severini 1998, Steinka 1999c, Steinka
2001a,b). From data it results that packing system has a significant influence on the behaviour
of micro-flora present in a product during its storage (table 12).
Table 12. Equations of linear correlation for the influence of tvarog
storage time on allochthonous micro-flora count
Type of
organisms
micro-
Enterococcus sp.
Escherichia coli
Staphylococcus
aureus CP
Mould
Yeast
Psychrotrophs
Lactic acid cheese packed into PA/PE
laminate
Equation
r
Y=38473+43157t
0.299
Y=1725.3-141.6t
-0.348
Y=861.67-6.600t
-0.021
Lactic acid cheese packed into Cryovac
laminate
Equation
r
Y=1575e2-126et
-0.239
Y=170.42-14.29t
-0.344
Y=129.17+10.714t
0.157
Y=7170.4+307.86t
Y=6845e2+53759t
Y=8445e2-102E2t
y=72.917+15.893t
Y=-148e3+66775t
Y=-295.6+274.02t
Steinka 2003a, t - storage time.
0.000
0.481
-0.090
0.170
0.631
0.261
193
Application of modified atmosphere in packing of lactic acid cheese does not guarantee
inhibition of growth of all types of micro-organisms present in a product before storage
(Kuncewicz 1997a,b). The research of Kuncewicz showed that application of 80% of CO2
additive for packing tvarogs limited the growth of mould and coliforms during refrigerating
storage, however it did not inhibit the growth of yeast.
Vacuum packing of tvarogs in conditions without Good Manufacture Practice also does
not guarantee the reduction of micro-flora during storage of products in refrigerating
conditions (Steinka 1999c).
An attempt to create model predicting changes of quality and safety of hermetically
packed lactic acid cheese had to take interactions occurring micro-flora present in tvarogs into
account. Changes of micro-flora population count present in tvarogs could result from the
change of conditions occurring in the space between the packaging and the products during
storage.
In lactic acid cheese packed with vacuum system and into Cryovac, the different
tendency in behaviour as well as varied dynamics of change of micro-organism population
count is observed.
Table 13. Tendency of changes of tvarog allochthonous micro-flora
Type of micro-flora
Enterococci
Escherichia coli
Moulds
Yeasts
Psychrotrophic
bacteria
Coagulase
positive
Staphylococci
Coagulase negative
Staphylococci
Type of packaging
PA/PE
Equation describing tendency
of changes
R2
Cryovac
Equation
describing
tendency of changes
r2
y = -0.82x2 + 4.28x + 0.32
y = 0.07x2 - 1.27x + 4.5
y = 1.21x2 - 4.77x + 7.6
y = -0.27x2 + 1.61x + 3.71
y = -0.15x2 + 0.59x + 5.31
0.999
0.997
0.999
0.999
0.999
y = 0.74x2 - 3.55x + 8.08
y = -1.15x + 3.4167
y = -1.675x2 + 5.515x+0.97
y = 0.41x2 - 0.44x + 3.6
y = 0.49x2 - 1.41x + 3.43
0.999
0.997
0.999
0.999
0.999
y = 0.205x2 - 0.355x + 2.97
0.999
y = 0.21x2 - 1.02x + 3.58
0.999
y = 0.255x2 - 0.525x + 3.71
0.999
y = -0.43x2 + 1.54x + 1.8
0.999
x-storage time.
Analyses of data also indicate the existence of significant variation in the course of
function describing changes in count of all other tested groups of facultative anaerobic
bacteria such as enterococci, staphylococci, E. coli after 14 days.
Linear equations cannot be used for describing changes of tvarog micro-flora (table 12).
The courses of these functions and consistency of predicted data with empirical data for both
tvarog packing systems are not identical. Coefficients of linear correlation r indicate weak or
lack of linear correlation between storage time and the behaviour of surface micro-flora
population.
Differences in tendencies of changes of micro-organisms present in tvarogs depending on
packing system can be observed. It is confirmed by the derived equations describing
tendencies of changes presented in table 13.
Due to the possibility of occurrence of multi-species population occupying the surface of
tvarogs as well as lack of predictive models concerning tvarogs, it became important and
194
Izabela Steinka
necessary to create such a predictive model for evaluation of quality of stored products, which
will take interaction occurring among surface micro-flora into account.
The research of Steinka et al. proved that the level of micro-flora present in tvarogs
showed diversification dependent on packing method (Steinka et al. 1998, 2001c Steinka
2001a). In tvarogs packed into cryovac, after 14 days of storage, the lower number of
Enterococcus sp. and Escherichia coli by 1 log cfu/g on the average was detected in
comparison with tvarogs packed into PA/PE. The count of coagulase-negative
Staphylococcus aureus, mould and psychrotrophs was higher by 2 logarithmic cycles on the
average in tvarogs packed into PA/PE. The level of yeast and coagulase-positive
staphylococci in tvarogs packed into both types of packaging was similar after storage
(Steinka 2003a).
Equation of linear correlation determined for evaluation of influence of storage time on
the dynamics of population changes showed that only 1.53-19.7 % of variability could be
explained with the help of linear models.
Models of changes of micro-flora populations present in tvarogs packed into Cryovac
laminates were characterised by low coefficients of determination R2 at the level of 0.0260.3716.
Microbiological data were subjected to multiple regression analysis. Determined
coefficients of semi-partial correlation are presented in tables 14 and 15.
Values of partial correlations allowed evaluation of the influence of interactions among
micro-organisms on changes in count of individual groups of micro-organisms in lactic acid
cheese (table 14). The obtained test results showed that enterococci, mould and psychrotrophs
had the greatest influence on determining changes of surface micro-flora of tvarogs packed
into PA/PE had.
In lactic acid cheese packed into cryovac, the significant reciprocal influence of
facultative anaerobic bacteria on changes of other micro-organism populations was detected
(table 15).
Table 14. Coefficients of multifactor regression correlation in equations of
micro-organism interactions in tvarogs packed into PA/PE
Type of interactions between micro-organisms in tvarogs packed
into PA/PE
r
2
r
Enterococcus sp.
E. coli
Yeast
Psychrotrophs
-0.202
-0.153
0.235
0.066
Staphylococcus aureus CP
Yeast
Mould
Mould
Psychrotrophs
Enterococcus sp.
Psychrotrophs
0.257
-0.155
-0.117
0.190
-0.155
-0.175
0.215
0.214
0.013
0.024
0.036
0.060
0.046
0.060
0.046
0.046
Yeast
Mould
0.249
0.184
0.062
0.033
Staphylococcus aureus CN
Mould
Yeast
Psychrotrophs
Steinka 2003a, CP- coagulase-positive Staphylococcus aureus, CN- coagulase-negative Staphylococcus
aureus.
195
Table 15. Coefficients of multifactor regression correlation in equations
of micro-organism interactions in tvarogs packed into Cryovac
Type of interactions between micro-organisms in tvarogs packed into Cryovac
r
2
r
Enterococcus sp.
E.coli
Enterococcus sp.
Yeast
Mould
0.146
0.753
0.767
0.409
0.411
0.020
0.021
0567
0.589
0.167
0.169
0.000
Enterococcus sp.
Yeast
Escherichia coli
0.294
0.252
-0.120
0.086
0.063
0.014
Mould
Yeast
Psychrotrophs
Mould
0.678
0.329
-0.206
0.668
0.460
0.108
0.042
0.447
E. coli
Psychrotrophs
Steinka 2003a, CP- coagulase-positive Staphylococcus aureus, CN- coagulase-negative Staphylococcus
aureus.
Equations presented in this paper describing variability of surface micro-flora of tvarogs,
depending on storage conditions suggest the existence of factors other than time that
influence changeability of micro-organism populations.
Coefficients of linear correlation determined for equations describing population of
staphylococci in both packing systems show that the behaviour of these micro-organisms is
probably dependant not only on atmosphere occurring inside the packaging in both packing
system, but also on other factors requiring further research.
The above-mentioned observations are the reasons for which it is difficult to evaluate
unequivocally the behaviour of staphylococci and to compare it with predictions obtained
with the help of a predictive computer program called Pathogen Modelling Program.
From predictions obtained as a result of simulations of Pathogen Modelling Program for
model conditions at pH 4.7, it results that time necessary for achieving reduction in
staphylococci count by only 1 logarithmic cycle at temperatures 4, 6 and 8°C is equal to 11.3,
13 and 14 days respectively. Data obtained through simulation of Pathogen Modelling
Program show a low rate of variability in these micro-organism count in model conditions,
what is also consistent with tendencies observed in tvarogs (Steinka 2003a).
According to Kimur, the behaviour of staphylococci and Escherichia coli is dependant on
the level of carbon dioxide and oxygen in the environment (Kimura et al. 1998). The
tendencies of staphylococcus growth observed in tested cheese coming from Cryovac and
PA/PE laminates show a significant meaning of atmosphere composition within the space
under packaging surface for the growth of this group of micro-organisms. Temperature is not
a factor that limits absolutely the growth of staphylococci. Their slow growth below the
temperature of 10°C is observed in different types of food (Lee Wong et al. 2002).
In tested tvarogs, the significant reduction in number of Escherichia coli rods during
storage is observed. From literature, it results that this pehnomena is closely connected with
sensitivity of rods to action of organic acids (Hsiao et al. 1999).
196
Izabela Steinka
Adams et al. (1995) proves that E. coli bacteria are sensitive to low pH values of the
environment. However, from model research it results that during production and storage of a
product at room temperature conditions, the reduction of Escherichia coli cells occurs not
before the acidity reaches the value of pH 3.4. Although Buchanan et al. (1992) did not
observe the growth of E. coli at the temperature of 4°C, Jordan et al. (1999) detected the
ability of non-toxicogenic strains of E. coli O157:H7 to survive in the environment of pH 3.0,
at the temperature of 37°C. This research showed that even after 3 days, it was possible to
identify the presence of a significant number of cells that survived in such conditions. This
allowed assuming that the growth of Escherichia coli in a product was not influenced by the
packing system, but by a low temperature and reciprocal antagonistic interactions occurring
among the micro-organisms.
The size of enterococci population detected in tvarogs can be related to the literature
information determining the level of contamination of unripened cheese (Baumgartner et al.
2001, Centeno et al. 1999).
In the literature, there are no models available describing the growth of fungi in vacuumpacked unripened cheese such as tvarog. However, the issue of determining the number of
these micro-organisms during storage of unripened cheese in conditions of modified
atmosphere was undertaken in several papers (Fedio et al. 1994, Maniar et al. 1994, Westal et
al. 1998).
Yeast constituted quantitatively predominant micro-flora in tvarogs packed with both
systems. Changes in populations showed high linear correlation with time of storage in
refrigerating conditions. The dynamics of growth of yeast in vacuum-packed products
confirmed tendencies observed by Westal (Westal et al. 1998). From data obtained by Westal,
it resulted that as much as 25% of tested cottage cheese with additives packed in modified
6
atmosphere showed the significant increase in yeast count in a product ranging from 10 up
8
to 10 cfu/g after 2-5 days. The qualitative and quantitative composition of yeast in cottage
cheese, as well as production of spores remained in a strong dependence on percentage
composition of modified atmosphere.
The tendencies of changes of psychrotropic micro-organisms observed in tvarogs are
hard to be related to the models accessible in literature. The survival rate of Pseudomonas sp.
during storage of cottage cheese was presented by Brocklehurst and Lund (Brocklehurst and
Lund 1988). There are only a few publications mentioning changes of psychrotroph
populations during tvarog storage. Tests conducted on cottage cheese aiming at determination
of this micro-flora were performed by Fedio et al. 1994, Maniar et al. 1994, Neugebauer et al.
2005. Evaluation of changes of psychrotrophs populations in tvarogs packed with a hermetic
and vacuum system was conducted by Steinka et al. 1999b.
Packing tvarogs into Cryovac laminates is often preceded by blowing nitrogen through
the product surface, what causes that the initial concentration of carbon dioxide at tvarog nonvacuum packing is different in comparison with its content in vacuum packaging.
Complete modification of gaseous atmosphere involving addition of 100% N2 during
packing of unripened cheese is commonly applied in many countries (Adams et al. 2000).
Interpretation of change in micro-organism count in hermetically-packed tvarogs gives
rise to many difficulties. In tested tvarogs packed with vacuum system, the existence of
interactions were detected among micro-organisms that are typical in model conditions and
difficult to precise unequivocally.
197
CHARACTERISTICS OF INTERACTIONS OCCURRING AMONG
MICRO-ORGANISMS IN HERMETICALLY-PACKED TVAROGS
The results of tests conducted on tvarogs (Steinka 2003a) allow saying that in vacuumpacking conditions, a major part of interactions occurring among micro-organisms had
antagonistic character. It was indicated by negative values of correlation coefficients. In these
tvarogs, the antagonistic interactions between yeast and enterococci, yeast and staphylococci,
Escherichia coli rods and psychrotrophs as well as fungi and staphylococci were detected.
The interactions between bacteria and fungi are more often observed in mould cheese. The
antagonistic influence of Penicillium roqueforti on such pathogens as Escherichia coli or
Staphylococcus aureus was described by Larsen (1997). The antagonism of fungi in relation
to pathogens was conditioned by proteolytic and lipolytic action of fungi. High activity of
enzymes decomposing proteins and fats results in high activity in inhibiting bacteria cells
(Larssen 1997).
It turns out that metabolites of fungi such as acetaldehyde and benzaldehyde play a
significant role in antagonism occurring between fungi and pathogenic bacteria.
Fungi of Penicillium type show the ability to inhibit Staphylococcus aureus and Listeria
monocytogenes at the temperature of 150C as soon as after 6 days. Mould occurring in tvarogs
include most of all Penicillium expansum and Aspergillus flavus. Their metabolic activity
could contribute to inhibition of growth of staphylococci cells, however this inhibition was
not effective.
In tested lactic acid cheese, the growth stimulation occurred in the case of yeast and
staphylococci, as well as yeast, mould and psychrotrophs. The direction of changes indicated
reciprocal actions stimulating the growth of one population by the other.
In laboratory conditions, the antagonistic action of Escherichia coli described in literature
concerned staphylococci. In tested tvarogs, this type of interactions was observed in the case
of Cryovac packaging. The synergistic interactions between coagulase-negative staphylococci
population and Escherichia coli rods was detected in tvarogs packed into cryovac.
The results of multifactor analysis did not confirm such a strong antagonistic interaction
between staphylococci and psychrotrophs as were observed in the previous testing (Steinka
2001b) of vacuum-packed tvarogs.
In model conditions of growth, the interactions between Escherichia coli and
Enterococcus faecalis both of synergistic and antagonistic character are observed (Usajewicz
1995). In tested tvarogs, the interactions of synergistic character occurring between these
bacteria reflect the tendency occurring in model conditions of mixed culture described by
Usajewicz (1995). The synergism between these bacteria was detected in tvarogs packed into
cryovac.
From conducted model research concerning growth of facultative anaerobic bacteria in
lactic acid curd, it results that the behaviour of some micro-organisms determined in a tvarog
differs from the one detected in curds (Steinka 2003a). Low temperature and the atmosphere
occurring inside the vacuum packaging lower the dynamics of growth of populations and the
metabolic activity of lactic acid bacteria.
The observed changes in count of lactic acid streptococci in curds produced in model
conditions and in stored tvarogs could be described with the help of polynomial equations of
198
Izabela Steinka
the third and fourth order. Significant differences in the course of curves illustrating those
changes were indicated in the case of non-hermetic and vacuum packaging (Steinka 2003a).
Antagonistic influence of lactic acid streptococci on micro-organisms present in tvarogs
could be significantly lowered, due to conditions occurring inside the packaging. Despite the
acknowledged antagonistic properties of lactic acid bacteria against pathogenic bacteria,
lactic acid cheese can also constitute the medium wherein the growth of such micro-flora as
staphylococci occurs (Ingham 1996, Belickova et al. 2001, Masa-Calpe 1996, Steinka 2001c,
Steinka 2004).
From the research of Kornacki (2002), it results than even at correctly conducted process
of souring the milk with application of active lactic acid cultures, the reduction in count of
micro-flora originating from postproduction contamination is not always obtained. It concerns
e.g. coli rods, which are sensitive to action of lactic acid bacteria, and which number was not
reduced during industrial production of tvarog, using butter cultures.
Changes of staphylococci population observed in tvarogs during product storage probably
do not result from the antagonism of Escherichia coli, because the count of faecal bacteria
was too low to inhibit Staphylococcus aureus. In order to inhibit the growth of staphylococci
effectively, more than 100-fold number of rods in relation to number of staphylococci, as well
as temperature higher than 150C are necessary (Steinka 2001 b).
The insignificant inhibition of growth of staphylococci population observed in tested
tvarogs was probably caused by the growth of mould.
It was stated that reduction in number of cells belonging to Staphylococcus aureus
species could not result from antagonistic action of yeast in relation to these staphylococci.
The correlation coefficients showed the stimulating influence of yeast on staphylococci in
both packing system. It was confirmed by model tests conducted on lactic acid curds. In
tvarogs, no inhibiting influence of yeast on majority of micro-organisms groups was detected,
despite the fact that yeast constituted predominant micro-flora in hermetically-packed
tvarogs.
Slow reduction of Staphylococcus aureus in products did not occur similarly to the
experiments performed in laboratory conditions. However, in tvarogs packed into cryovac, a
strong synergistic relations among populations of yeast, mould and psychrotrophs was
observed.
The character of interactions occurring among micro-organisms in tvarogs could result
from variability of gaseous atmosphere inside the packaging. Research of Westal proved a
small inhibiting influence of modified atmosphere on the growth of yeast in products (Westal
1998). Test results obtained by Westal were controversial in relation to the theory of Fedio
and Alves, who confirmed the increase in tvarog stability depending on the level of
atmosphere modification in MAP system.
In conditions of tvarog hermetic packing, it is hard to indicate unequivocally the
synergism, antagonism or antibiosis between two micro-organisms, because tvarogs presented
in mentioned cases constitute the bases for growth of multi-component population composed
of many species of fungi and bacteria.
It is hard to separate the influence of one group on the others, if it is considered that the
growth of certain micro-organism is influenced by metabolites of 7 groups of microorganisms at the same time. It is also difficult to separate their common influence on chemical
and physical characteristics of a products as well as basic packaging properties.
199
Application of response surface models as well as equations describing them in order to
evaluate the microbiological quality allowed defining changes occurring in tvarogs, taking at
least three groups of micro-organisms into account (Steinka 2003a).
The advantage of applied method was the possibility to predict magnitude of population
changes, depending on variability of two other species during storage.
The exact knowledge of these interactions is necessary for conducting observations of
changes in microbiological quality and safety, in order to compare obtained values with valid
microbiological standards for tvarogs. The obtained surface response models allowed
defining changes in time, depending on the initial size of tested populations.
In this regard, mathematical equations describing this variability allowed predicting
strictly defined interactions occurring in a products. However, surface response models have
some certain limitations, which concern among others a small number of relationships that
they can illustrate. Despite the above-mentioned limitations, the surface response models
constitute an assumption for interpretation of observed phenomena.
In order to illustrate the interactions occurring in both types of hermetically-packed
tvarogs, the dynamic model should be developed, which will consider all interactions
occurring in a given time both among the micro-organisms and between the products and
packaging.
DEVELOPMENT OF MATHEMATICAL MODEL FOR EVALUATION
OF QUALITY OF LACTIC ACID CHEESE
Development of a model was based on an assumption that interactions occurring among
micro-flora present on the tvarog surface and the interactions between them and the
packaging constituted a base for determining a mathematical model of dynamic interaction
among micro-organisms.
Calculations were started from searching for the relationship between variables
X i (t ), i = 1,2,..., m,
of the form:
X i (t ) = a i 0 (t ) + a i1 (t ) X 1 (t ) + a i 2 (t ) X 2 (t ) + ... + a ii −1 (t ) X i −1 (t ) + a ii +1 (t ) X i +1 (t ) + ...
+ a im (t ) X m (t )
(6)
during time t , t ∈< 0, T >, for i = 1,2,..., m.
Unknown coefficients a ik (t ), at defined i, i = 1,2,..., m, for k = 0,1, ,..., m, k ≠ i, are
determined using the least squares method, minimising sums of squares of deviations between
empirical values given in table 16 and calculated according to the following formula (6)
200
Izabela Steinka
n
Δi = ∑ [ xij (t ) − a i 0 (t ) − a i1 (t ) x1 j (t ) − a i 2 (t ) x 2 j (t ) − ... − a ii −1 (t ) x1−1 j (t )
j =1
− a ii +1 (t ) x1+1 j (t )
− ... − a im (t ) x mj (t )] 2 , i = 1,2,..., m,
(7)
Table 16. Empirical values used for model development
Variable
X 1 (t )
X 2 (t )
X 3 (t )
X m −1 (t )
X m (t )
Realisation
number j
Variable realisation
1
x11 (t )
x 21 (t )
x31 (t )
x m −11 (t )
x m1 (t )
2
x12 (t )
x 22 (t )
x 32 (t )
x m −12 (t )
x m 2 (t )
3
x13 (t )
x 23 (t )
x33 (t )
x m −13 (t )
x m 3 (t )
n −1
x1n −1 (t ) x 2 n −1 (t ) x 3n −1 (t ) x m −1n −1 (t )
x mn −1 (t )
n
x1n (t )
x mn (t )
x 2 n (t )
x3n (t )
x m −1n (t )
Steinka 2003a.
From necessary condition of existence of function extreme Δi , i = 1,2,..., m,
∂Δi
= 0, k = 0,1, ,..., m, k ≠ i,
∂a ik
For each defined i, i = 1,2,..., m, the following system of equations was obtained
n
n
n
n
j =1
j =1
j =1
na i 0 (t ) + ∑ x1 j (t ) a i1 (t ) + ∑ x 2 j (t ) a i 2 (t ) + ... + ∑ xi −1 j (t ) a ii−1 (t ) + ∑ xi +1 j (t ) a ii+1 (t )
j =1
n
n
j =1
j =1
+ ... + ∑ x mj (t ) a im (t ) = ∑ xij (t )
n
n
n
n
j =1
j =1
j =1
j =1
∑ x1 j (t ) a i 0 (t ) + ∑ x1 j (t )x1 j (t ) a i1 (t ) + ∑ x 2 j (t )x1 j (t ) a i 2 (t ) + ... + ∑ xi −1 j (t )x1 j (t )
aii−1 (t )
n
n
n
j =1
j =1
j =1
+ ∑ xi +1 j (t )x1 j (t ) a ii+1 (t ) + ... + ∑ x mj (t )x1 j (t ) a im (t ) = ∑ xij (t )x1 j (t )
...
n
n
n
j =1
j =1
201
∑ xi −1 j (t ) a i 0 (t ) + ∑ x1 j (t )xi −1 j (t ) a i1 (t ) + ∑ x 2 j (t )x i −1 j (t ) a i 2 (t ) + ...
j =1
n
+ ∑ xi −1 j (t )xi −1 j (t ) a ii−1 (t )
j =1
n
n
n
j =1
j =1
j =1
+ ∑ xi +1 j (t )xi −1 j (t ) a ii+1 (t ) + ... + ∑ x mj (t )x i −1 j (t ) a im (t ) = ∑ xij (t )xi −1 j (t )
...
n
n
n
j =1
j =1
∑ xi +1 j (t ) a i 0 (t ) + ∑ x1 j (t )xi +1 j (t ) a i1 (t ) + ∑ x 2 j (t )xi +1 j (t ) a i 2 (t ) + ...
j =1
n
+ ∑ xi −1 j (t )xi +1 j (t ) a ii−1 (t )
j =1
n
n
n
j =1
j =1
j =1
+ ∑ xi +1 j (t )xi +1 j (t ) a ii+1 (t ) + ... + ∑ x mj (t )xi +1 j (t ) a im (t ) = ∑ xij (t )xi +1 j (t )
...
n
n
n
n
j =1
j =1
j =1
j =1
∑ x mj (t ) a i 0 (t ) + ∑ x1 j (t )x mj (t ) a i1 (t ) + ∑ x 2 j (t )x mj (t ) a i 2 (t ) + ... + ∑ x i −1 j (t )x mj (t )
a ii−1 (t )
n
n
n
j =1
j =1
j =1
+ ∑ xi +1 j (t )x mj (t ) a ii+1 (t ) + ... + ∑ x mj (t )x mj (t ) a im (t ) = ∑ xij (t )x mj (t )
i = 1,2,..., m,
from which the unknown equation coefficients can be determined
assuming that for each defined i, i = 1,2,..., m, :
⎤
⎡bi 00 (t ), bi 01 (t ),..., bi 0i −1 (t ), bi 0i +1 (t ),..., bi 0 m (t )
⎡a i 0 (t ) ⎤
⎥
⎢
⎥
⎢
⎥
⎢bi10 (t ), bi11 (t ),..., bi1i −1 (t ), bi1i +1 (t ),..., bi1m (t )
⎢a i1 (t ) ⎥
⎥
⎢
.
⎥
⎢.
⎥
⎢
⎥
⎢
⎥
⎢.
⎥
⎢.
⎥
⎢
⎥
⎢.
.
⎥
⎢
⎥
⎢
B
t
b
t
b
t
b
t
b
t
b
t
(
),
(
),...,
(
),
(
),...,
(
)
=
(
)
⎥
⎢
Ai (t ) = ⎢a ii −1 (t ) ⎥
i
ii −10
ii −11
ii −1i −1
ii −1i +1
ii −1m
⎥
⎢
⎢a (t )⎥
⎢bii +10 (t ), bii +11( t ) (t ),..., bii +1i −1 (t ), bii +1i +1 (t ),..., bii +1m (t )⎥
⎢ ii +1 ⎥ ,
⎥,
⎢.
⎥
⎢.
⎥
⎢
⎥
⎢
⎥
⎢.
⎥
⎢.
⎥
⎢
⎥
⎢.
.
⎥
⎢
⎥
⎢
⎥⎦
⎢
b
(
t
),
b
(
t
),...,
b
(
t
),
b
(
t
),...,
b
(
t
)
a
(
t
)
im1
imi −1
imi +1
imm
⎣ im 0
⎦⎥
⎣⎢ im
(8)
202
Izabela Steinka
⎡c i 0 (t ) ⎤
⎢
⎥
⎢c i1 (t ) ⎥
⎢.
⎥
⎢
⎥
⎢.
⎥
⎢.
⎥
⎢
⎥
C i (t ) = ⎢c ii −1 (t ) ⎥
⎢c (t )⎥
⎢ ii +1 ⎥ ,
⎢.
⎥
⎢
⎥
⎢.
⎥
⎢.
⎥
⎢
⎥
⎣⎢c im (t ) ⎦⎥
(9)
where:
n
bi 00 = n, bi 0l = ∑ x lj (t ), l = 1,2,..., m, l ≠ i,
j =1
(9a)
n
bik 0 = ∑ x kj (t ), k = 1,2,..., m, k ≠ i,
j =1
n
bikl = ∑ x lj (t )x kj (t ), k = 1,2,..., m, k ≠ i, l = 1,2,..., m, l ≠ i,
j =1
n
c i 0 = ∑ x ij (t ),
j =1
n
c ik = ∑ x ij (t )x kj (t ), k = 1,2,..., m,
j =1
systems of equations (8) can be expressed in a matrix form:
Bi (t ) Ai (t ) =C i (t ) for i = 1,2,..., m.
(10)
Hence, if matrix determinants Bi (t ), i = 1,2,..., m, are different from zero, then for each
defined i, i = 1,2,..., m, we determine unknown coefficients
a i 0 (t ), a i1 (t ), a i 2 (t ), a ii −1 (t ), a ii+1 (t ), a im (t )
of models from matrix equations
Ai (t ) = [ Bi (t )] −1 C i (t )
during time t , t ∈< 0, T >, where [ Bi (t )] −1 are inverse matrixes of a matrix Bi (t ).
(11)
203
By this, we identify approximate relationships between variables X i (t ), i = 1,2,..., m, in
defined time t , t ∈< 0, T > .
Figure 14 presents the algorithm of determining the parameters of mathematical model of
dynamic interactions between tvarog microbiological parameters and the packaging.
The obtained polynomial equation served for developing a computer program called
TWAROGI JMTPH, which takes the dynamic changes of micro-flora in time into account. In
developed model, the predictions concerning changes in properties of applied packaging were
also considered. The predictions applied to micro-biological parameters of products packed
with a vacuum system and using the technology of shrink-wrapping of product with cryovac.
The obtained predictions differed from each other as regards the absolute terms and values of
constant coefficients. Below, the exemplary prediction of yeast population for day 11 of
tvarog storage is presented:
YPA/PE=126032.78+5.82x1+436.02x2-97.19x3+12.12x4-306.39x5+4.19x7
(12)
Yc=118770003.92-2.69x1+215.21x2+45.98.19x3+14.04x4-281.14x5+3.39x7
(13)
where x1-enterococci, x2-E. coli, x3-coagulase positive Staphylococcus aureus, x4-coagulase
negative Staphylococcus aureus, x5 – mould, x7 –psychrotrophs
Developed computer program allows quick prediction of magnitude and type of changes
occurring in hermetically-packed tvarogs depending on packing technology of products.
Although multi-parameter models used for predicting microbiological quality of products
are criticised, they reflect conditions occurring in food to the much greater extent than other
models (Baranyi 1996, Steinka 2003a). In predicting quality and safety of products, the
mathematical models of a small number of parameters are most commonly acknowledged and
applied.
However, the disadvantage of the latter is that it omits many environmental factors
responsible for the dynamics of observed changes. Up till now, one of a few available linear
multi-parameter models was the model of Reinchart and Mohasci-Farkas (Ko³o¿yn –
Krajewska 2003). The above-mentioned model took the influence of four environmental
factors on inactivation of pathogenic bacteria into consideration.
The presented evaluation of changes in quality of products packed with different
technologies proves that the element of reciprocal interactions among micro-organisms, often
omitted in predicting, can significantly influence the predicting quality.
It should be also taken into consideration that in literature there are no models available
connected with predicting the quality of tvarogs. Therefore, the presented program can
constitute complementation of prediction models connected with evaluation of survival rate
of micro-organisms in products of animal origin and can be useful in optimising the quality of
hermetically packed tvarogs.
204
Izabela Steinka
START
v=1
i=1
Read in data
Determine matrixes
Bi(t), Ci(t)
Determine matrix
Ai(t)
i=m?
NO
i=i+1
YES
v=w?
NO
v=v+1
YES
Print matrix elements
Ai(t), i = 1,…,m
i=1
Determine matrixes
E, Fik
Determine matrix
Dik
i=m?
NO
i=i+1
YES
Print matrix elements
Dik, i = 1,…,m
Is it end ?
NO
YES
STOP
Figure 14. Algorithm of determining parameters of mathematical model of dynamic interactions occurring
among microbiological parameters of tvarogs.
205
THE INFLUENCE OF INTERACTIONS AMONG MICRO-ORGANISMS ON
PHYSICO-CHEMICAL PROPERTIES OF LACTIC ACID CHEESE STORED
IN REFRIGERATING CONDITIONS
Multidirectional interactions cause that tvarogs packed with different systems (vacuum,
MAP, atmosphere) differ from each other in physico-chemical (water content) and chemical
(concentration of hydrogen ions) properties.
Regardless of the applied packing system and the packaging hermetic properties, the loss
in water content was observed in tvarogs relating to the packing system and product storage
time.
As soon as after two days of tvarog storage, the decrease in water content from 0.6 g up
to 0.8 g could be observed in products packed into cryovac, depending on the packaging
tightness (figures 15 and 16). In tvarogs hermetically packed with vacuum system, the drop in
water content was equal to 0.9 g. Tvarogs coming from depressurised packaging indicated 1.2
g less water in a product, in comparison with control sample. The significant loss in weight by
drying of surface of tvarog packed into Cryovac coming from both hermetic and non-tight
packaging was detected after 7 days of product storage. Between day 7 and day 14 of storing
the product packed into cryovac, the insignificant decrease in water content was observed in
non-tight packaging and the insignificant increase in hermetic packaging.
75
74,5
74
y= 0,1164x2 - 0,9956x+ 75,246
73,5
R2 = 0,9857
%
73
72,5
72
71,5
y= 72,78x-0,0075
R2 = 0,2858
71
70,5
70
0
2
4
7
14
Time (days)
Vacuum
Non-vacuum
polynom.
Figure 15. Changes in water content in tvarog packed hermetically with different system
power
206
Izabela Steinka
After 4 days, loss of water content in vacuum-packed products was equal to 1.3 g and
1.2g for tight and non-tight packaging respectively, in comparison with control samples.
In vacuum packaging, the increase of water content in product was observed after 7 days
of storage resulting probably from falling of water present on the internal packaging surface.
After 14 days, water loss equal to 1.1g was detected in tvarogs coming from Cryovac
laminate, and it was higher by 0.5 g than the change observed on day 2 of product storage.
Changes in water phase of a product after 14 days of storage were equal to 1.3g for
tvarogs packed into PA/PE laminates and 1.1g for tvarogs packed into Cryovac.
The dynamics of changes of water content during storage of tvarogs were different in
PA/PE and Cryovac packaging. However, in the final period of storage, the magnitude of
changes in water phase of products packed hermetically with both systems were comparable,
despite the fact that during initial period of storage the higher loss in water content was
observed in vacuum packed tvarogs.
Changes in water content during storage of tvarogs packed into Cryovac could be
2
described by the equation y = - ax + bx + c, whereas the tendency of changes in water phase
n
of tvarogs packed into hermetic PA/PE laminates was illustrated by a power function y=ax .
However, the above-mentioned equation described only 28.6% of water phase variability
in a function of time. Unfortunately, coefficients of determination of other functions showed
even lower values. This fact evidences the existence of complex packaging-product
interactions observed in this packing system of tvarogs.
75
74,5
74
73,5
y= 74,225x-0,0108
R2 = 0,9541
73
Log cfu/g
72,5
72
y= 0,2257x2 - 1,4023x+ 74,066
R2 = 0,7407
71,5
71
70,5
0
2
4
7
14
Time (days)
Vacuum
Non-vacuum
power
polynom.
Figure 16. Changes of water content in tvarogs packed with different systems coming from depressurised
packaging.
207
In this research, the average water content on the day of purchase of tvarogs packed into
Cryovac was equal to 74.3%. Water content in vacuum-packed tvarogs was at the level of
73.0% during that time, what is consistent with values contained within the Standard for this
type of cheese. However, as soon as after two days of storage, the differences connected with
packaging hermetic properties were observed.
Changes in water phase of tvarogs manufactured in experimental conditions presented by
other authors showed significant fluctuations during refrigerating storage (Œmietana et al.
1997). From tests performed on lactic acid cheese coming from trade and subjected to storage
(Steinka 2004), it resulted that after 7 and 14 days of storage, tvarogs in vacuum packaging
showed a similar tendency as the one quoted by Œmietana. Whereas the tendency of changes
in water content in tvarogs packed into Cryovac was different from the one presented by
Œmietana.
Conducted numerous research showed that at significant level of contamination of
tvarogs with micro-flora, the biological factors should be taken into account for mathematical
description of the water fluctuation process. Water fluctuation between product surface and
the packaging is determined not only by breathing of a product and its barrier properties, but
also by micro-organism metabolism (Steinka 2005b).
Equations of trend lines observed during changes in water content within time periods
Ä2, Ä4, Ä7, Ä14 during tvarog storage are presented below.
Water fluctuations were tested in vacuum-packed tvarogs containing level of micro-flora
taken into account while developing the computer program (Steinka 2003a).
The trend of changes was described by quadratic equation of the following form
Y = 3.6x2 + 8.9333x – 6.9 r2 0.999
(14)
The obtained results proved the existence of the average linear correlation between initial
water content in tvarogs and its level after 14 days, what is showed by the equation:
Y14 = 67.651 + 0.0707• x0 r 0.4320
where: y- water content
(15)
At significant contamination with micro-flora, during storage of tvarogs, the insignificant
influence of micro-organisms on fluctuation of water phase between packaging and product
surface was observed.
Table 17 below presents equations of linear correlation reflecting the influence of microorganism count on changes of water content during storage of tvarogs.
Table 17. The influence of water on populations occupying tvarog surface
Type of micro-organism
Equation
Enterococcus sp.
Yeast
Psychrotrophs
Y=11003E-148e3x
Y=8593E3-104e3x
Y=1157E4-150e3x
Steinka 2003a, x-water.
2
r
-0,268
-0,244
-0,185
208
Izabela Steinka
As a result of analysis of multifactor regression of data obtained during tests on tvarogs
showing a high level of contamination with micro-flora, it was observed that the growth of
chosen types of micro-flora could contribute to the water fluctuation. The analysis of
coefficient values of semi-partial and partial correlations showed that in vacuum-packed
tvarogs, the populations of enterococci, yeast and psychrotrophs inter-reacted with other
micro-organisms and influenced the water fluctuation in tvarogs in 12.9%, 9% and 4.6%
respectively (Steinka 2003a).
From data analysis, it resulted that water phase fluctuation in tvarogs after 14 days of
storage was mostly influenced by interactions of yeast and psychrotrophs with other groups of
micro-organisms.
SAFETY OF LACTIC ACID CHEESE
Many years of microbiological research on lactic acid cheese (Steinka 1998-2006)
showed the presence of coagulase-positive and coagulase-negative staphylococci both in
tvarogs packed in a traditional way (parchment paper) and into hermetic packaging.
From literature it results that the growth of staphylococci in food is determined by
numerous factors (Neumeyer et al. 1990, Taub et al. 2003, Castillo-Rodriquez et al. 2002,
Pereira et al. 1991, Feehery et al. 2004, Inhram et al. 2004, Schaffener et al. 2001, VernozyRozynand et al. 1998, Post et al. 1988, Zurea-Cosano et al. 2004, Lindquist et al. 2002,
Sameshima et al. 1998, McCann et al. 2003, Pepe et al. 2006, Schaffener et al. 2001).
Application of different types of additives in food should limit staphylococci growth in
products.
Among other, Zurera–Cosano et al. (2004) tested the combined influence of temperature
o
7-19 C, acidity equal to 4.5-8.5 pH, content of NaCl equal to 0-8% and 0-200 ppm of nitrates
on the growth and lag phase of staphylococci in aerobic and anaerobic conditions. Authors
estimated parameters, comparing suitability of a surface response model and Davey model.
Two kinetic parameters were evaluated, and it turned out that using surface response model
allowed achieving better prediction as regards the bacteria growth in comparison with the
second model. It was evidenced by values of bias and accuracy factors equal to bf1=1.06 and
bf2=1.31 and af1= 1.17 and af2=1.37 respectively for aerobic and anaerobic conditions. In lag
phase, Davey model indicated higher values of coefficients for these conditions.
Stewart et al. (2002) investigated the influence of humidity, pH 4.5-7.0 and sorbate
concentration on the growth of staphylococci. Tests results showed that saccharose and
fructose constituted factors inhibiting the growth of staphylococci populations at neutral pH
value. Sodium chloride turned out to be a significant inhibitor of bacteria only at lower pH
values. Authors also presented that the addition of potassium sorbate contributed to inhibition
of growth, especially when pH value was lower than 6.0.
209
Table 18. The influence of bacteria on the behaviour of facultative
anaerobic bacteria populations in tvarogs depending on gaseous conditions
Type of
micro-organism
Vacuum conditions
Variable atmosphere,
micro-aerophilic conditions
N=5.941+1.5789NL
N=22.202-3.269NL
r -0.8053
r 0.9045
Escherichia coli
Yeast
r 0.2026
N=-1.706 +0.6677NL
N=25.407-4.137NL
r -0.6378
N=7.6124-0.6321NL
N=-10.39 + 2.5435NL
r -0.3622
r 0.2382
Steinka et al. 2003b, N-population count, Nbfm – LAB count.
Tests conducted on tvarogs indicate the significant meaning of the environment on type
and intensity of interactions occurring among micro-organisms. Inside the tvarog packaging
and above the product surface, various conditions are formed depending on packing system.
These could be micro-aerophilic or aerobic conditions, or modified atmosphere (MAP). This
is important not only for technical micro-flora and micro-flora re-infecting tvarogs. Table 18
presents interactions occurring among micro-organisms present on the surface of lactic acid
cheese in environment of different proportions of oxygen and carbon dioxide.
From presented data it results that the growth of facultative anaerobic micro-organisms is
dependent on the level of lactic acid bacteria, however the type and magnitude of this
influence is dependent on environment wherein these interactions are observed (Steinka
2003a). In the case of staphylococci, values of linear correlation coefficients were equal to r
0.904 for vacuum-packed tvarogs and r -0.805 for tvarogs packed into parchment paper. An
important issue is different direction of changes of staphylococci population under the
influence of lactic acid bacteria in both types of packaging.
The size of staphylococci population was not large in tested products. It was at the level
of 2 log jtk/g. No statistically significant differences were observed between sizes of
staphylococci populations in vacuum-packed tvarogs (hermetically) and tvarogs packed in a
traditional way (non-hermetically).
In traditionally packed tvarogs, the growth of lactic acid bacteria populations was
corresponding to the decrease in number of staphylococci, whereas in vacuum-packed tvarogs
– the growth of streptococci population count was correlated with the growth of
staphylococci.
The obtained results indicate high importance of packaging hermetic properties in
determining the dynamics of changes of population re-infecting lactic acid cheese.
Due to their physiology, staphylococci constitute the greatest problem among facultative
anaerobic micro-flora. They have a strong ability to repair sub-lethal damages resulting from
the process of product manufacture, what can be confirmed by research of many authors
(Steinka 1999a, 2003a). Moreover, from conducted research it results that their cluster
distribution in products is also the reason for improper evaluation of food.
210
Izabela Steinka
Table 19. Presence of staphylococci in tvarog samples
and on the packaging during 7 days of storage
Tvarogs before storage
Tvarogs after 7 days of storage (40C)
Surface layer
of a product
Packaging
2
[cm ]
Surface layer of a
product
Packaging
2
[cm ]
Presence of staphylococcus
23.1%
30.1%
61.5%
61.5%
Absence of staphylococcus
66.9%
69.9%
38.5%
38.5%
Percentage
contribution
of
tvarogs with presence and
absence of staphylococcus
Steinka et al. 1999a.
From data presented by many authors (Castillo-Rodriqueza et al. 2002, Walls et al. 1996,
Schaffener et al. 2001), it results that staphylococci give rise to difficulties in predicting food
safety and the predictive microbiology is moderately useful for determining safety of
products, in which these bacteria can occur.
From conducted observations it results that products of metabolism of these bacteria can
appear not before refrigerating storage of the products. Staphylococci can appear in tvarogs
after 7 days or later, although during postproduction period their presence was not detectable
(table 19).
Nevertheless, tvarog composition can have the significant influence on the behaviour of
staphylococci populations. From conducted research it results that after dropping
3
2
staphylococci in amount of 1 cm on 1cm of tvarog surface, and then vacuum-packing of the
products into PA/PE packaging, the behaviour of these micro-organisms differed depending
on the fat content. Lactic acid cheese manufactured by the same producer and originating
from one lot contained 15 and 30% of fat. Products after addition of Staphylococcus aureus of
0
inoculum 3 log cfu/mL were stored after repacking at the temperature of 6±2 C for the period
of 14 days. Analyses were carried out after 2, 4, 7 and 14 days.
The tendency of changes of staphylococci population count in fat tvarogs could be
expressed with a quadratic equation. In low-fat tvarogs, the decrease in lactic acid bacteria
(LAB) count was accompanied by the growth of staphylococci population. Variability in
number of these micro-organisms could be also described with a quadratic equation (figure
16).
In the case of fat tvarogs, the growth of lactic acid bacteria was accompanied by the
decrease of staphylococci count. From research it resulted that variability of lactic bacteria
count in both types of tvarogs was not significantly dependant on storage time and
temperature in 18.7% and 40% respectively (table 20).
In tested fat tvarogs a weak linear correlation (r 0.235) between storage time and
staphylococci count was observed. This can evidence the influence of lactic acid bacteria,
other micro-flora not defined in this research and the fat content in products. Similar
relationships were observed in the case of low-fat tvarogs (r 0.283).
6
y = -0,1733x3 + 1,4386x2 - 3,2981x + 6,38
5
R2 = 0,8138
4
y = -0.2658x4 + 3.1433x3 - 12.834x2 + 20.957x - 7.7
R2 = 1
Log cfu/g 3
2
1
0
0
2
4
7
14
Tim e (days)
LAB
polynom.
polynom.
Figure 17. The behaviour of staphylococci and lactic acid bacteria in fat tvarogs.
6
y = -0,277x + 5,075
R2 = 0,8113
5
4
y = -0,255x4 + 3,0267x3 - 12,17x2 + 19,148x - 5,98
Log
3 cfu/g
R2 = 1
2
1
0
0
LAB
2
4
Tim e (days)
7
linear
Figure 18. The behaviour of staphylococci and lactic acid bacteria in low-fat tvarogs.
14
polynom.
211
212
Izabela Steinka
Table 20 below presents equations of linear correlation, as well as equations describing
the tendency of changes in both types of tvarogs.
Table 20. Trend equations of changes of LAB and
staphylococci in stored tvarog of different fat content
Type
tvarog
of
Type of micro-organisms
Fat
Low-fat
4
3
2
Y = -0.1808x + 2.2083x - 9.3492x + 15.772x –
5.15
2
r 0.999
Y = -0.098x + 3.586;
2
r 0.235
3
2
Y = 0.0383x - 0.385x + 1.0467x + 2.662
2
r 0.3416
Y = 3.5854e-0.0297x
2
r 0.2419
Y = 3.4786x-0.0614
2
r 0.1673
Y = -0.255x4 + 3.0267x3 - 12.17x2 + 19.148x 5.98;
2
r 1
Y = 0.195x + 3.281
2
r 0.2839
Y = 0.3612Ln(x) + 3.5201
2
r 0.1574
3
2
Y = -0.0333x + 0.4707x - 1.616x + 5.036
2
r 0.6005
Y = 3.3189e0.0477x
2
r 0.2307
Starter cultures (Lactococcus spp +
Leuconostoc lactis)
3
2
y = -0.1733x + 1.4386x - 3.2981x + 6.38
2
r 0.8138
y = 0.2092Ln(x) + 4.3097
2
r 0.0846
y = 4.3287e0.0124x
2
r 0.0414
y = 0.064x + 4.318
2
r 0.049
y = -0.277x + 5.075
2
r 0.8113
y = -0.7409Ln(x) + 4.9534
2
r 0.9376
y = 4.962x-0.1685
2
r 0.938
Own study.
Table 21. Size of Staphylococcus aureus population
simulated with Pathogen Modelling Program
Concentration of
lactic acid
0
0.3
0.5
0.7
0.8
1
Magnitude of reduction of Staphylococcus areus count Log10cfu
4
Reduction time (days)
92.87
61.65
52.21
48.17
47.78
50.12
Developed on the basis of PMP v 5.1.
5
6
116.09
77.06
65.26
60.21
59.72
62.65
139.3
92.47
78.31
72.25
71.67
75.18
213
Computer simulation developed with Pathogen Modelling Program shows that in
conditions corresponding to different magnitudes of changes connected with action of
alkalising micro-flora, the level of staphylococci is varied (table 21).
From data obtained by Pathogen Modelling Program, it results that time of reduction of
0
staphylococci count by 1 logarithmic cycle at temp. 4 C and pH 4.7 is equal to 11.3 days.
In tested tvarog, no reduction in count of these bacteria was observed after 14 days. In
low-fat tvarog the increase in bacteria number by 1 logarithmic cycle during that time was
detected.
It evidences that in case of infection of tvarogs, starter cultures present therein will not
inhibit the growth of staphylococci in products of low fat content.
From previous research it also results that reciprocal interaction between lactic acid
bacteria and staphylococci present at this level in fat tvarogs will be dependent on the stage of
hermetic properties and type of applied packaging (Steinka et al. 2003c).
In literature, there are a few predictive models available, which allow evaluation of the
growth of these bacteria in food (table 22).
Table 22. Predicting changes in staphylococci count in
model conditions and in food
Type of product
Model conditions
Bread
Sterile food
Model conditions
Model conditions
Tvarogs
Type of described changes
Davey and surface response model of the growth
at several environmental conditions
Kinetics of dying out, death in variable
environmental conditions, quasi-chemical model
was compared with Gompertz model, and
probabilistic model integrated with quasichemical was applied
Defined environmental conditions. Gompertz
model and comparison of obtained data with
PMP and FMM predictions
Environmental conditions. Gompertz model –
growth of staphylococci.
Kinetic models, environmental factor influence
on „growth/no growth”
Source
Zurera-Cosano 2004
Polynomial survival rate
Steinka 2003
Taub 2003
Walls 1996
McCann 2003
Stewart 2002
Own study.
An attempt of developing such a model was also made by Steinka (2003a), Steinka et al.
(2005a).
DEVELOPMENT OF THE PROGRAM FOR EVALUATION
OF STAPHYLOCOCCI GROWTH
The program was developed in Borland Delhi 2.0. language and serves for evaluation of
microbiological quality of lactic acid cheese vacuum-packed into PA/PE as well as shrinkwrapped with Cryovac packaging. Values of differences in predictions for tvarogs in both
types of packaging showed the higher dynamics of changes in bacteria count in tvarogs
214
Izabela Steinka
packed into Cryovac. It was observed that JMTPH computer program was useful for
predicting changes of staphylococci count in stored tvarogs. Type of packaging and the
packing system had the influence on evaluation of tvarog safety.
In the computer program used for predicting changes of these bacteria populations in
tvarogs packed into PA/PE laminates, 4 microbiological parameters were applied up to 7 days
of storage and 5 parameters during further storage period. In the case of prediction regarding
tvarogs packed into Cryovac, 6 microbiological parameters were applied. In conditions of
shrink-wrapping the product with Cryovac, no influence of yeast on the level of determined
staphylococci was observed in the second week of storage (table 23).
From predictions obtained for vacuum-packed tvarogs, it resulted that at maximum
product contamination equal to 3.32 log cfu/g, the level of staphylococci equal to 4 log10 cfu
in one gram of tvarogs remained between day 3 and day 21 of storage.
The prediction of change of coagulase-positive staphylococci population in tvarog during
storage is presented in table 23.
Table 23. Predictions of staphylococci growth in
tvarog depending on packing system
Day
of
storage
Parameters of mathematical model
Prediction
result
Log cfu/g
TVAROGS PACKED INTO PA/PE
3
Y=-3353.77+0.04 x1 +5.84 x2-0.11 x4+1.07 x5
4.11
7
Y=-1768.74+0.02x1+4.78x2-0.1x4+0.94x5
4.09
13
Y=608.79-0.01x1-3.17x2 +0.09x4+0.75x5+0.01x7
4.08
15
Y=1040.13-0.02x1+2.64x2-0.09x4+0.62x5+0.01x7
4.31
21
Y=3778.84-0.04 x1+1.04x2-0.08x4+0.49x5+0.02x7
4.06
TVAROGS PACKED INTO CRYOVAC
3
Y= 257.67 +0.01x1-+93.60x2-0.73x4-1.33x5+0.03x6-0.13x7
3.91
7
Y= 70.78-0.05x1+746.33x2-0.99x4-2.27x5+0.03x6+0.09x7
5.03
9
Y=-22.66+0.08x1+1072x2-0.06x4-2.271 213x5+0.01x6+0.76x7
5.14
15
Y=-303-0.16x1-2051.8x2-0.85x4+22.92x5-1.45x7
5.31
21
Y=-583.33-0.24x1+3030.90x2+1.64x4+33.72x5-0.01x6-2.11x7
5.48
From presented data the significant differences resulted in count of staphylococci
population in tvarogs, depending on packing way and type of applied packaging. Differences
between sizes of staphylococci populations determined in tvarogs packed into both types of
packaging could be observed as soon as from the day 3 of product storage. Difference values
in predictions obtained with the help of JMTPH computer program indicated the higher
dynamics of changes in tvarogs packed into Cryovac.
215
In optimum model conditions and at temperature of 220C, the growth of staphylococci
population shows significant dynamics. The increase in count of these bacteria by 3
logarithmic cycles can occur during 72 minutes. Simulation carried out with the Pathogen
Modelling Program for the temperature 40C and pH 4.7 showed that staphylococci reduction
time by 1 logarithmic cycle was equal to 11.3 days (6). This evidences the significant
resistance of these bacteria to the influence of low temperature and acid in the environment.
Computer simulations conducted with Pathogen Modelling Program showed that other microorganisms e.g. Salmonella spp., were characterised by different dying-out dynamics in
comparison with staphylococci population at the temperature of 60C and pH 4.7. Reduction in
number of rods by 1 and 2 logarithmic cycles occurred from 7 up to 14 hours respectively.
It also should be noticed that presented predictions developed using Pathogen Modelling
Program concerned the individual growth of micro-organisms without taking the presence of
other micro-organisms into account. Predicting the bacteria growth in model conditions in
many cases assumes the existence of microbiological rules obligatory for monocultures. From
our previous research it results that the behaviour of both staphylococci and Listeria spp. rods
in hermetically packed tvarogs was different than expected (Steinka et al. 1999b). Also the
growth of staphylococci in conditions occurring in food can proceed with different dynamics
than the one observed in model conditions, what was proved by research of Wallas et al.
(1997) and Smittle et al. (1994). From data obtained by other researchers it resulted that
temperature also did not constitute the factor that limited absolutely the growth of
staphylococci. The slow increase in staphylococci count below temperature of 10oC was
observed in different types of food by Lee Wong et al. (2002). The number of staphylococci
cells determined in tvarogs with JMTPH computer program presented in this paper was
similar to sizes of populations obtained by e.g. Belickov et al. (2001). The mentioned-above
1
4
authors isolated staphylococci from tvarogs at the level from 9x10 cfu/g up to 1.07x10 cfu/g.
Research conducted by those authors proved the presence of staphylococci in other fermented
dairy products such as sheep cheese, buttermilk and yoghurt, what can evidence the resistance
of staphylococci to antagonistic influence of lactic acid bacteria.
The above-menioned factors show that presented prediction of staphylococci changes
obtained with the help of JMTPH computer program can be actual and can reflect the
behaviour of population in conditions of hermetically packed tvarogs.
SURVIVAL RATE OF STAPHYLOCOCCI ON THE SURFACE OF TVAROGS
AND THE SYNTHESIS OF ENTEROTOXIN DURING STORAGE
One of the determinants of food safety, apart from the absence of vegetative forms of
pathogenic bacteria, is the absence of toxins released into food. The hazard of uncontrolled
synthesis is created by mostly such bacteria as Staphylococcus aureus. The intensity of
enterotoxin production by Staphylococcus aureus strains is dependent on environmental
conditions, among which the most significant are: temperature, environment pH value, redox
potential and gaseous atmosphere (Adams 1995). The synthesis of staphylococcal enterotoxin
is dependant on many factors such as: environment in which staphylococci population occurs,
compositions of a medium, micro-organism count and the presence of inhibiting substance.
216
Izabela Steinka
As it results from the literature, despite the antagonistic influence of other micro-flora
present in the environment (even lactic acid bacteria), in certain conditions the toxicogenesis
can occur.
In order to evaluate food safety, it is possible to apply microbiological predicting that
enables approximate assessment of population growth. The existing computer programs help
to determine lag phase, magnitude of population count reduction or the rate of its growth,
however they not always take all environmental conditions into account.
Therefore, it seems to be important to compare the growth and survival rate of
populations in model conditions and in monoculture with data obtained in food.
From research of Neumayer et al. (1990), it results that in a medium enriched with
ingredients occurring in such vegetables as pea or bean, the bacteria growth occurs with
significant dynamics in model conditions, however the concentration of produced enterotoxin
is highest in a medium where pea is present. Enterotoxin accumulated therein in amount of
14-15 ng per mL of a medium.
The presence of high concentrations of valine, cistine and arginine contributes to the
synthesis of SEA by staphylococcus aureus in amount smaller than SEB, SEC (Bergdol et al.
1989). Moreover, the same research also showed that glucose had inhibiting influence on the
production of SEB and SEC.
Opinions as regards number of staphylococci necessary for enterotoxin production are
varied. Halin–Dohnalek et al. (1989) indicated the level of 106 cfu/g in food environment of
high fat content. In sterile milk, this number is equal to 10 6,5 cfu/mL (Fukijawa et al. 2006).
Detectability of enterotoxin is not only dependant on the level of cells. Otero (1988) did
not detect the presence of enterotoxin in cheese even at the level of 108 cfu. Whereas Delbar
et al. (2006) detected enterotoxin after 24 hours in cheese, where number of staphylococci
was equal to 5.55-5.6 log10cfu/g. This confirms our observations (Steinka 2004).
While testing ready-to-serve food, Bahk et al. (2006) observed that as much as 29.73% of
samples showed the presence of staphylococci at the level > 105 cfu/g, what could favour
enterotoxin synthesis.
From tests conducted on hermetically packed tvarogs and tvarog coming from unsealed
packaging, it resulted that enterotoxin was formed more often in the latter. Research showed
that a small supply of oxygen to the product favoured the enterotoxin synthesis (Steinka
2004).
The presence of enterotoxic strains in food is observed in many different food products
(table 24).
Table 24. Contribution of toxicogenic strains among
staphylococci present in dairy products
Type of food
Milk, cheese
Milk from cows with mastitis
Data on the basis of Loir et al. 2003.
Contribution of toxicogenic strains
15.9 %
43%
72.8%
Source
Rosec 1997
Cordobo 1999
Akineden 2001
217
From research of Otero et al. it results that aerobic conditions cause the increase of
kinetics of staphylococci population growth, however they are not the reason for occurrence
of enterotoxin in tested cheese.
The significant factor influencing the production of enterotoxin is temperature. Literature
data evidence that the lowest temperature in which enterotoxin synthesis is observed is equal
to 70C (Adams et al. 1995).
According to Halin-Dohnalek et al. (1989), most of staphylococci strains present in sour
cream at the temperature of 370C synthesised enterotoxin as soon as after 18 hours. At 220C
this time was prolonged up to 52 hours. From research of these authors, it resulted that no
staphylococcus strain produced enterotoxin at 40C during 14 days. According to some
authors, heating chicken products and then storing them at the temperature of 40C guaranteed
elimination of enterotoxin (Pepe et al. 2006).
In lactic acid cheese tested by Steinka et al. (2001c, 2004), enterotoxin should not occur
due to the presence of lactic acid bacteria. From data obtained by Loir et al., it results that in
laboratory conditions – the acetic acid added to the medium has the greater inhibiting
influence on enterotoxin production than e.g. lactic acid. Whereas, basic pH constitutes a very
significant factor determining the production of toxins SEB, SEC and SED (Loir 2003). This
can be confirmed by research of Delbar et al. (2006), who observed the release of enterotoxin
by bacteria present in cheese at the increase of pH values.
The enterotoxin synthesis by Staphylococcus aureus is dependant on the presence of
accompanying micro-flora in the environment (Oter et al. 1988, Noleto et al. 1987,
Sameshima et al. 1998, Steinka 2004).
Sameshima (1998) tested the influence of Lactobacillus cultures on staphylococci in
fermented sausages. Inoculum was equal to 104 cfu for staphylococci and 107 cfu for
Lactobacillus. Enterotoxin was detected during fermentation at each temperature, if the
certain strain of lactic acid bacteria e.g. Lactobacillus acidophilus FERM P-15119 occurred in
the presence of staphylococci.
In the presence of L. rhamnosus and L. paracasei strains, the inhibition of toxin release
was also satisfactory. Lactic acid bacteria belonging to starter cultures do not always show the
identical ability to inhibit enterotoxin synthesis. It depends both on type of enterotoxin and
the inhibiting strain.
The influence of commercial starters on the growth of Staphylococcus aureus and the
production of C1 and C2 enterotoxins in model conditions was investigated by Otero et al.
1988.
Staphylococcus aureus FRI 137 strain producing enterotoxin C1 as well as FRI 361 and
L2 strains producing enterotoxin C2 grew well both individually and in the presence of
starters. This starter contained standard Lactococcus lactics spp. strains. Commercial starters
showed a weak inhibiting influence on S. aureus only in late phases of growth of these
bacteria.
In contrast, the enterotoxin synthesis was strongly inhibited after 18 hours in as much as
89% for Staphylococcus aureus FRI 137. Presence of the starter inhibited release of toxin in
80% by Staphylococcus aureus FRI 3 and in 69% by staphylococci L2 strain.
Enterotoxin C1 was both synthesised and accumulated during all phases of growth both
in monoculture and in mixed population. Unfortunately, the growth of other strains caused
reduction of its concentration after 24-36 hours (Otero et al. 1988).
218
Izabela Steinka
Extremely important research for understanding the character of staphylococci
toxicogenesis was conducted by Noleto et al. 1987, who evaluated production of
staphylococcal enterotoxin by Staphylococcus aureus in the presence of other pathogenic
bacteria such as: Bacillus cereus and Escherichia coli, Streptococcus faecalis, Pseudomonas
aeruginosa.
All staphylococci strains showed the growth and production of enterotoxin in the
presence of enterococci.
In tvarogs tested by Steinka (2004), count of enterococci was significant, what could be
the reason for stimulation of staphylococci to synthesise toxin.
From research it resulted that in model conditions, the metabolism ability of
staphylococci was also determined by the type of medium. Application of different medium
types allowed observing that this phenomenon occurred only when preponderance of
staphylococci over enterococci count was detected in the environment. Other behaviour of
staphylococci was observed in the presence of Bacillus sp. Staphylococci showed growth in
the presence of rods in both types of medium, however enterotoxin was produced only when
their inoculum was 10 versus 104 in relation to Bacillus sp.
Quantitive ratio of both populations necessary for enterotoxin production was dependent
on type of staphylococci strain used for medium inoculation. And so, e.g. FRI 196E strain
produced toxin in both types of applied medium even when inoculums of both bacteria were
equal.
Staphylococci did not produce enterotoxin only when Escherichia coli remained
preponderant in number in both medium types. In order to observe enterotoxin synthesis, the
count of staphylococci had to be significantly higher than number of rods (10 versus 104).
Other types of relationships were observed in the presence of Pseudomonas aeruginos.
Staphylococci did not produce enterotoxin when staphylococci inoculum exceeded 10 versus
3
4
10 or 10 .
From the research of Noleto, it resulted that enterotoxin was produced only when
staphylococci number was equal to or greater than number of accompanying species (Noleto
1987).
A very important condition favouring enterotoxin synthesis is also the presence of
inhibiting substances in the environment (Gonzales –Fandos et al. 1994).
Epidemiologic data suggest that the enterotoxin B (SEB) is seldom observed in food,
whereas enterotoxin of type A (SEA) and C (SEC) are predominant, and they are responsible
for more than 70% of contamination of food samples. Staphylococcal enterotoxins SEA and
SED are more often produced in food of basic pH, even at low number of cells. However,
even among staphylococci isolated from fermented milk, the significant amount belongs to
toxicogenic strains.
From research of Steinka (2004), it results that concentration of determined enterotoxin
was varied, and was higher in tvarogs packed with vacuum system then in tvarogs packed into
Cryovac films. Lack of packaging hermetic properties favoured the enterotoxin synthesis.
In samples of vacuum-packed tvarog coming from depressurised packaging, the 2-3-fold
higher enterotoxin concentration was observed in comparison with hermetic packaging.
0
0
Enterotoxin was detected in tvarogs stored in the temperature from 6 to 8 C for the
period of 7 and 14 days. Enterotoxin presence was not observed in samples taken for tests on
the day of introducing a product into the market.
219
However, the observed case of the increase in enterotoxin concentration in samples
coming from the same lot between day 7 and day 14 of product storage can suggest the
probable existence of this toxin synthesis.
The possibility of growth of Staphylococcus aureus strains producing enterotoxin in
fermented dairy products arouses controversy. As it results from the literature, despite the
antagonistic influence of other micro-flora present in the environment (even lactic acid
bacteria), in certain conditions the toxicogenesis can occur.
The necessity to evaluate the probability of staphylococci survival and the staphylococcal
enterotoxin synthesis in hermetically-packed products during storage at low temperature is
the reason for developing models determining the risk. For instance, the growth of
staphylococci after 14 days in tvarogs stored in hermetic packaging could not be described
with linear models, because they showed a low degree of equation matching.
NPA/PE = 214.86 + 1.3269•N7 r2
0.057
(16)
NCryovac = 236.63 – 0.0068•N7 r2
0.131
(17)
where
NPA/PE14 – staphylococci count in tvarogs packed into PA/PE laminated after 14 days
NCryovac 14 – staphylococci count in tvarogs packed into Cryovac laminated after 14
days
N7 – staphylococci count in tvarogs after 7 days of storage
Staphylococcal enterotoxin synthesis depending on storage time, hermetic properties and
packaging type as well as the ability of coagulase synthesis is presented in table 25.
Table 25. Models of staphylococcal enterotoxin synthesis in
dependence on the ability of coagulase synthesis and
number of staphylococci in tvarogs
Equation form
Ep7=-84.7853+0.425N0
r2
0.865
Ep7=79.4059+0.3342N0+56.6643K7
Erp7=211.122-0.134925N0
0.867
2
Erp14=300.907-230.4(K14)
Eb14=38.7367+74.0549K0-250.317K14+257.751K7-0.3713N14-0.0165N7
0.460
0.920
Erb14=-21.2696+3.21196N14 +1.74943N7 – 17002.1K14
0.856
0.176
Steinka 2004,
N- staphylococci count; 0,7,14 tvarog storage time
E- staphylococcal enterotoxin; K- coagulase;
Indexes: p - vacuum, b – non-vacuum, r – depressurised.
As a result of conducted research, staphylococcal enterotoxin was observed in the
insignificant percentage (4.5%) of tested samples coming both from tvarogs packed with
220
Izabela Steinka
vacuum system and those packed into Cryovac. Application of multifactor regression analysis
as well as data transformation allowed expressing the probability of occurrence of enterotoxin
in hermetically packed tvarogs with the help of linear and polynomial equations. When
enterotoxin was present in tvarogs packed into Cryovac, the statistically significant
relationships was also observed between the probability of enterotoxin occurrence and the
staphylococci population count during storage, as well as synthesis of coagulase by these
bacteria (table 25). Equation describing occurrence of enterotoxin after unsealing the nonvacuum packaging had quadratic form, what significantly evidences the influence of
environment on enterotoxin synthesis. Equation describing this relationship showed the
existence of weak connection between synthesis of enterotoxin and coagulase by
Staphylococcus aureus in these conditions. This can indicate the crucial importance in
evaluation of risk. In optimum model conditions, the growth of staphylococci count and the
production of enterotoxin show significant dynamics. At temperature of 220C, the growth of
staphylococci by 3 logarithmic cycles should occur after 72 minutes. According to Pathogen
Modelling Program, in aerobic conditions, at pH change and temperature drop to 10-120 C,
changes in staphylococci population count by 1 logarithmic cycle were not observed before
10-21 days.
Shorter time (by 11 days) of staphylococci breeding predicted with this program for
anaerobic conditions of growth show a significant meaning of redox potential for the growth
of these bacteria. Vernozy-Rozynand et al. (1998) suggest that enterotoxin production is a
slow process. In ripening cheese, the presence of enterotoxin was not observed in fresh curd,
but only after 21 days of ripening. The ability of staphylococcal enterotoxin synthesis does
not have to be connected with synthesis of coagulase, because there exist enterotoxic
coagulase-negative Staphylococcus aureus strains that produce enterotoxin, as well as other
species of enterotoxic staphylococci such as: Staphylococcus haemolyticus, Staphylococcus
warneri, Staphylococcus saprophyticus or Staphylococcus epidermidis.
METHODS OF OPTIMISING QUALITY OF TVAROGS
Before implementation of HACCP system into food production, tvarogs were
characterised by low microbiological quality before storage. The traditional packing system
connected with non-automated technological line can still arouse quality problems. The
conducted numerous attempts to optimise the quality of cottage cheese and tvarogs (Kornacki
et al. 1999, Kornacki et al. 2002 Molska 1992, Rosenthal et al. 1996 Herve et al. 1998,
Stanton et al. 1998, Neugebauer et al. 2005) indicated not only the problem of obtaining lactic
acid cheese of high stability level, but they also emphasised the significant influence of
micro-flora on achieving desired sensory features of these products. Microwaves and ionising
radiation are the directions of optimising microbiological quality of cottage cheese proposed
by Hevre et al. 1998 and Rosenthal et al. 1995. Kornacki et al. 1999 suggested enriching
starters used for tvarog production with addition of such bacteria as: Streptococcus salivarius
spp. termophilus, Lactobacillus delbrueckii bulgaricus, Bifidobacterium bifidum,
Lactobacillus acidophilus. Similar suggestions were made by Neugebauer et al. in relation to
cottage cheese (Neugebauer et al. 2005).
221
Kornacki et al. (2002) showed that application of traditional butter starters used for
production of tvarog made of raw material of low microbiological quality did not result in
reduction in number of coliforms and psychrotrophs, and even the growth of proteolytic
micro-organisms count in ready product was observed.
Therefore, it is necessary to find a method for optimising the quality of these products.
Optimisation of tvarog quality can be carried out with several methods:
•
•
•
Application of additives of biocide character
Modification of packing system
Application of safety predictions for instance with the help of a computer program
Optimisation with Biocides
Plant additives are often added to dairy products such as yoghurts, cottage cheese or
ripening cheese (Ahmed et al. 2002, Beckmang et al. 1996, Grega et al. 1999, 2001). They
include pieces of fruit, chives, onion, garlic, paprika, tomatoes, cucumbers, horseradish and
herbs. However, the data prove that some of the spices and herbs modify the metabolism of
starter cultures. This is the reason for changes in organoleptic properties of products
manufactured using those starters (Arora et al. 1999).
Various research concerning the behaviour of staphylococci in the presence of different
substances of plant origin has been conducted until now. For instance, some authors evaluated
the possibility of enterotoxin synthesis at variable concentration of garlic in the environment
(Gonzales-Fandos et al. 1994). Enterotoxins SEA and SEB were detectable at garlic
concentration not exceeding 1%, whereas SED was produced by staphylococci even at the
level of 2%. Generally, no additives are applied in tvarogs. Some additives of flavour
character are used as a supplement in cottage cheese. Some of them have also biostatic
properties. This concerns for example garlic, onion and herbs. However, from our research
(Steinka 2006a) it results that the presence of garlic in these products gives them a specific
bitter taste.
Searching for other plant additives e.g. mixture of rowan and aloe in model testing
performed on semi-products (lactic acid curds) showed varied influence on the facultative
anaerobic bacteria and fungi, which can be present in tvarogs (Steinka 2005c).
Table 26 presents changes in count of staphylococci, enterococci and yeast, depending on
plant additive.
Table 26. The influence of plant additives on facultative anaerobic micro-flora
Micro-organisms
Tvarog curd
Aloe arborescens
Y=0.13x+4.3
Sorbus aucuparia
Y=-0.2x+4.63
Enterococcus faecalis
Candida sp.
Y=3.11x-0.34
Y=0.94x+5.29
Y=-0.3x+3.07
Y=-0.76x+6.99
Steinka 2005d, x-value of control sample.
222
Izabela Steinka
The effort to find the appropriate conditions of adding aloe during production of lactic
acid curds encountered significant difficulties (Steinka 20002b, 2003b, 2003d). The attempts
to optimise the quality of ready lactic acid cheese with aloe aerosol were also made (Steinka
2003c).
In tvarog samples taken for tests during refrigerating storage, the differences were
noticed between sizes of micro-organism populations in products with aloe extract additive
and those where aloe aerosol was not added. The average values of population counts
indicated the stimulating action of aloe aerosol in relation to enterococci and yeast. From the
fourth day of storage of tvarogs with aloe additive, the increase in staphylococci count was
observed. The growth of yeast in tvarogs treated with aloe aerosol was observed during the
entire period of lactic acid cheese storage. Whereas, the effectiveness of aerosol action was
observed in relation to mould and staphylococci.
During storage of tested products, the inhibition of mould and staphylococci counts were
detected in samples with aloe extract additive. It was also observed that the presence of aloe
resulted in the inhibition of growth of Lactococcus sp. population during the first days of
product storage. From day 4 until day 7 of product storage, the growth of lactic acid bacteria
in tvarogs with additive was observed, and then the reduction in number of these bacteria was
noticed between day 7 and day 14 of tvarog storage.
The results of statistical analysis showed a high correlation (r 0.9697) between the
enterococci contamination level present in tvarogs not subjected to action of aerosol and
stored in packaging and the addition of aloe extract (table 27).
Table 27. Linear correlation between micro-organism populations
present in control tvarogs and in tvarogs with aloe aerosol additive
Type of
micro-organisms
Enterococcus sp.
Equation
of linear correlation
Ea= 13811+1.0894E
r
2
r
0.969
0.940
Sa=13.199+0.79701S
0.792
0.627
Yeast
Da=154600+0.71205D
0.708
0.500
Mould
GSa=191500+0164523GS
0.385
0.148
Lactococcus sp.
La =2971000+0.03452L
0.114
0.012
Steinka 2003b,
Ea - Enterococcus sp. in tvarogs with aloe additive; Sa- Staphylococcus aureus in tvarogs with aloe
additive; Da- yeast in tvarogs with aloe additive; GSa – staphylococci in tvarogs with aloe additive;
La - Lactococcus sp. in tvarogs with aloe additive; E- Enterococcus sp; S- Staphylococcus aureus;
D- yeast; L- Lactococcus sp.
High coefficient of determination r2 0.9403 showed that enterococci count in tvarogs
without additive was similar to number observed in tvarogs with aerosol additive. From
statistic analysis it resulted that the variance of enterococci count only in 6% could be
determined by the presence of aloe. Whereas, 37% of variance of staphylococci count in
tvarogs with aloe additive could result from the influence of aloe.
223
Basing on coefficient of determination, it was also proved that mould and yeast showed
varied susceptibility to aloe influence. In the case of yeast, more than 50% of variance of
these fungi count resulted from the action of aloe aerosol, whereas 85% of variance of mould
could result from the presence of aloe aerosol and the influence of this additive on fungi
populations.
Changes in number of bacteria and fungi in tvarogs stored with aloe additive, depending
on storage time and the behaviour of other micro-organism populations present in tvarogs
could be expressed with polynomial equations of the following form:
Y = a1x1 + a2x2 + a3x3 + a4x4 …
(18)
which are presented in table 28.
Table 28. The influence of storage time and the interactions among micro-organisms on
the population of micro-organisms in tvarogs with aloe aerosol additive
Equation of linear correlation
r
R2
Enterococcus sp.
Ea=
29479.82-2466.85t+1.1E-9.05S0.09D+0.16GS-0.01L
0.983
0.962
Staphylococcus
aureus
Sa=164.8455-14.2526t+0.0019E +0.7548S0.0002D-0.0001GS
0.802
0.593
Yeast
Da=134169.7-3827.7t-0.3E+3.3S+D-0.1GS
0.735
0.476
Mould
GSa=64808.98-1018.67t1.55E+36.38S+0.09D
+0.88 GS-0.02L
0.807
0.603
Steinka et al. 2003b.
The presented coefficients of determination of equations describing changes of
enterococci, staphylococci and yeast populations, taking interactions among micro-organisms
and action of aloe into account, were similar in both types of tested tvarogs (tables 27 and
28).
Coefficients of determination defined for those equations differed from each other by
2.18%, 3.41% and 2.55% respectively, indicating the insignificant influence of factors other
than aloe on changes of these micro-organisms populations (tables 27 and 28). In the case of
mould, differences in coefficients of determination of derived equations showed a great
influence of interactions occurring among micro-organisms present in products and the time
of tvarog storage on the level of fungi in tvarogs treated with aloe.
224
Izabela Steinka
In the case of mould population in tvarogs with aloe additive, the inhibition of its growth
was the combined effect of application of aloe, hermetic packaging, low temperature as well
as interactions occurring among the micro-organisms present in the product.
Table 29 presents the influence of lactic acid bacteria on the growth of individual groups
of micro-organisms in stored tvarogs as well as the influence of interactions among the microorganisms and the aloe aerosol on growth of these populations.
These relationships were expressed with quadratic equations (Second Order Polynomial).
Table 29. The influence of storage time, additive of aloe and lactic acid bacteria on
changes of secondary micro-flora population in stored tvarogs
Enterococcus sp
Equation form
Tvarogs stored without aloe
aerosol additive
E=29195+4361,14t-0,002L180,297 t2+3,203e-4tL+1,037e10L2
Staphylococcus
aureus
S=
1377,034-248,149t-8,123e5L+11,44t2+1,755e-5tL-1,059e12L2
Yeast
D=-35801,83+1,001e5t
+0,005L-5082,894t2+0,008tL6,035e-10L2
Mould
GS=22261,7+71775,96t-0,006L1966,29t2+0,002tL+2,338e-10L2
Tvarogs stored with aloe aerosol
additive
Ea= 24412,87-36566,1t
+0,03La+2653,61t2+0,017tLa
-3,923e-9La2
Sa= 1202,67-232,937t-5,122e-5La
+11,263t2 +1,223e-5tLa-1,014e12L 2
a
Da=72940,75+1,006e5t+0,085La
-6253,274t2+0,025tLa-7,192e-9
La2
GSa=-7391,507+35196,96t
+0,037La-702,675t2+0,011t La
-3,179e-9 La2
Steinka 2003b
Ea - Enterococcus sp. in tvarogs with sloe additive; Sa- Staphylococcus aureus in tvarogs with sloe
additive; Da- yeast in tvarogs with sloe additive; GSa – staphylococci in tvarogs with sloe additive;
La - Lactococcus sp. in tvarogs with sloe additive; E- Enterococcus sp; S- Staphylococcus aureus;
D- yeast; L- Lactococcus sp.; t- storage time.
From obtained data, it also results that the influence of lactic acid bacteria on the growth
of secondary micro-flora was influenced by aloe additive (table 29).
225
Second order polynomial equations describing the growth of staphylococci, enterococci
and mould in stored tvarogs differed among each other, if tvarogs were sprayed with aloe
aerosol. Only surface response models determining the influence of lactic acid bacteria on
yeast showed a very similar shape and direction of action in the case of tvarogs both without
and with aloe aerosol additive.
Changes of Lactococcus sp. populations under the influence of aloe could be expressed
by the equation of the following form:
La= -1.248e6 + 1.008e6t + 1.194L – 64381.85t2 – 0.043tL – 3.768e-9L2
(19)
where:
La – number of Lactococcus sp. in tvarogs with aloe additive
L – number of Lactococcus sp. in control tvarogs
t - storage time of tvarogs
Negative value of coefficient a in the equation indicated the direction of changes of
Lactococcus sp. population count under the influence of aloe, suggesting inhibition of growth
of lactic acid bacteria populations in tvarogs.
The bactericidal properties of aloe in relation to many bacteria are commonly known. In
food products its application is limited due to the presence of significant amount of aloin,
which excessive amount creates the hazard of excretory system hyperaemia and
nephropathogenesis. While aloin level in food products is not advantageous (special
regulations control the level), the small amount of aloe additive to food influences favourably
the intestine peristaltic motion as well as functioning of immunological system. There exist
data indicating the possibility to lower the adverse effect of aloin in the presence of lactic acid
bacteria (Steinka 2002b). Addition of small aloe amount can be applied in fermented food
with the help of lactic acid cultures.
From previously conducted research (Steinka 2001d,e 2002b), it resulted that the
presence of aloe in the form of a pulp influenced significantly the growth of certain types of
bacteria and fungi in lactic acid curd, as well as it affected animal organisms. The influence
on micro-organisms was varied, depending on type of micro-organisms, bacteria species,
presence of other micro-organisms and their count in tested environment (Steinka 2001d,f).
It was showed that the additive of aloe in the form of aerosol into tvarogs of low
microbiological quality lowered the staphylococci count during 14 days of product storage in
hermetic packaging. Moreover, the aerosol stabilises the level of mould in these products.
However, this method of aloe application shows stimulation influence on the growth of
enterococci and yeast population in stored tvarogs.
226
Izabela Steinka
Aloe aerosol also cannot be applied for optimising the quality of tvarogs of high
contamination level with enterococci and yeast.
To sum up, optimising the quality of tvarogs of a signification level of contamination
with facultative anaerobic bacteria, using aloe aerosol and vacuum re-packing is possible, but
it requires more research to be conducted.
Optimising the Quality through Modification of the Packing System
This type of optimisation involves packing in clean air atmosphere.
From various research, it results that air in dairy plant can be the reason for
contamination of ready products.
The literature data report that department of fermented drink and cheese production can
show a higher level of contamination with micro-organisms in comparison with other
departments (Ren et al. 1992, Salustiano et al. 2003). Salustiano et al. detected the presence of
staphylococci in dairy plants (table 30).
Table 30. Contamination of air in different departments of dairy plant
Processing area
Mesophilic
Bacteria
CFU/m3
110-600
Aerobic
Yeast and moulds
Total coliform
CFU/m3
70-160
0.00-0.66
Milk acceptance
section
Cheese
100-920
90-610
0.33-1.66
Yoghurts
100-320
100-940
0.00-0.66
Own study on the basis of Salustiano et al. 2003.
The reasons for product contamination can be both traditional production technology, in
which pressing and draining can constitute the critical control points. In automated production
technologies, these stages do not create any hazard.
According to FIL IDF, the air quality of the highest purity class should be characterised
by OLD value not greater than 10 cfu/m3 while both fungi and yeast as well as pathogenic
bacteria should not be present at all. The lowest air class (i.e. D) allows the presence of ca.
10000 aerobic mesophilic bacteria and more than 100 fungi and 10 pathogenic bacteria.
Research conducted by Olbromska et al. 2005 showed that contact with personnel,
machines, air and most of all with packaging is often the reason for secondary contamination
determining the safety of dairy products.
However, research of Steinka et al. 1998 did not show the high contamination level of
packaging materials applied for packing lactic acid cheese and cottage cheese (table 31).
227
Table 31. Microbiological quality of materials for packing tvarogs
Packaging type
Mould
Yeast
cfu/25cm2
Parchment paper
11
0
PA/PE laminate
30
0
Frischaltenfoliae PE
44
22
Aluminium foil
33
0
Styrofoam tray
70
0
Steinka et al. 1998.
In the case of tvarogs, modification of the packing system is hard due to the consistency
and delicate structure of these products. Applying modification of traditional packing system
and substituting it with Styrofoam trays does not guarantee high quality of tvarogs as well.
Products packed in this way and wrapped with thin frischaltenfolie showed high count of
6
5
fungi. After storage, the level of yeast reached 1.1•10 cfu/g, while mould 4.3•10 cfu/g and
these counts were higher than in the case of tvarogs packed into other types of packaging.
Photo 1. Tvarogs packed onto Styrofoam trays wrapped with thin PA/PE foil.
It is possible to protect the product against changes of sensory properties resulting from
significant fungi count by avoiding the non-hermetic packaging, or storing the product for a
short period of time - not longer than 4 days.
There also exists the possibility to modify packaging materials. At the present, the project
of creating laminate of modified composition is at development stage. Among modifying
elements the followings are proposed: starch and two biocides.
228
Izabela Steinka
Optimisation with the Help of Prediction Models
Among the possibilities of optimising the quality and safety of tvarogs, there is also
microbiological predicting. The behaviour of multi-species populations in stored tvarogs as
well as change of basic packaging properties can be evaluated with Twarogi JMTPH
computer program (Steinka 2003a).
For evaluation of staphylococcal enterotoxin synthesis, the probabilistic model was
developed taking storage time, staphylococci and yeast populations counts in tvarogs into
account. Development of computer program called TEG required application of Boolean
expression, which helped to precise the series of conditions that have to be fulfilled in tvarogs
for the occurrence of enterotoxin synthesis.
E = [(GN = 0) ∧ (GP ≥ 4)] ∨ {((GN + GP ) ≥ 5) ∧ [(GP > 3.5) ∨ (GN > 3.4 + 0.1t )
∨ (GP / D > 0.6) ∨ (GN / D > 0.7) ∨ ( GP − GN /(GP + GN ) ≤ 0.2)]}
(20)
where:
GN - coagulase negative Staphylococcus aureus count, GP - coagulase positive
Staphylococcus aureus count, D - yeast count, t - time
In a computer program developed in Delhi 7.1, the staphylococci count, storage time and
size of predominant population in tvarogs were also taken into account. The result of program
operation is obtaining the answer that negates or confirms the presence of staphylococcal
enterotoxin in a products (present-absent).
The example of computer simulation is presented in table 32 below.
Table 32. Predicting the presence of staphylococcal enterotoxin
with TEG computer program
Staphylococcus
aureus
CP
count
2.78
Staphylococcus
aureus CN count
Yeast
count
Storage time
of tvarogs
3.44
5.58
14
Result of simulation
of enterotoxin
presence
Present
2.32
2.11
3.89
7
Absent
Steinka et al. 2007.
229
CONCLUSION
Tvarogs constitute the important of many nutrients. Their nutritious and taste values
evidence that they are significant diet components for both adults and children. The
microbiological quality, taking safety of products into account, has been constantly
improving.
The interactions occurring among tvarog allochthonous micro-flora influence the growth
of all micro-organisms present in a product. The dynamics of growth of individual types of
these micro-organisms can be evaluated using JMPTH computer program.
The packaging hermetic properties determines significantly the direction of changes of
allochthonous micro-flora under the influence of lactic acid bacteria.
The packing system as well as hermetic properties and type of packaging influence the
growth of staphylococci count in a product. The probabilistic model is suitable for assessing
the presence of enterotoxin in products, depending on the level of staphylococci and yeast.
There also exists a possibility to optimise the quality of lactic acid cheese, using biostatic
plant additives or through modification of the composition of packaging material.
REFERENCES
[1]
Adams M.R., Moss M.O. (1995). Food Microbiology. London. The Royal Society of
Chemistry.
[2] Adams M.R., Moss M.O. (2000). Food Microbiology. London. The Royal Society of
Chemistry. pp 112, 141, 211.
[3] Ahmed A.K., Johnson K.A. (2000). Horticultural development of Australian native
edible plants. Austral. J. Botany, 48, 417-426.
[4] Alves R.M., Sarantopoulos C.I., van Dender A.G.F., Faria J. (1996) Stability of sliced
Mozzarella cheese in modified atmosphere, J. Food Prot., 59, 8, 838-844.
[5] Arora D.S., Kaur J. (1999). Antimicrobial activity of spices. Int. J. Antimicrobial Ag.,
12, 257-262.
[6] Ashenafi M. (1990). Microbial quality of ayib, a traditional Ethiopian cottage cheese,
Int. J. Food Microbiol., 10, 3-4, 263-268.
[7] Bahk G.J., Hong C.H., Oh D.H., Ha S. D., Park K. H., Todd E. C. (2006). Modelling
the level of contamination of Staphylococcus aureus in ready–to-eat kimbab in Korea,
J. Food Prot., 69, 6, 1340-1346.
[8] Baranyi J., Ross T., McMeekin T.A., Roberts T.A. (1996). Effects of parametrization
on the performance of empirical models used in predictive microbiology, Food
Microbiol., 13,83-91.
[9] Baumgartner A., Kuefer M., Rohner P. (2001). Occurrence and antibiotic resistance of
Enterococci in Various Ready–to-Eat. Foods Activ. Fur Lenbensmittelhygiene 52, 124,16-19.
[10] Beckmanng., Koszegl D., Sonnensche in B., Limbeck R.: On the microbial status of
herbs and spices. Fleischwirtchaft 70, 240-243, 1996.
230
Izabela Steinka
[11] Belickova E., Tkacikova L., Nass H. T., Vargova M., Ondrasovic M., Ondrasovicova
O., Obsitikova Toth L. (2001). Staphylococci plate counts in foods of milk origin. Vet.
Med. –Czech. 46, 1, 24-27
[12] Benkeroum N., Sandine W.E. (1988). Inhibitory action of nisin against Listeria
monocytogenes. J. Dairy Sci. 71, 3237 -3245.
[13] Bergdol M.S. (1995) Importance of staphylococci that produce nanogram quantites of
enterotoxin. Zentralbl. Bacteriol., 282,1, 1-6.
[14] Bertola N. A., Bevilcaqa A., Zaritzky N. (2001). Reological Behaviour of White and
Cream Cheese. Int. Congress on Engineering and Food Technomic Publishing
Company, Inc Lancaster,573-577.
[15] Bolton L.F., Frank J.F. (1999). Defining the growth/no growth interface for Listeria
monocytogenes in Mexican –style cheesebased on salt, pH and moisture content. J.
Food Prot., 62, 601-609.
[16] Bozukart H., Erkman O. (2001). Predictive modeling of Yersinai enterocolitica
inactivation I Turkish feta during storage. J Food Engeneering 47, 2, 81-87.
[17] Brocklehurst T. F., Lund B. M. (1988). The Effect of pH on the Initiation Growth of
Cottage Cheese Spoilage Bacteria, 6, 43 - 49.
[18] Brody A.L. (1989) Controlled/Modified Atmosphere Vacuum Packaging of Foods.
Food and Nutrition Press. Inc.,179.
[19] Brouilaud-Delarte A., Maire M., Colette C., Mattei C., Lahellec C. (1997). Predictive
microbiology of dairy products: influence of biological factors affecting growth of
Listeria monocytogenes. J AOAC Int., 80,4,913-919. Md 403
[20] Buchanan R, L., Klawitter L, A. (1992). The effect of incubation temperature initial pH
and sodium chloride on the growth kinetics of Escherichia coli 0 157 : H7. Appl.
Environ. Microbiol, 58, 2513 - 2516.
[21] Cais D., Wojciechowski J. (1996). Zmiany wybranych cech jakościowych serów
twarogowych w trakcie ich przechowywania. Przegl. Mlecz. 6, 177-179.
[22] Castilejo -Rodriquez et al. A.M., Garcia Gimeno R.M., Zurera-Cosano G., Barco –
Alcala E., Rodriquez –Perez M.R.(2002) Assessment of mathematical models for
predicting Staphylococcus aureus growth in cooked meat products. J.Food Prot., 65, 4,
659-665.
[23] Centeno J.A., Menende S., Harmida Ma. Rodriquez – Otero J.L. (1999). Effects of the
Addition of Enterococcus faecalis in Cebreiro Cheese Manufacture, International J.
Food Microbiol., 48, 97-111.
[24] Champagne C.P., Laing R.R., Roy D., Mafu A.A., Grifith M.W. (1994). Psychrotrophs
in dairy products: their effects and their control. Crit. Rev., Food Sci. Nutr., 34, 1, 1-30.
[25] Chen et al. J.H., Hotchkiss J.H. (1993). Growth of Listeria monocytogenes and
Clostridium sporogenes in cottage cheese in modified atmosphere packaging. J. Dairy
Sci., 76, 972-977.
[26] Chojnowski W., Żuraw J., Sell J., Jęsiak Z. (1997). Materiale form 4th National
Scientific Session. Postęp w technologii, technice i organizacji mleczarstwa. Olsztyn,
204-205.
[27] Crofcheck C.L., Payne F.A., Nokes S.E.(1999). Predicting the cutting time of cottage
cheese using light backscatter measurements. Transaction of the ASAE,42, 4, 1039-1045.
231
[28] Delbes C., Alomar J., Chougui N., Martin J.F., Montel M.C. (2006). Staphylococcus
aureus growth and enterotoxin production during the manufacture of uncooked, semihard cheese from cows’ raw milk. J. Food Prot. 69, 9, 2161-2167.
[29] Dixon, N.M., Kelly D. B. (1988). The inhibition by CO2 of the growth and metabolism
of microorganisms. J. Appl. Bacteriol., 67,109.
[30] Elliot S.C., Vuillemard J.C., Emond J.P. (1998). Stability of shredded Mozzarella
cheese under modified atmospheres. J. Food Sci. 63, 6, 1075-1080.
[31] Farrag S. A., Marth E. H. (1992) Interactions between Listeria monocytogenes and
other psychrotrophic bacteria i dairy foods: review. Food Aust., 44, 281-284, 286.
[32] FDA /CFSAN. 2001. Microbiological Safety of Controlled and modified atmosphere
Available
from:
packaging
of
fresh
and
fresh-cut
produce.
www.cfsan.fda.gov/comm/ift3-6.html. 30.03.07
[33] Fedio W. M., Macleod A., Ozimek L. (1994). The Effect of Modfied Atmosphere
Packing on the Growth of Microorganisms in Cottage Cheese. Milschwissenschaft
49,11, 622-629.
[34] Feehery F. E., Ross E.W., Doona C.J. (2004). Quasi chemical modeling of
Staphylococcus aureus growth-decline kinetics in intermediate moisture meats as
functions of humectans, anti-microbials, and acidulants. IFT Annual Meeting, 12-16.07.
Las Vegas, Session 30, Food Microbiology: Meat, poultry and seafood.
[35] Fukijawa H., Morozumi S. (2006) Modelling Staphylococcus growth and enterotoxin
production in milk.Food Microbiol. 23, 3, 260-267.
[36] George S. M., Lund B. M., Brocklehurst T. F. (1988). The effect of pH and temperature
initiation of growth of Listeria monocytogenes. Letters in Appl. Microbiol.6, 153 – 156.
[37] Gonzales –Fandos E., Garcia-Lopez M.L., Sierra M.L., Otero A. (1994).
Staphylococcal growth and enterotoxins (A-D) and thermonuclease synthesis in the
presence of dehydrated garlic. J. Appl. Bacteriol., 77,5, 549-552.
[38] Grega T., Sady M., Wszołek M. (2001). Ocena jakości jogurtów z dodatkiem ziarna
amarantusa (Amaranthus cruenthus). Przegl. Mlecz., 5, 223-226.
[39] Halin –Dohnalek M.I., Marth E. H. (1989). Growth and production of enterotoxin A by
Staphylococcus aureus in cream. J. Dairy Sci., 72, 9, 2266-2275.
[40] Herve A.G., Tang J., Luedecke L., Feng H. (1998). Dielectric properties of Cottage
Cheese and Surface Treatment Using Microwaves. J. Food Engineer. 37,389-410.
[41] Hicks S. J., Lund B., M. (1991). The survival Listeria monocytogenes in cottage cheese.
J. Appl. Bact., 70, 308.
[42] Holly A., von Holzapfel W.H. Dykes G.A. (1992). Bacterial Populations Associated
with Viena Sausage Packaging. Food Microbiology 9 (1), 45-53.
[43] Honer C. (1988). Closing the freshness gap with CAP and MAP. Dairy Foods 89, (3)
53.
[44] Hsiao CH., P., Siebert K. J. (1999). Modeling the Inhibitory Effects of Organic Acids
on Bacteria. Int. J. Food Microbiol., 47,189-201.
[45] Ingham S., Losinski J.A., Dropp B., Vivio L.L., Buege D.R., Research note: Evaluation
of Staphylococcus aureus growth potential in ham during a slow-cooking process: use
of predictions derived from the U.S. Department of Agriculture Pathogen Modeling
Program 6.1 Predictive model and an inoculation study. J. Food Prot., 2004, 67, 7,
1512-1516.
232
Izabela Steinka
[46] Jackson T. C., Acuff G.R, Vanderzant C., Sharp T.R., Savell J.W. (1992). Identification
and Evaluation of Volatile Compounds Associated with Vacuum and Modfied
Atmosphere Packaged Beef Strip Loins. Meat Sci., 13, 175-179.
[47] Jordan K. N., Oxford L., O Bryan C. P. (1999). Survival of Low - pH stress by
Escherichia coli O157:H7. Appl. and Environm. Microbiol, 3048-3055.
[48] Kimura B., Toshiyama T., Fuji T., J. (1999). Carbon Dioxide Inhibition of Escherichia
coli and Staphylococcus aureus on pH – adjusted Surface in Model System. Food Sci.,
64,2, 367-370.
[49] Kołożyn-Krajewska D. (2003). Higiena produckji żywności. Wydawnictwo SGGW.
Warszawa.
[50] Kornacki K., Maciejska A., Klebukowska L. (1999). Modyfikacja szczepionek do
produkcji nie dojrzewających serów twarogowych. 7th Scientific Session ‘Postęp w
technologii technice i organizacji mleczarstwa’. Olsztyn 15-16.02.1999, 237-242.
[51] Kornacki K., Klebukowska L., Pruszyńska M. (2002). Wpływ rodzaju szczepionek
bakterii fermentacji mlekowej na jakość mikrobiologiczną twarogów., 8th Scientific
Session ‘Postęp w technologii technice i organizacji mleczarstwa’, Olsztyn 21-22.02.
2002, 375-384.
[52] Kujawski M., Rymaszewski J., Cichosz G., Łaniewska –Moroz, Fetliński A. (1994).
Wpływ bakterii fermentacji propionowej na tworzenie cech smakowo-zapachowych
sera i twarogów. Przegląd mleczarski 10, 263-266.
[53] Larssen A.G., Knochl S. (1997). Antimicrobial activity of food-related Penicillium sp.
Against pathogenic bacteria in laboratory media and a cheese. J. Appl. Microbiol., 83,
111-119.
[54] Le Loir Y., Baron F., Gautier M. (2003). Staphylococcus aureus and food poisoning.
Genet. Mol. Res. 2, 1, 63-76.
[55] Lee Wong A., Bergdol M.S. (2002). Staphylococcal food poisoning, 231-248. clavier
[56] Linquist R., Sylven S., Vagshoim I. (2002) Quantitative microbial risk assessment
exemplified by Staphylococcus aureus in unripened cheese made from raw milk. Int. J.
Microbiol, 78,1-2, 155-170.
[57] Maniar A.B., Marcy J.E., Bishop J.R., Duncan S. E. (1994). Modified Packaging to
Maintain Direct - Set Cottage Cheese. J. Food Sci., 59, 6, 1305.
[58] Masa-Calpe (1996). Microbiological quality of cheeses: importance of good handling
practices. Aliment. 270, 69-72.
[59] McCann T.L., Eifert D., Gennings C., Schilling M.W., Carter W.H. (2003). A
predictive model with repeated measures analysis of Staphylococcus aureus growth
data. Food Microbiol., 20,2, 139-147.
[60] Moir C.J., Eyles M.J., Devey J.A. (1993). Inhibition of pseudomonas in cottage cheese
by packaging in atmospheres containing carbon dioxide. Food Microbiol., 10,345-351.
[61] Molska I., Kielak I., Lapińska H. (1992). Wpływ termizacji i przechowywania mleka na
jakość mikrobiologiczną i trwałość sera twarogowego. Przem. Spoż. 2,42-46.
[62] Neugebauer K.A., Gilliand S.E. (2005). Antagonistic action of Lactobacillus
delbrueckii spp. Lactis RM2-5 toward spoilage organisms in cottage cheese. J. Dairy
Sci. 88,4, 1335-1341.
[63] Neumayer L., Kramer J. (1990). Production of enterotoxin A and thermonuclease by
Staphylococcus aureus in legumes. Int. J. Food Microbiol., 10, 3-4, 225-233.
233
[64] Nguyen-the C, Carlin F. (1994). The microbiology of minimally processed fresh fruits
and vegetables. Crit. Rev. Food Sci. Nutr., 43, 4, 371-401.
[65] Nicolai B.M., Van Impe J.F., Verlinden B., Martens T., Vandewalle J., De
Baerdsmsaeker J. (1993). Predictive Modelling of Surface Growth of Lactic Acid
Bacteria in Vacuum-Packed Meat. Food Microbiol. 10, 229-238.
[66] Noleto A.L., Malburg J. L. M., Bergdoll N.M.S. (1987). Production of staphylococcal
enterotoxin in mixed cultures. Appl. Environ. Microbiol., 53, 10, 2271-2274.
[67] Olborska K., Lewicki P.P. (2005). Zagrożenia w procesie pakowania produktów
mleczarskich. 5th Scientific Conference on Quality and Safety of Food. Bia³obrzegi,
17-18.11, 44-45.
[68] Otero A., Garcia M.C., Garcia M.L., Prieto M., Moreno B. (1988). Behaviour of
Staphylococcus aureus strains, producers of enterotoxins C1 or C2, during the
manufacture and storage of Burgos cheese. J. Appl., Bacteriol., 64, 2, 117-122.
[69] Panfil-Kuncewicz H., Kuncewicz A., Bohdziewicz K., Kornacki K., K³êbukowska L.,
(1997b). Trwałość przechowalnicza twarogów pakowanych w próżni i w modyfikowanej
atmosferze. MateriałyXXVI Sesji KTiChŻ PAN 1997b, 85-88.
[70] Panfil-Kuncewicz H., Kuncewicz A., Szpendowski J. (1997a). Pakowanie twarogów w
atmosferze dwutlenku węgla. Materiały VI Sesji Naukowej ‘Postęp w technologii,
technice i organizacji mleczarstwa’ Olsztyn, 294-295.
[71] Pathogen Modeling Program www.arserc.gov/mfs/PATHOGEN.HTM
[72] Pepe O., Blaiotta G., Bucci F., Anastasio M., Aponte M., Villani F. (2006).
Staphylococcus aureus and staphylococcal enterotoxin A in breaded chicken products:
detection and behaviour during the cooking process. Appl. Environ. Microbiol., 72,11,
7057-7062.
[73] Pereira J.L., Salzberg SP., Bergdol M.S. (1991). Production of staphylococcal
enterotoxin D in foods by low-enterotoxin–producing staphylococci. Int. J. Microbiol,
14,1, 19-25.
[74] Philips C.A. (1996). Review: Modified atmosphere packaging and its effects on the
microbiological quality and safety of produce. Int. J., Food Sci Technol., 31, 463-479.
[75] Piccinnin D., Shelef L.A. (1995). Survival of Listeria monocytogenes in Cottage
cheese. J. Food Protect., 58,2,128-131.
[76] Pieczonka W. (1993). Jakość organoleptyczna twarogów kozich uzyskanych z
mrożonego mleka lub skrzepu. Przegląd Mlecz. 10, 284-286.
[77] Poirazi P., Leroy F., Georgalaki M.D., Aktypis A., De Vuyst L., Tsakalidou E. (2007).
Use of Artificial Networks and a Gamma-concept –based approach to model growth of
and bacteriocin production by Streptococcus macedonicus ACA-DC 198 under
simulated conditions of kasseri cheese production. Appl. Environ., Microbiol., 73, 3,
768-776.
[78] Post L.S., Lee D.A., Solberg M., Furgang D., Specchio J. (1988). Development of
Staphylococcal Toxin and Sensory Deteroration during Storage. J. Food Sci., 53(2),
383-387.
[79] Ren T.J., Frank F.J. (1992). A survey of four fluid milk processing plants for airborne
contamination using various sampling methods. J. Food Protect. 55, 38-42
234
Izabela Steinka
[80] Rosenthal I., Rosen B., Berstein S. (1996). Surface pasteurization of Cottage cheese.
Milschwissenschaft 51,4,198-201
[81] Ryster E. T., Marth E. H., Doyle M. P. (1985). Survival of Listeria monocytogenes
during manufacture and storage cottage cheese. J. of Food Protect., 48, 746 –750.
[82] Salustiano V.C., Andrade N.J., Brandao S.C.C., Azeredo R.M.C., Lima S.A.K.L.
(2003). Microbiological air quality of processing areas in a dairy plants as evaluated by
the sedimentation technique and a one-stage air sample. Braz. J. Microbiol., 34, 255259.
[83] Sameshima T., Magome C., Tekeshita K., Arihara K., Itoh M., Kondo Y. (1998). Effect
of intestinal Lactobacillus starter cultures on the behaviour of Staphylococcus aureus in
fermented sausage. Int. J. Food Microbiol., 41, 1, 1-7.
[84] Schaffener D.W., Vora P., Duffy S. (2001). Initiative modeling survival of Escherichia
coli and Staphylococcus aureus with probability distribution functions. Society for Risk
Analysis. www. riskworld.com/abstract/2001
[85] Severini C., Bressa F., Romani S., Dalla Rosa M. (1998). Physical and Chemical
Changes in Vacuum Packaged Permigano Reggiano Cheese during Storage at 25,2 and
0
[86]
[87]
[88]
[89]
[90]
[91]
[92]
[93]
[94]
[95]
– 25 C. Journal of food Quality 21, 355-367.
Sims G.R., Glenister D.A., Brocklehurst T.F., Lund B.M. (1989). Survival and growth
of ford poisoning bacteria following inoculation into cottage cheese varieties. Int. J.,
Food . Microbiol., 9, 3, 173-195.
Śmietana Z., Świegoń J., Szpendowski J., Bohdziewicz K. (1997). Propozycja
techniczno-technologiczna produkcji tradycyjnych serów twarogowych. Materiały VI
Sesji Naukowej ‘Postęp w technologii, technice i organizacji mleczarstwa’ Olsztyn,
198-200.
Smittle R.B., Flowers R.S. (1994). Predictive Modeling and Microbiological Food
Studies SCOPE 9, 1-5,7.
Stańczak B., Szczawiński J., Pęcinek J. (2000). Survival of Listeria monocytogenes in
cottage cheese. Med.Wet., 56, 4, 251-254.
Stanton C., Gardiner G., Lynch P.B., Collins J.K., Fitzgerald G., Ross R.P. (1998)
Probiotic Cheese. Int. Dairy J. 8, 491-496.
Steinka I., Przybyłowski P. (1998). Jakość mikrobiologiczna kwasowych serów
twarogowych a metody pakowania. Przem. Spoż. 11, 47- 49.
Steinka I., Stankiewicz J. (1999a). System pakowania twarogów - aspekty higieniczne.
Żywność, 21 (4), 106-116.
Steinka I., Stankiewicz J. (1999b). Influence of Vacuum Packing and Low
Temperatures on the Level of Pathogenic Psychrotrophs in Cottage Cheese. Joint
Proceedings WSM Gdynia, Hochschule Bremerhaven, 21, 63-67, 1999b.
Steinka I. (1999c). Wpływ hermetycznego pakowania na jakość twarogów i twarożków.
Zeszyty Naukowe WSM w Gdyni 30, 53-62.
Steinka I., Pukszta T. (2000). Influence of Mycota in Cottage Cheese on Establishing
the Product Quality. Joint Proceedings. WSM Gdynia, Hochschule Bremerhaven, 13,
84-92.
235
[96] Steinka I. (2001a). Importance of Packaging Tightness for the Quality of Lactic Acid
th
Cheese Packed in Plastic Films, Proceedings of the 13 IGWT Symposium
Commodity Science in global quality perspective, Maribor, 2-8 09. 2001, 751-755.
[97] Steinka I. (2001b). The effect the Interaction between Microorganisms Present in the
Vacuum Packed Lactic Acid Cheese has on the Microbiological Quality. Joint
Proceedings, WSM Gdynia- Hochschule Bremerhaven, 14, 41-48.
[98] Steinka I., Kurlenda J. (2001c). Ocena zagrożeń mikrobiologicznych związanych z
systemem i hermetyką pakowania twarogów. Medycyna Weterynaryjna, 57, (10),757761.
[99] Steinka I. (2001d). Próba zastosowania aloesu w fermentowanych przetworach
mleczarskich. Żywienie Człowieka i Metabolizm Suplement, 785-792.
[100] Steinka I. (2001e). Possibility to Apply Aloe Vera Solution to Optimize the Quality of
the Lactic Acid Cheese Curd, Dairy Conference, Cairo 3-8.11.2001, 235-242.
[101] Steinka I. (2001f) Assessment of the efficacy of Aloe vera added to Propionibacterium
rd
growth medium. 3 International Symposium Propionibacteria, 8-11.07. 2001, Zurich,
35.
[102] Steinka I., Kurlenda J. (2002a). Determination of Microbiological Quality Indicates of
Vacuum-Packed Cottage Cheese and Prediction of their Changes during Storage. Polish
Journal of Food and Nutral Sciences 11(2), 199-206.
[103] Steinka I. (2002b). Toxic Test Possibilities Testing the New Supplement to Lactic Acid
Cheese. Joint Proceedings, WSM Gdynia, Hochschule Bremerhaven, 15, 61-66.
[104] Steinka I. (2003a). Wpływ interakcji opakowanie–produkt na jakość mikrobiologiczną
hermetycznie pakowanych twarogów. Wydawnictwo AM Gdynia, 1-135.
[105] Steinka I., Kukulowicz A. (2003b). Jakość i bezpieczeństwo twarogów związane ze
sposobem pakowania produktów. Żywienie Człowieka i Metabolizm, 30, 3/4, 888-892.
[106] Steinka I., Kukulowicz A. (2003c). Próba optymalizacji jakości twarogów za pomocą
aerozolu aloesowego. Brom. Chem. Toksykol. 36, 4, 341-346.
[107] Steinka I. (2003d). Sposób antygronkowcowej suplementacji skrzepu twarogowego
P346068, Biuletyn Urzędu Patentowego, 17(721), 3.
[108] Steinka I. (2004) Ocena prawdopodobieństwa występowania gronkowców i
enterotoksyny gronkowcowej w twarogach pakowanych w laminaty z tworzyw
sztucznych, Roczn. PZH, 55, 1, 89-98.
[109] Steinka I. (2005a). Wyznaczanie jakości higienicznej kwasowych serów twarogowych
wytwarzanych w różnych warunkach. Brom. i Chem. Toksykol., Suplement, 373-376.
[110] Steinka I. (2005b). Wpływ jakości mikrobiologicznej twarogów na fazę wodną w
warunkach pakowania hermetycznego. Roczniki PZH 56, 3, 275-281.
[111] Steinka I., Blokus A. (2005c). Próba uwzględnienia interakcji między drobnoustrojami
w procesie prognozowania jakości twarogów i ich opakowań. Joint Proceedings
Wydawnictwo Akademia Morska, Gdynia, XVIII, 14-21.
[112] Steinka I. (2005d) Comparison of biostatic action of Sorbus aucuparia and Aloe
arborescens under model conditions and in food. The IX International Congress Actual
Problems of creation of new medicinal preparations of nutral origin Phytopharm 2005,
St. Petersburg June 22-25, 381-383.
[113] Steinka I, Nowaczyk M. (2006a). Wpływ dodatków roślinnych na wybrane cechy
twarożków smakowych. Handel Wewnętrzny 6, 422-427.
236
Izabela Steinka
[114] Steinka I. (2006c). Ocena jakości twarogów dostępnych w handlu przed nowelizacją
wymagań mikrobiologicznych. Jakość towarów i usług w obrocie. Wydawnictwo WSG
Bydgoszcz , Volume II, 167-174.
[115] Steinka I. Blokus A. (2007). Szacowanie wielkości populacji zdolnej do syntezy
enterotoksyny gronkowcowej w twarogach, unpublished data
[116] Steinka I., Parisi S. (2006b). The influence of cottage cheese manufacturing technology
and packing method on the behaviour of micro-flora. Joint Proceedings, AM Gdynia,
Hochschule Bremerhaven, 19, 30-37.
[117] Stewart C. M., Cole M.B., Legan J.D., Slade L., Vanden M.H., Schaffener D.W.
(2002). Staphylococcus aureus growth boundaries: moving towards mechanistic
predictive models based on solute-specific effects, Appl. Environ. Microbiol., 68,4,
1864-1871.
[118] Tamagnini L.M., de Sousa G.B., Gonzales R.D., Reveill J., Budde C.E. (2005).
Behaviour of Yersinai enterocolitica and Salmonella typhimurium in Crottin goat’s
cheese. Int. J. Food Microbiol., 99,2, 129-134.
[119] Taub I. A., Feeherry F.E., Ross E.W., Kustin K., Doona C.J. (2003). A quasi –chemical
kinetics model for the growth and Heath of Staphylococcus aureus In intermediate
moisture bread. J. Food Sci., 68, 8, 2530-2537.
[120] Turhan M., Kaletunc G. (1992). Modeling of salt diffusion In white cheese during longterm brining. J. Food Sci., 57,5, 1992.
[121] Tyszkiewicz I. (1992) Przechowywanie mięsa w atmosferze gazów ochronnych,
Gospodarka Mięsna 8, 20-22.
[122] Usajewicz I. (1995) Oddziaływanie paciorkowców rodzaju Enterococcus na wzrost oraz
aktywność metaboliczną bakterii grupy coli i Clostridium spp. Zeszyty Naukowe
Akademii Rolniczo Technicznej. Olsztyn
[123] Usajewicz I. (2000). Przeżywalność S. ureus, S. galinorum i E.coli w kefirze oraz w
mleku ukwaszonym przez kultury L. plantarum i L. casei SHIROTA, Materiały Naukowe
Szkoła letnia ‘Bakterie fermentacji mlekowej- klasyfikacja, metabolizm, genetyka,
wykorzystanie’. Kazimierz Dolny, 59.
[124] Vernozy-Rozynand C., Meyrand A., Mazuy A., Mazuy C., Delignette-Muller M.L.,
Joubert G., Perrins G., Lapeyere C., Richard Y. (1998). Behaviour and enterotoxin
production by Staphylococcus aureus during the manufacture and ripening raw goats
milk lactic cheeses. J. Dairy Res. 65, 273-281.
[125] Walls I., Scott V.N. (1997). Validation of Predictive Mathematical Models Describing
the Growth of Listeria monocytogenes. J. Food Protect. 60, (9), 1142-1145.
[126] Walls I., Scott V.N.,Dane B. T. (1996). Validation of predictive mathematical models
describing growth of Staphylococcus aureus. J. Food Prot., 59, 1, 11-15(5).
[127] Westal S., Filtenborg O. (1998). Spoilage Yeasts of Decorated Soft Cheese Packed in
Modfied Atmosphere. Food Microbiology 15, 243-249.
[128] Zagory D. (1995). Principles and practice of modified atmosphere packaging of
horticultural commodities. Lancaster, PA, Technomic Publishing Co Inc. 175-204.
[129] Ziółkowski T., Staniewska K., Panfil-Kuncewicz H. (2003). Metody pakowania a
bezpieczeństwo i trwałość twarogów i serów dojrzewających. Przegl. Mlecz., 7, 269272.
[130] Zurera –Cosano G., Castillejo-Rodriguez A.M., Garcia-Gimeno R. M., Rincon –Leon
F. (2004). Performanc e of response surface and Davey model for prediction of
237
Staphylococcus aureus growth parameters under different experimental conditions. J.
Food Prot., 67, 6, 1138-1145.
Chapter 3
THE DEVELOPMENT OF ENGINEERING
TECHNOLOGY TO IMPROVE THE QUALITY OF
PRODUCTION OF TROPICAL FRUIT
IN DEVELOPING COUNTRIES
B. Jarimopas1, P. Sirisomboon2,
R. Sothornwit3 and A. Terdwongworakul4
1,3,4
Faculty of Engineering at Kamphaengsaen, Kasetsart University,
Kamphaengsaen, Nakohn Pathom, Thailand
2
Department of Agricultural Engineering, Faculty of Engineering,
King Mongkut’s Institute of Technology Ladkrabang, Bangkok, Thailand
ABSTRACT
Many developing countries are rich in agricultural and food resources but are unable
to maximize the export income they earn from them because they lack value-adding
technology. In other words, developing countries typically must sell their products in
cheap unfinished form to nations which possess the technology that adds profitability to
these goods. Accordingly, if developing countries wish to earn more revenue for the
improvement of their people’s employment and education, they must develop food
engineering technology alongside other food science technologies. These efforts at
technological self-improvement should be supported by the developed countries as the
reduction of the knowledge and income gaps between the industrialized and developing
worlds will do much to further global peace and happiness.
The desired trend for food engineering research is to focus on developing
engineering technology that will help to improve tropical fresh produce quality. This
chapter discusses three facets of this trend. The first aspect concerns the physical
properties of tropical fruit and vegetables, which consist of post-harvest loss, physical
characteristics, mechanical properties, firmness, friction, and non-destructive quality
grading techniques relating to mangoes, mangosteen, durian, sweet tamarind, guava,
tangerines, snake egg plants, white long radish and lime. The second aspect concerns
innovations in machinery and devices used with mangosteen, durian, young coconut, dry
240
B. Jarimopas, P. Sirisomboon, R. Sothornwit et al.
over-mature coconut and baby corn. State of the art design, operating principles and key
performance tests of tropical fruit machinery and inventions will be reviewed. The third
aspect concerns packaging technology, particularly that which is directed towards the
extension of the shelf life of the aforementioned tropical fresh produce.
There are three current realities which inform this book. They are as follows: that
there is a high incidence of post-harvest loss and a corresponding magnitude of shortage
in research and development work on tropical fresh produce; that the global flow of
information is increasing while agricultural labor is becoming scarcer and more
expensive; and that tropical produce engineering technology must be thoroughly
understood. Accordingly, we make two recommendations: for producer countries to
instigate a dramatic increase in the research and development that they conduct into
tropical fresh produce, and in the support that they provide for this research; and that the
research trend should cover all economic tropical fruit and vegetable goods grown in the
producer countries and all aspects of engineering technology that they use, with a
particular emphasis on developing computerized non-destructive techniques for quality
assurance.
INTRODUCTION
If the task of science is to understand the composition of nature, the goal of engineering
is to employ that scientific understanding in the quest to create new things. In other words,
engineers who wish to improve the production of tropical fresh fruit and vegetables first must
understand the natural behavior of tropical fresh produce. Only when they possess this
knowledge can they develop innovations in production processes, devices and machinery.
The next goal for engineers is to improve the distribution and preservation processes; that is,
they must seek to improve the packaging that holds produce together and protects it from the
adverse conditions of handling, transport and environment. Indeed, the drive to improve
packaging has become of paramount importance due to the modern recognition of its capacity
to secure standard qualities of freshness, uniformity, flawlessness and attractive appearance.
Great opportunities exist today to increase export sales of tropical fruit and vegetables.
This is implied by the comparatively low level of sales that currently exist. To clarify, the
United States Department of Agriculture (2004) reports that exports to the world market of
four temperate region fresh fruit and vegetables (apples, pears, potatoes, tomatoes) in 2002
were valued at more than USD5250 m., while exports by Thailand in 2006 of tropical fresh
fruit and vegetables produced only USD172 m. in income (Customs Department, 2007).
Thus, in effect, the huge markets of the US, the EU, Japan and China are challenging
developing countries to improve their fruit and vegetable production technology, especially
their engineering technology. As noted before, improvements in engineering technology
should include developments in knowledge of the natural behavior of tropical fresh produce
and the creation of innovative packaging technology for this produce.
The natural behavior of tropical fresh produce relates to its physical properties.
Innovations in this area occur when developments are made in primary processing and postharvest machinery, and in devices which facilitate the production and consumption of tropical
fresh produce. Packaging technology relates to packaging for distribution and for extension of
shelf life of produce.
Development of Engineering Technology to Improve the Quality of Production… 241
However, at present, the investment into the research and development of tropical fresh
produce is comparatively very low. A Google Scholar search in April 2007 found that 79%
more research (≅ 233) is conducted into apples, peaches and pears than the leading tropical
fresh fruit (durian, longan, mangosteen, mango, young coconut, pineapple, pumelo, rambutan,
rose apple, dragon fruit) in terms of their physical properties and associated nondestructive
techniques. Meanwhile, 92.3% more research in the same areas is conducted into tomatoes,
potatoes and carrots (≅ 298) than into the dominant tropical fresh vegetables (egg plant, snake
egg plant, Chinese radish, chilli, Chinese cabbage, cabbage, kale, water morning glory).
Accordingly, there is a serious shortage of knowledge in these aspects of engineering
technology with regard to tropical fruit and vegetables. This chapter reviews and discusses the
current body of knowledge relating to the natural properties of tropical produce and
engineering innovations associated with these products, and then suggests a future trend for
research and development which it is hoped will help to redress the serious imbalances
described above.
1. PHYSICAL PROPERTIES OF TROPICAL FRESH
PRODUCE IN DEVELOPING COUNTRIES
1.1. Post-Harvest Loss and Physical Characteristics
of Selected Tropical Fresh Fruit
Longan is one of Thailand’s major export fruits. The fruit are usually presented in
bunches and, after manual harvesting, undergo sorting, handling, packaging and
transportation. The first step of this post-harvest process is to separate twin fruit and broken
branches and leaves from the gross product, a procedure which typically results in the
retention of 78.5-87.0% of marketable fruit (Jarimopas, 1985). The usual effect of handling,
packaging and transportation of the fruit is that some mechanical damage is caused in the
form of fruit rupture and berry-dropping, with average losses running at 9.0% in two stacking
containers and 14.8% in four stacking containers. The containers are cylindrical bamboo
baskets which are piled directly on top of each other without cushioning. Mechanical damage
is lowest in containers placed at the tops of stacks and is highest in containers placed at the
lowest levels, possibly due to the higher compressive loads exerted by the upper containers.
Another major export fruit in Thailand is mangosteen. This fruit has been investigated for
post-harvest loss occurring at grading-buying points in the orchards and at retailer locations.
Table 1 shows the various kinds of loss recorded from samples taken at the grading-buying
points. The relevant fruit were stored at ambient temperatures until ripe, and were inspected
and analyzed. The sampling survey was carried out in two provinces - Chantaburi in the east,
and Chumpon in the south - both of which are major mangosteen production areas in
Thailand. Samples were collected three times: at the beginning, the middle, and the end of the
harvesting season. The greatest loss (48.6%) was due to rough surface, which greatly reduces
the value of the fruit. The second greatest loss (33.9%) was due to internal defects (although it
should be noted that mangosteen might have more than one defect (Pushpariksha and
Jarimopas, 2006a)).
242
To determine the post-harvest loss at the retailing stage, sampling was performed at
representative sites of the most typical vending locations: at supermarkets, open markets, and
mobile retailers (those who sell fruit from utility vehicles such as pick-up trucks). The
sampled fruit was kept at room temperature for 3-4 days before being inspected and analyzed.
Losses recorded in rank of frequency were due to rough surface (83.8%), hard rind (33.4%),
translucent flesh and gummosis (26.9%), and decay (6.9%). The incidence of hard rind fruit,
which is caused by mechanical injury, increased tremendously from the wholesaler to the
retailer stages due to unsatisfactory packaging and inefficient handling and transit procedures.
To clarify, mangosteen in Thailand which are intended for local consumption (rough fruit
typically are not exported) usually are packed with minimal protection and care into paperlined reusable plastic containers before being transported by small trucks from the eastern and
southern provinces to Bangkok. However, despite the high quantity of rough fruit found at
local retailers, cracked fruit are generally absent because they have been culled out by the
wholesalers. The quantity of fruit with internal disorders (translucent flesh and gummosis)
tends also to be relatively low at retail point of sale because fruit with these defects tend to
decay after they leave the wholesalers and accordingly are sorted out by the retailers
(Pushpariksha et al., 2006).
Post-harvest loss of rose apple fruit was ascertained with respect to two variables: variety
(the Thongsamsri and Toonklao strains) and transport destination (retailers and wholesalers).
Samples from retail locations were drawn from three mobile vendors, large open markets, and
popular supermarkets around Bangkok and provincial cities. Wholesale samples were taken
from three large fruit markets in Bangkok. The rose apples were manually harvested, packed
and transported by trucks to all the above vending locations. Post-harvest loss was quantified
in terms of abrasion and bruising damage. Two parameters of the damage evaluation were:
Average damage per fruit (D x ) =
Total area of each damage type on fruit surface
Total fruit of the package
(1)
Number of damaged fruit in a package
×100
Total fruit of the package
(2)
Average damage percentage per package ( D y ) =
With regard to post-harvest damage of the premium Thongsamsri variety found at
wholesalers, the average damage due to bruising was 0.45 cm2/fruit (Dx) or 23.3% (Dy), while
that due to abrasion was 0.66 cm2/fruit (Dx) or 72.2% (Dy). At the retailers, the average
damage due to bruising was 1.45 cm2/fruit (Dx) or 56.8% (Dy), while abrasion was 0.95
cm2/fruit (Dx) or 78.1% (Dy). With regard to the Toonklao variety (a popular variety which is
cheaper and less sweet than the Thongsamsri strain), damage was found to be higher at retail
point of sale locations than at wholesalers. The major damage was bruising and abrasion. The
average bruising and abrasion were 0.22 cm2/fruit (Dx) or 26.7% (Dy) , and 0.45 cm2/fruit
(Dx) or 58.3% (Dy), respectively at the wholesalers while at retailers, average bruising and
abrasion were 0.61 cm2/fruit (Dx) or 61.7% (Dy), and 1.21 cm2/fruit (Dx) or 90.0% (Dy),
respectively (Toomsaengthong et al., 2006).
We turn now to studies conducted into maturity grading and sizing of fresh tropical fruit.
To evaluate the maturity of two Thai mango cultivars (Nam Dokmai and Chok Anan),
Kittawee and Jarimopas (2006) attempted to measure the specific gravity (SG) of samples
every two days for 40 days starting from when the fruit were immature until they were over-
ripe by using the technique suggested by Mohsenin (1996). Good correlation was found
between SG and maturity (based on time T after fruit set) for the Nam Dokmai variety while
poor correlation occurred with reference to the Chok Anan strain. The regression equation for
the Nam Dokmai analysis was SG = 0.87+0.0016T (R2 = 0.90).
Sizing of produce is in general based on its dimensions. Sizing is not only useful for
packaging, but also adds value to the produce (Jarimopas, 2006). Pushpariksha and Jarimopas
(2006) studied physical characteristics of mangosteen by measuring the following variables of
newly harvested fruit of four sizes (large, medium, small and undersize): weight, maximum
diameter Dmax, minimum diameter, volume, diameter of calyx circumscribing circle Dc, and
height with and without calyx. Table 2 shows the physical characteristics of fresh mangosteen
related to size. The dimension ratio (DR), which was the ratio between Dc and Dmax, was
proposed as a parameter to identify undersize fruit. It was found that the DR of the
marketable mangosteen (excluding those that were undersized) was greater than 1. Therefore,
DR could be a suitable parameter for undersize sorting. Since the weight of mangosteen
stored at ambient temperatures dropped 14% in 2 weeks while their diameter decreased only
0.3%, mangosteen sizing by dimension would probably return more consistent results than
sorting by weight.
1.2. Mechanical and Textural Properties
Studies have been conducted into the mechanical and textual properties of tropical fruit
such as mango and sweet tamarind and vegetables including snake egg plant and white long
radish. Parameters of these properties includes rupture force, rupture deformation, the slope
of the force-deformation curve, the Poisson’s ratio, modulus of elasticity, and firmness.
Friction properties will also be reviewed and discussed in this section. A discussion of the
technical experience of testing and measurement of the physical properties is also included.
Table 3 (Chaiyapong and Jarimopas, 2006) shows the mechanical properties with respect
to the rupture force FR, rupture deformation DR, and firmness expressed by the slope of the
force-deformation curve S (Jarimopas and Kittawee, 2007) of the Thai popular mature mango
“Nam Dokmai”. The experiment was performed with slow compression of the fruit by a 4mm
plunger driven by the universal testing machine UTM (INSTRON 5569) at a loading rate of
20 mm/min. The compression test was controlled by ripeness (unripe, ripe) and fruit
orientation (5 points of loading application – figure 1). FR, DR and S were significantly
affected by ripeness and fruit orientation at the significance level of 5%. The top edge and the
bottom edge of the mature and unripe mango statistically exhibited the highest and the lowest
FR, respectively. Specifically, the FR of the bottom edge and the head of the mature and
unripe mango were insignificantly different, with the greatest and the lowest slope S recorded
at the top edge and the tail of the fruit, respectively. This implies the maximum firmness of
mango occurs at the top edge and the minimum firmness at the tail.
When mango is ripe, the ripening process has changed flesh cells to totally soluble solids,
which results in reduction of the strength of the maximum FR of the ripe fruit to one-eleventh
of that of the unripe fruit. The maximum FR of the ripe mango in this experiment occurred at
the cheek (the most convex part of the fruit) while the FR of every point of load application
was statistically indifferent, except at the fruit head where FR was the least. Firmness in terms
of the slope of the ripe mango dropped to about one eleventh of that of the unripe fruit, while
244
firmness of every load application point was statistically indifferent. However, the slope
could not differentiate the maturity of Nam Dokmai and Chok Anan mangoes (Jarimopas and
Kittawee, 2007).
The Poisson’s ratio μ and modulus of elasticity E of the mango were also determined by
means of uniaxial compression with the INSTRON 5569 until 50% of rupture force. The
sample was cylindrical mature Nam Dokmai flesh measuring 15 mm in diameter by 30 mm in
length. The resulting μ and E was 0.24±0.05 and 3.39±0.3 MPa, respectively (Chaiyapong
and Jarimopas, 2006).
Sirisomboon et al. (in press) have conducted a preliminary study which intended to add to
the progress towards the design of a firmness tester suitable for mango maturity classification.
They have designed an experiment which consisted of two parts: probe selection, followed by
evaluation of the selected probe in mango maturity classification using a texture analyzer. In
the first part, mango samples (Mangifera indica L. variety Namdokmai) at three different
stages of maturity (120 fruit each at 60, 70 and 80% maturity, comprising a total sample size
of 360 fruit) were tested. These different maturity stages were classified by farmers through
sensory evaluation. A texture analyzer (TA-XT2i, Stable Micro System, UK) with 4 probes
including a 5, 10, and 15 mm diameter spherical stainless steel probe and a 75- mm diameter
circular flat aluminum plate probe were used to measure the firmness of the mango samples.
Thirty mango fruit at each stage of maturity were subjected to a compression test at a
maximum force of 3 N and probe speed of 0.2 mm/s (as no bioyield point appeared during the
procedure, this can be considered a non-destructive test). Each probe was compressed on the
cheek of one side of the fruit. The result showed that the 5-mm diameter spherical stainless
steel probe provided the best performance due to its minimum value of standard deviation,
coefficient of variation and variance. According to the Duncan’s test the means of the
firmness values tested by the probe at different stages of maturity were significantly different
(p<0.05). This indicated that the three different maturity stages (60, 70, and 80% of full
ripeness) could be classified by firmness.
The second stage of the experiment again involved the use of 360 mangoes of the same
variety selected according to the three different stages of maturity described above. Each of
the 360 fruit samples was measured for firmness and classified into three firmness categories:
greater than 13.0 N/mm; 13.0 - 11.6 N/mm; and less than 11.6 N/mm. A texture analyzer with
a 5 mm diameter spherical stainless steel probe was used to measure the firmness of the
samples. A total of 80 fruit of each firmness category were randomly sampled and were
divided into 4 groups (20 fruit each). The first group was immediately measured for soluble
solids while the other three groups were ripened through exposure to calcium carbide (CaC2)
at approximately 25°C (room temperature) for one, two and three days respectively. The
soluble solids content was measured each day by a digital refractometer (Atago, PR-32,
Japan) and expressed in % Brix. The experiment was conducted because the soluble solids
content is one of the indices of the maturity of mango fruit. Therefore, if the mangoes, which
were classified into different firmness categories by the probe, had corresponding differences
in soluble solids content, then the maturity of mangoes could also be classified by firmness.
The authors concluded that sugar developed better in the softer mangoes than in the harder
ones; in other words, they ripened faster.
The results showed that lower firmness indicated higher levels of soluble solids at each
ripening stage. The soluble solids at day 1, 2 and 3 of the ripening stage were significantly
different between different firmness categories. The first category (>13.0 N) and the third
category (<11.6 N) had different soluble solids but they were not different from the second
category (13.0-11.6 N). This indicated that a texture analyzer with a 5-mm spherical probe
could classify the maturity into two different stages: namely, the 60% and 80% stages of full
ripeness. However, the technique could not detect the difference between 60% and 70% of
full ripeness or between 70% and 80% of full ripeness, which are distinctions needed by
growers in determining fruit maturity. The author indicated that further study is needed to
develop a firmness tester that can work nondestructively online with high resolution in
classifying the maturity of mangoes during harvesting time. Also required is the development
of a firmness tester based on the direct measurement of force and deformation at a force level
not higher than the bioyield force of the fruit; in other words, nondestructive measurement
may be more appropriate for a nondestructive system than other indirect measurements such
as acoustic firmness testers. An additional point in favor of a direct measurement tester is that
it can be adapted to an online system and made to be independent of the effects of operatorinstrument interaction.
Our attention now is focused on experimental work concerning sweet tamarind
(Tamarindus Indica L.) This is a favorite fruit of both Thais and foreigners, as can be seen
from its export value in 2000 of roughly USD4 million. Tamarind has a sweet and sour flavor
and is rich in nutrients (figure 2).
The mature sweet tamarind presents as a pod, which contains a seed enclosed by flesh
and a shell. A distinctive feature of the tamarind is that the shell cleanly separates from the
flesh; however, tamarind currently suffers a considerable amount of mechanical damage
during post-harvest handling, packaging and distribution due to lack of information about the
physical and mechanical properties of the fruit.
Of recent interest is research conducted into the mechanical properties of two commercial
cultivars of sweet tamarind (the “Sitong” and “Srichompoo” cultivars). The research was
motivated by concern about the prevalence of pod shell cracking, which usually occurs during
the packaging process. Thirty pods of each cultivar, newly harvested and of uniformly
medium size, were compressed with a 3mm spherical plunger that was driven by a UTM at 25
mm/min. The drop impact tester developed by Chen et al. (1996a) was also used. The
experiment included three control factors: cultivar, maturity (immature and mature) and pod
surface profile (convex and concave). The mechanical properties included weight, dimension,
specific gravity, slope of force deformation curve and firmness index (peak acceleration
divided by the corresponding contact impact time) (Jarimopas et al., 2005a). The Sitong pods
were physically bigger, heavier, and denser than the Srichompoo fruit (table 4).
The strength of each pod shell was investigated by means of two properties: firstly, the
slope of the force deformation curve S under plunger slow compression; secondly, the
application of firmness index FI through the impact set-up. Table 5 shows that the slope and
the firmness index of the Sitong shells were higher than those of the Srichompoo variety at
the same level of maturity. Additionally, it was found that the S and FI of the shells of
immature sweet tamarind were higher than those of mature fruit from the same cultivar. It is
speculated that this is because tamarind flesh tends to separate from its shell when it
approaches maturity. Moreover, the pods that were tested had been hung out to dry for several
246
weeks. Accordingly, the shells were drier and thus were likely to be more fragile and more
prone to cracking.
The surface pod profile significantly influenced the slope of the force-deformation
response of the pod shell at a significance level of 5% (table 6). The convex shell had a higher
slope than the concave shell in both cultivars. Accordingly, it can be deduced from plate and
shell theory that yield stress due to compression on the shell of the convex side was higher
than that of the concave side (Timoshenko and Goodier, 1970), which in turn caused the S of
the convex shells of sweet tamarind pods to be greater than the S of the concave shells.
As mentioned in our introduction to this section, work has also been conducted into the
mechanical and textural properties of vegetables such as snake eggplant and long white
radishes. These vegetables have been of great significance to the local Thai market for a
considerable time and are usually consumed fresh. In recent times, a strong export market has
developed for the vegetables, and thus production requirements and standards have risen. A
higher standard implies standardization, which in turn requires knowledge of physical and
mechanical properties which to date have been only sketchily understood.
Jarimopas et al. (2006a) and Jarimopas et al. (2006b) note that the most significant
problem facing consumers and sellers of stored vegetables is that the vegetables quickly lose
their quality after harvesting. A few days after being collected, snake eggplant are softer and
their skin wilts, while the texture of the radish flesh changes from firm to spongy.
Accordingly, the modulus of elasticity E of each vegetable was determined with respect to
storage time as well as Poisson’s ratio μ. An experiment was conducted in which cylindrical
samples taken from the intact vegetables were subjected to two kinds of contact loading tests
(radial compression and die loading) with regard to two control factors (orientation and
storage time). The radial compression method used 15 mm x 30 mm cylindrical samples
while the die loading method used a 3.2 mm cylindrical probe. The testing instrument was the
UTM (INSTRON 5569) with a loading rate of 25 mm/min (ASAE Standard, 1998).
It was found that the storage time t significantly affected (p<0.05) modulus of elasticity
of the white long radish and the snake egg plant. The modulus of elasticity decreased
exponentially with t. The equation of relationship between modulus of elasticity and t is
shown in table 7. The average μ along the fruit axis was 0.252±0.082 while the μ along the
transverse axis was 0.166±0.047. The μ of the axial and the transverse samples of the long
white radish was 0.444±0.07 and 0.384±0.08, respectively. The position of snake egg-plant
sample along its body did not significantly affect E.
It was also ascertained that the firmness of snake egg-plant reduced with respect to
storage time. Orientation of preparation of sample of snake egg plant and white long radish
(axial and transverse) significantly affected μ at the significance level of 5%. Difference of μ
of a certain vegetable suggests that the assumption of fresh produce as an elastic material
ought to be carefully considered because the produce does not, in reality, behave
isotropically. However, in the case of this particular experience, the elasticity modulus
decreased by 30% with respect to the corresponding drop in weight. This might explain that
new fresh vegetables initially feature cells full of moisture. However, after storage in ambient
air for a week, the lost moisture causes the cells to deform, resulting in wilted skin and
reduced firmness.
With regard to the variable of friction, it can be said that it is an important mechanical
property of fresh produce. Conveying and processing machines are designed with regard to
friction (Wang, 1963; Mohsenin, 1996). Jarimopas et al. (2005b) developed the simple
electro-mechanical type and measured the coefficient of friction C and rolling angles A of
fruits. A typical device consists of a steel frame (300 mm wide by 500 mm long) with an
adjustable inclined surface. The angle of inclination θ of the surface of the machine discussed
in this context was computer-controlled and C and A results were displayed. The static
friction coefficient CS was the tangent of θ when the fruit started sliding, while the kinetic
friction coefficient Ck was the tangent of θ when the fruit uniformly slide along the inclined
plane after minor disruptive contact. The θ corresponding to the start of rolling of the fruit
was the rolling angle.
The experiment described here included three variables: produce (lime, tangerine, guava),
contact surface (galvanized sheet metal, plywood, plastics), and fruit orientation (opposite
stem side, stem side, cheek), which controlled the variation of Cs, Ck and A. The produce and
contacting surface significantly affected Cs and Ck (p<0.01) while the produce and the
orientation significantly influenced A (tables 8, and 9). Ck was less than Cs with regard to
identical forms of produce and contact surfaces, which corresponds with the claims made by
Mohsenin (1996).
The highest coefficient of friction for lime and tangerine was returned when the
experiment was conducted on plastic surfaces, while the results for guava were maximized on
plywood. The lowest coefficient of friction of all the produce was recorded when galvanized
steel was used. Depending on the contact surface, lime and guava exhibited respectively the
smallest and the greatest friction coefficient. For all produce, the orientation of opposite stem
side gave the greatest A because this orientation presented the greatest contact area to the
inclined surface. Rolling started when the line of produce weight passing through controid
was out of the contact area. The cheek contacted the inclined surface least.
Pushpariksha et al (2006) replicated the experiment concerning the static coefficient of
friction of mangosteen using the device developed by Jarimopas et al (2005b). In this
experiment, measurement was controlled by mangosteen type (normal surface, rough
surface), contact surface (plexiglass, plywood, galvanized steel sheet) and direction of
mangosteen slide (longitudinal, transverse to the fruit axis). All the fruit used in this
experiment was newly-harvested, uniform mangosteen. It was found that the mangosteen
type, contact surface and fruit sliding direction significantly affected Cs at a significance level
of 5% (table 10) and that the Cs of the mangosteen sliding along the transverse axis was
greater that that recorded by that moving in a longitudinal direction. Furthermore, the Cs of
normal mangosteen moving along plexiglass was higher than that recorded by rough
mangosteen, which probably results from the fact that mangosteen typically has a smooth,
waxed surface (and the cohesion of the surface of smooth fruit is likely to be greater than that
of rough fruit.)
248
1.3. Testing and Measurement
1.3.1. Contact Loading Technique
Contact loading is an important means of determining the mechanical and textural
properties of agricultural and food material. To attain efficient and successful testing and
measurement the following factors should be considered.
(A) Sample support: when a fruit sample is subjected to contact loading -- even when the
phenomenon of concern is at the upper contact point -- the support of the fruit sample which
creates the lower contact point must be considered (figure 3). The fruit, assumedly an elastic
body, stands at rest on a rigid support while its uppermost point is compressed with a flat
plate or a plunger. The lower contact point at the bottom of the fruit meanwhile is also
supported and compressed but the fruit is deformed because of greater support rigidity.
Theoretically, the lower contact point is considered to be stationary but, in reality, it is not
because of the fruit’s deformation. Thus, this affects the movement of the area of interest –
the upper contact point -- and, consequently, produces error in the deformation reading. In
order to produce an insignificant deformation of the fruit at the lower contact point, the fruit
should be supported with a large enough contact area so that compression is distributed in a
way that imparts very small contact stress and therefore also minimal deformation. To
facilitate the desired stability, moistened sand has been used by several researchers
(Chaiyapong and Jarimopas, 2007; Sarakan, 2006; Meeklangsaen et al., 2007; Vanichang and
Jarimopas, 2007) to support fruit including mango, rose apple, young coconut and dragon
fruit (figure 4). The chief advantages of this method are that moistened sand not only
improves stability but also can be manipulated to fit any fruit shape.
(B) Proper compression head. Questions often arise about which kind of contact loading
test and which compression head size should be used. With regard to determining the
mechanical properties of dragon fruit, the equipment that historically been deployed include a
flat plate, the die and the plunger probes. However, in helping to determine loading rate,
compression probes also significantly affect rupture force FR, rupture deformation, modulus
of elasticity and firmness. For example, the modulus of elasticity of the flat plate EFP at the
loading rate of 250 mm/min is 10.3% higher than when it is applied at 25 mm/min and is
23.7% higher than at a rate of 2.5 mm/min. Ultimately, the change of modulus of elasticity of
the cylindrical and the spherical probes due to loading rate change is close to 100%.
On the other hand, FR of fresh produce as a result of using die and ball heads is
customarily low because of the small contact area required. This lower contact area provides
greater opportunities for repeat testing of produce, which enables the orientation effect or
homogeneity or consistency of produce to be investigated, while the use of a flat plate results
in a large contact area and deformation at rupture force. Hence, with regard to flat plate
testing, it is often difficult to perform repeat tests using the same produce. According to the
ASAE Standard (1998), the modulus of elasticity of a curved material subjected to a flat plate
and a spherical indenter is
E FP
0.338 K 3 / 2 F (1 − μ 2 ) ⎡ 1
1⎤
=
+
⎥
⎢
D3 2
⎣ R1 R1′ ⎦
1
2
(1)
0.338K 3 / 2 F (1 − μ 2 ) ⎡ 1
1 4⎤
Eb =
⎢ + ′+ ⎥
32
D
⎣ R1 R1 d ⎦
1
2
(2)
In order to more easily use a ball head, the ball size should be manufactured so that d <<
R1 (about 10 times or more). Eb is then simplified to
Eb = 0.676
(1 − μ ).
2
d
1
2
F
D
3
(3)
2
Eb is dependent on the FD graph while μ and d (ball diameter) are kept constant.
Ed =
(1 − μ ) F
2
dd
(4)
D
(Mohsenin, 1996)
d d = die diameter (m)
Due to the comparatively greater flexibility of the design of the die and ball head, they
are considered to be highly compatible with produce size and structure. Conversely, the flat
plates that typically accompany UTM are usually too big for use with small stone fruit,
especially in mechanical damage studies. However, in cases where the use of flat plate is
mandated, the radial compression method may be an efficient approach. Jindal and Techasena
(1985) suggested the model of radial compression estimating modulus of elasticity of potato
as follows:
(
)
1.927 1 − μ 2 d10.2 F
ER =
L
D1.2
when
ER
μ
d1
L
(5)
= modulus of elasticity by radial compression test (MPa)
= Poisson’s ratio
= sample diameter (m)
= sample length (m)
The radial compression test requires the preparation of a sample of a cylindrical shape as
well as the measurement of d1 and L. The modulus of elasticity also is dependent on the
force-deformation response of the sample. However, if consistent sample preparation occurs,
reliable ER can be expected.
The low mass plunger impacter developed by Chen et al. (1996a) is widely applicable in
research which attempts to determine the mechanical and bruising properties of fruit (Chen et
250
al., 1996b; Jarimopas and Kittawee, 2007; Sarakan, 2006; Jaren et al., 1992; Corea et al.,
1992). Jarimopas and Kittawee (2007) enumerate its desirable features as follows:- i) the
measured acceleration signal increases, ii) both the magnitude of the calculated firmness
index and the rate of change of firmness index with respect to fruit firmness increase, iii) the
error due to movement of the fruit during the impact is minimized, iv) fruit damage caused by
the impact is minimized, and v) high speed sensing is applicable.
With regard to the determination of modulus of elasticity, a die seems to be the best head
for producing less complication and variation in E. This is because E depends directly on the
force-deformation ratio while μ and dd, are constant (see equation 3). A good alternative if the
condition to apply equation 3 holds is the low mass plunger probe. Determining the elasticity
modulus by means of FP and plunger head requires the measurement of radius of curvature in
two orthogonal planes, while radial compression necessitates good sample preparation and
measurement of sample dimension. It should be recalled that greater measurement and
replication requirements are likely to produce greater errors and testing and analyzing times.
(C) Effect of the size of the compression head. Jarimopas and Srirungruaug (2006)
investigated the relationship between impact and bruising in young coconut fruit by the use of
varying plungers (12, 24 ,48, and 96 gm/head) dropping on intact mature young coconut of
medium size (≅ 1.35 kg/fruit). Strong linear correlations were obtained between bruise
volume V and impact energy U (R2 > 0.99). The regression equations for different impact
heads were:V
V
V
V
=1161.3U-21.0
=1261.1U-20.6
=1333.1U-33.4
=1936.6U-94.2
(12 g impactor)
(24 g impactor)
(48 g impactor)
(96 g impactor)
The regression equations indicated the impact head variation caused variation in bruise
susceptibility (coefficient of U).
1.3.2. The Effect of Mechanical Loading upon Varying Mechanical Properties of Fruit
and Vegetables (Orientation Effect)
Mechanical loading applied to different points on the surface of a fruit or a vegetable can
cause different mechanical responses. For example, testing shows that a popular Thai papaya
(“Khagdum”) which is packed in the typical reusable plastic container in a vertical orientation
demonstrates 31% more bruising than if it is packed in a horizontal orientation (Chonhenchob
and Singh, 2005). This may be because the power spectrum density of package acceleration is
higher in a vertical direction than in a horizontal direction (Jarimopas et al., 2005c). In
another example, the abrasions to rose apple which occur because of handling and transit
vibration and which are the dominant form of damage to this fruit more often occur in the
section close to the stem (tail) than that in the head (Toomsaengtong et al., 2006). This
phenomenon was experimentally explained with reference to rose apples by means of slow
compression using a 4 mm plunger, which showed that the rupture force FR of the tail and
head were 5.50 and 8.89 N respectively. The smaller FR of the tail seems to indicate that there
is less mechanical resistance in this section than in the head, which leaves the tail more
vulnerable to damage. Similarly, with regard to “Nam Dokmai” mango, fruit orientation has
been described to influence FR and S of the fruit response (Chaiyapong and Jarimopas, 2007).
1.4. Sound and Ultrasound Properties
Sonic vibration occurs in the audible frequency range from about 20 Hz to about 15kHz.
An object vibrates at sonic frequencies when excited either by means of free vibration or
forced vibration. The object resonates at particular frequencies at which the amplitude is at
peak. The resonant frequencies as vibration characteristics are governed by elasticity, mass,
geometry and density. Fruit and vegetables also behave similarly when caused to vibrate.
A number of tropical fruits are evaluated for their internal quality by tapping and
listening to the generated sound. The ripeness or maturity level is judged from the pitch of the
sound. Experienced graders generally are very accurate in relating sound to ripeness and
maturity level. As a result, over the past 15 years, much research has been conducted into
objectively using sound production to predict maturity, especially with regard to durian and
pineapple. In such sound measurement experiments, fruit are caused to show a sonic (or
acoustic) vibration.
Initial research into modeling forced vibration in order to study vibration characteristics
of fruit was initially conducted by Abbott et al. (1968). They subjected apples to an acoustic
range of frequencies by a mechanical exciter. A series of resonant frequencies was displayed
and the second resonant frequency was found to be related to flexural vibration. The apple
mass and its firmness influence the second resonant frequency. The stiffness coefficient f2m
(where f was the second resonant frequency and m was the mass) was formulated to
compensate for the difference in mass. This stiffness coefficient was later corrected in terms
of dimension by Cooke (1972) as f2m2/3.
Following this, Yamamoto et al. (1980) modeled the free vibration mode of vibration for
watermelons in the early 1980s. They excited the fruit to vibrate freely by hitting it with a
wooden ball pendulum and recording the produced sound. Watermelon firmness indices
expressed as functions of the resonant frequency, mass, and density were correlated with
firmness and sensory scores.
Comparing the forced vibration to the free vibration in terms of displayed series of
resonant frequencies, the lowest resonant frequency of the forced vibration is found to
represent the interaction between the fruit mass and the force induced by local deformation of
the fruit on the vibrator. While this may not be the case for the free vibration where a series of
resonant frequencies are detected (Chen, 1996), what is in common for both modes of
vibration is that they represent the mechanical properties of the whole fruit (Abbott, 1999).
Implementation of sonic vibration to detect tropical fruit qualities is mainly of the free
vibration configuration, which closely replicates the way the graders test the firmness of fruit.
Research into quality detection of tropical fruit thus focuses on the application of this sonic
vibration configuration. For example, Terdwongworakul et al. (1997, 1998) found that the
resonant frequency based function of durian decreases progressively in the days after full
bloom (figure 6 and figure 7). They established this by measuring the sonic vibration of Thai
durians developing on trees (all samples were allowed to continue growing on trees so that
the small variation in samples was maintained (figure 5)). The size difference was
compensated for by measuring the volume of each sample by the water replacement method
and taking into account the density-based mass of representative samples of each stage of
maturity.
Meanwhile, research conducted in Indonesia by Haryanto et al. (2001) attempted to
determine the acoustic properties of durian fruit which in daily farm practice are graded
252
according to the evaluation of multiple parameters. In 2006, Terdwongworakul and Neamsorn
studied the changes in stem strength related parameters and resonant frequency in association
with durian maturity, which is referred to as pulp dry matter percentage. They indicated that
the area under the force-deformation curve of the stem was most positively correlated with
the dry matter percentage at a correlation coefficient of r = 0.808. On the other hand, a
negative relationship was found between resonant frequency and dry matter percentage (r = 0.448). A multiple linear regression analysis indicated that the area under the forcedeformation curve and the resonant frequency could be used in linear combination at a
multiple coefficient of correlation of r (0.844).
Another fruit that is subject to acoustic measurement is pineapple. Boonmung et al.
(2006) have fused resonant frequency, firmness and soluble solid measurement by employing
artificial neural networks (ANNs) to evaluate pineapple internal quality. They successfully
developed ANN model that is able to classify pineapple into three classes at accuracy of more
than 83%.
Nondestructive forced vibration has also been proposed as a method for determining
maturity levels of durian. Kongrattanaprasert et al. (2001) applied mechanical oscillation to
durian samples at regions between the prickles located at the middle of the fruit, after which
they recorded the frequency response through the use of laser Doppler techniques.
Classification of durians into immature and mature categories using pulp dry matter
percentage as a reference index was achieved with 90% accuracy by means of finger printpattern matching of power spectral density.
Another method involves the use of ultrasonic waves, which interact with materials by
transmittance, reflectance, refraction or diffraction. Parameters which are successfully used to
evaluate the quality of horticultural produce are wave propagation velocity, attenuation and
reflection, although unsuccessful results have been reported when high-frequency 1 MHz
ultrasound is used to distinguish between damaged and undamaged apple tissue (Upchurch et
al., 1987). This is believed to be because the structure and air spaces in apple tissue block the
ultrasonic wave transmission, which in turn makes it difficult to obtain useful information.
The application of low frequency (50 kHz) ultrasonic on the other hand has been of some
successes in determining acoustic properties of certain fruits and vegetables (Mizrach et al.,
1989).
Attempts to use ultrasonic measurement to determine durian quality was first reported by
Budiastra et al. (1999), as shown in figure 8. Kongrattanaprasert et al. (2001) later performed
a series of data transformations, including wavelet transformation. The transmission
ultrasonic pattern eventually was matched with the reference finger print-pattern by
correlation and 95% accuracy in terms of classifying durian into different maturity levels was
achieved. Ultrasonic transmission measurement (figure 9) was also found to be useful in
classifying mangosteen (Nasution et al., 2005)
1.5. Light Properties
Appearance is the primary property of fruit and vegetables that consumers judge quality
by. A fruit or vegetable’s “appearance” is actually the information that is contained in the
light reflected back from the agricultural product. However, when a light beam illuminates an
agricultural product, only about 4% of the incident light is reflected at the outer surface as
regular or specular reflectance (figure 10). The remaining 96% of the incident energy is
transmitted through the surface into the cellular structure of the product, where it experiences
scattering in all direction at small interfaces and absorbance by cellular constituents (Birth,
1976). An optically dense product such as fruit or vegetable alters the path length traveled by
the light, which makes it difficult to penetrate due to the complex physical structure of
tissues. Thus, the majority of the light energy penetrates only to a very short distance before
being scattered back to the surface and leaving the fruit at the vicinity of the point of
incidence. This type of reflection is perceived as “color” and termed “body reflectance”.
According to Birth (1976), light must be transmitted through the pigment within the cells
in order to give a colored appearance. The remaining scattered light energy penetrates deeper
into the fruit tissues, diffuses, and is then absorbed by various constituents of the fruit. This
light energy eventually exits the fruit some distance away from the point of incidence and
carries useful chemical-related information of the fruit. This type of reflection, which varies
with the constituents and, the light wavelength and path length, is termed “diffuse
reflectance”.
The ripening of fruit is associated with color change. For example, bananas change from
green to yellow as they ripen, which is caused by the reduction in chlorophyll and the
resulting unmasking of carotenoid. An early experiment by Finney et al. (1967) using
spectrophotometric techniques to measure color changes in banana peel showed that the color
change is related to flesh firmness.
Birth et al. in 1978 attempted to determine papaya maturity using a nondestructive optical
technique but reported unsuccessful results when attempting to differentiate immature papaya
from mature green papaya through evaluation of surface color (the degree of yellow-orange
coloration in a papaya’s flesh determines its maturity, with papaya changing color from white
to light yellow-orange to bright orange as it matures). This failure was because direct
transmittance (with the fruit between the source and the detector) provides inadequate signals
as a result of the characteristic shape of the fruit. However, by using a fiber optics system to
measure the transmittance of the papaya, Birth et al. (1978) obtained useful transmittance and
found high correlations between chlorophyll, carotene, and soluble solids concentration and
the transmittance at different stages of maturity.
A good example of optical characteristics application to evaluate firmness and
yellowness of mango can be found in the investigation conducted by Jha et al. (2006). In this
study, the authors measured the spectra of mango in the visual wavelength range 400–700 nm
using a handheld colorimeter in order to predict the firmness and yellowness index with
reference to maturity and ripening stages during growth and storage. The relative reflectance
was analyzed using comparative calibration models encompassing partial least squares
regression (PLS1 and PLS2), principal component regression (PCR) and multiple linear
regression (MLR). They showed that the PLS2 model derived from smoothed and
subsequently MSC treated spectra in the wavelength range of 530–550 nm provided the best
results. This in turn proves that color information obtained from the whole range of 530-550
nm provides a better nondestructive prediction model than information ascertained from just a
few wavelengths.
254
1.6. Near Infrared Properties
Matter molecules respond to near infrared (NIR) radiation in the wavelength range 700 or
770 to 2500 nm by vibrational absorption. They vibrate at fixed frequencies when energized
by radiation and therefore absorb light energy of that particular frequency or wavelength
(Mohsenin, 1984). Water, carbohydrates, fats and protein (i.e. functional groups that contain a
hydrogen atom e.g. OH, CH, NH) absorb light in the NIR region.
NIR spectra contain a large amount of useful physical and chemical information about
molecules. Nevertheless, this information cannot be always extracted from the spectra in
straightforward analysis. The difficulty of this information extraction is probably due to two
major reasons. One is that an NIR spectrum comprises NIR bands, which have their origins in
overtones and combinations of fundamentals. These bands strongly overlap with each other,
resulting in strong multicollinearity. The other comes from the fact that NIR spectroscopy
deals with real samples containing various components and thus yields poor signal-to-noise
(SN) ratio, baseline fluctuations, and severe overlapping of bands (Ozaki et al., 2007). The
NIR spectra are therefore normally broad and much weaker than IR bands. In addition, it is
often difficult to assign the NIR bands because of the overlapping of bands and complicated
combinations of vibrational modes.
Hydrogen bonding also causes a band shift for particular bands. For example, the NIR
band often experiences the problems of unwanted spectral variation and baseline shifts. The
sources of the variation and the baseline shifts may originate from 1) light scattering, 2) path
length variation causing poor reproducibility, 3) variations in temperature, density, and
particle size of samples and 4) various kinds of noises from a detector, an amplifier, or an AD
converter. The precise and proper spectral analysis of NIR spectra is needed in order to allow
extraction of useful information from NIR spectra to prevent incorrect interpretation.
Pretreatment methods of data are crucially important in NIR spectroscopy. Some of the
pretreatment methods encompass noise reduction, baseline correction, resolution
enhancement, and centering and normalization.
Near infrared spectroscopy has been used as a non destructive method for determining
the maturity degree of mango fruits Thai cultivars Nam Dokmai and Chok Anan (Mahayothee
et al., 2002). The reflectance spectra were collected in the integrating sphere using FT-NIR
spectrometer in the wavelength range from 650 to 2500 nm and the NIR spectra of the mango
were subjected to multivariate calibration techniques using principal component analysis
(PCA). The calibration model was validated using full cross-validation and it was found that
the ripening time and weight loss of both mango cultivars were highly correlated with the
reflectance of NIR illumination. NIR spectroscopy was also reported for the taste evaluation
of the fruit, with the mango being graded into four different groups: sweet-sour, sweet, sour
and tasteless (Saputra et al., 1995 and Susanto et al., 2000)
Application of NIR spectroscopy to another important fruit, mangosteen, has also been
investigated. The prediction of internal translucent flesh disorder in intact mangosteen fruit by
using short wavelength near infrared (SW-NIR) transmittance spectroscopy was investigated
by Teerachaichayut et al. (2007). In this experiment, the NIR absorption spectra of 193
mangosteen samples were obtained in the wavelength range from 640 to 980 nm on four sides
of each sample. The best result from a discriminant analysis for leave-one-out crossvalidation was 92.0% classification accuracy, with the results showing that the hardening
pericarp disorder influenced the accuracy of the classification.
1.7. Image Properties
Visual inspection by humans can be used to evaluate the quality of fruit and vegetables
provided that the external image is related to the quality of the produce. Accordingly, effort
has been invested in automating visual inspection in the form of a machine vision system, The
external features that can be analyzed by the machine vision system are usually color, shape
and defects, although in the past it was difficult to process the images and extract useful
feature information at an acceptable speed. However, due to the declining cost and increasing
speed of the hardware, the machine vision or image analyzing system has rapidly gained
popularity as an automatic sorting system. Research has mostly been conducted into the area
of optimum configuration in order to minimize unwanted features in the image, and also into
developing the efficiency of algorithms that extract the required information for further
analysis.
1.8. Recommended Future Research Directions
The preceding literature review has attempted to illuminate the factors responsible for the
high post-harvest loss of tropical fresh produce. We have argued as a result of this review that
the goal of producing tropical fresh produce at the standard required by local and export
markets demands greater understanding of the physical, mechanical, textural, electrical, light,
electromagnetic and sound characteristics of the produce.
Nevertheless, it appears that research into tropical fruit is still a relatively neglected area.
A count of papers returned on the academic search engine Google Scholar (April 2007) shows
that research into the physical properties of the dominant tropical fresh fruits (durian, longan,
mangosteen, mango, young coconut, pineapple, pumelo, rambutan, rose apple, dragon fruit)
and related nondestructive analysis techniques occurs at a level that is at 21% (≅ 233) of that
conducted into fruits such as apples, peaches and pears. Similarly, research into dominant
tropical vegetables such as egg plant, snake egg plant, Chinese radish, chilli, Chinese
cabbage, cabbage, kale, water morning glory occurs at a much lower level (7.7%) that
applied to tomatoes, potatoes and carrots (≅ 298). More research into tropical fruit and
vegetables will help define mechanisms and thresholds with regard to the variety of produce,
property, physical, physiological and breeding factors, which in turn will help lead to the
development of new post-harvest techniques and machinery as well as new ways to make use
of under-grade or culled produce.
Accordingly, a desired-for trend in research into tropical fruit and vegetables is for an
increase in knowledge of fundamentals relating to a) their physical, mechanical and bruising
properties in order to support mechanical sizing, conveying, handling, packaging and
associated machinery, b) non-destructive properties in order to support high precision sorting,
sizing and the associated machinery, c) textural properties in order to support breeding
development, and the food product related to the fresh produce out of the export marketing
quality. Research into the non-destructive properties should be informed by grower
experience (for example, the identification of watermelon and pineapple maturity by sound
(Boonmung et al., 2006; Kawano, 1994) which has led to the commercial development of a
watermelon maturity sorting device), while the bulk of future inquiry should be directed
256
towards those tropical fresh fruit and vegetables which are well known and accepted by
foreign markets (namely baby corn, okra, egg plant and chilli).
Table 1. Post-harvest loss of mangosteen fruit at wholesale level
Post-harvest Loss (%)
Fruit cracking
Hard rind
Rough surface
Internal defects
Translucent flesh
Gummosis
Translucent flesh and Gummosis
Decay
Chantaburi
1.2
0.8
37.2
Chumpon
1.3
3.3
59.9
average
1.3
2.1
48.6
14.6
10.0
4.6
1.6
15.0
12.0
8.5
1.3
14.8
11.0
6.6
1.5
Table 2. Physical characteristics of large, medium,
small and undersize mangosteen fruit
Physical characteristics
Weight (gm)
Volume (cm3)
Maximum diameter of fruit (mm)
Minimum diameter of fruit (mm)
Diameter of calyx circumscribing circle
(mm)
Height of fruit with stem end (mm)
Height of fruit without stem end (mm)
Dimension ratio
Large
102
105.2
60.3
57.9
51.8
Medium
81
80.3
56.0
54.4
47.8
Small
65
66.9
51.4
49.9
49.6
Undersize
44
44.6
44.4
43.3
47.4
65.5
51.7
0.86
63.6
48.3
0.85
59.6
43.1
0.96
55.0
37.2
1.06
Table 3. Statistical mechanical properties of Nam Dokmai
Mango with the variation of maturity and point of loading application
Point of
loading
application
1
2
3
4
5
•
Rupture
force (N)
70.43±
8.72 b*
60.77±
10.88 c
65.56±
12.31 cb
59.66±
4.47 c
82.35±
5.86 a
Mature
Rupture
deformation
(mm)
5.64±
0.59 c
7.05±
1.04 b
8.80±
1.21 a
5.33±
0.81 c
5.76±
0.77 c
Slope
(N/mm)
14.42±
1.32 b
10.78±
1.09 c
9.62±
1.52 c
12.90±
2.10 c
16.01±
0.39 a
Rupture
force (N)
7.14±
0.65 a
5.97±
0.84 b
6.52±
0.91 ab
6.96±
1.00 a
6.87±
1.06 a
Ripe
Rupture
deformation
(mm)
5.00±
0.58 ab
4.23±
0.65 c
5.35±
0.90 a
4.68±
0.69 cb
4.29±
0.73 c
Slope
(N/mm)
1.34±
0.14 a
1.42±
0.32 a
1.38±
0.18 a
1.41±
0.19 a
1.48±
0.20 a
Means followed by the same letter in the same column are insignificantly different at p < 0.05.
Table 4. Physical characteristics of Sitong and Srichompoo sweet tamarind pod
Cultivar
Sitong
Srichompoo
Physical characteristics
Weight (g)
Width (cm)
Length (cm)
25.14 ± 4.88
16.48 ± 2.72
16.08 ± 2.62
11.80 ± 2.65
2.43 ± 0.15
2.16 ± 0.11
Thickness
(cm)
2.09 ± 0.12
1.76 ± 0.09
Specific gravity
1.0093 ± 0.0120
0.9980 ± 0.0033
Table 5. Statistics of slope and firmness index of Sitong
and Srichompoo sweet tamarind pod with maturity variation
Cultivar
Sitong
Firmness Index (m/s3)
0.242a
0.217a
0.224a
0.169b
Maturity
Immature
Mature
Immature
Mature
Srichompoo
Slope (N/mm)
1.095a
1.074a
0.764b
0.689b
* Means followed by the same letter in the same column of a particular cultivar are insignificantly
different at p < 0.05.
Table 6. Statistics of slope of sweet tamarind pod with different surface profile (N/mm)
Cultivar
Sitong
Concave
17.04b
Convex
22.93c
Srichompoo
Concave
10.92a
Convex
12.23a
* Means followed by the same letter in the same row are insignificantly different at p < 0.05.
Table 7. Poisson’s ratio and Young’s modulus of selected tropical vegetables
Vegetables
Snake Egg
plant
White Long
radish
Poisson’s ratio
Axial
sample
0.252±0.082
Transverse
sample
0.166±0.047
0.444±0.07
0.384±0.08
Young’s modulus (E)
(Equation of E with respect to storage time t) (MPa)
Radial compression
Die loading
Fruit axis
Transverse axis
Fruit axis
ER,T=0.531e-0.04t
ED=0.524e-0.07t
ER,a=0.476e-0.03t
2
2
(R =0.81)
(R =0.95)
(R2=0.99)
ER,a=9.05e-0.08t
ER,a=8.66e-0.08t
ER,a=3.07e-0.084t
(R2=0.99)
(R2=0.95)
(R2=0.94)
Table 8. Statistics of coefficient of friction for each
combination of produce and contacting surface
Produce
Lime
Tangerine
Guava
Friction
coefficient
Cs
Ck
Cs
Ck
Cs
Ck
Contacting surface
Galvanized sheet
metal
0.39± 0.021a*
0.37± 0.020a
0.60± 0.054a
0.51± 0.047a
0.85± 0.12a
0.79± 0.120a
Plywood
Plastics
0.44± 0.062a
0.41± 0.078ab
0.61± 0.086a
0.56± 0.083a
0.92± 0.084a
0.87± 0.070a
0.55± 0.049b
0.50± 0.030b
0.91± 0.12b
0.89± 0.150b
0.91± 0.092a
0.83± 0.081a
* Means followed by the same letter in the same row of the same friction coefficent type are
insignificantly different at p < 0.01.
258
Table 9. Average values of rolling angle (degree) for each
different combination of produce and orientation
Produce
Orientation
Opposite stem side
21.30± 0.79c*
20.88± 0.59c
20.81± 0.85c
Lime
Tangerine
Guava
Stem side
13.44± 0.54b
13.36± 0.77b
16.01± 0.19b
Cheek
6.90± 0.85a
8.22± 0.15a
11.54± 1.51a
* Means followed by the same letter in the same row are insignificantly different at p < 0.01.
Table 10. Coefficients of static friction of normal and rough surface mangosteen fruits
Description
Normal surface fruits
Longitudinal axis
Transverse axis
Rough surface fruits
Longitudinal axis
Transverse axis
Plexiglass
Plywood
Galvanized steel
0.4553f
0.4553f
0.3663c
0.3772cd
0.3340b
0.3371b
0.3058a
0.3324b
0.3804cde
0.3915de
0.3762cd
0.3965e
* Means followed by the same letter are not significantly different at probability < 0.05 according to
Duncan’s multiple range test.
2
4
1
5
3
Figure 1. Illustration of “Nam Dokmai” mango with points of loading application ( 1- Cheek, 2-Head, 3-Tail,
4-Bottom edge, 5- Top edge).
a) Srichompoo
b) Sitong
Figure 2. Sweet Tamarind.
Figure 3. Theoretical contact loading.
Moistened sand
Figure 4. Plunger compression test with moistened sand supporting fruit sample.
260
FFT ANALYZING RECORDER
SOUND LEVEL METER
DURIAN
Figure 5. Instrumentation configuration for measuring the acoustic vibration of durian.
Exponentia Index
3000000
2500000
2000000
M1
M2
1500000
M3
1000000
M4
M5
500000
M6
0
40
50
60
70
80
90
100
110
120
130
140
Number of days after blossom
Figure 6. Change of resonant frequency index or exponential index, 2/3f2ln(m) (where f is the resonant
frequency and m is the mass) with number of days after blossom.
Stiffness coefficient
60000000
50000000
40000000
30000000
M1
20000000
M2
M3
10000000
M4
0
M5
40
50
60
70
80
90
100
110
120
130
140
M6
Number of days after blossom
Figure 7. Change of stiffness coefficient f2m2/3 (where f is the resonant frequency and m is the mass) with
number of days after blossom.
Ultrasonic tester
Digitizing
oscilloscope
PC Lab. card
Personal
computer
T
R
Figure 8. Ultrasonic instrumentation setup for durian ultrasonic measurement (Budiastra et al., 1999).
262
Ultrasonic tester
Digitizing
oscilloscope
PC Lab. card
Personal
computer
Figure 9. Experimental setup for nondestructive evaluation for mangosteen quality using ultrasonic wave
(Nasution et al., 2005).
Incident light
Regular reflectance
Body reflectance
Absorbance
Transmittance
Figure 10. A simplified schematic representation showing the interaction between light and a fruit.
2. INNOVATIONS OF TROPICAL FRESH PRODUCE MACHINERY
2.1. Durian Maturity Sorting Device
Production of fresh durian always encountered the problem of fruit contaminant, i.e.
matured fruit contaminated with the immature fruit intentionally or unintentionally. The
production of quality fruit for export requires detection and segregation of the immature out
of the mixture. Recently, Chawapradit et al. (2000) developed the durian maturity sorting
device.
2.1.1. Concept of the Design
Three points of view supported the design of the durian maturity sorting device, i.e. a) the
natural frequency fn of durian decreased as the fruit was getting matured, b) consistency of fn
was dependent on the consistency of the knocking area of durian surface, c) double knock
was undesired, only one knock was required for a test.
2.1.2. Design and Operation
Figure 11 showed the durian maturity sorting device comprising 50 cm x 70 cm steel
frame with two floors and the knocking mechanism. The knocking mechanism consisting of
teflon head and pneumatic solenoid valve was installed in the second floor in the middle of
the durian maturity sorting device. The teflon head hit the durian from the bottom. The teflon
head restored to its original position by gravity after switch was shut to prevent double
knocks. The durian fruit was placed on top of the frame on A and B stands, resulting in the
contact c and d. The fruit weight deformed stand spring so that the fruit lowered and
contacted metallic plates beside at a and b, giving rise to consistent knocking area regardless
of durian size. The knock was controlled by pneumatic solenoid valve. The knocking sound
was transmitted through microphone, converted to electrical signal, processed through the
signal conditioning circuit and analyzed by computer program. The natural frequency of each
durian fruit was recorded and implemented for maturity separation. fn of the mature durian of
120 days after pollination ranged from 600 to 720 Hz.
2.1.3. Performance Evaluation
Performance test indicated that the durian of maturity difference less than 7 days
contributed the sorting error of about 15%. For the durian of maturity difference more than 7
to 14 days, the sorting error was zero. The practical unit consists of 2 durian maturity sorting
devices connected to conveyor and controlled by 2 operators to place and remove durian fruit
interchangeably and continuously. The system capacity amounted to 1,500 fruit or 6 tons per
hour.
2.2. Mangosteen Sizing Machine
Mangosteen is a locally prized tropical fruit. Despite its importance, sorting of the fruit
for local and export consumption has largely been manual and inefficient. There are two main
sizing systems currently being used. The first is a tangerine mechanical sizer that uses
264
perforated cylinders to sort the fruit. However, this method is not appropriate for sizing
mangosteens because of the fruit’s large calyxes, which puts the fruit at risk of getting stuck
in circular holes. Due to the absence of appropriate commercially available sizing machinery,
mangosteens therefore have been historically sized by weight, not by dimensions. One
commercially available mangosteen sizing machine of this type features 10 kg load cells and
microcomputer control and weighs fruit dynamically in a continuous packing line.
Nevertheless, there are many disadvantages in this approach, including high initial and
operating costs and complicated maintenance procedures.
A desirable mangosteen sizing machine is one that uses the diameter of the fruit body as
sizing parameter. This is because mangosteen does not have a spherical appearance despite
having a large calyx, and thus rather spherical bodies. The basis of design features a rotating
conical-shape disk and a metering board with gaps of increasing size arranged along the
periphery of the disk (figure 12). Mangosteens are fed onto one section of the rotating disk
and the combined centrifugal and gravitational force moves the fruit toward the periphery
until contact with the metering board is attained. The tangential force then rolls the fruit along
the metering board, where they are sized and allowed to drop through gaps according to their
dimensions.
The mangosteen sizing machine (figure 13) comprises a rotating disk, a sizing board, a
feeding tray, receiving trays, and a power drive, all attached to a steel frame, which rides on
four small wheels. The frame is 820 mm wide by 820 mm long by 960 mm high and made of
40 mm by 40 mm steel L-beams. The rotating disk is made of 9.5-mm thick steel plate and is
600 mm in diameter. The top surface is formed into a conical shape with a 10 degree slope,
which allows the fruit to roll down to the sizing gaps by gravity. The center of the disk is
connected to a 50-mm diameter steel shaft which is driven by a 187 W, 220 V electric motor
through a 1:40 gear reducer and pulleys. Above the edge of the rotating disk is a 50 mm wide
by 6 mm thick vertically adjustable steel sizing board curved along the disk circumference.
The feeding and receiving trays are made of 1.0-mm thick steel sheet while the rotating disk,
the sizing board and the feeding and receiving trays are all lined with 3 mm thick rubber foam
to protect the mangosteen from mechanical damage. The factory prototpe contained a 400
mm feed opening. In operation, mangosteens are continuously poured onto the feeding tray
and then rolled down onto the rotating disk in clusters of 6 to 10 fruit at a time. Each fruit is
then brought into contact with the sizing board and the rim of the rotating disk through
gravitational and centrifugal forces. The fruit move along the sizing board and drop down to
the receiving tray whenever the diameter of the fruit is less than the sizing gap. Small fruit
thus will be sized before big fruit.
The disk diameter, disk speed and type of metering gap significantly affected the sizing
performance. The most efficient configuration of the factory prototype was a rotating disk
speed of 21 rpm using a step-type metering gap, resulting in sizing error of 22.8%, and
capacity of 1,026 kg/hr with minimal fruit damage (0.48%). The tested machine showed
better performance than currently existing commercial models (sizing error of 44% and
capacity of 500 kg/h) and manual sizing (153.4 kg/h with error of 33.4%). An engineering
economic analysis showed that the break even point and pay back period for the factory
model would be 46,020 kg/yr and 6 ½ months, respectively. (Jarimopas et al., 2007a)
2.3. Semi-Automatic Young Coconut Fruit Trimming Machine
Young coconut is one of the most popular fruit varieties. The edible parts include the
sweet juice at the core of the fruit and the soft flesh attached to the inner surface of the shell.
The juice contains glucose, vitamins, hormones and minerals, and is widely considered to be
a refreshing drink. The flesh contains carbohydrates, calcium and phosphorus, and is
commonly used in desserts (Pechsmai, 2002). Young coconut is the immature fruit of coconut
palms, which can be easily grown in South East Asia. The trimming process is manually done
which, required skilled labor, and is extremely hazardous. Currently, workers must shear the
husk off the green fruit with a long sharp knife. The inner white husk is then finely sheared to
form a conical shaped top, a slightly tapered cylindrical body, and a flat base. The final shape
has a pentagonal profile (figure 14) After it has been trimmed, the fruit is dipped into a
sodium metabisulfide solution to prevent surface browning. The shortage of experienced
labor and the high production cost has created an urgent need for mechanical trimming
machines.
The prototype is based on the lathe cutting machine mechanism. The principles
underlying the design were: i) the final product must have a pentagonal shape ii) the trimming
mechanism must be based on the lathe cutting technique iii) the construction must be rugged,
compact and transportable, iv) the mechanism must be uncomplicated, strong and must resist
vibration, v) it must be capable of being operated by one person.
The machine comprised: a) power transmission, b) control, c) shoulder and body knives,
d) base cutter, e) fruit holder, f) crest holder and, g) shaft holding pedicel (figure 15). In
operation, a young fruit was first firmly mounted between the crest holder and the shaft
holding pedicel, so that fruit axis was aligned with horizontal line. The fruit was rotated and
then trimmed by the body knife. Next, the fruit holder was manually fastened to the trimmed
body, while the crest holder was pulled away from the fruit to its retracted position. The
shoulder knife then trimmed the fruit until a sharp crest was achieved. A foam rubber pad
covered the crest, and the crest holder again held the fruit by pressing against the padded
crest. Next, the fruit holder was opened and the trimmed fruit rotated. Finally, the base knife
descended to cut the fruit base, producing the complete trimmed fruit. The finished fruit was
then dipped in sodium metabisulfide solution to prevent browning.
The two angles in orthogonal planes of shoulder knife (γ,α1), the two angles in
orthogonal planes of body knife (α2,β), the trimmed fruit speed significantly influenced the
trimming performance. The appropriate operating conditions were: shoulder knife γ = 560, α1
266
= 610, body knife β = 760, α2 = 610, trimmed fruit speed = 300 rpm. The corresponding
trimming performance was 21 fruit/h, untrimmed green area of 1.1% , remaining fibrous area
of 0.2%. The sample to be trimmed had to be uniform size and shape and newly-harvested
(Jarimopas et al., 2007b).
2.4. Semi-Automatic Young Coconut Fruit Opening Machine
The young coconut fruit that was already trimmed needed opening for consumption
because the edible part of both flesh and juice was inside the fruit shell. Opening of the
trimmed coconut is traditionally obtained by manual impact cutting with big sharp knife. The
cutting process was much likely to endanger the operator and juice was usually spilled off.
Besides, the appearance of opening looks unclean and not neat. Hence, the semi-automatic
young coconut fruit opening machine was developed to achieve safe, nice, clean and fast
opening with minimum loss.
Jarimopas et al. (1989) comparatively investigated three mechanism of opening the
trimmed young coconut, i.e. impact, shearing and cutting. The cutting was the proper means
mechanically opening the coconut because easy and complete opening with little spilled-off
juice was obtainable. Based on this mechanism, the trimmed young coconut can be cut open
by moving two rigid sharp knives in the same horizontal plane toward each other cutting the
stationary coconut placed in between.
The machine comprised two triangular stainless steel sharp knives (figure 16). Each knife
was fixed to the two shafts with thread on their surface at the left and the right sides. The
threads of each half of each shaft were in opposite direction to drive the knives traveling
toward each other. The shafts were driven by gears and ¼ hp 220 v electric motor with switch
to turn on, off the machine and to control forward and rearward travel of the knives. There
was an adjustable platform in the middle of the machine to support the varying size of
trimmed young coconut. In operation, the trimmed young coconut was first placed on the
adjustable platform. The operator would adjust the platform vertically so that the coconut
could be cut open with sufficiently wide opening. The machine was then switched on to move
the knives forward to completely cut open the coconut and to move the knives backward. The
machine was turned off and the open coconut was removed.
The opening machine could open the trimmed young coconut including the big, medium,
small sizes (117 mm ≤ fruit height ≤ 137 mm) at the average opening time of 8.5 sec/fruit
with the spilled-off juice about 4.7% and opening width of about 80 mm. Juice and flesh was
clean and well acceptable (Jarimopas and Pechsmai, 2001). It was not commercialized
because it was noisy. Besides, the cutting knives sometimes got stuck during cutting and the
design did not look safe enough for operator.
2.5. Young Coconut Fruit Opening Device
As mentioned earlier of the necessity of opening the trimmed young coconut,
Supsomboon (1998) invented the young coconut fruit opening device.
In this case, the device was so designed to be handy and for one usage to support personal
consumption. Opening mechanism is sawing.
The device comprised a metallic rectangular strip one long side of which featured lots of
teeth of saw; plastic holder to hold the strip ; and a plastic knife (figure 17). To open the
trimmed young coconut fruit (figure 14), the plastic holder with the strip underneath was put
over the crest of the fruit, manually pressed and turned around to and fro. The teeth of the
strip sheared the mesocarp and shell till rupture, the young coconut was then open. The
plastic knife facilitated opening in case of incomplete cut.
Testing the opening device revealed that it took 41.4 seconds to open a trimmed coconut
with spilled-off juice of 3.8%. Some sawdust of mesocarp and shell was found in the juice
(Jarimopas and Pechsmai, 2001). The device has already been patented.
2.6. General Purpose Coconut Dehusking Machine
Ripe coconut fruit is extensively used for fresh consumption and cooking of various
dishes in many countries. In order to utilize the coconut it must be first dehusked to get the
fruit enclosed with shell (figure 18). Then, the shell of the fruit will be so cracked that the
white firm flesh can be scratched into small pieces. Next, the small pieces of white flesh with
some water will be squeezed to get coconut milk for further cooking. The dehusking was
traditionally practiced with sharp knife and strong labor. Nature of the work is dangerous and
indeed requires the replacement of machine. Kwangwaropas and Sukjareon (1997)
recognized the problem and developed the general purpose coconut dehusking machine.
Coconut growers manually dehusk the ripe coconut mesocarp by tearing. A knife was
impact cut first longitudinally to partition the mesocarp, then the partitioned mesocarp was
removed by tearing. The developed machine featured the mechanism imitating the manual
tearing.
Figure 19 showed the general purpose coconut dehusking machine consisting of frame,
two 105 mm dehusking rollers, polishing brushes, power and transmission system. The frame
was made of welded steel construction. The dehusking rollers featured 6 fins welded to roller
surface and inclined to roller axis like spiral. The roller rotated at 49 rpm. The polishing set
consisted of two shafts each of which had eleven 175 mm diameter by 25 mm thick steel
268
brushes. The general purpose coconut dehusking machine was powered by a 2 hp, 220 v
electric motor. The power was further transmitted by chain driving the dehusking rollers and
brushes. In operation, the dry ripe coconut was first put onto the operating dehusking rollers
with the lid closed. Vertical compression at the lid plus friction force of the roller fins caused
pressing and pulling a portion of husk (or dry mesocarp) out of the shell. The rotating rollers
turned the coconut as simultaneously as they repeated tearing other portions of husk. It took
5-8 seconds to complete dehusking. The dehusked fruit further rolled by gravity due to
slightly inclined setting of the machine to polishing brushes. It took 8 seconds to get the
dehusked coconut completely polished.
Mechanical dehusking process could be averagely fulfilled in 4.8 seconds/fruit. Power
consumption for dehusking and dehusking plus polishing was 1.77 and 0.82 hp respectively.
The machine could make complete dehusking. The machine could further dehusk fresh
coconut satisfactorily and spent dehusking time as similarly as the machine did with the dry
ripe coconut. The machine has already been patented.
2.7. Unripe Durian Cutting Machine
Exporting fresh durian is nowadays performed under standard (Office of Thai
Agricultural Commodity and Food Standard, 2003). The mature durian fruit that does not
meet size, shape and internal defect standard is a lot. Since its internal quality is good, an
alternative to make value added to the under grade durian is needed, at least to save the
income of the fruit growers. The durian, normally harvested mature and unripe, is very firm
and tough. Moreover, its surface is full of sharp thorns. A strong and skillful man with sharp
knife can cut and open it. The fried raw flesh of durian has been successfully accepted in
several markets.
Opening durian fruit was accomplished by hydraulic cutting in vertical plane with
alignment to fruit axis and section wall.
Figure 20 showed the unripe durian cutting machine comprising 38 mm x 38 mm x 3 mm
rectangular steel frame welded construction, 9x18x0.3 cm typical stainless steel knife, 2direction hydraulic system with 35 cm stroke, 0.75 kw 220 V electric motor. The stem of an
unripe mature durian fruit was first cut off. Then, the durian fruit was mounted to the unripe
durian cutting machine at its center with the fruit stem pointing upward. The knife was
hydraulically moved down to touch the fruit axis while the knife edge was aligned along a
section wall. Next, the knife was switched on to move through to cut the fruit and then the
knife went up to repeat cutting the next section. The operator controlled the cutting at his foot
on the paddle switch. Cutting control was attained semi-automatically by the hydraulic
system with the operator manually rotating the fruit to set alignment.
The 95 kg unripe durian cutting machine, requiring one operator, was capable of cutting
the unripe, mature “Hmontong” durian fruit at the capacity of 350 kg/hr with flesh loss of
1.6%. A strong and experienced man could succeed durian cutting of 80 kg/hr. Electrical
power consumption was 540 watt-hour. Economic analysis indicated the cost of mechanical
cutting durian was approximately 1.5 USD/ton with the payback period of 0.63 year.
2.8. Baby Corn Husking and Flesh Separating Machine
In the early 1970s, Thailand was the first country to seriously start cultivating baby corn.
Since then Thailand has become known as an exporter of baby corn. Production of baby corn
is on a steadily increasing trend and thus making Thailand among the world leaders in baby
corn production. At present, exporters are faced with the problem of insufficient supply of
fresh baby corn cob when demand is high. Lack of skilled workers to husk the corn is a major
factor. There have been a number of researches that attempted to develop the baby corn
husking machine. The recent development of baby corn husking and flesh separating machine
is reported as follows.
The baby corn husking machine was designed based on the following physical property
relationships. Terdwongworakul and Suppattakul (2005) investigated the relationship
between the ear thickness and the ear diameter with the purpose to obtain the basis for the
design. The relationship was such that as the diameter of the ear increases from the silk end
(starting at the flesh tip inside), the ear husk is thinner. The relationship is consistent up to the
point where the ear diameter is greatest. Then from the greatest diameter point to the stem
end, the relationship is reversed as depicted in figure 21. That is the ear diameter relates
positively with the ear husk thickness.
This relationship governs the design of the cutting mechanism. The cutter of the
mechanism has to be designed to cut through the silk end and just makes slice trace along the
husk contour up to the stem end. The cut at the silk end opens the husk and such initiates the
cut path from which the subsequent husking operation will be able to remove the husk. The
husk will be torn aside by the husking rollers subsequently. The other useful relationship
depicts that the greater the maximum ear diameter the greater the ear thickness (figure 22).
This means the baby corns must be graded according to their biggest ear diameter prior to
being loaded into the husking machine to control the consistency of the thickness.
The husking machine consists of four main components (figure 23): a pair of feeding
rollers, a cutting mechanism, a pair of conveying rollers, and a pair of threaded husking
rollers. The feeding rollers have V-shaped groove at the middle to accommodate for varying
ear size. An ear is fed manually through the V-shaped groove and the rotating action of the
rollers forces and feed the ear to enter the cutting mechanism. The four-bar linkage cutter is
designed based on three coupler position synthesis. The coupler of the linkage is the cutter of
the mechanism. The ear is cut as it moves forcibly by the feeding rollers. The ear silk end is
270
cut through whereas along the ear contour, the husk is sliced open by the controlled action of
the four-bar linkage cutter. The conveying rollers ((C) in figure 23) pulls the cut ear from the
cutting mechanism and at the same time acts to feed the ear into the husking rollers ((D) in
figure 23) as showed in figure 24.
The husking action of the husking rollers is controlled by a cam operation. The threaded
husking rollers comprise the first and second husking rollers, each of which is made left-hand
threaded and right-hand threaded to the center, respectively. The two-way thread on the roller,
when rotating, will grip the husk and silk and take them from the center towards both ends of
the roller promoting the tearing and separating actions. In action, the first roller rotates
statically whereas the second roller will epicycle around a shaft of the first roller. Figure 25
illustrates the sequential action of the threaded husking rollers. The plane of the husking
rollers initially is vertical making the first roller be on top of the second roller in order to be
ready for receiving the silk end into the gap between the rollers. As soon as the silk end is
captured by the teeth of the husking rollers, the cam will make the plane of the rollers turn to
the horizontal position. The husk and silk are not only pulled towards ends of the roller but
also pulled through the gap or downwards as presented in figure 25.
The flesh is forced to move ahead over the rollers and thus separated from the husk and
silk simultaneously. When finished, the timer of the controller will terminate the cam action
and let the husking roller be back to the original position or the upright position. The machine
is therefore ready for the next ear to be fed and separated from the husk.
The tests performed to evaluate the performance of the machine showed that the
separation efficiency is 84.0% with the obtained flesh without husk attached to the flesh
(Terdwongworakul and Suppattakul, 2005). The silk remaining on the flesh accounts to
approximately 1.7%. However, each ear takes about 30 seconds for the complete operation.
The husking time could be reduced by improvement on the husking operation.
2.9. Recommended Research Trend
So far there has been serious shortage of several appropriate machinery a) supporting
certain postharvest operations to produce standard tropical fresh perishables, b) facilitating
eating the fresh produce, and c) supporting production of the undergrade produce to get value
added product. Durian, mangosteen, longan, pumelo, pineapple, mango, rambutan, rose apple
are either well-known tropical fruit or are gaining popularity in the world market. Hundreds
of million people in this planet are suffering nutritional deficiencies that the nutrition
ingredients they need prevail in the tropical fresh produce.
Table 11 listed the unavailability of machinery relating the postharvest process and fruit.
Trend of the research should direct mostly to the development of the sorting and sizing
machine. The machines are rather selective for fruit. Mechanical sizer, characterized by 3
grade sizing (small, medium, large), approximately 20% error, and 1-4 ton/hr capacity, is
primarily recommended to be developed to support those tropical fruit. The mechanical sizer
is basically rugged, easily repaired, has low cost that suits grower income in the developing
and under developed countries. The mechanical sizer can well support the production of
tropical fresh product to local markets and supermarkets. This engineering means will
perhaps lift up the quantity and standard of production to a certain extent. The perforated
cylindrical sizer for tangerine in Thailand is a distinct example. More than 600 perforated
cylindrical sizers widely support the tangerine becoming the basic fruit distributed in every
local market and supermarket (Jarimopas, 2006). However, the development of hi-technology
sorting machine with built-in sizer should be developed in parallel because exporting
production required high standard (error 5-10%) that the mechanical sizer cannot perform.
Besides, the hi-technology sorting machine will use less space in the packing line, rendering
the shorter line and the lower cost for exporting production.
Development of proper packing line integrating the sizing, sorting machines to other
conventional postharvest machinery like, washing, surface drying, weighing machines is also
required for cooperatives to support the quality fruit production for local market and export.
Introduction of the packing line featuring machinery and a small number of experienced
operators to replace that featuring a lot of labour is essential. This is because the problem of
worker shortage and expensiveness is invading the countries producing fresh produce.
There are several tropical fresh fruits that are strange to foreigners. The edible part is
inside the fruit whose peel is too hard to manually open. To promote eating and marketing the
fruit the device or machine facilitating eating tropical fresh fruit must be developed.
Appropriate machinery should be based on ease of use, inexpensiveness, sufficient efficiency,
easy maintenance, and minimum damage.
Table 11. Recommended trend of research and development of
postharvest machinery of tropical fresh fruit
Fruit
Durian
Postharvest machinery of tropical fresh fruit
Sorting
Sizing
Eating facility
U
U
Longan
Mangosteen
U (Device sorting
internal defects is
unavailable)
U
U
U
A
Not necessary
U
Mango
Pineapple
Young coconut
U
U
U
A
U
U
Not necessary
U
A
Pumelo
U
U
U
Rambuttan
U
U
U
Rose apple
Dragon fruit
U
U
U
U
Not necessary
Not necessary
Note : U = Unavailable ; A = Available ; Uf = undergrade fruit.
Management
of
Undergrade fruit
There
is
unripe
durian
cutting
machine
Dryer
Undefined process of
Uf
Local market
Feed stuff factory
Uf
Uf
Uf
Local market
Local market
272
Fruit
Figure 11. Durian maturity sorting device.
Figure 12. Sizing concept.
Figure 13. Mangosteen sizing machine (1 frame ; 2 feed opening ; 3 rotating disk ; 4 receiving tray ;
5 metering gap).
Figure 14. Young coconut fruit: (I) untrimmed, (II) trimmed.
Figure 15. Semi-automatic young coconut fruit trimming machine; (1 fruit holder ; 2 shoulder knife ; 3 body
knife ; 4 base cutter ; 5 control switch ; 6 electric motor drive).
274
Figure 16. Semi-automatic young coconut fruit opening machine.
a) 1 = metallic strip with plastic holder
2 = plastic knife
Figure 17. Young coconut fruit opening device.
Figure 18. Intact dry mature coconut fruit (left) with husk, (right) dehusked fruit.
Figure 19. General purpose coconut dehusking machine.
276
Figure 20. Unripe durian cutting machine.
Figure 21. The relationship between ear diameter and ear husk thickness. The starting end of the arrow
represents the silk end of the ear being pertinent to the flesh tip inside.
Figure 22. The relationship between average ear husk thickness and maximum ear diameter.
Figure 23. Baby corn husking and flesh separting machine consisting of (A) a pair of feeding rollers, (B) a
cutting mechanism, (C) a pair of conveying rollers, and (D) a pair of threaded husking rollers.
278
Figure 24. The operation of the baby corn husking and flesh separating machine consisting of a) feeding
rollers forces the ear into the cutting mechanism, b) the ear is cut along the contour by the cutting mechanism
and the conveying rollers feeds the cut ear into the husking rollers, and c) the ear husk is being separated by
the duhusking rollers.
Figure 25. The sequential action of the threaded husking rollers.
3. PACKAGING OF TROPICAL FRESH PRODUCE
Packaging of tropical fresh produce covers packaging for distribution and for extension
of the produce shelf life. The content of this aspect is divided into three topics, namely the
present status, interior packaging management, and edible film development.
3.1. Present Status
Packaging for distribution accounts for wholesale and retail packaging. For a certain
developing country like Thailand, typical wholesale packaging for fresh produce was kheng,
plastic bag, crate and corrugated box (Jarimopas, 2006). Figure 26 showed kheng which was
made of either bamboo or plastics. The bamboo kheng could carry load of 4 to 200 kg,
depending on size, design and quantity of bamboo used. Kheng is cheap, irreusable and easily
deformable when loaded. Because of its shape like frustum, stacking is impractical because
the upper kheng will damage the produce of the lower kheng. This renders inefficient
utilization of the truck space during transit and transportation cost cannot be reduced. Related
weight, capacity and compressive resistance were given in table 12. Due to wide availability
and inexpensiveness, plastic bag is popularly used for packaging fresh fruit and vegetables.
Instead of protection, the plastic bag rather collect produces in a place to ease handling and
shipping because its structure is thin plastic laminar which is not rigid. The produce
contacting the bag could be easily exerted by external force and consequently damaged.
Besides, the produce inside the bag could be further pressed in chain through contacts of
neighboring produces resulting additional damages. Based on plastics design, the plastics of a
bag was either uniform laminar or net with holes or without holes (figure 27). Based on
construction material, the plastic bag is made of linear low density polyethylene (LLDPE),
low density polyethylene (LDPE), high density polyethylene (HDPE), polypropylene (PP)
and polystyrene (PS). Crate is made of HDPE plastics of two designs, i.e. 45 litre rectangle
and 45 litre trapezoid (figure 28). The compressive resistance of crate was as high as 840 kg.
The structure of crate is more rigid than plastic bag and kheng.
Consequently, crate was found to protect mango bruising better than kheng did
(Chonhenchob and Singh, 2003). The full rectangular crate occupied the truck space as
equally as the empty crate because such a crate is rigid and not collaspsible. Even though the
empty trapezoidal crate could be piled up and occupied less truck space, this increased the
transportation cost of returning the empty crate. Crate is reusable and well ventilated but
limitedly printed. Each crate costing about 4.5 USD may last as long as 10 years. The crate
made of recyclable plastics costing about 3 USD may be out of order in 5 years. The
corrugated paper CP box is popularly used for transporting fresh fruit and vegetable to both
local and exporting markets. This is because the CP box has smooth surface facilitating
printing and not damaging the produce. The corrugated paper was light, degradable,
recyclable and needs little space before box assembly. The box assembly is easy and
sufficiently strong to protect the produce inside. Disadvantage of the CP box is low
ventilation and the paper absorbs moisture which reduces its strength. Table 13 presented the
specifications of corrugated paper box for exporting fresh fruit and vegetable recommended
by Thailand Packaging Center. According to US Standard the CP box for fresh produce must
280
bear a) the compressive stress of 19.3 kg/cm2, b) 210-220 cm stacking height. The CP box
was so designed to well meet OECD standard for palletization, i.e. 80 cm x 120 cm or 100 cm
x 120 cm. Generally, CP box capacity was 12 kg for typical produce and 5 kg for bruise
susceptible produce. The recommended design of CP box was for packaging banana,
rambutan, durian, fresh vegetable, guava, tomato, egg plant, papaya, mangosteen, longan,
pomelo, grape. Amongst corrugated box, plastic crate, and kheng, corrugated box with foam
net provided the best protection. Mangoes packaged in kheng showed the highest mechanical
damage and weight loss (Chonhenchob and Singh, 2004).
The typical retail packagings for fresh produce included bag, foam tray, kheng and box.
Bags are the most popular retail packaging because they are cheap but their performance was
the poorest among packagings (Peleg, 1985). Bags are mostly plastic in the form of either
laminar or net. The net is often used to package tangerine and sweet tamarind. The netted
tangerines came in a corrugated paper box from the producer to facilitate retailing whenever
the box is opened. Disadvantages of the bags are a) the produce inside the bags were injured
because of mutual impact among produce during handling and transport, b) absence of
individual produce separation, c) low package density and d) since the produces inside the
bag could not be clearly seen, this urged the buyer to manually explore the bag which added
produce damage. Foam tray, made of polystyrene, was applicable for intact and peeled fruit.
Foam tray formed a retail packaging with stretch film. Transparency of the stretch film
provided clear vision attracting buyers. They could also inspect the packaged produce.
Besides, the stretch film tightened the produce to the tray not to move when loaded. This not
only collected the produce together for easy carriage but also prevented bruising due to
mutual impact. Another advantage of the stretch film was to reduce transpiration of the
produce. Kheng was available for the capacity of 1 to 2 kg/container and was applicable
limitedly to local grape. Box was divided into two categories, i.e. paper box and plastics box.
The paper box was made of paperboard coated with wax and structured with a plastic top
window providing visual observation to buyers. The plastic box was made of PVC (polyvinyl
choride) with holes for ventilation. The paper box and plastic box were available for sweet
tamarind and strawberry respectively. For better protection of fruit, cushioning material like
foam net or air bubble plastic sheet was used to wrap the fruit before packaging (figure 29).
Chinese apple, dragon fruit, papaya were primarily wrapped with foam net and then packaged
in the wholesale packaging like corrugated box before shipping. This not only reduced
transportation bruising due to fruit contact impact but also facilitated retailing without
repackaging. Popularity of the air bubble plastic sheet to wrap the fruit was less as compared
with foam net. Thongkamthamachat and Timinkul (2000) found that performance of bruise
protection of Chinese apple and guava by commercial foam net to impact was better than that
by commercial air bubble sheet. Degree of bruise protection of the apple under impact varied
as the size of foam net thread. No bruise was found in an apple wrapped with 5 mm thread
foam net while bruising was detected in an apple wrapped with 1.5 mm thread foam net under
the impact energy of 1.1 J or less (Jarimopas et al., 2003).
3.2. Interior Packaging Management
Rose apple, mangosteen, mango, rambutan, longan and sweet tamarind were nowadays
packed in the aforementioned wholesale packagings. Considerable damages of the packaged
fruit remained which indicated that only the wholesale container was insufficient to protect
the produces from mechanical damage. Management of the produces inside the packages with
cushioning materials was additionally required. One way to implement this was the
application of existing cushioning material with different design of interior packaging. Design
criteria was a packaged fruit a) must not contact its neighboring fruit and package body, b)
must not move in side the package, c) must not bear vertical load, d) can be wrapped with
cushioning material to reduce damage (Peleg, 1985; Jarimopas, 2006).
The sweet tamarind in corrugated box shipped from the orchard to the wholesaler
depicted the total damage of 22 and 29.5% for Sitong and Srichompoo cultivars. Rachanukroa
et al. (2006) demonstrated the concept of mechanical damage reduction of the packaged sweet
tamarind by means of mixing small foam ball to the sweet tamarind at varying mixing ratio
and packing them in the corrugated box. The more the proportion of foam ball was, the more
the amount of damage decreased. In parallel, packing density also reduced. Further research
should be made to find the appropriate proportion between sweet tamarind and foam ball
while maintaining proper packing density in a wholesale container. Rachanukroa et al. (2007)
utilized the above concept with the single face corrugated paper to design a retail packaging
of 15 cm diameter by 20 cm height sleeve. The 1 kg sleeve was filled with sweet tamarind
mixed with 5 mm foam ball at 30% mixing ratio. Drop test evaluated that the sleeve could
produce damage of sweet tamarind of Sitong and Srichompoo cultivar at the level of 1 and 1
5
3
of the maximum damage in typical retail packaging.
Chaiyapong and Jarimopas (2007) attempted to utilize foam net, single wall corrugated
paper, shredded paper with fruit stacking variation to improve packaging of intact Nam
Dokmai mango for export. Typically, 24 flawless mature mangoes were packed in 24.5 cm x
35 cm x 25 cm, double wall, full telescope corrugated box in two layers with some shredded
paper distributing on the bottom of the box. Twelve fruits were placed on each layer with
their cheeks turning downwards. The improved packaging used the same size container
packaged with mango cushioned with foam net. The cushioned fruit was placed diagonally on
shredded paper at the bottom of the box. The shredded paper was spreaded over the cushioned
fruit and a piece of single wall corrugated paper followed. The second, the third and the
fourth layer was obtained by repeating the previous arrangement. Each layer comprised 8
cushioned mangoes. The 4-layer box of wrapped mangoes weighed 17.5 kg while the typical
box of bare mango weighed 10 kg. Performance test by means of vibration simulation was
applied to the typical export and the improved packaging. Table 14 showed that the improved
4-layer container exhibited potential packaging over the current container because it could
carry about 33 %more mango with less than half of the bruising that the current box gave.
Another management concerned with mangosteen packaging. Pushpariksha et al. (2006)
made up 8 different interior designs with 2 kinds of wholesale container (corrugated
fiberboard box and reusable crate). The corrugated fiberboard boxes (CFB) were packages for
export while reusable plastic container (RPC) was used for domestic market. The
experimented design were
282
1.CFB-1T Corrugated fiberboard box/Pattern-packed/Tray pack/1 layer
2.CFB-1C Corrugated fiberboard box/Pattern-packed/Cell pack/1 layer
3.CFB-2CP Corrugated fiberboard box/Pattern-packed/Cell pack/2 layers with Shredded
paper
4.CFB-3T Corrugated fiberboard box/Pattern-packed/Tray pack/3 layer
5.CFB-F
Corrugated fiberboard box/Pattern-packed/Foam net
6.CFB-FP Corrugated fiberboard box/Pattern-packed/Foam net and Shredded paper
7.RPC-R Reusable crate/Random-packed with paper liner
8.RPC-FH Reusable crate/Pattern-packed with paper liner/Foam net/Horizontal
9.RPC-FV Reusable crate/Pattern-packed with paper liner/Foam net/Vertical
No. 1, 2 and 7 were the current packagings. No. 3,4,5,6,8,9 were the developed
packagings. The various packaging systems shown in figure 30-33 were tested by simulated
vibration. All mangosteen samples for the tests were maunally harvested and carefully
handled from orchards. After tests, the mangosteens were stored at ambient temperature for
24 hours before the mechanical damages were evaluated. Four types of mechanical damages
on mangosteen were torn or detached calyx, scratched stem-end, hard rind and skin abrasion.
The amount of hard rind was less when fruit was isolated even in tray, cell or foam net
compared with the RPC-R. Abrasion was low in tray pack but high in cell pack. One layer
pack has excessive space resulting in tremendous damages on calyx and stem-end. Damages
were high in packages of CFB-F, RPC-FH, RPC-FV. This was speculated that foam net could
not well protect mangosteen because foam net slipped of the fruit when top layer fruits
bounced in head space. Using shredded paper in the head space would perhaps reduce this
problem. Packaging performance included not only mechanical damages but also packing
density. Overall packing density of CFB types were quite low (18-25%) as compared with
RPC types (40-50%) except CFB-F and CFB-FP (≅ 37%). Using foam net instead of internal
partition or separator in CFB-F and CFB-FP packages could improve their packing density.
By the way, foam net application as cushioning material in RPC type would decline its
packing density about 10%. The corrugated fiberboard box with three layers of expanded
polystyrene tray exhibited the best protection, yielding the lowest overall percentage of
damages, i.e. hard rind 5.6%, skin abrasion 9.3%, calyx’s damage 23.3%, and scratch on
stem-end 2.2%.
Even though foam net has been extensively used as fruit cushion, its very long
degradable life threatens human life. An attempt to determine proper cushioning material out
of agricultural waste and recyclable material to substitute foam net was recently made.
Jarimopas et al. (2006) compared the cushioning performance of dry banana string, dry water
hyacinth, single face corrugated paper, new and used double wall corrugated paper to protect
bruising of the stored “Fuji” Chinese apple. The cushioning materials of concern were
wrapped up the apple samples and impacted by a simple ballistic pendulum. Results of the
impact test indicated that, based on the lowest bruise susceptibility and the highest bruise
threshold, the single face corrugated paper with corrugators facing out of the fruit could best
protect the apple sample. The bruise threshold of the single face corrugated paper and the
foam net was 0.75 and 0.475 J respectively. The banana string and water hyacinth featured
several hitches according to their structure of netting which caused many small bruising. This
phenomenon was undesired.
Shredded (s) paper is often used below and top of a package, especially corrugated box,
as cushion. The knowledge about applying the s-paper as cushion to wrap up a fruit is
limitedly available. At present, the use of foam net is widely spreaded because of acceptable
impact protectionability and operation convenience. However, its difficult degradability
becomes increasingly problematic. An effort to find the s-paper which is recyclable, cheap
and easily degradable as an alternative cushioning material was executed. The s-paper was set
into three conditions of width (3 and 6 mm), and type (used A4 office paper and used
newspaper paper), the s-paper density (36, 48, 60, 72 kg/m3). The set s-paper was applied to
cushion the Chinese stored apple of Red Fuji cultivar. The cushioned fruits were impacted at
the constant energy of 2 J by a ballistic pendulum and the resulting impact bruising was
analyzed. Results showed that the s-paper made of 3 mm wide, used A4 office paper, with 60
kg/m3 density in a cloth sack could protect apple bruising under the threshold impact energy
of 1.4 J which is 87% higher than that of the foam net. The s-paper could practically make
good protection on rose apple fruit with damage 2.4 times less than that of the foam net.
3.3. Edible Films and Coatings for Fresh Produce
3.3.1. Definition and History of Edibl Films and Coatings
Edible film is defined as a stand-alone film used for food separation layer, wrap or casing
and pouch. On the other hand, edible coating is an edible film formed as coating such as
coating on surface of oranges and other fruits. Edible films and coatings have a potential to
extend the shelf life and quality of fresh produce, adding value to the edible film-forming
polymer, and reducing synthetic packaging materials. Edible films and coatings provide
barriers to oxygen and carbon dioxide, aroma, oil and moisture, depending on the nature of
the edible film-forming materials (Donhowe and Fennema, 1993; Krochta, 1997). In addition,
they enhance the appearance and integrity of food, carrier of antioxidant, flavor, color and
antimicrobial. Several materials were used to form edible films, such as protein,
polysaccharide and lipids. Coating fruits and vegetables has been performed since the 12th
century in China by waxing of oranges and lemons to prolong the storage time (Hardenburg,
1967). Edible films and coatings have been used to reduce the moisture loss and improve
appearance of whole fresh produce; for example, citrus and apple (Baldwin and Baker, 2002).
Moreover, the behavior of consumers is aware of the healthy eating habits and less time to
prepare food. This is a driving force for fresh-cut fruits in the market. However, fresh-cut
fruits are subject to undesirable physiological changes such as color, texture, aroma, and
overall appearance that cause a short fruit shelf life and quality loss. Therefore, edible films
and coatings can delay ripening, undesirable changes and thus extend fresh produce shelf life.
The prolonged shelf life will expand both the shipping distance of fresh produce and selling
in the market.
3.3.2. Edible Films and Coatings for Fresh Produce
Generally, the purpose of using edible coatings for fresh produce is to enhance the natural
barrier, if existing, or to restore it in cases where washing and handling has detached it.
Recently, it is emphasized the use of edible coatings in terms of creating an internal modified
atmosphere of fresh fruits which will delay ripening and senescence (Baldwin, 1994).
Selected the appropriate coating permeability to gases helps decrease internal O2 and increase
284
internal CO2 between coated fresh produce and the environment; thus, retarding the
metabolism. High CO2 concentration inside fruit tissues decreases the ethylene synthesis and
essential hormone for ripening resulting to delay ripening (Saltveit, 2003). Reviews related to
edible coatings for fresh produce can be found in Baldwin (1994), Wong et al. (1994),
Baldwin and Baker (2002) and Olivas and Barbosa-Canovas (2005).
3.3.3. Composition of Edible Coatings for Fresh Produce
Several materials such as lipids, resins, carbohydrates and proteins or hydrocolloids can
use as edible coatings for fresh produce. There are advantages and disadvantages in each
material; therefore, most commercial fresh produce coatings contain a mixture of components
so called composite coatings (Kester and Fennema, 1986). The characteristics of some
commercially coatings for fruits and vegetables are shown in table 15. For example,
SemperFresh coatings on different varieties of whole mangoes only retarded ripening in some
varieties at the concentration studied (Carrillo Lopez et al., 1995)
3.3.4. Lipids and Resins
Generally, lipid-based coatings provide good water vapor barrier and reduce the moisture
loss, shriveling and shrinkage of coated fresh produce. Lipid coatings are relatively permeable
to gases resulting in less modification of fresh produce internal atmosphere. These cause
anaerobic conditions and off-flavor finally (Baldwin and Baker, 2002). In general, lipids can
be included in the formulation of edible coatings in a single layer of lipid-based film, or lipids
dispersed in a network formed by hydrocolloids (protein or polysaccharide) or a secondary
layer over a hydrocolloid (Olivas and Barbosa-Canovas, 2005). Unfortunately, lipid coatings
alone cannot form good structural integrity so they require the use of hydrocolloids to form
the film matrix (Baldwin et al., 1997). Besides, the appearances of lipid films are generally
opaque, rigid and present waxy taste or may not adhere well to the hydrophilic surfaces
(Baldwin et al., 1995; Perez-Gago and Krochta, 2001). Beeswax, acetylated monoglycerides,
fatty alcohols and fatty acids are lipids used incorporated with proteins or polysaccharides to
elicit the best practice for fresh produce, especially fresh-cut fruits. Carnauba, candelilla or
polyethylene waxes can offer quite high gloss coating for a high shine consumer satisfaction
such as apples and citrus fruits (Baldwin et al., 1997).
Resin-based coatings provide very glossy, high shine appearance on fresh produce and
appropriate used on apples and citrus. Resin materials are shellac and wood rosin (Hernandez,
1994). Resin coatings offer fairly effective in reducing in moisture loss but excellent barriers
to gases (Hagenmaier and Shaw, 1992). Be aware of the anaerobic respiration and flavor
changes which are usually undesirable can occur.
3.3.5. Hydrocolloids (Proteins and Polysaccharides)
Protein and polysaccharide (hydrocolloid) coatings are excellent gas barriers. Therefore,
they are more effective for ripening control by creating a gentle modified atmosphere and a
gloss on fresh produce. However, they generally provide limited water vapor barrier due to
their hydrophilic nature so they are not effective in reducing moisture loss (Kester and
Fennema, 1986; Gennadios and Weller, 1990; Park and Chinnan, 1990; Gennadios et al.,
1994). The common approach to reduce the moisture loss of hydrocolloid coatings is to add
lipids in the formulation.
Proteins used in coatings are zein, soy protein, wheat gluten, whey protein, casein, gelatin
and collagen. Protein films and coatings have a potential to some fruits such as whey protein
coatings for apples (Cisneros-Zevellos and Krochta, 2003a; Cisneros-Zevellos and Krochta,
2003b), whey protein coatings on fresh-cut mangoes (Plotto et al., 2004), whey protein
coatings on oranges (Sothornvit, 2005), whey protein based composite coatings on fresh-cut
apples (Perez-Gago et al., 2005; Perez-Gago et al., 2006) and wheat gluten-based films and
coatings on refrigerated strawberry (Tanada-Palmu and Grosso, 2005). Furthermore, it has
been used with vegetables such as sodium caseinate/stearic acid emulsion coatings on peeled
carrots (Avena-Bustillos et al., 1994a), calcium caseinate-acetylated monoglyceride aqueous
emulsions coating on zucchini (Avena-Bustillos et al., 1994b), whey protein isolate, sodium
caseinate or sodium caseinate/beeswax emulsion coatings on green bell pepper
(Lerdthanangkul and Krochta, 1996) and zein films on fresh broccoli (Rakotonirainy et al.,
2001). The reason to use protein-based coatings on fresh-cut fruits is that it can provide
nutritional value in the fresh produce. It was recommended to label on the marketing display
to inform the type of the coatings such as animal-, resin-, or beeswax-based. The reason is
they might cause the allergic reaction or intolerances to certain proteins such as lactose or
gluten intolerances for some consumers (Baldwin and Baker, 2002). Moreover, the
vegetarians would not accept to consume animal-derived protein coatings such as gelatin and
milk protein. One approach to overcome this problem is using the natural materials such as
banana flour to form banana films (Sothornvit and Pitak, 2007) which can apply on the fresh
produce and no allergen concern. Banana flour films possessed good mechanical properties
and oxygen barrier. In addition, fruit and vegetable purees such as peach, strawberry, apricot,
apple, pear, carrot and broccoli are an alternative for edible films and coatings (McHugh et
al., 1996; McHugh and Olsen 2004). Fruit and vegetable films under certain relative humidity
(RH) and temperature imparted good gas barriers but poor water vapor barrier. Moreover,
fruit films apply on the same fresh-cut fruits might benefit both quality and shelf life such as
apple film incorporated with beeswax, pectin, glycerol, ascorbic acid and citric acid showed a
significant reduction of moisture loss and browning in fresh-cut apples (McHugh and Senesi,
2000). This may solve the problem of allergic reaction and more attractive to vegetarian
consumers.
Polysaccharides used in coatings are carrageenan, maltodextrin, methylcellulose,
carboxymethyl cellulose, pectin, alginate and starch. Polysaccharide films and coatings also
have a potential to some fruits such as chitosan films covered in the carton boxes of fresh
mangoes (Srinivasa et al., 2002), potato starch-based edible coatings on guava (Quezada
Gallo et al., 2003), hydroxypropyl methylcellulose-lipid edible composite coatings on plum
(Perez-Gago et al., 2003), carboxymethycellulose, chitosan and starch coatings on fresh-cut
mangoes (Plotto et al.,2004), hydroxypropyl methylcellulose-lipid edible composite coatings
on fresh-cut apples (Perez-Gago et al., 2005), chitosan coatings on sliced mangoes (Chien et
al., 2007), alginate coatings on fresh-cut apples (Olivas et al., 2007).
3.3.6. Composite and Bilayer Films and Coatings
Combination of hydrocolloids and lipids can be applied in forms of a composite films and
coatings where all components are mixed into one homogeneous coating layer. Alternatively,
the combination forms two layers, one with hydrocolloids and the other with lipids which is
called bilayer films and coatings. The goal is to improve the barrier characteristics of
composite and bilayer films and coatings by taking advantage of good moisture barrier
286
property of lipids and good gas barrier properties of hydrocolloids. Bilayer films have more
effective than composite films. However, composite films are easy to apply on fresh produce
because it requires one application and one drying step and adhere better to a larger number
of surfaces of polar and non-polar characteristics (Perez-Gago and Krochta, 2001). The
important issue is the orientation of lipid molecules within the coating. For fresh-cut fruits
coated with hydrocolloid-lipid emulsion, the lipid fraction of the coatings tends to orient
towards the outside to the environment which is lower humidity which hydrocolloids are
generally more affinity to fruit surfaces than lipids. It was shown that coated apple cylinders
with a mixture of polysaccharides (pectin, carrageenan, alginate and microcrystalline
cellulose) and the second layer of acetylated monoglyceride, reduced the moisture loss 12-14
times compared to uncoated apples (Wong et al., 1994).
3.3.7. Additives
Additives such as antibrowning agents, antimicrobial agents, firming agents, plasticizers,
nutraceutical, volatile precursor, flavors and color can be helped to improve functional,
nutritional, organoleptic and mechanical properties of films and coatings (Olivas and
Barbosa-Canovas, 2005). Mostly, additives are necessarily used for fresh-cut produce to
prevent browning reaction, loss of firmness and microbial growth. Combination of
antibrowning and firming agent to the edible coatings effectively prolonged shelf life of apple
slices (Lee et al., 2003). However, the usual additive used to improve mechanical properties
of edible films and coatings is a plasticizer, which is a low molecular weight nonvolatile
substance, to reduce biopolymer chain-to-chain interaction, resulting in film flexibility
(Sothornvit and Krochta, 2000; Sothornvit and Krochta, 2001). Plasticizers increase not only
flexibility but also water vapor permeability of film. Fruits and vegetables are often stored
under high RH (85-99%) to reduce the water vapor gradient compared to inside the fruits
(100% RH) to prevent moisture loss from transpiration (Baldwin and Baker, 2002). The high
storage RH can increase fruit coating permeability (Lerdthanangkul and Krochta, 1996);
therefore, reducing modified atmosphere ability of edible coatings within fruits and
vegetables.
Some researches applied different compositions of edible coating on fresh-cut fruits and
the results as shown in table 16.
3.4. Refrigerated Storage and Packaging
Controlled temperature is the key factor to maintain the quality of fresh produce.
Maintenance of the cold chain or refrigerated storage is the best way to minimize all forms of
deterioration after harvesting, such as moisture loss, softening, bruising, unwanted ripening,
texture degradation, color change, mold or rot growth. The rate of deterioration of fresh
produce is related to the rate of respiration. Good refrigerated storage and appropriate
packaging are the significant management to keep fresh quality of produce, leading to greater
satisfaction and increased demand. Generally, the export of fresh produce often involves long
journey times. Therefore, refrigerated storage is required from production to retail sale. The
breakdown in temperature control at any stage will impact on the final quality of fresh
produce; although, the visible effect may not appear until several days later. In general,
maintenance of fresh produce at optimum low temperatures is necessary and some scientific
postharvest investigations on citrus fruits can be viewed from Schiffmann-Nadel et al. (1971),
Nordby et al. (1987), Paull (1999) and Henriod (2006).
The use of air freight allows perishable produce to be rapidly transported around the
world. Using the right combination of packaging, refrigerated storage and handling
procedures can maintain the quality of fresh produce. Fresh fruit and vegetable continue
respiration which produces carbon dioxide, water and heat. The heat produced by respiration
results in warming of the produce and needs to keep it cool by refrigeration. The refrigerated
storage will lower the rate of respiration with limited heat accumulation resulting in lower
rate of deterioration. Different types of produce have different rates of respiration. The higher
rate of respiration is more highly perishable and temperature control is very critical. Ethylene
causes fresh produce ripening and deterioration in some produce. Keeping fresh produce cool
also reduces the production of ethylene (https://www.business.vic.gov.au/busvicwr/_assets/
main/lib60167/maintainingcoldchain_airfreight_perish.pdf).
During non-refrigerated transport stage, the simple cooling agents such as wet or dry ice
or gel packs are needed to maintain the correct produce temperature. When using refrigerants,
it is needed to be aware of the freezing or chilling injury to fresh produce so the location and
amount of refrigerant used is the critical points. Ensure refrigerants and packagings used are
matched. For example, wet ice requires packaging which will hold liquids and ensure that the
form of packaging used such as chipped, flaked, block, will not damage to the produce during
packing, handling or transportation. Dry ice requires sufficient ventilation to prevent an
accumulation of CO2 which will harmful to most fresh produce.
Conventional refrigerated storage room needs to concern three factors which are
temperature, relative humidity and air movement.
3.4.1. Temperature
Temperature control is based on tight, well-insulated structure, sufficient refrigeration
capacity for maximum demand, and control of refrigerant flow through the system by means
of thermostats and /or pressure-controlled expansion valves.
3.4.2. Relative Humidity
Relative humidity (RH) is the percentage of saturation of air with water vapor at a given
temperature. As the temperature of air increases, its water-holding capacity increases as well.
As RH of air decreases, its vapor pressure (VP) decreases. As VP decreases, the capacity of
the air for removing water from moist sources increases. Therefore, it is important to maintain
a high VP and as small a VP differential between the stored product and the storage air as
possible.
3.4.3. Air Movement
Air movement must be in sufficient volume to remove respiratory heat and heat entering
the room through exterior surfaces and door ways and has a uniform flow of air.
3.4.4. Storage for Fresh Produce
Proper storage of fresh produce can affect both quality and safety. To maintain quality of
fresh produce, certain perishable fresh fruits and vegetables should be stored in a clean
refrigerator at a temperature of 40 oF or below. The purposes are to minimize growth of
microorganisms and reduce enzyme activity. Packaging or storage also helps control
288
respiration rate and ripening. Most of the leaf, stem, bud and root vegetables are stored at a
few degrees above their freezing point. Storage life of most of the leafy vegetables is only a
few weeks, even in optimum environments. However, those root crops, such as carrots,
horseradish can store for several months held in ventilated storage. Refrigerated storage is
used each year for a part of each of these crops, that either to be stored for prolonged periods
or held in areas where outside temperature is not favorable for ventilation. Other produces,
which for reasons of economy are usually stored under ventilation, may be placed in
refrigerated storage during the later holding period for marketing beyond the season feasible
from ventilated storage such as potatoes, carrots, sweet potatoes, dry onions and cabbage.
For a long term storage, it is necessary to maintenance of as low temperature as possible
(close to 0 oC), high air relative humidity up to 85-95% and % CO2 in air related to the
vegetable species (Dauthy, 1995). This will minimize respiration and transpiration of fresh
produce. Leafy vegetables should be promptly cooled as close to 0 oC (32 oF) as possible and
held there throughout marketing. Wilting, diseases and disorders increase in severity as
temperature increases. Vegetables have to be handled and transported as soon as possible in
the storage conditions.
3.5. Recommended Research Trend
3.5.1. Research of Interior Packaging Management of Tropical Fresh Produce Should
Be Conducted into 2 Directions
One is to develop new design of interior packaging based on utilizing the available
cushioning materials to get minimum damage, high packing density at reasonable packaging
cost. The other is to develop new cushioning material protecting fresh fruit and vegetable.
The research trend should include development of related application technique of the
agricultural wastes as well as recyclable materials for efficient produce cushioning. One
successful example on application of the treated waste water to irrigate the plants in dessert
was recently shown. The developing countries which produces a lot of tropical fresh produce
are rich of produce waste. The countries may take this similar problem as challenge to make
use of the produce waste especially as an alternative packaging cushioning material.
3.5.2. It Needs To Be Taken into Account that the Maximum Storage Life of a
Harvested Crop Depends on Its Production History and Quality and Maturity at
Harvest
Refrigerated storage adds cost to the produce and requires storage method. The correct
storage technique is governed by the types of produce (its temperature from harvest and its
respiration rate as well as produce quality), the storage temperature and humidity best suited
to the produce and intended storage life, without chilly injury or microbial spoilage.
Refrigerated storage rooms are well established for designing and installing and common use
for fresh produce. However, the unsuccessful operation in the developing countries was due
to the significant common problems which are untrained or unmotivated supervision,
deterioration of produce quality during storage, improper use of facilities and underutilization of refrigeration space (Choi, 2002). These problems could be attributed to
inadequate planning and management performance. The successful operation of cold storage
is dependent on some knowledge of costing, specific commodity requirements, refrigeration
technology, and produce marketing. Good management of refrigerated storage needs
knowledge and experience of storage conditions of the commodities, directions for loading of
the rooms and maintaining a hygiene, management, control and maintenance of refrigerated
equipment and staff training (Choi, 2002).
3.5.3. The Use of Edible Coating Should Be Used in Combination with other Methods
Such as Low Temperature Storage, Controlled Atmosphere or Modified Atmosphere
Packaging to Enhance Stability of Fresh-Cut Produce
Tropical and subtropical fruits are subject to chilling injury; thus, application of edible
coatings is awareness. Fresh whole and fresh-cut produce have different characteristics which
need to further study the effect of each edible film and coatings for each commodity. To
overcome the allergen problem and vegetarian concern, fruit and vegetable coatings itself can
open the good opportunity to investigate and can develop as commercial coatings in the
future. Furthermore, the natural color and flavor of each fruit and vegetable itself might be
attractive to consumers, especially children and teenager. However, consumer perception and
safety issue from microbial growth of edible films and coatings wait for future studies prior to
commercialize. Finally, edible films can provide convenient for use as wrappers and it is still
under investigation.
Table 12. General characteristics of wholesaling container
Wholesaling container
Wide mouth kheng
Cylindrical kheng
Vegetable kheng
Wooden crate
Plastic crate
Corrugated box
Capacity
(litre)
11-237
40-188
40-82
40
45
22-60
Weight
(kg)
0.25-4.65
0.7-0.9
0.18-0.58
6.0-7.0
2.33
0.45-1.5
Compressive resistance
(kg)
80-200
67
4-43
>5,000
840
400-1,000
Source: Jarimopas (2006).
Table 13. Corrugated paper box recommended by Thailand Packaging
Center for exporting fresh fruit and vegetable
Produce
Transportation
type
Banana
Rambutan
without
foam tray
Rambutan with foam
tray
Durian
Fresh vegetable
Guava
Tomato
Mango
Carrying
weight
(kg)
125
5
Compressive
resistance (kg)
Ship
Airplane
Outside
dimension
(cm)
50x40x23
40x30x10
890
600
Maximum
stacking
layers
9
15
Airplane
40x30x10
4
600
15
Short distance
airplane
Long distance
airplane
Airplane
Airplane
Air conditioned
truck
Airplane
48x45x23
12
460
6
48x45x3
12
800
6
45x35x20
40x30x10
40x30x12
3-10
5
5-6
650
600
570
8
15
18
50x30x10
5
700
15
290
Table 13. (Continued)
Produce
Transportation
type
Outside
dimension(cm)
Carrying
weight (kg)
Compressive
resistance (kg)
Papaya (0.5-0.7
kg)
(1.2-1.5 kg)
(1.2-1.5 kg)
Mangosteen
without foam
tray
Mangosteen
with foam tray
Longan
Pumelo (38-46
cm
circumference)
Airplane
45x35x10
5
800
Maximum
stacking
layers
15
Airplane
Ship
Airplane
40x30x35
40x30x35
40x30x10
12
12
5
490
600
600
4
6
15
Airplane
40x30x10
4.5
600
15
Airplane
Ship
40x30x10
50x40x25
5
18
600
860
15
10
Airplane
Airplane
45x35x20
40x30x10
6
5
650
600
8
15
Grape
Source : Amornrat (1988).
Table 14. Performance comparison between the current
and the developed wholesale packaging for exporting mango
Performance
Parameter
Bruising (%)
Packing density (%)
Packaging cost
(USD/kg mango)
Count number
Packing weight (kg)
•
Mango
without
cushion (export)
15.0±5.6c
37.8d
0.05b
Cushioned mango with stacking layers
2
3
2.50±3.07a*
5.83±2.35ab
25.22b
28.25c
0.070c
0.023a
4
7.22±1.89b
23.14a
0.027a
24
10
16
7.5
36
17.5
24
11.5
Means followed by the same number in the same row are insignificantly different at p < 0.05.
Table 15. Some commercially coatings for fruits
Edible coating (Company)
Semperfresh (Surface System
Intl. Ltd.)
PacRite products (American
Machinery Corp.)
Vector 7, Apl-Brite 300C,
Citrus-Brite
300C
(Solutec
Corp.)
Primafresh Wax (S.C. Johnson)
Major ingredients
sucrose esters of fatty acids, sodium
carboxymethyl cellulose
water-based,
carnauba-shellac
emulsions, shellac and resin water
emulsions, water based mineral oil
fatty acid emulsions
shellac-based with morpholine; AplBrite and Citrus-Brite are carnaubabased
carnauba-wax emulsion
Shield-Brite products (Pace Intl.
Shield-Brite)
Sta-Fresh
products
(Food
Machinery Corp.)
shellac/ carnauba-based, natural wax
vegetable oil/wax and xanthan gum
natural, modified naturaland synthetic
resin and combination
adapted from USFDA, 2001
Applications
most fruits and vegetables,
nectarines
apples, citrus, peaches, plums,
nectarines
apples and citrus
apples, citrus and other firm
surfaced fruit
citrus, pears, stone fruit
citrus, apples, stone fruits,
pomegranates, pineapple and
cantaloupes
Table 15. (Continued)
Edible coating (Company)
Fresh Wax products (Fresh Mark
Corp.)
Apple Britex 559, Melon Wax
551, Banana Wax 509, Pineapple
Wax 510 and other fruit coating
products (Brogdex Co.)
Fresh SealTM (CPG Technologies
of Agway, Inc. to produce)
Nature
SealTM,
AgriCoat
(Mantrose Bradshaw Zinsser
Group)
Major ingredients
shellac and wood resin, oxidized
polyethylene wax, white oil/paraffin
wax
carnauba wax emulsions with or
without fungicides, high shine resinbased, carnauba-based emulsion,
vegetable oil, resin-based and
concentrated polyethylene emulsion
wax
cellulose derivatives and emulsifiers
composite polysaccharide
Applications
citrus, cantaloupes, pineapples
and apples
apples,
melon,
bananas,
avocado,
papaya,
mango,
pineapple, stone fruits and
lemons
avocado, cantaloupe, mangoes
and papaya
sliced apples, pears avocados,
and bananas
Table 16. Different edible coatings on fresh-cut fruits
Fruit
apple slices1
Edible coating
carrageenan
apple slices1
WPC + CMC
cut apple2
WPI + beeswax
apple slices3
calcium caseinate +
CMC, WPC + CMC
apple puree + beeswax
or vegetable oil
Nature SealTM, CMC
and soy protein
CMC
cut apple4
apple slices5
sliced mango6
apple
cylinders7
double
coating:
carrageenan/AMG
Pectin/AMG
Alginate/AMG
MCC/AMG
Additives
AA, OA, CA, Gly,
PEG
AA, OA, CaCl2,
Gly
Gly
CaCl2, Gly
AA, CA, Gly
AA, PS, soy oil,
CaCl2
Lecithin, PEG, BA,
CA
AA, CA, CaCl2 and
NaCl
Results
prolong shelf life by 2 weeks in packed
trays at 3 oC
20% decrease in initial respiration rate,
firm and good sensory
inhibit browning, no significant reduce
weight loss
delay browning
effective of wraps over the coatings on
moisture loss
prolong shelf life by 1 week in
overwrapped trays at 4 oC
retard color change
reduce the rate of carbon dioxide and
ethylene accumulation of 50-70% and
90%, respectively. Alginate films
presented the best water vapor barrier.
WPC = whey protein concentrate, CMC = carboxymethyl cellulose, WPI = whey protein isolate, AMG
= acetylated monoglyceride, MCC = microcrystalline cellulose, AA = ascorbic acid, OA = oxalic
acid, CA = citric acid, Gly = glycerol, PEG = polyethylene glycol, PS = potassium sorbate, BA =
benzoic acid.
1
Lee et al. (2003), 2 Perez-Gago et al. (2003), 3 Le Tien et al. (2001), 4 McHugh and Senesi (2000), 5
Baldwin et al. (1996), 6 Nisperos-Carriedo and Baldwin (1994), 7 Wong et al. (1994).
292
a) Bamboo kheng for banana
for longan
for garlic
for cabbage
for lettuce
b) Bamboo kheng
c) Ratan made kheng for pumpkin
Figure 26. Different design of wholesale packaging “Kheng”.
d) Plastic kheng for durian
a) Plastic bag for green onion
b) Netted plastic bag for red onion
c) Plastic without holes containing lime
Figure 27. Plastic bag.
a) Trapezoidal
294
b) Rectangular
Figure 28. Plastic crate.
a) Foam net
Figure 29. Cushioning material.
b) Air bubble plastic sheet
CFB-1T
(Thermoformed foamed polyethylene tray)
CFB-3T
(Expanded polystyrene tray)
Figure 30. Tray pack in corrugated fiberboard box
CFB-1C
CFB-2CP
Figure 31. Cell pack in corrugated fiberboard box
CFB-F
Figure 32. Packaging systems using foam net with and wihout shredded paper
CFB-FP
296
RPC-R
RPC-FH
RPC-FV
Figure 33. Reusable plastic containers
CONCLUSION
A review of 129 relevant publications has been conducted. Several terms have been
clarified; “engineering technology of tropical fresh produce”, which concerns physical
properties, innovations and packaging; and “physical properties”, which – with regard to
mango, sweet tamarind, guava, tangerine, mangosteen, durian, snake egg plant, white long
radish and lime -- consist of post-harvest loss, physical characteristics, mechanical properties,
firmness, friction, and associated non-destructive techniques. The discussion of innovations
concerned inventions of machinery and devices associated with durian, mangosteen, young
coconut fruit, dry over-mature coconut and baby corn. Finally, the discussion of packaging
technology related to developments in packaging which improves the distribution and
extension of shelf life of selected tropical fresh produce. Owing to the current high postharvest loss and comparative underinvestment in tropical fresh produce research and
development, it is the position of the leaders that the countries which produce tropical fresh
produce should dramatically increase their funding of research and development in all the
engineering technology aspects discussed in the review.
ACKNOWLEDGEMENT
The authors gratefully acknowledge Professor Paul Chen, Professor Emeritus,
Department of Biological and Agricultural Engineering, University of California, Davis to
technically review majority of the chapter.
REFERENCES
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
Abbott, J.A. (1999). Quality measurement of fruits and vegetables. Post-harvest
Biology and Technology, 15, 207-225.
Abbott, J.A., Bachman, G.S., Childers, N.F., Fitzgerald, J.V., and Matusik, F.J.
(1968). Sonic techniques for measuring texture of fruits and vegetables. Food
Technology 22(5), 101-112.
Anonymous. Maintaining the Cold Chain: Air Freight of Perishables, Victorian
Airfreight Council. 2 April 2007. Available from: https://www.business.vic.gov.au/
busvicwr/_assets/main/lib60167/maintainingcoldchain_airfreight_perish.pdf
ASAE Standard. (1998). Compression test of food materials of convex shape. ASAE
S368.3 Mar 95, American Society of Agricultural Engineering, 2950 Niles Road, East
Lansing, Michigan MI 49085.
Avena-Bustillos, R.J., Cisneros-Zevallos, L.A., Krochta, J.M. and Salveit, M.E., Jr.
(1994a). Application of casein-lipid edible film emulsions to reduce white blush on
minimally processed carrots. Postharvest Biol. Technol., 4, 319-329.
Avena-Bustillos, R.J., Krochta, J.M., Salveit, M.E., Jr., Rojas-Villegas, R.J. and
Sauceda-Perez, J.A. (1994b). Optimization of edible coating formulation on zucchini
to reduce water loss. J. Food Eng., 21, 197-214.
Baldwin, E.A. (1994). Edible coatings for fresh fruits and vegetables: past, present,
and future. In J.M. Krochta, E.A. Baldwin and M.O. Nisperos-Carriedo (Eds.), Edible
coatings and films to improve food quality. (pp. 25-64). Lancaster, PA, Technomic.
Baldwin, E.A. and Baker, R.A. (2002). Use of proteins in edible coatings for whole
and minimally processed fruits and vegetables. In A. Gennadios (Ed.), Protein-Based
Films And Coatings. (pp. 501-516). FL, CRC Press.
Baldwin, E.A., Nisperos-Carriedo, M.O. and Baker, R.A. (1995). Edible coatings for
lightly processed fruits and vegetables. HortScience, 30, 35-38.
Baldwin, E.A., Nisperos-Carriedo, M.O., Chen, X. and Hagenmaier, R.D. (1996).
Improving storage life of cut apple and potato with edible coating. Postharvest Biol.
Technol., 9, 151-163.
Baldwin, E.A., Nisperos-Carriedo, M.O., Hagenmaier, R.D. and Baker, R.A. (1997).
Use of lipids in edible coatings for food products. Food Technol., 51, 56-62.
Birth, G. S., MaGee, J. B., Cavalette, C., and Chan, H. (1978). An optical technique
for measuring papaya maturity. American Society of Agricultural Engineering, Paper
No. 78-3071, St. Joseph, Mich.
Birth, G.S. (1976). How light interacts with foods. In Gaffney, J.J.Jr. (Ed.), Quality
Detection in Foods. (pp. 6-11) American Society for Agricultural Engineering, St.
Joseph, MI.
298
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
Boonmung, S., Chomtee, B., and Kanlayasiri, K. (2006). Evaluation of artificial
neural networks for pineapple grading. Journal of Texture Studies, 37, 568-579.
Budiastra, I.W., Trisnobudi, A., and Purwadaria, H.K. (1999). Utrasonic system for
automation of internal quality evaluation of durian. Proceedings of 14th World
Congress of IFAC, Beijing, China, 5-9 July, Pergamon Press.
Carrillo Lopez, A., Valdez Torres, J.B., Rojas Villegas, R. and Yahia, E.M. (1995).
Ripening and quality of mango fruit as affected by coating with “Semperfresh”. Acta
Hort., 370, 203-211.
Chaiyapong, S., and Jarimopas, B. (2006). Mechanical properties of Nam Dokmai
mango fruit. Proceeding of the 7th National Seminar on “Research Enhancing the
Potential of Thai Agricultural Commodities in the World Market”, Organized by Thai
Society of Agricultural Engineering and Faculty of Engineering, Mahasarakhanm
University, 23-24 January 2006, Mahasarakhanm, Thailand.
Chaiyapong, S., and Jarimopas, B. (2007). Development of Thai mango wholesale
packaging. Proceeding of the International Conference on Agricultural, Food and
Biological Engineering and Post Harvest/Production Technology, organized by Thai
Society of Agricultural Engineering, American Society of Agricultural and Biological
Engineers, and Faculty of Engineering, Khon Kaen University, 21-24 January, Sofitel
Raja Orchid Hotel, Khon Kaen, Thailand.
Chawapradis, C., Tangpinitkul, N., and Krisanaseranee, S. (2000). Maturity
determination of Durian fruit by sonic response. In Research Report on Research
Program for Development of Production and Marketing of Durian for Export,
supported by National Research Council of Thailand, Bangkok, 38-81 (in Thai).
Chen, P. (1996). Quality evaluation technology for agricultural products. Proceedings
International Conference Agricultural Machinery Engineering, Seoul, Korea, 1, 171204.
Chen, P., (1978). Use of optical properties of food materials in quality evaluation and
materials sorting. Journal of Food Process Engineering, 2 (4), 307-322.
Chen, P., Ruiz-Altisent, M., and Barreiro, P. (1996a). Effect of impacting mass on
firmness sensing of fruits. Transaction of the ASAE, 39(3),1019-1023.
Chen, P., Tjan, Y., and Ruiz-Altisent, M. (1996b) A low-mass impact sensor for highspeed firmness sensing of fruit. Proceedings of the International Conference on
Agricultural Engineering AgEng, 96, Paper no. 96F-003, Madrid, Spain, September
23-26, 1996.
Chien, P.J., Sheu, F. and Yang, F.H. (2007). Effects of edible chitosan coating on
quality and shelf life of sliced mango fruit. J .Food Eng., 78, 225-229.
Choi, J.U. (2002). Cold and CA storage; In D. Kim (Coordinator). Postharvest
Technology of Fresh Produce for ASEAN Countries, 2002 (pp. 187-211). ASEANROK Postharvest Program, Korea Food Research Institute.
Chonhenchob, V. and Singh, S.P. 2003. A comparison of corrugated boxes and
reusable plastic containers for mango distributions. Packaging Technology and
Scienc., 16, 231-237.
Chonhenchob, V. and Singh, S.P. 2004. Testing and comparison of various packages
for mango distribution. Journal of Testing and Evaluation, 32(1), 69-72.
[28]
[29]
[30]
[31]
[32]
[33]
[34]
[35]
[36]
[37]
[38]
[39]
[40]
[41]
[42]
[43]
Chonhenchob, V., and Singh, S.P. 2005. Packaging performance comparison for
distribution and export of papaya fruit. Packaging Technology and Science, 18, 125131.
Cisneros-Zevallos, L. and Krochta, J.M. (2003a). Whey protein coatings for fresh
fruits and relative humidity effects. J. Food Sci., 68, 176-181.
Cisneros-Zevallos, L. and Krochta, J.M. (2003b). Dependence of coating thickness on
viscosity of coating solution applied to fruits and vegetables by dipping method. J.
Food Sci., 68, 503-510.
Cooke, J.R. 1972. An interpretation of the resonant behavior of intact fruits and
vegetables. Transactions of the ASAE, 15(6), 1075-1080.
Correa, P., Ruiz-Altisent, M., and Dela Plaza, J.L. (1992) Physical parameters in
relation to physiological changes of avocado during ripening (20 0C) and cold storage
(6 0C) in different conditions. Proceedings of AGENG 92, Paper No. 9211-16, 1992.
Dauthy, M.L. (1995). FAO Agricultural Services Bulletin No. 119; Fruit and
Vegetable Processing; Food and Agriculture Organization of the United Nations,
Rome,
2
April
2007.
Available
from;
http://www.fao.org/docrep/V5030E/V5030E0r.htm
Donhowe, G. and Fennema, O. (1993). Water vapor and oxygen permeability of wax
films. J. American Oil Chemists Society, 70, 867-873.
Finney, E. E., BenGera, I., and Massie, D. R. (1967). An objective evaluation of
changes in firmness of ripening bananas using a sonic technique, Journal of Food
Science, 32(6), 642-646.
Gennadios, A. and Weller, C.L. (1990). Edible films and coatings from wheat and
corn proteins. Food Technol., 44, 63-39.
Gennadios, A., McHugh, T.H., Weller, C.L. and Krochta, J.M. (1994). Edible
Coatings and Films Based on Proteins. In J.M. Krochta, E.A. Baldwin and M.O.
Nisperos-Carriedo (Eds.), Edible Coatings And Films To Improve Food Quality. (pp.
201-277). Lancaster, PA, Technomic.
Hagenmaier, R.D. and Shaw, P.E. (1992). Gas permeability of fruit coating waxes. J.
Amer. Soc. Hort Sci., 117, 105-109.
Hardenburg, R.E. (1967). Wax and related coatings for horticultural products.
Bibliography. Agr .Res. Bul 51-15. U.S. Dept. of Agric., Washington, DC.
Haryanto, B., Budiastra, I.W., Purwadaria, H.K., and Trisnobudi, A. (2001).
Determination of acoustic properties of durian fruit. Proceedings 2nd IFAC-CIGR
Workshop on Intelligent Control for Agricultural Application, Bali, Indonesia, 22-24
August 2001. Pergamon Press.
Henriod, R.E. (2006). Postharvest characteristics of navel oranges following high
humidity and low temperature storage and transport. Postharvest Biol. Technol., 42,
57-64.
Hernandez, E. (1994). Edible Coatings from Lipids and Resins. In J.M. Krochta, E.A.
Baldwin and M.O. Nisperos-Carriedo (Eds.), Edible Coatings And Films To Improve
Food Quality. (pp. 279-303). Lancaster, PA, Technomic.
Jaren, C., Ruiz-Altisent, M., and Perez de Rueda, R. (1992). Sensing physical stage of
fruits by their response to non-destructive impacts. Proceedings of AGENG 92, Paper
no. 9211-113.
300
[44]
[45]
[46]
[47]
[48]
[49]
[50]
[51]
[52]
[53]
[54]
[55]
[56]
[57]
[58]
[59]
Jarimopas, B. (1985). Reduction of Post-harvest Mechanical Loss of Longan.
Unpublished FAO/RAPA Research Report, Bangkok. 41 p.
Jarimopas, B. 2006. Post-harvest Sorting Machinery, Packaging and Packing House
of Fruit. Thai Society of Agricultural Engineering, Khon Kaen, Thailand 216 p.
Jarimopas, B., and Kittawee, U. (2007). Firmness properties of mangoes.
International Journal of Food Properties. (in press).
Jarimopas, B., and Pechsmai, A. (2001). Comparative test between a machine and a
device opening young coconut fruits. Thai Agricultural Research Journal, 19(3), 175184.
Jarimopas, B., and Ruttanadat, N. (2007b). Development of a young coconut fruit
trimming machine. Journal of Food Engineering, 79, 752-757.
Jarimopas, B., and Srirungruang, T. (2006). Young coconut fruit bruising under
impact. Agricultural Science Journal, 37(5) Supplement , 240-243.
Jarimopas, B., Jandapradit, S., and Wongsim, K. (2006a). Physical characteristics and
some mechanical properties as essential to quality sorting of Sitong and Srichompoo
sweet tamarinds. Proceeding of the 6th National Seminar on “Toward Kitchen of The
World by Agricultural Engineering”, organized by Thai Society of Agricultural
Engineering and Faculty of Agricultural Engineering and Technology,
Ratchamangchala University of Technology at Thanyaburee, 30-31 March, Grand
Miracle Hotel, Bangkok.
Jarimopas, B., Jinanuwong, S., Pushpariksha, P., Bupata, C., and Srirungruang. T.
(2006a). Poisson’s ratio and Young’s Modulus of white long radish. Thai Society of
Agricultural Engineering Journal, 12(1), 54-59.
Jarimopas, B., Phoetiniyom, K., Boonrin, S., and Khantoe, C. (1989). Development of
opening mechanism of Thai young coconut. National Agricultural Machinery Center
Newsletter, July-August , 4-6.
Jarimopas, B., Piamkla, N. and Sawangnet, P. (2003). Comparative study on the
capacity of foam net to reduce mechanical damage of apple due to impact. Thai
Society of Agricultural Engineering. 10(1), 44-49.
Jarimopas, B., Sayasoonthorn, S., Singh, S. P. and Singh, J. (2006). Test method to
evaluate bruising during impacts to apples and compare cushioning materials. Journal
of Testing and Evaluation. (in press)
Jarimopas, B., Singh, S.P., and Saengnil, W. (2005c). Measurement and analysis of
truck transport vibration levels and damage to packaged tangerines during transit.
Packaging Technology and Science, 18, 179-188.
Jarimopas, B., Timkhum, P., and Roongratana-ubol, K. (2005b). A simple electromechanical device for measuring coefficient of friction and rolling angles of fruits.
Kamphaengsaen Academic Journal, 3(1), 68-76.
Jarimopas, B., Toomsaengtong, S., Inprasit, C. (2007a). Design and testing of a
mangosteen sizing machine. Journal of Food Engineering, 79, 745-751.
Jarimopas, B., Vichukit, S., Sirisawat, B., Jaisin, N., and Pushpariksha, P. (2006b).
Poisson’s ratio and modulus of elasticity of snake egg plant. Kamphaengsaen Science
Journal, 4(1), 92-100.
Jha, S.N., Kingsly, A.R.P., and Chopra, S. (2006). Non-destructive determination of
firmness and yellowness of mango during growth and storage using visual
spectroscopy. Biosystems Engineering, 94(3), 397–402.
[60]
[61]
[62]
[63]
[64]
[65]
[66]
[67]
[68]
[69]
[70]
[71]
[72]
[73]
[74]
[75]
Jindal, V.K. and Techasena, On_Rawee. 1985. Compression tests for measuring the
firmness of potatoes. ASAE Paper no. 85-1072. American Society of Agricultural
Engineering, St. Joseph, MI 49085.
Kawano, S. 1994. Quality inspection of agricultural products by nondestructive
techniques in Japan. Farming Japan. Vol 28-1:14-19.
Kester, J.J. and Fennema, O.R. (1986). Edible films and coatings: A reviews. Food
Technol., 40, 47-59.
Kittawee, U. and Jarimopas, B. (2006). Firmness sensing of mango fruit subjected to
mechanical loading. Agricultural Science Journal, 37(2) (Suppl.) : 237-241.
Kongrattanaprasert, S., Arunrungrusmi, S., Pungsiri, B., Chamnongthai, K., and
Okuda, M., (2001). Nondestructive murity dtermination of drian by force vibration.
2001 IEEE International Symposium on Circuits and Systems, May 6-9, Australia.
Kongrattanaprasert, W., Arunrungrusmi, S., Pungsiri, B., Chamnongthai, K., and
Okuda, M. (2001). Nondestructive maturity determination of durian by force vibration
and ultrasonic. International Journal of Uncertainty, Fuzziness and Knowledge-Based
Systems, 9(6), 703-719.
Krochta, J.M. (1997). Film, edible. In A.L. Brody and K.S. March (Eds). The Wiley
Encyclopedia Of Packaging Technology. (pp. 397-401). NY. John Wiley and Sons.
Kwangwaropas, M., and Sukjaroen, A. (1997). Research and Development of a
General Purpose Coconut Dehusking Machine. Research Report funded by Kasetsart
University Research and Development Institute, Kasetsart University, Bangkok. 28 p.
Le Tien, C., Vachon, C., Mateescu, M.A. and Lacroix, M. (2001). Milk protein
coatings prevent oxidative browning of apples and potatoes. J. Food Sci., 66, 512516.
Lee, J.Y., Park, H.J., Lee, C.Y. and Choi, W.Y. (2003). Extending shelf-life of
minimally processed apples with edible coatings and antibrowning agents. Lebensm.Wiss U.-Technol. 36, 323-329.
Lerdthanangkul, S. and Krochta, J.M. (1996). Edible coating effects on postharvest
quality of green bell peppers. J. Food Sci., 61, 176-179.
Mahayothee, B., Leitenberger, M., Neidhart, S., Muhlbauer, W., and Carle, R. (2002).
Non-destructive determination of fruit maturity of Thai mango cultivars by near
infrared spectroscopy. Proceedings of International Symposium Sustaining Food
Security and Managing Natural Resources in Southeast Asia-Challenges for the 21st
Century, January 8-11, 2002, Chiang Mai, Thailand.
McHugh, T.H. and Olsen, C.W. (2004). Tensile Properties of Fruit and Vegetable
Edible Films. United Stated-Japan Cooperative Program In Natural Resources, 104108.
McHugh, T.H. and Senesi, E. (2000). Apple wraps: a novel method to improve the
quality and extend the shelf-life of fresh-cut apples. J. Food Sci., 65, 480-485.
McHugh, T.H., Huxsoll, C.C. and Krochta, J.M. (1996). Permeability properties of
fruit puree edible films. J. Food Sci., 61, 88-91.
Meeklangsaen, W., Jarimopas, B., Terdwongworakul, A., and Chantong, S. (2007).
Some physical characteristics, mechanical, sound, and physiological properties of a
young coconut fruit. Proceedings of of the 7th National Seminar on “Research
Enhancing the Potential of Thai Agricultural Commodities in the World Market”,
302
[76]
[77]
[78]
[79]
[80]
[81]
[82]
[83]
[84]
[85]
[86]
[87]
[88]
[89]
[90]
[91]
Organized by Thai Society of Agricultural Engineering and Faculty of Engineering,
Mahasarakhanm University, 23-24 January 2006, Mahasarakhanm, Thailand.
Mizrach, A.N., Galili, N., and Rosenhouse, G. (1989). Determination of fruit and
vegetable properties by ultrasonic excitation. Transactions of the ASAE, 32(6), 20532058.
Mohsenin, N.N. (1984). Electromagnetic Radiation Properties of Foods and
Agricultural Products, Gordon and Breach Science Publishers, New York.
Mohsenin, N.N. (1996). Physical Properties of Plant and Animal Materials. Gordon
and Breach Publishers, New York, 891 p.
Nasution, D., Suroso, A., Budiastr, I.W., Trisnobudi, A., and Purwadaria, H.K.
(2005). Sortation of mangosteen using ultrasonic as a non-destructive evaluation
system. Proceedings of National Seminar on Innovative Post-harvest Technology for
Agro-based Industry, Bogor, Indonesia, 7-8 September 2005.
Nisperos-Carriedo, M.O. and Baldwin, E.A. (1994). Method of increasing the stability
of fruits, vegetables or fungi and composition thereof. US Patent 5, 376, 391.
Nordby, H.E., Purvis, A.C. and Yelenosky, G. (1987). Lipids in peel of grapefruit and
resistance to chilling injury during cold storage. HortScience, 22, 915-917.
Office of Thai Agricultural Commodity and Food Standard. (2003). Durian. Thai
Agricultural Commodity and Food Standard. TACFS 3-2003, Ministry of Agricultural
and Cooperative, Bangkok, Thailand, 6 p.
Olivas, G.I. and Barbosa-Canovas, G.V. (2005). Edible coatings for fresh-cut fruits.
Critical Reviews in Food Science and Nutrition, 45, 657-670.
Olivas, G.I., Mattinson, D.S. and Barbosa-Canovas, G.V. (2007). Alginate coatings
for preservation of minimally processed ‘Gala’ apples. Postharvest Biology and
Technology., doi:10.1016/j.postharvbio.2006.11.018.
Ozaki, Y., Morita, S., and Du, Y. (2007). Spectral analysis. In Ozaki, Y., McClure,
W.F., and Christy, A.A., (Eds.), Near-Infrared Spectroscopy in Food Science and
Technology.(pp. 47-72). John Wiley and Sons, New Jersey.
Park, H.J. and Chinnan, M.S. (1990). Properties of edible coatings for fruits and
vegetables. ASAE Paper No. 90-6510, 19 pp.
Paull, R.E. (1999). Effect of temperature and relative humidity on fresh commodity
quality. Postharvest Biol. Technol., 15, 263-277.
Pechsmai, A. (2002). Design and development of a young coconut peeling machine.
Master Engineering Thesis, Department of Agricultural Engineering, Graduate
School, Kasetsart University, Kamphaengsaen, Nakohnpatom, Thailand. 97 p. (in
Thai)
Perez-Gago, M.B. and Krochta, J.M. (2001). Lipid particle size effect on water vapor
permeability and mechanical properties of whey protein-beeswax emulsion films. J.
Agric. Food Chem., 49, 996-1002.
Perez-Gago, M.B., Rojas, C. and del Rio, M.A. (2003). Effect of hydroxypropyl
methylcellulose-lipid edible composite coatings on plum (cv. Autumn giant) quality
during storage. J. Food Sci., 68, 879-883.
Perez-Gago, M.B., Serra, M. and del Rio, M.A. (2006). Color change of fresh-cut
apples coated with whey protein concentrate-based edible coatings. Postharvest Biol.
Technol., 39, 84-92.
[92]
[93]
[94]
[95]
[96]
[97]
[98]
[99]
[100]
[101]
[102]
[103]
[104]
[105]
[106]
Perez-Gago, M.B., Serra, M., Alonso, M., Mateos, M. and del Rio, M.A. (2005).
Effect of whey protein- and hydroxypropyl methylcellulose-based edible composite
coatings on color change of fresh-cut apples. Postharvest Biol. Technol., 36, 77-85.
Plotto, A., Goodner, K.L. and Baldwin, E.A. (2004). Effect of polysaccharide coatings
on quality of fresh cut mangoes (Mangifera indica). Proc. Fla. State Hort. Soc., 117,
382-388.
Pushapriksha, P., Singh. S. P., and Jarimopas, B. (2006). Post-harvest loss and
performance comparison of wholesale packaging of mangosteen fruit under simulated
vibration. Proceedings of the 15th IAPRI World Conference on Packaging, Oct 3-5,
2006, Tokyo., 285-289.
Pushpariksha, P., and Jarimopas, B. (2006). Post-harvest damages and some
mechanical properties of mangosteen fruits. Agricultural Science Journal,. 37(2)
Supplement , 242-245.
Quezada Gallo, J.A., Diaz Amaro, M.R., Gutierrez Cabrera, D.M.B., Castaneda
Alvarez, M.A., Debeaufort, F. and Voilley, A. (2003). Application of edible coatings
to improve shelf-life of Mexican guava. Acta Hort., 599, 589-594.
Rachanukroa, D. Singh, S. P. and Jarimopas, B. (2006). Postharvest damage and
performance comparison of sweet tamarind wholesale packaging. Proceedings of the
15th IAPRI World Conference on Packaging, October 4-5, 2006, Tokyo. p 209-213.
Rachanukroa, D. Singh, S. P., and Jarimopas, B. (2007). Development of sweet
tamarind pod retail packaging. Proceeding of the International Conference on
Agricultural, Food and Biological Engineering and Post Harvest/Production
Technology, organized by Thai Society of Agricultural Engineering, American
Society of Agricultural and Biological Engineers, and Faculty of Engineering, Khon
Kaen University, 21-24 January, Sofitel Raja Orchid Hotel, Khon Kaen, Thailand.
Rachanukroa, D., Singh, S. P., and Jarimopas, B. (2006). Postharvest damage and
performance comparison of sweet tamarind wholesale packaging. Proceedings of the
15th IAPRI World Conference on Packaging, Oct 3-5, 2006, Tokyo., 209-213.
Rakotonirainy, A.M., Wang, Q. and Padua, G.W. (2001). Evaluation of zein films as
modified atmosphere packaging for fresh broccoli. J. Food Sci., 66, 1108-1111.
Ryall, A.L. and Lipton, W.J. (1979). Handling, Transporatation and Storage of Fruits
and Vegetables, Vegetables and Melons, (Vol. 1, pp 293-306). Westport, CT: AVI
Publishing Company, Inc.
Salveit, M.E. (2003). Is it possible to find an optimal controlled atmosphere?
Postharvest Biol. Technol., 27, 3-13.
Saputra, D., Budiastra, I.W., and Purwadaria, H.K. (1995). Classification of mango by
near infrared diffuse reflectance. Proceedings of Food Processing Automation IV,
Chicago, ILL, USA, 3-5 November, 1995, ASAE.
Sarakan, S. (2006). Mechanical Properties of Thai Rose Apple Fruit. Unpublished
Master Engineering Thesis, Department of Agricultural Engineering, Graduate
School, Kasetsart University, Kamphaengsaen, Nakohnpatom, Thailand 184 p.
Schiffmann-Nadel, M., Lattar, F.S. and Waks, J. (1971). The response of grapefruit to
different storage temperatures. J. Am. Soc. Hortic. Sci., 96, 87-90.
Sihawong, S. (2005). Design and testing of a machine cutting and opening umpire
durian for durian chip processing using hydraulic system. Kasetsart Journal, 36(5-6)
supplement, 133-136.
304
[107] Sirisomboon, P., Boonmung, S., Pornchaloempong P., and Pithuncharurnlap, M. (in
press). A Preliminary Study on Classification of Mango Maturity by Compression
Test. International Journal of Food Properties.
[108] Sothornvit, R. and Krochta, J.M. (2000). Plasticizer effect on oxygen permeability of
beta-lactoglobulin films. J. Agri. Food Chem., 48, 6298-6302.
[109] Sothornvit, R. and Krochta, J.M. (2001). Plasticizer effect on mechanical properties of
beta-lactoglobulin films. J. Food Eng., 50, 149-155.
[110] Sothornvit, R. and Pitak, N. (2007). Oxygen permeability and mechanical properties
of banana films. Food Research International, 40, 365-370.
[111] Sothornvit, R. (2005). Edible film formation and properties from different protein
sources and orange coating application. Acta Hort,. 682, 1731-1738.
[112] Srinivasa, P.C., Baskaran, R., Ramesh, M.N., Harish Prashanth, K.V. and
Tharanathan, R.N. (2002). Storage studies of mango packed using biodegradable
chitosan film. Eur. Food Res.Technol., 215, 504-508.
[113] Supsomboon, T. (1998). Young coconut fruit opening device. National Research
Council of Thailand Report. p 80-83. Ministry of Science, Technology and
Environment.
[114] Susanto, Suroso, Budiastra, I.W., and Purwadaria, H.K. (2000). Classification of
mango by artificial neural network based on Near Infrared Diffuse Reflectance.
Prodeedings of 2nd IFAC/CIGR International Workshop on Bio-Robotics II, Sakai,
Osaka, Japan, 25-26 November, 2000, Pergamon Press.
[115] Tanada-Palmu, P.S. and Grosso, C.R.F. (2005). Effect of edible wheat gluten-based
films and coatings on refrigerated strawberry (Fragaria ananassa) quality. Postharvest
Biol. Technol., 36, 199-208.
[116] Teerachaichayut, S., Kil, K.Y., Terdwongworakul, A., Thanapase, W., and Nakanishi,
Y. (2007). Non-destructive prediction of translucent flesh disorder in intact
mangosteen by short wavelength near infrared spectroscopy. Post-harvest Biology
and Technology, 43 (2), 202-206.
[117] Terdwongworakul, A., and Neamsorn, N. (2006). Non-destructive maturity
measurement of “Montong” durian using stem strength and resonant frequency. KKU
Engineering Journal, 33(5) 555-563. (in Thai).
[118] Terdwongworakul, A., and Suppattakul, P. (2005). Development of baby corn
husking machine using rollers, Proceeding of NSTDA Annual Conference 2005, 28-30
March 2005, Science park of Thailand, National Science and Technology
Development Agency, Thailand (in Thai).
[119] Terdwongworakul, A., Srichonpet, S., Poniyom, K., and Sukchareon, A. (1997).
Investigation of change of exponential frequency index as related to durian maturity.
Proceedings of 5th International Symposium on Fruit, Nut, and Vegetable Production
Engineering, 3-10 September 1997, UC Davis, California USA.
[120] Terdwongworakul, A., Srichonpet, S., Poniyom, K., and Sukchareon, A. (1998).
Frequency index as related to maturity stage of 'Montong' durian. Journal of the
National Research Council, 30(1-2), 25-38. (in Thai).
[121] Thongkamthamachat, S. and Timinkul, A. (2000). Comparative study on the
performance of foam net and air bubble plastic sheet protecting fruit under impact. M.
Eng. Special Problem Report. Department of Agricultural Engineering, Graduate
School, Kasetsart University, Kamphaengsaen, Nakohnpathom, Thailand. 25 p.
[122] Timoshenko, S. P., and Goodier, J.N. (1970). Theory of Elasticity. McGraw-Hill
Kogakusha, Ltd.
[123] Toomsaengthong, S., Singh. S. P, and Jarimopas, B. (2006). Post-harvest loss and
development of wholesale packaging of fresh rose apple. Proceeding of the 15th
IAPRI World Conference on Packaging, Oct 3-5, 2006, Tokyo, 280-284.
[124] Upchurch, B.L., Miles, G.E., Stroshine, R.L., Furguson, E.S., and Emerson, F.H.
(1987). Ultrasonic measurement for detecting apple bruises. Transactions of the
ASAE, 30(3), 803-809.
[125] USFDA. (2001). Microbiological safety of controlled and modified atmosphere
packaging of fresh and fresh-cut produce. In Analysis And Evaluation Of Preventive
Control Measures For The Control And Reduction/Elimination Of Microbial Hazards
On Fresh And Fresh-Cut Produce. 2 April 2007. Available from:
http://www.cfsan.fda.gov/~comm/ift3-toc.html
[126] Vanichang, J., and Jarimopas, B. (2007). Some mechanical, physiological and light
properties of dragon fruit. Proceedings of of the 7th National Seminar on “Research
Enhancing the Potential of Thai Agricultural Commodities in the World Market”,
Organized by Thai Society of Agricultural Engineering and Faculty of Engineering,
Mahasarakhanm University, 23-24 January 2006, Mahasarakhanm, Thailand.
[127] Wang, J.K. (1963). Design of a ground berry husking machine. Transactions of the
ASAE, 6(4), 211-213.
[128] Wong, D.W.S., Camirand, W.M. and Pavlath, A.E. (1994). Development of Edible
Coatings for Minimally Processed Fruits and Vegetables. In J.M. Krochta, E.A.
Baldwin and M.O. Nisperos-Carriedo (Eds.), Edible Coatings And Films To Improve
Food Quality. (pp. 65-88). Lancaster, PA, Technomic.
[129] Yamamoto, H., Iwamoto, M., and Haginuma, S. (1980). Acoustic impulse response
method for measuring natural frequency of intact fruits and preliminary applications
to internal quality evaluation of apples and watermelons. Journal of Texture Studies,
11, 117-136.
Chapter 4
DEVELOPMENT OF GEL PRODUCTS CONTAINING
FRUIT PIECES USING OSMOTIC TREATMENTS
WITHOUT BY-PRODUCT GENERATION
N. Martínez-Navarrete*, M.M. Camacho*,
E. García-Martínez* and M.E. Martín-Esparza*
Polytechnic University. Food Technology Department – Institute of Food
Engineering for Development. Camino de Vera s/n. 46022. Valencia, Spain
ABSTRACT
Fruits are products of a very important nutritional interest. Nevertheless, and mainly
due to their relatively short shelf-life and modern-day eating habits, the level of
consumption is below that recommended by the World Health Organization. In this
sense, the development of foods with a high fresh or processed fruit content, that
maintain the nutritional and sensorial properties of the fresh fruit, may contribute to
stimulating the interest of the consumer, thus increasing the product consumption.
Osmotic dehydration (OD) techniques have been widely applied in fruit processing, since
they require little energy and allow us to obtain high quality products. However, its
industrial use may be limited by the management of the osmotic solution (OS). To solve
this problem, the re-use of the OS in more than one OD cycle, with or without a previous
re-concentration stage, may be considered. When there is no re-concentration, the re-use
will be limited by the possible microbiological contamination and by the progressive
dilution that takes place after each OD cycle, which may affect the kinetics of the osmotic
process. On the other hand, as some native hydrosoluble compounds, such as volatiles,
acids, minerals, vitamins and phytochemicals, will be released together with water into
the OS during OD, its management as an ingredient in some product formulation seems
*
[email protected]
*
[email protected]
*
[email protected]
*
[email protected]
308
N. Martínez-Navarrete, M.M. Camacho, E. García-Martínez et al
to be an interesting alternative. To this end, this work analyses the viability of
formulating a fruit-gel product with the osmodehydrated fruit (strawberry, kiwi or
grapefruit) and the re-used OS obtained from the dehydration step, in order to diminish
the loss of flavour, aroma and functional components of the fruit and avoid the generation
of by-products in the process. In this study, the number of OS re-use cycles has been
optimized, on the basis of its microbial recounts, the dilution level, the solution
enrichment in fruit bioactive compounds, the fruit-solution ratio used during the
dehydration step and the fruit-gel ratio in the final product. The kind and concentration of
gelling agents, which best favour the properties of aspect (transparency) and texture of
the gels, taking the peculiar composition of the re-used OS used as gelling medium into
account, have been identified. The conditions in which the fruit pieces are mixed with the
gelling solution have also been studied and defined. Finally, the fruit-gel product
formulation conditions have been optimized, on the basis of its sensory acceptance and its
compositional stability during storage, ensuring the thermodynamic equilibrium between
the fruit and the gel when mixed. The microbiological stability of the product was of at
least 15 days in refrigerated storage. During this time, the evolution of some properties
such as phytochemicals, vitamins, acids, volatile compounds, colour and texture was
studied.
INTEREST OF DEVELOPMENT OF GEL PRODUCTS
CONTAINING FRUIT PIECES
Fruits are an important part of the human diet, contributing some micro-nutrients, such as
fibre, minerals, acids and vitamins. They also contain other non-nutritive substances, called
phytochemicals, that mainly include terpenes and phenolic compounds, some of which are
important from a sensorial point of view (King and Young, 1999; Belnstein, 2001). All these
compounds may be included in the group of bioactive substances, as their intake seems to
have a significant impact on the prevention of some diseases such as different kinds of cancer,
cerebro and cardiovascular diseases, (Klein and Kurilich, 2000; Wargovich, 2000; Kaur and
Kapoor, 2001; Hertog, Hollman, and Van de Putte, 1993), strokes, Alzheimer's disease,
cataracts and some of the functional declines associated with ageing (Rui-Hai-Liu, 2003). Its
biological effects include antioxidant activity (Ming-Liu et al., 2002; Prior and Guohua-Cao,
2000; Wolfe et al., 2003), antimutagenic (Wargovich, 2000), antibacterial and angioprotective
properties (Venant et al., 1989).
Nevertheless, in general, fruits are products with a relatively short post-harvest life-span,
mainly due to their high water content. This fact, together with modern-day eating habits
(easy, quick-to-eat food, food purchased with a relatively long life utility), have led to a drop
in the consumption of fresh fruit, especially among the young, which has been replaced by
juices, dairy products with added fresh or processed fruits, preserves, confectioneries, etc.
(Torreggiani and Bertolo, 2001). Although there is an ample supply of this type of products, it
is important to point out that many of them have minimum fruit content, which is replaced, in
many cases, by a great number of additives. In this sense, developing another kind of food
with a high content in fresh or minimally processed fruit seems to be of great interest. The
latter will lead to a longer product shelf-life while maintaining the nutritional and sensorial
properties (aroma, flavour, colour and texture) of the fresh fruit, thus trying to stimulate the
interest of the consumer and to contribute to the acceptance of the product.
Development of Gel Products Containing Fruit Pieces Using Osmotic…
309
The possibility of developing fruit-gel products has been studied since the 1980s. In fact,
in a conducted bibliographical revision, numerous patents have been found, some of them
related to the selection or preparation method of the gelling agents (Gliksman and Farkas,
1974; Shank, 1985; Prest and Buckley, 1986; Musson and Prest 1988) and others that
describe diverse products. Among these can mainly be found products like “artificial fruit”.
These are made with either texturized fruit-flavoured gels (Cheney et al., 1984) or with added
fruit juice or crushed fruit (Fleck and Schindler, 1991; Jensen, 1991) or both and, in some
cases, they are shaped like a fruit (Trilling and Smadar, 1984; Elisabelar and Albelda, 1985;
Okonogi et al., 1989; Kaletunc et al., 1990). Dehydrated fruit-gels have also been described
(Arnstein et al., 1974; Wust et al., 1985) that are sometimes used to simulate the presence of
pieces of fruit in the elaboration of products like ice creams, cereals, jams, etc. (Walter and
Funk, 1998; Aoki et al., 2000; Gordon et al., 2001).
Nevertheless, no references have been found describing a gel product that includes an
important proportion of fresh or processed fruit portions. If the hydrocolloids are selected
carefully, the resulting food could be highly attractive to the eyes of the consumer, as long as
it is possible to formulate a gel with not only a high level of transparency, thus allowing the
content and type of fruit to be identify, but also with a high nutritious value and one that is
easy to consume. A reasonable shelf-life must be contemplated by theses products, one which
offers suitable commercialization margins, as much in terms of its security as of any changes
in its physical and sensorial properties. From this point of view, it is more advisable to
manufacture the product with partially dehydrated fruit. However, it is crucial that this
product maintains, as far as possible, the highest quality characteristics of the fresh fruit.
Osmotic dehydration (OD) with sugared solutions has been widely applied for minimal
fruit processing (Fito et al., 2001, Alzamora et al., 1997; Tapia de Daza et al., 1999). Its
application is technologically simple, since it consists of submerging the sample into a high
osmotic pressure solution at temperatures that can be moderate, so that a two-way mass
transfer is established: water and some natural soluble substances flow out of the fruit into the
osmotic solution (OS), and in the opposite direction, soluble solutes may be transferred from
the solution to the fruit. This method has received considerable attention due to the low
energy requirements (Taiwo et al., 2001) and fruit quality improvement (Heng, Guilbert and
Cup, 1990; Panagiotou, Karathanos and Maroulis, 1998), compared to alternative processes.
As fruits are not submitted to high temperatures, sensory attribute changes, such as colour,
aroma, flavour and texture, are minimised (Heng et al., 1990; Raoult-Wack, 1994; Fito et al.,
1995). Moreover, in comparison with other traditional drying treatments, OD only slightly
affects the food structure because water elimination does not involve phase changes (Forni et
al., 1987; Pinnavaia et al., 1988; Giangiacomo et al., 1994). Despite the above mentioned
advantages, one limitation to the industrial application of OD may be the management of the
osmotic solution (Torreggiani and Bertolo, 2001; Dalla-Rosa and Giroux, 2001). During OD, it
must be taken into account that the fruit releases some of its natural components into the
external solution, together with water. Some of these components, like soluble fibre, organic
acids, mineral salts, vitamins and phytochemicals, are interesting from the nutrition and health
point of view. For this reason, the use of OS as an ingredient in new product formulation is an
interesting alternative for its final management. In this case, the previous re-usability of OS in
several OD cycles would suppose, in addition to a decrease in generated by-products, that more
and more of these bioactive compounds are accumulated. There are authors who propose that it
be used as a syrup for fruit canning or as a component of carbonated fruity soft drinks (Dalla-
310
Rosa and Giroux, 2001). However, the development of products that not only use all the
dehydrated fruit but also all the OS necessary for its dehydration would be kinder on the
environment and would allow for a greater supply of fruit products in the market. In the face of
modern-day eating habits, this would be of great interest as it would both encourage fruit
consumption and also make it easier, thus promoting a healthier diet. The use of OS in the
formulation would not only contribute to improving the aroma and flavour of the fruit, but also to
recovering some of the micro-nutrients and other bioactive substances lost by it during the
osmotic processing. In this sense, some investigations reflect, for example, the possibility of
elaborating stable jams from OD fruit and the OS, without the use of a heat treatment. These
jams would be of a higher quality than conventional ones, in which the high cooking
temperatures entail undesirable changes in the sensorial (colour, texture, flavour) and nutritional
(mainly loss of vitamin C) properties (Shi et al., 1996; García-Martinez et al., 2002b).
As the objective is to extend the supply of this type of foods, this chapter describes the
methodology followed in order to develop a fruit-gel product, formulated from dehydrated fruit
and the actual osmotic solution used in the dehydration operation. The intention is to obtain a
product with a relatively long shelf-life (at least 15 days in refrigeration) by means of a
manufacturing process which is viable, economically profitable and that does not, as far as
possible, generate any by-products. Therefore, re-using the osmotic solution in successive OD
cycles before its final use in the formulation of the product has been considered. The
optimisation of the number of re-use cycles depends on the dilution level reached by the OS
after each OD cycle, related to the dehydration level of the obtained fruit, the microbiological
aspects, the fruit-solution ratio in the dehydration step and the fruit-gel ratio in the final
product. The presence in the OS of bioactive compounds that come from the fruit will
constitute an additional advantage, from the nutritional point of view of the developed
product. By using the osmotic solution as gelling medium, the kind of gelling agents and their
concentration which provide the best properties of aspect and texture to the gels, also have to
be considered. The operating conditions of the step when the fruit pieces are mixed with the
gelling solution (mixing step) are defined. Another aspect of interest relating to the quality of
the product and its changes during storage, and which is considered in this chapter, is the
fruit-gel interaction, which defines the transport of components (mainly water), if neither
phase is near the thermodynamic equilibrium. This transport may alter the properties of the
gel and the fruit, changing the quality of the product to a remarkable extent. It is therefore
necessary to adjust the water activity of the fruit and gel phases when designing this type of
products. All these questions are developed in the following sections.
THE USE OF OSMOTIC DEHYDRATION FOR THE
FORMULATION OF FRUIT-GEL PRODUCT’S
Osmosis is a phenomenon that occurs when two liquids or gases with different
concentrations of a certain substance are separated by a membrane permeable only to some
components. The differences in chemical potential of the components on both sides of the
membrane will promote the flow of those to which this membrane is permeable, in an attempt
by the system to reach thermodynamic equilibrium. The characteristic tissue of the fruits is
cellular in structure, so that most of its liquid fraction finds bulkhead by membranes that are
311
selectively permeable to the water. Thus, when a fruit is submerged in a concentrated sugar
solution, an osmotic dehydration takes place. However, simultaneous to the osmotic
mechanism, capillary and diffusion mechanisms promote a solute outflow from the fruit
towards the external solution and a solute inflow from the solution towards the fruit. The
interchange of all these components will continue until the system reaches thermodynamic
equilibrium. Normally, however, the rate of water flow in the osmotic processes is high
during the first 2-3 hours and the interchange of solutes takes place during the first 30 min of
treatment (Conway et al., 1983; Giangiacomo et al., 1987; Martínez-Monzó, 2002). As the
interchange of matter from these levels of concentration occurs much more slowly, in
practical terms (with a reasonable processing time), OD is not advisable to obtain reductions
in water content of over 50%. This means foods with an aw>0.90.
Mass transfer rates during OD operations depend on factors such as type, size and
geometry of the sample, type and concentration of the osmotic medium, degree of agitation of
the solution, working pressure, temperature and sample to solution ratio (Taiwo et al., 2001).
At a macroscopic level, the OD operation has been modelled for many foods in general, in
particular for many fruits, under different process conditions (Fito et al., 2001; Fito and
Chiralt, 1997; Talens, 2002). This allows us to know how much process time is needed to
reach a desired concentration level in the product.
The fruits selected for the development of the gel product were kiwifruit (Actinidia
chinensis P. var. Hayward), grapefruit (Citrus paradise var. Star Ruby), pineapple (Ananas
comosus) and strawberry (Fragaria ananassa var. Camarosa). In the first three cases, the
fruits were cut into 1 cm thick slices, the kiwifruit had an external diameter of 4,4 cm and the
pineapple of 8.5 cm, and they were dehydrated until a final water content of 75%. The
strawberry was cut in half and dehydrated until reaching a water content of 80%. The osmotic
treatment was carried out with a 55 ºBrix sucrose solution, at 30 ºC while being stirred
continuously. In every case but one it was processed at atmospheric pressure. The exception
was grapefruit, in which a 10 min vacuum pulse (50 mbar) was applied at the beginning of the
process, in order to accelerate the fruit’s dehydration. The ratios of fruit:osmotic solution
were 1:4 for strawberry, 1:5 for grapefruit, 1:5, 1:10 and 1:20 for kiwifruit and 1:20 for
pineapple. Under these conditions, the total process times were 1 h for kiwifruit, 3 h for
grapefruit and strawberry and 2 h for pineapple. The previously mentioned operating
conditions were established on the basis of prior experiments of dehydration kinetics carried
out on each fruit (García-Pinchi, 1998; Talens, 2002; Valero, 2003; Moraga, 2007) and the
results obtained from the study of different factors, like the temperature or the ratio of
fruit:OS applied in the osmotic treatment. Thus, in the case of the strawberry, the effect of
temperature both on the process time and on some quality characteristics of the obtained fruit,
such as the citric and ascorbic acid contents, texture, colour and aroma, was evaluated. An
experiment was performed under the same conditions as mentioned above, but at 20 ºC,
which meant that twice the process time without significantly improving the quality of the
strawberry (Penagos, 2006). The study to evaluate the influence of the ratio of fruit:OS was
carried out on kiwifruit. Some aspects of this study are mentioned in the following
paragraphs, although the final conclusion obtained was that, under the tested conditions,
working with the smallest amount of OS, does not affect the dehydration kinetics of the fruit.
However, it has to be pointed out that all the fruit pieces have to be totally submerged in the
OS, which also conditions the required OS volume. This was the reason why it was necessary
to work with a ratio of 1:20 in the case of pineapple.
312
One of the aims of the designed product was to avoid by-product generation. In OD
processes, the by-product is the osmotic solution used for fruit dehydration. When this must be
discharged as wastewater, the main problem to be considered is related to the high
biochemical oxygen demand (BOD5). For this reason, prior to being drained into the public
sewer, a preliminary sanitation must be carried out by using ion exchange resins, reverse
osmosis, micro- and ultra-filtration, etc. (Dalla-Rosa and Giroux, 2001), which increases the
process cost. As an alternative to OS management, the possibility of re-using it in successive
OD cycles and its final use in food formulations may be considered. When re-using it, with or
without a previous re-concentration stage, the possible microbiological contamination must
be considered. The re-concentration stage and hygienization would also suppose an additional
cost to the process, whereas its re-usability without previous treatments will be mainly limited
by the changes that take place during the process. This is because the progressive OS dilution
after each OD cycle could cause a slowing down of the mass transfer rate and the consequent
extension of the osmotic process.
Thus, the first aspect to be tackled in this study, prior to developing the fruit-gel product,
was to determine the viability of the direct re-use of the OS in further OD processes,
achieving the same efficacy with respect to the dehydration level reached by the fruit without
affecting its microbiological quality. An exhaustive parallel analysis of the effect of the
osmotic dehydration on the composition of the fruits, as well as on the changes suffered by
the OS during its re-usability, was carried out. The aim of this study was to know if the final
use of OS in the elaboration of the product proposed in this chapter was of interest, on the
basis of an enrichment in micro-nutrients and other bioactive substances that come from the
fruit. Successive OD operations or cycles were programmed for every fruit being tested, so
that in each cycle the fruit was renewed but the OS was re-used in the subsequent cycles, with
no previous re-concentration treatment. In each cycle, the soluble solids (ºBrix) and aw of the
fruits and OS before and after the OD were analyzed, as well as the water content (xw) of the
fruit before and after the OD. In the case of kiwifruit, the influence of the fruit:OS ratio on the
characteristics of the obtained dehydrated fruit was verified.
As to the characteristics of the fresh fruit, the analysis of variance (ANOVA) carried out by
studying the ºBrix, xw and aw of different batches of each fruit used in the study showed
significant differences (α<0.05) in xw and ºBrix. Nevertheless, this compositional variability, that
seems to be normal in this kind of raw material, was not reflected by significant differences in the
aw of the pieces (α>0.05). Table 1 shows the mean values of these properties in the fruits under
study.
Table 1. Water content (xw), soluble solid content (ºBrix) and water
activity (aw) of different batches of the fresh fruits implied in all the OD cycles
Fruit
ºBrix
aw
Kiwifruit
Grapefruit
Pineapple
Strawberry
14.9±0.6
12.5±0.6
12±1
8,0±1,4
0.987±0.006
0.9895±0.0012
0.989±0.001
0,994±0,002
Values expressed as mean±standard deviation.
xw
(g water/100g sample)
83.6±0.6
86.4±0.6
87±2
-
313
Figure 1 and tables 2 and 3 show the results obtained with kiwifruit, with which 10
successive OD cycles were programmed working with three fruit:OS ratios: 1:20, 1:10 and 1:5,
and with the other three fruits under study. Figure 1 shows the decrease in the soluble solid
content and the increase in the water activity observed in the OS after each of the different
OD cycles considered and, in the case of kiwifruit, for the three fruit:OS ratios considered. As
expected, the greater the number of OS re-uses and the higher the dehydrated fruit ratio (1:5),
the greater the syrup dilution.
Figure 1. Mean ºBrix (full symbols) and aw (hollow symbols) values of osmotic solution (OS) at different
osmotic dehydration cycles and fruit:OS ratios.
■ Kiwifruit (1:20), ■ Kiwifruit (1:10), ■ Kiwifruit (1:5)
♦Grapefruit (1:5), ▲ Pineapple (1:20), • Strawberry (1:4). Lines correspond to predicted values from
correlation equations fitted between both variables (table 4): (—) ºBrix; (---) aw..
Table 2 shows ºBrix, xw and aw of dehydrated kiwifruit. If the progressive OS dilution
observed when re-using it had a significant effect on the osmotic dehydration kinetics, a
different dehydration level in the fruit processed in each OD cycle could be expected. The
statistical study carried out using an ANOVA, taking the cycle factor into account for each
fruit:OS ratio, only showed a significantly (α<0.05) greater soluble solid content in the 1:20
fruit:OS ratio and for the first two cycles, thus confirming a greater effectiveness of the OD
process in these cases. In all the other cases, the observed differences of these two properties
may be related more to differences in the raw matter than to the diluting effect of the OS, as
no clear cycle-related tendencies can be pointed out. Nevertheless, aw was not significantly
affected by the re-use of the OS. Similar results were obtained with grapefruit, pineapple and
strawberry during 8, 15 and 7 consecutive OD cycles with the same OS, respectively (Table
3). From this point of view, an OD process consisting of a ratio of fruit:OS of around 1:5 and
the re-usal of the OS for different subsequent OD cycles, can be recommended. Under these
conditions, and in the programmed time, it is possible to obtain fruit with the same stability
314
(aw), while reducing the generated waste, which is important in order to make the OD process
more profitable.
Table 2. ºBrix, aw and xw (g/100 g dehydrated fruit) of osmodehydrated kiwifruit obtained
when re-using the same osmotic solution for different cycles of osmotic dehydration
Cycles
1
2
3
6
10
Fruit:OS
1:20
1:10
1:5
1:20
1:10
1:5
1:20
1:10
1:5
1:20
1:10
1:5
1:20
1:10
1:5
ºBrixa
27.90
23.13
23.40
27.27
22.60
22.57
23.83
23.00
22.57
21.57
21.83
22.10
21.67
22.40
21.60
awb
0.979
0.981
0.981
0.980
0.978
0.980
0.981
0.981
0.979
0.979
0.980
0.983
0.982
0.978
0.979
xwc
69.9
76.5
74.3
74.1
75.4
75.9
70.7
75.3
75.2
76.8
76.2
76.3
75.5
75.7
77.2
a
Reproducibility lower than 0.15
c
Reproducibility lower than 0.2.
b
Table 3. ºBrix, aw and xw (g/100 g dehydrated fruit) of osmodehydrated grapefruit,
pineapple and strawberry obtained when re-using the same osmotic solution for
different cycles of osmotic dehydration
Cycles
1
2
3
4
5
6
7
8
9
12
15
Grapefruit (1:5)
ºBrixa
awb
23.0
0.981
23.1
0.979
24.3
0.976
21.4
0.986
22.3
20.0
0.983
22.5
21.7
0.980
xwc
76
74
76
78
80
78
Pineapple (1:20)
ºBrixa
awb
23.5
0.978
xwc
77
24.3
0.978
76
23.0
0.980
75
22.5
0.979
76
22.0
21.0
23.0
0.980
0.981
0.978
77
78
76
Strawberry (1:4)
ºBrixa
awb
14.4
0.981
13.2
0.979
13.4
0.981
11.6
0.986
13.6
0.979
11.6
0.988
11.6
0.984
a
c
Reproducibility lower than 3.
b
For all the above-mentioned properties, it was possible to propose simple empirical
equations (linear or polynomic) that allow us to predict their value based on the number of OS
uses (Table 4). These equations could be useful for determining the number of OD cycles that
can be carried out depending on which final water or soluble solid content is desired in the
OS, taking any possible final use into account.
315
Table 4. Parameters of the model (y=a+bx+cx2) fitted to predict ºBrix and
water activity (aw) of osmotic solution as a function of osmotic dehydration cycles. R2:
determination coefficient
Propiedad
Fruit
a
b
(*)
Kiwifruit
53.894
-1.156
Grapefruit
55.096
-2.4116
ºBrix
Pineapple
54.967
-0.4435
Strawberry
55.392
-4.0413
Kiwifruit(*)
0.922
0.0053
Grapefruit
0.9186
0.0089
aw
Pineapple
0.915
0.0022
Strawberry
0.9185
0.01
(*)
The fruit:OS ratio of 1:5 was the only one considered for kiwifruit.
c
0.0998
0.1669
-0.0005
-0.00004
-0.003
R2
0.9775
0.9982
0.9650
0.9972
0.993
0.9801
0.9650
0.9972
As concerns the microbiological aspects of the OS, which could also limit its re-use, it is
well known that osmotolerant or osmophilic micro-organisms are particularly tolerant to high
concentrations of sucrose and cause numerous problems in industrial activities where large
amounts of sugar are used. In this case, the presence in the syrup of viable micro-organisms
(counts in Plate Count Agar for 48–72 h at 30 ºC) and yeasts and moulds (counts in
Sabouraud Chloramphenicol Agar for 3–5 days at 30 ºC) were considered in the studies
carried out on kiwifruit (García-Martínez et al., 2002a) and grapefruit (Moraga et al., 2005).
The number of colony forming units (CFU) per ml of syrup was negligible in both cases (less
than 10 CFU for yeasts and moulds and ranging between <25 and <100 for total viable microorganisms). In general, the number of micro-organisms increased with the syrup uses, but it
did not reach a critical value that could not guarantee the microbiological stability of the
process (counts were always lower than 102 UFC/ml for yeasts and moulds and 104 for viable
micro-organisms, the legal limit for fruit and derivate products according to the
Microbiological Norm, Real Decree 670/1990 of May 25, B.O.E. 31-5-90), thus confirming
the possibility of OS re-usage. The pH of the OS after fruit OD, lower than 3.5 in every case,
probably contributes to this fact. In any case, in order to ensure a greater stability of the
osmodehydrated fruit in the gel formulated products considered in this study, a mild thermal
treatment of the OS before each cycle (heating to 72ºC for 30 s) has been proven to reduce
micro-organism counts (Moraga et al., 2005).
As regards the effect of OD on the micro-nutrients of the different fruits under
consideration, analyses of majority minerals (calcium and magnesium by atomic absorption
spectrometry, potassium and sodium by atomic emission spectrometry and phosphorus by
spectrophotometry, according to the method described by de la Fuente et al., 2003), ascorbic
acid (AA) (AOAC 985.33, 1997), citric acid (CA) (AOAC 985.33, 1997) and total pectin
(determined from the galacturonic acid, AGU, present in the fruit as described by Contreras et
al., 2005) were performed. These analyses allowed us to confirm the loss of hydrosoluble
components of the fruits as a result of the osmotic dehydration. Quantitatively, these are small
losses, yet since the compounds in question are also present in small amounts in the fruits,
they turn out to be important from the point of view of the nutritious value, as can be
observed in table 5. Thus, for the different fruits, average losses in the order of 25% of their
ascorbic acid and citric acid, 43% of their minerals and 20 % of the total pectin have been
316
quantified. In general, these losses depend neither on the number of re-uses of the OS nor on
the fruit:OS ratio (García-Martínez et al., 2002a; Peiró et al., 2006; Peiró-Mena et al., 2007;
Penagos, 2006).
Table 5. Citric acid (CA), ascorbic acid (AA), galacturonic acid (AGU) and minerals lost
by the different fruits during osmotic dehydration. Values correspond to mg of
compound loss/100 mg of the compound present in the fresh fruit
Compound
CA
AA
AGU
Ca
Mg
K
P
Na
Grapefruit
25±5
12±7
18±7
28±5
29±9
57±10
40±9
59±10
Pinneaple
34±8
non detected
21±9
59±21
26±10
44±13
30±12
41±13
Kiwifruit
22±5
30±5
9±3
23±17
11±7
20±7
55±12
10±1
Strawberry
12
35
-
Values expressed as mean±standard deviation.
In the case of grapefruit and strawberry, the flow of phytochemicals was also studied. In
strawberry the antocyanins, referred to pelargonidine – 3 glucoside, the main one present in
this fruit (Torreggiani et al., 1998;), were quantified, following the method described by
Alarcao-E-Silva et al. (2001). The amount present in the fresh fruit was found to be 19
mg/100 g. The osmotic treatment caused an antocyanin loss of 32%, part of which was
incorporated into the OS, thus conferring the reddish tonality particular to the strawberry. In
grapefruit, on the other hand, the analysis by reverse-HPLC of a methanol-water extract,
allowed us to identify and quantify 7 flavonoids: naringin, narirutin, hesperidin,
neohesperidin, poncirin, didymin and naringenin. Of these, the first three were the major
ones, being present in amounts of 103, 44 and 14.8 mg/100g, respectively whereas the rest
appear in quantities of between 5 and 8 mg/100 g. Losses in the order of 20%, referred to the
component present in the fresh fruit, were quantified for all of them, during the dehydration.
The incorporation into the OS of the components lost by kiwifruit, grapefruit and
pineapple during their dehydration, and which depends on the number of re-use cycles, was
studied (figures 2 and 3). In every case, a progressive compound enrichment in the osmotic
solution was observed, with a practically linear evolution. The increase in the citric acid
promoted a decrease in the pH of the OS, changing from around 6.5 when prepared, to nearly
3.5 just after the first OD cycle, with no greater changes in the rest of the OD cycles. As AC
is a weak acid, the observed change in its concentration from cycle 1 does not affect the pH.
Similar behaviour has been observed by Valdez-Fragoso et al., (1998) who studied changes in
60 ºBrix OS when used successively in apple dehydration after a reconcentration process. As
for the phytochemicals, some of the major flavonoids lost by grapefruit were also partially
recovered in the OS, naringin being the most abundant (9.6 mg/100 g OS re-used in eight OD
cycles).
317
Figure 2. Mean values (numerical values also appear in the table) of citric acid (CA), ascorbic acid (AA) and
galacturonic acid (AGU) analysed in the osmotic solution (OS) when re-used for different osmotic
dehydration cycles of kiwifruit (fruit:OS ratio of 1:5), grapefruit and pineapple.
Figure 3. Mean values (numerical values also appear in the table) of different minerals analysed in the osmotic
solution (OS) when re-used for different osmotic dehydration cycles of kiwifruit (fruit:OS ratio of 1:5),
grapefruit and pineapple.
318
Additionally, it was wanted to know the effect that the incorporation of these compounds
had on OS electrical conductivity and viscosity, as these two physical properties are relevant
for the characteristics of the gel that is going to be formulated to obtain the product.
The electrical conductivity (EC) of the syrup depends on its sugar concentration,
temperature, the chemical composition of the water used in its preparation and, probably, on
the type and concentration of the soluble components coming from the fruit. The distilled
water used to prepare OS had an EC = 4.13 ± 0.02 μS/cm which changed to 12.38 ± 0.05
μS/cm when sucrose was added to obtain the 55 ºBrix osmotic solution. For all the fruits
under study, compositional changes of OS during the OD process promoted an increase in EC
over the course of the OD cycles, as is shown in figure 4. When the EC of the OS was
compared to that of sucrose solutions which had the ºBrix of OS obtained after each OD cycle
(data shown in figure 1), much greater values were observed in the former (figure 4). From
these results, the observed progressive enrichment in soluble components coming from the
fruits may be confirmed as being mainly responsible for the observed EC increase. By means
of a stepwise multiple regression analysis procedure, Ca, Mg, P, AA and AC were found to be
the main components responsible for this EC increase in grapefruit (Peiró et al., 2006) and
pineapple (Peiró-Mena et al., 2007). The smaller amount of these compounds present in the
OS re-used for pineapple dehydration (figures 2 and 3), probably due to the lower fruit:OS
ratio used in the osmotic step in this case, may be what is responsible for the much lower EC
values obtained in this OS.
Figure 4. Mean values of electrical conductivity (EC) of the osmotic solution (OS) when re-used for different
osmotic dehydration (OD) cycles of kiwifruit with a fruit:OS ratio of 1:5 (■), grapefruit (♦) and pineapple
(▲). EC of a sucrose solution with the same ºBrix as the OS after different OD cycles of kiwifruit (□),
grapefruit (◊) and pineapple () also appears. Lines correspond to predicted values from correlation equations
fitted between both variables (table 6).
319
From the point of view of the viscosity studies, the OS obtained from the different OD
cycles of every fruit under consideration showed Newtonian behaviour when the flow-curve
was obtained in a Physica Rheolab MC1 rheometer at 25 ºC (shear rate sweep from 0 to 150
s-1 in 90 s) using a concentric cylinder sensor (internal radius=12.5 mm, external
radius=13.56 mm, height=37.5 mm). As observed in figure 5, with the re-use of OS a sharp
decrease in viscosity (μ) was observed, due to the fact that it becomes more diluted. For
pineapple OS, the lower fruit ratio dehydrated in each OD cycle led to a much less dilution
and so, much greater viscosity values. In this case, when the results obtained were compared
with the viscosity of sucrose solutions with the same ºBrix as the osmotic solutions obtained
after different OD cycles (data shown in figure 1; Pancoast and Junk, 1980), higher viscosity
values of the re-used OS were observed (figure 5). The pectin content detected in the OS may
be responsible for the observed differences, as this component contributes to an increase in
the viscosity. From these results, it can be deduced that both the sugar and pectin content, are
what is responsible for the OS viscosity.
Figure 5. Mean viscosity values (μ) of the osmotic solution (OS) when re-used for different osmotic
dehydration (OD) cycles of kiwifruit with a fruit:OS ratio of 1:5 (■), grapefruit (♦) and pineapple (▲).
Viscosity of a sucrose solution with the same ºBrix as OS after different OD cycles of kiwifruit (□),
grapefruit (◊) and pineapple () also appears. Lines correspond to predicted values from correlation equations
fitted between both variables (table 6).
Both EC and μ, were well correlated with the number of syrup uses by means of linear or
second grade polynomic relationships (Table 6). Lines in figures 4 and 5 show the predicted
values using these equations. These equations could be useful for determining the number of
OD cycles that can be carried out depending on what the OS is to be used for (in certain food
formulations) and so, which are its desired final properties. On the other hand, practical
equations were found to correlate EC and μ with OS ºBrix for all the cycles being studied
(table 7). Despite the close correlation obtained, it has to be remembered that, as commented
320
on above, μ and, especially, EC, are related to the presence of other fruit soluble solutes in the
OS, apart from sugar. So, the equations are only useful for predicting these two properties in
re-used osmotic solutions.
Table 6. Parameters of the model (y=a+bx+cx2) fitted to predict osmotic solution
electrical conductivity (EC) and viscosity (μ), depending on the cycles of re-use. R2:
determination coefficient
Property
EC
Fruit
Kiwifruit(*)
Grapefruit
Pineapple
Kiwifruit(*)
Grapefruit
Pineapple
a
-0.0144
0.9186
6.6309
0.0339
20.402
24.005
b
0.0514
51.679
8.8851
-0.0043
-3.1306
-0.9555
c
0
0
0
0.0002
0.1931
0.019
R2
0.9915
0.9949
0.9910
0.9708
0.9698
0.9885
(*)
Table 7. Parameters of the model (y=a+bx+cx2) fitted to predict EC and μ as a function
of ºBrix of re-used osmotic solutions. R2: determination coefficient
Fruit
Kiwifruit(*)
Grapefruit
Pineapple
Property
EC (mS/cm)
(mPa*s)
EC (mS/cm)
(mPa*s)
EC (mS/cm)
(mPa*s)
a
0.0025
368.3
5294.3
4175.5
3741.7
127.73
b
-0.2792
-16.712
-80.65
-157.78
-122.3
-5.7532
c
7.8876
0.1993
1.5418
1.4963
0.991
0.0703
R2
0.9998
0.9873
0.9927
0.9986
0.9899
0.975
(*)
From the results commented on above, the direct re-use of the OS in successive OD
cycles may be recommended, as there were no stability problems detected in the obtained
fruit, from either the point of view of the water activity or the microbiological counts.
Nevertheless, this implies that changes in the composition of the OS, related to the
incorporation of water and fruit soluble solutes, become more and more significant. These
affect some physical characteristics, such as EC and μ, which may be relevant when using the
spent osmotic solution for a gel formulation.
OPTIMIZATION OF PRODUCT FORMULATION IN A
PROCESS WITHOUT BY-PRODUCT GENERATION
Once the possibility of OS re-use was verified, both from the point of view of the
characteristics of the obtained fruit as well as from the interest of its use related to the
presence of fruit bioactive substances, the key to formulating the gel product from all the
dehydrated fruit and with the greatest quantity of the OS used in the osmotic process were
considered in order to avoid wastewater.
To find out some of the product’s possible problems, some first formulations were carried
out with and without dehydrated kiwifruit (obtained in the conditions described in the
321
previous chapter and using a fruit:OS ratio of 1:5), working with different solvent means and
gelling agents. As solvent means, sucrose solutions of 55ºBrix and pH=4 (SS1), simulating the
OS after one OD cycle, sucrose solutions of 40ºBrix and pH=3.5 (SS10), simulating the OS
after ten OD cycles, and finally the actual OS obtained after 10 OD cycles (OS10) were tested.
To select the gelling agents, food gelatine was dissolved in the OS10 according to the
manufacturer’s specifications. The fact that this system does not gel is probably due to the
presence of actinidine, a proteolytic enzyme characteristic of kiwifruit (Préstamo, 1995). This
enzyme may be liberated into the osmotic solution during the OD process, interfering with the
helicoidal three-dimensional net formation that characterizes the gelling process of this
collagen derivative (Imeson, 1997). For this reason, and because of the cultural problems of
using it in some diets due to its animal origin, gelatine was discarded for the formulation of
the product. Carrageenan was then tested, at concentrations of 0.5, 0.6 and 0.75 %, dissolved
in warm SS1 and SS10. Gels with different characteristics were obtained depending on the
hydrocolloid concentration (Ribé et al., 2001). From this study, 0.6% carrageenan
concentration was selected as providing the best consistency. Nevertheless, in OS10 no gel
was obtained at this concentration, probably due to the fact that sucrose, ions (as deduced
from the mineral analysis carried out, figure 3) and carrageenan all compete for the water.
Nevertheless, an interesting characteristic of the gels formulated with the OS10 was the
absence of syneresis, evident when SS was used. In order to favour carrageenan gel
formation, other tests were carried out adding locust bean gum, due to the synergic character
described for both gelling agents (Camacho et al., 1999). Nevertheless, gels obtained in this
case showed lower consistency and greater syneresis than the ones formulated only with
carrageenan. This can be a consequence of the pH and ionic strength of the OS10 and also of
the temperatures used for the hydrocolloids dissolution. At pH <4.5 and temperatures over
80ºC, the hydrolysis of the glycoside chains of the locust bean gum takes place, due to acid
catalysis and thermal degradation processes and so, maximum viscosity was not reached
(Imeson, 1997). For all these reasons, it was decided to use only carrageenan but at an
increased concentration of 0.75 %.
Once the hydrocolloid and its concentration were optimized, the process of dosing and
mixing the gel with the dehydrated fruit was standardized. First, the ratio of the product’s
gel:fruit phase was optimized. To this end, ratios of 70:30, 65:35, 60:40 and 50:50 were
tested. Of these, 65:35 and 60:40 were the ones that allowed us to obtain a homogeneous
product, with a balanced content of each component and one that behaved satisfactorily when
it was turned out of the tub, not breaking the gel. As regards the mixing step, it was tested by
previously combining all the gel phase and the fruit and pouring the set into polystyrene tubs.
This leads to a heterogeneous product, with the kiwifruit in the top half of the product, which
was broken while turning it out of the tub. Flotation of the kiwifruit prior to the gel of the
system was a consequence of the low viscosity of the gel phase, due to its high temperature
when mixing with the fruit. These disadvantages were avoided by alternating layers of gel
phase, gel phase with fruit and gel phase again, in a ratio of 30:40:30. In order to avoid the gel
layers separating after the product is turned out, the temperature of the mixing process was
optimized, so that, after placing the first gel layer in the tub at 50ºC, it was introduced in a
bath with water at 20ºC for a few seconds until the walls were observed to gel. At this
moment the gel:kiwifruit layer was added at 50ºC, placed again in the bath at 20ºC and,
finally, the last gel layer was added. The product prepared in this way was allowed to gel for
at least 24 h at 8ºC before turning it out for analysis.
322
Following this methodology, and as it has been described in chapter 2, a batch of gel
products was prepared from OD kiwifruit and the OS obtained after 10 consecutive cycles of
fruit dehydration. Before proceeding to mix the gel phase with the dehydrated fruit, both were
analyzed separately, as to soluble solids and water activity. In addition, fruit water content
was also controlled. The same analyses were repeated 24 h after the product’s elaboration and
after one and two weeks of chilled storage (8 ºC), during which time syneresis was also
controlled. Results of aw and ºBrix analysis revealed that, initially, the product was not in
thermodynamic equilibrium, as the initial aw of the dehydrated kiwifruit was greater than that
of the gel (0.985 ± 0.001 and 0.947 ± 0.001, respectively). This means that the kiwifruit, with
an initial ºBrix of 18.4 ± 0.5 and humidity of 80.29 ± 0.04 %, is still dehydrated inside the gel,
which leads to a simultaneous increase of the gel’s aw. The product equilibrium was reached
after between 7 and 14 days of chilled storage (final gel and kiwifruit aw = 0.966 ± 0.001).
Syneresis was not observed during the period of time being studied, thus indicating that all
the water lost by the kiwifruit was incorporated by the structure of the gel. These results
suggest the need to formulate a thermodynamically stable product, in order to avoid major
fruit dehydration during storage. This will need the OS to be diluted until it reaches the same
aw as the dehydrated fruit.
To know the microbiological stability of the product total viable micro-organism, yeast
and mould counts were carried out at 24 h, 7, 14 and 30 days. Up to 15 days, counts were
lower than the permitted maximums established by the Microbiological Norm, Real Decree
670/1990 of May 25 (B.O.E. 31-5-90), as 105 UFC/g product for total viable and 104 UFC/g
product for moulds and yeasts. After one month, visual symptoms of contamination appeared
and the counts were over the allowed limit.
When formulating the product, the way of presenting the fruit inside the gel was taken
into account. Some tests were carried out with the fruit pieces obtained directly after the OD
(whole slices of kiwifruit, half slices of grapefruit and strawberry halves) and also with these
pieces cut into different sizes. Sensory evaluations did not show marked preferences, as,
although visually whole fruit is preferable, it was easier to consume when cut into pieces.
Nevertheless, this aspect concerns neither the previously described stages of product
formulation, nor the product’s stability which will be described later. To evaluate the sensory
acceptance of the formulated product, the colour, flavour, aroma and texture of the gel, the
dehydrated kiwifruit and the whole product, were tested. A consumption test was also carried
out and the results indicated that 80% of the panellists would buy it, which shows that the
formulated product was well accepted. Nevertheless, it was suggested that the gel should be
more consistent and not as sweet. To achieve this, the dilution of the OS may be
recommended, which, in turn, would improve the carrageenan chain extension, thus
increasing the gelling power. In addition, as has been shown in previous paragraphs, this OS
dilution is necessary in order to increase its aw until near that of the dehydrated fruit. In fact,
other subsequent sensory tests confirmed that the sweetness of the gel formulated with the OS
that has been diluted until reaching thermodynamic equilibrium with the fruit, was suitable.
In order to know the quantity of water to be added to OS, the use of Norrish’ equation for
a sucrose-water solution (eq. 1) is proposed, which relates the molar water fraction (xw) and
molar soluble solid fraction (xs) with the water activity of the solution (aw).
aw = xwexp(-6.47xs2)
(1)
323
In order to apply eq. (1), it is necessary to know the aw of the OS which will be equal to
that of the dehydrated fruit. On the other hand, as it is assumed that the solution is only made
up of water and sucrose, which are the major components, xw is equal to (1-xs). Therefore,
both of them can be determined. Transforming molar fractions to mass fractions allows us to
obtain the ºBrix of the diluted OS. From this data and the ºBrix of the OS obtained after the
dehydration process, the quantity of water that is necessary to add, in order to obtain the same
water activity as the dehydrated fruit (thermodynamic equilibrium), must be calculated.
On the other hand, as one of the objectives of the proposed product was to avoid byproduct generation, the number of re-uses of the OS in successive OD cycles must be
optimized, so that all the dehydrated fruit obtained after the different OD cycles and the spent
solution from the last usage are used in the formulation, while always taking into account the
required dilution level. To this end, different experiments were programmed with grapefruit,
kiwifruit and strawberry. For each fruit, a set of consecutive OD cycles were programmed
under the conditions described in section 2, with the only difference being that the spent OS
in one cycle was directly re-used in further ones, without any re-concentration treatment. The
weight, ºBrix and water activity of both dehydrated fruit and OS, were measured after each
OD cycle. From these data, the calculated amount of water that is necessary to add to the OS
for the product to reach thermodynamic stability and the selected gel:fruit ratio in the final
formulation, it is possible to determine the number of OD cycles that must be carried out to
design a closed process.
As an example, table 8 shows data from the strawberry experiment. In this case, seven
consecutive OD cycles (fruit:OS ratio of 1:4) were programmed. The mean value of
osmodehydrated strawberry aw obtained from all the cycles was 0.983. Applying eq. 1 with
this aw value allowed us to calculate the amount of water that needed to be added to the OS
depending on the number of re-uses, to obtain the weight of equilibrated OS shown in table 8.
To formulate the product a gel:fruit ratio of 60:40 was considered in this case. The fruit and
OS quantities necessary were calculated taking into account that 250 ml PET tubs were to be
used, in which 200 g of fruit-gel product can fit. The amount of equilibrated OS available
after each OD cycle and the accumulated osmodehydrated strawberry allowed us to calculate
the number of tubs that could be prepared by using either all the obtained dehydrated fruit or
all the OS. As can be observed in table 8, the optimum re-use of the OS would be five
consecutive OD cycles, as by-product generation is the smallest. In this case, a total of 26
tubs will be obtained and just 24 g of strawberry (0.7 %) and 467 g of equilibrated OS (13 %)
will be left over. Following the same procedure but using kiwifruit and grapefruit (dehydrated
at a fruit:OS ratio of 1:5) and with a final gel:fruit ratio of 65:35, it was possible to estimate
the optimum number of OS re-use cycles in order to minimize by-product generation as 4.
324
Figure 6. Scheme showing the optimized process for fruit-gel product formulation, using osmotic treatments,
without by-product generation.
325
Table 8. Weight and water activity of osmodehydrated strawberry (mODS and awODS)
and weight and ºBrix of osmotic solution (mOS and ºBrixOS) obtained after each OD
cycle. Number of gel fruit product tubs that could be obtained by using all the
equilibrated OS (TOSeq) or all the osmodehydrated strawberry (TODS)
obtained after the corresponding OD cycles
(1)
Cycle
mODS (g)
aw ODS
mOS (g)
ºBrixOS
mOSeq(1) (g)
TOSeq
TODS
1
410
0.981
2257
52.2
5034.9
42.0
5.1
2
394
0.979
2230
48.1
4583.9
38.2
10.1
3
421
0.981
2216
45.0
4261.5
35.5
15.3
4
450
0.986
2160
41.5
3830.8
31.9
20.9
5
430
0.979
2141
39.2
3586.6
29.9
26.3
6
485
0.988
2077
37.1
3293.0
27.4
32.4
7
462
0.984
2034
35.5
3085.8
25.7
38.2
Weight of equilibrated OS obtained when diluted to reach the same water activity as osmodehydrated
strawberry, calculated as explained in the text.
Therefore, with the results obtained from this part of the study, it is possible to propose
the gel product formulation process which contains the highest quantity of osmodehydrated
fruit pieces and which does not generate by-products. Figure 6 schematizes the corresponding
process.
CHARACTERIZATION AND STABILITY OF THE PRODUCT
In order to evaluate product changes during refrigerated storage (14 days), at 8ºC, two
different experimental designs were programmed on grapefruit and strawberry gel products.
In both cases, the aim was to achieve thermodynamic equilibrium between the dehydrated
fruit and the gel matrix. On the one hand, tubs were prepared with just one fruit piece inside
the gel matrix. These were used to study, under more controlled conditions, changes in
colour, mechanical properties and volatile profile in both the fruit and the gel matrix. On the
other hand, tubs prepared following the optimized formulation process, thus ensuring the
adequate gel:fruit ratio, were used to analyze compositional changes in the fruit and the gel
matrix, and to evaluate sensorial acceptance of the product.
Colour changes in the product were observed to be dependent on the pigment content of
the fruit included in the gel. The visual aspect of the fruits was not perceived to change during
product storage, although significant differences in CIEL*a*b* colour-coordinates (obtained
from the fruit surface with a spectrocolorimeter Minolta CM 3600D, D65-10 º) were detected.
As an example, table 9 shows the L*a*b* evolution of the osmodehydrated strawberry inside
the gel matrix at different storage times, as well as hue angle (h*ab=arctg b*/a*) and chrome
or saturation index (C*ab=(a*2+b*2)0.5) attributes. An increase in luminosity and a decrease in
a* and b* was observed. As a consequence of these changes, hue angle and chrome decreased
throughout storage, leading to a redder but less pure strawberry colour. As regards the gel, the
326
colour was not affected in the case of grapefruit and kiwifruit, but with strawberry it
immediately turns red. Transparency of gel was not lost with any of the fruits, which is a
desired characteristic as it helps to identify the fruit pieces inside the product.
Table 9. Values of CIEL*a*b* coordinates, chrome (C*ab) and hue (h*ab)
measured on osmodehydrated strawberry during storage of fruit-gel product. ∆E:
colour difference, related to sample at t=0, due to storage time
Time
(days)
0
L*
a*
b*
C*ab
h*ab
∆E
29±2a
23.4±1.5a
10.7±1.3a
26±a
24±3a
---
2
33.9±0.4b
20.6±1.2ab
6.72±0.07b
22±2b
18.1±1.9b
6.64±1.17a
14
31.8±1.8
ab
12.1±0.5
c
3.5±0.5
b
12.6±0.4
c
16±2
b
13.66±0.12b
Values expressed as mean±standard deviation. Within column, values with the same following letter do
not differ significantly from each other (p>0.05).
Several factors may contribute to the colour changes observed in the strawberry product.
In the case of the fruit, these may be physical changes on the surface that may affect its
reflectance, pigment losses as a result of lixiviation, oxidation or enzymatic action, or further
fruit dehydration (Contreras, 2006). Changes in the gel phase will more probably only be due
to the incorporation of anthocyanins coming from the strawberry. In this sense, the evolution
of the pelargonidine-3-glucoside was controlled during chilled storage of the product.
Measurements were taken both in the fruit and in three concentric zones in the gel matrix
around the fruit position. For fruit analysis, the anthocyanin concentration was referred to the
osmodehydrated fruit weight at storage time t=0. A significant pigment decrease was
observed in the first 2 storage days, changing from 14.9 to 7.2 mg/100g. No additional
decrease was observed after 14 storage days (7.4 mg/100g). Nevertheless, no correlation was
observed between fruit pigment concentration and colour coordinates, as the degradation of
free anthocyanins does not always have an immediate effect on visual colour changes (Skrede
et al., 1992) and because of the possible contribution of changes in the other factors
mentioned above. As regards the gel phase, figure 7 shows the average values for pigment
concentration in the three different zones considered in the gel matrix, during storage time. As
expected, significantly higher values were obtained for zone A (closer to the fruit position),
followed by zone B and zone C. In all of them, it can be observed that the longer the storage
time, the greater the anthocyanin content. This behaviour is coherent with a pigment
migration from the fruit to the gel matrix and within the matrix itself, as a consequence of its
hydrosoluble character. Both the temperature of the gel at the moment of introducing the fruit
(40ºC), together with the cellular damage caused by osmotic treatment, could be responsible
for the intense pigment diffusion from the vacuoles of the external cells to the gel matrix in
the first moments of storage. In this case, there was a close correlation observed between the
a* colour coordinate and the hue angle with the anthocyanin content (figure 8).
327
mg pgn 3 g/100g sample
1.4
zone A
1.2
zone B
1
zone C
0.8
0.6
0.4
0.2
0
0
2
15
storage time (days)
y = 0.124x + 0.207
R² = 0.747
1.4
pgn 3 g (mg/100 g sample)
pelargonidine 3-glucoside (mg/100 g sample)
Figure 7. Evolution of the pelargonidine-3-glucoside (pgn 3 g) content, during product storage, in three
concentric zones of the gel matrix around the strawberry piece (zone A, the closest to the fruit and C, the
furthest away).
1.2
1.0
0.8
0.6
0.4
0.2
Zone A
Zone B
y = -0.018x + 1,519
R2 = 0.744
1.4
1.2
1.0
0.8
0.6
0.4
0.2
Zone A
Zone C
Zone B
Zone C
0.0
0.0
0
2
4
a*
6
8
0
50
h*ab
100
Figure 8. Relationship between pelargonidine-3-glucoside (pgn 3 g) and a* colour coordinate and hue angle
(h*ab).
Texture is one of the main quality attributes for fruit and fruit based products, mainly
when the fruits in question are especially fragile and perishable (Sanz et al., 1999). In this
sense, when the stability of the formulated gel product is considered, possible changes in the
mechanical properties of the gel matrix and the fruit during its refrigerated storage have to be
taken into account. Different mechanical tests (puncture and shear) were carried out to
evaluate this aspect in the product. In every case a small although significant decrease of the
fruit’s resistance to fracture was observed after two storage days, but there were no other
328
significant changes during the rest of the storage time (Table 10 shows the results for the
strawberry gel product). Nevertheless, this decrease in the fruit’s resistance does not seem to
be a consequence of the gel being present, as the observed changes were of the same order as
those shown by the osmodehydrated fruit when not included in the gel matrix (Penagos,
2006). There were no observed changes in the mechanical properties of the gel matrix during
storage.
Table 10. Fracture force (Ff) and deformation at fracture (Df) of osmodehydrated
strawberry included in the gel matrix at different storage times
Ff (N)
Time (days)
0
2
14
Df (mm)
Shear test
Puncture test
Shear test
Puncture test
6.8±0.3a
2.0±0.2b
2.4±0.3b, c
6.4±1.6a
2.6±0.4b
2.5±0.3c
13.8±0.9a
5.3±0.8b
9.1±0.9c
0.32±0.03a
0.40±0.02b
0.41±0.05b
Values expressed as mean±standard deviation. Within column, values with the same following letter do
not differ significantly from each other (p≤0.05).
The volatile profile of the strawberry gel product was analysed by using the “purge and
trap” method for the extraction and using a GC/MS for compound identification and
quantification (Otson and Chan, 1987). A total of 28 compounds could be identified and
quantified (relative area of each compound referred to the internal standard is shown in figure
9): sixteen esters, seven alcohols, four aldehydes and one foranone (furaneol). In dehydrated
strawberry, the family of ester compounds was the major fraction, representing about 57% of
the total quantified volatile compounds. These “key compounds” (ester family) are not only
important from the quantitative point of view, but have also been reported to be relevant
components of the original strawberry aroma (Schreier, 1980; Dirinck, Schreyen and Schamp,
1981; Douillard and Guichard, 1989; Talens et al., 2003). Migration of alcohols and furaneol
compounds into the osmotic solution may be responsible for the smaller concentration
observed in the osmodehydrated fruit, when compared to fresh fruit (Talens et al., 2003;
Penagos, 2006). The highest relative areas (related to concentration) in dehydrated strawberry
were shown by 2 hexenal E (2.286), butanoic acid 3 methyl ethyl ester (2.124) and butanoic
acid ethyl ester (2.112). Individual compound analysis during storage showed a small transfer
of some volatile components from osmodehydrated strawberry to the gel matrix, such as
methylacetate, butanoic acid 3 methyl ethyl ester, or butanoic acid octyl ester. In general, a
decrease in all the quantified compounds was observed during product storage, except for
ethanol, which may be due to sugar fermentation.
7.5
Relative Area
6.5
5.5
4.5
3.5
329
Fruit 0 days
Fruit 2 days
Fruit 15 days
Gel 0 days
Gel 2 days
Gel 15 days
2.5
Relative Area
1.5
1
methyl acetate
butanoic acid ethyl ester
ethylacetate
propanoic acid ethyl ester
acetic acid prophyl ester
butanoic acid methyl ester
butanoic acid 3 methyl ethyl ester
butanoic acid 2 methyl ethyl ester
butanoic acid octyl ester
butanol acetate
2 butenoic acid ethyl ester
acetic acid penthyl ester
hexanoic acid methyl ester
acetic acid octyl ester
benzonoic acid ethyl ester
acetic acid fenylethyl ester
1 pentan 3 ol
ethanol
1 butanol
1 pentanol
2 hexen 1 ol E
3 hexenol Z
dodecanol
methyl 2 butenal
hexanal
2 hexenal E
nonanal
3(2H) foranone 5 ethyl
0
Volatile compounds
Figure 9. Strawberry and gel volatile profile obtained at different storage times of the product.
All the fruits showed similar results when comparing the product’s compositional
evolution during storage. To illustrate this, the results for the grapefruit gel product are shown
in the following paragraphs. In the fruit included inside the gel, a slight dehydration was
observed during product storage, more accused during the first 48 h (Table 11). This could be
related to an effect of the carrageenan, which decreases the gel´s aw, thus removing the
pretended thermodynamic equlibrium (equal water activities) with the dehydrated fruit, as can
also be observed in table 11. In this sense, it would be necessary to consider the presence of
carrageenan in eq. 1 calculations. Nevertheless, despite the variations observed in the water
330
content of the dehydrated fruit and the initial difference in aw between the fruit and the gel at
t=0, these are so small that no significant changes, either in the fruit or in the gel’s aw over
storage time, were appreciated.
Table 11. Water content (xw, g water/100g sample), ºBrix (g soluble solids /100 g liquid
fraction), water activity (aw) ascorbic acid (AA, g /100g sample) and citric acid (CA, g /
100 g sample) of the osmodehydrated grapefruit included in the gel structure (ODG) at
different storage times. ºBrix and aw of the gel matrix (GEL)
0
30.2
GE
L
20.1
0.976
0.970
xwa
FD
O
80.9
42
4.5
1497
168
1
28.8
20.3
0.975
0.966
78.4
29
7.3
1140
328
2
4
7
10
14
30.5
28.5
29.6
28.1
29.1
20.1
19.5
22.2
21.6
23.6
0.974
0.979
0.977
0.980
0.975
0.963
0.976
0.972
0.974
0.976
77.8
77.7
75.8
76.6
74.6
32
31
28
27
22
9.0
8.2
9.3
6.7
6.7
1211
1269
1181
1122
998
365
425
484
471
542
t (days)
awb
ºBrixa
ODG
ODG
GEL
AAc (mg/100g)
CAd (mg/100g)
ODG
GEL
ODG
GEL
Values expressed as mean±standard deviation. aReproducibility lower than 0.6. bReproducibility lower
than 0.005. cReproducibility lower than 3 in ODG and 1 in GEL. dReproducibility lower than 100
in ODG and 30 in GEL.
In all the products under study, whereas the ascorbic and citric acid contents of the gel
increased, those of the fruit decreased (Table 11). This, together with the increase of the
electrical conductivity of the gel detected until the seventh day (from 822 to 963 6 μS/cm in
the grapefruit product, for example) and the decrease in the pH (from 3.15 before introducing
the grapefruit to 2.80 after 24 h of product storage), would indicate that, together with the
water liberated by the fruit into the gel during the storage of the product, as commented on
above, a flow of soluble water substances takes place (ascorbic acid, mineral salts and organic
acids).
The evolution of galacturonic acid, minerals and flavonoids during storage was only
analyzed in the grapefruit gel product. Although a decrease was observed in the AGU of the
dehydrated fruit (from 1590 to 1258 mg AGU/100g), which was more significant in the first
four days, no changes in the gel’s AGU content were detected (mean value of 259 mg
AGU/100g). This can be due to the enzymatic action of poligalacturonase, which is abundant
in the grapefruit (Riov, 1975). As for Na and Ca content during storage (figure 10), there was
a slight decrease observed in the gels and yet a progressive enrichment in the grapefruit. This
would indicate a certain reincorporation of both minerals into the fruit. The opposite trend
was found for P evolution (figure 10). Dehydrated fruit showed a significant increase in Mg
and K during the first 24 h, with no additional changes, either in the fruit or in the gel,
observed during the rest of storage. During this time, the fruit showed mean values of 6 ±
1mg Mg/100g and 109 ± 10 mg K/100g, whilst in gel they were 2,5 ± 0,2 mg Mg/ 100g and
95 ± 3mg K/ 100g. In the case of flavonoids, there was no detected evolution of these
compounds in the osmodehydrated grapefruit included in the gel. An analysis of these
compounds in the gel matrix revealed the presence of only naringin, poncirin and naringenin.
Naringin, the most abundant in the OS, was present in smaller quantities in the gel (10
331
mg/100g OS vs. 3.7 mg/100 g gel). The other minor phenols present in the OS, with the
exception of naringenin, were not detected in the gel matrix. This was as expected, as the OS
is diluted prior to formulating the gel product. The presence of naringenin in the gel matrix
may be explained as it is a hydrolysis product of naringin, which is the main phenol present in
the OS, but also the one that most decreases in gel.
ODG
GEL
mg Na/100g sample
5
4
3
2
1
0
mg Ca/100g sample
20
15
10
5
0
12
mg P/100g sample
10
8
6
4
2
0
0
1
2
4
t (days)
7
10
14
Figure 10. Evolution of Na, Ca and P content in osmodehydrated grapefruit (ODG) and in gel during storage.
332
From these results, if any changes are observed in the fruit and gel compounds during
chilled storage, they are so small that the compositional stability of the product seems to be
guaranteed.
A panel made up of 30 untrained tasters took part in a test to determine the level of
acceptance of the colour, aroma, flavour, texture and fruit content of a gel product formulated
with strawberry. A hedonic scale of 5 points was used. As observed in figure 11, the attributes
of colour and aroma were the most widely accepted, followed by strawberry content and
flavour. The gel texture, however, turned out to be slightly soft. On the other hand, before the
product was tasted and only from a visual point of view, it was asked if they would buy the
product and 90 % of the panellists answered affirmatively. The same question was repeated
once the tasting was over, but this time the percentage fell to 77 %, due to the low consistency
of the gel which may easily be improved by slightly increasing the concentration of
carrageenan.
AROMA
2
1
0
FRUIT CONTENT
COLOUR
-1
-2
TEXTURE
TASTE
Figure 11. Results of the sensory acceptance evaluation of strawberry gel product.
CONCLUSIONS
During the osmotic dehydration of fruits with sucrose solutions, compositional changes
take place, both in the fruit and in the OS. On one hand, fruit water loss leads to a dilution of
the OS which, nevertheless, does not prevent it from being re-used in successive dehydration
cycles, without affecting the prearranged dehydration level of the fruit or causing
considerable microbiological contamination. At the same time, changes observed in the fruit
allow us to recommend a fruit:OS ratio of 1:4 or 1:5 for the dehydration operation, as using a
greater quantity of OS would only contribute to increasing the by-product generation.
Osmotic dehydration of fruits leads to a loss in micro-nutrients and other bioactive
substances, which has been verified and quantified. Nevertheless, a progressive enrichment in
the osmotic solution when it is re-used during successive cycles of fruit dehydration has been
observed, which turns it into an attractive ingredient for food formulation. This, together with
333
the optimization of the fruit:OS ratio, would help to make the osmotic process more
profitable, both from an economic and environmental point of view.
With this in mind, this work proposes the methodology to formulate a gel product from
osmodehydrated fruit and the actual osmotic solution used for its dehydration, with a good
sensory acceptance and a microbiological stability of at least 15 days of chilled storage. The
process has been optimized to avoid by-product generation. To this end, the re-use of OS for
4-5 consecutive fruit OD cycles is recommended, depending on the fruit:OS ratio during the
dehydration operation and on the fruit:gel ratio in the final product, which may range between
65:35 and 60:40. In order to achieve compositional stability of the gel product during its
storage, the OS must be diluted before the gelling agent is incorporated, so that its water
activity is the same as that of the dehydrated fruit. Although carrageenan looks like the most
appropriate gelling agent due to the compositional characteristics of the OS, its concentration
must be adapted, since gels formulated from the OS present less consistency than expected.
The dosing and mixing of the ingredients must be done by layers and under controlled
temperature conditions, to obtain a homogeneous product that is easy to turn out.
ACKNOWLEDGEMENTS
Authors thank the Ministerio de Educación y Ciencia and the Fondo Europeo de
Desarrollo Regional (FEDER) for the financial support throughout the projects AGL200201793 and AGL 2005-05994. Also, our most sincere thanks to Rebeca Peiró Mena and Lucas
Penagos Vélez, who have contributed to data shown in this chapter with results obtained
while doing their PhD Thesis.
REFERENCES
[1]
[2]
[3]
[4]
[5]
Alarcao-E-Silva, M.; Leitão, A.; Aznhaira, H. and Leitão, M. (2001). The arbutus
berry_ studies on its color and chemical characteristics at two mature stages. Journal of
Food Composition and Analysis, 14, 27-35.
Alzamora, S.M.; Gerschenson, L.N.; Vidales, S.L. and Nieto, A. (1997). Structural
changes in minimal processing of fruits: some effects of blanching and sugar
impregnation. In P. Fito; E. Ortega-Rodríguez and G.V. Barbosa-Cánovas (eds). Food
Engineering. 2000. USA, Chapman and Hall.
Aoki, K.; Shiotani, T. and Sasaki, J. (2000). Jelly foods containing agar, xanthan gum
and locust bean gum. European Patent Application. EP 1 074 183 A2 (EP1074183A2)
Arnstein, R.; Bonet, G.; Charette, J. and Steiner, J.P. (1974). Improvements to
powdered food preparations having gelling and/or thickening properties and to the
processes for obtaining them and food compositions containing these preparations.
French Patent Application. 2 185 367 (2185367)
Belnstein, J. (2001). The protective factors of fruit and vegetables. Food Technology
International, 10, 12-14.
334
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
Camacho, M.M.; Martínez-Navarrete, N. and Chiralt, A. (1999). Propiedades
funcionales de la goma de garrofín y sus aplicaciones en la industria de alimentos. Una
revisión. Alimentación, equipos y tecnología, XVIII (3): 103-110.
Cheney, P.A.; Stares, J. and Vernon, A.J. (1984). Food product thickened or gelled with
carrageenan and glucomannan. United States Patent. US 4 427 704 (US4427704)
Contreras, C. (2006). Influencia del método de secado en parámetros de calidad
relacionados con la estructura y el color de manzana y fresa deshidratadas. Ph.D.
Thesis. Universidad Politécnica de Valencia (Spain).
Contreras, C.; Martín, M.E.; Martínez-Navarrete, N. and Chiralt, A. (2005). Effect of
vacuum impregnation and microwave application on structural changes which occurred
during air-drying of apple. Lebensmittel-Wissenschaft und Technologie, 38 (2005) 471–
477.
Conway, J.; Castaigne, F.; Picard, G. and Vovan, X. (1983). Mass transfer
considerations in the osmotic dehydration of apples. Canadian Institute of Food Science
and Technology Journal, 16(1): 25-29.
Dalla-Rosa, M. and Giroux, F. (2001). Osmotic treatments (OT) and problems related
to the solution management. Journal of Food Engineering, 49: 223-236.
De la Fuente, M.A.; Montes, F.; Guerrero, G. and Juárez, M. (2003). Total and soluble
contents of calcium, magnesium, phosphorus and zinc in yoghurts. Food Chemistry, 80,
573-578.
Dirinck, P.J.; De Pooter, H.L.; Willaert, G.A. and Schamp, N.M. (1981). Flavor quality
of cultivated strawberries: The Role of the Sulfur Compounds. Journal of Agricultural
Food Chemistry, 29, 316-321.
Douillard, C. and Guichard, E. (1989). Comparison by multidimensional analysis of
concentrations of volatile compound in fourteen frozen strawberry varieties. Sciences
Des Aliments, 9, 61-83.
Elisabelar, J. and Albelda, G. (1985). New food product based on concentrated grape
juice and its production. French Patent Application. FR 2 563 701 A1 (FR2563701A1)
Fito, P.; Andrés, A.; Pastor, R. and Chiralt, A. (1995). Mass transfer behaviour and
structure changes during osmotic dehydration (VOD) of foods. In: A. Lenart, and P. P.
Lewicki (eds). Osmotic dehydration of fruits and vegetables. (5-19). Warsaw: Warsaw
Agricultural University Press.
Fito, P. and Chiralt, A. (1997). Osmotic dehydration: an approach to the modelling of
solid-liquid food operations. In P. Fito; E. Ortega-Rodríguez and G.V. BarbosaCánovas (eds). Food Engineering 2000. USA, Chapman and Hall.
Fito, P.; Chiralt, A.; Barat, J.M.; Spiess, W.E.L. and Behsnilian, D. (2001). Osmotic
dehydration and vacuum impregnation. Application in food industries. Technomic
Publishing Company, Inc.
Fleck, C. and Schindler, W. (1991). Food products which may be reconstituted as a gel,
and their manufacture. French Patent Application; FR 2 649 299 A1, FR 89-09188
(19890707).
Forni, E.; Torreggiani, D.; Crivelli, G.; Mastrelli, A.; Bertolo, G. and Santelli, F.
(1987). Influence of osmosis time on the quality of dehydrofrozen kiwifruit. Acta
Horticulturae, 282, 425-433.
335
[21] García-Martínez, E.; Martínez-Monzó, J.; Camacho, M.M. and Martínez-Navarrete, N.
2002a. Characterisation of reused osmotic solution as ingredient in new food product
formulation. Food Research International, 35 (2-3), 307-313.
[22] García-Martínez, E.; Ruiz-Díaz, G.; Martínez-Monzó, J.; Camacho, M.M.; MartínezNavarrete, N.; Chiralt, A. (2002b). Jam manufacture with osmodehydrated fruit. Food
Research International, 35 (2-3), 301-306.
[23] García-Pinchi, R. (1998). Deshidratación osmótica al vacío por pulso (PVOD) del kiwi
(Actinidia chinensis P.). PhD Thesis. Universidad Politécnica de Valencia (Spain).
[24] Giangiacomo, R.; Torreggiani, D. and Abbo, E. (1987). Osmotic dehydration of fruit.
Sugars exchange between fruit and extracting syrups. Journal of Food Processing and
Preservation, 11(3): 183-195.
[25] Giangiacomo, R.; Torreggiani, D.; Erba, M.L. and Messina, G. (1994). Use of
osmodehydrofrozen fruit cubes in yogurt. Italian Journal of Food Science, 6(3), 345350.
[26] Gliksman, M. and Farkas, E.H. (1974). Gum gelling system xanthan-tara dessert gel.
United States Patent. 3 784 712 (3784712)
[27] Gordon, D.L.; Roy, S.; Ryan, A.L. and Schwenn, K.S. (2001). Gel products fortified
with calcium and method of preparation. International Patent Application. WO
01/43564 A1 (WO01/43564A1)
[28] Heng, K.; Guilbert, S. and Cuq, J.L (1990). Osmotic dehydration of papaya: influence
of process variables on the product quality. Sciences des Aliments. 10(4): 831-848.
[29] Hertog, M.G.L.; Hollman, P.C.H. and Putte,B van de. (1993). Content of potentially
anticarcinogenic flavonoids of tea infusions, wines, and fruit juices. Journal of
Agricultural and Food Chemistry, 41(8): 1242-1246.
[30] Imeson, A. 1997. Thickening and Gelling Agents for food. Londres. Blackie Academic
and Professional
[31] Jensen, V.M. (1991). Vegetable foodstuff, especially for use as cold cuts as well as a
production method therefor. International Patent Application; WO 91/01650, DK 893915 (19890810).
[32] Kaletunc, G.; Nussinovitch, A. and Peleg, M.T. (1990). Alginate texturization of highly
acid fruit pulps and juices. Journal of Food Science, 55 (6): 1759-1761.
[33] Kaur, C. and Kapoor, H.C. (2001). Antioxidants in fruits and vegetables – the
millenniums’s health. International Journal of Food Science and Technology, 36(7),
703-725.
[34] King, A. and Young, G. (1999). Characteristics and occurrence of phenolic
phytochemicals. Journal of the American Dietetic Association, 99(2), 213-218.
[35] Klein, B.P. and Kurilich, A.C. (2000). Processing Effects of Dietary Antioxidants from
Plant Foods. HortScience, 35(4), 580-584.
[36] Martínez-Monzó, J. (2002). Cambios físico-químicos en mnzanas Granny Smith
asociados a la impregnación a vacío. Aplicación en congelación. PhD Thesis.
Universidad Politécnica de Valencia (Spain).
[37] Ming-Liu; Xiu-Qi-Li; Weber, C; Chang-Yong-Lee; Brown, J. and Rui-Hau-Liu. (2002).
Antioxidant and antiproliferative activities of raspberries. Journal of Agricultural and
Food Chemistry, 50(10), 2926-2930.
336
[38] Moraga, M. J. (2007). Pomelo mínimamente procesado por deshidratación osmótica.
Cambios en las propiedades físicas durante el almacenamiento. PhD Thesis,
Universidad Politécnica de Valencia (Spain). In press.
[39] Moraga, M.J.; Moraga, G.; Martínez-Navarrete, N. and Chiralt, A. (2005). Effect of the
re-use of the osmotic solution on the stability of osmodehydro-refrigerated grapefruit.
In: Fito, P. and Toldrá, F. (Eds). Innovations in tradicional foods INTRADFOOD 2005.
Proceedings. (Vol. I., 513-516) London, Elsevier.
[40] Musson, G.D. and Prest, C.T. (1988). Edible gels. European Patent Application. EP 0
290 251 A1 (EP0290251A1)
[41] Okonogi, S.; Yuguchi, H.; Tanai, S. and Morimoto, K. (1989). A method of
manufacturing jelly products having fibrous texture. European Patent Application; EP
0 334 466 A1, JP 88-56130 (19880311).
[42] Otson, R, and Chan, C. (1987). Sample Handling and Analysis for 51 Volatile Organics
by an Adapted Purge and Trap GC-MS Technique. International Journal of
Environmental Analytical Chemistry, 30, 4: 275-287.
[43] Panagiotou, N.; Karathanos,V.T. and Maroulis, Z.B. (1998). Mass transfer modelling of
the osmotic dehydration of some fruits. International Journal of Food Scienc and
Technology, 33(3): 267-284.
[44] Pancoast, H. M., and Junk, W. R. (1980). Handbook of sugars. Westport, Avi
Publishing Company.
[45] Peiró, R.; Camacho, M. M. and Martínez-Navarrete, N. (2007). Compositional and
physicochemical changes associated to successive osmodehydration cycles of pineapple
(Ananas comosus). Journal of Food Engineering, 79, 842-849.
[46] Peiró, R.; Dias, V. M. C.; Camacho, M. M. and Martínez-Navarrete, N. (2006).
Micronutrient flow to the osmotic solution during grapefruit osmotic dehydration.
Journal of Food Engineering, 74, 299-307.
[47] Penagos, L. (2006). Influencia del procesado esmótico en las características de un
producto gelificado formulado con la fresa deshidratada y la disolución osmótica. PhD
[48] Pinnavaia, G.; Dalla-Rosa, NI. and Lerici, C.R. (1988). Dehydrofreezing of fruit using
direct osmosis as concentration process. Acta Alimentaria Polonica, 14, 51-57.
[49] Prest, C.T. and Buckley, K. (1986). Gellable polysaccharide gum compositions. UK
Patent Application. GB 2 168 366 A (GB2168366A)
[50] Préstamo. G. (1995). Actinidin in kiwifruit cultivars. Zeitsschrift fuer Lebensmittel
Untersuchung und Forschung A., 200: 64-66.
[51] Prior, R.L. and Guohua-Cao. (2000). Antioxidant phytochemicals in fruits and
vegetables diet and health implications. HortScience, 35(4) 588-592.
[52] Raoult-Wack, A.L. (1994). Recent advances in the osmotic dehydration of foods.
Trends in Food Science and Technology, 5: 255-260.
[53] Ribé, S.; García-Martínez, E.; Martínez-Monzó, J.; Camacho, M.M. and MartínezNavarrete, N. (2001). Caracterización de geles de carragenato obtenidos a partir de
disoluciones azucaradas. In Fito, P., Chiralt, A., Andrés, A. and Martínez-Navarrete, N.
(Eds.) Series de Ciencia e Ingeniería de Alimentos. Investigación del postgrado del
IAD-DTA. Año 2000.(123-143). Valencia, Editorial de la Universidad Politécnica de
Valencia.
337
[54] Riov, J. 1975. Polygalacturonase activity in citrus fruit. Journal of Food Science, 40(1),
201-202.
[55] Rui-Hai-Liu. (2003). Protective role of phytochemicals in whole foods: implications for
chronic disease prevention. Applied Biotechnology, Food Science and Policy, 1(1), 3946.
[56] Sanz, C.; Pérez, A.G.; Olias, R. and Olias, J.M. (1999). Quality of strawberries packed
with perforated polypropylene. Journal of Food Science, 55, 1049-1053.
[57] Schreier, P. (1980). Quantitative composition of volatile constituents in cultivated
strawberries Fragaria x ananassa c.v. Senga Sengara, Senga Litessa and Senga
Gourmella. Journal of Science and Food Agriculture, 31, 487-494.
[58] Shank, J.L. (1985). A method of preparing a gelled food product. European Patent. EP
0 073 907 B1 (EP0073907B1)
[59] Shi, X.Q.; Chiralt, A.; Fito, P.; Serra, J.; Escoin, C. and Gasque, L. (1996). Application
of Osmotic Dehydration Technology on Jam Processing. Drying Technology, 14: 841847.
[60] Skrede,G.; Wrolstad,,R.E.; Lea, P. and Enersen, G. (1992). Color stability of strawberry
and blackcurrant syrups. Journal of Food Science, 57(1): 172-177.
[61] Taiwo, K.A.; Angersbach, A.; Ade-Omowaye, B.I.O. and Knorr, D. (2001). Effects of
pretreatments on the diffusion kinetics and some quality parameters of osmotically
dehydrated apple slices. Journal of Agricultural and Food Chemistry, 49 (6): 28042811.
[62] Talens, P. (2002). Tratamientos osmóticos en la crioprotección de fresa y kiwi. PhD
[63] Talens, P.; Escriche, I.; Martínez-Navarrete, N. and Chiralt, A. (2003). Influence of
osmotic dehydration and freezing on the volatile profile of kiwi fruit. Food Research
[64] Tapia de Daza, M.S., López-Malo, A., Consuegra, R., Corte P. and Welti-Chanes, J.
(1999). Minimally processed papaya by vacuum osmotic dehydration techniques. Food
Science and Technology International, 5(1), 43-52.
[65] Torreggiani, D. and Bertolo, G. (2001). Osmotic pre-treatment in fruit processing:
chemical, physical and structural effects. Journal of Food Engineering, 49: 247-253.
[66] Torreggiani, D.; Forni, E.; Maestrelli, A. and Quadri, F. (1998). Influence of osmotic
dehydration on texture and pectic composition of kiwifruit slices. Proceedings of the
11th International Drying Symposium, A: 930-937.
[67] Trilling, D.M. and Smadar, Y. (1984). Production of shaped food products. United
States Patent. US 4 436 759 (US4436759)
[68] Valdez-Fragoso, A.; Welti-Chanes, J. and Giroux, F. (1998). Properties of sucrose
solution reused in osmotic dehydration of apples. Drying Technology, 6 (7) 1429-1445.
[69] Valero, M.J. (2003). Evaluación de la reutilización de la disolución osmótica en la
deshidratación osmótica de piña (Ananas comosus). Proyecto Final de Carrera.
Universidad Politécnica de Valencia (Spain).
[70] Venant,A.; Borrel, S.; Mallet, J. and Neste, E-van (1989). Gel permeation
chromatography as a method for the simultaneous clean up of organochlorine,
organophosphate and polychlorinated biphenyl residues in fat extracts. Analusis,
17(1/2): 64-66
338
[71] Walter, D.L. and Funk, D.F. (1998). Fabricated fruit pieces and method of preparation.
United States Patent. US 5 718 931 (US5718931)
[72] Wargovich, M.J. (2000). Anticancer properties of fruits and vegetables. HortScience,
35(4), 573-575.
[73] Wolfe, K; Xianzhong, W. and Rui-Hai-Liu. (2003). Antioxidant activity of apple peles.
Journal of Agricultural and Food Chemistry, 51(3), 609-614.
[74] Wust, U.; Zehle, G. and Huenecke, H. (1985). Manufacture of dried fruit-like products.
German Democratic Republic Patent. DD 220 495 (DD220495).
Chapter 5
QUALITY ASPECTS OF DEHYDRATED AND
REHYDRATED FRUIT IN RELATION
TO DRYING METHOD
C. Contreras, M.E. Martín-Esparza,
A. Chiralt and N. Martínez-Navarrete
Food Technology Department, Institute of Food Engineering for Development.
Polytechnic University. P.O. Box 22012, 46071. Valencia, Spain
ABSTRACT
The development of new attractive dehydrated fruit-based products, to be consumed
as dried or rehydrated, with high quality and reasonable shelf-life, will increase and
diversify its availability in the market. In this sense, it is necessary to optimize the
dehydration operation conditions to achieve not only the maximum process efficiency
and control, but also various characteristics in the final product in relation to colour,
texture, water activity, nutritive value, etc. Air drying has been the most frequently
selected process for industrial food dehydration, due to its efficiency, versatility and easy
management. However, it is known that it provokes considerable changes in sensory and
nutritional quality. Some research works refer to the advantages of applying microwaves
to convective drying associated with the fast volumetric heating of the product due to its
high penetration power. On the other hand, the application of certain pre-treatments
before drying operation, such as vacuum impregnation or vacuum pulsed osmotic
dehydration, could help to enhance the stability and quality attributes, as high
temperatures are not employed and specific solutes can be incorporated into the porous
structure. In this chapter the advantages of microwave application to convective drying of
apple and strawberry are pointed out. These are related to the great reduction in process
time and to the fact that they allow obtaining a dehydrated product with a greater
resistance to deformation and fracture and a greater stability during commercialization.
Nevertheless, its use is not recommendable when the product has to be used or eaten after
its rehydration, as the structural damage caused by microwaves decreases the mechanical
resistance and the retention capacity of the incorporated liquid phase. The colour of
dehydrated or rehydrated product is more affected by microwave treatments when the
fruit pigment content is relevant, as occurs with strawberry anthocyanins. Application of
340
C. Contreras, M.E. Martín-Esparza, A. Charalt et al
a previous vacuum impregnation/osmotic dehydration step with sugared solutions is
always recommended.
DEHYDRATED AND REHYDRATED FRUITS,
A TRADITIONAL MARKET
Most fruits are consumed when fresh, but their market availability is commonly limited
by the seasonal production throughout the year and its short shelf life, mainly due to fungal
attack and mechanical damage during distribution. Nowadays, the research and development
of preservation techniques which lead to high nutritional quality products with the most
similar sensorial characteristics to those of fresh food, is of special interest. In this sense,
preservation methods that enlarge the shelf-life of the fruits, increasing their market
availability, such as freezing, freeze-drying, dehydration, etc., are very useful [1,2].
Nevertheless, all of them induce modification of fruit quality attributes (texture, colour, and
flavour) to a different extent.
Dehydration is a widely used traditional preservation technique for processing plantbased foods despite the possible existence, in some cases, of adverse effects on nutritional and
organoleptic qualities. Several references distinguish between drying and dehydration
techniques. Drying refers to leaving food in the sun to reduce water content while dehydration
is an artificial drying process [3]. In either case, final water content of about 2 % in the food
may be achieved.
The advantage of dried or dehydrated fruits is that they are natural foods available at any
time, with a longer preservation time than fresh fruit and easier to consume. They are widely
consumed as a dried product (powder or snack) or as a semi-moist ingredient in prepared
foods and may also be rehydrated before their final use. Traditionally, dried fruits are used in
a lot of industrial areas such as pastry, lacteous, hostelry and restoration, dietetics, ecologic,
artisan and sports foods, etc. Their several utilities make them very useful in our daily diet,
alone or mixed, with milk, chocolate, in cookies, in jams or confitures, etc. Despite good
prospects, the trade market of this kind of product is still modest. Nevertheless, if the drying
process has been well optimized, the consumption of dried/rehydrated fruit may help to
increase the daily intake contributing to a recommended healthy diet. From this point of view,
the development of new, consumer-attractive and high quality dried fruit products is desirable
in order to widen product availability and diversify the market, particularly as nowadays fresh
fruit consumption is below that recommended in the consumers’ diet.
Good raw materials are needed to obtain high quality dried products. Nevertheless, the
drying conditions must also be optimized to obtain not only economic processes but also the
desired product characteristics related to color, texture, water activity, nutritional value, etc.
This includes the possible application of some pre-treatments prior to drying itself. Finally,
good storage and distribution conditions must be ensured.
Quality Aspects of Dehydrated and Rehydrated Fruit...
341
FOOD DRYING PROCESS. APPLICATION OF
MICROWAVE TECHNOLOGY
The drying process consists of removing part of the water in the product up to a certain
threshold value. This allows the product to be stored for a longer period of time, since the
activities of the micro-organisms, enzymes and some chemical reactions are slowed down [4].
Different techniques are used to reach this purpose. However hot-air drying is the most
common process in the case of fruits and vegetables and implies elimination of water by
evaporation. The kinetics of this drying process is limited by the rate at which water diffuses
from the interior to the surface of the product from which it is evaporated. The longer or more
difficult the diffusion path the slower the drying. Increasing the ambient temperature, thereby
evaporating surface water faster, it is possible in some cases to speed up drying. However,
this is also limited by the rate at which the interior water can reach the surface [5].
Conventional heat also has a particularly difficult time reaching the wet inner areas, because
the dry external surface layers have low thermal conductivity [6]. This may imply the
continuous heating of the surface. As a consequence, high temperatures or long drying times
with this method may cause serious damage to the product’s flavour, colour and nutrients,
reducing bulk density and rehydration capacity of the dried product [7].
Microwave processing has been successfully applied on a commercial scale in some food
processes such as cooking (meat and poultry), precooking (bacon), tempering (meat, poultry,
fish, butter, fruit), baking (dough), pasteurizing (ready meals and pasta) or drying (pasta,
snacks, fruits and vegetables) and results in a substantially reduced processing time leading to
increased production capacity [5,7]. In this case, the energy of the electromagnetic waves
interacts with water molecules, ions, and other food components (some solutes such as sugar
and salt) to generate heat. Weaker interactions occur with other food components, such as fat
[8]. The conversion of microwave energy into heat is achieved by dipole rotation and ionic
conduction. The relative importance of these two mechanisms of heat transfer depends to a
large extent on the temperature, due to its effect on ion mobility and characteristic dielectric
relaxation times. At the commonly used frequencies for microwave heating, it is mostly the
water component in food that makes heating possible. Microwaves interact with water
molecules, which allow them to penetrate the food, although with attenuated energy. Thus
heat will be generated not only at the food surface, but within the food as well [8]. This
supposes an internal evaporation of water and therefore an internal pressure gradient, which
effectively pumps water to the surface. From this point of view, the heating process may be
non uniform at lower water contents. Nevertheless, the volumetric heating of the product
when microwaves are applied implies a faster drying than in a conventional process.
Combined convective-microwave heating may be of interest, as microwaves will
selectively heat the wet internal areas, thus increasing moisture transport from inside toward
the surface of the product, and the superficial water may be easily removed by hot air.
In any case, heat transfer in microwave processes is more difficult to study due to the
complex interaction of the microwaves with the food, and a complete engineering description
of this process, that includes physical, chemical, biological and sensory aspects, is simply not
available. In fact, conventional heating produces a simpler more intuitive and predictable
heating pattern than microwave heating [8]. In this sense, this chapter tries to contribute to the
study of the effect of microwave application to conventional hot air drying, considering heat
342
transfer mechanisms and drying kinetics of the process as well as quality aspects of the
products.
To this end different drying experiences were programmed with Granny Smith apple and
Camarosa strawberry. The mean fresh apple composition was: water content (xw)
0.858±0.005 g/g sample, soluble solids (xs) 0.12±0.04 g/g sample and water activity (aw)
0.991±0.002. Slices (7 mm thick) were obtained perpendicular to the apple axis; these were
not peeled but the core was taken out with a cylindrical 20 mm diameter core borer. The mean
fresh strawberry composition was: xw 0.912±0.013 g/g sample, xs 0.08±0.23 g/g sample and
aw 0.991±0.003. The strawberries were cut in half. The fruits were dried by air drying (AD)
and by combined air-microwave technique (A/MWD), using a modified household
microwave oven coupled to an analytical balance to control the weight of the sample during
the process, and connected to a computer [9]. The equipment allows us to control air
temperature, air velocity and microwave power. The air velocity was kept at a constant value
of 2.5 m/s inside the cavity and relative humidity ranged between 35-45 %. Apple slices were
placed suspended from a support perpendicular to the airflow. Air temperature was 30 ºC and
microwave incident power 0.5 W/g. Strawberry halves were placed cut side up on the dryer
grid to favour the mass transfer. In this case, air temperature was 40 ºC and microwave
incident power 0.2 W/g. All fruit samples were dried to 10 g water/100 g sample and each
drying treatment was done in triplicate.
PRE-DRYING TREATMENTS
During drying, changes in the quality of foodstuffs occurs, the greater the water
elimination or process time, the greater the changes. Nevertheless, the obtained product must
satisfy the consumer’s expectations in various quality aspects such as flavour, colour, texture
and nutritional value, among others. Several works [10-14] suggest application of pretreatments such as vacuum impregnation and/or osmotic dehydration prior to drying process
in order to contribute to the preservation of colour and texture.
Vacuum impregnation (VI) of a porous product consists of exchanging the internal gas or
liquid occluded in open pores for an external liquid phase, due to the action of hydrodynamic
mechanisms promoted by pressure changes [15,16]. The operation is carried out in two steps
after the product immersion in the liquid phase. In the first step, vacuum pressure (50–100
mbar) is imposed on the system for a short time (5–15 min), thus promoting the expansion
and outflow of the product’s internal gas. In the second step the atmospheric pressure is
restored in the system and compression leads to a great volume reduction of the remaining
gas in the pores and so to the subsequent inflow of the external liquid in the porous structure.
Compression can also reduce the pore size depending on the mechanical resistance of the
solid matrix. Coupling of deformation and impregnation in the sample depends on the
characteristic times of each phenomenon, which are respectively defined by the sample
mechanical properties and by the pressure drop during the flow of the liquid into the pores
[12].
In the last few years, the application of VI has been claimed as a useful way of
introducing liquids into the porous structure of some foods [17,18]. In this way, it allows the
embedding of a solution with some specific solutes into the porous product in order to adapt
343
its composition to certain quality or stability requirements (acids, criopreservative agents,
vitamins, minerals, browning substances, sugar, salt, etc.). With this procedure, not only the
product composition but also its physical and chemical properties may be changed in order to
improve some food characteristics [19]. In this sense it has been used to introduce calcium
salts into peeled apples, tomatoes or potatoes in order to increase parenchimatic tissue
firmness [20,21], extend the shelf-life [22] and prevent structure collapse [23]. Besides, mass
transfer is improved without modifications of the original cellular structure, leading to shorter
process times such as in cheese salting [24], cod salting and desalting [25,26] or ham curing
[27].
The osmotic dehydration (OD) of fruits is based on the principle of the natural cell wall
acting as a semi-permeable membrane. In OD, a cellular tissue is immersed in a concentrated
solution of sugars or salts in order to promote intra-cellular water loss, due to differences in
the water chemical potential established between the external solution and the internal liquid
phase of the cells. Nevertheless, due to the open structure of the tissue in the intercellular
spaces and to the presence of possible damaged external cells during product manipulation,
diffusion of internal and external solutes also occurs. This contributes to a net opposite flux of
water and solutes that allow the tissue to become concentrated with a determined ratio solute
gain/water loss, depending on process conditions. In addition to mass fluxes in the tissue,
structural changes and cell alteration also occur. These phenomena provoke changes not only
in the macroscopic properties of the sample, such as optical and mechanical properties, which
are related to product appearance and texture, respectively, but also in cell physiology and
biochemical reactions, which in turn can provoke several chemical modifications in the tissue
[28]. Hydrodynamic mechanisms are promoted to a great extent when pressure changes are
imposed on the system such as in VI processes. Vacuum treatments have an important effect
on water transfer during the OD. When VI is applied at the beginning of an OD treatment, the
process is called pulsed vacuum osmotic dehydration (PVOD). OD under vacuum makes it
possible to obtain a higher diffusional rate of water transfer. Several researches could be
consulted to increase knowledge of VI/DO/PVOD processes and their mechanism transport,
mass transfer, modelling or the response of some properties of fruits to these processes [1517,29,30].
In recent years, OD/PVOD of fruits, as an alternative intermediate step or as a pretreatment technology, has received increasing attention in the field of fruit preservation
processes in order to reduce energy consumption and improve the quality of the fruit product
[31,32]. Different studies have been carried out related to the use of osmotic processes to
obtain several kinds of fruit products or food ingredients such as minimally processed or
intermediate moisture fruits [33], or to their application as a pre-treatment in air drying [3437] or freezing [38,39]. When applied prior to drying, the osmotic step has been found to
reduce the degree of structural collapse which occurs during air drying, as reflected by a 2530 % increase in the final sample volume. As some examples, the work of [36,37], carried out
with peach cubes pre-treated by using 60 % sorbitol osmotic solution supplemented with 1 %
ascorbic acid and 0.5 % NaCl showed a lower structural collapse, retaining better surface
smoothness. Colour stability during air dehydration was also improved by the osmotic step
with sorbitol showing the highest protective effect. On the other hand, when studying air
drying and the combination osmotic-air drying of strawberry, the pre-dried samples showed a
much better tissue organization than the strawberries frozen without pre-treatment with a
greatest texture improvement of the fruit after thawing [40].
344
In this study, the influence of VI/OD was also considered when applied prior to AD and
A/MWD processes. To this end, some additional experiments were carried out with apple and
strawberry. Apple slices were impregnated with a commercial and isotonic apple juice (same
aw as fresh apple) by applying vacuum pressure (50 mbar) for 5 minutes and then restoring
the atmospheric pressure, keeping the samples immersed in the isotonic solution for 10 more
minutes (VI samples). Strawberry halves were pre-treated with a osmotic dehydration step,
carried out with 55 ºBrix sucrose solution at 20 ºC, under stirring conditions, by applying a
vacuum pressure pulse (50 mbar) for 5 minutes and then restoring the atmospheric pressure,
keeping the samples immersed for 3h more (PVOD samples). A mass ratio 1:20 for fruit
sample:osmotic agent was used. After these processes, samples were taken out of the
corresponding solutions and gently blotted (with a paper towel) to remove adhering solution.
These pre-treated samples were submitted to the same drying processes as non pre-treated
ones.
The xw, xs and aw of samples were controlled before and after pre-treatments. As
compared to raw material, VI of apple with isotonic solution did not change these properties
significantly, being in this case xw (0.862±0.003 g/g VI sample), xs (0.12 ±0.02 g/g VI
sample), and aw (0.992±0.002). Nevertheless, due to the osmodehydration, the xw and aw of
strawberry decreased to 0.863±0.009 g/g PVOD sample and 0.985±0.002, respectively, and xs
increased to 0.121±0.012 g/g PVOD sample.
HEAT TRANSFER MECHANISM AND DRYING KINETICS
Microwave application has been shown to significantly reduce convective drying time of
fruits and vegetables [41-43]. In this study, the time implied in combined convectivemicrowave drying treatments was around 75-85 % shorter than corresponding convective air
drying times (table 1). Pre-treated samples increased the convective drying time process up to
10 % due to the increase in its liquid phase volume. Convective-microwave drying time was
not influenced by VI or PVOD pre-treatments.
A kinetic study was carried out in order to propose accurate models for both drying
processes. To this end, registered continuous weight data and initial water content of pretreated or non pre-treated samples were used. Kinetic behaviour was dependent on drying
method. In all AD samples a falling rate period was identified, as corresponds to an internal
control of mass transfer, governed by intrinsic product properties and the internal resistance to
water diffusion [44,45]. Nevertheless, all A/MWD samples showed two differentiated
behaviours. Initially, a relatively constant period was observed. It can be justified if water
evaporation on the product-air interface occurs at a similar rate to water diffusion from the
inner to the product’s surface, due to the vapour partial pressure gradient generated by
internal water evaporation. With the drying progress, the lower mobility of the remaining
water molecules induces a decrease in the microwave power absorption. From this moment,
air drying begins to play a relevant role and a second falling rate period is observed.
The common and easy to interpret semi-empirical Page’s equation [46], described by Eq.
1 was used to describe the convective drying kinetics of apple slices and strawberry halves.
(X tw − X ew )
(X ow
− X ew )
345
= exp (− k * t n )
(1)
where Xw is the water content (g/g dry matter) with superscripts: o (initial condition), t (at
time t) or e (at equilibrium condition), t is time process (h), k is the drying constant (h-1) and n
is a dimensionless exponent.
As in drying experiences carried out the values of the equilibrium moisture content were
much smaller than Xwo, Xwe may be assumed to be zero. The fitting of Ln (-Ln (Xwt/Xwo)
versus Ln (t) allows obtaining k and n parameters (table 1).
Related to A/MWD samples, the initial drying constant period was described through a
simple linear equation (Xwt= Xwo-b*t). The falling rate period was also modelled by Page’s
equation (table 1).
Table 1. Process time (t), kinetics constants (k, n and b), and root mean square deviation
(RMSD) for each drying treatment. Values are expressed as mean±standard deviation
Strawberry
Apple
VI AD
AD
PVOD AD
AD
t (h)
28.9±0.8
17.9±0.3
41.4±1.2
37±2
k (h-1)
0.121 ±0.016
0.20±0.03
0.09±0.02
0.108±0.009
1.02±0.04
1.03±0.02
0.98±0.02
0.99±0.05
0.0024
0.0027
0.0046
0.0074
n
(1)
RMSD
VI A/MWD
A/MWD
PVOD A/MWD
A/MWD
t (h)
3.81±0.12
3.9±0.3
10.9±0.9
9.5±0.6
b (h-1)
2.6±0.3
2.5±0.3
1.16±0.06
2.05±0.14
k (h )
1.48±0.03
1.42±0.24
0.57±0.13
0.577±0.114
n
0.97±0.04
1.08±0.02
0.91±0.11
1.01±0.17
RMSD(1)
0.0076
0.0039
0.0026
0.0033
-1
(1)
RMSD =
(
1 z t
t
∑ X w −exp, i − X w −pre, i
z i=1
)
2
where Xwt-exp,i is the experimental water content, Xwt-
is the predicted water content and z is the observation number. Corresponds to the highest
RMSD value, among replicates, for each drying treatment.
pre,i
During convective drying, pre-treatment significantly decreased k drying constant, related
to the increase in drying time commented on above. This can be explained by the increase in
the liquid phase volume promoted by pre-treatments, especially in apple where no
simultaneous dehydration occurs. The increase on sugar concentration in the intercellular
spaces of pre-treated samples during drying can also contribute to difficult water transport.
No influence was observed on n parameter. For combined air-microwave drying, pre-
346
treatment only affected significantly during the first strawberry drying period, resulting in
lower b values (slower rates).
QUALITY OF DEHYDRATED AND REHYDRATED FRUIT
Quality characteristics of dried fruits are very different to those of fresh ones. An
important aspect that must be considered when optimizing the drying process is the
nutritional value of the product. In the case of fruits, the maximal retention of organic acids,
minerals, vitamins, fibre, phytochemicals, etc. has to be an objective in order to ensure its
functional role in the human diet. Nevertheless, despite the interest of consumers in the
healthy aspects of foods, other quality parameters are implied in the selection of the preferred
ones. In this sense, product appearance is of great interest and customer depends mainly on
shape, size and optical properties (colour, translucency and brightness).
Optical properties of tissue predetermine our expectation of both flavour and quality,
because they inform about another aspects of the product such as maturity, sanitary state,
pigment’s concentration, etc. Thus, it is important not to underestimate the influence that
these physical properties have on the consumer. When colour deterioration occurs
extensively, it results in visually unacceptable products. From a physical point of view,
optical properties depend on the way in which the food interacts with the visible
electromagnetic radiation. Structural and compositional aspects are implicated in such
interaction and so, despite the great influence of pigments presence on colour, they are not the
only element responsible for visual perception of this property.
Food texture is also a determinant factor in positive consumer opinion. The main factors
that contribute to mechanical properties of plant tissue are cell turgor, which is one of the
most important ones, cell bonding force through middle lamella, cell wall resistance to
compression or tensile forces, density of cell packaging that defines the free spaces with gas
or liquid, and various other factors common to other products, such as sample size and shape,
temperature and strain rate [47]. Fruits and vegetables soften when heated partly due to the
loss of turgor, but also due to a variety of enzymatic and chemical changes in the cell wall
matrix polysaccharides [48].
In development of new products, colour and texture are important quality parameters
because consumers have increased their expectations and requirements for attractive colours
and different textures.
Optical Properties
Optical properties of the fruit may change considerably during any drying process. The
causes of these changes are of chemical and physical nature: (1) Water loss implies an
increase in the effective pigment concentration, which could enhance selective light
absorption [28]; (2) Degradation or loss of fruit pigments and development of browning
during pre-treatments or drying process; (3) Exchange of internal gas in the pores for external
liquid near the sample surface due to the action of hydrodynamic mechanisms which may
occur during VI/PVOD pre-treatment. Changes in pigment concentration is mainly related to
347
colour changes, whereas the partial substitution of gas by liquid induces a more homogenous
refractive index in the tissue, which promote light absorption against scattering, the product
thereby gaining transparency.
Changes in product translucency induced by a process can be analysed by the spectral
distribution of Kubelka Munk coefficients (ratio between light absorption (K) and scattering
(S)), obtained from reflectance spectra when measured on black and white backgrounds [49].
When the mentioned spectra were obtained from the samples considered in this study,
fresh apple and strawberry samples, as well as pre-treated strawberry, behave as an infinitely
thick layer as no influence of the background was detected in reflectance measurements.
Nevertheless, VI apple slices showed translucency, due to the commented effect of air
exchange for impregnation liquid (figure 1). VI also affected fresh apple CIEL*a*b* colour
co-ordinates (figure 2), promoting a significant L* (lightness) decrease due to the greater light
penetration depth in the less opaque samples. Moreover, a* values increased to less negative
values, thus decreasing the greenness of sample, and b* values decreased turning to less
yellowness. This promoted a significant lower chrome of VI samples although hue angle was
not affected. The global colour difference between fresh apple before and after VI pretreatment (ΔE= [Δa*2+Δb*2+ΔL*2]0.5) was ±31. In strawberry (figure 2) the previous osmotic
dehydration supposed a significant decrease of a*, b* and chrome, whereas luminosity and
hue angle were not affected. In this case ΔE was ±10.
Figure 1. Spectral distribution of Kubelka-Munk coefficients (K/S) of fresh and vacuum impregnated (VI)
apple samples before and after drying treatment.
348
Figure 2. L* values and a*,b* chromatic diagram of fresh (○) and dried samples (∆ AD, □ A/MWD). Hollow
symbols pre-treated samples; full symbols non pre-treated samples.
349
Drying treatments decreased translucency of pre-VI apple and promoted changes in
measured colour co-ordinates (figures 1 and 2). AD or A/MWD dried apple slices showed
higher L*, a* and b* values than initial fresh fruit. In samples without pre-treatment, the
shorter process time needed when microwave application, provoked less global colour
changes (ΔE= ±11) than in the convective process (ΔE= ±15). In pre-VI samples, the increase
in sugar amount and a possible no enzymatic browning may be responsible for the observed
highest ΔE value with respect to the fresh non pre-treated sample (±17 in A/MWD and ±22 in
AD samples).This greater colour change could be a negative characteristic in the obtained
product and so the use of this pre-treatment will be limited when the principal objective of the
process is to obtain a final product with a similar appearance to raw material. For dried
strawberry halves (figure 2), the clearest effect was the increase in sample lightness promoted
by microwaves application (greater L* values), which could be related to the sample
discoloration at surface level in line with the higher temperature reached in the sample during
drying. Nevertheless, hue angle was not affected by drying treatment, which could be an
advantage for the product’s acceptance.
On the other hand, the colour of fruits is due to the presence of pigment groups, such as
chlorophylls, carotenoids, anthocyanins, etc. They are susceptible to colour deterioration
during heat treatment. In this sense, the thermal process optimisation may be desirable to
prevent degradation of natural pigments. Stability of strawberry anthocyanin during drying
process was studied, considering the pelargonidine-3-glucoside (Pgd) as the major
anthocyanidin of this fruit [50]. Fresh strawberry showed 34±6 mg Pgd/100 g fresh sample.
Neither PVOD nor AD treatments affected the content of the studied pigment, whereas
microwave application induced a significant anthocyanin degradation (20±4 mg Pgd/100 g
fresh sample), probably associated with the higher temperature reached by the samples in this
case. No significant correlations were observed between CIEL*a*b* colour co-ordinates and
anthocyanin concentration. This agrees with that reported by other authors [51] and can be
explained by the heterogeneous distribution of pigments in the fruit and the influence of the
surface structure on reflectance. Nevertheless, the higher L* values in air-microwave dried
samples may be related to the suggested anthocyanin degradation caused by microwaves on
the sample surface, where reflectance was measured.
Structural Aspects
Thermal treatment of fruits may cause important structural modifications, which are
related to alterations in cell wall and middle lamella components. These accumulative
changes could result in different tissue texture. The mechanical properties are closely related
to the developed structure as a result of induced deformations in cells (shrinkage/swelling)
and intercellular spaces, ruptures of cellular bonds and changes in cell wall polymers taking
place throughout the drying process. Also the glassy or rubbery physical state achieved by the
product’s liquid phase will affect the mechanical response. On the other hand, behaviour of
dried samples during rehydration will be closely related to structural damage occurred during
drying. An approach in this sense has been carried out with the samples considered in this
study, analyzing all these aspects before and after drying treatments.
350
As to the structure and functional properties, pectin is very important when compared to
other cell wall polymers because of its chemical sensitivity and thermal vulnerability. Pectin
is an important component on the primary cell wall and middle lamella and it has a relevant
structural role. The dominant feature of pectin is a linear chain of α-(1,4)-linked Dgalacturonic acid units in which varying proportions of the acid groups are present as
methoxyl (methyl) esters. Pectin may be broken down into pectinic acid and finally pectic
acid. Galacturonic acid units compose more than 65 % of pectin structure. Pectin may be
separated into calcium sensitive and non calcium sensitive fractions. The former appears to
have blocks of galacturonic acid which are de-esterified and are believed to come from the
middle lamella region, whilst the non calcium sensitive pectin comes from the primary cell
wall [52]. Two different pectin fractions, oxalate soluble (OSP) and water soluble (WSP)
pectin, may be analysed by selective extraction procedures of the total pectin (TP), as
described by [53], and respectively related to them. Galacturonic acid (GalA) content in the
different fractions may be determined colorimetrically at 520 nm by using the mhydroxydiphenyl method [54]. The difference between TP and the sum of WSP and OSP,
analyzed with mentioned procedures in samples under study, was taken into account to
estimate the amount of non extractable pectin (NXP), which was the protopectin fraction.
Different kinds of fruits contain different types and quantities of pectin. For example,
apple or banana contain high total pectin content (in the range of 0.5 to 1.6 g/100 g), while
soft fruits, such as cherries and strawberries contain lower amounts (0.2-0.7 g/100 g) [55].
The TP in apple and strawberry used in this study was 0.844±0.003 and 0.53±0.08 g
GalA/100 g of fresh sample, respectively. Of the whole pectin content of apple, about 55 %
corresponds to NXP, 37 % to WSP and 8 % to OSP. A different behaviour was observed in
strawberry, for which the OSP represent the major pectic fraction in the fresh sample (about
53 %) and the NXP the lower one (about 19 %). The lower esterification degree of strawberry
pectin is responsible for the greater amount of OSP. This pectin fraction can bind calcium
forming a cross-link structure [42]. In this sense, calcium-treatments contribute to maintain
structural integrity of fruits with a high OSP fraction [56].
After drying process pectin content was again analysed in samples with and without pretreatment and compared with initial raw material. The difference between the pectin content
in dried and fresh samples, in both cases referring to the mass of the corresponding initial
fresh sample, is shown in figure 3. Drying processes induced a pectin solubilisation, as a
decrease in NXP was quantified. Also an effect on the calcium pectin bonding occurs, thus
decreasing the OSP fraction. These changes contribute to the observed WSP increase. Both
pre-treatments and microwave application enhance the observed changes. On the one hand
this may be a consequence of the temperature effect [13], so that the greater heating reached
in microwave treated samples will favour pectin solubilisation. On the other hand, as a result
of the vacuum step during pre-treatment, intercellular spaces become full of an aqueous phase
which will be in contact with middle lamellae, thus favouring the pectin solubilisation
phenomenon during subsequent drying process. From these results it can be concluded that
the pectin fractions of non pre-treated air dried samples will be the less affected, while the
pre-treated ones dried with microwave application will change the most. Nevertheless, if the
sugar content of the sample is increased during pre-treatment, as in the case of PVOD
strawberry, no additional pectin solubilisation occurs during microwave treatment, probably
due to a certain pectin-sugar interaction that will protect it from the changes induced by the
351
high temperatures. In fact, it has been reported in a previous work [57] that cells protected by
sugars exhibited less damage to the middle lamella and less severe shrinkage during drying.
Figure 3. Difference in diverse pectic fractions between dried and fresh samples. (■) WSP, water soluble
pectin; (■) OSP, oxalate soluble pectin; and (□) NXP, non extractable pectin.
As commented above, both drying treatments and pre-treatments applied to studied
samples promoted changes in native solutes, due to changes in pectin composition and
increase in the sugar content of the samples. Changes in the average molecular weight of the
solutes present in the fruits liquid phase may affect the glass transition temperature (Tg) that
characterises the glassy to rubbery state transition [58,59]. Glassy and rubbery are amorphous
states, characterized by a disorderly molecule state presenting a metastable configuration,
achieved when imposed changes to the system occur faster than crystallization rate. In a
352
drying process, when the solubility limit of solutes is achieved, its separation in the form of
crystals is not frequent due to kinetic problems. In this situation, the remaining liquid phase
will be in a rubbery or glassy state depending on the final temperature and water content of
the product. As both are non equilibrium states, they may evolve to a crystalline stable state,
the greater the temperature or the water content, the quicker the evolution. Nevertheless, on a
kinetic level, the glassy state is considered to be much more stable than the rubbery one,
which shows a greater molecular mobility. In fact, in practical terms related to foods, the
glassy state may be considered as much stable as the crystalline one. Changes in molecular
mobility associated with the glass transition are related to changes in mechanical and
diffusional properties of foods [59].
In order to analyse the effect of pre-treatments and drying treatments applied to apple and
strawberry on the physical state of the remaining liquid phase, the Tg of dried products was
analysed by differential scanning calorimetry (DSC 5200Co, Seiko Instruments). Obtained
results are shown in table 2. Significant differences were detected among samples dried with
different treatments. As the final water content of the samples was of the same order,
differences may be explained taking into account the final composition of the solutes present
in dried samples. Table 2 shows the soluble solid fraction (xs) determined in the samples
submitted to DSC analysis, as well as the WSP fraction (xWSP). Soluble solid fraction was
determined from the soluble solid fraction in the liquid phase (ºBrix/100) of pre-treated or
fresh samples and applying the corresponding mass balances for drying operation. As can be
observed in table 2, osmotically pre-treated strawberry samples showed a significantly greater
soluble solid content due to the external sucrose gain. Nevertheless, the ratio xWSP/xs was
lower in pre-treated ones. From these data a lower average molecular weight seems to
correspond to soluble compounds of liquid phase in PVOD pre-treated samples. This fact
agrees with the lower Tg values observed for them. In non pre-treated apple samples, the Tg
value was in the expected range taking into account the xWSP/xs value, related to strawberry
ones. Nevertheless, in the case of vacuum impregnated apple, the Tg of samples was much
greater. Other compounds with higher molecular weight comming from commercial apple
juice used for sample impregnation, could contribute to the behaviour of aqueous phase in
these cases. These samples were the only ones in a glassy state at normal storage temperature
of the dried product.
Table 2. Soluble solids (xs), water soluble pectin fraction (xWSP) and glass transition
temperature (Tg) for dried samples. Values are expressed as mean±standard deviation
Sample
Apple
VI AD
VI A/MWD
AD
A/MWD
Strawberry
PVOD AD
PVOD A/MWD
AD
A/MWD
xs
xWSP
(g/g dried sample)
xWSP/xs
Tg
(ºC)
0.63±0.03
0.66±0.04
0.69±0.02
0.77±0.04
0.021±0.003
0.023±0.002
0.019±0.002
0.022±0.003
0.032±0.03
0.035±0.04
0.027±0.02
0.028±0.02
39.3±0.4
40.3±0.3
3.12±0.12
4.51±0.14
0.82±0.07
0.81±0.08
0.71±0.06
0.69±0.05
0.022±0.002
0.019±0.002
0.024±0.002
0.028±0.003
0.025±0.004
0.023±0.003
0.034±0.03
0.041±0.004
-1.0±0.3
-1.6±0.3
3.1±0.7
6.3±0.6
353
As has been described, changes in pectin solubility occurring during drying may affect
the cell bonding forces supporting the cellular structure and thus the mechanical behaviour of
dried and rehydrated samples. Also the glassy or rubbery state will affect. Mechanical
response may be interpreted by means of some physical parameters measured through a
puncture test with a Universal Texture Analyzer (TA.XT2, Stable Micro Systems). For this
purpose, a cylindrical 2 mm diameter punch was used at a penetration rate of 1.5 mm/s until
total sample penetration. Temperature during the test was 25 ºC. Parameters obtained from
the force-penetration depth curves were: the maximum force required to punch the sample
(Fmax) and the slope (Si) of the curve in the linear zone prior to fracture point. The peak of
maximum force is related to the product resistance to fracture or sample firmness [60] and the
slope of the curve is related to sample resistance to deformation (rigidity).
Fresh sample behaviour was considered in order to compare the mechanical response of
dried samples with the initial fruit performance. The force to penetrate fresh apple increased
to Fmax which kept relatively constant until the end of the test (7.8±0.9 N). For fresh
strawberry halves, two fracture peaks, related with the resistance (firmness) offered by the
strawberry epidermis (1.3±0.2 N at a penetration depth of 1.5±0.2 mm) and the pulp (2.3±0.6
N at 12.1±0.9 mm), to punch advance were observed. After drying process (figure 4), samples
showed a viscoelastic behaviour with a greater deformability (lower Si) before fracture, and
with only one fracture peak followed by an abrupt fall in force, regardless of kind of fruit and
drying conditions. Higher values of slope and maximum force were obtained for pre-treated
samples and also for A/MWD samples. Both process conditions promoted the dried sample
mechanical rigidity and resistance. However, microwave influence was not significantly
evident in VI samples. Gas-liquid interchange occurred during vacuum impregnation of
samples, also as the increase in sugar content in osmodehydrated samples, could favour the
generation of an extra compact cell matrix during drying. The greater pectin content detected
in the aqueous phase in A/MWD samples will agree with the more rigid, less deformable
observed structures.
Figure 4. Continued on next page.
354
Figure 4. Force-penetration depth curves for air (a) and air-microwave (b) dried samples.
The different impact of treatments on cellular structure may also be observed in
rehydrated samples (in distilled water at 20 ºC for 8h). To this end, the same mechanical test
conditions were used but punch diameter was 4 mm. Microwave applications, in either pretreated or non pre-treated samples, implied a significant decrease in the mechanical
parameters, in agreement with the observed changes in pectin fractions by microwave action.
As has been commented, the microwave favours the WSP increase. This has been related to a
greater mechanical resistance of dehydrated samples, due to the higher viscosity of the liquid
residual fraction. Nevertheless, the water incorporated during rehydration may attenuate the
compositional effect of the liquid phase. However, the OSP fraction, which decreased with
this treatment, confers resistance to the middle lamella and cell wall. This could have a more
relevant influence in the mechanical response of the rehydrated samples. A better mechanical
response of rehydrated pre-treated samples than non pre-treated ones was observed, especially
for strawberry halves, despite the fact that the decrease in OSP was greater in these cases.
This seems to indicate that pre-treatment helped to preserve the fruit matrix structure much
better whereas microwave application provokes a greater structural alteration.
In rehydrated apple samples, the rehydration ratio (RR) and the capacity of liquid phase
retention (CLPR in Eq. 2) were evaluated (table 3). The RR was expressed as the weight ratio
between the rehydrated and dehydrated samples [46]. The rehydration study was not carried
out with strawberry because an important colour loss was observed.
CLPR =
(
)
rh
M rh * x rh
w + xs − mL
(
M o * 1 − x ow
)
(2)
355
where M is the sample weight (g), xw is the water content (g/g), xs is the soluble solid content
(g/g), mL is the liquid phase weigh (g) after sample centrifugation (10 min at 4000 rpm).
Superscript o corresponds to the sample prior to dehydration and rh to the rehydrated sample.
Table 3. Rehydration ratio (RR) and capacity of liquid phase retention (CLPR) for
dried apple samples. Values are expressed as mean±standard deviation
Sample
VI AD
VI A/MWD
AD
A/MWD
RR
0.65±0.02
0.70±0.03
0.569±0.017
0.63±0.02
CLPR (g LF/g dry solid)
2.02±0.09
1.68±0.08
2.62±0.10
2.32±0.08
VI and A/MWD samples showed the greater RR and lower CLPR values, associated with
promoted structural changes. Both the effect of vacuum pressure during pre-treatment and the
porous structure generated when microwave is applied [61,62] will explain the greater water
incorporation but also the lower capacity to retain the liquid incorporated.
CONCLUSION
Microwave application to hot air drying provokes a great reduction in process time and
changes in pectin solubility, resulting in an increase in the water soluble fraction and a
decrease in both the oxalate soluble fraction and the residual pectins. As a consequence, when
applying microwaves, dried strawberry and apple showed a higher mechanical resistance.
However, the structural damage associated with dehydration is reflected in the lower
mechanical resistance of the corresponding rehydrated samples and also in a lower capacity to
retain the liquid phase. On the other hand, microwave application induces an increase in
luminosity of the strawberry, which shows an anthocyanin content loss. Related to pretreatments, vacuum impregnation of apple increases translucency and highlights the colour
changes that take place during drying, although the osmotic pre-treatment did not
significantly affect the strawberry colour. Both kinds of pre-treatments implied higher process
times when using convective drying but no significant differences were found when applying
microwaves. Nevertheless, both promoted pectic solubilization which, together with the
higher sugar content when dried, could explain the higher mechanical resistance observed in
the pre-treated samples when dried. At the same time, the sugar added during the osmotic pretreatment of strawberry contributes to a better mechanical response of the tissue when
rehydrated. Taking into account all these considerations, it is recommended to use these pretreatments and microwave application to hot air drying in order to obtain dried apple or
strawberry with a high mechanical resistance, although colour changes would be greater in
these cases, especially in apple. The higher the sugar introduced into the product with the pretreatment, the higher the resistance of the dried fruit to fracture. If the objective of the process
is mainly to obtain a product with good mechanical response to further rehydration, pretreatments are recommended as well, but not microwave application to convective drying.
356
ACKNOWLEDGEMENTS
The authors would like to thank the Spanish Ministry of Education and Science and the
European Regional Development Fund for financial support throughout the project AGL
2005-05994.
REFERENCES
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
Suutarinen, J.; Honkapää, K.; Heiniö, R.; Autio, K.; and Mokkila, M. (2000). The
effect of different prefreezing treatments on the structure of strawberries before and
after jam making. Lebensmittel Wissenschaft und Technologie, 33, 188-210.
Moraga, G.; Martínez-Navarrete, N.; and Chiralt, A. (2004). Water sorption isotherms
and glass transition in strawberries: influence of pretreatment. Journal of Food
Engineering, 62, 315-321.
Wilhelm, L. R.; Suter, D. A.; and Brusewitz, G. H. (2004). Drying and dehydration.
In: St. Joseph, Mich: American Society of Agricultural Engineers (Eds.), Food and
Process Engineering Technology. (259-284) ASAE Technical Library.
Ozkan, A. I.; Akbudak, B.; and Akbudak, N. (2007) Microwave drying characteristics
of spinach. Journal of Food Engineering, 78 (2), 577-583.
Schiffmann, R. (2001). Microwave processes for the food industry. In: A. Datta and
R. Anantheswaran (Eds.), Handbook of microwave technology for food applications.
(299-352). New York: Marcel Dekker. Inc.
Data, A. (2001). Fundamentals of heat and moisture transport for microwaveable food
product and process development. In: A. Datta and R. Anantheswaran (Eds.),
Handbook of microwave technology for food applications (115-166). New York:
Marcel Dekker. Inc.
Ruíz, G.; Martínez-Monzó, J.; Fito, P.; and Chiralt, A. (2003). Modelling of
dehydration-rehydration of orange slices in combined microwave/air drying.
Innovative Food Science and Emerging Technologies, 4, 203-209.
Fleischman, G. (2001). Safety in microwave processing. In: In: A. Datta and R.
Anantheswaran (Eds.), Handbook of microwave technology for food applications.
(471-497). New York: Marcel Dekker. Inc.
Martín, M. E.; Martínez-Navarrete, N.; Chiralt, A.; and Fito, P. (2003). Diseño y
construcción de una instalación experimental para el estudio de la cinética de secado
combinado por aire caliente y microondas. Alimentación. Equipos y Tecnología, 181,
101-107.
Alvarez, C.; Aguerre, R.; Gómez, R.; Vidales, S.; Alzamora, S.; and Gerschenson, L.
(1995). Air dehydration of strawberries: effects of blanching and osmotic
pretreatments on the kinetics of moisture transport. Journal of Food Engineering, 25,
167-178.
Torreggiani, D.; Forni, E.; Maestrelli, A.; and Quadri, F. (1999). Influence of osmotic
dehydration on texture and pectic composition of kiwifruit slices. Drying Technology,
17 (7-8), 1387-1398.
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
357
Fito, P.; Andrés, A.; Barát, J.; and Abors, A. (2001). Introducción al secado de
alimentos por aire caliente. España: Universidad Politécnica de Valencia.
Contreras, C.; Martín, M. E.; Martínez-Navarrete, N.; and Chiralt, A. (2005). Effect of
vacuum impregnation and microwave application on structural changes which
occurred during air-drying of apple. Lebensmittel Wissenschaft und Technologie, 38,
471-477.
Contreras, C.; Martín, M. E.; Martínez-Navarrete, N.; and Chiralt, A. (2007).
Influence of osmotic pre-treatment and microwave application on properties of air
dried strawberry related to structural changes. European Food Research and
Technology, 224 (4), 499-504.
Fito, P. (1994). Modelling of vacuum osmotic dehydration of food. Journal of Food
Fito, P.; and Pastor, R. (1994). Non-diffusional mechanisms occurring during vacuum
osmotic dehydration. Journal of Food Engineering, 21, 513-519.
Fito, P.; Andrés, A.; Chiralt, A.; and Pardo, P. (1996). Coupling of hydrodinamic
mechanism and deformation-relaxation phenomena during vacuum treatments in solid
porous food-liquid systems. Journal of Food Engineering, 27, 229-240.
Chiralt, A.; Fito, P.; Andrés, A.; Barat, J. M.; Martínez-Monzó, J.; and MartínezNavarrete, N. (1999). Vacuum impregnation: a tool in minimally processing of foods.
In: F. Oliveira and J. C. Oliveira (Eds.), Processing of Foods: Quality Optimization
and Process Assesment. (341-356). Boca Ratón: CRC Press.
Gras, M.; Vidal-Brotons, D.; Betoret, N.; Chiralt, A.; and Fito, P. (2002). The
response of some vegetables to vacuum impregnation. Innovative Food Science and
Emerging Technologies, 3 (3), 263-269.
Archer, R.W. (1962). Firming processed apples with calcium. Canner/Packer, 13:28.
Drake, S. R.; and Spayd, S. E. (1983). Influence of calcium treatment on Golden
Delicious apple quality. Journal of Food Science, 48, 403.
Conway, J.; and Sams, C. E. (1983). Calcium infiltration of Golden Delicious apples
and its effect on decay. Phytopathology, 73, 1068.
Bangerth, F.; Dilley, D. R.; and Dewey, D. H. (1972). Sterilization in Food
Technology. New York: McGraw-Hill Book Company, Inc
Chiralt, A.; and Fito, P. (1996). Sating of Manchego type cheese by vacuum
impregnation. In: P. Fito; E. Ortega-Rodríguez; and G. Barbosa-Cánovas (Eds.), Food
Engineering. 2000 (214). New York: Chapman and Hall.
Andrés, A.; Rodríguez-Barona, S.; Barat, J. M.; and Fito, P. (2002). Mass transfer
kinetics during cod salting operation. Food Science and Technology International, 8
(5), 309-314.
Barat, J. M.; Rodríguez-Barona, S.; Andrés, A.; and Visquert, M. (2004) Mass
transfer analysis during the cod desalting process. Food Research International, 37
(3), 203-208.
Barat, J. M.; Grau, R.; Pagán-Moreno, M. J.; and Fito, P. (2003). Simultaneous brine
thawing-salting operation during spanish cured ham manufacturing. Meat Science, 66,
603-608.
Chiralt, A.; and Talens, P. (2005). Physical and chemical changes induced by osmotic
dehydration in plant tissues. Journal of Food Engineering, 67 (1-2), 167-177.
358
[29]
[30]
[31]
[32]
[33]
[34]
[35]
[36]
[37]
[38]
[39]
[40]
[41]
[42]
[43]
Biswal, R. N.; Wilhelm, L. R.; Rojas, A.; and Mount, J. R. (1997).Moisture diffusivity
in osmotically concentrated diced sweet potato during air drying. Transactions of the
American Society of Agricultural Engineers, 40 (5), 1383-1390.
Ghosh, P. K.; Agrawal, Y. C.; Jayas, D. S.; and Kumbhar, B. K. (2004). Mass transfer
kinetics model of osmotic dehydration of carrots. Transactions of the American
Society of Agricultural Engineers, 47 (4), 1179-1185.
Shi, X. Q.; Fito, P.; and Chiralt, A. (1995). Influence of vacuum treatment on mass
transfer during osmotic dehydration of fruits. Food Research International, 28 (5)
445-454.
Shi, X. Q.; Chiralt, A.; Fito, P.; Serra, J.; Escoin, C.; and Gasque, L. (1996).
Application of osmotic dehydration technology on jam processing. Drying
Technology, 14 (3/4), 841-857.
Alzamora, S. M.; Cerrutti, P.; Guerrero, S.; and López-Malo, A. (1995). Minimally
processes fruits by combined methods. In: G. Barbosa-Cánovas and J. Welti-Chanes
(Eds.), Food preservation by moisture control: fundamentals and applications. (463492). Lancaster, USA: Technomics Publishing.
Alvarez, C.; Aguirre, R.; Gómez, R.; Vidales, S.; Alzamora, S.; and Gerschenson, L.
(1995). Air dehydration of strawberries: effects of blanching and osmotic
pretreatments on the kinetics of moisture transport. Journal of Food Engineering, 25,
167-178.
Nieto, A.; Salvatori, D.; Castro, M. A.; and Alzamora, S. M. (1998). Air drying
behaviour of apples as affected by blanching and glucose impregnation. Journal of
Food Engineering, 36 (1), 63-79.
Riva, M.; Campolongo, S.; Avitabile-Leva, A; Maestrelli, A; and Torreggiani, D.
(2005). Structure-property relationships in osmo-air-dehydrated apricot cubes. Food
Research-International, 38 (5), 533-542.
Riva, M.; Cortellino, G.; Maestrelli, A.; and Torreggiani, D. (2001) Structure collapse
and colour changes in osmo-air-dehydrated peach cubes. Food Science and
Biotechnology, 10 (6), 598-601.
Torreggiani, D.; and Bertolo, G. (2001). Osmotic pre-treatments in fruit processing:
chemical, physical and structural effects. Journal of Food Engineering, 49 (2-3), 247253.
Maestrelli, A.; Lo Scalzo, R.; Lupi, D.; Bertolo, G.; and Torreggiani, D. (2001).
Partial removal of water before freezing: cultivar and pre-treatments as quality factors
of frozen muskmelon (Cucumis melo, cv reticulatus Naud.). Journal of Food
Engineering, 4 (2-3), 255-260.
Sormani, A; Maffi, D; Bertolo, G; and Torreggiani,D. (1999). Textural and structural
changes of dehydrofreeze-thawed strawberry slices: effects of different dehydration
pretreatments. Food Science and Technology International, 5 (6), 479-485.
Funebo, T.; and Ohlsson, T. (1998). Microwave assisted air dehydration of apple and
mushroom. Journal of Food Engineering, 38, 353-367.
Lin, T. M.; Durance, T. D.; and Scaman, C. H. (1998). Characterization of vacuum
microwave, air and freeze dried carrot slices. Food Research International, 3 (2) 111117.
Maskan, M. (2000). Microwave/air and microwave finish drying of banana. Journal
of Food Engineering, 44, 71-78.
[44]
[45]
[46]
[47]
[48]
[49]
[50]
[51]
[52]
[53]
[54]
[55]
[56]
[57]
[58]
[59]
[60]
359
Mulet, A. (1994). Drying modelling and water diffusivity in carrots and potatoes.
Journal of Food Engineering, 22 (1-4), 329-348.
Wang, Z.; Sun, J.; Liao, X.; Chen, F.; Zhao, G.; Wu, J.; and Hu, X. (2007).
Mathematical modeling on hot air drying of thin layer apple pomace. Food Research
International, 40 (1), 39-46.
Giri, S. K.; and Prasad, S. (2007). Drying kinetics and rehydration characteristics of
microwave-vacuum and convective hot-air dried mushrooms. Journal of Food
Engineering, 78 (2), 512-521.
Maltini, E.; Torreggiani, D.; Rondo Brovetto, B.; and Bertolo, G. (1993). Functional
properties of reduced moisture fruits as ingredients in food systems. Food Research
International, 26 (6), 413-419.
Sapers, G.; Cooke, P.; Heidel, A.; Martin, S.; and Miller, R. (1997) Structural
Changes Related to Texture of Pre-Peeled Potatoes. Journal of Food Science, 62 (4),
797–803.
Hutchings, J. (1999). Food color and appearance (2d edition). Gaithersburg, Maryland:
Aspen Publishers.
Torreggiani, D.; Forni, E.;Guercilena, I.; Maestrelli, A.; Bertolo, G.; Archer, G. P.;
Kennedy, C. J.; Bone, S.; Blond, G.; Contreras-Lopez, E.; and Champion, D. (1999).
Modification of glass transition temperature through carbohydrates additions: effect
upon colour and anthocyanin pigment stability in frozen strawberry juices. Food
Research International, 32 (6), 441-446.
Skrede, G.; Wrolstad, R.; Lea, P.; and Enersen, G. (1992). Color stability of
strawberry and blackcurrant syrups. Journal of Food Science, 57, 172-177.
Imeson, A. (1997). Thickening and gelling. Agents for food. London, UK: Blackie
Academia and Professional.
Yu, L.; Reitmeier, C.; and Love, M. (1996). Strawberry Texture and Pectin Content as
Affected by Electron Beam Irradiation. Journal of Food Science, 61, 844-846.
Kinter, P.; and Van Buren, J. (1982). Carbohydrate interference and its correction in
pectin analysis using the m-Hydroxydiphenyl method. Journal of Food Science, 47,
756-764.
Badui, S. (2006). Química de los alimentos (4th edition). México: Pearson Addison
Wesley.
Lara, I.; García, P.; and Vendrell, M. (2004).Modifications in cell wall composition
alter cold storage of calcium-treated strawberry (Fragariaxananassa Duch.) fruit.
Postharvest Biology and Technology, 34, 331-339.
Tregunno, N.; and Goff, H. (1996). Osmodehydrofreezing of apples: structural and
textural effects. Food Research International, 29, 471-479.
Rao, M (1998). Phase/State Transitions in Foods. Chemical, structural and
rheological changes. New York: Marcel Dekker.
Roos Y (1995). Phase Transitions in Food. San Diego: Academic Press.
Prothon, F.; Ahrné, L.; Funebo, T.; Kidman, S.; Langton, M.; and Sjoholm, I. (2001).
Effects of combined osmotic and microwave dehydration of apple on texture,
microstructure and rehydration characteristics. Lebensmittel Wissenschaft und
Technologie, 34, 95-101.
360
[61]
[62]
Andrés, A.; Bilbao, C.; and Fito, P. (2004). Drying kinetics of apple cylinders under
combined hot air–microwave dehydration. Journal of Food Engineering, 63 (1), 7178.
Bilbao-Sáinz, C.; Andrés, A.; and Fito, P. (2005). Hydration kinetics of dried apple as
affected by drying conditions. Journal of Food Engineering, 68 (3), 369-376.
Chapter 6
PEST CONTROL USING HIGH PRESSURE CARBON
DIOXIDE AS AN ADVANCED TECHNOLOGY
Mustafa Bayram
University of Gaziantep, Faculty of Engineering,
Department of Food Engineering, 27310-Gaziantep-TURKEY
ABSTRACT
Food products are always under the risk of infestation by pests. In view of the
competitive markets, there has been increasing demand for quality in foods in terms of
freedom from pest and pesticide contaminants. Also, it is very important for trade
purpose suffer economic and quality losses. Zero tolerance of insect pest in foods has
been adopted in some of countries and there is a tendency to achieve this goal in overall
the world.
The governments, the food industries and exporters are dependent on fumigation as a
quick and effective tool for insect pest control in food commodities. Fumigants are
widely used for pest elimination in these commodities. Toxic substances have therefore
been used to destroy for example pests, as well as their eggs, larvae, cocoons and adults.
Currently used substances, such as methyl bromide, hydrogen phosphide, ethylene
dioxide, malathion etc., are characterized by more or less serious problems. In recent
years, that fumigation technology based on the chemical control of products has been
facing threats/constraints because of regulatory concerns, the development of resistance,
handling hazards, residues, food safety, cost, carcinogenicity, involvement in ozone
depletion, resurgence, environmental pollution and other factors. Reliance upon
fumigation as an overall solution to infestation problems in food products has become
questionable. The chemical action of fumigants upon commodities and the environment
has necessitated the withdrawal of many fumigants from the market. Also, some of them
are being phase out their uses at the international level.
Due to becoming the target of increasing criticism of toxic substances, such concerns
have led to the development of non-chemical methods for the control of insect pests that
infest food commodities. One such method is the high pressure carbon dioxide
application, which mainly involves the use of CO2 at high pressure (10-40 bar) for food
fumigation. It is a new effective, non-chemical, non-residual, safe, fast and
environmentally friendly method for the food industry. It has been generated and
362
Mustafa Bayram
developed within last 20 years. Carbon dioxide is a fumigant and being used to
control pests in the food industry. After extensive testing, high pressure carbon
dioxide fumigation can be accepted as the advanced pest control technology for the
future. Nowadays, it is particularly indispensable for the gentle, safe, natural and organic
food products. If operation time for the fumigation is constraint and non-chemical
treatments are required, this technique is suitable for conventional products.
INTRODUCTION
Storage of food in safe must maintain quality and quantity. In order to obtain this safe
storage, food products should be protected from environmental effects, microorganisms, high
moisture, high temperature, insects, rodents, animals, mites, odors and contaminations etc.
Pests can cause structural damage and threaten food safety and employee health. Protecting
consumers from pathogens that cause food poising, pneumonia and conjunctivitis is serious
matter.
The one of the most important defects caused during storage is insect damage. The
destruction also begins before storage and then continues during storing with the rate of
quality loss depending on storage conditions. If all contaminations is prevented, that rate is
slowest when the food is driest and coolest, since growth rate of insect depends on moisture
and temperature.
Insects are a hazard to stored food products in several ways. For example in grain
industry, some devour whole kernels, others consume broken kernels and dust. All cause rises
in grain temperature and moisture. All contaminate the grain, and particles of insects may get
into grain products where, though harmless, they are aesthetically objectionable (Bailey,
1974).
Grain-infesting insects are very sensitive to temperatures. They multiply slowly or not at
all below 15.56oC, and they cannot survive in temperature of 41.67oC or above. They appear
to thrive best at about 29oC, and at that level their life cycles may be as short as 30 days.
These insect may get into grain in the field, harvesting machinery, farm bins or trucks,
country elevators, or during bin-site storage, so that after 80 days of storage at temperatures
above 21.11oC any lot of stored grain is likely to show evidence of insects. Insects infesting
stored products can be controlled by different ways (Bailey, 1974).
INSECTS
Insects are a major cause of loss in stored food products. They not only consume these
materials but also contaminate them with insect fragments, feces, webbing, ill-smelling
metabolic products, and with a variety of microflora; they therefore constitute a major
sanitation and quality-control problem (Cotton and Wilbur, 1974).
Insects may be classified in different groups. However, it will be suitable to classify them
within two groups such as insects that develop inside and outside food. For example, weevils
deposit their eggs inside food; lesser grain borers and Angoumois grain moths deposit eggs
outside of, and their newly hatched larvae promptly tunnel into, the kernels. Bran bugs, flour
and bran beetles are insects that grow outside of the product. Their eggs usually are laid
Pest Control Using High Pressure Carbon Dioxide...
363
indiscriminately among the kernels or throughout the product. For the most part the larvae are
free-living, though several species tunnel under the germ covering where the larvae develop
as “hidden infestation” (Cotton and Wilbur, 1974).
Insects require optimum condition to continue their life like other organism. However,
they are very resistant organisms, and they exist over the world before human. In addition,
their species are very much.
The most important food-infesting insects live inside the foods during much of their lives,
it is difficult for food handlers to determine the extent of infestation in their products. There
are, however, various techniques and procedures that can be of great help in evaluating
infestations. The simplest and most practical determination can be done using visual
techniques (by eye, magnifier or microscope), stains, specific gravity separation methods,
radiography (X-ray), ninhydrin-impregnated paper, measuring temperature, crackingflotation, measuring carbon dioxide production, measuring uric acid content, traps, ELISA,
NMR, NIR, acoustic and aural etc. (Cotton and Wilbur, 1974; Rajendran, 2003).
A few of more than 100 species of stored-product insects and mites found in product
cause serious damage; the others are fungus feeders, scavengers, predators and parasites
(Abramson et. al., 2001). Insects have four life stages: egg, larva, pupa and adult (figures 1
and 2).
Egg
The eggs may be laid either in the crevices of foods or in the dust and refuse within
storage areas. Some species, such as granary weevils, lay their eggs inside kernels.
Larva
The larva is the only stage during which the insect grows. It consumes several times its
own weight in food, and as the larval skin cannot stretch, it periodically moults allowing it to
increase in size. Cast-off skins found in foods indicate that insects are, or were, present.
Pupa
The pupa, which forms after the last larval molt, does not feed. In some species, the pupa
is enclosed in a cell, or cocoon, constructed by the larva. During the pupal stage, the insect
undergoes extreme internal and external changes that lead to the development of the adult.
Adult
Adults of stored-product insects are between 0.1 and 1.7 cm long. They have three pairs
of legs and their bodies are divided into three parts: head, thorax and abdomen. The head
includes the mouthparts and sense organs; the thorax bears the legs and wings; and the
364
Mustafa Bayram
abdomen contains the reproductive organs. Adults move in the spaces between food particles
and can penetrate deeply into a bulk of products, with the exception of moths and spider
beetles. Some stored-product insects can fly and are widely distributed. Beetles have poorly
developed wings and some species are unable to fly, although the rusty grain beetle, the red
flour beetle and the lesser grain borer fly well.
Figure 1. Life cycles of stored product insects: A, a beetle and B, a moth (Source: Abramson et. al., 2001).
Figure 2. Stages of vermin (egg, larva, pupa and adult, respectively) (DKSH, 2007).
Stored-product beetles often appear similar but have differing behaviour patterns and
status as pests. It is important to determine which species are present before taking remedial
action. A detailed identification guide is now available (Bousquet, 1990) to help determine
which species are present. The characteristic features of the main beetle species occurring on
stored products are as follows (Abramson et. al., 2001):
Rusty Grain Beetle
This beetle (figure 3, Plate Ia, b) is the most serious pest of stored product. It usually
feeds on the germ (embryo) part of a whole seed. Heavy infestations cause grain to spoil and
heat. The adult is a flat, rectangular, shiny, reddish-brown beetle, 0.2 cm long and has long,
bead-shaped antennae that project forward in a “V”. It moves rapidly in warm and can fly
when the air temperature is above 23°C. Eggs are laid in the crevices of kernels and in grain
365
dust. The tiny larvae penetrate and feed on the germ of damaged kernels. Eggs become adults
in wheat in about 21 days at 14.5% moisture content and 31°C.
Sawtoothed Grain Beetle
These beetles (figure 3, Plate Ic) are more common in oats than in wheat, barley or
canola. The adult is brown, is about 0.3 cm long, and has six tooth-like projections on each
side of the thorax. In warm grain it takes about 22 days to develop from egg to adult under
optimal conditions of 31 to 34°C and 14 to 15% moisture content.
Indianmeal Moth
This moth (figure 3, Plate Id) is common on corn and processed feeds and foods, and
throughout the country in warehouses and stores.
Granary Weevil
This weevil (figure 3, Plate Ie) is one of the most destructive pests of stored grain in the
world. The adults have a distinctive snout, with which they bore into grain kernels. The
female deposits a single egg in a hole in each kernel and then seals the opening with a
gelatinous plug. The larvae feed on the endosperm and complete their development within the
kernel. The pupae develop into adults that chew holes in the side of the kernels as they
emerge. Development from egg to adult takes 25 to 35 days under optimal conditions of 26 to
30°C and 14% moisture content. The granary weevil adult is about 0.3-0.4 cm long and
cannot fly. When disturbed, they fold their legs under their body and appear to be dead.
Rice Weevil
This weevil (figure 3, Plate If) has been found in storage and in some prairie elevators in
recent years. It is 0.2 to 0.4 cm long and has four distinct reddish orange spots on the wing
covers, which are folded over the abdomen. It completes development from egg to adult in 28
days at 30°C and 14% moisture content. Adult rice weevils can fly, and attack a wide range of
cereals other than rice; larvae develop and pupate within the kernel.
366
Mustafa Bayram
Figure 3. Insects found in food products (Source: Sinha and Watters, 1985).
Yellow Mealworm
These insects (figure 4, Plate IIa) are the largest found in stored grain. They are not
common pests on farms. They first infest animal feeds and then move into stored grain that is
going out of condition. The adults are black beetles about 1.5 cm long; the larvae are yellow
367
and 0.2 to 2.8 cm long. Yellow mealworms prefer dark, damp places in a granary or a feed
bin. The adults live for several months and the larvae may take 1 to 2 years to change into
pupae under harsh conditions. Because of their relatively large size, they are easily visible and
often appear to be more numerous than they actually are. Their presence indicates poor
storage and sanitation conditions.
Figure 4. Insects found in food products (Source: Sinha and Watters, 1985).
368
Mustafa Bayram
Cadelles Cadelles
(figure 4, Plate IIb) are shining black or dark reddish-brown beetles about 1.25 cm long,
which makes them the largest of the major stored grain damaging insects. Their larvae range
between 1.58 and 2.54 cm long; they are creamy white with a black head, two black or dark
plates on the upper part of the segment just behind the head, and a dark plate with two stout
dark projections on the tip of the abdomen (Cotton and Wilbur, 1974).
Red Flour Beetle
This pest (figure 4, Plate IIc, d) develops on stored grains and oilseeds on farms and in
primary elevators. The adult is reddish brown and 0.4 cm long. Larvae and adults feed on
broken kernels. Complete development from egg to adult occurs in about 28 days under
optimal conditions of 31°C and 15% moisture content. Slower development occurs at
moisture contents as low as 8%. Adults fly in warm weather or may be blown by the wind
into farmhouses or other buildings.
Confused Flour Beetle
The adult (figure 4, Plate IIe) resembles that of the red flour beetle and is difficult to
distinguish without a microscope or magnifying glass. Larvae and adults feed on flour, animal
feed and other ground material. Unlike the red flour beetle, the confused flour beetle is more
common in flour mills than elsewhere, and the adults do not fly.
The summarized information about pests is tabulated in table 1 and 2 for beetles, and
moths.
Table 1. Stored-product beetles found in food products (Source: Sinha and Watters, 1985)
Table 2. Stored-product moths found in food products (Source: Sinha and Watters, 1985)
371
PEST CONTROL IN GENERAL USES
The insect pests of stored food product have certain temperature, moisture, air humidity,
ambient air composition, and food requirements, which directly affect their abundance, and
hence their ability to cause damage. By controlling these conditions, insects can be controlled
and killed. However, absolute control requires advanced techniques.
To prevent and control infestations it should be known where and when insects occur.
Surveys have shown that most empty storages are infested with low numbers of insects and
mites. Animal feeds, trucks and farm machinery are other sources of insect infestations. Some
insects can fly as well as walk, which increases their ability to infest stored products.
The insect control may be defined as the preventing contamination of adult insects to
products (cross contamination), growth of insects, stopping incubation of eggs, sustainability
of clearness of good products and killing eggs, larvas, pupas and adults using effective
methods. Practically, there are a lot of techniques to kill them such as physical, chemical and
biological. Some of them have still been used traditionally. Recently, high pressure carbon
dioxide system has effectively been used in industry. In order to compare it with other
techniques, they will be explained briefly.
Cooling, heating, irradiation, diatomaceous earth, impact-pneumatic auger, controlled
and modified atmospheres, chemicals (phosphine, carbon dioxide, malathion), biological
control, cleaning, sanitation, drying and aeration are general techniques used widely to
control insects. The most important methods selected before the explaining high pressure
carbon dioxide method are given below.
Cooling and Heating
Insects being poikilotherms are sensitive to large temperature changes in the
environment. Increase or decrease in temperatures outside the optimum range of 25-32 oC
results in developmental delay, drop in reproduction, and mortality at the end. Insects are
killed rapidly by heat rather than by cold treatment. Tolerance to heat treatments varies
depending on the insect species, stage, and age of the insect, and its physiological state.
Product is also affected from heating e.g. losing germination ability, physicoshemical changes
etc. Moreover, product after heating should be cooled immediately for safe storage
(Rajendran, 2003). A method to control insect infestations in winter is to lower food
temperature. This can be done by mixing and transferring infested products from one granary
to another which will lower food temperatures about 10°C in the winter; or by transferring
part of the product to a truck or small pile exposed to low air temperature, leaving it to cool
for one or more days and then returning it to the granary. However, aeration systems are
much more effective at lowering the food temperature. Insects do not develop or feed at
temperatures below 10°C. At temperatures below 0°C, the insects will die eventually
Abramson et. al. (2001). The effect of temperature on the insects can be summarized using
figure 5.
372
Mustafa Bayram
70
60
Death of insects in minutes
50
Death of insects in one day
Temperature (oC)
40
Growth of insects is slower
30
Growth of insects is faster
20
Growth of insects is slower
10
Death of insects in weeks, months
0
-10
Death of insects in days, months
-20
Death of insects in minutes
-30
min.
max.
Effectiveness
Figure 5. The effect of temperature on the growth of insects.
Irradiation
Ionizing radiation for insect control using gamma-radiation emitted from cobalt-60 and
cesium-137, or accelerated electrons of less than 10-V energy from a cathode is applied on
stored products. The treatment causes mortality as well as sterility in food insect pests and the
effect occurs at all temperatures (Rajendran, 2003).
Diatomaceous Earth
Control of insects can be achieved by using a nontoxic dust made from prehistoric
diatoms. Inert dusts, such as wood ash, paddy husk ash, kaolins, lime, and clay materials;
have been traditionally used for grain preservation. They act as a desiccant, absorbing water
from the insect body and may also have an abrasive action. They act slowly and take 20 or
more days to cause insect mortality (Rajendran, 2003). When insects come in contact with
this dust, the waxy covering on their skin is absorbed, leaving them prone to dehydration and
death. The product is applied to grain as it is augered into the bin, and is most effective when
applied to dry grain at harvest (Abramson et. al. 2001).
373
Impact-Pneumatic Auger
(Abramson et. al. 2001) Most free-living adult and larvae insect pests are killed during
bin unloading by using a “grain-vac.” Insects are killed by abrasive contact and impact as the
grain and insects are moved through the discharge tube. Better control is achieved when there
is a 90° bend in the tube; this causes more contact of insects with the sidewalls of the tube.
Controlled and Modified Atmosphere
Normal atmosphere consisting of 78 % nitrogen, 21 % oxygen, 0.03 % carbon dioxide,
and the balance argon and other gases. The objective of modified atmosphere treatment is to
attain a composition of atmospheric gases rich in CO2 and low in O2, or a combination of
these two gases at normal or altered atmospheric pressure within the treatment enclosure, for
the exposure time necessary to control the storage pests. Various terms used in reference to
MA storage for the control of storage insect pests or the preservation of food have appeared in
the literature to define the same method of treatment but using different means to attain the
same scope of control without adversely affecting the environment (Navorro, 2006). In a CA
treatment, the atmospheric composition in the treated enclosure is controlled or maintained at
a level lethal to insects. The modified gas composition, usually produced artificially, is
maintained unchanged by additionally generating the desired gases (CO2 or N2) or by further
purging the storage with these gases, supplied from pressurized cylinders or otherwise
(Navorro, 2006). The controlled atmospheres applied may be of either low-oxygen (0.5 %
oxygen and 99.5 % nitrogen) or high-carbon dioxide atmosphere (40-80 % carbon dioxide,
balance air) or burner gas (0.5 % oxygen, 13-21 % carbon dioxide, balance mainly nitrogen).
The choice between the three depends on local availability of the gases, suitability of the
structures, and afford-ability (Rajendran, 2003).
Chemicals
Approved insecticides are selected largely on the basis of i) low toxicity to mammals and
high toxicity to insects, ii) freedom from taint or odour on food, iii) non persistent
environmental effects, iv) safe, economical and easy use and v) presence of negligible
residues or toxic products in food. Some insecticides are more effective and longer lasting
than others. Premium-grade malathion, cyfluthrin, pyrethrum with piperonyl butoxide are at
present the insecticides registered for empty-bin treatments (Abramson et. al. 2001).
Methyl bromide has been an effective and important tool for controlling pests in food
processing facilities. However, the phaseout of methyl bromide has been an overshadowing
concern for producers globally since 1992, when 160 countries signed an amendment to the
Montreal Protocol environmental treaty that included methyl bromide as one of the several
identified ozone-depleting substances to be phased out of production (Buckley 2004, Methyl
Bromide Industry Government Working Group, 1998).
Fumigants are chemicals available as gases, liquids, and in solid formulations, but act on
the insect and other pests in gaseous state (Ranjendran, 2003). Fumigants generate toxic gases
that are used to control insects in stored grain. They are available for farm use only as solid
374
Mustafa Bayram
formulations. Fumigants are also toxic to humans and farm animals and, therefore, must be
applied only by trained people. Avoid inhaling the vapours (Abramson et. al. 2001) .
The gas fumigant sulfuryl fluoride is the probably the most anticipated new option for
structural fumigations. Phosphine is another methyl bromide option. Available in many
forms, it can be used for treating bulk grain storage, finished products, commodities in
transport and also structural spaces, although care must be taken to prevent corrosion to metal
and electronics. Phosphine tablets and pellets have been used for than 40 years. Aluminum
phosphide pre-pacs, and magnesium phosphide plates are especially suited for situations
where spent fumigant needs to be recovered. Cylinderized phosphine gas and phosphine
generator systems ae the newest applications to come out in recent years, and have everal
advantages over the pellets. Prime benefits are that flammability risks are reduced and there
are no spent residues to remove and dispose. Personal safety is enhanced because it’s remote
application eliminates the need to enter the fumigated area (Buckley, 2004).
Biological Control
There has been a growing tendency in favor of nonchemical methods. There are
situations in which biological control, which is residue-free but has species-specific action,
will play an active role. Control may be manifested by the action of predators, parasitoids, or
pathogens. Predators attack the immature stages of stored food insect pests. Parasitoids are
very small hymenopteran insects, parasitizing egg or larva (Rajendran, 2003).
HIGH PRESSURE CARBON DIOXIDE PROCESS (HPCO2PR)
FOR INSECT CONTROL
Food products may always be under the risk of infestation to a greater or lesser extent
(figure 6). Toxic substances have therefore been used to destroy for example insects, as well
as their larvae and eggs, up to now. Also, insects, pests and other vermin are a common and
very serious threat to commodities. However, these toxic substances were becoming the target
of increasing criticism. Insects damage to stored plant products due to pest infestation by
direct feeding damage (reduction in weight, destruction of seedlings, decrease in baking
quality or food value), pollution, transfer of micro-organisms and damage to the health of
humans and animals (allergies, poisoning). To avoid economic and reputation losses in the
markets, it is absolutely necessary to take measures against infestation and contamination.
However, the use of poison gas and insecticides can cause problem due to possible residues
such as prophylactic extermination, processing or packaging products directly after the
treatment, multiple treatments for long-term stored products, improper extermination of
pesticide from producer, pesticide use during cultivation, environmental pollution, industrial
safety and labor safety.
375
Figure 6. Egg, larva, pupa and adult on different food products (a) dried apricot, b) beans, c) chickpea, d)
lentils.
Biological treatment of products against all vermin (pest control) used to be a very
expensive and time consuming process. High pressure carbon dioxide process (HPCO2Pr) is a
new alternative method. Industrially, carbon dioxide is used as dry ice pellet, liquid and gas
for carbonation, refrigeration, crude oil recovery, pH control, deflashing, industrial cleaning,
electronics, preserving, baked goods manufacturing, inert blanketing and purging, shielding
gas, solvent, metallurgy (steel making), textiles, pressurization, papermaking, plastics,
agriculture, horticulture, food and chemical etc. It is a non-flammable, colorless, odorless gas,
about 1.5 times as heavy as air. Carbon dioxide can be added from an external source to a
sealed enclosure using either gas produced from a liquid supplied in pressurized cylinders or
from solid "dry ice". It is a compound formed by the combination of carbon and oxygen
atoms in a 1:2 ratio and proportioned by weight of about 27.3% carbon to 72.7% oxygen. It is
present in the atmosphere at a concentration of 0.03 percent by volume. It is a normal product
of human metabolism. It is a gas at normal atmospheric temperature and pressure. It is
relatively non reactive, non toxic and a slightly acidic gas.
Carbon dioxide treatment at atmospheric pressure as a fumigant remains slower-acting
than phosphine or methyl bromide. However, chemical solutions are not popular in recent
time. Therefore, high pressure with CO2 is an effective solution method for insects. Due to
that one, the study on high pressure carbon dioxide process has been continued for twenty
years. Carbon dioxide is not a residual gas due to its inert property. It is non-flammable,
ecologically friend gas that is safe for residual case. It is also used during packaging of food
product. In addition, it can be used repeatedly and prophylactically on the applications and
376
Mustafa Bayram
resulting in an extremely rapid and 100% effective treatment. As no pesticides or any other
undesirable chemicals are used, the process is suitable for HACCP, GMP, organic and
conventional rules and procedures.
Researches and Developments on the HPCO2Pr
Application of CO2 at atmospheric condition is long time request process. In order to
decrease the operation time, high pressure was started to use in CO2-insect treatments (figure
7). The Stored-Product Laboratory at Bordeaux investigated the use of high pressure and
carbon dioxide for insect/pest control at 1980’s. After extensive testing in the laboratory, a
high pressure fumigation chamber was designed and built in collaboration with MG SIAC
(Saint-Denis, France) (Fleurat-Lessard et. al. 1996). The first trials in the laboratory showed
that raising the CO2 pressure from 1 to 20 atmospheres reduced the time to control the
granary weevil (Sitophilus granarius) larvae from 18 days to 4 hours (Le Torc'h and FleuratLessard, 1991; Prozell and Reichmuth, 1991). Given the success of these first tests, the study
was expanded to insects that are more common in processed foods, the likely commodity for
this procedure. Eggs, larvae, and adults of the red flour beetle (Tribolium castaneum), the
hide beetle (Dermestes maculatus) and the Indian meal moth (Plodia interpunctella) were
placed in a pressurized chamber and sub-samples were removed at various times to check for
survival. Pupae were not used, as in a pretest they were shown to be more susceptible than the
other stages. Table 3 gives the minimum times needed to control insects. For the red flour
beetle the eggs are the most resistant stage, requiring just over 4 hours at 10 atmospheres and
1 hour at 19 atmospheres. Other insects at other stages are more susceptible than red flour
beetle eggs. Trials are also conducted with air in place of CO2. Hide beetles adults had 93%
and Indian meal moth adults have 100% mortality at 19 atmospheres after 2 hours, but all
three larval and egg stages are unaffected after 2 hours at 19 atmospheres (Fleurat-Lessard et.
al. 1996). After laboratory studies, a pre-industrial pilot pressure chamber with a capacity of
0.75 m3 and the ability to simulate the complete pressure treatment with a rapid rise in
pressure to 11 or 16 atmospheres, with a final stable pressure of 19 atmospheres was built and
tested. The pressure chamber was attached to a suite of 11 cylinders with 160 atmospheres of
CO2 and a heat exchanger for the injection of the gas into the chamber. The CO2 was injected
into the lower part of the chamber and the bags of insect-infested pet food placed at different
levels in the chamber to estimate the degree of gas stratification. The chamber was not purged
of air before the injection of CO2, causing a slight reduction in CO2 concentration
(approximately 1/19th). This may be the reason there were a few red flour beetle eggs that
survived in the top most level. To avoid this, the industrial scale chamber was designed to be
purged with one volume of CO2 before pressurization, and gas is introduced at several points
in the chamber (Fleurat-Lessard et. al. 1996). The pilot trials also determined the rates of
pressurization and depressurization that the packaging could tolerate. The initial pet food
packaging was too gas tight and often tore during the rapid changes in pressure. Replacing the
packaging with a more porous material, and the reducing the rates of pressure change solved
this problem (Fleurat-Lessard et. al. 1996).
377
Figure 7. Application time for CO2 at atmospheric condition (Carvex, 2007).
Table 3. The minimum duration necessary to completely control various insects at a
given stage under high pressure CO2 fumigation (Fleurat-Lessard et. al. 1996)
Stahl and coworkers (Rau, 1985; Stahl and Rau, 1985; Stahl et al, 1985; Gerard et al,
1988a,b) tested carbon dioxide under high pressure to kill insects and microbes of compressed
carbon dioxide against the cheese mite, Tyrophagus putrescentiae. Pohlen et al (1989),
Prozell and Reichmuth (1991), Le Torc’h and Fleurat-Lessard (1991), Nakakita and
Kawashima (1994), Reichmuth (1997), and Prozell et al (1997) also reported on the improved
efficacy of carbon dioxide under high pressure. Developmental stages of L. serricorne, O.
378
Mustafa Bayram
surinamensis, T. castaneum, T. confusum, Trogoderma granarium, Corcyra cephalonica (the
rice moth), Ephestia elutella, E. cautella, P. interpunctella, and Sitotroga cerealella
(Angoumois grain moth) were exposed (at a temperature of 20°C) to carbon dioxide at 37 bar
for 20 min, 30 bar for 1 hr, and 20 bar for 3 hr. These treatments resulted in 100% mortality
of all insects. Survivors of T. confusum were found after treatment with 10 bar for 20 hr.
Therefore, Adler et al (2000) concluded that extrapolation of laboratory results for carbon
dioxide and high pressures to field situations are risky. The rate of decompression of
pressurized chambers also have an adverse impact on insect mortality (Ulrichs, 1994; Ulrichs
et al, 1997a,b). Treatment with high-pressure carbon dioxide under different temperatures
may result in different rates of mortality. For example, at 15°C, 95% mortality of L.
serricorne was observed after 38.5 min of treatment, while the same level of control was
achieved within 1 min at 45°C (Ulrichs, 1995). With high pressures (20–40 bar), all types of
pests and their life stages can be killed within a short time. The relatively rapid control of
pests in all stages of development is based, on one hand, on the narcotic and acidifying effect
induced by the high solubility of carbon dioxide in cell fluid and, on the other hand, on the
destruction of the cells following the carbon dioxide pressure treatment during
depressurization (Adler et al, 2000) (Navarro, 2006).
Extremely short exposure times (a few hours) are needed to control all stages of storage
insects with carbon dioxide at pressures between 10 and 37 bar. Generally, increasing the
pressure reduces the lethal exposure time. Stahl et al (1985) and Stahl and Rau (1985) were
the first to report that pressurized carbon dioxide is lethal to insects (Navarro, 2006).
CO2 under high pressure followed by quick decompression was also introduced by Stahl
et al., (1985) and Gerald et al. (1988a). The greatest advantage of this method as a pest
control measure is its short lethal exposure period. Several researchers who investigated the
use of CO2 at high pressure on different insect pests of cereal grains have reported that the
exposure period can be reduced to less than an hour, regardless of the species or the
developmental stage (Prozell and Reichmuth, 1991; Reichmuth, 1991; Nakakita and
Kawashima, 1994; Reichmuth and Wohlgenmuth, 1994; Locatelli et al., 1999; Song et al.,
1999). In all these studies, the eggs were reported to be more tolerant than other
developmental stages. However, regarding the difference in the tolerance to CO2 of insect
eggs of different ages under high pressure, there is only one report, on Plodia interpunctella
(Hübner) (Reichmuth and Wohlgenmuth, 1994). Hence, the aim of this study was to provide
data on the effect of CO2 under high pressures on the mortality of C. maculatus egg of
different ages.
In the study of Shazalli et. al. (2004), their study was to provide empirical data on the
effect of ambient carbon dioxide (CO2) under high pressure on the mortality of
Callosobruchus maculatus (F.) eggs at different ages. The mortality of the eggs was assessed
in combinations of four CO2 pressures (15, 20, 25, and 30 bar) and five egg-age groups (one,
two, three, four and five days old) with 5, 10, 15, and 20 min exposure periods. The
investigations were carried out in an automated pilot plant (volume: 1.1 lt) at 25°C and 70%
R.H. After each exposure period the gas pressure was decreased to atmospheric level in one
second. One-day-old eggs were found to be the most tolerant, requiring 30 bar and 20 min
exposure for complete extermination. On the other hand, five-day-old eggs were the least
tolerant, requiring only 20 bar and 10 min. The tolerance of the eggs declined with age and
the mortality was influenced by the pressure level and the exposure period. To achieve 100%
mortality, increasing pressure was more effective than increasing exposure time. Decisions
379
regarding pressure and exposure time of CO2 should be made case by case, because the effect
of CO2 appears to vary depending on the age of the egg. The operational values are given in
table 4.
The egg stage is more tolerant than other developmental stages, and in fact it is
characterized by a low water content and very few cells, besides having the most stable form
as a sphere (Gerald et al., 1988a; Reichmuth and Wohlgenmuth, 1994). Reichmuth and
Wohlgenmuth (1994) studied the effect of egg age of P. interpunctella on mortality when
exposed to CO2 under high pressure, and concluded that 100% mortality of young eggs (24 h)
was achieved at 20 bar and 40 min. Locatelli et al. (1999) concluded that 20 bar and 15 min
were required to prevent P. interpunctella eggs of mixed ages (2–4 days old) from hatching.
These differences in the estimated 100% mortality levels show that the mortality of very
young eggs must be examined when insect pests are eradicated using high-pressure CO2.
Decisions regarding pressure and exposure time of CO2 should be made case by case, because
the effect of CO2 appears to vary depending on the age of the egg.
Table 4. Mean mortality of Callosobruchus maculatus eggs of different
ages exposed to CO2 under high pressure Shazalli et. al. (2004)
Commercial Applications
The stored-product pests laboratories at Bordeaux and Berlin investigated the use of
carbon dioxide at high pressure (Fleurat-Lessard, 1990; Reichmuth and Wohlgemuth, 1994).
After extensive testing in the laboratory, a high-pressure fumigation chamber was designed
and built in collaboration with the French company MG SIAC. The chamber can hold the
380
Mustafa Bayram
equivalent of the contents of one transport trailer. The unit is designed to recover at least 85%
of the carbon dioxide used (Navarro, 2006).
Gerard et. al. (1990) described a high-pressure chamber connected to a tank of liquid CO2
placed on a balance. This unit is commercially available and utilized in Germany (Navarro,
2006). The full scale pressure chamber of MG MIAG (Saint-Denis, France) has a working
capacity of 80 m3, enough space to treat 32 pallets of pet food or the equivalent of the
contents of one transport trailer. In a normal treatment cycle, pallets are loaded into the
chamber; the chamber is sealed and purged with one volume of CO2. The CO2 is injected into
the chamber, and it takes 90 minutes to obtain 19 atmospheres. This pressure is maintained
for 60 minutes and it takes 30 minutes to depressurize the chamber. The entire cycle with
loading, fumigation and unloading takes approximately four hours. The operation of
pressurizing and depressurizing is complicated by the desire to minimize the amount of CO2
lost during each fumigation. This is obtained by a patented system using two CO2 holding
tanks and a compressor. To verify the effectiveness of the unit, red flour beetle adults and
Indian meal moth larvae were placed in bags of pet food, the commodity to be fumigated, and
placed throughout the chamber. None of the 3200 red flour beetles or the 1600 Indian meal
moth survived the fumigation (Fleurat-Lessard et. al. 1996). There is another unit built in
Germany by another company that is used for fumigating spices.
CARVEX is a system constructor for HPCO2Pr in Germany which their system is carried
out by the Federal Biological Research Centre for Agriculture and Forestry of Germany. It is
an independent supreme authority in the domain of the Federal Ministry of Consumer
Protection, Food and Agriculture (Carvex, 2007).
The study of Martin Bauer (MABA-PEX) started as long ago as 1986. The first major
trials of the new MABA-PEX process took place in October 1987. All subsequent trials were
conducted in close cooperation with the Federal Institute of Biology in Brunswick and the
Department of Chemical Engineering at the University of Erlangen/Nuremberg (Martin
Bauer, 2007). Door of vessel is opened from upper section. It supplies low press to hinge
(figure8).
Figure 8.View from MABA-PEX system.
381
Over the last 10 years, DKSH Inc. (Holland) has developed a unique process for the
ecological and biological treatment of vermin, using a combination of CO2 and high pressure.
DKSH Inc. also applies their own single horizontal and vertical (figure 9) systems for their
raw materials used for pet feeds and others. Bulk commodities are treated in the vertical 70
m³ tank. Packaged products (when not airtight and/or vacuum packed) are treated in a
horizontal tank with a capacity of 14 europallets. A different opening and closing mechanism
is used on the gate mechanism of horizontal vessel. Frame at around the gate is rotated to lock
tooth.
Figure 9. Horizontal (left) and vertical (right) HPCO2Pr of DKSH Inc. (DKSH, 2007).
Tariş Co. (İzmir-Türkiye) uses two horizontal vessel systems made by Buse-Gastek
(Germany) to apply on dried grape and figure etc. The system contains a CO2 recovery
system (figure 10).
Figure 10. Two pressure chambers made by Buse-Gastek Co. for dried fruits and CO2 recovery system used
by Tariş Co.
382
Mustafa Bayram
Davert Inc. (Germany) uses two horizontal vessel systems made by Carvex Co.
(Germany) for organic products in packed form (figure 11). In this system similar to Tariş/
Buse-Gastek, the gate of horizontal vessel is open and closed by rotating gate on a bearing
(figure12). It is also jointed on hinge at side. Frame is not rotating. Their gate system is
different from DHSK Inc.
Figure 11. Double horizontal system with aspiration and heat exchanger components used by Davert Inc. for
organic products.
Figure 12. Gate system and bearing used by Tariş/Buse-Gastek and Davert/Carvex.
Tiryaki Group (Türkiye) uses its own vertical system for bulk grains and legumes either
for organic and conventional food products. It was developed by R and D team (Mustafa
Bayram, Faruk Kutbay, Süleyman Tiryakioğlu, Ahmet Tiryakioğlu) that is one of the high
capacity systems for the organic products (figure 13).
Commercially, these systems are also used under sub-contract protocols for different
companies.
383
Figure 13. Bulk product application with HPCO2Pr.
Operations
The influence of HPCO2Pr on the insects is (i) the effect of acidity of cell liquids and
hemolymph of insects through the dissolution of CO2 in the body fluid is fortified under
pressure (carbon dioxide is formed), (ii) effect of pressure, which is especially effective
during tension release, (iii) deoxygenation, (iv) dehydration during trying respiration of
insects, (v) sharp pressure change and explosion of insect egg, larva, pupa and body during
loading and discharging of CO2. The disinfestation effect of high pressure CO2 system
depends on various parameters, such as exposure time, species, phase of insects (figure 14),
pressure (figure 15), pressure drop rate, temperature (figure 16), etc. The parameters depend
on each other.
According to studies of Carvex (2007), the increase in temperature reduces required
exposure time, however high temperatures adversely affect product quality and low
temperatures increase required exposure time. In addition, if temperature is between 0 and
15°C, required exposure time increases. Out of this range, required exposure time decreases.
Also if pressure increases, the influence of the temperature decreases.
384
Mustafa Bayram
Figure 14. Effect phase of insects (Carvex, 2007).
Figure 15. Effect of pressure level on the insects (Carvex, 2007).
385
Figure 16. Effect of temperature for high pressure CO2 system (Carvex, 2007).
The treatment requirements include pressure-proof horizontal or vertical gas-tight vessels
(autoclaves). The high pressure CO2 process involves exposing the product in its gaspermeable original packaging materials e.g. bags and boxes (figure 17) (for horizontal vessel)
or bulk (for vertical vessel) to a pressurized carbon dioxide atmosphere. If the product is
packed in bags, bales, bundles, etc. and also marshaled on pallets, measures must be
implemented to ensure that the carbon dioxide can permeate the material completely. The
product to be treated is left in its original packaging and is transported on pallets into the
autoclave. Products are transported and loaded into vessel on a specially designed vehicle and
conveyors (figure 18). Once loaded, the vessel (if two vessels are used) is flooded with
gaseous carbon dioxide to the required final pressure. Liquid carbon dioxide in stock tank
(figure 19), this tank is 80 bar, another type storage tank are also hold between 18-20 bar
using conditioning system to decrease thickness of tank) is vaporized via a heat-exchange unit
(figure 20), introduced into the autoclave in gaseous form, and raised to the treatment
pressure. Over all processing time at each cycle is related to loading, discharging, processing
(e.g. 2 hr at 20 bar) etc (figure 21). The subsequent pressure equalization between vessels I
and II, which has been loaded in the meantime already represents a saving of 50% carbon
dioxide. Additional carbon dioxide can be taken to build up the necessary final pressure
following pressure equalization. If a single vessel is used instead of two vessels, the gas used
is discharged to atmosphere or recycled using recycling system. Due to the investment and
energy cost of recycling system (special compressor/pump for gas, coolers, regulators, tank,
climatic system etc.), it is not used widely. For two vessels and recovering systems, there is
also transfer risk of odors after applying gas and re-use it in subsequent operation. Therefore,
if the product has specific volatile odor, a single use should be applied.
386
Mustafa Bayram
Figure 17. Loading of packed products in vessel (Carvex, 2007).
Figure 18. Loading of products using conveyors and forklift (Carvex, 2007).
Figure 19. CO2 stock tank (on the left, Carvex, 2007) and high pressure CO2 fumigation with tanks for
recycling gas (on the right, Fleurat-Lessard et. al., 1996).
Figure 20. CO2 evaporator (heat exchanger) and fan system (Carvex, 2007).
Figure 21. Application time for high pressure CO2 system (Carvex, 2007).
387
388
Mustafa Bayram
After the operation, the remaining carbon dioxide in the vessel is then discharged through
a fan/compressor to atmosphere for the safety. Pressure drops back to ambient atmospheric
pressure. The gas is exhausted into the atmosphere in a short time (10–15 min) with the use of
a silencer (figure 22), to avoid a loud noise during release. The rate of decompression of
pressurized storages may also have an adverse impact on insect mortality. Penetration depth
and flow conditions during pressure build-up and relief were criteria that presented
particularly difficult problems initially. The capacity of system depends on the number of
cycle and vessel, size, chamber pressure limits and product bulk density etc. In order to help
the loading and discharging of products, two gates of vessel (figure 23) can be used.
However, its investment cost is higher than single one. If horizontal system is used for cubic
packaged product, the sides of cylindrical vessel should be filled and closed using brick,
cement or other bulking materials to decrease the cost of operation by decreasing head space
for gas (figure 24).
Figure 22. Silencer during CO2 disharging.
Figure 23. Two gates of vessel for inlet and outlet of product (Carvex, 2007).
389
Figure 24. Filling of side of cylindrical horizontal vessel by materials.
Table 5. The product applied with HPCO2Pr
Dried fruits and berries
Apples cubes, flakes,
Apples pieces
Figs
Pears, cubes, slices
Apricots cubes, wholes
Banana slices, brokens
Banana slices, wholes
Coconut flakes
Cranberries
Elder berries
Juniper berries
Mountain-ash (rowan) berries
Mango cubes
Melon (Cantaloupe) berries
Papaya cubes, red/orange
Papaya cubes, green
Pineapple cubes, slices
Raisins
Rose hips, wholes
Tutti-frutti (fruit mix)
Sour cherry
Dried vegetables and spices
Carrot flakes, cubes
Green beans, sliced
Green cabbage, flakes
White cabbage, flakes
Green leek, flakes
Onion flakes
Onion powder
Garlic flakes
Garlic powder
Garlic granules
Red bell peppers (flakes)
Parsley stems
Potato cubes
Red beets flakes
Tomato flakes, wholes
Pepper berries
Paprika powder
Mushroom
Cinnamon
Coriander
Aniseed
Eggplant
Pepper
Others
Dried chillies
large (4-6 cm) stemless
small (2-4 cm) Malawi
Turkish delight (lokum)
Seeds
Pulse rice
Lentil
Chickpea
Dried beans
Beans
Sesame seeds
Pistachio nuts
Coconuts
Hazelnuts
Other nuts
Pet feeds
Animal feeds
Wood
Pallet
Furniture
Historical materials
Organic products
Textile/fabric
Products Applied with High Pressure Carbon Dioxide System
The products including dried fruits, berries, angelica root, valerian root, birch leaves,
stinging nettle, fennel, rosehip, hibiscus, chamomile, peppermint, sage leaves, yarrow, and
senna leaves) in various cutting sizes (whole product, concise product, finely cut product,
pulvis subtilis) and various types of packaging (paper sacks, jute sacks, pressed bales, boxes
390
Mustafa Bayram
and crates, drums and tape fabric sacks) can be applied using horizontal and vertical systems
(Martin Bauer, 2007; DKSH, 2007). The most common product list is given in table 5.
THE EFFECT OF SYSTEM ON PRODUCT QUALITY
According to the documentation of Martin Bauer (2007), apart from insecticidal efficacy,
the subsequent laboratory experiments investigated such product specific parameters as
appearance and organoleptic properties (smell and taste of the product and tea infusion),
drying losses, extract content, color value, and constituent substances. GC and HPLC
methods were used to test the constituent substances, as well as the methods described in the
pharmacopoeias. The results indicate a 100% mortality rate and no differences in quality
between treated and untreated drugs. The products were tested again after 6 weeks, 3 months,
6 months and 12 months. Here again, no differences are found between untreated and treated
products. Other products have been tested and analyzed in order to verify the results obtained
at that time. No changes are found that could have been attributed to the pressurized carbon
dioxide treatment. However, the R and D Department of Tariş-Türkiye (Karabat, 2007)
studies on the effect of moisture content of product on color change of products during
treatment with HPCO2Pr.
During discharging CO2 from the horizontal HPCO2Pr, if the discharging of gas is fast,
the packages explore. Therefore, the discharging rate should be regulated and controlled.
Cost of HPCO2Pr
The investment costs of horizontal and vertical system change around 300,000-500,000 €
and 100,000-400,000 €, respectively, which depend on capacity, size, number and pressure.
In general, horizontal system is more expensive than vertical one due to special gate of vessel.
The CO2 suppliers rent their CO2 stock tanks to commodities. Therefore, the investment cost
decreases. If CO2 recycling system is preferred, it highly increases the cost. Some companies
manufacture their systems to decrease the investment cost. The operation time depends on
capacity should be calculated very well. If the capacity is low and there is no time limit, the
thickness of vessel can be selected thinner at low pressure long time.
The processing cost of the system depends on the cost of CO2 supplied in country,
pressure applied, space in vessel, bulk density of product, duration and specie of pest etc.
Therefore, operational cost can change from one to the other. According to value of
CARVEX Co., if the double horizontal chamber system (diameter: 2 m, length: 5.2 m, max.
working pressure 32 bar) with cylinder lining is used for products on pallets, the processing
cost of the system is 3.0, 4.7, 6.4 and 10.4 €/pallet at 10, 15, 20 and 30 bar, respectively. The
dimension of one pallet is width of 1.2 m, length of0.85 m, height of 1.5 m and volume of
1.53 m³.
The R and D Department of Tariş Co. investigated and compared the cost of CO2 with
other systems. According to the results, the processing costs of 1, 1, 0.5 and 10 USD/ton of
product on pallet are found for methyl bromide, atmospheric CO2 treatment, phosphine and
HPCO2Pr (with 50% recovery), respectively (Karabat, 2007). This cost is less when vertical
391
system with 50% recovery is used for bulk products e.g. 5.5-6 USD/ton. Both prices are valid
at Türkiye (the unit bulk price of CO2 in Türkiye is 350-500 USD/ton of CO2).
As seen, HPCO2Pr is expensive, therefore, a good working time chart should be prepared
before the selection and investment of system. For that purpose figure 25 can be used. In this
figure, the price factors of pressure, length and diameter of vessel are compared.
According to the report of Fleurat-Lessard et. al. (1996) on MG SIAC system, currently
the unit does six fumigations a day, at a cost of approximately $300 CAN to cover the
electricity and 300-400 kg of CO2 needed for each fumigation. The unit cost approximately
$850,000 CAN in 1995 to build, and the pet food company, Royal Canin, intends to build
another two units, which will enable them to treat 15 truck loads of product a day. The one
pressurized unit replaces eight fumigation units that used phosphine and took three days per
fumigation. This system is appropriate for any packaged food or animal feed product that has
a non airtight packaging, is a high value product, the manufacturer needs a rapid treatment
and a high assurance that the product is free from infestation.
Figure 25. Price factors of parameters for HPCO2Pr vessel.
CHEMICAL AND PHYSICAL PROPERTIES OF CO2 (CITED FROM BOC)
Food grade carbon dioxide is supplied as a liquid in pressurized cylinders. Liquid CO2
changes to a gas when released from the cylinder. The rate of release of gas from the cylinder
is controlled by a regulator designed specifically for carbon dioxide. High pressure tubing is
used to pass the gas from the regulator to the entry port located at the base of the storage silo
or enclosure.
392
Mustafa Bayram
Solid "dry ice" is also a useful source of gaseous CO2. At sub-zero temperatures, carbon
dioxide changes directly from a solid to a gas. Dry ice is supplied as blocks, crushed ice or
pellets. Crushed ice or pellets rapidly change to a gas and are best for initial gas addition.
Blocks are useful to make up gas loss during treatment due to their slower release. Dry ice is
best suited for use in gastight containers or low volume sheeted stacks. Place the dry ice on
the commodity surface prior to sealing or at the base of the container or stack.
Table 6. Properties of CO2
Properties
Specific gravity
Density, lbs/ft3
Values
1.5289 at 1 atm and 70 °F
solid: -109.25 °F = 97.6 lb/cu. ft.
liquid: +1.7 °F, 300 psig = 63.36 lb/cu. ft.
liquid: 70 °F, 830 psig = 47.35 lb/cu. ft.
liquid: -69.8 °F = 73.5 lb/cu. ft.
Specific volume, lbs/ft3
Normal boiling point
Specific heat-gas-varies (at constant pressure
of 1 atmosphere)
Viscosity-gas at atmospheric pressure
Heat of vaporization
Solubility of carbon dioxide
Carbon Dioxide is obtained as a by-product
from one of several sources
Purification methods
8.57 at 1 atm and 60 °F
8.74 at 1 atm and 70 °F
-109.35 °F
70 °F.......................................0.20 BTU/lb
(at constant volume)...............0.15 BTU/lb
70 °F temperature..........
...0.015 centipoise
liquid at 0 °F...................... ....0.14 centipoise
Solid: -109.25 °F = 246.6 BTU/lb
Liquid: +1.7 °F, 300 psig = 119.2 BTU/lb
Liquid: +70 °F, 839 psig = 63.9 BTU/lb
Dissolved in water, carbon dioxide forms carbonic acid
(H2CO3)
Becomes chemically active in moisture or high heat
Readily dissolves in most liquids
Amount is affected by temperature and pressure
Under normal conditions water dissolves its own volume of
carbon dioxide
The greater the pressure, the more CO2 a liquid can hold
Once the pressure is released, CO2 escapes in the
effervescent characteristic of uncapped soft drinks
The colder the liquid, the more CO2 it can hold
Carbon dioxide flows downhill, settles in the bottom, and
displaces air
Ammonia Plants
Fermentation ethanol plants
Hydrogen Plants within refineries
Ethylene oxide
Natural gas process plants
Extractions from flue gases from the burning of natural gas
or fuels
In some parts, CO2 is obtained from CO2 wells at extremely
high concentrations and pressures
Zinc Oxide Beds
Dryers
Adsorbers
Noble Catalyst Beds
Carbon Beds
Molecular Sieve Beds
Water Wash Columns
Potassium Permanganate Beds
393
Table 7. Hazardous and emergencies for CO2
Carbon dioxide hazards
Handling leaks and emergencies
Heavier than air-accumulates in low or confined areas
Asphyxiant;
− Even in normal concentrations of oxygen carbon dioxide can
paralyze the respiratory system
− Concentrations of 10% CO2 or more can cause unconsciousness or
death
The seriousness of the symptoms of asphyxiation experienced
depends on the concentration levels and length of exposure
Carbon dioxide should only be used in areas with good ventilation
Ventilate areas to prevent the formation of toxic concentrations of
carbon dioxide.
If carbon dioxide content exceeds 3% you must wear an SCBA to
enter that area.
Avoid contact of the skin or eyes with cold carbon dioxide.
Evacuate the immediate area if the leak is large.
If water spray is used to dissipate leak, a dense fog may form as well
as carbonic acid.
Leak will dissipate itself given time if the ambient temperature is
above freezing.
REFERENCES
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
Abramson, D., Demianyk, C. J., Fields, P. G., Jayas, D. S., Mills, J. T., Muir, W. E.,
Timlick, B., & White, N. D. G. (2001). Protection of farm-stored grains, oilseeds and
pulses from insects, mites and moulds. In N.D. G. White, Protection of farm-stored
grains, oilseeds and pulses from insects, mites and moulds (pp:1-56, Pub. No: 1851/E
“revised”), Manitoba: Cereal Research Centre, Canadian Agriculture and Agrifood
Canada Publ.
Adler, C., Corinth, H. G., and Reichmuth, C. (2000). Modified atmospheres. In B.
Subramanyam and D. W. Hagstrum, (Eds.). Alternatives to Pesticides in StoredProduct (pp. 105-146). Boston, USA, Kluwer Academic Publishers.
Bailey, J. E. (1974). Whole grain storage. In C. M. Christensen, Storage of cereal
grains and their products (pp. 333-360), St. Paul, Minnesota: AACC Press.
Bauer, M. (2007). Product safety and technical documentation. Martin Bauer Co.,
Germany.
Bousquet, Y. (1990). Beetles: associated with stored products in Canada: An
identification guide. Biosystematics Research Centre Research Branch, Agriculture
Canada Publication, 1-214.
Buckley, E. (2004). A mill’s sanitation toolbox. World Grain, April, 46-49.
Carvex, 2007. Verfahrenstechnologies für Lebensmittel und Pharma GmbH, Technical
documentation. Carvex Co., Germany.
Cotton, R. T., & Wilbur, D. A. (1974). Insects. In C. M. Christensen, Storage of cereal
grains and their products (pp. 194-225), St. Paul, Minnesota: AACC Press.
DKSH, (2007). High pressure treatment: Rapid and environmentally friendly solution
for extending the shelf life of commodities. DKSH Brochure, Holland.
394
Mustafa Bayram
[10] Fleurat-Lessard, F. (1990). Effect of modified atmospheres on insects and mites
infesting stored products. In M. Calderon and R. Barkai-Golan, (Eds.), Food
Preservation by Modified Atmospheres (pp. 21-38). Boca Raton, FL, CRC Press Inc.
[11] Fleurat-Lessard, F., Fields, P. and Le Torc'h J. (1996). Methyl bromıde alternatıves: a
European perspectıve. Workshop on Alternatives to Methyl Bromide, Toronto Canada,
May 30-31, 1996, pp 83-90.
[12] Gerard, D., Kraus, J., and Quirin, K. W. (1988a). Rückstandsfreie Druckentwesung mit
natürlicher Kohlensaure. [Residue-free pressure disinfestation with natural carbon
dioxide]. Gordian, 88, 90-94.
[13] Gerard, D., Kraus, J., Frohlingsdorf, B., Jerga, C. and Dallüge, A. (1990).
Rückstandsfreier Vorratsschutz für Arznei- und Teedrogen. [Residue free stored
product protection of medical and tea drugs]. Dtsch. Apoth. Ztg., 130, 2014-2018.
[14] Gerard, D., Kraus, J., Quirin, K. W., and Wohlgemuth, R. (1988b). Anwendung von
Kohlendioxid (CO2) unter Druck zur Bekampfung vorratsschadlicher Insekten und
Milben. [Use of carbon dioxide (CO2) to control stored product pest insects and mites].
Pharm. Ind., 50, 1298-1300.
[15] Karabat, S. (2007). Personel communication, Tariş R-D Department, İzmir, Türkiye.
[16] Le Torc’h, J. M., and Fleurat-Lessard, F. (1991). The effects of high pressure on
insecticide efficiency of modified atmospheres against Sitophilus granarius (L.) and S.
oryzae (L.) (Coleoptera: Curculionidae). In F. Fleurat-Lessard and P. Ducom (Eds.),
Proc. 5th Int. Work. Conf. Stored-Product Protection (pp. 847-856). Bordeaux, France.
[17] Locatelli, D. P., Suss, L. and Frati, M. (1999). The use of high pressure carbon dioxide
(20 bar) to control some insect of foodstuffs. In Z. Jin, Q. Liang, Y. Liang, X. Tan and
L. Guam (Eds.), Proc. 7th Int. Work. Conf. Stored-Product Protection (pp. 671–675).
Beijing, P. R. China, Sichuan Publishing House of Sci. and Tech.
[18] Maba-Pex, (2007). Advertising brochures.
[19] Methyl Bromide Industry Government Working Group, (1998). Integrated Pest
Management in Food Processing:Working Without Methyl Bromide. Sustainable Pest
Management Series S98-01.
[20] Nakakita, H. and Kawashima, K. (1994). A new method to control stored-product
insects using carbon dioxide with high pressure followed by sudden pressure loss. In E.
Highley, E. J. Wright, H. J. Banks and B. R. Champ (Eds.), Proc. 6th Int. Work. Conf.
Stored-Product Protection (pp. 126-129). Canberra, Australia, CAB International.
[21] Navarro, S. (2006). Modified Atmospheres for the Control of Stored-Product Insects
and Mites. In J.W. Heaps (Ed.), Insect Management for Food Storage and Processing,
(Second Edition, pp. 105-146), St. Paul, MN, AACC International.
[22] Pohlen, W., Rau, G., & Finkenzeller, F. (1989). Erste praktische Erfahrungen mit einem
Verfahren zur Druckentwesung mit Kohlendioxid. [First practical experiences with a
procedure to disinfest with pressurised carbon dioxide]. Pharm. Ind. 51: 917- 918.
[23] Prozell, S. and Reichmuth, C. (1991). Response of the granary weevil Sitophilus
granarius (L) (Coleoptera; Curculionidae) to a controlled atmosphere under high
pressure. In F. Fleurat-Lessard and P. Ducom (Eds.), Proc. 5th Int. Work. Conf. StoredProduct Protection (pp. 911-918). Bordeaux, France.
[24] Prozell, S., Reichmuth, C., Ziegleder, G., Schartmann, B., Matissek, R., Kraus, J.,
Gerard, D., and Rogg, S. (1997). Control of pests and quality aspects in cocoa beans
and hazelnuts and diffusion experiments in compressed tobacco with carbon dioxide
[25]
[26]
[27]
[28]
[29]
[30]
[31]
[32]
[33]
[34]
[35]
[36]
[37]
395
under high pressure. In E. J. Donahaye, S. Navarro and A. Varnava, (Eds.), Proc. Int.
Conf. on Controlled Atmosphere and Fumigation in Stored Products (pp. 325-333).
Nicosia, Cyprus, Printco Ltd.
Rajendran, S. (2001). Alternatives to methyl bromide as fumigants for stored food
commodities. Pesticide Outlook, December, 249-253.
Rajendran, S. (2003). Grain storage: perspectives and problems. In A. Chakraverty,
A.S. Mujumdar, G.S.V. Raghavan and H.S. Ramaswamy, (Eds.), Handbook of
Postharvest Technology (Chapter 8, pp. 183-214). N.Y. USA, Marcel Dekker Inc. N.Y.
Rau, G. (1985). Die Anwendung von verdichtetem Kohlendioxid zur
Qualitiitsverbesserung von Drogen. [Application of pressurized carbon dioxide to
improve the quality of drugs.] Ph.D. dissertation, University of the Saarland,
Saarbrücken, Germany. 100 pp.
Reichmuth, C and R. Wohlgenmuth (1994) Carbon dioxide under high pressure of 15
bar and 20 bar to control the eggs of the Indian meal moth Plodia interpunctella
(Hubner) (Lepidoptera: Pyralidae) as the most tolerant stage at 25°C. In E. Highley, E.
J. Wright, H. J. Banks and B. R. Champ (Eds.), Proc. 6th Int. Work. Conf. StoredProduct Protection (pp. 163-171). Canberra, Australia, CAB International.
Reichmuth, C. (1991). New techniques in fumigation research today. In F. FleuratLessard and P. Ducom (Eds.), Proc. 5th Int. Work. Conf. Stored-Product Protection
(pp. 701-725). Bordeaux, France.
Reichmuth, C. (1997). There is no resistance of stored-product moths against treatment
with carbon dioxide under high pressure. In E. J. Donahaye, S. Navarro and A.
Varnava, (Eds.), Proc. Int. Conf. on Controlled Atmosphere and Fumigation in Stored
Products (pp. 519-525). Nicosia, Cyprus, Printco Ltd.
Shazalli, M. E. H., Imamura, T. and Miyanoshita, A. (2004). Mortality of eggs of the
cowpea bruchid, Callosobruchus maculatus (F.) (Coleoptera: Bruchidae) in carbon
dioxide under high pressure. Appl. Entomol. Zool. 39, 49–53.
Sinha, R.N. and Watters, F.L. (1985). Insect pests of flour mills, grain elevators, and
feed mills and their control. Agric. Can. Publ., 1776. 290.
Song, W., Yang, H. and Wang, H. (1999). The effect of high pressure carbon dioxide,
nitrogen and their mixture on the mortality of two species of stored-product insects. In
Z. Jin, Q. Liang, Y. Liang, X. Tan and L. Guam (Eds.), Proc. 7th Int. Work. Conf.
Stored-Product Protection (pp. 706–709). Beijing, P. R. China, Sichuan Publishing
House of Sci. and Tech.
Stahl, E. and Rau, G. (1985). Neues Verfahren zur Entwesung. [A new method for
disinfestations]. Anz. Schadlingskd. Pflanzensch. Umweltsch., 58, 133-136.
Stahl, E., Rau, G. and Adolphi, H. (1985). Entwesung von Drogen durch KohlendioxidDruckbehandlung (PEX-Verfahren). [Disinfestation of drugs by pressure treatment with
carbon dioxide (PEX procedure)]. Pharm. Ind., 47, 528-530.
Stahl, E., Rau, G. and Adophi, H. (1985). Entwesung von Drogen durch kohlendioxide
Drukbehandlung (PEX-verfahren). Pharmazeutische Industrie, 47, 528–530.
Ulrichs, C. (1994). Effects of different speed of build up and decrease of pressure with
carbon dioxide on the adults of the tobacco beetle Lasioderma serricorne (Fabricius)
(Coleoptera: Anobiidae). . In E. Highley, E. J. Wright, H. J. Banks and B. R. Champ
(Eds.), Proc. 6th Int. Work. Conf. Stored-Product Protection (pp. 214-216). Canberra,
Australia, CAB International.
396
Mustafa Bayram
[38] Ulrichs, C. (1995). Zur Empfindlichkeit des Tabakkafers Lasioderma serricorne
(Fabricius) (Coleoptera: Anobiidae) gegnüber Behandlung mit Kohlenstoffdioxid unter
Hochdruck. [Susceptibility of the tobacco beetle Lasioderma serricorne (Fabricius)
(Coleoptera: Anobiidae) towards treatment with carbon dioxide under high pressure.] (2
Fiche.) Diplomarbeit, Fachbereich Biologie, Freie Universitat Berlin, Verlag DHS
Hansel-Hohenhausen, Egelsbach, 2, 134.
[39] Ulrichs, C., Reichmuth, C. and Rassmann, W. (1997a). Carbon dioxide under high
pressure to control the tobacco beetle Lasioderma serricorne. In E. J. Donahaye, S.
Navarro and A. Varnava, (Eds.), Proc. Int. Conf. on Controlled Atmosphere and
Fumigation in Stored Products (pp. 335-341). Nicosia, Cyprus, Printco Ltd.
[40] Ulrichs, C., Reichmuth, C., Tauscher, R. and Westphal, K. (1997b). Rate of gas
exchange during treatment of compressed tobacco with nitrogen or carbon dioxide for
pest control. In E. J. Donahaye, S. Navarro and A. Varnava, (Eds.), Proc. Int. Conf. on
Controlled Atmosphere and Fumigation in Stored Products (pp. 343-347). Nicosia,
Cyprus, Printco Ltd.
Chapter 7
EFFECTS OF PERMEATION ON MASS TRANSFER
COEFFICIENT FOR LAMINAR NON-NEWTONIAN
FLUID FLOW IN MEMBRANE MODULES DURING
CLARIFICATION/CONCENTRATION OF FRUIT JUICE
Sirshendu De*, Sunando DasGupta and S. Ranjith Kumar
Department of Chemical Engineering; Indian Institute of Technology,
Kharagpur; Kharagpur - 721 302; India
ABSTRACT
Membrane based clarification and concentration of fruit juice has become a popular
unit operation in modern fruit juice processing industries. The well known membrane
modules used for this purpose are tubular and spiral wound modules. Therefore, design of
these modules is of utmost industrial importance. The key parameter for design of
membrane modules is mass transfer coefficient. Most of the fruit juices have nonNewtonian rheology, e.g., power law, ellis fluid, etc. Till today, the mass transfer
coefficient for such systems used is approximated from the corresponding relations
developed for Newtonian fluids. Hence, a detailed fluid flow modeling with nonNewtonian rheology is urgently warranted. In the present work, this aspect is attempted.
The expressions of the mass transfer coefficients are derived from the first principles for
laminar, non-Newtonian fluid flow in a porous conduit. The effects of the permeation are
incorporated quantitatively in the mass transfer coefficient from a theoretical basis. The
analysis is carried out for various non-Newtonian rheologies. Effects of the operating
conditions, i.e., Reynolds number, permeate flux, etc. on mass transfer coefficient are
also investigated. Two flow geometries are considered. Flow through a tube and that
through a rectangular thin channel, which are useful for the design of the tubular and
spiral wound cross flow membrane modules. The developed relations of mass transfer
coefficients would be of tremendous help to the design engineers.
*
Corresponding author: Sirshendu De; Tel: + 91 – 3222 – 283926; Fax: +91 – 3222 – 2755303; E Mail:
[email protected]
398
1. INTRODUCTION
The mass transfer coefficient is an important parameter for designing membrane
separation modules, where the flow occurs through a porous conduit. Therefore, accurate
estimation of the mass transfer coefficient is necessary. These coefficients are generally
calculated from the Sherwood number correlations, obtained from the heat and mass transfer
analogies. The major limitations of these correlations are, (i) they are applicable for nonporous conduits, (ii) the effects of pressure on the mass transfer coefficient are not
incorporated, (iii) it is assumed that the mass transfer boundary layer is fully developed and
(iv) the property variations with concentration remain unaccounted. Therefore, the standard
correlations lead to inaccurate estimation of the mass transfer coefficient. One way to avoid
this is to carry out a detailed numerical simulation of the fluid and the mass transfer in the
membrane modules [1,2] and the subsequent estimation of the mass transfer coefficient. But,
this method is not attractive to the engineers due to the extensive computation effort and
complications. The available mass transfer coefficient correlations had been reviewed in
detail [3,4]. The shortcomings of these correlations as stated earlier have been extensively
discussed in detail in both the reviews. The alternative approaches, like velocity variation
technique [3] or osmotic pressure model [4,5], are also examined. But, both of these methods
have their own limitations.
The effect of the permeation is extremely important in the mass transfer. The effect is two
fold; first, it enhances the mass transfer and second, it stabilizes the laminar flow by delaying
the onset of laminar to turbulent transition [3].
Membrane based separation processes are used extensively in various process industries,
e.g., food processing [6], dairy products [7], clarification and concentration of fruit juice
[8,9], polymer concentration, separation and fractionation [10], biomedical applications [10],
protein concentration and separation [11], etc. Most of the fruit juices, polymeric solutions,
blood, etc. follow non-Newtonian rheology. Power law is the commonest rheology of these
non-Newtonian process streams [12]. The Sherwood number relations for the non-Newtonian
fluids are scarce in literature. Most of the available relations are empirical or semi-empirical
in nature and these are for power law fluids only [13-15]. The generalized expressions of
Sherwood number including the effects of membrane permeation for Newtonian laminar flow
as well as the turbulent flow regimes are already developed [16,17]. The Sherwood number
relations for the entire range of the power law fluids, from pseudoplastic to dilatant, have
been developed both for the laminar and turbulent flow regimes [18,19]. The present work is
aimed at the developing expressions of the Sherwood numbers for three non-Newtonian
fluids, namely, Ellis, Reiner-Philippoff and Eyring fluids in a tube. The analysis is applicable
for laminar cross flow in reverse osmosis (RO) as well as in ultrafiltration (UF).
2. THEORY
2.1. Flow Through a Tube
The theoretical developments of the tubular flow for Ellis, Eyring and Reiner-Philippoff
fluids are presented herein. The flow geometry is shown in figure 1.
Effects of Permeation on Mass Transfer Coefficient for Laminar...
399
Figure 1. Schematic of the flow geometry in the tube.
2.1.1. Ellis Fluid
The rheology of the Ellis fluid is [20],
−
(
dv x
= ϕ 0 + ϕ 1 τ rx
dr
α −1
)τ
rx
(1)
The laminar velocity profile of the Ellis fluid can be obtained by solving the x-component
equation of motion and using Eq.(1),
⎧⎪ Fϕ R 2
vx = ⎨ 0
⎪⎩ 2
for 0 ≤ r ≤ R,
⎛ ⎛ r ⎞2 ⎞ F α
⎛ ⎛ r ⎞ α +1 ⎞⎫⎪
α +1 ⎜
⎜1 − ⎜ ⎟ ⎟ +
ϕ R 1 − ⎜ ⎟ ⎟⎬
⎜ ⎝ R ⎠ ⎟ α +1 1
⎜ ⎝ R ⎠ ⎟⎪
⎠
⎝
⎠⎭
⎝
(2)
dP
u
where, F = (- dx ). F, can be expressed as a function of average velocity ( 0 ) over the
cross-section of the channel as,
400
R
∫ v rdr
x
u0 =
0
R
∫ rdr
0
⎧
⎛ R2
u 0 = ⎨ Fϕ 0 ⎜⎜
⎝ 4
⎩
or,
⎫
⎞ Fα
⎟⎟ +
ϕ1 R α +1 ⎬
⎠ α +3
⎭
(
)
(3)
The steady state solute mass balance in the concentration boundary layer is obtained as,
vx
∂c
∂c D ∂ ∂c
(r )
+ vr
=
∂x
∂r r ∂r ∂r
(4)
by neglecting the diffusive flux compared to the convective flux in the axial direction.
Considering a thin concentration boundary layer adjacent to the wall, the curvature
effects may be neglected and the problem may be treated as though the wall were flat [20]. If
the distance from the wall is denoted as y=R-r, the fluid may be regarded as being confined
between a flat mass-transfer surface extending from y=0 to y=∞. Therefore, the solute mass
balance equation (Eq. (4)) can be expressed as,
vx
∂c
∂c
∂ 2c
+ vy
=D 2
∂x
∂y
∂y
(5)
The x-component velocity profile is expressed by Eq. (2). By substituting r=R-y in Eq. (2)
y2
2
and neglecting R and the higher order terms in the binomial expansion of the Eq. (2)
(since the thickness of the concentration boundary layer is small), the simplified velocity
profile becomes,
v x = {Fϕ 0 R 2 + F α ϕ1 R α +1 } y
0
≤
y
≤
R
,
R
for
(6)
v
Since the x-component velocity x is large enough compared to the permeate flux, the ycomponent velocity can be approximated as [21], assuming no solute adsorption on the
membrane surface,
v y = −v w
The initial and boundary conditions of Eq. (5) are,
(7)
401
c = c0
at x = 0 ,
(8)
c = c0
at y = ∞,
(9)
At the membrane surface, the net solute flux towards the membrane is zero at the steady
state. Therefore, the boundary condition at the membrane surface is,
at y = 0,
v w (c − c p ) + D
∂c
=0
∂y
(10)
Rr = 1 −
Eq. (10) can be expressed in terms of real retention of the membrane (
which is constant for a membrane solute system [22],
at y = 0,
v w cRr + D
∂c
=0
∂y
cm
cp
),
(11)
Inserting the velocity profiles, Eqs. (6) and (7) in Eq. (5) and after nondimensionalization, the following equation is obtained,
A1 y *
*
∂c *
∂ 2c*
* ∂c
−
Pe
x
=
w
∂x *
∂y * ∂y *2
( )
(12)
where,
3
α
α ⎛ d ⎞
vw d
x
y c* = c ,
*
⎜
{
}
A
F
R
F
R
ϕ
ϕ
=
+
1
0
1
x = , y = ,
Pe w =
⎜ LD ⎟⎟
c0
⎝
⎠ and
L
d
D ,
d = 2R .
*
The rheological parameter A1 can be expressed in terms of Reynolds and Schmidt
numbers as,
⎛d
A1 = Fϕ 0 R + F α ϕ1 R α ⎜⎜
⎝ u0
{
}
⎞⎛ u 0 d 2
⎟⎟⎜⎜
⎠⎝ LD
⎞
⎟
⎟
⎠ or,
d2
d α +1 ⎫⎛
d⎞
1 ⎧
α
+ F ϕ1 α ⎬⎜ Re Sc ⎟
A1 =
⎨ Fϕ 0
u0 ⎩
L⎠
2
2 ⎭⎝
402
d⎞
⎛
A1 = A11 ⎜ Re Sc ⎟
L⎠
⎝
or
(13)
where, the non-dimensional rheological parameter becomes,
A11 =
Fϕ 0
Re =
and
d2
d α +1
+ F α ϕ1 α
2
2
u0
(14)
ρu 0 d
μ eff
Sc =
μ eff
ρD
,
The effective viscosity is generally expressed for the non-Newtonian fluid as [12],
μ eff =
Fd 2
32u 0
(15)
The derivation of Eq. (15) is presented in the appendix. The non-dimensional boundary
conditions for Eq. (5) become,
at x = 0 , c = 1
(16)
*
at y = ∞, c = 1
(17)
*
*
*
and at y = 0,
*
Pe w c * R r +
∂c *
=0
∂y *
(18)
Eq. (12) is a parabolic partial differential equation with one of the boundary at infinity.
Hence, it admits a similarity solution. The similarity parameter in this case is derived in the
appendix and is expressed as,
η = A1
1
3
y*
1
x* 3
(19)
In terms of the similarity parameter, Eq (12) becomes an ordinary differential equation,
⎞ dc *
d 2c* ⎛η 2
⎜
B
+
+
1⎟
⎟ dη = 0
dη 2 ⎜⎝ 3
⎠
(20)
403
where, B1 is a constant and is given as,
B1 =
Pe w
A1
1
x*
1
3
3
or
Pe w
B1 =
A11
1
x*
d 1
3
(Re Sc ) 3
L
1
3
(21)
The transformed boundary conditions become,
*
at η = ∞ , c = 1
(22)
dc *
+ B1 Rr c * = 0
η
=
0
,
d
η
at
(23)
The solution of Eq. (20) with the boundary conditions, Eqs. (22) and (23) is,
⎛ η3
⎞
c * (η ) = K 1 ∫ exp⎜⎜ −
− B1η ⎟⎟dη + K 2
⎝ 9
⎠
(24)
The integration constants, K 1 and K 2 are obtained using Eqs. (22) and (23) as,
K1 = −
B1 Rr
1 − B1 Rr I 1
K2 =
and
(25)
1
1 − B1 Rr I 1
(26)
∞
⎛ η3
⎞
− B1η ⎟⎟dη
I 1 = ∫ exp⎜⎜ −
⎝ 9
⎠
0
where,
(27)
The constant B1, can be expressed in terms of length averaged dimensionless permeate
flux
(Pe ) from Eq. (21),
w
1
Pe w =
∫ Pe w dx = 1 .5 A11
*
0
1
3
d⎞
⎛
⎜ Re Sc ⎟
L⎠
⎝
1
3
B1
404
or,
B1 = 0.67
Pew
1
d 1
( A11 3 )(Re Sc ) 3
L
(28)
Estimation of the Mass Transfer Coefficient
The definition of mass transfer coefficient is,
⎛ ∂c ⎞
k (c m − c0 ) = − D⎜⎜ ⎟⎟
⎝ ∂y ⎠ y =0
(29)
In terms of the similarity parameter, Eq. (29) is expressed as
(
)
Sh c m − 1 = −
cm
*
*
A11
1
3
d⎞
⎛
⎜ Re Sc ⎟
L⎠
⎝
* 13
x
1
3
⎛ dc * ⎞
⎜⎜
⎟⎟
⎝ dη ⎠ η = 0
(30)
⎛ dc * ⎞
⎟⎟ are expressed in terms of the integration constants K1 and K 2 as,
and ⎜⎜
d
η
⎝
⎠η = 0
A11
Sh = −
1
3
d⎞
⎛
⎜ Re Sc ⎟
L⎠
⎝
* 13
x
1
3
K1
K2 −1
(31)
Substituting K 1 and K 2 from Eqs. (25) and (26), the Sherwood number profile along the
membrane length becomes,
( )
Sh x =
*
A11
1
d 1
(Re Sc ) 3
L
x 3 I1
3
*1
(32)
The definite integral I1, can be expressed in terms of non-dimensional, length averaged
flux (
Pew
) using Eqs. (27) and (28),
⎞
⎛
⎟
⎜ η3
Pe
w
I 1 = ∫ exp⎜ −
η ⎟dη or,
− 0.67
1
d 1
⎜ 9
0
A11 3 (Re Sc ) 3 ⎟⎟
⎜
L
⎠
⎝
∞
3
⎛ η
⎞
− 0.67λeff 1η ⎟⎟dη
I 1 = ∫ exp⎜⎜ −
⎝ 9
⎠
0
405
∞
where,
Pe w
λeff 1 =
A11
1
3
(33)
(34)
d 1
(Re Sc ) 3
L
The length averaged Sherwood number becomes, (from Eq. (32)),
1
1
3
1
1.5
( A11 ) (Re Sc d ) 3
ShL = ∫ Sh( x )dx =
L
I1
0
*
*
(35)
Based on the extent of permeation, results of various cases are discussed below.
Case 1: No Permeation
In this case,
Pew
∞
∫
⎛ η3 ⎞
⎟⎟dη = 1.8575
⎝ 9 ⎠
=0 and hence, I 1 = exp⎜⎜ −
0
Therefore, the expression for average Sherwood number is,
1
d 1
ShL = 0.81( A11 ) 3 (Re Sc ) 3
L
(36)
Case 2: With Permeation (RO/UF System)
To trap the effects of suction as well as the non- Newtonian behavior, I1 is evaluated
numerically for various values of λeff 1 (in the range of λeff 1 , between nearly 0 and 16,
typically encountered in RO/UF), and the inverse of the integral is plotted against λeff 1 , in
figure 2. The results are fitted in polynomial function of
more than 0.99, as
λeff 1 with a correlation coefficient
406
[
1
= 0.54 1 + 0.74λ eff 1 + 0.12λ 2eff 1 − 8.4 × 10 −3 λ3eff 1
I1
]
(37)
The expression of the average Sherwood number from Eq. (35) is then,
d⎞
⎛
Sh L = 0.81 × ( A11 ) ⎜ Re Sc ⎟
L⎠
⎝
1
1
3
3
[1 + 0.74λ
eff 1
+ 0.12λ 2eff 1 − 8.4 × 10 −3 λ3eff 1
]
(38)
Case 3: ϕ1 = 0 , Newtonian Fluid
In this case,
gradient ( −
F=
ϕ0
becomes inverse of the viscosity (μ) of the solution. Hence, the pressure
dP
= F ) from Eq. (3) becomes,
dx
4u 0 μ
,
R2
(39)
The rheological parameter A11 is simplified from Eq. (14),
A11 =
Fd 2
2μu 0
(40)
Using Eq.(39), the value of A11 is obtained as 8. Therefore, from Eq.(38), the expression
of the length averaged Sherwood number becomes,
1
[
d⎞ 3
⎛
Sh L = 1.62⎜ Re Sc ⎟ 1 + 0.74λ eff 1 + 0.12λ 2 eff 1 − 8.4 × 10 −3 λ3 eff 1
L⎠
⎝
where from Eq. (34), λeff 1 is,
λeff 1 = 0.5
Pe w
d 1
(Re Sc ) 3
L
]
(41)
(42)
Hence, Eq. (41) can be written as,
⎡
⎤
1
2
3
⎥
d⎞ 3⎢
Pe w
Pe w
Pe w
⎛
−3
+ 0.03
− 1.05 × 10
Sh L = 1.62⎜ Re Sc ⎟ ⎢1 + 0.37
⎥
1
2
d
d
d
L⎠ ⎢
⎝
(Re Sc ) 3
(Re Sc ) 3
(Re Sc ) ⎥
L
L
L ⎦⎥
⎣⎢
(43)
407
It may be noticed that this result coincides with the reported one for the mass transfer
coefficient with permeation for Newtonian fluid [16] in a porous tube.
For, no permeation i.e.,
Pe w
d⎞
⎛
Sh L = 1.62⎜ Re Sc ⎟
L⎠
⎝
1
=0 and Eq. (43) becomes,
3
(44)
which is identical with the Leveque solution [3].
Case 4:
ϕ0 = 0 , Power Law Fluid
In this case, the pressure gradient is obtained from Eq. (3) as,
1
⎧ 2α +1 u 0 (α + 3) ⎫ α
F =⎨
⎬
α +1
⎩ ϕ1 d
⎭
(45)
From Eq. (14), rheological parameter A11 becomes,
F α ϕ1 d α +1
A11 =
u 0 2α
(46)
Using Eqs. (45) and (46), A11 becomes
A11 = 2(α + 3)
(47)
Therefore, the expression of average Sherwood number is (from Eq. 38),
1
[
1 ⎛
d⎞
Sh L = 1.02(α + 3) 3 ⎜ Re Sc ⎟ 1 + 0.74λ eff 1 + 0.12λ 2 eff 1 − 8.4 × 10 −3 λ3 eff 1
L⎠
⎝
where,
3
]
(48)
λeff 1 is (from Eq. 34),
λeff 1 =
0.794 Pe w
d 1
(α + 3) (Re Sc ) 3
L
1
3
(49)
408
It may be noted here that in the definition of Re and Sc, the viscosity is μeff. The
expression of μeff is shown in the appendix.
2.1.2. Reiner-Philippoff Fluid
The rheological equation for Reiner-Philippoff fluid is [20],
⎛
⎜
dv x ⎜
1
−
=⎜
μ0 − μ∞
dr
⎜ μ∞ +
2
⎜
1 + (τ rx τ s )
⎝
⎞
⎟
⎟
⎟τ rx
⎟
⎟
⎠
(50)
An analysis of the equation of motion in x-direction yields the following equation,
1 d
(r τ rx ) = − dP = F
r dr
dx
(51)
The solution of the above equation using Eq. (50) yields the laminar velocity profile as,
vx =
2
F ⎧⎪ R 2 ⎛⎜ ⎛ r ⎞ ⎞⎟
−
1
− C ln (2 μ 0 − μ ∞ ) + μ 0 a 2 r 2 + C ln (2μ 0 − μ ∞ ) + μ 0 a 2 R 2
⎜
⎟
⎨
μ 0 ⎪⎩ 2 ⎜⎝ ⎝ R ⎠ ⎟⎠
(
where, a = − F
)
(
⎫
)⎪⎬
(52)
⎪⎭
τs
⎛μ −μ ⎞
∞
⎟
and C = ⎜⎜ 0
2 ⎟
2
μ
a
0
⎝
⎠
The term F can be related with
tube as follows,
u0 =
u 0 using the definition of average velocity (Eq. 3) in the
⎛ 2μ − μ
2 F ⎪⎧ R 4 CR 2
+
− C ⎜⎜ 0 2 ∞
2 ⎨
2
μ 0 R ⎪⎩ 8
⎝ 2μ 0 a
⎫
⎞ ⎛
μ0a 2
2 ⎞⎪
⎟ ln⎜1 +
⎟
⎟ ⎜ (2μ − μ ) R ⎟⎬⎪
0
∞
⎠ ⎝
⎠⎭
Inside the very thin concentration boundary layer, r=R-y and y << R , hence,
(53)
y2
and
R2
higher order terms are neglected, to get the approximate velocity profile as,
vx =
F
μ0
Ry
(54)
409
The solute mass balance equation and its boundary conditions within the concentration
boundary layer remain in the same form as Eqs. (12), Eqs.(16-18). Only, A1 is replaced by A2.
A2 = A22 Re Sc
where, A22 =
d
L
(55)
Fd 2
2μ 0 u 0
(56)
In the definition of Re and Sc in Eq. (55), μeff is expressed by Eq. (15), where F can be
calculated from Eq. (53) for a known u0 , rheological parameters and tube radius.
The concentration profile is obtained by solving Eq. (12) and Eqs. (16-18) using the
similarity method with the similarity parameter,
ξ = A2
1
3
y*
x
*1
(57)
3
Using the similar calculation steps as discussed in detail for the Ellis fluid, profile of
Sherwood number along the membrane length becomes,
Sh( x ) =
*
( A22 )
I2x
1
*1
3
3
d 1
(Re Sc ) 3
L
(58)
∞
⎛ ξ3
⎞
where, I 2 = ∫ exp⎜⎜ −
− 0.67λeff 2ξ ⎟⎟dξ
⎝ 9
⎠
0
and
λeff 2 =
PeW
(60)
d 1
( A22 ) (Re Sc ) 3
L
1
(59)
3
The length averaged Sherwood number becomes,
( A ) 3 ⎛ Re Sc d ⎞
1.5 22
1
ShL =
I2
⎜
⎝
⎟
L⎠
1
3
Based on the extent of permeation, following simplifications are discussed.
(61)
410
Case 1
No permeation:
PeW
ShL = 0.81( A22 )
1
3
=0 and I2=1.8575. Hence, the average Sherwood number is,
d⎞
⎛
⎜ Re Sc ⎟
L⎠
⎝
1
3
(62)
Case 2: With Permeation
In this case, I2 is evaluated by numerical integration for various values of
is plotted with
λeff 2 and 1 / I 2
λeff 2 in figure 2. The expression of the length averaged Sherwood number is
given by Eq. (38), replacing A11 by A22 and
λeff 1 by λeff 2 .
Case 3: μ 0 = μ ∞ = μ , Newtonian fluid
In this case, as for Ellis fluid, A22 = 8 and the length averaged Sherwood number becomes
similar to Eq. (41), replacing λ eff 1 by λeff 2 , while λeff 2 is expressed by Eq. (42). Therefore,
the final expression for the length averaged Sherwood number is identical with Eq. (43).
2.1.3 Eyring Fluid
The rheological equation for the Eying fluid is [20],
1 dv x ⎞
⎟
⎝ B dr ⎠
⎛
τ rx = ASinh −1 ⎜ −
(63)
An analysis of x-component equation of motion results in Eq. (51). Using Eqs. (51) and
(63), the expression of the x-component velocity profile becomes,
vx =
B
{Cosh(KR ) − Cosh( Kr )}
K
where, K =
(64)
F
A
The relation between the cross sectional average velocity u0 and F can be obtained as
before (from Eq. 3),
u0 =
⎫
2B ⎧ R
1
R2
(
)
(
)
Sinh
KR
(
1
Cosh
KR
)
Cosh( KR )⎬
+
−
−
2 ⎨
2
2
KR ⎩ K
K
⎭
Inside the concentration boundary layer, r=R-y and y << R , hence
411
(65)
y2
and higher order
R2
terms are neglected, to get the velocity profile as,
v x = [BSinh( KR )]y
(66)
boundary layer remain in the same form as Eq. (12) and Eqs. (16-18), with A1 is replaced by
A3 ,
d
L
A3 = A33 Re Sc
(67)
where,
A33 =
Bd
Kd
Sinh(
)
u0
2
(68)
The definition of Re and Sc, in Eq. (68), μeff is expressed by the Eq. (15), where F can be
calculated from Eq. (65) for a known value of u0 , rheological parameters and channel height.
similarity method with similarity parameter,
φ = A3
1
3
y*
x
*1
(69)
3
Using the similar calculation steps as discussed in detail for the Ellis fluid, the Sherwood
number profile along the membrane length becomes,
( A33 ) 3 ⎛
1
Sh( x ) =
*
I3x
∞
∫
*1
3
1
3
⎛ φ3
⎞
− 0.67λeff 3φ ⎟⎟dφ
⎝ 9
⎠
where, I 3 = exp⎜⎜ −
0
d⎞
⎜ Re Sc ⎟
L⎠
⎝
(70)
(71)
412
and
λeff 3 =
PeW
(72)
d 1
( A33 ) (Re Sc ) 3
L
1
3
( A33 ) 3 ⎛
1
ShL = 1.5
d⎞
⎜ Re Sc ⎟
L⎠
⎝
I3
1
3
(73)
The simplifications with various extents of permeation are as follows,
Case 1: No Permeation, PeW =0
The length averaged Sherwood number becomes
ShL = 0.81( A33 )
1
d⎞
⎛
3 Re Sc
⎟
⎜
L⎠
⎝
1
3
(74)
As earlier, I3 is evaluated numerically for various values of
λeff 3 and 1 / I 3 versus λeff 3
is plotted in figure 2. The Sherwood number relationship is given by Eq. (38), replacing A11
and A33 and λeff 1 by λeff 3 .
413
10
1/I1,2,3
8
6
4
2
0
0
2
4
6
8
10
12
14
16
λeff1, eff2, eff3
Figure 2. Variation of the definite integrals I1,2,3 with
λeff 1, eff 2, eff 3
for tubular geometry.
2.2. Flow through a Rectangular Channel
The theoretical developments of the rectangular thin channel for Ellis, Eyring and ReinerPhilippoff fluids are presented herein. The flow geometry is shown in figure 3.
Figure 3. Schematic of the flow geometry in the rectangular channel.
414
2.2.1. Ellis Fluid
The rheology of the Ellis fluid is [20],
−
(
dv x
= ϕ 0 + ϕ1 τ
dy
α −1
yx
)τ
(75)
yx
The laminar velocity profile of the Ellis fluid can be obtained by solving the x-component
equation of motion using Eq.(75),
α +1
⎡
⎧ ⎛
y ⎞ Fα
y ⎞ ⎫⎪⎤
⎛
α +1 ⎪
for 0 ≤ y ≤ h, v x = ⎢ Fϕ 0 hy⎜1 −
ϕ 1 h ⎨1 − ⎜1 − ⎟ ⎬⎥
⎟+
⎪⎩ ⎝ h ⎠ ⎪⎭⎦⎥
⎝ 2h ⎠ α + 1
⎣⎢
⎡
⎛
⎝
for h ≤ y ≤ 2h, v x = ⎢ Fϕ 0 hy ⎜1 −
⎢⎣
where, F = (-
⎧ ⎛ y ⎞α +1 ⎫⎪⎤
y ⎞ Fα
α +1 ⎪
h
+
ϕ
⎟
⎨1 − ⎜ − 1⎟ ⎬⎥
1
2h ⎠ α + 1
⎪⎩ ⎝ h ⎠ ⎪⎭⎥⎦
(76)
(77)
dP
u
). F, can be expressed as a function of average velocity ( 0 ) over the
dx
cross-section of the channel as,
2h
∫ v dy
x
u0 =
0
2h
∫ dy
0
or,
⎧
⎛ h2
u 0 = ⎨ Fϕ 0 ⎜⎜
⎝ 3
⎩
⎫
⎞ Fα
⎟⎟ +
ϕ1 (h α +1 )⎬
⎠ α +2
⎭
(78)
The solute mass balance in the concentration boundary layer is obtained as,
∂ 2c
∂c
∂c
=D 2
+ vy
vx
∂y
∂x
∂y
(79)
The x-component velocity profile is expressed by Eq. (76). Since the thickness of the
y2
concentration boundary layer is small, 2 and the higher order terms in the binomial
h
expansion of the Eq. (76) are neglected and the simplified velocity profile becomes,
{
for 0 ≤ y ≤ h, v x = Fϕ 0 h + F
2
α
ϕ 1 hα +1 }
y
h
415
(80)
v
Since the x-component velocity x is large enough compared to the permeate flux, the ycomponent velocity can be approximated as expressed in Eq.(7). The boundary conditions of
Eq.(79) are given in Eqs.(8-11). Inserting the velocity profiles and after nondimensionalization, the following equation is obtained,
A10 y *
*
∂ 2c*
∂c *
* ∂c
=
Pe
x
−
w
∂y * ∂y *2
∂x *
( )
(81)
where,
x* =
v d
x
y
c
, c * = , Pew = w e and
, y* =
L
de
c0
D
{
α
A = Fϕ 0 h + F ϕ 1 h
0
1
α
}
⎛ de3 ⎞
⎜
⎟
⎜ LD ⎟
⎝
⎠
The equivalent diameter for a thin channel is defined as
d e = 4h [23].The rheological
0
parameter A1 can be expressed in terms of Reynolds and Schmidt numbers as,
{
α
A = Fϕ 0 h + F ϕ 1 h
0
1
α
}
⎛ de
⎜⎜
⎝ u0
2
⎞⎛ u 0 d e
⎜
⎟⎟
⎜
⎠⎝ LD
⎞
⎟
⎟
⎠
or,
α +1
2
⎧⎪
de
d e ⎫⎪⎛
d ⎞
α
ϕ
ϕ
F
F
+
⎜ Re Sc e ⎟
⎨ 0
1
α ⎬
L⎠
4
4 ⎪⎭⎝
⎪⎩
de ⎞
0
0 ⎛
or A1 = A11 ⎜ Re Sc
⎟
L⎠
⎝
A10 =
1
u0
(82)
where, the non-dimensional rheological parameter becomes,
2
α +1
d
d
Fϕ 0 e + F α ϕ 1 e α
4
4
A110 =
u0
(83)
416
and Re =
μ eff
ρu 0 d e
, Sc =
ρD
μ eff
The effective viscosity is generally expressed for the non-Newtonian fluid as [12]
μ eff
2
Fd e
=
32u 0
(84)
The derivation of Eq. (84) is presented in the appendix.
The non-dimensional boundary conditions for Eq. (81) are given by Eqs.(16-18). Eq. (81)
is a parabolic partial differential equation with one of the boundary at infinity. Hence, it
admits a similarity solution. The similarity parameter in this case is derived in the appendix
and is expressed as,
η 0 = A10
1
y*
1
x* 3
3
(85)
In terms of the similarity parameter, Eq (81) becomes an ordinary differential equation,
d 2c*
dη 0
2
⎛η0 2
⎞ *
0 ⎟ dc
⎜
+
+ B1
=0
⎜ 3
⎟ dη
⎝
⎠ 0
(86)
0
where, B1 is a constant and is given as,
B 10 =
Pe w
0
1
A
1
x*
1
3
3
or
Pe w
B 10 =
0
11
A
1
d 1
3
(Re Sc e ) 3
L
x*
1
3
(87)
The transformed boundary conditions become,
at
η 0 = ∞ , c* = 1
dc *
η
=
0
,
0
at
+ B10 R r c * = 0
dη 0
(88)
(89)
417
The solution of Eq. (86) with the boundary conditions, Eqs. (88) and (89) is,
⎛ η 3
⎞
c * (η 0 ) = K 10 ∫ exp⎜ − 0 − B10η 0 ⎟dη 0 + K 20
⎜ 9
⎟
⎝
⎠
0
(90)
0
The integration constants, K 1 and K 2 are obtained using Eqs. (88) and (89) as,
K 10 = −
B10 R r
(91)
1 − B10 R r I 10
and K 2 =
0
1
1 − B10 R r I 10
(92)
⎛ η03
⎞
− B10η 0 ⎟dη 0
where, I = ∫ exp⎜ −
⎜ 9
⎟
0
⎝
⎠
∞
0
1
(93)
0
The constant B1 , can be expressed in terms of length averaged dimensionless permeate
flux
(Pe ) from Eq. (87),
w
1
Pe w =
∫ Pe
1
0 3
11
dx = 1 .5 A
*
w
0
d ⎞
⎛
⎜ Re Sc e ⎟
L ⎠
⎝
1
3
B 10
or,
Pe w
B10 = 0.67
0
11
(A
1
3
(94)
d 1
)(Re Sc e ) 3
L
Estimation of Mass Transfer Coefficient
From the definition of mass transfer coefficient, in terms of similarity parameter, Eq. (29)
is expressed as
(
)
Sh c m − 1 = −
*
0
11
A
1
3
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
* 13
x
1
3
⎛ dc *
⎜⎜
⎝ dη 0
⎞
⎟⎟
⎠η 0 = 0
(95)
418
cm
*
⎞
0
0
⎟⎟
are expressed in terms of the integration constants K 1 and K 2 as,
⎠η 0 = 0
⎛ dc *
⎝ dη 0
and ⎜⎜
0
11
A
1
3
Sh = −
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
* 13
x
0
1
3
K 10
K 20 − 1
(96)
0
Substituting K 1 and K 2 from Eqs. (91) and (92), the Sherwood number profile along
the membrane length becomes,
( )
Sh x =
*
A110
1
3
1
x * 3 I 10
(Re Sc
d e 13
)
L
(97)
0
The definite integral I 1 , can be expressed in terms of non-dimensional, length averaged
flux (
Pew
) using Eqs. (93) and (94),
⎛
⎞
3
⎜
⎟
η
Pe
w
η 0 ⎟dη 0 or,
I 10 = ∫ exp⎜ − 0 − 0.67
1
d 1
⎜ 9
⎟
0
A110 3 (Re Sc e ) 3
⎜
⎟
L
⎝
⎠
3
∞
⎞
⎛ η
I 10 = ∫ exp⎜ − 0 − 0.67λ 0eff 1η 0 ⎟dη 0
⎟
⎜ 9
0
⎠
⎝
∞
where,
Pe w
λ0eff 1 =
0
11
A
1
3
(98)
(99)
d 1
(Re Sc e ) 3
L
The length averaged Sherwood number becomes, (from Eq. (97)),
1
( )
1.5
Sh L = ∫ Sh( x )dx = 0 A110
I1
0
*
*
1
3
(Re Sc
d e 13
)
L
Based on the extent of permeation, results of various cases are discussed below.
(100)
419
Case 1: No Permeation
Pew
In this case,
∞
⎛ η03 ⎞
⎟dη = 1.8575
⎜ 9 ⎟ 0
⎠
⎝
=0 and hence, I 1 = exp⎜ −
0
∫
0
Therefore, the expression for average Sherwood number is,
Sh L = 0.81( A110 ) 3 (Re Sc
1
d e 13
)
L
(101)
Case 2: With Permeation (RO/UF System)
0
To trap the effects of suction as well as the non- Newtonian behavior, I 1 is evaluated
λ 0eff 1 (between nearly 0 and 16, typically encountered in
numerically for various values of
RO/UF), and the inverse of the integral is plotted against λ eff 1 , in figure 4. The results are
0
fitted in polynomial function of
λ 0eff 1 with a correlation coefficient more than 0.99, as
[
1
= 0.54 1 + 0.743λ0eff 1 + 0.105(λ0eff 1 ) 2 − 9.66 × 10 −3 (λ0eff 1 ) 3
0
I1
]
(102)
The expression of the average Sherwood number from Eq. (100) is then,
d ⎞
⎛
Sh L = 0.81 × ( A ) ⎜ Re Sc e ⎟
L⎠
⎝
0
11
Case 3:
1
3
1
3
[1 + 0.743λ
0
eff 1
+ 0.105(λ0eff 1 ) 2 − 9.66 × 10 −3 (λ0eff 1 ) 3
]
(103)
ϕ1 = 0, Newtonian Fluid
In this case,
gradient ( −
F=
ϕ0
becomes inverse of the viscosity of the solution. Hence, the pressure
dP
= F ) from Eq. (78) becomes,
dx
3u 0 μ
,
h2
(104)
0
The rheological parameter A11 is simplified from Eq. (83),
420
2
A110 =
Fd e
4μu 0
(105)
0
Using Eq.(104), the value of A11 is obtained as 12. Therefore, from Eq.(103), the
expression of the length averaged Sherwood number becomes,
1
[
d ⎞
⎛
ShL = 1.85⎜ Re Sc e ⎟ 1 + 0.743λ0eff 1 + 0.105(λ0eff 1 ) 2 − 9.66 × 10 −3 (λ0eff 1 ) 3
L⎠
⎝
3
λ0eff 1 = 0.44
where from Eq. (99), λ eff 1 is,
0
]
Pe w
d 1
(Re Sc e ) 3
L
(106)
(107)
Hence, Eq. (106) can be written as,
⎡
⎤
1
2
3
⎥
de ⎞ 3 ⎢
Pe w
Pe w
Pe w
⎛
−4
+ 0.02
− 8.05 × 10
ShL = 1.85⎜ Re Sc ⎟ ⎢1 + 0.32
1
2
d ⎥
d
d
L⎠ ⎢
⎝
(Re Sc e ) 3
(Re Sc e ) 3
(Re Sc e ) ⎥
L
L
L ⎦⎥
⎣⎢
(108)
It may be noticed that this result coincides with the reported one for the mass transfer
coefficient with permeation for Newtonian fluid [16].
For, no permeation i.e.,
Pe w
d ⎞
⎛
ShL = 1.85⎜ Re Sc e ⎟
L⎠
⎝
1
=0 and Eq. (108) becomes,
3
(109)
which is identical with the Leveque solution [3].
Case 4:
ϕ0 = 0 , Power Law Fluid
In this case, the pressure gradient is obtained from Eq. (78) as,
1
⎧⎪ 4α +1 u 0 (α + 2) ⎫⎪ α
F =⎨
⎬
⎪⎩ ϕ1 d e α +1 ⎪⎭
(110)
0
From Eq. (83), rheological parameter A11 becomes,
421
F α ϕ1 d e
A110 =
α +1
(111)
u 0 4α
0
Using Eqs. (110) and (111), A11 becomes
A110 = 4(α + 2)
(112)
Therefore, the expression of average Sherwood number is (from Eq. 103),
1
[
d ⎞
⎛
Sh L = 1.28(α + 2) ⎜ Re Sc e ⎟ 1 + 0.73λ 0eff 1 + 0.105(λ 0eff 1 ) 2 − 9.66 × 10 −3 (λ0eff 1 ) 3
L⎠
⎝
1
where,
3
3
]
(113)
λ 0eff 1 is (from Eq. 99),
λ0eff 1 =
0.63Pe w
(114)
d 1
(α + 2) (Re Sc e ) 3
L
1
3
It may be noted here that in the definition of Re and Sc, the viscosity is μeff. The
expression of μeff is shown in the appendix.
The rheological equation for Reiner-Philippoff fluid is [20],
⎛
⎜
dv x ⎜
1
−
=⎜
μ0 − μ∞
dy ⎜
μ0 +
2
⎜
1 + (τ yx τ s )
⎝
⎞
⎟
⎟
⎟τ yx
⎟
⎟
⎠
(115)
An analysis of the equation of motion in x-direction yields the following equation,
dτ yx
dy
=−
dp
=F
dx
(116)
The solution of the above equation using Eq. (115) yields the laminar velocity profile as,
vx =
(
)
(
)
F ⎧ ⎛ y ⎞
2
2
2 2 ⎫
⎨hy ⎜1 − 2h ⎟ − C ln (2 μ 0 − μ ∞ ) + μ 0 a (h − y ) + C ln (2 μ 0 − μ ∞ ) + μ 0 a h ⎬
⎠
μ0 ⎩ ⎝
⎭
(117)
422
where, a = − F
τs
⎛μ −μ ⎞
∞
⎟
and C = ⎜⎜ 0
2 ⎟
2
μ
a
0
⎠
⎝
The term F can be related with
the channel as follows,
u0 =
u 0 using the definition of average velocity (Eq. 78) in
3
F ⎧h3
2 2
−1 ⎛ h ⎞ ⎫
⎟⎟⎬
⎨ − Ch ln ((2 μ 0 − μ ∞ ) + μ 0 a h ) + 2Ch − 2C 2 tan ⎜⎜
μ0h ⎩ 3
⎝ C ⎠⎭
(118)
y2
and higher order terms are
Inside the Concentration Boundary layer, where
h2
neglected, the velocity profile becomes,
vx =
F
μ0
hy
(119)
0
0
boundary layer remain in the same form as Eqs. (81), (16-18). Only, A1 is replaced by A2 .
0
A20 = A22
Re Sc
de
L
(120)
2
where, A22 =
0
Fd e
4μ 0 u 0
(121)
In the definition of Re and Sc in Eq. (120), μeff is expressed by Eq. (84), where F can be
calculated from Eq. (118) for a known u0 , rheological parameters and channel half height.
The concentration profile is obtained by solving Eq. (81) and Eqs. (16-18) using the similarity
method with the similarity parameter,
1
0 3
2
ξ0 = A
y*
x
*1
(122)
3
Using the similar calculation steps as discussed in detail for the Ellis fluid, profile of
Sherwood number along the membrane length becomes,
Sh( x ) =
*
0
( A22
)
0
2
I x
1
*1
3
(Re Sc
3
d e 13
)
L
423
(123)
⎞
⎛ ξ03
where, I = ∫ exp⎜ −
− 0.67λ 0eff 2 ξ 0 ⎟dξ 0
⎟
⎜ 9
0
⎠
⎝
∞
0
2
and
λ0eff 2 =
(124)
PeW
(125)
d 1
( A ) (Re Sc e ) 3
L
1
0
22
3
Sh L
(A )
= 1.5
0
22
0
2
1
3
I
d ⎞
⎛
⎜ Re Sc e ⎟
L ⎠
⎝
1
3
(126)
Based on the extent of permeation, following simplifications are discussed.
Case 1: No permeation
PeW
0
=0 and I 2 =1.8575. Hence, the average Sherwood number is,
( )
Sh L = 0.81 A
0
22
1
3
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
1
3
(127)
0
In this case, I 2 is evaluated by numerical integration for various values of
λeff 2 and
1 / I 20 is plotted with λ 0eff 2 in figure 4. The expression of the length averaged Sherwood
0
0
number is given by Eq. (103), replacing A11 by A22 and
λ 0eff 1 by λ 0eff 2 .
424
Case 3: μ 0 = μ ∞ = μ , Newtonian Fluid
0
In this case, as for Ellis fluid, A22 = 12 and the length averaged Sherwood number
becomes similar to Eq. (106), while
λ 0eff 2 is expressed by Eq. (107). Therefore, the final
expression for the length averaged Sherwood number is identical with Eq. (108).
2.2.3. Eyring Fluid
The rheological equation for the Eying fluid is [20],
⎛
1 dv ⎞
x
⎟⎟
τ yx = ASinh −1 ⎜⎜ −
⎝ B dy ⎠
(128)
An analysis of x-component equation of motion results in Eq. (116). Using Eqs. (116)
and (128), the expression of the x-component velocity profile becomes,
vx =
B
{Cosh(K (h − y )) − Cosh(Kh)}
K
(129)
⎛ dP ⎞
⎜−
⎟
F ⎝ dx ⎠
=
where, K =
A
A
The relation between the cross sectional average velocity u0 and F can be obtained as
before (from Eq.78),
u0 =
B ⎧2
⎫
⎨ Sinh(Kh ) − 2hCosh(Kh )⎬
2 Kh ⎩ K
⎭
Inside the Concentration Boundary layer, where
(130)
y2
and higher order terms are
h2
neglected, the velocity profile becomes,
v x = B Sinh( Kh) y
(131)
0
boundary layer remain in the same form as Eq. (81) and Eqs. (16-18), with A1 is replaced by
A30 ,
de
L
A30 = A330 Re Sc
425
(132)
where,
A330 =
Bd e
Kd
Sinh( e )
u0
4
(133)
The definition of Re and Sc, in Eq. (133), μeff is expressed by the Eq. (84), where F can
be calculated from Eq. (130) for a known value of u0 , rheological parameters and channel
height.
similarity method with similarity parameter,
1
0 3
3
φ0 = A
y*
x
*1
(134)
3
Using the similar calculation steps as discussed in detail for the Ellis fluid, the Sherwood
number profile along the membrane length becomes,
Sh( x
*
(A )
)=
0
33
I 30 x
1
*1
3
3
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
1
3
(135)
⎞
⎛ φ 3
0
where, I = ∫ exp⎜ − 0 − 0.67λ eff 3φ 0 ⎟dφ 0
⎟
⎜ 9
0
⎠
⎝
∞
0
3
and λ eff 3 =
PeW
0
d 1
( A ) (Re Sc e ) 3
L
1
0
33
(136)
(137)
3
Sh L
(A )
= 1.5
0
33
0
3
I
1
3
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
1
3
The simplifications with various extents of permeation are as follows,
(138)
426
Case 1: No Permeation, PeW =0
The length averaged Sherwood number becomes
ShL = 0.81(A
0
33
)
1
d ⎞
3⎛
⎜ Re Sc e ⎟
L⎠
⎝
1
3
(139)
As earlier,
I 30 is evaluated numerically for various values of λ 0 and 1 / I 30 versus
eff 3
λ 0eff 3 is plotted in figure 4. The Sherwood number relationship is given by Eq. (103),
0
replacing A11 by
A330 and λ 0 by λ 0 .
eff 1
eff 3
10
1/I1,2,3
8
6
4
2
0
0
2
4
6
8
10
12
14
λeff1, eff2, eff3
Figure 4. Variation of the definite integrals
I 10, 2,3
with
λ 0 eff 1, eff 2, eff 3 for rectangular channel.
16
427
3. RESULTS AND DISCUSSION
3.1. Tubular Geometry
3.1.1. Ellis Fluid
Aqueous solution of carboxymethyl cellulose (CMC) follows Ellis fluid behavior.
Various rheological parameters of the CMC solutions are given below [20],
ϕ 0 = 0.2891 cm2 s-1 dyne-1, ϕ = 0.028 cm2α s-1 dyne-α, α =1.707 for 0.6% CMC and
1
ϕ 0 = 0.421 cm2 s-1 dyne-1, ϕ = 0.2724 cm2α s-1 dyne-α, α =1.185 for 1.5% CMC
1
solution. In order to calculate the Sherwood number, first F (i.e., −
dP
) is fitted with the
dx
average velocity (u0), using the following steps,
i) a value of u0 is assumed.
ii) using the rheological parameters and assumed values of u0 and channel geometry R
(0.001 m), F is obtained from Eq. (3) using Newton-Raphson iteration method.
iii) μ eff is calculated using the F value from step (ii) by Eq. (15).
iv) Reynolds number is calculated from its definition
ρu 0 d
and is checked whether it
μ eff
is lying within the laminar flow regime ( Re ≤ 2200 ).
Using the above method, F is evaluated for various value of u0 and is fitted as a function
of u0. The tubular channel radius (R) is considered to be 0.001 m in this study. The
relationship of F with u0 is presented below,
F = − 1 . 1 × 10 5 u 0 + 1 . 8 × 10 5 u 0 + 9 . 8 × 10 3 , for 0.6% CMC solution
2
(140)
F = 2 . 8 × 10 5 u 0 + 5 . 5 × 10 3 , for 1.5% CMC solution
(141)
where, F is in Pa/m and u0 is in m/s.
Using Eq. (14), A11 is evaluated at u0 =0.3 m/s and its values are,
A11 = 9.66 , for 0.6% CMC solution
= 8.23 , for 1.5% CMC solution
142)
The profiles of Sherwood numbers along the channel length are obtained from Eq. (32),
428
1
( )
d⎞ 3
2.13 ⎛
Sh x =
Sc
Re
⎜
⎟ , for 0.6% CMC solution
*1
L⎠
I1 x 3 ⎝
*
1
2.02 ⎛
d⎞ 3
= *1 ⎜ ReSc ⎟ , for 1.5% CMC solution
L⎠
I1 x 3 ⎝
The values of the permeation parameter, λeff 1 is obtained from Eq. (34),
λeff 1 =
=
0.469 Pe w
d⎞
⎛
⎜ Re Sc ⎟
L⎠
⎝
0.495PeW
d⎞
⎛
⎜ Re Sc ⎟
L⎠
⎝
1
1
(143)
for 0.6% CMC solution
3
(144)
3
The length averaged Sherwood numbers are obtained from Eq. (38) as,
⎤
⎡
⎥
⎢
2
3
PeW
PeW
d⎞ 3
PeW
⎛
−4
⎥
0
.
026
8
.
67
10
ShL = 1.73⎜ Re Sc ⎟ ⎢1 + 0.35
+
−
×
1
2
⎥
d
3
3
L⎠ ⎢
⎛
⎞
⎝
d⎞
d⎞
⎛
⎛
Re
Sc
⎜
⎟
⎥
⎢
Re
Re
Sc
Sc
⎜
⎟
⎜
⎟
L ⎠⎥
⎝
⎢⎣
L⎠
L⎠
⎝
⎝
⎦
1
⎤
⎡
⎥
⎢
2
3
3
PeW
PeW
PeW
−3
⎥
= 1.64⎛⎜ Re Sc d ⎞⎟ ⎢1 + 0.366
+ 0.029
− 1.02 × 10
1
2
⎥
d
3
3
L⎠ ⎢
⎛
⎞
⎝
d⎞
d⎞
⎛
⎛
⎜ Re Sc ⎟ ⎥
⎢
⎜ Re Sc ⎟
⎜ Re Sc ⎟
L ⎠⎥
⎝
⎢⎣
L⎠
L⎠
⎝
⎝
⎦
(145)
1
The variation of the Sherwood number along the channel length for values of
Re Sc
d
PeW
= 103 and 105 for
=200 is shown in figure 5. It is observed from the figure
L
that, the Sherwood number decreases along the tube length. The decline is sharp in the
upstream of the channel and gradual thereafter. This is due to the fact that the build up of the
concentration boundary layer over the membrane surface becomes sluggish at the
downstream of the channel because of the forced convection imposed by the cross flow. This
reduces the concentration difference between the membrane surface and the bulk of the
solution. Therefore, the Sherwood number and consequently, the mass transfer coefficient
429
decreases along the channel length. It may be observed from figure 5 that the Sherwood
number is more at higher Re Sc
d
Pe
at the same level of the permeate flux ( w ). This
L
indicates that at higher Reynolds number, forced convection is more due to higher cross flow
velocity, which enhances the mass transfer coefficient. It may also be observed that the
Sherwood number profiles for both concentrations of CMC solution almost coincide at
Re Sc
d
d
=103 and they differ marginally at Re Sc =105.
L
L
340
320
300
280
Re Sc d/L=10
*
Sh(x )
260
5
240
0.6% CMC
220
200
1.5% CMC
180
160
Re Sc d/L=10
140
120
0.0
0.2
3
0.4
0.6
x
0.8
1.0
*
Figure 5. Variation of Sherwood number along the tube length for the Ellis fluid at
Pe w = 200
.
The variation of the length averaged Sherwood number with the average wall Peclet
number is presented in figure 6, for Re Sc
d
=103 and 105. It is evident from the figure that
L
the Sherwood number increases with the wall Peclet number. This implies the mass transfer
coefficient increases with the extent of permeation. As permeation increases, the convective
solute flux through the membrane increases and at the steady state, to maintain the solute
balance, the backward diffusion from the surface to the bulk also increases. This leads to an
enhancement of the mass transfer coefficient. It may also be observed that at lower Re Sc
Sherwood number for both concentrations of CMC becomes identical.
d
,
L
430
400
Re Sc d/L=10
5
1.5% CMC
__
ShL
Re Sc d/L=10
3
0.6% CMC
200
0
0
100
200
300
400
__
Pew
Figure 6. Variation of length averaged Sherwood number with the average dimensionless permeate flux for
the Ellis fluid for flow through a tube.
The effects of permeation on Sherwood number can be quantified from Eq. (145). The
ratio of Sherwood number with permeation to that without permeation (
below,
PeW
⎡
⎤
⎢
⎥
2
3
PeW
PeW
PeW
−4
⎥,
Q = ⎢1 + 0.35
0
.
026
8
.
67
10
+
−
×
1
2
⎢
⎥
d
3
3
⎛
⎞
d⎞
d⎞
⎛
⎛
⎜ Re Sc ⎟ ⎥
⎢
⎜ Re Sc ⎟
⎜ Re Sc ⎟
L ⎠⎥
⎝
⎢⎣
L⎠
L⎠
⎝
⎝
⎦
=0) is presented
for 0.6% CMC
solution,
⎡
⎤
⎢
⎥
2
3
PeW
PeW
PeW
−3
⎥,
0
.
029
1
.
02
10
+
−
×
= ⎢1 + 0.366
1
2
⎢
⎥
d
3
3
⎛
⎞
d⎞
d⎞
⎛
⎛
⎜ Re Sc ⎟ ⎥
⎢
⎜ Re Sc ⎟
⎜ Re Sc ⎟
L ⎠⎥
⎝
⎢⎣
L⎠
L⎠
⎝
⎝
⎦
solution
for
1.5%
CMC
(146)
431
The variation of Q with the average wall Peclet number is shown in figure 7. It is
observed from the figure that the permeation results in about 2 times increase in the
Sherwood number for Re Sc
PeW
d
d
PeW
=105 and
=400, whereas for Re Sc =103, at
L
L
=400, permeation causes about six fold increase in the Sherwood number.
6
5
Re Sc d/L=10
5
1.5% CMC
3
0.6% CMC
Re Sc d/L=10
Q
4
3
2
1
0
100
200
300
400
500
Length Averaged Pe NO
Figure 7. Variation of Q with the average dimensionless permeate flux for Ellis fluid for flow through a tube.
A typical set of rheological parameters for Reiner-Philippoff fluid is given below [20],
μ 0 = 0.0215 Kg/m.s, μ = 0.00105 Kg/m.s and τ s = 0.0073 N/m2.
∞
As discussed in section 3.1 F versus u0 relationship becomes,
F = 8.6 × 10 4 u 0 + 0.014
(147)
u
For a typical velocity, 0 =1.18 m/s, rheological parameters and tube geometry, A22 is
evaluated from Eq. (56) as 8. From Eq. (55) A2 becomes,
d⎞
⎛
A2 = 8⎜ Re Sc ⎟
L⎠
⎝
(148)
432
The Sherwood number profile along the tube length is obtained from Eq. (58) as,
d⎞
⎛
2⎜ Re Sc ⎟
L
Sh x* = ⎝ *1 ⎠
x 3 I2
1
3
( )
(149)
The value of suction parameter
λ eff 2 = 0.5
λeff 2 in this case is obtained from Eq. (60),
PeW
d⎞
⎛
⎜ Re Sc ⎟
L⎠
⎝
1
(150)
3
The length averaged Sherwood number is obtained from Eq. (38) as,
⎡
⎤
⎢
⎥
2
3
PeW
PeW
PeW
⎛ Re Scd ⎞ 3 ⎢
⎥
−3
+
−
×
0
.
03
1
.
05
10
ShL = 1.62⎜
⎟ ⎢1 + 0.37
1
2
⎥
d
3
3
⎛
⎞
⎝ L ⎠
d⎞
d⎞
⎛
⎛
⎜ Re Sc ⎟ ⎥
⎢
⎜ Re Sc ⎟
⎜ Re Sc ⎟
L ⎠⎥
⎝
⎢⎣
L⎠
L⎠
⎝
⎝
⎦
1
(151)
The ratio (Q) of the average Sherwood number with permeation to that without
permeation (
PeW
=0) is expressed as,
⎡
⎤
⎢
⎥
3
2
PeW
PeW
PeW
⎢
⎥
−3
Q = ⎢1 + 0.37
− 1.05 ×10
+ 0.03
1
2
d
⎞⎥
⎛
d⎞ 3
d⎞ 3
⎛
⎛
⎢
⎜ Re Sc ⎟ ⎥
⎜ Re Sc ⎟
⎜ Re Sc ⎟
L ⎠⎥
⎝
⎢⎣
L⎠
L⎠
⎝
⎝
⎦
(152)
The variation of the Sherwood number along the channel length for Re Sc
d
= 103 and
L
Pe
W =200, is shown in figure 8. The results show the usual
105 at the wall Peclet number,
trend. The variation of the length averaged Sherwood number with the average wall Peclet
number is shown in figure 9. The ratio Q with the extent of suction (
figure 10. The figures show the expected trend.
PeW
) is presented in
433
340
320
300
280
260
5
Re Sc d/L=10
*
Sh(x )
240
220
200
180
3
160
Re Sc d/L=10
140
120
0.0
0.2
0.4
0.6
x
0.8
1.0
*
Figure 8. Variation of Sherwood number along the tube length for the Reiner-Philippoff fluid at
Pe w = 200
.
400
Re Sc d/L=10
5
300
3
__
ShL
Re Sc d/L=10
200
100
0
0
100
200
300
400
__
Pew
the Reiner-Philippoff fluid for flow through a tube.
434
6
5
5
3
Re Sc d/L=10
Re Sc d/L=10
Q
4
3
2
1
0
100
200
300
400
500
__
Pew
Figure 10. Variation of Q with the average dimensionless permeate flux for Reiner-Philippoff fluid for flow
through a tube.
3.1.3. Eyring Fluid
The typical values of the rheological parameters for Eyring fluid are [23],
A= 600 N/m2, B= 200 S-1
The expression of F with u0 is obtained as before,
F = 2.0 × 10 7 u 0 − 2.2 × 10 7 u 0 + 9.7 × 10 6 u 0 + 1.5 × 10 5
3
2
(153)
u 0 =0.3 ms-1 and R=0.001 m, the value of A is found out
33
A = 9.875 . From Eq. (67),
from the Eq. (68) as 33
For an average velocity of
d⎞
⎛
A3 = 9.875⎜ Re Sc ⎟
L⎠
⎝
The Sherwood number profile along the channel length is obtained from Eq. (70) as,
(154)
435
( )
2.15 ⎛
d⎞
Sh x = *1 ⎜ Re Sc ⎟
L⎠
x 3 I3 ⎝
*
1
3
(155)
The value of the permeation parameter,
λ eff 3 = 0.466
λ eff 3 is obtained from Eq. (72) as,
Pe W
d⎞
⎛
⎜ Re Sc ⎟
L⎠
⎝
1
(156)
3
⎤
⎡
⎥
⎢
2
3
PeW
PeW
PeW
⎛ Re Scd ⎞ ⎢
−3
⎥
1
0
.
345
0
.
026
1
.
06
10
ShL = 1.74⎜
−
×
+
+
⎟
1
2
⎥
d
3
3
⎞
⎛
⎝ L ⎠ ⎢
d⎞
d⎞
⎛
⎛
⎜ Re Sc ⎟ ⎥
⎢
⎜ Re Sc ⎟
⎜ Re Sc ⎟
L
⎠ ⎥⎦
⎝
⎢⎣
L⎠
L⎠
⎝
⎝
1
3
(157)
Q, the ratio of average Sherwood number with suction to that without suction is given as
⎡
⎤
⎥
⎢
2
3
PeW
PeW
PeW
⎥
−4
0
.
023
9
.
78
10
+
−
×
Q = ⎢⎢1 + 0.346
1
2
d
⎛
⎞⎥
d⎞ 3
d⎞ 3
⎛
⎛
⎢
⎜ Re Sc ⎟ ⎥
⎜ Re Sc ⎟
⎜ Re Sc ⎟
L ⎠⎥
⎝
⎢⎣
L⎠
L⎠
⎝
⎝
⎦
(158)
d
= 103 and
L
Pe
figure 13. The figures show the expected result.
PeW
) is presented in
436
350
300
Re Sc d/L=10
5
*
Sh(x )
250
200
150
3
Re Sc d/L=10
100
0.0
0.2
0.4
0.6
x
0.8
1.0
*
Figure 11. Variation of Sherwood number along the tube length for the Eyring fluid at
Pe w = 200
.
400
5
Re Sc d/L=10
300
3
__
ShL
Re Sc d/L=10
200
100
0
0
100
200
300
400
__
Pew
the Eyring fluid for flow through a tube.
437
6
3
Re Sc d/L=10
5
Q
4
5
Re Sc d/L=10
3
2
1
0
100
200
300
400
500
__
Pew
Figure 13. Variation of Q with the average dimensionless permeate flux for Eyring fluid for flow through a
tube.
3.2. Rectangular Geometry
3.2.1. Ellis Fluid
Using the method described in section 3.1.1 for CMC solution F is evaluated for various
value of u0 and is fitted as a function of u0. The rectangular channel half height (h) is
considered to be 0.001 m in this study. The relationship of F with u0 is presented below,
F = 9 . 58 × 10 4 u 0 + 1 . 5 × 10 4
, for 0.6% CMC solution
(159)
F = 2 . 09 × 10 5 u 0 + 6 . 7 × 10 3 , for 1.5% CMC solution
(160)
0
Using Eq. (83), A11 is evaluated at u0 =0.3 m/s and its values are,
A110 = 12.33 , for 1.5% CMC solution
= 13.7 , for 0.6% CMC solution
(161)
438
The profiles of Sherwood numbers along the channel length are obtained from Eq. (97),
1
de ⎞ 3
2.39 ⎛
Sh x =
Sc
Re
⎜
⎟ , for 0.6% CMC solution
1
0 * 3 ⎝
L
⎠
I1 x
( )
*
1
2.31 ⎛
d ⎞3
= 0 *1 ⎜ Re Sc e ⎟ , for 1.5% CMC solution
L⎠
I1 x 3 ⎝
The values of the permeation parameter,
λ0eff 1 =
=
0.418 Pe w
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
0.433PeW
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
1
1
(162)
λ 0eff 1 is obtained from Eq. (99),
3
(163)
3
The length averaged Sherwood numbers are obtained from Eq. (103) as,
⎡
⎢
2
3
PeW
PeW
PeW
⎛ Re Scd e ⎞ 3 ⎢
−4
Sh L = 1.93⎜
+ 0.018
− 7.06 × 10
⎟ ⎢1 + 0.31
1
2
d
L
⎛
⎝
⎠ ⎢
de ⎞ 3
de ⎞ 3
⎛
⎛
⎜ Re Sc e
Sc
Sc
Re
Re
⎜
⎟
⎜
⎟
L
⎢
⎝
L ⎠
L ⎠
⎝
⎝
⎣
1
⎤
⎥
⎥
⎥
⎞⎥
⎟
⎠ ⎥⎦
=
⎡
⎢
2
3
PeW
PeW
PeW
⎛ Re Scd e ⎞ 3 ⎢
−4
+ 0.02
1.87⎜
− 7.84 × 10
⎟ 1 + 0.316
1
2
d
L ⎠ ⎢
3
3
⎛
⎝
d
d
⎛
⎞
⎛
⎞
⎢
e
e
⎜ Re Sc e
Re
Re
Sc
Sc
⎜
⎟
⎜
⎟
L
⎢
⎝
L⎠
L⎠
⎝
⎝
⎣
1
⎤
⎥
⎥
⎞ ⎥⎥
⎟
⎠ ⎥⎦
(164)
The variation of the Sherwood number along the channel length for values of
Re Sc
de
PeW
= 103 and 105 for
=200 is shown in figure 14. It is observed from the
L
figure that, the Sherwood number decreases along the channel length. The decline is sharp in
439
the upstream of the channel and gradual thereafter. This is due to the fact that the build up of
the concentration boundary layer over the membrane surface becomes sluggish at the
downstream of the channel because of the forced convection imposed by the cross flow. This
reduces the concentration difference between the membrane surface and the bulk of the
solution. Therefore, the Sherwood number and consequently, the mass transfer coefficient
decreases along the channel length. It may be observed from figure 14 that the Sherwood
number is more at higher Re Sc
de
Pe
at the same level of the permeate flux ( w ). This
L
indicates that at higher Reynolds number, forced convection is more due to higher cross flow
velocity, which enhances the mass transfer coefficient. It may also be observed that the
Sherwood number profiles for both concentrations of CMC solution almost coincide at
Re Sc
de
d
=103 and they differ marginally at Re Sc e =105.
L
L
360
340
320
300
280
5
Re Sc de/L=10
*
Sh(x )
260
240
0.6% CMC
220
1.5% CMC
200
180
160
140
120
0.0
3
Re Sc de/L=10
0.2
0.4
0.6
0.8
1.0
*
x
Figure 14. Variation of Sherwood number along the channel length for the Ellis fluid at
Pe w = 200
.
The variation of the length averaged Sherwood number with the average wall Peclet
number is presented in figure 15, for Re Sc
de
=103 and 105. It is evident from the figure that
L
the Sherwood number increases with wall Peclet number. This implies the mass transfer
coefficient increases with the extent of permeation. As permeation increases, the convective
solute flux through the membrane increases and at the steady state, to maintain the solute
balance, the backward diffusion from the surface to the bulk also increases. This leads to an
440
enhancement of the mass transfer coefficient. It may also be observed that at lower
Re Sc
de
, Sherwood number for both concentrations of CMC becomes identical.
L
400
5
Re Sc de/L=10
1.5% CMC
__
ShL
3
0
Re Sc de/L=10
0.6% CMC
200
0
100
200
300
400
__
Pew
the Ellis fluid for flow through the rectangular channel.
The effects of permeation on Sherwood number can be quantified from Eq. (164). The
ratio of Sherwood number with permeation and without permeation (
below,
PeW
⎡
⎢
2
3
PeW
PeW
PeW
⎢
−4
+ 0.018
− 7.06 × 10
Q = ⎢1 + 0.31
1
2
d
⎛
de ⎞ 3
de ⎞ 3
⎛
⎛
⎢
⎜ Re Sc e
⎜ Re Sc
⎟
⎜ Re Sc
⎟
L
⎢
⎝
L ⎠
L ⎠
⎝
⎝
⎣
=0) is presented
⎤
⎥
⎥ , for 0.6% CMC
⎞ ⎥⎥
⎟
⎠ ⎥⎦
solution,
⎡
⎤
⎢
⎥
2
3
PeW
PeW
PeW
−4
⎢
⎥,
+ 0.02
− 7.84 × 10
= 1 + 0.316
1
2
⎢
⎥
d
3
3
⎛
⎞
d ⎞
d ⎞
⎛
⎛
⎜ Re Sc e ⎟ ⎥
⎢
⎜ Re Sc e ⎟
⎜ Re Sc e ⎟
L ⎠⎥
⎝
L⎠
L⎠
⎝
⎝
⎣⎢
⎦
for
1.5%
CMC
solution
(165)
441
The variation of Q with the average wall Peclet number is shown in figure 16. It is
observed from the figure that the permeation results in about 5 times increase in the
Sherwood number for Re Sc
PeW
de
d
PeW
=105 and
=400, whereas for Re Sc e =103, at
L
L
=400, permeation causes about three fold increase in the Sherwood number.
5
1.5% CMC
4
3
Re Sc de/L=10
0.6% CMC
Q
3
5
Re Sc de/L=10
2
1
0
0
100
200
300
400
__
Pew
Figure 16. Variation of Q with the average dimensionless permeate flux for Ellis fluid for flow through the
rectangular channel.
For a typical set of rheological parameters for Reiner-Philippoff fluid, as discussed in
section 3.1.2, F versus u0 relationship becomes,
F = 6.45 × 10 4 u 0 + 0.03
(166)
For a typical velocity,
u 0 =1.18 m/s, rheological parameters and channel height, A 0 is
22
evaluated from Eq. (121) as 12.52. From Eq. (120),
A20 becomes,
442
d ⎞
⎛
A20 = 12.52⎜ Re Sc e ⎟
L⎠
⎝
(167)
d ⎞
⎛
2.32⎜ Re Sc e ⎟
L⎠
⎝
Sh x * =
* 13 0
x I2
1
3
( )
(168)
The value of suction parameter
λ 0eff 2 = 0.43
λ 0eff 2 in this case is obtained from Eq. (125),
Pe W
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
1
(169)
3
⎛ Re Scd e ⎞
Sh L = 1.88⎜
⎟
L
⎝
⎠
1
3
⎡
⎢
2
3
PeW
PeW
PeW
⎢
−4
+
+
1
0
.
32
0
.
02
7
.
68
10
−
×
⎢
1
2
d
⎛
de ⎞ 3
de ⎞ 3
⎛
⎛
⎢
⎜ Re Sc e
Sc
Sc
Re
Re
⎜
⎟
⎜
⎟
L
⎢
⎝
L ⎠
L ⎠
⎝
⎝
⎣
⎤
⎥
⎥
⎞ ⎥⎥
⎟
⎠ ⎥⎦
(170)
The ratio (Q) of the average Sherwood number with suction and without suction
(
PeW
=0) is expressed as,
⎡
⎤
⎢
⎥
3
2
PeW
PeW
PeW
⎢
⎥
−4
Q = ⎢1 + 0.32
+ 0.02
− 7.68 × 10
2
1
⎥
d
3
3
⎞
⎛
e
de ⎞
de ⎞
⎛
⎛
⎢
⎥
Sc
Re
⎜
⎟
⎜ Re Sc ⎟
⎜ Re Sc ⎟
L ⎠⎥
⎢⎣
⎝
L
L
⎝
⎠
⎝
⎠
⎦
(171)
de
= 103 and
L
Pe
PeW
) is presented in
443
340
320
300
280
240
5
*
Sh(x )
260
Re Sc de/L=10
220
200
180
160
3
Re Sc de/L=10
140
120
0.0
0.2
0.4
0.6
0.8
1.0
*
x
Figure 17. Variation of Sherwood number along the channel length for the Reiner-Philippoff fluid at
Pe w = 200
.
400
5
Re Sc de/L=10
300
3
__
ShL
Re Sc de/L=10
200
100
0
0
100
200
300
400
__
Pew
the Reiner-Philippoff fluid for flow through the rectangular channel.
444
Figure 19. Variation of Q with the average dimensionless permeate flux for Reiner-Philippoff fluid for flow
through the rectangular channel.
3.2.3. Eyring Fluid
For typical values of the rheological parameters for Eyring fluid as discussed in section
3.1.3, the expression of F with u0 is obtained as before,
F = 3 × 10 5 + 5.44 × 10 6 u 0 − 4.65 × 10 6 u 0
For an average velocity of
the Eq. (133) as
2
(172)
u 0 =0.3 ms-1 and h=1 mm, the value of A330 is found out from
A330 = 16.54 . From Eq. (132),
d ⎞
⎛
A30 = 16.5353⎜ Re Sc e ⎟
L⎠
⎝
(173)
445
( )
d ⎞
2.55 ⎛
Sh x = * 1 0 ⎜ Re Sc e ⎟
L⎠
x 3 I3 ⎝
*
1
3
(174)
The value of the permeation parameter,
λ0eff 3 = 0.39
λ 0eff 3 is obtained from Eq. (137) as,
Pe W
d ⎞
⎛
⎜ Re Sc e ⎟
L⎠
⎝
1
(175)
3
⎛ Re Scd e ⎞
Sh L = 2.06⎜
⎟
L
⎝
⎠
1
3
⎡
⎢
2
3
PeW
PeW
PeW
⎢
−4
1
0
.
28
0
.
016
5
.
73
10
+
+
−
×
⎢
1
2
d
⎛
de ⎞ 3
de ⎞ 3
⎛
⎛
⎢
⎜ Re Sc e
Re
Re
Sc
Sc
⎜
⎟
⎜
⎟
L
⎢
⎝
L ⎠
L ⎠
⎝
⎝
⎣
⎤
⎥
⎥
⎥
⎞⎥
⎟
⎠ ⎥⎦
(176)
Q, the ratio of average Sherwood number with suction to that without suction is given as
⎡
⎢
2
3
PeW
PeW
PeW
⎢
−4
Q = ⎢1 + 0.28
0
.
016
5
.
73
10
+
−
×
1
2
d
⎛
de ⎞ 3
de ⎞ 3
⎛
⎛
⎢
⎜ Re Sc e
Sc
Sc
Re
Re
⎜
⎟
⎜
⎟
L
⎢
⎝
L ⎠
L ⎠
⎝
⎝
⎣
⎤
⎥
⎥
⎥
⎞⎥
⎟
⎠ ⎥⎦
(177)
de
= 103 and
L
Pe
PeW
) is presented in
446
350
250
*
Sh(x )
300
5
Re Sc de/L=10
200
150
100
0.0
3
Re Sc de/L=10
0.2
0.4
0.6
0.8
1.0
*
x
Figure 20. Variation of Sherwood number along the channel length for the Eyring fluid at
Pe w = 200
.
400
Re Sc de/L=10
5
300
__
ShL
Re Sc de/L=10
3
200
100
0
0
100
200
300
400
__
Pew
the Eyring fluid for flow through the rectangular channel.
447
5
4
3
Re Sc de/L=10
3
5
Q
Re Sc de/L=10
2
1
0
100
200
300
400
__
Pew
Figure 22. Variation of Q with the average dimensionless permeate flux for Eyring fluid for flow through the
rectangular channel.
4. CONCLUSION
The Sherwood number relations incorporating the effects of permeation are derived from
the first principles for a laminar flow in a tubular module and rectangular channel for three
non-Newtonian fluids. Effects of permeation on the mass transfer coefficient have been
quantified. Because of permeation, the Sherwood number can increase several times
compared to that without permeation depending upon the permeate flux. The derived
analytical expressions are useful to the engineers for design of the tubular and spiral wound
membrane modules for flow of the non-Newtonian fluids covered in this study.
NOMENCLATURE
A
A1,A2,A3
A10 , A20 , A30
rhelogical parameter in Eyring fluid
dimensionless parameters in Eqs.(12), (55) and (67)
A11,22,33
dimensionless parameters in Eqs.(82), (120) and (132)
dimensionless rheological parameters in Eqs.(14), (56) and (68)
A110 , 22,33
dimensionless rheological parameters in Eqs.(83), (121) and (132)
B
B1
rhelogical parameter in Eyring fluid
constant in Eq.(21)
448
B10
constant in Eq.(87)
c
c0
cp
c*
cm
D
d
F
f
I1,2,3
solute concentration, kg/m3
feed concentration, kg/m3
permeate concentration, kg/m3
dimensionless concentration
membrane surface concentration, kg/m3
solute diffusivity, m2/s
tube diameter, m
pressure gradient across the channel length (-dP/dx), Pa/m
friction factor
definite integrals in Eqs. (27), (59) and (71)
I 10, 2,3
definite integrals in Eqs. (93), (124) and (136)
K
K1,2
parameter in Eq.(64)
integration constants in Eq.(24)
K 10, 2
integration constants in Eq.(96)
k
L
P
Pew
mass transfer coefficient, m/s
channel length, m
pressure, Pa
dimensionless permeate flux (wall Peclet number)
Pe w
R
Re
Rr
r
Sh
length averaged non-dimensional permeate flux
tube Radius, m
Reynolds number
real retention of the membrane
radial direction, m
Sherwood number
ShL
length averaged Sherwood number
Sc
u0
vx
vy
vw
x
x*
y
y*
Schmidt number
average velocity across the cross section, m/s
x-component velocity, m/s
y-component velocity, m/s
permeate flux, m3/m2s
axial dimension, m
dimensionless axial dimension
dimension normal to the flow direction, m
dimensionless normal dimension
Greek letters:
α
δ
δ*
ϕ0 , ϕ
Ellis fluid rheological parameter
concentration boundary layer thickness, m
dimensionless concentration boundary layer thickness
1
Ellis fluid rheological parameters
τ yx
μ0 , μ∞
μ eff
449
Shear stress, Pa
rheological parameters in Eq.(50), Pa.s
effective viscosity, Pa.s
η , ξ , φ ,η 0 , ξ 0 , φ 0
similarity parameters
ρ
density, kg/m3
τs
rheological parameters in Eq.(50), Pa
REFERENCES
[1]
Bouchard, C. R.; Carreau, P. J.; Matsuuara, T.; Sourirajan, S. (1994). Modeling of
ultrafiltration: prediction of concentration polarization effects. J. Membrane Sci., 97,
215-229.
[2] Kleinstreuer, C ; Paller, M. S. (1983). Laminar dilute suspension flows in plate and
frame ultrafiltration units. AIChE J., 29, 533-539.
[3] van den Berg, G. B; Racz, I. G.; Smolders, C. A. (1989). Mass transfer coefficients in
cross flow ultrafiltration, J. Membrane Sci., 47, 25-50.
[4] Gekas, V; Hallstrom, B. (1987). Mass transfer in the membrane concentration
polarization layer under turbulent cross flow. I. Critical literature review and adaptation
of existing Sherwood correlations to membrane operations. J. Membrane Sci., 80, 153169.
[5] De, S.; Bhattacharjee, S.; Bhattacharya, P. K. (1995). Development of correlations for
mass transfer coefficient in ultrafiltration systems. Develop. Chemical Engg. Mineral
Proc., 3, 187-206.
[6] Girard, B.; Fukumoto, L. R. (2000). Membrane processing of fruit juices and
beverages: a review. Crit. Rev. Food Sci. Nutrition, 40 (2), 91-157.
[7] Cheryan, M. Ultrafiltration Handbook, Technomic Publishing Co. Ltd.: Lancaster, PA,
1986, pp. 349-369.
[8] Pepper, D.; Orchard, A.C. J.; Merry, A. J. (1985). Concentration of tomato juice and
other fruit juices by reverse osmosis. Desalination, 53, 157-166.
[9] Thomas, R. L.; Gaddis, J. L.; Westtfall, P. H.; Titus, T. C.; Ellis, N. D. (1987)
Optimization of apple juice production by single pass metallic membrane ultrafiltration.
J. Food Sci., 52, 1263-1266.
[10] Aptel, P., and Clifton, M. (1983). Ultrafiltration. In P. M. Bungay, H. K. Lonsdale and
M. N. de Pinho (Eds.), Synthetic Membranes: Science, Engineering and Applications
(pp. 249-305). Dordrecht : D. Reidel Publishing Co.
[11] Porter, M. C. (2005). Ultrafiltration. In Handbook of Industrial Membrane Technology
(pp. 136-256). New Delhi: Crest Publishing House.
[12] Chhabra, R. P.; Richardson, J. F.; Non-Newtonian flow in the Process Industries:
Fundamentals and Engineering Applications; Butterworth Heinemann: Oxford, 1999,
pp. 77.
450
[13] Charcosset, C; Choplin, C. (1996). Ultrafiltration of non-Newtonian fluids. J.
Membrane Sci., 115, 147-160.
[14] Howell, J. A; Field, R.; Wu, D. (1996). Ultrafiltration of high viscosity solutions:
theoretical developments and experimental findings. Chem. Engg. Sci., 51, 1405-1415.
[15] Pritchard, M.; Howell, J. A.; Field, R.; Wu, D. (1995). The ultrafiltration of viscous
fluids. J. Membrane Sci., 102, 223-235.
[16] De, S.; Bhattacharya, P. K. (1997). Prediction of mass transfer coefficient with suction
in the applications of reverse osmosis and ultrafiltration. J. Membrane Sci., 128, 119131.
[17] Minnikanti, V. S.; DasGupta, S.; De, S. (1999). Prediction of mass transfer coefficient
with suction for turbulent flow in cross flow ultrafiltration. J. Membrane Sci., 137, 227239.
[18] Ranjan, R.; DasGupta, S.; De, S. (2004). Mass transfer coefficient with suction for
laminar non-Newtonian flow in application to membrane separations. J. Food Engg.,
64, 53-61.
[19] Ranjan, R; DasGupta, S.; De, S. (2004). Mass transfer coefficient with suction for
turbulent non-Newtonian flow in application to membrane separations. J. Food Engg.,
65, 533-541.
[20] Bird, R. B.; Stewart, W. E.; Lightfoot, E. N. Transport Phenomena; Wiley: N.Y.,1960;
pp 13-14.
[21] De, S.; Bhattacharjee, S.; Sharma, A.; Bhattacharya, P. K. (1997). Generalized integral
and similarity solutions of the concentration profiles for osmotic pressure controlled
ultrafiltration. J. Membrane Sci., 130, 99-121.
[22] Opong, W. S.; Zydney, A. L. (1991). Diffusive and convective protein transport
through asymmetric membranes. AIChE J., 37, 1497-1510.
[23] Yurusoy, M.; (2003). A study of pressure distribution of a slider bearing lubricated with
Powell-Eyring fliuid, Turkish J. Eng. Env. Sci., 27, 299-304.
[24] White, F. M. Viscous Fluid Flow; McGraw Hill Inc.: Singapore, 1991; pp. 123.
APPENDIX
A.1. Effective Viscosity ( μ eff )
From the definition of friction factor, f [12],
f =
τw
1 2
ρu 0
2
(A1)
From the definition of the wall shear stress [12],
d
⎛ dP ⎞ d
⎟ =F
4
⎝ dx ⎠ 4
τ w = ⎜−
From Eqs. (A1) and (A2), the expression of friction factor becomes,
(A2)
f =
Fd 2
2 ρu 02
451
(A3)
16
Re
For laminar flow, f =
Hence, from Eqs.(A3) and (A4),
(A4)
μ eff =
Fd 2
32u 0
(A5)
A.2. Similarity Parameter
Evaluating Eq.(12) at the edge of the concentration boundary layer,
Δc * Δc *
A1δ
≈ *2
x*
δ
*
(A6)
1
⎛ x* ⎞ 3
*
⎟⎟
From the above equation, δ = ⎜⎜
⎝ A1 ⎠
Similarity parameter is defined as, η =
y*
δ*
= A11 / 3
y*
x *1 / 3
(A7)
A.3. Effective Viscosity for Power Law Fluid
Flow Through a Tube
In this case,
F =2
α +1
α
ϕ 0 = 0 . From Eqs.(46) and (47), the explicit expression of F becomes,
1
(α + 3)α u 0α
1
1
ϕ1α d
α +1
α
(A8)
From Eqs. (A5) and (A8), the expression of effective viscosity is obtained in this case,
452
1−α
1
1 ⎛ u ⎞ α ⎛ 2(α + 3) ⎞ α
⎟
μ eff = ⎜ 0 ⎟ ⎜⎜
16 ⎝ d ⎠ ⎝ ϕ1 ⎟⎠
Flow through a Rectangular Thin Channel
In this case,
F =4
α +1
α
(A9)
ϕ 0 = 0 . From Eqs.(111) and (112), the explicit expression of F becomes,
1
(α + 2)α u 0α
1
(A10)
α +1
α
1
ϕ1α d e
From Eqs. (A5) and (A10), the expression of effective viscosity is obtained in this case,
μ eff
1⎛u
= ⎜⎜ 0
8 ⎝ de
⎞
⎟⎟
⎠
1−α
α
1
⎛ 4(α + 2) ⎞ α
⎟⎟
⎜⎜
⎝ ϕ1 ⎠
(A11)
Chapter 8
EFFECT OF SMOOTH ROLL GRINDING CONDITIONS
ON REDUCTION OF SIZINGS IN THE WHEAT FLOUR
MILLING PROCESS
Department of Carbohydrate Food Engineering, Faculty of Technology,
University of Novi Sad, Bulevar Cara Lazara 1, 21 000 Novi Sad, Serbia
ABSTRACT
A laboratory roll stand Variostuhl, equipped with smooth rolls (250 mm diameter,
100 mm length), was used to examine, under simulated commercial conditions, the effect
of roll speed and roll differential on the reduction of sizings and coarse middlings from
the primary break passages of the wheat flour milling process. The samples were
obtained from the industrial mill, intercepting the sizings and coarse middlings from the
1st, 2nd and 3rd break stage that normally would have gone to the purification system, as
well as intercepting the purified sizings (cleaned middlings) that normally would have
gone to the reduction system of the wheat flour milling process. As roll velocity increases
flour release was increased, milling energy consumption rose while flour quality (as
determined by ash content) was not affected. By increasing roll velocity it is possible to
increase feed rate to the rolls and, therefore, the disposable roll surface is used more
efficiently. Flour release rose when differential was increased from 1.1 up to 1.25 but
decreased when differential increased from 1.25 up to 5.0. Increasing roll differential led
to an increase in milling energy consumption. These effects can be explained by the
relative contribution of compressive and shearing forces acting on the particles passing
through the grinding zone of the smooth rolls. Considering the results obtained in this
study (flour release, flour quality and milling energy consumption) a differential of 1.25,
relative to a fast roll speed of 5 m/s could be designated as optimal.
454
INTRODUCTION
The modern wheat flour milling process involves breaking open the grain, scraping off as
much endosperm from the bran and germ, and then gradually reducing the chunks of
endosperm into flour [1]. Repeated breakage (by roller milling) and separation (by sifting and
purifying) in the gradual reduction process allows effective removal of bran and germ from
endosperm and highly efficient recovery of flour, relatively free from bran contamination
[2,3].
This is possible due to the differences in structural and mechanical characteristics
between the anatomic parts of the wheat kernel. The three parts of the wheat kernel, bran,
germ and endosperm, differ in relative toughness and friability, giving different breakage
patterns on roller milling. These differences are exaggerated by adding water to the wheat
prior to milling, in a process known as conditioning or tempering. The need and advantages
of proper conditioning are well established [4,5].
During comminution operations, both material properties and milling methods affect
particle breakage [6]. The factors affecting particle size reduction can be classified into those
arising from the pshysicochemical properties of the material and those related to the design
and operation of the milling equipment [7]. The material is stressed by the action of the
processing equipment, and the stress is absorbed internally by the material as strain energy.
When the local strain energy exceeds some critical level, which is a function of the material
properties, fracture occurs along lines of weakness [8]. In wheat flour milling, the
predominant comminution tool is the roller mill in which the feed material is passed between
two counter-rotating rolls of, usually 250 mm diameter and with either a corrugated or
smooth finish [9]. The rolls are separated by a small gap and rotate at different speeds.
Particle size reduction is achieved by passing cleaned and conditioned wheat through a series
of break (fluted) and reduction (smooth) rolls. For fracture to occur in a wheat endosperm
particle during roller milling, the stress in the region that fractures must exceed internal
forces. Wheat endosperm exhibits viscoelasticity when fracturing, a condition intermediate
between complete brittleness and gross plastic yielding [10].
In a roller mill, particles are subjected to shear and compressive forces. Previous work of
Austin et al. [11, 12] and Hague [8] studied the situation of a particle being drawn into the nip
of smooth rolls counter rotating at the same speed. However, for most grain grinding
operations, the two rolls run at different speeds. If two rolls were to rotate at different speeds,
shear stress would be induced in the particles [13]. Figure 1 shows the idealized situation for
one particle (assumed to be perfectly spherical in shape) being drawn into the grinding zone
of the rolls (in reality a collection of particles are passing through the grinding zone). The
grinding zone is from the point where a particle is initially engaged between two rolls to the
point at which the gap is at minimum. Particles passing through the grinding zone of the roller
mill are subjected to shear forces from contact between points on the particles and the roll
surfaces, and compressive forces on the particles as a whole. Shear force from the side of the
fast roll (FF) tends to draw particle into the roll nip while shear force from the side of the slow
roll (FS) tends to eject it because of the different speeds of the rolls. Particle is also subjected
to the compressive forces (FF1 and FS1) reaching the maximum at the line connecting the
centers of the cross section of the rolls [14]. Once the particle is drawn into the roll nip, the
strain increases as the particle goes toward the roll nip, and the particle is crushed. The
Effect of Smooth Roll Grinding Conditions on Reduction of Sizings…
455
particles are held on the slow roll [15] while the rotation of the fast roll causes both
compressive and shear deformation. The reduction in size resulting from particle fracture
occurs after a given amount of deformation. This deformation will be ductile or brittle
depending on the applied stresses and the particle components upon which the stresses act
[16]. The roll parameters: the gap between the rolls, uniformity and the feed rate of stocks to
rolls, the roll velocities (speeds), the roll differential (the ratio of speeds of the fast and slow
rolls), and the type and condition of roll surface, influence the magnitude of the stress and the
relative contributions of compressive and shearing forces. The magnitude and the nature of
the forces acting on particles will determine the degree of particle size reduction, energy
required for grinding and bran contamination of the flour [17].
FS
FF1
FS1
α
fast roll
slow roll
FF
Figure 1. Idealized grinding zone and forces acting on an individual particle.
Fast and slow roll velocities, vf and vs respectively, roll differential (vf / vs), as well as
difference between the fast and slow roll velocity (vf – vs), have strong influence on the
treatment the particles receive in the grinding zone. Shear strain arises from the action of roll
differential. A larger differential gives a larger shear strain, compressive strain remains
constant [13] but the ratio between compressive and shearing forces is altered. With the
increase of roll velocity and roll differential the degree of particle size reduction also
increases. However, to study the effectiveness of the wheat flour milling process, along with
the quantity rates (break release, flour yield, particle size distribution of the output),
qualitative analyses (such as ash or protein content in the flour or size fraction of the output)
are of great importance [18] considering that, along with size reduction, efficient separation
of the bran and germ from the endosperm of the wheat kernel has to be achieved.
456
The main goal of the wheat flour milling industry is to produce a selection of flours of
defined quality followed by low investment and energy costs. The trend in recent years has
been to shorter mill flows necessitating increased feed rate to rolls. The faster the roll, the
larger the capacity [8]. As roll velocity increases the particles are drawn through the grinding
zone more quickly which also contribute to increased degree of particle size reduction.
The ribbon theory for flour production, presented by Perry and Chilton [19], predicts that
grinding action is proportional to the ratio of roll velocity to feed rate. Increased feed rate
reduces the amount of grinding any given particle receives. When roll velocity is increased
the feed ribbon spreads out, reducing the load in the grinding zone. The increased grinding
action on particles resulting from reduced ribbon width causes greater flour release as roll
velocity increases. The results of Scanlon et al. [16,17] support the ribbon theory. In their
investigation of smooth roll grinding conditions on farina milling, they found that by
increasing roll velocity or decreasing feed rate flour release was increased, milling energy
consumption rose and flour quality (as determined by ash content and color) was improved.
They also reported that increasing roll differential led to an increase in flour starch damage,
flour water absorption and milling energy consumption and a deterioration in flour quality
(ash and color). The effect of increasing the differential up to 1.5 was to increase flour yield.
Similar results were reported by Evers et al. [20] as differential was increased to 1.25. Further
increasing the magnitude of the shear forces imparted by the differential had little effect on
flour release, in fact the amount of flour decreased.
The purpose of this work was to examine, under simulated commercial conditions, the
effect of roll speed and roll differential on the reduction of sizings and coarse middlings from
the primary break passages of the wheat flour milling process. The changes were observed in
the degree of particle size reduction, flour yield, flour ash and milling energy requirements
and discusses in terms of the forces acting on the particles.
MATERIALS AND METHODS
Sample Preparation
The samples were obtained from the commercial mill intercepting the sizings and coarse
middlings from the 1st, 2nd and 3rd break stage that normally would have gone to the
purification system, as well as intercepting the purified sizings (clean middlings) that
normally would have gone to the reduction system of the wheat flour milling process. Sizings
and coarse middlings are the coarsest endosperm separates of the primary breaks representing
a mixture of pure endosperm, endosperm with various degrees of attached bran, and bran
particles. The purpose of the purifier is to separate the middlings into these fractions. The
clean separations from the purifier are sent to the head end of the reduction system [9].
Sizings and coarse middlings from the first and second break passages, particle size range
560-1000 μm, which according to the flow sheet would have gone to the same section of the
purifier, were intercepted (sample A in the following text). Stream leaving the purifier, that
normally would have gone to the front passages of the reduction system, consisted of particles
457
passing through 950 and 1000 μm bolting cloths (22 GG1 and 20 GG respectively), obtained
by purification of the sample A, was intercepted and designated as sample B. Sizings and
coarse middlings from the fine side of the second break passage, particle size range 560-850
μm, and from the third break passage, particle size range 530-850 μm, which according to the
flow sheet would have gone to same section of the purification system, were intercepted
(sample C in the following text). Stream leaving the purifier, obtained by purification of the
sample C and consisted of particles passing through 600 and 670 μm bolting cloths (32 GG
and 30 GG respectively), was intercepted and designated as sample D.
In each of the investigated samples, moisture and ash contents have been determined
according to ICC standard methods No. 110/1 [21] and 104/1 [22] respectively.
Rolls
Samples were milled on the laboratory roll stand Variostuhl; model C Ex 2 (Miag,
Braunschweig, Germany). It is a single pass, fully variable test mill, which uses full scale
diameter rolls (250 mm – diameter and 100 mm – length) to simulate commercial flour
milling conditions. Rolls are interchangeable to allow fluted rolls to be studied in different
dispositions, as well as the use of smooth rolls. It also provides wide range of roll speeds (up
to 18 m/s) and roll differentials (up to 1:85). Increasing the speed of the fast roll the slow roll
speed also increases according to differential which remains constant. Changing the speed of
the slow roll it is possible to change roll differential because fast roll speed remains constant.
Feed rate and roll gap are also adjustable.
Milling Conditions
The samples were separated into 1 kg batches and milled on a Miag Vario mill using
smooth rolls. Roll gap was set at 0.10 mm, for the grinding runs with sample A and B, and at
0.08 mm, for the grinding runs with sample C and D. Roll gaps were set using the indicator
on the mill and checked with a feeler gauge. All samples were feed at the rate of 0.4 kg/m/s.
The effect of roll speed on milling results was investigated using a constant roll
differential of 1.25 relative to fast roll speeds of 3, 4, 5 and 6 m/s. The effect of roll
differential on milling results was investigated setting the constant speed of the fast roll at 5
m/s relative to roll differentials of 1.1, 1.25, 1.50, 1.75, 2.0, 3.0 and 5.0. Tables 2 and 3
summarize experimental range of variables tested.
Analysis
Sieve analysis of obtained stocks was performed on the Bühler laboratory sifter (gyratory
in horizontal plane), model MLU-300 (Uzwil, Switzerland). Different stacks of sieves that
have been used (tables 2 and 3), were chosen according to results of the preliminary sieve
1
GG – grit gauze
458
analysis of stocks following the milling of the investigated samples at different roll speeds
and roll differentials.
All samples were sieved for 3 min and stock held on each sieve and the bottom collecting
pan was weighed. Three samples were milled and sifted at the same conditions. The weight
distribution among the streams was highly reproducible.
Moisture and ash contents in flour and other size fraction of the milling output have been
determined according to ICC standard methods No. 110/1 [21] and 104/1 [22] respectively.
The milling energy consumption during all grinding runs was determined from the
wattmeter fitted as an integral part of the Variostuhl laboratory roll stand. Power readings that
have been recorded (P, kW) correspond to operation with the material flow. The milling
energy consumption, E kJ/kg, was calculated by Eq. (1):
E=
Pt
(1)
m
Here m (kg) is the mass of flour obtained and t (s) is the time of the grinding run
determined by the chronometer.
RESULTS AND DISCUSION
Sample Characteristics
Ash content in the samples A and C is considerably higher compared to the ash content of
the samples B and D (table 1). Ash is concentrated in the bran and the ash content increases
from the inner to the outer part of the wheat kernel [23], with over the half the total in the
pericarp, testa and aleurone [24]. Higher ash content indicates that the samples A and C are
relatively enriched in bran and germ compared to samples B and D. However, it was to be
expected considering that samples B and D were obtained by purifying the samples A and C
respectively. As it was mentioned earlier in a chapter, the purpose of the purifier is to separate
sizings and coarse middlings into three fractions: pure endosperm, endosperm with attached
bran, and bran particles. Samples A and C represent a mixture of these fractions while in
samples B and D pure endosperm particles, relatively free from bran and germ, dominate.
This is important because of the differences of the mechanical properties. Endosperm and
bran do not break in the same way under the same stresses. Bran, being tough and fibrous, is
more prone to the ductile fracture imparted by shear forces than to brittle fracture. In contrast,
under dominating compressive forces, the bran particles remain relatively intact while brittle
endosperm is crushed into many small pieces. Arnold and Roberts [25], studying the stress
distribution in wheat grains, concluded that under compression the bran does not carry any of
the applied load, serving only to contain the endosperm material.
Moisture contents of the samples are within usual range (table 1). At these values,
differences in the structural and mechanical characteristics between the particles that originate
from different anatomic parts of the wheat kernel still exist, and therefore efficient separation
of the remaining bran from the endosperm, along with the particle size reduction, was
possible.
459
Table 1. Particle size range, moisture and ash content of the investigated samples
Sample
A
B
C
D
Size range [μm]
560 – 1000
670 – 1000
530 – 850
530 – 670
Moisture content (%)
14.6
14.4
14.6
14.3
Ash content (%)dm
1.04
0.54
1.55
0.54
dm – dry matter basis.
Table 2. Summary of experimental range of variables tested
(the effect of roll speed)
Sample
Roll
surface
A
Roll
gap
[mm]
Feed rate
[kg/m/s]
Differential
Fast roll
speed
[m/s]
0.4
1.25
3; 4; 5; 6
0.10
B
0.10
Smooth
C
0.08
D
0.08
Sieve
openings*
[μm]
570, 400,
250, 150
450, 350,
250, 150
570, 400,
250, 100
450, 350,
250, 100
*along with the bottom collecting pan.
Table 3. Summary of experimental range of variables tested
(the effect of roll differential)
Sample
Roll
surface
A
Roll
gap
[mm]
Feed rate
[kg/m/s]
Fast
roll
speed [m/s]
Differential
0.4
5
1.10; 1.25;
1.50; 1.75;
2.0; 3.0; 5.0
0.10
B
0.10
Smooth
C
0.08
D
0.08
Sieve
openings*
[μm]
570, 400,
250, 100
450, 350,
250, 100
570, 400,
250, 100
400, 350,
250, 100
*along with the bottom collecting pan.
The Effect of Roll Speed
Changes in the particle size distribution of the stocks, brought about by the increase of
the roll speed, followed the same trends for all investigated samples (figure 2). By increasing
fast roll speed, yield of two largest size fractions of the milling output (>570 μm and 400-570
μm - samples A and C; >450 μm and 350-450 μm - samples B and D) tends to decrease while
the quantity of the medium sized stocks and both flour fractions (fine: <100 μm and coarse:
100-250 μm - samples C and D and fine: <150 μm and coarse: 150–250 μm – samples A and
B) increased. Flour production (<250 μm) was directly related to roll speed (figure 3a).
460
Similar results were reported by Scanlon et al. [17] as well as Schumacher [26] and support
the ribbon theory of Perry and Chilton [19] mentioned earlier in a chapter. The increased
grinding action on particles resulting from reduced ribbon width causes greater flour release
as roll velocity increases. As roll velocity increases the particles are drawn through the
grinding zone more quickly, enhancing their brittleness, which would also contribute to
increased flour production [17].
Sample A
35
Yield of the milling output size fractions [%]
45
Size fractions [ μm ]
>570
400-570
250-400
150-250
<150
40
35
30
25
20
15
10
3
5
30
25
20
15
10
6
3
45
40
Size fractions [μm ]
>570
400-570
250-400
100-250
<100
Sample C
25
20
15
10
4
5
6
Fast roll speed [m /s]
45
4
50
30
Sample B
5
5
35
>450
350-450
250-350
150-250
<150
40
>450
350-450
250-350
100-250
<100
35
30
Sample D
25
20
15
10
5
5
3
4
5
6
3
4
5
6
Figure 2. Effect of fast roll speed on the weight percentage of various streams.
Under the present grinding conditions (smooth rolls, constant roll differential of 1.25 and
constant roll gap), a larger roll speeds would induce a larger shear strain, compressive strain
remains constant but the ratio between compressive and shearing forces is altered. As it was
mentioned earlier in chapter, the nature of deformation depends not only on the applied
stresses but as well on the particle components upon which the stresses act. Compressive
stresses, compared to shear, are more effective in causing the disintegration of the brittle
endosperm material. This explains why the flour release and degree of particle size reduction
in general are not even more noticeable under present grinding conditions.
Flour release, obtained by milling the samples B and D (following the purification) is
higher compared to samples A and C (before the purification). Samples B and D, mainly
consisted of pure endosperm particles, are relatively free from bran while samples A and C
represent a mixture of pure endosperm, endosperm with various degrees of attached bran, and
bran particles. Bran takes on some portion of the forces in the grinding zone which would be
otherwise directed to the reduction of the endosperm explaining the lower flour yield and
461
milling efficiency in general. However, different stacks of sieves that have been used for
sieve analysis make the comparison of the degree of particle size reduction between
investigated samples more difficult.
Milling energy consumption exhibited similar relationship to flour release as roll speed
was altered. By increasing roll speed milling energy consumption slightly rose (figure 3b).
The goal of the wheat flour milling industry is to produce a selection of flours of defined
quality at lowest possible price. Therefore, the consumption of energy in the process, since
large part of it is energy required for grinding, should be observed as energy consumption
relative to the mass of produced flour. Eq. (1) defines milling energy consumption relative to
the mass of flour obtained. Therefore, increase of the flour release contributes to the decrease
of milling energy consumption calculated on the basis of eq. (1). Since flour release was
directly related to roll speed there was only slight increase of the milling energy consumption
following the increase of roll speed. However, by increasing roll speeds power requirement
increases and therefore the rolls should be run at lowest possible speed to handle the capacity.
This means that rolls with small loads should be run at lower speeds than rolls with heavy
loads [9]. On the other hand, increasing roll speed can be used to form a similar feed flow
pattern when an increase in feed rate is desired [27]. The faster the roll, the larger the capacity
[8]. These are very important considerations in the modern wheat flour milling process
because trend in recent years has been to shorter mill flows necessitating increased feed rate
to rolls to retain or even increase the capacity. With slow rolls the demands for increased
capacity could not be met.
It was mentioned earlier in a chapter that bran takes on some portion of the forces in the
grinding zone contributing to the lower degree of particle size reduction that is reduced
milling efficiency. This is the reason why milling energy consumption, at the same fast roll
speed, is constantly higher for the samples A and C (before purification) compared to samples
B and D (following the purification) respectively (figure 3b).
By increasing roll speed flour quality, as determined by ash content, was not affected
(table 4). It shows that increasing roll speed wasn’t followed by increased grinding of the bran
which would otherwise increase flour ash, considering that ash is concentrated in the bran and
the ash content increases from the inner to the outer part of the wheat kernel. Ash content of
the flour obtained by milling samples A and C is constantly higher compared to the ash
content of the flour obtained by milling samples B and D respectively. However, it was to be
expected considering that samples B and D were obtained by purifying the samples A and C
respectively, and that initial ash content of the samples A and C is higher compared to
samples B and D.
Table 4. Ash content of flour (<250 μm) obtained by milling
the investigated samples at different fast roll speed
Fast roll speed [m/s]
3
4
5
6
Ash content of flour (%)dm
Sample
A
B
C
0.46
0.42
0.52
0.47
0.38
0.51
0.45
0.41
0.50
0.45
0.39
0.50
D
0.44
0.45
0.41
0.40
Milling energy consumption [kJ/kg]
Flour release (%)
462
36
34
32
30
28
26
24
22
20
18
Sample:
A
B
C
D
a
3
4
5
6
5
6
160
b
150
140
130
120
110
100
90
3
4
Figure 3. Effect of fast roll speed on a – the release of flour and b – milling energy consumed.
The Effect of Roll Differential
The particle size distribution of the stock followed the same trends for all investigated
samples (figure 4). A differential of 1.25 appears to be a turning point. Increasing roll
differential from 1.1 up to 1.25 led to a decrease of the yield of two largest size fractions of
the milling output while the quantity of medium sized stocks and both flour fractions (fine:
<100 μm and coarse: 100-250 μm) increased. Quite opposite to that, further increase of the
roll differential, from 1.25 up to 5.0, led to an increase in the yield of the largest size fractions
of the milling output while the quantity of medium sized stocks and both flour fractions
decreased. This decrease in the degree of particle size reduction, imparted by increase of the
roll differential, is caused by two primary reasons. Firstly, the most effective way of grinding
bran is by cutting actions of the corrugated rolls. Since smooth rolls have been used in the
experiment there was no cutting action of the rolls. Secondly, with roll differential closer to 1
the compressive forces dominate in the grinding zone. As the roll differential increased
greater shear stresses were imposed altering the relative contributions of compressive and
shearing forces. All investigated samples, especially samples B and D, are composed
primarily of endosperm. Compressive stresses, compared to shear, are more effective in
causing the disintegration of the brittle endosperm material. These are the reasons why the
milling efficiency is higher in the region of small roll differentials.
463
Size fractions [μm]
>570
400-570
250-400
100-250
<100
50
65
55
Sample A
45
40
35
30
25
20
15
10
5
60
>450
350-450
250-350
100-250
<100
Sample B
55
50
45
40
35
30
25
20
15
10
5
0
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
1.0
1.5
2.0
Roll differential
Sample C
35
30
>570
400-570
250-400
100-250
<100
15
3.5
4.0
4.5
5.0
10
5
Sample D
45
40
20
3.0
Roll differential
45
25
2.5
40
35
30
>400
350-400
250-350
100-250
<100
25
20
15
10
5
0
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
1.0
1.5
2.0
2.5
Roll differential
3.0
3.5
4.0
4.5
5.0
Roll diferential
Figure 4. Effect of roll differential on the weight percentage of various streams.
For all investigated samples flour release, as measured by the 250 μm sieve, reached its
maximum at roll differential of 1.25 (figure 5a). Further increasing the magnitude of the shear
forces imparted by the differential resulted in decrease of the flour yield. It points out that
flour particles are more likely formed by compressive fracture than shear. Similar results were
seen by Evers et al [20] as well as Scanlon et al [16, 17]. Flour release, obtained by milling
samples A and C is lower compared to those obtained by milling samples B and D. Again it
could be attributed to the fact that bran takes on some of the forces in the grinding zone which
would be otherwise directed to the reduction of endosperm.
Milling energy consumption exhibited a near linear response to roll differential (figure
5b). Increasing roll differential from 1.1 up to 1.25 caused very small decrease of milling
energy consumption while further increase of roll differential led to a significant increase in
milling energy consumption. In fact, decrease in the degree of particle size reduction is
followed by increase in milling energy consumption. The reasons for the decrease in the
degree of particle size reduction have been explained earlier in a chapter. The relationship
between roll differential and milling energy consumption observed in the current study
concurs with the results of Scanlon et al [16, 17], Wanzenried [28] and Zwingelberg et al
[29].
Flour release (%)
464
34
32
30
28
26
24
22
20
18
16
14
12
10
Milling energy consumption [kJ/kg]
1.0
800
Sample:
A
B
C
D
a
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
4.0
4.5
5.0
Roll differential
b
700
600
500
400
300
200
100
0
1.0
1.5
2.0
2.5
3.0
3.5
Figure 5. Effect of roll differential on a – the release of flour and b – milling energy consumed.
Increased roll differential caused increased flour ash (table 5). The deterioration of flour
quality as differential increases can be attributed to bran powdering since increased
differential induce more tearing of the bran. Bran being tough and fibrous is more prone to
the ductile fracture imparted by shear forces than to brittle fracture. As a result, flour ash
increases because of greater bran contamination of flour. It also explains why the ash content
of flour obtained by milling samples A and C is constantly higher, under the same roll
differential, compared to the ash content of flour obtained by milling samples B and D
respectively. However, it was to be expected considering that samples B and D were obtained
by purifying the samples A and C respectively, and that initial bran and therefore ash content
of the samples A and C is higher compared to samples B and D.
Table 5. Ash content of flour (<250 μm) obtained by milling
the investigated samples at different roll differentials
Roll differential
1.10
1.25
1.50
1.75
2.00
3.00
5.00
Ash content of flour (%)dm
Sample
A
B
0.43
0.35
0.43
0.36
0.45
0.40
0.46
0.39
0.48
0.43
0.51
0.44
0.55
0.47
C
0.50
0.50
0.54
0.54
0.59
0.63
0.71
D
0.40
0.42
0.43
0.43
0.45
0.48
0.50
465
CONCLUSION
The effects of smooth roll grinding conditions on reduction of sizings can be explained
on the basis of the forces imparted on the particles in the grinding zone. With constant feed
rate to rolls, by increasing roll speed the load in the grinding zone is reduced. Particles are
subjected to greater grinding action, causing more fracture, which results in increased flour
release while flour quality as determined by the ash content is not affected. By increasing roll
speed milling energy consumption rose. However, increasing roll speed can be used to form a
similar feed flow pattern when an increase in feed rate is desired. This way the disposable roll
surface is used more efficiently. Setting the roll differential at 1.25 flour release reaches
maximum while the milling energy consumption is at minimum. As differential is increased
greater shear forces are imparted to the particles causing greater bran contamination of flour
and, therefore, deterioration of flour quality caused by increased flour ash.
Considering results obtained in this study (flour release, flour quality and milling energy
consumption) a differential of 1.25, relative to a fast roll speed of 5 m/s could be designated
as optimal for smooth roll grinding of sizings.
REFERENCES
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
Bass, E.J. (1988). Wheat flour milling. In Y. Pomeranz (Ed.), Wheat: Chemistry and
Technology. (Vol.2, 3rd edition, pp. 1-68). St.Paul, Minnesota: American Association
of Cereal Chemists.
Sudgen, T.D. and Osborne, B.G. (2001). Wheat flour milling. In D.A.V. Dendy, and
B.J.Dobraszczyk (Eds.), Cereals and Cereal Products: Chemistry and Technology.
(pp. 140-181). New York, Aspen Publishers.
Owens, W.G. (2001). Wheat, corn and coarse grains milling. In W.G. Owens (Ed.),
Cereals Processing Technology. (pp. 27-52).Cambridge, UK: Woodhead Publishing
Ltd.
Lockwood, J.F. (1960). Flour Milling. Stockport, Cheshire, England: Henry Simon
Ltd.
Shellenberger, J.A. (1980). Advances in milling technology. In Y. Pomeranz (Ed.),
Advances in Cereal Science and Technology. (Vol. 3, pp. 227-270). St.Paul,
Minnesota: American Association of Cereal Chemists.
Scanlon, M.G. and Lamb, J. (1995). Fracture mechanism and particle shape formation
during size reduction of a model food material. Journal of Material Science, 30, 25772583.
Campbell, G.M., Bunn, P.J., C.Webb, C., and Hook, S.C.W. (2001). On predicting
roller milling performance Part II: The breakage function. Powder Technology, 115,
243-255.
Haque, E. (1991). Application of Size Reduction Theory to Roller Mill Design and
Operation, Cereal Foods World, 36, 368-374.
Posner, E.S., and Hibbs, A.N. (2005). Wheat Flour Milling. St. Paul, Minnesota:
American Association of Cereal Chemists.
466
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
MacRitchie, F. (1980). Physiochemical aspects of some problems in wheat research.
In Y. Pomeranz (Ed.), Advances in Cereal Science and Technology (Vol. 3, pp. 271326). St.Paul, Minesota: American Association of Cereal Chemists.
Austin, L.G., van Orden, D.R., and Perez, J.W. (1980). A preliminary analysis of
smooth roll crushers. International Journal of Mineral Processing, 6, 321-336.
Austin, L.G., van Orden, D.R., McWilliams, B., and Perez, J.W. (1980). Breakage
parameters of some materials in smooth roll crushers. Powder Technology, 28, 245251.
Fang, C., and Campbell, G.M. (2002). Stress-Strain Analysis and Visual Observation
of Wheat Kernel Breakage During Roller Milling Using Fluted Rolls. Cereal
Chemistry, 79, 511-517.
Мерко, И.Т.: Совершенствование технологических процессоб сортовога помола
пшеницы, Колос, Москва, 1979.
Scott, J.H. (1951). Flour Milling and Processes (2nd ed.). London, Chapman and Hall.
Scanlon, M.G., Dexter J.E., and Biliaderis, C.G. (1988). Particle-Size Related
Physical Properties of Flour Produced by Smooth Roll Reduction of Hard Red Spring
Wheat Farina, Cereal Chemistry, 65, 486-492.
Scanlon, M.G., and Dexter, J.E. (1986). Effect of Smooth Roll Grinding Conditions
on Reduction of Hard Red spring Wheat Farina, Cereal Chemistry, 63, 431-435.
Farrel, E.P., and Ward, A.B. (1965). Flow rates and analyses for ash and protein of all
streams in the Kansas State University pilot flour mill. Association of Operative
Millers-Bulletin, March, 2842-2847.
Perry, R.H., and Chilton, C.H. (1973). Chemical Engineer`s Handbook (5th ed.). New
York, NY: McGraw-Hill.
Evers, A.D., Baker, G.J., and Stevens, D.J. (1984). Production and measurement of
starch damage in flour. Part 1. Damage due to roller milling of semolina. Starch, 36,
309-312.
ICC Standard No. 110/1: Determination of Moisture Content of Cereals and Cereal
Products (Practical Method).
ICC Standard No. 104/1: Determination of Ash in Cereals and Cereal Products
Pomeranz, Y. (1988). Chemical composition of kernel structure. In Y. Pomeranz
(Ed.), Wheat Chemistry and Technology (Vol.2, 3rd edition, pp.97-158). St.Paul,
Minnesota: American Association of Cereal Chemists.
Kent, N.L. (1975). Technology of cereals. Oxford: Pergamon Press.
Arnold, P.C., and Roberts, A.W. (1966). Stress distributions in loaded wheat grains.
Journal of Agricultural Engineering Research, 11, 38-43.
Schumacher, F. (1966). Spiral, cut, pressure among technical aspects of grinding with
roller mills. Am. Miller Process., 94(5), 29.
Schumacher, F. (1967). Technical aspects of grinding with roller mills. Association of
Operative Millers – Bulletin, January, 2956.
Wanzenried, H. (1970). Grinding with smooth rolls. Association of Operative Millers
– Bulletin, September, 3195.
Zwingelberg, H., Meyer, D., and Gerstenkorn, P. (1983). Beeinflussung der
Mehlausbeute und Mehlqualität von Weizen durch Glattwalzen unterschiedlicher
Beschaffenheit. Getreide Mehl Brot, 37, 112.
Chapter 9
AN EFFECT OF RELATIVE AIR HUMIDITY ON THE
CONTENT OF VOLATILE COMPOUNDS IN ROASTING
COCOA BEANS
Wieslawa Krysiak,*1 Teresa Majda and Ewa Nebesny1
1
Institute of Chemical Technology of Food; Institute of Food Chemistry Principles
Technical Univeristy of Lodz (TUL), 90-924 Lodz, st. Stefanowskiego 4/10
ABSTRACT
The Ivory Coast cocoa beans were convectively roasted at 135°C, at the air flow rate
of 1.0 m/s and relative air humidity (RH) of 0.4%, 2.0% and 5.0%. Volatile components
of raw and roasted beans were analyzed by SPME/GC/GCMS and identified by
comparing their retention indices with that of standards included in a database and their
mass spectra with standard spectra included in NIST computer library. Almost 100
different volatile compounds were identified in examined samples of roasted cocoa. They
ranked among aldehydes, ketones, alcohols, esters, monoterpenes, pyrazines, acids,
lactones, furan derivatives, and sulfur-containing compounds. It was found that a rise in
the relative air humidity from 0.4% to 2.0 and 5.0% increased the contents of pyrazines,
volatile acids, esters, furan derivatives, and sulfur-containing compounds in a headspace
of roasted cocoa. In contrast, the contents of alcohols and aldehydes in the headspace
were considerably lower when the cocoa beans were roasted at the relative air humidity
of 5.0% as compared to that when less humid air was used for convective heating.
Keywords: cocoa beans; convective roasting; roasting of cocoa beans; relative air humidity;
volatile components in roasted cocoa beans.
*
Wieslawa Krysiak: e-mail: [email protected], [email protected]
468
INTRODUCTION
Roasting is one of principal technological operations in cocoa beans processing. It
reduces water, volatile acids and tannins contents, produces a characteristic chocolate aroma,
enhances brown coloration of cocoa beans, facilitates separation of shells from nibs and
destroys microbial contamination. One of the most important effects derived by roasting is the
development of a characteristic and pleasant chocolate aroma [3, 6, 19, 20, 33]. It appears
when precursors of aroma generated during fermentation and drying of cocoa beans combine
with each other during roasting.
Maillard reactions rank among the principal processes occurring during roasting and
contributing to generation of the appropriate aroma, changes in texture and stronger brown
coloration [5, 6, 9, 19, 21, 29, 30, 33, 37, 38, 39]. Chemistry of these reactions depends on
temperature and water activity of raw material [36, 37], concentration and structure of
reducing sugars and amino acids, and pH of material [37]. The presence of small amounts of
water is thought to favor Maillard reactions because water enables the transport of reacting
molecules [44, 46]. However, when water content is too high, pyrazines and other important
aromatic substances are not formed.
Alkyl derivatives of pyrazine were found to be the most important components of roasted
cocoa aroma [6, 7, 15, 24, 42, 48]. Their odor threshold is 4-490ng/g [17]. One of the factors
affecting the content of pyrazines in aroma of roasted cocoa is the geographic origin of cocoa.
It was found that cocoa beans from Ghana contained 698μg/100 g of these compounds, while
the Mexican cocoa of Tabasco variety – only 142 μg/100g [19, 41]. Concentration of
pyrazines in roasted cocoa depends also on the genotype of cocoa seeds and parameters of
unit processes such as fermentation [1, 2, 6, 10, 18, 30, 40], drying and roasting [6, 7, 15, 21,
33, 41, 42, 45].
The most abundant pyrazines identified in cocoa beans are pyrazine, 2,5dimethylpyrazine, 2,6-dimethylpyrazine, trimethylpyrazine and tetramethylpyrazine, [6, 7, 31,
33, 40]. The contents of pyrazine and tetramethylpyrazine [41] are significantly higher in
roasted cocoa than in raw material.
The ultimate steps of Maillard reactions are aldol condensation and polymerization of
aldehyde amines, which generate aldimines and ketimines, and next the heterocyclic nitrogen
compounds [38].
It was found that [17] the unique chocolate aroma of roasted cocoa was derived by
reaction of phenylacetic aldehyde and 3-methylbutane. The aldol condensation yields 2phenyl-5-methyl-2-hexanal. The other aromatic compounds generated during roasting are 3methylbutanal [17, 31], phenylacetaldehyde, 2-methyl-3-furan, 2-ethyl-3,5-dimethyl pyrazine
and 2,3-diethyl-5-methyl pyrazine [3]. Ziegleder [31] proposed to determine the roast level of
cocoa beans on the basis of methylfuran concentration.
Cocoa beans are roasted at 130 – 1500C for 15-45 min. The maximum temperature on
their surface is 120 – 140oC [32, 34, 44, 45, 47]. Usually whole beans are roasted. In one of
several variants of this process, the surface of material is moisturized to make the separation
of shells from nibs easier. Moisturizing of the surface of cocoa beans is achieved by spraying
with water, steaming or increasing humidity of air in a roaster [4, 13, 16, 44].
Presented studies aimed at estimation of the relationship between the relative air humidity
and concentration of aroma components in the headspace of roasted cocoa beans.
An Effect of Relative Air Humidity on the Content…
469
MATERIALS AND METHODS
The Ivory Coast cocoa beans (Forastero cultivar, Ivory Coast) were applied for the
studies. The cocoa beans were sorted and the medium-size fraction was selected for further
experiments to provide uniform processing of all roasted beans.
Roasting of Cocoa Beans
Raw cocoa beans were convectively roasted in a forced air flow drying tunnel [26, 27,
28]. The parameters of thermal processing were as follows:
•
•
•
temperature of 1350C;
air flow rate of 1.0 ms-1 (it was earlier found to be the optimum flow rate [26]);
relative air humidity of 0.4%, 2.0% and 5.0%.
Presented parameters of thermal processing of cocoa beans refer to the air, which was in
a direct contact with roasted beans. Process of roasting was conducted without air circulation.
Measurements of spent air parameters were also carried out (results not presented).
Air temperature was measured by YCY meter (type YC-262 coupled with NiCr-NiAl
sensor), and the rate of its flow was determined using the coupled THERM 2285-2B meter
equipped with 9915 S120 sensor (produced by AHLBORN).
The relative humidity of “dry” air was calculated according to the following equation
(presented for the temperature of 110°C):
RH=100×
Y`× P
`
0.622 × ( Psat )110 0 C + Y × ( Psat )110 0 C
where: RH - relative air humidity [%],
Y’ – absolute air humidity at 20°C [kg H2O/kg dry air]; 0.0087729 kg H2O/kg dry air;
P- pressure of saturated steam [Pa]; 101 x 103 Pa;
(Psat)110°C – pressure of steam at 110°C [Pa], 143.2653 x 103 Pa [Manual of Engineer:
Sugar Manufacturing, p. 52 (Dobrzycki et al. 1973)].
Air humidity was increased using saturated steam produced in a steam generator.
Relative humidity of this air was determined using the coupled THERM 2285-2B meter
equipped with FHA636-HR2 sensor (produced by AHLBORN).
The precision of measurements of temperature, air flow rate and its humidity was +1 °C,
+0.05 ms-1 and +0.5%, respectively.
Each time, batches of cocoa beans (200 g) were spread to form a monolayer during
roasting. The process was terminated when the water content of material dropped to
approximately 2%, since this value is regarded as optimal for further steps of cocoa
processing, such as crushing or butter pressing [40].
470
Determination of Chemical Composition of Cocoa Beans’ Headspace
Samples of raw and roasted cocoa beans were ground in a laboratory mill WZ-1 (ZBBPP,
Poland), and approximately 5g portions were weighed to glass vials (5×10 cm). Concentration
of volatiles was determined by solid phase microextraction coupled with gas chromatography
and mass spectrometry SPME-GC-GC/MS. Volatiles were adsorbed using a SPME unit
(Supelco) consisting of a length (2 cm plug) of fused silica fiber coated with divinylbenzene
/carboxen/polydimethylsiloxane DVB/Carboxen/PDMS (thickness of 50/30 μm).
Microextraction of volatile aroma components was carried out for 0.5 h. It was preceded by
30 min stabilization of ground cocoa at 600C. Desorption of these compounds occurred at
2500C in a sampler of gas chromatograph. GC analyses were carried out using HRGC 5300
gas chromatograph (CARLO-ERBA INSTRUMENTS, series Mega) equipped with flame
ionisation detector (FID) and SSL injector. GC/MS analyses were conducted using GC 8000
gas chromatograph (FISONS INSTRUMENTS) equipped with SSL injector and coupled with
MD 800 mass detector. In both cases aroma components were separated on Quadrex capillary
column (30 m x 0.32 mm x 0.5 μm) fused with 007-FFAP stationary phase. Nitrogen was the
carrier gas (flow rate of 1ml/min) when analyses were conducted using HRGH 5300 gas
chromatograph. The temperature was increased (40C/min) from 400C (3 min isothermal
period) to 2450C (a final 30 min isothermal period). The temperature of injector and detector
was 2500C. The same parameters were maintained when aroma components were separated
using GC 8000 gas chromatograph. In this case helium was the carrier gas (flow rate of
0.8ml/min) and ionisation energy was 70 eV.
The volatile components of aroma were identified by comparison of both their retention
indices with that of standards included in a database and their mass spectra with spectra of
compounds included in NIST computer library.
Calculation and Statistics
Determinations of the headspace composition were carried out in triplicate. Results are
expressed as weight% of total volatiles (mean + SD). Percentage content of each headspace
component was calculated as follows: the sum of surface areas below peaks of all volatiles
was taken as 100% and then the weight% of each compound was calculated on the basis of
surface area below the respective peak. The results were subjected to statistical analysis,
which included determination of a mean surface area below each peak (table 1), calculation of
standard deviation of the latter and one-way analysis of variation (ANOVA) at the
significance level p≤0.05.
RESULTS AND DISCUSSION
Many different factors, such as the variety of cocoa, post-harvest treatment, fermentation
and roasting conditions determine the aroma of cocoa, which is characteristic of chocolate
products. The aroma is affected both by substances contained within the raw cocoa beans and
by newly generated components, which are products of pyrolysis of sugars and nitrogen
471
compounds. In early phases of roasting this aroma can be acetic, beer-like, bread-like or
another. A loss of easily evaporating components of raw cocoa is of importance for the
ultimate aroma of roasted cocoa and thereby for the quality of chocolate.
Gas chromatography of aroma components of raw and convectively roasted cocoa beans
(either in “dry” (RH of 0.4%) or in “humid” air (RH of 2 or 5.0%)), revealed approximately
100 volatile compounds, ranking among aldehydes, ketones, alcohols, esters, monoterpenes,
pyrazines, acids, lactones, furyl derivatives and sulfur compounds. All these substances, their
retention indices (RI) and percentage contents determined on the basis of surface area under
their peaks (the sum of surface area under all the peaks is equivalent to 100%) are displayed
in table 1.
Table 1. The effect of relative air humidity during roasting on headspace composition of
roasted cocoa*.
*Roasting was carried out at 1350C and air flow rate of 1.0 m/s. Values of relative air
humidity were 0.4, 2.0 and 5.0%. The headspace composition of raw and convectively
roasted cocoa beans was determined by SPME/GC/GCMS
Peak
no
Compound
RI
1.
2.
3.
4.
5.
6.
7.
methanthiol
acetaldehyde
dimethyl sulfide
noidentified
isobutyraldehyde
propionaldehyde
acetic
acid
methyl
acetate
tetrahydro-2-methylfuran
2-methylfuran
butyraldehyde
pivaldehyde(2,2dimethylpropanal)
isovaleric aldehyde
2,5-dimethylfuran
2-pentanon
2-methyl-2-pentanal
3-methyl-3-buten-2-one
2-ethyl-5-methyl-furan
2-butanal
methyl-3-butenoate
dimethyl disulfide
hexanal
2-ethylacrolein
2-pentanol
3-penten-2-one
β-myrcene
hyptanone
isoamyl alcohol
2,4-nonadienal
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20
21.
22.
23.
24.
25.
26.
27.
28.
Roasted at RH of
0.4%;
τ=35 min
Raw
cocoa
beans
697
715
763
809
}829
RT
2.18
2.27
2.52
2.82
}3.05
0.10a
0.20
0.18
0.20a
}0.3
841
3.18
Roasted at
Roasted at RH
RH
of
of 5.0%;
2.0%;
τ=60 min
τ=45 min
Surface area of GC peak (%)
0.10a
0.14a
0.07a
b
0.13
0.28
0.25b
0.35
0.36
0.61
0.22a
0.20a
0.20a
0.73
}2.47
}2.42
1.03
1.15b
1.92
3.07
}887
}3.72
}0.09
}0.11
916
924
4.22
4.38
1.35
1.16b
928
982
995
}102
9
1054
1060
1079
1099
1113
1125
1133
1146
1180
1199
1222
1235
4.48
5.65
5.92
}6.93
7.72
7.92
8.53
9.15
9.67
traces
10.38
10.85
12.08
12.97
13.63
14.13
1.11b
}-
1.31
1.17b
0.94
0.16
0.80
1.25
2.45b
0.08
0.46
}0.24b
2.79b
0.02
0.34
}0.20b
2.56b
3.07
}0.12
0.98
}0.03
0.12b
1.14
1.14
0.57
0.24b
traces
0.07b
7.33
0.01b
0.54
0.24b
0.13b
0.10b
0.77
1.21
0.28
0.20bbb
0.06b
6.02
0.05b
0.43
0.27bbb
0.16b
0.09b
0.22
0.06
0.15
0.02
0.33
1.16
0.34
0.49
0.15b
0.08
traces
2.54
0.06
0.58
0.42
1.09
3.09
0.22
0.35
2.44
472
Peak
no
Compound
RI
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
Styrene
methylpyrazine
isobutyl methyl ether
noidentified
3-methyl-2-hexanal
2,5-dimethylpyrazine
ethylpyrazine
trans-linalool oxide
metyl trisulfide
2-ethyl-5-methylpyrazine
2-nonanon
2-ethyl-6-methylpyrazine
trimethylpyrazine
ester?
2-ethyl-3,5dimethylpyrazine
acetic acid
2-ethyl-3,6dimethylpyrazine
cis-linalool oxide
3-furalaldehyde
tetramethylpyrazine
ethylene glycol acetate
6-methyl-6vinylpyrazine
2-furyl-methyl-ketone
2-heptanol
pyrrole
benzaldehyde
linalool
2,3-butandiol
3-methyl-pyrrole
isobutyric acid
dimethyl sulfooxide
1,3-butandiol
3(2H)-piridazinone
pyridinecarboxylic acid
derivative
3-butenoic acid
benzenacetaldehyde
acetophenone
3-furanmethanol
isovaleric acid
1-methyl-2pyrrolidinone
2-acetylo-3methylpyrazine
ketone ?
1279
1290
1309
1328
}134
6
1351
1357
1365
1370
1382
1400
1406
1412
1426
1450
1466
RT
15.78
16.18
16.90
17.62
}18.2
7
18.47
18.70
19.00
19.17
19.60
20.28
20.48
20.72
21.20
22.05
22.62
}147
4
}22.9
0
}19.82b
19.85b
0.04
13.62
0.50
37.85
traces
1489
}149
8
1505
1515
23.40
}23.7
2
23.98
24.32
0.18b
}1.39
śl
0.82
traces
0.14
0.12
}traces
0.04b
0.26
0.14b
1.67
traces
0.03b
0.35
traces
1534
}154
6
1556
1584
1589
1597
1607
1617
1622
1639
1650
24.95
}25.3
8
25.72
26.67
26.83
27.13
27.45
27.77
27.93
28.47
28.82
0.10b
}0.22
0.09b
}1.20
10.37
traces
0.35b
0.03
0.15
0.34
0.70
0.30b
7.46
0.05
0.36b
0.24
0.45
0.27
0.52
0.46
0.28b
0.06b
1.36
0.08
2.25
0.39
1.86
0.19
1.33
0.06
1.93
0.27
0.13
traces
3.26
0.90
5.07
4.11
3.09
0.07
0.53
1670
}167
7
1684
1690
1710
29.47
}29.6
8
29.92
30.10
30.72
1.30
}7.95
traces
5.61
traces
0.93
7.43
0.05
}1.50
1.99b
4.30b
traces
1.58
7.87
traces
1.99b
4.74b
traces
1715
30.88
0.07a
0.32b
0.34b
0.04a
1728
31.28
0.20a
0.20a
0.14a
0.14a
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
Roasted at RH of
0.4%;
τ=35 min
Roasted at
Roasted at RH
RH
of
of 5.0%;
2.0%;
τ=60 min
τ=45 min
0.51
0.39
0.34
3.30b
3.73ba
3,96a
0.73b
0.62b
0.66b
1.66
1.44
0.18a
0.39
}3.13
}3.65
1.68
1.84b
1.93b
2.00b
b
b
0.65
0.69
0.62b
b
b
0.18
0.20
0.46
0.30
0.21
0.48
0.09
0.13
0.03
0.11
0.18b
0.20b
0.59b
0.53b
0.54b
b
b
0.51
0.60
0.47b
0.01
0.93b
1.01b
0.04
0.11b
0.10b
b
b
0.51
0.65
0.52b
Raw
cocoa
beans
0.87
traces
0.37
0.18
0.08
}0.05
traces
0.04
0.07
traces
0.50
14.42
-
473
Peak
no
Compound
RI
73.
2-methyl-5-transpropenylpyrazine
valeric acid
2,3-hexandiol
2-pentanoic acid
methylbenzyl alcohol
iso-amyl benzoate
hexanoic acid
methoxyphenol
benzyl alcohol
phenyl ethyl alcohol
methylcinnamaldehyde
maltol
ketone methyl pyrrol-2yl
noidentified
furaneol
noidentified
noidentified
4H-pyran-4-one-2,3dihydro-3,5-dihydroxy6-methyl
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
Roasted at RH of
0.4%;
τ=35 min
Raw
cocoa
beans
1777
RT
32.78
Roasted at
Roasted at RH
RH
of
of 5.0%;
2.0%;
τ=60 min
τ=45 min
0.07a
0.09a
0.10a
0.10a
1801
1825
1839
1844
1855
1868
1897
1911
1948
1972
2003
2014
33.53
34.23
34.62
34.78
35.10
35.48
36.30
36.72
37.72
38.40
38.69
39.55
0.12
0.09b
0.07b
0.25b
0.11b
0.41b
0.16
0.30
2.02b
0.36b
0.88
0.24
0.17
0.08b
0.24b
0.10b
0.36b
0.28
0.23a
2.09b
0.34b
0.02
1.66
0.03
0.10b
traces
0.25b
0.12b
0.31b
0.21
0.15
1.39
0.10
traces
0.66
0.99
0.25a
1.41
0.08
2072
2079
2083
2096
2317
41.10
41.28
41.40
41.75
47.33
0.28
0.15b
0.10
0.08
1.43b
0.41
0.23
0.19
0.14
1.53b
0.50
0.19b
0.39
1.20
-
}0.15
RI-retent index, RT-retention time
Values in each line bearing the same letters are not significantly different (p>0,050 from one another.
Changes in contents of aroma components are also shown in two representative
chromatograms (figures 1 and 2). Numbers of compounds in the table 1 are the same as in
figures 1 and 2.
Table 2 presents the relationship between the number of individual compounds in each of
the groups found in the headspace of cocoa beans roasted at 1350C and air flow rate of
1.0m/s, and the relative air humidity (0.4; 2.0 or 5.0%).
Presented results prove that the number of volatile compounds in the headspace of
roasted cocoa is higher than in that of raw cocoa irrespective of the relative air humidity. Our
finding is consistent with results of other researchers who were involved in studies on cocoa
aroma [6, 7, 10, 15, 17, 20, 21, 24, 33, 38, 40, 41, 42, 45].
The dominating headspace components of raw and roasted cocoa were found to be
pyrazines, aldehydes and alcohols. The contents of volatile acids, ketones and sulfur
compounds were lower. Small amounts of esters and furans were also detected.
Figure 1. Representative GC chromatogram of volatile components of raw cocoa beans.
Figure 2. Representative GC chromatogram of volatile components of convectively roasted cocoa beans (T=1350C, v=1,0m/s, RH=0,4%, τ=35 min).
476
Table 2. The number of compounds within each of the groups of volatile compounds
identified in raw and convectively roasted cocoa beans and its dependence on the
humidity of air used for roasting (temperature and air flow rate were maintained at
1350C and 1.0m/s, respectively)
Group of compounds
Cocoa beans
Raw
Roasted at RH of 0.4%;
τ=35 min
Pyrazines
Alcohols
Aldehydes
Ketones
Acids
Sulfur compounds
Esters
Furans
10
13
12
6
6
3
2
1
13
13
13
7
7
3
5
4
Roasted at RH of
2.0%;
τ=45 min
14
14
13
7
7
4
4
4
Roasted at RH of
5.0%;
τ=60 min
14
14
13
6
5
4
4
4
Pyrazines
Pyrazines rank among the most important volatile components of roasted cocoa aroma.
They impart the characteristic aroma to roasted products [5, 6, 7, 17, 19, 20, 21, 23, 40, 41
42].
The number of pyrazines rose from 10 (included in the headspace of raw cocoa) to 13 -14
(table 2) during roasting at 1350C regardless of the relative air humidity. Raw cocoa beans
contained the following pyrazines: methylpyrazine, 2.3-dimethylpyrazine, 2-ethyl-5methypyrazine, 2-ethyl-6-methypyrazine, trimethylpyrazine, 2-ethyl-3,5-dimethypyrazine, 2ethyl-3,6-dimethypyrazine, tetramethylpyrazine, 6-methyl-6-vinylpyrazine and 2-acetyl-3methylpyrazine. Five of them were hardly detectable and the contents of other five were very
low (0.04-0.1%). Also Keeney [23], Jinap et al. [121], Reineccius et al. [40], Sanagi et al.
[41] found these pyrazines in raw cocoa beans.
Irrespective of the relative air humidity, the process of roasting not only increased the
contents of these pyrazines, which were detected in the headspace of raw cocoa beans but also
generated the new compounds, mainly dimethylpyrazines, such as 2,5-dimethylpyrazine and
2,6-dimethylpyrazine. 2,5-dimetylopyrazine was found to convey the nutty aroma to
thermally processed products [6, 19]. Our results are consistent with findings of Jinap et al.
[21], Keeney [23] and others [6, 7, 31, 33, 40].
The relative air humidity had no explicit impact on formation or disappearance of
pyrazines. Hence the increased water content in air impaired neither Maillard reactions nor
formation of pyrazines and the aroma of cocoa beans was not less rich [44].
The other important factors affecting the quality of roasted cocoa are the ratios of
dimethylpyrazines (DMP) to trimethylpyrazines (TMP) and dimethylpyrazines (DMP) to
tetramethylpyrazines (TMP). According to Bonvehi et al. [6], Eun-Jung-Lee et al. [14] and
Fadini et al. [15] both these ratios should not be lesser than 1 and their low values indicate
that synthesis of aroma components was impaired. The ratios (DMP)/(TMP) and
(DMP)/(TMP) determined in this work exceeded 1 irrespective of roasting conditions.
477
Alcohols
The headspace of raw and roasted cocoa beans contained 13 and 14 different alcohols,
respectively. Alcohols impart the fruity and plant-like hint [21]. The most abundant alcohols
in raw cocoa headspace were isoamyl alcohol, 2,3-butandiol, 1,3 butandiol and pentanol
(3.09; 5.07; 3.09 and 1.44%, respectively) [35]. The contents of other alcohols were lower
and usually did not exceed 1.0% (0.58-0.09%).
Alcohol content was reduced during roasting because of their volatilization with steam
and/or thermal degradation. The same phenomenon was observed by Jinap et al. [21].
The content of alcohols in the headspace of roasted cocoa beans was higher when the
relative air humidity was 5.0%, most probably because of rapid formation of empty space
between the kernel and shell (the so termed “balloon effect”) what hampered the evaporation
of volatile compounds from the beans [25, 28, 44].
The new alcohol was formed during roasting of cocoa beans (undetectable in the
headspace of raw beans) regardless of the relative air humidity. It was 2-heptanol, which
imparts the fruity, herbal, and sharp aroma [21]. The other alcohols important for sensory
properties are linalol and phenyl ethyl alcohol. Linalol is responsible for the flower hint of
thermally processed products [44]. It was particularly abundant in cocoa beans roasted at the
relative air humidity of 5.0%. According to Świechowski [44] this alcohol is derived from
pyrazines at high temperature and humidity.
Carbonyl Derivatives
Aldehydes
Carbonyl compounds were found to be important components of cocoa aroma [19, 21,
43]. As much as 20 different aldehydes and ketones were detected in the aroma of roasted
cocoa.
Aldehydes are products of Stecker degradation of free amino acids and like pyrazines
rank among the principal aroma components formed during roasting. They can be also
derived by oxidation of lipids, which occurs at high water content [2, 19].
11 aldehydes were detected in raw cocoa beans. The most abundant of them were:
benzaldehyde and benzenacetaldehyde (3.26 and 1.50%, respectively). The contents of acetic,
isobutyric, propionic and butyric aldehydes were lower than 0.5% (0.1-0.35%). These
compounds could be the result of selfoxidation and degradation of fatty acids [2, 8].
The number of aldehydes rose from 12 to 13 during roasting, irrespective of the relative
air humidity. Their content was the highest in cocoa beans roasted using “dry” air (RH of
0.4%). Application of more humid air (RH of 2.0 or 5.0%) reduced the amounts of aldehydes
and their depletion was more pronounced at the highest RH value. It could result from the
longer time of processing (60 min) and evaporation of these highly volatile substances with
steam. Also according to Jinap et al. [21] the longer time of roasting decreases the contents of
these compounds. The most susceptible to distillation with steam were benzaldehyde and
benzenacetaldehyde. Their contents increased 3 and 5 fold, respectively, when cocoa beans
were roasted with “dry” air but when the relative air humidity was increased to 2.0 and 5.0%
their contents were 30-70% lower as compared to that achieved at RH of 0.4%.
478
Changes in the contents of ketones during roasting of cocoa beans were like in case of
aldehydes.
Esters
Esters impart the fruity taste and aroma to plant products. The content of methyl acetate,
which was one of two esters detected in the headspace of raw cocoa beans, reached 1.11%.
Roasting increased the number of these compounds to 3 (RH of 5.0%) or 4 (RH of 0.4 and
2.0%).
Percentage contents of esters rose with humidity of air used for roasting. For instance, the
contents of methyl acetate increased by 4, 73 and 177% for RH of 0.4; 2.0 and 5.0%,
respectively. This character of changes could result from the longer time of roasting when RH
was higher. It favored condensation of methanol and acetic acid. The latter is one of abundant
components of raw cocoa beans and GC analysis revealed that its content was decreased
during roasting. Also Jinap et al. [21] found that longer roasting at 1400C beneficially affected
esters formation.
Volatile Acids
Acetic acid was the most abundant volatile acid (above 37%) in raw cocoa beans. The
contents of isovaleric (14.42%) and isobutyric (4.11%) acids were also appreciable.
Percentage contents of other acids, like hexanoic and butenoic (1.0-1.5%) were lower.
Depletion of undesirable acidic substances, mainly acetic acid, is one of the goals of
roasting of cocoa beans [19, 20, 22, 25, 34, 44, 47]. Concentrations of acetic, isobutyric,
isovaleric, hexanoic and pentanoic acids were reduced by roasting, regardless of air humidity.
The ultimate content of acids was decreased with a rise in RH with the exception of isovaleric
acid. It was believed to result from more advanced evaporation of volatile acids with steam
during longer roasting at higher RH.
Although the content of isovaleric acid was also reduced (by 50-70%) during roasting, its
highest percentage content was detected in the headspace of cocoa beans roasted at RH of
5.0%, like in case of valeric acid.
The abundance of isovaleric acid and the presence of valeric acid in the headspace of
cocoa beans roasted at RH of 5.0% brought about the relatively high acidity of this material.
The similar phenomenon was reported earlier by one of the authors [25].
Furans
The raw cocoa beans contained only one volatile furan derivative, i.e. 2,5-dimethylfuran
(0.98%) while the roasted material contained 4 of them. These compounds are generated by
degradation or caramelisation of sucrose [12]. Because the concentration of the latter in raw
cocoa beans is very low (approximately 1.0%), so the degradation of sugars due to Maillard
reactions occurring during roasting is also believed to be the source of these compounds [11,
42]. The majority of furans impart the sweet and caramel-like aroma of burnt sugar.
The contents of furans in the headspace of roasted cocoa beans increased with the relative
air humidity and was the highest for RH of 5.0%. The highest rise was observed for 2,5dimethylfuran (3 folds increment). The same tendency was observed for 2-methylfuran and
tetrahydro-2-methylfuran. It was arguably caused by longer time of roasting when RH was
greater. Elevated humidity and longer thermal processing beneficially affected Maillard
reactions occurring in cocoa beans [21]. Water concentration of 3% was found to favor the
479
non-enzymatic browning. In the atmosphere of more humid air, particularly at RH of 5.0%,
water content of 3.0% in cocoa beans subjected to roasting is maintained for 30 min whereas
in the “dry” air (RH of 0.4%) – only for 20 min [27].
Sulfur Compounds
Raw cocoa beans contained dimethyl sulfide, dimethyl disulfide and methanthiol (0.18,
2.54% and 0.10%, respectively). Because of very low thresholds these compounds enhance
the intensity of aroma of other aromatic substances. The number of these compounds rose to 5
during roasting in the atmosphere of more humid air (RH of 2.0 or 5.0%). The headspace of
roasted cocoa beans contained also methyl trisulfide and dimethyl sulfoxide. Their contents
were higher for RH of 2.0%. When cocoa beans were convectively heated with “dry” air, only
methyl trisulfide was generated during roasting. The application of more humid air resulted in
depletion of dimethyl disulfide. Its content was reduced 4.5, 9 and 17 folds for RH of 0.4, 2.0
and 5.0%, respectively. It was distilled with steam during longer roasting, like other very
volatile substances. The other reason of their disappearance was degradation to dimethyl
sulfide, which caused a rise in concentration of the latter (by 2% for RH of 0.4 and 2.0%, and
3.5 fold for RH of 5.0%).
Summary
The conclusions drawn from the results of the determinations are as follows:
•
•
•
•
GC/MS chromatography revealed almost 100 different volatile compounds in the
headspace of cocoa beans convectively roasted at 135°C;
these substances include aldehydes, ketones, alcohols, esters, monoterpenes,
pyrazines, acids, lactones, furan derivatives, and sulphur-containing compounds;
a rise in air humidity from 0.4% to 2 and 5% increased the content of pyrazines,
volatile acids, esters, furan derivatives, and sulfur-containing compounds.
the content of alcohols and aldehydes was significantly reduced when cocoa beans
were roasted at the relative air humidity of 5%.
REFERENCES
[1]
[2]
[3]
[4]
Abeygunasekera D. D., Mubarak A., M., Jansz. E., R. (1989). The volatiles of cocoa
by GC/MS analysis and sensory evaluation with special emphasis on the effect of
fermentation time and maturation. Journal of the National Science Council of Sri
Lanka, 17 (2), 229-235.
Abeygunasekera D. D., Jansz. E., R. (1991). Effect of the maturation process on
fermented cocoa bean. I. Free amino acids and volatile carbonyls. Journal of the
National Science Council of Sri Lanka, 17 (1), 23-33.
Belitz H.-D., Grosch W. (1999). Food Chemistry. Cocoa and Chocolate, 2nd ed.,
Berlin, Springer-Verlag, 894-903.
Benz K.: Debacterization of Cocoa Beans Gains Increasing Acceptance. Available
since 2003, http://www.buhlergroup.com/sc/en/publikationen.asp
480
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
Bonvehi J.S., Coll F.V. (1997). Evaluation of bitterness and astringency of
polyphenolic compounds in cocoa powder. Food Chemistry, 60, 365-370.
Bonvehi J.S., Coll F.V. (2002). Factors affecting the formation of alkilpyrazines
during roasting treatment in natural and alkalinized cocoa powder. J. Agric. Food
Chem., 50, 3743-3750.
Bonvehi J.S. (2005). Investigation of aromatic compounds in roasted cocoa powder.
European Food research and tenchnology, 221 (1-2), 19-29.
Boosfeld J., et. al.. (1993). Characterization of unsaturated aldehydes in green coffee.
15th Scientific Symposium on Coffee, Sinscinati, Available since 2003,
http://www.asic-café.org/
Brito E.S., Narain N. (2003). Effect of pH distillate volume on monitoring aroma
quality of bittersweet chocolate. Food Quality and Preference, 14, 219-226.
Cros E. (1999). Cocoa flavor development. Effects of post-harvest processing.
Manufacturing and Confectioner, 79 (2), 70-77.
Czerny M., Mayer F., Grosch W. (1999). Sensory study on the character impact
odorants of roasted Arabica coffee. J. Agric. Food Chem., 47, 695-699.
De Maria C. A. B., et al. (1996). Composition of green coffee water-soluble fractions
and identification of volatiles formed during roasting. Food Chemistry, 55 (5), 203207.
Dodson C. (1996). Fruitful new opportunities in food processing industry. FoodTech-Europe, 3(2), 52, 54, 56.
Eung-Jung-Lee et al. (2000). Changes in flavor components during microwave
roasting of cocoa mass. Journal of the Korean Society of Food Science and Nutrition,
29 (3),384-388.
Fadini A. L., Garcia N-H-P. (1997). Evolution of pyrazines during the roasting of
cacao beans (Theobroma cacao, L.) variety Forastero. Coletanea-do-Instituto-deTecnologia-de Alimentos, 1999, 27(1/2), 69-74.
Finken H. (1996). A new thermal cocoa process. Food Marketing and Technology, 4,
25-27.
Grabowska J. (2002). Aroma compounds. In: Food Chemistry. Ed. Z.E. Sikorski.,
Warsaw, PWN, 427-456.
Groot H. (2003). Cocoa aroma- a complex puzzle. Susswaren, (7-8), 20-21.
Hoskin J.C., Dimick P.S. (1994). Chemistry of flavour development in chocolate. In
Industrial chocolate manufacture and use. II-nd ed., Chapman and Hall, , 102-111.
Jinap S., Dimick P.S., Hollender R. (1995). Flavour evaluation of chocolate
formulated from cocoa beans from different countries. Food Control, 6, 105-110.
Jinap S., Wan Rosli W.I., Russly A.R., Nordin L.M. (1998). Effect of roasting time
and temperature on volatile component profiles during nib roasting of cocoa beans
(Theobroma cacao). J. Sci. Food Agric., 77, 441-448.
Jinap S., Zeslinda A. (1995). Influence of organic acids on flavour perception of
Malaysian and Ghanian cocoa beans. J. Food Sci. Technol., 32, 27-33.
Keeney P.G. (1972). Various interactions in chocolate flavor. JAOCS, 49, 567-572.
Koehler P.E., Odell G.V. (1970). Factors affecting the formation of pyrazine
compounds in sugar-amine reactions. J. Agr. Food Chem., 18, 895-898.
[25]
[26]
[27]
[28]
[29]
[30]
[31]
[32]
[33]
[34]
[35]
[36]
[37]
[38]
[39]
[40]
[41]
[42]
[43]
481
Krysiak W. (2001). Physico-chemical changes in cocoa bean roasted in changing air
conditions. In Proceedings of the XIIth seminar of Properties of Water in Food ed.
P.P. Lewicki, Warsaw Agricultural University Press, 107-119.
Krysiak W., Iciek J., Motyl-Patelska L. (2003). Infulence of roasting conditions on
selected physico-chemical properties of cocoa bean. Inzynieria Chemiczna i
Procesowa, 24 (3),509-524.
Krysiak W., Motyl-patelska L. (2005). Effects of roasting conditions on the degree of
lipid migration from cocoa bean kernel. Inzynieria Chemiczna i Procesowa, 26
(4),817-829.
Krysiak W., Motyl-Patelska L. (2006). Effects of air parameters on changes in
temperature inside roasted cocoa beans. Acta Agrophysica, 7 (1),113-128.
Martins S.I.F.S., Jongen W.M.F., van Boeckel M.A.J.S. (2001). A review of Maillard
reaction in food and implications to kinetic modelling. Trends Food Sci. Technol., 11,
364-373.
Mascaros A. (1993). Sensory properties of cocoa. Origin, processing and evaluation.
Alimentaria (244), 85-89.
McFarlane I. (1994). Instrumentation. In Industrial chocolate manufacture and use.
II-nd ed., Chapman and Hall, 281-311.
Minifie B.W. (1981). Chocolate, cocoa and confectionery: In Science and
Technology. Pitman Press, 15, 25-28.
Misnawi , Jinap S., Jamilah B., Nazamid S. (I). (2004). Effect of polyphenol
concentration on pyrazine formation during cocoa liquor roasting. Food Chem.,
85,73- 80.
Nebesny E., Rutkowski J. (1998). Effect of roasting and secondary fermentation on
cocoa bean enrichment. Pol. J. Food Nutr. Sci., 7/48, 437-444.
Oberparleiter S., Ziegleder G. (1997). Amyl alcohols as indicative of raw cocoa bean
quality. Zeitschrift-fuer-Lebensmittel-Untersuchung-und-Forschung-A/Food Reserch
and Technology, 204 (2), 156-160.
Őzdemir M., Devres Y.O. (2000). Analysis of color development during roasting of
hazelnuts using response surface methodology. J. Food Eng., 45, 17-24.
Őzdemir M., Devres Y.O.(I). (2000). Kinetics of color changes of hazelnuts during
roasting. J. Food Eng., 44, 31-38.
Pijanowski E., Dłużewski M., Dłużewska A., Jarczyk A. (1997). In Food technology,
VI ed., Warsaw, WNT, 88,120,192.
Redgwell R.J., Trovato V., Curti D. (2003). Cocoa bean carbohydrates: roastinginduced changes and polymer interactions. Food Chemistry, 80, 511-516.
Reineccius G.A., Keeney P.G., Weissberger W. (1972). Factors affecting the
concentration of pyrazines in cocoa beans. J. Agr. Food Chem., 20, 202-206.
Sanagi M.M., Hung W.P., Yasir S.M. (1997). Supercritical fluid extraction of
pyrazines in roasted cocoa beans. Effect of pod storage period. J. Chromatography A,
785, 361-367.
Shibamoto T., Akiyama T., Sakaguchi M., Enomoto Y. et. al. (1979). A study of
pyrazine formation. J. Agric. Food Chem., 27, 1027-1031.
Silwar R. (1988). Quantitative determination of steam-volatile aroma constituents.
Café, caco, The, 32 (3), 243-250.
482
[44]
[45]
[46]
[47]
[48]
Świechowski Cz. (1996). Chocolate manufacturing. Roasting of cocoa beans –
comparison of methods. Bakery and Confectionery Rev., 4, 20-22.
Świechowski Cz. (1994). Thermal processing of cocoa beans. Bakery and
Confectionery Rev., 1, 35-37.
Świtka J. (1994). Water as ingredient of food. In Chemical and functional properties
of ingredients of food ed. Z.E. Sikorski. Warsaw, WNT, 63-64.
Wyczański S. (1994). Confectionery. Warsaw, WSiP, 249-252,257,264.
Zamalloa W., A., Pezoa N., H., Meireles M., A., A. (1995). The extraction of volatile
components from cocoa beans with a micro-extractor and using subcritical CO2.
Ciencia-e-Tecnologia-de-Alimentos, 15 (1), 70-73.
Chapter 10
BULGURATION: COMBINED COOKING
AND DRYING OPERATION
Mustafa Bayram
Assoc. Prof. Dr., University of Gaziantep, Faculty of Engineering,
Department of Food Engineering, 27310-Gaziantep-TURKEY
ABSTRACT
Cooking and drying are two main unit operations used widely in food processing.
Consecutive cooking and drying operations supplies perfect properties to gain to food
products and called as bulguration. Individually, the former method is used nearly for all
food products before consumption. Cooking is a well-known way to destruct
microorganisms, insect, insect eggs and larvaes for food safety. Also, it increases the
digestive property of food with starch gelatinization, protein gelation and textural
softening. However, it is very difficult to store this product without drying due to its high
moisture content after cooking. Therefore, food products should be dried. Drying is
required to prolong storage time of food products. Bulguration is the gaining of the some
functional characteristics on the finished product such as the resistance to mold
contamination, insect attacks and radiation, inactivation of enzymes and microorganisms,
encapsulation of numerous nutritional components in food products, easy preparation
after bulguration due to semi and ready-to-eat form, obtaining long shelf-life having
economical products with safety, decreasing undesired components e.g. phytic acid in
contrast to increasing desired one e.g. folate/folic acid. As raw materials, cereals, pulses,
seeds, vegetables, fruits etc. can be used.
Recently, the use of bulguration in the food industry dramatically increases as an
optimal method due to above situations. Bulguration is an ancient technique; however,
the modern technology re-discovered it. In this chapter, the techniques of bulguration are
explained with examples. Also, the results of the recent researches are given.
484
Mustafa Bayram
INTRODUCTION
Cooking and drying operations are well-known processes individually. However, the
evaluation of their combination is limited in the literature. Recently, bulguration as a
combination of cooking and dying has been studied by the researchers. During bulguration,
significant functional properties are gained to finished product. Globally, cereal/legumesbased foods are prepared as a dry finished form using roasting and extrusion operations.
However, bulguration technique is different, due to its specific processing steps - i.e. cooking
in water and subsequent drying. It should be noted, and also added to the production method
specifications for the processing of cereals and legumes, that bulguration is more suitable to
cereals and legumes than other methods. For example, extrusion and roasting equipments are
more expensive, and they work at high temperatures (~150-180°C). These high temperatures
cause high (and costly) energy consumption, high nutrition loss, high quality loss (primarily
color) and the formation of undesired and unhealthy byproducts, such as i.e. hydroxylmethyl
furfural (HMF, a Maillard-Amidori browning reaction byproduct), acrylamide etc. In turn,
cereals and legumes with and without blending with other ingredients could be produced
using bulguration technique, instead of extrusion and roasting. Such products would be both
healthier and cheaper (Bayram, 2007).
Bulgurated product has been regarded as being the nutritional equivalent of whole raw
material but more stable and resistant to attack by insects and vermin. The simple processing
and low-fuel requirements for food preparation were additional advantages, which supply
high resistance to humid and hot environmental conditions Bayram, 2007).
Bulguration’s benefits can be summarized as follows (Bayram, 2000, 2005, 2007;
Bayram and Öner, 2002, 2005; Bayram et.al., 2004a, b, c, d, e):
•
•
•
•
•
increases nutrient absorption due to high mineral and insoluble cellulose fiber content
of cereals and legumes, and also prevents constipation and intestinal cancer risk
the finished product can be classified as a functional foods
this process using grains is suitable for vegetarian diets
is a good processing for expectant women and babies, due to folate/folic acid content of
cereals and legumes. Folate/folic acid is important in the development of babies’ brains,
particularly during the first three months of pregnancy. However, folate/folic acid is
continuously broken down by metabolism and must therefore be continually
replenished through nutrition. (Consequently, bulguration plays a very important role
for pre-natal brain development and the health of expectant mothers). For example,
folate/folic acid content of wheat-bulgur (Shepherd, et. al., 1965; Pence et. al., 1964)
varies between 41-150 μg/100 g, which depends on wheat species and processing
parameters. Its folate/folic acid content is higher than some unbulgurated-food products
such as patent flour: 13, white bread: 25, brown bread: 45, wholemeal bread: 40, raw
brown rice: 49, plain popcorn: 3, raw pearl barley: 20, orange: 31, grapefruit: 26, rye
crispbread: 35 and wheatgerm bread: 46 μg/100 g (McKevith, 2002, 2004; Calhoun et.
al. 1960).
has the best property to decrease the available phytic acid content (a mineral-binding
antinutrient), while simultaneously increasing its bran content (high fiber, high
mineral). The decrease in phytic acid content is about 18.9-33.9% due to cooking and
•
•
•
•
•
•
•
485
drying operations. During cooking and drying, heat causes the degradation of phytic
acid (Özkaya et. al., 2004; Lasztity and Lasztity, 1990).
resistant to mold contamination due to the cooking and drying operations
resistant to insect attacks and formation of larva due to the cooking and drying
operations
inactivates microorganisms and enzymes
nutrients (minerals and vitamins) originally present in the grain and legumes are reabsorbed with water into the kernel during the cooking operation, thereby curbing the
loss of nutrients
provides a longer shelf life than other food materials
is economical due to pre-processing of product before consumption
lends itself to easy home preparation, as it is pre-cooked. is used in ready-to-eat or
semi-ready-to-eat food products.
According to literature, there are different kinds of bulgurated-food-products such as
wheat-bulgur, corn-bulgur, barley-bulgur, soy-bulgur, rye-bulgur, triticale-bulgur, lentilbulgur, chickpea-bulgur, rice-bulgur (called as parboiled rice) etc. (Bayram et.al., 2004a, b;
Elgun et.al., 1990; Köksel et.al., 1999; Bayram et. al., 2004c, d, e; Singh and Dodda, 1979).
Some of them are also produced commercially. The number of the plants for the bulguration
of wheat now stands around 600 worldwide (comprising 500 in Türkiye, 15-20 in the United
States and Canada, 4-6 in the EU, 10-15 in Arabic countries). For example, more-than one
million metric tones of bulgurated wheat are produced annually in Türkiye. The production
capacity is totally 250,000-300,000 tons/year in USA and Canada. The annual per-capita
consumption of bulgurated wheat in the major producer country, Türkiye, reflects its
economical and nutritional value. Turkish consumption of bulgurated-wheat is 2.5-3.5 and
1.5-2.5 times greater than consumption of pasta (macaroni) and raw-rice, respectively, with
an average annual consumption of about 12 kg/person. In the eastern and southern parts of
Türkiye, consumption averages 25 kg/person, whereas in Syria, Iraq, Iran, Israel, Lebanon,
Arabia i.e. Middle East countries, (consumption averages 30-35 kg/person). Due to increased
demands for bulguration, some pasta and flour plants in these areas have integrated their
systems for bulguration operation and new factories are planned or are under construction.
Recently, new bulguration factories have been constructed in Europe (3, 10-15).
BULGURATED PRODUCTS
Bulgurated-Wheat
In the literature, there is a lot of knowledge about wheat-bulgur, especially produced
from durum-wheat due to its yellow color and hard texture (Bayram, 2000, 2006; Bayram and
Öner, 2002, 2005).
486
Mustafa Bayram
Bulgurated-Barley
Traditions and customs control the consumption of barley as a human food. Barley was
once used extensively in the diets of rural areas in England, Denmark, Near East and Far East
(Kent, 1975; Munch, 1981). Taste and appearance factors along with its poor baking quality
have limited the use of barley in human foods and the consumption of barley has declined in
the last century. Nonetheless, barley is suitable for a wide range of food applications. It can
be processed into a number of palatable, nutritious food products or blended with other foods
(Bhatty, 1986; Newman and Newman, 1991).
Barley has also been promoted in many parts of the world for its ability to contribute to a
healthy life. The high level of soluble fibre in barley is reputed to reduce heart disease
(Newman et. al., 1989; McIntosh et. al., 1991; Klopfenstein and Hoseney, 1987), colon
cancer (McIntosh et. al., 1993) and post-prandial glucose concentrations (Jenkins et. al.,
1978). Reducing the levels of post-prandial glucose is an important tool for controlling
glucose levels in diabetic subjects12. The ability of barley to reduce heart disease is thought
to result from reduced levels of blood cholesterol. Soluble, (1Æ3; 1Æ4)- b-D-glucan (bglucan) is believed to be the barley component most responsible for this hypocholesterolemic
activity (Bhatty, et. al., 1993). Using barley for bulguration is, therefore, be a way of
increasing the nutritional value of this food (Köksel et. al. 1999).
Three barley cultivars (Hordeum vulgare L.) were processed by Köksel et. al. (1999) for
bulguration by pressure cooking or cooking at atmospheric pressure. The effect of processing
on levels of thiamine, riboflavin, minerals (Fe, Cu, Zn, Mn, Ca, Mg) as well as the phytic acid
and beta-glucan was investigated. Significant decreases (p<0·05) were observed in ash,
riboflavin and thiamine contents during bulguration. Neither the cooking methods nor the
dehulling process had significant influence on the content of Fe, Cu, Zn or Mg. However, the
Mn and Ca content of the finished product were significantly (p<0·05) lower compared with
the corresponding raw barleys. For all cultivars total P and phytate P contents were
significantly (p<0·05) lower compared with the corresponding raw barleys. In contrast, levels
of beta-glucan were significantly higher in processed product vs raw barley. Protein contents
of the samples did not change significantly during bulguration. Bulguration using barley
appeared to retain most of the nutritional value of raw barley, in particular it showed high
levels of soluble dietary fibre.
Bulgurated Triticale
Bulguration of triticale was studied by Singh and Dodda (1979). Bulgurated triticale of
acceptable quality was prepared from two commercially available cultivars of triticale by
boiling 10 min and cooking for 3 min or 10 min at 15 psi and 120°C. Moisture contents of 3241% were needed to achieve a desirable level of gelatinization of starch. They evaluated
protein, amino acids, gross energy, crude fat, thiamine, riboflavin, folic acid, vitamin E,
calcium, iron, copper, phosphorus, manganese, zinc, potassium, sodium and magnesium.
488
Mustafa Bayram
Activation energy can be used to explain the degree of the effect of temperature during
cooking (Eq. 1) on the rates of the changes of the physical and chemical properties of product.
k=A.exp(-Ea/RT)
(1)
where k is rate order (min-1), A is frequency factor (min-1), Ea is activation energy (J), R is gas
constant (8314 J/K) and T is absolute temperature (K).
Instead of activation energy concept many researchers in the food field have used the Q10
approach for temperature acceralation where the Q10 is the increase in rate for a 10oC
temperature increase (Eq. 2), (Labuza, 1984).
ln Q10 = [10*Ea]/[R*T*(T+10)]
(2)
In addition to previous quantities, z-value can be used to explain the influence of
temperature on product properties during cooking using Eqs. (3 and 4). Also, it can be used to
calculate the cook value and control the cooking process (Eq. 5). The z-value is defined as the
necessary temperature rise needed for 10-fold increase in the rate. Differential practical
cooking processes take place at the varying temperatures. Hence, the effect of each process
must be described in a different way.
log k= p+d τ
(3)
z=1/d
(4)
t
C=
∫
10(τ-Tr)/z dt
(5)
0
where p and d are constant, z is the temperature range over which the rate changes 10-fold
(°C), C is cooking value (min), Q10 is the ratio of the rate at one temperature to that at a
temperature 10°C higher, t is time (min), τ is actual process temperature (K) and Tr is
reference temperature (100°C).
The z-value was evaluated using d-value with Eq. (3). Low values of z, or high values of
d indicate that the temperature is very important. The influence of temperature on the rate
constant k (Eq. 3) is also considerable, thus the intensity of a rate is determined mainly by
temperature. On the other hand high values of z or low values of d indicate that temperature is
of secondary importance. For microorganisms, for instance, the z-values are much lower, for
heat resistant enzymes and most vitamins z-values are higher [Harada et. al., 1985). The zvalue is also used to evaluate the cook value for thermal processing of food materials in Eq.
(5).
Ea, Q10 and z-values can be used effectively to predict temperature effect on the physical
properties of the product during the cooking operation. Also, these values can be used to
determine the optimum cooking parameters for bulguration.
During bulguration, the behavior and properties of the raw material kernel should be well
analyzed because of whole kernel form of bulguration product. Therefore, some studies are
available in the literature. For example, in the study of Bayram et. al. (2004a), the effect of
487
Bulgurated-Corn
Bulguration of corn was studied by Elgun et. al. (1990) to determine the effects of the
maturation stage (milk, yellow, or ripe) and cooking form (on the cob or shelled) of Narman
sweet corn on some selected parameters obtained for bulguration. Also, physical and
chemical properties of products were examined. During cooking below 95 oC for
approximately 60 min, there was an increase in the dry matter content and color intensity of
cooking wastewater. As the grain matured, the amount of material diffused into the cooking
wastewater decreased. The yellow stage corn provided the hardest and most vitreous
endosperm texture to the finished product after drying and showed the highest resistance to
grinding, whereas the milky state corn bulgur showed the lowest resistance. On a raw material
basis, the yields of the pilav bulgur (greater than 1.5 mm) and total bulgur (greater than 0.5
mm) increased sharply with grain maturation, especially in the ripe stage. In either total or
yellow color intensity of the bulgur fractions, the yellow stage corn bulgur showed the highest
values with amberlike yellowness and brightness. Increasing particle size from the bulgur
flour (less than 0.5 mm) to the pilav bulgur (less than 1.5 mm) increased the color intensity.
Ash, fiber, and protein contents of the all bulgurs decreased with maturation, but fat content
increased. In general, the finer the corn bulgur fraction is the higher the ash, fiber, protein,
and fat contents. In conclusion, the best stages were yellow corn for bulgur color, appearance,
and functionality; milky corn for nutritional value; and ripe corn for bulgur yield.
PRINCIPLES OF BULGURATION
Bulguration can be discussed in two steps such as cooking and drying. Both are very
critical operations during bulguration.
There is also a range of important chemical reactions, which help to develop flavour and
texture during cooking. The first group contains the enzymatic reactions. There are natural
chemical reactions that affect the food. All foods contain enzymes- there are many different
enzymes that are present in different foods-in nature these enzymes control biochemical
reactions essential for the life of the organism. The second group of reactions is those which
affect sugars and carbohydrates when they are heated. Many disaccharide and oligosaccharide sugars will undergo a process known as hydrolysis when heated with some water
(Barham, 2001).
Cooking time and temperature affect product due to water absorption. The effects of the
processing variables and the modeling of the cooking operation are necessary to
systematically design the cooker and to understand the effects of cooking on the production.
Kinetics deal with the changes in a system, their associated levels, the rate at which the
changes occur and the mode and mechanism by which the changes are affected.
Understanding the behaviour of product during cooking is of practical importance since it
governs the subsequent operations and quality of the final product. Hence, modelling the
changes during cooking has attracted considerable attention. Determination of the cooking
mechanism and the prediction of the changes are also essential to the control of the cooking
operation. (Bayram, Öner, Eren, 2004a).
489
the cooking time and temperature on the dimensions and crease of the wheat kernel was
studied during bulguration. Wheat was cooked at 87, 92 and 97°C for 140 minutes. The
change of the length, two widths, weight, volume and density for the wheat kernel were
determined during the cooking operation. In addition, in order to determine the effect of
cooking time and temperature, rates, activation energy, Q10 and z-values were determined.
Negative percent change values and the rate constant for the length and density of the wheat
kernel were obtained at different cooking temperature (P>0.05). A positive rate constant was
determined for other properties. The crease side width increased gradually at each cooking
temperature between 6.95-68.05%. Cooking time also significantly affected the change of the
crease side (P<0.05). The secondary width was affected significantly (P<0.05) by the cooking
temperature and time, and its value changed between 9.95-69.00%. The big change for the
secondary width was obtained at 97°C. The crease has important guarding property for the
length and secondary width and it also guards the kernel for the secondary width against the
internal force up to 97°C.
The volume of the kernel also increased (27.35-185.20%) during the cooking operation
significantly (P>0.05), and has greater percent change value than the weight (19.25-160.70%)
due to high amount of swelling of the wheat kernel. Therefore, density changed negatively.
Ea, Q10 and z-values were determined for all physical properties of the wheat kernel and
found that cooking temperature significantly affected the change of the c, W and ρ values
(Bayram et. al., 2004a).
Also, the same dimensions were evaluated by Bayram et.al. (2004b). Physicochemical
quantities (activation energy, enthalpy, entropy and Gibbs free energy) as kinetic models were
used to describe the changes of physical attributes of the wheat kernel during cooking. Rate
constant for the length and density of the wheat kernel were obtained as negative in contrast
to positive rate constant values of the widths, weight and volume of the wheat kernel.
Influence of cooking temperature on the physical properties of the wheat kernel was also
detected from kinetic models and it was found that, the rate of the change in the secondary
width, weight and density of wheat kernel were more sensitive to temperature due to their
greater activation energies as 5.95x107, 5.26x107 and 6.11x107 J, respectively. In contrast,
width of the wheat kernel required less amount of energy due to crease side. All of the
changes in physical properties illustrated the non-spontaneous property with their activation
Gibbs free energy values.
A lot of quality parameters (cooking degree, colour, size, shape etc.) are obtained during
this critical operation. During bulguration, the cooking can be controlled with the
amylose/iodine, centre cutting, DSC and light scattering methods to determine the cooking
degree based on starch gelatinization. Excess cooking causes significant deformation on the
intact kernel during the cooking operation. During cooking, the two most important criteria’s
are the protection of the wholeness of the kernel i.e. no deformation, and getting complete
cooking i.e. absence of an opaque white centre (100% gelatinization, the gelatinized
endosperm is essentially translucent but the ungelatinized starch appears in the endosperm as
central white spots). Deformed kernel cannot be used for subsequent bulguration operation
i.e. drying. Therefore, cooking conditions should be well arranged to complete gelatinization
without darkening the product or making it so sticky as to interfere with subsequent drying.
Determination of the gelatinization degree of starch in wheat and triticale during the
cooking operation based on the traditional centre cutting method was also used by Smith et.
al. (1964), and Singh and Dodda (1979). Their evaluation scales for cooking of intact wheat
490
Mustafa Bayram
were given as follow; a product with a white centre count below 5% was considered to be
adequately gelatinized and rated as excellent; a count below 10% as good, below 20% as fair,
and above 20% as poor (unacceptable).
The gelatinization of starch in solid foods occurs with water absorption. Absorbed water
migration in solid foods has been widely analysed using the concept that water migration is
driven by the water content gradient. This principle was also applied in the case of cooking
starchy food (Suzuki, Aki, Kubota, and Hosaka, 1977; Bakshi and Singh, 1980; Watanabe,
Fukuoka, Tomiya, and Mihori, 2001).
For the automation of the cooking operation for bulguration, the diffusion of high
intensity light through the kernel (especially for durum wheat) can also be used to determine
the gelatinization degree based on translucent and opaque parts of the intact kernel. Light will
pass through the translucent part easily and colour differences can differentiate the gelatinized
part in the centre of the kernel (Bayram, 2004).
BULGURATION OPERATION
The cooking operation can be made in hot water under high or atmospheric pressures.
However, the soaking operation before the cooking operation can be used to control moisture
content of finished product. If pressure is obtained directly with live-steam, soaking should be
made to reach the moisture to 40-50%. In general, during soaking, temperature is raised to 5080 oC and moisture content is increased to 40-50 %.
Figure 1. Open-to-atmosphere cooker.
Figure 2. Screen-atmospheric cooker.
Figure 3. Direct steam inject continuous pressure cooker.
491
492
Mustafa Bayram
Figure 4. Pressure-drum cooker.
Cooking can be made using open-to-atmosphere cooker (Figure 1), screen-atmospheric
cooker (Figure 2), steam jacketed screw cooker, direct steam inject continuous pressure
cooker (Figure 3), belt in water type cooker, screw-silo combination systems and pressuredrum (Figure 4) cookers. During the cooking operation, first step is gelation of starch and/or
protein in product. In the cooking systems, temperature, time, water absorption and gelation
of starch/protein should be controlled. In the pressure cooker, it remains enough time (5-20
minutes) under 1-3 atms of pressure. This procedure insures complete cooking without
discoloration. After cooking, vacuum or cooling can be applied to evaporate surface water
and also to prevent stickiness of products.
For drying during bulguration which depends on raw material, fluidized bed dryer,
radiofrequency, tower (Figure 5), mixing type dryer can be used. The purpose is the removal
of 40-50% of initial moisture of cooked product. Drying must be gradual at comparatively
low temperature and preferably with continuous movement or frequent turning/moving
product. Drying is made with tower dryer for 6-8 hours by using hot air between 70-140 oC
until moisture of wheat decreases under 13 %.
Of all food preservation methods, that of drying foods has received the most widespread
and enthusiastic publicity in recent years. Actually, drying is one of the oldest methods of
food preservation. Techniques have been passed from one generation to another based on
what worked and what didn't. Methods used for drying food have become sophisticated over
time.
The benefit of drying during bulguration is to remove moisture from cooked product to
prevent growing molds, yeast and bacteria. When foods are sufficiently dehydrated (dried),
microorganisms cannot grow and foods will not spoil. Therefore, its shelf-life increases. By
the way, bulguration supplies high resistant semi-ready to eat food product using different
raw materials.
493
Figure 5. View from tower-type dryer.
Of all food preservation methods, that of drying foods has received the most widespread
and enthusiastic publicity in recent years. Actually, drying is one of the oldest methods of
food preservation. Techniques have been passed from one generation to another based on
what worked and what didn't. Methods used for drying food have become sophisticated over
time.
The benefit of drying during bulguration is to remove moisture from cooked product to
prevent growing molds, yeast and bacteria. When foods are sufficiently dehydrated (dried),
microorganisms cannot grow and foods will not spoil. Therefore, its shelf-life increases. By
the way, bulguration supplies high resistant semi-ready to eat food product using different
raw materials.
REFERENCES
[1]
[2]
[3]
Bakshi, A. S. and Singh, R. P. (1980). Kinetics of water diffusion and starch
gelatinization during rice parboiling. Journal of Food Science, 45, 1387-1392.
Barham, P. (2001). The science of cooking (pp. 32-33). Berlin, Germany, Springer
Verlag.
Bayram, M. (2000). Bulgur around the world. Cereal Foods World, 45, 80-82.
494
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
Mustafa Bayram
Bayram, M. (2005). Modelling of cooking of wheat to produce bulgur. Journal of Food
Bayram, M. (2005). Bulgur: The product of ancient world and mystery. In M. Bayram,
A. Avcı and O. Arslan, (Eds.), Bulgur (pp:22-23). Gaziantep, Türkiye, University of
Gaziantep and Bulgur Industrialists Association Press.
Bayram, M. (2006). Determination of the cooking degree for bulgur production using
amylose/iodine, centre cutting and light scattering methods. Food Control, 17, 331-335.
Bayram, M. (2007). Application of bulgur technology to food aid program. Cereal
Foods World, (inpress).
Bayram, M. and Öner, M. D. (2002) Bulgur: The new old wheat. World Grain,
November, 51-53.
Bayram, M. and Öner, M.D. (2005). Stone, disc and hammer milling of bulgur. Journal
of Cereal Science, 41, 291-296.
Bayram, M., Öner, M.D. and Eren, S. (2004a). Effect of the cooking time and
temperature on the dimensions and crease of the wheat kernel during the bulgur
production. Journal of Food Engineering, 64, 43-51.
Bayram, M., Öner, M.D. and Eren, S. (2004b). Thermodynamics of the dimensional
changes in the wheat kernel during cooking for bulgur production. Food Science and
Technology International, 10, 243-253.
Bayram, M., Kaya, A. and Öner, M. D. (2004c). Changes in properties of soaking water
during production of soy-bulgur. Journal of Food Engineering, 61, 221-230.
Bayram, M., Öner, M.D. and Kaya, A. (2004d). Influence of soaking on the dimensions
and colour of soybean for bulgur production. Journal of Food Engineering, 61, 331339, 2004.
Bayram, M., Kaya, A. and Öner, M. D. (2004e). Water absorption, leaching and color
changes during the soaking for production of soy-bulgur. Journal of Food Process
Bhatty, R.S. (1933). Nonmalting uses of barley. In A.W. MacGregor and R.S. Bhatty,
(Eds.), Barley: Chemistry and Technology (pp. 355-417), St. Paul, MN, AACC.
Bhatty, R.S. (1986). The potential of hull-less barley-a review. Cereal Chemistry, 63,
97-103.
Calhoun, W. K., Hepburn, F. N. and Bradley, W. B. (1960). The distribution of the
vitamins of wheat in commercial mill products. Cereal Chemistry, 37, 755 - 761.
Elgun, A., Ertugay, Z. and Certel, M. (1990). Corn Bulgur: Effects of corn maturation
stage and cooking form on bulgur-making parameters and physical and chemical
properties of bulgur products. Cereal Chemistry, 67, 1-6.
Harada, T., Tirtohusodo, H. and Paulus, K. (1985) Influence of temperature and time on
cooking kinetics of potatoes. Journal of Food Science, 50, 459-462, 472.
Jenkins, D.J.A., Wolever, T.M.S., Leeds, A.R., Gassull, M.A., Haisman, P., Dilawari,
J., Goff, D.V., Metz, G.L. and Alberti, K.G.M.M. (1978). Dietary fibres, fibre
analogues, and glucose tolerance: importance of viscosity. British Medical Journal, 1,
1392–1394.
Kent, N.L. (1975). Technology of cereals with special reference to wheat, (2nd edition,
pp 226–240), New York, USA, Pergamon Press.
Klopfenstein, C.F. and Hoseney, R.C. (1987). Cholesterol low-conering effect of betaglucan enriched bread. Nutrition Reports International, 36, 1091–1097.
495
[23] Köksel, H, Edney, M. J. and Özkaya, B. (1999). Barley bulgur: Effect of processing and
cooking on chemical composition. Journal of Cereal Science 29, 185–190.
[24] Labuza, T. P. (1984). Application of chemical kinetics to deterioration of foods.
Journal of Chem. Education, 61, 348-357.
[25] Lasztity, R. and Lasztity, L. (1990). Phytic acid in cereal technology. In Y. Pomeranz
(Ed.), Advances in Cereal Science and Technology, (Volume 10, pp. 309-371), St. Paul,
MN, AACC.
[26] McIntosh, G.H., Jorgensen, L. and Royle, P. (1993). The potential of insoluble dietary
fiber from barley to protect from DMH-induced intestinal tumours in rats. Nutritional
Cancer, 19, 213–221.
[27] McIntosh, G.H., Whyte, J.,McArthur, R. and Nestel, P.J. (1991). Barley and wheat
foods. Influence on plasma cholesterol concentrations in hypercholesterolemic men.
American Journal of Clinical Nutrition, 53, 1205–1209.
[28] McKevith, B. (2002). Folate and folic acid. British Nutrition Foundation Nutritional
Bulletin. 1-16.
[29] McKevith, B. (2004). Nutritional aspects of cereals. British Nutrition Foundation
Nutritional Bulletin, 29, 111-142.
[30] Munck, L. (1981). Barley for food, feed and industry. In Y. Pomeranz and L. Munck
(Eds.), Cereals: A renewable resource, theory and practice (pp. 427–459), AACC, St.
Paul, MN.
[31] Newman, R.K. and Newman, C.W. (1991). Barley as a food grain. Cereal Foods
World, 36, 800-805.
[32] Newman, R.K., Lewis, S.E., Newman, C.W., Boik, R.J. and Ramage, R.T. (1989).
Hypochoesterolemic effect of barley foods on healthy men. Nutritional Reports
[33] Özkaya, H., Özkaya, B., Bayrak, H. and Gökpınar, F. Bulgurun fitik asit içeriğine
prosesin etkisi. Geleneksel Gıdalar Sempozyumu, Van Yüzünyıl Üniversitesi, VanTürkiye, 23-24.Eylül.2004.
[34] Pence, J.W., Ferrel, R.E. and Robertson, J.A. (1964). Effects of processing on Bvitamin and mineral contents of bulgur. Food Technology, May, 171-174.
[35] Shepherd, A. D., Ferrel, R.E., Bellard N. and Pence J. W. (1965). Nutrient composition
of bulgur and lye peeled bulgur. Cereal Science Today, December, 590-592.
[36] Singh, B. and Dodda, M. (1979). Studies on the preparation and nutrient composition of
bulgur from triticale. Journal of Food Science, 44, 449–452.
[37] Smith, G.S., Barta, E.J. and Lazar, M.E. (1964). Bulgur production by continuous
atmospheric pressure process. Food Technology, 18, 89-92.
[38] Suzuki, K., Aki, M., Kubota, K., and Hosaka, H. (1977). Studies on the cooking rate
equations of rice. Journal of Food Science, 42, 1545-1548.
[39] Watanabe, H., Fukuoka, M., Tomiya, A., and Mihori, T. (2001). A new non-Fickian
diffusion model for water migration in starchy food during cooking. Journal of Food
Chapter 11
WATER SORPTION ON FOODSTUFFS ALTERNATIVE MODELS
Sylwester Furmaniak1, Artur P. Terzyk*1,
Leszek Czepirski2, Ewa Komorowska-Czepirska2,
Joanna Szymońska3 and Piotr A. Gauden1
1
N. Copernicus University, Department of Chemistry,
Physicochemistry of Carbon Materials Research Group,
Gagarin St. 7, 87-100 Toruń, Poland
2
AGH – University of Science and Technology,
Faculty of Fuels and Energy, al. Mickiewicza 30,
30-059 Cracow, Poland
3
Agriculture University, Department of Chemistry,
al. Mickiewicza 24/28, 30-059 Cracow, Poland
ABSTRACT
It is well known that sorption isotherms of foodstuffs are very important for design,
modeling and optimization of important processes for example drying, aeration,
predicting of stability and quality during packaging and storage of food. Many literature
reviews conclude that the BET (and its modifications) and the GAB sorption isotherm
equations are the most popular and applicable for description of isotherms of foodstuffs.
We showed recently the applicability of the GDW model for description of water
sorption on different foodstuffs. Moreover, it was also shown that the GAB model (also
widely applied in food science) is the special case of the GDW equation. In this review
we present the current state of art and also an attempt of application of different models
of water sorption, namely CMMS, DD and modified CDS for description of water
sorption data on different starch samples and other foodstuffs.
*
Corresponding author: Artur P. Terzyk; e-mail:[email protected] URL:http://chem.uni.torun.pl/_aterzyk/
498
Sylwester Furmaniak, Artur P. Terzyk, Leszek Czepirski et al.
1. INTRODUCTION
It is well known that sorption isotherms of foodstuffs are very important for design,
modeling and optimization of important processes for example drying, aeration, predicting of
stability and quality during packaging and storage of food [1-3]. Many literature reviews
conclude that the BET (and its modifications) and the GAB sorption isotherm equations are
the most popular and applicable for description of isotherms of foodstuffs [1,4-6]. It was
shown recently the applicability of the GDW model for description of water sorption on
different foodstuffs (pineapple, macaroni, sardine, pistachio nut paste, chickpea seeds, lentil
seeds, potato and on green peppers) [7,8]. Moreover, it was also shown that the GAB model
(also widely applied in food science) is the special case of the GDW equation [8]. Obtained
results explained the total failure of the BET model in description of multitemperature data
and the similarities between the GAB and GDW. Finally the general mechanism of water
sorption on foodstuffs was also proposed [8]. This mechanism can be of the GAB or GDW
type, depending on the arrangement and features of the primary water sorption sites. If the
geometrical constraints for creation of the BET – like type clusters do not occur on surface,
and if each from primarily sorbed water molecules convert only into one secondary sorption
site, one can say that the mechanism follows the GAB scenario. Contrary, in the case of rough
or porous surfaces, where there are the geometric constraints for creation of secondary sites,
and/or where one primary site produces more than one secondary site, the mechanism of
water sorption is of the GDW type.
All models discussed above originate from adsorption science, therefore it is interesting
to check the validity of different (i.e. alternative) approaches to describe water sorption data
on foodstuffs. In this review we also present the current state of art and an attempt of
application of GAB, GDW, CMMS, simplified DD and modified CDS models for description
of water sorption data on different starch granules and other foodstuffs.
2. MODELS
First studied model is the Generalized D’Arcy and Watt (GDW) one proposed previously
for description of adsorption of water on carbonaceous adsorbents [9], and next applied
successfully for description of water sorption on many foodstuffs [7,8]. It was applied in the
form:
Me =
mKhr 1 − k (1 − w ) hr
⋅
1 + Khr
1 − khr
(1)
where Me is the moisture equilibrium content, hr – relative humidity, m – the maximum
adsorption value on the primary sorption centers. K and k are the kinetic constants related to
sorption on primary and secondary centres, and w is the parameter determining what part of
water molecules sorbed on primary sorption sites convert into the secondary sorption sites.
Water Sorption on Foodstuffs - Alternative Models…
499
Next studied model is proposed in 2000 (to description of adsorption of alcohols on
polymers) by Malakhov and Volkov [10] and widely propagated by Rutherford et al. (to
description of water sorption on different adsorbents) [11-13] and others [14,15]. This new
equation of cooperative the multimolecular sorption (called the CMMS) assumes that the
sorption process follows the scenario of cooperative filling of channels (interrelated
nanovoids) of the sorbent, and this process is combined with the growth of associates of
sorbed molecules within the sorbent bulk. The final sorption equation, which can be reduced
to the Henry’s, Langmuir, Ising and/or BET models, can be written as:
Me =
mK0 hr
(2)
( 1 − K as hr ) ( K0 hr + ω 2 ( 1 − K as hr ) )
where:
2
⎛
⎛
4K0 hr
K1 hr
K1 hr ⎞
1⎜
+ ⎜1 −
+
ω = 1−
⎟
2⎜
1 − K as hr
1 − K as hr ⎠ 1 − K as hr
⎝
⎝
⎞
⎟
⎟
⎠
(3)
and m is the maximum sorption on primary sites, K0 is the equilibrium constant for sorption
of the central unit on the primary sites, K1 – the equilibrium constant for sorption of the side
unit on the primary side, Kas – the equilibrium constant for sorption of the site associate.
As the reference model we used the GAB one [1,4-6]. This model, widely accepted as
valid and the most popular in the field of food engineering, is applied in the form:
Me =
mCKhr
(1 − Khr )(1 − Khr + CKhr )
(4)
where m is the monolayer capacity, C is the kinetic constant related to the sorption in the first
layer, K is the kinetic constant related to multilayer sorption.
Finally, since the mentioned above concepts are more or less applicable to description of
water sorp

Focus on Food Engineering Research and Developments

Transcription

Similar documents

March 18

Introducing - Auburn DECA

Drinks Menu

It IS the gift that counts

STATUS OF DRAGON FRUIT PRODUCTION IN MALAYSIA

- Cantigny

whirlpool® hybridcaretm dryer

Bon Appetit Catering Guide - Bon Appetit at Willamette University

Wine List - La Pentola Hermanus

catering menu - Lucky Eagle Casino

The Effect of Lactobacillus acidophilus on the health of human skin