Document 6591849

CSE 246
Data Structures and Algorithms
Graphs
Graph data structure
 Graph is an ADT.
 A graph is a set of vertices and edges
𝐺 = {𝑉, 𝐸}
𝑉={v1,v2,v3,…,vn},
𝐸={e1,e2,e3,…,en}
 An Edge connects exactly two vertices.
 A vertex can have any number of edges connected to it.
2
Quratulain
Graphs
 Edge might be directed or undirected.
 Weighted graphs. Additional information on edges.
3
Quratulain
Terms to remember
 graph
 path
 vertex (pl vertices)‫‏‬
 cycle
 edge
 Hamiltonian
 edge cost
 Eulerian
 undirected graph
 planar graph
 directed graph
 acyclic directed graph
 simple graph
 forest
 loop
 tree
Graph Applications
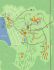
 Modelling a road network with vertexes as towns and edge costs as




distances.
Modelling a water supply network. A cost might relate to current
or a function of capacity and length. As water flows in only 1 direction,
from higher to lower pressure connections or downhill, such a network
is inherently an acyclic directed graph.
Internet traffic modelling. Dynamically modelling the status of a
set of routes by which traffic might be directed over the Internet.
Flight scheduling. Minimising the cost and time taken for air travel
when direct flights don't exist between starting and ending airports.
Using a directed graph to map the links between pages within a
website and to analyse ease of navigation between different parts of the
site.
Graph Applications
 The Seven Bridges of Königsberg is a problem inspired by an
actual place and situation.
 The question is whether it is possible to walk with a route
that crosses each bridge exactly once, and return to the
starting point. In 1736, Leonhard Euler proved that it was
not possible."
Source: http://en.wikipedia.org/wiki/Seven_Bridges_of_Koenigsberg
6
Quratulain
Three cottage problem
Source: http://en.wikipedia.org/wiki/Three_cottage_problem
"The three cottage problem is a well-known mathematical
puzzle. It can be stated like this:
Suppose there are three cottages on a plane (or sphere) and
each needs to be connected to the gas, water, and electric
companies. Is there a way to do so without any of the lines
crossing each other?"
Three cottage problem
"The three cottage problem is a well-known mathematical
puzzle. It can be stated like this:
Suppose there are three cottages on a plane (or sphere) and
each needs to be connected to the gas, water, and electric
companies. Is there a way to do so without any of the lines
crossing each other?"
 Source: http://en.wikipedia.org/wiki/Three_cottage_problem
8
Quratulain
Data structure to store Graphs
 To select data structure for graph:
 First programmer need to understand the application data.
 Then construct a graph.
 The choice and design of data structure(s) will influence and be
influenced by program performance and memory usage
requirements.
9
Quratulain
Data structures to store graph
 Adjacency list
 Adjacency matrix.
 Incident list
Source:
http://interactivepython.org/courselib/static/pythonds/Graphs/graphintro.html
10
Quratulain
Adjacency matrix
 implement a graph is to use a two-dimensional matrix.
11
Quratulain
Adjacency list
 A more space-efficient way to implement a sparsely
connected graph is to use an adjacency list
12
Quratulain
Graph search algorithms
 Breadth first search
 Depth first search
13
Quratulain
Depth first search
 The depth-first search uses a stack to remember where it
should go when it reaches a dead end.
14
Quratulain
Depth first search Example
 Knight’s tour graph
15
Quratulain
Breadth first search
 the algorithm likes to stay as close as possible to the starting
point. It visits all the vertices adjacent to the starting vertex,
and only then goes further. This kind of search is
implemented using a queue
16
Quratulain
Breadth first search Example
 Word ladder graph
17
Quratulain
Graph Analysis
18
Quratulain