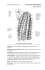Math 180B (P. Fitzsimmons) Final Exam Solutions Each problem is

Math 180B
(P. Fitzsimmons)
Final Exam
Solutions
Each problem is worth 10 points.
1. The non-negative random variables X and Y have joint density function f given by the formula
xe−x(1+y) , x > 0, y > 0
f (x, y) =
0,
otherwise.
(a) Find the marginal density fX (x).
(b) Find E[X].
(c) Find the conditional density fY |X (y|x) of Y , given that X = x.
Solution. (a) Integrate: For x > 0,
Z
∞
Z
∞
fX (x) =
f (x, y) dy =
∞
Z ∞
−x
=e
xe−xy dy
xe−x(1+y) dy
0
0
=e
−x
.
(If x ≤ 0 then fX (x) = 0.) The fourth equality follows because y 7→ xe−xy is the exponential
density with parameter x.
(b) From (a) we know that X has the exponential distribution with parameter 1. Therefore,
E[X] = 1/1 = 1. Or, referring to the definition (and integrating by parts)
Z
E[X] =
0
∞
∞
xe−x dx = −xe−x − e−x = 1.
0
(c) For x > 0 and y > 0,
fY |X (y|x) = f (x, y)/fX (x) =
xe−x(1+y)
= xe−xy .
e−x
That is, the conditional distribution of Y , given that X = x, is exponential with parameter x.
2. (a) The random variables X and Y have a bivariate normal distribution with E[Y ] = 0,
Var(X) = Var(Y ) = 1. In addition, you know that E[X|Y = y] = 2 − .3y for all y.
(a.1) Find E[X].
(a.2) Find Cov(X, Y ).
(b) [CORRECTED STATEMENT] The random variables Z and W have a bivariate normal distribution with E[Z] = E[W ] = 0, Var(Z) = Var(W ) = 1, and correlation ρ ∈ (−1, 1). Given
that P[Z + W ≤ 1] = .8413, find the value of ρ. [Hint: .8413 = Φ(1), where Φ is the standard
normal distribution function.]
Solution. (a.1) By the Law of the Forgetful Statistician,
E[X] = E [E[X|Y ]] = E[2 − .3Y ] = 2 − .3E[Y ] = 2.
1
(a.2) (Method 1) Using the LotFS again, and the assumption that E[Y ] = 0,
Cov(X, Y ) = E[XY ] = E [E[X|Y ]Y ] = E[(2 − .3Y )Y ]
= E[2Y − .3Y 2 ] = 2E[Y ] − .3E[Y 2 ] = −.3.
(Method 2) We know that when X and Y have a bivariate normal distribution, then
E[X|Y = y] = µX +
σX
ρ · (y − µY ),
σY
∀y,
which under the present assumptions (and the result of part (a.1)) reduces to
E[X|Y = y] = 2 − ρ · y,
∀y.
On the other hand, we are told that E[X|Y = y] = 2 − .3y for all y. It follows that Corr(X, Y ) =
ρ = −.3. Because X and Y both have variance equal to 1, their covariance coincides with their
correlation. That is, Cov(X, Y ) = −.3.
(b)
3. A Markov chain {Xn : n = 0, 1, 2, . . .} has state space {0, 1, 2} and transition matrix


.7 .2 .1
P =  0 .6 .4  .
.5 0 .5
(a) Fine P[X2 = 1|X0 = 2].
(b) Find P[X17 = 1, X18 = 2|X15 = 2].
Solution. As a start,

.54 .26
2

P = P · P = .20 .36
.60 .10

.20
.44  .
.30
(2)
(a) P[X2 = 1|X0 = 2] = P2,1 = (P2 )2,1 = .10.
(2)
(b) By the Markov property, P[X17 = 1, X18 = 2|X15 = 2] = P2,1 · P1,2 = .10 · .4 = .04.
4. Consider a Markov chain {Xn : n = 0, 1, 2, . . .} with state space {0, 1, 2} and transition matrix


0 1/2 1/2
P= 0
0
1 .
1/3 2/3 0
(a) Explain why P is regular.
(b) Find the “stationary distribution” for P; that is, the row vector π = [π0 , π1 , π2 ] such that
πP = π and π0 + π1 + π2 = 1.
(c) Suppose that P[X0 = 0] = .2, P[X0 = 1] = .3, and P[X0 = 2] = .5. Find limn→∞ P[Xn = 1].
Solution. (a) By examining the “transition graph” of this Markov chain, it becomes clear that it
is irreducible (any two states communicate) and that
(3)
(2)
P0,0 > 0 and P0,0 > 0.
2
Because the greatest common divisor of 2 and 3 is 1, state 0 has period 1. By irreducibility,
the chain is aperiodic. As we know, is a Markov chain on a finite state space is aperiodic and
irreducible, then it is regular.
(b) The equation π = πP amounts to the system
π0 = (1/3)π2
π1 = (1/2)π0 + (2/3)π2
π2 = (1/2)π0 + π1 .
Solving the first equation for π2 and then substituting into the second equation leads to
(1/2)π0 + 2π0 = π1 ,
which simplifies to
π1 = (5/2)π0 .
Thus π has the form
π = [ π0
(5/2)π0
3π0 ] .
If the entries of π are to sum to 1 we must have π0 = 2/13. Consequently
π = [ 2/13
5/13
6/13 ] .
(n)
(c) Because this Markov chain is regular, we know that for each i, limn→∞ Pi,1 = π1 = 5/13.
Therefore,
2
2
X
X
5
5
(n)
lim P[Xn = 1] =
P[X0 = i] · Pi,1 =
P[X0 = i] ·
=
.
n→∞
13
13
i=0
i=0
(The specific values of P[X0 = i] are a red herring—they don’t matter at all.)
5. A Markov chain X = {Xn : n = 0, 1, 2, . . .} with state space {0, 1, 2} has transition matrix


1/2 1/2 0
P =  0 1/3 2/3  .
0 2/3 1/3
(n)
(a) Explain why P0,0 = 2−n for n = 1, 2, . . ..
(b) Is state 0 transient or recurrent? (Explain.)
(c) The subset {1, 2} forms a communicating class for the Markov chain X. The transition matrix
˜ obtained by deleting row 0 and
for X restricted to this class is the 2 × 2 matrix (call it P)
˜ is doubly stochastic. Use these observations to find
column 0 from P. Observe that P
(n)
lim Pi,j
n→∞
for i = 0, 1, 2 and j = 1, 2. (You can do this in your head—no pen or pencil needed!)
Solution. (a) This Markov chain stays for a while in state 0 (if started there) and then moves to
state 1; because P1,0 = P2,0 = 0 the chain never thereafter returns to state 0. Thus, there is just
one way to start in state 0 and then be in state 0 at time n ≥ 1:
(n)
P0,0 = P[X1 = 0, X2 = 0, . . . , Xn = 0|X0 = 0] = P0,0 · P0,0 · · · P0,0 = (1/2)n .
3
P∞
P∞
(n)
(b) By part (a), n=1 P0,0 = n=1 2−n = 1 < ∞. Therefore state 0 is transient.
e has only strictly
(c) The 2 × 2 sub matrix of P corresponding to states 1 and 2, call it P,
positive entries (and is therefore regular), and is evidently doubly stochastic. It therefore has the
uniform distribution on {1, 2} as its unique stationary distribution. In short, the Markov chain
restricted to starting points in {1, 2} is recurrent, and
(†)
(n)
lim Pi,j =
n→∞
1
2
for i = 1, 2 and j = 1, 2. If i = 0 then by part (a) the chain eventually reaches state 1 and from
then on moves in {1, 2}, and (†) applies to yield
(n)
lim P0,j =
n→∞
1
2
as well.
6. A bug walks randomly on the graph below. At each step the bug moves to an adjacent node,
choosing from the available destinations with equal probability. Assuming that the bug starts in
state 0, what is the probability that it gets to state 2 before state 4?
Solution. Define vi = P[reach 2 before 4|X0 = i]. Clearly v2 = 1 and v4 = 0. By first-step analysis:
v0 = (1/2)v1
v1 = (1/3)v0 + (1/3)v1 + (1/3)
v3 = (1/3)v1 + (1/3).
Let’s clear out the fractions first:
2v0 = v1
3v1 = v0 + v1 + 1
3v3 = v1 + 1.
Using the first equation, eliminate v1 from the second to obtain
(6.1)
5v0 = v3 + 1
Do the same with the third equation to obtain
(6.2)
3v3 = 2v0 + 1.
This 2 × 2 system is readily solved: Multiply (6.1) by 3, add this to (6.2) and then cancel the 3v3
from both sides to get 15v0 = 2v0 + 4. Therefore v0 = 4/13.
4
7. Customers arrive at a store in accordance with a Poisson process {X(t) : t ≥ 0} of rate 3 per
hour. The successive arrival times of the customers are labelled W1 , W2 , . . . as usual. (Convention:
W0 = 0.) Suppose that customer number N is the first customer to arrive after time 2. The
number N is random and is the unique positive integer such that WN −1 ≤ 2 < WN .
(a) Show that {WN > 2 + s} = {X(2 + s) − X(2) = 0}.
(b) Find P[WN > 2 + s] for s > 0.
(c) From part (b) we see that WN − 2 has a familiar distribution. Use this to find E[WN ].
Solution. (a) WN > 2 + s means that the first customer to arrive after time 2 actually arrives after
time 2 + s. This is the case if and only if no one arrives during the time interval (2, 2 + s], which
is the same as saying that X(2) = X(2 + s).
(b) In view of (a),
P[WN > 2 + s] = P[X(2 + s) − X(2) = 0] = e−3s ,
because the increment X(2 + s) − X(2) has the Poisson distribution with parameter 3s.
(c) By part (b), the random variable WN − 2 has the exponential distribution with parameter
3. Therefore E[WN − 2] = 31 . Finally, E[WN ] = 2 + 13 = 7/3.
8. Let {X(t) : t ≥ 0} be a Poisson process of rate λ > 0, and let 0 < s < t be two times. Compute
the following:
(a) P[X(s) = 2, X(t) = 5].
(b) E[X(t)|X(s) = 2].
(c) Corr(X(s), X(t)).
Solution. (a) Because X(s) and X(t) − X(s) are independent:
P[X(s) = 2, X(t) = 5] = P[X(s) = 2, X(t) − X(s) = 3] = P[X(s) = 2] · P[X(t) − X(s) = 3]
= e−λs
(λs)2 −λ(t−s) (λ(t − s))3
λ5 s2 (t − s)3
·e
= e−λt
.
2!
3!
12
(b) Observe that X(t) = X(s) + [X(t) − X(s)]. Therefore
E[X(t)|X(s) = 2] = E[X(s) + [X(t) − X(s)]|X(s) = 2] = 2 + E[X(t) − X(s)|X(2) = 2].
But X(s) and X(t)−X(s) are independent, so E[X(t)−X(s)|X(2) = 2] = E[X(t)−X(s)] = λ(t−s).
Therefore E[X(t)|X(s) = 2] = 2 + λ(t − s).
(c) As in part (b), the random variable X(s) and X(t) − X(s) are independent, hence their
covariance is 0. Therefore
Cov(X(s), X(t)) = Cov(X(s), X(t) − X(s)) + Cov(X(s), X(s)) = 0 + Var(X(s)) = λs.
In addition, Var(X(t)0 = λt, so
Cov(X(s), X(t))
λs
Corr(X(s), X(t)) = p
=√
=
λs · λt
Var(X(s)) Var(X(t))
5
r
s
.
t
9. Let {X(t) : t ≥ 0} and {Y (t) : t ≥ 0} be independent Poisson processes with respective
parameters λ and µ. Let T = min{t ≥ 0 : Y (t) = 1} be the random time of the first event in the
Y process. Determine P[X(T ) = k] for k = 0, 1, 2, . . ..
Solution. (Method 1) The random variable T has the exponential distribution with parameter µ
and is independent of the X process. Therefore, by the Law of Total Probability,
Z
∞
P[X(t) = k]µe−µt dt
P[X(t) = k] =
0
=
=
=
=
=
∞
(λt)k −µt
e−λt
e
dt
k!
0
Z
µ · λk ∞ −(µ+λ)t k
e
t dt
k!
0
Z ∞
µ · λk
e−u uk du
(µ + λ)k+1 k! 0
µ · λk
· k!
(µ + λ)k+1 k!
k
µ
λ
.
µ+λ µ+λ
Z
The fourth equality results from the change of variables u = (µ + λ)t.)
(Method 2) Let us create the X and Y processes by starting with a Poisson process {Z(t) :
t ≥ 0} with rate µ + λ, and then coloring the points of Z at random, independently of each
other, either red (with probability p = λ/(µ + λ)) or green (with probability q = µ/(µ + λ)); the
(Poisson) process of red points is then {X(t) : t ≥ 0} and the green points {Y (t) : t ≥ 0}. In
terms of this coloring, the event {X(T ) = k} is just the event that the first k arrivals (in the
Z process) are painted red and the (k + 1)st is painted green. The probability of this is clearly
pk q = (λ/(µ + λ))k (µ/(µ + λ)), as before.
10. Let W1 , W2 , . . . be the arrival times of a Poisson process {X(t) : t ≥ 0}, of rate 2. Find
E[W1 W2 · · · WX(t) ]. [The empty product, which occurs if X(t) = 0, is understood to equal 1.]
Solution. We use the Law of Total Probability and the uniform distribution law for the arrival
6
times of a Poisson process, conditional on the number of arrivals:
E[W1 W2 · · · WX(t) ] =
=
=
=
=
=
∞
X
n=0
∞
X
n=0
∞
X
n=0
∞
X
n=0
∞
X
n=0
∞
X
n=0
P[X(t) = n]E[W1 W2 · · · Wn |X(t) = n]
P[X(t) = n]E[U(1) U(2) · · · U(n) ]
P[X(t) = n]E[U1 U2 · · · Un ]
P[X(t) = n](t/2)n
e−2t
(2t)n
(t/2)n
n!
e−2t
(t2 )n
n!
2
= e−2t · et = e−t(2−t) .
7