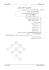עצים בינארים

‫עיצוב תכנה‬
‫‪1‬‬
‫עצים בינאריים‬
‫עצים בינאריים ‪BinTreeNode -‬‬
‫עץ ‪-‬‬
‫מבנה נתונים (גרף) המורכב מצמתים המקיימים ביניהם יחס של הורה ובנים ‪ /‬צאצאים‪.‬‬
‫צומת ‪ -‬חוליה ולה תכונות‪ - info :‬הפניה לטיפוס המידע‪ ,‬והפניות לצמתים אחרים‪.‬‬
‫קשת ‪ -‬הפניה היוצאת מצומת אב לצומת בן‪.‬‬
‫כל עץ מורכב מצומת שורש )‪ (root‬שהוא הצומת הראשון בעץ‪.‬‬
‫לכל צומת פרט לשורש יש הורה ‪ /‬אב )‪.(perent‬‬
‫כל צומת יכול להיות הורה לצמתים רבים אחרים‪,‬‬
‫וכל הצמתים הללו הם בניו של ההורה‪.‬‬
‫כל הצמתים שהם בניו של אותו הורה הם צמתים אחים‪.‬‬
‫כל צומת בעץ הוא צאצא )‪ (descendent‬של כל הצמתים שמעליו‪.‬‬
‫כל צומת הוא אב קדמון של כל צאצאיו‪.‬‬
‫מספר בניו של הצומת קובעים את דרגתו ‪ -‬דרגת צומת )‪.(degree‬‬
‫לצומת שלו ‪ 3‬בנים נקבעת דרגה ‪ 3‬ואילו לצומת שאין לו בנים כלל נקבעת דרגה ‪.0‬‬
‫צומת שדרגתו ‪ 0‬קרוי עלה )‪.(leaf‬‬
‫עץ בינארי )‪ - (BinTreeNode‬עץ שבו הדרגה המקסימאלית של כל אחד מצמתיו הוא ‪ .2‬כלומר ‪ -‬לכל צומת‬
‫יש שתי הפניות ‪ left‬ו‪ right -‬לשני בנים‬
‫מסלול ‪ -‬רצף של צמתים‪/‬קשתות היוצאות מצומת אחת עד צומת שני‪.‬‬
‫רמת עץ )‪ ,(tree level‬זוהי השכבה בה מצוי הצומת הרחוק ביותר מהשורש‪ .‬השורש בעץ מסומן כרמה ‪ ,0‬בניו של‬
‫השורש נמצאים ברמה מספר ‪ ,1‬בני בניו ברמה ‪ 2‬וכך הלאה‪.‬‬
‫רמה של צומת הינה מספר הקשתות שיש לעבור כדי להגיע משורש העץ עד הצומת המבוקש‪.‬‬
‫גובה עץ או עומק העץ הוא מספרה של הרמה הגבוהה ביותר בעץ‪.‬‬
‫מספר הקשתות לאורכו של המסלול הארוך ביותר היוצא מן השורש ומסתיים בעלה‪.‬‬
‫תת‪-‬עץ‪-‬שמאלי ‪ -‬עץ בינארי ששורשו הוא הבן השמאלי של צומת נתון‪.‬‬
‫תת‪-‬עץ‪-‬ימני ‪ -‬עץ בינארי ששורשו הוא הבן הימני של צומת נתון‪.‬‬
‫בן הוא תמיד שורש של תת‪-‬עץ )‪.(sub-tree‬‬
‫רמה מלאה ‪ -‬רמה בעץ שקיימים בה כל הצמתים‪.‬‬
‫עץ בינארי מלא (עץ שלם) ‪ -‬עץ שכל רמה בו היא רמה‪-‬מלאה‪.‬‬
‫עץ בינארי לחלוטין ‪ -‬עץ שדרגת כל צומת בו היא ‪ 0‬או ‪2‬‬
‫(כלומר ‪ -‬אין צומת שלו בן יחיד)‪.‬‬
‫‪www.kadman.net‬‬
‫הילה קדמן‬
‫עיצוב תכנה‬
‫‪2‬‬
‫עצים בינאריים‬
‫דוגמאות לעצים שאינם עצים בינאריים‪:‬‬
‫‪www.kadman.net‬‬
‫הילה קדמן‬
‫עיצוב תכנה‬
‫תרגיל‪:‬‬
‫‪3‬‬
‫אלו מהמשפטים הבאים נכון לגבי העץ שלהלן‪:‬‬
‫א‪.‬‬
‫‪ A‬הוא אב קדמון של כל צמתי העץ‪----------------------------------------- .‬‬
‫ב‪.‬‬
‫‪ B‬הוא אב קדמון של ‪------------------------------------------------------ .G‬‬
‫ג‪.‬‬
‫‪ F‬הוא צאצא של ‪ E ,C‬ו‪---------------------------------------------------.G-‬‬
‫ד‪.‬‬
‫‪ D‬הוא ברמה ‪--------------------------------------------------------------- .2‬‬
‫ה‪.‬‬
‫‪ G‬הוא אח של ‪------------------------------------------------------------- .B‬‬
‫ו‪.‬‬
‫‪ C‬הוא אב קדמון של ‪ F‬ו‪-------------------------------------------------- .D-‬‬
‫ז‪.‬‬
‫רמתם של אחים בעץ זהה‪---------------------------------------------------- .‬‬
‫תרגיל‪:‬‬
‫עצים בינאריים‬
‫כמה אבות קדמונים יש לצומת ברמה ‪ n‬בעץ בינארי ?‬
‫‪www.kadman.net‬‬
‫הילה קדמן‬
‫עיצוב תכנה‬
‫‪www.kadman.net‬‬
‫‪4‬‬
‫עצים בינאריים‬
‫הילה קדמן‬
‫עצים בינאריים‬
‫עיצוב תכנה‬
5
:‫תרגיל‬
:‫עקוב אחרי קטע הקוד וצייר את העץ המתקבל‬
Java
BinTreeNode<Integer> bt = new BinTreeNode<Integer>(7);
BinTreeNode<Integer> t1 = new BinTreeNode<Integer>(5);
BinTreeNode<Integer> t2 = new BinTreeNode<Integer>(2);
bt.setLeft(t1);
bt.setRight(t2);
t1.setRight (new BinTreeNode<Integer>(new BinTreeNode<Integer>(4),
1,
null));
t2.setLeft(new BinTreeNode<Integer>(null,
8,
new BinTreeNode<Integer>(12)));
t1 = t1.getRight();
t1.setRight(new BinTreeNode<Integer> (15));
t2.setRight(new BinTreeNode<Integer>(new BinTreeNode<Integer>(-4),
9,
new BinTreeNode<Integer>(72)));
‫הילה קדמן‬
www.kadman.net
‫עצים בינאריים‬
‫עיצוב תכנה‬
6
:‫תרגיל‬
:‫עקוב אחרי קטע הקוד וצייר את העץ המתקבל‬
C#
BinTreeNode<int> bt = new BinTreeNode<int>(7);
BinTreeNode<int> t1 = new BinTreeNode<int>(5);
BinTreeNode<int> t2 = new BinTreeNode<int>(2);
bt.SetLeft(t1);
bt.SetRight(t2);
t1.SetRight (new BinTreeNode<int> (new BinTreeNode<int> (4),
1,
null));
t2.SetLeft
(new BinTreeNode<int> (null,
8,
new BinTreeNode<int> (12)));
t1 = t1.GetRight();
t1.SetRight (new BinTreeNode<int> (15));
t2.SetRight (new BinTreeNode<int> (new BinTreeNode<int> (-4),
9,
new BinTreeNode<int> (72)));
‫הילה קדמן‬
www.kadman.net
‫עיצוב תכנה‬
‫‪7‬‬
‫עצים בינאריים‬
‫סריקת עץ בינארי‪:‬‬
‫סריקה בסדר תחילי ‪pre order -‬‬
‫‪1.‬‬
‫‪.2‬‬
‫‪.3‬‬
‫בקר בשורש‪.‬‬
‫סרוק תת‪-‬עץ השמאלי בסדר תחילי‪.‬‬
‫סרוק תת‪-‬עץ ימני בסדר תחילי‪.‬‬
‫סריקה בסדר תוכי‬
‫‪1.‬‬
‫‪2.‬‬
‫‪.3‬‬
‫‪in order -‬‬
‫סרוק תת‪-‬עץ השמאלי בסדר תוכי‪.‬‬
‫בקר בשורש‪.‬‬
‫סרוק תת‪-‬עץ ימני בסדר תוכי‪.‬‬
‫סריקה בסדר סופי ‪post order -‬‬
‫‪1.‬‬
‫‪2.‬‬
‫‪.3‬‬
‫סרוק תת‪-‬עץ השמאלי בסדר סופי‪.‬‬
‫סרוק תת‪-‬עץ ימני בסדר סופי‪.‬‬
‫בקר בשורש‪.‬‬
‫שלושת שיטות הסריקה מעידים על מיקומה של פעולת הביקור בשורש בין ‪ 3‬הפעולות‪.‬‬
‫קיימת שיטת סריקה נוספת ‪ -‬סריקה לפי רמות‪.‬‬
‫‪‬‬
‫שחזור עץ בינארי על פי ‪ 2‬מסריקותיו‪.‬‬
‫‪www.kadman.net‬‬
‫הילה קדמן‬
‫עיצוב תכנה‬
‫‪8‬‬
‫סריקת העץ בשיטות השונות‪:‬‬
‫‪ABDEGJCFHKI‬‬
‫סריקה בסדר תחילי‪:‬‬
‫‪DBJGEACHKFI‬‬
‫סריקה בסדר תוכי‪:‬‬
‫‪DJGEBKHIFCA‬‬
‫סריקה בסדר סופי‪:‬‬
‫‪PreOrder‬‬
‫‪InOrder‬‬
‫‪PostOrder‬‬
‫תרגיל‪:‬‬
‫עצים בינאריים‬
‫מהו סדר הביקור בצמתים בכל אחת משלוש שיטות הסריקה?‬
‫‪www.kadman.net‬‬
‫הילה קדמן‬
‫עיצוב תכנה‬
‫‪9‬‬
‫עצים בינאריים‬
‫אוסף פעולות רקורסיביות‪:‬‬
‫‪‬‬
‫‪‬‬
‫מספר הצמתים בעץ‬
‫סכום הצמתים בעץ‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫עלה?‬
‫מספר העלים בעץ‬
‫סכום העלים‬
‫מספר הצמתים שערכם ‪x‬‬
‫‪‬‬
‫‪‬‬
‫מספר בנים ימניים בעץ‬
‫מספר צמתים זוגיים‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫מספר הבנים של צומת נתון‬
‫מספר הנכדים של צומת נתון‬
‫עץ פרו ורבו (‪ - )2004‬מחזיר אמת אם קיים צומת ולו לפחות שני נכדים משני הבנים‪.‬‬
‫מספר‪-‬סבים בעץ‬
‫‪‬‬
‫האם‪-‬נמצא? )‪(bt, x‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫האם כל הצמתים אי‪-‬זוגיים?‬
‫ בגרות ‪2004‬‬‫עץ פרו ורבו‬
‫ממוין‪-‬רמות? ‪ -‬אמת אם ערך כל אב קטן מערך בניו‪ ,‬ושקר אחרת‬
‫עץ‪-‬ממוצע? ‪ -‬אמת אם ערך כל צומת שווה לממוצע הערכים של בניו‪.‬‬
‫‪‬‬
‫‪‬‬
‫גובה‪-‬עץ‬
‫ערך מקסימאלי בעץ‬
‫‪‬‬
‫האם‪-‬אחים? )‪(bt1, bt2‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫האם‪-‬הורה? (‪)bt1, bt2‬‬
‫ בגרות ‪2000‬‬‫סבא רבא‬
‫ מחזיר הפניה לצומת ההורה של הצומת‪ .‬הצוןמת אינו שורש העץ‬‫מצא‪-‬הורה (צומת)‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫ האם קיים מסלול שערכי כל צמתיו זהה‪.‬‬‫מסלול‪-‬אחיד‬
‫עץ‪-‬מלא? ‪ -‬כל הרמות מלאות (הקשר שבין מספר הצמתים ‪ N‬וגובה העץ ‪)2^k == n :K‬‬
‫עץ בינארי לחלוטין (עץ מלא) ‪ -‬עץ שדרגת כל צומת בו היא ‪ 0‬או ‪2‬‬
‫‪www.kadman.net‬‬
‫הילה קדמן‬
‫עיצוב תכנה‬
‫‪www.kadman.net‬‬
‫‪10‬‬
‫עצים בינאריים‬
‫הילה קדמן‬