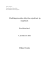Luku 1 Yhden selittäjän lineaarinen regressio

Luku 1
Yhden selitt¨
aj¨
an lineaarinen
regressio
T¨am¨a luku on tiivistelm¨a Jørgensenin kirjan luvusta 1. T¨ass¨a luvussa k¨asitell¨a¨an
yksinkertaisilla tarkasteluilla yhden selitt¨aj¨an lineaarista regressiota, mutta
suoraviivaisia laskuja ei ole t¨ass¨a laskettu auki, vaan ne esitet¨a¨an luennoilla
tai j¨atet¨a¨an lukijan tarkistettavaksi. Luvussa 2 tarkastellaan sitten yleist¨a lineaarista regressiota k¨aytt¨am¨all¨a hienostuneempia matemaattisia ty¨okaluja.
1.1
Regressiomalli
Analysoitavana on n:n havaintoyksik¨on suuruinen aineisto, jonka muuttujista yksi, y, on luonteeltaan selitett¨av¨a ja toinen, x, selitt¨a¨a selitett¨av¨an
muuttujan y vaihtelua. Olkoot
(x1 , y1 ), . . . , (xn , yn )
vastaavat havainnot. Muuttujien x ja y v¨alinen yhteyden ajatellaan olevan
osapuilleen lineaarinen. Kutsumme muuttujaa y selitett¨av¨aksi muuttujaksi
tai vasteeksi (dependent variable, response variable). Kutsumme muuttujaa
x selitt¨av¨aksi muuttujaksi (independent variable, explanatory variable).
Ajattelmme, ett¨a yi :t ovat vastaavien satunnaismuuttujien Yi havaittuja
arvoja. Sen sijaan ajattelemme, ett¨a selitt¨av¨at muuttujat xi ovat ei-satunnaisia
eli vakioita. T¨allainen oletus on luonteva, jos xi :t ovat kokeen suunnittelijan
valittavissa olevia lukuja.
Joissakin tapauksissa lineaarista regressiota sovelletaan tilanteessa, jossa
ei ole luontevaa olettaa, ett¨a xi :t ovat vakioita, vaan on luontevaa olettaa, ett¨a
ne ovat tiettyjen satunnaismuuttujien X1 , . . . , Xn havaittuja arvoja. T¨all¨oin
1
ajatellaan, ett¨a koko analyysi tehd¨a¨an ehdollistamalla selitt¨avien muuttujien havaittuihin arvoihin, eli t¨all¨oin tarkastellaan selitett¨avien muuttujien
Y1 , . . . , Yn ehdollista jakaumaa ehdolla X1 = x1 , . . . , Xn = xn .
Yhden selitt¨aj¨an lineaarisessa mallissa tehd¨a¨an seuraavat oletukset. Selitt¨avien muuttujien arvot xi ovat kiinteit¨a annettuja lukuja. Havaintoja yi
vastaavat satunnaismuuttujat Yi ovat riippumattomia, ja ne noudattavat jakaumaa
Yi ∼ N (µi , σ 2 ), i = 1, . . . , n,
jossa keskiarvot µi = EYi toteuttavat yht¨al¨ot
µi = β1 + β2 xi ,
i = 1, . . . , n.
Keskiarvoille tehty oletus on rakenneoletus: se kertoo, miten selitett¨av¨an
muuttujan vaihtelu riippuu selitt¨av¨ast¨a muuttujasta. Normaalisuusoletus on
jakaumaoletus, joka kertoo, mink¨alaista satunnaisvaihtelua mallissa on rakenneosan lis¨aksi. Mallissa on kolme parametria, vakiotermi (intercept) β1 ∈
R, kulmakerroin (slope) β2 ∈ R ja varianssiparametri σ 2 ∈ R + .
Toinen tapa esitt¨aa¨ sama malli on kirjoittaa
Yi = β1 + β2 xi + i ,
i = 1, . . . , n,
jossa virheet i ∼ N (0, σ 2 ) riippumattomasti, ja i on havaintoyksikk¨o¨on i
liittyv¨a ei-havaittu satunnaismuuttuja.
Mallissa tehd¨a¨an siis seuraavat oletukset, jotka alla luetellaan tilastolisen
analyysin j¨arkevyyden kannalta summittaisessa t¨arkeysj¨arjestyksess¨a.
(i) Yi :n odotusarvo riippuu lineaarisesti xi :st¨a.
(ii) Muuttujat Y1 , . . . , Yn ovat riippumattomia.
(iii) Muuttujan Yi varianssi on vakio (homoskedastisuus).
(iv) Muuttujalla Yi on normaalijakauma.
N¨am¨a oletukset pit¨aisi yritt¨a¨a verifioida aineiston ja sit¨a koskevan taustatiedon perusteella. Hajontakuvio on t¨at¨a varten t¨arke¨a apuv¨aline, ja siit¨a voi
yritt¨a¨a arvioida (i) lineaarisuutta ja (iii) vakiovarianssisuutta. Normaalisuutta (iv) voi yritt¨a¨a tutkia residuaalikuvioiden avulla. Riippumattomuutta (ii)
ei voida verifioida aineistosta, vaan se yleens¨a oikeutetaan koetta koskevalla
taustatiedolla.
2
1.2
Parametrien SU-estimaatit
Johdamme parametrien suurimman uskottavuuden estimaatit eli SU-estimaatit.
Mallin mukaan Yi ∼ N (β1 + β2 xi , σ 2 ) riippumattomasti, joten uskottavuusfunktio on
n
Y
1
2
2 −1/2
2
L(β1 , β2 , σ ) =
(2πσ )
exp − 2 (yi − β1 − β2 xi ) ,
2σ
i=1
josta logaritminen uskottavuusfunktio saadaan kirjoitettua muotoon
`(β1 , β2 , σ 2 ) = log L(β1 , β2 , σ 2 )
n
n
1 X
2
= − log(2πσ ) − 2
(yi − β1 − β2 xi )2
2
2σ i=1
n
1
= − log(2πσ 2 ) − 2 D(β1 , β2 ).
2
2σ
Kutsumme poikkeamien neli¨osummaa D(β1 , β2 ) nimell¨a devianssi.
T¨ast¨a muodosta huomaamme seuraavaa. Oli σ 2 > 0 mik¨a tahansa kiinte¨a
arvo, niin logaritmisen uskottavuusfunktion maksimoi parametrien β1 ja β2
suhteen ne arvot, jotka minimoivat devianssin D(β1 , β2 ).
Kirjoitetaan nyt rakenneyht¨al¨o muotoon
EYi = µi = β1 + β2 xi = β1 + β2 (xi − x¯) + β2 x¯
ja uudelleenparametroidaan malli k¨aytt¨am¨all¨a alkuper¨aisten selitt¨avien muuttujien arvojen sijasta keskistettyj¨a arvoja
ti = xi − x¯.
T¨all¨oin malli muuntuu muotoon
EYi = µi = α + β2 ti ,
jossa otettiin k¨aytt¨o¨on uusi parametri
α = β1 + β2 x¯.
Uudessa mallissa parametreina ovat α, β2 ja σ 2 . Alkuper¨aisen mallin parametri β1 saadaan laskettua uusista parametreist¨a kaavalla
β1 = α − β2 x¯,
3
ja muut kaksi parametria ovat samoja alkuper¨aisess¨a ja keskistetyss¨a mallissa.
Parametrien α, β2 ja σ 2 avulla ilmaistuna logaritminen uskottavuusfunktio on samaa muotoa kuin alkuper¨aisten parametrien avulla ilmaistuna sill¨a
erolla, ett¨a devianssin lausekkeena on
˜
D(α,
β2 ) =
n
X
(yi − α − β2 ti )2 .
i=1
Derivoimalla devianssin lauseketta kahteen kertaan, saadaan selville, ett¨a
mik¨ali St > 0, devianssilla on yksik¨asitteinen minimipiste kohdassa
α
ˆ = y¯,
Sty
βˆ2 =
,
St
jossa
n
y¯ =
1X
yi ,
n i=1
Sty =
n
X
ti yi ,
i=1
St =
n
X
t2i .
i=1
(Aina St ≥ 0, ja jos St = 0, niin kaikki xi :t ovat yht¨asuuria, eik¨a lineaarinen
malli ole mielek¨as!)
Keskistetyn mallin parametrien α ja β2 SU-estimaatit ovat edell¨a johdetut
α
ˆ ja βˆ2 . Alkuper¨aisen mallin parametrien β1 ja β2 SU-estimaatit ovat
βˆ1 = α
ˆ − βˆ2 x¯.
(SU-estimaatin invarianssiominaisuus!)
Huomaa, ett¨a sovitettu regressiosuora y = βˆ1 + βˆ2 x kulkee aina aineiston
painopisteen (¯
x, y¯) kautta, sill¨a edellisen nojalla
βˆ1 + βˆ2 x¯ = y¯.
Jos varianssi σ 2 > 0 kiinnitet¨a¨an, ja log-uskottavuusfunktio maksimoidaan muiden parametrien suhteen, niin tulokseksi saadaan
˜ 2 ) = − n log(2πσ 2 ) − 1 D(βˆ1 , βˆ2 ).
`(σ
2
2σ 2
T¨at¨a σ 2 :n funktioita kutsutaan parametrin σ 2 logaritmiseksi profiiliuskottavuusfunktioksi. Parametrin σ 2 SU-estimaatti saadaan ratkaistua ratkaisemalla t¨am¨an funktion maksimipiste. Derivoimalla SU-estimaatille saadaan
johdettua kaava
n
σ
ˆ2 =
1
1X
D(βˆ1 , βˆ2 ) =
(yi − βˆ1 − βˆ2 xi )2 .
n
n i=1
4
1.3
Estimaattorien ominaisuuksia
Kun puhumme estimaattoreista, tarkoitamme estimaatteja vastaavia satunnaismuuttujia. Oletamme, ett¨a lineaarinen malli pit¨a¨a paikkansa, ja tutkimme satunnaismuuttujien
Pn
n
X
ti Yi
1
S
tY
α
ˆ = Y¯ =
Yi , βˆ2 =
= Pi=1
n
2
n i=1
St
i=1 ti
jne. jakaumia (ts. estimaattorien otantajakaumia, sampling distribution) ja
muita ominaisuuksia.
1.3.1
Tyhjent¨
avyys
Tilastollisessa mallissa, jossa havaintovektorin Y = (Y1 , . . . , Yn ) yhteisjakaumalla on parametrina tai parametrivektorina θ, tunnusluku T = t(Y ) on
tyhjent¨av¨a, jos Y :n ehdollinen jakauma ehdolla T ei ole θ:n funktio. T¨all¨oin
tunnusluku T sis¨alt¨a¨a parametrista yht¨a paljon tietoa kuin alkuper¨ainen havaintovektori. Tilastollisen p¨a¨attelyn teorian nojalla tiedet¨a¨an, ett¨a tunnusluku T on tyhjent¨av¨a silloin ja vain silloin, kun havaintojen (yhteis)tiheys fY
voidaan kirjoittaa faktoroidussa muodossa
fY (y; θ) = g(t(y); θ)h(y),
∀y, θ.
(My¨os satunnaismuuttujan T otosvastinetta kutsutaan tyhjent¨av¨aksi tunnusluvuksi.)
T¨am¨an perusteella on helppo n¨aytt¨aa¨, ett¨a yhden selitt¨aj¨an lineaarisessa
regressiossa tunnusluku
t(y) = (Sy , y+ , Sty )
on tyhjent¨av¨a, jossa
Sy =
n
X
1
yi2 ,
y+ =
n
X
1
yi ,
Sty =
n
X
ti yi .
1
Pienill¨a laskuilla n¨ahd¨a¨an t¨am¨an perusteella, ett¨a my¨oskin parametrien SUestimaattorit (ˆ
α, βˆ1 , σ
ˆ 2 ) muodostavat tyhjent¨av¨an tunnusluvun.
1.3.2
Regressiokertoimien estimaattorien jakaumat
Palautetaan ensin mieleen kahden satunnaismuuttujan U ja V v¨alinen kovarianssi, joka m¨a¨aritell¨a¨an kaavalla
Cov(U, V ) = E[(U − EU )(V − EV )].
5
Muuttujan U varianssi Var U on sama kuin Cov(U, U ). Yksinkertainen lasku
osoittaa, ett¨a kovarianssi on bilineaarinen (eli lineaarinen molempien argumenttien suhteen) ts., jos αi :t ja βj ovat vakioita ja Ui :t ja Vj :t satunnaismuuttujia, niin
X
X
X
αi Ui ,
βj Vj ) =
αi βj Cov(Ui , Vj ).
Cov(
i
j
ij
Koska muttujien Y1 , . . . , Yn yhteisjakauma on moniulotteinen normaalijakauma eli multinormaalijakauma, ja koska keskistetyn mallin SU-estimaattorit
α
ˆ ja βˆ2 ovat niiden lineaarikombinaatioita, on niiden yhteisjakauma kaksiulotteinen normaalijakauma. Helposti saadaan johdettua tulokset
α
ˆ ∼ N (α,
σ2
),
n
2
σ
βˆ2 ∼ N (β2 , ),
St
sek¨a
Cov(ˆ
α, βˆ2 ) = 0.
Siis keskistetyn mallin parametrit α
ˆ ja βˆ2 ovat korreloimattomia. Koska niiden yhteisjakauma on kaksiulotteinen normaalijakauma, t¨ast¨a seuraa, ett¨a
ne ovat per¨ati riippumattomia.
Alkuper¨aisen mallin kertoimien β1 ja β2 SU-estimaattorien yhteisjakauma
on my¨oskin kaksiulotteinen normaalijakauma, ja laskemalla saadaan selville,
ett¨a
2
1
x
¯
2
βˆ1 ∼ N β1 , σ
+
n St
ja
σ2
,
St
joten alkuper¨aisen mallin estimaattorit ovat korreloituneita ja riippuvia. Jos
x-arvot sijaitsevat kaukana origosta (¯
x on iso verrattuna arvoon St ), niin vaˆ
kiotermin estimaattorin β1 varianssi on suuri, eli estimaattori βˆ1 on ep¨astabiili.
T¨am¨an takia kannattaa useimmiten k¨aytt¨a¨a keskistetty¨a mallia, jonka kertoimien tulkinta on lis¨aksi usein mielekk¨a¨amp¨a¨a kuin keskist¨am¨att¨om¨an mallin
parametrien tulkinta.
Huomaa, ett¨a regressiokertoimien estimaattorit ovat harhattomia ja ett¨a
niiden jakaumat riippuvat (tuntemattomasta) varianssiparametrista σ 2 , mink¨a
vuoksi n¨ait¨a tuloksia ei voi suoraan k¨aytt¨a¨a esim. parametrien luottamusv¨alien
johtamiseen.
Cov(βˆ1 , βˆ2 ) = −¯
x
6
1.3.3
Varianssiparametri
T¨ass¨a luvussa johdetaan se t¨arke¨a tulos, ett¨a σ
ˆ 2 on riippumaton regressioparametrien estimaattoreista. T¨at¨a varten tarkastellaan ensin residuaalien
ri = y i − µ
ˆi = yi − βˆ1 − βˆ2 xi = yi − α
ˆ − βˆ2 ti
ominaisuuksia, jossa
µ
ˆi = βˆ1 + βˆ2 xi = α
ˆ + βˆ2 ti
on i:s sovite (fitted value). Olkoon Ri residuaalia ri vastaava satunnaismuuttuja,
Ri = Yi − βˆ1 − βˆ2 xi = Yi − α
ˆ − βˆ2 ti .
Nyt
ERi = EYi − E α
ˆ − ti E βˆ2 = 0,
ja pienill¨a laskuilla havaitaan, ett¨a
Cov(Ri , α
ˆ ) = Cov(Ri , βˆ2 ) = 0.
Nyt satunnaismuuttujilla α
ˆ , βˆ2 ja Ri on yhteisjakaumana multinormaalijakauma, sill¨a ne saadaan lineaarikombinaatioina satunnaismuuttujista Y1 , . . . , Yn ,
joilla on multinormaalijakauma. Koska multinormaalijakaumassa korreloimattomuudesta seuraa riippumattomuus, on Ri riippumaton parista (ˆ
α, βˆ2 ).
Koska
n
1X 2
R ,
σ
ˆ2 =
n i=1 i
seuraa, ett¨a my¨os σ
ˆ2 on riippumaton parista (ˆ
α, βˆ2 ). Yhdistettyn¨a edell¨a johˆ
q β2 t¨ast¨a seuraa, ett¨a keskistetyn mallin kaikki kolme
dettuun tulokseen α
ˆ−
parametriestimattoria ovat kesken¨a¨an riippumattomia. Keskist¨am¨att¨om¨ass¨a
mallissa n¨ahd¨a¨an vastaavilla laskuilla, ett¨a σ
ˆ 2 on riippumaton parista (βˆ1 , βˆ2 ).
Satunnaismuuttujan Ri reunajakauma on normaalijakauma, jonka varianssi saadaan laskettua helposti k¨aytt¨am¨all¨a edell¨a johdettuja riippumattomuustuloksia. Ri :n jakaumaksi saadaan
1
t2i
2
Ri ∼ N 0, σ 1 − −
n St
Osoittautuu, ett¨a varianssiparametrin SU-estimaattorin jakauma on skaalausta vaille tietty χ2 -jakauma (khiin neli¨o tai khii toiseen). Palautetaan mieleen χ2 -jakauman m¨a¨aritelm¨a. Olkoot Z1 , . . . , Zk riippumattomia standardinormaalijakaumaa noudattavia satunnaismuuttujia. T¨all¨oin satunnaismuuttujalla
U = Z12 + · · · + Zk2
7
on χ2 -jakauma k:lla vapausasteella (degrees of freedom, df ), eli
U ∼ χ2 (k).
Tunnetusti t¨am¨an jakauman odotusarvo on k ja varianssi on 2k.
Luvun 2 tuloksista selvi¨a¨a aikanaan, ett¨a
D(βˆ1 , βˆ2 ) =
n
X
Ri2 ∼ σ 2 χ2 (n − 2),
i=1
(kahden parametrin estimointiin kuluu kaksi vapausastetta), joten
Eσ
ˆ2 =
n−2
1
ED(βˆ1 , βˆ2 ) = σ 2
.
n
n
SU-estimaattori σ
ˆ 2 on siis alasp¨ain harhainen, ja sen sijasta tavallisesti k¨aytet¨a¨an
harhatonta estimaattoria
n
1
1 X 2
Ri =
D(βˆ1 , βˆ2 ).
σ
˜ =
n − 2 i=1
n−2
2
1.4
Residuaalit
Edellisess¨a kappaleessa johdettiin residuaalia vastaavalle satunnaismuuttujalle jakaumana
1
t2i
2
Ri ∼ N 0, σ 1 − −
.
n St
Sovitteelle µ
ˆi saadaan helposti johdettua jakauma
1
t2i
2
µ
ˆ i ∼ N µi , σ
+
.
n St
Sellaisessa suuressa otoksessa, jossa my¨os St on suuri, residuaalien varianssit
menev¨at kohti arvoa σ 2 ja sovitteiden varianssit kohti nollaa.
Residuaalien avulla voidaan yritt¨a¨a selvitt¨a¨a, ovatko havainnot Yi normaalijakautuneita. Jos lineaarinen malli pit¨a¨a paikkansa, residuaalit ovat
normaalijakautuneita, niiden varianssi on osapuilleen σ 2 , ja ne ovat osapuilleen (mutta ei tarkalleen) korreloimattomia. Residuaalien normaalisuutta voidaan selvitt¨a¨a vertaamalla residuaalien jakaumaa normaalijakaumaan
normaalisen kvantiilikuvion (eli fraktiilikuvion) (normal probability plot, normal QQ plot) avulla. Siin¨a piirret¨a¨an pistekuvio, jossa toiselle akselille piirret¨a¨an arvot
ui = Φ−1 ((i − 1/2)/n),
8
jossa Φ−1 on standardinormaalijakauman kertym¨afunktion k¨a¨anteisfunktio,
ja toiselle akselille arvot r(i) , jossa r(i) on i:nneksi pienin residuaaleista,
r(1) ≤ r(2) ≤ · · · ≤ r(n) .
Kirjassa suositellaan, ett¨a j¨arjestetyt residuaalit esitet¨aa¨n vaaka-akselilla ja
ui :t pystyakselilla, mutta usein akselit valitaan toisin p¨ain.
Jos lineaarisen mallin oletukset pit¨av¨at paikkansa, pisteet asettuvat suunnilleen origon kautta kulkevalle suoralle, jonka kulmakerroin on σ −1 , mik¨ali
residuaali esitet¨a¨an vaaka-akselilla ja σ, mik¨ali ne esitet¨a¨an pystyakselilla.
1.5
Parametreja koskeva p¨
a¨
attely
Jos mallin parametrit β1 ja β2 tunnettaisiin, niin varianssiparametri σ 2 voitaisiin estimoida lausekkeella n1 D(β1 , β2 ), sill¨a
D(β1 , β2 ) ∼ σ 2 χ2 (n).
Varianssiparametrin SU-estimaattorin alasp¨ainen harha syntyy siit¨a, ett¨a
t¨ah¨an lausekkeeseen sijoitetaan tuntemattomien parametrien tilalle niiden
SU-estimaattorit, jotka lasketaan minimoimalla t¨at¨a samaista lauseketta.
Kuten jo mainittiin, varianssiparametrille k¨aytet¨a¨an tavallisesti harhaisen
SU-estimaattorin sijasta harhatonta estimaattoria
n
σ
˜2 =
1 X 2
1
Ri =
D(βˆ1 , βˆ2 ).
n − 2 i=1
n−2
Palautetaan mieleen (Studentin) t-jakauma. Jos satunnaismuuttujat
U ∼ N (0, 1),
V ∼ χ2 (k)
ovat riippumattomia, niin satunnaismuuttujalla
U
Z=p
V /k
on t-jakauma k:lla vapausasteella, eli Z ∼ t(k).
Edell¨a johdimme tuloksen
2
σ
βˆ2 ∼ N (β2 , ),
St
9
mink¨a motivoimana m¨a¨arittelemme estimaattorin βˆ2 keskivirheen (standard
error, s.e.) eli estimaattorin otantajakauman keskihajonnan otosestimaatin
kaavalla
σ
˜
s. e.(βˆ2 ) = √ ,
St
jossa siis tuntemattoman varianssiparametrin sijalle on sijoitettu sen harhaton estimaatti σ
˜2.
Parametrin β2 t-testisuure m¨a¨aritell¨a¨an kaavalla
βˆ2 − β2
.
s. e.(βˆ2 )
t(Y ) =
Seuraavaksi osoitetaan, ett¨a t(Y ):ll¨a on t-jakauma n − 2:lla vapausasteella,
(kun m¨a¨aritelm¨ass¨a k¨aytetty β2 on ko. parametrin todellinen arvo). Nyt
√
(βˆ2 − β2 ) St /σ
t(Y ) =
√
s. e.(βˆ2 ) St /σ
jossa osoittajan ja nimitt¨aj¨a ovat riippumattomia satunnaismuuttujia, koska
q σ
βˆ2 −
˜ 2 . Osoittajan jakauma on N (0, 1), ja nimitt¨aj¨a on neli¨ojuuri lausekkeesta
χ2 (n − 2)
σ
˜2
∼
,
σ2
n−2
miss¨a k¨aytettiin tietoa
(n − 2)˜
σ 2 ∼ σ 2 χ2 (n − 2).
Siis t(Y ) ∼ t(n − 2).
T¨at¨a tulosta voidaan k¨aytt¨a¨a parametria β2 koskevien testien konstruoin(0)
tiin sek¨a sen luottamusv¨alin laskemiseen. Olkoon β2 annettu vakio (kulma(0)
kertoimen β2 kohdalla tyypillisesti β2 = 0), ja tarkastellaan hypoteesia
(0)
H0 : β2 = β2 ,
k¨aytt¨am¨all¨a kaksisuuntaista vastahypoteesia
(0)
HA : β2 6= β2 .
T¨all¨oin voidaan k¨aytt¨a¨a tunnuslukua
(0)
βˆ2 − β2
t(Y ) =
,
s. e.(βˆ2 )
10
0.2
0.0
−6
−4
−2
0
2
4
6
Kuva 1.1: Kaksisuuntaisen t-testin kriittinen alue koostuu kahdesta
h¨ant¨aalueesta, joihin kumpaankin j¨a¨a osuus a/2 todenn¨ak¨oisyysmassasta.
jonka jakauma on t(n − 2) silloin, kun H0 p¨atee. Nollahypoteesin kannalta
kriittisi¨a ovat ne tapaukset, joissa |t(Y )| on suuri. Nollahypoteesi hyl¨at¨aa¨n
merkitsevyystasolla a, jos
|t(y)| > t1−a/2 (n − 2),
miss¨a oikealla puolella oleva merkint¨a tarkoittaa sit¨a pistett¨a, jossa t(n − 2)
jakauman kertym¨afunktio saavuttaa arvon 1 − a/2, ks. kuvaa 1.1. (T¨ass¨a
k¨aytettiin hyv¨aksi t-jakauman symmetrisyytt¨a.)
Palautetaan mieleen, ett¨a testin p-arvo eli havaittu merkitsevyystaso tarkoittaa todenn¨ak¨oisyytt¨a, ett¨a nollahypoteesin p¨atiess¨a testisuuretta vastaava satunnaismuuttuja saa arvon, joka on yht¨a suuri tai suurempi kuin nyt
havaittu testisuureen arvo. Yll¨aolevan testin p-arvo on
PH0 (|t(Y )| ≥ t(y)) = 2(1 − G(|t(y)|)),
jossa G on jakauman t(n − 2) kertym¨afunktio (ja jossa j¨alleen k¨aytettiin
hyv¨aksi t-jakauman symmetrisyytt¨a).
Koska todenn¨ak¨oisyydell¨a 1 − a p¨atee ep¨ayht¨al¨o
|t(Y )| =
|βˆ2 − β2 |
< t1−a/2 (n − 2),
s. e.(βˆ2 )
niin ratkaisemalla t¨am¨a ep¨ayht¨al¨o parametrin β2 suhteen p¨a¨adyt¨a¨an seuraavaan parametrin β2 luottamusv¨aliin luottamustasolla 1 − a,
[βˆ2 − t1−a/2 (n − 2) s. e.(βˆ2 ), βˆ2 + t1−a/2 (n − 2) s. e.(βˆ2 )].
11
Parametrien β1 ja α kohdalla testisuureet konstruoidaan samalla periaatteella. Esimerkiksi parametrin β1 kohdalla l¨ahdet¨a¨an liikkeelle tuloksesta
x¯2
2 1
ˆ
β1 ∼ N (β1 , σ ( + )),
n St
jonka perusteella βˆ1 :n keskivirheeksi m¨aa¨ritell¨a¨an
s
1 x¯2
s. e.(βˆ1 ) = σ
˜
+ ,
n St
ja sen t-testisuureeksi m¨aa¨ritell¨a¨an
t(Y ) =
βˆ1 − β1
.
s. e.(βˆ1 )
T¨am¨an j¨alkeen konstruoida testej¨a ja luottamusv¨alej¨a parametrille β1 kuten
edell¨a β2 :lle.
Varianssiparametrin kohdalla l¨ahdet¨a¨an liikkeelle tiedosta
σ
˜2
χ2 (n − 2)
∼
,
σ2
n−2
2
josta saadaan johdettua hypoteesi¨a H0 : σ 2 = σ(0)
koskeva testi sek¨a seuraavaa luottamustason 1 − a luottamusv¨ali
"
#
(n − 2)˜
σ2
(n − 2)˜
σ2
,
χ21−a/2 (n − 2) χ2a/2 (n − 2)
jossa χ2b (k) tarkoittaa sit¨a pistett¨a, jossa χ2 (k)-jakauman kertym¨afunktio saa
arvon b.
12
Luku 2
Yleinen lineaarinen malli
Huomautus: yleinen lineaarinen malli on englanniksi general linear model.
Yleistetty lineaarinen malli, generalized linear model, on taas aivan eri asia.
2.1
Lineaarinen malli lineaarialgebran k¨
asitteill¨
a
Kehit¨amme seuraavaksi geometrisen l¨ahestymistavan lineaarisen mallin k¨asittelyyn.
Tarkastelemme havaintovektoria y, vastaavaa satunnaisvektoria Y sek¨a sen
odotusarvovektoria µ vektoriavaruuden R n pistein¨a, jossa
 
 
 
µ1
y1
Y1
 .. 
 .. 
 .. 
T
y = (y1 , . . . , yn ) =  .  , Y =  .  , µ =  .  .
µn
Yn
yn
Yleisess¨a lineaarisessa mallissa asetetaan lineaarisia rajoitteita keskiarvovektorille µ.
Yhden selitt¨aj¨an lineaarisessa regressiossa oletettiin, ett¨a
µi = β1 + β2 xi ,
i = 1, . . . , n.
Voimme esitt¨aa¨ t¨am¨an rakenneoletuksen vektorimerkinn¨oill¨a muodossa
µ = β1 1 + β2 x,
jossa k¨aytettiin seuraavia n-komponenttisia pystyvektoreita
 
 
1
x1
 .. 
 .. 
1 = . ,
x =  . .
1
xn
13
Toisin sanoen malli voidaan ilmaista siten, ett¨a µ on kahden annetun vektorin
1 ja x lineaarikombinaatio eli µ kuuluu n¨aiden kahden vektorin viritt¨am¨a¨an
aliavaruuteen.
M¨
a¨
aritelm¨
a. Yleisess¨a lineaarisessa mallissa oletetaan, ett¨a havaintoja yi
vastaavat satunnaismuuttujat Yi ovat riippumattomia ja ett¨a
Yi ∼ N (µi , σ 2 ),
i = 1, . . . , n,
jossa keskiarvovektori µ (joka on parametri eli tuntematon vakiovektori) toteuttaa rajoitteen (hypoteesin, rakenneoletuksen)
µ ∈ L,
jossa L on annettu (tunnettu ja ei-satunnainen) avaruuden R n aliavaruus ja
σ 2 > 0 on parametri (eli tuntematon vakio).
Palautetaan mieleen lineaarialgebran k¨asitteit¨a. Joukko L ⊂ R n on aliavaruus, jos on voimassa
x, y ∈ L ja a, b ∈ R
⇒
ax + by ∈ L.
Erityisesti nollavektori kuuluu jokaiseen aliavaruuteen.
Vektorit x1 , . . . , xk ∈ L muodostavat aliavaruuden L kannan, jos
(i) ne viritt¨av¨at L:n, eli mik¨a tahansa L:n alkio y voidaan esitt¨a¨a niiden
lineaarikombinaationa y = a1 x1 + · · · + ak xk .
(ii) joukko {x1 , . . . , xk } on lineaarisesti riippumatton (eli vapaa) ts.
a1 x1 + · · · + ak xk = 0
⇒
a1 = · · · = ak = 0.
Lineaarialgebrasta tiedet¨a¨an, ett¨a jokaisella R n :n aliavaruudella on olemassa
kanta ja ett¨a jokaisella L:n kannalla on yht¨a monta kantavektoria. T¨at¨a tarvittavaa kantavektoreiden lukum¨a¨ar¨a¨a kutsutaan aliavaruuden dimensioksi, dim(L). Huomaa, ett¨a kantavektoreiden lineaarisen riippumattomuuden
ansiosta vektorin x ∈ L esitys kantavektoreiden lineaarikombinaationa on
yksik¨asitteinen.
Jos x1 , . . . , xk on lineaarisen mallin aliavaruuden L kanta, niin rakenneoletus µ ∈ L voidaan ilmaista muodossa
µ=
k
X
xj βj = Xβ,
j=1
14
jossa X on tunnettu vakiomatriisi, jonka sarakkeet (pystyvektorit) ovat x1 , . . . , xk ,
ja kerroinvektori β = (β1 , . . . , βk )T on parametri, eli se on tuntematon vakiovektori. Matriisia X kutustaan t¨all¨oin asetelmamatriisiksi (design matrix )
tai mallimatriisiksi (model matrix ). Huomaa, ett¨a t¨all¨a kurssilla mallimatriisin sarakkeet ovat aina lineaarisesti riippumattomia (ellei erityisesti toisin
mainita). On hy¨odyllist¨a tarkastella lineaarista mallia toisaalta tietyn kannan
(ja tietyn mallimatriisin) avulla lausuttuna ja toisaalta koordinaattivapaasti
eli pelk¨ast¨a¨an aliavaruuden L avulla ilmaistuna.
Joskus aliavaruudelle L k¨aytet¨a¨an kahta eri kantaa ja mallimatriisia
µ = X1 β
ja µ = X2 ψ.
Kun n × k-mallimatriisin X1 sarakkeet esitet¨a¨an n × k-mallimatriisin X2
sarakkeiden muodostaman kannan avulla, p¨aa¨dyt¨aa¨n esitykseen
X1 = X2 A,
jossa k × k-matriisin A sarakkeet ovat lineaarisesti riippumattomat (sill¨a
muuten X1 :n sarakkeet olisivat lineaarisesti riippuvat). T¨am¨an takia A on
k¨a¨antyv¨a matriisi. Koska µ = X1 β = X2 ψ = X2 Aβ, on
ψ = Aβ
ja β = A−1 ψ.
Aliavaruuden L kannan vaihto on sama asia kuin t¨allainen lineaarisen mallin
lineaarinen uudelleenparametrointi.
Vektoreiden x, y ∈ R n sis¨atulo on
T
T
x·y =x y =y x=
n
X
xi yi ,
i=1
ja vektorin x normi on
kxk =
√
xT x.
Vektorit x ja y ovat ortogonaaliset eli toisiaan vastaan kohtisuorat, jos
xT y = 0, mik¨a voidaan ilmaista merkinn¨all¨a x ⊥ y. Pythagoraan lause
sanoo, ett¨a
x ⊥ y ⇒ kx + yk2 = kxk2 + kyk2 .
Aliavaruuden L ortogonaalikomplementti L⊥ on
L⊥ = {x ∈ R n : x ⊥ z
L⊥ on tunnetusti aliavaruus.
15
∀z ∈ L}.
Jos L on aliavaruus ja y ∈ R n , niin tunnetusti on olemassa yksik¨asitteinen
vektori pL (y) ∈ L siten, ett¨a
y − pL (y) ∈ L⊥
tai ekvivalentisti siten, ett¨a
y − pL (y) ⊥ z
∀z ∈ L.
Vektoria pL (y) kutsutaan vektorin y ortogonaaliprojektioksi aliavaruuteen L.
Huomaa, ett¨a ortogonaaliprojektio pL (y) on pistett¨
a y l¨
ahin aliavaruuden L piste, eli pL (y) on optimointiteht¨av¨an
ky − zk = min! rajoitteella z ∈ L,
yksik¨asitteinen ratkaisu, sill¨a jos z ∈ L, niin Pythagoraan lauseen mukaan
ky − zk2 = ky − pL (y)k2 + kpL (y) − zk2 ≥ ky − pL (y)k2 ,
ja ep¨ayht¨al¨o on aito, jos z 6= pL (y).
Ortogonaaliprojektio on lineaarinen kuvaus, sill¨a kun y1 , y2 ∈ R n
esitet¨a¨an muodossa
yj = pL (yj ) + (y − pL (yj )),
j = 1, 2,
jossa pL (yj ) ∈ L ja y − pL (yj ) ∈ L⊥ , niin havaitaan, ett¨a kaikille skalaareille
α1 , α2 p¨atee
α1 y1 + α2 y2 = [α1 pL (y1 ) + α2 pL (y2 )] + [α1 (y1 − pL (y1 )) + α2 (y2 − pL (y2 ))],
jossa oikean puolen ensimm¨ainen termi kuuluu aliavaruuteen L ja toinen
termi aliavaruuteen L⊥ . N¨ain ollen
pL (α1 y1 + α2 y2 ) = α1 pL (y1 ) + α2 pL (y2 )
∀y1 , y2
∀α1 , α2 .
Koska kuvaus y 7→ pL (y) on lineaarinen, sen v¨alit¨a¨a tietty n × n-matriisi H,
eli
pL (y) = Hy, ∀y
Luvussa 2.2.1 annetaan matriisille H lauseke k¨aytt¨am¨all¨a mielivaltaista aliavaruuden L kantaa.
16
Ortogonaaliprojektion k¨asittely on yksinkertaista, jos aliavaruudelle L
tunnetaan ortogonaalinen kanta e1 , . . . , ek , eli kanta, jonka vektorit ovat kesken¨a¨an kohtisuorat (ja kaikille aliavaruuksille l¨oytyy ortogonaalinen kanta).
T¨all¨oin ortogonaaliprojektio saadaan lausekkeella
pL (y) =
k
X
ej · y
e.
2 j
ke
k
j
j=1
T¨am¨a todistetaan tarkistamalla, ett¨a lausekkeen oikea puoli kuuluu aliavaruuteen L kaikilla y ja ett¨a y:n ja v¨aitetyn lausekkeen erotus on kohtisuorassa
L:n kantavektoreita vastaan.
Mielivaltainen aliavaruuden kanta voidaan ortogonalisoida Gramin–Schmidtin
ortogonalisointiprosessilla. Otetaan k¨aytt¨o¨on merkint¨a
S ⊂ Rn
span S,
tarkoittamaan joukon S viritt¨am¨a¨a aliavaruutta (eli pienint¨a aliavaruutta, joka sis¨alt¨a¨a joukon S.) Olkoon a1 , . . . , ak aliavaruuden L kanta, ja m¨a¨aritell¨a¨an
Lj = span{a1 , . . . , aj }.
M¨aa¨ritell¨a¨an e1 = a1 ja sen j¨alkeen
ej = aj − pLj−1 (aj ),
j = 2, . . . , k.
T¨all¨oin e1 , . . . , ej on aliavaruuden Lj ortogonaalinen kanta, ja erityisesti e1 , . . . , ek
on aliavaruuden L ortogonaalinen kanta. Yll¨a ortogonaaliprojektio pLj−1 (aj )
saadaan laskettua helposti, sill¨a indeksin j kohdalla yll¨a olevassa iteraatiossa
tunnetaan aliavaruuden Lj−1 ortogonaalinen kanta e1 , . . . , ej−1 .
Jos L1 ja L2 ovat aliavaruuksia, niin my¨os niiden leikkaus ja summa ovat
aliavaruuksia. Aliavaruuksien L1 ja L2 summa on juokko
L1 + L2 = {v1 + v2 : v1 ∈ L1 , v2 ∈ L2 }.
Aliavaruudet L1 ja L2 ovat ortogonaaliset, mik¨a voidaan ilmaista merkinn¨all¨a L1 ⊥ L2 , jos v1 ⊥ v2 kaikilla v1 ∈ L1 ja v2 ∈ L2 . T¨all¨oin aliavaruuksien L1 ja L2 summaa kutsutaan ortogonaaliseksi suoraksi summaksi,
ja sit¨a merkit¨a¨an
L 1 ⊕ L2 .
(Huomaa, ett¨a monissa muissa l¨ahteiss¨a merkint¨a¨a L1 ⊕ L2 k¨aytet¨a¨an my¨os
aliavaruuksien suoralle summalle, jossa summattavilta aliavaruuksilta vaaditaan ainoastaan, ett¨a L1 ∩ L2 = {0}, mik¨a tietenkin pit¨a¨a paikkansa, jos L1
ja L2 ovat ortogonaalisia.)
17
Jos L2 ⊂ L1 ⊂ R n ovat aliavaruuksia, niin L2 :n ortogonaalikomplementti L1 :ss¨
a on
L1 L 2 = L 1 ∩ L⊥
2 = {x ∈ L1 : x ⊥ z
∀z ∈ L2 }.
Erityisesti tavanomaiselle ortogonaalikomplementille L⊥ voidaan k¨aytt¨aa¨ merkint¨a¨a R n L.
2.2
SU-estimaatit
Tarkastelemme lineaarista mallia µ ∈ L, jossa L on aliavaruus. Uskottavuusfunktio on
n
Y
1
2 −1/2
2
2
L(µ, σ ) =
(2πσ )
exp − 2 (yi − µi )
2σ
i=1
1
2 −n/2
2
= (2πσ )
exp − 2 ky − µk .
2σ
Oli σ 2 > 0 mik¨a tahansa arvo, niin µ:n suhteen t¨am¨an funktion maksimoi se
µ ∈ L, joka minimoi lausekkeen ky − µk2 , ja t¨am¨an teht¨av¨an ratkaisu on
µ
ˆ = pL (y).
Argumentin µ suhteen maksimoitu uskottavuusfunktio eli parametrin σ 2 profiiliuskottavuusfunktio on
1
2
2
2 −n/2
2
˜
L(σ ) = L(ˆ
µ, σ ) = (2πσ )
exp − 2 ky − µ
ˆk .
2σ
Varianssiparametrin σ 2 > 0 SU-estimaatti l¨oydet¨a¨an maksimoimalla t¨at¨a
funktiota, ja maksimipisteeksi saadaan helpoilla laskuilla
σ
ˆ2 =
1
ky − µ
ˆ k2
n
olettaen, ett¨a y 6∈ L. Jos y ∈ L, niin σ 2 :n SU-estimaatti ei ole m¨aa¨ritelty.
(Uskottavuusfunktio l¨ahestyy t¨ass¨a tapauksessa ¨a¨aret¨ont¨a, kun σ 2 l¨ahestyy
nollaa, mutta arvo nolla ei kuulu parametriavaruuteen.) Jos lineaarinen malli pit¨a¨a paikkansa ja L on avaruuden R n aito aliavaruus, niin tapauksen
{Y ∈ L} todenn¨ak¨oisyys on nolla, joten rajoitus y 6∈ L ei ole huolestuttava.
Kootaan tulokset lauseeksi.
18
Lause 1. Lineaarisen mallin µ ∈ L SU-estimaatit ovat olemassa jos ja vain
jos y 6∈ L, ja t¨all¨oin niill¨a on lausekkeet
1
µ
ˆ = pL (y),
σ
ˆ 2 = ky − µ
ˆ k2 .
n
Uskottavuusfunktion maksimiarvo on
n
n
L(ˆ
µ, σ
ˆ 2 ) = (2πˆ
σ 2 )− 2 e− 2
Varianssiparametrin SU-estimaatin σ
ˆ 2 sijasta sille tullaan k¨aytt¨am¨a¨an
estimaattia
1
σ
˜2 =
ky − µ
ˆk2 ,
jossa k = dim(L).
n−k
T¨ass¨a y = (y − µ
ˆ) + µ
ˆ, jossa y − µ
ˆ ∈ L⊥ ja µ
ˆ ∈ L, joten termit ovat
ortogonaalisia. Pythagoraan lauseen nojalla ko. estimaatin lauseke voidaan
kirjoittaa my¨os muodossa
1
σ
˜2 =
(kyk2 − kˆ
µk2 ).
n−k
2.2.1
Ortogonaaliprojektion matriisiesitys
Olkoon x1 , . . . , xk lineaariavaruuden L kanta ja olkoon
X = x1 , . . . , x k
matriisi, jonka sarakkeina on kyseiset kantavektorit. Jos µ ∈ L, niin
µ=
k
X
xj βj = Xβ
j=1
jollekin β ∈ R k , ja t¨am¨a esitys on yksik¨asitteinen. Koska my¨os µ
ˆ ∈ L, on
ˆ jolla
olemassa yksik¨asitteinen β,
ˆ
µ
ˆ = pL (y) = X β.
T¨all¨oin µ
ˆ = X βˆ on parametrin µ SU-estimaatti aliavaruutta L vastaavassa
ˆ
lineaarisessa mallissa. Seuraavaksi johdamme lausekkeen estimaatille β.
ˆ
Kerroinvektorin β lauseke voidaan johtaa joko derivoimalla (kuten kirjassa) tai seuraavalla geometrisella tarkastelulla. Koska vektorit x1 , . . . , xk
muodostavat L:n kannan, seuraavat asiat ovat ekvivalentteja.
X βˆ = pL (y)
⇔ y − X βˆ ⊥ z ∀z ∈ L
⇔ y − X βˆ ⊥ xj ∀j = 1, . . . , k
ˆ = 0.
⇔ X T (y − X β)
19
Edell¨a johdettua yht¨al¨o¨a
X T X βˆ = X T y
kutsutaan normaaliyht¨
al¨
oksi (tai normaaliyht¨al¨oiksi tai normaaliyht¨al¨oryhm¨aksi).
Koska X:n sarakkeet muodostavat kannan, ovat ne lineaarisesti riippumattomia. Todistamme seuraavaksi, ett¨a t¨ast¨a seuraa se seikka, ett¨a X T X on
s¨
a¨
anno
¨llinen matriisi, eli ett¨a t¨all¨a matriisilla on olemassa k¨a¨anteismatriisi.
Ensinn¨akin X T X on k × k-neli¨omatriisi, ja toisekseen seuraava implikaatioketju
X T Xa = 0
⇒
(aT X T )(Xa) = 0
⇒
Xa = 0
⇒
a=0
osoittaa, ett¨a matriisin X T X nolla-avaruus koostuu nollavektorista. T¨am¨an
takia matriisi X T X on s¨aa¨nn¨ollinen.
Siis βˆ voidaan ratkaista normaaliyht¨al¨ost¨a, jolloin saadaan
βˆ = (X T X)−1 X T y.
T¨am¨an j¨alkeen ortogonaaliprojektio µ
ˆ saadaan lausekkeesta
pL (y) = µ
ˆ = X βˆ = X(X T X)−1 X T y = Hy,
miss¨a otettiin k¨aytt¨oo¨n merkint¨a
H = X(X T X)−1 X T .
Lineaarikuvauksen pL v¨alitt¨av¨a¨a n × n-matriisia H kutsutaan hattumatriisiksi. (Selitys: sovitevektorille µ
ˆ k¨aytet¨a¨an usein merkint¨a¨a yˆ, joten hattumatriisi laittaa hatun y:n p¨a¨alle, yˆ = Hy.) Voidaan my¨os sanoa, ett¨a H on
projektiomatriisi aliavaruuteen L.
Laskemalla n¨ahd¨a¨an, ett¨a hattumatriisi on idempotentti ja symmetrinen,
ts.
HH = H ja H T = H.
K¨a¨ant¨aen, jos P on idempotentti ja symmetrinen matriisi, niin se on
projektiomatriisi aliavaruuteen
R(P ) = {P x : x ∈ R n }
eli kuvauksen x 7→ P x kuva-avaruuteen eli P :n sarakkeiden viritt¨am¨a¨an aliavaruuteen. (Kirjassa k¨aytet¨a¨an merkint¨a¨a span{P } ≡ R(P ).) T¨am¨a tarkistetaan seuraavilla laskuilla.
1) P y ∈ R(P ) kaikilla y (tietenkin).
20
2) Tarkistetaan, ett¨a y − P y on kohtisuorassa aliavaruutta R(P ) vastaan:
y − P y ∈ R(P )⊥
∀y
⇔ P T (I − P )y = 0 ∀y,
mutta j¨alkimm¨ainen identiteetti on tietenkin tosi symmertrisyyden ja
idempotenttisuuden takia.
2.2.2
Kerroinvektorin estimaattorin jakauma
Jostain syyst¨a kirjan luvussa 2 ei tehd¨a t¨ass¨a teht¨avi¨a yksinkertaisia huomiota kerroinvektorin estimaattorin jakaumasta. Ensin kertaamme multinormaalijakauman ominaisuuksia.
Satunnaisvektori Y = (Y1 , . . . , Yk )T on vektori, jonka komponentit Yj
ovat satunnaismuuttujia. Sen odotusarvovektori on komponenttien odotusarvoista koottu vektori ts. vektorin odotusarvo m¨a¨aritell¨a¨an laskemalla
odotusarvo komponentti komponentilta,
  

Y1
EY1
  

EY = E  ...  =  ... 
Yk
EYk
Satunnaismatriisi ja sen odotusarvo m¨a¨aritell¨a¨an samaan tapaan.
Jos Z on satunnaismatriisi ja A, B ja C ovat vakiomatriiseja, joiden dimensiot ovat yhteensopivia, niin odotusarvon lineaarisuudesta ja matriisioperaatioiden m¨a¨aritelmist¨a seuraa, ett¨a
E[AZB + C] = A(EZ)B + C.
Kahden satunnaisvektorin U ja V kovarianssimatriisi m¨a¨aritell¨a¨an kaavalla
Cov(U, V ) = E[(U − EU )(V − EV )T ],
joten sen alkio (i, j) on E[(Ui −EUi )(Vi −EVi )T ] = Cov(Ui , Vj ). Jos A ja a ovat
vakiomatriisi ja vakiovektori siten, ett¨a lauseke AU + a on hyvin m¨a¨aritelty,
ja B ja b ovat vakiomatriisi ja vakiovektori siten, ett¨a lauseke BV + b on
hyvin m¨a¨aritelty, niin koska
AU + a − E[AU + a] = A(U − EU ),
BV + b − E[BV + b] = B(V − EV ),
on
Cov(AU + a, BV + b) = E[(A(U − EU )(V − EV )T B T ] = A Cov(U, V )B T .
21
T¨am¨a kaava pit¨a¨a sis¨all¨a¨an luvussa 1.3.6 k¨aytetyn kovarianssin bilineaarisuusominaisuuden.
Satunnaisvektorin Y kovarianssimatriisi (eli varianssi-kovarianssimatriisi)
on
Cov(Y ) = Cov(Y, Y ) = E[(Y − EY )(Y − EY )T ],
jonka alkio kohdassa (i, j) on E[(Yi − EYi )(Yj − EYj )] = Cov(Yi , Yj ). Kovarianssimatriisi on aina v¨ahint¨aa¨n positiivisesti semidefiniitti (ja usein per¨ati
positiivisesti definiitti). Edell¨a johdetun kaavan nojalla
Cov(AY + b) = A Cov(Y )AT ,
kun A on vakiomatriisi ja b vakiovektori.
Multinormaalijakauma eli moniulotteinen normaalijakauma voidaan m¨a¨aritell¨a l¨ahtem¨all¨a liikkeelle satunnaisvektorista U = (U1 , . . . , Uk ),
jonka komponentit ovat riippumattomia ja noudattavat standardinormaalijakaumaa, Uj ∼ N (0, 1). T¨all¨oin satunnaisvektorilla U on tiheysfunktio
k
Y
1 2
1
1
√ e− 2 ui = (2π)−n/2 exp(− uT u),
fU (u) =
2
2π
j=1
u = (u1 , . . . , uk )T .
Merkit¨aa¨n t¨all¨oin, ett¨a U ∼ N (0, I). Huomaa, ett¨a EU = 0 ja Cov(U ) = I.
T¨am¨an j¨alkeen sanotaan, ett¨a satunnaisvektorilla Y on multinormaalijakauma, jos se voidaan esitt¨a¨a muodossa
Y = AU + b,
jossa A on vakiomatriisi ja b vakiovektori. Voidaan osoittaa, ett¨a multinormaalijakauman m¨a¨ar¨a¨av¨at jakauman odotusarvovektori sek¨a kovarianssimatriisi, ja multinormaalijakaumalle odotusarvolla µ ja kovarianssimatriisilla Σ
k¨aytet¨a¨an merkint¨a¨a N (µ, Σ).
Multinormaalijakaumalla on mm. seuraavat ominaisuudet.
• Jos Y noudattaa multinormallijakaumaa, niin Y :n komponentit noudattavat yksiulotteista normaalijakaumaa, ja yleisemmin, jos C on vakiomatriisi ja d on vakiovektori, niin satunnaisvektori CY + d noudattaa multinormaalijakaumaa. T¨am¨a n¨ahd¨aa¨n l¨ahtem¨all¨a liikkeelle esityksest¨a Y = AU + b, jossa U ∼ N (0, I) ja huomaamalla, ett¨a
CY + d = (CA)U + (Cb + d).
• Jos Σ on positiivisesti definiitti (jolloin se on my¨os ei-singulaarinen),
niin jakaumalla N (µ, Σ) on tiheysfunktio
1
T −1
−n/2
−1/2
f (y) = (2π)
det(Σ)
exp − (y − µ) Σ (y − µ) .
2
22
• Jos Σ on singulaarinen, niin multinormaalijakauma N (µ, Σ) on my¨os
singulaarinen ts. se ei ole jatkuva jakauma eik¨a diskreetti jakauma
(paitsi jos Σ = 0, jolloin jakauma on diskreetti).
• Jos Y noudattaa multinormaalijakaumaa, ja sen osavektorit
U = (Y1 , . . . , Yj )T ,
V = (Yj+1 , . . . , Yk )
ovat korreloimattomia ts. Cov(U, V ) = 0, niin ne ovat per¨ati riippumattomia. (T¨ah¨an ominaisuuteen vedottiin lukuisia kertoja luvussa 1).
T¨am¨an ominaisuuden todistaminen onnistuisi n¨app¨ar¨asti k¨aytt¨am¨all¨a
jakauman karakteristista funktiota. Ei-singulaarisessa tapauksessa ominaisuuden voi todistaa my¨os k¨aytt¨am¨all¨a tiheysfunktion lauseketta.
Multinormaalijakauman avulla ilmaistuna lineaarisen mallin µ = Xβ oletukset (rakenneoletus ja jakaumaoletus) voidaan molemmat ilmaista kaavalla
Y ∼ N (Xβ, σ 2 I),
sill¨a onhan mallin mukaan
Yi = µi + σ
Yi − µi
= µi + σUi ,
σ
jossa satunnaismuuttujat Ui ∼ N (0, 1) riippumattomasti, ja µi = [Xβ]i .
Koska kerroinvektorin SU-estimaattori on
βˆ = (X T X)−1 X T Y,
jossa X ja siten my¨os (X T X)−1 X T on vakiomatriisi, niin βˆ noudattaa multinormaalijakaumaa, jonka odotusarvovektori ja kovarianssimatriisi lasketaan
seuraavaksi.
Odotusarvovektori on
E βˆ = (X T X)−1 X T EY = (X T X)−1 X T Xβ = β,
joten βˆ on harhaton. Kovarianssimatriisi on
ˆ = (X T X)−1 X T Cov(Y )[(X T X)−1 X T ]T
Cov(β)
= (X T X)−1 X T (σ 2 I)X(X T X)−1 = σ 2 (X T X)−1 .
Siis βˆ noudattaa (ei-singulaarista) multinormaalijakaumaa
βˆ ∼ N (β, σ 2 (X T X)−1 ).
23
My¨os sovitevektori
µ
ˆ = X βˆ = X(X T X)−1 X T Y = HY
sek¨a residuaalivektori
R=Y −µ
ˆ = (I − H)Y
noudattavat multinormaalijakaumaa, koska ne saadaan lineaarisilla muunnoksilla multinormaalijakaumaa noudattavasta vektorista Y . Laskemalla n¨ahd¨a¨an,
ett¨a
µ
ˆ ∼ N (µ, σ 2 H),
R ∼ N (0, σ 2 (I − H)).
N¨am¨a molemmat multinormaalijakaumat ovat singulaarisia (ellei malli ei ole
triviaali). My¨os µ
ˆ:n ja R:n yhteisjakauma on singulaarinen multinormaalijakauma, jossa
Cov(ˆ
µ, R) = 0,
joten satunnaisvektorit µ
ˆ ja R ovat riippumattomia. Koska varianssiparametrin estimaattori
σ
˜2 =
1
kRk2 ,
n−k
k = dim(L)
on satunnaisvektorin R funktio, ovat µ
ˆ ja σ
˜ 2 riippumattomia. Samalla tavalla
n¨ahd¨a¨an, ett¨a my¨os βˆ ja σ
˜ 2 ovat riippumattomia.
2.3
Uskottavuusosam¨
a¨
ar¨
atestin ja F -testin v¨
alinen
yhteys
Tilastollisen p¨a¨attelyn perusty¨okalu lineaarisessa mallissa on ns. F -testi. T¨ass¨a
luvussa esitell¨a¨an ko. testi sek¨a osoitetaan, ett¨a se on ekvivalentti uskottavuusosam¨aa¨r¨atestin kanssa.
Olkoot L1 ja L2 kaksi sis¨akk¨aist¨a aliavaruutta siten, ett¨a L2 on L1 :n aito
aliavaruus, eli
L2 ⊂ L 1 ,
ja k2 = dim(L2 ) < k1 = dim(L1 ).
Oletamme, ett¨a aliavaruutta L1 vastaava lineaarinen malli on voimassa, ja
tahdomme testata hypoteesia
H0 : µ ∈ L2
k¨aytt¨am¨all¨a vastahypoteesia HA : µ ∈ L1 \ L2 .
24
Uskottavuusosam¨aa¨r¨atesti (likelihood ratio test) perustuu testisuureeseen
Q(y) =
L(ˆ
µ1 , σ
ˆ12 )
,
L(ˆ
µ2 , σ
ˆ22 )
jossa (ˆ
µ1 , σ
ˆ12 ) ovat parametrien (µ, σ 2 ) SU-estimaatit k¨aytt¨am¨all¨a mallia L1 ja
(ˆ
µ2 , σ
ˆ22 ) SU-estimaatit k¨aytt¨am¨all¨a mallia L2 . Osoittajassa on uskottavuusfunktion maksimiarvo mallin L1 ja nimitt¨aj¨ass¨a mallin L2 vallitessa. Koska
parametriavaruudet ovat sis¨akk¨aiset (L2 ⊂ L1 ), on L(ˆ
µ1 , σ
ˆ12 ) ≥ L(ˆ
µ2 , σ
ˆ22 ),
joten Q(y) ≥ 1.
Suuret testisuureen Q(y) arvot ovat kriittisi¨a H0 :n kannalta: jos Q(y)
on suuri, niin uskottavuusfunktion maksimi mallissa L2 on selv¨asti pienempi kuin uskottavuusfunktion maksimi mallissa L1 . Nollahypoteesi µ ∈ L2
hyl¨at¨a¨an merkitsevyystasolla α, jos Q(y) > c, jossa c m¨a¨ar¨aytyy ehdosta
PL2 (Q(Y ) > c) = α.
Seuraavaksi muokkaamme testisuureen Q(y) lauseketta. Lauseen 1 mukaan
2 − n2 − n2
σ
ˆ1
ky − µ
ˆ 1 k2
L(ˆ
µ1 , σ
ˆ12 )
=
=
Q(y) =
L(ˆ
µ2 , σ
ˆ22 )
σ
ˆ22
ky − µ
ˆ 2 k2
T¨ass¨a
y−µ
ˆ2 = (y − µ
ˆ1 ) + (ˆ
µ1 − µ
ˆ2 ),
jossa termit ovat ortogonaalisia, sill¨a y−ˆ
µ1 ∈ L ⊥
ˆ1 −ˆ
µ2 ∈ L1 . Pythagoraan
1 ja µ
lauseen mukaan
ky − µ
ˆ2 k2 = ky − µ
ˆ1 k2 + kˆ
µ1 − µ
ˆ 2 k2 ,
ja kun t¨am¨a sijoitetaan Q(y):n lausekkeeseen, se saadaan muotoon
Q(y) =
ky − µ
ˆ 2 k2
ky − µ
ˆ 1 k2
n2
=
kˆ
µ1 − µ
ˆ 2 k2
1+
ky − µ
ˆ 1 k2
n2
Seuraavaksi m¨a¨arittelemme F -testisuureen hypoteeseille H0 : µ ∈ L2 kaavalla
kˆ
µ1 − µ
ˆ2 k2 /(k1 − k2 )
F (y) =
.
ky − µ
ˆ1 k2 /(n − k1 )
Huomaa, ett¨a uskottavuusosam¨a¨ar¨an testisuure Q(y) saadaan soveltamalla
bijektiivist¨a aidosti kasvavaa funktiota testisuureeseen F (y). Uskottavuusosam¨aa¨r¨atestin kriittinen alue on muotoa Q(y) > c ja F -testin kriittinen
alue on muotoa F (y) > d, joten n¨am¨a testit ovat samoja.
25
0.4
0.0
0
2
4
6
8
Kuva 2.1: F -testin kriittinen alue merkitsevyystasolla α koostuu kyseess¨a
olevan F -jakauman siit¨a oikeanpuoleisesta h¨ant¨aalueesta, johon j¨a¨a todenn¨ak¨oisyysmassasta α:n verran.
Suuret testisuureen F (y) arvot ovat kriittisi¨a H0 :n kannalta. Tulemme
my¨ohemmin todistamaan, ett¨a nollahypoteesin p¨atiess¨a (eli kun µ ∈ L2 ) F testisuureen jakauma on F -jakauma vapausasteilla k1 − k2 ja n − k1 , eli
F (Y ) ∼ F (k1 − k2 , n − k1 ),
kun H0 p¨atee eli kun µ ∈ L2 .
Palautetaan t¨ass¨a yhteydess¨a mieleen F -jakauman m¨a¨aritelm¨a. Jos satunnaismuuttujat U1 ∼ χ2 (f1 ) ja U2 ∼ χ2 (f2 ) ovat riippumattomia, niin
t¨all¨oin osam¨a¨ar¨a
U1 /f1
∼ F (f1 , f2 ),
U2 /f2
miss¨a F (f1 , f2 ) on (Fisherin) F -jakauma vapausasteilla f1 ja f2 . V¨alitt¨om¨asti
n¨aemme, ett¨a jos T ∼ t(f ), niin T 2 ∼ F (1, f ).
Kun testataan hypoteesia H0 : µ ∈ L2 merkitsevyystasolla α, verrataan
F -testisuureetta F (y) arvoon d, joka m¨a¨ar¨at¨a¨an siten, ett¨a nollahypoteesin
p¨atiess¨a hypoteesi hyl¨at¨a¨an todenn¨ak¨oisyydell¨a α, eli
PL2 (F (Y ) > d) = α,
ks. kuvaa 2.1. Kun k¨ayt¨amme hyv¨aksi sit¨a tietoa, ett¨a F (Y ):ll¨a on H0 :n
vallitessa F -jakauma, niin n¨aemme, ett¨a
d = F1−α (k1 − k2 , n − k1 ),
26
jossa Fβ (f1 , f2 ) tarkoittaa sit¨a pistett¨a, jossa ko. F -jakauman kertym¨afunktio
saa arvon β. T¨am¨an testin p-arvo on
PL2 (F (Y ) ≥ F (y)) = 1 − G(F (y)),
miss¨a G on jakauman F (k1 − k2 , n − k1 ) kertym¨afunktio.
2.4
Yhden selitt¨
aj¨
an lineaarinen regressio
uudestaan k¨
asiteltyn¨
a
K¨asittelemme yhden selitt¨aj¨an lineaarista regressiota keskistetyss¨a muodossa,
EYi = µi = α + β2 ti , jossa ti = xi − x¯,
i = 1, . . . , n,
eli mallin rakenneoletus on
µ = α1 + β2 t,
jossa t = (t1 , . . . , tn )T .
Huomaa, ett¨a
a) vektorit 1 ja t ovat lineaarisesti riippumattomia, mik¨ali t ei ole muotoa
a1. Koska ti -arvojen keskiarvo on nolla, vektorit 1 ja t ovat lineaarisesti
riippumattomia silloin ja vain silloin, kun
St =
n
X
t2i > 0.
i=1
Jos St > 0, vektorit 1 ja t muodostavat kaksiulotteisen aliavaruuden
span{1, t} kannan.
P
b) Vektorit 1 ja t ovat ortogonaalisia, sill¨a 1T t = ni=1 ti = 0.
Oletetaan, ett¨a St > 0. T¨all¨oin 1 ja t ovat lineaarisesti riippumattomia,
ja lineaarisen mallin mallimatriisi X on
X = [1, t],
joten
T
1 1 1T t
n 0
X X= T
=
,
t 1 tT t
0 St
T
27
Pn
y
n¯
y
i
X y = Pni=1
=
,
t
y
S
ty
i=1 i i
T
josta
T
−1
(X X)
1/n
0
=
,
0 1/St
α
ˆ
y¯
T
−1 T
= (X X) X y =
.
Sty /St
βˆ2
Regressiokertoimien estimaattorien jakauma on
2
α
ˆ
α
α
σ /n
0
2
T
−1
∼N
, σ (X X)
=N
,
.
β2
β2
0
σ 2 /St
βˆ2
Oletetaan, ett¨a yhden selitt¨aj¨an lineaarinen malli pit¨a¨a paikkansa, ja johdetaan F -testisuure hypoteesille H2 , ett¨a selitt¨av¨a muuttuja on mallissa tarpeeton, eli hypoteesille
H2 : β2 = 0.
Alkuper¨ainen malli vastaa aliavaruutta
L1 = span{1, t}
ja hypoteesia H2 vastaa aliavaruus
L2 = span{1}.
T¨ass¨a
L2 ⊂ L1 ,
ja
dim(L2 ) = 1 < dim(L1 ) = 2.
Mallin L1 p¨atiess¨a sovite on
µ
ˆ1 = α
ˆ 1 + βˆ2 t = y¯1 + βˆ2 t,
ja mallin L2 p¨atiess¨a taas
yT 1
1 = y¯1.
k1k2
N¨ain ollen F -testisuure hypoteesille β2 = 0 on
µ
ˆ2 =
F (y) =
kˆ
µ1 − µ
ˆ2 k2 /(2 − 1)
βˆ22 St
=
,
ky − µ
ˆ1 k2 /(n − 2)
σ
˜2
miss¨a σ
˜ 2 on varianssiparametrin estimaatti mallissa L1 ,
1
σ
˜2 =
ky − µ
ˆ1 k2 .
n−2
Palautetaan mieleen luvusta 1.5, ett¨a t-testisuure hypoteesille β2 = 0 on
βˆ2
t(y) = √ ,
σ
˜ / St
joten F -testisuureen ja t-testisuureen v¨alill¨a on yhteys
F (y) = t2 (y).
T¨ast¨a seuraa, ett¨a t¨alle hypoteesille F -testi ja (kaksisuuntainen) t-testi ovat
samoja.
28
2.5
Lis¨
a¨
a jakaumateoriaa
T¨ass¨a kappaleessa osoitetaan, ett¨a aikaisemmin m¨a¨aritellyll¨a F -testisuureella
on nollahypoteesin p¨atiess¨a todellakin F -jakauma Sivutuotteena johdetaan
se tulos, ett¨a aliavaruutta L vastaavassa yleisess¨a lineaarisessa mallissa varianssiparametrin estimaattorin jakauma on seuraava skaalattu khiin neli¨o,
σ
˜2 =
1
σ2 2
kY − µ
ˆ k2 ∼
χ (n − k),
n−k
n−k
jossa k = dim(L).
2.5.1
Multinormaalijakauman N (0, σ 2 I) ominaisuuksia
Kirjoitamme lineaarisen mallin muodossa
Y = µ + ,
µ ∈ L,
jossa virhevektorin = (1 , . . . , n )T komponentit ovat riippumattomia, ja
niill¨a on jakauma N (0, σ 2 ), joten virhevektorilla on multinormaalijakauma
N (0, σ 2 I).
Seuraavaksi osoitamme, ett¨a jos esit¨amme virhevektorin miss¨a tahansa
R n :n ortonormeeratussa kannassa, niin koordinaattien yhteisjakauma on edelleen N (0, σ 2 I). Olkoon e1 , . . . , en avaruuden R n ortonormeerattu kanta ts.
kantavektorit ovat kesken¨a¨an ortogonaalisia ja kunkin pituus on yksi. Muodostetaan neli¨omatriisi A asettamalla kantavektorit A:n sarakkeiksi,
A = [e1 , . . . , en ].
T¨all¨oin A on ortogonaalinen matriisi, eli
A−1 = AT .
Ortogonaalisen matriisin determinantti on joko +1 tai −1, sill¨a
1 = det(I) = det(AT A) = det(AT ) det(A) = det(A)2 .
Olkoot ϕ1 , . . . , ϕn satunnaisvektorin koordinaatit ortonormeeratussa kannassa e1 , . . . , en , jolloin
n
X
ϕi ei = Aϕ,
=
i=1
jossa ϕ = (ϕ1 , . . . , ϕn ). T¨ast¨a n¨ahd¨a¨an satunnaisvektorien ja ϕ v¨alinen
yhteys,
ϕ = AT ⇔ = Aϕ.
29
Lause 2. Jos A on ortogonaalinen matriisi ja ∼ N (0, σ 2 I), niin satunnaisvektorin ϕ = AT jakauma on N (0, σ 2 I).
Todistus. Satunnaisvektorin tiheysfunktio on
1
2 −n/2
2
f (x) = (2πσ )
exp − 2 kxk ,
2σ
ja satunnaisvektorin ϕ tiheysfunktio fϕ saadaan kaavalla
1
2 −n/2
2
fϕ (y) = f (Ay) | det(A)| = (2πσ )
exp − 2 kyk ,
2σ
jossa k¨aytettiin hyv¨aksi tulosta kAyk2 = y T AT Ay = y T y = kyk2 .
Palautetaan mieleen kappaleesta 2.1, ett¨a merkint¨a L1 ⊕ L2 tarkoittaa
kahden ortogonaalisen aliavaruuden ortogonaalista suoraa summaa. Laajennamme merkinn¨an koskemaan useampaa kuin kahta aliavaruutta. Merkint¨a
U = L1 ⊕ · · · ⊕ Lr
tarkoittaa aliavaruuksien L1 , . . . , Lr ortogonaalista suoraa summaa, eli sit¨a,
ett¨a aliavaruudet Li ja Lj ovat ortogonaalisia, kun i 6= j, ja ett¨a U :n alkiot
ovat muotoa
u = v1 + · · · + vr , jossa vj ∈ Lj .
Lause 3. Olkoon ∼ N (0, σ 2 I) ja olkoot L1 , . . . , Lr avaruuden R n ortogonaalisia aliavaruuksia siten, ett¨a
R n = L1 ⊕ · · · ⊕ Lr .
Olkoon ki = dim(Li ) ja olkoon pi ortogonaaliprojektio aliavaruuteen Li .
T¨all¨oin
(i) p1 (), . . . , pr () ovat riippumattomia.
(ii) kpi ()k2 ∼ σ 2 χ2 (ki ), i = 1, . . . , r.
Todistus. Muodostetaan kullekin aliavaruudelle Lj ortonormeerattu kanta,
ja luetellaan kantavektorit per¨akk¨ain siten, ett¨a ensin luetellaan L1 :n kantavektorit, sitten L2 :n kantavektorit jne. ja viimeiseksi Lr :n kantavektorit.
T¨all¨oin lopputulos, e1 , . . . , en , on R n :n ortonormeerattu kanta, koska aliavaruudet Lj ovat ortogonaalisia. Konstruktion perusteella Lj :n kantavektorit
ovat
enj−1 +1 , . . . , enj ,
j = 1, . . . , r
30
kun m¨aa¨ritell¨a¨an n0 = 0 ja
n j = k1 + · · · + kj ,
j = 1, . . . , r.
M¨a¨aritell¨a¨an ortogonaalinen matriisi A siten, ett¨a sen sarakkeet ovat ortonormaalit kantavektorit e1 , . . . , en ja m¨aa¨ritell¨aa¨n satunnaisvektori ϕ kaavalla
ϕ = AT ⇔ = Aϕ.
T¨all¨oin ortogonaaliprojektiolla pj on esitys
nj
X
pj () =
ϕi ei .
i=nj−1 +1
Lauseen 2 mukaan satunnaismuuttujat ϕ1 , . . . , ϕn ovat riippumattomia, ja
kukin niist¨a noudattaa normaalijakaumaa N (0, σ 2 ). Niinp¨a satunnaisvektorit
p1 (), . . . , pr ()
ovat riippumattomia, sill¨a pj () riippuu vain muuttujista
ϕi ,
i = nj−1 + 1, . . . , nj ,
ja t¨ass¨a indeksijoukot ovat erillisi¨a eri j:n arvoilla. Pythagoraan lauseen ja
χ2 -jakauman m¨a¨aritelm¨an nojalla p¨atee lis¨aksi
2
kpj ()k =
nj
X
i=nj−1 +1
ϕ2j
=σ
nj
X
2
ϕ 2
j
i=nj−1 +1
σ
∼ σ 2 χ2 (kj ).
2.5.2
Parametrien estimaattorit
Tarkastellaan lineaarista mallia µ ∈ L1 , eli
Y = µ + ,
µ ∈ L1 ,
∼ N (0, σ 2 I),
jossa dim(L1 ) = k1 . Esitet¨aa¨n R n ortogonaalisena suorana summana
R n = L1 ⊕ L⊥
1,
ja olkoot pL1 ja pL⊥1 vastaavat ortogonaaliset projektiot.
31
Lauseen 3 mukaan
kpL⊥1 ()k2 ∼ σ 2 χ2 (n − k1 ).
Lis¨aksi
pL⊥1 (Y ) = Y − pL1 (Y ),
ja toisaalta
pL⊥1 (Y ) = pL⊥1 (µ) + pL⊥1 () = pL⊥1 ().
Edell¨a pL⊥1 (µ) = 0, sill¨a µ ∈ L1 . T¨am¨an takia
σ
˜2 =
1
σ2
1
kY − pL1 (Y )k2 =
kpL⊥1 ()k2 ∼
χ2 (n − k1 ),
n − k1
n − k1
n − k1
joka tulos saatiin nyt vihdoin viimein todistettua, vaikka sit¨a on sovellettu
jo useissa yhteyksiss¨a aikaisemmin. Erityisesti estimaattori σ
˜ 2 on harhaton,
Eσ
˜ 2 = σ2.
Koska
µ
ˆ = pL1 (Y ) = pL1 (µ) + pL1 () = µ + pL1 (),
n¨ahd¨a¨an lausetta 3 soveltamalla, ett¨a sovitevektori µ
ˆ ja estimaattori σ
˜ 2 ovat
kesken¨aa¨n riippumattomia, mink¨a asian tiesimme jo luvun 2.2.2 perusteella.
2.5.3
F-testi
Tarkastelemme kahta sis¨akk¨aist¨a aliavaruutta
L2 ⊂ L1 ,
k2 = dim(L2 ) < k1 = dim(L1 ),
ja oletamme, ett¨a aliavaruutta L2 vastaava lineaarinen malli pit¨a¨a paikkansa.
Olkoot p1 ja p2 ortogonaaliprojektiot aliavaruudelle L1 ja L2 , jolloin
µ
ˆ1 = p1 (y),
µ
ˆ2 = p2 (y).
F -testisuure L2 :lle L1 :n vallitessa on
F (y) =
kp1 (y) − p2 (y)k2 /(k1 − k2 )
ky − p1 (y)k2 /(n − k1 )
Osoitamme seuraavaksi, ett¨a L2 :n vallitessa F -testisuureella on jakauma
F (Y ) ∼ F (k1 − k2 , n − k1 ),
32
kun µ ∈ L2 .
Oletetaan siis, ett¨a µ ∈ L2 . Esitet¨a¨an R n seuraavan kolmen aliavaruuden
ortogonaalisena suorana summana,
R n = L2 ⊕ (L1 L2 ) ⊕ L⊥
1,
jossa aliavaruuksien dimensiot ovat k2 , k1 − k2 ja n − k1 , ja jossa ortogonaaliprojektiot ko. aliavaruuksiin ovat p2 , p1 − p2 ja y 7→ y − p1 (y). Lausetta 3
soveltamalla saadaan selville, ett¨a
kp2 ()k2 ∼ σ 2 χ2 (k2 )
kp1 () − p2 ()k2 ∼ σ 2 χ2 (k1 − k2 )
k − p2 ()k2 ∼ σ 2 χ2 (n − k1 ),
ja ett¨a n¨am¨a kolme satunnaismuuttujaa ovat riippumattomia.
Koska µ ∈ L2 ⊂ L1 , on µ = p1 (µ) = p2 (µ), joten
p1 (Y ) − p2 (Y ) = p1 (µ) + p1 () − p2 (µ) − p2 () = p1 () − p2 ()
Y − p1 (Y ) = µ + − p1 (µ) − p1 () = − p1 ().
Siis, kun µ ∈ L2 ,
kp1 () − p2 ()k2 /(k1 − k2 )
kp1 (Y ) − p2 (Y )k2 /(k1 − k2 )
=
kY − p1 (Y )k2 /(n − k1 )
k − p1 ()k2 /(n − k1 )
∼ F (k1 − k2 , n − k1 ),
F (Y ) =
jossa tarvittiin sit¨a tietoa, ett¨a osoittaja ja nimitt¨aj¨a ovat riippumattomia ja
jossa osoittajan ja nimitt¨aj¨an varianssiparametrit kumosivat toisensa.
F-testisuureen n¨akee usein esitett¨av¨an muodossa
F (y) =
(RSS2 − RSS1 )/(k1 − k2 )
,
RSS1 /(n − k1 )
jossa RSSj on j¨a¨ann¨osneli¨osumma (residual sum of squares) mallista µ ∈ Lj ,
eli
RSSj = ky − pLj (y)k2 .
T¨am¨a kaava on tietenkin yht¨apit¨av¨a edell¨a esitetyn kaavan kanssa (HT).
2.5.4
F-testi, kun rajoitteet ovat muotoa Aβ = 0
K¨ayt¨ann¨oss¨a malli µ ∈ L1 spesifioidaan useimmiten tietyn mallimatriisin
avulla, µ = Xβ, ja rajoitettu malli µ ∈ L2 annetaan usein muodossa
Aβ = 0,
33
jossa A on annettu q × k-matriisi, jonka vaakarivit ovat lineaarisesti riippumattomia. T¨all¨oin alkuper¨aisen mallin aliavaruus L1 = R(X), ja rajoitetun
mallin µ ∈ L2 aliavaruus L2 on
L2 = {µ ∈ R n : ∃β ∈ R k siten, ett¨a µ = Xβ ja Aβ = 0}.
T¨all¨oin voidaan edet¨a sill¨a tavalla, ett¨a q kappaletta parametreista βj eliminoidaan rajoitusehtojen avulla. Esimerkiksi, jos q = 1 ja rajoitusehtona on
β1 + β2 = 0, niin t¨all¨oin voidaan esim. β1 eliminoida kaavalla β1 = −β2 ja ilmaista rajoitettu malli parametrien β2 , . . . , βk avulla. T¨am¨an j¨alkeen voidaan
ratkaista µ
ˆ2 ja k¨aytt¨a¨a edell¨a kehitetty¨a kaavaa F -testisuureelle.
T¨ass¨a tilanteessa voidaan antaa my¨os eksplisiittinen kaava F -testisuureelle.
Er¨as hy¨odyllinen muoto on
F (y) =
ˆ
βˆT AT [A(X T X)−1 AT ]−1 Aβ/q
,
σ
˜2
(*)
jossa βˆ on alkuper¨aisest¨a mallista µ ∈ L1 laskettu estimaatti
βˆ = (X T X)−1 X T y,
ja σ
˜ 2 on alkuper¨aisen mallin µ ∈ L1 varianssiparametrin estimaatti.
Kaavan (*) voi johtaa l¨ahtem¨all¨a liikkeelle siit¨a, ett¨a F -testisuureen osoittajassa oleva neli¨omuoto on y:n ortogonaaliprojektion pituuden neli¨o aliavaruudelle L1 L2 . Lis¨aksi tarvitaan se tieto, ett¨a matriisin
X(X T X)−1 AT
sarakkeet muodostavat kannan aliavaruudelle L1 L2 . T¨am¨a todistetaan tarkistamalla, ett¨a kyseisen matriisin sarakkeet ovat lineaarisesti riippumattomia sek¨a laskemalla seuraavasti.
v ∈ L 1 L2 = L 1 ∩ L ⊥
2
⇔ v = Xβ ja (Aβ 0 = 0 ⇒ β 0 X T Xβ = 0)
⇔ v = Xβ ja X T Xβ ∈ N (A)⊥ = R(AT )
⇔ v = Xβ ja X T Xβ = AT z jollekin z ∈ R q
⇔ v = X(X T X)−1 AT z jollekin z ∈ R q .
Lopuksi kaava (*) johdetaan soveltamalla luvun 2.2.1 teoriaa k¨aytt¨am¨all¨a
kantana matriisin X(X T X)−1 AT sarakkeita.
34
2.6
t-testin ja F -testin v¨
alinen yhteys
Tarkastellaan lineaarista mallia µ = Xβ, jonka mallimatriisi on X. Luvussa
2.2.2 johdettiin kerroinvektorin β SU-estimaattorille tulos
βˆ ∼ N (β, σ 2 C),
jossa C = (XX T )−1 .
Olkoon cij matriisin C alkio kohdassa (i, j). Kerroinvektorin β = (β1 , . . . , βk )
alkion βj keskivirhe on
√
s. e.(βˆj ) = σ
˜ cjj
ja sen t-testisuure on
t(y) =
βˆj − βj
.
s. e.(βˆj )
Kirjoitetaan vastaava satunnaissuure t(Y ) muodossa
√
(βˆj − βj )/(σ cjj )
p
t(Y ) =
,
σ
˜ 2 /σ 2
jossa osoittajassa on standardinormaalijakaumaa noudattava satunnaismuuttuja, ja nimitt¨aj¨ass¨a on neli¨ojuureen sis¨all¨a siit¨a riippumaton satunnaismuuttuja, jolle
σ
˜2
1
∼
χ2 (n − k).
2
σ
n−k
Siis t-jakauman m¨a¨aritelm¨an nojalla
t(Y ) ∼ t(n − k),
mink¨a perusteella voidaan muodostaa hypoteesia βj = 0 koskeva t-testi samalla tavalla kuin luvussa 1.5. T¨allaisessa testiss¨a tutkitaan, onko kerrointa
βj vastaava selitt¨aj¨a tarpeellinen lineaarisessa mallissa, kun malli sis¨alt¨aa¨
muut selitt¨av¨at muuttujat.
Hypoteesia βj = 0 voidaan testata my¨os F -testill¨a. T¨am¨a vastaa rajoitetta Aβ = 0, jossa A = eTj ja ej on R n :n standardikannan j:s vektori.
K¨aytt¨am¨all¨a luvun 2.5.4 kaavaa (*) F -testisuureeksi saadaan
F (y) =
βˆj2 /cjj
,
σ
˜2
joten
F (y) = t2 (y),
mist¨a seuraa, ett¨a testit ovat samat.
Kirjassa vastaava lasku lasketaan ilman kaavaa (*), ja laskut ovat huomattavasti hankalampia kuin yhden selitt¨aj¨an tapauksessa.
35
2.7
Luottamusjoukot ja affiinit hypoteesit
2.7.1
Luottamusellipsoidi
Oletetaan, ett¨a satunnaisvektori Y noudattaa lineaarista mallia n×k-mallimatriisilla
X eli ett¨a
Y = µ + , µ = Xβ, ∼ N (0, σ 2 I).
Tarkastellaan hypoteesia H2 : β = β0 , jossa β0 on annettu k-komponenttinen
vektori. Emme voi testata t¨at¨a hypoteesia suoraan F -testill¨a, sill¨a ko. hypoteesi on µ:n avulla ilmaistuna sama kuin
µ ∈ {µ0 },
jossa µ0 = Xβ0 ,
ja joukko {µ0 } on aliavaruus t¨asm¨alleen silloin, kun µ0 = 0 eli kun β0 = 0. Sen
sijaan tarkastelemme muunnettua mallia, jossa hypoteesi H2 on ekvivalentti
aliavaruuden {0} kanssa.
M¨a¨aritell¨a¨an satunnaisvektori Y 0 kaavalla Y 0 = Y − Xβ0 . T¨all¨oin Y 0
noudattaa lineaarista mallia mallimatriisilla X, sill¨a
Y 0 = Y − Xβ0 = X(β − β0 ) + = Xβ 0 + ,
miss¨a uuden mallin parametrin β 0 ja alkuper¨aisen mallin parametrin β v¨alill¨a
on yhteys
β 0 = β − β0 .
Alkuper¨aisen mallin hypoteesi β = β0 on sama kuin uuden mallin hypoteesi β 0 = 0. Kehitet¨a¨an seuraavaksi F -testisuureen lauseketta uuden mallin
hypoteesille β 0 = 0 eli aliavaruudelle L2 = {0}.
Uudessa mallissa
µ
ˆ1 = X βˆ0 ja µ
ˆ2 = 0,
miss¨a uuden mallin kerroinvektorin β 0 SU-estimaattorille p¨atee kaava
βˆ0 = (X T X)−1 X T Y 0 = (X T X)−1 X T (Y − Xβ0 ) = βˆ − β0 ,
jossa βˆ on alkuper¨aisen mallin kerroinvektorin β SU-estimaattori. Niinp¨a F testisuureen osoittajassa on neli¨omuoto
kˆ
µ1 − µ
ˆ2 k2 = kX βˆ0 k2 = kX(βˆ − β0 )k2 = (βˆ − β0 )T X T X(βˆ − β0 ).
Nimitt¨aj¨ass¨a on varianssiparametrin estimaatti uudessa mallissa, kun µ ∈
L1 = R(X) eli
1
1
1
ˆ 2,
ky 0 − X βˆ0 k2 =
ky − Xβ0 − X(βˆ − β0 )k2 =
ky − X βk
n−k
n−k
n−k
36
joten nimitt¨aj¨a on sama kuin varianssiparametrin estimaatti σ
˜ 2 alkuper¨aisess¨a
mallissa. F -testisuureen lauseke ja sen jakauma on
F (Y ) =
(βˆ − β0 )T X T X(βˆ − β0 )/k
∼ F (k, n − k),
σ
˜2
kun β = β0 .
F -testisuureen avulla voidaan johtaa luottamusjoukko parametrivektorille β. Jos on annettu luottamustaso 1 − a (jossa 0 ≤ a ≤ 1), niin todenn¨ak¨oisyydell¨a 1 − a on voimassa
(
)
ˆT T
ˆ
k (β0 − β) X X(β0 − β)/k
β ∈ β0 ∈ R :
≤ F1−a (k, n − k)
σ
˜2
jossa F1−α (f1 , f2 ) on se piste, jossa F (f1 , f2 )-jakauman kertym¨afunktio saa
arvon 1 − α. T¨am¨a luottamusjoukko on R k :n ellipsoidi, jonka keskipiste on βˆ
ja jonka muodon m¨a¨ar¨a¨a matriisi X T X.
Luottamusellipsoidin visualisointi on tietenkin hankalaa, jos k > 3.
2.7.2
Luottamusv¨
alit
Yksitt¨aiselle kertoimelle βj , 1 ≤ j ≤ k voidaan muodostaa luottamusv¨ali
luvussa 2.6 johdetun tuloksen
t(Y ) =
perusteella, jossa
βˆj − βj
∼ t(n − k)
s. e.(βˆj )
√
s. e.(βˆj ) = σ
˜ cjj
ja jossa cjj on matriisin (X T X)−1 j:s l¨avist¨aj¨aalkio.
T¨ast¨a tuloksesta seuraa (samanlaisilla laskuilla kuin luvussa 1.5), ett¨a
luottamustasolla 1 − a kertoimelle βj p¨atee luottamusv¨ali
βˆj ± s. e.(βˆj ) t1−a/2 (n − k),
jossa t1−a/2 (n − k) on se piste, jossa t(n − k)-jakauman kertym¨afunktio saa
arvon 1 − a/2.
Varoitus: jos kaikille kertoimille muodostetaan luottamusv¨alit t¨all¨a tavalla, niin todenn¨ak¨oisyys, ett¨a kaikki komponentit saisivat samalla kerralla
arvon, joka osuu luottamusv¨aliin ei ole 1 − a.
37
2.7.3
Affiini hypoteesi
Tarkastellaan lineaarista mallia µ ∈ L1 sek¨a siit¨a rajoitettua mallia
H2 : µ ∈ x 0 + L2 ,
miss¨a x0 ∈ L1 on annettu vakio ja L2 ⊂ L1 annettu aliavaruus. T¨ass¨a joukko
x0 + L2 = {v ∈ R n : v = x0 + z jollekin z ∈ L2 }
on affiini aliavaruus, ja kutsumme vastaavaa hypoteesia affiiniksi hypoteesiksi. Affiini aliavaruus x0 + L2 ⊂ L1 oletusten x0 ∈ L1 ja L2 ⊂ L1 takia.
Hypoteesia H2 testataan siirtym¨all¨a tarkastelemaan satunnaisvektoria
Y 0 = Y − x0 = µ − x0 + = µ0 + .
Alkuper¨aisin mallin hypoteesi µ ∈ L1 on uudessa mallissa aliavaruutta L1
vastaava lineaarinen malli ja alkuper¨aisen mallin hypoteesi µ ∈ x0 + L2 on
uudessa mallissa aliavaruutta L2 vastaava hypoteesi.
T¨all¨a tekniikalla saadaan affiini hypoteesi muunnettua uuden mallin lineaariseksi hypoteesiksi, jonka j¨alkeen voidaan soveltaa F -testi¨a.
T¨arke¨a erikoistapaus affiinista mallista on se, jossa tarkasteltavat mallit
ovat
µ = Xβ
sek¨a siit¨a rajoitettu alimalli
µ = Xβ
ja Aβ = c,
jossa A on q × k-matriisi, jonka vaakarivit ovat lineaarisesti riippumattomia,
ja c ∈ R q on annettu vektori, joka on valittu siten, ett¨a yht¨al¨oll¨a Aβ = c on
(ainakin yksi) ratkaisu, eli c ∈ R(A). T¨all¨oin luvun 2.5.4 kaavaa (*) soveltamalla saadaan yksinkertaisilla laskuilla F -testisuure kehitetty¨a muotoon
F (y) =
(Aβˆ − c)T [A(X T X)−1 AT ]−1 (Aβˆ − c)/q
,
σ
˜2
jossa βˆ on rajoittamattoman mallin µ = Xβ kerroinvektorin estimaatti, eli
βˆ = (X T X)−1 X T y,
ja σ
˜ 2 on rajoittamattoman mallin varianssiparametrin estimaatti.
38
2.8
Tyhjent¨
avyys
Uskottavuusfunktio mallissa µ = Xβ, jossa X:n sarakkeet ovat lineaarisesti
riippumattomat on
1
2
2 −n/2
2
L(β, σ ) = (2πσ )
exp − 2 ky − Xβk .
2σ
Koska
ky − Xβk2 = y T y − 2y T Xβ + β T X T Xβ,
niin uskottavuusfunktio riippuu havainnoista y ainoastaan tunnusluvun
(y T y, y T X)
kautta. (Muista, ett¨a X on vakiomatriisi!) Faktorointikriteerin nojalla kyseinen tunnusluku on tyhjent¨av¨a.
My¨os tunnusluku
ˆ σ
(β,
˜2)
on tyhjent¨av¨a, sill¨a kyseinen pari saadaan bijektiivisell¨a kuvauksella parista
(y T y, y T X), mik¨a n¨ahd¨a¨an kaavoista
βˆ = (X T X)−1 X T y
1
1
ˆ
σ
˜2 =
(kyk2 − kˆ
µk2 ) =
(y T y − βˆT X T X β).
n−k
n−k
2.9
Ep¨
akeskeiset jakaumat ja F -testin voima
Kirjan luvussa 2.9 k¨asitell¨a¨an F -testin voimafunktiota eli todenn¨ak¨oisyytt¨a,
ett¨a nollahypoteesi hyl¨at¨a¨an (eli testi toimii oikein) silloin, kun vaihtoehtohypoteesi pit¨a¨a paikkansa. T¨at¨a todenn¨ak¨oisyytt¨a tarkastellaan mallin parametrien µ ja σ 2 funktiona. Osoittautuu, ett¨a F -testin voimafunktio voidaan
esit¨a¨a k¨aytt¨am¨all¨a ns. ep¨akeskeist¨a F -jakaumaa.
39
Luku 3
Yhden otoksen malli sek¨
a
yksisuuntainen
varianssianalyysi
3.1
Yhden otoksen lineaarinen malli
Tarkastelemme mallia, jossa satunnaismuuttujat Yi ovat riippumattomia, ja
Yi ∼ N (β, σ 2 ),
i = 1, . . . , n,
jolloin keskiarvovektori µ = EY toteuttaa yht¨al¨on
µ = β1,
eli mallimatriisi X = 1. T¨ast¨a saadaan helposti estimaattorit sek¨a niiden
jakaumat,
2
σ
βˆ = Y¯ ∼ N (β, )
n
n
X
1
σ2 2
σ
˜2 =
(Yi − Y¯ )2 ∼
χ (n − 1).
n − 1 i=1
n−1
Hypoteesia H0 : β = β0 voidaan testata t-testill¨a, jossa testisuure ja sen
jakauma ovat
βˆ − β0
Y¯ − β0
√ ∼ t(n − 1).
t(Y ) =
=
ˆ
σ
˜/ n
s. e.(β)
Luottamustason 1 − α luottamusv¨ali parametrille β on
σ
˜
y¯ ± √ t1−α/2 (n − 1)
n
40
3.2
Parivertailu
Tarkastelemme mallia
Yi = Ui2 − Ui1 ,
i = 1, . . . , n,
jossa parit (U11 , U12 ), . . . , (Un1 , Un2 ) ovat riippumattomia ja samoin jakautuneita ja jossa
Yi ∼ N (β, σ 2 ),
i = 1, . . . , n
riippumattomasti. Sen sijaan yhden parin satunnaismuuttujat Ui1 ja Ui2 saavat olla riippuvia. Tilanne, jossa havaintojen erotuksilla on yksiulotteinen
normaalijakauma syntyy erityisesti silloin, jos parilla (Ui1 , Ui2 ) on kaksiulotteinen normaalijakauma. Kiinnostuksen kohteena on hypoteesi H0 : β = 0,
jonka vallitessa parin havainnoilla on sama odotusarvo.
T¨ass¨a mallissa Ui1 voisi esim. olla vasteen arvo yksik¨olle i ennen tietty¨a
k¨asittely¨a, ja Ui2 vaste k¨asittelyn j¨alkeen. Toinen tapaus, jossa t¨am¨a malli
on paikallaan on se, jossa yksik¨on tietty¨a ominaisuutta mitataan kahdella
eri menetelm¨all¨a: Ui1 on yksik¨ost¨a i tehty mittaus menetelm¨all¨a yksi ja Ui2
yksik¨ost¨a i tehty mittaus menetelm¨all¨a kaksi.
Parivertailussa eli parittaisessa t-testiss¨a yksinkertaisesti vain sovelletaan
yhden otoksen lineaarisen mallin kaavoja erotuksiin Yi .
3.3
Yksisuuntainen varianssianalyysi
Indeksoimme nyt vastemuuttujat kahdella indeksill¨a i ja j. Indeksi i ∈ {1, . . . , k}
kertoo ryhm¨an ja j indeksoi tapauksia ryhm¨an sis¨all¨a. Ryhm¨ass¨a i indeksi j
saa arvot 1, . . . , nj , jossa nj ≥ 1. Usein ryhm¨at vastaavat erilaisia k¨asittelyj¨a
(treatment). Ryhm¨an i havaintoja vastaavat satunnaismuuttujat ovat
Yi1 , Yi2 , . . . , Yini .
Mallin mukaan vasteen keskiarvo on vakio kussakin ryhm¨ass¨a, mutta voi
vaihdella ryhm¨ast¨a ryhm¨a¨an,
Yij ∼ N (βi , σ 2 ),
i = 1, . . . , k,
j = 1, . . . , ni ,
jossa satunnaismuuttujat Yij ovat eri indekseill¨a kesken¨a¨an riippumattomia,
ja havaintojen kokonaislukum¨a¨ar¨a on
n = n1 + n2 + · · · + nk .
41
Vastaavat havaitut suureet ovat yij . Kiinnostuksen kohteena on nollahypoteesi, jonka mukaan vasteen odotusarvo ei riipu ryhm¨ast¨a i. T¨at¨a nollahypoteesia vastaa F -testisuure, joka voidaan tulkita tiettyjen varianssiestimaattorien suhteeksi, mink¨a perusteella (melkoisen harhaanjohtava) nimitys varianssianalyysi lienee aikanaan valittu.
Yksisuuntainen varianssianalyysi on tavallaan yhden selitt¨aj¨an lineaarisen
mallin yleistys: siin¨a kuvaillaan vastevektorin Y riippuvuutta faktorista I,
jossa


 
Y11
1
 .. 
 .. 
 . 
.


 
 Y1n1 
1


 
 Y21 
2
 . 
.
 . 
.
.


.
Y =
I =  .
,
 Y2n2 
2
 . 
.
 .. 
 .. 


 
Y 
k 
 k1 
 
 .. 
 .. 
 . 
.
Yknk
k
Kussakin kohdassa faktorin I arvo (eli sen taso) kertoo, mist¨a ryhm¨ast¨a
vastaava havainto on per¨aisin vektorissa Y . Joskus faktorin I tasot syntyv¨at
diskretoimalla jatkuvan muuttujan X vaihteluv¨ali, jolloin yksisuuntainen varianssianalyysi esitt¨aa¨ mielivaltaista riippuvuutta t¨am¨an selitt¨av¨an muuttujan ja vastemuuttujan v¨alill¨a (kun vasteella on vakiovarianssinen normaalijakauma).
Otetaan k¨aytt¨o¨on merkint¨a Y¯i+ ryhm¨an i keskiarvolle
ni
1 X
¯
Yij ,
Yi+ =
ni j=1
i = 1, . . . , k,
sek¨a merkint¨a Y¯++ kaikkien havaintojen keskiarvolle
k
n
i
1 XX
Y¯++ =
Yij .
n i=1 j=1
Vastaavia otosvektorista y laskettuja suureita merkit¨aa¨n vastaavasti y¯i+ ja
y¯++ .
M¨a¨aritell¨a¨an vektorit ei siten, ett¨a vektori ei koostuu ryhm¨an i indikaattorimuuttujista (dummy variable), eli
ei = (0, . . . , 0, 1, . . . , 1, 0, . . . , 0)T ,
| {z }
ni kpl
42
i = 1, . . . , k,
jossa arvo yksi esiintyy niiss¨a kohdissa, miss¨a havaintovektorin Y arvo on
per¨aisin ryhm¨ast¨a i. Kutsumme vektoria ei ryhm¨an i osoitinvektoriksi (dummy vector). T¨all¨oin
EY = µ = β1 e1 + · · · + βk ek ,
joten malli on lineaarinen. Vektorit ei ovat ortogonaalisia, sill¨a
(
0, kun i 6= l
eTi el =
ni , kun i = l.
Koska oletuksen mukaan kukin ni ≥ 1, ovat vektorit e1 , . . . , ek lineaarisesti
riippumattomia ja siten muodostavat aliavaruuden
L1 = span{e1 , . . . , ek }
kannan. Mallimatriisi on
X = [e1 . . . ek ].
Koska kantavektorit (mallimatriisin sarakkeet) ovat ortogonaalisia, ovat
estimaattorit sek¨a niiden jakaumat helppo johtaa. Projektio aliavaruuteen
L1 on
k
k
X
X
eTi Y
ei =
Y¯i+ ei ,
p1 (Y ) =
T
e
e
i=1
i=1 i i
joten kertoimien estimaattorit ja niiden jakaumat ovat
2
σ
βˆi = Y¯i+ ∼ N (βi , ),
ni
i = 1, . . . , k.
Kertoimien estimaattorit ovat kesken¨a¨an riippumattomia. Varianssiparametrin estimaattori ja sen jakauma (mallissa µ ∈ L1 ) on
σ
˜12
ni
k
1
1 XX
σ2 2
2
=
ky − p1 (y)k =
(Yij − Y¯i+ )2 ∼
χ (n − k).
n−k
n − k i=1 j=1
n−k
Testattava nollahypoteesi on
H2 : β1 = β2 = · · · = βk ,
jota vastaa aliavaruus L2 = span{1}. Vastaava projektio on
p2 (Y ) = Y¯++ 1.
43
Nollahypoteesia testataan tuttuun tapaan F -testill¨a, jonka testisuure ja
sen jakauma nollahypoteesin ollessa tosi on
F (Y ) =
kp1 (Y ) − p2 (Y )k2 /(k − 1)
∼ F (k − 1, n − k).
σ
˜12
Osoittajassa esiintyy suure
kp1 (y) − p2 (y)k2 =
ni
k X
X
(¯
yi+ − y¯++ )2 =
i=1 j=1
k
X
ni (¯
yi+ − y¯++ )2 ,
i=1
jota k¨aytt¨am¨all¨a F -testisuure saadaan muotoon
Pk
1
yi+ − y¯++ )2
i=1 ni (¯
k−1
,
F (y) = 1 Pk Pni
¯i+ )2
i=1
j=1 (yij − y
n−k
joka voidaan tulkita ryhmien v¨alisen varianssin ja ryhmien sis¨aisen varianssin
osam¨a¨ar¨aksi.
F -testisuureelle voidaan johtaa muita lausekkeita k¨aytt¨am¨all¨a kaikille lineaarisille malleille p¨atevi¨a identiteettej¨a (HT)
kp1 (y) − p2 (y)k2 = ky − p2 (y)k2 − ky − p1 (y)k2 = kp1 (y)k2 − kp2 (y)k2 .
Jos nollahypoteesi hyl¨at¨a¨an, voidaan seuraavaksi olla kiinnostuneita muotoa
H3 : βi = βl
olevista hypoteeseista. T¨am¨an hypoteesin t-testisuure on helppo johtaa, sill¨a
riippumattomuuden ansiosta
1
1
2
+
.
Var(βˆi − βˆl ) = σ
ni nl
Hypoteesin H3 t-testisuure on
t(Y ) =
βˆ − βˆl
qi
σ
˜1 n1i +
,
1
nl
jolla on jakaumana t(n − k) hypoteesin H3 ollessa tosi.
Yksisuuntainen varianssianalyysi voidaan parametroida eri tavoilla. Usein
malli kirjoitetaan muodossa
EYij = µij = α + δi ,
44
j = 1, . . . , ni ,
jossa on n¨aenn¨aisesti k + 1 kerroinparametria (varianssiparametrin lis¨aksi).
Hypoteesi β1 = · · · = βk = 0 vastaa uudessa parametroinnissa ehtoa δ1 =
· · · = δk = 0.
Uudessa parametroinnissa vasteiden odotusarvojen muodostama vektori
saa esityksen
k
X
µ = α1 +
δi ei ,
i=1
mutta t¨ass¨a tarvitaan jokin sidosehto, P
ennen kuin mallin parametrit ovat
yksik¨asitteisi¨a eli identifioituvia: koska i ei = 1, t¨ass¨a α voitaisiin muuten
valita mielivaltaisesti ja sitten valita δi = βi − α. Sidosehto voidaan valita
esim. siten, ett¨a seuraava ortogonaalisuusehto toteutuu
k
X
(
δi ei )T 1 = 0,
i=1
mik¨a on yht¨apit¨av¨a¨a ehdon
k
X
ni δi = 0
i=1
kanssa. T¨all¨oin kertoimien SU-estimaateiksi saadaan
α
ˆ = y¯++
βˆ = βˆi − α
ˆ = y¯i+ − y¯++ .
Varoitus: eri tilasto-ohjelmissa saatetaan k¨aytt¨a¨a varianssianalyysiss¨a
erilaisia parametrointeja.
Varianssianalyysiss¨a voidaan my¨os testata sit¨a mallin oletusta, onko varianssi vakio ryhmiss¨a. T¨all¨oin tarkastellaan alkuper¨aisen vakiovarianssisen
eli homoskedastisen mallin sijasta heteroskedastista mallia
Yij ∼ N (µi , σi2 ),
jossa vakiovarianssinen malli vastaa hypoteesia
σ12 = · · · = σk2 .
T¨am¨an hypoteesin testaukseen kehitetty erilaisia testej¨a.
• Jos ryhmi¨a on kaksi, voidaan k¨aytt¨aa¨ F -testi¨a (HT).
• Muussa tapauksessa voidaan k¨aytt¨a¨a Bartlettin testi¨a (joka on kuvailtu
kirjan luvussa 3.5) tai Levenen testi¨a.
N¨aist¨a F -testi ja Bartlettin testi ovat herkki¨a mallin normaalijakaumaoletukselle. Levenen testi on t¨alle oletukselle v¨ahemm¨an herkk¨a, mist¨a syyst¨a
sit¨a usein suositellaan.
45
Luku 4
Usean selitt¨
aj¨
an malleja
4.1
Toistot ja lineaarisen mallin puuttellisuuden testaus
(Vrt. kirjan luku 4.1)
Joskus voi olla etua siit¨a, ett¨a lineaarista mallia tarkastellaan varianssianalyysin (analysis of variance, ANOVA) mallin alimallina. T¨am¨a on mahdollista, jos k¨aytett¨aviss¨a on toistoja, eli havaintoja, joissa x-komponentti
on vakio.
Takastellaan yhden selitt¨aj¨an lineaarista regressiota, jossa kullakin xarvolla xi on saatu ni toistoa, eli mallia
Yij ∼ N (β1 + β2 xi , σ 2 ),
i = 1, . . . , k,
j = 1, . . . , ni ,
jossa satunnaismuuttujat Yij ovat riippumattomia, ja jossa ryhmien lukum¨a¨ar¨a
k > 2. T¨am¨a malli on yksisuuntaisen varianssianalyysimallin
Yij ∼ N (δi , σ 2 ),
i = 1, . . . , k,
j = 1, . . . , ni ,
alimalli. Lineaarisessa regressiossa toistojen kera on nimitt¨ain voimassa lis¨aehto
eli nollahypoteesi
H0 : δi = β1 + β2 xi ,
i = 1, . . . , n.
Edell¨a yhden selitt¨aj¨an malli on tietenkin yhden selitt¨aj¨an malli, ja sen parametrien estimointi sujuu tuttuun tapaan. Yhden selitt¨aj¨an mallia verrataan
malliin, jonka dimensio on k, mink¨a takia t¨at¨akin asiaa voidaan tarkastella
otsikon “monen selitt¨aj¨an malleja” alla
Huomaa, ett¨a pystymme estimoimaan varianssiparametrin ANOVA-mallista
(toistojen avulla) tekem¨att¨a mit¨a¨an oletusta vasteen odotusarvon ja selitt¨aj¨an
46
funktionaalisesta muodosta, ja voimme testata lineaarista regressiota ANOVAmallin alimallina F -testill¨a. L¨ahestymistapaa kutsutaan nimell¨a lack of fit
-testaus, mallin puutteellisuuden testaus. Varianssin vakioisuus joudutaan
tietenkin olettamaan F -testiss¨a, mutta sit¨akin puolta voidaan halutessa testata Bartlettin testill¨a, Levenen testill¨a tai graafisilla tarkasteluilla.
ANOVA-mallissa varianssiparametrin estimaattoriksi tulee
σ
˜12
ni
k
1 XX
=
(Yij − Y¯i+ )2 ,
n − k i=1 j=1
ja F -testisuureeksi saadaan yksinkertaisilla laskuilla
Pk
ni (Y¯i+ − βˆ1 − βˆ2 xi )2 /(k − 2)
F (Y ) = i=1
.
σ
˜12
Nollahypoteesin vallitessa F (Y ) noudattaa jakaumaa F (k − 2, n − k).
T¨am¨a l¨ahestymistapa voidaan tietenkin helposti yleist¨a¨a siihen tapaukseen, jossa tahdotaan testata monen selitt¨aj¨an lineaarista mallia vertaamalla
sit¨a yksisuuntaiseen ANOVA-malliin, kunhan k¨aytett¨aviss¨a on toistoja (HT).
4.2
Kovarianssianalyysi: regressiosuorien vertailu
(Vrt. kirjan luku 4.2)
Tarkastellaan yhden selitt¨aj¨an regressiota, jossa havainnot tulevat yhdest¨a k:sta ryhm¨ast¨a. Tavoitteena on vertailla tuloksena saatavia k:ta regressiosuoraa. Tekniikkaa kutsutaan nimell¨a kovarianssianalyysi (analysis of covariance, AN(O)COVA), ja nimi jountuu ilmeisesti siit¨a seikasta, ett¨a selitt¨avi¨a muuttujia on tapana kutsua my¨oskin kovariaateiksi. Tarkasteltava
malli on
Yij ∼ N (β1i + β2i xij , σ 2 ),
i = 1, . . . , k,
j = 1, . . . , ni ,
jossa satunnaismuuttujat Yij ovat riippumattomia. Vasteen vaihtelua selitt¨av¨at
skalaari xij ja lis¨aksi indeksi¨a i vastaava luokkamuuttuja eli faktori. Kiinnostuksen kohteena on se kysymys, onko regressiosuorilla eroa. Tavallisesti tarkastellaan ensin, ovatko kulmakertoimet samat, ja sen j¨alkeen voidaan viel¨a
tarkastella, ovatko my¨os regressiosuorien vakiot samoja.
J¨arjestet¨a¨an kahdella indeksill¨a indeksoidut vasteet yhdeksi vektoriksi Y
siten, ett¨a ensin luetellaan ryhm¨ast¨a yksi saadut vasteet, sitten ryhm¨ast¨a
kaksi saadut vasteen jne., eli
Y = (Y11 , . . . , Y1n1 , Y21 , . . . , Y2n2 , . . . , Yk1 , . . . , Yknk )T .
47
T¨all¨oin odotusarvovektori µ = EY voidaan esitt¨aa¨ summana
µ=
k
X
(β1i ei + β2i ui ),
i=1
jossa
ei = (0, . . . , 0, 1, . . . , 1, 0, . . . , 0),
| {z }
ryhm¨
ai
ja
ui = (0, . . . , 0, xi1 , . . . , xini , 0, . . . , 0),
|
{z
}
ryhm¨
ai
joten malli on lineaarinen. Esim. kahden ryhm¨an tapauksessa
 


 


1
x11
0
0
 .. 
 .. 
 .. 
 .. 
.
 . 
.
 . 
 


 


1
x 
0
 0 
µ = β11   + β21  1n1  + β12   + β22 
.
0
 0 
1
 x21 
.
 . 
.
 . 
 .. 
 .. 
 .. 
 .. 
0
0
1
x2n2
Kertoimien β1i ja β2i estimoiminen on helppoa. Estimaateiksi tulee samat arvot, jotka saataisiin tekem¨all¨a erikseen k lineaarista regressiota, joista
i:nness¨a on mukana vain ryhm¨ast¨a i saadut havainnot. T¨am¨a perustuu siihen
seikkaan, ett¨a eri ryhmi¨a i ja j vastaavat kantavektorit ovat ortogonaalisia,
eli
eTi ej = eTi uj = uTi ej = uTi uj = 0,
kun i 6= j.
Varianssiparametrin estimaatiksi saadaan
σ
˜12
ni
k
1 XX
(yij − βˆ1i − βˆ2i xij )2 .
=
n − 2k i=1 j=1
Sitten voidaan testata hypoteesia, ett¨a kaikki kulmakertoimet ovat samoja, eli
H2 : β21 = β22 = · · · = β2k ,
mik¨a vastaa alimallia
Yij ∼ N (β1i + β2 xij , σ 2 ),
i = 1, . . . , k,
j = 1, . . . , ni .
T¨at¨a alimallia voidaan testata F -testill¨a, ja testisuureelle on kohtalaisen helppoa johtaa konkreettinen, k¨asinlaskuihinkin soveltuva lauseke.
48
Jos hypoteesi H2 hyv¨aksyt¨a¨an, voidaan viel¨a testata, ovatko regressiosuorien vakiotkin samoja eli H2 :n alihypoteesia
H3 : β11 = β12 = · · · = β1k .
Hypoteesi H3 vastaa tavallista yhden selitt¨aj¨an lineaarista regressiota. Testaus onnistuu j¨alleen kerran F -testill¨a.
On tietenkin mahdollista testata ensin regressiosuorien vakioiden yht¨asuuruutta
ja vasta sitten kulmakertoimien yht¨asuuruutta, mutta t¨ah¨an j¨arjestykseen
liittyy ongelmia. Regressiosuorien vakioiden arvot riippuvat nimitt¨ain x-akselin
origion paikan valinnasta, mink¨a takia vakioiden vertailu ei v¨altt¨am¨att¨a ole
mielek¨ast¨a. Jos x-arvot ovat kaukana origosta, hyv¨aksyt¨a¨an vakioiden yht¨asuuruus
hyvin helposti, sill¨a t¨all¨oin vakioiden estimaattoreilla on suuri varianssi.
Huomaa, ett¨a t¨ass¨a luvussa teemme per¨akk¨ain monta testi¨a. Sivuutamme
t¨ass¨a esityksess¨a kuitenkin t¨allaisiin per¨att¨aisiin testeihin liittyv¨an ongelmakent¨an.
4.3
Ennusteen luottamusv¨
ali ja uuden vasteen ennustev¨
ali
(Vrt. kirjan luku 4.5)
Tarkastelemme yleist¨a lineaarista mallia, jossa odotusarvovektori µ =
Xβ, ja X on n × k-matriisi. Odotusarvovektorin i:s komponentti on
µi =
k
X
xij βj = xT[i] β,
j=1
jossa xT[i] on matriisin X i:s vaakarivi. Olkoon x0 = (x01 , . . . , x0k )T uusi, annettu, selitt¨aj¨avektorin arvo. Tarkastelemme kahta samantapaista teht¨av¨a¨a,
jotka liittyv¨at uuteen vasteeseen Yx0 selitt¨aj¨avektorin arvolla x0 . Oletamme,
ett¨a uuden vasteen jakauma on
Yx0 ∼ N (xT0 β, σ 2 ),
ja ett¨a Yx0 on riippumaton aineistosta Y1 , . . . , Yn . Johdamme seuraavaksi
• luottamusv¨alin vasteen Yx0 odotusarvolle eli lineaariselle ennusteelle
µx0 = xT0 β
• ennustev¨alin satunnaismuuttujalle Yx0 .
49
Huomaa, ett¨a µx0 on parametrivektorin funktio, mutta Yx0 on satunnaismuuttuja, mink¨a vuoksi teemme eron niille johdettujen v¨alien nimitysten
suhteen.
Ensiksi johdamme luottamusv¨alin selitt¨aj¨avektoria x0 vastaavalle lineaariselle ennusteelle
µx0 = xT0 β.
Sen piste-estimaattori on
ˆ
µ
ˆx0 = xT0 β,
ja t¨am¨an estimaattorin jakauma on
µ
ˆx0 ∼ N (xT0 β, xT0 (σ 2 C)x0 ),
jossa C = (X T X)−1 .
Estimaattorin keskivirhe on edellisen perusteella
q
s. e.(ˆ
µ x0 ) = σ
˜ xT0 Cx0 ,
jossa σ
˜ 2 on varianssiparametrin tavanomainen estimaattori. Tuttuun tapaan
µ
ˆ x0 − µ x0
∼ t(n − k),
s. e.(ˆ
µ x0 )
josta saadaan luottamustason 1 − a luottamusv¨aliksi
µ
ˆx0 ± s. e.(ˆ
µx0 )t1−a/2 (n − k)
=µ
ˆx0 ± t1−a/2 (n − k) σ
˜
q
xT0 Cx0
Yhden selitt¨aj¨an lineaarisessa regressiossa, jossa
µi = β1 + β2 xi = α + β2 (xi − x¯)
uutta x-pistett¨a u0 vastaa (mallin keskist¨am¨att¨om¨ass¨a muodossa) selitt¨aj¨avektori
x0 = (1, u0 )T . Yksinkertaisilla laskuilla (HT) saadaan t¨ast¨a huomiosta regressiosouran luottamustason 1 − a luottamusv¨aliksi pisteess¨a x = u0
s
1 (u0 − x¯)2
βˆ1 + βˆ2 u0 ± t1−a/2 (n − 2) σ
˜
+
.
n
St
Regressiosuoran luottamusv¨ali on kapeimmillaan pisteess¨a u0 = x¯.
Uuden vasteen ennustev¨alin johtamiseksi tarkastellaan ensin yleist¨a lineaarista mallia µ = Xβ. Satunnaismuuttujan Yx0 paras ennuste on tietenkin
µ
ˆx0 , mink¨a takia tarkastellaan satunnaismuuttujaa Yx0 − µ
ˆx0 . Sen varianssi
50
on (toisistaan v¨ahennett¨avien satunnaismuuttujien riippumattomuuden nojalla)
Var(Yx0 − µ
ˆx0 ) = σ 2 + σ 2 xT0 Cx0 .
Koska σ
˜ 2 on riippumaton sek¨a satunnaismuuttujasta Yx0 ett¨a satunnaismuuttujasta µ
ˆx0 joiden yhteisjakauma on multinormaalijakauma, on
Y −µ
ˆ x0
p x0
∼ t(n − k).
σ
˜ 1 + xT0 Cx0
Jos on annettu 0 < a < 1, niin jakaumatuloksen perusteella todenn¨ak¨oisyydell¨a
1 − a on voimassa
Y −µ
ˆx0 x0
≤ t1−a/2 (n − k),
p
σ
˜ 1 + xT0 Cx0 josta saadaan ratkaistua, ett¨a todenn¨ak¨oisyydell¨a 1 − a uusi vaste Yx0 saa
arvon v¨alilt¨a
q
µ
ˆx0 ± t1−a/2 (n − k) σ
˜ 1 + xT0 Cx0 .
T¨am¨a on uuden vasteen ennustev¨ali.
Yhden selitt¨aj¨an lineaarisen regression tapauksessa uutta x-pistett¨a u0
vastaa taas selitt¨aj¨avektori x0 = (1, u0 )T , ja ennustev¨aliksi uudelle vasteelle
saadaan
s
1 (u0 − x¯)2
βˆ1 + βˆ2 u0 ± t1−a/2 (n − 2) σ
˜ 1+ +
.
n
St
Huomautus: Johdetut luottamus- ja ennustev¨alit ovat voimassa vain
selitt¨aj¨avektorin arvolla x0 eli pisteess¨a x0 . T¨allaisten v¨alien lis¨aksi on mahdollista johtaa v¨alej¨a, jotka ovat voimassa simultaanisesti eli yht¨aaikaisesti
kaikilla selitt¨aj¨avektorin arvoilla.
4.4
4.4.1
T¨
aydent¨
avi¨
a huomioita lineaarisista malleista
Muunnokset
Joskus linaarisia malleja sovelletaan vasta sen j¨alkeen, kun alkuper¨aisiin selitt¨aviin muuttujiin ja selitett¨av¨a¨an muuttujaan on ensin sovellettu muunnoksia. Kirjan luvussa 4.3.2 tarkastellaan esimerkki¨a, jossa puun tilavuutta v
yritet¨a¨an ennustaa sen rinnankorkeushalkaisijan d ja pituuden h avulla. Halkaisija ja pituus voidaan helposti mitata kasvavasta puusta, mutta tilavuuden mittaaminen onnistuu luotettavasti vain kaatamalla puu ensin. Aineisto
51
koostuu tietyn puulajin yksil¨oist¨a tehdyist¨a mittauksista (di , hi , vi ). Ensiksi
yritet¨a¨an yht¨al¨o¨a
v = β1 + β2 d + β3 h
vastaavan mallin sovitusta. Residuaalikuvioista n¨ahd¨a¨an, ett¨a mallin oletukset eiv¨at t¨ayty.
Sovitettu malli on asiaa koskevan tiedon valossa huono. Jos puun runko olisi muodoltaan sylinteri tai kartio, niin tilavuus saataisiin molemmissa
tapauksissa kaavalla
v = cd2 h,
jossa c on vakio. J¨arkev¨ampi malli saadaan siirtym¨all¨a logaritmeihin, ja sovittamalla mallia
log v = β1 + β2 log d + β3 log h,
jota vastaavat residuaalikuviot n¨aytt¨av¨at j¨arkevilt¨a.
Logaritmisella asteikolla esitetyss¨a lineaarisessa mallissa oletetaan, ett¨a
log Vi = β1 + β2 log di + β3 log hi + i ,
jossa Vi on tilavuutta vastaava satunnaismuuttuja ja jossa virheet i ∼ N (0, σ 2 )
riippumattomasti. Alkuper¨aisell¨a asteikolla ilmaistuna mallin oletus on, ett¨a
Vi = eβ1 dβi 2 hβi 3 ei .
Huomaa, ett¨a alkuper¨aisell¨a asteikolla virhe on multiplikatiivinen eik¨a additiivinen. Alkuper¨aisen asteikon virheen, exp(i ), jakauma on lognormaalinen,
eli t¨am¨an satunnaismuuttujan logaritmilla on normaalijakauma.
Mallia tarvitaan tilavuuden ennustamiseen puun halkaisijan ja pituuden
avulla. Jos uudelle puulle saadaan tilavuuden logaritmille ennustev¨ali [l, u],
niin v¨ali saadaan muunnettua alkuper¨aiselle asteikolle soveltamalla logaritmin k¨a¨anteisfunktiota eli eksponenttifunktiota. Ts. ennustev¨ali tilavuudelle
on [exp(l), exp(u)].
4.4.2
Selitt¨
ajien lis¨
a¨
aminen
Lineaarisessa mallissa oletetaan, ett¨a selitett¨avist¨a muuttujista koostetulla
satunnaisvektorilla Y on esitys
∼ N (0, σ 2 I),
Y = Xβ + ,
jossa X on tunnettu vakiomatriisi. Erityisesti oletetaan, ett¨a virhevektorin
komponentit i ovat riippumattomia ja i ∼ N (0, σ 2 ). Virheiden riippumattomuutta ei voida todistaa aineistoa tarkastelemalla, vaan t¨am¨a oletus pit¨a¨a
52
todentaa koetta koskevalla taustatiedolla (jos aineisto on jo annettu) tai
hyv¨a¨all¨a kokeen suunnitelulla (jos aineiston ker¨a¨amist¨a vasta suunnitellaan).
Usein lineaarisessa mallissa on mukana alkuper¨aisten selitt¨ajien ohessa
niiden funktioita kuten esim. yhden selitt¨aj¨an kvadraattisia termej¨a, eri selitt¨ajien tuloja tai muita sopivia kantafunktioita. T¨am¨a on mahdollista, koska
lineaarisen mallin oletusten mukaan malli on lineaarinen parametriensa eik¨a
alkuper¨aisten selitt¨ajien suhteen.
Mahdollisia alkuper¨aisten selitt¨ajien funktioita on tietysti rajattomasti,
mink¨a takia usein lineaarisia malleja sovitetaan siten, ett¨a lopullisessa mallissa k¨aytett¨av¨at selitt¨aj¨at valitaan suuresta joukosta kandidaatteja soveltamalla F -testej¨a tms. ty¨okaluja. T¨ass¨a yhteydess¨a on paikallaan varoitus.
Lopullisen mallin ep¨avarmuudesta saadaan liian optimistinen kuva, mik¨ali
t¨all¨oin tuijotetaan vain lopullisen mallin parametrien ep¨avarmuutta kuvaavia tunnuslukuja, ts. jos k¨aytet¨a¨an vain t¨all¨a kurssilla k¨asiteltyj¨a asioita.
4.4.3
Lineaaristen mallien rajoitukset
Lineaarisia malleja ei voida soveltaa kaikkissa tilanteissa. Jos esimerkiksi selitett¨av¨a muuttuja on bin¨aa¨rinen, eiv¨at lineaarisen mallin oletukset taatusti
pid¨a paikkaansa. Jos Yi voi saada vain arvot 0 ja 1 ja lis¨aksi on k¨aytett¨aviss¨a
yksi selitt¨aj¨a xi , niin ns. logistinen malli voi sopia selitt¨am¨a¨an vasteen Yi
vaihtelua. Mallissa oletetaan, ett¨a Yi :t ovat riippumattomia ja ett¨a
log
P (Yi = 1)
= β0 + β1 xi .
1 − P (Yi = 1)
Logistinen malli on erikoistapaus ns. yleistetyist¨a lineaarisista mallista, joita
varten on olemassa pitk¨alle kehitetty teoria ja hyvi¨a tietokoneohjelmia.
Joskus teoria kertoo, ett¨a vaste on muotoa
Yi = f (xi , β) + i ,
i ∼ N (0, σ 2 )
jossa funktio f riippuu parametrivektorista β ep¨alineaarisesti, ja kiinnostuksen kohteena on parametrivektorin arvo. T¨all¨oin oikea l¨ahestymistapa on
ep¨alineaarinen regressio.
53