computational fluid dynamics model for tacoma

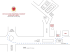
Proceedings of FEDSM’03:
4TH ASME.JSME JOINT FLUIDS ENGINEERING CONFERENCE
July 6-11, 2003 - Honolulu, Hawaii
FEDSM2003-45514
COMPUTATIONAL FLUID DYNAMICS MODEL FOR TACOMA
NARROWS BRIDGE UPGRADE PROJECT
Kristian Debus, Jonathan Berkoe, Brigette
Rosendall
Bechtel National Inc., P.O. Box 193965, San Francisco,
California 94119-3965
ABSTRACT
The purpose of this work was to validate and apply a
commercial computational fluid dynamics code with a hybrid
RANS/LES turbulence computational model for a flow past a
bluff body ultimately to help in the design of the caisson
anchoring system during construction of a new adjacent span of
the Tacoma Narrows Bridge.
INTRODUCTION
The new Tacoma Narrows Bridge will be designed as a
suspension bridge and operated parallel to the existing Tacoma
Narrows crossing in Tacoma, Washington (see Figure 1). This
is the largest suspension bridge built in the USA in the last 40
years, and the first time a major suspension bridge has been
constructed parallel and so near to an existing bridge.
Fig. 1 Rendering of future new span (shown on left)
of Tacoma Narrows Bridge
Tacoma Narrows Constructors has commissioned a study
involving the use of CFD modeling in support of the Tacoma
Narrows Bridge Expansion Project. During the construction
Farzin Shakib
ACUSIM Software, Inc., 2685 Marine Way, Suite 1215,
Mountain View, California 94043
of the new caissons a complex, cable-supported anchoring
system will be used to control the positions of the caissons
located 65 feet from the existing bridge piers. During
installation, the caissons will be subjected to current-driven
loads and vortex shedding. The CFD model results for the East
and West pier configurations will provide input data to the
dynamic mooring analysis of the flow-structure interactions to
determine the expected and maximum forces on the anchoring
system cables.
CFD is an especially important tool in this case due to the
lack of relevant field measurement data for similar structures or
experimental scale model data for similar configurations.
PROBLEM DESCRIPTION
The forces and moments determined from the CFD
analysis are used to guide the dynamic simulation and design a
cable-supported anchoring system. A preliminary design of
this anchoring system at the east side of the span is shown is
Figure 2 with the new caisson (square cross section) on the left
Fig. 2 Anchor system design layout for the East side
1
Copyright © #### by ASME
and the existing pier on the right. The anchor positions are
indicated by the dots and are distributed around the caissons.
Positioning of the anchors and attached cables is based on the
expected current-induced load distribution during installation,
installation logistics, riverbed soil considerations, and water
depth. Additionally and of critical importance, it has been
stipulated that the existing bridge structure cannot be touched
by any of the anchors or cables. This results in a very complex
design procedure that will be unique for each side of the span.
Since the Tacoma Narrows is a tidal channel, the current
flow cycles through opposing directions, referred to as flood
and ebb. During flood conditions maximum flow speeds of 9
knots (4.6 m/s) at the East piers and 7 knots (3.6 m/s) at the
West piers can occur. In the ebb direction the maximum
velocity for both sides is around 7 knots (3.6 m/s). For flood
direction, the caisson is positioned in the wake of the pier
where the effects of vortex shedding prevail; for the ebb
direction, the upstream caisson is subjected primarily to drag
forces.
In summary, the key technical challenges for this analysis
are as follows:
• The transverse loads on the caisson – particularly
during the flood flow direction scenario in which the
caisson lies in the wake of the existing pier – are
significant and may critically affect the stability of the
structure. These loads are induced by the current flow
adjacent to the caisson and also by the shedding and
subsequent flow recirculation of vortices in the wake
region. The vortex shedding phenomena is explicitly
transient (time-varying) and unsteady (see Figure 3).
• The Reynolds number of the flow around the piers is
on the order of 108 (100 million). No literature has
been found applying CFD in this range of Reynolds
number. The implication of the high Reynolds
number is the difficulty in predicting the flow
separation points and vortex shedding frequencies in
the wake regions.
• It has been observed at the existing bridge that the
vortices shed from the pier are directed downward. It
is also believed that the downward direction to the
vortices is coupled to the transverse components of the
vortex formation.
These considerations necessitated the development of a fully
three-dimensional modeling approach. The commercial CFD
code, AcuSolve, was chosen for the model because its equalorder pressure/velocity coupling results in fast convergence and
was developed to run very efficiently on parallel platforms.
Also, the hybrid RANS/LES turbulence model is the most
appropriate choice for high Reynolds number flows around
bluff bodies. By using this methodology it was possible to
achieve excellent accuracy with relatively fast solution times.
CFD MODEL DESCRIPTION
Solution Methodology
AcuSolve solves the transient turbulent incompressible
Navier-Stokes equations
∇ ⋅u = 0
ρ
Du
= −∇p + ∇ ⋅ τ
Dt
These are, respectively, the conservation of mass and
momentum in three-dimensions. Here D / Dt = ∂ / ∂t + u ⋅ ∇
is the material derivative; u is the velocity vector; ρ is the
density; p is the pressure; and τ is the stress tensor which is
the sum of contributions from the viscous and turbulence
Reynolds stress, modeled as
τ = ( µ + µt )(∇u + ∇T u )
where µ and µ t are, respectively, the molecular and turbulent
eddy viscosities.
The one-equation Spalart-Allmaras (SA) RANS turbulence
model with the Detached-Eddy Simulation (DES) modification
is used to model the eddy-viscosity. The SA RANS model may
be written as
2
Dν~
~~ 1
 ν~ 
2
~
~
~
= cb1S ν + ∇ ⋅ (ν + ν )∇ν + cb 2 (∇ν ) − cw1 f w  
Dt
σ
d
(
)
Where ν~ is the unknown field; see [Spalart 92] for details and
~
definition of S and f w and constants σ , cb1 , cb 2 , and cw1 . ν~ is
closely related to kinematic eddy viscosity. The turbulence
eddy viscosity is then given by
µ t = ρν~
χ3
χ +c
3
3
v1
χ = ρν~ / µ
The DES model is obtained by replacing the distance to the
nearest wall, d , by
~
d = min(d , C DES ∆)
Fig. 3 Complex flow structures in the wake region of
the existing pier (east side) at Tacoma Narrows
Here ∆ is a local measure of element size and CDES is a
constant; see [Spalart 97] for details.
It is well known that RANS turbulence models can be very
effective in resolving boundary layers and free-stream flows.
However, they do a poor job in capturing free shears. On the
other hand, LES turbulence models can be effective in
capturing the free shear, while they need unattainable mesh
resolution to capture boundary layers, especially at high
Reynolds numbers. For well-generated meshes, DES is
2
Copyright © #### by ASME
designed to naturally switch between RANS and LES where
appropriate. The mesh spacing in the boundary layers is of the
order of boundary layer thickness. Consequently, in the
boundary layer, DES reverts to the “RANS mode” to predict
the boundary layer and flow separations. Away from the walls,
and when production and destruction terms are balanced, the
~
length scale d = C DES ∆ of the model yields a Smagorinsky
LES eddy viscosityν~ ∝ S∆ . In short, DES attempts to
provide the best of both worlds.
The above equations constitute a system of five equations
with five unknowns. These equations are solved using the
Galerkin/Least-Squares finite element technology; see [Hughes
87] and references therein for in-depth description.
Equal-order nodal interpolations for all working variables,
including pressure, are used with low-order elements.
Moreover, the semi-discrete generalized- α method of [Hulbert
93] is used to resolve the time dependencies.
The Galerkin finite element formulation provides the base
algorithm. Galerkin formulation, which is equivalent to centraldifference formulation in finite differences, does not yield
stable discretization for the solution of the incompressible
Navier-Stokes equations. The stability difficulties arise from
two main sources: (1) the divergence-free constraint, i.e., the
continuity equation; and (2) the convective term in the
momentum equations. The least-squares operator is designed
to add the needed stability without sacrificing accuracy.
AcuSolve improves performance in three ways: (1) it
solves the coupled velocity/pressure system, yielding
substantially faster convergence; (2) its architecture has been
implemented from the ground up for vector and cache-based
super-scalar machines; (3) it is designed for coarse-grain
parallel machines. Domain decomposition is used to break and
distribute the elements and nodes to different processors.
Message Passing Interface (MPI) is used to communicate
between the processors. All the algorithms are designed
specifically to perform on coarse-grain parallel machines.
2
Model Geometry and Bathymetry
The CFD model was set up as a rigid body system
submerged in water. The complex bathymetry (based on actual
mapping of the riverbed) was imported to the meshing tool
from a CAD model. The bathymetry data was converted using
Microstation (Bentley, Inc.) to a surface model suitable for
export to the CFD meshing software. Separate models were
created for the East and West piers. Each of these models
extended sufficient distance into the channel to allow for
specification of far-field boundary condition.
Fig. 4 Computational domain for the west side with
bathymetry and pier/caisson configuration
Figure 4 shows the West pier model including the surface
bathymetry, caisson/pier configuration, boundary locations, and
coordinate system orientation.
An unstructured hybrid mesh with tetrahedral and
prismatic elements for the boundary layers was created using
the Tetra module of the ICEM-CFD software (ANSYS, Inc.).
To reduce run time and memory usage the prismatic elements
were converted to tetra, leading to a mesh size of
approximately 3.5 million elements. Figure 5 shows a plot of
the mesh around the new caisson with the prismatic elements
on the caisson surface. The mesh density was increased in the
wake region behind the caisson to optimize grid resolution and
capture the vortex shedding and recirculation areas.
Fig. 5 Computational mesh with prismatic elements
on the caisson and pier
Boundary Conditions
Simulations were carried out for 9 different scenarios at
the East and West piers under ebb and flood conditions.
Measured current velocity data obtained for the Tacoma
Narrows showed maximum flow speeds of 9 knots (4.6 m/s) at
the East piers and 7 knots (3.6 m/s) at the West piers.
Maximum flows were used to provide the Project team ‘worst
case scenario’ data.
HR Wallingford in the UK had been commissioned to
carry out scale-model rigid body tests on the East piers. For
the flood direction, measured velocity profiles from the tests
were scaled up (velocity magnitude for HRW model was 0.463
m/s) and applied at the upstream inlet boundary of the CFD
model. The far-field side boundaries and the water surface
3
Copyright © #### by ASME
boundary were set as symmetry boundaries. For the ebb
direction, a uniform velocity of 3.6 m/s was applied at the inlet
boundary.
For the West side, data from the scale model was not made
available since the Project decided to rely solely on CFD
modeling for determining the rigid body loads there.
Additionally, there was not sufficient measured current velocity
data available to specify the expected approach angle with a
high degree of confidence. Therefore it was decided to model a
range of flow angles to determine the sensitivity of the results
and to use an additional source model for projecting the inlet
flow conditions.
OEA Inc. (Ocean Engineering Associates, Inc.) had
previously been assigned to determine the flow skew angles at
Tacoma Narrows using a two-dimensional computer model
(RMA2: US Army Corps of Engineers). These depth average
data were used to determine the maximum flow angles at
relevant flow velocities. The extracted model data were applied
using a bi-linear interpolation scheme at the inlets just as the
HRW measurement data had been used for the East piers flood
scenario. For the ebb cases, the inlet and exit boundaries in the
far wake were placed at about 6.5R and 20R (R being the
diameter of the existing pier at ~35 meters) from the center of
the existing pier, respectively. In order to apply the boundary
conditions retrieved from the OEA simulation the boundaries
for the flood case simulations were placed at 15R and 26R.
Fig. 6 Flow around a square cylinder at Re=1.15 105
The Reynolds numbers evaluated ranged from Re = 105
(HRW model scale size) up to Re = 108 (full scale) into the
super critical flow regime. The results for drag coefficients and
Strouhal numbers were in good agreement with data from the
literature for the smooth cylinder at Re = 105 and in excellent
agreement for the square cylinder (the measured value for
square cyclinder should be close to 2.0 [Delany 53]). At the
full scale Reynolds number an extrapolation for experimental
data from literature [Achenbach 68] confirmed the confidence
in the chosen method (see Figures 7 through Figure 9). In
particular the square cylinder test case was considered most
relevant due to its similarity to the actual shape of the caissons.
Since the modeling of flow separation around square cyclinders
is more repeatable (and numerically more robust) than for
circular cylinders, extrapolation to higher Reynolds numbers
from the limited range of available data was done with greater
confidence.
Computer Simulations
All simulations were run on a Compaq ES40 server using
four 667 MHz Alpha processors running in parallel and
equipped with four gigabytes (Gb) of memory (RAM). The
runs were typically initialized by computing an approximate
steady state solution, and then running in transient mode for
many cycles until repeatability in the solution behavior (based
on both forces and drag coefficients) was observed. The
computation time varied depending on the model size and flow
conditions, but typically required about four days.
CFD MODEL VALIDATION
The first step was to run benchmark simulations and
compare the results to measured data for standard similar bluff
body configurations such as circular and square cylinders. A
velocity vector plot from the square cylinder simulation is
shown in Figure 6.
Fig. 7 Drag coefficient at Re=1.15 105 for circular and
square cylinder test cases
Fig. 8 Drag coefficient at Re=1.15 108 for full-scale
circular cylinder test case
4
Copyright © #### by ASME
Fig. 11 Flow streamlines around East side caisson for
4.6 m/s flood direction
Fig. 9 Achenbach - Drag coefficients measured for
circular cylinders at up to Re = 107
CFD MODEL RESULTS
The project deliverables were the forces in x-y-z direction,
the moments (Mx, My, Mz) for the new caissons and the
existing piers, and the drag and lift coefficients in x-y-z
direction, in addition to the respective time history of the
frequency oscillations. All simulations except as noted below
were based on the maximum draft before the caisson touched
the riverbed.
Figures 10 through 12 show results for the east side flood
flow case. While it is difficult to present images of transient
vortex shedding in a “snapshot” type of graphic, both the
velocity vector plot and the streamline plot indicate the high
degree of turbulence and unsteady eddy formation surrounding
the caisson, and in particular in the “shadowed” zone between
the pier and caisson. The degree of “shadowing” created by the
pier is naturally very sensitive to the flow angle – in this case,
the east side caisson is almost completely in the wake region.
Thus, as shown in Figure 12, the transverse (y-direction) force
time history is highly variable, and in fact shows occurrences
of peak loads that exceed even the drag force on the pier. Also
note the relative small magnitude of the drag (x-direction) force
on the caisson, due to its poistion in the wake of the pier.
Fig. 12 Force time history for East side caisson and
pier for 4.6 m/s flood direction
Figure 13 shows the velocity field at the surface for the
east side ebb case, which is in effect what the visual appearance
of the flow from above would look like. This can be contrasted
with the velocity field shown in Figure 14, taken near the
bottom, where the effect of the bathymetry on the field can be
observed. Such is the power of CFD that it allows the analyst a
level of detail impossible to obtain even in an experiment.
Figure 15 compares the force time history on the caisson of
the flood and ebb cases for the east side. For the flood
direction, the transverse loads driven by the effects of vortex
shedding dominate the overall force. For the ebb direction, the
drag and transverse loads are comparable. Since the caisson is
suspended above the riverbed bottom, a relatively small but
measureable lift (z-direction) force is observed as well. Both
flow directions produce significant loads of comparable
magnitude and need to be considered from a design standpoint.
Fig. 10 Velocity vectors at mid-depth around East
side caisson and pier for 4.6 m/s flood direction
5
Copyright © #### by ASME
Fig. 13 Velocity vectors at the surface around East
side caisson and pier for 3.6 m/s ebb direction
Fig. 14 Velocity vectors near the bottom around East
side caisson and pier for 3.6 m/s ebb direction
Fig. 15 Force time history for East side caisson for
4.6 m/s flood and 3.6 m/s ebb direction
Figure 16 compares the force time history of the east and
west caissons for the ebb flow direction. The measurable
variations can be attributed to relatively slight differences in
flow direction, caisson orientation, and bathymetry.
Fig. 16 Force time history for East and West side
caissons for 3.6 m/s ebb direction
CONCLUSIONS
The Tacoma Narrows Bridge Expansion Project presents a
good example of the value of CFD modeling. While bridge
design would at first glance appear to be far less of a challenge
from a fluid dynamic standpoint than an aircraft or ship, in fact
the Reynolds numbers involved in this case are extraordinarily
high, so much so that neither relevant scale model data nor
proven design correlations are readily available to the team. In
such cases it is easy for engineers and designers to overlook the
complexities of the actual situation, and difficult to even apply
a universal factor of conservatism with a high degree of
confidence and without excessive cost.
In recognizing the challenge in using CFD modeling for
such flow conditions due to the high Reynolds number,
unsteady nature of the flow, and degree of accuracy required
for fluid-structure force calculations, a unique commercial
solver package AcuSolve™, based on a hybrid RANS/LES
turbulence model (referred to as DES) and the finite element
methodology, combined with a detailed CAD model and an
unstructured prismatic and tetrahedral mesh, was employed.
This approach proved to be fast, reliable, and very stable – all
required for a real-world engineering project.
The accuracy of the CFD methodology employed was
partially confirmed by successful comparison with
experimental data from recognized benchmark cases, and
additionally by a peer review of bridge and offshore platform
designers. More conclusive confidence in the accuracy of the
CFD model results will require agreement with scale model
tests of the actual caisson configuration, scheduled to be
undertaken in the coming weeks.
REFERENCES
[Hughes 87] T.J.R. Hughes, “Recent Progress in the
Development and Understanding of SUPG Methods with
Special Reference to the Compressible Euler and Navier-Stokes
Equations,” Int. J. Numer. Methods Fluids, 1261-1275 (1987).
[Hulbert 93] J. Chung and G.M. Hulbert, "A time
integration algorithm for structural dynamics with improved
numerical dissipation: The generalized-a method", J. Appl.
Mech. 60 371-75, (1993).
6
Copyright © #### by ASME
[Shakib 89] F. Shakib, “Finite Element Analysis of the
Compressible Euler and Navier-Stokes Equations," Ph.D.
Thesis, Department of Mechanical Engineering, Stanford
University, 1989.
[Spalart 92] P.R. Spalart and S.R. Allmaras, “A OneEquation Turbulence Model for Aerodynamics Flows,” AIAA
Paper No. 92-0439, 1992.
[Spalart 97] P.R. Spalart, W.H. Jou, M. Strelets, and S.R.
Allmaras, “Comments on the Feasibility of LES for Wings, and
on Hybrid RANS/LES Approach” Advances in DNS/LES, 1st
AFOSR Int. Conf. on DNS/LES, Aug. 4-8, 1997, Greyden
Press, Columbus OH.
[Achenbach 68], E. Achenbach, “Distribution of local
pressure and skin friction around a circular cylinder in crossflow up to Re = 5.0 106, J . Fluid Mech. 34, 625-639, 1968.
[Delany 53] Noel K. Delany, Norman E. Sorenson, 'LowSpeed Drag of Cylinders of Various Shapes', NACA (National
Advisory Committee for Aeronautics), Ames Aeronautical
Laboratory, Moffett Field, Calif., November 1953
7
Copyright © #### by ASME