Lecture 8: Parametric Analysis of Variance

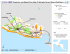
Parametric Analysis of Variance
The same principles used in the two-sample means test can be
applied to more than two sample means.
In these cases we call the test analysis of variance.
The null hypothesis for analysis of variance (AOV or
ANOVA) is:
H0 : μ1 = μ2 … = μk
And this may be applied over both time and space.
Assumptions of analysis of variance testing:
1. Observations between and within samples are random and
independent (methodological issue).
2. The observations in each category are normally distributed (run
normality tests on each group).
3. The population variances are assumed to be equal (homogeneity
of variances test).
j
i
Obs 1
Obs 2
Obs 3
Obs 4
Obs 5
Generic Data Set
Group1
X1,1
X1,2
X1,3
X1,4
X1,5
Group2
X2,1
X2,2
X2,3
X2,4
X2,5
Group3
X3,1
X3,2
X3,3
X3,4
X3,5
Note that i denotes rows and j denotes columns.
AOV:
• Compares the variation within the groups (columns)
to the variation among the group means.
− If the variation among the group means is much
greater than within the groups, reject H0.
− If the variation among the group means is not
much greater than within the groups, accept H0.
There are 3 pieces of information that need to be determined to
perform AOV:
TSS (total sum of squares) – the sum of the squared deviations of
the observation from the overall mean.
BSS (between sum of squares) – the sum of the squared deviations
between the groups.
WSS (within sum of squares) – the sum of the squared deviations
with the groups.
We will use this set of equations because they are
easier to calculate.
k
TSS = ∑
i =1
ni
2
X
∑ ij − C
j =1
2

 ni
 X ij 

ni  ∑
j =1
 −C

BSS = ∑
ni
i =1
WSS = TSS − BSS
(
X )
∑∑
where C =
ij
N
2
We test for differences among the groups using the F test.
• The standard F test is simply a ratio of variances.
• Here the F test is slightly modified to take into account:
1. The number of groups.
2. Differences in the number of group members.
The F statistic is calculated as:
F=
BSS
k −1
WSS
N −k
where k is the number of groups and N is the total sample size.
This is basically the sample size weighted ratio of the within group
variation to the between group variation.
There are 2 types of degrees of freedom for the F statistic:
• k – 1 (where k is the number of columns) for the numerator.
• N – k (where N is the total sample size) for the denominator.
Note that the table from the book is different than the web table.
• Book p values are < or > a set alpha level.
• Web table p values can be a range.
A few words on Sum of Squares…
• In all cases, the sum of squares is a measure of total variation
from the mean in a data set.
• If the sum of squares is large, then the data set has a lot of
variation. This makes it more difficult to reject Ho (find a
difference).
• If the sum of squares is small, then the data set has little
variation. This makes it earier to reject Ho (find a difference).
• Once the sum of squares has been determined there are
many ways of using the information.
In AOV the sum of squares is partitioned into 3 distinct types.
• This is because we are working with subsets of the total
data set (3+ groups).
It can be thought of as performing multiple and simultaneous
difference in means tests (t-tests).
Understanding the role of the total sum of squares (TSS) is
straightforward: it is the total amount of variation in the data
set.
TSS = ∑ ∑ ( X ij − X ij )
i
2
j
is equivalent to
k
TSS = ∑
i =1
ni
∑X
j =1
2
ij
−C
(
X )
∑∑
where C =
ij
N
2
For TSS the data are pooled together.
The between sum of squares (BSS) is the “treatment”
variance.
• We want to compare these to each other.
BSS = ∑ n j ( X j − X ij ) 2
j
is equivalent to
2

 ni
 ∑ X ij 

ni 
j =1
 −C

BSS = ∑
ni
i =1
We are examining the distance between the means of each group (A and B).
The within sum of squares (WSS) can be thought of
as the “error” variance.
• We want to factor out variation within the groups.
WSS =
∑∑
i
( X ij − X j ) 2
j
is equivalent to
WSS = TSS − BSS
The F test is simply the ratio between the error variance (within
groups) and the treatment variance (between groups).
F=
BSS
k −1
WSS
N −k
IF the ratio is small then the difference is also small (accept Ho).
IF the ratio is large then the difference is also large (reject Ho).
Tarascan Village Percent Population Employed
Mountain Group
Meseta Group
Lake Group
Mountain
Meseta
Lake
We will drop the towns along the highways since we are interested only in rural towns.
Lake
Quiroga
San Andres
San Jeronimo
Erongaricuaro
Ihuatzio
Jaracuaro
Puacuaro
Santa Fe
Uricho
Zurumutaro
Tzintzuntzan
Ajuno
51.55
54.12
36.61
48.73
59.91
49.09
50.52
71.19
33.22
54.68
46.38
37.52
Meseta
Arantepacua
Comachuen
La Mojonera
Nahuatzen
Pichataro
Quinceo
San Isidro
San Juan
Sevina
Tingambato
Turicuaro
Mountain
37.88
36.72
31.08
44.39
46.90
32.64
44.32
32.76
40.76
44.72
37.63
Ahuiran
Angahuan
Charapan
Cocucho
Corupo
Nurio
Pomacuaran
San Felipe
San Lorenzo
Urapicho
47.56
47.21
45.92
24.41
38.92
39.14
48.09
36.11
38.64
29.90
Normality Tests by Group
Ho: Village economic activity measurements are not significantly
different than normal.
qLake
37.97
=
= 3.61
10.52
nLake= 12
qcritical = 2.80 – 3.91
Accept Ho.
qMeseta
15.82
=
= 2.86
5.53
nMeseta= 11
qcritical = 2.74 – 3.80
Accept Ho.
qMountain =
23.68
= 2.97
7.97
nMountain= 10
qcritical = 2.67 – 3.69
Accept Ho.
All village groups are not significantly different than normal (w/s
qLake 3.61, p > 0.05, qMeseta 2.86, p > 0.05, qMountain 2.97, p > 0.05)
Equality of Variances Test (Hartley Test1)
Ho: The group variances are not significantly different.
FMax
Max s 2
=
Min s 2
Group variances: Lake = 110.67
Meseta = 30.60
Mountain = 63.54
df = k − 1, nMax
df = 2, 12
110.67
FMax =
= 3.62
30.60
FCritical = 4.16
The group variances are not significantly different (F3.89, p > 0.05).
1
SPSS uses the less conservative Levene’s Test.
• The Hartley test is VERY sensitive to the normality assumption.
Even small deviations from normal can influence the results.
• The test works best when the group sample sizes are equal. If
the group sizes are roughly equal, use the group with the
largest sample for determining the df and the smaller of the
two dfs reported.
• If in doubt, double check using the SPSS Levene’s test.
Hypotheses
Ho: There is no significant difference in the percent working
population among the three Tarascan village groups.
Ha: There is a significant difference in the percent working
population among the three Tarascan village groups.
Use between for two-group testing and among for 3+ group
testing.
Lake
Quiroga
San Andres
San Jeronimo
Erongaricuaro
Ihuatzio
Jaracuaro
Puacuaro
Santa Fe
Uricho
Zurumutaro
Tzintzuntzan
Ajuno
Column Sums
n1 = 12
n2 = 11
n3 = 10
ntotal = 33
51.55
54.12
36.61
48.73
59.91
49.09
50.52
71.19
33.22
54.68
46.38
37.52
593.5
Meseta
Arantepacua
Comachuen
La Mojonera
Nahuatzen
Pichataro
Quinceo
San Isidro
San Juan
Sevina
Tingambato
Turicuaro
Mountain
37.88
36.72
31.08
44.39
46.90
32.64
44.32
32.76
40.76
44.72
37.63
429.8
Ahuiran
Angahuan
Charapan
Cocucho
Corupo
Nurio
Pomacuaran
San Felipe
San Lorenzo
Urapicho
47.56
47.21
45.92
24.41
38.92
39.14
48.09
36.11
38.64
29.90
395.9
k
TSS = ∑
i =1
ni
∑X
j =1
2
ij
−C
Lake
Quiroga
San Andres
San Jeronimo
Erongaricuaro
Ihuatzio
Jaracuaro
Puacuaro
Santa Fe
Uricho
Zurumutaro
Tzintzuntzan
Ajuno
Column Sums
51.55
54.12
36.61
48.73
59.91
49.09
50.52
71.19
33.22
54.68
46.38
37.52
593.5
Sum of the observations
(∑∑ X )
where C =
2
ij
N
x2
2657.4
2928.9
1340.4
2374.9
3589.6
2409.9
2552.2
5068.2
1103.8
2990.1
2151.5
1407.8
30574.6
Meseta
Arantepacua
Comachuen
La Mojonera
Nahuatzen
Pichataro
Quinceo
San Isidro
San Juan
Sevina
Tingambato
Turicuaro
37.88
36.72
31.08
44.39
46.90
32.64
44.32
32.76
40.76
44.72
37.63
x2
1434.9
1348.7
965.7
1970.4
2199.6
1065.7
1964.5
1072.9
1661.3
1999.8
1416.0
Mountain
Ahuiran
Angahuan
Charapan
Cocucho
Corupo
Nurio
Pomacuaran
San Felipe
San Lorenzo
Urapicho
47.56
47.21
45.92
24.41
38.92
39.14
48.09
36.11
38.64
29.90
429.8 17099.5
395.9 16246.9
Sum of the squared observations
Total observation sum = 593.5 + 429.8 + 395.9 = 1419.2
(∑∑ X )
ij
k
Total squared sum = 30574.6 + 17099.5 + 16246.9 = 63921
x2
2262.2
2228.4
2108.9
596.0
1515.1
1532.3
2313.0
1303.9
1493.3
893.9
ni
∑ ∑X
i =1
j =1
2
ij
k
TSS = ∑
i =1
ni
2
X
∑ ij − C
where
j =1
(1419.2) 2
C=
= 61034.2
33
TSS = 63921 − 61034.2 = 2886.8
(
X )
∑∑
C=
ij
N
2
2

 ni
 ∑ X ij 

ni 
j =1
 −C

BSS = ∑
ni
i =1
Lake n=12
x2
Meseta n=11
x2
Mountain n=10
x2
Quiroga
51.55
2657.4
Arantepacua
37.88
1434.9
Ahuiran
47.56
2262.2
San Andres
54.12
2928.9
Comachuen
36.72
1348.7
Angahuan
47.21
2228.4
San Jeronimo
36.61
1340.4
La Mojonera
31.08
965.7
Charapan
45.92
2108.9
Erongaricuaro
48.73
2374.9
Nahuatzen
44.39
1970.4
Cocucho
24.41
596.0
Ihuatzio
59.91
3589.6
Pichataro
46.90
2199.6
Corupo
38.92
1515.1
Jaracuaro
49.09
2409.9
Quinceo
32.64
1065.7
Nurio
39.14
1532.3
Puacuaro
50.52
2552.2
San Isidro
44.32
1964.5
Pomacuaran
48.09
2313.0
Santa Fe
71.19
5068.2
San Juan
32.76
1072.9
San Felipe
36.11
1303.9
Uricho
33.22
1103.8
Sevina
40.76
1661.3
San Lorenzo
38.64
1493.3
Zurumutaro
54.68
2990.1
Tingambato
44.72
1999.8
Urapicho
29.90
893.9
Tzintzuntzan
46.38
2151.5
Turicuaro
37.63
1416.0
Ajuno
37.52
1407.8
593.5
30574.6
395.9
16246.9
Column Sums
429.8 17099.5
(593.5) 2 (429.8) 2 (395.9) 2
BSS =
+
+
− 61034.2 = 786.5
12
11
10
Only used to calculate the WSS
TSS = 2886.8
BSS = 786.5
WSS = 2886.8 − 786.5 = 2100.3
F=
BSS
k −1
WSS
N −k
786.5
393.25
3
−
1
=
= 5.62
F=
2100.3
70.01
33 − 3
df =
(k-1) = (3-1) = 2,
(n-k) = (33-3) = 30
To get the probability range on this table, read DOWN the column.
F = 5.62
Since 5.62 > 3.32 reject Ho
There is a significant difference in the percent employed population
among the three groups of Tarascan villages (F5.62, 0.01 > p > 0.005).
Test of Homogeneity of Variances
PctAct
Levene
Statistic
.876
df1
df2
2
Sig.
.427
30
ANOVA
Pc tAct
Between Groups
W ithin Groups
Total
Sum of
Squares
786.816
2095.240
2882.056
df
2
30
32
Mean Square
393.408
69.841
F
5.633
Sig.
.008
Multiple Comparisons
Dependent Variable: PctAct
LSD
(I) Group
1
2
3
(J) Group
2
3
1
3
1
2
Mean
Difference
(I-J)
10.3886*
9.8698*
-10.3886*
-.5188
-9.8698*
.5188
Std. Error
3.4885
3.5783
3.4885
3.6515
3.5783
3.6515
*. The mean difference is s ignificant at the .05 level.
Sig.
.006
.010
.006
.888
.010
.888
95% Confidence Interval
Lower Bound Upper Bound
3.264
17.513
2.562
17.178
-17.513
-3.264
6.938
-7.976
-17.178
-2.562
-6.938
7.976
Comparing our results to those of SPSS:
TSS
BSS
WSS
F
p
SPSS
2882.1
786.8
2095.2
5.63
0.008
Us
2886.6
786.8
2100.3
5.62
0.01 - 0.005
Multiple Comparison (AOV Post Hoc) Tests
• Available in SPSS to compare all group pairs.
• Used to determine which means are significantly different.
• Similar to (but not exactly like) performing two group means
tests while holding the other group(s) constant.
• The post hoc test listed below are useful for non-paired
comparisons and non treatment-control comparisons.
For treatment-control (e.g. before- after) comparisons, use the
Dunnet test.
LSD (Fisher test)
• The Least Significant Difference test assumes that if the null
hypothesis is incorrect, as indicated by a significant F-test, Type I
errors are not really possible.
• LSD test has been criticized for not sufficiently controlling for Type
I errors.
• Although this is the first test on the list in SPSS, it is probably not
the best.
Bonferroni
• Probably the most commonly used post hoc test because it is
flexible, simple to compute, and can be used with any type of
statistical test.
• The traditional Bonferroni tends to lack power.
• The Bonferroni overcorrects for Type I error.
Sidak
• A relatively simple modification of the Bonferroni formula that
would have less of an impact on statistical power but retain much
of the flexibility of the Bonferroni method.
• This approach is convenient but has not received any systematic
study.
• It is unlikely that a single, simple correction will result in the most
efficient balance of Type I and Type II errors.
Tukey (Tukey’s HSD)
• The HSD (honest significant difference) has greater power than
the other tests under most circumstances.
• Requires equal sample sizes.
• If sample sizes are unequal, the Tukey-Kramer test is used by
SPSS which computes the harmonic mean of the sample sizes
for each group, slightly lowering the power of the test.
Games-Howell
• This test can be used when variances are unequal and also
takes into account unequal group sizes.
• Severely unequal variances can lead to increased Type I error,
and with smaller sample sizes, more moderate differences in
group variance can also lead to increases in Type I error.
• This test appears to do better than the Tukey HSD if variances
are very unequal (or moderately so in combination with small
sample size) or can be used if the sample size per cell is very
small (e.g., <6).
• This is probably the most reliable post hoc test, but also the most
conservative.
Probabilities from 5 Post Hoc Tests
Group
Comparisons
1–2
GamesHowell
0.021
Tukey HSD
0.015
LSD
0.006
Bonferroni
0.017
Sidak
0.017
1–3
0.053
0.026
0.010
0.029
0.029
2–3
0.984
0.989
0.888
1.000
0.999
Note that the differences are slight, except for the GamesHowell test.