economic convergence and territorial disparities in eastern europe

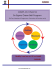
CCI3
ECONOMY AND MANAGEMENT
ECONOMIC CONVERGENCE AND TERRITORIAL DISPARITIES IN
EASTERN EUROPE – THE FUNCTIONAL NEIGHBORHOOD AND THE
ESTIMATION OF THE SIGMA REGIONAL CONVERGENCE TRENDS
Alexandru Rusu, Assist. Prof., PhD, Andreea Mihaela Buraga, PhD Student, ”Al.
Ioan Cuza” University of Iași
Abstract: The inclusion of the territorial dimension in the analysis of the sigma regional
convergence provides a better understanding of the trends describing the reduction of the
regional disparities. Using a mobile Gaussian kernel of variable size that weights the
GDP/inhab. for each NUTS3 of the studied area, we calculate a local sigma convergence
coefficient that can be mapped. Once the cartographic and the spatial analysis are combined,
they depict better the gradients that shape the Eastern European countries and the trends at
work in the reduction or the increase of the regional disparities. Estimating the proper size of
the functional neighborhood allows us to explain how the economic convergence is
accelerated or stopped by geographical factors - state frontiers, years of EU adhesion or
spatial autocorrelation in the GDP distribution.
Keywords: sigma convergence, territorial disparities, functional neighborhood, territorial
endowment, Eastern Europe
1) Introduction
Despite the new challenges and the new topics of major interest fueled by the
worldwide financial crisis, the regional economic convergence in the EU still remains an
important theme of research in various disciplines, such as economy, territorial planning or
political studies. Our paper proposes a methodological framework that enables a better
visualization of the territorial disparities, even in a strong context of regional resilience. The
Eastern European countries recently admitted in the EU are the perfect laboratory for testing
the different theories of economic convergence at regional scale. They generally present high
rhythms of GDP growth, during the 2001-2008 period and they seem to catch-up the
differences of performance and welfare that separate them from the Western core of the
Union. In the same time, this rhythm of GDP growth is unequally distributed in the Eastern
European space, deteriorating the unstable equilibrium of revenues and productivity at local
scale (NUTS3). The economic growth that characterizes these Eastern European economies
has also a problematic influence on the state of the territorial cohesion and the increase of the
territorial disparities becomes a strong theme of debate for policy makers and decision takers.
Our intention is to elaborate a methodology that captures the dynamics of the territorial
876
CCI3
ECONOMY AND MANAGEMENT
disparities for the studied area, using spatial analysis and tools that upgrade classical
econometric indicators like the sigma convergence (Montfort, 2008; Dao et al., 2013). In a
first part, we will present a literature review of the concepts that shaped our research - the
economic convergence and the functional neighborhood. The main corpus of this paper is
dedicated to the elaboration of the methodology and the analysis of the results we obtained in
exploring the GDP convergence trends, for 2001-2011. Finally, we present the theoretical
limits of our approach and possible solutions to improve the methodology we propose.
2) Literature review and concepts
In the view of the main studies treating the economic convergence issue, we notice
that this concept, generating contradictions and still insufficiently explored, is more the
privilege of economic (Chatterji, 1992; Barro and Sala-i-Martin, 1992; Canova and Marcet,
1995; de la Fuente, 1995; Galor, 1996; Krugman, 1991, 1995, 2008; Brasili and Gutierrez,
2004; Jóźwik and Ponikowski, 2014; Dall‘erba and Le Gallo, 2006; Cuestas et al., 2013),
political and administrative sciences. However, the economic convergence seems to be among
the concerns of geographers, economists and policy makers, by integrating the spatial
dimension of the data needed to estimate the level of convergence of regional economies,
proposing a multiscale approach to measure regional disparities (Gaile, 1984; Armstrong,
1995; Martin, 2000; Grasland, 2012; Bourdin, 2013). Philippe Montfort (2008) considered
that ―the omission of the space variable from the regional beta-convergence process leads to
biased results‖.
The basis of the works centered on the concept of convergence is the neoclassical
theory of the economic growth, developed by Robert Solow (1956), according to which ―the
convergence process between unequal developed countries it is possible‖. Solow insists on
the principle that the initial regional disparities decay with time, each region converging to a
growth rate of the revenue per inhabitant, long-term, called ―the steady state‖. The theoretical
approaches which study the concept of regional convergence focused on the so-called
„catching-up‖ process, less economic performant regions making significant efforts to catchup the rich regions. Gerschenkron (1952) was the first who exposed the idea of ‖the
advantages of relative backwardness‖, according to which the poor states imitate and the
developed ones inovate. Because the imitation process is easier and involves lower costs, the
less developed countries shows favorable conditions of a faster growth rate compared with the
rich ones.
Quoting the Convergence report of the European Comission the convergence process
represents a ‖sine-qua-non condition of the stability and the prosperity of the community
space, a condition of the integration of the remoted regions and of the cohesion.‖ The large
number of definitions of the economic convergence corresponds to different concepts and can
be divided on two levels: the beta-convergence (β) and the sigma-convergence (σ) (Sala-iMartin, 1996).
The so-called hypotesis of β-convergence refers to ‖the process by which the less
economic performant states register faster growth rates than the rich ones, making possible
the recovering of the existing economic disparities‖. Therefore, the economic growth should
lead to a ―steady state of the economies, with a growth rate dependent only on levels of
technological progress and employment growth‖ (Montfort, 2008). Also, the growth rate of
poor economies should be higher, while the level of income and/or GDP per inhabitant has to
equal that of the developed ones. The β-convergence can be absolute, when the process is
independent of the initial conditions of the economies, or conditioned, when we suppose that
economies are identical in terms of technologies, economic politics, more precisely when
877
CCI3
ECONOMY AND MANAGEMENT
economies are dependent on the endogeneous factors (Barro and Sala-i-Martin, 1996;
Montfort, 2008; Bourdin, 2013).
The concept of sigma-convergence makes reference to ―the reduction in time of the
interregional disparities‖, by comparing an indicator of dispersion, calculated for the end of
the analyzed period, with the value of the same indicator for the beginning of the studied
period (Montfort, 2008).
The topics of beta and sigma convergence are complementary, because these measure
the convergence process in different ways, offering distinct solutions. Sala-i-Martin (1994,
1996) stressed that beta-convergence is a more interesting concept, because it can be used for
showing the existence of convergence models within different economies, how fast this
process manifests, if the convergence process is absolute or conditioned, total or partial.
3) Methodology and data quality check
The data we use in this article are collected from official sources, the major provider
being the EUROSTAT. In order to analyze the dynamics of the territorial disparities, we have
build a database that contains time-series of GDP at NUTS3 scale. These time-series cover the
period of 2001-2011, partially capturing the effects of the economic convergence on the
Eastern European states. The indicator we retained in our analysis is the GDP per inhabitant,
excluding other variables such as the GDP in purchasing power index for reasons of spatial
comparability of data. The geometry for the mapping process and spatial analysis is provided
by GISCO, the GIS division of the EUROSTAT. Once the indicators being collected, they
were explored for possible outliers using LISA (local indicators for spatial association) and,
with the exception of the false positive flags, no significant outliers were detected.
The spatial database we created was populated with values for all the 234 NUTS3 in
an area composed by the Baltic States (Estonia, Latvia and Lithuania), former centralized
economies from Eastern Europe (Bulgaria, Czech Republic, Hungary, Poland, Romania and
Slovakia) and Austria. The selection of the last country has two reasons. In a first place, from
a historical point of view Austria presents many affinities with the countries from Central
Europe. Secondly, taking into account the relative high values of the GDP/inhab. of the
Austrian NUTS3, we have considered that these values can serve as a reference for better
capturing the dynamics of the GDP, for the other countries retained in the studied area. An
alternative option to also include the Eastern Germany's NUTS3 was rejected due to the fact
that economic convergence process was a matter of national policy, after the reunification and
is less linked to geo-political processes like the EU adhesion.
The database enabled us to explore the process of the sigma convergence at national
scale, showing a large variety in the increase or decrease of the territorial disparities. If
Austria is the most stable country showing an insignificant reduction of the internal
disparities, countries like Romania and Bulgaria present a constant increase in the lack of
territorial cohesion. Contrary, Hungary has a trend of constant reduction of the territorial
disparities, even more spectacular in a country marked by huge inequalities of NUTS3
demographic and economic size. Despite the fact that there is a shortage of comparable sigma
convergence analysis at NUTS0 (country level) in the literature, which makes this regional
depiction an insight in the problems of economic catching-up of the Eastern European states,
we signal some limits of NUTS0 approach on the topic of sigma convergence :
- the administrative geometry of the Eastern European countries makes impossible a
proper comparison of the sigma convergence. Some selected countries have only 5 NUTS3
regions (e.g. Estonia) and calculating the standard deviation of the yearly GDP/inhab. is
statistically limited. In the same time, countries like Poland (66 NUTS3) or Romania (42
878
CCI3
ECONOMY AND MANAGEMENT
NUTS3) are more suitable for the analysis of the national sigma convergence. Basically, we
do not deal with comparable geographical objects, in order to explore the dynamics of the
territorial disparities.
Figure 1 - Sigma convergence process at national scale (2001-2011)
- reporting the sigma convergence to the national scale in a globalizing world is a
matter of creation of an artificial bounding area. The classical and statistical method is not
able to intercept the effects of the economically dynamic borders in the reduction/increase of
the territorial disparities. Such is the case for the Austro-Hungarian border or the state frontier
between Romania and Hungary.
These limitations invite researchers to propose new ways of approach on the sigma
convergence and the measure of the territorial disparities. As already signaled in the literature
review, encouraging results were obtained by Grasland (2012) and Dao et al. (2014), in the
frame of the ESPON Programme, while the necessity to spatially weight the trends of the
local sigma convergence were already indicated by Monfort (2008).
Figure 2 - The conceptual framework of the functional neighborhood
The methodology we propose enables mapping the sigma convergence trends and it is
based on the concept of functional neighborhood. Using a Gaussian kernel of variable size,
879
CCI3
ECONOMY AND MANAGEMENT
the indicator used to measure the sigma convergence (GDP/inhab.) was weighted with the
distance separating the NUTS3 retained for the analysis. The distance function we used is set
to decrease the contributions of the NUTS3 place in the functional neighborhood as follows:
- a first Gaussian span was set at 100 km (approximately 2 hours of car drive
distance). A NUTS3 situated at this 100 km distance will contribute with 50 % of its
GDP/inhab. in the calculation of the local sigma convergence.
- the second Gaussian span was set at 200 km (approximately 4 hours of car drive
distance). A NUTS3 situated at this 200 km distance will contribute with 50 % of its
GDP/inhab. in the calculation of the local sigma convergence.
This mathematical model of local sigma convergence describes a functional
neighborhood that is replicated for each NUTS3 from the studied area (Grasland, 2012). The
weighted values are summed and then different calculations are implemented - local average
and local standard deviation of the weighted values. The ratio between the local standard
deviation and the local average provides the coefficient of variation (sigma convergence) for
each NUTS3. These values are available for all the yearly indicators in the database
(GDP/inhab. 2001- 2011) and they can be mapped.
The mathematical model contains a set of parameters that indicates the starting
assumptions in the exploration of the local convergence. It is derived from the model of
spatial potential of interaction and we remind that a numerous number of weighted distance
functions can be implemented in the calculation of the sigma convergence (inverse distance
weight, squared inverse distance weight, exponential decay of the distance, logarithmic decay
of the distance etc.).
The formalization of the model is build using this algorithm:
where :
a = ln(0.5)/GS2
Dij = distance between the NUTS3
GS = the Gaussian span set to control the distance decay function.
b = the distance decay parameter, generally set to the value of 2.
The local sigma convergence is calculated using this formula:
LSC = SD/(
)/n)
where:
SD = the local standard deviation of the weighted GDP/inhab. values.
Any intervention on the parameters operating in the model will have an impact on the
calculation of the sigma convergence. Assuming different values for the parameters, one can
obtain an unlimited number of different functional neighborhood contexts.
880
CCI3
ECONOMY AND MANAGEMENT
Figure 3 - Different approaches of the functional neighborhood.
In the example of the figure 3, three different hypotheses were used. For the f1
example, the value of the Gaussian span was set to 100 km and the weighted function to 0.33.
Using this distance function, only 33% of the GDP/inhab. would have participated in the
elaboration of the local sigma convergence, at 100 km from each NUTS3 in the studied area.
In the case of the f2 example, the Gaussian span was set to 200 km and the probability of
collection to 0.5 (50%). In the last case, the Gaussian span is set to 300 km, but the value of
the weighted function is blocked at 0.66 (66%), with an intervention on the distance decay
parameter b (1.5).
Figure 4 - Synthetic results of the functional neighborhood methodological
approach of the sigma convergence
The implementation of the methodological frame of the local sigma convergence
evaluation is a step by step calculation process. The elaboration of the distance matrix
between all the 234 NUTS3 in the studied area provided a table of 54522 lines. The
GDP/inhab. dataset for 2001-2011 was joined to this table and two types of functional
neighborhood (2 and 4 hours time distance neighborhood) were calculated as weighting
functions. The GDP/inhab. dataset at NUTS3 level was multiplied with the distance weighting
functions and the results were summarized, in order to allow the estimation of the local
standard deviation of the GDP/inhab. and the local average. The two statistical indicators
were finally used for the calculus of the local sigma convergence for 2001, 2008 (the starting
year of the financial crisis) and 2011.
The data we obtained served for two purposes: a basic cartographic exploration of the
territorial distribution of the local sigma convergence, doubled by more advanced spatial
881
CCI3
ECONOMY AND MANAGEMENT
analysis of the territorial disparities. The basic mapping of the local sigma convergence shows
interesting patterns in the distribution of the territorial disparities. The general trend observed
on the maps indicates a reduction of the territorial disparities between 2001 and 2011, at
NUTS3 level. However, at regional and national scale, the conservation of some areas of
strong disparities on the axis Vienna-Krakow-Warsaw and around Bucharest suggests that the
mechanism of economic growth is strongly related to the metropolitan endowment of the
Eastern European urban system. Budapest and Sofia are also generators of territorial
disparities, at regional scale (2 hours or 4 hours of functional neighborhood), but in a more
limited manner. The more advanced exploration of the local sigma convergence with tools of
spatial analysis is presented in the section dedicated to the results and discussions.
4) Results and discussions
The main intention of our study is to propose a methodological framework to estimate
the local sigma convergence. Applying techniques of spatial analysis to these indicators is one
way to derive policy recommendations for decision makers dealing with the issue of territorial
disparities. This final step in the analysis can signal the progress made in the promotion of
more cohesive territories, but it can also flag the regional stakes and the areas where the
objective of territorial cohesion is unlikely to be soon implemented.
Figure 5 - Annual average change rate of the local sigma convergence (2001-2011)
- 2 hours time distance of functional neighborhood
The dataset containing the local sigma convergence indicators for 2001-2011 was used
to calculate an average annual change rate, for two contexts of functional neighborhood - 2
hours and 4 hours time distance. The map presented in the figure 5 emphasizes the uneven
distribution in this change rate. While NUTS3 regions from Austria, Western Hungary,
Western Slovakia or the Romanian-Hungarian border show a steady rhythm of decrease for
882
CCI3
ECONOMY AND MANAGEMENT
the territorial disparities, the NUTS3 surrounding the capital-regions of Bucharest and Sofia
behave differently. The gradients at work in the dynamics of the territorial disparities are no
longer West-East oriented; they are complicated by numerous other factors that can be
explained by territorial advantages: economically active borders, metropolitan endowment or
demographic stability.
Figure 6 - Annual average change rate of the local sigma convergence (2001-2011)
- 4 hours time distance of functional neighborhood
Changing the scale of analysis to a 4 hours time distance functional neighborhood will
smooth the trends observed on the previous map. In this case, regions like the North-East
NUTS2 change completely the dynamic of territorial disparities evolution. The spatial
smoothing provides the image of a macro-region where the trends regarding the territorial
cohesion are divided. Austria, Czech Republic, Hungary and Slovakia claim a reduction of the
disparities, Romania and Bulgaria are in an opposite situation, Poland remains stable, while
the Baltic States are a synthetic image of three trends overlapped. Each scale of functional
neighborhood and the conclusions of the spatial analysis proposed address different types of
policy makers and decision takers. For example, the functional neighborhood of 2 hours is
rather suitable for decisions concerning the intermediate area, like the NUTS2 regions. The
analysis of the sigma convergence in a functional neighborhood of 4 hours is more likely to
be useful for territorial planning at national and regional scale. The combination of these two
scales by a qualitative typology places each NUTS3 in one specific class.
883
CCI3
ECONOMY AND MANAGEMENT
Figure 7 - NUTS3 typology based on the annual average change rate of the local
sigma convergence
The four classes obtained by the NUTS3 typology are interesting by their spatial
distribution and by the policy recommendations that can be addressed, in the frame of applied
spatial analysis. For example, for counties (NUTS3) placed in the first class (reduction of the
territorial disparities in both functional neighborhood contexts) policies aiming the increase of
their economic competitiveness should be considered. The regional classification we propose
can also be considered as a territorial impact assessment tool, measuring the results of the
rolled-back strategies in the reduction territorial disparities.
5) Conclusions
The main objective of our research was to elaborate a methodological framework that
enables the estimation of the local sigma convergence, passing from the territorial scale of
reference (national, macro-region) to the spatial one. This translation is possible using the
concept of functional neighborhood that is based on a mobile Gaussian kernel of variable size.
Choosing two different spatial contexts (2 hours and 4 hours of functional neighborhood), we
implemented our methodology and obtained indicators describing the levels of territorial
disparities for the 2001-2011 period. These indicators were explored using spatial analysis
tools and they served to elaborate a NUTS3 typology concerning the annual average change
rate of the local sigma convergence.
884
CCI3
ECONOMY AND MANAGEMENT
The limits of our approach are derived mostly from the formalization of the functional
neighborhood model. Taking into account that the model is based on three different
parameters - the potential of GDP collection, the Gaussian span and the distance decay
function, the lack of empirical studies providing calibration for these parameters is clearly a
limit for our approach. In order to calibrate one parameter in the model, like the potential of
GDP collection, one would need a yearly matrix of commercial flows between the NUTS3,
matrix that is not available at this geographical level. A second limit that we observed in our
research is provided by the impossibility to properly define a spatially weighted standard
deviation for the coefficient of dispersion needed in the calculation of the local sigma
convergence.
Despite these limitations, there is a promising potential of applied spatial analysis on
the topic of the local sigma convergence. The results might be an alternative and distinctive
method to propose policy recommendations that take into account both the geographical and
economical factor of the NUTS3 performance.
Acknowledgement
This work was supported by the strategic grant POSDRU/159/1.5/S/133652, cofinanced by the European Social Fund within the Sectorial Operational Program Human
Resources Development 2007 – 2013
6) Bibliography
Armstrong, H., (1995) –„An appraisal of the evidence from cross-sectional analysis
of the regional growth process within the European Union, in Convergence and Divergence
among European Regions‖, Eds. Armstrong H. and Vickerman, R. (Pion Limited), pag. 4165.
Barro, R., Sala-i-Martin, X., (1992) – „Convergence‖, Journal of Political Economy,
nr. 100 (2), pag. 223–251.
Barro, R., Sala-i-Martin, X., (1997) – „Technological diffusion, convergence, and
growth‖, Journal of Economic Growth, nr. 2, pag. 1–27.
Bourdin, S., (2013) – „Vers une réduction des inégalités régionales dans l‘Union
européenne ? Une approche multiscalaire des trajectoires de convergence‖, ASRDLF 2013,
Appel à communication.
Brasili, C., Gutierrez, L., (2004) – „Regional convergence across European Union‖,
Development and Comp Systems0402002, EconWPA.
Canova, F., Marcet, A., (1995): „The Poor stay Poor : non Convergence Accross
Country and Regions‖, CEPR Workshop on Empirical Macroeconomics, Brussels.
Chatterji, M., (1992) – „Convergence clubs and Endogenous Growth‖ , Oxford
Review of Economic Policy, nr. 8 , p. 57-69.
Cuestas, J.C., Monfort M, Ordóñez, J., (2010) – „Real Convergence in Europe: A
Cluster Analysis‖, Sheffield Economic Research Paper Series, nr. 2012023.
Dall'Erba, S., Le Gallo, J., (2008) – „Regional convergence and the impact of
European structural funds over 1989-1999: a spatial econometric analysis‖, Regional
Science, vol. 87, pag. 219-244.
Dao, H., Plagnat, P., Rousseaux, V., (2013) – „Sigma-convergence as a measure of
territorial cohesion‖, published in Science in support of European Territorial Development
and Cohesion, Luxembourg, p. 32-37.
de la Fuente, A., (1995) – „Catch-up, Growth and Convergence in the OECD", CEPR
Discussion Paper, nr. 1274.
885
CCI3
ECONOMY AND MANAGEMENT
Gaile, G.L., (1984) – „Measures of spatial inequality‖. In: Gaile GL, WilImott CJ
(eds) Spatial statistics and
Models, D. Reidel, p. 223-233.
Galor, O., (1996) – „Convergence? Inferences from Theoretical models‖, The
Economic Journal, nr. 106, p. 1056-1069.
Gerschenkron, A., (1952) - „Economic Backwardness in Historical Perspective‖, The
Progress of Underdeveloped Areas, Chicago University Press.
Grasland, C., (2012) – „Transformation of regional indicators with functional
neighborhood‖ (presentation), ESPON Open Seminar, Aalborg, June 2012.
Jóźwik, B., Ponikowski, H., (2014) – „Real convergence, economic crises and EU
cohesion policy‖, Cambridge Conference Business & Economics.
Krugman, P., (1991) – „Increasing returns and economic geography‖, Journal of
Political Economy, nr. 99 (3), pag. 483 – 499.
Le Gallo, J., Dall’Erba, S., (2006) - „Evaluating the temporal and spatial
heterogeneity of the European convergence process: 1980-1999‖, Journal of Regional
Science, nr. 46, p. 269-288.
Martin, R., (2000) – „EMU versus the regions? Regional convergence and divergence
in Euroland‖, ESRC Centre for Business Research, University of Cambridge, Working Paper,
nr. 179.
Montfort, P., (2008) – „Convergence of EU régions. Measures and Evolution‖,
DG Politique Régionale, Bruxelles, document de travail, n°1, 20 p.
Solow, R., (1956) – „A Contribution to the Theory of Economic Growth‖, Quarterly
Journal of Economics LXX(1), pag. 65-94.
***(2013) – „Success for Convergence Regions‘ Economies‖, ESPON Final Report.
***(2012) – „Convergence Report‖, European Economy 3, European Commission.
***(2007) – „Regional disparities and Cohesion: What strategies for the future‖,
European Parliament.
http://database.espon.eu/db2/
http://epp.eurostat.ec.europa.eu/portal/page/portal/eurostat/home/
886