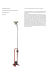Experiment05

Name:
Laboratory Section:
Laboratory Section Date:
Partners’ Names:
Grade:
Last Revised on January 6, 2016
EXPERIMENT 5 - New
Part 1: Equivalence of Energy: Heat, Mechanical
Part 2: Equivalence of Energy: Heat, Electrical, Light
0. Pre-Laboratory Work [2 pts]
1.
A 90kg person jumps from a 30m tower into a tub of water with a volume of 5m3 initially
at 20°C. Assuming that all of the work done by the person is converted into heat to the water,
what is the final temperature of the water? It’s helpful to first find the work done by the
person to the water tub and then the amount of heat equivalent to that work. Make sure you
have the correct value for the mass of the water. Include units. [1pt]
2.
In both Section 3.1 (part 1) and Section 3.2.1 (part 2) you are asked to continue taking
temperature measurements even after the heat source has been turned off. What effect are we
trying to observe and how do we use this effect in our data analysis? [1pt]
1 of 20
Name:
Laboratory Section:
Laboratory Section Date:
Partners’ Names:
Grade:
Last Revised on January 6, 2016
EXPERIMENT 5 - New
Part 1: Equivalence of Energy: Heat, Mechanical
Part 2: Equivalence of Energy: Heat, Electrical, Light
1. Introduction and Purpose
Conservation of Energy is one of the foundational principles in Physics. As a consequence of
this principle, we expect that when energy changes forms, there should be the same amount of
energy before and after that change. Different forms of energy relevant in this experiment
include mechanical work, electrical work, heat (thermal energy), and light. The purpose of this
experiment is to observe the conversion of energy from one form to another. Mechanical and
electrical work are generally measured in Joules, whereas thermal energy (heat) is usually
measured in Calories. Calories and Joules should be proportional to one another, since they are
just different units of measure for the same physical quantity (energy). In part Ι, you will
measure that proportionality constant between Joules and Calories (i.e. the proportionality
between mechanical work and heat), known as Joule’s constant. The accepted value of Joule's
constant is 4.19 J/cal. In part ΙΙ, your TA will assign you one of two possible procedures: (1)
You will use a light bulb to convert electrical energy into either heat, from which you will again
determine Joule’s constant, or (2) you will convert electrical energy into heat and light, allowing
the light energy from the light bulb to escape. By comparing your results with another group,
you will be able to calculate the efficiency of the conversion of electrical energy to light. The
efficiency of a light-bulb at producing light would be determined by how much of the energy put
into the bulb is converted into light: a high-efficiency bulb converts most of the electrical energy
it is given into light, whereas a low-efficiency bulb only converts a small fraction of that energy
to light, and wastes the rest in other forms (nominally heat).
In summary, you will do the following:
Ι. Conversion of Mechanical Energy into Heat
ΙΙ. Conversion of Electrical Energy (TA will assign 1 or 2 below)
1. Conversion of Electrical Energy into Heat
2. Conversion of Electrical Energy into Heat and Light
2 of 20
2. Theory
2.1 Conversion of Mechanical Energy into Heat (Part 1)
In this experiment, a measurable amount of work is performed by turning a crank. The crank
drives the rotation of an aluminum cylinder, which is subject to friction from a rope looped
around the cylinder several times, supporting a mass. When the system is set up correctly,
turning the crank will just lift that supported mass off the ground—when this occurs, we know
that the force of friction between the aluminum cylinder and the rope is equal to the gravitational
force F = Mg on the mass. If we know the average force, and we know the number of turns of
the crank (there is a counter on the hardware), then we can compute how much work we have
put into the system. We assume that all of this work is converted to heat through friction, and
that we should subsequently be able to make a connection between the amount of work put into
the system and the temperature of the aluminum cylinder over time. Specifically, we expect that
the mechanical work performed and the thermal energy gained by the cylinder will be
proportional.
There is a thermistor embedded in the aluminum. By measuring the resistance of the
thermistor using a multimeter, we can monitor the temperature change of the cylinder (and thus
compute the thermal energy transferred to the cylinder). Finally we calculate the ratio of
mechanical work performed (in Joules) to heat gained by the cylinder (in Calories), in order to
compute Joule's Constant Jmechanical = 4.19 J/Cal, or the mechanical equivalence of heat. (Note
that we notate Jmechanical = Jm throughout the manual, in order to contrast this result with the
corresponding one in the second half of the lab, which will be notated Jelectrical = Je).
We go through the process for computing the amount of mechanical work performed by
turning the crank. The torque required to support a mass M is given by
Equation 5.1
τ = MgR
where g is the graviational accelerating near Earth's surface, and R is the radius of the aluminum
cylinder being cranked. The work performed by this torque is given by W = τθ, where θ is the
angle through which the cylinder has been rotated. Each complete turn of the crank adds 2π to θ.
It then follows that if we have
performed a total of N turns of the crank in the experiment, the
total mechanical work must equal to:
W = τθ = ( 2πN ) MgR
Equation 5.2
This completes the calculation of the mechanical work we put into the system.
Next we consider how to compute the heat Q imparted to the cylinder from the measured
temperature change. The general formula to compute the heat required to change the temperature
of an object by a certain amount is given by:
Equation 5.3
Q = mcΔT
The mass of the object being heated is m, and c is the specific heat of the material. For us, the
object being heated is the aluminum cylinder. Its mass m can be measured (it should be about
200 g), and the specific heat of aluminum is 0.220 (cal/g oC). ΔT is the change in temperature
experienced by the object being heated, and is a measured quantity. We will calculate this a few
different ways, discussed in the post-lab.
We can then finally find Joule's Constant:
W
J m = ( J / cal )
Equation 5.4
Q
Any remaining details in the calculations are discussed in section 3.1.
3 of 20
2.2 Conversion of Electrical Energy into Heat and Light (Part 2)
Another form of energy that we use on a daily basis is electrical energy. When a light switch
is flipped on, electrons flow through the filament of the lamp. Electrons collide with the nuclei of
the lattice of the lamp’s filament, causing them to vibrate with larger amplitude. The energy due
to the vibrating electrons is radiated away as electromagnetic waves called photons (light
particles). This radiation is what people identify as “light” and/or “heat.” A regular incandescent
light bulb produces a light spectrum consisting of the infrared, the visible and the ultraviolet. If
the light bulb is submerged under water, the infrared and ultraviolet parts of the spectrum are
absorbed by the water causing the water temperature to increase. The visible part of the spectrum
passes through water1.
The amount of electrical energy consumed by the light bulb, EConsumed , is calculated by
multiplying the power P used, by the amount of time Δt the light bulb is on. The power P is
found by multiplying the voltage V with the electric current I through the light bulb— P = IV .
Assuming that the light bulb used the entire electrical energy it consumed to produce the
radiation energy E Produced , we have
E Produced = EConsumed = PΔt = IVΔt .
Equation 5.5
If V is in Volts and I in Amps, then P is in Watts and the energy E is in Joules.
If the light bulb is surrounded by material that will absorb almost all of the photons and
whose specific heat is known, the total heat can be found again by using Equation 5.3. In this
experiment, the materials that surround the light bulb are the water, water jar and thermometer.
The amount of heat ΔQ associated with the temperature change ΔT is
Equation 5.6
ΔQ = DΔT ,
where for this setup D is given by
cal ⎞
⎛ cal ⎞
⎛
D = mwater cwater +23 ⎜ o ⎟ +Vthermometer ⎜ 0.46 3 o ⎟ .
Equation 5.7
⎝ C⎠
⎝
cm C ⎠
This is a generalization of equation 5.3; instead of one term mcΔT, we now have several terms
playing the role of mc for each of the different substances and objects in the water.
In Part 3.2.1 of the experiment (Conversion of Electrical Energy into Heat), a small amount
of India ink is added to the water to capture the otherwise escaping visible spectrum of light. In
order to further reduce the heat lost to the air, the water jar is inserted into a Styrofoam
Calorimeter insulator. By adding India ink and insulating the jar, one can assume the entire
electrical energy produced by the light bulb is converted to heat and no heat is lost to the air. The
electrical Joule’s constant J electrical = J e can then be calculated based on Equ. 5.5 through 5.8,
E
IV Δt
J e = Produced =
.
Equation 5.8
DΔT
ΔQ
In Part 3.2.2 of the experiment (Conversion of Electrical Energy into Heat and Light) no
India ink is added and the jar is not insulated. Because the visible part of the spectrum is not
absorbed in this case, all the radiation does not go into producing heat and thus Equation 5.8 is
not applicable in this case. However, the visible light producing efficiency can be calculated
from the following,
− Eabsorbed
E
E
, Equation 5.9
VisibleLightProducingEfficiency = visible = produced
E produced
E produced
1
If you consider the composition of your eyes, you can understand why the light that passes through water is
“visible”.
4 of 20
where Evisible is the energy of the visible light and Eabsorbed is the radiation energy absorbed by
the water. Since the absorbed radiation energy Eabsorbed is the heat absorbed by the water,
Eabsorbed can be calculated according to
Eabsorbed = JΔQ .
Equation 5.10
where J = 4.19
J
is the accepted value of Joule’s constant. The amount of heat ΔQ
cal
transferred to the water must be found using Equations 5.6 and 5.7.
3. Laboratory Work
3.1 Conversion of Mechanical Energy (Part 1)
Preparing the Apparatus
The apparatus for this lab must be set up carefully in order to obtain a good result. The
overall apparatus is shown in Fig. 5.1. A multimeter (ohmmeter) will be used to determine the
temperature of the cylinder as shown in Fig. 5.2 and described below. We convert mechanical
work into heat through friction between a nylon rope and aluminum cylinder, as described in
section 2.1. The source of mechanical energy will be provided by you—the aluminum cylinder
will be turned by a crank. You should do the following to ensure your hardware is set up
correctly.
1. You should have the crank apparatus set up on the table top as shown in Fig. 5.3.
Measure the mass of the aluminum cylinder, and replace it by screwing in the knob (see
Fig 5.3). There are two brushes on the crank apparatus—make sure that they in contact
with the side of the aluminum cylinder with the brass slip rings exposed, as shown in Fig.
5.4. The brushes establish an electrical contact with the thermistor inside the cylinder,
which is used to monitor the cylinder's temperature.
2. Spray some powdered graphite on the cylinder. This acts as a lubricant. The graphite is
harmless so long as it is not inhaled (so avoid spraying it near your face).
3. Mass the bucket and whatever masses have been placed in it. The total M = Mbucket + Min
is taken to be the mass supported by the rope. We neglect the rope's mass. A total M of 23 kg is recommended.
4. Tie the nylon rope to the bucket, leaving relatively little extra rope hanging down below
the bucket. (You will need as much of the rope's length above as possible.)
5. Align the bucket with the slot on the edge of the table-top crank apparatus, such that the
nylon rope passes vertically through the slot. Wrap the rope several times around the
aluminum cylinder (4-5 turns recommended), keeping some tension in the rope as it is
wrapped. (It should be wrapped tightly).
6. Tie the rope to rubber band anchored to the base-plate of the crank, as shown in Fig. 5.1.
The rubber band should be through the hook in such a way that it creates two loops. (One
loop is not strong enough to maintain proper tension in the rope for most rubber bands—
loop it through so that it is doubled up. Ask you TA/TI for help if needed.) Pull the
rubber band's loops towards the aluminum cylinder before tying that end of the rope off,
so that when you are not cranking the rubber band maintains some tension in the rope.
Make sure the rope does not cross over itself anywhere on the cylinder.
7. Turn the crank a few times. How much does the mass rise off the floor? The amount of
friction between the rope and cylinder is determined by the tension in the rope, and the
number of turns of the rope around the cylinder. If the mass rises more than 3cm from the
floor, there is too much friction between the rope and aluminum cylinder. In this case
5 of 20
either re-tie the string to the rubber band such that it is looser, or unwind one turn of the
rope around the cylinder. If the mass does not entirely leave floor, there is not enough
friction, and you should either add a turn or re-tie the rope to the rubber band to make it
tighter. To correctly calculate the force of the hanging mass, all of the mass must leave
the floor when you are cranking.
8. Ideally the mass will just leave the floor when you crank, and fall back to the floor if you
stop cranking but hold on to the crank handle. Keep playing with step 7 until this happens.
9. Use the banana-plug connectors to attach the ohmmeter (see Figs. 5.2 and 5.4), and set it
to the 200 kΩ setting or similar resistive range. Your apparatus is ready to go! Some tips
about setting up multimeters are provided at the end of the instructions (p. 10).
Using the Apparatus (Data Collection)
We now describe the experimental procedure which uses the apparatus described above.
1. Make sure the turn counter for the crank is reset to zero. (Turn the knob of the counter to
reset it.)
2. Make sure your Ohmmeter is on, and record your starting resistance R for time t = 0, in
6 of 20
3.
4.
5.
6.
7.
table 5.1. Note that a table and function for converting the resistance measured across the
thermistor to a temperature can be found below. It is most efficient to record all of the
resistances in the experiment and then make conversions at the end.
Start your hand timer, and begin cranking the apparatus. Every thirty seconds you should
briefly stop cranking in order to record the resistance and number of revolutions in table
5.1. (Note that the thermistor's reading will vary while the apparatus is being cranked, but
will quickly settle to a steady value when it is not being cranked. The person cranking
should stop for less than five seconds at each thirty second interval, just long enough for
a lab partner to record N and R, and then resume.)
Continue performing step three for thirty second intervals until your recorded
temperature has risen 10-12 oC. You can eyeball this from the table above (or the reduced
table on the apparatus itself) while doing the experiment, and then do more careful
temperature calculations once data collection is over. A total cranking time of about 5
minutes (300 seconds), in which 500-700 revolutions of the crank are performed would
be typical.
At a thirty second interval at which you have achieved the temperature change of
approximately 10-12 oC, stop cranking. Mark this time as tstop.
However long you were cranking the system, continue to monitor it for that long again
every thirty seconds. (Continue taking data without cranking until the time reaches 2tstop..
Clearly N no longer changes, but the resistance should rise slowly as the temperature of
the aluminum cylinder decreases as it gradually tries to return to equilibrium with the
environment.) This step is in place in order to make a rough estimate of how much
energy was lost as heat dissipating into the environment. A change of 1-4 oC in this step
would be typical. Talk to your TA if you observe something outside of this range.
Convert all of your resistance data to temperatures using the table and/or function below.
The table will allow you to convert to temperatures with an acceptable degree of
precision in the absence of a good calculator for evaluating the function. If you are able
to use the functional form to get data however, your results will be much nicer. The
function is:
T ( R ) = ( 67.03) − ( 0.7136 ) R + (3.801∗10 −3 ) R 2 − (8.680 ∗10 −6 ) R 3
Equation 5.11
This function requires input of R in kΩ in order to obtain a result in degrees Celsius.
Figure 5.1
Figure 5.2
7 of 20
Figures 5.5 and 5.6 visualize the data from the table below. (Equation 5.11 is an approximation
of the actual curve, but we see from figure 5.6 that it is a good one over the temperature range of
interest. The function is shown in green, and the table data below in blue.)
8. Follow the instructions and questions in the post-lab in order to complete the analysis of
the data.
3.2 Conversion of Electrical Energy (Part 2)
To be able to compare more data in the allotted time, you will be collecting data for only half
this section and will be utilizing results from other groups to complete the analysis. Before you
begin this section, the Lab TA or TI will assign your group to complete EITHER Part 3.2.1
OR Part 3.2.2. DO NOT DO BOTH. You are asked to share your data with the laboratory
section by writing your results on the chalk board as soon as you have them available, and in turn
you will be using results of others to answer some of the questions.
8 of 20
Introduction
Introduction (Part 2)
In
In Part
Part 3.2.1,
3.2.1, Conversion
Conversion of
of Electrical
Electrical Energy
Energy into
into Heat
Heat (With
(With Ink
Ink &
& Insulator),
Insulator), we
we are
are
assuming
assuming all
all the
the energy
energy produced
produced by
by the
the light
light bulb
bulb is
is absorbed
absorbed by
by the
the water
water when
when calculating
calculating
JJElectrical
Electrical .. A
A 35-Watt
35-Watt incandescent
incandescent lamp
lamp is
is immersed
immersed in
in aa known
known quantity
quantity of
of water
water with
with aa small
small
amount
of
India
ink
added
to
make
it
opaque
to
the
visible
light,
so
as
to
absorb
the
visible
light.
amount of India ink added to make it opaque to the visible light, so as to absorb the visible light.
The
The water
water jar
jar is
is inserted
inserted into
into aa Styrofoam
Styrofoam Calorimeter
Calorimeter insulator
insulator to
to prevent
prevent heat
heat from
from escaping
escaping to
to
the
air.
The
temperature
of
the
water
is
measured
with
a
thermometer.
By
monitoring
the
water
the air. The temperature of the water is measured with a thermometer. By monitoring the water
temperature,
temperature, the
the heat
heat produced
produced by
by the
the lamp
lamp can
can be
be calculated.
calculated. The
The ratio
ratio between
between the
the electrical
electrical
energy
that
flows
into
the
lamp
and
the
heat
produced
by
the
lamp
determines
the
energy that flows into the lamp and the heat produced by the lamp determines the Joule’s
Joule’s
constant
constant for
for the
the electrical
electrical energy.
energy.
In
In Part
Part 3.2.2,
3.2.2, Conversion
Conversion of
of Electrical
Electrical Energy
Energy into
into Heat
Heat and
and Light
Light (Without
(Without Ink
Ink &
& Insulator),
Insulator),
the
the efficiency
efficiency of
of the
the incandescent
incandescent lamp
lamp is
is measured.
measured. The
The details
details are
are similar
similar to
to the
the first
first part,
part, but
but
no
no India
India ink
ink is
is added
added to
to the
the water
water and
and the
the jar
jar is
is not
not insulated.
insulated. Without
Without the
the ink,
ink, some
some (not
(not all)
all) of
of
the
the energy
energy from
from the
the lamp
lamp is
is absorbed
absorbed into
into the
the water,
water, but
but the
the visible
visible light
light energy
energy escapes.
escapes. To
To
determine
determine the
the amount
amount of
of visible
visible light
light energy,
energy, the
the heat
heat transferred
transferred into
into the
the water
water is
is subtracted
subtracted
from
from the
the total
total energy
energy produced
produced by
by the
the light
light bulb,
bulb, which
which is
is the
the same
same as
as the
the total
total electrical
electrical energy
energy
itit consumed.
consumed. The
The ratio
ratio between
between the
the light
light energy
energy and
and the
the electrical
electrical energy
energy gives
gives the
the light
light
producing
efficiency
of
the
bulb.
producing efficiency of the bulb.
3.2.1
3.2.1 Conversion
Conversion of
of Electrical
Electrical Energy
Energy into
into Heat
Heat (With
(With Ink
Ink &
& Insulator)
Insulator) (Part 2)
Procedure
Procedure
1.
1. Measure
Measure the
the room
room temperature.
temperature.
2. Weigh
Weigh the
the jar
jar assembly
assembly including
including the
the lid
lid and
and record
record its
its mass
mass m
mJar
2.
inSection
Section4.2.1.
4.2.1.
Jar in
3.
3. Remove
Remove the
the lid
lid of
of the
the jar
jar and
and fill
fill itit to
to the
the indicated
indicated water
water level.
level. Do not overfill. Filling
beyond
beyond this
this level
level can
can significantly
significantly reduce
reduce the
the life
life of
of the
the lamp.
lamp. Close
Close the
the lid.
lid.
4.
4. Make
Make the
the electrical
electrical connections
connections with
with aa DC
DC power
power supply,
supply, two
two multimeters
multimeters (one
(one acting
acting as
as
aa voltmeter
voltmeter and
and the
the other
other as
as an
an ammeter)
ammeter) and
and wires
wires with
with banana
banana plug
plug connectors.
connectors. The
The
voltmeter
voltmeter is
is to
to measure
measure the
the voltage
voltage difference
difference between
between the
the two
two terminals
terminals of
of the
the lamp
lamp and
the
the ammeter
ammeter is
is to
to measure
measure the
the current
current through
through the
the lamp.
lamp. (See
(See Figures 5.7, 5.8)
Figure 5.8
Figure 5.7
5.
5. Turn
Turn on
on the
the power
power supply
supply and
and quickly
quickly adjust
adjust the
the power
power supply
supply voltage
voltage to
to about
about 9.8
9.8 volts.
volts.
At
At this
this voltage
voltage the
the ammeter
ammeter should
should read
read about
about 2.2
2.2 amps.
amps. Shut
Shut the
the power
power off
off right
right away.
away.
Do
Do not
not leave
leave the
the power
power on
on long,
long, otherwise
otherwise itit will
will raise
raise the
the water
water temperature
temperature before
before the
the
= VI
VI .).)
measurement
P=
measurement takes
takes place
place later.
later. Do
Do not
not let
let power
power exceed
exceed 35
35 watts! ( P
99 of
of 20
20
6. Add enough India ink to the water, so the lamp filament is just barely visible when the
lamp is illuminated.
7. Insert the jar into a Styrofoam Calorimeter insulator.
8. Insert a thermometer through the hole in the top of the jar. You may want to swirl the jar
slightly while in contact with table to reach an equilibrium temperature (room
temperature). When swirling, hold the rubber part of the insulator in order to reduce the
heat going into the jar from your hand.
9. When ready, turn the power supply on and start the timer.
10. On Table 5.2, record the current, voltage, and temperature of water with respect to time
in constant intervals of 60 seconds. Keep an eye on the ammeter and voltmeter
throughout the measurement to be sure these values do not change significantly.
Continually swirl the jar gently the whole time! As in Step 8, hold the rubber part of the
insulator.
11. When the temperature increases by about 8°C, shut off the power but do not stop the
timer. Record the time tstop and temperature.
12. As done in Section 3.1, continue to take temperature readings in 60-seconds intervals
until the timer reads 2t stop . Continue swirling the water gently.
13. Remove the jar from the insulator. Note how much of the thermometer is immersed in the
water. Remove the thermometer from the jar. Calculate Vthermometer —an estimate volume
of the portion of the thermometer that was immersed in the water. Record it in Section
4.2.1.
14. Weigh the jar assembly including the water m jar +mwater = m j+w and record it in Section
4.2.1. Discard the water.
3.2.2 Conversion of Electrical Energy into Heat and Light (Without Ink & Insulator)
Procedure (Part 2)
1. Without the India ink and Styrofoam Calorimeter insulator, follow Steps 3 – 14 of
Section 3.2.1. You wish to allow visible light to escape. Since you will not be using the
Styrofoam calorimeter insulator hold the lid of the jar when swirling instead. Record your
data in Table 5.3.
Instruction Appendix: Notes on Wiring Multimeters (Part 2)
1. One wire always goes to the common (COM) port on a multimeter.
2. Where the second wire goes depends on the quantity you want to measure. The other
choices may include any of the following: (A), (mA), (V and/or Ω).
3. In order to measure voltage (voltmeter), the second wire goes to the (V) port. The
multimeter should then be turned to an appropriate voltage reading setting, depending on
the size of the voltage being measured. Take care to note whether the device is set to
measure a voltage for an alternating source (AC or ~), or direct source (DC or –). There
are no alternating sources in this lab.
4. Voltages are always measured across two different points in the circuit, and a voltmeter
should consequently be wired in parallel with the circuit element(s) of interest.
5. In order to measure a current the second wire should go either to the (mA) or (A) port.
(Some multimeters may not have both). The (mA) port is more sensitive than the (A)
port, and therefore has higher numerical resolution / precision for small currents. Putting
too much current through a (mA) port however will blow the fuse, and then that port will
no longer work until the fuse is replaced. For larger currents (closer in order of magnitude
10 of 20
to an amp as opposed to a milliamp), always use the (A) port. The currents in this lab are
large enough that you should not ever plug into a (mA)-only port today. Once again turn
the device to an appropriate setting for current readout to make measurements.
6. Currents travel through loops in a circuit. An ammeter should therefore be placed within
the loop of interest (or in series with the circuit element(s) of interest).
7. On devices set up to measure resistances, you would generally use the same port as for
voltage. Turn the device to an appropriate Ω setting and proceed with measurements once
it is wired. This is the case you are interested in for the first half of the lab, where you are
measuring a resistance across the aluminum cylinder's thermistor to get a temperature
reading.
11 of 20
Name:
Laboratory Section:
Laboratory Section Date:
Partners’ Names:
Grade:
Last Revised on January 6, 2016
EXPERIMENT 5 - New
Part 1: Equivalence of Energy: Heat, Mechanical
Part 2: Equivalence of Energy: Heat, Electrical, Light
For Mechanics courses (PHY113, PHY121) do only part 1
4. Post-Laboratory Work [20 pts]
4.1 Conversion of Mechanical Energy into Heat [10pts]
Time (sec)
0
30
60
90
120
150
180
210
240
270
300
330
360
390
420
450
480
510
540
570
600
630
660
690
720
750
780
R (kΩ)
N (Revs)
Temp (°C)
Time (sec)
R (kΩ)
N (Revs)
Temp (°C)
Time (sec)
R (kΩ)
N (Revs)
Temp (°C)
Table 5.1
Convert R into T using T ( R ) = ( 67.03) − ( 0.7136 ) R +( 3.801∗10 −3 ) R 2 − ( 8.680 ∗10 −6 ) R 3 where R
must be entered in kΩ , or use the table on page 8.
12 of 20
1. Plot temperature versus time of the data
from Table 5.1 on Graph 5.1. Draw two
best-fit straight lines—one for the time
between 0 and t stop and the other between
t stop and 2t stop . As shown on Figure 5.7,
mark on the y -axis the initial ( Tinitial ), peak
( T peak ) and final ( T final ) temperatures.
These three temperatures must be based on
the two best-fit straight lines, not the data
Figure 5.3: Temperature vs. Elapsed Time.
points themselves. The initial temperature
Tinitial is at the y-intercept of the first line;
the peak temperature T peak is at the intersection of the two lines; the final temperature T final
is when the time is 2t stop . Include title and axis labels with units. [2pts]
Graph 5.1
13 of 20
2. The peak temperature in Graph 5.1 may not be exactly the same as the temperature when you
stopped cranking. Why might it be possible to for the temperature reading to rise a bit more
after you stop putting energy into the system? [1pt]
3. Calculate the work done to lift the mass while cranking, using equation 5.2. Next compute
what we will call ( ΔT )Uncorrected = ΔTu , which is the temperature change between your starting
temperature at t=0 and peak temperature. (If your peak temperature and stop temperature are
different, as discussed in question 2, use the peak). Then compute Qu using ΔTu and equation
5.3. Finally, compute Jmechanical,uncorrected = Jmu using the above quantities and equation 5.4. [2
pt]
Total Number of Revolutions N = __________
Hanging Mass M =
__________
Aluminum Mass m =
Radius of Aluminum cylinder R =
ΔTu (°C) = TPeak − TInitial =
__________
4. While cranking, some heat was likely lost to the air due to ambient cooling. Estimate the
temperature change due to this effect by computing ΔTambient = ΔTa = Tpeak − Tfinal . Then
compute a corrected temperature change ΔTcorrected = ΔTc = ΔTu + ΔTa . Repeat the calculation
from question 3 above to obtain J mechanical,corrected = J mc . [1 pt]
14 of 20
5. Which of the two values Jmu or Jmc is closer to the accepted value of J = 4.2 J/cal? (The value
which corrects for ambient cooling may not always be better.) Explain what you observe.
(Hint: Why might measuring ambient cooling relative to the peak over-estimate the amount
of heat lost to the environment during cranking?) [2pt]
6. Compute the average of Jmu and Jmc. You can call the average Jm. Compute the standard
deviation based on those two numbers, and the error in the mean Jm. Does your average agree
with the accepted value? [1pt]
7. Discuss one major source of error in this experiment besides the ambient/radiant cooling, and
how it may have affected the measured Joule’s constant. Had that error been removed, would
it have increased the measured Joule’s constant or decreased it? Explain. [1pt]
15 of 20
4.2 Conversion of Electrical Energy [9pts] (Part 2)
CIRCLE WHICH SECTION
YOU ARE ASSIGNED:
m Jar (grams) =
m Jar + mWater (grams) =
mWater (grams) =
Section 3.2.1
With India Ink
Section 3.2.2.
Without India Ink
__________
__________
__________
VThermometer (cm3) =
__________
(Estimate Vthermometer as a cylinder, making appropriate measurements with the calipers. The
relevant volume is the portion of the thermometer that is submerged.)
Time
(sec)
Temperature
(°C)
Voltage
(V)
Current
(A)
Time
(sec)
Table 5.2
16 of 20
Temperature
(°C)
Voltage
(V)
Current
(A)
8. Plot the water temperature versus time of the data from Table 5.2 on Graph 5.2, as was done
in Question 1. Referring to Figure 5.4, draw two best-fit straight lines and mark on the y axis the initial, peak and final temperatures ( TInitial , TPeak and TFinal , respectively).
Include title, axis labels with units. What is the uncorrected temperature change
ΔTUncorrected = TInitial − TPeak ? [2pt]
Graph 5.2
9. As done as in Question 4, find ( ΔT )Corrected based on the Question 8’s graph. Record your
answer below and in Table 5.3. Include units and show calculation work. [1pt]
17 of 20
10. Calculate the quantity D using Equation 5.7. Record your answer below and in Table 5.3.
Include units and show calculation work. [1pt]
11. Using Equation 5.5, calculate the total amount of electrical energy consumed by the light
bulb, EConsumed . If the voltage and current changed, use an average value of the power
P = VI in your calculations. Record your answer below and in Table 5.3. Include units and
show calculation work. [1pt]
Once you have completed Questions 9, 10, & 11, place your values for (ΔT )Corrected ,
D , and
EConsumed
on the board in the appropriate section (either “Section 3.2.1 Results” or “Section
3.2.2 Results”). Then, by selecting a set of data that is consistent with the majority of the class’s
data, complete the second half of Table 5.3 using data from another group.
(ΔT )Corrected
Section 3.2.1: Conversion of
Electrical Energy into Heat using
Ink and Insulator
D
EConsumed
Table 5.3
18 of 20
Section 3.2.2: Conversion of
Electrical Energy into Heat and
Energy (No Ink or Insulator)
12. By applying D and ( ΔT )Corrected from Section 3.2.1 to Equation 5.6, calculate the total heat
ΔQ1 absorbed by the water containing the India ink, the jar and the thermometer. Then,
using D and (ΔT )Corrected from section 3.2.2, calculate the total heat ΔQ2 absorbed by the
set-up that does not include the India ink. Include units and show calculation work. [1pt]
13. Calculate Joule’s constant J e by applying ΔQ1 from Question 12 and EProduced = EConsumed
from Section 3.2.1 to Equation 5.8. Include units and show calculation work. [1pt]
14. By what fraction of the accepted Joule’s constant J = 4.19
J
does your J e differ from it,
cal
⎛ J −J⎛
i.e. what is ⎜ e
? What is the more accurate of J mu and J mc you found in Question 5?
⎝ J ⎜⎝
Compare: which one of J m and J e is closer to the accepted value J ? Explain. [1pt]
19 of 20
15. Find EAbsorbed by the water without the ink, the jar, and the thermometer by expressing the
heat ΔQ2 found in Question 12 in units of Joules using Equation 5.10. [1pt]
16. Calculate the efficiency of the lamp in producing light using Equation 5.9. Is the
incandescent lamp more efficient as a light producing source or as a heat source? Explain.
(You have access to data in which the visible spectrum is allowed to escape / is not absorbed
into the water as heat, and another data set in which the entire spectrum is absorbed. Think
about how these should differ.) [1pt]
20 of 20