Derivative Finanzprodukte mit Kreditrisiko

70
KAPITEL 5. KREDITRISIKO AM EINZELGESCHÄFT
Derivative Finanzprodukte mit Kreditrisiko
Neben den primären Finanzprodukten, gibt es inbesondere am Sekundärmarkt, also bei den derivativen Produkten die Problematik des Kreditrisikos. So gibt es z.
B. Kreditderivative wie die Kreditversicherung. Hier geht es um die Versicherung
von Kreditportfolien. Dafür müssen wir zunächst wieder ein Modell für die Ausfallanzahl unterstellen. Es handelt sich hierbei wieder um einen nicht-stetigen stochastischen Prozess, der aber strukturell einfacher als der Zählprozess ist, den wir
in Abschnitt 5.1 kennen lernen werden. Der Grund ist zum einen, dass es sich um
ein altes versicherungs-mathematisches Modell handelt, aber auch der, dass die Parametrisierung einfacher ist.
Seien E1 , E2 , . . . unabh. exp(h)-verteilte Zufallsvariablen und definiere
Sn :=
n
X
Ei .
i=1
Mit der Interpretation der Ei als Wartezeiten zwischen dem i-ten und (i − 1)-ten
Ereignis, und E1 als Wartezeit bis zum ersten Ereignis, ist Sn die Zeit des n-ten
Ereignisses.
Nt := sup{n : Sn ≤ t}
(5.9)
zählt die Ereignisse, die bis zum Zeitpunkt t eingetreten sind. Nt wird Erneuerungsprozess (auch Punkt- oder Zählprozess) genannt und z. B. in Sheldon (1996) oder
Kingman (1993) untersucht.
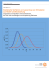
Ein potenzieller Verlauf von Nt ist in der Abbildung 5.3 dargestellt.
Es gilt
(i) N0 = 0.
(ii) Nt , t ≥ 0 besitzt unabh. Zuwächse.
Beweis: Die Ei sind unabhängig und das in t aktuelle Ei gehorcht der gedächtnislosen Exponentialverteilung.
5.2. BEWERTUNG VON FINANZINSTRUMENTEN
71
NH(t)
6
2
1
-
0
τ1
τ2
|{z}
|{z}
E1
t
E2
Abbildung 5.3: Verlauf eines Erneuerungsprozesses
(iii) Nt+u − Nt ∼ P oisson(hu). D. h. Nt ist stationär, hängt also nicht von t ab.
Insbesondere gilt Nu ∼ P oisson(hu).
Beweis: hier nicht
(iv) E(Nt+u − Nt ) = hu = V ar(Nt+u − Nt ).
(v) Nt < ∞ und
Nt
t
→ h für t → ∞.
Beweis: E Ntt = h, V ar Ntt =
h t→∞
⇒
t
0
(vi) Nt − ht ist ein Martingal.
Beweis: E(Nt+u − Nt ) = hu ⇒ EdNt = hdt damit ist der Kompensator
Rt
EdNs = ht und ⇒ Nt − ht ein Martingal.
0
Beweis: Nt+u − Nt ∼ P oisson(hu).
(vii) Nt ist ein Markoff-Prozess.
Beweis: hier nicht
Die zu erwartende Anzahl der Ereignisse in einem Interval [t, t + u] ist proportional
zur Länge (vi) mit Faktor h, der Intensitätsrate heißt. Da h konstant ist, heißt Nt
homogener Poisson-Prozess.
Hängt h von t ab, so definiere H(t) =
Rt
0
h(s)ds und Nt , so dass
72
KAPITEL 5. KREDITRISIKO AM EINZELGESCHÄFT
(i) N0 = 0
(ii) Nt , t ≥ 0 besitzt unabhängige Zuwächse.
(iii) Nt+u − Nt ∼ P oisson(H(t + u) − H(t)), h(s) > 0 ∀s ≥ 0.
(iv) (iii) ist gleichbedeutend mit P (Nt+u −Nt = n) =
(siehe Formel (6.1)).
R t+u
1
(
n! t
h(s))n exp{−
R t+u
t
h(s)ds}
Interessant und nützlich ist
Theorem 5.2.4 Wenn Nt die kum. Intensität H(t) besitzt, so hat NH −1 (t) die Intensität h ≡ 1.
Beweis: Übung
Eine weitere Verallgemeinerung stellt der Cox-Prozess dar, bei dem h zusätzlich zu
t auch noch von einem Prozess Zt abhängt.
Definition: Sei h(t), 0 ≤ t < ∞ ein potenziell zufälliger nicht-negativer Intensitätsprozess. Ein Punktprozess Nt , 0 ≤ t < ∞ mit N0 = 0 heißt Cox-Prozess, falls
für 0 ≤ t1 < t2 < . . . tk < ∞ gilt
=E
(
1
n1 ! . . . n k !
P (Nt1 − N0 = n1 , . . . , Ntk − Ntk−1 = nk )
¸ni
· Z tk
¸)
k ·Z ti
Y
h(s)ds exp −
h(s)ds
i=1
ti−1
0
Bemerke, dass analog zu Satz 5.2.4 gilt:
Theorem 5.2.5 Sei h(t, Zt ) = h(t) 0 ≤ t ≤ ∞ ein zufälliger Intensitätsprozess und
N ein homogener Poissonprozess mit Parameter 1, welcher unabhängig von h sei.
Rt
Setze Ht = 0 h(s)ds. Dann ist
Ñt = NHt
ein Cox-Prozess mit Intensität h(t).
5.2. BEWERTUNG VON FINANZINSTRUMENTEN
73
Nun wollen wir das Ereignis Ausfall des Kontrahenten vor Laufzeitende des Geschäfts”
verhältnisses“ modellieren. Sei T das Laufzeitende und τ der Konkurszeitpunkt. Es
geht also um {τ ≤ T }. Wir betrachten einen Cox-Prozess Ñ (in t), bzw. einen
Standard Poissonprozess N in Ht .
Setze
τ = τ1 = Ẽ1 Zeitpunkt des ersten Ausfalls
n
X
Ẽi für n > 1.
τn =
i=1
Betrachte ein (einmalige) Zahlung XT . Besteht Erfüllungsrisiko, so ist der Zahlungsstrom
I{τ >T } XT ,
wobei XT zufällig oder fest sein kann.
Nun ist
{τ > T } = {ÑT = 0} mit Ñ als betrachtetem Cox-Prozess
= {NHT = 0} wegen Satz 5.2.5
= {HT < E1 } d. h. Konkurs nach Laufzeitende
(auf der transformierten Skala)
½Z T
¾
=
h(s, Zs )ds < E1
0
Die Wahrscheinlichkeit dieses Ereignisses hängt von der gemeinsamen Verteilung
R∞Rx
von Zs und E1 ab, da P (X > Y ) = 0 0 f (x, y)dxdy. Wir müssen also Annahmen
über die gemeinsame Verteilung der beiden Seiten machen. Bedingt gilt jedoch unter
Unabhängigkeit
P (τ > T | Zs , 0 ≤ s ≤ T ) = e−
RT
0
h(s,Zs )ds
,
(5.10)
da die kumulative Verteilungsfunktion von E1 P (E1 ≤ t) = 1 − e−t ist. Zur Plausibilisierung sei bemerkt, dass bei einem Pfad von Zt mit großer Intensität h(t, Zt )
die rechte Seite klein, also die frühe Ausfallwahrscheinlichkeit groß ist.
74
KAPITEL 5. KREDITRISIKO AM EINZELGESCHÄFT
Sei weiter einschränkend H(∞) = ∞, d. h. es gibt unendlich viele Sprünge τi . Des
Weiteren betrachten wir das Modell ohne Wiedereinbringung (engl. zero recovery“).
”
Der Wert der Auszahlung I{τ >T } XT beträgt in t:
E{e−
RT
t
Hier stellt e−
f
ru
du
RT
t
XT I{τ >T } | Ft }.
f
ru
du
den Abdiskontierungsfaktor bei Terminzinskurve ruf (siehe For-
mel (2.3)) dar. Zu kann von ruf abhängen. Hingegen nehmen wir an, dass E1 (konditional) unabhängig von den anderen stochastischen Größen ist.
E(e−
= E[e−
RT
t
f
ru
du
RT
t
f
ru
du
XT I{τ >T } | Ft )
XT E[I{τ >T } | Ft , XT , Zu , ruf , 0 ≤ u ≤ T ] | Ft )]
wegen E(X) = E(E(X|Y )) und E(E(X|Y )|Z) = E(E(X|Z)|Y ).
Die innere Erwartung ist
µ
Z T
Z
P E1 >
h(s, Zs )ds | E1 >
0
0
u
¶
h(s, Zs )ds, 0 ≤ u ≤ t .
Da 1{E1 >t} einen Markoff-Prozess darstellt, ist dieses gleich
¶
µ
Z t
Z T
h(s, Zs )ds
h(s, Zs )ds | E1 >
P E1 >
0
0
RT
RT
P (E1 > 0 h(s, Zs )ds)
= 1{τ >t} e− t h(s,Zs )ds .
= 1{τ >t}
Rt
P (E1 > 0 h(s, Zs )ds)
Somit erhalten wir die Fundamentalformel:
³ RT f
´
³ RT f
´
E e− t ru du XT 1{τ >T } | Ft = 1{τ >t} E e− t (ru +hu )du XT | Ft
Die Größe ht ist bisher die allgemeinste Definition des Kreditrisikoaufschlags (engl.
credit spread“). Es gibt zu dem Thema eine extensive Literatur, z. B. betrachten
”
Bielecki and Rutkowski (2002) diesen Fall (Seite 221ff). Duffie and Singleton (1999)
geben die Formel für zufällige (positive) Wiedereinbringungsquoten an. Außerdem
werden aktuell die Annahmen der Modelle weiter verringert (siehe Collin-Dufresne
et al. (2004)).
Bemerke
5.2. BEWERTUNG VON FINANZINSTRUMENTEN
75
(i) Falls der Konkurs schon eingetreten ist, verbleibt nur der Wert 0.
(ii) Falls τ > t ist, kann man wie gewöhnlich ohne Kreditrisiko vorgehen und muss
nur die Zinsen erhöhen. ht . Je höher ht dieser ist desto geringer ist die Bonität
des Kontrahent.
Es ergibt sich, dass die Theorie eine direkte Verallgemeinerung zur Überlebenszeitanalyse bei deterministischen Ausfallwahrscheinlichkeiten darstellt. Kommen wir auf
das Bespiel der zero-coupon Anleihe mit Nominal 1 (ohne risikofreien Zins) zurück.
Sei
n RT
o
P (t, T ) = E e− t h(s,Zs )ds | Ft
Es gilt
1{τ >t} P (t, T ) = E(1{τ >T } | Ft )
Beweis: Fundamentalformel mit rtf ≡ 0 und XT = 1.
(5.11)
¤
Also ist P (t, T ) die bedingte Wahrscheinlichkeit, dass der Kontrahent nicht vor
T ausfällt. Formel (5.1) impliziert eine Überlebenswahrscheinlichkeit von P (τ >
T |τ > t) = e−
RT
t
h(s)ds
für deterministisches h(s). h(s) ist hierbei die Hazardrate des
Ausfallzeitpunkts.
Bemerkung: Bewertung von Anleihen (engl. bond pricing“)
”
Aus den angestellten Überlegungen - insbesondere aus Formel (5.11) - ergibt sich
direkt die Preisbildung einer ausfallgefährdeten - aber noch nicht ausgefallenen Anleihe (Bond) mit Nominal 1.
B̄0 (t, T ) = E(e−
RT
t
f
ru
du
1{τ >T } | Ft ) = 1{τ >t} P (t, T )B(t, T )
wobei rtf deterministisch ist. Die Bewertung einer nicht-ausfallgefährdeten Anleihe
- mit Nominal 1 - B(t, T ) haben wir in Formel (5.28) hergeleitet. Dort allerdings
noch mit konstantem Zins.
76
KAPITEL 5. KREDITRISIKO AM EINZELGESCHÄFT
B(T, T )
−B̄0 (T, T ) Summe DDP
Ohne Konkurs
+1
−1
0
Mit Konkurs
+1
0
1
Tabelle 5.1: Hedgingstrategie für DDP
Um einen Bogen zu den anfänglichen Überlegungen zur Bewertung derivativer Produkte (ohne Kreditrisiko) zu schlagen, soll hier ein derivatives Produkt mit Ausfallrisiko betrachtet werden.
Die digitale Konkursversicheurng. (engl. digital default put“).
”
Ein DDP hat im Zeitpunkt des Ausfalls eine Auszahlung von 1, sonst eine von 0.
Betrachte zunächst den Fall, dass die Zahlung ggf. erst in T erfolgt. Dann beträgt
der Barwert und damit der Preis in t
D(t, T ) = E(e−
= E(e−
RT
t
f
ru
du
RT
f
du
ru
t
1{τ ≤T } | Ft )
(1 − 1{τ >T } ) | Ft )
= B(t, T ) − B̄0 (t, T )
mit B̄0 als endfälliger ausfallgefährdeter Anleihe (engl. zero coupon defaultable
”
bond“).
Denselben Preis erhält man durch Replikation mit zwei Anleihen mit Nominal 1.
Betrachte das Portoflio aus einer gekauften nicht-ausfallgefährdeten Anleihe und
einer verkauften ausfallgefährdeten Anleihe. Die Auszahlungen im Zeitpunkt T sind
in der Tabelle 5.1 dargestellt.
Für den realistischen Fall, dass der Ausfallzeitpunkt gleich dem Zahlungszeitpunkt
ist, folgt (siehe Formel (5.10), wobei 0 mit t wegen der Gedächnislosigkeit der ExpVerteilung ausgetauscht werden kann):
D(t, T ) = 1{t<τ } E(e−
Rτ
t
f
ru
du
P (τ > x | ruf , u ≤ T, Zs , s ≤ T, {τ ≤ s}, s ≤ t) = e−
|
{z
}
1{τ ≤T } | Ft )
Rx
t
h(s)ds
:=GT
Somit hat τ auf x > t die bedingte Dichte h(x)e−
Rx
t
h(s)ds
1{τ >t} .
1{τ >t}
5.2. BEWERTUNG VON FINANZINSTRUMENTEN
Also:
D(t, T ) = E{1{t<τ ≤T } e−
Rτ
t
f
ru
du
Rτ
| Ft }
f
t ru du
| GT ) | Ft }
= E{E(1{t<τ ≤T } e−
Z T R
Rx
x f
= E{1{τ >t}
e− t ru du h(x)e− t hu du dx | Ft }
t
Z T
Rx f
= 1{τ ≥t} E(
h(x)e− t (ru +hu )du dx | Ft )
t
Z T
Rx f
⇒ D(t, T ) =
E(h(x)e− t (ru +hu )du | Ft )dx
t
77