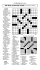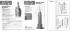KenKen Lesson 4: Talking KenKen     KENKEN RULES 

 KenKen Lesson 4: Talking KenKen KENKEN RULES 1. Every square in the grid will contain one number. • In a 5 x 5 puzzle, use the numbers 1–5. • In a 6 x 6 puzzle, use the numbers 1–6. 2. Do not repeat numbers in any row or column. 3. A cage is a heavily outlined set of squares. The numbers in the squares within a cage must combine (in any order) to produce the target number in the top corner. You must use the mathematical operation next to the target number. 4. Cages with just one square should be filled in with the target number in the top corner. (Hint: This is a good place to start solving the puzzle.) KenKen Lesson 4
Puzzle 4A Puzzle 4B Puzzle 4C Puzzle 4D KenKen is a registered trademark of Nextoy, LLC: © 2009 Nextoy
Page 1 KenKen Lesson 4: Talking KenKen OVERVIEW Students work in small groups to develop and compare solution strategies.
NCTM STANDARDS Communication
• organize and consolidate mathematical thinking through communication;
• communicate mathematical thinking coherently and clearly to peers, teachers, and others;
• analyze and evaluate the mathematical thinking and strategies of others;
• use the language of mathematics to express mathematical ideas precisely.
PROCEDURE 1. Review these KenKen terms with students:
• A square is an individual box in a KenKen puzzle.
• Squares are arranged in rows and columns. A row is a horizontal line of squares. A column
is a vertical line of squares.
• A cage is a heavily outlined set of squares. A cage can have one or more squares.
• Each cage has a target number and operation in the corner.
• A combination is a set of numbers that can possibly complete a cage.
• An arrangement is a set of numbers that can complete a cage in a specific order.
2. Tell students that sharing solution strategies provides practice with clear mathematical thinking and
communication. Emphasize that mathematical language must be precise and consistent to avoid
confusion.
3. Have students look at Puzzle 4A. Invite them to consider how they might begin to solve this puzzle.
Read aloud this strategy to model unclear mathematical thinking:
First I’ll fill in the ones. Then I’ll look for some boxes I can fill in. I know this one with the
25 has only one way to go, so I can fill it in. That means I can fill in the squares in the one
with 4 in it too.
Ask: Why was that description confusing? (The language is not comprehensible and consistent. It is
difficult to follow the description because the actions to follow are not consistently clear. The logical
thinking also is muddy.)
4. Model a clear explanation of the same solution strategy:
I will begin by filling in the cages with only one square. Then, I will look for cages that only
have one possible combination and arrangement. I know that there is only one way to fill in
the 25x cage. It must use the numbers 1, 5, and 5, and the 1 must be in the corner. Once I fill
those in, I also can fill in the 4x cage. There are two possible combinations for that cage: 1, 1,
and 4 or 1, 2, and 2. I know that 1, 1, and 4 cannot be used because there already is a 1 in the
third row. So the 4x cage must be filled with 1, 2, and 2. The 1 must be placed in the corner.
Ask: Why was that description easier to follow? (The language is clear and consistent. It uses
specific terms, including square, cage, combination, and row.)
KenKen Lesson 4
Grades 6-8
KenKen is a registered trademark of Nextoy, LLC: © 2009 Nextoy
Page 2
5. Point out that the clearer description refers to the third row. Explain that to refer to squares clearly,
the rows should be numbered from top to bottom. Columns can be numbered from left to right.
6. Have teams work together to solve Puzzle 4A. Encourage them to take turns solving cages. After
solving a cage, students should carefully explain their thinking processes. Suggest to students that
they consider the remaining cages in this order: 6+, 4–, 12+, 2÷, 24x in the third column, 24x in the
first and second columns, 12x if they need help. Have students compare their solution strategies.
Discuss how to communicate clearly when talking about solving KenKen puzzles. Use these
questions to guide discussion:
• Which cages were easiest to solve? Which were most difficult? Why?
• What words do you have to use carefully when explaining how to solve a KenKen puzzle?
• What advice would you give to someone trying KenKen for the first time?
7. Point out that identifying specific squares can be difficult when talking about a KenKen puzzle.
Some solvers prefer to name each square with a letter. Show students Puzzle 4B. Point out that each
square has been named with a letter in the corner. Explain that students can use this system to name
the squares in any KenKen puzzle. To model the benefits of naming squares, ask: What number
must go in square D? Why? (3; The 15x cage must hold 3 and 5. D must hold the 3 because there is a
3 in the fifth column in square T.) What number must go in square A? Why? (4; The 3+ cage must
be filled with 1 and 2. This means 4 is the only unused number in the first row.)
8. Have teams work together to solve Puzzle 4B. Encourage students to use letter names to help
describe their thinking. Suggest that students consider the remaining squares in this order: H, I, U,
Q, P, Y, X, R, S, N, M, C, B, G, F, J, O, K, L, V, W if they need help. Tell them they can use letter
names for squares at any time to discuss KenKen puzzle solutions. These letter names are
particularly helpful when discussing more challenging puzzles.
EXTEND THE LESSON Challenge students to solve Puzzles 4C and 4D. Have student pairs or teams talk through each step of
their solutions. Then have teams compare their solution strategies.
Puzzle 4C: Point out that this KenKen puzzle only uses multiplication. Review these terms to help
students discuss possible combinations: factors are numbers multiplied together; a product is the result
of multiplying two or more factors. Suggest that students consider the cages in this order: 10x in first
row, 4x, 15x, 5x, 48x, 24x, 40x, 10x in second and third rows if they need help,.
Puzzle 4D: Point out that to name the squares in a 6x6 puzzle, students can use double letters after z:
AA, BB, CC, and so on. If students need help, suggest they begin by considering numbers that must go
in the 11+ and 3÷ cages in the first column. They can determine one number that must go in the 20x
cage and then complete the cages in this order: 20x, 11+ in first row, 4x, 3÷, 8+, 72x, 11+ in sixth
column, 1–, 24x, 40x, 6+, 15x, 11+ in first column, 3–.
COMING UP IN NEXT WEEK’S LESSON Lesson 5: KenKen Notation
Students learn notation methods to help keep track of logical deduction as they solve KenKen puzzles.
KenKen Lesson 4
Grades 6-8
KenKen is a registered trademark of Nextoy, LLC: © 2009 Nextoy
Page 3
PUZZLE ANSWERS KenKen Lesson 4
Puzzle 4A Puzzle 4B Puzzle 4C Puzzle 4D Grades 6-8
KenKen is a registered trademark of Nextoy, LLC: © 2009 Nextoy
Page 4