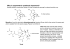Applications of Renormalization Group Methods in Nuclear Physics – 3 Dick Furnstahl

Transcription

Applications of Renormalization Group
Methods in Nuclear Physics – 3
Dick Furnstahl
Department of Physics
Ohio State University
HUGS 2014
Outline: Lecture 3
Lecture 3: Effective field theory
Recap from lecture 2: How SRG works
Motivation for nuclear effective field theory
Chiral effective field theory
Universal potentials from RG evolution
Extra: Quantitative measure of perturbativeness
Outline: Lecture 3
Flow equations in action: NN only
√
In each partial wave with k = ~2 k 2 /M and λ2 = 1/ s
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
√
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 ) +
(k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
Basics: SRG flow equations
[e.g., see arXiv:1203.1779]
Transform an initial hamiltonian, H = T + V , with Us :
Hs = Us HUs† ≡ T + Vs ,
where s is the flow parameter. Differentiating wrt s:
dHs
= [ηs , Hs ]
ds
with
ηs ≡
dUs †
U = −ηs† .
ds s
ηs is specified by the commutator with Hermitian Gs :
ηs = [Gs , Hs ] ,
which yields the unitary flow equation (T held fixed),
dHs
dVs
=
= [[Gs , Hs ], Hs ] .
ds
ds
Very simple to implement as matrix equation (e.g., MATLAB)
Gs determines flow =⇒ many choices (T , HD , HBD , . . . )
SRG flow of H = T + V in momentum basis
Takes H −→ Hs = Us HUs† in small steps labeled by s or λ
dHs
dVs
=
= [[Trel , Vs ], Hs ]
ds
ds
√
with Trel |k i = k |k i and λ2 = 1/ s
For NN, project on relative momentum states |k i, but generic
X
dVλ
(k , k 0 ) ∝ −(k − k 0 )2 Vλ (k , k 0 )+ (k + k 0 − 2q )Vλ (k , q)Vλ (q, k 0 )
dλ
q
Vλ=3.0 (k , k 0 )
1st term
2nd term
Vλ=2.5 (k , k 0 )
First term drives 1 S0 Vλ toward diagonal:
2 2
Vλ (k, k 0 ) = Vλ=∞ (k , k 0 ) e−[(k − k 0 )/λ ] + · · ·
dHs
dVs
=
= [[Trel , Vs ], Hs ]
ds
ds
√
X
dVλ
dλ
q
Vλ=2.5 (k , k 0 )
1st term
2nd term
Vλ=2.0 (k , k 0 )
2 2
Vλ (k, k 0 ) = Vλ=∞ (k , k 0 ) e−[(k − k 0 )/λ ] + · · ·
dHs
dVs
=
= [[Trel , Vs ], Hs ]
ds
ds
√
X
dVλ
dλ
q
Vλ=2.0 (k , k 0 )
1st term
2nd term
Vλ=1.5 (k , k 0 )
2 2
Vλ (k, k 0 ) = Vλ=∞ (k , k 0 ) e−[(k − k 0 )/λ ] + · · ·
Outline: Lecture 3
“Traditional” nucleon-nucleon interaction
(from T. Papenbrock)
Local nucleon-nucleon interaction for non-rel S-eqn
Depends on spins and isospins of nucleons; non-central
longest-range
part is one-pion-exchange potential
−mπ r
3
3
e
+
Vπ (r) ∝ (τ1 ·τ2 ) (3σ1 · ˆr σ2 · ˆr − σ1 · σ2 )(1 +
) + σ1 · σ2
2
mπ r
(mπ r )
r
Characterize operator structure of shorter-range potential
central, spin-spin, non-central tensor and spin-orbit
{1, σ1 · σ2 , S12 , L · S, L2 , L2 σ1 · σ2 , (L · S)2 } ⊗ {1, τ1 · τ2 }
Tensor =⇒
deuteron wf is
mixed S (L = 0)
and D (L = 2)
Non-zero
quadrupole
moment
V(r) (MeV)
200
S=1, T=0 deuteron
proton-neutron
L = 0 relative state
100
S=0,T=1
0
Argonne v18
-100
The quantum numbers of the deuteron
have the deepest potential well!
-200
-300
0
1
2
3
r (fm)
4
5
6
Problems with Phenomenological Potentials
The best potential models can describe with χ2 /dof ≈ 1 all of the
NN data (about 6000 points) below the pion production threshold.
So what more do we need?
Some drawbacks:
Usually have very strong repulsive short-range part =⇒
requires special (non-systematic) treatment in many-body
calculations (e.g. nuclear structure).
Difficult to estimate theoretical errors and range of
applicability.
Three-nucleon forces (3NF) are largely unconstrained and
unsystematic models. How to define consistent 3NF’s and
operators (e.g., meson exchange currents)?
Models are largely unconnected to QCD (e.g., chiral
symmetry). Don’t connect NN and other strongly interacting
processes (e.g., ππ and πN). Lattice QCD will be able to
predict NN, 3N observables for high pion masses. How to
extrapolate to physical pion masses?
Alternative: Use Chiral Effective Field Theory (EFT)
QCD and Nuclear Forces
Quarks and gluons are the fundamental QCD dof’s, but . . .
At low energies (low resolution), use “collective” degrees
of freedom =⇒ (colorless) hadrons. Which ones?
Different EFTs depending on scale of interest
LQCD
scale&
separa)on&
ab initio
CI
DFT
collective
models
Resolution
constituent
quarks
Effective theories
[H. Georgi, Ann. Rev. Nucl. Part. Sci. 43, 209 (1993)]
One of the most astonishing things about the world in which we live is
that there seems to be interesting physics at all scales.
To do physics amid this remarkable richness, it is convenient to be able to
isolate a set of phenomena from all the rest, so that we can describe it
without having to understand everything. . . . We can divide up the
parameter space of the world into different regions, in each of which there
is a different appropriate description of the important physics. Such an
appropriate description of the important physics is an “effective theory.”
The common idea is that if there are parameters that are very large or
very small compared to the physical quantities (with the same dimension)
that we are interested in, we may get a simpler approximate description
of the physics by setting the small parameters to zero and the large
parameters to infinity. Then the finite effects of the parameters can be
included as small perturbations about this simple approximate starting
point.
E.g., non-relativistic QM: c → ∞
E.g., chiral effective field theory (EFT): mπ → 0, MN → ∞
E.g., pionless effective field theory (EFT): mπ , MN → ∞
Goals: model independence (completeness) and error estimates
Classical analogy to EFT: Multipole expansion
If we have a localized charge distribution
ρ(r) within a volume characterized by
distance a, the electrostatic potential is
Z
ρ
φ(R) ∝ d 3 r
|R − r|
If we expand 1/|R − r| for r R, we get the multipole expansion
Z
q
1 X
1 X
ρ
=
+ 3
Ri Pi +
(3Ri Rj − δij R 2 )Qij + · · ·
d 3r
|R − r|
R
R
6R 5
i
ij
=⇒ pointlike total charge q, dipole moment Pi , quadrupole Qij :
Z
Z
Z
q = d 3 r ρ(r)
Pi = d 3 r ρ(r) ri
Qij = d 3 r ρ(r)(3ri rj − δij r 2 )
Hierarchy of terms from separation of scales =⇒ a/R expansion
Can determine coefficients (LECs) by matching to actual distribution
(if known) or comparing to experimental measurements
Completeness =⇒ model independent (cf. model of distribution)
Effective Field Theory Ingredients
General procedure for building an EFT . . .
1
Use the most general L with low-energy dof’s consistent with
global and local symmetries of underlying theory
2
Declaration of regularization and renormalization scheme
3
Well-defined power counting =⇒ small expansion parameter
General procedures:
QFT: trees + loops → renormalization
Include long-range physics explicitly
Short-distance physics captured in a
few LEC’s (calculated from underlying
or fit to data). Check naturalness.
General procedure for building an EFT . . .
1
global and local symmetries of underlying theory
What are the low-energy dof’s for QCD?
What are the relevant symmetries?
2
What choices are there?
Will we be able to use dimensional regularization?
3
Well-defined power counting =⇒ small expansion parameter
Usually Q/Λ. What are the QCD scales?
General procedures:
QFT: trees + loops → renormalization
Include long-range physics explicitly
Short-distance physics captured in a
few LEC’s (calculated from underlying
or fit to data). Check naturalness.
Outline: Lecture 3
Symmetries of the QCD Lagrangian
Besides space-time symmetries and parity, what else?
Is SU(3) color gauge “symmetry” in the EFT?
Consider chiral symmetry . . .
LQCD = q L i/
DqL + q R i/
DqR −
D
/ ≡/
∂ − igsG
/ aT a ;
M=
qL,R =
mu
0
1
(1 ± γ5 )q ,
2
0
md
1
Tr Gµν Gµν −q R MqL − q L MqR
2
T a = SU(3) Gell-Mann matrices
SU(2) quark mass matrix
projection on left,right-handed quarks
mu and md are small compared to typical hadron masses
(5 and 9 MeV at 1 GeV renormalization scale vs. about 1 GeV)
M ≈ 0 =⇒ approximate SU(2)L ⊗ SU(2)R chiral symmetry
Chiral Symmetry of QCD
What happens if we have a symmetry of the Hamiltonian?
Could have a multiplet of equal mass particles
Could be a spontaneously broken (hidden) symmetry
Experimentally we notice
Isospin multiplets like p,n or Σ+ ,Σ− ,Σ0 (that is, they have
close to the same mass). So isospin symmetry is manifest.
But we don’t find opposite parity partners for these states with
close to the same mass. The “axial” part of chiral symmetry is
spontaneously broken down!
Isospin symmetry is “vectorial subgroup” with L = R
The pions are pseudo-Goldstone bosons. The symmetry is
explicitly broken by the quark masses, which means the pion is
2
light (mπ2 MQCD
) but not massless.
Chiral symmetry relates states with different numbers of pions
and dictates that pion interactions get weak at low energy =⇒
pion as calculable long-distance dof in χEFT!
Specific answers for chiral EFT:
1
the global and local symmetries of the underlying theory
2
3
Well-defined power counting =⇒ expansion parameters
Effective Field Theory Ingredients: Chiral NN
Specific answers for chiral EFT:
1
the global and local symmetries of the underlying theory
Left = Lππ + LπN + LNN
chiral symmetry =⇒ systematic long-distance pion physics
2
momentum cutoff and “Weinberg counting” (still unsettled!)
=⇒ define irreducible potential and sum with LS eqn
use cutoff sensitivity as measure of uncertainties
3
Well-defined power counting =⇒ expansion parameters
{p, mπ }
use the separation of scales =⇒
with Λχ ∼ 1 GeV
Λχ
P∞
chiral symmetry =⇒ VNN = ν=νmin cν Q ν with ν ≥ 0
naturalness: LEC’s are O(1) in appropriate units
Chiral Lagrangian
Unified description of ππ, πN, and NN · · · N
Lowest orders [Can you identify the vertices?]:
1
1
gA
1
∂µ π · ∂ µ π − mπ2 π 2 + N † i∂0 +
τ σ · ∇π − 2 τ · (π × π)
˙ N
2
2
2fπ
4fπ
1
1
− CS (N † N)(N † N) − CT (N † σN)(N † σN) + . . . ,
2
2
2c1 2 2 c2 2 c3
†
2
= N 4c1 mπ − 2 mπ π + 2 π˙ + 2 (∂µ π · ∂ µ π)
fπ
fπ
fπ
c4
− 2 ijk abc σi τa (∇j πb )(∇k πc ) N
2fπ
D
1
−
(N † N)(N † στ N) · ∇π − E (N † N)(N † τ N) · (N † τ N) + . . .
4fπ
2
L(0) =
L(1)
Infinite # of unknown parameters (LEC’s),
but leads to hierarchy
P
of diagrams: ν = −4 + 2N + 2L + i (di + ni /2 − 2) ≥ 0
Nucleon-nucleon force up to N3LO
Ordonez et al. ’94; Friar & Coon ’94; Kaiser et al. ’97; Epelbaum et al. ’98,‘03; Kaiser ’99-’01; Higa et al. ’03; …
Chiral expansion for the 2N force:
(0)
(3)
(2)
(4)
V2N$=$V2N$$+V2N$+$V2N$+$V2N$+$…
Short4range'LECs'are'
fi9ed'to'NN4data
LO:
2 LECs
NLO:
renormalization of 1π-exchange
N2LO:
7 LECs
renormalization of contact terms
leading 2π-exchange
Single4nucleon'LECs'are'
fi9ed'to'πN4data
subleading 2π-exchange
N3LO:
sub-subleading 2π-exchange
15 LECs
renormalization of contact terms
3π-exchange (small)
figure from H. Krebs
Chiral effective field theory for two nucleons
Epelbaum, Meißner, et al.
1S0
3S1
80
150
Also Entem, Machleidt
100
40
Organize by (Q/Λ)ν where
Q = {p, mπ }, Λ ∼ 0.5–1 GeV
LπN + match at low energy
Qν
1π
2π
4N
50
0
0
-40
0
0.1
0.2
0.3
0
0.1
0.2
0.3
0.2
0.3
0.2
0.3
1D2
3P0
80
12
40
8
0
4
0
0
0.1
0.2
0.3
0
0.1
3G5
3D3
6
0
0
-0.4
-6
-0.8
-1.2
-12
0
0.1
0.2
0.3
0
0.1
1S0
3S1
80
150
100
40
Q = {p, mπ }, Λ ∼ 0.5–1 GeV
Qν
Q0
1π
2π
—
50
0
0
-40
0
0.1
0.2
0.3
0
0.1
4N
0.2
0.3
0.2
0.3
0.2
0.3
1D2
3P0
80
12
40
8
0
4
0
0
0.1
0.2
0.3
0
0.1
3G5
3D3
6
0
0
-0.4
-6
-0.8
-1.2
-12
0
0.1
0.2
0.3
0
0.1
1S0
3S1
80
150
100
40
Q = {p, mπ }, Λ ∼ 0.5–1 GeV
Qν
Q0
Q1
1π
2π
—
50
0
0
-40
0
0.1
0.2
0.3
0
0.1
4N
0.2
0.3
0.2
0.3
0.2
0.3
1D2
3P0
80
12
40
8
0
4
0
0
0.1
0.2
0.3
0
0.1
3G5
3D3
6
0
0
-0.4
-6
-0.8
-1.2
-12
0
0.1
0.2
0.3
0
0.1
1S0
3S1
80
150
100
40
Q = {p, mπ }, Λ ∼ 0.5–1 GeV
Qν
Q0
1π
2π
50
0
0
-40
0
0.1
0.2
0.3
0
0.1
4N
0.3
80
12
40
8
0
4
0.2
0.3
0.2
0.3
—
0
Q1
0
0.1
0.2
0.3
0
0.1
3G5
3D3
Q2
0.2
1D2
3P0
6
0
0
-0.4
-6
-0.8
-1.2
-12
0
0.1
0.2
0.3
0
0.1
1S0
3S1
80
150
100
40
Q = {p, mπ }, Λ ∼ 0.5–1 GeV
Qν
1π
Q0
2π
50
0
0
-40
0
0.1
0.2
0.3
0
0.1
4N
0.3
80
12
40
8
0
4
0.2
0.3
0.2
0.3
—
0
Q1
0
0.1
0.2
0.3
0
0.1
3G5
3D3
Q2
Q3
0.2
1D2
3P0
6
0
0
-0.4
-6
-0.8
-1.2
-12
0
0.1
0.2
0.3
0
0.1
1S0
3S1
80
150
100
40
Q = {p, mπ }, Λ ∼ 0.5–1 GeV
Qν
1π
Q0
2π
50
0
0
-40
0
0.1
0.2
0.3
0
0.1
4N
0.2
0.3
0.2
0.3
0.2
0.3
1D2
3P0
80
12
40
8
0
4
—
0
Q1
0
0.1
0.2
0.3
0
0.1
3G5
3D3
Q2
Q3
Q4
many
6
0
0
-0.4
-6
-0.8
-1.2
many
→
− 4 (15)
∇
-12
0
0.1
0.2
0.3
0
0.1
Phase Shift [deg]
NN scattering up to N3 LO (Epelbaum, nucl-th/0509032)
60
1
S0
40
20
Phase Shift [deg]
Phase Shift [deg]
0
3
S1
100
0
3
P0
0
3
P1
-10
-20
-10
3
P2
40
20
-30
-20
15
ε1
4
0
0
1
D2
10
2
-2
40
D2
30
-30
0
3
D3
5
20
D1
-20
0
3
3
-10
5
0
ε2
-1
-2
0
10
0
P1
-30
0
10
1
-10
-20
50
0
-20
Phase Shift [deg]
150
-3
-5
0
50
100
150
200
Lab. Energy [MeV]
250
0
50
100
150
200
Lab. Energy [MeV]
250
-4
0
50
100
150
200
Lab. Energy [MeV]
250
Theory error bands from varying cutoff over “natural” range
NN scattering up to N3 LO (Epelbaum, nucl-th/0509032)
Phase Shift [deg]
Phase Shift [deg]
0
3
1
F3
-1
-2
2
0.5
-5
3
0
3
F4
2.5
2
-3
0
ε3
-3
-4
0
0
3
0.5
1
G5
-0.2
H5
-0.5
-0.4
-1
-0.6
50
100
150
200
Lab. Energy [MeV]
250
3
H4
0.4
0.3
0.2
0.1
-1.5
0
G3
-2
2
0.5
3
-1
4
1
F3
-2
6
1.5
3
-1
1
-4
0
0
Phase Shift [deg]
F2
1.5
-3
-0.8
0
3
2.5
0
50
100
150
200
Lab. Energy [MeV]
250
0
0
50
100
150
200
Lab. Energy [MeV]
250
Theory error bands from varying cutoff over “natural” range
Few-body chiral forces
At what orders? ν = −4 +
2N + 2L +
P
i (di
+ ni /2 − 2),
so adding a nucleon
suppresses by Q 2 /Λ2 .
Power counting confirms
2NF 3NF > 4NF
NLO diagrams cancel
3NF vertices may appear
in NN and other
processes
Fits to the ci ’s have
sizable error bars
dimensional analysis counting
Status of chiral EFT forces [H. Krebs, TRIUMF Workshop (2014)]
Zwei-Nukleon-Kraft
Two-nucleon
force
Drei-Nukleon-Kraft
Three-nucleon
force
Vier-Nukleon-Kraft
Four-nucleon
force
nder Beitrag
LO (Q0)
r 1. NLO
Ordnung
(Q2)
2LO (Q3)
r 2.NOrdnung
3LO (Q4)
r 3.NOrdnung
converged
not yet converged
accurate description of NN at
least up to Elab ~ 200 MeV
higher orders in progress
converged ??
impact on few- & many-N
systems?
Also in progress: versions with ∆ included =⇒ better expansion?
!
Summary: Conceptual basis of (chiral) effective field theory
Separate the short-distance
(UV) from long-distance (IR)
physics =⇒ defines a scale
Exploit chiral symmetry =⇒
hierarchical treatment of
long-distance physics
Use complete basis for
short-distance physics
=⇒ hierarchy a` la multipoles
Summary: Conceptual basis of (chiral) effective field theory
Separate the short-distance
(UV) from long-distance (IR)
physics =⇒ defines a scale
Exploit chiral symmetry =⇒
hierarchical treatment of
long-distance physics
Use complete basis for
short-distance physics
From
=⇒ hierarchy a` la multipoles QCD
QCD to nuclear physics
From QCD to nuclear physics
QCD
ChPT
T
T
T
=
ChPT
T
⇡
⇡
=
[H. Krebs]
NN'interac/on'is'strong:(resumma-ons/nonperturba-ve(methods(needed
|pi | M ⇥ mN
1/mN J(expansion:(nonrela-vis-c(problem(((((((((((((((((((((((((((((()(
Generate a nonrelativistic
✓ X
◆
NN'interac/on'is'strong:(resumma-ons/nonperturba-ve(methods(needed
A
◆
A
2
⇥2 ✓ X
i
3 i
+ O(mN⇥
) +
V4N+ +
..+
. |V4N +
= .E|
2N +3V
+V
O(m
) 3N++V2N
V3N
.. |
N
potential
for many-body
2m
i=1 2mN
1/m
i | N M ⇥ mN
i=1|p
N J(expansion:(nonrela-vis-c(problem(((((((((((((((((((((((((((((()(
methods (controversies!)
...
the(QM(AJbody(p
= E|
the(QM(AJbody(problem
derived&within&ChPT
✓ X
◆ (((((Construct(effec-ve(poten-al(perturba-vely
A
⇥2i
3 2i
3Vdraw
+ O(mN⇥
) +
VO(m
+
Vthe
. . . | 4N +
= .E|
Where/how
do
draw
2Nwe
3N++
4N
+
)
V2N
++
Vline?
. if
. |we =
E| it in different places?
3N + VWhat
N
2m
=1 2mN
A
X
.
◆
How do we draw the line in an EFT? Regulators!
In coordinate space, define R0
to separate short and long
distance
In momentum space, use Λ to
separate high and low momenta
Much freedom how this is done
=⇒ different scales / schemes
How do we draw the line in an EFT? Regulators!
In coordinate space, define R0
to separate short and long
distance
In momentum space, use Λ to
separate high and low momenta
Much freedom how this is done
=⇒ different scales / schemes
Non-local regulator in momentum (e.g., with n = 3 for N3 LO):
VCHPT (p, p0 ) −→ e−(p
2
/Λ2 )n
VCHPT (p, p0 )e−(p
02
/Λ2 )n
Local regulator in coordinate space for long-range and delta function:
4
4
Vlong (r) −→ Vlong (r)(1 − e−(r /R0 ) ) and δ(r) −→ Ce−(r /R0 )
Or local in momentum space [Gazit, Quaglioni, Navratil (2009)]
Rough relation:
Λ = 450 . . . 600 MeV ⇐⇒ R0 = 1.0 . . . 1.2 fm
What does changing a cutoff do in an EFT?
(Local) field theory version in perturbation theory (diagrams)
∆Λc
Loops (sums over intermediate states) ⇐⇒ LECs
d
+
=0
dΛc
| {z }
| {z }
R Λc d 3 q C0 MC0
Λc
(2π)3 k 2 −q 2 +i
C0 (Λc )∝
2π 2
+···
Momentum-dependent vertices =⇒ Taylor expansion in k 2
Claim: Vlow k RG and SRG decoupling work analogously
SRG (“T” generator)
“Vlow k ”
Outline: Lecture 3
S. Weinberg on the Renormalization Group (RG)
From “Why the RG is a good thing” [for Francis Low Festschrift]
“The method in its most general form can I think be understood as
a way to arrange in various theories that the degrees of freedom
that you’re talking about are the relevant degrees of freedom for
the problem at hand.”
Improving perturbation theory; e.g., in QCD calculations
Mismatch of energy scales can generate large logarithms
RG: shift between couplings and loop integrals to reduce logs
Nuclear: decouple high- and low-momentum modes
Identifying universality in critical phenomena
RG: filter out short-distance degrees of freedom
Nuclear: evolve toward universal interactions
Nuclear: simplifying calculations of structure/reactions
Make nuclear physics look more like quantum chemistry!
RG gains can violate conservation of difficulty!
Use RG scale (resolution) dependence as a probe or tool
Flow of different N3 LO chiral EFT potentials
1
S0 from N3 LO (500 MeV) of Entem/Machleidt
1
S0 from N3 LO (550/600 MeV) of Epelbaum et al.
Decoupling =⇒ perturbation theory is more effective
hk |V |k i+
X hk |V |k 0 ihk 0 |V |k i
k0
(k 2
−
k 0 2 )/m
+· · · =⇒ Vii +
X
j
Vij Vji
(ki2
1
+· · ·
− kj2 )/m
3
3
hk |V |k i+
k0
(k 2
−
k 0 2 )/m
+· · · =⇒ Vii +
X
j
Vij Vji
(ki2
1
+· · ·
− kj2 )/m
Approach to universality (fate of high-q physics)
Run NN to lower λ via SRG =⇒ ≈Universal low-k VNN
Off-Diagonal Vλ (k , 0)
1.0
k′ < λ
−1
λ = 5.0 fm
0.5
1
Vλ
S0
Vλ(k,0) [fm]
0.0
q≫λ
−0.5
C0
Vλ
−1.0
k<λ
550/600 [E/G/M]
600/700 [E/G/M]
500 [E/M]
600 [E/M]
−1.5
−2.0
0.0
=⇒
0.5
1.0
1.5
2.0
−1
k [fm ]
2.5
3.0
3.5
q λ (or λ) intermediate states
=⇒ replace with contact term:
C0 δ 3 (x − x0 )
[cf. Left = · · · + 12 C0 (ψ † ψ)2 + · · · ]
As resolution changes, shift high-k details to contacts, e.g., C0
1.0
k′ < λ
−1
λ = 4.0 fm
0.5
1
Vλ
S0
Vλ(k,0) [fm]
0.0
q≫λ
−0.5
C0
Vλ
−1.0
k<λ
550/600 [E/G/M]
600/700 [E/G/M]
500 [E/M]
600 [E/M]
−1.5
−2.0
0.0
=⇒
0.5
1.0
1.5
2.0
−1
k [fm ]
2.5
3.0
3.5
C0 δ 3 (x − x0 )
[cf. Left = · · · + 12 C0 (ψ † ψ)2 + · · · ]
1.0
k′ < λ
−1
λ = 3.0 fm
0.5
1
Vλ
S0
Vλ(k,0) [fm]
0.0
q≫λ
−0.5
C0
Vλ
−1.0
k<λ
550/600 [E/G/M]
600/700 [E/G/M]
500 [E/M]
600 [E/M]
−1.5
−2.0
0.0
=⇒
0.5
1.0
1.5
2.0
−1
k [fm ]
2.5
3.0
3.5
C0 δ 3 (x − x0 )
[cf. Left = · · · + 12 C0 (ψ † ψ)2 + · · · ]
1.0
k′ < λ
−1
λ = 2.5 fm
0.5
1
Vλ
S0
Vλ(k,0) [fm]
0.0
q≫λ
−0.5
C0
Vλ
−1.0
k<λ
550/600 [E/G/M]
600/700 [E/G/M]
500 [E/M]
600 [E/M]
−1.5
−2.0
0.0
=⇒
0.5
1.0
1.5
2.0
−1
k [fm ]
2.5
3.0
3.5
C0 δ 3 (x − x0 )
[cf. Left = · · · + 12 C0 (ψ † ψ)2 + · · · ]
1.0
k′ < λ
−1
λ = 2.0 fm
0.5
1
Vλ
S0
Vλ(k,0) [fm]
0.0
q≫λ
−0.5
C0
Vλ
−1.0
k<λ
550/600 [E/G/M]
600/700 [E/G/M]
500 [E/M]
600 [E/M]
−1.5
−2.0
0.0
=⇒
0.5
1.0
1.5
2.0
−1
k [fm ]
2.5
3.0
3.5
C0 δ 3 (x − x0 )
[cf. Left = · · · + 12 C0 (ψ † ψ)2 + · · · ]
1.0
k′ < λ
−1
λ = 1.5 fm
0.5
1
Vλ
S0
Vλ(k,0) [fm]
0.0
q≫λ
−0.5
C0
Vλ
−1.0
k<λ
550/600 [E/G/M]
600/700 [E/G/M]
500 [E/M]
600 [E/M]
−1.5
−2.0
0.0
=⇒
0.5
1.0
1.5
2.0
−1
k [fm ]
2.5
3.0
3.5
C0 δ 3 (x − x0 )
[cf. Left = · · · + 12 C0 (ψ † ψ)2 + · · · ]
NN VSRG universality from phase equivalent potentials
1
0.3 (a)
0.0
0.3
0.6
0.9
1.2
2
3
k [fm−1 ]
1
S0
λ=∞
1
2
k [fm−1 ]
3
1.5
1.0
0.5
0.0
0.5
1.0
1.5
2.0
2.5
1
3
1
δ(k) [degrees]
S0
160
120
80
40
0
40 (b)
S1
2
k [fm−1 ]
3
(b)
3
V(k,k) [fm]
1
δ(k) [degrees]
60
45
30
15
0
15 (a)
V(k,k) [fm]
V(k,k) [fm]
δ(k) [degrees]
Diagonal elements collapse where phase equivalent [Dainton et al, 2014]
S1
λ=∞
1
2
k [fm−1 ]
3
10
P1
20
30
(c)
0.6 (c)
0.5
0.4
0.3
0.2
0.1
0.0
1
2
k [fm−1 ]
1
3
P1
λ=∞
1
2
k [fm−1 ]
3
NN VSRG universality from phase equivalent potentials
1
0.3 (a)
0.0
0.3
0.6
0.9
1.2
2
k [fm−1 ]
1
3
S0
λ = 1.5 fm−1
1
2
k [fm−1 ]
3
1
3
1
δ(k) [degrees]
S0
160
120
80
40
0
40 (b)
S1
2
k [fm−1 ]
1.5
1.0 3 S1
0.5 λ = 1.5 fm−1
0.0
0.5
1.0
1.5
2.0
2.5
1
2
k [fm−1 ]
10
(b)
3
P1
20
30
(c)
3
V(k,k) [fm]
1
δ(k) [degrees]
60
45
30
15
0
15 (a)
V(k,k) [fm]
V(k,k) [fm]
δ(k) [degrees]
Diagonal elements collapse where phase equivalent [Dainton et al, 2014]
0.6
0.5
0.4
0.3
0.2
0.1
0.0
1
2
k [fm−1 ]
1P
(c)
1
3
λ = 1.5 fm−1
1
2
k [fm−1 ]
3
Result: local decoupling!
0
20
30
V(k,k) [fm]
1
P1
70
4 5 6 7 8
k [fm ]
−1
(a)
0 1 2 3 4 5 6 7 8
klab [fm−1 ]
(c)
ISSP λ = ∞
AV18 λ = ∞
ISSP λ = 1.5
AV18 λ = 1.5
P1
50
60
klab [fm ]
1
40
−1
0.6
0.4
0.2
0.0
0.2
0.4
0 1 2 3
ISSP
AV18
10
δ(klab) [degrees]
Use 1 P1 as example
(for a change :)
0
ISSP
10
AV18
20
1P
1
30
40
50
60 (c)
70
0 1 2 3 4 5 6 7 8
0.6
1
0.4
V(k,k) [fm]
What if not phase equivalent
everywhere?
δ(klab) [degrees]
Use universality to probe decoupling
P1
0.2
0.0
0.2
0.4
(b)
ISSP λ = ∞
AV18 λ = ∞
ISSP λ = 1.5 fm−1
AV18 λ = 1.5 fm−1
0 1 2 3 4 5 6 7 8
k [fm−1 ]
Result: local decoupling!
δ(klab) [degrees]
Use 1 P1 as example
(for a change :)
0
ISSP
10
AV18
20
1P
1
30
40
50
60 (c)
70
0 1 2 3 4 5 6 7 8
V(k,k) [fm]
klab [fm−1 ]
0.6
0.4
0.2
0.0
0.2
0.4
0 1 2 3
1
P1
(c)
ISSP λ = ∞
AV18 λ = ∞
ISSP λ = 1.5
AV18 λ = 1.5
4 5 6 7 8
k [fm ]
−1
0
ISSP
10
AV18
20
30
1P
1
40
50
60
70
80
(a)
90
0 1 2 3 4 5 6 7 8
klab [fm−1 ]
0.6
1
0.4
V(k,k) [fm]
What if not phase equivalent
everywhere?
δ(klab) [degrees]
Use universality to probe decoupling
P1
0.2
0.0
0.2
0.4
(b)
ISSP λ = ∞
AV18 λ = ∞
ISSP λ = 1.5 fm−1
AV18 λ = 1.5 fm−1
0 1 2 3 4 5 6 7 8
k [fm−1 ]
Outline: Lecture 3
S. Weinberg on the Renormalization Group (RG)
From “Why the RG is a good thing” [for Francis Low Festschrift]
“The method in its most general form can I think be understood as
a way to arrange in various theories that the degrees of freedom
that you’re talking about are the relevant degrees of freedom for
the problem at hand.”
Improving perturbation theory; e.g., in QCD calculations
Mismatch of energy scales can generate large logarithms
RG: shift between couplings and loop integrals to reduce logs
Nuclear: decouple high- and low-momentum modes
Identifying universality in critical phenomena
RG: filter out short-distance degrees of freedom
Nuclear: evolve toward universal interactions
Nuclear: simplifying calculations of structure/reactions
Make nuclear physics look more like quantum chemistry!
RG gains can violate conservation of difficulty!
Use RG scale (resolution) dependence as a probe or tool
1
1
hk |V |k i+
k0
(k 2
−
k 0 2 )/m
+· · · =⇒ Vii +
X
j
Vij Vji
(ki2
1
+· · ·
− kj2 )/m
3
3
hk |V |k i+
k0
(k 2
−
k 0 2 )/m
+· · · =⇒ Vii +
X
j
Vij Vji
(ki2
1
+· · ·
− kj2 )/m
Convergence of the Born series for scattering
Consider whether the Born series converges for given z
T (z) = V + V
1
1
1
V +V
V
V + ···
z − H0
z − H0 z − H0
If bound state |bi, series must diverge at z = Eb , where
(H0 + V )|bi = Eb |bi
=⇒
V |bi = (Eb − H0 )|bi
Convergence of the Born series for scattering
Consider whether the Born series converges for given z
T (z) = V + V
1
1
1
V +V
V
V + ···
z − H0
z − H0 z − H0
If bound state |bi, series must diverge at z = Eb , where
(H0 + V )|bi = Eb |bi
=⇒
V |bi = (Eb − H0 )|bi
For fixed E, generalize to find eigenvalue ην [Weinberg]
1
V |bi = |bi
Eb − H0
=⇒
1
V |Γν i = ην |Γν i
E − H0
From T applied to eigenstate, divergence for |ην (E)| ≥ 1:
T (E)|Γν i = V |Γν i(1 + ην + ην2 + · · · )
=⇒ T (E) diverges if bound state at E for V /ην with |ην | ≥ 1
Weinberg eigenvalues as function of cutoff Λ/λ
3
Consider ην (E = −2.22 MeV)
S1 (Ecm = -2.223 MeV)
2.5
Deuteron =⇒ attractive
eigenvalue ην = 1
free space, η > 0
2
Λ ↓ =⇒ unchanged
| ην |
1.5
1
0.5
0
2
3
4
5
-1
Λ [fm ]
6
7
eigenvalue ην = 1
But ην can be negative, so
V /ην =⇒ flip potential
eigenvalue ην = 1
3
eigenvalue ην = 1
free space, η > 0
free space, η < 0
2
Hard core =⇒ repulsive
eigenvalue ην
Λ ↓ =⇒ reduced
1.5
| ην |
S1 (Ecm = -2.223 MeV)
2.5
1
0.5
0
2
3
4
5
-1
Λ [fm ]
6
7
3
2.5
eigenvalue ην = 1
Hard core =⇒ repulsive
eigenvalue ην
Λ ↓ =⇒ reduced
In medium: both reduced
ην 1 for Λ ≈ 2 fm−1
=⇒ perturbative (at least for
particle-particle channel)
-1
kf = 1.35 fm , η > 0
-1
kf = 1.35 fm , η < 0
1.5
| ην |
free space, η > 0
free space, η < 0
2
S1 (Ecm = -2.223 MeV)
1
0.5
0
2
3
4
5
-1
Λ [fm ]
6
7
Weinberg eigenvalue analysis of convergence
Born Series: T (E) = V + V
1
1
1
V +V
V
V + ···
E − H0
E − H0 E − H0
For fixed E, find (complex) eigenvalues ην (E) [Weinberg]
1
V |Γν i = ην |Γν i
E − H0
=⇒
T (E)|Γν i = V |Γν i(1+ην +ην2 +· · · )
=⇒ T diverges if any |ην (E)| ≥ 1
[nucl-th/0602060]
Im η
Im η
1
3
S0
−3
S1− D1
1
−2
−1
3
1
−3
1
−2
−1
1
Re η
−1
AV18
CD-Bonn
−2
3
N LO (500 MeV)
−3
Re η
AV18
CD-Bonn
3
N LO
−1
−2
−3
Lowering the cutoff increases “perturbativeness”
Weinberg eigenvalue analysis
(repulsive) [nucl-th/0602060]
Im η
1
0
S0
1
S0
1
−0.2
−2
−1
1
Re η
−1
−2
-1
Λ = 10 fm
-1
Λ = 7 fm
-1
Λ = 5 fm
-1
Λ = 4 fm
-1
Λ = 3 fm
-1
Λ = 2 fm
3
−3
ην(E=0)
−3
N LO
−0.4
−0.6
Argonne v18
2
N LO-550/600 [19]
−0.8
3
N LO-550/600 [14]
3
N LO [13]
−1
1.5
2
2.5
-1
Λ (fm )
3
3.5
4
(repulsive) [nucl-th/0602060]
Im η
3
0
S1− D1
−3
3
−2
−1
−0.5
1
Re η
−1
−2
−3
3
S1− D1
1
ην(E=0)
3
−1
-1
Λ = 10 fm
-1
Λ = 7 fm
-1
Λ = 5 fm
-1
Λ = 4 fm
-1
Λ = 3 fm
-1
Λ = 2 fm
3
N LO
Argonne v18
2
N LO-550/600
−1.5
3
N LO-550/600
3
N LO [Entem]
−2
1.5
2
2.5
-1
Λ (fm )
3
3.5
4
(ην at −2.22 MeV vs. density)
3
1
S1 with Pauli blocking
0.5
ην(Bd)
-1
Λ = 4.0 fm
-1
Λ = 3.0 fm
-1
Λ = 2.0 fm
0
-0.5
-1
0
0.2
0.4
0.6
0.8
-1
1
1.2
1.4
kF [fm ]
Pauli blocking in nuclear matter increases it even more!
at Fermi surface, pairing revealed by |ην | > 1

Applications of Renormalization Group Methods in Nuclear Physics – 3 Dick Furnstahl

Transcription

Similar documents

Chiral Spectrometer Product Information

ISIS Accelerator and Targets (R. Williamson)

02/19 - MSU Chemistry

INSTRUCTION MANUAL FOR CHIRALPAK ZWIX(+) and CHIRALPAK ZWIX(-)

N EW ETTER Asomex® by Emcure

Why is asymmetric synthesis important?

Chiral Minimal Surface Geometries for Photonic Crystal Design