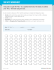
Metric Measurement Worksheet kh da BASE dcm gram (g)

Name___________________________________
Per. ______
Metric Measurement Worksheet
kilo, hecto, deka, (base—no prefix), deci, centi, milli
k h da BASE d c m
gram (g)
liter (L)
meter (m), etc.
Part 1: Metric Units
Choose an appropriate metric prefix and/or base unit for the following (h, da, and d prefixes will
not be used):
ANSWER: mg
1. Mass of ibuprofen in 1 Advil tablet Ex. mass: grams, and small: milli
2. Mass of a person
3. Mass of a slice of cheese
4. Volume of a sample of hydrochloric acid for a chemistry experiment
5. Volume of a bathtub
6. Thickness of a quarter
7. Height of a building
8. Distance from Katy to NYC
9. Length of your arm
Part 2: Metric Conversions
1.
2.
3.
4.
5.
6.
7.
8.
1 km
1g
5.70 g
0.8 kL
783 kg
459 mm
10 m
0.375 L
=
=
=
=
=
=
=
=
_____________ m
_____________ cg
_____________ mg
_____________ L
_____________ g
_____________ m
_____________ cm
_____________ mL
9.
10.
11.
12.
13.
14.
15.
4.37 cm
75 daL
25 L
5000 m
0.012 g
500 mg
789 mL
=
=
=
=
=
=
=
_____________ m
_____________ L
_____________ dL
_____________ km
_____________ mg
_____________ g
_____________ L
Name_________________________________
Per. ______
Scientific Notation Worksheet
When using scientific notation:
1. a. Should numbers greater than or equal to 10 be expressed with positive or
negative powers of 10? (circle one)
b. Should numbers less than 1 be expressed with positive or negative
powers of 10? (circle one)
2. What about a number that falls between 1 and 10? Ex. 7
Express the following in scientific notation:
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
985,000
0.000087
8.845
0.0232
0.75
7,456,921
65,510
200
0.0002
1100
4550.7
4
________________
________________
________________
________________
________________
________________
________________
________________
________________
________________
________________
________________
Express the following in regular notation:
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
8.99 x 10 – 2
2.95 x 10 3
5.443 x 10 4
1.97 x 10 – 6
3.4 x 10 – 1
6.0002 x 10 3
2.55 x 10 – 5
7.9998 x 10 2
4.008 x 10 – 2
9.999 x 10 7
4 x 10 – 3
___________________________
___________________________
___________________________
___________________________
___________________________
___________________________
___________________________
___________________________
___________________________
___________________________
___________________________
Name___________________________________________ Period____________________ Date___________
Measuring with Precision
Below are three meter sticks. As you proceed down the page, each meter stick has a smaller division marked.
When you read any scale, you always record the measurement by reading the smallest interval (division) on
the scale and then estimate the next smallest division (“record what you know plus one more”). As you
proceed down the page, you can see how your measurement becomes more precise and you have more
significant digits in your reading. A significant digit is a digit that has physical meaning.
Directions: For the metric ruler below, record the correct reading. Hint: what is the smallest interval?
a. _______
b. _______
c. _______
d. _______
e. _______
f.
_______
Name___________________________________________ Period____________________ Date___________
Measuring Volume
What volume is indicated on each of the graduated cylinders below? The unit of volume is mL.
What temperature is indicated on each of the thermometers below? The unit for temperature is oC.
a) _______
b) _______
c) _______
Name: _________________________________
Period: _____
Significant Figures Worksheet #1
Determine how many significant figures are in each of these numbers.
1) 2.03
11) 1.0030
21) 0.00872
2) 0.0224
12) 967 000
22) 0.000008
3) 10.05
13) 0.00967
23) 0.800008
4) 5000000
14) 900.0
24) 500 000 000
5) 1.0
15) 0.005
25) 708
6) 0.1005
16) 500
26) 0.908
7) 0.002030
17) 0.050
27) 78 000
8) 1.005
18) 0.005670
28) 780.00
9) 0.004300
19) 0.1110
29) 0.00600
10) 1000.1
20) 670 000.
30) 20.040
Determine how many significant figures are in each of these numbers.
31) 7.080 x 107
33) 5 x 1017
35) 1.080 x 1012
32) 4.0 x 104
34) 4.50 x 107
36) 3.40 x 108
Perform the following calculations and express the answer with unit and in proper significant figures.
37) 210.6 mm + 14.57 mm =
42) 500 km x 32 km =
38) 74.000 cm + 8.6 cm =
43) 8560.0 m x 1000 m =
39) 84 cm + 111.7 cm =
44) 0.100 cm x 0.85 cm =
40) 84.34 g – 5.2 g =
45) 9200 g ÷ 873 g =
41) 9.81 cm – 3.151 cm =
46) 985 m2 ÷ 500. m =
Name: ___________________________________
Chemistry - Significant Figures Worksheet #2
How many sig figs does each of the following have?
1.
0.02
11. 8040
2.
0.020
12. 0.0300
3.
501
13. 699.5
4.
501.0
14. 2.00 x 102
5.
5000
15. 0.90100
6.
5000.
16. 90100
7.
6051.00
17. 4.7 x 10-8
8.
0.0005
18. 10800000.
9.
0.1020
19. 3.01 x 1021
10. 10001
20.
0.000410
Calculate the following and express your answer with unit and in the proper number of sig figs:
21. 1.35 cm x 2.467 cm = __________________
22. 1035 g / 82 mL = ___________________
23. 12.01 mm + 35.2 mm + 6 mm = ______________
24. 55.46 g - 28.9 g = __________________
25. 0.21 m x 3.2 m x 100.1 m = _____________________
26. 0.15 mg + 1.15 mg + 2.051 mg = ____________________
27. 15 g / 6 mL = ____________________
28. 505 mL - 450.25 mL = ____________________________
29. 1.252 cm x 0.115 cm x 0.012 cm = __________________
30. 1.278 x 103 m2 / 1.4267 x 102 m = ____________________
Introduction to Dimensional Analysis Worksheet
1. Equivalents – Please write the equivalents for each of the items in the provided
space:
a. 1 week = ____7_____ days
f. 1 pint = _________ cups
b. 365 days = _________ year
g. 1 week = _________ days
c. 4 quarts = _________ gallon
h. 1 mile = ________ feet
d. 2.54 cm = _________ inch
i. 60 sec = _________ min
e. 12 inches = ________ foot
j. 120 min = ________ hours
2. Conversion factors equal to one – Any number over itself is equal to one. For
example, 139/139 = 1. Likewise, 3/3 = 1. In the same way, 1 week/7 days = 1. Use
the equivalents from part 1 above and write each one as a fraction equal to 1.
1 week
a. _____7 days___________
f. ____________________
b. ____________________
g. ____________________
c. ____________________
h. ____________________
d. ____________________
i. ____________________
e. ____________________
j. ____________________
3. Multiplying by one – Any value multiplied by one is that same value. For
example, 139 x 1 = 139. Use the fractions equal to one from part 2 to multiply each
value below by “1”. Carefully choose the fraction you write so you can cancel the
unit provided and end up with the unit requested.
a. 21 days x _______ = ______ weeks
f. 5 cups x _______ = ______ pints
b. 272 days x _______ = ______years
g. 3.2 weeks x _______ = ______ days
c. 1.6 gallons x _______ = ______ quarts
h. 590 ft x _______ = ______ miles
d. 6 inches x _______ = ______ cm
i. 400 sec x _______ = ______ min
e. 39 inches x _______ = ______ ft
j. 325 min x _______ = ______ hours
Name___________________Class________Date____
I.
Dimensional Analysis Practice with Metric Units
1. 453 cm x _______
= _______ m
2. 13.4 mm x _______ = _______ m
3. 0.12 m x _______
= _______hm
4. 15.0 km x _______ = _______ m
5.
3.2 km x ______ x ______ = ______ mm
1 hr
II.
1 hr
DA Practice with Imaginary Units
6. 58 whoas x
= ___ uhoh’s
7. 0.25 bogs x
= ___ cocos
8. 155 popos x
= ___ dodos
9. 0.122 shays x
= ___ toes
10. 29 hobos x
= ___ momos
III. DA Practice with Miscellaneous Units
11. 6.00 yr x
= ___ day
12. 7.5 x 106 in x
= ___ mi
13. 50.0 yd x
= ___ in
14. 15 mi x
= ___ yd
15. 2.0 gal x
= ___ cups
Name
Date
Period
Dimensional Analysis/Factor Label Practice
Using the conversion factors in your notes and a PENCIL, solve the following. Show work next to
each problem and box your answer.
Steps for solving:
1. identify unit given
2. identify unit you’d like to convert to
3. identify conversion factor(s) needed
4. set up using the DA technique only and solve
5. round answer to the correct number of sig figs
1.
137 lbs = ? oz
2.
25 yds = ? ft
3.
46 pints = ? gallons
4.
6 days = ? seconds
5.
6 500 943 oz = ? tons
6. 72 inches = ? feet
7.
1 year = ? seconds
8.
64 oz = ? lbs
9.
12 feet = ? inches
10. 89 374 seconds = ? weeks
11. 29 years = ? seconds
Name
Date
Dimensional Analysis Practice
Period
Single Step Conversions
1. How many quarts are in 3.0 gallons of milk?
2. Cork has a density of 0.35 g/mL. What is the volume of 20. g of cork?
3. One mole of oxygen has a mass of 32 g. What is the mass of 5.5 moles of oxygen?
4. If one mole of gas has a volume of 22.4 L, how many moles are there in 25.0 L of gas?
5. If one mole of nitrogen has a mass of 28 g, how many moles of nitrogen gas are in 7.0 g of
nitrogen gas?
6. A large nugget of naturally occurring silver metal has a mass of 3.20 x 10 4 troy ounces. What is the
mass in kilograms if 1 troy ounce is equivalent to 0.0311 kg?
7. If 1 mole of octane produces 5450. kJ of heat when burned, how many moles of octane must be
burned to produce 15,100. kJ of heat?
Multiple Step Conversions
8. An old barometer hanging on the wall of a mountain hut has a reading of 27.0 inches of mercury.
1 inch of mercury equals 0.0334 atm (“atmospheres”) and 1 atm = 101.3 kPa (“kilopascals”), what
is the pressure reading of the barometer, in kPa?
9. Sugar costs $0.98/kg. 1 metric ton = 1000 kg. How many metric tons (“t”) of sugar can you buy for
$350.?
10. Solve the following using the fact that beakers cost $8.40 per dozen.
a. Harry drops 3 dozen beakers. How much will Harry’s chemistry teacher charge him? (sig figs
don’t apply)
b. Harry breaks another batch of beakers and is charged $13.30, what was the number of
beakers that he broke? (give the actual number, not how many dozen)
11. An ancient Celtic chicken farmer wished to purchase a gift for his wife. The gift was worth 2 horses.
At the local market, 3 horses were worth 5 cows, 1 cow was worth 4 hogs, 3 hogs were worth 4
goats, and 1 goat cost 9 chickens. How much was the gift going to cost the farmer, who had to pay in
chickens? (sig figs don’t apply)
12. In a primitive society, the following exchange rates exist:
1 fot = 5 vum, 2 sop = 3 tuz, 4 bef = 3 tuz, 9 fot = 2 bef
(a) A man has 4 sop and wants to convert all of it into vum. How many vum will he get? (sig figs don’t
apply)
(b) A woman needs to pay for some food costing 12 sop. She has only fot in her purse. How many fot
should she pay? (sig figs don’t apply)
Metric Conversions (use DA, not decimal hopping)
13. Write the conversion factor between each of the following:
a. kg and g
b. mL and L
14. Convert the following:
a. 25 kg into grams
b. 50.0 mL into L
15. If 1 L of granite has a mass of 5.50 kg,
a. what is the mass of 7.00 L of granite?
b. what is the volume occupied by 22 kg of granite?
c. what is the mass, in grams of 5.00 mL of granite?