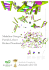Sedimentation and Electrophoretic Migration of DNA Knots and

J. Mol. Biol. (1998) 278, 1±3
COMMUNICATION
Sedimentation and Electrophoretic Migration of DNA
Knots and Catenanes
Alexander V. Vologodskii1, Nancy J. Crisona2, Ben Laurie3
Piotr Pieranski4, Vsevolod Katritch5, Jacques Dubochet6
and Andrzej Stasiak6*
1
Department of Chemistry
New York University
New York, NY 10003, USA
2
Department of Molecular and
Cell Biology, University of
California, Berkeley, CA 94720
USA
3
A.L. Digital, London, England
4
Institute of Physics, Poznan
University of Technology
60-965, Poznan and Institute of
Molecular Physics
60-159, Poznan, Poland
5
Department of Chemistry
Rutgers the State University of
New Jersey, New Brunswick
NJ 08903, USA
Various site-speci®c recombination enzymes produce different types of
knots or catenanes while acting on circular DNA in vitro and in vivo. By
analysing the types of knots or links produced, it is possible to
reconstruct the order of events during the reaction and to deduce the
molecular ``architecture'' of the complexes that different enzymes form
with DNA. Until recently it was necessary to use laborious electron
microscopy methods to identify the types of knots or catenanes that
migrate in different bands on the agarose gels used to analyse the products of the reaction. We reported recently that electrophoretic migration
of different knots and catenanes formed on the same size DNA molecules
is simply related to the average crossing number of the ideal representations of the corresponding knots and catenanes. Here we explain this
relation by demonstrating that the expected sedimentation coef®cient of
randomly ¯uctuating knotted or catenated DNA molecules in solution
shows approximately linear correlation with the average crossing number
of ideal con®gurations of the corresponding knots or catenanes.
# 1998 Academic Press Limited
6
Laboratoire d'Analyse
Ultrastructurale, BaÃtiment de
Biologie, Universite de
Lausanne, CH-1015
Lausanne-Dorigny, Switzerland
*Corresponding author
Keywords: DNA knots; DNA catenanes; DNA sedimentation; DNA
topology; DNA gel electrophoresis
We investigated recently the relation between
ideal geometric representations of knots or catenanes and the physical behaviour of knotted or
catenated DNA molecules (Katritch et al., 1996,
1997; Stasiak et al., 1996; Laurie et al., 1998). Ideal
geometric con®gurations of knots or catenanes are
the trajectories that allow maximal radial expansion of a virtual tube of uniform diameter centred
around the axial trajectory of the knot (Grosberg
et al., 1996; Katritch et al., 1996). In characterizing
ideal geometric forms of knots and catenanes we
have chosen scale-independent measures, such as
the ratio between the length and the diameter of
the tube used to generate ideal con®gurations
(Grosberg et al., 1996), or the average crossing
number, which describes how many crossings one
0022±2836/98/160001±03 $25.00/0/mb981696
perceives on average when the knot or catenane is
viewed from an in®nite number of directions equisampling the sphere (Katritch et al., 1996). When
different knots are made from the same length of
tube, the radial expansion of the tube becomes
more limited as the number of crossings, or
complexity, of the knot increases. As a result, the
ideal con®gurations of knots get more and more
compact as the average crossing number increases
(see Figure 1). The analogous situation applies to
DNA knots made from molecules of the same
length. The more complex the knot, the more compact its structure. Knowing that the electrophoretic
mobility of the molecules with the same molecular
mass and the same overall charge increases with
compactness of the molecules, we expected that
# 1998 Academic Press Limited
2
Figure 1. Linear relation between the electrophoretic
migration of different DNA knots and the compactness
of ideal con®gurations of the corresponding knots.
Torus and twist knots were produced by site-speci®c
recombination mediated by a mutant form of the Gin
recombinase acting on a 7 kb plasmid. All of the knots
have the same molecular mass since they arise from the
same unknotted substrate molecules (Crisona et al.,
1994). Before gel electrophoresis, the knotted DNA
molecules were nicked to eliminate supercoiling of the
molecules so that the difference in the knot type was the
only reason for the electrophoretic separation of knots
into different bands. The DNA from each band was analysed by electron microscopy using the RecA coating
method (Krasnow et al., 1983) and identi®ed as the knot
type drawn. Drawings of the knots present the ideal
geometric con®guration of each knot type. To help
visual tracing of the knots, the tubes forming ideal geometric representations are presented with a smaller
diameter than in their maximally expanded con®gurations (Katritch et al., 1996). However, the axial trajectory remains unchanged. Note that with increasing
complexity of the knots, the overall dimensions of the
knots decrease, although the total length of the DNA is
the same. Notice also that knots migrate with a speed
directly proportional to the average crossing number of
their ideal con®gurations.
the speed of electrophoretic migration of different
knots made from DNA molecules of the same
length would increase with the average crossing
number measured for the ideal con®guration of the
corresponding knot. In fact this correlation turned
out to be approximately linear (Figure 1) as preliminarily described by Stasiak et al. (1996). Trying
to explain this linear correlation between the
migration of different types of knots and the average crossing number of their ideal con®gurations,
we observed that one standard measure of molecular compactness, the mean of inverse distances
measured on ideal representations of different
Physical Behaviour of DNA Knots and Catenanes
knots having the same axial length, was directly
proportional to the average crossing number of
ideal con®gurations of the corresponding knots
(Stasiak et al., 1996). However, knotted DNA molecules in solution do not adopt ideal geometric
con®gurations. Therefore, in the present study, we
decided to calculate the molecular compactness of
knotted DNA molecules undergoing thermal
motion and thus not adopting regular trajectories
of ideal con®gurations. One of us (A.V.) developed
recently a method to calculate the expected
sedimentation coef®cient of DNA molecules with a
given topology (Rybenkov et al., 1997). Since the
sedimentation coef®cient is an accepted measure of
molecular compactness of molecules in solution,
the values obtained are more suited to be compared with electrophoretic migration than the
average inverse distance calculated for the ideal
con®gurations of the corresponding knots or
catenanes. We decided therefore to simulate an
equilibrium set of thermally agitated DNA
molecules forming different types of knots and to
calculate the time-averaged sedimentation coef®cient for the different knot types tied on a torsionally relaxed DNA chain 3600 bp long, the size of a
typical bacterial plasmid. Figure 2(a) shows that
there is a linear correlation between the average
crossing number of ideal con®gurations of knots
and the computed sedimentation coef®cient of
knotted polymers forming a given type of knot.
The slight deviation from linearity may result from
inaccuracies of the modelling approach or may
indicate that in fact linearity only approximates a
more complex relation.
We reported recently that the compactness of
ideal con®gurations of catenanes correlates well
with the electrophoretic migration of different
types of DNA catenanes (Laurie et al., 1998). We
therefore decided to calculate the sedimentation
coef®cients of different types of DNA catenanes
formed by two torsionally relaxed DNA molecules
of 3600 bp each and to compare them with the
compactness of ideal catenanes of a given type. As
shown in Figure 2(b) there is an approximately linear relation between the calculated sedimentation
coef®cients of different types of DNA catenanes in
solution and the average crossing number of their
ideal representations. Since the electrophoretic
mobility of different DNA knots and catenanes is
proportional to the average crossing number of
their ideal geometric representations, there is a
colinearity of the sedimentation coef®cient with the
electrophoretic migration of DNA knots and catenanes analysed on agarose gels run at low voltage
(Crisona et al., 1994). This last observation may
advance our understanding of the gel electrophoretic separation of cyclic polymers.
The results presented here strengthen the
evidence that ideal con®gurations of knots and
catenanes contain information about the actual
physical behaviour of knotted and catenated polymers in solution (Katritch et al., 1996, 1997; Stasiak
et al., 1996; Laurie et al., 1998). Earlier studies by
3
Physical Behaviour of DNA Knots and Catenanes
and the gel migration of the corresponding DNA
knots (Simon, 1996).
Acknowledgements
We thank Alicja Stasiak and Eric Larquet for help in
preparation of the Figures. This work was supported by
Swiss National Science Foundation grant 31-42158.94,
Foundation Herbette University of Lausanne, US public
Health Service grants GM34809, GM31657-15 and GM
54215, Polish Scienti®c Committee grant 8T11-F01008P04 and by A. L. Digital.
References
Figure 2. Linear relation between the compactness of
ideal con®gurations of (a) knots and (b) catenanes, and
the sedimentation coef®cients of DNA molecules forming knots and catenanes of a given type. To calculate
the sedimentation coef®cients of knotted or catenated
DNA molecules in solution, it is necessary to create a
rich ensemble of con®gurations corresponding to
momentary conformations of thermally agitated DNA
molecules with a required size and topology. The
approach of Metropolis Monte Carlo simulations was
used to create a Boltzmann population (ca 106 con®gurations) of the desired type of DNA molecules (Katritch
et al., 1996; Vologodskii et al., 1992). For each con®guration, the sedimentation coef®cient was then calculated
using the Kirkwood-Riseman approximation (Bloom®eld
et al., 1974). Finally, the average of the obtained sedimentation coef®cient values for individual conformations was taken as the time-averaged sedimentation
coef®cient for molecules of a given size and topology.
The sedimentation coef®cient of unknotted circles of
3600 bp was calculated to be 16.35 S.
other authors also demonstrated the connection
between the entropy of knotted polymers and the
ideal con®gurations of corresponding knots
(Grosberg et al., 1996) and investigated the relation
between energy-minimized con®gurations of knots
Bloom®eld, V. A., Crothers, D. M. & Tinoco, I. (1974).
Physical Chemistry of Nucleic Acids, Harper & Row,
New York.
Crisona, N. J., Kanaar, R., Gonzalez, T. N., Zechiedrich,
E. L., Klippel, A. & Cozzarelli, N. R. (1994).
Processive recombination by wild-type Gin and an
enhancer-independent mutant. Insight into the
mechanisms of recombination selectivity and
strand exchange. J. Mol. Biol. 243, 437 ± 457.
Grosberg, A. Y., Feigel, A. & Rabin, Y. (1996). Florytype theory of a knotted ring polymer. Phys. Rev.
ser. A, 54, 6618± 6622.
Katritch, V., Bednar, J., Michoud, D., Scharein, R. G.,
Dubochet, J. & Stasiak, A. (1996). Geometry and
physics of knots. Nature, 384, 142 ± 145.
Katritch, V., Olson, W. K., Pieranski, P., Dubochet, J. &
Stasiak, A. (1997). Properties of ideal composite
knots. Nature, 388, 148± 151.
Krasnow, M. A., Stasiak, A., Spengler, S. J., Dean, F.,
Koller, T. & Cozzarelli, N. R. (1983). Determination
of the absolute handedness of knots and catenanes
of DNA. Nature, 304, 559± 560.
Laurie, B., Katritch, V., Dubochet, J. & Stasiak, A. (1998).
Geometry and physics of links. Biophys. J. 74, in the
press.
Rybenkov, V. V., Vologodskii, A. V. & Cozzarelli, N. R.
(1997). The effect of ionic conditions on the conformations of supercoiled DNA. I. Sedimentation
analysis. J. Mol. Biol. 267, 299± 311.
Simon, J. (1996). Energy functions for knots: beginning
to predict physical behavior. In Mathematical
Approaches to Biomolecular Structure and Dynamics
(Mesirov, J. P., Shulten, K. & Sumners, D. W., eds),
pp. 39±58, Springer-Verlag, New York.
Stasiak, A., Katritch, V., Bednar, J., Michoud, D. &
Dubochet, J. (1996). Electrophoretic mobility of
DNA knots. Nature, 384, 122.
Vologodskii, A. V., Levene, S. D., Klenin, K. V., FrankKamenetskii, M. & Cozzarelli, N. R. (1992).
Conformational and thermodynamic properties of
supercoiled DNA. J. Mol. Biol. 227, 1224 ±1243.
Edited by M. Yaniv
(Received 23 August 1997; received in revised form 2 February 1998; accepted 4 February 1998)