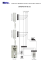Modeliranje električnih strojev

Modeliranje električnih strojev
Laboratorijska vaja 1
Ime in priimek:
Datum in ura:
1
Ocena poročila:
Besedilo naloge
S preizkusoma kratkega stika in prostega teka določite elemente nadomestnega vezja
enofaznega transformatorja. Z nadomestnim vezjem analizirajte izbrano obratovalno stanje
transformatorja.
2
Vezalni načrt
DIGITALNI W-METER
ENOFAZNI
TRANSFORMATOR
1.1
2.1
1.2
2.2
(a)
(b)
L
N
Slika 1: Vezalni načrt za (a) preizkus prostega teka in (b) preizkus kratkega stika.
3
Opis merilnih metod
Za enofazni transformator bomo uporabili nadomestno vezje kot je prikazano na sliki 2.
Elementov nadomestnega vezja transformatorja je šest, predstavljajo pa:
R1 –
R2' –
X1 –
X2' –
R0 –
X0 –
upornost primarnega navitja,
upornost sekundarnega navitja (reducirana na primarno število ovojev),
stresano reaktanco primarnega navitja,
stresano reaktanco sekundarnega navitja (reducirano na primarno število ovojev),
moč na tem uporu predstavlja izgube v železu (PFe),
reaktanca magnetenja (tok skoznjo predstavlja magnetilni tok).
I1
R1
X2'
X1
R2'
I2'
I0
U1
R0
X0
U2'
Slika 2: Nadomestno vezje enofaznega transformatorja.
Elemente nadomestnega vezja enofaznega transformatorja lahko določimo z različnimi
metodami. Pri transformatorjih, kjer so impedance zaporedne (serijske) veje (R1, X1, R2', X2')
1-1
Modeliranje električnih strojev
dosti manjše od impedanc v vzporedni (paralelni, prečni) veji (R0, X0), elemente največkrat
izračunamo s pomočjo rezultatov preizkusa kratkega stika in preizkusa prostega teka
transformatorja.
3.1 Preizkus kratkega stika transformatorja
Pri preizkusu kratkega stika transformatorja je sekundarno navitje kratko sklenjeno, primarno
navitje pa napajamo s tako napetostjo Uk, da je kratkostični tok Ik enak nazivnemu toku
transformatorja (Ik = In). Ker so serijske impedance (R1, X1, R2', X2') zanemarljivo majhne napram
paralelnim (R0, X0), lahko tok v paralelno vejo zanemarimo in nadomestno vezje dobi obliko, ki
je prikazana na sliki 3.
Ik
R1
X2'
X1
R2'
Uk
Slika 3: Poenostavljeno nadomestno vezje transformatorja v kratkem stiku.
V kratkem stiku gre torej za zaporedno vezavo upornosti in stresanih reaktanc obeh navitij, kar
pomeni, da bomo s tem preizkusom lahko določili kratkostično impedanco:
Z k = R1 + jX 1 + R2 + jX2′ = Rk + jX k ,
(1)
Za izračun kratkostične impedance ter elementov vezja potrebujemo naslednje podatke
preizkusa kratkega stika transformatorja: kratkostično napetost Uk, kratkostični tok Ik ter
kratkostično moč Pk.
S pomočjo kratkostične napetosti in toka izračunamo absolutno vrednost kratkostične
impedance:
Zk =
Uk
,
Ik
(2)
ki jo nato razstavimo na upornost in reaktanco:
Rk =
Xk =
Pk
,
Ik 2
(3)
2
Z k − Rk2 .
(4)
Upoštevajoč poenostavljeno nadomestno vezje za kratek stik velja:
Rk = R1 + R2′ ,
(5)
X k = X 1 + X 2′ .
(6)
Točne delitve impedanc med primarno in sekundarno stranjo ne poznamo, zato utemeljeno
privzamemo, da sta serijski impedanci primarne in sekundarne strani enaki. Tako izračunamo
elemente serijske veje:
R
R1 = R2′ = k ,
2
(7)
1-2
Modeliranje električnih strojev
X
X 1 = X 2′ = k .
2
(8)
Na ta način sicer dobimo približne vrednosti, ki pa v našem primeru zadostujejo. Za točnejše
določanje upornosti R1 in R2’ lahko v določenih primerih uporabimo tudi enosmerno merjenje
upornosti posameznih navitij, za točnejše določanje stresanih reaktanc pa žal ni kakšne
enostavne metode.
3.1.1 Kratkostična napetost
Poleg elementov nadomestnega vezja pa dobimo s preizkusom kratkega stika tudi vrednost
kratkostične napetosti, ki je karakterističen podatek transformatorja. Kratkostična napetost je
padec napetosti na upornostih navitij in stresanih reaktancah, ko je transformator nazivno
obremenjen. Največkrat se podaja v odstotkih nazivne napetosti, tako da je relativna
kratkostična napetost:
uk =
Uk
⋅ 100% .
U1n
(9)
Ob poznanem cosϕk lahko izračunamo še induktivni in ohmski padec napetosti pri nazivnem
(kratkostičnem) toku, ki pa sta seveda sorazmerna vrednostima Rk in Xk:
uR = uk ⋅ cos ϕk ,
(10)
ux = uk ⋅ sin ϕk oz. ux = uk2 − uR2 .
(11)
Faktor moči v kratkem stiku (cosϕk) izračunamo s pomočjo izmerjene moči kratkega stika (Pk):
cos ϕk =
Pk
.
U k ⋅ Ik
(12)
3.2 Preizkus prostega teka transformatorja
V prostem teku transformatorja je primarno navitje napajano z nazivno napetostjo, sekundarno
navitje pa je odprto. Ker skozi elementa R2' in X2' ne teče tok, ju lahko opustimo in nadomestno
vezje dobi obliko, ki je prikazana na sliki 4.
Ip
Up
R1
Ip
X1
R0
Up
X0
Slika 4: Nadomestno vezje transformatorja
v prostem teku.
R0
X0
Slika 5: Poenostavljeno nadomestno vezje
transformatorja v prostem teku.
S preizkusom kratkega stika smo že določili elementa R1 in X1, zato bi, upoštevajoč znano vezje, s
pomočjo preizkusa prostega teka izračunali še preostala elementa R0 in X0. Impedanca
nadomestnega vezja transformatorja v prostem teku je:
Z p = Rp + jX p = R1 + jX 1 +
R0 ⋅ jX 0
.
R0 + jX 0
(13)
Ker sta padca napetosti na R1 in X1, zaradi majhnih vrednosti serijskih impedanc, zanemarljiva v
primerjavi z napetostjo na paralelni veji, lahko vezje poenostavimo do te mere, da v njem ostane
le paralelna veja z elementoma R0 in X0 (slika 5). Sedaj lahko zapišemo:
1-3
Modeliranje električnih strojev
Zp R0 ⋅ jX 0
.
R0 + jX 0
(14)
Za izračun elementov vezja izmerimo naslednje podatke prostega teka transformatorja:
napetost prostega teka Up, tok prostega teka Ipt ter moč prostega teka Pp.
Elemente vezja bi lahko izračunali s pomočjo impedance prostega teka (13 in 14), vendar bomo
v našem primeru le-te izračunali s pomočjo delovne in jalove moči. Delovna moč prostega teka
Pp, ki predstavlja predvsem izgube v železu, se v nadomestnem vezju troši na uporu R0, zato
izračunamo:
R0 =
U p2
Pp
.
(15)
Podobno izračunamo še reaktanco X0 s pomočjo jalove moči:
(U
Qp = S p2 − Pp2 =
X0 =
U p2
Qp
2
p
⋅ Ip ) − Pp2 ,
(16)
.
(17)
3.3 Nelinearno nadomestno vezje
Elementa R0 in X0 ponavadi določimo pri nazivni napetosti transformatorja. Takó določeno
nadomestno vezje ponavadi zadostuje za analize različnih stacionarnih obratovalnih stanj
transformatorja, saj transformator pri nazivni napetosti tudi večino časa obratuje. Za obravnavo
prehodnih pojavov pa takšno nadomestno vezje ne zadostuje in predstavlja preveliko
poenostavitev. Zaradi nelinearnih magnetnih lastnosti feromagnetnega materiala imata
nelinearno karakteristiko predvsem elementa R0 in X0. Da bi razširili uporabnost nadomestnega
vezja, izmerimo še celotno karakteristiko prostega teka (od 0 do 1,1 Un) in izračunamo
odvisnost obeh elementov od primarne napetosti (R0 = f(U) in X0 = f(U)).
3.4 Uporaba nadomestnega vezja
Nadomestno vezje z linearnimi elementi bomo uporabili za izračun obratovalnega stanja
enofaznega transformatorja (slika 6).
I1
R1
X2'
X1
R2'
I2'
I0
~
U1
R0
X0
U2'
Rb'
Slika 6: Vezje za izračun obratovalnega stanja transformatorja.
Na primarne sponke pripeljemo nazivno napetost (U1), na sekundar pa priključimo upornost,
katere vrednost izračunamo s pomočjo nazivnih podatkov transformatorja:
Rb =
U2n U2n2
.
=
I2n
Sn
(18)
1-4
Modeliranje električnih strojev
Če ima transformator prestavo (p) različno od ena, je potrebno upornost bremena reducirati na
primarno stran:
Rb′ = Rb ⋅ p2 .
(19)
Izmenično vezje rešimo analitično z uporabo metod za reševanje električnih vezij, lahko pa
uporabimo tudi katerega od računalniških programov za numerične analize vezij (npr. Spice). Za
izbrano obratovalno stanje izračunamo izgube v bakru (PCu), izgube v železu (PFe), sekundarno
napetost (U2') in izkoristek transformatorja (η).
4
Vprašanja za razmislek
a)
b)
Katere izgube v transformatorju krije moč kratkega stika? Utemeljite odgovor.
Na čem temelji privzeta enakost primarnih in sekundarnih elementov nadomestnega
vezja?
Zakaj so izgube prostega teka predvsem izgube v železu?
Zakaj višina napajalne napetosti vpliva predvsem na vrednosti elementov R0 in X0?
Kakšen faktor moči lahko pričakujemo v prostem teku in kakšnega v kratkem stiku
transformatorja? Utemeljite odgovor.
Kaj se spremeni pri določevanju elementov nadomestnega vezja, če gre za trifazni
transformator?
c)
d)
e)
f)
5
Priporočena literatura
[1]
[2]
Damijan Miljavec, Peter Jereb, Električni stroji - temeljna znanja, Ljubljana, 2005.
Peter Jereb, Damijan Miljavec, Vezna teorija električnih strojev, Založba FE in FRI,
Ljubljana, 2009.
France Avčin, Peter Jereb, Preizkušanje električnih strojev, Tehniška založba Slovenije,
Ljubljana, 1983.
Danilo Makuc, Analiza nadomestnega vezja transformatorja s programskim paketom SPICE
OPUS, učno gradivo dostopno na:
http://les.fe.uni-lj.si/mes/predloge/spice/Transformator_SPICE.pdf
[3]
[4]
6
Nevarnosti pri delu
POZOR, NEVARNOST ELEKTRIČNEGA UDARA!
NAPAJALNA IZMENIČNA NAPETOST DO 270 V. OB NEPRAVILNI PRIKLJUČITVI
MERJENCA OBSTAJA NEVARNOST INDUCIRANJA VISOKE NAPETOSTI.
MERILNO VEZJE, INSTRUMENTE IN NAPRAVE VEDNO VEŽITE, PRIKLAPLJAJTE ALI
ODKLAPLJAJTE V BREZNAPETOSTNEM STANJU!
MED MERITVIJO SE NE DOTIKAJTE MERILNIH VEZI, PRIKLJUČNIH SPONK IN
MERJENCA!
1-5
Modeliranje električnih strojev
Priprava na laboratorijsko vajo 1
Izračunajte elemente nadomestnega vezja enofaznega transformatorja z nazivnimi podatki:
Sn = 200 VA, U1n = 230 V, U2n = 24 V, f = 50 Hz. Rezultati meritev so:
– preizkus prostega teka: P0 = 12 W, I0 = 150 mA;
– preizkus kratkega stika: Pk = 6,9 W, uk = 3,5 %.
1-6