Integralregning - Sct. Knuds Gymnasium

Udgave 2.1
Integralregning
Infinitesimalregning
Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette
som et redskab til bestemmelse af arealer under funktioner. Noterne er
supplement til kapitel III side 101 til 122 i Vejen til matematik B2. Endvidere er
der supplerende materiale omkring omdrejningslegemer fra A2.
Sct. Knud Gymnasium
Henrik S. Hansen
Indhold
Infinitesimalregning ............................................................................................................................. 1
Integralregning ..................................................................................................................................... 1
Integrering og det ubestemte integral................................................................................................... 2
Sætning: Stamfunktioner .................................................................................................................. 2
Sætning: Bestemmelse af stamfunktion ........................................................................................... 2
Arealer og bestemte integraler ............................................................................................................. 4
Sætning: Arealfunktion .................................................................................................................... 5
Sætning: Det bestemte integral......................................................................................................... 6
Sætning: Integralet som grænseværdi for summer ........................................................................... 7
Sætning: Regneregler for det bestemte integral ............................................................................... 8
Areal mellem grafer ............................................................................................................................. 9
Rumfang ............................................................................................................................................... 9
Sætning: Rumfanget af et omdrejningslegeme .............................................................................. 10
Integration ved substitution ................................................................................................................ 12
Sætning: Integration ved substitution ............................................................................................. 12
Henrik S. Hansen, Sct. Knuds Gymnasium
Infinitesimalregning
Infinitesimalregning er en gren inden for matematikken, grundlagt af Isaac Newton og Gottfried
Leibniz med skabelsen af differentialregning. Der var en lang kontrovers om, hvorvidt det var
Newton eller Leibniz, der skabte infinitesimalregningen. Den almindelige konsensus er, at begge
opdagede den uafhængigt af hinanden, men at Newton kom først, og Leibniz publicerede først.
Infinitesimalregning beskæftiger sig med "uendeligt små" ændringer af kontinuerte funktioner, dvs.
matematiske funktioner, der beskriver noget, der ændrer sig "glat". Et eksempel er bevægelse; man
kan ikke bevæge sig fra et sted til et andet uden at have været alle steder imellem.
For at forstå begrebet "uendeligt lille" (differentielt) kan man som analogi betragte fotografering: Vi
tænker på et fotografi som et billede taget på et bestemt tidspunkt, men i virkeligheden er billedet
eksponeret i et kort tidsrum. Jo kortere man kan gøre eksponeringstiden, jo mindre ser man rystelser
etc. Hvis eksponeringstiden kunne gøres uendelig kort, ville billedet blive perfekt.
Infinitesimalregningen kan groft sagt opdeles i to intimt relaterede discipliner: Differentialregning
og integralregning. Vi vil i det efterfølgende kigge nærmere på integralregningen.
Integralregning
I noterne om differentialregning så vi hvordan at væksten til en bestemt
-værdi på en graf kunne
bestemmes ud fra differentialkvotienten. Vi blev i stand til at differentiere og dermed finde en
funktion, som kunne bestemme differentialkvotienten (væksthastigheden – hældningen på tangenten
i punktet) ud fra en given x-værdi. Når vi differentierede en funktion
fik vi
også kaldet
den afledede funktion.
Eks. hvis vi har
så kunne vi gætte på at
da vi netop fik
. Det antog vi som sandt
. Faktisk har vi lige lavet integrationsprøven 
når vi differentierede
Integralregning handler om arealer og kan opfattes som det modsatte af at differentiere. Nå vi
integrerer
får vi en ny funktion
og denne kaldes en stamfunktion.
Definition (video)
En funktion
kaldes en stamfunktion til
En stamfunktion til funktionen
∫
, hvis
.
∫
betegnes også som
kaldes også for det ubestemte integral af
, og
Henrik S. Hansen, Sct. Knuds Gymnasium
⇔
kaldes integranden.
1
Integrering og det ubestemte integral
Ud fra definitionen kan vi opstille følgende sætning:
Sætning: Stamfunktioner
Hvis
er en stamfunktion til
så må alle funktioner af typen
, hvor c er en
konstant, være stamfunktioner til
Bevis: (video)
Da
er en stamfunktion til
, må der gælde at
. Vi kigger da på
Hermed bevist.
Hvis det handler om at arbejde modsat af at differentiere, så må følgende sætning gælde:
Sætning: Bestemmelse af stamfunktion
Hvis
så vil en vilkårlig stamfunktion
kunne bestemmes ved
, hvor c er en vilkårlig konstant, og
Bevis (video)
Vi benytter definitionen af stamfunktion
⇔
Da dette nu er vores
er sætningen bevist.
I praksis kalder vi det integrationsprøven, når vi ”prøver” at differentiere den tiltænkte
om det giver
og se
Vi kunne også kalde det at ”gætte” en stamfunktion.
Eksempelvis:
Vi ved at
så må
da
Når vi bestemmer stamfunktionen, så bestemmer vi det ubestemte integral.
Lav opgave 121 side 119, øvelse 1.18 (a,c,e) side 107, opgave 122 side 119 og opgave 123 side 119
Henrik S. Hansen, Sct. Knuds Gymnasium
2
Vi kan se, at når vi bestemmer det ubestemte integral, så får vi et konstantled. Hvis vi skal angive
en værdi for dette led, så skal vi blot kende et punkt
som integralet/stamfunktionen
løber igennem.
Eksempel
Bestem stamfunktionen til
som går gennem punktet (2,15)
Vores vilkårlige stamfunktion må være
⇔
Vi bestemmer c ved at løse
Altså bliver stamfunktionen
Lav opgave 127 side 119 og opgave 128 side 120
Henrik S. Hansen, Sct. Knuds Gymnasium
3
Arealer og bestemte integraler
Differentiering kunne benyttes til at bestemme
væksthastigheder. Integrering benyttes til at bestemme
arealet mellem funktionsgrafen og x-aksen. (video)
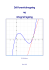
Lad os kigge på en genstand, der falder i det frie rum. Vi
kan indtegne grafen som følgende.
angiver faldhastigheden efter x sekunder.
Eks. falder vores genstand efter 4 sekunder med
m/s
Men hvor langt er den faldet efter de 4 sekunder?
Da grafen for
meter
giver os hastigheden til en bestemt tid, så må
120
kunne give os information om, hvor langt den er nået til en
100
bestemt tid. Hvis vi bestemmer stamfunktionen til f(x) og antager
80
at den er falder med 0 m/s idet den slippes. (gennem punktet (0,0) )
60
så får vi følgende
40
F(x) = 4.91*x^2
(4 , 78.56)
.
20
Vi kan se at
meter
1
2
3
4
5
sekunder
Hvis vi kigger på den første graf igen, så må vi kunne bestemme den tilbagelagte afstand ved at
kigge arealet under grafen. Grunden til dette er tid*hastighed=distance.
y
y
f(x) = 9.82x
Vi inddeler intervallet i lige store dele
50
50
med længden
40
40
denne afstand mindre. Dette resulterer i
30
30
(som graferne viser) n-pinde. Hver pind
20
20
har arealet højde gange bredde. Der vil
10
10
gælde at
og gør hele tiden
∑
.
1
2
3
4
5
6
f(x) = 9.82x
x
1
2
3
4
meter/sekund
Når vi så lader
så vil
∑
∫
5
x
6
f(x) = 9.82*x
50
40
I vores eksempel vil arealet under graf væren som vist på figuren.
Lad os se nærmere på det…….
integral = 78.56
30
20
10
1
Henrik S. Hansen, Sct. Knuds Gymnasium
2
3
4
5
6
sekunder
4
Sætning: Arealfunktion
Arealfunktionen
for en kontinuert funktion
Arealfunktionen er altså en stamfunktion til
er differentiabel og der gælder
.
Bevis: (video)
Vi opfinder en såkaldt arealfunktion
y
, idet vi lader
f(x)
betegne arealet under grafen fra a til b. Funktionen er blot en
bagvedliggende funktion til
, men med den funktion at den
til en given x-værdi angiver arealet undergrafen. Der gælder at
er kontinuert og differentiabel.
A(6)
Arealfunktionen opfylder, at når vi beregner
giver størrelsen af arealet af undergrafen fra a og til 6.
Endelig er
x
a
2
3
5
4
6
b
hele arealet undergrafen fra a til b.
Vi ser stadig på en vores positive og voksende funktion
f(x)
f(x)
y
Vi kigger på
som er
.
Vi kigger på det som tre arealer, og opstiller en undersum
og en oversum
og da
x
a
og
får vi
da
b
den er kontinuert og differentiabel.
Endvidere vil
Da
Dermed må
når
hele tiden er ”klemt inde” vil
i grænseområdet.
være en stamfunktion til
Hermed bevist
Henrik S. Hansen, Sct. Knuds Gymnasium
5
Som det fremgår af figuren, så er arealet under grafen lig med funktionens værdi i tallet b, dvs at
Arealet af under vores graf kan altså nu bestemmes hvis vi kender stamfunktionen
bestemmer en stamfunktion
. Hvis vi
som tidligere nævnt, så kan vi ikke vide, om det netop er
, vi
har fundet, eller en anden stamfunktion. Men vi ved dog at de kun adskiller sig ved en konstant.
Altså at
Sætning: Det bestemte integral
Lad
være en stamfunktion til
kaldes det bestemte integral af
. Tallet
og man skriver
∫
Bevis: (video)
Vi har tidligere vist at arealfunktionens værdi i tallet b er givet ved
Da
er en stamfunktion så kan den kun adskille sig fra
ved en konstant.
, da
Altså bliver
fås
∫
Hermed bevist
Det gode er her, at vi kan bruge en vilkårlig stamfunktion, da c går ud med hinanden.
Eksempelvis:
Bestem det bestemte integral for
på intervallet [-2;1]. (arealet mellem graf
og x-aksen)
Henrik S. Hansen, Sct. Knuds Gymnasium
6
10
∫
8
(
6
)
4
integral = 3.
2
-3
-2
-1
1
2
3
-2
Altså fandt vi det bestemte integral til 3. Grafisk ser løsningen ud
-4
-6
som på grafen til højre.
-8
-10
Lav øvelse 2.10 side 115, øvelse 2.11 side 115, opgave 129 side 120, opgave 131 side 120 og
opgave 139 side 121
Det bestemte integral er altså vores areal. Areal under x-aksen er negativt og areal over x-aksen er
positivt. Vores eksempel ovenover viser altså at største delen af arealet ligger over x-aksen.
Det skal her kort nævnes, at vi også kan kigge på arealet mellem graf og x-asken som en sum af
middelværdier.
Hvis vi i stedet for over- og undersummer skabe en middelsum af n lige store delintervaller, som det
ses på nedenstående tegning, så vil vi når vi lader antallet af delintervaller stige nærme os arealet
under grafen.
Sætning: Integralet som grænseværdi for summer
For en funktion, der er kontinuert i intervallet
gælder, at en middelsum på intervallet har en
grænseværdi for
som er lig med integralet fra a til b (altså arealet under grafen)
∑
∫
for
Bevis: (video)
Vi tegner en tænkt kontinuert, ikke negativ og glat
kurve, og inddeler denne i n lige store delintervaller
med bredden .
Vi vælger nu i hvert interval en tilfældig x-værdi
og hertil bestemmes funktionsværdien.
,
Nu kan vi tegne et rektangel med bredden
og
højden
, og når vi samler alle arealerne fås
følgende sum:
Henrik S. Hansen, Sct. Knuds Gymnasium
7
∑
Vi kan se at hvis vi sætter antallet af delintervaller op, så
nærmer summen sig det aktuelle areal.
∑
∫
for
Hermed bevist.
Da vi tidligere mødte det bestemte integral for første gang var det som værdien af en arealfunktion.
Integralet var lig med et areal. Så længe vi kigger på en positiv og kontinuert funktion så er det lige
meget hvad vi vælger. Areal, det bestemte integral og middelsum er samme tal.
Sætning: Regneregler for det bestemte integral
1. Sum og differensregel
∫
∫
∫
2. Konstantregel
∫
∫
3. Indskudsregel
∫
∫
∫
Bevis (video)
1. Jf. sætningen om det bestemte integral må der gælde at
(
∫
∫
)
∫
Tilsvarende for minus. Hermed bevist
2. Jf. sætningen om det bestemte integral må der gælde at
∫
(
)
∫
Henrik S. Hansen, Sct. Knuds Gymnasium
8
Hermed bevist.
3. Jf. sætningen om det bestemte integral må der gælde at
∫
∫
∫
Hermed bevist.
Areal mellem grafer
På grafen til højre ser vi to positive og kontinuerte grafer. Der er
markeret en punktmængde M hvor der gælder for alle x i
intervallet
at
y
f(x)
Det er umiddelbart klart, at arealet af M må være lig med arealet
under g minus arealet under f.
∫
∫
g(x)
M
∫
x
a
Prøv at kontrollere dette, når det oplyses at
b
og
Lav øvelse 3.4 side 208 A2, opgave 279 side 234 A2 og opgave 280 A2
Rumfang
Integraler blev benyttet til at bestemme arealer i planen mellem grafer og linjer, men hvis vi drejer
dette areal rundt om eksempelvis x-aksen får vi et omdrejningslegeme, som vi kan bestemme
rumfanget af. (video)
Henrik S. Hansen, Sct. Knuds Gymnasium
9
Tidligere så vi at arealet i planen var givet som uendelige mange tynde pinde med arealet gælde at
∑
, som resulterede i ∫
.
Det vi skal se nu er uendelig mange cylindere med
arealet
eller hos os
(hvor vi
tænker os at cylinderen ligger ned).
Vi må altså få rumfanget til
Når vi lader
får vi
∑
.
∫
∫
Sætning: Rumfanget af et omdrejningslegeme
Det omdrejningslegeme der fremkommer, når punktmængden
{
} altså arealet mellem graf og x-aksen, drejes 360° omkring
|
x-aksen, har rumfanget
∫
Bevis: (video)
Vi vælger at inddele omdrejningslegemet i mindre
skiver med bredden
mindre
. Således får vi
skiver. Jo
jo flere skiver.
Finder vi rumfanget af alle
disse skiver tilsammen, så har
vi rumfanget af
omdrejningslegemet.
Som under arealet i planen kigger vi først på et voksende interval. Vi får et
undervolumen og et overvolumen i forhold til det korrekte volumen.
Da vi har valgt
fås følgende
Henrik S. Hansen, Sct. Knuds Gymnasium
10
Vi lader nu
og får dermed
Vi integrerer på begge sider og får
∫
Hermed er sætningen vist. Beviset føres tilsvarende for
Eksempelvis. Grafen for
konstant eller aftagende
og linjen
afgrænser en punktmængde M.
y
f(x)
6
5
4
Hvor stort bliver rumfanget af den figur som fremkommer når
3
g(x)
2
punktmængden roteres 360 rundt om x-aksen?
M
1
Den nedre og øvre grænse kan bestemmes til
eller
1
2
3
4
5
6
x
Det er umiddelbart klart, at vi finder punktmængden M ved
∫ (
)
y
(overvej hvorfor)
f(x)
6
5
4
Men vi skal bestemme rumfanget af omdrejningslegemet omkring x-
3
aksen. Så vi må trække rumfanget af den figur, som fremkommer ved
1
roterer punktmængden under f(x), fra rumfanget af den cylinder som
2
-1
-2
g(x)
M
1
2
3
4
5
6
M
-3
fremkommer ved at rotere g(x).
-4
-5
-6
∫
∫
∫
∫
Lav øvelse 5.5 side 225 A2, øvelse 5.7 side 225 A2 og opgave 288 side 235 A2
Henrik S. Hansen, Sct. Knuds Gymnasium
11
x
Integration ved substitution
Ved hjælp af følgende regneregel, kan man beregne mange integraler. Desværre er det ikke altid at
reglen virker. Metoden er baseret på følgende sætning
Sætning: Integration ved substitution
For differentiable funktioner f og g gælder, at hvis
∫ (
)
hvor
(
er kontinuert, så er
)
er en stamfunktion til
Et lommebevis: Ovenstående kan via Leibniz. Først sætter vi
∫
(
∫
. Nu kan vi skrive det som
)
Bevis: (video)
Da der skal gælde at
, kan vi differentiere højre siden, og får vi integranden fra
venstreside, så har vi bevist sætningen.
Ifølge sætningerne om differentiering af en sum og af en sammensat funktion fås
( (
)
)
( (
))
(
)
(
)
Hermed bevist.
I praksis benyttet vi sjældent sætningen direkte, men udnytter Leibniz´skrivemåde.
Eksempelvis. Beregn det ubestemte integral ∫
Først sætter vi
her efter bestemmes
Nu kan vi indsætte (substituere) dette ind i integralet
∫
∫
∫
Vi har altså fundet ∫
Hvis I skal lave den samme beregning i TI, så vil I få forskellige output afhængig af om TI er
Henrik S. Hansen, Sct. Knuds Gymnasium
12
indstillet til grader eller radianer. Husk på at når funktionen er bygget op på sinus eller cosinus, og
når vi indsætter et reelt tal (ikke et antal grader), så skal den stå i radianer.
I grader bliver output

sin2 x - 5  x

   

-28.6479cos2. x - 2.5 


I radianer fås følgende output

 sin 2 x - 5  x

   

-.5cos 2.x - 5.


Lav øvelse 1.20 side 202 A2,
Henrik S. Hansen, Sct. Knuds Gymnasium
13