Suhteelliset frekvenssijakaumat ja summafrekvenssijakaumat

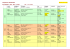
2 Aineiston kuvaaminen graafisesti
1
2.2 Suhteelliset frekvenssijakaumat ja summafrekvenssijakaumat
Suhteelliset jakaumat ja summafrekvenssijakaumat muodostetaan suorasta jakaumasta. Laskemalla frekvenssit yhteen järjestyksessä f1 , f 2 ,..., f l saadaan summafrekvenssijakauma
f1
saadaan suhteellinen frekvenssijan
f
f
kauma (kuva 1, sarake 1 ). Prosenttisista frekvensseistä pi  100  1 saadaan prosenttinen
n
n
frekvenssijakauma (kuva 1, sarake p i ). Laskemalla prosenttiset frekvenssit yhteen järjestyk-
(kuva 1, neljäs sarake). Suhteellisista frekvensseistä
sessä p1 , p2 ,..., pk saadaan prosenttinen summafrekvenssijakauma (kuva 1, viimeinen sarake). Kuvassa 2 ovat tiedostossa Synnytys.xlsx1 olevan havaintomatriisin sarakkeesta x10
(lapsen paino) muodostetut kaikki erilaiset frekvenssijakaumat.
Kuva 1. Suhteelliset frekvenssi- ja summafrekvenssijakaumat
Kuva 2. Lapsen painon suhteelliset frekvenssi- ja summafrekvenssijakaumat
1
tiedosto http://users.metropolia.fi/~pasitr/opas/Ran15a/02/esim/Synnytys.xlsx
2
Tilastomatematiikka
Suhteellisista summafrekvensseistä muodostuva summakäyrä on suhteellinen summakäyrä
eli otoskertymäfunktio (kuva 3). Usein suhteelliset summafrekvenssit esitetään prosenttilukuina, jolloin käyrä on prosenttinen summakäyrä ([20], 81). Lapsen painon summafrekvenssijakauma (kuva 2, sarake summafrekvenssi) on esitetty graafisesti kuvassa 4.
Kuva 3. Summakertymäfunktion periaate
Kuva 4. Lapsen painon summakertymäfunktio