Johns Hopkins University Tristan A. Sharp, Lars Pastewka, Mark O

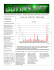
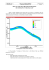
Johns Hopkins University
Scale effects in static friction between rough solids
Tristan A. Sharp, Lars Pastewka, Mark O. Robbins
Dislocations decrease
static friction
Method: Molecular Dynamics
and Greens Function - MD
sandia.gov
Introduction
Understanding small-scale deformation and energy dissipation
between contacting solids is important in applications that range
from nanoscale mechanical devices to jet engines. Even finelysmoothed parts exhibit roughness, and contact between solids
generally occurs only at asperities, often approximated as
spheres. Here, we use molecular dynamics simulation to
investigate sliding of a single asperity and to identify scale
effects of the static friction coefficient, μ.
(eV / Å)
Force on surface atoms
𝐹𝑓𝑢𝑙𝑙
Rigid spherical asperity
radius R
~O(Nsurface) runtime
Processor-seconds per MD step
Error
𝐹𝑓𝑢𝑙𝑙 − 𝐹𝑔𝑓𝑚𝑑
If a>bcore, the sphere need not overcome the corrugation
stress all at once. Nucleation of a dislocation results in
partial slip. Dislocation annihilation at the center moves
the contact one Burger’s vector, b.
Friction trace:
Static friction
1000
GFMD
slope ≈ 2
System size, linear dimension L
σx
Surface atoms’ displacement, u (Å)
(4.07 Å unit cell)
Also, implemented on GPU. Also, fewer
atoms means shorter convergence time
-1.5
0
Shear force, fx
(L-J units)
1.5
0
dislocation nucleated
0
Sliding distance
6σ
Scale effects in friction
Contact Stresses
p
Isotropic elastic flat
Young’s modulus, E
Poisson ratio, ν = 0.5
bcore:
Dislocation core size
Elastic-interfacial energy balance: bcore = bE/3τavg
Full
slope ≈ 3
slope = 2
Slide, x-dir
σx
O(u2) convergence
slope = 1
Atomic diameter, b = 21/6 σ
Shear stress, σx
before nucleation
after nucleation
To study large systems, we helped develop a parallel, multi-scale simulation
package which accelerates molecular dynamics simulation. The acceleration is
achieved by replacing part of a solid with its Greens function response. The
method requires calculating the energy about a reference state and Taylor
expanding to second order in the atomic displacements, u. Once the Greens
function is calculated, calculations can be performed quickly, scaling with the
number of atoms on the surface of the solid, Nsurface.
μ
Static friction coefficient s. contact radius
Tomlinson regime
μ constant
Contact radius, a
We simulate the quasistatic sliding of an asperity composed of a
bent lattice, choosing the lateral spacing of the surface atoms to
be commensurate with the lattice of the substrate. Repulsive
Lennard-Jones (LJ) interactions produce a square (x-y) lattice of
atomic corrugations. The substrate is controlled by the Green’s
function of isotropic linear elasticity4.
model2,
Simple dislocation
adapted
Hertzian dislocation model
Full MD
Peierls stress
arrests dislocations
(a2/Rb)x(16m/9π)
NSF IGERT 0801471; AFOSR FA9550-0910232; OCI-0963185
References:
1 JA Hurtado and Kim. Proc. R. Soc. Lond. A. 1999 1471-2946
2 Yanfei Gao J. Mech. Phys. Solids 58 (2010) 2023-2032
4 L. Pastewka, T. Sharp, M. O. Robbins. PRB 86 075459 (2012)
5 S. Plimpton. J Comp Phys, 117, 1-19 (1995)
Shear stresses at the edge cannot exceed the normal pressure, p, times the
corrugation max slope, m. This explains the correspondence with the Mindlin
continuum model (which uses Hertz pressure and a local friction coefficient, μ0).
In the simulations, atomic corrugation slope mimics the role of μ0. Applying
sufficient stress causes the sphere to coherently hop one atomic diameter..
Small contact regime: static friction requires overcoming corrugation
stress (m x pressure) over the full contact area.
Large contact regime: friction drops as (a2/R)-1/2 due to contact edge
stress maximum nucleating dislocations.
printed by
Very large contact regime: Peierls stress dominates
www.postersession.com