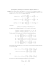technische universität münchen

TECHNISCHE UNIVERSITÄT MÜNCHEN
Zentrum Mathematik
Mathematik für Physiker 2
(Analysis 1)
Prof. Dr. Oliver Matte
Max Lein
Wintersemester 2010/2011
Lösungsblatt 11
(14.01.2011)
Zentralübung
88. Eine glatte Funktion
Zeigen Sie, dass die Funktion f : R −→ R,
{
f (x) =
e− x
0
1
x>0
,
x≤0
beliebig oft differenzierbar ist.
Lösung:
Für x ̸= 0 ist f (x) beliebig oft differenzierbar, als Komposition unendlich oft differenzierbarer
Funktion.
f ist stetig bei x = 0, denn limx→0+ e− x = 0 = f (0) = limx→0− f (x). Weiter ist offenbar
) 1
(
1
limx→0− f (k) (x) = 0 für alle k ∈ N. Für x > 0 ist f ′ (x) = x12 e− x , f ′′ (x) = − x23 + x14 e− x .
1
Allgemein ist f (k) (x) = pk ( x1 ) e− x mit Polynomen pk vom Grad 2k, denn
1
f (k+1) (x) =
d ( (1) −1 ) ( 1 ′ (1)
pk x e x = − x2 pk x +
dx
{z
|
)
1
p (x)
x2 k
}
e− x .
1
1
=:pk+1 ( x )
Wegen limx→0+
1
xn
e− x = limx→∞
1
xn
ex
= 0, da 0 ≤
xn
ex
≤
xn (n+1)!
xn+1
→ 0 für x → ∞, folgt sofort
lim f (k) (x) = 0
x→0+
und damit per Induktion
f (k−1) (x) − f (k−1) (0) l’H
= lim f (k) (x) = 0.
x→0
x→0
x
f (k) (0) = lim
f ist also beliebig oft (stetig) differenzierbar, mit f (k) (0) = 0 für k ∈ N0 .
f HxL
1.0
f HxL
0.030
0.025
0.8
0.020
0.6
0.015
0.4
0.010
0.2
0.005
x
-0.05
0.00
0.05
0.10
0.15
0.20
0.25
0.30
1
x
0
2
4
6
8
10
89. Die Landau-Symbole
(
)
Seien f, g : R \ {x0 } −→ C. Wir sagen, dass{ f (x) = O g(x) für x} → x0 , falls r, C > 0 existierten
(
)
derart, dass |f (x)| ≤ C |g(x)| für alle x ∈ ξ ∈ R | |ξ − x0 | < r erfüllt ist und f (x) = o g(x) ,
(x)|
falls limx→x0 |f
|g(x)| = 0. Zeigen Sie:
(i) x2 = O(x2 ) für x → ±∞, 0
(iv) x2 = O(x) für x → 0
1
= O(|x|−s ) für x → ±∞, s > 0
(v) √
2s
1+x
(
)
(vi) x = o x ln |x| für x → 0
(ii) x2 ̸= o(x2 ) für x → 0
(iii) x2 = o(x) für x → 0
Lösung:
(
)
Anschaulich bedeutet f (x) = o g(x) für
( x →
) x0 “f geht schneller als g gegen 0 oder f wächst
langsamer als g gegen ∞” und f (x) = O g(x) für x → x0 “f geht mindestens so schnell gegen 0
wie g oder wächst höchstens so langsam wie g gegen ∞.” Man nennt O und o auch “little o” und
“big o;” in der Physik ist O gang und gebe.
(i) Offensichtlich gilt für alle x0 ∈ R
lim sup
x→x0
x2
= lim 1 = 1
x2 x→x0
und somit per Definition x2 = O(x2 ) für x → ±∞ und x → 0.
(ii) Nach Teilaufgabe (i) ist lim supx→0
(iii) Aus lim supx→0
x2
x
x2
x2
= 1 ̸= 0 und daher auch x2 ̸= o(x2 ) für x → 0.
= limx→0 x = 0 folgt per Definition x2 = o(x) für x → 0.
2
x
2
(iv) Da
( lim )supx→0 x = limx→0 x = 0, folgt
( auch
) x = O(x). Ganz allgemein gilt: ist f (x) =
o g(x) für x → x0 , gilt auch f (x) = O g(x) für x → x0 . Umgekehrt ist das falsch.
(v) Setzen wir die Abschätzung
1
1
1
0≤ √
≤√
=
s
2s
2s
|x|
1+x
x
in den Quotienten der Funktionen ein, erhalten wir
0≤
√ 1
1+x2s
1
|x|s
|x|s
|x|s
=√
≤
= 1,
|x|s
1 + x2s
der Quotient ist beschränkt und somit gilt
√ 1
1+x2s
= O(|x|−s ) für x → ±∞.
(vi) Wir bilden den Grenzwert des Quotienten der beiden Funktionen für x → 0,
lim
x→0
x
1
= lim
= 0,
x ln |x| x→0 ln |x|
(
)
also gilt x = O x ln x .
2
90. Taylor-Polynome und Taylor-Reihen
Für eine n Mal stetig differenzierbare Funktion f : R −→ R definieren wir für k ≤ n das TaylorPolynom kter Ordnung um den Entwicklungspunkt a als
Tk f (x) :=
k
∑
f (l) (a)
l!
l=0
(x − a)l .
Falls f beliebig oft differenzierbar ist und die Potenzreihe T f (x) := limk→∞ Tk f (x) für alle |x − a| <
ρ, ρ > 0, konvergiert, so heißt T f die Taylor-Reihe von f um den Entwicklungspunkt a. Zeigen Sie:
dl
T f
dxl k
l
d
(l) (a) = f (l) (a) für alle l ≤ k.
= Tk−l f (l) sowie dx
l Tk f (a) = Tk−l f
(
)
(ii) f (x) − Tk f (x) = o (x − a)k für x → a und k ≤ n.
(i) Tk f erfüllt
(iii) Interpretieren Sie das Ergebnis aus Teilaufgabe (ii) anschaulich.
(iv) Deuten Sie T1 f und T2 f , die Taylor-Polynome erster und zweiter Ordnung, anschaulich.
√
(v) Entwickeln sie die relativistische kinitesche Energie E(p) = m2 + p2 , m > 0, für kleine
Impulse. Geben Sie die ersten drei nichtverschwindenden Terme an.
(vi) Geben Sie das Taylor-Polynom nter Ordnung und die Taylor-Reihe zu f aus Aufgabe 88 um
x = 0 an und interpretieren Sie das Ergebnis.
Lösung:
(i) Für k = 0 folgt sofort aus der Definition
Tk f (a) =
k
∑
f (l) (a)
l!
l=0
(a − a)l =
f (0) (a)
= f (a).
0!
Für die erste Ableitung der Taylor-Reihe gilt
∑ f (l) (a)
∑ f (l+1) (a)
d
Tk f (x) =
lxl−1 =
xl
dx
l!
l!
k
k−1
l=1
l=0
= Tk−1 f ′ (x).
Wir erhalten also rekursiv für k ≤ n sofort
dl
Tk f (x) = Tk−l f (l) (x)
dxl
und somit auch
dl
T f (a)
dxl k
= Tk−l f (l) (a) = f (l) (a).
)
(
(ii) Wir zeigen die Behauptung, f (x) − Tk f (x) = o (x − a)k für x → a, getrennt für k = 0 und
1 ≤ k ≤ n. Für k = 0 folgt sofort
(
)
f (x) − T0 f (x)
= lim f (x) − f (a) = 0
0
x→a
x→a
(x − a)
(
)
und somit f (x) − T0 f (x) = o (x − a)1 = o(1), da f stetig in a ist.
lim
Für 1 ≤ k ≤ n benutzen wir folgendes Faktum, welches wir im Anschluß beweisen werden:
es existiert ein ξ ∈ (x, a) bzw. ξ ∈ (a, x) derart, dass
f (x) − Tk f (x)
f (k) (ξ) − f (k) (a)
=
(x − a)k
k!
3
(1)
gilt. Da x → a auch ξ → a impliziert (es gilt x < ξ < a oder a < ξ < x) und f n(Mal stetig)
differenzierbar ist, geht die rechte Seite gegen 0 und wir haben f (x) − Tk f (x) = o (x − a)k
gezeigt.
Nun zum Beweis von Gleichung (1) per Induktion: Für k = 1 erhalten wir aus dem Mittelwertsatz und T1 f (a) = f (a) sofort
(
) (
)
)
f (x) − T1 f (x) − f (a) − T1 f (a)
f (x) − T1 f (x)
d(
=
=
f − T1 f (ξ)
1
(x − a)
x−a
dx
′
′
′
′
= f (ξ) − T0 f (ξ) = f (ξ) − f (a)
für ein ξ ∈ (x, a) bzw. ξ ∈ (a, x) (je nachdem, ob x > a oder x < a ist). Da f ′ per Annahme
stetig ist und( x → a) auch ξ → a impliziert, geht die rechte Seite gegen 0 und wie haben
f − T1 f = o (x − a) bewiesen.
Sei nun ohne Einschränkung x > a (die Argumente für x < a sind analog). Für den Induktionsschritt k → k +1 ≤ n brauchen wir den verallgemeinerten Mittelwertsatz (Satz 9.2.4 aus
der Vorlesung): Sind f, g : [a, b] −→ R zwei stetige Funktionen, die auf (a, b) differenzierbar
sind. Dann existiert ein ξ ∈ (a, b) mit
(
)
(
)
f (b) − f (a) g ′ (ξ) = g(b) − g(a) f ′ (ξ).
Falls g(b) − g(a) ̸= 0 und g ′ (ξ) ̸= 0 sind, ist das äquivalent zu
f ′ (ξ)
f (b) − f (a)
= ′ .
g(b) − g(a)
g (ξ)
In diesem Fall identifizieren wir f mit f − Tk f , g mit (x − a)k und b mit x.
Nun zum Induktionsschritt k → k + 1: wir benutzen die in Teilaufgabe (i) nachgewiesene
d
Rekursion dx
Tk f = Tk−1 f ′ und setzen sie in den relevanten Quotienten ein: es existiert ein
η ∈ (x, a) mit
(
)
(
) (
)
d
f (x) − Tk+1 f (x) − f (a) − Tk+1 f (a)
f (x) − Tk+1 f (x)
dx f − Tk+1 f (η)
=
= d
(x − a)k+1
(x − a)k+1 − (a − a)k+1
(x − a)k+1 dx
=
1
k+1
f ′ (η)
− Tk+1−1
(η − a)k
f ′ (η)
=
1
k+1
f ′ (η)
f ′ (η)
− Tk
(η − a)k
x=η
.
Nun können wir iterativ fortfahren, da f ′ eine n − 1 Mal stetig differenzierbare Funktion
ist und somit die Bedingungen für die Induktionsvoraussetzung selbst erfüllt. Das heißt, es
existiert ein ξ ∈ (a, η) ⊂ (a, x) mit
f ′ (η) − Tk f ′ (η)
=
(η − a)k
=
dk ′
f (ξ)
dxk
k
d
′
− dx
f (k+1) (ξ) − Tk−k f (k+1) (ξ)
k Tk f (ξ)
=
k!
k!
f (k+1) (ξ) − T0 f (k+1) (ξ)
f (k+1) (ξ) − f (k+1) (a)
=
.
k!
k!
Eingesetzt in die vorherige Gleichung liefert das Gleichung (1) für k + 1.
(iii) Das Ergebnis aus Teilaufgabe (ii) besagt, dass der Fehler zwischen f und dem Taylor-Polynom
kter Ordnung schneller als (x − a)k gegen 0 strebt, also das Taylor-Polynom lokal (das heißt
in einer Umgebung von a) die Funktion f approximiert.
(iv) Das Taylor-Polynom erster Ordnung T1 f (x) = f (a) + f ′ (a) (x − a) ist die Tangentengerade
zu f am Punkt a. Das Taylor-Polynom zweiter Ordnung T2 f (x) = f (a) + f ′ (a) (x − a) +
1 ′′
2
2 f (a) (x − a) ist die Anschmiegparabel von f am Punkt a.
4
(v) Da E eine gerade Funktion ist, E(−p) = E(+p), tragen nur gerade Polynome bei. Um also den
dritten nichtverschwindenden Term auszurechnen, müssen wir (mindestens) das Taylorpolynom vierter Ordnung ausrechnen!
Anstatt √
E vier Mal abzuleiten, kann man sich das Leben erheblich vereinfachen, indem man
f (x) = m2 + x um x = 0 Taylor-entwickelt (falls m > 0, ist f glatt) und dann E(p) = f (p2 )
ausnutzt:
√
f (x) = m2 + x
f (0) = m
1
1
f ′ (x) = √
f ′ (0) =
2m
2 m2 + x
1
1
f ′′ (x) = −
f ′′ (0) = − 3
3/2
2
4m
4(m + x)
Daher ist
T2 f (x) = m +
1 1
1! 2m x
2
−
⇒ T4 E(p) = T2 f (p ) = m
2
1 1
2! 4m3 x
4
1 2
1
+ 2m
p − 8m
3p .
Man schreibt auch
E(p) =
√
m2 + p2 = m +
1 2
2m p
−
1
p4
4m3
+ O(p6 ).
(vi) Wie wir aus Aufgabe 88 wissen, verschwindet f und alle seine Ableitungen bei x = 0, f (k) (0) =
0 für alle k ∈ N0 . Somit verschwinden für alle n ∈ N0 das Taylor-Polynom Tn f (x) = 0 und die
Taylor-Reihe T f (x) = 0. Moral von der Geschicht’: nicht jede unendlich oft differenzierbare
Funktion lässt sich durch ihre Taylor-Reihe approximieren!
5
Hausaufgaben
88. Eigenschaften der reellen Logarithmusfunktion
[11 Punkte]
R+
Sei l :
−→ R die Umkehrfunktion der in Aufgabe 80 untersuchten Funktion e : R −→ R+ .
Zeigen Sie:
(i) l(1) = 0, l(xy) = l(x) + l(y) und l ist streng monoton wachsend und stetig,
(ii) l(x) ≤ x − 1 für x, y > 0,
(iii) limy→x
l(y)−l(x)
y−x
=
1
x
für x > 0.
Lösung:
(i) Aus e(0) = 1 folgt l(1) = 0 [1]. Seien x, y > 0, dann gibt es u, v ∈ R mit x = e(u), y = e(v)
[1]. Somit ist
(
)
(
)
l(xy) = l e(u)e(v) = l e(u + v) = u + v = l(x) + l(y).
[1]
Sei nun x < y. Wir zeigen l ist in x stetig und l(x) < l(y) (strenge Monotonie): Wähle a =
u − 1, b = v + 1. Da e : [a, b] → [e(a), e(b)] streng monoton wachsend und stetig ist, ist auch
l : [e(a), e(b)] → [a, b] streng monoton wachsend und stetig [1]. Da x, y ∈ [e(a), e(b)], ist l in
x stetig und l(x) < l(y) [1].
(ii) Aus e(x) ≥ 1 + x folgt wegen der Monotonie von l, dass x ≥ l(1 + x), falls x > −1 ist [1].
Verschiebung ergibt l(x) ≤ x − 1 für x > 0 [1].
(iii) Sei (yn ) eine Folge in R+ \ {x}, yn → x > 0 [1]. Wir setzen vn = l(yn ), u = l(x) [1]. Wegen
der Stetigkeit von l gilt vn → u [1]. Nun ist
vn − u
1
1
l(yn ) − l(x)
n→∞
=
−−−→
= .
yn − x
e(vn ) − e(u)
e(u)
x
[1]
Bemerkung: Die Funktion exp erfüllt die Bedingungen an die Funktion x 7→ e(x) von Aufgabe 80. Somit besitzt die Umkehrfunktion log alle hier für die Funktion x 7→ l(x) gezeigten
Eigenschaften. Das exp und log hierdurch schon eindeutig bestimmt sind werden wir in Kürze
zeigen können (Mittelwertsatz der Differentialrechnung).
6
89. Die allgemeine Potenz auf R
(
Seien x, y ∈ R und a > 0. Wir definieren ax := ex ln a . Zeigen Sie a
Lösung:
( x )y [1] x ln ax [1] xy ln a
a
= e
= e
= axy
7
)
x y
[2 Punkte]
= axy .
90. Ableiten von Funktionen auf R
[20 Punkte]
(i) Berechnen Sie die erste Ableitung von
f (x) = ln
1+
√
1 + x2 √
− 1 + x2 .
x
1
(ii) Definiere für n ∈ N die Funktion fn (x) = xn−1 e x , x ̸= 0. Zeigen Sie, dass gilt:
1
dn
ex
fn (x) = (−1)n n+1
n
dx
x
(iii) Es seien f1 , . . . fn im Punkte x0 differenzierbare Funktionen, die in x0 nicht verschwinden,
fj (x0 ) ̸= 0 für alle j = 1, . . . , n. Zeigen Sie, dass für alle n ∈ N gilt:
d ∏n
n
∑
f
(x)
j
f ′ (x0 )
j=1
dx
x=x0
∏n
=
f (x0 )
j=1 fj (x0 )
j=1
(iv) Zeigen Sie, dass
f (x) =
ln(1 + x)
x
für x > 0 streng monoton fallend ist.
Lösung:
(i) Wir schreiben zuerst f um als
√
√
(
)
f (x) = ln 1 + 1 + x2 − ln x − 1 + x2 .
Das vereinfacht die Rechnung beträchtlich! Die Ableitung ist dann gegeben durch
1
[1] 1 (1 + x2 )− /2 2x 1 1
1
√
f ′ (x) = 2
− − 2 (1 + x2 )− /2 2x
x
1 + 1 + x2
x
x
1
[2]
√
= √
.
(
)− −√
2
2
x
1+x 1+ 1+x
1 + x2
(ii) Die Behauptung wird induktiv bewiesen. Leiten wir fn ein Mal nach x ab, erhalten wir
(
)
1
1
d ( n−1 1 )
1
d
fn (x) =
x
e x = (n − 1) xn−2 e x + xn−1 e x − 2
dx
dx
x
1
1
= (n − 1) xn−2 e x − xn−3 e x = (n − 1) fn−1 (x) − fn−2 (x).
[1]
(2)
Da die rechte Seite fn−1 und fn−2 enthält, müssen wir für den Induktionsanfang n = 1 und
n = 2 beweisen [1]:
d ( 0 1)
ex
ex
x e x = − 2 = (−1)1 1+1
dx
x
x
(
)
1
1
1
d ( 1)
ex
1
x ex = ex − x 2 = 1 −
ex
dx
x
x
((
) )
)
)
(
(
2
1
1
d
1
d
1 1
1
1
f2 (x) =
1−
ex = + 2 ex + 1 −
ex − 2
dx2
dx
x
x
x
x
1
d
f1 (x) =
dx
d
f2 (x) =
dx
1
[1]
1
= (−1)2
ex
x2+1
[1]
8
Nun zum Induktionsschritt: wir benutzen Gleichung (2) um die n + 1te Ableitung von fn+1
umzuschreiben als
n
) [1] dn
dn+1
d dn−1
[1] d (
f
(x)
=
n
f
(x)
−
f
(x)
=
n
f
(x)
−
fn−1 (x)
n+1
n
n−1
n
dxn+1
dxn
dxn
dx dxn−1
(
1
1 )
x
x
d
[1]
n e
n−1 e
= n (−1) n+1 −
(−1)
x
dx
xn
1
(
)
1
1
ex
[1]
= n (−1)n n+1 + (−1)n −n x−n−1 e x + x−n e x (−x−2 )
x
1
1
x
ex
[1]
n e
n+1
= −(−1) n+2 = (−1)
.
x
x(n+1)+1
Damit ist die Behauptung bewiesen.
(iii) Die einzige Schwierigkeit besteht darin, die einzelnen Schritte korrekt aufzuschreiben:
∑n
∏n
′
d ∏n
j=1 fj (x0 )
n
k=1 fk (x0 )
f
(x)
[2] ∑ fk′ (x0 )
j=1 j
j̸=k
dx
x=x0 [2]
∏n
∏n
=
=
fk (x0 )
j=1 fj (x0 )
j=1 fj (x0 )
k=1
(iv) Die Ableitung von f ist
1
[1] 1 1
[1] x − (1 + x) ln(1 + x)
−
f ′ (x) =
ln(1 + x) =
x 1 + x x2
x2 (1 + x)
Mit Aufgabe xyz (ii) kann f ′ von oben beschränkt werden durch
f ′ (x) ≤
ln(1 + x) − (1 + x) ln(1 + x) [1] −x ln(1 + x)
=
< 0,
x2 (1 + x)
x2 (1 + x)
die Funktion ist streng monoton fallend [1].
9
91. Kurvendiskussion
[16 Punkte]
Diskutieren Sie die Funktion
f (x) = x ln |x| .
Geben Sie den Definitionsbereich, Grenzwerte an den Lücken, Verhalten bei 0 und ±∞, Extrema
und gegebenenfalls die stetige Fortsetzung an. Begründen Sie Ihre Antworten! Skizzieren Sie den
Graphen und zeichnen Sie alle relevanten Informationen ein.
Lösung:
Definitionsbereich: Der Definitionsbereich ist R \ {0} [1], da die Funktion x 7→ ln x nur auf R+
definiert ist. Wir bemerken, dass die Funktion ungerade ist, das heißt f (−x) = −f (x).
Ableitungen: Um die Ableitung auszurechnen, schreiben wir f als
{
−x ln(−x) x < 0
f (x) =
x ln x
x>0
[1]
und leiten für x > 0 und x < 0 getrennt ab. Wir berechnen die erste und zweite Ableitung zu
{
− ln(−x) − 1 x < 0
f ′ (x) =
[1]
+ ln x + 1
x>0
{
− x1 x < 0
′′
f (x) =
[1]
+ x1 x > 0
und schließen daraus, dass die Funktion für x < 0 konvex und für x > 0 konkav ist [1].
!
Extrema: Setzen wir f (x) = 0, so erhalten wir für x > 0
ln x + 1 = 0 ⇔ ln x = −1 ⇒ xc1 = 1/e
[1]
und analog für x < 0 den zweiten Kandidaten xc2 = −1/e [1]. Daraus ergibt sich f (1/e) = −1/e =
−f (−1/e). Da f ′′ (x) < 0 für x < 0 und f ′′ (x) > 0 für x > 0 ist (1/e, −1/e) ein lokales Minimum [1]
und (−1/e, 1/e) ein lokales Maximum [1].
Grenzwert an der Definitionslücke: Da f (−x) = −f (x) gilt
(
)
lim f (x) = lim −x ln(−x) = lim x ln x
x↗0
x↗0
x↘0
1/x
ln x
= lim
= lim (−x)
1
x↘0 /x
x↘0 −1/x2
x↘0
= lim f (x) = lim
x↘0
[1]
=0
und wir können f in 0 mit f˜(0) = 0 stetig fortsetzen [1]. Die stetige Fortsetzung ist aber in 0 nicht
differenzierbar.
Asymptotik: Da x 7→ x und x 7→ ln x für x → ∞ auch gegen ∞ streben, erhalten wir mit f (−x) =
−f (x) auch
lim f (x) = ±∞.
[1]
x→±∞
10
Variationstabelle: [2]
x
f (x)
f ′ (x)
f ′′ (x)
(−∞, −1/e)
−
−
−1/e
1/e
0
−
(−1/e, 0)
0
0
(0, 1/e)
1/e
−
+
−1/e
0
+
+
−
(1/e, ∞)
−
+
Graph: [2]
1.5
f (x) = x ln |x|
Extrema
1
0.5
0
-0.5
-1
-1.5
-2
-1.5
-1
-0.5
11
0
0.5
1
1.5
2
92. Ableitung von Umkehrfunktionen
[10 Punkte]
Zeigen Sie folgende Gleichungen:
(i)
d
1
arctan x =
dx
1 + x2
√
(
)
(ii) arcsinh x := sinh−1 x = ln x + 1 + x2
Lösung:
Ganz allgemein gilt
d −1
1
f (x) = ′ ( −1 ) .
dx
f f (x)
(i) Die Ableitung des Tangens berehcnet sich zu
d
d sin x
1
1
sin2 x
tan x =
= cos x ·
+ sin x · (−1) · (− sin x) ·
=
1
+
dx
dx cos x
cos x
cos2 x
cos2 x
2
= 1 + tan x.
[1]
Daher erhalten wir
d
[1]
arctan x =
dx
d
dx
1
1
1
(
)=
.
(
)=
2
1
+
x2
1 + tan arctan x
tan arctan x
[1]
(ii) Zwei stetige Funktionen f, g : D ⊂ R −→ R sind genau dann gleich, wenn an einem Punkt
x0 ∈ D gilt f (x0 ) = g(x0 ) sowie auf ganz D auch f ′ = g ′ gilt [1]. Sei beispielsweise x0 = 0.
Dann folgt aus
(
)
sinh 0 = 12 e0 − e0 = 0
auch arcsinh 0 = 0 [1]. Die rechte Seite gibt auch 0, denn
√
(
)
ln 0 + 1 + 0 = ln 1 = 0.
[1]
Die Ableitung der linken Seite
d
arcsinh x =
dx
d
dx
1
1
1
[1]
∗
(
)=
√
(
) =
(
)
cosh arcsinh x
sinh arcsinh x
1 + sinh2 arcsinhx
1
=√
1 + x2
[1]
stimmt mit der Ableitung der rechten Seite
√
x
√
) [1] 1 + √1+x2
d (
x
+
1 + x2
1
1
√
√
√
ln x + 1 + x2 =
=
‘= √
[1]
dx
x + 1 + x2
x + 1 + x2 1 + x2
1 + x2
√
(
)
überein. Damit ist arcsinh x = ln x + 1 + x2 . Im mit ∗ markierten Schritt ist 1 + sinh2 x =
cosh2 x benutzt worden.
12