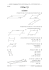משמעות גיאומטרית של דטרמיננטות = u. נסמן זויית ביניהם ב־ α. ניקח שני וקט

משמעות גיאומטרית של דטרמיננטות = u. נסמן זויית ביניהם ב־ α. ניקח שני וקט

‫אלכס גולדוורד ולביא קרפ‬
‫אלגברה ליניארית‬
‫משמעות גיאומטרית של דטרמיננטות‬
‫‪ ‬‬
‫‪ ‬‬
‫‪x1‬‬
‫‪y1‬‬
‫ניקח שני וקטורים ‪ .u =   , v =  ‬נסמן זויית ביניהם ב־ ‪.α‬‬
‫‪x2‬‬
‫‪y2‬‬
‫נחשב שטח של מקבילית ‪ S‬שנוצרת ע״י הווקטורים האלה‪.‬‬
‫‪u‬‬
‫‪v‬‬
‫נשתמש במכפלה סקלרית ‪ u · v = |u||v| cos α = x1 y1 + x2 y2‬ובנוסחה לשטח של מקבילית‪.‬‬
‫‪S = |u||v| sin α‬‬
‫‪2‬‬
‫= )‪S 2 = |u|2 |v|2 sin2 α = |u|2 |v|2 (1 − cos2 α) = |u|2 |v|2 − (|u||v| cos α‬‬
‫‬
‫‬
‫‪2‬‬
‫= ) ‪x21 + x22 y12 + y22 − (x1 y1 + x2 y2‬‬
‫= ‪x21 y12 + x21 y22 + x22 y12 + x22 y22 − x21 y12 − 2x1 y1 x2 y2 − x22 y22‬‬
‫‪2‬‬
‫) ‪x21 y22 + x22 y12 − 2x1 y1 x2 y2 = (x1 y2 − x2 y1‬‬
‫מסקנה‪.S = |x1 y2 − x2 y1 | :‬‬
‫ניתן לקבל את הנוסחה הנ״ל בדרך גיאומטרית ללא עזרה של מכפלה סקלרית‪ .‬לשם כך נכניס את המקבילית‬
‫שלנו למערכת צירים כך שהמוצא משוטף של הווקטורים ‪ u, v‬יהיה בראשית הצירים‪.‬‬
‫אז‪,‬‬
‫) ‪SOABD = SOEBF − 2(SOEA + SAEB‬‬
‫‪SOEBF = (x1 + y1 ) (x2 + y2 ) = x1 x2 + x1 y2 + x2 y1 + y1 y2‬‬
‫‪2SOEA = x2 (x1 + y1 ) = x1 x2 + x2 y1‬‬
‫‪2SAEB = y1 (x2 + y2 ) = x2 y1 + y1 y2‬‬
‫‪SOABD = x1 y2 − x2 y1‬‬
‫כמובן‪ ,‬מה שנעשה נכון רק לגבי המצב המצוייר ועל מנת להשלים את ההוכחה יש לעבור על כל המצבים‬
‫האפשריים‪.‬‬
‫‪1‬‬