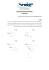תרגיל בית מספר 1#
Transcription
תרגיל בית מספר 1#
אוניברסיטת תל אביב -בית הספר למדעי המחשב מבוא מורחב למדעי המחשב ,אביב 3102 תרגיל בית מספר - 4להגשה עד 6במאי בשעה 325:: קיראו בעיון את הנחיות העבודה וההגשה המופיעות באתר הקורס ,תחת התיקיה .assignmentsחריגה מההנחיות תגרור ירידת ציון /פסילת התרגיל. הנחיות ספציפיות לתרגיל זה: תשובות לשאלות 2 ,1א' 4 ,3 ,א' 5 ,יש לממש בקובץ השלד ( )skeleton.pyהמצורף לתרגיל זה .אין לצרף לקובץ ה py-את הקוד ששימש לפתרון יתר השאלות .לא לשכוח לשנות את שם הקובץ למספר ת"ז שלכם לפני ההגשה ,אך להשאיר את הסיומת .py שימו לב שבקובץ השלד יש קוד שמבצע בדיקות של כמה מקרים פשוטים (חלק בעזרת assertוחלק בעזרת - doctestלפרטים נוספים על .)doctestהיעזרו בקוד זה כדי לוודא נכונות הפלטים שלכם עבור אותם מקרים .פתרונות שלא עובדים נכון במקרים פשוטים אלו לא יתקבלו .כמובן ,על הקוד שלכם להיות נכון לכל קלט תקין ,ולא רק למקרים שבדוגמאות .אסור לשנות את כותרות הפונקציות שעליכם לממש בקובץ השלד. תשובות לכל שאר השאלות יוגשו בקובץ docx ,docאו pdfיחיד. בסה"כ מגישים שני קבצים בלבד .עבור סטודנט שמספר ת"ז שלו הוא 012345678הקבצים שיש להגיש הם ( 012345678.docxאו .docאו ).pdfו.012345678.py - הקפידו לענות על כל מה שנשאלתם. במסמך התשובות ,תנו תשובות קולעות וברורות ,כל תשובה באורך 4שורות לכל היותר בפונט בגודל .12מטרת הגבלת אורך התשובה היא כפולה: .1על מנת שנוכל לבדוק את התרגילים שלכם בזמן סביר. .2כדי להרגיל אתכם להבעת טיעונים באופן מתומצת ויעיל ,ללא פרטים חסרים מצד אחד אך ללא עודף בלתי הכרחי מצד שני .זוהי פרקטיקה חשובה במדעי המחשב. עמ' 1מתוך 7 CC BY-NC-SA 3.0 אוניברסיטת תל אביב -בית הספר למדעי המחשב מבוא מורחב למדעי המחשב ,אביב 3102 שאלה 0 עליכם לממש מחלקה בשם ( Vectorוקטור) אשר מתארת נקודה במרחב תלת-ממדי .R3וקטור מיוצג ע"י מרחקו משלושת הצירים – – X, Y, Zאשר מתארים את מיקום הוקטור במרחב .שלושת מרחקים אלו הם משתנים פנימיים של המחלקה וקטור .המחלקה תהיה ,immutableכלומר ,לאחר יצירת מופע חדש של וקטור המתודות של המחלקה לעולם לא ישנו את המשתנים הפנימיים שלו ,אלא יחזירו מופע חדש של המחלקה. בקובץ התרגיל כבר מתוארת המחלקה ועליכם לממש את המתודות שלה .במתודות שמקבלות וקטור נוסף כמשתנה (למשל ,מתודת __ )__addיש צורך לבדוק את הטיפוס של המשתנה הנוסף כפי שהודגם בתרגול. לתשומת לבכם ,אמנם בשאלה זו מספר רב של סעיפים ,אך את רוב המתודות ניתן לממש בשורת קוד בודדת. לבדיקה עצמית 5בתיעוד כל פונקציה כתוב טסט פשוט ,שמאפשר לכם לבדוק את נכונות המימוש שלכם לפונקציה .הבדיקה היא באמצעות .doctest א. ממשו את הבנאי __ .__initהבנאי יקבל את מרחק הוקטור משלושת הצירים x,y,zכשלושה מספרים וישמור אותם במשתנים פנימיים מטיפוס .floatלא ייתנו ערכי ברירת-מחדל למשתני הבנאי. דוגמא: )>>> u = Vector(1,0,2 ב. ממשו את המתודה .to_tupleהמתודה אינה מקבלת ארגומנטים (מלבד )selfומחזירה tuple באורך 3ובו המרחק של הוקטור מציר ה ,X-ציר ה Y -וציר ה ,Z-לפי הסדר הזה .שימו לב שהמתודה __ __reprכבר ממומשת אך היא נעזרת במתודה to_tupleלפעולתה. דוגמא: )(>>> u.to_tuple )(1.0, 0.0, 2.0 ג. ממשו את המתודה __ :__eqמתודה זו בודקת האם שני וקטורים שווים .המתודה מקבלת בנוסף ל self-וקטור נוסף ,other ,ומחזירה Trueאך ורק אם שני הוקטורים שווים ואחרת מחזירה המתודה .False דוגמא: )>>> u == Vector(1,1,1 False )>>> u == Vector(1,0,2 True עמ' 2מתוך 7 CC BY-NC-SA 3.0 אוניברסיטת תל אביב -בית הספר למדעי המחשב מבוא מורחב למדעי המחשב ,אביב 3102 ד. ממשו את אופרטור החיבור ע"י מימוש המתודה __ :__addהמתודה מקבלת שני וקטורים ( self, )otherומחזירה וקטור חדש שהוא סכום הוקטורים מהקלט .שימו לב שחיבור וקטורים הוא לפי איברים – למשל ,המרחק של הוקטור החדש מציר ה X-הוא סכום מרחקי וקטורי הקלט מציר ה.X- דוגמא: )>>> u + Vector(1,-3,4 )(2.0, -3.0, 6.0 >>> u )(1.0, 0.0, 2.0 ה. ממשו את אופרטור החיסור ע"י מימוש המתודות __ __negו :__sub__-מכיוון שחיסור הוא חיבור בנגדי ,ממשו תחילה את המתודה __ __negשמחזירה את הוקטור השלילי לוקטור זה, כלומר ,הוקטור שהסכום איתו ייתן ( .)0,0,0לאחר מכן ממשו את המתודה __ __subבעזרת המתודות __ __negו.__add__- דוגמא: >>> -u )(-1.0, 0.0, -2.0 )>>> u – Vector(4,3,2 )(-3.0, -3.0, 0.0 ו. ממשו את אופרטור הכפל בסקלר ע"י מימוש המתודה __ :__mulהמתודה תקבל מספר שהוא סקלר ותחזיר וקטור חדש שהוא המכפלה של הוקטור בסקלר – כל אחד מערכי הוקטור מוכפל בסקלר .שימו לב ,עליכם לוודא כי המשתנה בקלט הינו אכן מספר – intאו floatע"י שימוש בפונקציה ,isinstanceכפי שהודגם בתרגול. דוגמא: >> u * 2 )(2.0, 0.0, 4.0 >>> u * u AssertionError: ז. ממשו את המתודה innerשמקבלת וקטור נוסף כמשתנה ומחשבת את המכפלה הפנימית .חישוב המכפלה הפנימית של שני וקטורים מחזיר סקלר ( )floatלפי הנוסחה הבאה ,עבור המכפלה הפנימית של הוקטורים :u, v עמ' 3מתוך 7 CC BY-NC-SA 3.0 אוניברסיטת תל אביב -בית הספר למדעי המחשב מבוא מורחב למדעי המחשב ,אביב 3102 דוגמא: ))>>> u.inner(Vector(1,2,4 9.0 ))>>> u.inner(Vector(-2,3,1 0.0 ח. ממשו את המתודה normאשר מחשבת את הנורמה של וקטור :ממשו את המתודה בעזרת המתודה innerוהפונקציה sqrtמהמודול .mathהמתודה תחזיר את השורש של המכפלה הפנימית של הוקטור עם עצמו ,ולא תקבל ארגומנטים (מעבר ל.)self- דוגמא: )(>>> u.norm 2.2360679774997898 )(>>> Vector(1,2,2).norm 3.0 שאלה 3 א .כתבו פונקציה ) k_select(lst, kשמקבלת רשימת מספרים lstבאורך nומספר שלם 0≤k<n ומחזירה את המספר ה k+1-בגודלו ברשימה – הוא המספר שיש בדיוק kמספרים שקטנים ממנו ממש. על המימוש להיות רקורסיבי ואין להשתמש בפונקציות sortedאו .sortניתן להניח שהמספרים בקלט יחודיים ,כלומר ,שאין מספרים שחוזרים על עצמם .אם kקטן מדי או גדול מדי יש לזרוק שגיאה באמצעות .assert הנחיה :המימוש יתבצע באופן דומה למימוש Slowsortשהודגם בתרגול: עבור רשימה באורך nיש לבחור כציר ( )pivotאת האיבר הראשון ברשימה יש לחלק את הרשימה לשתי תתי-רשימות – oהאיברים שקטנים ממש מהציר ברשימה אחת – "קטנים" oהאיברים שגדולים ממש מהציר ברשימה שניה – "גדולים" יש לבדוק ,לפי אורכי "קטנים" ו"גדולים" ולפי kהאם האיבר ה k-נמצא ברשימה "קטנים", "גדולים" או שאולי הוא איבר הציר. אם הוא באחת הרשימות ,יש למצוא אותו ע"י קריאה רקורסיבית על הרשימה המתאימה. שימו לב שכל קריאה ל k_select-מייצרת קריאה רקורסיבית אחת לכל היותר. דוגמאות הרצה: )>>> k_select([5,4,7,6,8,2,3], 2 4 )>>> k_select([5,4,7,6,8,2,3], 5 7 )>>> k_select([5,4,7,6,8,2,3], 0 2 ב .בהינתן קלט תקין ,מצאו מה סיבוכיות הזמן של האלגוריתם שמומש בסעיף א' בתלות באורך הקלט עבור המקרה הטוב ביותר ,ונמקו בקצרה .ציינו גם מהו הקלט שמתאים למקרה זה. עמ' 4מתוך 7 CC BY-NC-SA 3.0 אוניברסיטת תל אביב -בית הספר למדעי המחשב מבוא מורחב למדעי המחשב ,אביב 3102 ג. ד. בהינתן קלט תקין ,מצאו מה סיבוכיות הזמן של האלגוריתם שמומש בסעיף א' בתלות באורך בקלט עבור המקרה הגרוע ביותר ,ונמקו בקצרה .ציינו גם מהו הקלט שמתאים למקרה זה. השוו בעזרת הפונקציה clockבמודול timeאת זמן הריצה של הפונקציה שממשתם בסעיף א' לעומת זמן הריצה של מימוש בעזרת :sorted ]>>> sorted(lst)[k לצורך ההשוואה ,השתמשו ברשימת המספרים מ 1-עד ,nמסודרים אקראית: >>> import random ])>>> lst = [i for i in range(1, 100 (>>> random.shuffle(lst מהי מסקנתכם? האם יש הבדל בתשובתכם עבור רשימה באורך 10ועבור רשימה באורך ?1,000,000 שאלה 2 בשאלה זו עליכם לכתוב את הפונקציה הרקורסיבית ).choose_sets(lst, k הפונקציה מקבלת רשימה של איברים lstומספר שלם ,kומחזירה רשימה המכילה את כל הרשימות השונות באורך kשניתן ליצור מאיברי ,lstללא חשיבות לסדר האיברים .כלומר ,את כל האפשרויות לבחור kאיברים מתוך הרשימה ,lstללא חשיבות לסדר הבחירה .ניתן להניח שאיברי הרשימה lst יחודיים ,כלומר ,שאין איברים שחוזרים על עצמם. שימו לב: כאן אנו מעונינים ממש באפשרויות השונות לבחור kאיברים ,ולא רק בכמה אפשרויות כאלו יש. הערך המוחזר הוא רשימה של רשימות ,וכל אחת מהרשימות הללו הינה בדיוק באורך .k סדר הרשימות בתוך רשימת העל אינו חשוב. כאמור ,הסדר הפנימי בכל תת-רשימה אינו חשוב ,ואסור שיהיו כפילויות .לדוגמא ,הרשימה ] [1,2,3שקולה לרשימה ].[3,2,1 הנחיה: ניתן לקבל את כל התת-רשימות באורך kע"י איסוף של כל תת-הרשימות שמכילות את האיבר הראשון ברשימה וכל תת-הרשימות שאינן מכילות את האיבר הראשון ברשימה. שימו לב לערך ההחזרה של מקרה הבסיס (תנאי ההתחלה). ניתן להניח כי הקלט תקין – אין חזרות של איברים ברשימת הקלט ו 0≤k≤n-הוא מספר שלם, כאשר nהוא אורך הרשימה .lst דוגמאות הרצה: (>>> choose_sets([1,2,3, 4], 0 [[]] (>>> choose_sets([1,2,3, 4], 2 [[]]4 ,3[ ,]2 ,4[ ,]2 ,3[ ,]1 ,4[ ,]1 ,3[ ,]1 ,2 (>>> choose_sets([1,2,3, 4], 4 עמ' 5מתוך 7 CC BY-NC-SA 3.0 אוניברסיטת תל אביב -בית הספר למדעי המחשב מבוא מורחב למדעי המחשב ,אביב 3102 [[]]4 ,3 ,2 ,1 (>>> choose_sets(['a','b','c','d','e'], 4 ]]'[['d', 'c', 'b', 'a'], ['e', 'c', 'b', 'a'], ['d', 'e', 'b', 'a'], ['c', 'd', 'e', 'a'], ['b', 'c','d', 'e שאלה 4 א. בשאלה זו תממשו את אלגוריתם המיון Selection sortבאופן רקורסיבי ,בפונקציה ).selection_sort(lst הנחיה: בהינתן קלט של רשימה ,הפונקציה מוצאת את האיבר המינימלי ברשימה. כעת ניתן לקרוא שוב לפונקציה על אותה רשימה ללא האיבר המינימלי הנ"ל ,ובכך מקטינים את הרשימה שהפונקציה מקבלת באיבר אחד ואורך הקלט משתנה מ n-ל .n-1-זהו הפירוק של הרקורסיה. תנאי העצירה הוא רשימה בגודל .1 אין צורך לבדוק את טיפוס הקלט וניתן להניח שהוא מטיפוס .list דוגמא: )]>>> selection_sort([5, 4, 6, 3 ][3, 4, 5, 6 ])>>> lst = [random.randint(1, 55) for i in range(100 (>>> selection_sort(lst) == sorted(lst True ב. ג. ד. מה סיבוכיות הזמן של Selection sortבמקרה הגרוע ביותר? הסבירו בקצרה. האם יש הבדל בין הסיבוכיות במקרה הגרוע ביותר לבין הסיבוכיות במקרה הטוב ביותר? מה עומק הרקורסיה עבור רשימה בגודל ?n שאלה : עץ בינארי ( )binary treeהינו מבנה נתונים נפוץ במדעי המחשב .עץ בינארי מורכב מקודקודים ()nodes המכילים ערכים .לכל קודקוד לכל היותר שני קודקודים בנים :בן ימני ובן שמאלי .החיבור בין קודקוד לבנו נקרא קשת ) .(edgeהקודקוד שבראש העץ נקרא שורש ( .)rootהקודקודים בתחתית העץ (אשר להם אין קודקודים בנים) נקראים עלים ( .)leavesלשם המחשה ,מובא עץ בינארי לדוגמא (הציור לקוח מתוך האתר :)http://www.squidoo.com/computer-trees עמ' 6מתוך 7 CC BY-NC-SA 3.0 אוניברסיטת תל אביב -בית הספר למדעי המחשב מבוא מורחב למדעי המחשב ,אביב 3102 עץ בינארי יכול להכיל קודקוד אחד (שהינו גם שורש העץ וגם עלה בו זמנית) ,או אפילו להיות עץ ריק (אינו מכיל קודקודים כלל). בשאלה זו נחשב את גובהו של עץ בינארי נתון. נגדיר תחילה מחלקה המייצגת קודקוד בעץ .כל קודקוד מכיל שלושה שדות: .1ערך הקודקוד .2הבן הימני של הקודקוד (או Noneאם לא קיים) .3הבן השמאלי של הקודקוד (או Noneאם לא קיים). הבנאי (__ )__initשל המחלקה נתון בקובץ הקוד המצורף. א .הוסיפו למחלקה Nodeמתודה בשם add_childהמוסיפה בן לקודקוד קיים .המתודה מקבלת שני ארגומנטים )1( :הצד שאליו מתווסף הבן ו )2(-הבן שיש להוסיף (אובייקט מטיפוס Nodeבעצמו), ומעדכנת את הקודקוד הקיים .הצד יצוין על ידי האותיות (מחרוזות באורך L )1או ( Rשמאל וימין, בהתאמה) בלבד .אין צורך לבדוק האם כבר קיים בן בצד המבוקש. לאחר הוספת המתודה ,אם נריץ את הפונקציה build_diagramהנתונה בקובץ הקוד ,נקבל את העץ המתואר בתרשים הנ"ל .אפשר להניח שפעולת ההוספה אינה יוצרת מעגלים בעץ (אין צורך לבדוק זאת). ב .הוסיפו מתודה בשם ) is_leaf(selfהמחזירה Trueאם הקודקוד הינו עלה (קצה העץ) ,ואחרת מחזירה .False ג .כתבו פונקציה רקורסיבית בשם tree_heightהמקבלת עץ ומחשבת את "גובה" העץ .גובה של עץ מוגדר כמספר הקשתות בענף הארוך ביותר (למשל ,עבור העץ שדוגמה התשובה היא .)2ענף הוא מסלול של קודקודים שמוביל משורש לעלה. הפונקציה אינה שייכת למחלקה .Node עץ מצוין על ידי שורשו ,ועל כן הפונקציה מקבלת למעשה אובייקט מסוג Nodeשהוא שורש העץ או Noneבמקרה של עץ ריק. סוף. עמ' 7מתוך 7 CC BY-NC-SA 3.0