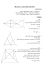מדריך למורה – טענות, הנמקות והסקת מסקנות על

Transcription

‫על טענות‪ ,‬הנמקות והסקת מסקנות – מדריך למורה‬
‫מבנה כללי של המבוא‬
‫פרק זה הינו פרק מבוא לפרק הגיאומטריה האוקלידית ומטרתו לתת מוטיבציה לעיסוק במבנה הדדוקטיבי של‬
‫גיאומטריה‪ .‬בלימודי הגיאומטריה בכיתה ז וגם בחלק מההוראה בכיתה ח‪ ,‬ניסחנו טענות והצדקנו אותן על‬
‫סמך חקירה ובדיקה של מקרים פרטיים ועל סמך דדוקציות מקומיות או על ידי הוכחות בעלות שלב אחד‪.‬‬
‫לעתים‪ ,‬הדוגמאות שעסקנו בהן היו דוגמאות גנריות (כמו למשל‪ ,‬בנושא של משפט פיתגורס)‪.‬‬
‫מטרת המבוא היא להע לות את הצורך בהוכחות כלליות על ידי המחשה של הבעייתיות של הסקת מסקנות על‬
‫סמך מקרים פרטיים ויחד עם זאת להראות שבתחומים מתמטיים אחרים (כמו אלגברה) כבר למדנו כלים‬
‫שמאפשרים לקבוע נכונות של טענה מסוימת באופן כללי‪.‬‬
‫אנו ערים לכך שבכיתות ח רבות כבר החלו בהוכחות דדוקטיביות מסודרות‪ ,‬עם זאת‪ ,‬אנו חושבים שפעילות זו‬
‫מתאימה כפעילות לפתיחת השנה‪ ,‬כיוון שהיא מחדדת שנית את הצורך בהוכחות פורמליות‪ ,‬היא פעילות מהנה‬
‫ומעוררת עניין‪ .‬היא מדגישה את המטרה המרכזית של הוראת הגאומטריה בכיתה ט והיא פיתוח מיומנויות‬
‫ההוכחה בגאומטריה‪ ,‬הכוללות מיומנויות היסק ומיומנויות כתיבה‪.‬‬
‫הפרק נפתח בשתי פעילויות בהן ההכללה ברורה כביכול‪ ,‬אך למעשה ההכללה שמסתמנת על סמך מספר‬
‫מצומצם של מקרים פרטיים במקרה אחד היא שגויה ובמקרה שני היא נכונה‪.‬‬
‫המטרה של שתי הפעילויות יחד היא לעורר אצל התלמידים קונפליקט וצורך ביישובו באמצעות כלים מתמטיים‬
‫חזקים יותר מאשר בחינת מספר דוגמאות‪.‬‬
‫להלן תיאור הפעילויות והדגשים בהן‪.‬‬
‫פעילות ‪ – 1‬חקירה‪ :‬מספר‬
‫הנקודות על המעגל ומספר‬
‫האזורים הנוצרים בעיגול –‬
‫עמ' ‪197‬‬
‫הפעילות עוסקת במציאת מספר‬
‫אזורים שנוצרים מחולקת מעגל‬
‫לאזורים על‪-‬ידי מיתרים‪ .‬למעשה‬
‫מדובר במספר אזורים מקסימאלי‬
‫שמתקבל לאחר העברת ‪n‬‬
‫מיתרים‪ .‬מספר זה מתקבל כאשר‬
‫אין שלושה מיתרים שעוברים דרך‬
‫נקודה אחת‪.‬‬
‫למשל‪ ,‬אם בסרטוט המעגל עם ‪6‬‬
‫נקודות‪ ,‬המיתר ‪ AD‬היה עובר דרך‬
‫נקודת החיתוך של המיתרים ‪CF‬‬
‫ו‪ EB -‬מספר האזורים היה קטן‬
‫יותר‪.‬‬
‫נקודה זו מתחילה להיות רלוונטית‬
‫רק כאשר מספר הנקודות על היקף המעגל הן ‪ 6‬ומעלה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪1‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר כתום‪ ,‬חלק א‬
‫מספר הנקודות על המעגל‬
‫(‪)n‬‬
‫מספר האזורים הנוצרים בעיגול‬
‫‪2‬‬
‫‪3‬‬
‫‪2‬‬
‫‪4‬‬
‫עבור ‪ 5‬נקודות על היקף המעגל או פחות‪ ,‬מסתמנת החוקיות‪:‬‬
‫‪4‬‬
‫‪5‬‬
‫‪6‬‬
‫‪8‬‬
‫‪16‬‬
‫‪31‬‬
‫‪n1‬‬
‫‪ . 2‬אולם חוקיות זו נשברת עבור המקרה של‬
‫‪ .n=6‬עבור ‪ 6‬נקודות על היקף המעגל‪ ,‬המספר המקסימאלי של אזורים הוא ‪ .31‬למעשה החוקיות‬
‫‪n1‬‬
‫‪2‬‬
‫אינה מתקיימת גם בהמשך‪ ,‬אולם קיימת חוקיות אחרת‪ ,‬שהכרתה היא מעבר לחומר לימוד של תכנית‬
‫הלימודים לחט"ב‪.‬‬
‫בפעילות ‪ 2‬ראינו כי על‪-‬מנת להראות שהשערה מסוימת נכונה בכל המקרים‪ ,‬יש להוכיח זאת באופן כללי‪,‬‬
‫שמכסה את כל המקרים‪ .‬על מנת להפריך השערה‪ ,‬כלומר להראות שהיא אינה נכונה בכל המקרים‪ ,‬מספיק‬
‫לתת דוגמה נגדית אחת‪ ,‬כלומר‪ ,‬דוגמה שמקיימת את תנאי הבעיה אבל לא את המסקנה (כפי שהראיתם‬
‫בפעילות ‪.)1‬‬
‫פעילות ‪ – 2‬חקירה‪ :‬מספר אלכסונים במצולע – עמ' ‪198‬‬
‫הפעילות עוסקת בחקירת מספר אלכסונים במצולע‪ .‬בפעילות זו ההכללה שהתלמידים ימצאו בעקבות מספר‬
‫דוגמאות נכונה‪.‬‬
‫להלן הטבלה המתקבלת לאחר הפתרון‪:‬‬
‫‪ - n‬מס'‬
‫הצלעות במצולע‬
‫מס' הקדקודים‬
‫במצולע‬
‫מס' האלכסונים היוצאים‬
‫מכל קדקוד‬
‫סה"כ מספר‬
‫האלכסונים‬
‫סרטוט‬
‫‪4‬‬
‫‪4‬‬
‫‪1‬‬
‫‪2‬‬
‫‪5‬‬
‫‪5‬‬
‫‪2‬‬
‫‪5‬‬
‫‪6‬‬
‫‪6‬‬
‫‪3‬‬
‫‪9‬‬
‫‪7‬‬
‫‪7‬‬
‫‪4‬‬
‫‪14‬‬
‫‪N‬‬
‫‪n‬‬
‫‪n-3‬‬
‫)‪n(n- 3‬‬
‫‪2‬‬
‫____________________________________________________________________________________________________________‬
‫‪2‬‬
‫ב‪ .‬מספר הקדקודים במצולע בעל ‪ n‬צלעות גם הוא ‪n‬‬
‫מספר האלכסונים היוצאים מכל קדקוד הוא ‪.n-3‬‬
‫הסבר לחישוב מספר האלכסונים היוצאים מכל קדקוד‪ :‬מכל קדקוד יוצאים אלכסונים לכל הקדקודים‬
‫האחרים מלבד לשני הקדקודים הסמוכים לו והוא עצמו‪ ,‬לכן מורידים ‪ 3‬מסך כל הקדקודים‪.‬‬
‫ג‪ .‬הביטוי המתאר את מספר האלכסונים במצולע בעל ‪ n‬צלעות )‪n(n- 3‬‬
‫‪2‬‬
‫‪.‬‬
‫הסבר לחישוב מספר האלכסונים במצולע בעל ‪ n‬צלעות‪ :‬מכל קדקוד יוצאים ‪ n-3‬אלכסונים וכל אחד‬
‫מהם משותף לשני קדקודים‪ .‬כיוון שספרנו כל אלכסון פעמיים יש לחלק את התוצאה ב‪.2 -‬‬
‫ד‪ .‬הביטוי נכון עבור כל מצולע‪ .‬במשולש )‪ (n=3‬אין אלכסונים ואילו במתומן‪ ,‬מכל קדקוד יוצאים ‪ 5‬אלכסונים‪,‬‬
‫לכן סה"כ ‪ 20‬אלכסונים‪.‬‬
‫תרגילים – עמ' ‪198‬‬
‫עמ' ‪.1 198‬‬
‫‪ 13‬הוא מספר ראשוני‪ .‬אם נהפוך את סדר הספרות שלו נקבל את המספר ‪ ,31‬שגם הוא מספר ראשוני‪.‬‬
‫באופן דומה‪ :‬גם ‪ 17‬וגם ‪ 71‬שניהם מספרים ראשוניים‪ .‬האם תופעה זו נכונה לכל המספרים הראשוניים?‬
‫הסבירו כיצד קבעתם זאת‪.‬‬
‫תשובה‪ :‬לא‪ ,‬להלן דוגמה סותרת‪ 23 :‬ראשוני‪ 32 ,‬זוגי‬
‫‪.2‬‬
‫‪2‬‬
‫נורית הבחינה בתופעה מעניינת‪ :‬אם מציבים מספרים טבעיים בביטוי האלגברי‪ ,n + n + 17 :‬מתקבלים‬
‫מספרים ראשוניים‪ .‬היא העלתה השערה שתופעה זו נכונה לכל מספר‬
‫‪2‬‬
‫‪1 + 1 + 17 = 19‬‬
‫טבעי‪.‬‬
‫‪2‬‬
‫א‪ .‬בדקו את נכונות ההשערה של נורית עבור חמישה מספרים‬
‫‪2 + 2 + 17 = 23‬‬
‫טבעיים‪ .‬כמה קיבלתם?‬
‫‪n‬‬
‫הראשוני‬
‫‪1‬‬
‫‪19‬‬
‫‪2‬‬
‫‪23‬‬
‫‪3‬‬
‫‪29‬‬
‫‪4‬‬
‫‪37‬‬
‫‪5‬‬
‫‪47‬‬
‫‪6‬‬
‫‪59‬‬
‫‪7‬‬
‫‪73‬‬
‫‪8‬‬
‫‪89‬‬
‫‪9‬‬
‫‪107‬‬
‫‪10‬‬
‫‪127‬‬
‫האם זה מספיק כדי להוכיח את ההשערה? לא‬
‫ב‪.‬‬
‫ארז אומר שאם נציב ‪ n = 17‬נקבל מספר שאינו ראשוני (מספר פריק)‪ .‬האם ארז צודק?‬
‫‪2‬‬
‫כן‪ 19*17=)17+1+1(17=17 +17+17 ,‬מספר המתחלק ב‪ 17-‬וב‪19-‬‬
‫ג‪.‬‬
‫האם דבריו של ארז מוכיחים את ההשערה של נורית?‬
‫האם דבריו של ארז מפריכים את ההשערה של נורית? הסבירו‪.‬‬
‫מפריכים את ההשערה של נורית‪ ,‬כי זו דוגמה שמקיימת את התנאים אך לא את המסקנה‪.‬‬
‫תרגילים נוספים‬
‫בנושא באתר‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪3‬‬
‫החלטנו לשלב באתר הספר ובמדריך למורה מספר תרגילים מתחום האלגברה הממחישים את הרעיון שהובא‬
‫בפעילויות ‪ 1‬ו‪ 2-‬בתחום הגאומטריה‪ ,‬שמספר דוגמאות לעתים מעיד על הכללה נכונה‪ ,‬אך לא תמיד‪.‬‬
‫בתרגילים מוצגים מקרים בהם ההכללה נכונה ולתלמידים יש כלים אלגבריים להוכיח זאת ותרגילים בהם‬
‫הכללה איננה נכונה וישנה הכוונה בתרגיל או צפייה שהתלמידים יאתרו דוגמה נגדית מתאימה להפריך את‬
‫ההשערה‪.‬‬
‫תרגילים אלו הם רשות ואינם חלק מתכנית הלימודים‪.‬‬
‫לפניכם שישה תרגילים נוספים‪ ,‬שאינם מופיעים בספר לתלמיד‪ .‬להלן הפתרונות של תרגילים ובעמ' ‪8 - 7‬‬
‫במדריך‪ ,‬יש דף עבודה לתלמיד לשכפול‪.‬‬
‫תרגילים נוספים שאינם מופיעים בספר לתלמידים‬
‫‪ .1‬התבוננו בסדרת תרגילי הכפל שבמסגרת‪.‬‬
‫‪12 ∙ 11 = 132‬‬
‫‪12 ∙ 11 = 132‬‬
‫‪26 ∙ 11 = 286‬‬
‫‪26 ∙ 11 = 286‬‬
‫התרגילים האחרונים‪ .‬הקיפו בעיפרון צבעוני את‬
‫‪32 ∙ 11 = 352‬‬
‫‪32 ∙ 11 = 352‬‬
‫הספרה הראשונה ואת הספרה האחרונה בכל‬
‫‪45 ∙ 11 = 495‬‬
‫‪45 ∙ 11 = 495‬‬
‫מכפלה‪.‬‬
‫= ‪62 ∙ 11‬‬
‫‪62 ∙ 11 = 682‬‬
‫האם הבחנתם בחוקיות כלשהי? נסחו אותה‬
‫= ‪81 ∙ 11‬‬
‫‪81 ∙ 11 = 891‬‬
‫א‪ .‬העתיקו את התרגילים ורשמו תוצאות לשני‬
‫במילים‪.‬‬
‫התרגיל‬
‫ב‪ .‬ודאי שמתם לב שהספרות שסימנתם בצבע הן‬
‫הפתרון‬
‫הספרות של המספר שכפלתם ב‪ 11 -‬והספרה האמצעית היא סכומן‪.‬‬
‫שערו‪ :‬האם החוקיות הזאת מתקיימת רק עבור התרגילים הרשומים בתוך המסגרת?‬
‫ג‪.‬‬
‫שערו‪ :‬האם החוקיות הזאת מתקיימת לכל מכפלה של מספר דו‪-‬ספרתי ב‪?11-‬‬
‫ד‪ .‬הציעו תרגילי כפל ב‪ 11 -‬של מספרים דו‪-‬ספרתיים נוספים ובדקו את השערותיכם‪.‬‬
‫ה‪ .‬כמה מקרים‪ ,‬לדעתכם‪ ,‬מספיק לבדוק על מנת לדעת אם השערותיכם נכונות או לא?‬
‫החוקיות שמסתמנת מבדיקת המקרים הפרטיים היא שכאשר כופלים מספר דו‪-‬ספרתי ב‪ ,11 -‬מתקבל מספר‬
‫תלת ספרתי שבו ספרת המאות וספרת האחדות זהות לספרות של המספר‬
‫הדו‪-‬ספרתי והספרה האמצעית היא סכומן‪.‬‬
‫חוקיות זו אינה נכונה לכל מספר דו‪-‬ספרתי‪ .‬בתור דוגמה נגדית מספיק לקחת מספר דו‪-‬ספרתי שסכום ספרותיו‬
‫גדול מ‪ .9-‬למשל‪ ,75 ,38 ,46 ,‬וכדומה‪.‬‬
‫בתרגיל זה מתקבלת חוקיות שנכונה עבור מספר מקרים בודדים‪ ,‬אך היא אינה נכונה בכל המקרים‪ .‬במטרה‬
‫להפריך את ההשערה הראשונית הצגנו דוגמאות נגדיות (דוגמאות סותרות)‪.‬‬
‫המסקנה שעולה מתרגיל זה היא שכאשר רוצים לקבוע אם תכונה מסוימת מתקיימת בכל המקרים‪ ,‬לא די‬
‫בבדיקה של מקרים פרטיים ‪ -‬יש צורך בהוכחה כללית או אם מספר המקרים סופי‪ ,‬יש לבדוק את כולם‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪4‬‬
‫‪.2‬‬
‫=‪1+2+3‬‬
‫התבוננו בתרגילי חיבור של שלושה מספרים עוקבים‪.‬‬
‫= ‪12 + 13 + 14‬‬
‫א‪ .‬העתיקו למחברת את התרגילים ופתרו אותם‪.‬‬
‫מה משותף לכל התוצאות שקיבלתם?‬
‫ב‪ .‬האם שמתם לב שכל התוצאות שהתקבלו שוות למכפלת המספר‬
‫= )‪(-3) + (-2) + (-1‬‬
‫האמצעי ב‪ ?3 -‬האם‪ ,‬לדעתכם‪ ,‬תכונה זו מתקיימת רק עבור‬
‫ארבעת הסכומים הרשומים בתוך המסגרת?‬
‫ג‪.‬‬
‫=‪1+2+3‬‬
‫= ‪12 + 13 + 14‬‬
‫הציעו שלשות נוספות של מספרים עוקבים ובדקו האם גם עבורן‬
‫מתקיימת התכונה‪.‬‬
‫= )‪(-3) + (-2) + (-1‬‬
‫= ‪39 + 40 + 41‬‬
‫ד‪ .‬שערו‪ :‬האם התכונה שמצאתם מתקיימת לכל שלושה מספרים‬
‫עוקבים? כמה מקרים לדעתכם צריך לבדוק על מנת להסיק האם‬
‫ההשערה נכונה או שגויה? הציעו דרך להצדיק זאת ללא בדיקה של דוגמאות נוספות?‬
‫פתרון‬
‫ההשערה שעולה לאחר בדיקת מספר מקרים פרטיים בפעילות זו היא‬
‫שהסכום המתקבל בכל תרגיל שווה למכפלת המספר האמצעי ב‪.3 -‬‬
‫תכונה זו אכן מתקיימת לכל סכום של שלושה מספרים שלמים עוקבים‪.‬‬
‫‪1+2+3=6‬‬
‫‪12 + 13 + 14 = 39‬‬
‫ניתן להראות זאת באופן אלגברי‪:‬‬
‫ההשערה מתייחסת למספרים עוקבים‪.‬‬
‫‪(-3) + (-2) + (-1) = -6‬‬
‫נסמן את המספר האמצעי ב‪.n -‬‬
‫‪39 + 40 + 41 = 120‬‬
‫המספר העוקב ל‪ n-‬הוא‪.n+1 :‬‬
‫המספר הקודם ל‪ n-‬הוא‪.n-1 :‬‬
‫הביטוי אלגברי לסכום של שלושה מספרים עוקבים הוא‪:‬‬
‫(‪.)n-1) + n + (n+1‬‬
‫נפתח סוגריים ונקבל‪)n-1) + n + (n+1) = n - 1 + n + n + 1 = 3n :‬‬
‫קיבלנו‪ :‬סכום של שלושה מספרים עוקבים כלשהם שווה ל‪ ,3n -‬כלומר‪ ,‬למכפלת המספר האמצעי ב‪.3 -‬‬
‫הוכחנו שתכונה זו אכן נכונה לכל שלושה מספרים עוקבים בעזרת חוקים אלגבריים (כמו חוק החילוף וחוק‬
‫הקיבוץ)‪.‬‬
‫מסקנה‪ :‬על מנת להראות שהשערה מסוימת נכונה בכל המקרים יש להוכיח זאת בצורה לוגית‪.‬‬
‫‪4‬‬
‫‪ .3‬חשבו את ערכי החזקות של ‪ 11‬עד ‪.11‬‬
‫א‪ .‬באיזו חוקיות אתם מבחינים?‬
‫שערו האם החוקיות הזאת מתקיימת גם בחזקות גבוהות יותר‪.‬‬
‫‪5‬‬
‫‪6‬‬
‫ב‪ .‬בדקו את השערתכם עבור ‪ 11‬ו‪ .11 -‬האם החוקיות שמצאתם‬
‫נשמרת? הסבירו מדוע‪ .‬החוקיות איננה נשמרת‪ ,‬ניתן לראות בטבלה‬
‫למטה מה קורה כאשר החזקה שווה ל‪ 5 -‬או ל‪.6-‬‬
‫‪n‬‬
‫‪1‬‬
‫‪2‬‬
‫‪3‬‬
‫‪4‬‬
‫‪5‬‬
‫‪6‬‬
‫פָּ לִ ינ ְְדרֹום‪ ,‬הוא מספר‬
‫שקריאתו מימין לשמאל‬
‫ומשמאל לימין נותנת‬
‫אותו מספר‪.‬‬
‫‪11‬‬
‫‪121‬‬
‫‪1331‬‬
‫‪14641‬‬
‫‪161051‬‬
‫‪1771561‬‬
‫____________________________________________________________________________________________________________‬
‫‪5‬‬
‫‪.4‬‬
‫עבור כל אחת מהטענות שלפניכם קבעו אם היא נכונה או לא והצדיקו את קביעתכם‪.‬‬
‫א‪.‬‬
‫סכום של שני מספרים אי‪-‬זוגיים כלשהם הוא מספר‪-‬זוגי‪.‬‬
‫הטענה נכונה‪ .‬נכתוב שני מספרים אי‪-‬זוגיים כלשהם‪ 2a+1 :‬ו‪ ,2b+1 -‬נחבר ביניהם ונקבל‪:‬‬
‫)‪ (2a+1)+(2b+1)=(2a+2b)+2=2(a+b)+2= 2(a+b+1‬שהוא כפולה של ‪ 2‬ולכן בוודאות‪,‬‬
‫מספר זוגי‪.‬‬
‫ב‪ .‬אם ‪x  6‬‬
‫אז ‪ x‬הוא מספר חיובי‪ .‬לא נכון‪ ,‬דוגמה סותרת ‪x=-7, |-7|>6‬‬
‫ג‪( an  0 .‬הוא חיובי) עבור ‪ n‬זוגי ו‪ 0 -‬‬
‫‪ . a‬נכון‪ ,‬גם אם ‪ ,a<0‬העלאתו בחזקה זוגית‪ ,‬מבטלת את‬
‫שליליותו‪.‬‬
‫‪.5‬‬
‫בדקו את נכונות החישובים בסדרת התרגילים שלפניכם‪.‬‬
‫‪(1‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪2  1  1 1‬‬
‫‪2‬‬
‫‪2‬‬
‫‪4  1  1 1 ( 3‬‬
‫‪4‬‬
‫‪4‬‬
‫‪3  1  1 1 (2‬‬
‫‪3‬‬
‫‪3‬‬
‫הוסיפו שלושה תרגילים הבנויים לפי התבנית שבתרגילים‪ .‬האם הבחנתם בחוקיות כלשהי?‬
‫‪6 1  1 1‬‬
‫‪6‬‬
‫‪6‬‬
‫‪5 1  1 1‬‬
‫‪5‬‬
‫‪5‬‬
‫‪7 1  1 1‬‬
‫‪7‬‬
‫‪7‬‬
‫מצאו ביטוי אלגברי המתאר את החוקיות שמצאתם ובדקו אם היא מתקיימת לכל מספר טבעי המופיע‬
‫במכנה‪.‬‬
‫‪ a  1  1 1‬חוקיות המתקיימת לגבי כל מספר טבעי‬
‫‪a‬‬
‫‪a‬‬
‫‪ .6‬לפניכם מספר שוויונות שבהם מתקיימת חוקיות מסוימת‪.‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2 -1 =2+1‬‬
‫א‪ .‬בדקו את נכונות השוויונות במסגרת והוסיפו במחברתכם‬
‫‪3 -2 =3+2‬‬
‫שלוש דוגמאות נוספות‪.‬‬
‫‪4 -3 =4+3‬‬
‫ב‪ .‬סמנו את המספר הראשון ב‪ ,n -‬כמו בשורה האחרונה‬
‫‪….‬‬
‫ברשימה שלפניכם‪ .‬איזה ביטוי מתקבל? הוכיחו שהחוקיות‬
‫‪2‬‬
‫‪n - …. = n + ….‬‬
‫מתקיימת לכל מספר טבעי ‪.n‬‬
‫ג‪.‬‬
‫האם חוקיות זו מתקיימת גם למספרים שאינם טבעיים?‬
‫רמז‪:‬‬
‫‪2‬‬
‫)‪(n-1) =(n-1)(n-1‬‬
‫פתרון‪:‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫)‪n – (n-1) = n - n +2n-1=2n-1=n+(n-1‬‬
‫נשים לב‪ ,‬כי בפיתוח האלגברי לא התבססנו על העובדה כי ‪ n‬מספר טבעי‪ ,‬ולכן החוקיות מתקיימת גם‬
‫למספרים שאינם טבעיים‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪6‬‬
‫דף עבודה בנושא טענות ומסקנות – תרגילים נוספים‬
‫‪ .1‬התבוננו בסדרת תרגילי הכפל שבמסגרת‪.‬‬
‫א‪ .‬העתיקו את התרגילים ורשמו תוצאות לשני התרגילים האחרונים‪.‬‬
‫הקיפו בעיפרון צבעוני את הספרה הראשונה ואת הספרה‬
‫האחרונה בכל מכפלה‪.‬‬
‫האם הבחנתם בחוקיות כלשהי? נסחו אותה במילים‪.‬‬
‫ב‪ .‬ודאי שמתם לב שהספרות שסימנתם בצבע הן הספרות של‬
‫המספר שכפלתם ב‪ 11 -‬והספרה האמצעית היא סכומן‪.‬‬
‫‪12 ∙ 11 = 132‬‬
‫‪26 ∙ 11 = 286‬‬
‫‪32 ∙ 11 = 352‬‬
‫‪45 ∙ 11 = 495‬‬
‫= ‪62 ∙ 11‬‬
‫= ‪81 ∙ 11‬‬
‫שערו‪ :‬האם החוקיות הזאת מתקיימת רק עבור התרגילים‬
‫הרשומים בתוך המסגרת?‬
‫ג‪ .‬שערו‪ :‬האם החוקיות הזאת מתקיימת לכל מכפלה של מספר דו‪-‬ספרתי ב‪?11-‬‬
‫ד‪ .‬הציעו תרגילי כפל ב‪ 11 -‬של מספרים דו‪-‬ספרתיים נוספים ובדקו את השערותיכם‪.‬‬
‫ה‪ .‬כמה מקרים‪ ,‬לדעתכם‪ ,‬מספיק לבדוק על מנת לדעת אם השערותיכם נכונות או לא?‬
‫‪ .2‬התבוננו בתרגילי חיבור של שלושה מספרים עוקבים‪.‬‬
‫א‪ .‬העתיקו למחברת את התרגילים ופתרו אותם‪.‬‬
‫מה משותף לכל התוצאות שקיבלתם?‬
‫=‪1+2+3‬‬
‫= ‪12 + 13 + 14‬‬
‫ב‪ .‬האם שמתם לב שכל התוצאות שהתקבלו שוות למכפלת‬
‫המספר האמצעי ב‪ ?3 -‬האם‪ ,‬לדעתכם‪ ,‬תכונה זו מתקיימת‬
‫רק עבור ארבעת הסכומים הרשומים בתוך המסגרת?‬
‫= )‪(-3) + (-2) + (-1‬‬
‫ג‪ .‬הציעו שלשות נוספות של מספרים עוקבים ובדקו האם גם עבורן מתקיימת התכונה‪.‬‬
‫ד‪ .‬שערו‪ :‬האם התכונה שמצאתם מתקיימת לכל שלושה מספרים עוקבים? כמה מקרים‬
‫לדעתכם צריך לבדוק על מנת להסיק האם ההשערה נכונה או שגויה? הציעו דרך להצדיק‬
‫זאת ללא בדיקה של דוגמאות נוספות?‬
‫‪ .3‬חשבו את ערכי החזקות של ‪ 11‬עד ‪.114‬‬
‫א‪ .‬באיזו חוקיות אתם מבחינים?‬
‫שערו האם החוקיות הזאת מתקיימת גם בחזקות גבוהות יותר‪.‬‬
‫ב‪ .‬בדקו את השערתכם עבור ‪ 115‬ו‪ .116 -‬האם החוקיות שמצאתם נשמרת? הסבירו מדוע‪.‬‬
‫פָּ לִ ינ ְְדרֹום‪ ,‬הוא מספר‬
‫שקריאתו מימין לשמאל‬
‫ומשמאל לימין נותנת‬
‫אותו מספר‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪7‬‬
‫‪ .4‬עבור כל אחת מהטענות שלפניכם קבעו אם היא נכונה או לא והצדיקו את קביעתכם‪.‬‬
‫א‪.‬‬
‫סכום של שני מספרים אי‪-‬זוגיים כלשהם הוא מספר‪-‬זוגי‪.‬‬
‫ב‪ .‬אם ‪ x  6‬אז ‪ x‬הוא מספר חיובי‪.‬‬
‫ג‪.‬‬
‫‪( an  0‬הוא חיובי) עבור ‪ n‬זוגי ו‪. a  0 -‬‬
‫‪ .5‬בדקו את נכונות החישובים בסדרת התרגילים שלפניכם‪.‬‬
‫‪(1‬‬
‫‪2  1  1 1‬‬
‫‪2‬‬
‫‪2‬‬
‫‪4  1  1 1‬‬
‫‪4‬‬
‫‪4 )3‬‬
‫‪3  1  1 1‬‬
‫‪3‬‬
‫‪3 (2‬‬
‫א‪ .‬הוסיפו שלושה תרגילים הבנויים לפי התבנית שבתרגילים‪ .‬האם הבחנתם בחוקיות כלשהי?‬
‫ב‪ .‬מצאו ביטוי אלגברי המתאר את החוקיות שמצאתם ובדקו אם היא מתקיימת לכל מספר‬
‫טבעי המופיע במכנה‪.‬‬
‫‪ .6‬לפניכם מספר שוויונות שבהם מתקיימת חוקיות מסוימת‪.‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2 -1 =2+1‬‬
‫א‪ .‬בדקו את נכונות השוויונות במסגרת והוסיפו‬
‫במחברתכם שלוש דוגמאות נוספות‪.‬‬
‫‪3 -2 =3+2‬‬
‫‪4 -3 =4+3‬‬
‫ב‪ .‬סמנו את המספר הראשון ב‪ ,n -‬כמו בשורה האחרונה‬
‫ברשימה שלפניכם‪ .‬איזה ביטוי מתקבל? הוכיחו‬
‫שהחוקיות מתקיימת לכל מספר טבעי ‪.n‬‬
‫ג‪ .‬האם חוקיות זו מתקיימת גם למספרים שאינם טבעיים?‬
‫‪….‬‬
‫‪2‬‬
‫‪n - …. = n + ….‬‬
‫רמז‪:‬‬
‫‪2‬‬
‫)‪(n-1) =(n-1)(n-1‬‬
‫____________________________________________________________________________________________________________‬
‫‪8‬‬
‫הגיאומטריה האוקלידית ‪ -‬עמ' ‪199‬‬
‫מטרת חלק זה במבוא היא לתת הסבר כללי לתלמידים מהי אכסיומה ומה ההבדל בינה לבין משפט‪ .‬אבחנה‬
‫זאת נעשת במטרה להציג לתלמידים את הרעיון של "ארגז כלים"‪ ,‬המכיל אכסיומות ומאגר משפטים שלמדנו‬
‫שבהם ניתן להשתמש להנמקת טענות נוספות‪ .‬אחת המיומנויות הדרושות לתלמידים‪ ,‬היא אחבנה בין תנאי‬
‫הטענה (הנתונים) לבין התוצאות אותן צריך להוכיח‪ .‬זו מטרת תרגיל ‪ 3‬בפרק זה‪.‬‬
‫הנחות היסוד (אכסיומות)‬
‫במבוא זה ניתן קצת רקע היסטורי על‬
‫הנחות היסוד (אכסיומות)‪ .‬הן מוצגות‬
‫כאוסף של הנחות אותן החליטו‬
‫המתמטיקאים לקבל ללא הוכחה‪.‬‬
‫הנחות אלה מהוות בסיס התחלתי‬
‫בבניית של אוסף הכלים והחוקים‬
‫שבאמצעותם ניתן יהיה להוכיח באופן‬
‫כללי טענות בגאומטריה‪ .‬אוסף זה‬
‫מכונה בפרק "ארגז הכלים"‪.‬‬
‫בעמוד האחרון של הספר מופיע ארגז‬
‫כלים ראשוני והוא כולל את הנחות‬
‫היסוד והמשפטים שעל‪-‬פי תכנית‬
‫הלימודים של כיתה ט‪ ,‬עליהם ורק‬
‫עליהם‪ ,‬אפשר להתבסס בתחילת‬
‫השנה‪.‬‬
‫להלן הרשימה ‪:‬‬
‫א‪.‬‬
‫כלל המעבר (טרנזיטיביות)‪ :‬שני עצמים גיאומטריים ששווים‪/‬חופפים לעצם שלישי שווים‪/‬חופפים‬
‫ביניהם‪.‬‬
‫ב‪.‬‬
‫כלל החיבור (לקטעים)‪ :‬שני קטעים‪ ,‬שכל אחד מהם מחולק לשני קטעים זרים‪ ,‬שווים אם הקטעים‬
‫שמרכיבים אותם שווים בהתאמה‪.‬‬
‫ג‪.‬‬
‫כלל החיבור (לזוויות)‪ :‬שתי זוויות‪ ,‬שכל אחת מהן מחולקת לשתי זוויות זרות‪ ,‬שוות אם הזוויות‬
‫המרכיבות אותן שוות בהתאמה‪.‬‬
‫ד‪.‬‬
‫בין כל שתי נקודות עובר קו ישר יחיד‪.‬‬
‫ה‪ .‬סכום זוויות צמודות הוא ‪ 180‬מעלות‪.‬‬
‫ו‪.‬‬
‫זוויות קודקודיות שוות זו לזו‪.‬‬
‫ז‪.‬‬
‫משפטי החפיפה במשולש‪ :‬צ‪.‬ז‪.‬צ ‪ ,‬ז‪.‬צ‪.‬ז‪ ,‬צ‪.‬צ‪.‬צ וניצב ויתר‪.‬‬
‫ח‪ .‬במשולש שווה‪-‬שוקיים התיכון לבסיס‪ ,‬הגובה לבסיס וחוצה זווית הראש מתלכדים‪ .‬כמו כן‪ ,‬זוויות‬
‫הבסיס שוות‪.‬‬
‫ט‪.‬‬
‫אם שני קווים הם מקבילים אזי זוויות מתחלפות ביניהם שוות‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪9‬‬
‫י‪.‬‬
‫סכום הזוויות במשולש הוא ‪ 180‬מעלות‪.‬‬
‫יא‪ .‬סכום הזוויות הפנימיות במצולע קמור‪ ,‬בעל ‪ n‬צלעות‪ ,‬הוא ‪ ) n - 2) ·180‬מעלות‪.‬‬
‫יב‪ .‬זווית חיצונית למשולש שווה לסכום שתי הזוויות הפנימיות שאינן צמודות לה‪ ,‬ובפרט גדולה מכל זווית‬
‫פנימית שאינה צמודה לה‪.‬‬
‫יג‪ .‬סכום שתי צלעות במשולש גדול מהצלע השלישית‪.‬‬
‫יד‪ .‬משפט פיתגורס‪.‬‬
‫טו‪ .‬שני משולשים שכל זוויותיהם שוות בהתאמה הם דומים‪.‬‬
‫"ארגז כלים" ‪ -‬הכינו פנקס קטן (או שלושה דפים נפרדים בסוף המחברת) ורכזו בו את האכסיומות‬
‫ואת כל המשפטים שהוכחנו וצרו "ארגז כלים"‪ .‬בכל פעם שנוכיח משפט חדש או תכונה חדשה הוסיפו אותם‬
‫לרשימה שלכם‪ .‬כך יהיה לרשותכם "ארגז הכלים" מעודכן וזמין‪ .‬בעמוד האחרון של הספר מופיעים הנחות‬
‫יסוד ומשפטים שכבר למדנו בכיתות ז ו‪-‬ח וניתן להשתמש בהם מבלי להוכיח אותם‪.‬‬
‫התלמידים מתבקשים להכין פנקס קטן שבו ירכזו את האכסיומות והמשפטים שהם מוכיחים בשיעורי‬
‫גיאומטריה‪ .‬מומלץ לבקש מהתלמידים להביא פנקס זה לכל שיעור גיאומטריה ולהיעזר בו בפתרון תרגילים‪.‬‬
‫אפשרות אחרת היא לרשום את ארגז הכלים בעמודים האחרונים של המחברת‪.‬‬
‫פעילות ‪ – 3‬נתונים ומסקנות ‪ -‬עמ' ‪200‬‬
‫פעילות ‪ 3‬נועדה להדגיש את החשיבות של זיהוי מרכיבי הטענה‪ :‬הנתונים‪ ,‬או תנאיי הטענה והמסקנה שאותה‬
‫מסיקים על סמך הנתונים הללו‪ .‬כאשר הטענה מנוסחת כמשפט תנאי‪" :‬אם___אז___" קל לזהות את מרכיבי‬
‫הטענה‪ ,‬אולם טענות רבות בגיאומטריה אינן נוסחות באופן זה‪ ,‬למשל‪" ,‬אלכסונים של מלבן שווים באורכם"‪.‬‬
‫ניסוח זה מקשה על זיהוי מרכיבי הטענה‪.‬‬
‫פעילות זו מאפשרת לתלמידים להתמקד בזיהוי מרכיבי הטענה ולהתאמן בפעולת הזיהוי בסיטואציה כיתתית‬
‫עם תיווך‬
‫המורה‬
‫ובהמשך גם‬
‫באופן עצמאי‬
‫בתרגיל ‪ 3‬עמ'‬
‫‪ .200‬יהיה‬
‫תרגול נוסף‬
‫בנושא גם‬
‫בפרק הדלתון‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪10‬‬
‫להלן פתרונות חלקיים‪:‬‬
‫ב‪ .‬מרובע שבו האלכסונים שווים זה לזה וחוצים זה את זה הוא מלבן‪.‬‬
‫אם במרובע ה אלכסונים שווים זה לזה וחוצים זה את זה אז המרובע הוא מלבן‪.‬‬
‫ג‪ .‬האלכסונים במלבן שווים זה לזה וחוצים זה את זה‪.‬‬
‫אם מרובע הוא מלבן אז האלכסונים שלו שווים זה לזה וחוצים זה את זה‪.‬‬
‫ד‪ .‬המנה של שני מספרים שמכפלתם חיובית היא מספר חיובי‪.‬‬
‫אם מכפלה של שני מספרים היא מספר חיובי אז גם המנה שלהם היא מספר חיובי‪.‬‬
‫תרגילים‬
‫עמ' ‪200‬‬
‫‪.3‬‬
‫בכל אחת מהטענות שלפניכם זָהו ורשמו במחברת מה נתון ומהי המסקנה שאותה צריך להוכיח‪.‬‬
‫א‪ .‬אם ספרת היחידות של מספר שלם היא ‪ ,0‬המספר מתחלק ב‪.5 -‬‬
‫נתון‪ :‬שספרת היחידות של מספר שלם היא ‪ 0‬צריך להוכיח כי‪ :‬המספר מתחלק ב‪.5 -‬‬
‫ב‪ .‬מלבן שכל צלעותיו שוות זו לזו הוא ריבוע‪.‬‬
‫נתון‪ :‬מלבן שכל צלעותיו שוות זו לזו צריך להוכיח כי‪ :‬המלבן הוא ריבוע‪.‬‬
‫ג‪.‬‬
‫אם שתי צורות חופפות זו לזו‪ ,‬אז הן שוות בשטחן‪.‬‬
‫נתון‪ :‬שתי צורות חופפות זו לזו צריך להוכיח כי‪ :‬הן שוות בשטחן‪.‬‬
‫ד‪ .‬אם בשני משולשים ישרי‪-‬זווית שווים בהתאמה שני ניצבים‪ ,‬אז המשולשים חופפים‪.‬‬
‫נתון‪ :‬הניצבים של שני משולשים ישרי‪-‬זווית שווים בהתאמה צריך להוכיח כי‪ :‬המשולשים חופפים‪.‬‬
‫ה‪ .‬אם סכום הספרות של מספר מתחלק ב‪ , 3 -‬אז המספר מתחלק ב‪.3 -‬‬
‫נתון‪ :‬סכום הספרות של מספר מתחלק ב‪ 3-‬צריך להוכיח כי‪ :‬המספר מתחלק ב‪.3-‬‬
‫____________________________________________________________________________________________________________‬
‫‪11‬‬
‫על מצולעים וזוויות – מדריך למורה‬
‫מבוא על הפרק‪:‬‬
‫סכום הזוויות במצולע‪ :‬נתון טכני או פלא טבע?‬
‫בחרנו לפתוח את השנה עם נושא שמאפשר שיעורים פעילים‪ ,‬מתחבר לנושאים מציאותיים ומזמן הפתעות‪.‬‬
‫סכום הזוויות הפנימיות של מצולע תלוי אך ורק במספר הצלעות שלו‪.‬‬
‫ואחרי שנחקור ונלמד שסכום הזוויות הפנימיות במצולע גדל ככל שמספר הצלעות גדל‪ ,‬מצפה לנו הפתעה גדולה יותר‪ :‬סכום‬
‫הזוויות החיצוניות של מצולע קבוע בכל המצולעים הקמורים‪ ,‬ללא קשר למספר הצלעות של המצולע‪.‬‬
‫בעמוד הבא מופיעה ערכת מצולעים משוכללים לגזירה שמכילה מצולעים משוכללים שונים שאורך הצלע שלהם זהה‪.‬‬
‫כדאי לתת לתלמידים את הערכות לגזירה בשקית שתאפשר להם לעשות שימוש בערכה‪ ,‬לדוגמה בתרגיל ‪.17‬‬
‫בנוסף‪ ,‬מבחינה מתמטית יכולנו להתחיל ממצולע כללי ואחר כך לדבר על מצולעים משוכללים‪ .‬במקרה זה בחרנו לתת בעיה‬
‫בתוך הקשר של ריצוף‪ ,‬ולכן התחלנו ממצולעים משוכללים‪ ,‬בלי להגיע להכללות‪ .‬המשכנו למצולעים כלליים‪ ,‬ולאחר קבלת‬
‫נוסחה לחישוב סכום הזוויות חזרנו למצולעים משוכללים וקיבלנו נוסחה לחישוב של כל הזווית במצולעים משוכללים‬
‫ובמצולעים שאינם משוכללים‪.‬‬
‫רעיון זה אינו כה פשוט לתלמידים ולכן במסגרת הפעילויות והתרגילים אנו מחדדים נקודה זו‪ .‬שימו לב‪ ,‬כי תרגיל ‪ 1‬הינו‬
‫פעילות הכנה לפעילות ‪ .2‬בתרגיל ‪ 1‬ניתן חישוב זוויות של מחומש משוכלל ואלו בפעילות ‪ 2‬התלמידים מתבקשים לחשב את‬
‫הזוויות של מחומש שאינו משוכלל‪ .‬מטרת שתי הפעילויות היא להבהיר לתלמידים כי לא הסתמכנו על תכונות מצולע‬
‫משוכלל ולכן התהליך נכון לכל המצולעים‪ .‬לחדד זאת‪ ,‬אנו עושים את אותו התהליך בדיוק עבור מחומש משוכלל ועבור‬
‫מחומש שאינו משוכלל‪ ,‬כדי לסייע למי שלא הגיע למסקנה עצמאית‪.‬‬
‫_________________________________________________________________________‬
‫‪12‬‬
‫___‬
‫מדריך למורה לכיתה ט – ספר כתום‪ ,‬חלק א‬
‫_________________________________________________________________________‬
‫‪13‬‬
‫___‬
‫הצעה לפעילות מקדימה לפעילות ‪ 1‬בספר הלימוד‪:‬‬
‫הפעילות הבאה אינה מופיעה בספר הלימוד‪ .‬פעילות זו היא פעילות רשות המכינה לקראת הפעילויות על סכום זוויות‬
‫במצולע‪ .‬מטרות הפעילות הן לרענן ידע קודם ויצירת הקשר מציאותי לעיסוק בזוויות של מצולעים‪ .‬בעמוד הבא מופיע דף‬
‫הפעילות לשכפול לתלמידים‪.‬‬
‫בוטיק השוקולד המשולש‪.‬‬
‫בוטיק השוקולד של חומי ידוע בזכות משולשי השוקולד המשובח הנמכרים בו‪.‬‬
‫חומי מסדר את משולשי השוקולד במארזים‪ ,‬בשכבה אחת‪ ,‬כך שהם ממלאים את‬
‫כל המארז מבלי להשאיר רווח‪ .‬הוא יודע שעיצוב האריזה חשוב לקידום המכירות לא‬
‫פחות מאשר טעמו המשובח של השוקולד‪.‬‬
‫א‪ .‬משולשי השוקולד הם שווי צלעות‪ .‬מה מידת הזווית של‬
‫משולש שווה צלעות? ‪60‬‬
‫ב‪ .‬התבוננו בסרטוט של אריזת מתנה ריקה ל‪ 6 -‬משולשי שוקולד‪ ,‬וחשבו את סכום‬
‫הזוויות בנקודה ‪360 . A‬‬
‫‪A‬‬
‫ג‪ .‬הסבירו מדוע סכום הזוויות שקיבלתם מבטיח שניתן להניח את השוקולדים סביב‬
‫הנקודה ‪ A‬באופן שלא יעלו זה על זה‪ .‬סכום הזוויות סביב נקודה אחת שווה‬
‫בדיוק לסכום ‪ 6‬הזוויות של המשולשים שווי‪ -‬הצלעות‪.‬‬
‫ד‪ .‬חשבו את מידותיהן של זוויות המשושה‪2  60 = 120 .‬‬
‫ה‪ .‬חשבו את סכום הזוויות של משושה משוכלל‪6  120 = 720 .‬‬
‫ו‪.‬‬
‫חומי נוהג למכור שוקולד גם באריזות משולשות‪ ,‬גדולות יותר‪ .‬הסבירו מדוע ניתן‬
‫לסדר את משולשי השוקולד בשורות ישרות (ראו סרטוט)‪.‬‬
‫‪ 3‬זוויות של משולש שווה‪-‬צלעות יוצרות זווית שטוחה‪.‬‬
‫רמז‬
‫‪:‬‬
‫ז‪ .‬הציעו מארזים נוספים שניתן לסדר בהם ‪ 6‬משולשי שוקולד‪.‬‬
‫דוגמאות אפשריות‪:‬‬
‫ח‪ .‬הציעו מארז שניתן לסדר בו ‪ 10‬משולשי שוקולד‪.‬‬
‫דוגמאות אפשריות‪:‬‬
‫ט‪ .‬האם ניתן לסדר ‪ 9‬משולשי שוקולד במארז שצורתו משולש שווה צלעות? הסבירו או הדגימו‪.‬‬
‫סידור של ‪ 9‬משולשי שוקולד‪:‬‬
‫_________________________________________________________________________‬
‫‪14‬‬
‫___‬
‫בוטיק השוקולד המשולש‬
‫בוטיק השוקולד של חומי ידוע בזכות משולשי השוקולד המשובח הנמכרים בו‪.‬‬
‫חומי מסדר את משולשי השוקולד במארזים‪ ,‬בשכבה אחת‪ ,‬כך שהם ממלאים את‬
‫כל המארז מבלי להשאיר רווח‪ .‬הוא יודע שעיצוב האריזה חשוב לקידום המכירות‬
‫לא פחות מאשר טעמו המשובח של השוקולד‪.‬‬
‫א‪ .‬משולשי השוקולד הם שווי צלעות‪.‬‬
‫מה מידת הזווית של משולש שווה צלעות?‬
‫ב‪ .‬התבוננו בסרטוט של אריזת מתנה ריקה ל‪ 6 -‬משולשי שוקולד‪ ,‬וחשבו את‬
‫סכום הזוויות בנקודה ‪. A‬‬
‫‪A‬‬
‫ג‪ .‬הסבירו מדוע סכום הזוויות שקיבלתם מבטיח שניתן להניח את השוקולדים סביב‬
‫הנקודה ‪ A‬באופן שלא יעלו זה על זה‪.‬‬
‫רמז‬
‫‪:‬‬
‫ד‪ .‬חשבו את מידותיהן של זוויות המשושה‪.‬‬
‫ה‪ .‬חשבו את סכום הזוויות של משושה משוכלל‪.‬‬
‫ו‪.‬‬
‫חומי נוהג למכור שוקולד גם באריזות משולשות‪ ,‬גדולות יותר‪ .‬הסבירו מדוע ניתן‬
‫לסדר את משולשי השוקולד בשורות ישרות (ראו סרטוט)‪.‬‬
‫ז‪ .‬הציעו מארזים נוספים שניתן לסדר בהם ‪ 6‬משולשי שוקולד‪.‬‬
‫ח‪ .‬הציעו מארז שניתן לסדר בו ‪ 10‬משולשי שוקולד‪.‬‬
‫ט‪ .‬האם ניתן לסדר ‪ 9‬משולשי שוקולד במארז שצורתו משולש שווה צלעות? הסבירו או הדגימו‪.‬‬
‫_________________________________________________________________________‬
‫‪15‬‬
‫___‬
‫פעילות ‪ – 1‬זוויות במשושה ומתומן משוכלל – עמ' ‪201‬‬
‫מטרתן של השאלות הראשונות של הפעילות היא לעורר סקרנות‪ ,‬ולגרום‬
‫לתלמידים לייחס משמעות לתוצאות החישוביות‪ ,‬ולא לחלוף עליהן במהירות‪.‬‬
‫אפשר‪ ,‬במקום להיצמד להוראות‬
‫הפעילות‪ ,‬לתת לתלמידים משימה‬
‫פתוחה לחשב את סכום הזוויות‬
‫במתומן‪.‬‬
‫תשובות‪:‬‬
‫א‪.‬‬
‫משולשי השוקולד הם‬
‫משולשים שווי‪-‬צלעות בהם כל‬
‫זווית שווה‬
‫ל – ‪.60‬‬
‫ב‪.‬‬
‫סכום הזוויות סביב נקודה אחת‬
‫שווה בדיוק לסכום ‪ 6‬הזוויות‬
‫של המשולשים שווי‪ -‬הצלעות‪.‬‬
‫לכן ניתן לארגן את משולשי‬
‫השוקולד במארז משושה‪.‬‬
‫באופן דומה‪ ,‬כל שלושה‬
‫משולשים שווי‪-‬צלעות יוצרים‬
‫זווית שטוחה ולכן ניתן לסדר‬
‫את משולשי השוקולד במארז‬
‫משולש כמדוגם בסרטוט‪.‬‬
‫ג‪.‬‬
‫לא ניתן לסדר את משולשים‬
‫שווי‪ -‬צלעות בקופסה בצורת‬
‫מתומן בשכבה אחת בלי‬
‫להשאיר רווחים‪ .‬התלמידים יכולים לנסות לענות על השאלה בעזרת ערכת המצולעים או להעלות השערה‪ .‬אפשר‬
‫לערוך הצבעה בין התלמידים ובהמשך לבדוק אתם האם צדקו בהשערתם‪.‬‬
‫ד‪.‬‬
‫השיקול של גיל נכון‪ .‬סידור המשולשים בקופסה כולל גם את "מילוי" הפינות‪ .‬בהמשך‪ ,‬כאשר נדע שמידת הזווית של‬
‫מתומן משוכלל היא ‪ .135‬המספר ‪ 135‬אינו מתחלק ב‪ ,60 -‬ולכן לא ניתן למלא את פינת הקופסה במשולשים‪.‬‬
‫ה‪.‬‬
‫אם גיל ידע את סכום הזוויות יוכל לחלק את הסכום ב‪ 8 -‬ולדעת מה גודלה של כל זווית‪ .‬על‪-‬פי ההצעה של גיל‬
‫מתקבלים ‪ 6‬משולשים‪ .‬סכום הזוויות ב‪ 6 -‬משולשים הוא ‪.1080‬‬
‫‪.1080 : 8 = 135‬‬
‫_________________________________________________________________________‬
‫‪16‬‬
‫___‬
‫חלוקת המתומן למשולשים‬
‫התקבלו‬
‫נעביר את כל האלכסונים‬
‫שיוצאים מקדקוד אחד‬
‫ונספור את מספר‬
‫המשולשים שהתקבלו‪.‬‬
‫‪6‬‬
‫משולשים‬
‫חישוב סכום הזוויות במתומן‬
‫סכום הזוויות‬
‫במתומן משוכלל‪:‬‬
‫‪1080‬‬
‫נכפול את מספר‬
‫המשולשים ב‪.180 -‬‬
‫מידת כל זווית‪:‬‬
‫חישוב מידת הזווית‬
‫כדי לדעת את מידתה‬
‫של כל זווית נחלק את‬
‫סכום הזוויות ב‪.8 -‬‬
‫‪1080:8=135‬‬
‫ו‪.‬‬
‫כן‪ .‬זווית של מתומן משוכלל (‪ )135º‬גדולה מזווית של משושה משוכלל (‪.)120º‬‬
‫ז‪.‬‬
‫אי אפשר‪ .‬המספר ‪ 135‬אינו מתחלק ב‪ , 60 -‬ולכן לא ניתן "למלא" את פינת הקופסה במשולשים‪.‬‬
‫מצולע הוא קו שבור סגור (שאינו חותך את עצמו)‪.‬‬
‫מצולע שכל צלעותיו שוות זו לזו וכל זוויותיו שוות זו לזו נקרא מצולע משוכלל‪.‬‬
‫ריבוע הוא מרובע משוכלל‪.‬‬
‫משולש שווה‪-‬צלעות הוא משולש משוכלל‪.‬‬
‫מארז השוקולד בפעילות ‪ 1‬הוא בצורת משושה משוכלל‪.‬‬
‫מצולע משוכלל בעל ‪ 8‬צלעות נקרא מתומן משוכלל‪.‬‬
‫המצולע ‪ LMNOP‬הוא מחומש (בעל חמש צלעות) לא משוכלל כי הצלע ‪ PO‬לא שווה באורכה לצלע ‪.ON‬‬
‫‪ ‬היא זווית של המצולע ‪ LMNOP‬כי ‪ MN‬ו‪ ON -‬צלעות של המצולע‪.‬‬
‫‪ ‬אינה זווית של המצולע כי ‪ PM‬אינה צלע של המצולע‪.‬‬
‫_________________________________________________________________________‬
‫‪17‬‬
‫___‬
‫תרגילים – חישובי זוויות במצולעים משוכללים אחרים – עמ' ‪203 – 202‬‬
‫תרגיל ‪ 1‬הינו פעילות הטרמה לפעילות ‪ .2‬בתרגיל ‪ 1‬התלמידים מתבקשים לחשב את הזוויות של מחומש משוכלל‪ .‬חשוב‬
‫לשאול את התלמידים‪ ,‬האם בחישוב סכום הזוויות השתמשנו בכך כי המצולע משוכלל? ומה אפשר ללמוד מזה?‬
‫מטרתנו שיסיקו שכיוון שלא השתמשנו בתכונות של המצולע המשוכלל אזי זה נכון גם למצולע שאינו משוכלל‪ .‬לחיזוק אנו‬
‫עושים את אותו התהליך בדיוק עבור מחומש שאינו משוכלל בפעילות ‪( 2‬ראו הקדמה לפרק ופעילות ‪)2‬‬
‫עמ' ‪ .1 202‬בעזרת ההצעה של גיל חשבו את סכום הזוויות ואת מידת כל זווית במחומש משוכלל‪.‬‬
‫חלוקת המחומש למשולשים‬
‫התקבלו‬
‫שיוצאים מקדקוד אחד‬
‫ונספור את מספר‬
‫המשולשים שהתקבלו‪.‬‬
‫‪3‬‬
‫מחומש משוכלל‬
‫סכוםשל‬
‫הזוויות‬
‫חישוב סכום‬
‫הזוויות‬
‫חישוב‬
‫סכום הזוויות‬
‫במחומש משוכלל‪:‬‬
‫במחומש‬
‫‪3 180=540‬‬
‫חישוב מידת הזווית של מחומש משוכלל‬
‫מידת כל זווית ‪:‬‬
‫‪540 :5=108‬‬
‫‪ .2‬חשבו את מידת הזווית של מצולע משוכלל בעל ‪ 15‬צלעות‪.156 .‬‬
‫סכום הזוויות הפנימיות במצולע קמור – עמ' ‪203‬‬
‫מצולע קמור הוא מצולע שכל אלכסוניו פנימיים‬
‫(נמצאים בתוך המצולע)‪.‬‬
‫מצולע שאינו קמור ‪-‬‬
‫מצולע קמור ‪-‬‬
‫לפחות אחד מהאלכסונים חיצוני‪.‬‬
‫כל אלכסוניו פנימיים‪.‬‬
‫אלכסוניו פנימיים‪.‬‬
‫בהגדרה של מצולע קמור חשוב לשים לב שמצולע הוא קמור‪ ,‬אם כל אלכסוניו פנימיים‪ .‬די באלכסון חיצוני אחד כדי‬
‫שהמצולע לא יהיה קמור‪ ,‬אז מתקבל מצולע קעור‪ .‬קיימות הגדרות נוספות‪ ,‬שקולות למצולע קמור‪ .‬הבחירה בהגדרה‬
‫הנוכחית מבוססת על העובדה שהיא מאפשרת לבדוק בקלות אם המצולע קמור‪.‬‬
‫_________________________________________________________________________‬
‫‪18‬‬
‫___‬
‫תרגילים ‪ 3-7‬מיועדים לעזור לתלמידים להב חין בין מצולעים קמורים ומצולעים שאינם קמורים ובין אלכסון פנימי לאלכסון‬
‫חיצוני‪ .‬ניתן לתת אותם כתרגילים או כחלק מהפעילות הכיתתית‪.‬‬
‫כפי שצוין בעמוד קודם‪ ,‬קיימות הגדרות נוספות‪ ,‬שקולות למצולע קמור‪ .‬המצולע ‪ TMALCUH‬מאפשר להרחיב ולחזור‬
‫עם התלמידים על הידוע להם מבית הספר היסודי‪ ,‬כי אי‪-‬קמירות של הצורה נובעת גם מהמצב של אלכסון שלא כולו‬
‫בתוך המצולע‪ ,‬כפי שקורה לדוגמה באלכסון ‪.CT‬‬
‫‪S‬‬
‫‪R‬‬
‫‪U‬‬
‫‪E‬‬
‫‪O‬‬
‫‪H‬‬
‫‪L‬‬
‫‪A‬‬
‫‪K‬‬
‫‪H‬‬
‫‪T‬‬
‫‪K‬‬
‫‪O‬‬
‫‪V‬‬
‫‪A‬‬
‫‪P‬‬
‫‪E‬‬
‫‪C‬‬
‫‪A‬‬
‫‪U‬‬
‫‪M‬‬
‫‪T‬‬
‫עמ' ‪ .3 203‬המחומש ‪ HOUSE‬הוא מחומש קמור כי כל אלכסוניו פנימיים‪ .‬העתיקו אותו למחברת וסרטטו את כל‬
‫האלכסונים‪ .‬זהו בין הסרטוטים מצולע קמור נוסף‪ .‬מצולע קמור נוסף ‪.PARKET‬‬
‫‪ .4‬העתיקו למחברת את המשושה ‪ PARKET‬וסרטטו את כל האלכסונים שמתחברים לקדקוד ‪.P‬‬
‫לכמה משולשים האלכסונים מחלקים את המשושה? לארבעה משולשים‪.‬‬
‫‪ .5‬המרובע ‪ KOVA‬אינו קמור‪ .‬העתיקו אותו למחברת וסרטטו בו אלכסון פנימי ואלכסון חיצוני‪.‬‬
‫אלכסון פנימי ‪ .KV‬אלכסון חיצוני ‪.AO‬‬
‫‪ .6‬המצולע ‪ MALCHUT‬אינו קמור‪ .‬זהו בו שני אלכסונים חיצוניים ושלושה אלכסונים פנימיים‪.‬‬
‫אלכסונים חיצוניים‪ .HL ,TH :‬אלכסונים פנימיים‪ ML ,AT ,MU ,UC :‬ו‪.AC -‬‬
‫‪ .7‬במצולע ‪ MALCHUT‬האלכסון ‪ LU‬חלקו בתוך המצולע וחלקו מחוץ למצולע‪.‬‬
‫זהו במצולע זה אלכסון נוסף עם אותה התכונה‪.CT .‬‬
‫‪ .8‬סרטטו משושה שאינו קמור‪ .‬לדוגמה‪:‬‬
‫_________________________________________________________________________‬
‫‪19‬‬
‫___‬
‫הפעילות עוסקת במצולע קמור כללי‪ ,‬לאו דווקא מצולע משוכלל‪ .‬דרך החישוב שהוצגה לחישוב סכום הזוויות במצולע משוכלל‬
‫מתאימה גם כאן ‪ .‬בפעילות אנו מסבים את תשומת ליבם של התלמידים לכך שכאשר אנו מדברים על זוויות אנו מתייחסים‬
‫לזוויות הפנימיות של המצולע‪.‬‬
‫פעילות ‪ – 2‬סכום הזוויות של מצולע קמור – עמ' ‪203‬‬
‫א‪ .‬האם אפשר‪ ,‬לדעתכם‪ ,‬לסרטט מרובע שסכום הזוויות שלו שונה מאשר ‪?360‬‬
‫אם אפשר ‪ -‬הדגימו‪.‬‬
‫אם אי‪-‬אפשר ‪ -‬הסבירו מדוע‪.‬‬
‫שימו לב!‬
‫בדרך כלל‪ ,‬אם לא מציינים‬
‫אחרת‪ ,‬כשמדברים על זוויות של‬
‫מצולע מדברים על הזוויות‬
‫הפנימיות (בתוך המצולע)‬
‫ב‪ .‬גיל טוען שהשיטה שלו מתאימה לחישוב סכום הזוויות בכל מצולע‪ ,‬גם אם אינו משוכלל‪ .‬הראו בעזרת השיטה של גיל‬
‫שסכום הזוויות בכל מחומש הוא ‪.540‬‬
‫חלוקה למשולשים‬
‫התקבלו ______‬
‫שיוצאים מקדקוד אחד‪.‬‬
‫חישוב סכום הזוויות במחומש‬
‫סכום הזוויות במחומש‪:‬‬
‫___=‪___180‬‬
‫השלימו את הטבלה‪:‬‬
‫מספר הצלעות במצולע‬
‫‪3‬‬
‫‪4‬‬
‫‪6‬‬
‫‪5‬‬
‫‪8‬‬
‫‪10‬‬
‫‪n‬‬
‫סרטוט‬
‫מספר המשולשים‬
‫כשמעבירים אלכסונים‬
‫מקדקוד אחד‬
‫‪1‬‬
‫‪2‬‬
‫‪3‬‬
‫‪4‬‬
‫‪6‬‬
‫‪8‬‬
‫‪n–2‬‬
‫סכום הזוויות במצולע‬
‫‪180‬‬
‫‪360‬‬
‫‪540‬‬
‫‪720‬‬
‫‪1080‬‬
‫‪1440‬‬
‫)‪180(n – 2‬‬
‫הערה‪ :‬נשים לב‪ ,‬כי במשולש אין אלכסונים ולכן יש משולש אחד‪.‬‬
‫_________________________________________________________________________‬
‫‪20‬‬
‫___‬
‫ג‪ .‬בכמה גדל סכום הזוויות של מצולע כאשר מוסיפים לו צלע אחת? נסו להסביר בדרכים אחדות‪.‬‬
‫כאשר מגדילים באחד את מספר הצלעות של המצולע סכום הזוויות גדל ב‪ .180 -‬תופעה זו בולטת בטבלה‪ ,‬וניתן גם‬
‫להסביר אותה באמצעות הנוסחה שהתקבלה‪ ,‬ובאמצעות העובדה שהוספה של צלע מוסיפה משולש אחד‪ ,‬ולכן סכום הזוויות‬
‫גדל ב‪.180 -‬‬
‫ד‪ .‬בעמודה השמאלית של הטבלה קיבלתם נוסחה לחישוב סכום הזוויות במצולע‪.‬‬
‫נוסיף את הנוסחה לארגז הכלים‪:‬‬
‫במצולע קמור בעל ‪ n‬צלעות סכום הזוויות הפנימיות הוא )‪.180(n–2‬‬
‫הסבירו את הנוסחה‪.‬‬
‫מצולע קמור בעל ‪ n‬צלעות אפשר לחלק ל‪ (n – 2( -‬משולשים‪.‬‬
‫סכום הזוויות במשולש הוא ‪ .180‬על מנת לחשב את סכום הזוויות הפנימיות של משולש יש לכפול את מספר המשולשים‬
‫ב‪.180 -‬‬
‫פעילות ‪ – 3‬מידת הזווית של מצולע משוכלל – עמ' ‪205‬‬
‫מספר הצלעות במצולע‬
‫המשוכלל‬
‫‪3‬‬
‫‪4‬‬
‫‪5‬‬
‫‪6‬‬
‫‪7‬‬
‫‪10‬‬
‫‪n‬‬
‫סכום הזוויות במצולע‬
‫‪180‬‬
‫‪360‬‬
‫‪540‬‬
‫‪720‬‬
‫‪900‬‬
‫‪1440‬‬
‫)‪180(n – 2‬‬
‫מידת כל זוויות‬
‫‪60‬‬
‫‪90‬‬
‫‪108‬‬
‫‪120‬‬
‫‪128.57‬‬
‫‪144‬‬
‫‪180(n – 2)/n‬‬
‫_________________________________________________________________________‬
‫‪21‬‬
‫___‬
‫עמ' ‪205‬‬
‫‪ .9‬לפניכם ‪ 4‬סרטוטים‪:‬‬
‫א‬
‫ב‬
‫ג‬
‫ד‬
‫א‪ .‬ציינו באיזה מהסרטוטים מופיע מצולע קמור‪ .‬א‪ ,‬ד‬
‫ב‪.‬‬
‫באיזה מהסרטוטים מופיעה צורה שאיננה מצולע? ב‬
‫‪ .10‬חשבו את סכום הזוויות במצולע קמור בעל ‪ 12‬צלעות‪ .‬אם המצולע הוא משוכלל ‪ -‬מה מידתה של כל זווית‪.‬‬
‫נציב בנוסחה‪ ;180(12 – 2)= 1800º :‬כיוון שהמצולע משוכלל כל הזוויות שוות ולכן מידת הזווית היא‪150º :‬‬
‫שאלה ‪ 11‬מחדדת את ההבנות של תוצאות הטבלה בפעילות ‪.3‬‬
‫‪ .11‬האם נכון ש‪?...‬‬
‫אם כן ‪ -‬נמקו‪ .‬אם לא ‪ -‬הביאו דוגמה נגדית‪.‬‬
‫א‪ .‬לכל המצולעים עם ‪ 10‬צלעות יש אותו סכום זוויות‪ .‬נכון‪ .‬תרגיל זה מספק הזדמנות להתייחס לדרך למצוא את‬
‫מידת הזווית של מצולע עם מספר צלעות נתון לא כאל עובדה טכנית‪ ,‬אלא כאל תופעה מפתיעה‪ :‬סכום הזוויות של‬
‫מצולע תלוי רק במספר הצלעות שלו‪.‬‬
‫ב‪ .‬ככל שמספר הצלעות של מצולע משוכלל יותר גדול כך סכום הזוויות שלו יותר גדול‪ .‬נכון‪ .‬אפשר לראות באמצעות‬
‫הנוסחה או על פי הדרך בה הגענו לנוסחה‪ :‬ככל שמספר הצלעות גדול יותר כך נחלק את המצולע ליותר משולשים‪.‬‬
‫ג‪ .‬ככל שמספר הצלעות של מצולע משוכלל יותר גדול כך סכום הזוויות שלו יותר קטן‪ .‬לא נכון‪ ,‬כנאמר בסעיף ב‪.‬‬
‫*‪ .12‬האם קיים מצולע משוכלל שמידת הזווית שלו ‪ ?40‬אם כן ‪ -‬כמה צלעות במצולע זה?‬
‫אם לא ‪ -‬הסבירו כיצד ניתן לדעת זאת‪ .‬לא‪.‬‬
‫שני הסברים אפשריים‪:‬‬
‫הסבר הקשור לטענה הנכונה מתרגיל ‪:10‬‬
‫ככל שמספר הצלעות של מצולע משוכלל גדול יותר‪ ,‬כך זווית המצולע גדולה יותר‪ .‬אנחנו יודעים שבמשולש הזווית היא ‪60º‬‬
‫ולכן לא תיתכן זווית קטנה יותר‪.‬‬
‫הסבר נוסף‪ ,‬אם נציב ‪ 40‬בנוסחה לא נקבל ‪ n‬שלם ולכן לא קיים מצולע משוכלל שמידת הזווית שלו היא ‪.40‬‬
‫*‪ .13‬האם קיים מצולע משוכלל שמידת הזווית שלו ‪ ?170‬אם כן ‪ -‬כמה צלעות במצולע זה?‬
‫אם לא ‪ -‬הסבירו כיצד ניתן לדעת זאת‪ 36 .‬צלעות‪.‬‬
‫נבדוק כבדומה לתרגיל ‪ 170 :12‬‬
‫‪180   n  2‬‬
‫‪n‬‬
‫‪ .‬פתרון המשוואה הוא ‪ .n = 36‬לכן נסיק שקיים מצולע משוכלל שמידת‬
‫הזווית שלו ‪ ,170‬ושלמצולע זה ‪ 36‬צלעות‪.‬‬
‫_________________________________________________________________________‬
‫‪22‬‬
‫___‬
‫עמ' ‪206‬‬
‫‪Q‬‬
‫‪ .14‬במחומש ‪ PQRST‬כל הזוויות שוות‪ .‬חשבו את מידת הזווית ‪.∡D‬‬
‫תרגיל זה מפ גיש את התלמידים עם מצולע שאיננו משוכלל‪ ,‬למרות שכל זוויותיו‬
‫שוות זו לזו‪ .‬חישוב מידתן של זוויות המחומש נעשה כמו במצולע משוכלל‪.‬‬
‫‪∡QPT = ∡PTS = 108‬‬
‫חישוב זווית פנימית במחומש‬
‫‪∡DPT = ∡PTD = 72‬‬
‫זוויות אלו צמודות לזוויות ‪108‬‬
‫‪P‬‬
‫‪R‬‬
‫‪S‬‬
‫‪D‬‬
‫‪T‬‬
‫חישוב זווית במשולש ‪DPT‬‬
‫‪∡D = 36‬‬
‫‪ .15‬חשבו את מידתה של הזווית המסומנת ב‪ x -‬על‪-‬פי נתוני הסרטוט‪.X = 128º .‬‬
‫בתרגיל ‪ 16‬כדאי לבקש כתיבה מקוצרת של הנימוקים‪ ,‬כדי לא להאפיל על יופיו‬
‫של המחומש המשוכלל ושל הכוכב שבו כתיבה מייגעת של נימוקים‪.‬‬
‫‪ .16‬במחומש המשוכלל ‪ YAROK‬האלכסונים נפגשים‬
‫בנקודות ‪ ,S ,E ,P ,B‬ו‪.T -‬‬
‫א‪ .‬מה מידת הזווית ‪108 ?∡KYA‬‬
‫(אפשר להיעזר בטבלה של פעילות ‪).3‬‬
‫ב‪ .‬חשבו את זוויות המשולש ‪ORA‬‬
‫(זכרו שכל הצלעות של המחומש ‪ YAROK‬שוות זו לזו‪).‬‬
‫המשולש ‪ ∆ORA‬הוא שווה‪-‬שוקיים‪ .‬מידת זווית הראש היא ‪108‬‬
‫ומכאן שהמידות של הזוויות האחרות הן ‪.36‬‬
‫ג‪ .‬חשבו את זוויות המשולש ‪.SER‬‬
‫נשים לב למשולשים החופפים על פי צ‪.‬ז‪.‬צ‪:‬‬
‫‪ORA  RAY  AYK  YKO  KOR‬‬
‫‪12 3‬‬
‫מהחפיפות נסיק‪:‬‬
‫‪∡O1 = ∡O3 = ∡K1 = ∡K3 = ∡Y1 = ∡Y3 = ∡A1 = ∡A3 = ∡R1 = ∡R3 = 36‬‬
‫ומכאן נוכל להמשיך ולחשב את כל הזוויות בסרטוט‪ .‬בפרט‪:‬‬
‫‪∡R2 = ∡R – ∡R1 – ∡R2 = 108 – 2  36 = 36‬‬
‫‪∡OSR = 180 – ∡O1 – ∡R3 = 180– 2  36 = 108‬‬
‫‪3‬‬
‫‪2‬‬
‫‪1‬‬
‫‪2‬‬
‫‪3‬‬
‫‪2‬‬
‫‪2 1‬‬
‫‪3‬‬
‫‪1‬‬
‫‪21‬‬
‫‪1‬‬
‫‪3‬‬
‫‪∡S1 = 180 – ∡OSR = 180 – 108 = 72‬‬
‫_________________________________________________________________________‬
‫‪23‬‬
‫___‬
‫ד‪ .‬הוכיחו כי אלכסוני המחומש מחלקים את זוויותיו ל‪ 3 -‬זוויות שוות‪.‬‬
‫במהלך פתרון סעיף ג כבר קיבלנו‪.∡R1 = ∡R2 = ∡R3 = 36 :‬‬
‫* ה‪ .‬מצאו משולש דומה למשולש ‪ ORA‬שאינו חופף לו‪.‬‬
‫כמה משולשים כאלה קיימים בסרטוט?‬
‫חמישה משולשים דומים ל‪ ORA -‬ואינם חופפים לו‪:‬‬
‫‪.OSR ,REA ,APY ,YBK ,KTR‬‬
‫נסיק זאת על מתוך חשבון הזוויות‪.‬‬
‫(אפשר גם להוכיח כי ‪.)OSR  REA  APY  YBK  KTR‬‬
‫* ו‪ .‬מצאו משולש דומה למשולש ‪ SER‬שאינו חופף לו‪.‬‬
‫כמה משולשים כאלה קיימים בסרטוט? ‪ 5‬משולשים‪ ,‬למשל ‪.KRY‬‬
‫* ז‪ .‬הוכיחו שהמחומש ‪ BPEST‬הוא מחומש משוכלל‪.‬‬
‫מחשבון הזוויות מקבלים שהמידות של כל זוויות המחומש ‪ BPEST‬הן ‪.108‬‬
‫ניתן להראות באמצעות חפיפת משולשים שכל הצלעות המחומש ‪ BPEST‬שוות‪.‬‬
‫זוויות חיצוניות במצולעים – עמ' ‪207‬‬
‫זווית הנוצרת בין אחת הצלעות של מצולע קמור לבין המשך הצלע הסמוכה נקראת‬
‫זווית חיצונית למצולע‪ .‬זווית זו צמודה לזווית פנימית במצולע‪.‬‬
‫שימו לב‪ :‬ליד כל קדקוד יש שתי זוויות חיצוניות‪.‬‬
‫מדוע שתי הזוויות החיצוניות שליד אותו קדקוד שוות זו לזו?‬
‫חשוב לשים לב‪ ,‬כי רק במצולעים קמורים ניתן לדבר על זווית חיצונית למצולע‪ .‬כדאי להזכיר עובדה זו כאשר עוברים לעסוק‬
‫בסכום הזוויות החיצוניות של מצולע שאינו משוכלל‪.‬‬
‫נשים לב כי הנושא‪ :‬זווית חיצונית למשולש נלמד בכיתה ז‪ ,‬חלק ג‪ ,‬עמ' ‪ .168-170‬המשפטים על זווית חיצונית במשולש‬
‫הם משפטים שימושיים בהמשך לימודי הגיאומטריה‪.‬‬
‫לאחר שעסקנו בסכום הזוויות הפנימיות של מצולעים‪ ,‬ראינו שהוא גדל ככל שגדל מספר הצלעות של מצולע‪ ,‬וראינו שסכום‬
‫הזוויות יכול להיות גדול מאד‪ ,‬מזומנת לנו הפתעה‪ :‬סכום הזוויות החיצוניות של מצולע קבוע בכל המצולעים הקמורים והוא‬
‫‪ . 360‬האתנחתא בסוף הפרק ממחישה מדוע סכום הזוויות החיצוניות בכל המשולשים שווה לסכום הזוויות סביב נקודה‬
‫אחת‪.‬‬
‫פעילות ‪ – 4‬סכום הזוויות החיצוניות במצולע – עמ' ‪207‬‬
‫את פעילות ‪ 4‬כדאי לתת לתלמידים כעבודה עצמית ואחר כך לסכם את הדיון בכתה‪ ,‬ולהדגיש את המיוחד במשפט‪.‬‬
‫המפגש עם מגוון דוגמאות שבכולן סכום הזוויות החיצוניות של המצולע הוא ‪ 360‬מטרתו לעורר מוטיבציה להבין את‬
‫התופעה ולהוכיח אותה‪.‬‬
‫התופעה מוסברת באמצעות חקר של מספר מצולעים משוכללים‪ :‬משושה‪ ,‬מתומן‪ ,‬משולש וריבוע וניסיון להכליל מהן‪.‬‬
‫_________________________________________________________________________‬
‫‪24‬‬
‫___‬
‫ניתן כמובן גם להוסיף את המחומש המשוכלל‪ :‬במחומש סכום הזוויות‪ ,‬הפנימית והחיצונית‪ ,‬ליד כל קודקוד הוא ‪ .180‬לכן‬
‫סכום כל הזוויות פנימיות וחיצוניות‪ ,‬הוא ‪ .900‬נפחית את סכום הזוויות הפנימיות‪ ,540 ,‬ונקבל שסכום הזוויות החיצוניות‬
‫הוא ‪.360‬‬
‫ההוכחה הכללית‪ ,‬שהיא דומה מאד אינה מוצגת בספר‪:‬‬
‫בכל קדקוד סכום הזווית הפנימית והזווית החיצונית של המצולע הוא ‪ .180‬לכן סכום הזוויות הפנימיות והחיצוניות ביחד‬
‫הוא ‪ .180n‬נפחית ממספר זה את סכום הזוויות הפנימיות ונקבל‪.180  n – 180(n – 2) = 360 :‬‬
‫פעילות ‪ – 4‬סכום הזוויות החיצוניות במצולע –‬
‫עמ' ‪207‬‬
‫נתבונן במצולע ‪.ABCDEF‬‬
‫בכל אחד מהקדקודים קיימות שתי זוויות חיצוניות שוות זו לזו‪.‬‬
‫‪B‬‬
‫‪C‬‬
‫כשמדברים על סכום הזוויות החיצוניות במצולע מדברים על זווית אחת בכל קדקוד‪,‬‬
‫‪A‬‬
‫‪D‬‬
‫כלומר מסכמים את מידות כל הזוויות באותה מגמה‪:‬‬
‫הזוויות המסומנות בסרטוט א או הזוויות המסומנות בסרטוט ב‪.‬‬
‫‪E‬‬
‫‪B‬‬
‫‪C‬‬
‫‪B‬‬
‫‪C‬‬
‫א‪.‬‬
‫‪F‬‬
‫ב‪.‬‬
‫‪A‬‬
‫‪D‬‬
‫‪E‬‬
‫או‬
‫‪F‬‬
‫‪A‬‬
‫‪D‬‬
‫‪E‬‬
‫‪F‬‬
‫א‪ .‬מידת הזווית הפנימית של משושה משוכלל היא ‪ .120‬מה מידת הזווית החיצונית במשושה משוכלל?‬
‫ב‪ .‬חשבו את סכום הזוויות החיצוניות במשושה משוכלל‪.‬‬
‫רמזים‪:‬‬
‫מה מידת זווית פנימית במתומן משוכלל?‬
‫מה מידת זווית חיצונית במצולע משוכלל?‬
‫*ג‪ .‬חשבו את סכום הזוויות החיצוניות במתומן משוכלל‪.‬‬
‫מה מידתה של כל זווית חיצונית במתומן משוכלל?‬
‫ד‪ .‬חשבו את סכום הזוויות החיצוניות במצולעים הבאים‪:‬‬
‫א‪ .‬משולש שווה‪-‬צלעות‬
‫ב‪ .‬ריבוע‬
‫האם גיליתם משהו מיוחד?‬
‫_________________________________________________________________________‬
‫‪25‬‬
‫___‬
‫ה‪ .‬ומה אם המצולע אינו משוכלל?‬
‫נתבונן במחומש ‪ .KATOM‬בכל קדקוד מסומנת זווית חיצונית‬
‫וזווית פנימית‪.‬‬
‫‪ .∡K1 + ∡K2 = 180‬הסבירו מדוע‪ .‬זווית שטוחה שווה ל‪.180º -‬‬
‫באופן דומה גם‪:‬‬
‫‪,∡A1 + ∡A2 = 180‬‬
‫‪,∡T1 + ∡T2 = 180‬‬
‫‪,∡O1 + ∡O2 = 180‬‬
‫‪. ∡M1 + ∡M2 = 180‬‬
‫הסבירו מדוע סכום כל הזוויות הפנימיות (המסומנות ב‪ )1 -‬והזוויות החיצוניות (המסומנות ב‪ )2-‬ביחד הוא‪:‬‬
‫‪.5  180 = 900‬‬
‫סכום הזוויות הפנימיות במחומש הוא ‪.540‬‬
‫לכן סכום הזוויות החיצוניות הוא ‪900 – 540 = 360º‬‬
‫באופן דומה אפשר להראות כי בכל מצולע‪ ,‬גם אם אינו משוכלל‪ ,‬סכום הזוויות החיצוניות הוא ‪.360‬‬
‫נוסיף לארגז הכלים‪:‬‬
‫סכום הזוויות החיצוניות בכל מצולע קמור הוא ‪. 360º‬‬
‫ניתן לתת דוגמה נוספת על מתומן‪:‬‬
‫_________________________________________________________________________‬
‫‪26‬‬
‫___‬
‫אתנחתא – עמ' ‪208‬‬
‫האתנחתא מציגה שתי נקודות מבט שמאירות את העובדה המפתיעה‪ :‬הגדלת מספר הצלעות של מצולע קמור לא משפיעה‬
‫על סכום הזוויות שלו שנשאר תמיד ‪ - 360‬סכום הזוויות מסביב לנקודה‪.‬‬
‫מבט מרחיק לכת‬
‫דמיינו שאתם מתבוננים במצולע ממקום רחוק‪ :‬מקצה החדר‪ ,‬מקצה הרחוב‪ ,‬מפסגת הר‪ ,‬ואולי מהירח‪.‬‬
‫ככל שמתרחקים‪ ,‬המצולע נראה יותר ויותר קטן עד אשר סכום הזוויות החיצוניות נראה כמו סכום הזוויות מסביב לנקודה‪.‬‬
‫מהו סכום הזוויות מסביב לנקודה אחת?‬
‫מבעד לעדשת המצלמה‬
‫צמצם הוא רכיב בעדשה של מצלמה‪ ,‬שמאפשר בקרה על כמות האור העובר‬
‫דרכה‪ .‬הצמצם בנוי ממספר תריסים שיוצרים פתח בצורת מצולע משוכלל‪.‬‬
‫התריסים יכולים לנוע ולשנות את גודל הפתח וכך ניתן לווסת את כמות האור הנקלט‬
‫במצלמה‪.‬‬
‫חישבו על הזוויות של תריסי הצמצם כזוויות חיצוניות לחור הצמצם שנוצר כשהתריסים נפתחים‪.‬‬
‫מהו סכום הזוויות כשהצמצם סגור?‬
‫האם סכום הזוויות משתנה כשהצמצם פתוח?‬
‫נשים לב‪ :‬התריסים של צמצם המצלמה לא משתנים כשהצמצם נפתח אלא רק מתרחקים ממרכז החור‪ ,‬ולכן סכום הזוויות‬
‫כשהצמצם פתוח שווה לסכום הזוויות כשהצמצם סגור ‪.360 -‬‬
‫חשוב‪ :‬תרגילים אלה מתייחסים למצולעים קמורים בלבד‪ ,‬גם כשאין זה מוזכר בתרגיל‪.‬‬
‫מטרת התרגיל ‪ 17‬לומר שוב‪ ,‬בניסוחים אחדים‪ ,‬כי סכום הזוויות החיצוניות של כל מצולע קמור הוא ‪ ,360‬ובמילים אחרות‬
‫ לא קיים מצולע קמור שסכום הזוויות החיצוניות שלו שונה מ‪ .360 -‬הנתון המוצג בסעיף ג‪ ,‬סכום הזוויות החיצוניות של‬‫המצולע הוא ‪ ,360‬אינו מוסיף אינפורמציה ואינו מאפשר לדעת מהו מספר הצלעות של המצולע‪.‬‬
‫עמ' ‪209‬‬
‫‪ .17‬א‪ .‬מהו סכום הזוויות החיצוניות במצולע בעל ‪ 20‬צלעות?‬
‫ב‪ .‬האם קיים מצולע שסכום הזוויות החיצוניות שלו שונה מ‪ .360 -‬הסבירו‪.‬‬
‫שימו לב‪ ,‬תרגילים אלו‬
‫מתייחסים למצולעים‬
‫קמורים בלבד‪ ,‬גם כשאין‬
‫זה מוזכר בתרגיל‪.‬‬
‫ג‪ .‬במצולע משוכלל נתון כי סכום הזוויות החיצוניות שלו הוא ‪.360‬‬
‫האם ניתן להסיק מהנתון את מספר הצלעות של המצולע?‬
‫_________________________________________________________________________‬
‫‪27‬‬
‫___‬
‫תרגיל ‪ 18‬עוסק בריצוף באמצעות אריחים זהים‪ .‬מומלץ להיעזר בערכת המחשה המופיעה בתחילת ההנחיות לפרק‬
‫להצגת פתרון תרגיל זה‪.‬‬
‫עמ' ‪ .18 209‬האם אפשר לרצף משטח באמצעות אריחים זהים שצורתם‪:‬‬
‫א‪ .‬משולש שווה‪-‬צלעות‬
‫ב‪ .‬ריבוע‬
‫ג‪ .‬מחומש משוכלל‬
‫ד‪ .‬משושה משוכלל ה‪ .‬מתומן משוכלל ?‬
‫הסבירו את תשובותיכם‪.‬‬
‫הראינו כבר שאפשר לרצף עם ריבוע‪ ,‬משולש משוכלל ומשושה משוכלל‪ .‬למעשה אלו הצורות המשוכללות היחידות‬
‫שניתן לרצף בעזרתן משטח‪ .‬מידת הזווית של מחומש משוכלל היא ‪ .108º‬מספר זה אינו מחלק של ‪ 360‬ולכן אם‬
‫נצמיד שני מחומשים יוותר מרווח‪ ,‬ואם נצמיד שלושה מחומשים לקדקוד משותף הם יכסו זה את זה‪ .‬כדאי להמחיש‬
‫זאת באמצעות ערכת המצולעים המופיעה בתחילת המדריך‪.‬‬
‫שיקול דומה אפשר להראות לגבי מתומן משוכלל‪ .‬גם מידת הזווית שלו ‪ ,135º‬איננה מחלק של ‪.360‬‬
‫‪ .19‬בסרטוטים שלפניכם חשבו את ‪.x‬‬
‫א‪.‬‬
‫‪X = 44º‬‬
‫ג‪.‬‬
‫ב‪.‬‬
‫‪ .X = 66º‬יש לשים לב‪ ,‬ש‪ x -‬זווית פנימית‪.‬‬
‫‪X = 71º‬‬
‫‪ .20‬מהו סכום הזוויות בכוכב מחומש‪.‬‬
‫אתגר‪ :‬נסו לענות על השאלה בדרכים אחדות‪.‬‬
‫ניתן למצוא את סכום הזוויות של כוכב‬
‫מחומש בדרכים רבות‪.‬‬
‫רמז היעזרו במשפט‪ :‬זווית‬
‫חיצונית במשולש‪ ,‬שווה‬
‫לסכום שתי הזוויות הפנימיות‬
‫שאינן צמודות לה‪.‬‬
‫הדרך המוצגת כאן מפתיעה בפשטותה‬
‫ומתבססת על המשפט‪ :‬זווית חיצונית במשולש שווה לסכום שתי‬
‫הזוויות הפנימיות שאינן צמודות לה‪.‬‬
‫נסמן את זוויות הכוכב במספרים‪.‬‬
‫נתבונן בזוויות המשולש ‪:GFC‬‬
‫‪ .∡G = ∡1 + ∡3‬זווית זו חיצונית למשולש ‪.DEG‬‬
‫‪ .∡F = ∡2 + ∡5‬זווית זו חיצונית למשולש ‪.ABF‬‬
‫‪∡1 + ∡3 + ∡2 + ∡5 + ∡4 = ∡G + ∡F + ∡C = 180‬‬
‫אם אף תלמיד בכתה לא יציג פתרון זה מומלץ לסרטט על הלוח את‬
‫הסרטוט המצורף לפתרון‪ ,‬עם המשולש המודגש ועם סימון הזוויות ולתת לתלמידים לפענח את ההוכחה המסתתרת‬
‫בסרטוט‪.‬‬
‫_________________________________________________________________________‬
‫‪28‬‬
‫___‬
‫על מצולעים וזוויות ‪ -‬עיקרי הדברים – עמ' ‪209‬‬
‫בכל מצולע בעל ‪ n‬צלעות סכום הזוויות הפנימיות הוא )‪.180(n–2‬‬
‫במצולע משוכלל בעל ‪ n‬צלעות מידת כל זווית פנימית היא‬
‫‪180   n  2‬‬
‫‪n‬‬
‫‪.‬‬
‫במרובע קמור בעל ‪ n‬צלעות סכום הזוויות החיצוניות הוא ‪.360‬‬
‫זווית חיצונית במשולש שווה לסכום שתי הזוויות הפנימיות שאינן צמודות לה‪.‬‬
‫_________________________________________________________________________‬
‫‪29‬‬
‫___‬
‫משולש שווה‪-‬שוקיים – מדריך למורה‬
‫משולש שווה‪-‬שוקיים נלמד בכמה סבבים‪ .‬בכיתה ח מטרות ההוראה היו על פי תכנית הלימודים‪ ,‬ללמד את תכונות משולש‬
‫שווה‪-‬שוקיים ולעסוק במשפט‪ :‬במשולש שווה‪-‬שוקיים זוויות הבסיס שוות זו לזו‪ ,‬ולא ללמד ולעסוק במשפט ההפוך או במושג‬
‫"משפט הפוך" בהם נעסוק בהרחבה בהוראה בכיתה ט‪.‬‬
‫עם זאת‪ ,‬במסגרת ספרי "אפשר גם אחרת" לכיתה ח‪ ,‬חלק א‪ ,‬הצענו פעילויות הרחבה והעשרה מעבר לתוכנית הלימודים‬
‫שעוסקת במשפט ההפוך למשפט על זוויות הבסיס במשולש שווה‪-‬שוקיים וכן פעילות אינטגרטיבית העוסקת במשולשים‬
‫חופפים ומשולשים שווי‪-‬שוקיים הנוצרים על ידי ישרים במערכת צירים‪.‬‬
‫מורים שלא הספיקו ללמד פעילויות אלו בכיתה ח‪ ,‬מוזמנים לעיין בפעילויות ‪ 20‬ו‪ 21-‬עמודים ‪ 289-290‬ובתרגילים ‪134-137‬‬
‫ולשלב גם אותם בהוראה בהתאם לצורך‪.‬‬
‫זו אחת הסיבות שאנו קוראים לפרק זה מפגש חוזר והרחבה‪ ,‬כי למעשה משולש שווה‪-‬שוקיים נלמד בכיתה ח‪.‬‬
‫חשוב לציין כי עיקר התרגול בנושא משולש שווה‪-‬שוקיים נמצא בפרק הדלתון ולכן אין צורך להוסיף תרגילים לפרק מעבר‬
‫לתרגילים שכבר שובצו‪.‬‬
‫הפעילות הראשונה עוסקת במשפט ההפוך‪ ,‬מבלי לציין כי זהו משפט הפוך‪ .‬בהמשך ההוראה בכיתה ט‪ ,‬נשים דגש רב יותר‬
‫על משפט ישר ומשפט הפוך‪ ,‬אך בפרק זה נזרעים הזרעים הראשונים לרעיון ובפעילות ‪ 3‬אנו מחדדים לתלמידים את ההבדל‬
‫בין שני המשפטים‪.‬‬
‫פעילות ‪ – 1‬משולש בעל שתי זוויות שוות – עמ' ‪210‬‬
‫לפעילות ‪ 1‬שתי מטרות עיקריות‪ :‬מטרה ראשונה הוכחת המשפט ההפוך למשפט על זוויות הבסיס במשולש שווה‪-‬שוקיים‬
‫ומטרה שנייה היא עיסוק בכתיבת הוכחה פורמלית ומסודרת‪ .‬כדי להקל על התלמידים מחד ולתרגל אותם בכתיבת הוכחה‬
‫פורמלית מאידך‪ ,‬התחלנו ממקרה פרטי בו נתון כי זוויות הבסיס שוות ל‪ .70º -‬מקרה זה מפורט כדוגמה פתורה עם דגשים‬
‫מרכזים בכתיבת הוכחה‪ .‬כשלב שני‪ ,‬אנו מבקשים מהתלמידים להשלים את ההוכחה הכללית בהתאם להבנות שלהם‬
‫מההוכחה של המקרה הפרטי‪.‬‬
‫אנו לוקחים בחשבון שגם בכיתות ח עסקנו בכתיבת הוכחות והלמידה בכיתה ט מתבססת גם על התנסויות אלו‪.‬‬
‫________ ____________________________________________________________________________________________________‬
‫‪30‬‬
‫פעילות ‪ – 1‬משולש בעל שתי זוויות שוות‬
‫ראינו שבמשולש שווה‪-‬שוקיים זוויות הבסיס שוות‪.‬‬
‫‪A‬‬
‫האם כל משולש שיש לו זוג זוויות שוות הוא משולש שווה‪-‬שוקיים?‬
‫נבדוק תחילה מקרה פרטי‪.‬‬
‫נתון משולש שבו שתי זוויות שמידתן ‪∡B = ∡C = 70 .70‬‬
‫האם ניתן להסיק שהמשולש שווה‪-‬שוקיים?‬
‫כדי לבדוק זאת נוסיף למשולש את הגובה לצלע ‪.BC‬‬
‫‪C‬‬
‫חשבו את כל הזוויות בסרטוט‪.‬‬
‫‪70‬‬
‫לפי איזה משפט חפיפה ניתן להסיק שהמשולשים ‪ ADC‬ו‪ ADB -‬חופפים?‬
‫‪70‬‬
‫‪B‬‬
‫‪A‬‬
‫האם המשולש ‪ ∆ABC‬שווה‪-‬שוקיים? הסבירו‪.‬‬
‫להוכחה שני שלבים עיקריים‪:‬‬
‫‪1 2‬‬
‫א‪ .‬נראה ש‪∡A1 = ∡A2 -‬‬
‫ב‪ .‬נראה ש‪ ADB  ADC -‬ונסיק ש‪AB = AC -‬‬
‫נכתוב כעת את ההוכחה בצורה מאורגנת‪.‬‬
‫נתון‪∡B = ∡C = 70 :‬‬
‫השלב בהוכחה‬
‫צ"ל‪.AB = AC :‬‬
‫‪C‬‬
‫‪70‬‬
‫‪1 2‬‬
‫‪D‬‬
‫בניית עזר‪ :‬גובה לצלע ‪.BC‬‬
‫טענה‬
‫נימוק‬
‫‪∡B = ∡C = 70‬‬
‫נתון‬
‫‪∡D1 = ∡D2 = 90‬‬
‫‪ AD‬גובה לפי בניית עזר‪.‬‬
‫‪∡A1 =180 - 90 -70 = 20‬‬
‫חישוב שמתבסס על סכום הזוויות במשולש ‪. ADB‬‬
‫‪∡A2 =180 - 90 -70 = 20‬‬
‫חישוב שמתבסס על סכום הזוויות במשולש ‪. ADC‬‬
‫‪∡A1 = ∡A2‬‬
‫לפי החישוב שערכנו‪.‬‬
‫‪AD = AD‬‬
‫צלע משותפת‪.‬‬
‫נוכיח‬
‫‪∡D1 = ∡D2‬‬
‫זוויות ישרות‪.‬‬
‫‪ADB  ADC‬‬
‫‪∡A1 = ∡A2‬‬
‫הוכחנו בשלב א‪.‬‬
‫ז‪.‬צ‪.‬ז‬
‫‪AB = AC‬‬
‫צלעות מתאימות במשולשים חופפים שוות‪.‬‬
‫‪ ABC‬שווה‪-‬שוקיים‬
‫משולש בעל שתי צלעות שוות הוא שווה‪-‬שוקיים‪.‬‬
‫שלב א‪:‬‬
‫נוכיח ש‪-‬‬
‫‪∡A1 = ∡A2‬‬
‫שלב ב‪:‬‬
‫ונסיק‬
‫‪AB = AC‬‬
‫‪70‬‬
‫‪B‬‬
‫מ‪.‬ש‪.‬ל‬
‫________ ____________________________________________________________________________________________________‬
‫‪31‬‬
‫דגשים ביחס להוכחת המשפט ההפוך‪:‬‬
‫השאלה הראשונה בפעילות בעצם מחדדת את הרעיון של משפט הפוך‪ .‬כלומר‪ ,‬ידוע לנו כי בכל משולש שווה‪-‬שוקיים זוויות‬
‫הבסיס שוות‪ ,‬האם כל משולש שיש לו זוג זוויות שוות הוא משולש שווה‪-‬שוקיים?‬
‫מורים שמעוניינים‪ ,‬זו הזדמנות ראשונה להתייחס לכמת כל ולמשמעותו במתמטיקה‪ .‬בספר העיסוק המפורש בכמת "כל"‬
‫מתבצע בפרק הדלתון‪.‬‬
‫הדגשים בכתיבת ההוכחה‪:‬‬
‫הדגשים לכתיבת ההוכחה רלוונטיים לכתיבת ההוכחה של המקרה הפרטי והכללי כאחד ויכתבו כאן בהתייחס למקרה הכללי‪.‬‬
‫הדגש הראשון בפעילות הוא זיהוי מה נתון במשפט ומה צריך להוכיח‪ .‬כאמור‪ ,‬בפרק המבוא על טענות ומסקנות‪ ,‬למדנו‬
‫להבחין בין חלקי המשפט ולהבחין בין מה שנתון לבין מה שצריך להוכיח‪ ,‬כפעילות בפני עצמה (ראו עמ' ‪ .)200‬הפעם זהו‬
‫שלב ראשון בהוכחה‪ .‬השלב הבא בהוכחה הוא בניית עזר פשוטה‪ ,‬סרטוט גובה לצלע ‪ .BC‬אם טרם התייחסתם בכיתה ח‬
‫לרעיון של בניית עזר‪ ,‬כדאי להסבירו בקצרה‪.‬‬
‫"לקראת ההוכחה " הינו הסבר של רציונל ההוכחה בכללותו‪ ,‬לרוב בהסתכלות מהסוף להתחלה‪ .‬רציונל זה מסביר מה נרצה‬
‫לה וכיח בסוף התהליך ומה אנו זקוקים לשם כך‪ ,‬בדרך‪ .‬הסבר זה מסייע לתלמידים לראות את התמונה הכללית ולהבין את‬
‫שלבי הביניים של ההוכחה‪ .‬במקרה זה‪ ,‬את הצורך בהוכחת שוויון בין הזוויות ‪ ∡A1 = ∡A2‬לצורך הוכחת חפיפת משולשים‬
‫וחפיפת משולשים לצורך הסקת שוויון בין צלעות‪.‬‬
‫כמ ו כן‪ ,‬במסגרת הפעילות אנו מציעים דרך לכתיבת הוכחה‪ .‬לאורך הספר בכיתה ט נציג דרכים שונות לכתיבת הוכחה‬
‫פורמלית מדויקת מתמטית ובכך נאפשר לתלמידים לבחור בדרך המתאימה להם מחד ונכונה מתמטית מאידך‪.‬‬
‫בפעילות זו נציג את הטבלה בעלת שלוש עמודות‪ ,‬כדרך לכתיבת הוכחה מורכבת‪ .‬העמודה הראשונה מימין‪ ,‬מטרתה להציג‬
‫את השלב בהוכחה בהתאם למה שתואר ב"לקראת הוכחה"‪ .‬בהוכחות מורכבות‪ ,‬אנחנו מוכיחים משהו אחד במטרה להוכיח‬
‫משהו אחר ולתלמידים קשה לעקוב אחר מהלך המחשבה מהסוף להתחלה‪ .‬כדי לסייע להם‪ ,‬יצרנו את העמודה הימנית בה‬
‫מופיעים כל שלבי ההו כחה‪ .‬העמודה השנייה‪ ,‬מטרתה להציג את הטענה אותה אנו טוענים ועמודה השלישית והאחרונה את‬
‫הנימוק לטענה זו‪.‬‬
‫זוהי ההוכחה הפורמלית הראשונה ובמסגרתה אנו מציגים את הסיומת "מ‪.‬ש‪.‬ל" ‪.‬‬
‫מטרת סעיף ג בפעילות הינו לחדד את ההבדל בין שני ניסוחים מקובלים של המשפט‪:‬‬
‫ניסוח ראשון‪ :‬אם למשולש יש שתי זוויות שוות‪ ,‬אז הצלעות מולן שוות‬
‫ניסוח שני‪ :‬אם למשולש יש שתי זוויות שוות‪ ,‬אז המשולש שווה‪-‬שוקיים‪.‬‬
‫יתרונו של הניסוח השני‪ ,‬הוא קבלת שני משפטים הפוכים סימטריים‪ .‬בזכות הסימטריה‪ ,‬לתלמידים קל לעקוב להבחין כי אלו‬
‫שני משפטים הפוכים‪ .‬חסרונו בהשוואה לניסוח שהראשון‪ ,‬הינו המידע המתקבל‪ .‬בניסוח הראשון אנו מקבלים מידע גם מי הן‬
‫הצלעות השוות במשולש‪ .‬חשוב לדון על נקודות אלו עם התלמידים‪.‬‬
‫________ ____________________________________________________________________________________________________‬
‫‪32‬‬
‫האם יכולנו להראות שהמשולש שווה‪-‬שוקיים גם ללא מידע על מידות הזוויות?‬
‫‪A‬‬
‫נוכיח משפט‪ :‬אם למשולש יש שתי זוויות שוות‪ ,‬אז הצלעות מולן שוות‪.‬‬
‫נתון‪∡B = ∡C =  :‬‬
‫‪1 2‬‬
‫הוכיחו כי ‪.AB = AC‬‬
‫השלימו את החישובים והנימוקים החסרים בהוכחה הבאה‪:‬‬
‫שלב א‪:‬‬
‫נוכיח ש‪-‬‬
‫‪∡A1 = ∡A2‬‬
‫שלב ב‪:‬‬
‫נוכיח‬
‫‪C‬‬
‫‪1 2‬‬
‫‪D‬‬
‫טענה‬
‫נימוק‬
‫‪∡B = ∡C‬‬
‫נתון‪.‬‬
‫‪∡D1 = ∡D2 = 90‬‬
‫‪ AD‬גובה לפי בנייה‪.‬‬
‫‪∡A1 =180 - ∡B -∡D1‬‬
‫חישוב שמתבסס על סכום הזוויות במשולש ‪ABD‬‬
‫‪∡A1 = 90º- ∡B‬‬
‫הצבת ‪∡D1‬‬
‫‪∡A2 =180 - ∡B -∡D2‬‬
‫חישוב שמתבסס על סכום הזוויות במשולש ‪ACD‬‬
‫‪∡A2 = 90º- ∡B‬‬
‫הצבת ‪∡D2‬‬
‫‪∡A1 = ∡A2‬‬
‫שתיהן שוות ‪90º- ∡B‬‬
‫‪AD = AD‬‬
‫‪∡D1 = ∡D2‬‬
‫זוויות ישרות‪.‬‬
‫‪∡A1 = ∡A2‬‬
‫הוכחנו בשלב א‪.‬‬
‫‪ ADB   ADC‬‬
‫ז‪.‬צ‪.‬ז‬
‫‪B‬‬
‫ונסיק‬
‫‪AB = AC‬‬
‫‪AB = AC‬‬
‫צלעות מתאימות במשולשים חופפים שוות‪.‬‬
‫מ‪.‬ש‪.‬ל‬
‫הקיצור מ‪.‬ש‪.‬ל‪ .‬או מש"ל פירושו‪ :‬מה שהיה צריך‬
‫להוכיח‪ .‬נהוג לרשום קיצור זה בסיום ההוכחה‪.‬‬
‫משפט‪ :‬אם למשולש יש שתי זוויות שוות‪ ,‬אז הצלעות מולן שוות‪.‬‬
‫ג‪ .‬גלעד ה ציע לנסח את המשפט כך‪ :‬אם למשולש יש שתי זוויות שוות‪ ,‬אז המשולש שווה‪-‬שוקיים‪.‬‬
‫מה ההבדל בין שני הניסוחים?‬
‫משפט‪ :‬אם למשולש יש שתי זוויות שוות‪ ,‬אז המשולש שווה‪-‬שוקיים‪.‬‬
‫________ ____________________________________________________________________________________________________‬
‫‪33‬‬
‫פעילות ‪ – 2‬האם התבססנו רק על הידוע לנו? – עמ' ‪212‬‬
‫המטרה המרכזית של פעילות ‪ 2‬היא לעסוק בשגיאות נפוצות אצל תלמידים‪ .‬שגיאה אחת היא התבססות על מידע שאינו‬
‫נתון במהלך ההוכחה דבר שעלול ליצור מעגליות בהוכחה‪ .‬במקרה זה‪ ,‬התבססות על תכונות משולש שווה‪-‬שוקיים‪ ,‬לפני‬
‫שהוכח שהמשולש הוא משולש שווה‪-‬שוקים‪ .‬שגיאה נוספת היא השימוש במושג "זוויות בסיס" השמור לזוויות במשולש שווה‪-‬‬
‫שוקיים בלבד לפני שהוכחנו שהמשולש שווה‪-‬שוקיים‪ .‬הבהרה זו נעשת על ידי סעיף ב בו עדי מציעה ניסוח פשוט למשפט‬
‫שהוכח ועל התלמידים לזהות את הבעייתיות בניסוח המוצע‪.‬‬
‫מטרה משנית של הפעילות היא פיתוח מיומנות קריאת הוכחה‪ .‬במסגרת פעילות ‪ ,2‬התלמידים צריכים לקרוא הוכחה נתונה‬
‫ולזהות בה את השגיאה‪ .‬בפעילות מוצהר כי התלמיד שכתב את ההוכחה התבסס על מידע שאינו נתון ועל התלמידים לאתר‬
‫מהו המידע שלא ניתן היה להתבסס עליו‪.‬‬
‫פעילות ‪ 2‬היא הזדמנות לחדד ידע מתמטי על ידי דיון עם תלמידים בשגיאות נפוצות שלהם – שימוש במידע שאינו נתון‬
‫במסגרת ההוכחה ושימוש במושגים שמורים‪ ,‬שלא במקומם‪.‬‬
‫________ ____________________________________________________________________________________________________‬
‫‪34‬‬
‫פעילות ‪ – 3‬באיזה משפט השתמשנו בכל שלב של ההוכחה? – עמ' ‪213‬‬
‫המטרה המרכזית של‬
‫פעילות ‪ 3‬היא התייחסות‬
‫לאבחנה בין משפט‬
‫למשפט הפוך מבלי לציין‬
‫זאת בצורה מפורשת‪.‬‬
‫בפעילות התלמידים‬
‫מתנסים בהוכחה שיש‬
‫בה שימוש במשפט‬
‫ובמשפט ההפוך‪ .‬שימוש‬
‫בשני המשפטים במסגרת‬
‫הוכחה אחת‪ ,‬מחדדת‬
‫את ההבדל ביניהם‪.‬‬
‫בשלב הראשון נתון‬
‫שהמשולש הוא שווה‪-‬‬
‫שוקיים ולכן מותר לנו‬
‫להסיק כי זוויות הבסיס‬
‫שוות‪ .‬מאוחר יותר בגלל‬
‫שהוכחנו שוויון בין זוויות‪,‬‬
‫נוכל להסיק שוויון בין‬
‫הצלעות שמולן‪.‬‬
‫ההוכחה המלאה‪:‬‬
‫טענה‬
‫נימוק‬
‫‪∡A = ∡L‬‬
‫אם משולש הוא שווה‪-‬שוקיים אז זוויות הבסיס‬
‫שלו שוות‪.‬‬
‫‪1‬‬
‫‪A‬‬
‫‪2‬‬
‫‪A1 ‬‬
‫נתון ש‪ AG -‬חוצה את הזווית ‪.∡A‬‬
‫‪1‬‬
‫‪L‬‬
‫‪2‬‬
‫‪L1 ‬‬
‫נתון ש‪ LG -‬חוצה את הזווית ‪.∡L‬‬
‫‪1‬‬
‫‪1‬‬
‫‪A‬‬
‫‪L‬‬
‫‪2‬‬
‫‪2‬‬
‫חצאי זוויות שוות שווים‪.‬‬
‫‪AG = LG‬‬
‫אם במשולש יש שתי זוויות שוות אז הצלעות‬
‫מולן שוות‪.‬‬
‫‪ GAL‬שווה‪-‬שוקיים‬
‫משולש בעל שתי צלעות שוות הוא שווה‪ -‬שוקיים‬
‫מ‪.‬ש‪.‬ל‬
‫________ ____________________________________________________________________________________________________‬
‫‪35‬‬
‫פעילות ‪ – 4‬משולש בו גובה וחוצה‪-‬זווית מתלכדים – עמ' ‪214‬‬
‫מטרת פעילות ‪4‬‬
‫היא להציג ולהוכיח‬
‫תנאי נוסף המבטיח‬
‫שמשולש הוא‬
‫שווה‪-‬שוקיים‪ :‬אם‬
‫במשולש גובה לצלע‬
‫וחוצה זווית‬
‫מתלכדים אז‬
‫המשולש‬
‫שווה‪-‬שוקיים‪.‬‬
‫מטרה נוספת של‬
‫הפעילות היא‬
‫ההבנה של אופן‬
‫השימוש במשפטים‬
‫בהוכחות‪.‬‬
‫מטרת סעיף ג‪ ,‬היא‬
‫להבהיר לתלמידים‬
‫כי מהרגע שהוכחנו‬
‫משפט נוכל‬
‫להשתמש בו‬
‫בהוכחות חדשות‪,‬‬
‫ללא צורך בהוכחת‬
‫המשפט עצמו‪ ,‬בדיוק‬
‫כפי שמציע זמר‪.‬‬
‫חשוב להדגיש כי גם‬
‫דרכה של שיר נכונה‪.‬‬
‫________ ____________________________________________________________________________________________________‬
‫‪36‬‬
‫מטרת פעילות ‪ 5‬היא להוסיף עוד תנאי על התנאים המבטיחים שמשולש הוא שווה‪-‬שוקיים‪ :‬אם במשולש גובה לצלע ותיכון‬
‫לאותה צלע מתלכדים אז המשולש שווה‪-‬שוקיים‪ .‬מטרה נוספת של הפעילות היא חזרה ותרגול של ניסוח משפטים‬
‫מתמטיים בצורת אם‪ ...‬אז‪ ,...‬המקלה על התלמידים בזיהוי הנתון במשפט ומה צריך להוכיח‪ ,‬כפי שעשינו בפעילות‬
‫הפתיחה‪ ,‬פעילות ‪ – 3‬נתונים ומסקנות‪ ,‬עמ' ‪.200‬‬
‫פעילות ‪ – 5‬משולש בו גובה ותיכון מתלכדים – עמ' ‪215‬‬
‫א‪ .‬נסחו באמצעות "אם" ו"אז" את המשפט‪:‬‬
‫"משולש שבו תיכון לצלע הוא גם גובה לאותה צלע הוא משולש שווה‪-‬שוקיים"‪.‬‬
‫אם ______________________ אז _______________________‬
‫ב‪ .‬כדי להוכיח את המשפט נסרטט משולש ‪ ABC‬ונסמן ב‪ M -‬את אמצע הצלע ‪.BC‬‬
‫‪A‬‬
‫ג‪ .‬הוכיחו את המשפט שניסחתם‪.‬‬
‫נתון‪ :‬א‪BM=MC .‬‬
‫ב‪AM  BC .‬‬
‫הוכיחו ש ‪AMB  AMC‬‬
‫והסיקו מסקנה מהחפיפה‪.‬‬
‫על איזה משפט חפיפה תתבססו הפעם?‬
‫‪1 2‬‬
‫צ"ל‪_____ :‬‬
‫‪C‬‬
‫‪M‬‬
‫‪B‬‬
‫תבנית הוכחה‬
‫טענה‬
‫נימוק‬
‫‪∡M1 = ∡M2 = 90‬‬
‫‪ AM‬גובה לפי בנייה‪.‬‬
‫‪BM = MC‬‬
‫נתון תיכון‪.‬‬
‫‪AM = AM‬‬
‫‪AMB ≅ AMC‬‬
‫‪AB = AC‬‬
‫לפי צ‪.‬ז‪.‬צ‪.‬‬
‫צלעות מתאימות במשולשים חופפים‪.‬‬
‫מ‪.‬ש‪.‬ל‬
‫________ ____________________________________________________________________________________________________‬
‫‪37‬‬
‫תרגילים – עמ' ‪218 – 216‬‬
‫תרגיל ‪ 1‬הינו תרגול יכולת ההנמקה וזיהוי תכונות משולש שווה‪-‬שוקיים עליהן ניתן להתבסס‪.‬‬
‫כמו כן‪ ,‬התרגיל מאפשר שימוש במושגים ותכונות שנלמדו בכיתות ז‪-‬ח כמו‪ ,‬המעגל וזווית חיצונית במשולש‪.‬‬
‫עמ' ‪216‬‬
‫‪ .1‬הראו שהמשולשים הבאים הם שווי‪-‬שוקיים ורשמו מי הן שוקי המשולש‪.‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪A‬‬
‫ג‪.‬‬
‫‪L‬‬
‫‪46‬‬
‫ד‪.‬‬
‫‪W‬‬
‫‪P‬‬
‫‪45‬‬
‫‪130‬‬
‫‪30‬‬
‫‪50‬‬
‫‪M 80‬‬
‫‪S‬‬
‫‪C‬‬
‫‪K‬‬
‫‪45‬‬
‫‪30‬‬
‫‪67‬‬
‫‪60‬‬
‫‪V‬‬
‫‪B‬‬
‫זיהוי מידת הזווית‬
‫השלישית מתוך סכום‬
‫זוויות במשולש‪.‬‬
‫‪AC = AB‬‬
‫‪50‬‬
‫‪F‬‬
‫‪R‬‬
‫זיהוי מידת הזווית‬
‫השלישית מתוך סכום‬
‫זוויות במשולש‪.‬‬
‫‪LS = SV‬‬
‫חישוב זוויות על‬
‫סמך זווית‬
‫חיצונית‪.‬‬
‫‪MP = MF‬‬
‫חישוב זווית על‬
‫סמך זווית‬
‫חיצונית‪.‬‬
‫‪KW = KR‬‬
‫‪ A .2‬ו‪ B -‬הן נקודות על מעגל שמרכזו בנקודה ‪.M‬‬
‫‪B‬‬
‫‪M‬‬
‫א‪ .‬הוכיחו שהמשולש ‪ MAB‬שווה‪-‬שוקיים‪.‬‬
‫שתיים מצלעות המשולש הן רדיוסים של המעגל ולכן הצלעות שוות באורכן‪.‬‬
‫‪.AM=MB‬‬
‫‪A‬‬
‫ב‪ .‬הוכיחו‪.∡MBA =∡MAB :‬‬
‫נצפה כאן מהתלמידים שימוש במשפט אם משולש הוא שווה‪-‬שוקיים אז זוויות הבסיס שלו שוות‪.‬‬
‫‪ ,R ,G ,F .3‬ו‪ S -‬הן נקודות על מעגל שמרכזו בנקודה ‪.M‬‬
‫‪R‬‬
‫א‪ .‬נתון‪ .∡MFG = 15 :‬חשבו את ‪.150º . ∡FMG‬‬
‫בתרגיל זה‪ ,‬אנו רוצים שהתלמידים יעברו את השרשרת ההסקית הבאה‪:‬‬
‫‪M‬‬
‫‪S‬‬
‫יוכיחו כי המשולש ‪ FMG‬שווה‪-‬שוקיים כפי שהוכיחו בתרגיל ‪ 2‬בהתבסס על‬
‫הרדיוסים ‪ .FG = MG‬יסיקו מכך שאם המשולש הוא שווה‪-‬שוקיים אז זוויות‬
‫הבסיס שלו שוות וישתמשו בחישוב סכום זוויות במשולש לחישוב הזווית ‪.∡FMG‬‬
‫‪G‬‬
‫‪F‬‬
‫ב‪ .‬נתון‪ .∡SMR = 50 :‬חשבו את ‪65º . ∡MSR‬‬
‫גם כאן יש את אותה שרשרת הסקית כמו בסעיף א‪ .‬ניתן לפתור בכיתה את סעיף א ולתת לתלמידים לפתור את סעיף ב‬
‫באופן עצמאי בבית או בכיתה‪.‬‬
‫________ ____________________________________________________________________________________________________‬
‫‪38‬‬
‫הסרטוטים בעמוד זה‪,‬‬
‫מופיעים בהקטנה‪.‬‬
‫דוגמה פתורה ‪ -‬עמ' ‪216‬‬
‫חשבו את השטח ואת ההיקף של המשולש שווה‪-‬שוקיים שלפניכם‪.‬‬
‫‪N‬‬
‫הסבירו את החישובים‪ .‬היעזרו במשפט פיתגורס‪ .‬הסרטוט מופיע בהקטנה‪.‬‬
‫‪ 15‬ס"מ = ‪( NB‬מדוע?)‬
‫‪10‬‬
‫‪A‬‬
‫נחשב את אורך השוקיים בעזרת משפט פיתגורס‪:‬‬
‫לפי משפט פיתגורס‪NB2  AB2  152  102  325  18.027 :‬‬
‫‪30 B‬‬
‫= ‪AN = AV‬‬
‫לכן‪ ,‬ההיקף הוא‪ 66.054 :‬ס"מ‬
‫והשטח הוא‪ 150 :‬סמ"ר‪.‬‬
‫‪V‬‬
‫עמ' ‪ .4 217‬חשבו את השטח ואת ההיקף של כל המשולשים השווי‪-‬שוקיים שלפניכם‪ .‬הסבירו את החישובים‪.‬‬
‫‪20‬‬
‫א‪.‬‬
‫‪B‬‬
‫‪E‬‬
‫‪Y‬‬
‫‪21‬‬
‫ב‪.‬‬
‫היעזרו במשפט‬
‫פיתגורס‪.‬‬
‫‪Q‬‬
‫‪10‬‬
‫‪25‬‬
‫במידת הצורך דייקו עד ‪ 2‬ספרות‬
‫אחרי הנקודה העשרונית‪.‬‬
‫‪X‬‬
‫‪L‬‬
‫‪EL = BL  26.93‬‬
‫שטח‪ 250 :‬סמ"ר‬
‫היקף‪ 73.85 :‬ס"מ‬
‫‪YQ = QX = 21‬‬
‫שטח‪ 184.66 :‬סמ"ר‬
‫היקף‪ 78.93 :‬ס"מ‬
‫‪ .5‬חשבו את השטח ואת ההיקף של כל המשולשים השווי‪-‬שוקיים שלפניכם‪ .‬הסבירו את החישובים‪.‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪T‬‬
‫‪2.2‬‬
‫ג‪.‬‬
‫‪E‬‬
‫‪2.7‬‬
‫‪1.8‬‬
‫‪2.5‬‬
‫היעזרו במשפט‬
‫פיתגורס‬
‫‪D‬‬
‫‪A‬‬
‫‪Z‬‬
‫‪3.6‬‬
‫‪N‬‬
‫‪2‬‬
‫‪E‬‬
‫‪TN = TE = 2.2 ; h  1.96‬‬
‫שטח‪ 1.96 :‬סמ"ר‬
‫היקף‪ 6.4 :‬ס"מ‬
‫‪R‬‬
‫‪G‬‬
‫‪ZN = ZE = 2.7 ; h  2.55‬‬
‫שטח‪ 2.29 :‬סמ"ר‬
‫היקף‪ 7.2 :‬ס"מ‬
‫‪DA = DG = 2.5 ; h  1.73‬‬
‫שטח‪ 3.12 :‬סמ"ר‬
‫היקף‪ 8.6 :‬ס"מ‬
‫________ ____________________________________________________________________________________________________‬
‫‪39‬‬
‫בתרגילים הבאים רשמו תחילה‬
‫מה נתון ומה צריך להוכיח‪.‬‬
‫עמ' ‪217‬‬
‫‪ .6‬במלבן ‪ FARM‬הקטע ‪ MO‬חוצה את הזווית ‪ ∡M‬והקטע ‪ RO‬חוצה את הזווית ‪.∡R‬‬
‫‪A‬‬
‫‪F‬‬
‫א‪ .‬חשבו את זוויות המשולש ‪. MOR‬‬
‫‪1‬‬
‫סעיף א‪ ,‬הינו סעיף מדרגה‪.‬‬
‫‪R‬‬
‫‪ FARM‬מלבן ולכן‪∡R = ∡M = 90º ,‬‬
‫‪∡M1 = ∡M2 = 45º‬‬
‫‪O‬‬
‫‪2‬‬
‫‪2‬‬
‫‪1‬‬
‫‪M‬‬
‫(הקטע ‪ MO‬חוצה את הזווית ‪)∡M‬‬
‫‪( ∡R1 = ∡R2 = 45º‬הקטע ‪ RO‬חוצה את הזווית ‪)∡R‬‬
‫ב‪ .‬הוכיחו כי המשולש ‪ MOR‬שווה‪-‬שוקיים (‪.)OM = OR‬‬
‫מוצגת כאן דוגמה לאופן כתיבה אפשרי של ההוכחה גם ללא סעיף א‪.‬‬
‫‪( ∡M1 = ∡M2‬הקטע ‪ MO‬חוצה את הזווית ‪)∡M‬‬
‫נתון‪:‬‬
‫‪( ∡R1 = ∡R2‬הקטע ‪ RO‬חוצה את הזווית ‪)∡R‬‬
‫צריך להוכיח‪OM = OR :‬‬
‫הוכחה‪:‬‬
‫טענה‬
‫נימוק‬
‫‪∡M = ∡R = 90º‬‬
‫נתון כי ‪ FARM‬הוא מלבן‪.‬‬
‫‪1‬‬
‫‪1‬‬
‫‪M‬‬
‫‪R  45o‬‬
‫‪2‬‬
‫‪2‬‬
‫הקטעים ‪ MO‬ו‪ RO -‬חוצי‬
‫‪R2‬‬
‫‪M2 ‬‬
‫המשולש ‪ MOR‬שווה‪-‬שוקיים‪.‬‬
‫זויות‪.‬‬
‫זוויות השוות ל ‪.45º‬‬
‫אם במשולש יש שתי זוויות שוות אז המשולש שווה‪-‬שוקיים‪.‬‬
‫מ‪.‬ש‪.‬ל‬
‫________ ____________________________________________________________________________________________________‬
‫‪40‬‬
‫תרגיל ‪ 7‬דומה מאד לפעילות ‪ .3‬העובדה שנתון משולש שווה‪-‬צלעות מקצרת את השרשרת ההיסקית‪.‬‬
‫‪F‬‬
‫עמ' ‪ .7 217‬המשולש ‪ NOF‬הוא שווה‪-‬צלעות‪ .‬הקטע ‪ SF‬חוצה את הזווית ‪∡F‬‬
‫‪1‬‬
‫‪2‬‬
‫‪1‬‬
‫‪2‬‬
‫והקטע ‪ SO‬חוצה את הזווית ‪.∡O‬‬
‫‪S‬‬
‫הוכיחו כי המשולש ‪ SOF‬שווה‪-‬שוקיים‪.‬‬
‫‪N‬‬
‫נתון‪:‬‬
‫‪O‬‬
‫‪( ∡F1 = ∡F2‬הקטע ‪ SF‬חוצה את הזווית ‪)∡F‬‬
‫‪( ∡O1 = ∡O2‬הקטע ‪ SO‬חוצה את הזווית ‪)∡O‬‬
‫‪ NOF‬הוא שווה‪-‬צלעות‪.‬‬
‫צריך להוכיח‪SF = SO :‬‬
‫טענה‬
‫נימוק‬
‫‪∡F = ∡O = 60º‬‬
‫נתון כי ‪ NOF‬הוא שווה‪-‬צלעות‪.‬‬
‫‪1‬‬
‫‪1‬‬
‫‪F‬‬
‫‪O  300‬‬
‫‪2‬‬
‫‪2‬‬
‫‪1‬‬
‫‪1‬‬
‫‪F1 ‬‬
‫‪F‬‬
‫‪O  O1‬‬
‫‪2‬‬
‫‪2‬‬
‫עמ' ‪218‬‬
‫המשולש ‪SOF‬‬
‫אם במשולש יש שתי זוויות שוות אז המשולש שווה‪-‬שוקיים‪.‬‬
‫שווה‪-‬שוקיים‪.‬‬
‫מ‪.‬ש‪.‬ל‬
‫‪R‬‬
‫‪ .8‬המשולש ‪ ROM‬שווה‪-‬שוקיים‪ .‬נתון ש‪.∡ROT = ∡RMT -‬‬
‫א‪ .‬הוכיחו ש‪∡TOM = ∡TMO -‬‬
‫‪T‬‬
‫ב‪ .‬הוכיחו שהמשולש ‪ TOM‬שווה‪-‬שוקיים‪.‬‬
‫‪O‬‬
‫רעיון לפתרון‪ :‬באמצעות הפרש זוויות‪ .‬נתון ש‪ ROM -‬שווה‪-‬שוקיים ולכן זוויות הבסיס שוות‪.‬‬
‫‪M‬‬
‫נתון גם ש‪ ∡ROT = ∡RMT -‬מהפרש זוויות נקבל כי שתי זוויות של המשולש ‪ TOM‬שוות (סעיף א)‬
‫ולכן הוא משולש שווה‪-‬שוקיים (סעיף ב)‪.‬‬
‫סעיף א הינו סעיף מדרגה הנועד לכוון את התלמידים להוכחה המתבססת על חשבון זוויות והמשפט‬
‫‪R‬‬
‫"אם במשולש שתי זוויות שוות אז הצלעות מולן שוות"‪.‬‬
‫חלק מהתלמידים עשוי לנסות להתבסס על חפיפת משולשים ולהוסיף את הקטע ‪( RT‬ראו סרטוט)‬
‫כדי להוכיח את הטענה על ידי חפיפה של המשולשים ‪ RMT‬ו‪ .ROT -‬פעולה זו אינה נכונה כיוון‬
‫‪T‬‬
‫‪O‬‬
‫שהזוויות הש וות נמצאות מול הצלע המשותפת‪ ,‬ולא ניתן להיעזר בחפיפת משולשים להוכחת‬
‫הטענה‪.‬‬
‫‪M‬‬
‫מהלך ההוכחה דומה להוכחה שבפעילות ‪ ,3‬אלא שבמקום להתבסס על שוויון של חצאי זוויות שוות אנחנו מתבססים כאן על‬
‫הפרש של זוויות שוות‪.‬‬
‫התרגיל נועד לחזור ולדון בשאלה מתי אנו מתבססים על המשפט "אם משולש הוא שווה‪-‬שוקיים אז זוויות הבסיס שלו שוות"‬
‫ומתי על המשפט "אם במשולש שתי זוויות שוות אז הצלעות מולן שוות"‪.‬‬
‫________ ____________________________________________________________________________________________________‬
‫‪41‬‬
‫עמ' ‪218‬‬
‫‪.9‬‬
‫‪ M‬נקודה על הצלע ‪ SL‬של המשולש ‪ .SAL‬הסרטוט מופיע בהקטנה‪.‬‬
‫‪A‬‬
‫נתון‪1.5 :‬ס"מ = ‪SM = ML‬‬
‫‪AM  SL‬‬
‫‪ 2‬ס"מ = ‪. AM‬‬
‫א‪ .‬הוכיחו שהמשולש ‪ SAL‬שווה‪-‬שוקיים‪.‬‬
‫‪L‬‬
‫‪M‬‬
‫מטרת סעיף א הוא שימוש במשפט‪ :‬אם במשולש גובה ותיכון מתלכדים אז המשולש שווה‪-‬שוקיים‪.‬‬
‫‪S‬‬
‫על התלמידים לשים לב לנתונים ולזהות כי ‪ AM‬הינו תיכון וגם גובה‪.‬‬
‫ב‪ .‬חשבו את השטח ואת ההיקף של המשולש ‪ .SAL‬שטח‪ 3 :‬סמ"ר היקף‪ 8 :‬ס"מ‪.‬‬
‫מטרת סעיף ב שימוש בתכונות משולש שווה‪-‬שוקיים‪ ,‬משפט פיתגורס והמושגים היקף ושטח‪.‬‬
‫‪ .10‬המשולש ‪ ROM‬שווה‪-‬שוקיים‪ .‬הקטע ‪ RD‬חוצה את ‪ ∡R . ∡OTM‬זווית ראש‪.‬‬
‫‪R‬‬
‫הנקודה ‪ T‬נמצאת על ‪.RD‬‬
‫א‪ .‬הוכיחו כי ‪ .OTD  MTD‬לפי צ‪.‬ז‪.‬צ‪.‬‬
‫‪T‬‬
‫נשתמש במשפט שחוצה זווית הוא גם גובה וגם תיכון‪.‬‬
‫‪O‬‬
‫ב‪ .‬הוכיחו שהמשולש ‪ TOM‬שווה‪-‬שוקיים‪ .‬מתוך החפיפה נובע ‪.MT = OT‬‬
‫‪D‬‬
‫‪M‬‬
‫‪D‬‬
‫‪ .11‬המשולש ‪ DAF‬שווה‪-‬שוקיים (‪.)DA = DF‬‬
‫‪ DM‬הגובה לבסיס‪ K .‬נקודה על ‪.DM‬‬
‫א‪ .‬הוכיחו כי‬
‫‪ .AM = MF‬גובה במשולש שווה‪-‬שוקיים הוא גם תיכון‪.‬‬
‫‪F‬‬
‫ב‪ .‬הוכיחו שהמשולש ‪ KAF‬שווה‪-‬שוקיים‪.‬‬
‫‪K‬‬
‫‪M‬‬
‫‪A‬‬
‫רעיון לפתרון‪:‬‬
‫אפשרות א‪ :‬מנתוני הבעיה אנו רואי כי מתקיים המשפט ההפוך‪" :‬משולש שבו תיכון לצלע הוא גם גובה לאותה צלע‪,‬‬
‫הוא משולש שווה‪-‬שוקיים"‪ ,‬ולכן נקבל כי ‪ KAF‬שווה‪-‬שוקיים‪.‬‬
‫אפשרות ב‪ :‬באמצעות משפט חפיפה צ‪.‬ז‪.‬צ מוכיחים כי המשולשים ‪ KFM‬ו‪ KAM -‬חופפים‪.‬‬
‫________ ____________________________________________________________________________________________________‬
‫‪42‬‬
‫דלתון – מדריך למורה‬
‫הדלתון נבחר כמרובע הראשון שנלמד במסגרת שיעורי הגאומטריה בכיתה ט‪ ,‬כי הוראת הדלתון פשוטה מבחינה היסקית‪,‬‬
‫מאפשרת שימוש וחיזוק של ידע שנלמד בכיתות ז ו‪ -‬ח ונושא הדלתון חדש יחסית לתלמידים‪ .‬הרעיון בהוראת הגאומטריה‬
‫בכיתה ט‪ ,‬הוא לפתח בצורה הדרגתית את מיומנויות ההיסק וכתיבת ההוכחה‪ .‬לכן‪ ,‬בפרק זה נמנע מהוכחות מורכבות‬
‫ומרובות שלבים או הוכחות בדרך השלילה שאליהן נגיע בשלב מאוחר יותר של ההוראה‪ .‬לעומת זאת‪ ,‬יעשה שימוש רב בידע‬
‫שנרכש בכיתה ח בנושא חפיפת משולשים‪ ,‬משולש שווה‪-‬שוקיים‪ ,‬שוויון קטעים‪ ,‬שוויון זוויות‪ ,‬זוויות קדקודיות‪ ,‬זוויות צמודות‬
‫וכן תוצאות הנובעות מתכונות הדלתון‪ .‬סדר ההוראה מכתיב שימוש רב בחפיפת משולשים ובשאר הנושאים שהוזכרו קודם‬
‫לכן‪ ,‬כיוון שהתלמידים טרם למדו את תכונות המרובעים האחרים כדוגמת הריבוע ואינם יכולים לעשות שימוש בתכונות אלו‬
‫בהוכחות‪.‬‬
‫מרבית ההוכחות מבססות על חפיפת משולשים‪ ,‬ולכן במדריך למורה נציין את רעיון ההוכחה ולא נפרט את הדרך בה אנו‬
‫מצפים מהתלמידים לכתוב את ההוכחה‪ .‬פרק זה הוא הזדמנות מצוינת לתרגול דרכי כתיבת הוכחה‪ ,‬כי רוב ההוכחות עצמן‬
‫הן פשוטות‪.‬‬
‫בפרק הדלתון נעסוק גם בקישוריות בין אלגברה לבין גאומטריה על ידי שילוב תרגילים בנושא הדלתון ומערכת צירים‪.‬‬
‫תרגילים אלו יתבססו על נושאים שנלמדו בכיתה ח כמו שימוש במערכת צירים ופונקציה קווית‪ .‬כמו כן‪ ,‬קישוריות זו תתרום‬
‫לזריעת זרעים ראשונים להוראת גאומטריה אנליטית בעתיד‪ .‬בדרך הוראה מדורגת זו‪ ,‬אנו מאמינים כי יותר תלמידים יצליחו‬
‫וייהנו מלימודי הגאומטריה בהמשך‪.‬‬
‫שיקול נוסף לפתיחה עם הוראת הדלתון קשור לפרק העוקב‪ ,‬פרק בניות באמצעות סרגל ומחוגה‪ .‬בפרק זה חלק גדול‬
‫מהשיקולים וההצדקות קשור בתכונות הדלתון‪.‬‬
‫פרק הדלתון נפתח בהגדרה של דלתון‪ .‬ההגדרה שנבחרה היא‪ :‬דלתון הוא מרובע שלו שני זוגות זרים של צלעות סמוכות‬
‫השוות זו לזו‪ .‬ההגדרה מתייחסת רק לצלעות הדלתון‪ .‬זאת בהבדל מהגדרות שהיו נהוגות בעבר‪ ,‬כגון‪ :‬דלתון הוא מרובע‬
‫המורכב משני משולשים שווה‪-‬שוקיים בעלי בסיס משותף‪ .‬ההגדרה האחרונה‪ ,‬כוללת בתוכה את האלכסון המשני של הדלתון‬
‫שאיננו צלע של מרובע ולכן אנו נמנעים מלהשתמש בהגדרה זו‪.‬‬
‫כדאי להתעכב על מרכיבי הגדרת הדלתון‪ .‬למשל‪ ,‬מדוע נדרשים שני זוגות צלעות סמוכות שוות זו לזו‪ .‬כדאי לבקש‬
‫מהתלמידים לתת דוגמה למרובע שבו יש זוג אחד של צלעות סמוכות שוות ואיננו דלתון‪.‬‬
‫נקוד ה נוספת חשובה להתייחסות בהקשר להגדרת הדלתון הוא המושג "זרים" הכלול בהגדרה‪ ,‬ודורש הבהרה לתלמידים‪.‬‬
‫מה המשמעות זרים ומדוע יש לציין שני זוגות זרים?‬
‫הדוגמה הבאה יכולה לחדד נקודה זו‪:‬‬
‫בדוגמה יש שני זוגות של צלעות סמוכות השוות זו לזו ובכל זאת המרובע איננו דלתון‪.‬‬
‫תרגילים מתאימים לעורר דיון על ההגדרה של הדלתון ולשרש תפיסות שגויות הינם תרגילים ‪ 1‬ותרגיל ‪ .5‬תרגיל ‪ 1‬מכיל‬
‫דוגמאות ואי דוגמאות לדלתון ומציף נקודות חשובות להתייחסות‪ ,‬כגון המקרה של ריבוע‪ .‬תרגיל ‪ ,5‬עושה שימוש במשפט‬
‫הפוך למשולש שווה‪-‬שוקיים‪.‬‬
‫לפני פעילות ‪ 1‬וכחלק מהחזרה על הגדרות מוכרות לתלמידים מלימודים קודמים‪ ,‬ישנה גם התייחסות לדלתון קמור ודלתון‬
‫קעור‪ .‬בדומה להגדרת מצולע קמור ומצולע קעור‪ ,‬גם כאן אנו בוחרים בהגדרה המתבססת על האלכסונים‪ ,‬האומרת כי דלתון‬
‫קמור הינו מרובע שכל אלכסוניו הם פנימיים‪ .‬הגדרה זו מאפשרת בדיקה קלה מאוד‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪43‬‬
‫דלתון‬
‫דלתון הוא מרובע שלו שני זוגות זרים של צלעות סמוכות השוות זו לזו‪.‬‬
‫קדקוד ראש‬
‫אלכסון ראשי‬
‫קדקוד הנמצא בין שתי צלעות שוות נקרא קדקוד ראש‪.‬‬
‫הזווית שנוצרת בין שתי צלעות שוות נקראת זווית הראש‪.‬‬
‫הזוויות בשני הקדקודים האחרים נקראות זוויות צד‪.‬‬
‫אלכסון משני‬
‫האלכסון המחבר את קדקודי הראש נקרא אלכסון ראשי‪.‬‬
‫האלכסון האחר נקרא אלכסון משני‪.‬‬
‫קדקוד ראש‬
‫כשמעבירים את האלכסון המשני נוצרים שני משולשים שווי‪-‬שוקיים‪.‬‬
‫כל זוג צלעות שוות הן שוקיים באחד המשולשים‪ ,‬והאלכסון המשני הוא בסיס משותף‬
‫של שני המשולשים‪.‬‬
‫דלתון שהוא מרובע קמור (כל אלכסוניו פנימיים) נקרא דלתון קמור‪.‬‬
‫בדלתון קמור האלכסונים הם פנימיים‪ .‬לכן שני המשולשים השווי‪-‬שוקיים נמצאים‬
‫משני צדי האלכסון המשני‪.‬‬
‫דלתון שאינו קמור נקרא דלתון קעור‪ .‬בדלתון קעור האלכסון המשני חיצוני‪.‬‬
‫בדלתון קעור המשולשים השווי‪-‬שוקיים נמצאים בצד אחד‬
‫דלתון קעור‬
‫דלתון קמור‬
‫של האלכסון המשני‪.‬‬
‫מטרת פעילות ‪ 1‬היא לזהות לשים לב לדקויות שבהגדרת הדלתון ולהדגיש שהזיהוי מתבסס על הגדרת הדלתון ולא על דימוי‬
‫של הדלתון‪ .‬חלק מהסעיפים מתבססים ישירות על הנתונים‪ .‬באחרים יש צורך להתבסס על חפיפת משולשים כדי להוכיח‬
‫שהמרובע הוא דלתון‪ .‬נשים לב‪ ,‬כי לכל דוגמה יש מטרה לחדד היבט אחר של הגדרת הדלתון‪.‬‬
‫פעילות ‪ – 1‬האם ניתן להסיק שהמרובע דלתון? – עמ' ‪219‬‬
‫קבעו לגבי כל אחד מן המרובעים הבאים‪ ,‬אם ניתן להסיק מהנתונים שהוא דלתון‪ ,‬ונמקו את קביעתכם‪.‬‬
‫אם המרובע הוא דלתון‪ ,‬ציינו אם הוא דלתון קמור או דלתון קעור‪.‬‬
‫ב‪.‬‬
‫א‪.‬‬
‫ד‪.‬‬
‫ג‪.‬‬
‫ה‪.‬‬
‫‪45 45‬‬
‫‪27 27‬‬
‫ו‪.‬‬
‫ז‪.‬‬
‫ח‪.‬‬
‫ט‪.‬‬
‫‪45 45‬‬
‫____________________________________________________________________________________________________________‬
‫‪44‬‬
‫ב‪.‬‬
‫א‪.‬‬
‫ד‪.‬‬
‫ג‪.‬‬
‫ה‪.‬‬
‫‪45 45‬‬
‫‪27 27‬‬
‫דלתון קעור ‪-‬‬
‫ישנם שני זוגות‬
‫זרים של צלעות‬
‫סמוכות שוות‪.‬‬
‫יש אלכסון‬
‫חיצוני‪.‬‬
‫ו‪.‬‬
‫דלתון קמור ‪-‬‬
‫מעוין הוא דלתון‬
‫כי יש לו שני‬
‫זוגות זרים של‬
‫צלעות סמוכות‬
‫שוות‪ .‬הוא קמור‬
‫כי האלכסונים בו‬
‫פנימיים‪.‬‬
‫לא ניתן להסיק‬
‫שהמרובע הוא‬
‫דלתון ‪-‬‬
‫ישנם שני זוגות‬
‫זרים של צלעות‬
‫יש אלכסון‬
‫חיצוני‪.‬‬
‫יש רק זוג אחד של‬
‫שוות‪.‬‬
‫ז‪.‬‬
‫ניתן להוכיח לפי ז‪.‬צ‪.‬ז‬
‫שהאלכסון מחלק את‬
‫המרובע לשני‬
‫משולשים חופפים‪.‬‬
‫מהחפיפה נסיק שני‬
‫זוגות זרים של צלעות‬
‫ח‪.‬‬
‫ט‪.‬‬
‫‪45 45‬‬
‫חשוב להתעכב‬
‫עם התלמידים‬
‫על ההסבר מדוע‬
‫ריבוע הוא גם‬
‫דלתון‪.‬‬
‫דלתון ‪-‬‬
‫שני הזוגות של‬
‫הצלעות השוות אינן‬
‫סמוכות‪.‬‬
‫קיבלנו מקבילית‪.‬‬
‫ישנם שני זוגות של‬
‫שוות‪ ,‬אך הם אינם‬
‫זרים‪.‬‬
‫ניתן להוכיח לפי צ‪.‬ז‪.‬צ‬
‫שהאלכסון מחלק את המרובע‬
‫לשני משולשים חופפים ולהסיק‬
‫שקיימים שני זוגות זרים של‬
‫צלעות סמוכות שוות‪.‬‬
‫מטרת פעילות ‪ 2‬היא להתחיל לחקור את תכונות הדלתון ולהשתמש בידע שנרכש בכיתה ח בנושא חפיפת משולשים‪.‬‬
‫התלמידים עדין לא נדרשים לרשום הוכחה אלא להשלים הוכחה שנתונה להם‪ .‬חשוב לבנות את ההוכחה בכתה עם‬
‫התלמידים‪ .‬השלמת ההוכחה על פי הפעילות היא הזדמנות לשחזר את ההוכחה ולתרגל כתיבה של הוכחה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪45‬‬
‫פעילות ‪ – 2‬נחקור את תכונות הדלתון – עמ' ‪220‬‬
‫המרובע ‪ ALON‬הוא דלתון (‪.)ON = OL , AN = AL‬‬
‫נוכיח כי האלכסון הראשי מחלק את הדלתון לשני משולשים חופפים‪.‬‬
‫נתון‪ .ON = OL ,AN = AL :‬צ"ל‪ANO  ALO :‬‬
‫א‪ .‬השלימו את ההוכחה‪:‬‬
‫נימוק‬
‫טענה‬
‫‪AN = AL‬‬
‫נתון‬
‫‪ON = OL‬‬
‫נתון‬
‫‪AO = AO‬‬
‫צלע משותפת‬
‫‪ ANO ≅ ALO‬מ‪.‬ש‪.‬ל‬
‫לפי משפט חפיפה צ‪.‬צ‪.‬צ‬
‫ב‪ .‬רשמו זוגות של זוויות שוות שניתן להסיק מחפיפת המשולשים‪:‬‬
‫‪∡ANO = ∡ALO‬‬
‫‪∡OAL = ∡OAN‬‬
‫‪∡AOL = ∡AON‬‬
‫‪A‬‬
‫ג‪ .‬ומה אם הדלתון קעור?‬
‫הראו שגם במקרה זה האלכסון הראשי ‪ AC‬מחלק את הדלתון לשני משולשים חופפים‪,‬‬
‫ורשמו שלושה שוויונות בין זוויות הנובעים מחפיפת המשולשים‪.‬‬
‫גם הפעם המשולשים חופפים לפי ‪ 3‬צלעות‪ .‬נוכל להסיק‪:‬‬
‫‪∡ADC = ∡ABC‬‬
‫‪∡CAD = ∡CAB‬‬
‫‪C‬‬
‫‪∡DCA = ∡BCA‬‬
‫‪B‬‬
‫‪D‬‬
‫ד‪ .‬את השוויונות הנובעים מחפיפת המשולשים ננסח כתכונות של דלתון‪:‬‬
‫משפט‪ :‬בדלתון זוויות הצד שוות זו לזו‪.‬‬
‫משפט‪ :‬האלכסון הראשי של הדלתון חוצה את זוויות הראש‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪46‬‬
‫מטרת פעילות ‪ 3‬היא להדגיש את הכלליות של הוכחה‪ .‬בהוכחה לא התבססנו על אף תכונה שלא קיימת בכל דלתון ולכן מה‬
‫שהוכחנו תקף לכל דלתון‪ .‬אנחנו מוכיחים שהתוצאות של טענה מתקיימות בכל פעם שמתקיימים התנאים‪ ,‬ללא תלות בצורת‬
‫הדלתון‪ .‬שלושת הסעיפים של התרגיל בסעיף א נבדלים אך ורק בשמות הקדקודים‪ .‬די להוכיח פעם אחת שהאלכסון הראשי‬
‫של הדלתון חוצה את זוויות הראש של הדלתון‪ ,‬ולהשתמש במסקנה ביחס לכל דלתון‪ .‬הפעילות מדגישה גם את העובדה שלא‬
‫קיים דלתון שתכונותיו סותרות את מה שהוכחנו‪ ,‬או במילים אחרות‪ :‬לא קיימת דוגמה נגדית לטענה נכונה‪.‬‬
‫פעילות ‪ – 3‬האם יש צורך בהוכחה נפרדת? – עמ' ‪221‬‬
‫א‪ .‬מה דומה ומה שונה בשלושת התרגילים הבאים‪:‬‬
‫‪P‬‬
‫‪)1‬‬
‫‪Q‬‬
‫‪G‬‬
‫‪)2‬‬
‫‪)3‬‬
‫‪A‬‬
‫‪1 2‬‬
‫‪H‬‬
‫‪E‬‬
‫‪2 1‬‬
‫‪1‬‬
‫‪2‬‬
‫‪S‬‬
‫‪B‬‬
‫‪C‬‬
‫‪D‬‬
‫‪R‬‬
‫‪M‬‬
‫‪ SQ‬הוא האלכסון הראשי‬
‫‪ AC‬הוא האלכסון הראשי‬
‫‪ GM‬הוא האלכסון הראשי‬
‫של הדלתון ‪.SPQR‬‬
‫של הדלתון ‪.ABCD‬‬
‫של הדלתון ‪.EGHM‬‬
‫הוכיחו כי ‪∢Q1 = ∢Q2‬‬
‫הוכיחו כי ‪∢A1 = ∢A2‬‬
‫הוכיחו כי ‪∢G1 = ∢G2‬‬
‫שלושת התרגילים בסעיף א של פעילות ‪ 3‬נבדלים אך ורק בשמות הקדקודים‪ .‬די להוכיח פעם אחת שהאלכסון הראשי של‬
‫הדלתון חוצה את זוויות הראש של הדלתון‪ ,‬ולהשתמש במסקנה ביחס לכל דלתון‪.‬‬
‫‪A‬‬
‫‪D‬‬
‫ב‪ .‬האם ניתן לסרטט דלתון שהאלכסון שלו לא חוצה את זוויות הראש?‬
‫לא‪ .‬הוכחנו שבכל דלתון האלכסון הראשי חוצה את זוויות הראש‪ .‬מצב אחר לא ייתכן‪.‬‬
‫‪B‬‬
‫ג‪ ABCD .‬דלתון‪ A .‬ו‪ C -‬הם הקדקודים הראשיים של הדלתון‪.‬‬
‫‪C‬‬
‫הסבירו מדוע ‪.∢D = ∢B‬‬
‫הפעם אנחנו מתבססים על המשפט‪ :‬בדלתון זוויות הצד שוות זו לזו‪.‬‬
‫ד‪ .‬האם ניתן לסרטט דלתון שבו אחת מזוויות הצד ישרה וזווית הצד השנייה בת ‪?60‬‬
‫אם כן – מה גודלן של שאר זוויות הדלתון‪.‬‬
‫אם לא קיים דלתון כזה – הסבירו מדוע‪.‬‬
‫לא קיים דלתון כזה‪ .‬הוכחנו שבכל דלתוןן זוויות הצד שוות זו לזו‪ .‬לא יתכן מקרה שסותר את מה שהוכחנו‪.‬‬
‫בפעילות ‪ 2‬הוכחנו שהאלכסון הראשי של הדלתון חוצה את זוויות הראש‪ .‬תכונה זו מתקיימת בכל דלתון‪.‬‬
‫לכן בתרגילים בסעיף א בפעילות זו‪ ,‬לא היה צורך להשתמש שוב בחפיפת משולשים כדי להוכיח את שוויון הזוויות‪.‬‬
‫כיוון שהוכחנו שבכל דלתון האלכסון הראשי חוצה את זוויות הראש‪ ,‬לא קיים דלתון שהאלכסון הראשי שלו לא חוצה את‬
‫הזוויות האלו‪.‬‬
‫למעשה הוכחנו‪:‬‬
‫בכל דלתון האלכסון הראשי חוצה את זוויות הראש‪.‬‬
‫בכל דלתון זוויות הצד שוות‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪47‬‬
‫פעילות ‪ 4‬עוסקת בתכונות נוספות של הדלתון‪ ,‬ואף כאן מודגשת הכלליות של ההוכחה‪ .‬יש לשקול עד כמה לעסוק בדלתון‬
‫קעור‪ ,‬בהתאם לקבוצה‪.‬‬
‫פעילות ‪ – 4‬תכונות נוספות של אלכסוני הדלתון – עמ' ‪222‬‬
‫בפעילות זו נחקור תכונות נוספות של אלכסוני הדלתון‪.‬‬
‫ראינו שהאלכסון הראשי של הדלתון חוצה את זווית הראש‪.‬‬
‫‪A‬‬
‫‪ AC‬האלכסון הראשי של הדלתון ‪ P .ABCD‬נקודת המפגש של האלכסונים‪.‬‬
‫‪12‬‬
‫א‪ ∢A1 = ∢A2 .‬כי האלכסון הראשי של הדלתון חוצה את זוויות הראש‪.‬‬
‫ב‪ ADB .‬הוא משולש שווה‪ -‬שוקיים כי בדלתון הצלעות ליד קודקוד ראש שוות ומכאן ‪.AD = AB‬‬
‫‪B‬‬
‫‪P‬‬
‫‪D‬‬
‫‪C‬‬
‫ג‪ DP = PB .‬כי חוצה זווית הראש במשולש שווה‪-‬שוקייםהוא גם תיכון‪.‬‬
‫ד‪ AC  BD .‬כי חוצה זווית הראש במשולש שווה‪-‬שוקיים הוא גם גובה‪.‬‬
‫‪A‬‬
‫ה‪ .‬ואם הדלתון קעור?‬
‫‪12‬‬
‫נאריך את האלכסון הראשי עד למפגש עם האלכסון המשני‪ .‬נסמן ב‪ P -‬את נקודת‬
‫המפגש של חוצה הזווית עם האלכסון ‪.DB‬‬
‫‪C‬‬
‫חזרו על הסעיפים א‪-‬ג במקרה של דלתון קעור‪.‬‬
‫ההוכחות בדיוק כמו במקרה של דלתון קעור‪.‬‬
‫שני קטעים שאינם נחתכים‪ ,‬הנמצאים על‬
‫ישרים מאונכים‪ ,‬מאונכים גם הם‪.‬‬
‫‪B‬‬
‫‪P‬‬
‫‪D‬‬
‫ננסח את המסקנות כתכונות של הדלתון ונוסיף אותן לארגז הכלים‪:‬‬
‫משפט‪ :‬האלכסון הראשי של דלתון קמור חוצה את האלכסון המשני‪.‬‬
‫משפט‪ :‬האלכסון הראשי של הדלתון מאונך לאלכסון המשני‪.‬‬
‫ו‪ .‬נסחו מחדש את המשפטים תוך שילוב המילה "בכל"‪.‬‬
‫בכל דלתון קמור האלכסון הראשי חוצה את האלכסון המשני‪.‬‬
‫בכל דלתון האלכסון הראשי מאונך לאלכסון המשני‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪48‬‬
‫עמ' ‪ .1 222‬בכל אחד מהמקרים קבעו נכון‪/‬לא נכון והסבירו את תשובתכם‪.‬‬
‫א‪ .‬האם בכל דלתון האלכסון המשני חוצה את האלכסון הראשי? לא‪ ,‬למשל‬
‫ב‪ .‬האם קיים דלתון שבו האלכסון המשני חוצה את האלכסון הראשי? כן‪ ,‬למשל ריבוע‪ .‬אמנם התלמידים לא עסקו עדין‬
‫בתכונות הריבוע אך קל להסביר את הדוגמה אם מוסיפים לסרטוט של ריבוע עם אלכסונים את כל הזוויות‪.‬‬
‫ג‪.‬‬
‫האם קיים דלתון שבו האלכסון המשני לא חוצה את האלכסון הראשי? כן‪ ,‬התשובה כמו בסעיף א‬
‫ד‪ .‬האם בכל דלתון האלכסון המשני מאונך לאלכסון הראשי? כן‪ .‬כדאי להדגיש את ההבדל בין סעיף א לסעיף זה‪.‬‬
‫במקרה של חציה‪ ,‬קטע יכול לחצות קטע אחר מבלי שהשני יחצה אותו‪ .‬לעומת זאת ניצבות היא תכונה סימטרית‪.‬‬
‫אם ישר א מאונך לישר ב אז גם ישר ב מאונך לישר א כי הזווית ביניהם ישרה‪.‬‬
‫ה‪ .‬האם קיים דלתון שבו זוויות הצד ישרות? כן‪ ,‬למשל ריבוע‪.‬‬
‫ו‪.‬‬
‫האם בכל דלתון זוויות הצד ישרות? לא‪.‬‬
‫פעילות ‪ – 5‬סימטריה בדלתון – עמ' ‪223‬‬
‫בפעילות ‪ ,5‬זו הפעם הראשונה שאנו עושים שימוש במושג הסימטריה בכיתה ט‪ .‬נחזור ונדגים אותו גם בפרק המקבילית‪,‬‬
‫טרפז שווה‪-‬שוקיים‪ ,‬מלבן וריבוע‪ .‬הסימטריה הינה דרך המאפשרת לא לזנוח את השיקולים הבלתי פורמאליים ולאפשר‬
‫לתלמידים להסתייע בהם כחלק מהחשיבה הראשונית בבניית הוכחות לוגיות או כחלק מתהליך הפנמה של תכונות‬
‫המרובעים‪ .‬הסימטריה שאנו מזהים בסרטוט כולו או בחלקים בתוכו מהווים רמז קדם‪-‬היסקי‪ ,‬לדרך שבה כדאי לבחור‬
‫להוכיח באופן פורמלי‪ .‬נשים לב‪ ,‬שכמעט כל הוכחה במסגרת פרק הדלתון נשענת על הסימטריה שבו‪ .‬כיוון שלא הגדרנו‬
‫סימטריה בדרך פורמלית לא נשתמש בסימטריה ככלי להוכחת טענות‪ ,‬אלא רק להסבר לא פורמלי כמו בשלב הקדם‬
‫דדוקטיבי‪ .‬למשל‪ ,‬להוכחת תכונות שנוח לנו להצדיק מטעמי סימטריה נחפש חפיפת משולשים או תכונות של משולשים‬
‫שווי‪-‬שוקיים‪.‬‬
‫לאור נקודה זו‪ ,‬חשוב מאוד לדון עם התלמידים על ההבדל בין המחשה באמצעות קיפולי נייר לבין הוכחות של תכונות‬
‫הדלתון כפי שנעשה בפעילות ‪.2‬‬
‫המושג סימטריה מוצג בהקשר לאלכסון הראשי של הדלתון המחלק אותו לשני משולשים חופפים‪ .‬המובן הבסיסי של ציר‬
‫סימטריה שיקופית הוא קו קיפול‪ :‬אם נקפל את הדלתון לאורך קו זה יכסה החלק האחד את החלק השני במדויק‪ .‬זוהי גם‬
‫המשמעות של חפיפה‪ .‬כדאי להזכיר ולקשר לתלמידים משמעות זו של חפיפה‪ ,‬כפי שהכירו אותה בכיתה ז‪.‬‬
‫מתוך הבנת התלמידים את משמעות החפיפה נרצה כי יסיקו תכונות נוספות המודגמות על ידי ציר הסימטריה והן‪ :‬קיומם של‬
‫שני זוגות נפרדים של צלעות סמוכות שוות‪ ,‬שוויון זוויות הצד‪ ,‬חציית זוויות הראש של הדלתון‪ ,‬חציית האלכסון המשני‪.‬‬
‫בפעילות אנו מתייחסים גם לקיפול לאורך האלכסון המשני‪ ,‬במטרה להמחיש שלא תמיד נקבל ציר סימטריה בעת הקיפול‬
‫לאורך האלכסונים‪ ,‬כפי שקיבלנו בקיפול לאורך האלכסון הראשי‪ .‬העדר החפיפה בין המשולשים בולט מאוד בקיפולי נייר‪.‬‬
‫מטרת סעיף ז היא להראות כי האלכסונים מאונכים זה לזה‪.‬‬
‫מטרת סעיף ט להדגיש מקרה מיוחד‪ :‬כשמשקפים משולש ישר‪-‬זווית בניצב‪ ,‬מתקבל משולש שווה‪-‬שוקיים ולא דלתון‪.‬‬
‫ניתן להדגים את הסימטריה באמצעות שני יישומונים‪ .‬היישומון הראשון "שיקוף משולש בצלעו" מדגיש את הסימטריה‬
‫בדלתון‪ ,‬על ידי שיקוף משולש בצלעו וקבלת דלתון‪ .‬בישומון ניתן לשנות את המשולש ולראות שבכל המקרים (למעט‬
‫כשמשקפים משולש ישר‪-‬זווית בניצב) מתקבל דלתון‪ .‬חשוב לשקף את הדלתון בצלע אחת בכל פעם‪.‬‬
‫בישומון השני רואים איך לכל נקודה על צלע של הדלתון יש נקודה סימטרית על צלע אחרת‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪49‬‬
‫פעילות ‪ – 5‬סימטריה בדלתון – עמ' ‪223‬‬
‫לפעילות זו יישומון באתר‪.‬‬
‫‪‬‬
‫בפעילות זו נחקור את הסימטריה בדלתון‪ .‬עקבו אחר ההנחיות הבאות‪:‬‬
‫א‪ .‬סרטטו משולש על דף נייר לבן‪.‬‬
‫ב‪ .‬קפלו את המשולש לאורך אחת הצלעות‪ ,‬כך שהסרטוט יהיה בצד החיצוני של הקיפול‪.‬‬
‫(אם המשולש ישר זווית קפלו אותו לאורך היתר‪).‬‬
‫ג‪ .‬גזרו את הדף המקופל על‪-‬פי שתי הצלעות של המשולש שאינן מקופלות‪ .‬פתחו את הקיפול‪.‬‬
‫הסבירו מדוע קיבלתם דלתון‪.‬‬
‫גזרנו זוגות של צלעות ביחד וקיבלנו מרובע עם שני זוגות נפרדים של צלעות סמוכות שוות‪.‬‬
‫ד‪ .‬קו הקיפול הוא האלכסון הראשי של הדלתון‪ .‬כיצד מדגים הקיפול את תכונות האלכסון הראשי?‬
‫א‬
‫ב‬
‫‪‬‬
‫ג‬
‫ד‬
‫דלתון הוא צורה סימטרית‪.‬‬
‫האלכסון הראשי הוא ציר סימטריה של הדלתון‪.‬‬
‫כל אחד מהמשולשים משני צדי האלכסון הראשי הוא תמונת ראי של המשולש השני‪.‬‬
‫האלכסון הראשי מחלק את הדלתון לשני משולשים חופפים‪.‬‬
‫ה‪ .‬אילו תכונות נוספות של הדלתון מודגמות על‪-‬ידי הקיפול? שוויון זוויות הצד‪ ,‬האלכסון הראשי‬
‫חוצה את זוויות הראש ואת האלכסון המשני‪.‬‬
‫ו‪ .‬קפלו את הדלתון לאורך האלכסון המשני‪.‬‬
‫נזכור‪ ,‬כי מעוין הוא מרובע שצלעותיו‬
‫שוות זו לזו ולכן הוא סוג של דלתון‪.‬‬
‫בדלתון שאיננו מעוין האלכסון המשני איננו ציר סימטריה ‪-‬‬
‫המשולשים שנוצרים משני צדי האלכסון המשני אינם חו פפים ואינם מכסים זה את זה בעת הקיפול‪.‬‬
‫ז‪ .‬נקפל את הדלתון גם לאורך האלכסון הראשי‪.‬‬
‫איזו זווית נוצרה במפגש האלכסונים? הסבירו‪.‬‬
‫איזו תכונה נוספת מבליט הקיפול לאורך הציר הראשי של הדלתון?‬
‫האלכסון הראשי מאונך לאלכסון המשני‪.‬‬
‫ח‪ .‬האם נוכל ליצור גם דלתון קעור באמצעות "שכפול משולש"?‬
‫כן‪ ,‬אם נתחיל ממשולש קהה זווית כמו זה המסורטט ברמז‪ .‬האלכסון הראשי נמצא מול זווית חדה‪.‬‬
‫רמז‬
‫____________________________________________________________________________________________________________‬
‫‪50‬‬
‫ט‪ .‬מה יקרה אם נקפל משולש ישר‪-‬זווית לאורך אחד הניצבים‪ ,‬ונגזור את הדף כמודגם בפעילות?‬
‫יתקבל משולש שווה‪-‬שוקיים כבסרטוט‬
‫לפעילות מצורפים שני יישומונים דינמיים‬
‫יישומון א‪ :‬סימטריה בדלתון – שיקוף משולש בצלעותיו‪.‬‬
‫בצד השמאלי של היישומון נתון משולש שהתלמידים יכולים לשקף בכל אחת מצלעותיו‪ ,‬על פי בחירתו‪ ,‬ולקבל בכל פעם דלתון‬
‫אחר (דוגמאות א‪-‬ב)‪ .‬בצד הימני מופיעה משימת החקר‪.‬‬
‫התלמידים יכולים גם לשנות את המשולש באמצעות גרירת הקדקודים‪ ,‬והשיקוף ישתנה בהתאם‪.‬‬
‫כשמשקפים משולש ישר‪-‬זווית בניצב לא מתקבל דלתון אלא משולש שווה‪-‬שוקיים‪ .‬ראו דוגמה ג‪.‬‬
‫א‬
‫ג‬
‫ב‬
‫הפעילות מיועדת לחקור את הסימטריה בדלתון ואת הקשר בין תכונות הדלתון לבין הסימטריה השיקופית שלו ביחס לאלכסון‬
‫הראשי‬
‫____________________________________________________________________________________________________________‬
‫‪51‬‬
‫כיוון שהדלתון המתקבל ביישומון מתקבל על ידי הוספה למשולש הנתון משולש שהוא תמונת ראי שלו‪ ,‬שוויון זוויות הצד‪,‬‬
‫ושוויון זוגות של זוויות סימטריות‪ ,‬שבין האלכסון הראשי לבין צלעות הדלתון‪ ,‬בולט לעין‪.‬‬
‫השימוש ביישומון לא מוכיח את הסימטריה השיקופית של הדלתון אלא ממחיש אותה‪ ,‬ומקשר בין הסימטריה לבין תכונות‬
‫הדלתון‪.‬‬
‫משימות החקר המופיעות בחלק הימני של היישומון עם תשובות‪:‬‬
‫שיקוף משולש באחת מצלעותיו – פעילות חקר‬
‫לפניכם משולש ‪.ABC‬‬
‫היישומון מאפשר לכם לשקף את המשולש בכל אחת מצלעותיו ולחקור את הצורות המתקבלות על צג המחשב‬
‫א‪ .‬שקפו את המשולש בצלע ‪.AC‬‬
‫המשמעות של שיקוף המשולש ‪ ABC‬בצלע ‪ AC‬פירושה שהמשולש החדש שקיבלנו ‪ ABD‬הוא תמונת ראי של המשולש‬
‫‪.ABC‬‬
‫‪)1‬‬
‫‪)2‬‬
‫‪)3‬‬
‫‪)4‬‬
‫‪)5‬‬
‫איזו צלע היא תמונת ראי של הצלע ‪AD ?AB‬‬
‫איזו צלע היא תמונת ראי של הצלע ‪DC ?BC‬‬
‫הסבירו מדוע המרובע ‪ ABCD‬הוא דלתון‪ .‬למרובע שני זוגות נפרדים של צלעות סמוכות שוות‪.‬‬
‫זהו את זוויות הצד והסבירו מדוע הן שוות‪ ∢B .‬ו‪ ∢D -‬הן זוויות הצד‪ .‬הן שוות כיוון שהן זוויות מתאימות במשולשים‬
‫חופפים‪.‬‬
‫אילו תכונות של האלכסון הראשי מודגמות ביישומון? ניתן לראות שהאלכסון הראשי של הדלתון חוצה את זוויות‬
‫הראש‪ .‬ניתן גם לראות שהאלכסון הראשי מחלק את הדלתון לשני משולשים חופפים‪ .‬שוב‪ ,‬זו איננה הוכחה‪ .‬אנחנו‬
‫בנינו את הדלתון באמצעות שני משולשים חופפים‪.‬‬
‫ב‪ .‬שקפו את המשולש בצלע אחרת (שקפו בצלע אחת בכל פעם)‪.‬‬
‫‪ )1‬הסבירו מדוע גם הפעם התקבל על צג המחשב דלתון‪ .‬שוב התקבלו שני משולשים חופפים ומהחפיפה ניתן ללמוד‬
‫שלמרובע המופיע על הצג יש שני זוגות זרים של צלעות סמוכות שוות‪.‬‬
‫‪ )2‬רשמו תכונות של הדלתון שמודגמות באמצעות השיקוף‪ .‬הצלעות הסמוכות לקדקוד ראש שוות‪ .‬זוויות הצד שוות זו‬
‫לזו‪ .‬האלכסון הראשי חוצה את הזוויות‬
‫ג‪.‬‬
‫שקפו את המשולש באחת מצלעותיו וגררו את קדקודי המשולש ‪.ABC‬‬
‫האם תשובותיכם לסעיפים הקודמים מתאימות גם לאחר הגרירה? הסבירו‪ .‬אם הצלע שבה שיקפנו את המשולש‬
‫אינה מאונכת לצלע אחרת מתקבל דלתון‪ ,‬וכל התשובות לסעיפים הקודמים מתאימות‪ .‬לעומת זאת כאשר משקפים‬
‫משולש ישר‪-‬זווית באחד הניצבים לא מתקבל דלתון אלא משולש שווה‪-‬שוקיים (דוגמה ג במבוא לפעילות עם‬
‫היישומון)‪.‬‬
‫יישומון ב‬
‫פעילות ‪_5‬סימטריה בדלתון‬
‫ביישומון זה ניתן לראות שלכל נקודה על הדלתון‪ ,‬למעט הקדקודים‪ ,‬יש‬
‫נקודה סימטרית ביחס לאלכסון הראשי‪ ,‬הנמצאת על צלע סמוכה של‬
‫הדלתון‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪52‬‬
‫נבנה "תעודת זהות" לדלתון‪ .‬אם ידוע שמרובע הוא דלתון‪ ,‬אז בהכרח יש לו את כל התכונות שברשימה‪( :‬עמ' ‪)224‬‬
‫‪A‬‬
‫תכונות של דלתון‪:‬‬
‫‪L‬‬
‫הגדרה‪:‬‬
‫‪P‬‬
‫‪N‬‬
‫‪O‬‬
‫‪.1‬‬
‫אלכסוני הדלתון מאונכים זה לזה‪.‬‬
‫‪.2‬‬
‫האלכסון הראשי של דלתון חוצה את זוויות הראש‪.‬‬
‫‪.3‬‬
‫האלכסון הראשי של דלתון קמור חוצה את האלכסון המשני‪.‬‬
‫‪.4‬‬
‫בדלתון זוויות הצד שוות זו לזו‪.‬‬
‫דלתון הוא מרובע שלו שני זוגות זרים של צלעות‬
‫סמוכות השוות זו לזו‪.‬‬
‫מטרת פעילות ‪ 6‬היא לעסוק בניסוחים מתמטיים שקולים ומשמעותם‪ .‬זוהי התשתית הראשונית של מיומנויות ההיסק‬
‫בגאומטריה של התלמידים‪ .‬עליהם לדעת שטענה כללית מתייחסת לכמת "כל" גם במקרים שהמילה "כל" איננה מופיע‬
‫בטענה‪ .‬להלן דוגמאות שנ יתן לרשום אותן ללא הכמת "כל" והמשמעות זהה (אם נמחוק את המילה כל‪ ,‬המשמעות תשמר)‪:‬‬
‫בכל דלתון האלכסון הראשי חוצה את זוויות הראש‪.‬‬
‫האלכסון הראשי מחלק כל דלתון לשני משולשים חופפים‪.‬‬
‫האלכסון המשני מחלק כל דלתון לשני משולשים שווי‪-‬שוקיים‪.‬‬
‫באופן דומה נלמד את התלמידים כי גם הניסוח אם‪ ...‬אז‪ ...‬שקול לניסוח קודם‪:‬‬
‫אם מרובע הוא דלתון אז האלכסון הראשי חוצה את זוויות הראש‪.‬‬
‫הניסוח האחרון מאפשר לנו לזהות בקלות‪ ,‬מה נתון ומה צריך להוכיח‪.‬‬
‫כל משפט בגאומטריה מכיל אוסף של נתונים (או הנחות) ומסקנה שנובעת מהנתונים‪ .‬למשל‪:‬‬
‫אם מרובע הוא דלתון אז האלכסון הראשי חוצה את זוויות הראש‪.‬‬
‫נתונים‬
‫מסקנות‬
‫בכל פעם שנרצה להוכיח משפט או טענה נרשום תחילה את הנתונים ואת המסקנות אותן רוצים להוכיח‪.‬‬
‫כדי להוכיח משפט יש להראות באופן לוגי שהמסקנה נובעת מהנתונים‪.‬‬
‫אחת ממטרות הפעילות היא לחדד שנית את ההבנה שגם כאשר הכמת "לכל" איננו נכלל בניסוח הטענה‪ ,‬משמעותה של‬
‫הטענה זהה‪ .‬לדוגמה בסעיף ‪ 2‬המשמעות של הטענה "אלכסוני הדלתון מאונכים זה לזה"‪ ,‬היא שלא קיים דלתון שאלכסוניו‬
‫אינם מאונכים זה לזה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪53‬‬
‫פעילות ‪ – 6‬הוכחה מול המחשה – עמ' ‪224‬‬
‫בפעילות ‪ 5‬הראינו שהאלכסון הראשי של הדלתון שגזרנו חוצה את זוויות הראש של הדלתון‪.‬‬
‫האם נוכל להסיק מהקיפול שהאלכסון הראשי של כל דלתון חוצה את זוויות הראש? מדוע?‬
‫בפעילות ‪ 2‬הוכחנו משפט‪ :‬האלכסון הראשי של הדלתון חוצה את זוויות הראש‪.‬‬
‫פירושו של משפט זה במילים אחרות הוא‪ :‬בכל דלתון האלכסון הראשי חוצה את זוויות הראש‪.‬‬
‫הסבירו מדוע מההוכחה בפעילות ‪ 2‬נובע שבכל דלתון האלכסון הראשי חוצה את זוויות הראש‪.‬‬
‫לעתים אנחנו משתמשים בניסוח שקול‪:‬‬
‫אם מרובע הוא דלתון אז האלכסון הראשי שלו חוצה את זוויות הראש‪.‬‬
‫ניסוח באמצעות אם ואז מאפשר לנו לראות בקלות מה נתון ומהי המסקנה שאותה המשפט מוכיח‪.‬‬
‫לפניכם רשימה של משפטים שמתארים תכונות נוספות של הדלתון‪.‬‬
‫א‪ .‬נסחו כל אחד מהם מחדש באמצעות המילה "כל"‪.‬‬
‫ב‪ .‬נסחו כל אחד מהם מחדש באמצעות המילים "אם" ו"אז"‪.‬‬
‫‪ .1‬האלכסון הראשי של דלתון קמור חוצה את האלכסון המשני‪.‬‬
‫בכל דלתון קמור האלכסון הראשי חוצה את האלכסון המשני‪.‬‬
‫אם מרובע הוא דלתון קמור אז אלכסונו הראשי חוצה את אלכסונו המשני‪.‬‬
‫‪ .2‬אלכסוני הדלתון מאונכים זה לזה‪.‬‬
‫בכל דלתון האלכסונים מאונכים זה לזה‪.‬‬
‫אם מרובע הוא דלתון אז אלכסוניו מאונכים זה לזה‪.‬‬
‫‪ .3‬זוויות הצד של הדלתון שוות זו לזו‪.‬‬
‫בכל דלתון זוויות הצד שוות זו לזו‪.‬‬
‫אם מרובע הוא דלתון אז זוויות הצד שלו שוות זו לזו‪.‬‬
‫ג‪ .‬האם בכל דלתון האלכסון הראשי הוא ציר סימטריה של הדלתון? הסבירו‪ .‬כן‪.‬‬
‫התכונה האחרונה לא הוכחה כי אם הומחשה ולכן נחזור להמחשה‪ :‬כל דלתון נוכל לקפל לאורך האלכסון הראשי כך‬
‫שהחלקים יכסו זה את זה בדיוק‪.‬‬
‫תרגילים – עמ' ‪231 – 225‬‬
‫עמ' ‪225‬‬
‫‪ .2‬בדלתון ‪ .)BC = DC ,AB = AD( ABCD‬הסרטוט מופיע בהקטנה‪.‬‬
‫נתון‪ 5 ,∡BAC = 45 :‬ס"מ = ‪.∡BCD = 50 ,MB‬‬
‫חשבו‪:‬‬
‫א‪∡BAD = 90 .‬‬
‫ב‪∡ABM = 45 .‬‬
‫ג‪.‬‬
‫‪∡ACD = 25‬‬
‫ד‪∡BDC = 65 .‬‬
‫ה‪ 5 .‬ס"מ = ‪( AM‬נשים לב שהמשולש ‪ AMB‬שווה שוקיים‪).‬‬
‫____________________________________________________________________________________________________________‬
‫‪54‬‬
‫עמ' ‪225‬‬
‫‪.3‬‬
‫בכל אחד מהדלתונים הבאים חשבו את הגדלים המבוקשים על‪ -‬פי הנתונים‪ .‬פרטו ונמקו את צעדי החישוב‪.‬‬
‫א‪.‬‬
‫ג‬
‫‪.‬‬
‫ב‪.‬‬
‫‪∡BAD = 40‬‬
‫‪∡ABM = 70‬‬
‫‪∡BDC = 15‬‬
‫‪∡BCD = 150‬‬
‫‪∡BAD = 140‬‬
‫‪∡AMD = 90‬‬
‫‪∡ABM = 20‬‬
‫‪∡ABM = 32.5‬‬
‫‪∡ABC = 55‬‬
‫‪∡ACB = 57.5‬‬
‫‪∡ACD = 55‬‬
‫‪∡ADM = 22‬‬
‫‪∡ADC = 55‬‬
‫‪∡DAB = 125.5‬‬
‫‪∡ADC = 85‬‬
‫‪ .4‬מהו סכום הזוויות של דלתון? הוכיחו‪.‬‬
‫התשובה של טלי‪ :‬למדנו שסכום הזוויות במרובע הוא ‪ .360‬דלתון הוא מרובע ולכן סכום הזוויות שלו הוא‬
‫‪.360‬‬
‫התשובה של עמית‪ :‬סכום הזוויות בדלתון הוא בדיוק סכום הזוויות של שני‬
‫משולשים ולכן הוא שווה ל‪.360 -‬‬
‫מה דעתכם?‬
‫שתי התשובות נכונות אך חשוב לשים לב להבדלים‪ .‬טלי משתמשת בידע על סכום הזוויות בכל מרובע‪ .‬עמית‬
‫מוכיחה את הטענה מחדש בהסתמך על סכום הזוויות במשולש‪.‬‬
‫סידרת ההיסקים של טלי‪ :‬מרובע הוא דלתון‪ ,‬בכל מרובע סכום הזוויות הפנימיות הוא ‪  360‬סכום הזוויות‬
‫הפנימיות בדלתון הוא ‪.360‬‬
‫____________________________________________________________________________________________________________‬
‫‪55‬‬
‫עמ' ‪226‬‬
‫‪ .5‬בכל אחד מהסעיפים הבאים‪ ,‬קבעו אם המרובע ‪ ABCD‬דלתון‪.‬‬
‫‪D‬‬
‫‪A‬‬
‫‪C‬‬
‫א‪.‬‬
‫‪A‬‬
‫ב‪.‬‬
‫ד‪.‬‬
‫ג‪.‬‬
‫‪55‬‬
‫‪B‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪D‬‬
‫‪D‬‬
‫‪60‬‬
‫‪60‬‬
‫‪55‬‬
‫‪A‬‬
‫‪D‬‬
‫‪B‬‬
‫‪40‬‬
‫‪B‬‬
‫‪55‬‬
‫‪40‬‬
‫‪60‬‬
‫‪A‬‬
‫דלתון – בעזרת המשפט‬
‫ההפוך נוכיח כי יש שני‬
‫משולשים שווי‪-‬שוקיים‬
‫שהאלכסון המשני הוא בסיס‬
‫משותף לשניהם‪.‬‬
‫‪60‬‬
‫‪B‬‬
‫‪55‬‬
‫‪C‬‬
‫דלתון – בעזרת חישוב זוויות‬
‫במשולש ישר‪-‬זווית ומשפט הפוך‪,‬‬
‫נוכיח כי יש שני משולשים שווי‪-‬‬
‫שוקיים שהאלכסון המשני הוא בסיס‬
‫משותף לשניהם‪.‬‬
‫‪C‬‬
‫‪C‬‬
‫לא דלתון – מחישוב זוויות‪ ,‬נראה‬
‫כי אין זוג זוויות נגדיות שוות‪.‬‬
‫‪ ∡B = 110º‬ו‪. ∡D =125º -‬‬
‫‪ ∡A = 60º‬ו‪.∡C =55º -‬‬
‫בדלתון זוויות הצד שוות זו לזו‪ .‬ניתן‬
‫גם להראות שאין שני זוגות זרים של‬
‫צלעות סמוכות שוות‪.‬‬
‫מקרה זה מובא כדי להדגיש שלא‬
‫כל מרובע שניתן לחלק לשני‬
‫משולשים שווי‪-‬שוקיים הוא דלתון‪.‬‬
‫דלתון – לפי הזוויות‬
‫הנתונות נסיק כי יש לנו‬
‫שני משולשים שווי‪-‬צלעות‪,‬‬
‫שהאלכסון המשני משותף‬
‫להן‪.‬‬
‫‪D‬‬
‫‪ ABCD .6‬דלתון‪ A .‬ו‪ C -‬הם הקדקודים הראשיים של הדלתון‪.‬‬
‫‪Q‬‬
‫הנקודות ‪ P‬ו‪ Q -‬הן בהתאמה אמצעי הצלעות ‪ BC‬ו‪.DC -‬‬
‫הוכיחו (תוכלו להשלים נימוקים בתבנית ההוכחה) שהמרובע ‪APCQ‬‬
‫‪A‬‬
‫‪C‬‬
‫‪P‬‬
‫‪B‬‬
‫נשים לב‪ :‬השימוש בתבנית ההוכחה עם עמודה מיוחדת לשלבי ההוכחה מאפשר‬
‫לתת לתלמידים להשלים נימוקים בהוכחה‪ ,‬כשהשרשרת ההיסקית שמבטאת העמודה "תבנית ההוכחה" נמצאת לנגד‬
‫עיניהם‪.‬‬
‫א‪.‬‬
‫הוכחת החפיפה‬
‫‪ADQ  ABP‬‬
‫ב‪.‬‬
‫הוכחה ש‪-‬‬
‫‪ APCQ‬דלתון‬
‫נימוק‬
‫טענה‬
‫‪CD =CB‬‬
‫צלעות סמוכות ליד אותו קדקוד ראש בדלתון שוות זו לזו‪.‬‬
‫‪DQ = BP‬‬
‫חצאי קטעים שווים שווים זה לזה‪.‬‬
‫‪∡D = ∡B‬‬
‫זוויות הצד בדלתון שוות זו לזו‪.‬‬
‫‪AD = AB‬‬
‫צלעות סמוכות ליד אותו קדקוד ראש בדלתון שוות זו לזו‪.‬‬
‫‪ADQ  ABP‬‬
‫צ‪.‬ז‪.‬צ‬
‫‪AQ = AP‬‬
‫צלעות מתאימות במשולשים חופפים שוות זו לזו‪.‬‬
‫‪CQ = CP‬‬
‫חצאי צלעות סמוכות בדלתון שווים זה לזה‪.‬‬
‫‪ APCQ‬דלתון‪ .‬מ‪.‬ש‪.‬ל‬
‫מרובע עם שני זוגות זרים של צלעות שוות הוא דלתון (הגדרה)‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪56‬‬
‫עמ' ‪ .7 226‬אייל בנה עפיפון שצורתו דלתון (‪ .)BC = DC ,AB = AD‬כדי לקשט את העפיפון שלו אייל סימן על שתי צלעות של‬
‫הדלתון נקודות ‪ G‬ו‪ K -‬כך ש‪ .AG = AK -‬אייל צבע את המרובע החדש ‪ AGCK‬וטוען שגם מרובע זה דלתון‪.‬‬
‫‪A‬‬
‫הוכיחו‪:‬‬
‫‪K‬‬
‫א‪.‬‬
‫‪.BG = DK‬‬
‫ב‪.‬‬
‫‪.GBC  KDC‬‬
‫ג‪.‬‬
‫המרובע ‪ AGCK‬הוא דלתון‪.‬‬
‫‪G‬‬
‫‪B‬‬
‫‪D‬‬
‫סעיפי התרגיל מכוונים להוכיח שהמרובע דלתון על‪-‬פי חפיפת המשולשים בסעיף ב‪.‬‬
‫‪C‬‬
‫נשים לב שאפשר גם להוכיח ש‪ GC = KC -‬אם מסרטטים את האלכסון הראשי ומוכיחים את חפיפת‬
‫המשולשים ‪AGC  AKC‬‬
‫‪A‬‬
‫עמ' ‪ .8 227‬המרובע ‪ ABCD‬הוא דלתון (‪.)BC = DC ,AB = AD‬‬
‫‪ N‬נקודה על האלכסון הראשי‪.‬‬
‫‪D‬‬
‫הוכיחו (תוכלו להשלים נימוקים בתבנית ההוכחה)‪:‬‬
‫‪B‬‬
‫‪N‬‬
‫א‪.CNB  CND .‬‬
‫‪12‬‬
‫‪C‬‬
‫ב‪ .‬המרובע ‪ CBND‬הוא דלתון‪.‬‬
‫נימוק‬
‫טענה‬
‫‪∡C1 = ∡C2‬‬
‫האלכסון הראשי בדלתון חוצה את זוויות הראש‪.‬‬
‫א‪ .‬הוכחת החפיפה‬
‫‪BC = DC‬‬
‫נתון‪.‬‬
‫‪CNB  CND‬‬
‫‪CN = CN‬‬
‫צלע משותפת‬
‫‪CNB  CND‬‬
‫צ‪.‬ז‪.‬צ‬
‫‪BN = DN‬‬
‫צלעות מתאימות במשולשים חופפים שוות זו לזו‪.‬‬
‫‪ CBND‬דלתון‬
‫מרובע בעל שני זוגות זרים של צלעות סמוכות שוות הוא דלתון‪.‬‬
‫ב‪ .‬הוכחה ש‪CBND -‬‬
‫דלתון‬
‫____________________________________________________________________________________________________________‬
‫‪57‬‬
‫עמ' ‪ .9 227‬קבעו לגבי כל אחד מן המרובעים הבאים‪ ,‬האם ניתן להסיק מהנתונים שהוא דלתון‪ ,‬ונמקו את קביעתכם‪.‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪L‬‬
‫‪H‬‬
‫ג‪.‬‬
‫‪A‬‬
‫‪K‬‬
‫‪68‬‬
‫*ד‪.‬‬
‫‪68‬‬
‫‪R‬‬
‫‪N‬‬
‫‪E‬‬
‫‪M‬‬
‫‪B‬‬
‫‪54‬‬
‫‪Z‬‬
‫‪54‬‬
‫‪D‬‬
‫‪C‬‬
‫ניתן להסיק מהנתונים‬
‫שהמרובע הוא דלתון‪.‬‬
‫לא ניתן להסיק מהנתונים‬
‫שהמרובע הוא דלתון‬
‫קמור או קעור‪ .‬בסרטוט‬
‫מופיע דלתון קעור‪.‬‬
‫‪.10‬‬
‫‪F‬‬
‫‪F‬‬
‫‪C‬‬
‫לא ניתן להסיק שהמרובע‬
‫דלתון (גם לא ניתן להסיק‬
‫שאינו דלתון)‪ .‬אם המשולש‬
‫העליון שווה‪-‬צלעות אז‬
‫המרובע הוא דלתון‪.‬‬
‫‪E‬‬
‫דלתון‪ .‬ניתן להסיק‬
‫מהנתונים על שני זוגות‬
‫זרים של צלעות סמוכות‬
‫‪P‬‬
‫אנחנו יודעים בוודאות שהמרובע‬
‫אינו דלתון‪ Z .‬לא יכול להיות‬
‫קדקוד הראש‪ ,‬כי הזווית ‪ Z‬לא‬
‫נחצת על‪-‬ידי האלכסון ‪.ZN‬‬
‫הקדקוד ‪ N‬נמצא מול קדקוד ‪Z‬‬
‫ולכן גם הוא לא קדקוד ראש‪ .‬אלו‬
‫המרובע היה דלתון‪ ,‬אז קדקודי‬
‫הראש היו צריכים להיות ‪ F‬ו‪, P-‬‬
‫אבל ‪ FZ‬לא יכול להיות שווה‬
‫ל‪ FN -‬בגלל שבמקרה זה גם‬
‫זווית ‪ ∢FNZ‬היתה צריכה להיות‬
‫ישרה‪.‬‬
‫‪ TLV‬משולש שווה‪-‬שוקיים (‪ S .)LV = LT‬נקודה על הקטע ‪,LR‬‬
‫‪L‬‬
‫חוצה זווית הראש של המשולש‪.‬‬
‫‪V‬‬
‫הוכיחו כי המרובע ‪ TLVS‬הוא דלתון‪.‬‬
‫‪S‬‬
‫‪R‬‬
‫אפשר להוכיח על‪-‬ידי חפיפת המשולשים ‪ VLS  TLS‬על פי צ‪.‬ז‪.‬צ‬
‫והסקת שוויות הצלעות ‪. VS = TS‬‬
‫‪T‬‬
‫‪O‬‬
‫עמ' ‪ KOF .11 228‬משולש שווה‪-‬שוקיים (‪)KO = FO‬‬
‫‪1‬‬
‫‪ E‬נקודה מחוץ למשולש‪.∢K1 = ∢F1 .‬‬
‫‪F‬‬
‫‪K‬‬
‫‪1‬‬
‫א‪ .‬הוכיחו‪ :‬המרובע ‪ KOFE‬הוא דלתון‪ .‬נוכיח תחילה ש‪.FE = KE -‬‬
‫ב‪ .‬נתון גם‪ .∢O = 133 ,∢K1 = 53 :‬חשבו את זוויות הדלתון‪.‬‬
‫‪E‬‬
‫‪133 ,76.5 ,74 ,76.5‬‬
‫____________________________________________________________________________________________________________‬
‫‪58‬‬
‫עמ' ‪228‬‬
‫‪M‬‬
‫‪ MOR .12‬משולש שווה‪-‬שוקיים (‪.)MO = MR‬‬
‫‪ F‬נקודה בתוך המשולש‪.∢O1 = ∢R1 .‬‬
‫הוכיחו‪ MOFR :‬דלתון‪.‬‬
‫‪F‬‬
‫‪F‬‬
‫‪1‬‬
‫‪‬‬
‫טענה‬
‫נימוק‬
‫‪MO = MR‬‬
‫נתון‬
‫‪∢O1 = ∢R1‬‬
‫נתון‬
‫‪RF =OF‬‬
‫מול זוויות שוות במשולש (‪ )OFR‬מונחות צלעות שוות‪.‬‬
‫‪ MOFR‬דלתון‬
‫מרובע בעל שני זוגות נפרדים של צלעות סמוכות שוות הוא דלתון‬
‫‪O‬‬
‫‪1‬‬
‫‪R‬‬
‫‪ PET .13‬משולש שווה‪-‬שוקיים (‪ TH .)TP = TE‬הגובה לבסיס‪.‬‬
‫‪P‬‬
‫נתון‪.PA = EB :‬‬
‫הוכיחו‪ :‬המרובע ‪ HATB‬הוא דלתון‪.‬‬
‫‪A‬‬
‫‪H‬‬
‫כאן יש דרכי הוכחה אחדות שיתכן שתלמידים יעלו‪.‬‬
‫את שוויון הצלעות ‪ AT = BT‬מוכיחים כהפרש קטעים שווים‪.‬‬
‫‪T‬‬
‫‪E‬‬
‫‪B‬‬
‫את שוויון הצלעות ‪ AH = BH‬ניתן להוכיח באמצעות חפיפת המשולשים‬
‫‪ ΔAHP ≅ ΔBHE‬או באמצעות חפיפת המשולשים ‪.ΔAHT ≅ ΔBHT‬‬
‫בשני המקרים ההוכחות על פי צ‪.‬ז‪.‬צ‪.‬‬
‫‪K‬‬
‫‪ .14‬הנקודה ‪ T‬היא מפגש חוצי הזוויות של המשולש ‪ .KAV‬נתון‪.∡A = ∡V :‬‬
‫א‪ .‬הוכיחו‪ :‬המרובע ‪ KATV‬הוא דלתון‪.‬‬
‫‪T‬‬
‫ב‪ .‬נתון‪ .∢A1 = 30 :‬חשבו את זוויות הדלתון‪.‬‬
‫‪.30 ,240 ,30 ,60‬‬
‫‪V‬‬
‫‪1‬‬
‫‪1‬‬
‫‪A‬‬
‫הוכחה לסעיף א‪:‬‬
‫‪∡KAV = ∡KVA‬‬
‫נתון‬
‫‪KA = KV‬‬
‫מול זוויות שוות במשולש (‪ )KAV‬מונחות צלעות שוות‪.‬‬
‫‪∢A1 = ∢V1‬‬
‫חצאי זוויות שוות שווים זה לזה‪.‬‬
‫‪AT = VT‬‬
‫מול זוויות שוות במשולש (‪ )ATV‬מונחות צלעות שוות‪.‬‬
‫‪ KATV‬דלתון‬
‫מרובע בעל שני זוגות זרים של צלעות סמוכות שוות‬
‫הוא דלתון‪.‬‬
‫הערה למורה‪:‬‬
‫בפרק משולש שווה‪-‬שוקיים‬
‫למדנו את המשפט‪:‬‬
‫אם למשולש יש שתי זוויות‬
‫שוות אז הצלעות מולן שוות‪.‬‬
‫בנימוקים להוכחות נהוג‬
‫להשתמש בנוסח‪ :‬מול זוויות‬
‫שוות במשולש מונחות צלעות‬
‫הינכם יכולים לבחור באיזה‬
‫נוסח לנמק בהוכחות בכיתה‪.‬‬
‫ניתן ללמד את התלמידים גם‬
‫נוסח זה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪59‬‬
‫עמ' ‪228‬‬
‫‪ NET .15‬הוא משולש שווה‪-‬שוקיים (‪.)NE = ET‬‬
‫‪ - EA‬חוצה זווית הראש במשולש‪.‬‬
‫‪E‬‬
‫‪ AR‬ו‪ AC -‬מאונכים לשוקי המשולש ‪.NET‬‬
‫‪1 2‬‬
‫הוכיחו כי‪:‬‬
‫א‪= ∡A4 .‬‬
‫‪.∡A1‬‬
‫חישוב במשולשים ‪ ACT‬ו‪ARN -‬‬
‫ב‪= ∡A3 .‬‬
‫‪.∡A2‬‬
‫נתבסס על כך שחוצה זווית הראש במשולש שווה‪-‬שוקיים הוא גם‬
‫‪C‬‬
‫גובה לבסיס‪ ,‬ומכאן ‪ ∡A2‬ו‪ ∡A3 -‬משלימות זוויות שוות ל‪.90 -‬‬
‫‪R‬‬
‫‪2 3 4‬‬
‫‪1‬‬
‫‪T‬‬
‫‪A‬‬
‫ג‪ .ΔARE ≅ ΔACE .‬ז‪.‬צ‪.‬ז‬
‫‪N‬‬
‫ד‪ .‬המרובע ‪ RACE‬הוא דלתון‪ .‬מרובע בעל שני זוגות נפרדים של צלעות סמוכות שוות הוא דלתון‪ .‬שוויון הצלעות נובע‬
‫מהחפיפה בסעיף הקודם‪.‬‬
‫סידרת התרגילים ‪ 19 – 16‬בנויה מתרגילים דומים מאד‪ ,‬ומטרתה למקד את תשומת הלב בנתונים המשתנים משאלה‬
‫לשאלה‪ ,‬וגם לעזור לתלמידים שעדין מתקשים לנסח הוכחות לתרגל כתיבה של הוכחות פשוטות‪.‬‬
‫‪C‬‬
‫עמ' ‪229‬‬
‫‪B‬‬
‫‪G‬‬
‫‪ .16‬נתון‪ - GCKL :‬ריבוע‪.GB = KF .‬‬
‫‪F‬‬
‫א‪ .BGL  FKL .‬על פי צ‪.‬ז‪.‬צ‬
‫ב‪ - BCFL .‬דלתון‪.‬‬
‫מרובע בעל שני זוגות נפרדים של צלעות סמוכות שוות הוא דלתון‪.‬‬
‫‪L‬‬
‫‪K‬‬
‫‪ FL =BL‬שוויון הצלעות נובע מהחפיפה בסעיף הקודם‪ CF =BC .‬כחיסור קטעים שווים מקטעים שווים‪.‬‬
‫‪Q‬‬
‫‪ .17‬נתון‪ - PQRS :‬ריבוע‪.MQ = QT .‬‬
‫‪M‬‬
‫‪P‬‬
‫‪T‬‬
‫א‪.PMS  RTS .‬‬
‫ב‪.‬‬
‫‪ - SMQT‬דלתון‬
‫‪S‬‬
‫‪R‬‬
‫נשים לב‪ :‬השיקולים דומים מאד לאלו של תרגיל ‪ .16‬הפעם נתון שוויון של זוג קטעים שונה‪.‬‬
‫‪O‬‬
‫‪ .18‬נתון‪ - SONG :‬ריבוע‪.GP = GK .‬‬
‫א‪.‬‬
‫‪P‬‬
‫‪S‬‬
‫‪K‬‬
‫‪.GSP  GNK‬‬
‫ב‪ - GPOK .‬דלתון‪.‬‬
‫‪N‬‬
‫‪G‬‬
‫הפעם חפיפת המשולשים מתבססת משולשים ישרי‪-‬זווית השווים בניצב ויתר‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪60‬‬
‫‪D‬‬
‫‪E‬‬
‫עמ' ‪ .19 229‬נתון‪ - DESK :‬ריבוע‪.∢E1 = ∢E2 .‬‬
‫‪1‬‬
‫‪2‬‬
‫א‪.‬‬
‫‪ .DEL  SEV‬לפי ז‪.‬צ‪.‬ז‬
‫ב‪.‬‬
‫‪ - KLEV‬דלתון ‪.‬‬
‫‪L‬‬
‫‪S‬‬
‫‪K‬‬
‫‪V‬‬
‫בתרגיל ‪ 20‬יש סעיף העוסק בדמיון משולשים‪.‬‬
‫‪ LET .20‬משולש שווה‪-‬שוקיים (‪ HGER .)EL = ET‬דלתון‪.‬‬
‫‪ HE‬הוא האלכסון הראשי של הדלתון ‪.HGER‬‬
‫‪.HR  TE‬‬
‫‪E‬‬
‫‪G‬‬
‫‪. HG  LE‬‬
‫‪1 2‬‬
‫‪L‬‬
‫‪2‬‬
‫א‪ H .‬אמצע הצלע ‪ .LT‬האלכסון הראשי של הדלתון הוא חוצה זווית הראש של‬
‫‪1‬‬
‫‪R‬‬
‫הדלתון ולכן גם של המשולש‪ .‬חוצה זווית הראש במשולש ‪ LET‬הוא גם תיכון לבסיס‪.‬‬
‫‪H‬‬
‫‪0‬‬
‫ב‪ LGH  LHE .‬על פי ז‪.‬ז‪.‬ז‪ ∡G1 = ∡G2 = 90 .‬ו‪ ∡L -‬זווית משותפת‪.‬‬
‫ג‪.‬‬
‫‪T‬‬
‫‪ LG = TR‬נובע מהחפיפה‪.‬‬
‫עמ' ‪ .21 230‬אייל בנה עפיפון שצורתו דלתון‪ .‬כדי לקשט את העפיפון שלו אייל מדד מקצות‬
‫‪B‬‬
‫האלכסון ‪ AC‬שני קטעים שווים באורך ‪ 5‬ס"מ = ‪.AL = MC‬‬
‫‪C‬‬
‫אייל חיבר את הנקודות ‪ L‬ו‪ M -‬עם קדקודי הדלתון ‪ B‬ו‪( D -‬ראו סרטוט)‪.‬‬
‫‪L‬‬
‫‪M‬‬
‫‪A‬‬
‫הסרטוט מופיע בהקטנה‪.‬‬
‫אייל צבע את המרובע החדש ‪ BMDL‬בצבע ‪ ,‬וטען שגם הוא דלתון‪.‬‬
‫האם אייל צודק? הוכיחו את תשובתכם‪.‬‬
‫‪D‬‬
‫אייל צודק‪ .‬רעיון ההוכחה‪:‬‬
‫דרך א‪ :‬הוכחה על ידי חפיפה של שני משולשים ישרי‪-‬זווית ‪ ∆BLO  ∆BMO‬ו‪ ∆DLO  ∆DMO -‬השווים בשני נציביהם‪.‬‬
‫דרך ב‪ :‬האלכסון הראשי בדלתון חוצה את האלכסון המשני‪ .‬שמרנו על תכונה זו כאשר הורדנו קטעים שווים באורכם‬
‫מקטעים שווים‪ .‬שמרנו גם על תכונות המאונכות של האלכסונים‪.‬‬
‫לפי המשפט אם במשולש גובה הוא תיכון ‪ ,‬אז המשולש הוא שווה‪-‬שוקיים‪ .‬נקבל שני משולשים שווה‪-‬שוקיים ולכן גם נקבל‬
‫שני זוגות זרים של צלעות סמוכות שוות‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪61‬‬
‫‪L‬‬
‫עמ' ‪ .22 230‬עופרה בנתה עפיפון שצורתו דלתון‪ .‬כדי לקשט את העפיפון שלה‪ ,‬היא מדדה‬
‫‪T‬‬
‫מקצוות שני האלכסונים בדלתון קטעים שווים של ‪ 8‬ס"מ‪.‬‬
‫‪U‬‬
‫‪.LT = AU = RE = BS = 8‬‬
‫‪S‬‬
‫‪A‬‬
‫‪B‬‬
‫עופרה חיברה בין ארבעת הנקודות ‪ S, T, A, R‬שסימנה (ראו סרטוט)‪.‬‬
‫‪R‬‬
‫‪E‬‬
‫א‪ .‬עופרה טוענת שהצורה החדשה‪ STAR :‬היא דלתון‪.‬‬
‫האם עופרה צודקת? הוכיחו את תשובתכם‪.‬‬
‫עופרה צודקת‪ .‬רעיון ההוכחה‪ :‬כמו בתרגיל ‪.10‬‬
‫בתשובה לסעיף א יש כבר רמז לסעיף ב‪.‬‬
‫ב‪ .‬בועז טוען שכדי לסרטט דלתון מספיק לסמן שתי נקודות ‪ A‬ו‪ S -‬במרחקים שווים מקודקודי ‪ B‬ו‪ U -‬של הדלתון‪,‬‬
‫כפי שסימנה עופרה‪ ,‬אבל הנקודות ‪ R‬ו‪ T -‬יכולות להיות במרחקים שונים מהקדקודים ‪L‬‬
‫ו‪ E -‬של הדלתון‪.‬‬
‫האם בועז צודק? הוכיחו את תשובתכם‪.‬‬
‫בועז צודק‪ .‬ניתן לבקש מהתלמידים לנסות לסרטט‪ ,‬למשל‪ ,‬את המרובע‪ LSEA :‬ולבחון האם הוא דלתון?‬
‫בדרך הבנייה אותה מציע בועז‪ ,‬אנחנו כל הזמן שומרים על תנאי המשפט‪ :‬אם במשולש גובה הוא תיכון ‪ ,‬אז‬
‫המשולש הוא שווה‪-‬שוקיים‪ .‬ולכן תמיד נקבל שני זוגות זרים של צלעות סמוכות שוות‪.‬‬
‫‪ .23‬לפניכם רשימת טענות‪ .‬קבעו לגבי כל טענה אם היא נכונה ונמקו‪.‬‬
‫א‪ .‬אלכסוני הדלתון מאונכים זה לזה‪ .‬נכון‪ .‬הוכחנו משפט‪.‬‬
‫ב‪ .‬ריבוע הוא דלתון‪ .‬נכון‪ .‬לריבוע יש שני זוגות נפרדים של צלעות סמוכות שוות‪.‬‬
‫ג‪.‬‬
‫דלתון הוא ריבוע‪ .‬לא נכון‪ .‬ראינו דלתונים רבים שאינם ריבועים‪.‬‬
‫ד‪ .‬אין דלתון שהוא ריבוע‪ .‬לא נכון‪ .‬יש דלתון שהוא ריבוע כי כל ריבוע הוא דלתון‪.‬‬
‫ה‪ .‬אם במרובע יש שני זוגות של צלעות סמוכות שוות‪ ,‬אזי המרובע הוא דלתון‪.‬‬
‫לא נכון‪ .‬יכולות להיות ל מרובע שלוש צלעות שוות וצלע רביעית שונה ואז אין לו שני זוגות נפרדים של צלעות סמוכות‬
‫שוות‪ .‬ראו למשל דוגמה ח בפעילות ‪.1‬‬
‫____________________________________________________________________________________________________________‬
‫‪62‬‬
‫תרגיל ‪ 24‬הינו תרגיל בו הסרטוט אינו שלם ועל התלמידים להשלימו ולהיזכר במשמעות המושג אנך אמצעי לקטע‪.‬‬
‫‪B‬‬
‫עמ' ‪ .24 231‬הישר ‪ m‬הוא אנך אמצעי לקטע ‪.AB‬‬
‫הנקודות ‪ G‬ו‪ F -‬נמצאות על הישר ‪.m‬‬
‫‪G‬‬
‫‪P‬‬
‫הוכיחו כי ‪ AFBG‬דלתון‪.‬‬
‫‪F‬‬
‫‪m‬‬
‫‪A‬‬
‫אנך אמצעי לקטע ‪ ,AB‬פירושו אנך‬
‫החוצה את הקטע ‪.AB‬‬
‫הרעיון לפתרון‪:‬‬
‫התלמידים צריכים להכיר את מושג אנך אמצעי שטומן בתוכו שתי תכונות‪ :‬היותו אנך והיותו חוצה קטע‪ .‬קיבלנו מרובע בו‬
‫האלכסונים מאונכים זה לזה‪ ,‬ואחד מהם חוצה את השני‪ .‬מכאן שגם במשולש ‪ AGB‬וגם במשולש ‪ AFB‬יש תיכון שהוא‬
‫גם גובה ולכן שני המשולשים שווי‪-‬שוקיים‪.‬‬
‫‪ - LAMP .25‬ריבוע‪.‬‬
‫‪AP .∡P1 = ∡P2‬‬
‫‪R‬‬
‫‪A‬‬
‫‪.RC‬‬
‫‪2‬‬
‫‪C‬‬
‫‪L‬‬
‫‪1‬‬
‫ב‬
‫א‬
‫‪2‬‬
‫א‪∡R1 = ∡R2 .‬‬
‫ב‪ LRCP .‬דלתון‪.‬‬
‫‪M‬‬
‫‪1‬‬
‫‪P‬‬
‫הרעיון לפתרון‪:‬‬
‫ניתן לחשב את כל הזוויות בסרטוט‪ ,‬ולהוכיח את החפיפה של משולש א ומשולש ב על פי ז‪.‬צ‪.‬ז‬
‫כיצד נזהה שמרובע הוא דלתון?‬
‫כדי להוכיח שמרובע הוא דלתון‪ ,‬נשתמש במשפטי חפיפת משולשים שלמדנו‪.‬‬
‫בעזרתם נוכל להוכיח‪ ,‬שיש למרובע שני זוגות זרים של צלעות סמוכות שוות‪ ,‬או לזהות במרובע שני משולשים‬
‫שווי‪-‬שוקיים שהאלכסון המשני הוא בסיס משותף לשניהם‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪63‬‬
‫אתנחתא – יצירת מצולעים באמצעות דלתונים – עמ' ‪231‬‬
‫לפניכם שני דלתונים בשני גדלים שונים‪ .‬העתיקו כל דלתון פעמים וגזרו את‬
‫הדלתונים שקיבלתם‪.‬‬
‫א‪.‬‬
‫נסו להרכיב משני הדלתונים הגדולים ושני הדלתונים הקטנים מלבן‪.‬‬
‫ב‪.‬‬
‫נסו להרכיב מהדלתון הגדול ומהדלתון הקטן טרפז‪.‬‬
‫ג‪.‬‬
‫נסו להרכיב משני הדלתונים הגדולים ושני הדלתונים הקטנים מקבילית‬
‫שאיננה מלבן‪.‬‬
‫ד‪.‬‬
‫האם מכל שני דלתונים גדולים וקטנים ניתן לבנות מלבן? מקבילית?‬
‫‪90‬‬
‫טרפז? הסבירו‪.‬‬
‫‪‬‬
‫כדי ששני דלתונים יתחברו וייצרו טרפז זוויות הצד צריכות להיות‬
‫‪180-‬‬
‫ישרות‪.‬‬
‫‪90‬‬
‫אם יצרנו טרפ ז ישר זווית בדרך שיצרנו נוכל לשקף את הטרפז בשוק‬
‫הסמוכה לזוויות הישרות ולקבל טרפז שווה שוקיים מארבעה דלתונים‪.‬‬
‫משני טרפזים כאלה נוכל ליצור גם מלבן ומקבילית‪ ,‬כמו באיורים‬
‫ה‪.‬‬
‫הציעו דרך לרצף חדר (או חצר) באריחים שצורתם כצורת הדלתונים שלכם‪.‬‬
‫‪180-‬‬
‫‪90‬‬
‫‪‬‬
‫‪‬‬
‫‪90‬‬
‫‪180- 180-‬‬
‫‪‬‬
‫‪90‬‬
‫‪180-‬‬
‫נוכל להצמיד זה לזה את הצורות שיצרנו‪ ,‬למשל‪:‬‬
‫ניתן לקרוא על ריצוף עם דלתונים מיוחדים בקישור‪:‬‬
‫‪http://he.wikipedia.org/wiki/%D7%93%D7%9C%D7%AA%D7%95%D7%9F_%D7%A8%D7%99%D7 %‬‬
‫‪A6%D7%95%D7%A3‬‬
‫____________________________________________________________________________________________________________‬
‫‪64‬‬
‫‪‬‬
‫לפניכם הריצוף בצורות גדולות לגזירה והדגמה‪:‬‬
‫____________________________________________________________________________________________________________‬
‫‪65‬‬
‫מטרת פעילות ‪ 7‬להציג דרכים שונות לחישוב שטח דלתון על סמך ידע קודם של התלמידים או להוכיח אותן‪ .‬בפעילות זו‪,‬‬
‫בעת ההוכחה נדרשת טכניקה אלגברית‪.‬‬
‫‪‬‬
‫פעילות ‪ – 7‬שטח דלתון – עמ' ‪232‬‬
‫לפעילות זו יישומון באתר‪.‬‬
‫א‪ .‬בסרטוט הדלתון ‪ ,ROSH‬מופיעים האורכים של הקטעים בסנטימטרים‪ .‬הסרטוט מופיע בהקטנה‪.‬‬
‫דנה ושני מחשבות את שטח הדלתון‪.‬‬
‫‪S‬‬
‫‪ )1‬הציעו דרך משלכם לחישוב שטח הדלתון וחשבו את שטחו‪.‬‬
‫‪ )2‬שני מחשבת את שטח המשולש ‪ SOR‬ומכפילה אותו ב‪.2 -‬‬
‫‪3‬‬
‫‪O‬‬
‫מדוע היא עושה זאת? המשולשים חופפים‪.‬‬
‫חשבו את השטח בדרך של שני‪ .‬שטח כל משולש ‪ 7‬סמ"ר‪ .‬שטח הדלתון ‪ 14‬סמ"ר‪.‬‬
‫‪2‬‬
‫‪2‬‬
‫‪H‬‬
‫‪4‬‬
‫‪ )3‬דנה מחשבת את השטחים של ‪ 4‬משולשים ומחברת אותם‪.‬‬
‫חשבו את השטח בדרך של דנה‪.‬‬
‫שטח כל משולש תחתון ‪ 4‬סמ"ר‪ .‬שטח כל משולש עליון ‪ 3‬סמ"ר שטח הדלתון ‪14‬‬
‫‪R‬‬
‫סמ"ר‪.‬‬
‫‪)4‬‬
‫חשבו את מכפלת האלכסונים של הדלתון‪28 .‬‬
‫פי כמה גדולה מכפלת האלכסונים של הדלתון ‪ ROSH‬משטחו? פי ‪2‬‬
‫‪C‬‬
‫ב‪ .‬במרובע ‪ CTLD‬האלכסונים מאונכים זה לזה‪ .‬הסרטוט מופיע בהקטנה‪.‬‬
‫בסרטוט מופיעים האורכים של הקטעים בסנטימטרים‪.‬‬
‫‪ )1‬חשבו את שטחי ארבעת המשולשים הישרי‪-‬זווית שיוצרים אלכסוני המרובע‪.‬‬
‫‪ 14‬סמ"ר = ‪7.5+2.5+1+3‬‬
‫‪ )2‬הראו ששטח המרובע שווה למחצית מכפלת האלכסונים‪.‬‬
‫מכפלת האלכסונים ‪ .28‬אכן בדוגמה שטח המרובע שווה למחצית מכפלת האלכסונים‪.‬‬
‫‪T‬‬
‫‪D‬‬
‫הוכחה כללית בהמשך‪.‬‬
‫‪L‬‬
‫ג‪.‬‬
‫נוכיח כי בכל מרובע שאלכסוניו מאונכים זה לזה שטח המרובע שווה למחצית‬
‫מכפלת האלכסונים‪.‬‬
‫ההוכחה מתייחסת לדלתון קמור‬
‫בלבד‪ .‬ניתן להוכיח שהמסקנה נכונה‬
‫לכל דלתון באמצעות חיסור שטחים‪.‬‬
‫נתון‪ :‬אלכסוניו של המרובע ‪ CTLD‬מאונכים זה לזה‪.‬‬
‫צ"ל‪SCTLD = ½  TD  CL :‬‬
‫‪C‬‬
‫האלכסון ‪ TD‬מחלק את האלכסון ‪ CL‬לשני חלקים שאחד מהם‪,‬‬
‫‪ SL‬הוא הגובה לצלע ‪ TD‬במשולש ‪, TLD‬‬
‫‪ CS‬הוא הגובה לצלע ‪ TD‬במשולש ‪.CTD‬‬
‫נחשב את שטח המרובע ‪ CTLD‬כסכום שני המשולשים ‪ LTD‬ו‪:CTD -‬‬
‫‪D‬‬
‫‪SCTLD = SLTD + SCTD = ½  TD  LS + ½  TD  CS = ½  TD(LS+CS) = ½  TD  CL‬‬
‫מ‪.‬ש‪.‬ל‬
‫‪S‬‬
‫‪T‬‬
‫‪L‬‬
‫‪LS+CS = CL‬‬
‫____________________________________________________________________________________________________________‬
‫‪66‬‬
‫לפעילות מצורף יישומון "הקשר בין אלכסוני הדלתון לשטחו"‪.‬‬
‫ביישומון זה ניתן לקבוע את אורכי האלכסונים באמצעות המחוון הכחול והמחוון הירוק‪.‬‬
‫ברגע שקבענו את אורכי האלכסונים‪ ,‬ניתן לגרור את הנקודה ‪A‬וכך לשנות את הדלתון מבלי לשנות את אורכי אלכסוניו‪.‬‬
‫התלמידים מתבקשים לחקור את הקשר בין אורכי האלכסונים של הדלתון לשטח הדלתון‪.‬‬
‫נרשום זאת בארגז הכלים‪:‬‬
‫משפט‪ :‬שטח מרובע שאלכסוניו מאונכים זה לזה שווה למחצית מכפלת אלכסוניו‪.‬‬
‫דלתון הוא מרובע שאלכסוניו מאונכים זה לזה‪ .‬לכן נוכל לחשב את שטח הדלתון כמחצית מכפלת האלכסונים‪.‬‬
‫משפט‪ :‬שטח דלתון שווה למחצית מכפלת אלכסוניו‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪67‬‬
‫תרגילים – עמ' ‪236 – 233‬‬
‫עמ' ‪ .26 233‬באיורים למטה מופיעים דלתונים‪ .‬חשבו את שטחי הדלתונים על‪ -‬פי המידות הרשומות בסרטוט בסנטימטרים‪.‬‬
‫הסרטוטים מופיעים בהקטנה‪.‬‬
‫ב‪.‬‬
‫א‪.‬‬
‫ד‪.‬‬
‫ג‪.‬‬
‫‪ .27‬א‪ .‬חשבו את שטחי המרובעים‪ .‬ידוע כי אורך כל צלע של משבצת הוא יחידה אחת‪.‬‬
‫(‪ .14 )5( ;12.5 )4( ;8 )3( ;6 )2( ; 7.5 )1‬יחידות השטח הן המשבצות עליהן מסורטטים המרובעים‪.‬‬
‫ב‪ .‬זהו בין המרובעים את הדלתונים‪.5 ,3 ,2 .‬‬
‫כדאי לשים לב לבחירת הדוגמאות‪ :‬מעוין וריבוע הם דלתונים מיוחדים‪ .‬יש תלמידים שלא מזהים אותם כדלתונים בגלל‬
‫שיש להם שם ניפרד‪ .‬דוגמה ‪ 4‬נראית דומה לדלתון אך לא עונה על ההגדרה‪ ,‬אין צלעות שוות‪.‬‬
‫( ‪)2‬‬
‫( ‪)5‬‬
‫‪O‬‬
‫( ‪)4‬‬
‫( ‪)1‬‬
‫‪L‬‬
‫‪Z‬‬
‫‪E‬‬
‫( ‪)3‬‬
‫‪N‬‬
‫____________________________________________________________________________________________________________‬
‫‪68‬‬
‫‪A‬‬
‫סרטוטים בעמוד זה‬
‫מופיעים בהקטנה‪.‬‬
‫עמ' ‪ .28 233‬בדלתון ‪.)BC = DC ,AB = AD( ABCD‬‬
‫‪6‬‬
‫‪M‬‬
‫‪D‬‬
‫‪.∡ADC = ∡CBA = 90°‬‬
‫‪ 6‬ס"מ = ‪,AB‬‬
‫‪ 8‬ס"מ = ‪,CD‬‬
‫א‪.‬‬
‫חשבו את אורכי הקטעים‪ 10 :‬ס"מ = ‪ 3.6 ,AC‬ס"מ = ‪ 9.6 AM‬ס"מ = ‪. BD‬‬
‫ב‪.‬‬
‫חשבו את שטח הדלתון‪ 48 .‬סמ"ר‪.‬‬
‫‪C‬‬
‫נתון‪ 5 :‬ס"מ = ‪,RO‬‬
‫‪13‬‬
‫‪12‬‬
‫‪16‬‬
‫‪ 20‬ס"מ =‪.KL‬‬
‫‪B‬‬
‫‪8 6.4‬‬
‫‪ RKLM .29‬דלתון‪ O .RK = RM .‬נקודת מפגש האלכסונים‪.‬‬
‫‪ 13‬ס"מ = ‪,RM‬‬
‫‪4.8‬‬
‫‪4.8‬‬
‫‪8‬‬
‫‪ 4.8‬ס"מ = ‪. BM‬‬
‫‪3.6‬‬
‫‪6‬‬
‫‪12‬‬
‫‪5‬‬
‫‪13‬‬
‫חשבו את שטח הדלתון‪.‬‬
‫לאחר שנחשב באמצעות משפט פיתגורס את אורכי כל הקטעים שבסרטוט‬
‫נחשב את שטח הדלתון‪ 252 :‬סמ"ר‪.‬‬
‫(בפתרונות לתרגיל זה‪ ,‬בספר לתלמיד‪ ,‬יש שגיאה)‬
‫‪17‬‬
‫עמ' ‪ FROG .30 234‬דלתון‪ N .GF = GO .‬נקודת מפגש האלכסונים‪.‬‬
‫נתון‪ 20 :‬ס"מ = ‪,NR‬‬
‫‪ 8‬ס"מ = ‪,GN‬‬
‫‪15‬‬
‫‪ 17‬ס"מ =‪.GF‬‬
‫‪8‬‬
‫‪20‬‬
‫חשבו את שטח הדלתון ואת היקפו‪.‬‬
‫‪15‬‬
‫לאחר שנחשב באמצעות משפט פיתגורס את אורכי כל הקטעים שבסרטוט‬
‫נחשב את שטח הדלתון‪ 420 :‬סמ"ר‪.‬‬
‫‪ PQRT .31‬דלתון‪ M .PQ = PT .‬נקודת מפגש האלכסונים‪.‬‬
‫נתון‪,∡PQM = 45 :‬‬
‫‪,∡MQR = 60‬‬
‫‪ 3‬ס"מ = ‪.TM‬‬
‫‪45 45‬‬
‫א‪ .‬מצאו את גודל הזווית ‪45 .∡PTQ‬‬
‫‪45‬‬
‫‪60‬‬
‫ב‪ .‬מצאו את אורך הקטעים ‪ MQ‬ו‪ .TM -‬פרטו את חישובכם‪.‬‬
‫‪3‬‬
‫‪45‬‬
‫‪60‬‬
‫האלכסון הראשי חוצה את האלכסון המשני ולכן‪ 3 ,‬ס"מ = ‪.MQ = TM‬‬
‫ג‪ .‬מצאו את אורך הצלע ‪( QR‬רמז‪ :‬מהן זוויות המשולש ‪)? ΔMQR‬‬
‫המשולש ‪ TQR‬שווה‪-‬צלעות‪ .‬לכן ‪ 6‬ס"מ = ‪.QR = TQ‬‬
‫____________________________________________________________________________________________________________‬
‫‪69‬‬
‫ד‪ .‬חשבו את שטח הדלתון ואת היקפו‪.‬‬
‫על פי הזוויות הנתונות‪ ,‬המשולש ‪ MQP‬הינו משולש שווה‪-‬שוקיים‪ ,‬לכן ‪ 3‬ס"מ = ‪.PM = MQ‬‬
‫לפי משפט פיתגורס‪ 4.24 ,‬ס"מ = ‪.PQ = PT‬‬
‫היקף הדלתון‪ 20.48 :‬ס"מ = ‪.2PQ + 2RQ‬‬
‫בעזרת משפט פיתגורס במשולש ‪ MQR‬נמצא את אורך הקטע ‪ 5.2 :MR‬ס"מ = ‪. MR‬‬
‫‪1‬‬
‫שטח הדלתון‪ 24.6 :‬סמ"ר = ‪ 6  8.2‬‬
‫‪2‬‬
‫‪M‬‬
‫עמ' ‪ .32 234‬במרובע ‪ MNOP‬האלכסונים מאונכים זה לזה ונפגשים בנקודה ‪.T‬‬
‫נתון‪ 4 :‬ס"מ = ‪,PT‬‬
‫‪,∡MNT = 45‬‬
‫‪ 5‬ס"מ = ‪,MP‬‬
‫‪N‬‬
‫‪5‬‬
‫‪45‬‬
‫‪45‬‬
‫‪T‬‬
‫‪ 9.6‬ס"מ = ‪.TO‬‬
‫‪P‬‬
‫‪4‬‬
‫חשבו את שטח המרובע ואת היקפו‪.‬‬
‫‪9.6‬‬
‫יש לשים לב‪ ,‬כי אין מדובר פה בדלתון‪.‬‬
‫נחשב תחילה באמצעות משפט פיתגורס במשולש ‪ 3 :MTN‬ס"מ = ‪MT‬‬
‫‪O‬‬
‫כמו כן יש לשים לב שמשולש ‪ MTN‬הינו משולש שווה‪-‬שוקיים‪ ,‬לכן ‪ 3‬ס"מ = ‪ .NT = MT‬ולכן‪ 7 ,‬ס"מ = ‪NP‬‬
‫בעזרת משפט פיתגורס נמצא את אורך הקטע‪:‬‬
‫‪ 10.4‬ס"מ = ‪ . OP‬ולכן‪ 12.6 ,‬ס"מ = ‪MO‬‬
‫שטח המרובע הוא‪ 44.1 :‬סמ"ר;‬
‫בעזרת משפט פיתגורס נמצא את אורכי הצלעות החסרות‪:‬‬
‫‪ 4.24‬ס"מ = ‪ 5 ; MN‬ס"מ = ‪ 10.05 ; MP‬ס"מ = ‪NO‬‬
‫היקף המרובע‪ 29.69 :‬ס"מ‪.‬‬
‫תרגיל ‪ 33‬הוא ללא סרטוט‪ ,‬כי יש אינסוף אפשרויות לדלתונים העונים על הדרישות‪ .‬לא ידוע באיזו נקודה האלכסון‬
‫המשני חותך את האלכסון הראשי‪ .‬להלן מוצגות שתי‬
‫אפשרויות‪ .‬הסרטוטים מופיעים בהקטנה‪:‬‬
‫‪F‬‬
‫‪G‬‬
‫‪ EFGH .33‬דלתון‪ P .FG = EF .‬נקודת מפגש האלכסונים‪.‬‬
‫‪P‬‬
‫‪E‬‬
‫‪G‬‬
‫‪ 10‬ס"מ = ‪ .EG‬שטח הדלתון ‪ 40‬סמ"ר‪.‬‬
‫‪F‬‬
‫‪P‬‬
‫‪E‬‬
‫א‪ .‬מה אורך האלכסון ‪ 8 ? FH‬ס"מ = ‪; FH‬‬
‫‪H‬‬
‫ב‪ .‬האם ניתן לדעת על‪-‬פי הנתונים מהו אורך הקטע‬
‫‪H‬‬
‫‪ ?FP‬אין לנו מספיק מידע על האלכסון הראשי‪.‬‬
‫ניתן להמחיש לתלמידים באמצעות הסרטוטים שיש יותר מאפשרות אחת שהאלכסון המשני יחתוך את האלכסון‬
‫הראשי ויתקיימו כל התנאים‪.‬‬
‫ג‪ .‬האם ניתן לדעת על‪-‬פי הנתונים מהו אורך הקטע ‪ ? EP‬במידה וכן ‪ -‬חשבו‪.‬‬
‫כן‪ ,‬כי האלכסון הראשי חוצה את האלכסון המשני ולכן‪ 5 ,‬ס"מ = ‪; EP‬‬
‫במידה ולא ‪ -‬נמקו‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪70‬‬
‫עמ' ‪ .34 235‬לפניכם מרובעים במערכת צירים‪.‬‬
‫א‪.‬‬
‫‪.1‬‬
‫מי מהמרובעים במערכת הצירים הוא דלתון? הסבירו‪.‬‬
‫‪.4‬‬
‫‪4 ,3 ,2 ,1‬‬
‫ב‪.‬‬
‫‪.2‬‬
‫חשבו את השטח וההיקף של המרובעים‪.‬‬
‫היקפים (ביחידות אורך של מערכת הצירים)‪:‬‬
‫‪.18.55 .5 ; 18 .4 ;14.6 .3 ;13.42 .2 ;13.54 .1‬‬
‫‪.3‬‬
‫שטחים (ביחידות שטח שח מערכת הצירים)‪:‬‬
‫‪.5‬‬
‫‪17.5 .5 ;12 .4 ;16 .3 ;6 .2 ;9 .1‬‬
‫* ‪ .35‬הנקודות )‪ (0,4‬ו‪ (2,0) -‬הן קדקודים סמוכים של דלתון‪.‬‬
‫א‪ .‬מצאו שיעורים של עוד שתי נקודות שיכולות להיות שני הקדקודים האחרים‪,‬‬
‫אם ידוע שהאלכסון הראשי הוא על ציר ה‪ ,y -‬וסרטטו את הדלתון‬
‫במחברת‪ .‬כמה דלתונים שונים אפשר למצוא? נמקו‪.‬‬
‫ב‪ .‬מורן הציעה את הנקודות )‪ (0,-4‬ו‪.(-2,0) -‬‬
‫האם המרובע של מורן הוא דלתון?‬
‫ג‪ .‬מצאו שיעורים של עוד שתי נקודות שיכולות להיות שני הקדקודים האחרים‪ ,‬אם‬
‫ידוע שהאלכסון הראשי הוא על ציר ה‪ ,x -‬וסרטטו את הדלתון במחברת‪.‬‬
‫ד‪ .‬מורן אומרת שאם רוצים לבנות דלתון בהתאם להנחיות בסעיף ג‪ ,‬נקודה אחת‬
‫חייבת להיות )‪ .(0,-4‬הסבירו מדוע‪.‬‬
‫ה‪ .‬שני טוענת שבמקרה זה‪ ,‬הקדקוד הרביעי חייב להיות על ציר ‪ .x‬הסבירו מדוע‪.‬‬
‫ו‪.‬‬
‫לירי הוסיפה‪ :‬אם שני צודקת‪ ,‬אז יש אינסוף דלתונים כאלה‪ .‬הסבירו מדוע‪.‬‬
‫סעיף א‪ :‬קיימים אינסוף דלתונים אפשריים‪.‬‬
‫ידוע שהאלכסון הראשי הוא על ציר ה‪ .y -‬האלכסון המשני מאונך לו ועובר‬
‫בנקודה )‪ (2,0‬ולכן הוא על ציר ה‪.x -‬‬
‫כיוון שהאלכסון הראשי חוצה את האלכסון המשני הנקודה הנוספת על‬
‫האלכסון המשני חייבת להיות )‪ .(-2,0‬יש אינסוף אפשרויות לקבוע את‬
‫הנקודה הנוספת על האלכסון הראשי‪ .‬למעשה יכולנו לבחור כל נקודה‪,‬‬
‫למעט הנקודה הנתונה ולמעט ראשית הצירים‪ ,‬כדי שלא ייוצר משולש‪.‬‬
‫כאן מוצגות שתי דוגמאות‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪71‬‬
‫סעיפים ג – ו מנחים באמצעות שאלות למסקנה‪ ,‬כי ניתן לבנות אינסוף דלתונים בהתאם לתנאים הנדרשים בסעיף ג‪.‬‬
‫סעיפים ד –ה –ו מנחים את התלמידים לשים לב מהם התנאים המספיקים‪.‬‬
‫תנאי ראשון הינו התנאי של מורן‪ :‬ידוע שהאלכסון הראשי הוא על ציר ה‪.x -‬‬
‫האלכסון המשני מאונך לו ועובר בנקודה )‪ (0,4‬ולכן הוא על ציר ה‪.y -‬‬
‫כיוון שהאלכסון הראשי חוצה את האלכסון המשני הנקודה הנוספת על האלכסון‬
‫המשני חייבת להיות )‪ ,(-4,0‬כפי שטענה מורן‪.‬‬
‫התנאי השני הינו התנאי של שני‪ :‬כל נקודה נוספת חייבת להיות על האלכסון‬
‫הראשי הנמצא על ציר ה‪ ,x -‬כפי שטענה שני‪.‬‬
‫לירי צודקת יש אינסוף אפשרויות לקבוע את הנקודה הנוספת על האלכסון‬
‫הראשי (ציר ה‪ .)x-‬למעשה יכולנו לבחור כל נקודה‪ ,‬למעט הנקודה הנתונה‬
‫ולמעט ראשית הצירים‪ ,‬כדי שלא ייוצר משולש‪.‬‬
‫כאן מוצגות שתי דוגמאות‪ .‬דוגמה של דלתון קמור ודוגמה לדלתון קעור‪.‬‬
‫לפעילות זו יש דף להקרנה והדגמה בשני נוסחים‪:‬‬
‫שקף להקרנת השאלה‪ ,‬עם דלתון שאפשר לשנות את שיעורי קדקודיו באמצעות הוורד‪ .‬לשם כך נדרשת מיומנות בעבודה‬
‫עם כלי הסרטוט של הוורד‪ .‬שקף זה מופיע באתר הקורס בשם "הזיזו את הנקודות כך שהצורה תישאר דלתון"‪.‬‬
‫שקף (מופיע ב עמוד הבא) עם הגדלה של השאלה‪ .‬ניתן להקרינו על לוח לבן ולאפשר לתלמידים להשלים את הדלתון‬
‫במערכת הצירים‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪72‬‬
‫‪8‬‬
‫‪6‬‬
‫‪4‬‬
‫‪2‬‬
‫‪6‬‬
‫‪4‬‬
‫‪2‬‬
‫‪-2‬‬
‫‪-4‬‬
‫‪-6‬‬
‫‪-2‬‬
‫‪-4‬‬
‫‪-6‬‬
‫‪-8‬‬
‫סרטטו דלתון שהנקודות המסומנות הן קדקודים סמוכים שלו‬
‫שקף לשאלה ‪ ,35‬עמ' ‪235‬‬
‫____________________________________________________________________________________________________________‬
‫‪73‬‬
‫‪8‬‬
‫‪6‬‬
‫‪4‬‬
‫‪2‬‬
‫‪6‬‬
‫‪4‬‬
‫‪2‬‬
‫‪-2‬‬
‫‪-4‬‬
‫‪-6‬‬
‫‪-2‬‬
‫‪-4‬‬
‫‪-6‬‬
‫‪-8‬‬
‫סרטטו דלתון שהנקודות המסומנות הן קדקודים סמוכים שלו‬
‫והאלכסון הראשי שלו על ציר ה‪.y -‬‬
‫שקף לשאלה ‪ , 36‬עמ' ‪235‬‬
‫____________________________________________________________________________________________________________‬
‫‪74‬‬
‫עמ' ‪235‬‬
‫‪ .36‬הנקודות )‪ (0,3‬ו‪ (4,4) -‬הן קדקודים סמוכים של דלתון‪.‬‬
‫מצאו שיעורים של עוד שתי נקודות שיכולות להיות שני הקדקודים האחרים‬
‫א‪.‬‬
‫של הדלתון‪ ,‬אם ידוע שהאלכסון הראשי הוא על ציר ה‪ ,y -‬וסרטטו את‬
‫הדלתון במחברת‪.‬‬
‫מצאו שיעורים של עוד שתי נקודות שיכולות להיות שני הקדקודים האחרים‬
‫ב‪.‬‬
‫של הדלתון‪ ,‬אם ידוע שהאלכסון המשני הוא על ציר ה‪ ,y -‬וסרטטו את‬
‫הדלתון במחברת‪.‬‬
‫א‪ .‬ידוע שהאלכסון הראשי הוא על ציר ה‪ .y -‬האלכסון המשני מאונך לו‬
‫ועובר בנקודה )‪ (4,4‬ולכן הוא על הישר ‪.y=4‬‬
‫כיוון שהאלכסון הראשי חוצה את האלכסון המשני הנקודה הנוספת על‬
‫האלכסון המשני חייבת להיות )‪ .(-4,4‬יש אינסוף אפשרויות לקבוע את‬
‫הנקודה הנוספת על האלכסון הראשי‪ .‬למעשה יכולנו לבחור כל נקודה‪,‬‬
‫למעט הנקודה הנתונה )‪ ,(0,3‬ולמעט הנקודה )‪( (0,4‬כדי שלא ייוצר‬
‫משולש)‪.‬‬
‫כאן מוצגת דוגמה‪:‬‬
‫לפעילות זו יש דף להקרנה והדגמה בשני נוסחים‪:‬‬
‫שקף להקרנת השאלה‪ ,‬עם דלתון שאפשר לשנות את שיעורי קדקודיו באמצעות הוורד‪ .‬לשם כך נדרשת מיומנות בעבודה‬
‫עם כלי הסרטוט של הוורד‪ .‬שקף זה מופיע באתר הקורס בשם "הזיזו את הנקודות כך שהצורה תישאר דלתון"‪.‬‬
‫שקף (מופיע בעמוד הקודם ) עם הגדלה של השאלה‪ .‬ניתן להקרינו על לוח לבן ולאפשר לתלמידים להשלים את הדלתון‬
‫במערכת הצירים‪.‬‬
‫עמ' ‪236‬‬
‫‪ SHARON .37‬הוא משושה משוכלל‪ .‬הוכיחו כי ‪ SAON‬דלתון‪.‬‬
‫נתון‪ :‬משושה משוכלל‪.‬‬
‫‪;NO = SN‬‬
‫צ"ל‪:‬‬
‫‪AO = SA‬‬
‫נסו להוכיח ללא חישוב‬
‫מידת הזוויות‪.‬‬
‫‪H‬‬
‫‪A‬‬
‫‪N‬‬
‫‪R‬‬
‫‪S‬‬
‫טענה‬
‫נימוק‬
‫‪NS = NO‬‬
‫נתון משושה משוכלל‪.‬‬
‫‪∡SHA = ∡ARO‬‬
‫זוויות פנימיות במשושה משוכלל שוות‪.‬‬
‫‪OR = AR = SH = HA‬‬
‫נתון משושה משוכלל‪.‬‬
‫‪∆SHA  ∆ARO‬‬
‫לפי צ‪.‬ז‪.‬צ‬
‫‪AO = SA‬‬
‫צלעות מתאימות בין משולשים חופפים‪.‬‬
‫‪ SAON‬דלתון‬
‫‪O‬‬
‫מ‪.‬ש‪.‬ל‬
‫____________________________________________________________________________________________________________‬
‫‪75‬‬
‫עמ' ‪ .38 236‬הוכיחו או הפריכו‪:‬‬
‫‪A‬‬
‫א‪ .‬מרובע שאחד מאלכסוניו מחלק אותו לשני משולשים שווי‪-‬שוקיים הוא דלתון‪.‬‬
‫לא נכון‪ .‬אפשר לסרטט מרובע שמורכב משני משולשים שווי‪-‬שוקיים דומים כמו‬
‫‪D‬‬
‫‪55‬‬
‫‪55‬‬
‫בסרטוט‪ .‬המקרה מובא בתרגיל ‪( 5‬עמ' ‪ 226‬בספר לתלמיד ועמ' ‪ 56‬במדריך) וגם‬
‫‪B‬‬
‫בתרגיל זה‪ ,‬כדי להדגיש שלא כל מרובע שניתן לחלק לשני משולשים שווי‪-‬שוקיים‬
‫‪55‬‬
‫הוא דלתון‪.‬‬
‫‪55‬‬
‫‪C‬‬
‫ב‪ .‬מרובע שאחד מאלכסוניו מאונך לאלכסון השני הוא דלתון‪.‬‬
‫לא נכון‪ .‬יש דוגמאות נגדיות רבות‪ .‬לדוגמה‪:‬‬
‫ג‪ .‬מרובע שאחד מאלכסוניו הוא אנך אמצעי לאלכסון השני הוא דלתון‪.‬‬
‫נכון‪ .‬במקרה זה ה אלכסון מחלק את הדלתון לשני משולשים‪ ,‬שבכל אחד מהם התיכון הוא גם גובה‪ .‬מכאן שלמרובע‬
‫שני זוגות זרים של צלעות סמוכות שוות ולכן הוא דלתון‪.‬‬
‫ד‪ .‬מרובע שמורכב משני זוגות של משולשים חופפים הוא דלתון‪.‬‬
‫לא נכון‪ .‬כל מקבילית מהווה דוגמה נגדית לטענה‪.‬‬
‫ה‪ .‬מרובע שאלכסון שלו חוצה שתיים מזוויותיו הוא דלתון‪.‬‬
‫נכון‪ .‬במקרה זה האלכסון הראשי מחלק את הדלתון לשני משולשים חופפים‪ ,‬ומהחפיפה נסיק את קיומם של‬
‫תרגילים מסוג "האם קיים?" כמו בתרגיל ‪ 39‬הם הזדמנות מצוינת להסביר מדוע תופעה לא יכולה להתקיים‪.‬‬
‫‪ .39‬האם קיים?‬
‫א‪.‬‬
‫דלתון שהזווית בין אלכסוניו היא בת ‪ ?45º‬לא‪ .‬אלכסוני הדלתון תמיד מאונכים‪.‬‬
‫ב‪.‬‬
‫דלתון עם שלוש זוויות חדות? כן‪ .‬לדוגמה‪:‬‬
‫ג‪.‬‬
‫דלתון עם ארבע זוויות חדות? אין אף מרובע עם ‪ 4‬זוויות חדות‪.‬‬
‫לו היה מרובע כזה סכום הזוויות שלו היה קטן מ‪.360 -‬‬
‫ד‪.‬‬
‫דלתון עם ארבע זוויות ישרות? כן‪ .‬כל ריבוע הוא דלתון‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪76‬‬
‫עמ' ‪236‬‬
‫‪ .40‬לפניכם הטענה הבאה‪ :‬מרובע שאלכסוניו מאונכים זה לזה הוא דלתון‪ .‬שלושה תלמידים הציעו דרכים לקבוע האם‬
‫הטענה נכונה או שגויה‪ .‬מי צודק? נמקו את תשובתכם‪.‬‬
‫ירדן טוען‪ :‬הטענה נכונה כי למדנו את המשפט‪ :‬האלכסון הראשי של הדלתון מאונך לאלכסון המשני‪.‬‬
‫יעלה טוענת‪ :‬הטענה לא נכונה‪ .‬גם בריבוע האלכסונים מאונכים‪.‬‬
‫עופרי הצליחה לסרטט את המרובע הבא וטוענת כי זו הוכחה שהטענה איננה נכונה‪.‬‬
‫הטענה שהתלמידים דנים בה אינה נכונה‪ .‬לא כל מרובע שאלכסוניו מאונכים זה לזה הוא דלתון‪.‬‬
‫הנימוק של ירדן אינו רלוונטי‪ ,‬למרות שהמשפט עליו הוא מתבסס הוא משפט נכון‪ .‬אלכסוני הדלתון אכן מאונכים‪ ,‬אך לא‬
‫כל מרובע שאלכסוניו מאונכים הוא דלתון‪ .‬הטענה לא עוסקת בתכונות של הדלתון‪ ,‬אלא בתנאים המבטיחים שמרובע הוא‬
‫גם הנימוק של יעלה שגוי‪ .‬יעלה צודקת באמרה שגם בריבוע האלכסונים שווים‪ ,‬ובכל זאת הדוגמה שהביאה אינה דוגמה‬
‫נגדית לטענה הנידונה‪ ,‬כיוון שריבוע הוא בעצמו דלתון‪ .‬דוגמה נגדית צריכה לקיים את תנאי הטענה (במקרה זה "אלכסוני‬
‫המרובע מאונכים") וצריכה גם לא לקיים את התוצאות (במקרה זה לא לקיים את התוצאה שהמרובע דלתון)‪ .‬הדוגמה של‬
‫יע לה כן מקיימת את העובדה שהמרובע דלתון ולכן לא יכולה להיות דוגמה נגדית‪ .‬הדוגמה מבטאת טעות נפוצה של‬
‫תלמידים שלא מתייחסים אל ריבוע כאל דלתון‪.‬‬
‫הנימוק של עופרי מכיל דוגמה נגדית טובה‪ .‬אלכסוני המרובע מאונכים (תנאי הטענה מתקיימים) והמרובע אינו דלתון‬
‫(תוצאת הטענה לא מתקיימת)‪.‬‬
‫חשוב להדגיש שכדי לתת תשובה נכונה עופרי צריכה גם להסביר מה הדוגמה שלה מדגימה (מרובע עם אלכסונים‬
‫מאונכים שאינו דלתון)‬
‫‪ .41‬נתון מחומש עם כל אלכסוניו‪.‬‬
‫זהו במחומש כמה שיותר דלתונים לא חופפים‪ .‬כמה מצאתם?‬
‫מכל דלתון שמצאתם‪ ,‬כמה דלתונים חופפים לו?‬
‫קיימים שלושה דלתונים שונים‪ .‬אחד מהם הוא מעוין‪ .‬לכל אחד מהדלתונים יש עוד ארבעה חופפים לו‪.‬‬
‫____________________________________________________________________________________________________________‬
‫‪77‬‬

מדריך למורה – טענות, הנמקות והסקת מסקנות על

Transcription

Similar documents

סיכום גיאומטריה משולשים - תיכון תל-אביב

לחצו כאן

בניות בסיסיות בסרגל ומחוגה

תרגילי חזרה למבחן 27.01.2013

עיינו כאן - טיפוס טבעי

הקליקו כאן - קיבינימטיקה

Summer 2013 4-5.pdf - התיכון העירוני על שם בליך ר"ג

12. משולשים - עשר בריבוע

סיכום משפטים בגיאומטריה

זוויות משולשים קטעים מיוחדים זוויות בין ישרים משולשים חופפים