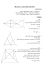בניות בסיסיות בסרגל ומחוגה

‫בניות בסיסיות בסרגל ומחוגה‬
‫על הפרק‬
‫בפרק זה לומדים התלמידים לתכנן את פעולותיהם כדי לממש בניה נדרשת‪ .‬תוך כדי כך הם מחזקים את מיומנויות ההוכחה‬
‫שאליהן נחשפו בפרק הקודם‪ .‬תרגילי הבנייה מבוססים באופן בלעדי על התוכן של פרקי הלימוד הקודמים‪ ,‬חפיפת משולשים‪,‬‬
‫משולש שווה‪-‬שוקיים ודלתון‪ ,‬וכך מחזקים ומבססים אותם‪.‬‬
‫בהמשך הלימוד יש לשלב בכל פרק חדש בניות מותאמות לתכנים החדשים שיילמדו‪.‬‬
‫פרק הבניות גם משמש מבוא לבניות עזר שתופענה בהוכחות בהמשך‪.‬‬
‫המיומנויות אותן חשוב לפתח בהדרגה בפרק הבניות‬
‫ הקדמת תכנון לביצוע‪.‬‬‫ יכולת הצדקה של כל שלב בביצוע‪.‬‬‫ זיהוי מקרים שבהם הנתונים מספיקים לבניית צורה יחידה‪ ,‬ומקרים בהם בנייה איננה אפשרית כלל‪.‬‬‫ זיהוי מקרים בהם הנתונים מספיקים לבניית צורה יחידה תומך בהטמעת הקשר שבין יחידּות צורה הנבנית‪ ,‬לבין חפיפתה‬‫לצורה אחרת שנבנתה לפי אותם נתונים‪.‬‬
‫ לזיהוי מקרים בהם בנייה היא בלתי אפשרית חשיבות בהפנמת הכלליות של הוכחה‪ .‬אם הוכחנו שלצורה יש תכונות‬‫הכרחיות אז דוגמה נגדית היא בלתי אפשרית‪ ,‬ולא נוכל לבנות צורה שתכונותיה סותרות את מה שהוכח‪.‬‬
‫ תרומה נוספת של זיהוי מקרים שבנייה היא בלתי אפשרית היא פיתוח היכולת לזהות מצבים בלתי אפשריים‪ .‬מיומנות זו‬‫תהיה חשובה במיוחד בפרק על הוכחות בדרך השלילה בהמשך השנה‪.‬‬
‫דגשים‪:‬‬
‫‪ .1‬כל בנייה תהיה מבוססת על תכנון מוקדם באופן שיספק את דרישות הבנייה על‪-‬פי הנתונים‪.‬‬
‫‪ .2‬כל בנייה תהיה מלווה בהוכחה המצדיקה אותה‪.‬‬
‫יוצאות מכלל זה הן הבניות הבאות‪ :‬העתקת קטע‪ ,‬חיבור קטעים או חיסורם (כולל הכפלת קטע נתון במספר טבעי)‪,‬‬
‫העתקת זווית‪ ,‬חיבור זוויות או חיסורן (כולל הכפלת זווית נתונה במספר טבעי)‪ .‬בספר לתלמיד בחלק מהבניות מופיעה‬
‫הצדקת הבנייה ובבניות אחרות התלמידים מתבקשים להצדיק את הבנייה בעצמם‪ .‬במקרים אלה הצדקת הבנייה‬
‫מופיעה במדריך למורה‪.‬‬
‫‪ .3‬יש להראות כיצד מחסור בדרישות הבנייה עלול לפגום ביחידּות של הצורה הנבנית‪ ,‬ולאפשר בנייה של צורות מתאימות‬
‫לנתונים שאינן חופפות‪ .‬בגוף המדריך נדגיש תרגילים שזו מטרתם‪.‬‬
‫‪ .4‬יש להראות כיצד עודף בדרישות הבנייה עלול למנוע את אפשרות הבנייה‪.‬‬
‫‪ .5‬יש לדעת לקשר בין דרישות בנייה המגדירות צורה יחידה לבין משפטי החפיפה‪.‬‬
‫‪ .6‬היחידּות של הצורה הנבנית גוררת את חפיפתה לכל צורה אחרת שנבנתה לפי אותן דרישות‪ .‬עובדה זו היא היבט נוסף‬
‫של מושג החפיפה‪.‬‬
‫הבניות יכולות להיעשות באמצעות סרגל חסר שנתות ומחוגה‪ ,‬או באמצעות אמצעי טכנולוגי המדמה זאת‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪62‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫על בניות באמצעים טכנולוגיים‬
‫‪.1‬‬
‫השימוש באמצעים הטכנולוגיים יכול לחסוך זמן רב ולהפוך את הנושא למהנה יותר‪ .‬אנחנו ממליצים לאפשר לתלמידים‬
‫להתנסות בבנייה באמצעות סרגל חסר שנתות ומחוגה בשלבים הראשונים של הנושא‪ ,‬ולשלב את הבנייה באמצעים‬
‫טכנולוגיים בהמשך‪ .‬לאחר ההתנסות בבנייה באמצעות סרגל חסר שנתות ומחוגה הכלים הטכנולוגיים יהיו ברורים יותר‬
‫לתלמידים‪ .‬מומלץ לשלב את השימוש בתוכנה לאחר הבנייה של חוצה זווית‪ .‬את הבנייה של שלושת האנכים‪ :‬אנך‬
‫אמצעי‪ ,‬אנך לישר מנקודה על הישר ואנך לישר מנקודה מחוץ לישר מומלץ לבצע גם ידנית וגם באמצעות התוכנה‪ .‬את‬
‫הבניות שבהמשך מומלץ לבצע בעיקר באמצעות התוכנה‬
‫‪.2‬‬
‫מיומנויות השימוש באמצעים טכנולוגיים יאפשרו לתלמידים להתנסות בהמשך בפעילויות חקר המבוססות על אמצעים‬
‫אלה‪.‬‬
‫‪.3‬‬
‫אחד היתרונות של בנייה באמצעות תוכנה דינמית נעוץ באפשרות לשנות‪ ,‬לאחר סיום הבנייה‪ ,‬את נתוני הבנייה‪,‬‬
‫ולראות כיצד משתנה הצורה שבנינו בהתאם לנתונים החדשים‪.‬‬
‫פותחת את הנושא פעילות ‪ 1‬הנושאת אופי של חידה‪ .‬כדאי להציג אותה לתלמידים בדיון כתתי כדי שיוכלו להציע הצעות‬
‫משלהם מבלי לראות את ההצעות בספר‪ .‬השימוש בחבלים מדמה את המחוגה‪ ,‬ומציאת הנקודה שמרחקיה מנקודות הציון‬
‫שבשאלה תואמים את הנתונים‪ ,‬כמוה כמציאת מפגש של שני מעגלים‪.‬‬
‫פעילות ‪ – 1‬מציאת האוצר – עמ' ‪221‬‬
‫שני ארכיאולוגים יצאו לגלות אוצר מטבעות‪ ,‬שלפי מקורותיהם מצוי באתר חפירות בו נמצאים מגדל ובאר מים‪ .‬במגילת קלף‬
‫שמצאו באותו אתר נאמר שהאוצר הוטמן במרחק ‪ 40‬מטרים מהמגדל‪ ,‬ובמרחק ‪ 50‬מטרים מבאר המים‪.‬‬
‫הארכיאולוגים גילו את המגדל ואת הבאר‪.‬‬
‫א‪ .‬הציעו דרך לגלות את האוצר‪.‬‬
‫ב‪ .‬אחד הארכיאולוגים הציע‪ :‬נקשור חבל באורך ‪ 40‬מטרים ליתד בבסיס המגדל‪ .‬נקשור‬
‫חבל באורך ‪ 50‬מטרים לשפת הבאר‪ .‬כל אחד משנינו יחזיק קצה של אחד החבלים‪.‬‬
‫כשנמצא נקודה משותפת שבה החבלים של שנינו יהיו מתוחים לכל אורכם – שם נתחיל‬
‫לחפור‪ .‬מה דעתכם?‬
‫ג‪.‬‬
‫הארכיאולוגים הגיעו למסקנה שהם יצרו משולש‪ .‬החבלים מתוחים על שתיים מצלעות‬
‫המשולש‪ .‬מי הצלע השלישית ? ומי הם הקדקודים?‬
‫הקדקודים הם המגדל‪ ,‬הבאר‪ ,‬ונקודת המפגש של החבלים‪ .‬הצלע השלישית היא הקטע‬
‫המחבר את הנקודות המציינות את הבאר והמגדל‪.‬‬
‫ד‪ .‬הארכיאולוגים פעלו לפי התכנית ולהפתעתם לא מצאו את האוצר‪.‬‬
‫מה יכולה להיות הסיבה לכך? ישנן כמובן סיבות רבות‪ ,‬למשל אי דיוקים במידע שבמגילת‬
‫הקלף‪ ,‬ומתאים להתייחס גם לסיבות אלה‪ .‬הסיבה המתמטית‪ :‬ישנה נקודה נוספת בה‬
‫החבלים יכולים להיפגש‪ ,‬מעברה השני של "הצלע השלישית"‪ .‬במונחים מתמטיים‪ :‬לשני‬
‫המעגלים יש שתי נקודות מפגש והארכיאולוגים חפרו בנקודה שבה לא נמצא האוצר‪.‬‬
‫ה‪ .‬בהנחה שהאוצר נמצא במקום שנאמר במגילת הקלף – הציעו לארכיאולוגים דרך לגלות‬
‫את האוצר‪ .‬לחפור בנקודה השנייה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪63‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫בפרק הבניות נעשה‬
‫שימוש רב במושגים‬
‫גאומטריים‪ ,‬חלקם מושגי‬
‫יסוד‪ ,‬וזו הזדמנות לדון‬
‫בהם‪ ,‬ולהסב את תשומת‬
‫לב התלמידים לכך שלא כל‬
‫מושג ניתן להגדרה‪ .‬נזכור‬
‫שהקווים והנקודות‬
‫הגאומטריים הם חסרי כל‬
‫עובי‪ ,‬דבר שלא ניתן‬
‫לממש במציאות‪ ,‬ואנחנו‬
‫למעשה בונים רק מודל של‬
‫המושגים האידיאליים‪ .‬אילו‬
‫היה לנקודה עובי היו קיימים ישרים‬
‫רבים שעוברים דרך כל שתי נקודות‪,‬‬
‫ולשני ישרים היתה יותר מאשר נקודה‬
‫משותפת אחת‪.‬‬
‫פעילות ‪ – 2‬העתקת משולש‬
‫בעזרת מחוגה וסרגל ללא‬
‫מידות – עמ' ‪222‬‬
‫פעילות ‪ 2‬נותנת ביטוי מתמטי‬
‫לרעיונות שעלו בפעילות ‪.1‬‬
‫למעשה‪ ,‬מתוארת כאן בנייה של‬
‫משולש על‪-‬פי ‪ 3‬צלעות‪ .‬תיאור‬
‫מסודר של בנייה זו יבוא מאוחר‬
‫יותר‪ .‬המטרה של הפעילות‬
‫הנוכחית היא לשים לב לאבני הבניין‬
‫היסודיות ביותר של הבניות‬
‫הגאומטריות‪ :‬העתקת קטע והעתקת‬
‫זווית‪ .‬במהלך הבנייה יש להעתיק‬
‫קטעים למקום אחר‪ .‬בנוסף‪,‬‬
‫הפעילות מדגישה שיחד עם‬
‫המשולש אנחנו מעתיקים את זוויותיו‬
‫ולכן הנחנו את הבסיס לבנייה‬
‫היסודית "העתקת זווית" שתגיע‬
‫בהמשך‪ .‬התבוננות זו מאפשרת‬
‫להציג את הבניות היסודיות בתוך‬
‫הקשר ולא להצניח אותן‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪64‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫שלבי הבנייה הם‪:‬‬
‫‪ .1‬העתקה של קטע‪( .‬הקטע ‪)AB‬‬
‫‪ .2‬סרטוט מעגלים (המעגל שמרכזו ב‪ A -‬והמעגל שמרכזו ב‪ .3 .)B -‬מציאת נקודות‬
‫המפגש בין המעגלים (הנקודה ‪ .4 ) C‬סרטוט קטע בין שתי נקודות‪( :‬סרטוט הצלעות ‪ AC‬ו‪.)BC -‬‬
‫בפעילות ‪ 2‬עשינו מהלך שלם של העתקת משולש למקום אחר‪.‬‬
‫בפעילויות ‪ 3‬ו‪ 4 -‬נעסוק במרכיבים של העתקת משולש למקום אחר‪ :‬העתקת קטע והעתקת זווית‪.‬‬
‫פעילות ‪ ,5‬בניית משולש על‪-‬פי צלעות היא כמעט חזרה על פעילות ‪ ,2‬אולם הפעם הדגש הוא על בנייה מתוך נתונים‪.‬‬
‫המסגרת הבאה היא מעין מבוא לפעילויות שיבואו‬
‫מה ידוע לנו על הזוויות במשולשים חופפים? מה נוכל להסיק מכך?‬
‫נשים לב כי במהלך ההעתקה של המשולש למקום אחר במישור‪ ,‬למדנו גם להעתיק זווית למקום אחר במישור‪,‬‬
‫כי יחד עם המשולש העתקנו את כל זוויותיו‪.‬‬
‫תהליך ההעתקה של זווית מבוסס על תהליך ההעתקה של משולש‪.‬‬
‫הידעתם?‬
‫מחוגה משמשת גם לשם מדידת מרחקים על מפות‪ .‬לשם כך קובעים את המרווח בין רגלי המחוגה כך שייצג מרחק ידוע‬
‫(לפי קנה המידה של המפה)‪ ,‬ואז סופרים כמה פעמים נכנס מרווח קבוע זה במסלול שאת אורכו רוצים למדוד‪.‬‬
‫על הרעיון של שימוש במחוגה למדידת מרחקים מבוסס תרגיל ‪.44‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪65‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 3‬העתקת קטע אל ישר נתון – עמ' ‪224‬‬
‫נתון הקטע ‪.AB‬‬
‫‪B‬‬
‫‪A‬‬
‫נעתיק את הקטע ‪ AB‬למקום אחר‪.‬‬
‫א‪ .‬העתקת קטע‬
‫נסרטט ישר ונסמן עליו נקודה ‪.C‬‬
‫נפתח את המחוגה כך שקצה אחד שלה יהיה בנקודה ‪A‬‬
‫‪D‬‬
‫והקצה השני בנקודה ‪.B‬‬
‫‪C‬‬
‫נשים את חוד המחוגה בנקודה ‪ C‬ונחוג מעגל שיחתוך את הישר‪.‬‬
‫נסמן את נקודת החיתוך באות ‪.D‬‬
‫הסבירו מדוע הקטע ‪ AB‬שווה לקטע ‪. CD‬‬
‫רדיוסים באותו מעגל שווים‪.‬‬
‫המעגל חותך את הישר בנקודה נוספת‪ .‬כיצד ידענו באיזו משתי נקודות החיתוך לסמן את הנקודה ‪? D‬‬
‫יכולנו לסמן כל אחת מהנקודות‪ .‬אין עדיפות לאחת הנקודות‪.‬‬
‫נשים לב כי כדי לקבל את הנקודה ‪ D‬לא היינו חייבים לסרטט את המעגל כולו‪ .‬יכולנו להסתפק בקשת של המעגל שעוברת‬
‫באחת משתי נקודות החיתוך של המעגל והישר‪.‬‬
‫מעתה‪ ,‬נסתפק לעתים בסרטוט קשת של המעגל במקום לסרטט את המעגל כולו‪.‬‬
‫באמצעות העתקת קטע נוכל גם לקבל כפולות של קטע במספר טבעי‪ ,‬וכן סכומים והפרשים של קטעים‪.‬‬
‫‪a‬‬
‫נתונים הקטעים ‪ a‬ו‪(a>b) b -‬‬
‫‪b‬‬
‫ב‪ .‬חיבור קטעים‬
‫כדי לחבר שני קטעים ‪ a‬ו‪ b -‬נעתיק תחילה על ישר את אחד הקטעים (לדוגמה‪.)a ,‬‬
‫בשלב הבא נעתיק על הישר את הקטע ‪ b‬באופן שקצה אחד שלו‬
‫‪a+b‬‬
‫הוא הקצה של קטע ‪ a‬ולקטעים רק נקודה משותפת אחת‪.‬‬
‫הקטע שיתקבל הוא חיבור של שני הקטעים ‪ a‬ו‪.b -‬‬
‫‪a‬‬
‫‪b‬‬
‫ג‪.‬‬
‫חיסור קטעים‬
‫כדי לחסר שני קטעים שונים זה מזה‪ ,‬נעתיק תחילה את הקטע הגדול‬
‫מבין השניים‪ .‬במקרה זה קטע ‪ .a‬בשלב הבא נעתיק את הקטע הקטן ‪,b‬‬
‫‪b‬‬
‫‪a - b‬‬
‫באופן שקצה אחד הוא הקצה של הקטע ‪ a‬והקצה השני מונח על הקטע ‪a‬‬
‫כמודגם בסרטוט‪ .‬הקטע המתקבל הוא חיסור של הקטע ‪ b‬מהקטע ‪.a‬‬
‫‪a‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪66‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫ד‪ .‬סרטטו באמצעות סרגל ומחוגה קטעים באורך‪:‬‬
‫‪)1‬‬
‫‪2a‬‬
‫‪)2‬‬
‫‪a-b‬‬
‫‪)3‬‬
‫‪)4‬‬
‫‪3b‬‬
‫‪3a+2b‬‬
‫ה‪ .‬רשמו את מהלך הבנייה של סרטוט הקטע באורך ‪.3b‬‬
‫נעתיק תחילה על ישר את הקטע ‪ .b‬בשלב הבא נעתיק שוב על הישר את הקטע ‪ b‬על‬
‫הישר כך שלשני הקטעים יש נקודה אחת משותפת‪ .‬כך קיבלנו את הקטע ‪ .2b‬בשלב‬
‫אנחנו משתמשים באותיות‬
‫אנגליות קטנות‪ b ,a ,‬וכו' גם גם‬
‫כשם של קטע וגם כאורך הקטע‪,‬‬
‫והפירוש ברור לפי ההקשר‪.‬‬
‫השלישי נחבר את הקטע ‪ b‬לקטע ‪ 2b‬ונקבל את הקטע ‪.3b‬‬
‫פעילות ‪ – 4‬העתקת זווית – עמ' ‪225‬‬
‫כדי להעתיק זווית אנחנו‬
‫למעשה יוצרים משולש‬
‫עם הזווית הנתונה‬
‫ומעתיקים אותו למקום‬
‫הדרוש‪ .‬נוח לבחור את‬
‫הנקודות ‪B‬ו‪ C -‬באותו‬
‫מרחק מ‪ .A -‬כך אפשר‬
‫לסמן את שתי הנקודות‬
‫באמצעות קשת שמרכזה‬
‫ב‪ .A -‬אנו חופשיים לקבוע‬
‫את אורך הרדיוס‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪67‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 5‬חיבור וחיסור זוויות – עמ' ‪226‬‬
‫החשיבות של חיבור וחיסור זוויות תבוא לידי ביטוי מאוחר יותר בתרגילים מורכבים‪ .‬אם‪ ,‬למשל‪ ,‬נרצה לבנות משולש שווה‪-‬‬
‫שוקיים בעזרת שוק וזווית בסיס‪ ,‬נמצא תחילה את זווית הראש באמצעות חיסור זוויות הבסיס מזווית שטוחה ונוכל לבסס את‬
‫הבנייה על זווית הראש‪ .‬ראו דוגמה פתורה בעמוד ‪.221‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪68‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילויות ‪ 8 – 6‬עוסקות בסרטוט משולש על‪-‬פי אוסף נתונים שתואם את אחד ממשפטי החפיפה צ‪.‬צ‪.‬צ‪ ,‬צ‪.‬ז‪.‬צ ו‪ -‬ז‪.‬צ‪.‬ז‪.‬‬
‫בניית משולש על‪-‬פי זווית ישרה‪ ,‬ניצב ויתר תילמד אחרי בניות הקשורות באנכים לסוגיהם‪ .‬אחת המטרות של העיסוק‬
‫בבניות שתואמות משפטי חפיפה היא להדגיש שנתונים שמתאימים למשפט חפיפה מגדירים משולש יחיד‪ .‬כל המשולשים‬
‫שנבנה על‪-‬פי אותם הנתונים יהיו משולשים חופפים‪.‬‬
‫מהלך הבנייה בפעילות ‪ 6‬זהה למהלך הבנייה בפעילות ‪ ,2‬ומאפשר חזרה אל הבנייה הראשונה שהוצגה‪ .‬חשוב לשים לב‬
‫להבדל בין שתי הפעילויות‪ .‬בפעילות ‪ 2‬היה נתון לנו המשולש כולו‪ .‬בבנייה לא התחשבנו בזוויות כי הבנייה בעזרת‬
‫הצלעות היא הנוחה ביותר‪ .‬בפעילות ‪ 6‬הנתונים היחידים שלנו הם צלעות המשולש‪.‬‬
‫כיוון שלא ראינו לנגד עינינו את המשולש בנוי איננו יודעים אם קיים משולש שתואם את הנתונים‪ ,‬ואכן‪ ,‬במצבים בהם סכום‬
‫שתי צלעות אינו גדול מהצלע השלישית לא נוכל לבנות את המשולש‪.‬‬
‫אחד הח סרונות של ההוראות המפורטות בספר הוא שהתלמידים מקבלים את הוראות הבנייה מן המוכן‪ .‬תכנון הבנייה ללא‬
‫הוראות יכול להיות מעניין יותר‪ .‬לכן ניתן ללמד את השיעור ללא ספרים פתוחים ולבקש מהתלמידים הצעות כיצד לבצע את‬
‫הבנייה‪.‬‬
‫הסעיף האחרון של פעילות ‪ 6‬מזמין את התלמידים לחשוב בעצמם על הדרך לבנות משולש לפי שתי צלעות והזווית‬
‫שביניהן‪.‬‬
‫אחת האפשרויות לארגן את הלמידה היא באמצעות למידה שיתופית‪ .‬התלמידים מתחלקים לזוגות או לשלשות‪ .‬בהתחלה‬
‫כל תלמיד מבצע פעילות אחרת‪ .‬אחר כך כל תלמיד מלמד את התלמידים האחרים בקבוצה את הבנייה מהפעילות שקיבל‪.‬‬
‫גם אם מארגנים את הלמידה בקבוצות חשוב לעצור ולשאול כיצד אנו יודעים שאכן קיבלנו את המשולש המבוקש‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪69‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 6‬בניית משולש כשנתונות ‪ 3‬צלעותיו – עמ' ‪227‬‬
‫נתונים ‪ 3‬קטעים‪ ,b ,a :‬ו‪.c -‬‬
‫‪c‬‬
‫‪b‬‬
‫‪a‬‬
‫ב‬
‫ד‬
‫ג‬
‫עלינו לבנות משולש ‪ ∆ABC‬שאורכי צלעותיו הם‪ AC = b ,BC = a :‬ו‪.AB = c -‬‬
‫א‪.‬‬
‫שלבי הבנייה‬
‫שלב א‪ :‬נעתיק את הקטע ‪ a‬ונסמן את קצותיו ב‪ B -‬ו‪.C -‬‬
‫שלב ב‪ :‬נשים את חוד המחוגה בנקודה ‪ C‬ונחוג קשת שאורך מחוגה ‪.b‬‬
‫שלב ג‪ :‬נשים את חוד המחוגה בנקודה ‪ B‬ונחוג קשת שאורך מחוגה ‪ .c‬נסמן ב‪ A -‬את מפגש שתי‬
‫הקשתות‪.‬‬
‫שלב ד‪ :‬נחבר את ‪ A‬עם ‪ B‬ועם ‪.C‬‬
‫‪A‬‬
‫‪c‬‬
‫‪B‬‬
‫‪a‬‬
‫‪C‬‬
‫שלב א‬
‫‪B‬‬
‫‪a‬‬
‫‪C‬‬
‫‪B‬‬
‫שלב ב‬
‫‪a‬‬
‫‪B‬‬
‫‪C‬‬
‫שלב ג‬
‫‪b‬‬
‫‪a‬‬
‫‪C‬‬
‫שלב ד‬
‫כיצד נוכיח שקיבלנו את הצורה המבוקשת? ‪ BC = a‬כיוון שהעתקנו את הקטע ‪ AC = b .a‬כיוון ש‪ AC -‬רדיוס של‬
‫מעגל שמחוגו ‪ AB = c .b‬כיוון ש‪ AB -‬רדיוס של מעגל שמחוגו ‪.c‬‬
‫ב‪.‬‬
‫ג‪.‬‬
‫בכל אחד מהסעיפים בנו‪ ,‬אם אפשר‪ ,‬משולש על‪-‬פי ‪ 3‬הקטעים הנתונים‪.‬‬
‫א‬
‫ג‬
‫ב‬
‫ד‬
‫האם בכל המקרים אפשר היה לבנות משולש מהקטעים הנתונים? הסבירו‪ .‬הנתונים בסעיפים ב ו‪-‬ד אינם מאפשרים‬
‫בניית משולש‪ .‬הם עומדים בסתירה למשפט "סכום שתי צלעות במשולש גדול מהצלע השלישית"‪ .‬בסעיף ב סכום‬
‫הצלעות הקצרות שווה לצלע הארוכה ולכן המעגלים נפגשים על הצלע הראשונה שסרטטנו (או על המשכה) ולא נותר‬
‫משולש‪ .‬בסעיף ד סכום הצלעות הקצרות קטן מהצלע הארוכה ולכן המעגלים לא נפגשים כלל‪.‬‬
‫ד‪.‬‬
‫במקרים בהם ניתן היה לבנות משולש בעזרת הקטעים הנתונים – האם ניתן היה לבנות משולשים שונים שאינם‬
‫חופפים? לא‪ .‬כל המשולשים שנבנה על‪-‬פי אותם נתונים יהיו חופפים על‪-‬פי צ‪.‬צ‪.‬צ‪.‬‬
‫ה‪.‬‬
‫נתון קטע ‪.a‬‬
‫‪a‬‬
‫אם אפשר‪ ,‬בנו משולש שאורך צלעותיו ‪?5a ,2a ,a‬‬
‫אם לא – הסבירו מדוע לא ניתן לבנות משולש כזה‪ .‬אי‪-‬אפשר‪.a + 2a <5a .‬‬
‫ו‪.‬‬
‫אילו היו נתונות לכם שתי צלעות והזווית שביניהן‪ ,‬כיצד הייתם מתכננים את הבנייה?‬
‫סעיף ו של פעילות ‪ 6‬הוא הקדמה לקראת פעילות ‪ ,7‬ונועד להזמין את התלמידים לחשוב על הבנייה לפני שייחשפו לה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪70‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 7‬בניית משולש לפי שתי צלעות וזווית שביניהן – עמ' ‪228‬‬
‫נתונים זווית ושני קטעים‪.‬‬
‫עלינו לבנות משולש ‪ ABC‬על‪-‬פי הנתונים‪.∡A =  ,AC = b ,AB = c :‬‬
‫‪‬‬
‫א‪ .‬שלבי הבנייה‬
‫שלב א‪ :‬נעתיק את הקטע ‪ c‬ונסמן את קצותיו ב‪ A -‬ו‪.B -‬‬
‫‪c‬‬
‫שלב ב‪ :‬נעתיק את הזווית ‪ ‬כך שקדקודה בנקודה ‪ A‬ואחת משוקיה‬
‫מכילה את ‪.AB‬‬
‫‪b‬‬
‫שלב ג‪ :‬על השוק השנייה של הזווית ‪ ,‬נעתיק את הקטע ‪ b‬כך שקצהו האחד‬
‫ב‪ .A -‬נסמן ב‪ C -‬את הקצה השני של הקטע‪.‬‬
‫שלב ד‪ :‬נחבר את ‪ C‬עם ‪.B‬‬
‫‪C‬‬
‫‪C‬‬
‫‪b‬‬
‫‪B‬‬
‫‪A‬‬
‫‪c‬‬
‫‪‬‬
‫‪B‬‬
‫‪c‬‬
‫שלב א‬
‫‪A‬‬
‫‪B‬‬
‫שלב ב‬
‫‪b‬‬
‫‪‬‬
‫‪c‬‬
‫‪A‬‬
‫‪B‬‬
‫שלב ג‬
‫‪‬‬
‫‪c‬‬
‫‪A‬‬
‫שלב ד‬
‫כיצד נוכיח שקיבלנו את המשולש המבוקש?‬
‫‪ ∡A = ‬כי בצענו העתקת זווית‪ AB = c .‬כיוון ש‪ AB -‬רדיוס של מעגל שמחוגו ‪.c‬‬
‫‪ AC = b‬כיוון ש‪ AC -‬רדיוס של מעגל שמחוגו ‪.b‬‬
‫ב‪ .‬האם ניתן לבנות על‪-‬פי הנתונים שקיבלנו משולש שונה מ‪? ABC -‬‬
‫לא‪ .‬כל משולש אחר עם אותם נתונים יהיה חופף לו על‪-‬פי צ‪.‬ז‪.‬צ‬
‫(‪)1‬‬
‫(‪)3‬‬
‫(‪)2‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪b‬‬
‫‪b‬‬
‫‪b‬‬
‫‪c‬‬
‫‪c‬‬
‫‪c‬‬
‫‪a‬‬
‫ג‪ .‬בכל סעיף בנו‪ ,‬אם אפשר‪ ,‬משולש ‪ ABC‬שבו‪.∡A =  ,AC = b , AB = c :‬‬
‫ד‪.‬‬
‫האם כל זוג קטעים וזווית מאפשרים סרטוט משולש כך שהקטעים הם צלעות במשולש והזווית נמצאת בין צלעות‬
‫אלה? כל עוד הזווית בין ‪ 0‬ל‪ 180 -‬ניתן לבצע את הבנייה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪71‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 8‬בניית משולש לפי שתי זוויות וצלע שביניהן – עמ' ‪229‬‬
‫נתונות שתי זוויות ונתון קטע‪.‬‬
‫‪.∡A =  ,∡B =  ,‬‬
‫עלינו לבנות משולש ‪ ABC‬על‪-‬פי הנתונים‪AB = c :‬‬
‫‪α‬‬
‫א‪ .‬שלבי הבנייה‬
‫שלב א‪ :‬נעתיק את הקטע ‪ c‬ונסמן את קצותיו ב‪ A -‬ו‪.B -‬‬
‫שלב ב‪ :‬נעתיק את הזווית ‪ ‬כך שקדקודה בנקודה ‪ A‬ואחת משוקיה מכילה את ‪.AB‬‬
‫שלב ג‪ :‬נעתיק את הזווית ‪ ‬כך שקדקודה בנקודה ‪ B‬ואחת משוקיה מכילה את ‪.AB‬‬
‫‪‬‬
‫נסמן ב‪ C -‬את נקודת המפגש של שוקי הזוויות ‪ ∡A‬ו‪.∡B -‬‬
‫נשים לב כי הסימון של הנקודה ‪ C‬השלים את בניית המשולש‪.‬‬
‫‪c‬‬
‫‪C‬‬
‫‪B‬‬
‫‪A‬‬
‫‪c‬‬
‫‪‬‬
‫‪B‬‬
‫‪A‬‬
‫‪c‬‬
‫שלב א‬
‫‪B‬‬
‫שלב ב‬
‫‪‬‬
‫‪‬‬
‫‪c‬‬
‫‪A‬‬
‫שלב ג‬
‫ב‪ .‬האם ניתן לבנות על‪-‬פי הנתונים שקיבלנו משולש שונה מ‪? ABC -‬‬
‫לא‪ .‬כל משולש אחר עם אותם נתונים יהיה חופף לו על‪-‬פי ז‪.‬צ‪.‬ז‪.‬‬
‫ג‪.‬‬
‫בכל סעיף בנו‪ ,‬אם אפשר‪ ,‬משולש ‪ ABC‬שבו‪.∡A =  ,∡B =  , AB = c :‬‬
‫‪)1‬‬
‫‪)2‬‬
‫(‪)1‬‬
‫‪)3‬‬
‫(‪)3‬‬
‫(‪)2‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪c‬‬
‫‪c‬‬
‫‪‬‬
‫‪‬‬
‫‪c‬‬
‫סעיף ‪ 3‬חשוב כי הוא מבליט את העובדה שלא קיים משולש עם שתי זוויות ישרות‪.‬‬
‫נקודה זו חשובה כי היא מספקת הסבר אינטואיטיבי לכך שישרים שמאונכים לאותו ישר לא יכולים להיפגש ולכן הם‬
‫מקבילים‪.‬‬
‫ד‪.‬‬
‫האם כל שתי זוויות וקטע מאפשרים לבנות משולש שבו הצלע הנתונה נמצאת בין שתי הזוויות הנתונות?‬
‫סכום הזוויות הנתונות צריך להיות קטן מ‪180 -‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪72‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תרגילים – עמ' ‪233 – 230‬‬
‫תרגילים לבניית משולש על‪-‬פי שלוש צלעות – עמ' ‪230‬‬
‫באתר מופיע קובץ עם נתונים לביצוע‬
‫במחשב של הבניות בעמוד זה‬
‫בנק נתונים‬
‫עבור תרגילי בנייה ‪ 7 – 1‬היעזרו בקטעים הנתונים‪:‬‬
‫‪a‬‬
‫עמ' ‪230‬‬
‫‪b‬‬
‫‪d‬‬
‫‪c‬‬
‫‪ .1‬א‪ .‬נתונים הקטעים ‪ a‬ו‪ .b -‬בנו משולש שווה‪-‬שוקיים עם צלעות אלה‪.‬‬
‫ב‪ .‬כמה אפשרויות קיימות לבניית המשולש בסעיף הקודם?‬
‫קיימות ‪ 2‬אפשרויות‪ :‬א‪ a .‬בסיס ו‪ b -‬שוק‪ .‬ב‪ b .‬בסיס ו‪ a -‬שוק‪.‬‬
‫‪ .2‬א‪ .‬נתונים הקטעים ‪ c‬ו‪ .d -‬בנו משולש שווה‪ -‬שוקיים עם צלעות אלה‪.‬‬
‫ב‪ .‬כמה אפשרויות קיימות לבניית המשולש בסעיף הקודם? בנו את כל המשולשים האפשריים‪.‬‬
‫קיימת אפשרות אחת‪ d :‬בסיס ו‪ c -‬שוק‪.‬‬
‫כיוון ש‪ 2d < c -‬אי‪-‬אפשר לבנות משולש שווה‪-‬שוקיים עם בסיס ‪c‬‬
‫ושוק ‪.d‬‬
‫‪ .3‬בנו משולש שווה‪-‬צלעות לפי צלעו ‪.b‬‬
‫‪ .4‬בנו דלתון לפי האלכסון הראשי ‪ a‬והצלעות ‪ b‬ו‪.c -‬‬
‫נקדים תכנון לביצוע‪ :‬נסרטט את הדלתון באופן סכמתי‪ .‬נשים לב‪ ,‬שהאלכסון הנתון מחלק אותו לשני משולשים‬
‫חופפים שצלעותיהם נתונות לנו ולכן נוכל לבנות את המשולשים ולקבל את הדלתון‪.‬‬
‫אפשר לתת לתלמידים את התרגיל כדוגמה פתורה עם שאלות לדיון (ראו בדף הבא)‪.‬‬
‫הדוגמה גם מצביעה על דרך נוחה לתיאור המהלך של בניות מורכבות‪ .‬בעמודה הימנית כותבים את שלבי הבנייה‬
‫באמצעות בניות יסודיות‪ .‬בעמודה השנייה מפרטים את המהלכים שבכל אחת מן הבניות האלה‪ .‬אפשר גם להוסיף‬
‫עמודה עם איורים‪.‬‬
‫דף העבודה מלווה בדף עם פתרונות והערות למורה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪73‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫דוגמה פתורה – בניית דלתון על‪-‬פי שתי צלעות שונות ואלכסון ראשי‬
‫א‪.‬‬
‫בדלתון ‪ ABCD‬נתון‪ . AC = c , CB = CD = b ,AB = AD = a :‬בנו את הדלתון‪.‬‬
‫‪a‬‬
‫‪b‬‬
‫‪c‬‬
‫ב‪ .‬ניתוח הבעיה‬
‫‪A‬‬
‫נסרטט סקיצה של דלתון עם אלכסון ראשי‪ .‬הסקיצה אינה מתבססת על הקטעים הנתונים‪.‬‬
‫נצבע את הקטעים שנתונים לנו ונתבונן בקשרים שביניהם‪.‬‬
‫ניתן לראות שהאלכסון הראשי מחלק את הדלתון לשני משולשים שכל צלעותיהם נתונות‪,‬‬
‫‪D‬‬
‫‪B‬‬
‫ולכן נוכל לבנות את שניהם ולקבל את הדלתון‪.‬‬
‫ג‪.‬‬
‫תיאור מהלך הבנייה‬
‫‪C‬‬
‫פירוט‬
‫השלב‬
‫‪A‬‬
‫‪‬‬
‫נעתיק את הקטע ‪ m‬ונכנה את קצותיו ‪ A‬ו‪.C -‬‬
‫‪‬‬
‫נחוג קשת שמרכזה בנקודה ‪ A‬ומחוגה ‪.a‬‬
‫בניית‬
‫‪‬‬
‫נחוג קשת שמרכזה בנקודה ‪ C‬ומחוגה ‪.b‬‬
‫המשולש‬
‫‪‬‬
‫נסמן ב‪ B -‬את מפגש שתי הקשתות‪.‬‬
‫‪‬‬
‫נחבר את ‪ B‬עם ‪ A‬ועם ‪.C‬‬
‫‪‬‬
‫בזאת יצרנו את המשולש ‪.ABC‬‬
‫‪‬‬
‫נשים את חוד המחוגה בנקודה ‪ A‬ונחוג קשת‬
‫שמחוגה ‪ a‬מהצד השני של ‪.AC‬‬
‫‪‬‬
‫נשים את חוד המחוגה בנקודה ‪ C‬ונחוג קשת‬
‫שמחוגה ‪ b‬כך שתחתוך את הקשת הראשונה‪.‬‬
‫נסמן ב‪ D -‬את מפגש שתי הקשתות‪.‬‬
‫‪‬‬
‫נחבר את ‪ D‬עם ‪ A‬ועם ‪.C‬‬
‫‪‬‬
‫בזאת יצרנו את המשולש ‪ ADC‬והשלמנו את‬
‫הדלתון‪.‬‬
‫‪ABC‬‬
‫‪B‬‬
‫‪C‬‬
‫בניית‬
‫המשולש‬
‫‪ADC‬‬
‫‪A‬‬
‫‪D‬‬
‫‪B‬‬
‫‪C‬‬
‫ד‪ .‬כיצד נוכל להיות בטוחים שהבנייה תואמת את הנתונים?‬
‫ה‪ .‬אור אומרת שאפשר גם אחרת לבנות את הדלתון‪" :‬העתקתי את הקטע ‪ m‬שהוא האלכסון ‪ .AC‬מהקדקוד ‪ A‬חגתי‬
‫קשת גדולה ברדיוס ‪ .a‬מהקדקוד ‪ C‬חגתי קשת גדולה ברדיוס ‪ .b‬הקשתות נפגשו ב‪ 2 -‬נקודות‪ .‬קראתי להן ‪ B‬ו‪-‬‬
‫‪ .D‬חיברתי כל אחת מהנקודות ‪ B‬ו‪ D -‬עם ‪ A‬ועם ‪ C‬וקיבלתי את הדלתון"‪.‬‬
‫האם הבנייה של אור נכונה? הסבירו‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪74‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫דוגמה פתורה – בניית דלתון על‪-‬פי שתי צלעות שונות ואלכסון ראשי ‪ -‬פתרונות והערות‬
‫דוגמה זו מדגימה את הנוחיות שבשימוש בצבעים במהלך תכנון הבנייה‪ .‬הצבעים מאפשרים לראות בקלות את מקומם של‬
‫החלקים הנתונים בצורה המבוקשת‪ ,‬ולבסס על כך את הבנייה של הצורה המבוקשת על‪-‬פי הסרטוט הסכמתי‪.‬‬
‫הבנייה שאור מציעה בסעיף ה היא יעילה יותר מאשר ההצעה הראשונה‪ .‬ניתן לסרטט את שני המשולשים בו זמנית על‪-‬ידי‬
‫סרטוט קשתות גדולות יותר שייפגשו בשתי נקודות‪.‬‬
‫הבנייה לא נעשתה כך מראש כדי להדגיש את העובדה שאחרי שלמדנו לסרטט משולשים על‪-‬פי נתונים שתואמים את משפטי‬
‫ההחפיפה נוכל להיעזר בהם על מנת לסרטט צורות שבמורכבות ממשולשים כאלה‪.‬‬
‫א‪ .‬בדלתון ‪ ABCD‬נתון‪ . AC = m , CB = CD = b ,AB = AD = a :‬בנו את הדלתון‪.‬‬
‫‪a‬‬
‫‪b‬‬
‫ב‪ .‬ניתוח הבעיה‬
‫‪m‬‬
‫נסרטט סקיצה של דלתון עם אלכסון ראשי‪ .‬הסקיצה אינה מתבססת על הקטעים הנתונים‪.‬‬
‫נצבע את הקטעים שנתונים לנו ונתבונן בקשרים שביניהם‪.‬‬
‫‪A‬‬
‫‪D‬‬
‫‪B‬‬
‫ניתן לראות שהאלכסון הראשי מחלק את הדלתון לשני משולשים שכל צלעותיהם נתונות‪,‬‬
‫ולכן נוכל לבנות את שניהם ולקבל את הדלתון‪.‬‬
‫‪C‬‬
‫ג‪.‬‬
‫תיאור מהלך הבנייה‬
‫פירוט‬
‫השלב‬
‫‪A‬‬
‫‪‬‬
‫נעתיק את הקטע ‪ m‬ונכנה את קצותיו ‪ A‬ו‪.C -‬‬
‫‪‬‬
‫נחוג קשת שמרכזה בנקודה ‪ A‬ומחוגה ‪.a‬‬
‫בניית‬
‫‪‬‬
‫נחוג קשת שמרכזה בנקודה ‪ C‬ומחוגה ‪.b‬‬
‫המשולש‬
‫‪‬‬
‫נסמן ב‪ B -‬את מפגש שתי הקשתות‪.‬‬
‫‪‬‬
‫נחבר את ‪ B‬עם ‪ A‬ועם ‪.C‬‬
‫‪‬‬
‫בזאת יצרנו את המשולש ‪.ABC‬‬
‫‪‬‬
‫נשים את חוד המחוגה בנקודה ‪ A‬ונחוג קשת‬
‫שמחוגה ‪ a‬מהצד השני של ‪.AC‬‬
‫‪‬‬
‫נשים את חוד המחוגה בנקודה ‪ C‬ונחוג קשת‬
‫שמחוגה ‪ b‬כך שתחתוך את הקשת הראשונה‪.‬‬
‫נסמן ב‪ D -‬את מפגש שתי הקשתות‪.‬‬
‫‪‬‬
‫נחבר את ‪ D‬עם ‪ A‬ועם ‪.C‬‬
‫‪‬‬
‫בזאת יצרנו את המשולש ‪ ADC‬והשלמנו את‬
‫הדלתון‪.‬‬
‫‪ABC‬‬
‫‪B‬‬
‫‪C‬‬
‫בניית‬
‫המשולש‬
‫‪ADC‬‬
‫‪A‬‬
‫‪D‬‬
‫‪B‬‬
‫‪C‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪75‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫ד‪ .‬כיצד נוכל להיות בטוחים שהבנייה תואמת את הנתונים?‬
‫את האלכסון הראשי העתקנו‪ .‬צלעות הדלתון הן מחוגים של מעגלים שניבנו עם הרדיוס המבוקש‪.‬‬
‫ה‪ .‬אור אומרת שאפשר גם אחרת לבנות את הדלתון‪" :‬העתקתי את הקטע ‪ m‬שהוא האלכסון ‪ .AC‬מהקדקוד‬
‫‪ A‬חגתי קשת גדולה ברדיוס ‪ .a‬מהקדקוד ‪ C‬חגתי קשת גדולה ברדיוס ‪ .b‬הקשתות נפגשו ב‪ 2 -‬נקודות‪.‬‬
‫קראתי להן ‪ B‬ו‪ .D -‬חיברתי כל אחת מהנקודות ‪ B‬ו‪ D -‬עם ‪ A‬ועם ‪ C‬וקיבלתי את הדלתון"‪.‬‬
‫האם הבנייה של אור נכונה? הסבירו‪.‬‬
‫ראו הסבר במבוא לדף העבודה‪.‬‬
‫תרגיל ‪ 5‬נועד לעסוק במצב בו אין מספיק נתונים כדי לסרטט צורה יחידה‪.‬‬
‫‪‬‬
‫עמ' ‪230‬‬
‫‪ .5‬א‪ .‬בנו דלתון ‪ ABCD‬לפי הנתונים‪.CB = CD = b , AB = AD = a :‬‬
‫ב‪ .‬כמה דלתונים שונים זה מזה אפשר לבנות על‪-‬פי הנתונים?‬
‫ניתן לבנות אינסוף דלתונים על‪-‬פי הנתונים‪.‬‬
‫דרך א‬
‫נוכל לקבוע נקודה ‪ ,A‬לסרטט מעגל ברדיוס ‪ a‬עם מרכז ‪ A‬ולקבוע עליו שתי‬
‫נקודות ‪ B‬ו‪ .D -‬מכל אחת מהנקודות ‪ B‬ו‪ D -‬נחוג מעגל ברדיוס ‪ .b‬את אחת‬
‫מנקודות המפגש של המעגלים נסמן ב‪ .C -‬אם המעגלים לא נחתכים נבחר נקודות‬
‫קרובות יותר על המעגל עבור ‪ B‬ו‪.D -‬‬
‫‪‬‬
‫באתר יש יישומון הדגמה לדרך בניה זו‪ :‬בניית דלתון על‪-‬פי צלעותיו ‪.1‬‬
‫ביישומון יש סרגל ניווט שמאפשר להתבונן בבנייה צעד אחר צעד‪ ,‬החל מסרטוט‬
‫הקטעים המשמשים כנתונים ועד לבניית שני דלתונים‪ ,‬האחד קמור והשני קעור‪.‬‬
‫כדאי להדגים איך גרירת הנקודות ‪ B‬ו‪ D -‬על המעגל משנה את הדלתון‪.‬‬
‫דרך ב אפשרות אחרת היא לקבוע שתי נקודות ‪ A‬ו‪ C -‬כקדקודים הראשיים של‬
‫הדלתון‪.‬‬
‫מהנקודה ‪ A‬כמרכז נחוג מעגל ברדיוס ‪ .a‬מהנקודה ‪ C‬כמרכז נחוג מעגל‬
‫ברדיוס ‪ .b‬נקודות המפגש ‪ B‬ו‪ D -‬הן קדקודי צד של הדלתון‪ .‬כיוון שיש לנו‬
‫אינסוף אפרויות לקבוע את הקדקודים הראשיים יש אינסוף אפשרויות לבנות את‬
‫הדלתון‪.‬‬
‫‪‬‬
‫באתר יש יי שומון הדגמה לדרך בניה זו‪ :‬בניית דלתון על‪-‬פי צלעותיו ‪.2‬‬
‫ג‪ .‬הציעו נתון נוסף כך שהנתונים יאפשרו לבנות דלתון אחד בלבד‪.‬‬
‫למשל‪ ,‬נוכל לקבוע את האלכסון הראשי ‪.AC = c‬‬
‫קביעת האלכסון המשני לא תבטיח משולש יחיד אלא תאפשר בניית שני משולשים‪ ,‬אחד קמור ואחד קעור‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪76‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪230‬‬
‫‪ .6‬א‪ .‬בנו דלתון ‪ ABCD‬לפי הנתונים‪.BD = c , CB = CD = b , AB = AD = a :‬‬
‫נקדים תכנון לביצוע‪:‬‬
‫כדי להתבונן בחלקי הדלתון הנתונים בתוך סרטוט של דלתון מתאים נניח שהצלחנו‬
‫‪B‬‬
‫לסרטט את הדלתון המבוקש‪.‬‬
‫חשוב להדגיש‪ :‬עדין איננו יודעים לסרטט את הדלתון הנתון ולכן אנחנו יוצרים‬
‫‪A‬‬
‫‪C‬‬
‫סרטוט סכמתי שחלקיו אינם תואמים בהכרח את הנתונים‪ .‬האלכסון מחלק את‬
‫הדלתון לשני משולשים שווי‪-‬שוקיים שכל אחד מהם ניתן לבנייה על‪-‬פי צ‪.‬צ‪.‬צ‪.‬‬
‫‪D‬‬
‫נבנה תחילה את המשולש ‪.ABD‬‬
‫למציאת הקדקוד ‪ C‬נבנה את המשולש ‪.CBD‬‬
‫ב‪ .‬כמה דלתונים שונים זה מזה אפשר לבנות על‪-‬פי הנתונים?‬
‫ניתן לבנות שני דלתונים‪ ,‬קמור וקעור‪.‬‬
‫ג‪ .‬כמה דלתונים קמורים שונים זה מזה אפשר לבנות על‪-‬פי הנתונים‪.‬‬
‫‪C‬‬
‫ניתן לבנות דלתון קמור אחד על‪-‬פי הנתונים‪.‬‬
‫‪D‬‬
‫‪ .7‬הסבירו מדוע לא ניתן לבנות דלתון שבו אורכי הצלעות ‪ a‬ו‪ 2a -‬ואורך האלכסון הראשי ‪ .3a‬שתי הצלעות יחד עם‬
‫האלכסון הראשי יוצרות משולש‪ .‬לא קיים משולש שצלעותיו‬
‫‪ 2a ,a‬ו‪ .3a -‬כיוון שבמקרה זה סכום שתי צלעות שווה לצלע השלישית‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪77‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תרגילים לבניית משולש לפי זווית צלע וזווית – עמ' ‪231‬‬
‫בנק נתונים‬
‫עבור תרגילי בנייה ‪ 18 – 8‬היעזרו בנתונים הבאים‪:‬‬
‫‪m‬‬
‫‪k‬‬
‫‪‬‬
‫עמ' ‪231‬‬
‫‪d‬‬
‫‪p‬‬
‫‪γ‬‬
‫‪‬‬
‫‪ .8‬בנו משולש שווה‪-‬שוקיים על‪-‬פי השוק ‪ k‬וזווית הראש ‪.∡A = ‬‬
‫‪ .9‬נתונים קטע ‪ m‬וזווית ‪ .‬בנו משולש שבו ‪ ∡A = ‬וצלעותיו ‪ AB = m‬ו‪.AC=2m -‬‬
‫האם כל צירוף של קטע וזווית מאפשר לבנות את המשולש המבוקש? כל עוד הזווית בין ‪ 0‬ל‪ 180 -‬ניתן לבצע את‬
‫הבנייה‪.‬‬
‫דוגמה פתורה – עמ' ‪231‬‬
‫בנו משולש שווה‪-‬שוקיים על‪-‬פי השוק ‪ p‬וזווית הבסיס ‪.β‬‬
‫היעזרו בסכום זוויות‬
‫במשולש‪.‬‬
‫פתרון‬
‫בנייה זו כרוכה בשלב הכנה‪ .‬תחילה נמצא את זווית הראש‪.‬‬
‫כיצד נדע את מידתה?‬
‫‪‬‬
‫הסבירו מדוע זו מידת זווית הראש‪.‬‬
‫‪‬‬
‫‪180-‬‬
‫לאחר שמצאנו את גודל זווית הראש‪ ,‬נוכל להמשיך ולבנות את המשולש על‪-‬פי שתי צלעות והזווית שביניהן‪.‬‬
‫‪ .10‬בנו משולש ‪ ABC‬שבו‪.AC = 2d ,AB = p ,∡A =  :‬‬
‫‪A‬‬
‫‪ .11‬א‪ .‬בנו דלתון ‪ ABCD‬שבו‪.∡B = ∡D =  ,CB = CD = k ,AB = AD = m :‬‬
‫‪m‬‬
‫‪α B‬‬
‫סרטוט סכמתי של הדלתון לפני הבנייה מראה‪ :‬הנתונים מאפשרים בנייה של המשולש‬
‫‪D‬‬
‫‪ ABC‬על‪-‬פי צ‪.‬ז‪.‬צ‪.‬‬
‫לאחר שנסרטט את הקטע ‪ AC‬נוכל להשלים את הדלתון על‪-‬ידי בניית המשולש ‪,ADC‬‬
‫‪k‬‬
‫או במילים אחרות למצוא את הקדקוד ‪ D‬כנקודת מפגש של שתי קשתות‪ :‬האחת מחוגה ‪m‬‬
‫ומרכזה ‪ .A‬השנייה מחוגה ‪ k‬ומרכזה ‪.C‬‬
‫‪C‬‬
‫נשים לב כי למרות הסימטריה של הדלתון הבנייה איננה סימטרית‬
‫ב‪ .‬האם יכולתם לקבוע מי הן הצלעות השוות על‪-‬פי הנתונים אודות הזוויות השוות?‬
‫הזוויות השוות הן זוויות צד‪ .‬מכאן ששני הקדקודים האחרים הם קדקודי ראש‪.‬‬
‫הצלעות היוצאות מכל קדקוד ראש שוות זו לזו‪.‬‬
‫בנו תחילה‬
‫את המשולש ‪.ABC‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪78‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫מטרת תרגיל ‪ 12‬להדגיש את הקשר בין תנאים שאינם מבטיחים חפיפת משולשים לבין תנאים שמאפשרים לבנות יותר‬
‫מאשר משולש אחד שעונה על הדרישות‪.‬‬
‫השתמשו בבנק הנתונים‬
‫מהעמוד הקודם‪.‬‬
‫עמ' ‪ .12 232‬נתונות שתי זוויות ‪ ‬ו‪. -‬‬
‫א‪ .‬בנו משולש ‪ ABC‬שבו ‪ ∡A = ‬ו‪.∡B =  -‬‬
‫נבנה קטע ‪ AB‬שרירותי‪ ,‬ובקצותיו נעתיק את הזוויות הנתונות‪.‬‬
‫ב‪ .‬בנו‪ ,‬אם אפשר‪ ,‬משולש נוסף שבו ‪ ∡A = ‬ו‪ ∡B =  -‬ואשר אינו חופף למשולש ‪.ABC‬‬
‫אם אי‪-‬אפשר לבנות – הסבירו מדוע‪.‬‬
‫כיוון שבנינו את הקטע ‪ AB‬כרצוננו‪ ,‬נוכל לשנות אותו ולקבל משולשים שאינם חופפים‪.‬‬
‫ג‪ .‬בנו‪ ,‬אם אפשר‪ ,‬משולש נוסף שבו ‪ ∡A = ‬ו‪ ∡B =  -‬ואשר אינו דומה למשולש ‪.ABC‬‬
‫אם אי‪-‬אפשר לבנות – הסבירו מדוע‪.‬‬
‫כיוון שכל שני משולשים שיש להן שתי זוויות שוות בהתאמה דומים‪ ,‬לא ניתן לבנות בנתוני השאלה משולשים‬
‫שאינם דומים‪.‬‬
‫‪ .13‬בנו משולש ‪ ABC‬שבו אורך ‪ ∡A =  ,AB = k‬ו‪.∡B =  -‬‬
‫האם מכל צירוף של צלע ושתי זוויות נוכל לבנות משולש? הסבירו‪.‬‬
‫הבניה היא בנייה סטנדרטית על פי ז‪.‬צ‪.‬ז‪ .‬סכום הזוויות הנתונות צריך להיות קטן מ‪.180 -‬‬
‫בנייה זו כרוכה‬
‫בשלב הכנה‪.‬‬
‫‪ .14‬בנו משולש ‪ ABC‬שבו ‪ ∡B =  ,AB = m‬והזווית החיצונית בקדקוד ‪ A‬שווה ל‪. -‬‬
‫בשלב ההכנה נבנה את הזווית הצמודה ל‪ . -‬כעת נוכל לבנות משולש על‪-‬פי ז‪.‬צ‪.‬ז‪.‬‬
‫האם כל צירוף של זוויות ‪ ‬ו‪  -‬מאפשר לבנות את המשולש המבוקש בסעיף‬
‫הקודם?‬
‫‪‬‬
‫הזווית החיצונית הנתונה צריכה להיות גדולה מהזווית הפנימית הנתונה‪.‬‬
‫‪‬‬
‫‪m‬‬
‫כדאי להעלות את השאלה אם נוכל לבנות משולש ‪ ABC‬שבו ‪ ∡A =  ,AB = m‬והזווית החיצונית בקדקוד ‪B‬‬
‫שווה ל‪ .  -‬התשובה שלילית כי הפעם הזווית החיצונית קטנה מזווית פנימית שאינה צמודה לה‪.‬‬
‫‪ ‬‬
‫‪ .15‬בנו דלתון שבו אורך האלכסון הראשי הוא ‪ , p‬וגודל זוויות הראש הוא‪ 2 :‬ו‪.2 -‬‬
‫‪p‬‬
‫כיוון שאלכסוני הדלתון חוצים זה את זה‪ ,‬חצאי זוויות הראש הם ‪ ‬ו‪ . -‬כעת נוכל לבנות לפי ז‪.‬צ‪.‬ז‬
‫שני משולשים חופפים עם צלע משותפת שהיא האלכסון הראשי‪.‬‬
‫‪ ‬‬
‫‪ .16‬בנו דלתון קמור שבו אורך האלכסון המשני הוא ‪ m‬וגודל הזוויות בין האלכסון המשני לבין צלעות‬
‫הדלתון הוא ‪ ‬ו‪. -‬‬
‫האלכסון המשני מחלק דלתון קמור לשני משולשים שווי‪-‬שוקיים עם בסיס משותף‪ .‬כל אחד מהם נוכל‬
‫‪‬‬
‫‪‬‬
‫‪ m ‬‬
‫לבנות על‪-‬פי ז‪.‬צ‪.‬ז‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪79‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫‪Q‬‬
‫עמ' ‪ .17 232‬בנו דלתון קעור שבו אורך האלכסון המשני הוא ‪ k‬וגודל הזוויות בין האלכסון‬
‫המשני לבין צלעות הדלתון הוא‪  :‬ו‪. -‬‬
‫הפעם האלכסון המשני נמצא מחוץ לדלתון‪ .‬כמו בתרגיל ‪ 15‬נבנה שני‬
‫‪S‬‬
‫משולשים שווי ‪-‬שוקיים עם בסיס ‪ .k‬האחד עם זווית בסיס ‪ ‬והשני עם זווית‬
‫בסיס ‪ .‬הפעם שני המשולשים בנויים מאותו צד של האלכסון המשני‪.‬‬
‫‪P‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪k‬‬
‫‪R‬‬
‫בניית דלתון עם זווית ראש נתונה – מה אפשר ללמוד מזה? – עמ' ‪232‬‬
‫תרגילים ‪ 19 - 18‬הם תרגילי מכינים לקראת בניית חוצה‪-‬זווית במשולש‪.‬‬
‫בניית חוצה הזווית מבוססת על בניית דלתון וסרטוט האלכסון הראשי שלו‪.‬‬
‫בתרגיל ‪ 18‬מספקים נתונים שמאפשרים בנייה יחידה של דלתון‪ .‬שלבי הבנייה הם בדיוק אלה שישמשו בהמשך לחצייה של‬
‫זווית תרגיל ‪ 19‬עושה צעד נוסף‪ .‬הפעם מבקשים לסרטט דלתון כשהנתון היחיד הוא אחת מזוויות הראש‪.‬‬
‫זהו בדיוק הנתון שמקבלים כאשר מתבקשים לחצות זווית‪.‬‬
‫בתרגיל ‪ 19‬שואלים במפורש מדוע בכל הדלתונים שבנינו התקבל חוצה זווית‪ .‬מטרת סעיף זה היא להאיר את העובדה‬
‫שבנינו חוצה זווית‪ ,‬במטרה שלפחות חלק מהתלמידים שיתבקשו לבנות חוצה זווית יוכלו להתבסס על התרגילים שבצעו זה‬
‫עתה ולתכנן בעצמם את הבנייה‪.‬‬
‫כאן גם נזרעים הזרעים הראשונים לקראת הבניות של אנך אמצעי לקטע‪ ,‬אנך לישר מנקודה על הישר ואנך לישר מנקודה‬
‫מחוץ לישר בפעילויות ‪ .12 - 10‬גם בשלוש הבניות האלה בונים דלתון‪ .‬הפעם האלכסון הראשי של הדלתון הוא הישר‬
‫המבוקש‪.‬‬
‫‪ .18‬א‪ .‬בנו דלתון קמור ‪ ABCD‬שבו‪.∡A =  ,CB = CD = k ,AB = AD = m :‬‬
‫בנו תחילה‬
‫את המשולש ‪.ABD‬‬
‫ב‪ .‬בנו דלתון קעור עם אותם נתונים‪.‬‬
‫הדרכה‪:‬‬
‫לפני שמחליטים על מהלך הבנייה נוח לפעמים להתבונן בסרטוט סכמתי של דלתון דומה‪ .‬בסרטוט‬
‫‪k‬‬
‫‪C‬‬
‫‪D‬‬
‫הסכמתי הצלעות והזוויות לא חייבות להתאים לנתונים‪.‬‬
‫הצלעות ‪ AD‬ו‪ AB -‬נמצאות על שוקי הזווית ‪ .‬לכן נוכל למצוא את מקום הקדקודים ‪ B‬ו‪ D -‬אם‬
‫נעתיק את הקטע ‪ m‬על שוקי הזווית‪.‬‬
‫‪k‬‬
‫‪B‬‬
‫‪m‬‬
‫‪‬‬
‫כיצד נמצא את מקומה של הנקודה ‪? C‬‬
‫‪m‬‬
‫‪A‬‬
‫אפשר לחשוב על הבנייה כעל פעולה בת שני שלבים‪ :‬בשלב הראשון בונים את המשולש ‪ ABD‬על‪-‬פי שתי צלעות וזווית‬
‫שביניהן‪ .‬בשלב השני בונים את המשולש ‪ BCD‬על‪-‬פי שלוש צלעות‪.‬‬
‫‪C‬‬
‫‪D‬‬
‫‪k‬‬
‫‪D‬‬
‫‪k‬‬
‫‪m‬‬
‫‪B‬‬
‫‪‬‬
‫‪m‬‬
‫‪B‬‬
‫‪m‬‬
‫‪‬‬
‫‪m‬‬
‫‪A‬‬
‫‪A‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪80‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪233‬‬
‫‪ .19‬נתונה זווית ‪ ‬שקדקודה בנקודה ‪.B‬‬
‫א‪ .‬בנו דלתון ‪ ABCD‬שהנקודה ‪ D‬היא אחד מקדקודי הראש שלו‪ ,‬ושתיים מצלעותיו נמצאות על שוקי הזווית‪.‬‬
‫מהלך הבנייה זהה לזה שבתרגיל ‪ .18‬ההבדל היחיד הוא שבתרגיל זה התלמיד קובע בעצמו את אורכי‬
‫הצלעות‪.‬‬
‫ב‪.‬‬
‫בנו דלתון נוסף שעונה על הדרישות‪ .‬מהלך הבנייה כמו בסעיף הקודם‪ .‬בחירה חדש של אורכי הצלעות מובילה‬
‫לקבלת דלתון שונה מהקודם‪.‬‬
‫ג‪.‬‬
‫מדוע בכל הדלתונים שניתן לבנות בדרך זו ‪? ∡ABD = ∡CBD‬‬
‫תוכלו לבחור את‬
‫אורכי הצלעות‪.‬‬
‫בכל הדלתונים שניבנו בדרך זו ‪ ∡B‬היא זווית ראש והאלכסון הראשי חוצה אותה‪.‬‬
‫למעשה נוכל לחצות כל זווית על‪-‬ידי בניית דלתון שהזווית הנתונה היא זווית ראש שלו‪.‬‬
‫בפעילות הבאה נלמד לחצות זווית נתונה באמצעות סרטוט דלתון‪.‬‬
‫פעילות ‪ – 9‬חציית זווית – עמ' ‪233‬‬
‫נתונה זווית ‪ .α‬נחצה את הזווית‪.‬‬
‫‪C‬‬
‫א‪ .‬תיאור הבנייה‬
‫‪α‬‬
‫שלב א‪ :‬מהקדקוד ‪ A‬של הזווית ‪ α‬נחוג קשת במחוג כלשהו‪.‬‬
‫‪D‬‬
‫‪A‬‬
‫הקשת תחתוך את שוקי הזווית בנקודות ‪ C‬ו ‪.D -‬‬
‫שלב ב‪ :‬מ‪ C -‬נחוג קשת במחוג כלשהו הגדול מ ‪.CD -‬‬
‫שלב ג‪ :‬מ‪ D -‬נחוג קשת באותו מחוג‪ .‬הקשתות ייחתכו בנקודה ‪.F‬‬
‫שלב ד‪ :‬נחבר את נקודה ‪ A‬ואת נקודה ‪.F‬‬
‫רמז‪ :‬זהו בסרטוט ארבעה‬
‫קדקודים של דלתון‪.‬‬
‫ב‪ .‬הוכיחו ש‪ AF -‬חוצה זווית‪.‬‬
‫‪C‬‬
‫‪F‬‬
‫‪α‬‬
‫‪D‬‬
‫‪A‬‬
‫תרגילים – חוצה זווית – עמ' ‪233‬‬
‫לסידרת התרגילים ‪ 22 – 20‬מטרות אחדות‪:‬‬
‫‪‬‬
‫לתרגל את הבנייה של חוצה זווית‪.‬‬
‫‪‬‬
‫לגוון את השיעורים באמצעות משימות חקר קטנות‪.‬‬
‫‪‬‬
‫להבליט את החשיבות של בניות גאומטריות שחושפות בעינינו תופעות מפתיעות‪.‬‬
‫‪‬‬
‫לחזק ולהמחיש תכנים קודמים‪.‬‬
‫‪o‬‬
‫חוצי זוויות צמודות מאונכים זה לזה (תרגיל ‪.)20‬‬
‫‪o‬‬
‫חוצי זוויות הבסיס במשולש שווה‪-‬שוקיים שווים זה לזה (תרגיל ‪.)21‬‬
‫‪o‬‬
‫זיהוי דלתון (תרגיל ‪.)22‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪81‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תרגיל ‪ 20‬מחזיר אותנו לתרגיל מהפרק על זוויות צמודות שמבליט תופעה מעניינת‪ :‬החוצים של זוויות צמודות מאונכים זה‬
‫לזה‪ .‬כעת התופעה מתגלה כתוצאה מהבנייה‪ .‬התלמידים מסרטטים זוויות צמודות שונות ואצל כולם חוצי הזווית מאונכים זה‬
‫לזה‪.‬‬
‫בניית חוצי הזווית בתוכנה דינמית למעשה יוצרת יישומון‪ .‬נוכל למדוד את הזווית בין חוצי הזווית ולגלות שהיא ישרה‪ .‬נוכל‬
‫לשנות את הזוויות הצמודות וחוצי הזווית יישארו מאונכים‪.‬‬
‫עמ' ‪233‬‬
‫‪ .20‬א‪ .‬סרטטו זוג זוויות צמודות‪.‬‬
‫ב‪ .‬חצו כל אחת מהזוויות הצמודות‪ .‬צבעו את חוצי הזוויות‪.‬‬
‫ג‪ .‬איזו זווית נוצרת בין חוצי הזוויות הצמודות? הסבירו את התופעה‪.‬‬
‫תרגיל ‪ 21‬מחזיר אותנו לתופעה שהכרנו בפרק "משולש שווה‪-‬שוקיים"‪ :‬במשולש שווה‪-‬שוקיים תוצי זוויות הבסיס שווים זה‬
‫לזה‪ .‬אם מבצעים את הבנייה באמצעות תוכנה דינמית ניתן לגרור את קדקודי המשולש‪ ,‬והתכונה‪ ,‬שוויון חוצי זוויות הבסיס‪,‬‬
‫נשמרת בכל המשולשים שמתקבלים על‪-‬ידי גרירה‪ .‬באתר יש קובץ הדגמה בשם למדריך_תרגיל ‪_20‬חוצי זוויות צמודות‪.‬‬
‫‪‬‬
‫‪ .21‬א‪ .‬סרטטו משולש שווה‪-‬שוקיים‪.‬‬
‫ב‪ .‬העבירו את חוצי זוויות הבסיס‪.‬‬
‫ג‪ .‬מה הקשר בין האורכים של חוצי זוויות הבסיס? הסבירו את התופעה‪.‬‬
‫בתרגיל ‪ 22‬מגלים תופעה חדשה‪ :‬ההמשכים של חוצי זוויות הבסיס יוצרים עם בסיס‬
‫‪ ‬‬
‫‪P‬‬
‫המשולש הנתון משולש שווה‪-‬שוקיים‪ .‬השוקיים של שני המשולשים הן ‪ 4‬צלעות של‬
‫דלתון‪ .‬כדי להוכיח שאכן מתקבל דלתון נראה שכל הזוויות המסומנות ב‪  -‬שוות‪.‬‬
‫באתר יש קובץ הדגמה בשם למדריך_תרגיל ‪_20‬חוצי זוויות חיצוניות‪.‬‬
‫‪.22‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪Q‬‬
‫‪‬‬
‫‪R‬‬
‫‪M‬‬
‫א‪ .‬סרטטו משולש שווה‪-‬שוקיים ‪.)PQ = PR( PQR‬‬
‫ב‪ .‬העבירו את החוצי‪-‬זוויות של הזוויות הצמודות לזוויות הבסיס של המשולש‪.‬‬
‫ג‪ .‬ההמשכים של חוצי הזוויות הצמודות לזוויות הבסיס נפגשים בנקודה ‪ .M‬מהו סוג המרובע ‪? PQMR‬‬
‫הוכיחו‪.‬‬
‫לקראת פעילויות ‪ 12 – 10‬ותרגילי ההכנה הקודמים להם (‪)25 - 23‬‬
‫שלו שת התרגילים הבאים הם תרגילי הכנה לפעילויות המציגות שלוש בניות של אנכים לישר נתון‪.‬‬
‫אנך אמצעי לקטע (תרגיל ‪ 23‬כהכנה לפעילות ‪ ,)10‬אנך לישר מנקודה על הישר (תרגיל ‪ 24‬כהכנה לפעילות ‪ )11‬ואנך‬
‫לישר מנקודה מחוץ לישר (תרגיל ‪ 25‬כהכנה לפעילות ‪ .)12‬שלוש הבניות של האנכים מבוססות על בנייה של דלתון‪.‬‬
‫עד לנקודה זו סביר להניח התלמידים כבר התנסו בלא מעט בניות וגם התנסו בניתוח בעיות לקראת הכנת תכנית בנייה‪.‬‬
‫יתכן וחלק מהתלמידים יכולים כבר להתמודד בעצמם עם השאלה כיצד ניבנה אנך אמצעי לקטע נתון‪ .‬עבור תלמידים‬
‫אלה ההתמודדות עם השאלה כיצד ניתן לבנות אנך היא הרבה יותר מעניינת מאשר פעולה על‪-‬פי הוראות‪.‬‬
‫חלק מהתלמידים יוכלו אולי לתכנן את בניות האנכים בעצמם אם יתנסו קודם בשאלות ההכנה‪ ,‬ולכם שאלות ההכנה‬
‫חשובות במיוחד‪.‬‬
‫תלמידים אחדים זקוקים אולי להדרכה צעד אחר צעד‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪82‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילויות ‪ 12- 10‬בספר מציגות את הבניות באופן מפורט מאד‪ ,‬וזאת על מנת שתוכניות הבנייה יהיו תמיד לרשות כל‬
‫תלמיד שרוצה לחזור ולהיעזר בהן‪.‬‬
‫אם נרצה שהתלמידים יתמודדו עם הבניות בעצמם נציג להם את האתגרים האלה בשיעור ללא ספרים‪.‬‬
‫נציג מספר אפשרויות לארגון הלמידה‪.‬‬
‫אפשרות א‬
‫‪‬‬
‫עיסוק בשלושת תרגילי ההכנה ברצף בעבודה עצמית בכתה או בשיעורי בית‪.‬‬
‫‪‬‬
‫דיון כתתי ותכנון משותף של בניית אנך אמצעי‪ ,‬ואז להציב בפני התלמידים את האתגר להתמודד עם שתי הבניות‬
‫האחרות בעצמם בעבודה בקבוצות‪.‬‬
‫‪‬‬
‫הצגת העבודה של הקבוצות במליאת הכתה‪.‬‬
‫אפשרות ב‬
‫כל תרגיל הכנה יוצג לתלמידים בסמוך לפעילות המתאימה לו‪ .‬כל אחת מהפעילויות תלווה בתרגילים שמתבססים עליה‬
‫אפשר ומומלץ לארגן את הלמידה של פעילויות ‪ 11‬ו‪ 12 -‬בדרך של למידה שיתופית‪.‬‬
‫מחלקים את הכתה לקבוצות של כ‪ 4 -‬תלמידים בקבוצה‪ .‬המטרה של מחצית מהקבוצות היא לבנות אנך לישר מנקודה על‬
‫הישר והמטרה של הקבוצות האחרות היא לבנות אנך לישר מנקודה מחוץ לישר‪.‬‬
‫בהתחלה התלמידים מנסים להתמודד עם האתגר בעצמם ובשלב מאוחר יותר‪ ,‬ובפרט אם קבוצה מתקשה‪ ,‬אפשר לתת‬
‫להם את הנחיות הבנייה‪.‬‬
‫תרגילי הכנה לפעילויות ‪ – 12 – 10‬עמ' ‪234‬‬
‫‪S‬‬
‫עמ' ‪ .23 234‬א‪ .‬נתון קטע ‪ .GS‬העתיקו את הקטע ‪ GS‬למחברת‪ ,‬בנו דלתון ‪GRST‬‬
‫ש‪ GS -‬הוא האלכסון המשני שלו‪.‬‬
‫‪G‬‬
‫ב‪ .‬סמנו ב‪ P -‬את מפגש האלכסונים מה מידת הזווית ‪ ? ∡RPS‬הסבירו‪.‬‬
‫ב‪ .‬בנו דלתון נוסף ש‪ GS -‬הוא האלכסון המשני שלו‪ .‬האם גם אלכסוניו נפגשים בנקודה ‪ ? P‬הסבירו‪.‬‬
‫ג‪ .‬כמה דלתונים ש‪ GS -‬הוא האלכסון המשני שלהם קיימים?‬
‫אתם יכולים לבחור‬
‫את אורכי הצלעות‪.‬‬
‫‪ .24‬א‪ .‬נתון ישר ‪ m‬ועליו נקודה ‪ .P‬בנו דלתון ‪ ABCD‬שהאלכסון המשני שלו ‪ AC‬מונח על הישר ‪ m‬והנקודה ‪P‬‬
‫היא מפגש האלכסונים שלו‪.‬‬
‫ב‪ .‬כמה דלתונים כאלה אפשר לבנות? אינסוף‬
‫ג‪ .‬האם יש ביניהם מעוין? כל הדלתונים שווי הצלעות הם מעויינים‪.‬‬
‫‪m‬‬
‫ד‪ .‬הוכיחו ש‪ AC -‬מאונך ל‪ BD .BD -‬הוא האלכסון הראשי של הדלתון והוא מאונך לאלכסון המשני ‪.AC‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪83‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫‪n‬‬
‫עמ' ‪ .25 234‬נתון ישר ‪ n‬ונתונה נקודה ‪ A‬מחוץ לישר‪.‬‬
‫‪A‬‬
‫בנו דלתון ‪ BACK‬שבו ‪ AC = AB‬והנקודות ‪ B‬ו‪ C -‬נמצאות על הישר ‪.n‬‬
‫א‪ .‬לפניכם שלבים בבנייה של נועם‪ .‬סדרו אותם על‪-‬פי הסדר‪.‬‬
‫שמתי את חוד המחוגה‬
‫בנקודה ‪ A‬וסרטטתי קשת‬
‫שפוגשת את המעגל בשתי‬
‫נקודות‬
‫‪1‬‬
‫סימנתי נקודת מפגש אחת‬
‫של הקשת והישר באות ‪B‬‬
‫ואת השנייה באות ‪.C‬‬
‫‪2‬‬
‫‪6‬‬
‫במקום שהקשתות נפגשות‬
‫סימנתי את הנקודה ‪.K‬‬
‫סרטטתי שתי קשתות עם‬
‫הרדיוס החדש‪ .‬באחת‬
‫המרכז בנקודה ‪ B‬ובשנייה‬
‫בנקודה ‪.C‬‬
‫‪4‬‬
‫הגדלתי קצת את המפתח של‬
‫המחוגה‪.‬‬
‫‪5‬‬
‫ב‪ .‬הוכיחו שאכן מתקבל דלתון‪.‬‬
‫עכשיו כשכל הקדקודים‬
‫מסומנים סרטטתי את‬
‫הדלתון‪.‬‬
‫‪3‬‬
‫‪n‬‬
‫(‪)1‬‬
‫‪n‬‬
‫(‪) 2‬‬
‫‪B‬‬
‫‪B‬‬
‫ג‪ .‬איזה דלתון מתאים לבנייה של נועם?‬
‫שני הדלתונים מתאימים לבנייה של נועם כי שני‬
‫‪A‬‬
‫המעגלים שבנה נחתכים בשתי נקודות‪.‬‬
‫‪K‬‬
‫‪K‬‬
‫‪A‬‬
‫‪C‬‬
‫‪C‬‬
‫ד‪ .‬ה אם נועם היה חייב לשנות את מפתח המחוגה במהלך הבנייה כדי לקבל דלתון?‬
‫לא‪ .‬אם לא היה משנה את מפתח המחוגה היה מתקבל מעויין‪ .‬גם במקרה זה היה מקבל דלתון כי מעויין הוא‬
‫דלתון‪.‬‬
‫ה‪ .‬האם בשני הדלתונים (‪ )1‬ו‪ AK ,)2( -‬מאונך ל‪ ? BC -‬הסבירו‪.‬‬
‫כן‪ .‬קטעים נחשבים מאונכים אם הם נמצאים על ישרים מאונכים‪ .‬קטעים מאונכים לא חייבים להיחתך‪ .‬אלכסוני כל‬
‫דלתון מאונכים‪.‬‬
‫בפעילויות ‪ 12 - 10‬נלמד לסרטט אנך לישר נתון באמצעות סרטוט דלתון‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪84‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 10‬בניית אנך אמצעי לקטע – עמ' ‪235‬‬
‫הצדקת הבנייה‪:‬‬
‫המשולשים ‪AEB‬‬
‫ו‪ ADB -‬הם‬
‫שווי ‪-‬שוקיים כי נוצרו‬
‫באמצעות קשתות שוות‪,‬‬
‫ולכן המרובע ‪ AEBD‬הוא‬
‫דלתון‪ .‬בדלתון האלכסון‬
‫הראשי מאונך לאלכסון‬
‫המשני וחוצה אותו‪.‬‬
‫למעשה המרובע ‪AEBD‬‬
‫הוא דלתון שווה‪-‬צלעות‪,‬‬
‫מעוין‪ ,‬כיוון שגם המשולשים‬
‫‪ AED‬ו‪ BED -‬שווי שוקיים‪ .‬כיוון שעדין לא למדנו את תכונות המעוין מתאים להוכיח את הנדרש על‪-‬פי תכונות הדלתון‪.‬‬
‫פעילות ‪ – 11‬העלאת אנך לישר מנקודה על הישר – עמ' ‪234‬‬
‫נתון ישר ‪ m‬ועליו נתונה נקודה ‪ .A‬כיצד נעלה אנך לישר בנקודה הנתונה?‬
‫פעלו על‪-‬פי ההדרכה והסבירו מדוע הישר המתקבל בבנייה אכן מאונך לישר ‪.m‬‬
‫‪K‬‬
‫‪F‬‬
‫‪A‬‬
‫נתון ישר ‪ m‬ועליו‬
‫נתונה נקודה ‪.A‬‬
‫‪F‬‬
‫‪F‬‬
‫‪A‬‬
‫‪A‬‬
‫‪G‬‬
‫‪m‬‬
‫‪K‬‬
‫‪L‬‬
‫שלב א‪ :‬נחוג סביב ‪A‬‬
‫מעגל במחוג כלשהו‪.‬‬
‫נסמן ב‪ F -‬ו‪ G -‬את‬
‫נקודות החיתוך של‬
‫המעגל והישר‪.‬‬
‫‪A‬‬
‫‪G‬‬
‫‪L‬‬
‫שלב ב‪ :‬נחוג קשת שמרכזה‬
‫‪ F‬במחוג כלשהו הגדול מ‪-‬‬
‫‪ .AF‬מהנקודה ‪ G‬נחוג קשת‬
‫באותו מחוג‪ .‬נסמן את נקודות‬
‫המפגש של הקשתות‬
‫ב‪ K -‬ו‪.L -‬‬
‫‪G‬‬
‫שלב ג‪ :‬נעביר ישר‬
‫דרך הנקודות ‪ K‬ו‪.L -‬‬
‫א‪ .‬הסבירו מדוע ‪ A‬אמצע הקטע ‪ AG .GF‬ו‪ AF -‬רדיוסים באותו מעגל‪.‬‬
‫ב‪ .‬הסבירו מדוע המרובע ‪ GKFL‬דלתון ‪ GK = KF .‬כרדיוסים של מעגלים שווים וכך גם ‪ GL‬ו‪.LF -‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪85‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫הסבירו מדוע ‪ KL‬עובר דרך הנקודה ‪ A .A‬אמצע הקטע ‪ GF‬על פי הבנייה (ראו סעיף ב)‪ .‬בדלתון האלכסון הראשי‬
‫ג‪.‬‬
‫חוצה את האלכסון המשני ולכן עובר בנקודה ‪.A‬‬
‫ד‪ .‬הסבירו מדוע ‪ KL‬מאונך ל‪ .AF -‬בדלתון האלכסון הראשי מאונך לאלכסון המשני‪.‬‬
‫אפשר גם אחרת‬
‫הבנייה המתוארת למעלה מבוססת על בנייה של דלתון (למעשה בנינו מעוין שהוא דלתון שווה‪-‬צלעות)‪.‬‬
‫אפשר להעלות אנך גם באמצעות סרטוט משולש שווה‪-‬שוקיים שבסיסו מונח על הישר ‪ m‬והנקודה ‪ A‬היא אמצע הבסיס‬
‫שלו‪.‬‬
‫ה‪ .‬לפניכם סדרה של מהלכי הבנייה‪ .‬תארו את המהלכים והוכיחו שאכן קיבלנו אנך לישר הנתון‪.‬‬
‫‪m‬‬
‫‪m‬‬
‫‪K‬‬
‫‪m‬‬
‫‪F‬‬
‫‪A‬‬
‫‪F‬‬
‫‪A‬‬
‫‪G‬‬
‫נתון ישר ‪ m‬ועליו‬
‫נתונה נקודה ‪.A‬‬
‫‪m‬‬
‫‪F‬‬
‫‪A‬‬
‫‪K‬‬
‫‪A‬‬
‫‪G‬‬
‫שלב ב‬
‫שלב א‬
‫נחוג סביב ‪ A‬מעגל‬
‫במחוג כלשהו‪ .‬נסמן‬
‫ב‪ F -‬ו‪ G -‬את נקודות‬
‫החיתוך של המעגל‬
‫והישר‪.‬‬
‫נחוג קשת שמרכזה ‪F‬‬
‫במחוג כלשהו הגדול‬
‫מ‪ .AF -‬מהנקודה ‪G‬‬
‫נחוג קשת באותו מחוג‪.‬‬
‫נסמן ב‪ K -‬את אחת‬
‫מנקודות המפגש של‬
‫הקשתות‪.‬‬
‫‪G‬‬
‫שלב ג‬
‫נעביר ישר דרך הנקודות‬
‫‪ K‬ו ‪.A -‬‬
‫הצדקת הבנייה‪ GKF :‬משולש שווה‪-‬שוקיים כי ‪ GF‬ו‪ GK -‬רדיוסים במעגלים שווים‪ A .‬אמצע ‪ GF‬לפי הבנייה‪.‬‬
‫במשולש שווה‪-‬שוקיים תיכון לבסיס הוא גם גובה לבסיס‪ ,‬ומכאן שהישר העובר דרך ‪ K‬ו‪ A -‬מאונך ל‪.m -‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪86‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 12‬הורדת אנך לישר מנקודה מחוץ לישר – עמ' ‪236‬‬
‫נתונים ישר ‪ k‬ונקודה ‪ A‬מחוץ לישר‪ .‬כיצד נסרטט אנך לישר שיעבור דרך ‪? A‬‬
‫א‪ .‬פעלו על‪-‬פי ההדרכה והסבירו מדוע הישר המתקבל בבנייה אכן מאונך לישר ‪.k‬‬
‫‪A‬‬
‫‪A‬‬
‫‪A‬‬
‫‪A‬‬
‫‪C‬‬
‫‪C‬‬
‫‪k‬‬
‫‪C‬‬
‫‪B k‬‬
‫‪B k‬‬
‫שלב א‪ :‬נחוג קשת שמרכזה‬
‫‪ A‬כך שתחתוך את הישר‪.‬‬
‫נסמן ב‪ B -‬ו‪ C -‬את נקודות‬
‫החיתוך של הקשת והישר‪.‬‬
‫שלב ב‪ :‬נחוג קשת שמרכזה ‪B‬‬
‫ומחוגה גדול ממחצית ‪.BC‬‬
‫מהנקודה ‪ C‬כמרכז נחוג קשת‬
‫באותו מחוג‪ .‬נסמן ב‪ P-‬את‬
‫מפגש הקשתות‪.‬‬
‫‪k‬‬
‫‪B‬‬
‫‪P‬‬
‫‪P‬‬
‫נתונים ישר ‪ k‬ונקודה ‪A‬‬
‫מחוץ לישר‪.‬‬
‫שלב ג‪ :‬נעביר ישר דרך הנקודות‬
‫‪ P‬ו ‪.A -‬‬
‫ב‪ .‬הסבירו מדוע ‪.AP  CB‬‬
‫הראו תחילה שהמרובע ‪ ACPB‬דלתון‪ .‬קיבלנו דלתון כי ‪ AB = AC‬ו‪.CP = BP -‬‬
‫בדלתון האלכסון הראשי מאונך לאלכסון המשני‪.‬‬
‫תרגילים – אנך אמצעי – עמ' ‪237‬‬
‫מטרת תרגיל ‪ 26‬להדגיש שניתן למצוא אמצע קטע באמצעות האנך האמצעי‪ .‬גם אם מבצעים את הבנייה באמצעות תוכנה‬
‫גרפית חשוב להדגיש שהכלי הגאומטרי למציאת אמצע קטע הוא האנך האמצעי‪.‬‬
‫עמ' ‪237‬‬
‫‪ .26‬סרטטו קטע ‪.AB‬‬
‫א‪ .‬מצאו את נקודת האמצע של הקטע‪.‬‬
‫ב‪ .‬חלקו את הקטע ל‪ 4 -‬חלקים שווים‪.‬‬
‫ג‪ .‬סמנו על הקטע ‪ AB‬נקודה ‪ P‬כך ש‪.AB = 8AP -‬‬
‫‪ .27‬בנו משולש שווה‪-‬שוקיים לפי אורך הבסיס ‪ a‬ואורך הגובה לבסיס ‪.ha‬‬
‫במשולש שווה‪-‬שוקיים הגובה לבסיס הוא גם תיכון לבסיס‪ .‬לכן ניבנה אנך אמצעי‪,‬‬
‫‪a‬‬
‫‪ha‬‬
‫נקצה עליו את הגובה ונקבל את קדקוד זווית הראש‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪87‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫‪ .28‬א‪ .‬סרטטו משולש שווה‪-‬שוקיים‪.‬‬
‫עמ' ‪237‬‬
‫ב‪ .‬סרטטו את התיכונים לשוקי המשולש‪.‬‬
‫ג‪ .‬מה הקשר בין אורכי התיכונים? הסבירו את התופעה‪.‬‬
‫תרגיל זה מחזיר אותנו אל תכונה של משולש שווה‪-‬שוקיים‪ :‬התיכונים לשוקי המשולש שווים זה לזה‪.‬‬
‫תרגילים – אנך מנקודה על הישר – עמ' ‪237‬‬
‫‪c‬‬
‫‪a‬‬
‫‪b‬‬
‫‪ .29‬נתונים ‪ 3‬קטעים ‪ ,b ,a‬ו‪.c -‬‬
‫בנו משולש ישר‪ -‬זווית שניצביו הם הקטעים ‪ ,b‬ו‪.c -‬‬
‫‪ .30‬א‪ .‬בנו משולש ישר‪-‬זווית שאורך ניצביו ‪ ,3a‬ו‪.4a -‬‬
‫ב‪ .‬הוכיחו שאורך היתר ‪ .5a‬לפי משפט פיתגורס‪ :‬אם אורך היתר ‪ x‬אז‬
‫‪x = (3a) + (4a) = 9a +16a = 25a  x = 5a‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫תרגילים – אנך מנקודה מחוץ לישר – עמ' ‪237‬‬
‫אחד השימושים של הורדת אנך לישר מנקודה מחוץ לישר הוא סרטוט גבהים במשולשים‪ .‬חלק מהתלמידים מתקשים‬
‫לסרטט גובה חיצוני‪ ,‬ולעתים אף מתקשים לזהות גובה כזה‪ .‬תרגיל ‪ 31‬מזמן חקירה של גבהים במשולש‪ ,‬שממנה עולה‬
‫תוצאה מפתיעה‪ :‬לא קיים משולש עם גובה חיצוני אחד‪.‬‬
‫במטרה לחסוך את סרטוט המשולשים הנתונים‪ ,‬לתרגילים אלו יש דפי עבודה לבנייה בסרגל ובמחוגה ויישומון‬
‫לתרגיל ‪ 31‬יש דף עבודה עם סרטוטים מוגדלים‬
‫גאוגברה‪.‬‬
‫לבנייה בסרגל ובמחוגה ויישומון גאוגברה‪.‬‬
‫שם הישומון‪:‬‬
‫לתרגיל ‪_31‬הורדת גבהים_קובץ עם קדקודים קבועים‬
‫עמ' ‪237‬‬
‫‪‬‬
‫‪ .31‬א‪ .‬בכל אחד מן המשולשים סרטטו את הגבהים‪.‬‬
‫‪P‬‬
‫‪B‬‬
‫‪F‬‬
‫‪A‬‬
‫‪W‬‬
‫‪F‬‬
‫‪N‬‬
‫‪D‬‬
‫‪L‬‬
‫‪T‬‬
‫‪E‬‬
‫‪R‬‬
‫ב‪ .‬סרטטו משולשים נוספים‪ ,‬חדי‪-‬זוויות‪ ,‬קהי‪-‬זווית וישרי‪-‬זווית וחקרו‪:‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪88‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫(‪ )1‬באיזה משולשים כל הגבהים נמצאים בתוך המשולש? במשולשים חדי‪-‬זוויות‪ .‬כל הזוויות החיצוניות קהות ולכן‬
‫אילו היה אפשר לסרטט גובה חיצוני היה מתקבל משולש שבו יש גם זווית ישרה וגם זווית קהה‪.‬‬
‫(‪ )2‬באיזה משולש לפחות אחד מהגבהים חיצוני? משולש קהה‪-‬זווית‪.‬‬
‫(‪ )3‬האם קיים משולש עם יותר מגובה אחד חיצוני? כל משולש קהה‪-‬זווית‪ .‬אם יש גובה חיצוני אז המשולש קהה‬
‫זווית‪ ,‬מהסיבות שצוינו בסעיף (‪ .)1‬במשולש כזה שני הגבהים אל הישרים המכילים את הצלעות שמול הזוויות‬
‫החדות חייבים להיות חיצוניים‪.‬‬
‫(‪ )4‬האם קיים משולש שבו רק אחד מהגבהים הוא חיצוני? ראו תשובה לסעיף (‪.)3‬‬
‫(‪ )5‬האם קיים משולש שבו אין אף גובה פנימי? לא קיים משולש כזה‪ .‬בכל משולש יש לפחות זווית חדה אחת ולכן‬
‫מהסיבה שתוארה בסעיף (‪ )1‬חייב להיות גובה פנימי‪.‬‬
‫לתרגיל ‪ 32‬יש דף עבודה עם סרטוטים מוגדלים‬
‫לבנייה בסרגל ובמחוגה ויישומון גאוגברה‪.‬‬
‫שם הישומון‪:‬‬
‫לתרגיל ‪_32‬מציאת משולשים דומים שנוצרים על‪-‬ידי‬
‫גבהים_ הורדת אנכים‬
‫‪‬‬
‫‪ .32‬לפניכם משולש ‪.ABC‬‬
‫עמ' ‪238‬‬
‫א‪ .‬בנו במשולש גובה ‪ CD‬לצלע ‪. AB‬‬
‫ב‪ .‬בנו במשולש גובה ‪ BE‬לצלע ‪ .AC‬סמנו ב‪ H -‬את מפגש הגבהים‪.‬‬
‫ג‪ .‬מצאו בסרטוט שני זוגות של משולשים דומים והוכיחו שהם דומים‪ .‬קיימים שלושה זוגות של משולשים דומים‪:‬‬
‫‪B‬‬
‫‪B‬‬
‫‪B‬‬
‫‪D‬‬
‫‪D‬‬
‫‪H‬‬
‫‪C‬‬
‫‪D‬‬
‫‪H‬‬
‫‪H‬‬
‫‪E‬‬
‫‪A‬‬
‫‪C‬‬
‫‪E‬‬
‫‪A‬‬
‫‪C‬‬
‫‪E‬‬
‫‪A‬‬
‫‪ .33‬א‪ .‬בנו משולש שווה‪-‬שוקיים‪.‬‬
‫ב‪ .‬בנו את הגבהים לשתי השוקיים‪.‬‬
‫ג‪ .‬מה הקשר בין שני הגבהים? הוכיחו את טענתכם‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪89‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫אנך מנקודה מחוץ לישר – דף עבודה‬
‫‪ .1‬א‪ .‬בכל אחד מן המשולשים סרטטו את הגבהים‪.‬‬
‫‪P‬‬
‫‪F‬‬
‫‪L‬‬
‫‪T‬‬
‫‪F‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A‬‬
‫‪W‬‬
‫‪E‬‬
‫‪N‬‬
‫‪R‬‬
‫ב‪ .‬סרטטו משולשים נוספים‪ ,‬חדי‪-‬זוויות‪ ,‬קהי‪-‬זווית וישרי‪-‬זווית וחקרו‪:‬‬
‫(‪ )1‬באיזה משולשים כל הגבהים נמצאים בתוך המשולש?‬
‫(‪ )2‬באיזה משולש לפחות אחד מהגבהים חיצוני?‬
‫(‪ )3‬האם קיים משולש עם יותר מגובה אחד חיצוני?‬
‫(‪ )4‬האם קיים משולש שבו רק אחד מהגבהים הוא חיצוני?‬
‫(‪ )5‬האם קיים משולש שבו אין אף גובה פנימי?‬
‫‪ .2‬לפניכם משולש ‪.ABC‬‬
‫א‪ .‬בנו במשולש גובה ‪ CD‬לצלע ‪. AB‬‬
‫ב‪ .‬בנו במשולש גובה ‪ BE‬לצלע ‪ .AC‬סמנו ב‪ H -‬את מפגש הגבהים‪.‬‬
‫ג‪ .‬מצאו בסרטוט שני זוגות של משולשים דומים והוכיחו שהם דומים‪.‬‬
‫‪B‬‬
‫‪A‬‬
‫‪C‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪90‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.34 238‬‬
‫בעיית חקר‬
‫א‪ .‬סרטטו זווית‪.‬‬
‫ב‪ .‬בנו את החוצה זווית‪.‬‬
‫ג‪ .‬סמנו נקודה על החוצה זווית‪.‬‬
‫ד‪ .‬הורידו מהנקודה שסימנתם אנכים לשתי שוקי הזווית‪.‬‬
‫ה‪ .‬מה הקשר בין אורכי האנכים שהורדתם? הסבירו את הקשר שמצאתם‪.‬‬
‫ו‪ .‬סמנו נקודה מחוץ לחוצה זווית‪ .‬הורידו ממנה אנכים לשוקי הזווית‪ .‬מה הקשר בין אורכי האנכים‬
‫שהורדתם?‬
‫תרגיל ‪ 34‬מדגים תופעה כפולה שניתן לנסח באמצעות טענה וטענה הפוכה‪:‬‬
‫‪‬‬
‫כל נקודה על חוצה הזווית נמצאת במרחקים שווים משוקי הזווית‪.‬‬
‫‪‬‬
‫כל הנקודות הנמצאות במרחקים שווים משני שוקי הזווית נמצאות על חוצה הזווית‪.‬‬
‫סעיף ה מדגים את הטענה הראשונה‪ .‬התלמידים מסמנים נקודה על חוצה הזווית ורואים שמרחקיה משתי שוקי הזווית שווים‪.‬‬
‫לשם כך חשוב להזכיר את המושג מרחק נקודה מישר‪ .‬ניתן לגרור את הנקודה על חוצה הזווית ולראות שהתופעה נשמרת‪.‬‬
‫סעיף ו מדגים את הטענה ההפוכה‪ :‬כאשר מורידים אנכים לשוקי הזווית מנקודה שאיננה על חוצה הזווית‪ ,‬מקבלים קטעים‬
‫שונים באורכם‪ .‬מכאן עולה ה השערה שאם נקודה איננה על חוצה הזווית אז מרחקיה משוקי הזווית אינם שווים זה לזה‪ .‬זהו‬
‫ניסוח שקול לטענה השנייה‪ :‬כל הנקודות הנמצאות במרחקים שווים משתי שוקי הזווית נמצאות על שוקי הזווית‪.‬‬
‫את שתי הטענות מוכיחים באמצעות חפיפת משולשים‬
‫בשנים מאוחרות יותר התלמידים ינסחו תופעה זו באמצעות המושג מקום גאומטרי‪:‬‬
‫חוצה הזווית הוא המקום הגאומטרי של כל הנקודות שמרחקיהן משתי שוקי זווית שווים זה לזה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪91‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 13‬בניית משולש ישר‪-‬זווית על‪-‬פי ניצב ויתר – עמ' ‪239‬‬
‫בפעילות ‪ 13‬אנו‬
‫מציעים שתי דרכים‬
‫לבנות משולש ישר‪-‬‬
‫זווית על‪-‬פי ניצב ויתר‪.‬‬
‫בסיכום הפעילות אנו‬
‫גם מציינים את‬
‫היתרונות של הדרך‬
‫הראשונה‬
‫כשמשתמשים בתוכנה‪,‬‬
‫ושל הדרך השנייה‬
‫כשבונים בסרגל‬
‫ומחוגה‪.‬‬
‫בבנייה הראשונה‬
‫סרטטנו גם את הישר‬
‫שעליו מונח הקטע כי‬
‫הוא דרוש להעלאת‬
‫האנך‪.‬‬
‫הצדקת הבנייה‬
‫הראשונה‪:‬‬
‫הזווית ‪ C‬ישרה כיוון‬
‫שהעלינו בנקודה זו‬
‫אנך‪.‬‬
‫‪ BC=a‬כיוון שהעתקנו‬
‫את הקטע ‪.a‬‬
‫‪ AB=c‬כרדיוס של‬
‫מעגל שמרכזו ב‪B -‬‬
‫ומחוגו ‪.C‬‬
‫הנתונים צריכים למלא את התנאי ‪ c>a‬כי היתר גדולה מהניצב‪.‬‬
‫בנתונים אלה ניתן לסרטט רק משולש אחד‪ .‬כל משולש אחר שנסרטט על‪-‬פיהם יהיה חופף למשולש ‪ ABC‬על‪-‬פי‬
‫המשפט‪ :‬משולשים ישרי‪-‬זווית השווים בניצב ויתר חופפים זה לזה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪92‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תיאור שלבי הבנייה השנייה‪:‬‬
‫שלב א‪ :‬נסרטט ישר‪ .‬נסמן עליו נקודה ‪ C‬ונחוג מעגל ברדיוס ‪ a‬שמרכזו ב‪ .C -‬נסמן את נקודות המפגש של‬
‫המעגל והישר ב‪ B -‬ו‪.D -‬‬
‫שלב ב‪ :‬נחוג שתי קשתות ברדיוס ‪ ,c‬האחת מרכזה בנקודה ‪ B‬והשנייה מרכזה בנקודה ‪.D‬‬
‫נסמן ב‪ A -‬את אחת מנקודות המפגש של הקשתות‪.‬‬
‫שלב ג‪ :‬נשלים את סרטוט צלעות המשולש ‪ ABC‬שהוא המשולש המבוקש‪.‬‬
‫ההצדקה של בנייה זו‪:‬‬
‫‪ BC = a‬כרדיוס המעגל שמרכזו ב‪.C -‬‬
‫‪ AB = c‬כרדיוס המעגל שמרכזו ב‪.B -‬‬
‫‪ ∡C = 90‬כיוון ש‪ AC -‬תיכון במשולש ‪ ABC‬שהוא משולש שווה‪-‬שוקים‪ ,‬ולכן גם גובה לבסיס‪.‬‬
‫הבנייה השנייה חוסכת את הצורך בהעלאת אנך לניצב הנתון‪.‬‬
‫כשמבצעים את הבנייה עם סרגל ומחוגה העלאת האנך כרוכה בשלבים אחדים‪ ,‬ולכן יש יתרון לבנייה השנייה‪.‬‬
‫כשמבצעים את הבנייה באמצעות תוכנה העלאת האנך היא פעולה מיידית‪ ,‬ולכן הבנייה הראשונה יותר נוחה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪93‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫בעוד זמן קצר‪ ,‬לאחר שנלמד בפרק המקבילים לסרטט ישר מקביל כשנדע לסרטט מקביל יהיה פתרון הרבה יותר פשוט‬
‫לבנייה שבדוגמה הפתורה‪ .‬לכן כדאי לשקול אם להציג את הדוגמה הפתורה כאן‪ ,‬במטרה לפתח את מיומנות התכנון‪ ,‬או‬
‫לדחות בנייה זו עד לאחר שהתלמידים ידעו לבנות מקביל לישר נתון ויוכלו לבצע בנייה פשוטה יותר‪.‬‬
‫דוגמה פתורה – עמ' ‪240‬‬
‫סרטטו משולש ‪ ABC‬על‪-‬פי הצלעות ‪ AB = c , BC = a‬ו‪ - hc -‬הגובה לצלע ‪AB‬‬
‫‪a‬‬
‫תכנון הבנייה‪:‬‬
‫‪c‬‬
‫בשאלה לא נאמר אם הגובה פנימי או חיצוני‪ ,‬ולכן נבחן כל מקרה בנפרד‪.‬‬
‫‪hc‬‬
‫מקרה א‪ :‬הגובה פנימי‬
‫נסרטט סקיצה של משולש ‪ ABC‬ובתוכו גובה ‪ CD‬ונדגיש את הנתונים‪.‬‬
‫אפשר לזהות בסרטוט משולש ישר‪-‬זווית‪ BCD ,‬שבו נתונים לנו ניצב ויתר‪.‬‬
‫‪hc‬‬
‫אחרי שנסרטט את המשולש ‪ BCD‬נוכל להשלימו למשולש ‪ , ABC‬כיוון שגם הצלע‬
‫‪B‬‬
‫‪ AB‬נתונה‪.‬‬
‫‪A‬‬
‫‪a‬‬
‫‪D‬‬
‫‪c‬‬
‫את הסקיצה מסרטטים לצורך‬
‫התכנון של הבנייה ולכן אין כל‬
‫חשיבות למידות של חלקיה‪.‬‬
‫מקרה ב‪ :‬הגובה חיצוני‬
‫נסרטט סקיצה של משולש ‪ ABC‬עם גובה חיצוני ‪.CD‬‬
‫‪C‬‬
‫הפעם אפשר לזהות מחוץ למשולש ‪ ABC‬משולש ישר‪-‬זווית ‪ BCD‬שבו נתונים לנו‬
‫‪D‬‬
‫ניצב וגובה‪.‬‬
‫‪a‬‬
‫גם הפעם‪ ,‬אם נבנה את המשולש ‪ BCD‬נוכל להשלימו למשולש ‪ ABC‬בעזרת‬
‫הצלע הנתונה ‪.AB‬‬
‫‪B‬‬
‫‪A‬‬
‫‪hc‬‬
‫‪D‬‬
‫‪c‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪94‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫מהלך הבנייה‬
‫סקיצה מתאימה לתיאור הבנייה‬
‫השלב בבנייה‬
‫תיאור הבנייה‬
‫בניית המשולש‬
‫‪BCD‬‬
‫נעתיק את הגובה ‪ .hc‬נסמן את קצותיו‬
‫‪ C‬ו‪.D -‬‬
‫בנקודה ‪ D‬נעלה אנך‪.‬‬
‫מהנקודה ‪ C‬נחוג קשת ברדיוס ‪a‬‬
‫שתחתוך את הישר‪.‬‬
‫נסמן ב‪ B -‬את נקודת המפגש של הקשת‬
‫והאנך‪( .‬הקשת פוגשת את האנך פעמיים‬
‫אך המשולשים הנוצרים חופפים)‬
‫קיבלנו את קדקודי המשולש ‪. BCD‬‬
‫נשלים את סרטוט הצלעות‪.‬‬
‫סרטוט המשולש‬
‫‪ABC‬‬
‫המקרה של גובה‬
‫פנימי‬
‫נאריך את הקטע ‪ BD‬מעבר לנקודה ‪.D‬‬
‫מהנקודה ‪ B‬כמרכז נחוג קשת ברדיוס ‪.c‬‬
‫נסמן את נקודת החיתוך של הקשת עם‬
‫המשך ‪ BD‬ב‪.A1 -‬‬
‫קיבלנו את כל קדקודי המשולש ‪.ABC‬‬
‫נשלים את סרטוט הצלעות‪.‬‬
‫סרטוט המשולש‬
‫‪ABC‬‬
‫המקרה של גובה‬
‫חיצוני‬
‫נאריך את הקטע ‪ BD‬מעבר ל‪.B -‬‬
‫מהנקודה ‪ B‬כמרכז נחוג קשת ברדיוס ‪.c‬‬
‫נסמן את נקודת החיתוך של הקשת עם‬
‫המשך ‪ BD‬ב‪.A2 -‬‬
‫קיבלנו את כל קדקודי המשולש ‪.ABC‬‬
‫נשלים את סרטוט הצלעות‪.‬‬
‫‪C‬‬
‫‪a‬‬
‫‪hc‬‬
‫‪D‬‬
‫‪B‬‬
‫‪C‬‬
‫‪B‬‬
‫‪A1‬‬
‫‪D‬‬
‫‪C‬‬
‫‪A2‬‬
‫‪B‬‬
‫נשים לב שקיבלנו שני משולשים שמקיימים את דרישות‬
‫הבנייה‪ A1BC :‬ו‪.A2BC -‬‬
‫‪D‬‬
‫‪C‬‬
‫הוכיחו שאכן שני המשולשים שקיבלנו עונים על הדרישות‪.‬‬
‫‪A2‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A1‬‬
‫‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪95‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪242‬‬
‫‪ .35‬דנה וחגית התבקשו לבנות דלתון קמור שבו צלע ‪ ,a‬אלכסון משני ‪ b‬ואלכסון ראשי ‪.c‬‬
‫לפניכם שתי תכניות הבנייה שלהן‪.‬‬
‫א‪ .‬קבעו איזו מהתכניות מבוססת היטב ובאיזו יש פגם‪ .‬נמקו את התשובה‪.‬‬
‫ב‪ .‬בחרו את הבנייה הנכונה ובנו את הדלתון‪.‬‬
‫ג‪ .‬האם כל צירוף של נתונים מאפשר לסרטט דלתון קמור?‬
‫התכנית של דנה‬
‫התכנית של חגית‬
‫א‪ .‬נסרטט קטע באורך ‪ .b‬נסמן את קצותיו‬
‫א‪ .‬נסרטט קטע באורך ‪ .c‬נסמן את קצותיו באותיות‬
‫‪ .C ,A‬אלה הם שני הקדקודים של הדלתון‬
‫שבקצות האלכסון הראשי‪.‬‬
‫באותיות ‪ .D ,B‬אלה הם שני הקדקודים של‬
‫הדלתון שבקצות האלכסון המשני‪.‬‬
‫ב‪ .‬מהנקודה ‪ A‬כמרכז נחוג מעגל ברדיוס באורך‬
‫‪ .a‬הקדקודים ‪ B‬ו‪ D -‬יהיו מונחים על מעגל זה‪.‬‬
‫ב‪ .‬נבנה אנך אמצעי לקטע‪ .‬על ישר זה יעבור‬
‫האלכסון הראשי של הדלתון‪.‬‬
‫ג‪ .‬נעביר אנך לאלכסון ‪ AC‬באורך הקטע ‪ ,b‬כך‬
‫שייחתך עם המעגל בנקודות ‪ B‬ו‪.D -‬‬
‫ג‪ .‬מהנקודה ‪ B‬כמרכז ‪ ,‬נחוג קשת ברדיוס ‪ .a‬נסמן‬
‫ד‪ .‬כעת כשכל הקדקודים נקבעו נסרטט את הצלעות‪:‬‬
‫‪ ABCD‬הוא הדלתון המבוקש‪.‬‬
‫באות ‪ A‬את נקודת החיתוך שלה עם האנך‬
‫האמצעי‪.‬‬
‫ד‪ .‬מהנקודה ‪ A‬נקצה על האנך האמצעי קטע‬
‫באורך ‪ c‬החותך את הקטע ‪ .BD‬נסמן את‬
‫קצה הקטע באות ‪. C‬‬
‫ה‪ .‬כעת‪ ,‬כשכל הקדקודים נקבעו‪ ,‬נסרטט את‬
‫הצלעות‪ ABCD :‬הוא הדלתון המבוקש‪.‬‬
‫ננתח את הבעייה באמצעות סרטוט סכמתי של דלתון‪ .‬האלכסון הראשי הוא אנך אמצעי לדלתון המשני‪ .‬הקושי בבנייה‬
‫שאנלנו איננו יודעים היכן‪ ,‬על האנך האמצעי‪ ,‬נמצאים קדקודי הדלתון‬
‫התוכנית של דנה נכונה‪:‬‬
‫במשולשים ‪ ABD‬ו‪ CBD -‬האנך האמצעי שבנינו לצלע ‪ BC‬הוא תיכון גם גובה‪ .‬מכאן שמשולשים אלה שווי‪-‬שוקיים‬
‫ולמרובע ‪ ABCD‬יש שני זוגות זרים של צלעות שוות‪.‬‬
‫את האלכסון המשני ‪ BD = b‬יצרנו על‪-‬ידי העתקת קטע‪.‬‬
‫האלכסון הראשי ‪ AC = c‬הוא רדיוס הקשת שמרכזה ‪.A‬‬
‫הצלע ‪ AB = a‬כרדיוס הקשת שמרכזה ב‪.B -‬‬
‫בתוכנית של חגית יש פגם‪:‬‬
‫אנחנו לא יודעים היכן הנקודות ‪ B‬ו‪ D -‬וגם לא יודעים איפה להעלות את האנך‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪96‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫לא כל צירוף נתונים מבטיח בניית דלתון קמור‪ .‬אם האלכסון הראשי קצר מהגובה של המשולש ‪ ABD‬נוכל לסרטט‬
‫רק דלתון קעור‪ .‬אם האלכסון הראשי שווה לגובה של המשולש הנתונים לא מאפשרים לסרטט דלתון‪.‬‬
‫כדי לענות על השאלה די להדגים מצב בו האלכסון הראשי קצר מגובה המשולש‪ .‬בכתה חזקה מאד אפשר לדון גם במקרה‬
‫‪2‬‬
‫‪b‬‬
‫בו לא מתקבל דלתון‪ ,‬ולקשר את הדיון למשפט פיתגורס‪ :‬אם ‪ c 2     a2‬אז גובה המשולש שווה לאלכסון הראשי‪ ,‬ולכן‬
‫‪2‬‬
‫לא ניתן לבצע את הבנייה‪.‬‬
‫מטרת פעילות ‪ 14‬היא לפתח את המיומנות של הקדמת תכנון לביצוע‪ .‬מומלץ לבצע את ההדרכה לתרגיל זה עם‬
‫התלמידים בכתה‪ ,‬כדי שהתלמידים יעלו בעצמם הרעיונות לתכנון הבנייה‪.‬‬
‫הביצוע של תרגיל זה באמצעות תוכנה דינמית הוא פשוט‪ ,‬בעוד שבבנייה ידנית אנו נדרשים לבנות אנך אמצעי‬
‫בשביל פעולה פשוטה כמו חציית קטע‪.‬‬
‫כאמור‪ ,‬אחד היתרונות של בנייה באמצעות תוכנה נעוץ באפשרות לשנות בסוף הבנייה את החלקים הנתונים‬
‫ולראות כיצד הצורה שבנינו משתנה בהתאם לנתונים החדשים‪.‬‬
‫אתנחתא – איורים גאומטריים ברקמות מסורתיות‪ ,‬אריגים ואריחי קרמיקה –‬
‫עמ' ‪242‬‬
‫אריגים מסורתיים רבים‪ ,‬משובצים בדוגמאות גאומטריות שעוברות מדור לדור‪ .‬כך גם רקמות עמים‪ ,‬שטיחים‪,‬‬
‫שמיכות טלאים‪ ,‬אריחי קרמיקה ועוד‪.‬‬
‫בנו את האיורים באמצעות תוכנה גרפית או סרגל ומחוגה‪ ,‬בהתאם לרמזים מתחת כל איור‪.‬‬
‫הרדיוסים של‬
‫רבעי העיגולים‬
‫שווים למחצית‬
‫צלע הריבוע‪.‬‬
‫ארבעת הקטעים‬
‫שעל כל אלכסון‬
‫שווים זה לזה‪.‬‬
‫אורך הצלע של כל‬
‫ריבוע פינתי שווה‬
‫למחצית אורך צלע‬
‫הריבוע הגדול‪.‬‬
‫לאיור שמימין נוסף‬
‫ריבוע שקדקודיו‬
‫באמצעי הצלעות של‬
‫הריבוע האמצעי‪.‬‬
‫תוכלו למצוא דוגמאות רבות נוספות ברשת האינטרנט‪ ,‬ואולי גם במשפחה‪.‬‬
‫בכל הבניות תחילה נבנה ריבוע ונסרטט את אלכסוניו‪.‬‬
‫בנייה א‪ :‬נחצה את הצלעות‪ ,‬נחוג רבעי מעגלים שמרכזם בקדקודים ומחוגם חצי צלע‪.‬‬
‫בנייה ב‪ :‬נחלק את הצלעות ל‪ 4 -‬חלקים שווים על ידי חציית הצלע פעמיים‪ ,‬ונוסיף את ארבעת הקטעים העוברים‬
‫דרך נקודות החלוקה‪.‬‬
‫בנייה ג‪ :‬נחצה כל קטע שמחבר את מפגש האלכסונים עם קדקוד‪ .‬נסרטט מרובע שקדקודיו בנקודות החלוקה‪.‬‬
‫כדאי לשאול מדוע מרובע זה הוא ריבוע‪.‬‬
‫בנייה ד‪ :‬נחצה את צלעות הריבוע הפנימי ונסרטט מרובע נוסף (אף הוא ריבוע) שקדקודיו בנקודות החלוקה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪97‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 14‬בניית משולש על‪-‬פי שתי צלעות ותיכון לאחת מצלעות אלה – עמ' ‪243‬‬
‫באתר מופיע קובץ עם נתונים‬
‫לביצוע בנייה זו במחשב‪.‬‬
‫עלינו לבנות משולש ‪ ABC‬ששתיים מצלעותיו הן ‪ , AC=b BC=a‬והתיכון לצלע ‪ AC‬הוא ‪. BD = m‬‬
‫‪m‬‬
‫‪a‬‬
‫‪b‬‬
‫א‪ .‬הדרכה בתכנון מהלך הבנייה‬
‫לפני שניגש לבנייה נבחן את הנתונים במטרה לגלות קשרים שיעזרו לנו לתכנן את צעדי הבנייה‪.‬‬
‫לשם כך אנו זקוקים לסרטוט‪.‬‬
‫‪A‬‬
‫איננו יודעים עדיין לסרטט את המשולש בהתאם לנתונים‪ ,‬ולכן נסרטט סקיצה מבלי להתחשב‬
‫‪b‬‬
‫‪2‬‬
‫בנתוני המשולש המבוקש‪:‬‬
‫‪m‬‬
‫נסרטט משולש‪ ,‬נסמן בו שתי צלעות ותיכון לאחת מהן‪ ,‬ונחפש קשרים שיוכלו לעזור לנו‪.‬‬
‫ניתן לראות‪:‬‬
‫‪b‬‬
‫= ‪.CD‬‬
‫את המשולש ‪ CBD‬אפשר לבנות על‪-‬פי שלוש צלעות‪,AC = b ,BD = m :‬‬
‫‪2‬‬
‫‪b‬‬
‫ולמצוא את הקדקוד ‪. A‬‬
‫לאחר שנעשה זאת נוכל לחבר לצלע ‪ CD‬קטע נוסף באורך‬
‫‪2‬‬
‫‪b D‬‬
‫‪2‬‬
‫‪C‬‬
‫‪a‬‬
‫‪B‬‬
‫ב‪ .‬בנו את המשולש על‪-‬פי מהלך הבנייה המתואר‬
‫‪b‬‬
‫‪ .I‬חצו את הקטע הנתון ‪ b‬לקבלת הקטע‬
‫‪2‬‬
‫‪.‬‬
‫‪ .II‬בנו את המשולש ‪ CBD‬על‪-‬פי ‪ 3‬צלעותיו‪ .‬רשמו את מהלך הבנייה‪.‬‬
‫‪b‬‬
‫‪ .III‬העתיקו על המשך הישר ‪ ,CD‬החל מהנקודה ‪ ,D‬את הקטע‬
‫‪2‬‬
‫‪ ,‬וסמנו את קצהו השני ב‪.A -‬‬
‫‪ .IV‬חברו את ‪ A‬עם ‪.B‬‬
‫ג‪ .‬לשם מה חצינו את הקטע ‪ ? b‬כדי לקבל את הצלע ‪ CD‬של המשולש ‪.CDB‬‬
‫ד‪ .‬כיצד אנחנו יודעים שקיבלנו את המשולש המבוקש? את התיכון והצלע ‪ CB‬קיבלנו במהלך הבנייה של המשולש‬
‫‪b‬‬
‫= ‪ .CD‬הצלע ‪ AC‬התקבלה כתוצאה מחיבור שני קטעים‬
‫‪ .CDB‬במהלך בניית משולש זה קיבלנו את הקטע‬
‫‪2‬‬
‫‪b‬‬
‫השווים ל‪. -‬‬
‫‪2‬‬
‫ה‪ .‬האם כל צירוף של נתונים מאפשר לבנות את המשולש?‬
‫לא‪ .‬צלעות המשולש ‪ CBD‬צריכות לקיים את המשפט‪ :‬סכום שתי צלעות במשולש קטן מהצלע השלישית‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪98‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תרגילים מעורבים ‪ -‬עמ' ‪245 - 244‬‬
‫עמ' ‪244‬‬
‫‪ .36‬א‪ .‬נתונים קטע ‪ a‬ושתי זוויות ‪ ‬ו‪.  -‬‬
‫ב‪ .‬בנו לפחות שני משולשים עם נתונים אלה‪.‬‬
‫בנק נתונים לתרגילים ‪43 - 36‬‬
‫מטרת תרגיל ‪ 36‬להדגיש שיש לשים לב מי הצלע הנתונה‪.‬‬
‫כמו כן התרגיל מדגיש את החשיבות של חפיפת משולשים על‪-‬פי‬
‫חלקים מתאימים שווים‪ .‬שוויון של צלעות אחרות לא מבטיח‬
‫חפייפת משולשים‪.‬‬
‫‪‬‬
‫להלן שני משולשים שעונים על דרישות הבנייה‬
‫‪‬‬
‫‪180--‬‬
‫‪‬‬
‫‪‬‬
‫‪a‬‬
‫‪‬‬
‫‪‬‬
‫‪a‬‬
‫קיים משולש נוסף שבו הזווית ‪ ‬נמצאת מול הצלע ‪.a‬‬
‫‪‬‬
‫‪ .37‬בנו‪ ,‬אם אפשר‪ ,‬משולש שווה‪-‬שוקיים לפי אורך הגובה לבסיס ‪ ,b‬וזווית‬
‫הבסיס ‪.‬‬
‫בתרגיל זה המוקד הוא תכנון מוקדם‪.‬‬
‫‪90-‬‬
‫‪a‬‬
‫הגובה מחלק את המשולש לשני משולשים‬
‫‪b‬‬
‫ישרי‪-‬זווית שבכל אחד מהם נתונים ניצב‬
‫‪‬‬
‫ובקצותיו זווית ישרה‪ ,‬וזווית שמידתה ‪.90-‬‬
‫‪c‬‬
‫‪ .38‬בנו‪ ,‬אם אפשר‪ ,‬משולש שווה‪-‬שוקיים לפי אורך הגובה לבסיס ‪ ,b‬וזווית הבסיס ‪.‬‬
‫לא ניתן‪ .‬זווית בסיס חייבת להיות חדה‪.‬‬
‫‪ .39‬בנו‪ ,‬אם אפשר‪ ,‬משולש שווה‪-‬שוקיים לפי אורך הגובה לבסיס ‪ ,b‬וזווית הראש ‪.‬‬
‫סרטוט סכמתי מראה שבדומה לתרגיל ‪ 37‬אפשר להתחיל עם בניית משולש ישר‪-‬זווית‪.‬‬
‫‪‬‬
‫הפעם נתונים ניצב ולצדדיו זווית ישרה וזווית ידועה ‪.‬‬
‫‪2‬‬
‫‪‬‬
‫‪2‬‬
‫‪ .40‬א‪ .‬בנו דלתון ‪ ABCD‬על‪-‬פי זוויות הראש ‪ ‬ו‪  -‬והאלכסון הראשי ‪.a‬‬
‫הבנייה כרוכה בשלב הכנה בו נחצה את הזוויות הנתונות‪ .‬עכשיו נוכל לבנות את שני המשולשים שיוצר האלכסון‬
‫הראשי על‪-‬פי ז‪.‬צ‪.‬ז‪.‬‬
‫ב‪ .‬כמה דלתונים שונים זה מזה ניתן לבנות על‪-‬פי הנתונים?‬
‫אחד‪ .‬כל משולש אחר שנבנה יהיה חופף למשולש שבנינו‪ ,‬ולכן יביא לבניית דלתון חופף לזה שבנינו‪.‬‬
‫ג‪ .‬איזה תנאי צריכות לקיים זוויות הראש של הדלתון כדי שהבנייה תהיה אפשרית?‬
‫סכום חצאי הזוויות צריך להיות קטן מ‪ ,180 -‬ומכאן שסכום הזוויות הנתונות צריך להיות קטן מ‪.360 -‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪99‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪ .41 244‬א‪ .‬בנו דלתון קעור ‪ ABCD‬על‪-‬פי זוויות הראש ‪ ‬ו‪ 2 -‬והאלכסון הראשי ‪.a‬‬
‫ב‪ .‬כמה דלתונים שונים זה מזה ניתן לבנות על‪-‬פי הנתונים?‬
‫אם הנתונים מאפשרים את הבנייה אז הבניה דומה לזו שבתרגיל ‪ 40‬ומאפשרת בניית דלתון קעור אחד‪.‬‬
‫ג‪ .‬החליפו את הזווית הנתונה ‪ ‬בזווית אחרת ‪ .‬איזה תנאי צריכה לקיים הזווית ‪ ‬כדי שהבנייה תהיה אפשרית?‬
‫הסבירו‪.‬‬
‫כדי שהדלתון יהיה קעור צריך להתקיים ‪ ,2 > 180‬ומכאן ‪ . > 90‬כיוון שמדובר בזוויות של מרובע צריך‬
‫להתקיים גם ‪ . < 120  2 +  < 360‬משני התנאים נקבל ‪.90 <  < 120‬‬
‫‪ .42‬הסבירו מדוע לא ניתן לבנות דלתונים שבהם‪:‬‬
‫א‪ .‬האלכסון הראשי מחלק את האלכסון המשני ביחס של ‪.2 : 1‬‬
‫כי האלכסון הראשי חוצה את האלכסון המשני‪.‬‬
‫ב‪ .‬אורכי הצלעות ‪ a‬ו‪ ,2a -‬וזוויות הראש שוות זו לזו‪.‬‬
‫כי אם זוויות הראש שוות זו לזו אז גם החצאים שלהן שווים ולכן האלכסון הראשי מחלק את הדלתון לשני משולשים‬
‫שווי ‪-‬שוקיים‪ .‬זה סותר את הנתון שאורכי הצלעות ‪ a‬ו‪.2a -‬‬
‫‪ .43‬בנו דלתון על‪-‬פי זווית הראש ‪ ,‬זווית צד ‪ ‬והאלכסון הראשי ‪.a‬‬
‫‪‬‬
‫התרגיל כרוך בשלב הכנה לבנות את הזווית‬
‫‪180   ‬‬
‫‪2‬‬
‫לנוחיותכם בעמוד הבא צילום מוגדל של המפה בשאלה ‪44‬‬
‫‪‬‬
‫‪180   ‬‬
‫‪2‬‬
‫‪‬‬
‫‪2‬‬
‫עמ' ‪ .44 245‬לפניכם מפה עם סרגל לקריאת מרחקים בהתאם לקנה המידה של המפה‪.‬‬
‫א‪ .‬היעזרו במחוגה כדי למצוא על המפה (בקירוב) את‪:‬‬
‫‪ .I‬אורכו של רחוב יסמין‪.‬‬
‫‪ .II‬המרחק בין הככר בשדרות בן גוריון פינת רחוב ז'בוטינסקי לככר ברחוב‬
‫בן גוריון פינת רחוב נחלת הר חב"ד‪.‬‬
‫ב‪ .‬מצאו על המפה‪ ,‬בעזרת המחוגה‪ ,‬זוגות של אתרים שהמרחק ביניהם הוא‪:‬‬
‫‪ 100 .I‬מטרים‪ 500 .II .‬מטרים‪.‬‬
‫‪ 1 .III‬ק"מ‪.‬‬
‫ג‪ .‬משפחת רפאל רוצה לגור בשכונה זו‪ ,‬במרחק של ‪ 500‬מטרים לכל היותר מקופת חולים לאומית ומחפשת‬
‫מודעות בעתון על דיר ות להשכרה‪ .‬ציינו את שמות הרחובות בהם יש אפשרות שימצאו דירה מתאימה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪100‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪101‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫סוגרת את הפרק משימת חקר אינטגרטיבית שמשלבת בין פרק הבניות‪ ,‬פרק הדלתון ופרק הפונקציות‪.‬‬
‫החלק הראשון של הפעילות יכול להתבצע עם או בלי טכנולוגיה‪.‬‬
‫בפרק זה משווים בין שתי דרכים לבניית דלתון על‪-‬פי אלכסוניו‪.‬‬
‫הדרך הראשונה "הבנייה של יובל" מאפשרת לבנות רק דלתונים קמורים‪ .‬הדרך השנייה‪" ,‬הבנייה של ליאור"‬
‫מאפשרת לבנות גם דלתונים קעורים‪ ,‬ולמעשה מאפשרת לבנות כל דלתון שניתן לבנות בנתונים הקיימים‪.‬‬
‫כיוון ששטח הדלתון הוא מחצית מכפלת אלכסוניו‪ ,‬השטחים של כל הדלתונים‪ ,‬הניתנים לבנייה בשתי הדרכים‪ ,‬שווים‪.‬‬
‫סביר להניח שלפחות חלק מהתלמידים יגלו זאת בעצמם‪.‬‬
‫החלק השני של הפעילות מבוסס על יישומון‪.‬‬
‫היישומון מאפשר לסרטט דלתונים רבים באמצעות "הבנייה של יובל"‪ ,‬ולראות כיצד משתנים השטח וההיקף של הדלתון‬
‫כאשר הדלתון משתנה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪102‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫לפעילות זו יישומון באתר‪.‬‬
‫‪‬‬
‫משימת חקר ‪ -‬דלתון עם אלכסונים נתונים ‪ -‬עמ' ‪246‬‬
‫‪ .1‬סרטטו בסרגל ובמחוגה דלתון ‪ ABCD‬על‪-‬פי אלכסוניו‪.‬‬
‫אלכסון ראשי‬
‫‪m‬‬
‫‪C‬‬
‫סמנו ב‪ P -‬את נקודת המפגש של האלכסונים‪.‬‬
‫‪A‬‬
‫‪ .2‬בנו דלתון נוסף עם אותם אלכסונים‪.‬‬
‫‪ .3‬לפניכם בניות של שני תלמידים‪:‬‬
‫אלכסון משני‬
‫‪D‬‬
‫‪k‬‬
‫‪B‬‬
‫הבנייה של יובל‬
‫הבנייה של ליאור‬
‫יובל סרטט תחילה קטע ‪ AC‬באורך ‪ ,m‬וסימן עליו נקודה ‪P‬‬
‫שתהיה מפגש האלכסונים‪.‬‬
‫בנקודה ‪ P‬יובל העלה אנך ל‪.AC -‬‬
‫‪k‬‬
‫שמרכזו בנקודה ‪.P‬‬
‫יובל חג מעגל ברדיוס‬
‫‪2‬‬
‫בנקודות המפגש של המעגל עם האנך סימן את הקדקודים ‪B‬‬
‫ו‪ ,D -‬חיבר את הקדקודים וקיבל דלתון‪.‬‬
‫ליאור סרטט תחילה קטע ‪ BD‬באורך ‪.k‬‬
‫ליאור העלה אנך אמצעי ל‪ P( .BD -‬אמצע ‪).BD‬‬
‫על האנך האמצעי ליאור סימן נקודה ‪.A‬‬
‫ליאור חג מעגל ברדיוס ‪ m‬שמרכזו ‪. A‬‬
‫ליאור סימן ב‪ C -‬את אחת מנקודות המפגש של המעגל עם‬
‫האנך האמצעי‪ ,‬חיבר את הקדקודים וקיבל דלתון‪.‬‬
‫‪A‬‬
‫‪B‬‬
‫‪D‬‬
‫‪P‬‬
‫‪A‬‬
‫‪B‬‬
‫‪D‬‬
‫‪C‬‬
‫‪C‬‬
‫הסבירו מדוע ‪ ABCD‬דלתון‪.‬‬
‫הסבירו מדוע ‪ ABCD‬דלתון‪.‬‬
‫א‪ .‬האם לדעתכם יש יתרון לאחת הבניות? הסבירו‪.‬‬
‫ב‪ .‬שערו‪ :‬האם שטחי הדלתונים שסרטטו יובל וליאור שווים זה לזה?‬
‫האם היקפי הדלתונים שסרטטו יובל וליאור שווים זה לזה?‬
‫נסו לבסס את השערתכם‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪103‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫‪‬‬
‫פתחו את היישומון שטח והיקף של דלתון קמור עם אלכסונים נתונים‪.‬‬
‫הדלתון ביישומון זה ניבנה בדרך של יובל‪.‬‬
‫גרירת הנקודה ‪ P‬משנה את הדלתון‪ ,‬אך האלכסונים נשארים מאונכים ואורכיהם‬
‫נשארים קבועים‪.‬‬
‫‪A‬‬
‫בחלק זה של הפעילות נחקור כיצד משפיע המיקום של הנקודה ‪ P‬על השטח‬
‫‪D‬‬
‫וההיקף של הדלתון ‪.ABCD‬‬
‫‪B‬‬
‫‪P‬‬
‫גררו את הנקודה ‪.P‬‬
‫על צג המחשב מתקבלים שני גרפים‪.‬‬
‫אחד הגרפים מתאר את השתנות שטח הדלתון כפונקציה של המרחק ‪.PC‬‬
‫הגרף השני מתאר את השתנות היקף הדלתון ‪ ABCD‬כפונקציה של המרחק‬
‫‪C‬‬
‫‪.PC‬‬
‫ג‪.‬‬
‫איזה גרף מתאים לכל אחת מן הפונקציות? הסבירו‪.‬‬
‫פונקציית השטח היא פונקציה קבועה ‪ y=6‬כיוון שכל הדלתונים המתקבלים הם שווי שטח‪.‬‬
‫פונקציית ההיקף ‪ . y  2 4  x2  2 4  (3  x)2 :‬כשמקלידים אותה בחלון הקלט מתלכדים הגרף שהתקבל‬
‫באמצעות הגרירה והגרף שהתקבל בעזרת ההצגה האלגברית של הפונקציה‪.‬‬
‫ד‪.‬‬
‫מצאו את החוק של כל אחת מן הפונקציות‪.‬‬
‫תוכלו להקליד את הפונקציה בחלון הקלט‬
‫ולבדוק אם הגרף מתלכד עם הגרף שקיבלתם‬
‫באמצעות העקבות‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪104‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫ה‪ .‬בנו את הדלתון בדרך של ליאור‪.‬‬
‫ו‪.‬‬
‫האם כל הדלתונים שנבנו בדרך של ליאור אף הם שווי שטח? כן‪.‬‬
‫פונקציית ההיקף דומה מאד לפרבולה אולם תבניתה איננה של פונקצייה ריבועית‪ .‬אפשר להסביר את הסימטריה באופן‬
‫גיאומטרי‪ ,‬כי כשהנקודה ‪ P‬נמצאת במרחק ‪ x‬מ‪ C -‬וכשהיא נמצאת באותו המרחק מ‪ A -‬מתקבלים דלתונים חופפים‪.‬‬
‫אתנחתא ‪ -‬תרגול בניות ואתגרים נוספים – עמ' ‪247‬‬
‫באמצעות הקישור הבא‪http://euclidthegame.org/Level1.html :‬‬
‫או בסריקת ה‪QR -‬‬
‫תוכלו להגיע אל משחק בניות ממוחשב בסרגל ומחוגה הכולל בניות שכבר ביצעתם ויכול לסייע בתרגול או ביצוע‬
‫בניות נוספות מתקדמות להרחבה ואתגר‪.‬‬
‫במשחק זה מתחילים עם בניות בסיסיות‪ ,‬ומתקדמים לבניות מתקדמות ומאתגרות‪.‬‬
‫כאשר מצליחים לבצע בנייה באמצעות כלים שכבר נרכשו‪ ,‬מתווסף בסרגל הכלים כלי חדש לביצוע הבנייה שזה‬
‫עתה הושלמה בהצלחה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪105‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫על ישרים מקבילים וזוויות – מדריך למורה‬
‫פרק המקבילים נפתח במפגש חוזר‪ ,‬כיוון שהתלמידים מכירים את המושגים ישרים מקבילים (כיתה ז חלק א עמ' ‪,)153‬‬
‫"זוויות מתחלפות בין מקבילים" ו"זוויות מתאימות בין מקבילים" (כיתה ז חלק ב עמ' ‪.)240‬‬
‫חשוב לשים לב‪ ,‬בכיתה ז הישרים המקבילים הוגדרו בתוכנית הלימודים ובספרי הלימוד‪ ,‬כישרים השונים זה מזה ומאונכים‬
‫לאותו ישר‪ .‬כל הפעילויות התבססו על הגדרה זו‪ .‬לעומת זאת בכיתה ט‪ ,‬אנו מסתמכים על ההגדרה הבאה‪ :‬שני ישרים‬
‫נקראים ישרים מקבילים אם הם ישרים הנמצאים באותו מישור ואינם נחתכים‪.‬‬
‫בפרק זה שלוש תוספות עיקריות למה שהתלמידים כבר מכירים מכיתות ז‪-‬ח‪:‬‬
‫א‪ .‬הגדרה שונה לישרים מקבילים‪.‬‬
‫ב‪ .‬בכיתה ז התלמידים הכירו את המושגים זוויות מתאימות וזוויות מתחלפות‪ .‬בפרק הנוכחי הוספנו את המושג "זוויות‬
‫חד‪-‬צדדיות בין ישרים מקבילים"‪ .‬זוויות חד‪-‬צדדיות אינן בתוכנית הלימודים‪ .‬יחד עם זאת זוויות סמוכות במקבילית‬
‫וזוויות ליד אותה שוק בטרפז הן זוויות חד‪-‬צדדיות בין ישרים מקבילים‪ ,‬והיכרות מוקדמת עם זוויות אלה מפשטת‬
‫את ההוראה כשעוסקים במקבילית ובטרפז‪.‬‬
‫ג‪.‬‬
‫בכיתה ח התלמידים הכירו משפטים בהם נתון שישרים מקבילים נחתכים על‪-‬ידי ישר שלישי‪ .‬בפרק הנוכחי יכירו‬
‫משפטים הפוכים לאלה שהכירו בכיתה ח‪ ,‬בעזרתם יוכלו לזהות ישרים מקבילים על‪-‬פי נתונים אודות הזוויות‪.‬‬
‫בעקבות הצגת המשפט ההפוך למשפט על זוויות בין מקבילים מוצג המושג "משפט הפוך"‪ .‬הקדשנו פעילויות אחדות להבחנה‬
‫בין מה נתון לבין מה צריך להוכיח‪ ,‬ולהבחנה באיזה משפט מתוך צמד משפטים‪ ,‬ישר או הפוך‪ ,‬נעשה שימוש בהוכחה של‬
‫טענות שונות‪.‬‬
‫פעילות ‪ – 1‬מפגש חוזר – עמ' ‪248‬‬
‫מטרת פעילות ‪ 1‬היא להציג את ההגדרה בה נשתמש‬
‫בכיתה ט ולערוך חזרה על כל מה שנלמד עד כה‬
‫בנושא ישרים מקבילים‪ :‬מושגים ומשפטים‪.‬‬
‫לדוגמה‪ ,‬הטענה‪ :‬אם שני ישרים מקבילים זה לזה‪,‬‬
‫אזי כל שתי זוויות מתחלפות ביניהם שוות זו לזו‪.‬‬
‫הוזכרה בכיתה ז‪ ,‬איננה ניתנת להוכחה‪ ,‬קיבלנו‬
‫אותה כהנחת יסוד‪.‬‬
‫הפעילות מתייחסת גם למושג מרחק בין ישרים‬
‫מקבילים‪ ,‬שהוא אורך האנך ביניהם‪ .‬כל האנכים בין‬
‫ישרים מקבילים הם שווי אורך‪ ,‬מכיוון שהמרחק בין‬
‫שני ישרים מקבילים הוא קבוע‪ .‬המרחק בין ישרים‬
‫מקבילים הוא אורך של קטע‪ ,‬ולכן תמיד חיובי‪.‬‬
‫בתום הפעילות התלמידים מתבקשים להוכיח את‬
‫המשפט‪ :‬אם ישר מאונך לאחד משני ישרים מקבילים‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪106‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫הוא מאונך גם לישר השני‪ .‬הוכחת משפט זה תאפשר חזרה על זיהוי זוויות מתחלפות או זוויות מתאימות ושימוש באחד משני‬
‫המשפטים שנלמדו בכיתה ז‪.‬‬
‫כפי שפרטנו במבוא‪ ,‬בחרנו להגדיר את המושג זוויות חד‪-‬צדדיות‪ ,‬למרות שהוא אינו נכלל בתכנית הלימודים‪ ,‬כי היכרות‬
‫מוקדמת עם זוויות אלה מפשטת את ההוראה כשעוסקים במקבילית ובטרפז‪.‬‬
‫זוויות חד‪-‬צדדיות‬
‫‪m‬‬
‫הזוויות ‪ ∡B3‬ו‪ ∡A3 -‬הן זוויות חד‪-‬צדדיות כי שתיהן מאותו צד של הישר החותך‪,‬‬
‫‪A‬‬
‫‪n‬‬
‫אבל שתיהן מצדדים שונים של הישרים ‪ m‬ו‪.n -‬‬
‫‪4‬‬
‫הזוויות ‪ ∡B2‬ו‪ ∡A4 -‬הן זוויות חד‪-‬צדדיות כי שתיהן מאותו צד של הישר החותך‪,‬‬
‫‪B‬‬
‫‪1‬‬
‫‪3‬‬
‫‪1‬‬
‫‪2‬‬
‫‪2‬‬
‫‪4‬‬
‫‪3‬‬
‫אבל שתיהן מצדדים שונים של הישרים ‪ m‬ו‪.n -‬‬
‫הישרים ‪ a‬ו‪ b -‬נחתכים על‪-‬ידי הישר ‪.c‬‬
‫‪c‬‬
‫‪c‬‬
‫זוויות שנמצאות מאותו צד של הישר החותך ‪,c‬‬
‫‪a‬‬
‫ומצדדים שונים של הישרים ‪ a‬ו‪ b -‬נקראות‬
‫‪a‬‬
‫זוויות חד‪-‬צדדיות‪.‬‬
‫‪b‬‬
‫זוויות חד‪-‬‬
‫צדדיות סומנו‬
‫באופן זהה‪.‬‬
‫‪b‬‬
‫פעילות ‪ – 2‬האם זה מקרי? – עמ' ‪249‬‬
‫פעילות ‪ 2‬נועדה להעלות‬
‫השערה בהקשר לסכום‬
‫זוויות חד‪-‬צדדיות בין ישרים‬
‫מקבילים‪ .‬בפעילות זו אנו‬
‫גם מלמדים את התלמידים‬
‫שכאשר מתגלה תופעה יש‬
‫לבדוק האם היא מקרית או‬
‫ניתן להוכיח אותה ולהכליל‪.‬‬
‫בפעילות ‪ 3‬אנו מוכיחים את‬
‫הטענה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪107‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 3‬הוכחת משפט זוויות חד‪-‬צדדיות – עמ' ‪250‬‬
‫מטרת פעילות ‪ - 3‬הוכחה של התופעה שזיהנו בפעילות ‪ 2‬והכללתה למשפט‪.‬‬
‫מורים שעובדים עם קבוצות ח זקות‪ ,‬מוזמנים לתת לתלמידים לנסות ולהוכיח את הטענה באופן עצמאי‪.‬‬
‫לעתים נוח לזהות את הישרים המקבילים ואת זוגות של זוויות ביניהם‪ ,‬בעזרת דמיון ויזואלי לאותיות‪ ,‬לפעמים מסובבות‬
‫כמודגם באיורים‪:‬‬
‫נוח לזהות זוויות מתחלפות בעזרת‬
‫האותיות ‪ Z‬או ‪ N‬או מ‪.‬‬
‫נוח לזהות זוויות מתאימות בעזרת‬
‫האותיות ‪ F‬או ע‪.‬‬
‫נוח לזהות זוויות חד‪-‬צדדיות בעזרת‬
‫האותיות ח או האות כ‪.‬‬
‫הידעתם? – עמ' ‪250‬‬
‫הידעתם? הינו קטע ההיסטורי עם מעט מידע על אכס יומות ועל אכסיומת המקבילים‪ .‬הינכם יכולים להמליץ לתלמידים לקרוא‬
‫את הקטע באופן עצמאי או לערוך סביבו דיון כיתתי‪ .‬נקודה הכרחית להתייחסות וחשובה בהמשך לבניות בסרגל ובמחוגה או‬
‫לבניית ישר מקביל בסביבה דינמית היא להתייחס למשמעות האכסיומה‪ :‬שדרך נקודה מחוץ לישר ניתן להעביר (באותו‬
‫מישור) רק מקביל אחד לישר הנתון‪.‬‬
‫מורים המעוניינים לפרט קצת יותר בכיתה‪ ,‬להלן מידע נוסף על זה המופיע בספר לתלמיד ובו פירוט חמשת האכסיומת‬
‫והויכוח שהתחולל סביבן‪.‬‬
‫מתמטיקאים משתדלים לנסח אכ סיומות באופן שייראה לאנשים כמובן מאליו על סמך ניסיונם‪.‬‬
‫את היסודות לגאו מטריה שאנו לומדים היום הניח המתמטיקאי היווני הגדול אוקלידס במאה השלישית לפני הספירה בספרו‬
‫יסודות (אלמנטים)‪ .‬אוקלידס הציג מערכת של מושגי יסוד‪ ,‬הגדרות ואכסיומות‪ .‬הספר יסודות הוא אחד המפורסמים ביותר‬
‫בתולדות האנושות‪ .‬יש אומרים כי אף ספר מדעי לא זכ ה להצלחה לאורך שנים כה רבות כמו ספר זה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪108‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫בהניחו את יסודות הגאומטריה אוקלידס ניסח חמש אכסיומות‪:‬‬
‫‪.1‬‬
‫בין כל שתי נקודות ניתן להעביר קטע ישר‪.‬‬
‫‪.2‬‬
‫כל קטע אפשר להמשיך לקו ישר‪.‬‬
‫‪.3‬‬
‫מכל נקודה אפשר לחוג מעגל בכל רדיוס נתון‪.‬‬
‫‪.4‬‬
‫כל הזויות הישרות שוות זו לזו‪.‬‬
‫‪.5‬‬
‫אם ישר חותך שני ישרים כך שמצד אחד שלו נוצרות זוויות חד‪-‬צדדיות פנימיות שסכומן קטן מסכום שתי זוויות‬
‫ישרות‪ ,‬אז בהמשך הישרים נחתכים זה עם זה באותו הצד של החותך שבו סכום הזוויות קטן משתי זוויות ישרות‪.‬‬
‫הדיון סביב האכ סיומה החמישית נמשך למעלה מאלפיים שנה‪ ,‬כשבמהלכן הציעו מתמטיקאים ניסוחים שקולים לאכסיומה זו‪,‬‬
‫שנחשבו בעיניהם ברורים יותר‪ .‬אחד הניסוחים המפורסמים ביותר‪ ,‬המכונה לעתים "אכסיומת המקבילים" הוא‪:‬‬
‫דרך נקודה מחוץ לישר ניתן להעביר (באותו מישור) רק מקביל אחד לישר הנתון‪.‬‬
‫הידעתם?‬
‫בגאומטריה מבחינים בין מושגים שלא ניתן להגדיר – מוש גי יסוד‪ ,‬כמו‪ :‬נקודה‪ ,‬קו‪ ,‬ישר‪ ,‬ומישור‪ ,‬לבין מושגים שאותם‬
‫מגדירים‪ ,‬כמו‪ :‬קטע‪ ,‬משולש‪ ,‬זווית ועוד‪ .‬כך גם מבחינים בין טענות המקובלות כנכונות ללא צורך בהוכחה – הנחות יסוד‪,‬‬
‫הנקראות אכסיומות‪ ,‬לבין טענות שדורשות הוכחה – משפטים‪.‬‬
‫את הטענות ניתן להוכיח או לה פריך בעזרת האכסיומות‪ ,‬משפטים אחרים שהוכחנו‪ ,‬והסקות לוגיות‪.‬‬
‫מטבע הדברים המתמטיקאים משתדלים להשתמש בכמה שפחות מושגי יסוד ובכמה שפחות אכסיומות‪.‬‬
‫כל מה שניתן להגדרה באמצעות מושגים קודמים מוגדר כך‪ ,‬וכל מה שניתן להוכחה באמצעות אכסיומות קיימות ומשפטים‬
‫המתבססים עליהן אינו מוצג כאכסיומה‪ ,‬אלא מוכח כמשפט‪.‬‬
‫את היסודות לגאומטריה שאנו לומדים היום הניח המתמטיקאי היווני הגדול אוקלידס במאה השלישית לפני‬
‫הספירה בספרו יסודות (אלמנטים)‪ .‬בהניחו את יסודות הגאומטריה אוקלידס ניסח חמש אכסיומות‪.‬‬
‫החמישית מבין האכסיומות היא אכסיומת המקבילים‪.‬‬
‫בעוד שארבע האכסיומות הראשונות לא עוררו כל ויכוח‪ ,‬בהיותן פשוטות וברורות‪ ,‬היו רבים שהתקשו לקבל‬
‫את האכסיומה החמישית‪ :‬מצד אחד‪ ,‬היא הרבה יותר מורכבת מהאחרות ולכן קשה היה להשלים עם הצורך לקבלה ללא‬
‫הוכחה‪ .‬מצד שני‪ ,‬מתמטיקאים רבים ניסו להוכיח את הטענה שמציגה האכסיומה החמישית ולהפכה למשפט‪ ,‬וכך לבסס את‬
‫יסודות הגיאומטריה על ארבע האכסיומות הראשונות בלבד‪.‬‬
‫הדיון סביב האכסיומה החמישית נמשך למעלה מאלפיים שנה‪ ,‬כשבמהלכן הציעו מתמטיקאים ניסוחים שקולים לאכסיומה זו‪,‬‬
‫שנחשבו בעיניהם ברורים יותר‪ .‬אחד הניסוחים המפורסמים ביותר‪ ,‬המכונה לעתים‬
‫"אכסיומת המקבילים" הוא‪ :‬דרך נקודה מחוץ לישר ניתן להעביר (באותו מישור) רק מקביל אחד לישר הנתון‪.‬‬
‫ניסוח שקול מוכר לכם הוא‪ :‬אם ישרים הם מקבילים אז ישר שחותך אותם יוצר זוויות מתאימות שוות‪.‬‬
‫ללא אכסיומת המקבילים לא ניתן להוכיח שסכום הזוויות במשולש הוא ‪.180‬‬
‫ללא אכסיומת המקבילים לא ניתן אפילו להוכיח שסכום הזוויות של כל המשולשים זהה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪109‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תרגילים – עמ' ‪252 – 251‬‬
‫עמ' ‪.1 251‬‬
‫‪B‬‬
‫‪y‬‬
‫נתון‪ - CPRN :‬מלבן‪.AN II DE .‬‬
‫‪D‬‬
‫‪P‬‬
‫על‪-‬פי הנתונים בסרטוט מצאו את הערכים של ‪ x‬ו‪.y -‬‬
‫‪A‬‬
‫‪C‬‬
‫‪56º‬‬
‫מטרת התרגיל היא להשתמש בידע קודם של התלמידים על תכונות המלבן‪ ,‬זוויות‬
‫‪x‬‬
‫‪42º‬‬
‫קדקודיות וסכום זוויות במשולש‪.‬‬
‫‪R‬‬
‫‪N‬‬
‫‪E‬‬
‫למציאת ‪ y‬שתי דרכים‪ :‬האחת להסתכל על סכום זוויות במשולש ‪ ABD‬והשנייה‬
‫להסתכל על סכום זוויות במשולש ‪.NBR‬‬
‫‪B‬‬
‫‪y‬‬
‫‪y = 180º – 42º –56º = 82º‬‬
‫‪D‬‬
‫‪P‬‬
‫‪42º‬‬
‫‪A 56º‬‬
‫‪ α = 56º‬זווית מתחלפות בין ישרים מקבילים ‪CP II NR‬‬
‫‪C‬‬
‫‪56º‬‬
‫‪ x = α = 56º‬זוויות מתאימות בין ישרים מקבילים ‪.AN II DE‬‬
‫‪42º‬‬
‫‪x‬‬
‫‪R‬‬
‫‪.2‬‬
‫‪α‬‬
‫‪N‬‬
‫‪E‬‬
‫נתון‪ .AB ll CD :‬הישר ‪ AE‬חוצה את הזווית ‪.∡A‬‬
‫והישר ‪ CF‬חוצה את הזווית ‪.∡C‬‬
‫חוצי הזוויות נפגשים בנקודה ‪.G‬‬
‫א‪ .‬סמנו‪ ∡BAE = α :‬ובטאו באמצעות ‪‬‬
‫את כל הזוויות בקדקודים ‪ A‬ו‪.C -‬‬
‫ב‪ .‬הוכיחו כי ‪.∡AGC = 90‬‬
‫הטכניקה המוצעת בהדרכה לתרגיל‪ ,‬ביטוי זוויות באמצעות משתנה היא שימושית‬
‫מאד ולכן כדאי להתעכב עליה‪.‬‬
‫ההדרכה מכוונת לדרך שבה נוח יותר לרוב התלמידים לעבוד באופן עצמאי‪:‬‬
‫‪‬‬
‫‪‬‬
‫‪( ∡C = 180 – 2‬זוויות חד‪-‬צדדיות בין ישרים מקבילים)‬
‫‪∡C1 = ∡C2 = 90 – ‬‬
‫‪∡AGC = 180 –  – (90 – ) = 90‬‬
‫‪1 2‬‬
‫כדאי להציע דרך נוספת‪ ,‬אלגנטית יותר‪.‬‬
‫נסמן‪:‬‬
‫‪∡ACG = ∡DCG =  ,∡BAG = ∡CAG = ‬‬
‫‪2 + 2 = 180‬‬
‫‪ +  = 90‬‬
‫‪∡AGC = 180 – ( + ) = 90‬‬
‫כדאי להציג גם דרך זו כיוון שהיא תשמש אותנו פעמים רבות בהמשך‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪110‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.3 251‬‬
‫‪E‬‬
‫‪B‬‬
‫‪1‬‬
‫לפניכם הדגל של מדינת טרינידד טובגו‪ .‬הדגל הוא בצורת מלבן שמורכב ממספר‬
‫‪A‬‬
‫‪2 1 2‬‬
‫צורות ג אומטריות (לצורך השאלה הניחו שהפסים הלבנים הינם ישרים חסרי עובי)‪.‬‬
‫נתון כי המשולש ‪ EBC‬הוא שווה‪-‬שוקיים‪ ,‬וכי ‪.AF ll EC‬‬
‫הוכיחו שגם המשולש ‪ ADF‬שווה‪-‬שוקיים‪.‬‬
‫‪C‬‬
‫‪D‬‬
‫‪F‬‬
‫עיקרי הפתרון‪:‬‬
‫אם המשולש ‪ EBC‬הוא שווה‪-‬שוקיים‪ ,‬אזי זוויות הבסיס שלו שוות ל ‪.45º -‬‬
‫‪⇒ ∡A1 = 45º ⇒ ∡A2= 45º ⇒ ∡F= 45º‬‬
‫סכום זוויות‬
‫במשולש‬
‫‪.4‬‬
‫‪ A‬זווית ישרה‬
‫במלבן‬
‫‪∡E1 = 45º ⇒ ∡E2 = 135º‬‬
‫סכום זוויות חד‪-‬‬
‫צדדיות בין מקבילים‬
‫זווית שטוחה‬
‫הישרים ‪ AB‬ו‪ CD -‬מקבילים זה לזה‪ CH .‬חוצה את הזווית ‪.∡ACD‬‬
‫א‪ .‬הוכיחו כי ‪ ACH‬הוא משולש שווה‪-‬שוקיים‪.‬‬
‫ב‪ .‬האם נתוני השאלה מאפשרים לקבוע אם ‪ ACH‬הוא שווה‪-‬צלעות?‬
‫ה מוטיב של חציית זווית שנוצרת בין החותך לאחד הישרים המקבילים‪ ,‬וזיהוי משולש‬
‫שווה‪-‬שוקיים חוזר בוואריאציות שונות בתרגילים רבים‪ ,‬ויחזור גם בתרגילים בפרק‬
‫המרובעים‪.‬‬
‫אחת המטרות של התרגיל היא לא להיתפס למראה עיניים‪.‬‬
‫ניתן להוכיח ש‪ ACH -‬משולש שווה‪-‬שוקיים‪ ,‬אולם לא ניתן להוכיח שהוא‬
‫שווה צלעות‪.‬‬
‫פתרון תרגיל ‪:4‬‬
‫א‪ .‬נסמן ב‪  -‬את חצאי הזווית ‪ .∡ACD‬גם ‪ ∡AHC = ‬ולכן‬
‫‪‬‬
‫המשולש שווה‪-‬שוקיים‪.‬‬
‫ב‪ .‬בשום מקום לא עשינו שימוש בגודלה של הזווית ‪ ,∡ACD‬ומכאן שאין לנו דרך‬
‫‪‬‬
‫‪‬‬
‫לקבוע את גודל הזוויות ולדעת אם ‪ ACH‬שווה‪-‬צלעות‪.‬‬
‫אם‪ ,‬למשל‪ ,∡ACD = 130 ,‬אז ‪∡HCA = ∡HCD = ∡AHC = 65‬‬
‫והמשולש אינו שווה‪-‬שוקיים‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪111‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫‪.5‬‬
‫‪‬‬
‫עמ' ‪251‬‬
‫‪.AP II BK‬‬
‫הקווים המרוסקים מחלקים את הזוויות המסומנות לשלושה חלקים שווים‪.‬‬
‫(ראו סרטוט)‪.‬‬
‫א‪ .‬מה מידת הזווית ‪ ∡G‬במרובע ‪?EFGH‬‬
‫ב‪ .‬מצאו זווית נוספת שנתוני השאלה מאפשרים לדעת את מידתה‪.‬‬
‫ג‪ .‬מצאו לפחות זווית אחת שנתוני השאלה אינם מאפשרים לדעת את מידתה‪.‬‬
‫הסבירו‪.‬‬
‫לתרגיל זה יש ישומון באתר‪ ,‬המאפשר המחשה טובה מה קורה כאשר משנים את מידות הזוויות‪ .‬אלו זוויות נשארות זהות‬
‫במידתן ואלו משתנות‪ .‬הישומון יסייע לתלמידים למצוא מענה לסעיפים ב ו‪-‬ג ולחפש נימוקים מתמטיים מדוע זה קורה‪.‬‬
‫א‪ .‬נסמן את שלושת החלקים השווים של ‪ ∡ABL‬ב‪ -‬‬
‫ואת שלושת החלקים השווים של ‪ ∡BAP‬ב‪. -‬‬
‫‪‬‬
‫‪‬‬
‫‪3 + 3 = 180‬‬
‫‪ +  = 60‬‬
‫‪‬‬
‫‪2 + 2 = 120‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪∡BGA = 180 – (2 + 2) = 60‬‬
‫ב‪ .‬נמצא לדוגמה את מידת הזווית ‪: ∡FEH‬‬
‫‪∡BEA = 180 – ( + ) = 120º‬‬
‫‪( ∡FEH = 120‬זוויות קדקודיות)‬
‫ג‪ .‬נתוני השאלה אינם מאפשרים לדעת את גודלן של הזוויות ‪ ‬ו‪ -‬אלא רק את סכומן‪ , +  = 60 ,‬ואת המידה של כל‬
‫זווית שהיא מכפלה של סכום זה‪ .‬למשל‪ ,‬לא ניתן גם לדעת את מידת הזווית ‪ ∡AHB‬כי )‪.∡AHB = 180 – ( + 2‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪112‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.6 252‬‬
‫המשולש ‪ ABC‬הוא שווה‪-‬שוקיים (‪ .)CA = CB‬הקטע ‪ CF‬הוא התיכון לבסיס‪ .‬הקטע‬
‫‪ EG‬מקביל לשוק ‪.∡ACB = 40 .BC‬‬
‫א‪ .‬הוכיחו כי המשולש ‪ ECD‬הוא שווה‪-‬שוקיים‪.‬‬
‫ב‪ .‬האם ניתן להוכיח שהמשולש ‪ ECD‬הוא שווה‪-‬שוקיים גם מבלי לדעת את מידת הזווית‬
‫‪?∡ACB‬‬
‫בפתרון תרגיל ‪ 6‬חישוב הזוויות בסעיף א מהווה הכנה לפתרון סעיף ב‪.‬‬
‫א‪ .‬נפתור בעזרת חשבון זוויות‪ ,‬ונקבל ‪.∡EDC = ∡FCB = 20‬‬
‫ב‪ .‬ניתן להוכיח שהמשולש ‪ ECD‬הוא שווה‪-‬שוקיים גם מבלי לדעת את מידת הזווית ‪.∡ACB‬‬
‫‪‬‬
‫‪‬‬
‫נסמן ‪.∡ACF = ∡FCB = ‬‬
‫‪( ∡EDC = ∡FCB = ‬זוויות מתחלפות בין הישרים המקבילים ‪ EG‬ו‪.)CB -‬‬
‫ומכאן שהמשולש ‪ ECD‬הוא שווה‪-‬שוקיים‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪113‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ –4‬כיצד נדע לזהות ישרים מקבילים? – עמ' ‪252‬‬
‫תעתועי ראיה תמיד מרתקים‬
‫את הדמיון‪ ,‬וכדאי להציע‬
‫לתלמידים לחפש תעתועים‬
‫נוספים באינטרנט‪.‬‬
‫שלוש התמונות מקורן בכתובת‬
‫‪http://www.neroyair.com/ti‬‬
‫‪me/pnay‬‬‫‪li/foll_ashlaya_optit/ashlay‬‬
‫‪a_optit_03.htm‬‬
‫בה ניתן למצוא תמונות רבות‬
‫נוספות‪.‬‬
‫תעתועי הראיה מוצגים כאן‬
‫לעורר צורך בדיון כיצד נזהה‬
‫שישרים הם מקבילים‪ ,‬והצגת‬
‫המשפטים ההפוכים לאלה‬
‫שהתלמידים כבר מכירים‪.‬‬
‫הקישור הבא מציג בניין במלבורן שבאוסטרליה שעיצובו מתעתע את הראייה‪:‬‬
‫‪. Digital Harbour Port 1010, in‬‬
‫‪Melbourne, Australia (photo by Chris‬‬
‫‪Lusby Taylor).‬‬
‫‪http://mathworld.wolfram.com/CafeWallIllusion.‬‬
‫‪html‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪114‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 5‬האם גם ההיפך נכון? – עמ' ‪253‬‬
‫מטרתה של פעילות ‪ 5‬היא לזרוע זרעים ראשונים לשני נושאים שילמדו לעומק בהמשך לימודי הגאומטריה בכיתה ט‪:‬‬
‫א‪ .‬משפטים ומשפטים הפוכים ‪ -‬למדנו בכיתה ז שאם ישר חותך שני ישרים אז כל שתי זוויות מתאימות שוות זו לזו‬
‫ומטרת הפעילות לבדוק האם גם ההיפך נכון? האם במצב בו ישר חותך שני ישרים אחרים נוצרות זוויות‬
‫שמתאימות שוות‪ ,‬ניתן להסיק שהישרים מקבילים? אנו עושים זאת כאן מבלי להדגיש יתר על המידה את מבנה‬
‫המשפט‪ .‬בפעילות ‪ 6‬אנו מחדדים את מבנה המשפט על‪-‬ידי הדגשה ועומדים על ההבדלים בין המשפטים על‪-‬ידי‬
‫שימוש בשני המשפטים להוכחה על אותו סרטוט‪ ,‬כאשר בכל פעם נתון מידע שונה וצריך להוכיח משהו אחר‪.‬‬
‫במטרה להדגיש את ההבדלים בין המשפטים בדרך נוספת‪ ,‬בתרגיל ‪ 1‬אנו נותנים הוכחה אשר בשלבים שונים‬
‫שלה נעשה שימוש במשפט אחד ומאוחר יותר במשפט ההפוך‪.‬‬
‫ב‪ .‬הוכחות בדרך‬
‫השלילה –‬
‫בהוכחות בדרך‬
‫השלילה נטפל‬
‫בצורה פורמלית‬
‫ומסודרת בפרק‬
‫המקבילית‪ ,‬אך‬
‫ההוכחה של‬
‫המשפט ההפוך‬
‫הינה למעשה‬
‫הוכחה בדרך‬
‫השלילה בצורה‬
‫רכה‪ .‬נעשה‬
‫שימוש בכלים של‬
‫הוכחה בדרך‬
‫השלילה מבלי‬
‫לומר זאת‬
‫מפורשות‪ .‬אנו‬
‫מניחים הנחה‬
‫שהישרים אינם‬
‫מקבילים ומקבלים‬
‫סתירה – מצב‬
‫בלתי אפשרי בו‬
‫סכום זוויות‬
‫במשולש אינו‬
‫‪ .180º‬ההוכחה מאוד אינטואיטיבית ולכן בחרנו בדרך זו‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪115‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫לבחירתכם שלוש אפשרויות להוראה של פעילות ‪:5‬‬
‫‪‬‬
‫מורים שמעוניינים‪ ,‬יכולים לדחות את ההוכחה עד אשר הנושא ילמד בצורה מסודרת ולהציג את הפעילות‬
‫במסגרת הוראת הנושא‪ :‬הוכחות בדרך השלילה‪.‬‬
‫‪ ‬הצגת הפעילות כפי שהיא מופיעה בספר‪ ,‬מבלי להתעמק במבנה של הוכחות בדרך השלילה‪.‬‬
‫‪ ‬התעמקות במבנה ההוכחה בדרך השלילה באמצעות הטבלה הבאה‪ ,‬כמעגל ראשון בספירלת הלמידה של‬
‫הוכחות בדרך השלילה (מתאים במיוחד לקבוצות של תלמידים מצטיינים)‪.‬‬
‫הערה חשובה‪ :‬הצגת מבנה ההוכחה בדרך השלילה כפי שהיא מופיעה בטבלה למטה‪ ,‬נועדה לשלוש מטרות‪:‬‬
‫‪.1‬‬
‫הפירוק של ההוכחה לשלבים עוזר להבין את תפקידו של כל מהלך‪ ,‬ויחזור על עצמו בהמשך השנה להוכחת משפטים‬
‫אחרים בדרך זו‪.‬‬
‫‪.2‬‬
‫לצורך השוואה עם הוכחות אחרות בדרך השלילה‪ ,‬בעת הוראת הנושא בהמשך השנה‪ .‬ייתכן ויהיו מורים שבזמן שילמדו‬
‫הוכחות בדרך השלילה אחרות‪ ,‬ירצו לחזור להוכחה זו לצורך השוואה‪ .‬טבלה זו תסייע להם‪.‬‬
‫‪ .3‬להוראה בכיתות חזקות במיוחד ‪ .‬אנו מאמינים כי במרבית הכיתות יתאים לדחות את הטיפול בהוכחות בדרך השלילה‬
‫לשלב מאוחר יותר בשנת הלימודים‪ ,‬אך לקבוצות מצטיינות ניתן להקדים את הוראת הנושא‪.‬‬
‫מבנה של הוכחה בדרך השלילה –‬
‫במקרה של "אם ישר חותך שני ישרים אחרים ונוצרות זוויות מתאימות שוות אז הישרים מקבילים"‬
‫שלבים בהוכחת המשפט ההפוך‬
‫שלבים בהוכחה בדרך השלילה‬
‫‪ .1‬חלוקה דיכוטומית של כל האפשרויות (תוצאה א או תוצאה ב)‬
‫הישרים מקבילים או הישרים חותכים זה את זה‪.‬‬
‫‪ .2‬בירור של השאלה‪:‬‬
‫מה היה קורה אילו היתה מתקיימת תוצאה ב?‬
‫אם הישרים חותכים זה את זה‪ ,‬קיימת נקודת מפגש‬
‫ביניהם ונוצר משולש‪ .‬חשבון הזוויות מראה כאילו סכום‬
‫הזוויות במשולש גדול מ‪.180º -‬‬
‫‪ .3‬תוך כדי הבירור מתבהרת תוצאה הכרחית שעומדת בסתירה‬
‫לנתון או לעובדה ידועה‬
‫הנחה כזאת מובילה למסקנה בלתי אפשרית‪ ,‬כיוון‬
‫שבכל משולש סכום הזוויות שווה ל‪!180º -‬‬
‫‪ .4‬הסתירה שהתבהרה שוללת את תוצאה ב‬
‫לא ייתכן שהישרים חותכים זה את זה‪.‬‬
‫‪ .5‬משלילת האפשרות האחרת נותרת אפשרות יחידה‬
‫והיא קיומה של תוצאה א‪.‬‬
‫מסקנה‪ :‬הישרים מקבילים‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪116‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫הצעה לדרך הפעלה בכיתה‪:‬‬
‫הצגת כל שורה בטבלה בהדרגה‪ ,‬כאשר המורה מציע את תוכן העמודה הראשונה והתלמידים צריכים להציע את תוכן‬
‫העמודה השנייה‪.‬‬
‫לדוגמה‪ :‬יש לנו חלוקה דיכוטומית של כל האפשרויות (תוצאה א או תוצאה ב)‪ .‬הציעו אלו שתי תוצאות אפשרויות ייתכנו‬
‫במקרה שלנו?‬
‫חזרה על מבנה קבוע בעת ניתוח הוכחות בדרך השלילה תסייע בעתיד‪ ,‬עם ריבוי המקרים‪ ,‬לראות את המבנה הכללי של‬
‫הוכחה בדרך השלילה ועל‪ -‬ידי כך נסייע לתלמידים להבין או אפילו לבנות הוכחות מסוג זה באופן עצמאי במקרים שונים‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪117‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תרגילים – עמ' ‪256 – 254‬‬
‫מטרת תרגיל ‪ 7‬היא להסב את תשומת לב התלמידים שכאשר אנו מזהים זוויות שנוצרות בין מקבילים וישר שחותך אותם‪,‬‬
‫חשוב מאד לציין מיהם הישרים המקבילים‪ .‬חלק מהתלמידים מיישמים את המשפטים על ישרים מקבילים שנחתכים על‪-‬ידי‬
‫ישר שלישי גם במצבים בהם הישרים הנחתכים אינם מקבילים‪ ,‬או כאשר אין להם דרך לקבוע אם הישרים מקבילים או לא‪.‬‬
‫מטרת תרגיל זה לחדד את הנקודה הזו ולכן מומלץ לדון בפתרון התרגיל בכיתה‪ .‬התרגיל גם מאפשר להתייחס למראה עיניים‬
‫שלעיתים מטעה מאוד‪ .‬גם תרגיל ‪ 10‬מטפל בהיבט זה‪.‬‬
‫עמ' ‪254‬‬
‫‪.7‬‬
‫בכל אחד מן הסעיפים זהו ישרים מקבילים‪ ,‬והסבירו לפי מה קבעתם שהישרים מקבילים‪.‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪c‬‬
‫‪d‬‬
‫‪k‬‬
‫‪m‬‬
‫‪a‬‬
‫‪p‬‬
‫‪b‬‬
‫‪g‬‬
‫הישרים ‪ m II k‬כי יש שתי זוויות מתאימות שוות‬
‫ומידתן היא ‪. 38º‬‬
‫הישרים ‪ p‬ו‪ g -‬אינם מקבילים כי הזוויות‬
‫המתאימות אינן שוות במידתן‪ .‬אחת היא ‪37º‬‬
‫ושנייה ‪ .38º‬בגלל הפרש של מעלה אחת הישרים‬
‫עלולים להראות מקבילים‪.‬‬
‫הישרים ‪ a II b‬כי יש שתי זוויות מתאימות שוות‬
‫ומידתן היא ‪. 143º‬‬
‫‪0‬‬
‫‪ , ∡C1=37‬משלימה לזווית שטוחה‪.‬‬
‫הישרים ‪ c II d‬כי יש שתי זוויות מתאימות שוות‬
‫ומידתן היא ‪. 37º‬‬
‫‪.8‬‬
‫הישר ‪ EF‬חותך את הישרים ‪ AB‬ו‪ .CD -‬נתון כי ‪.∡LKD = ∡ALK = ‬‬
‫א‪ .‬הסבירו מדוע ‪.∡ELB = ∡ALK‬‬
‫זוויות קדקודיות‬
‫ב‪ .‬הסבירו מדוע ‪.∡ELB = ∡LKD‬‬
‫שני גדלים השווים לגודל שלישי שווים ביניהם‪.‬‬
‫ג‪ .‬הסבירו כיצד ניתן להסיק מהשוויון האחרון שהישרים ‪ AB‬ו‪ CD -‬מקבילים‪.‬‬
‫באמצעות סעיפים א ו‪ -‬ב הוכחנו כי זוויות מתאימות שוות ולכן ‪.AB II CD‬‬
‫בתרגיל זה הוכחנו משפט‪:‬‬
‫אם הישר החותך שני ישרים יוצר זוויות מתחלפות שוות‪ ,‬אז הישרים הם מקבילים‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪118‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫‪.9‬‬
‫הוכיחו את המשפט‪:‬‬
‫אם הישר החותך שני ישרים יוצר זוויות חד‪-‬צדדיות שסכומן ‪ 180‬אז הישרים הם‬
‫מקבילים‪.‬‬
‫מטרת התרגיל לאפשר לתלמידים להוכיח משפט פשוט יחסית הנתון בצורה מילולית‬
‫היעזרו במשפטים קודמים להוכחת‬
‫המשפט בתרגיל ‪.9‬‬
‫בלבד ללא סרטוט מלווה‪.‬‬
‫לתלמידים שמתקשים להוכיח את המקרה הכללי ללא סרטוט‪ ,‬ניתן לתת סרטוט עם ערכים כפי שמודגם בסרטוט תחתון‪.‬‬
‫נתון‪  + α = 180º :‬צ"ל‪AG II BM :‬‬
‫‪K‬‬
‫הוכחה‪:‬‬
‫‪G‬‬
‫‪P‬‬
‫טענה‬
‫נימוק‬
‫‪α = 180º - β‬‬
‫נתון ‪ + α = 180º‬‬
‫‪∡PLM = 180º - ‬‬
‫זווית שטוחה‪.‬‬
‫‪∡PLM = α‬‬
‫שני גדלים השווים לגודל שלישי שווים ביניהם‪.‬‬
‫‪∡KPT = α‬‬
‫זוויות קדקודיות‪.‬‬
‫‪∡KPT = ∡PLM‬‬
‫שני גדלים השווים לגודל שלישי שווים ביניהם‪.‬‬
‫‪AG II BM‬‬
‫לפי המשפט‪ :‬אם ישר חותך זוג ישרים אחרים ונוצרות זוויות‬
‫‪α‬‬
‫‪M‬‬
‫‪β‬‬
‫‪A‬‬
‫‪L‬‬
‫‪C‬‬
‫‪B‬‬
‫‪41.66º‬‬
‫‪138.34º‬‬
‫מתאימות שוות אז הישרים מקבילים‪.‬‬
‫מ‪.‬ש‪.‬ל‬
‫בשלב זה מוצגות לתלמידים בצורה מאורגנת שלוש דרכים שונות בהן ניתן לוודא שישרים הינם מקבילים‪.‬‬
‫למדנו שלוש דרכים לוודא שישרים הם מקבילים (עמ' ‪:)255‬‬
‫מועדון הזוגות של ישרים מקבילים – אישור כניסה‬
‫כדי לאשר שזוג ישרים הם מקבילים‬
‫‪ .1‬הישרים יוצרים‪ ,‬עם ישר שלישי זוויות מתאימות שוות‪.‬‬
‫מספיק להראות שהם מקיימים‬
‫לפחות אחת הדרישות מהרשימה‬
‫משמאל‪.‬‬
‫או‬
‫‪ .2‬הישרים יוצרים‪ ,‬עם ישר שלישי זוויות מתחלפות שוות‪.‬‬
‫או‬
‫?‬
‫‪ .3‬הישרים יוצרים‪ ,‬עם ישר שלישי זוויות חד‪-‬צדדיות שסכומן ‪.180º‬‬
‫נשים לב‪ ,‬כי אם מתקיימת אחת הדרישות הישרים מקבילים ומכאן ניתן להסיק ששתי הדרישות האחרות מתקיימות גם הן‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪119‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.10 255‬‬
‫בכל אחד מהסעיפים נתונים שני ישרים ‪ a‬ו‪ ,b -‬קבעו האם הם מקבילים או לא‪ .‬נמקו את תשובתכם‪.‬‬
‫אם הישרים אינם מקבילים‪ ,‬באיזה צד יחתכו?‬
‫לתרגיל זה ייתכנו פתרונות בדרכים שונות‪ .‬נציג כאן את אחת הדרכים ובחלק מהמקרים נציין אפשרויות נוספות‪.‬‬
‫א‪.‬‬
‫‪A‬‬
‫ב‪.‬‬
‫‪a‬‬
‫‪50° 50°‬‬
‫‪135°‬‬
‫‪100°‬‬
‫‪a‬‬
‫‪α‬‬
‫‪α‬‬
‫‪b‬‬
‫‪46° ‬‬
‫‪b‬‬
‫נמצא את ערכה של הזווית המתחלפת (‪ )α‬או‬
‫המתאימה (‪ )‬ל ‪.135º -‬‬
‫‪.  = α =134 º‬‬
‫הזוויות המתחלפות (או המתאימות) אינן שוות ולכן‪,‬‬
‫הישרים אינם מקבילים‪.‬‬
‫הישרים עלולים להראות מקבילים כי ההפרש בין‬
‫הזוויות הוא מעלה אחת בלבד‪.‬‬
‫הישרים יחתכו בצד שמאל כי סכום הזוויות החד‪-‬‬
‫צדדיות שווה ל‪ 179º -‬ומכאן שיתקבל משולש עם‬
‫זווית בת מעלה אחת‪.‬‬
‫יש דרכים נוספות להוכיח שהישרים אינם מקבילים‪.‬‬
‫נמצא את ערכה של הזווית ‪ α‬המתחלפת עם ‪.100º‬‬
‫קיבלנו זוויות מתחלפות שוות ולכן‪ ,‬הישרים ‪.a II b‬‬
‫יש דרכים נוספות להוכיח שהישרים מקבילים‪ ,‬לדוגמה‬
‫על‪-‬ידי זוויות חד‪-‬צדדיות‪.‬‬
‫ד‪.‬‬
‫ג‪.‬‬
‫‪118°‬‬
‫‪a‬‬
‫‪b‬‬
‫‪a‬‬
‫‪α‬‬
‫‪45°‬‬
‫‪60°‬‬
‫‪b‬‬
‫‪30°‬‬
‫‪120°‬‬
‫‪60°‬‬
‫סכום הזוויות החד‪-‬צדדיות הוא ‪ 180º‬ולכן‬
‫הישרים ‪.a II b‬‬
‫קיימות כמובן אפשרויות נוספות‪ ,‬לדוגמה למצוא את‬
‫הזווית המתחלפת עם ‪ 60º‬ועוד‪.‬‬
‫הזווית ‪ 30º‬היא סוג של מסיח‪ .‬תלמידים עלולים‬
‫להשתמש בנתון זה ונתון שצריך להוכיח יחד ולהניח‬
‫שהזווית המתאימה שווה גם היא ‪.30º‬‬
‫עם זאת‪ ,‬ייתכן שיהיו תלמידים שישתמשו בנתון בדרך‬
‫נכונה אך ארוכה‪.‬‬
‫נמצא את ערכה של הזווית ‪ α‬המתאימה לזווית‬
‫‪ .60º‬מחישוב זוויות נקבל ‪ .62º‬מכאן נסיק‬
‫שזוויות מתאימות לא שוות ולכן הישרים אינם‬
‫מקבילים‪.‬‬
‫הישרים יחתכו בצד שמאל כי סכום הזוויות בצד‬
‫ימין הוא ‪ 182º‬ולא ייתכן שיתקבל משולש שסכום‬
‫זוויותיו מעל ‪.180º‬‬
‫ניתן כמובן גם למצוא את ערכה של הזווית‬
‫המתאימה ל‪ 118º-‬ודרכים מגוונות נוספות‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪120‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.11 256‬‬
‫לפניכם דגל של נפאל‪ .‬בשונה מרוב מדינות העולם‪ ,‬לדגל של נפאל אין צורה מלבנית‪.‬‬
‫‪A‬‬
‫א‪ .‬אילו זוויות צריך למדוד כדי לדעת האם הקטעים ‪ AB‬ו‪CD -‬‬
‫בדגל מקבילים זה לזה?‬
‫ניתן להשוות בין זוויות מתחלפות‪ α :‬ו‪ δ -‬כדי לקבוע האם ‪ AB‬מקביל ל‪.CD -‬‬
‫‪α‬‬
‫‪δC‬‬
‫‪B‬‬
‫ב‪ .‬אילו זוויות צריך למדוד כדי לדעת האם הקטעים ‪ CB‬ו‪ED -‬‬
‫‪‬‬
‫בדגל מקבילים זה לזה?‬
‫‪D‬‬
‫ניתן להשוות בין זוויות מתחלפות‪  :‬ו‪ δ -‬כדי לקבוע האם ‪ CB‬מקביל ל‪.ED -‬‬
‫‪.12‬‬
‫‪E‬‬
‫‪N‬‬
‫‪ SNOW‬הוא מלבן‪ .‬הנקודה ‪ K‬נמצאת על המשך ‪.SW‬‬
‫‪S‬‬
‫על‪-‬פי הנתונים בסרטוט הוכיחו‪:‬‬
‫‪67º‬‬
‫‪O‬‬
‫א‪.WN ll KO .‬‬
‫‪W‬‬
‫‪23º‬‬
‫ב‪ .‬המשולש ‪ ∆SOK‬הוא שווה‪-‬שוקיים‪.‬‬
‫‪K‬‬
‫א‪∡NWO = 90 – 67 = 23 .‬‬
‫‪( ∡NWO = ∡WOK = 23‬זוויות מתחלפות שוות)‬
‫ומכאן ‪WN ll KO‬‬
‫ב‪ .‬נוכיח כי ‪ SOW  KOW‬לפי משפט‬
‫‪.∡SOW = ∡NWO = 23‬‬
‫במשולש ‪ ∆SOK‬הקטע ‪ WO‬הוא חוצה זווית וגם גובה ומכאן שהמשולש שווה שוקיים‪.‬‬
‫‪D‬‬
‫‪F‬‬
‫‪.13‬‬
‫נתון‪.∡CEB = 55º ; ∡DEL = 65º ; ∡L1 = ∡L2 = ∡L3 :‬‬
‫‪H‬‬
‫קבעו האם הטענה נכונה או לא‪ ,‬על‪-‬פי הנתונים שבסרטוט‪.‬‬
‫נמקו את תשובתכם‪.‬‬
‫‪M‬‬
‫א‪∡KLE = ∡L1 .‬‬
‫כן‪.‬‬
‫ב‪.AB ll FG .‬‬
‫כן‪.‬‬
‫ג‪.CD ll KH .‬‬
‫לא‪.‬‬
‫‪A‬‬
‫‪2 3‬‬
‫‪L‬‬
‫‪1‬‬
‫‪E‬‬
‫‪K‬‬
‫‪B‬‬
‫‪C‬‬
‫‪G‬‬
‫ד‪ ∡BEL = ∡ELK .‬כן‪.‬‬
‫‪F‬‬
‫את כל המסקנות ניתן להסיק בעזרת חישוב הזוויות כפי שמופיע בסרטוט הבא‪:‬‬
‫בסעיף ג‪ ,‬יש זוג זוויות מתאימות לא שוות‪.‬‬
‫‪O‬‬
‫‪D‬‬
‫‪A‬‬
‫‪H‬‬
‫‪60‬‬
‫‪60‬‬
‫‪2 3 60‬‬
‫‪L 60 M‬‬
‫‪60‬‬
‫‪60‬‬
‫‪1‬‬
‫‪55‬‬
‫‪60‬‬
‫‪60‬‬
‫‪E‬‬
‫‪65‬‬
‫‪O‬‬
‫‪K‬‬
‫‪B‬‬
‫‪C‬‬
‫‪G‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪121‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.14 256‬‬
‫בסרטוט נתון‪.∡1 = ∡2 :‬‬
‫על‪-‬פי הנתונים בסרטוט קבעו אילו מבין הטענות שלפניכם נכונות ואילו לא‪ .‬נמקו את תשובותיכם‪.‬‬
‫חשוב לברר עם התלמידים מה ניתן להסיק מהנתון? אילו ישרים מקבילים?‬
‫א‪3 .‬‬
‫‪4‬‬
‫‪ .‬מהנתון‪ ,‬הישרים ‪ k II m‬ולכן‪ ,‬זוויות‬
‫‪b‬‬
‫מתאימות בין ישרים מקבילים‪.‬‬
‫ב‪6 .‬‬
‫‪4‬‬
‫‪ .‬לא ידוע‪.‬‬
‫ג‪6 .‬‬
‫‪5‬‬
‫‪ .‬לא ידוע‪.‬‬
‫ד‪7 .‬‬
‫‪5‬‬
‫‪ .‬מהנתון‪ ,‬הישרים ‪ k II m‬ולכן‪ ,‬זוויות‬
‫‪3‬‬
‫‪a‬‬
‫‪m‬‬
‫‪8‬‬
‫‪7‬‬
‫‪1‬‬
‫‪6‬‬
‫‪2‬‬
‫‪5‬‬
‫‪4‬‬
‫‪k‬‬
‫מתחלפות בין ישרים מקבילים‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪122‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 6‬על משפטים ומשפטים‬
‫הפוכים – עמ' ‪257‬‬
‫חלק מהתלמידים‪ ,‬בפרט בעת צעדיהם הראשונים‬
‫בגאומטריה דדוקטיבית‪ ,‬מתקשים להבחין בין‬
‫משפט לבין משפט הפוך‪ ,‬ובין מה שנתון בשאלה‬
‫לבין מה שהם מתבקשים להוכיח‪ .‬בפרט קשה‬
‫להם להבחין אם הם מנמקים טענה על סמך‬
‫משפט כלשהו או על סמך המשפט ההפוך לו‪.‬‬
‫המטרה של פעילות ‪ 6‬ושל התרגילים שבעקבותיה‬
‫היא להציג את המושג משפט הפוך ולעזור‬
‫לתלמידים להבחין מתי נידרש שימוש במשפט‬
‫ומתי במשפט הפוך לו‪.‬‬
‫העיסוק במשפטים הפוכים יימשך גם בפרקים‬
‫הבאים‪.‬‬
‫עד כה פגשנו במשפט ובמשפט ההפוך לו במשולש‬
‫שווה‪-‬שוקיים‪ ,‬מקרה בו שני המשפטים נכונים‪:‬‬
‫• במשולש שווה‪-‬שוקיים זוויות הבסיס שוות‪.‬‬
‫• אם למשולש יש שתי זוויות שוות‪ ,‬אז הצלעות‬
‫מולן שוות‪.‬‬
‫התלמידים מכירים גם משפטים ומשפטים הפוכים מלימודי האלגברה‪ .‬הדוגמאות המובאות הן מבית הספר היסודי‪ ,‬בנושא‬
‫סימני ההתחלקות‪ .‬המקרה הראשון מציג מצב בו שני המשפטים נכונים‪ :‬אם סכום הספרות של מספר מתחלק ב‪,3 -‬‬
‫המספר מתחלק ב‪ .3 -‬והמשפט ההפוך לו‪ :‬אם מספר מתחלק ב‪ ,3 -‬אז סכום ספרותיו מתחלק ב‪ .3 -‬המקרה השני מציג‬
‫מצב בו המשפט מתקיים‪ ,‬אך ההפוך לו‪ ,‬אינו נכון‪:‬‬
‫אם מספר מתחלק ב‪ 6 -‬אז סכום ספרותיו מתחלק ב‪ .3 -‬אבל המשפט ההפוך אינו נכון‪ :‬אם סכום הספרות מחלק ב‪ ,3-‬אז‬
‫המספר מתחלק ב‪ .6 -‬המספר חייב להיות גם זוגי‪ .‬חשוב להציג את שני המקרים ולדון בהם‪.‬‬
‫להלן התשובות לפעילות‪:‬‬
‫‪ .1‬בסרטוט שלפניכם הישר ‪ CH‬חוצה‬
‫‪ .2‬בסרטוט שלפניכם הישר ‪ CH‬חוצה את הזווית ‪.∡ACD‬‬
‫את הזווית ‪.∡ACD‬‬
‫נתון כי ‪.AC = AH‬‬
‫נתון כי ‪.AB II CD‬‬
‫הוכיחו כי ‪.AC = AH‬‬
‫הוכיחו כי ‪.AB II CD‬‬
‫כאן דרוש המשפט השני כדי להוכיח שהישרים מקבילים‪.‬‬
‫כאן דרוש המשפט הראשון‪.‬‬
‫אם ידוע שהישרים מקבילים אז אפשר‬
‫להסיק שהזוויות המתאימות שוות‪.‬‬
‫אם ידוע שהזוויות המתאימות הן שוות אז אפשר להסיק‬
‫שהישרים מקבילים‪.‬‬
‫בדרך הצגה זו באמצעות צבע אנו מבליטים לתלמידים מה נתון ולאיזה חלק במשפט הוא מתייחס ומה צריך להוכיח ולאיזה‬
‫חלק במשפט הוא מתייחס‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪123‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תרגילים – עמ' ‪260 – 258‬‬
‫בתרגיל ‪ 15‬אנו מוכיחים משפט הנחוץ לנו לבנייה באמצעות סרגל ומחוגה של ישר מקביל לישר נתון‪ .‬תרגיל ההוכחה מופיע‬
‫כאן כי הוא עושה שימוש במשפט ההפוך‪ :‬אם הז וויות המתאימות הן שוות אז הישרים מקבילים‪.‬‬
‫עמ' ‪.15 258‬‬
‫הוכיחו את המשפט‪ :‬ישרים שמאונכים לאותו ישר הם ישרים מקבילים‪.‬‬
‫תרגיל ‪ 16‬חשוב ושימושי מאד בעיקר בפרקים הבאים‪ ,‬כי במהלכו מוכחים את המשפט‪ :‬אם שני ישרים שונים מקבילים‬
‫לישר שלישי אז הם מקבילים זה לזה‪.‬‬
‫‪.16‬‬
‫ידוע כי ‪ a ll b‬וגם ‪.c ll a‬‬
‫צריך להוכיח כי ‪c ll b‬‬
‫בניית עזר‪ :‬נעביר ישר רביעי החותך את שלושת הישרים‪.‬‬
‫השלימו את הנימוקים בהוכחה‪:‬‬
‫טענה‬
‫נימוק‬
‫‪∡GTJ = ∡TKL‬‬
‫זוויות מתאימות בין המקבילים ‪ a‬ו‪.b -‬‬
‫‪∡GTJ = ∡KMN‬‬
‫זוויות מתאימות בין המקבילים ‪ a‬ו‪.c -‬‬
‫‪∡KMN = ∡TKL‬‬
‫שני גדלים השווים לגודל שלישי שווים ביניהם‪.‬‬
‫‪c ll b‬‬
‫לפי המשפט‪ :‬אם חותך של שני ישרים יוצר זוויות‬
‫מתאימות שוות אז הישרים הם מקבילים‪.‬‬
‫בתרגיל זה הוכחתם משפט‪:‬‬
‫אם שני ישרים שונים מקבילים לישר שלישי אז הם מקבילים זה לזה‪.‬‬
‫תרגילים ‪ 17‬ו‪ 18 -‬עושים שימוש בשני משפטים הפוכים על זוויות מתחלפות‪ .‬בכל אחד מהם‪:‬‬
‫בשלב הראשון של ההוכחה נתון ששני ישרים מקבילים ומסיקים שזוויות מתחלפות שוות‪.‬‬
‫בשלב השני יודעים שזוויות מתחלפות שוות ומסיקים שהישרים מקבילים‪.‬‬
‫בתרגיל ‪ 17‬מידות הזוויות נתונות במספרים ולכן תרגיל זה מטפל במקרה פרטי‪.‬‬
‫בתרגיל ‪ 18‬מידות הזוויות נתונות במשתנים ולכן תרגיל זה מטפל במקרה כללי‪.‬‬
‫אפשר לראות בתרגיל ‪ 17‬הכנה לתרגיל ‪.18‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪124‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫‪‬‬
‫‪.17‬‬
‫עמ' ‪258‬‬
‫בסרטוט שלפניכם‪.∡DCM = 50º ,∡AMC = 82º ,∡BAM = 32º :‬‬
‫‪B‬‬
‫צריך להראות‪.AB ll CD :‬‬
‫‪A‬‬
‫הדרכה‪ :‬דרך הנקודה ‪ M‬העבירו ישר ‪ EF‬כך ש‪.AB ll EF -‬‬
‫‪M‬‬
‫שימו לב‪ ,‬בשלב זה לא ניתן לקבוע ש‪ EF -‬מקביל גם ל‪.CD -‬‬
‫א‪ .‬מצאו את מידת הזווית ‪ .∡AME‬באיזה משפט השתמשתם?‬
‫‪D‬‬
‫‪ ∡AME = 32º‬על‪-‬פי המשפט אם ישרים הם מקבילים אז ישר שחותך אותם‬
‫‪C‬‬
‫‪A‬‬
‫‪B‬‬
‫יוצר זוויות מתחלפות שוות‪.‬‬
‫ב‪ .‬מצאו את מידת הזווית ‪.∡EMC‬‬
‫‪M‬‬
‫‪82 – 32 = 50‬‬
‫‪E‬‬
‫‪F‬‬
‫ג‪ .‬איזו מסקנה ניתן להסיק לגבי הישרים ‪ CD‬ו‪?EF -‬‬
‫נמקו על‪-‬פי משפט מתאים‪.‬‬
‫‪C‬‬
‫‪D‬‬
‫הישרים מקבילים לפי המשפט‪ :‬אם חותך של שני ישרים יוצר זוויות‬
‫מתחלפות שוות אז הישרים מקבילים‪.‬‬
‫בתרגיל זה השתמשנו בשני משפטים הפוכים על זוויות מתחלפות‪.‬‬
‫לתרגיל זה יישומון באתר‪:‬‬
‫גלו קשרים בין הזוויות _יישומון לתרגיל ‪17‬‬
‫בסעיף א היה נתון ששני ישרים מקבילים )‪ (AB ll EF‬והסקנו שזוויות מתחלפות שוות‪.‬‬
‫בסעיף ג מצאנו שזוויות מתחלפות שוות והסקנו מסקנה שהישרים מקבילים )‪.(EF ll CD‬‬
‫עמ' ‪.18 259‬‬
‫על‪-‬פי הנתונים בסרטוט‪ ,‬הוכיחו שהישרים ‪ EG‬ו‪ HK -‬מקבילים זה לזה‪.‬‬
‫‪E‬‬
‫‪G‬‬
‫‪β‬‬
‫הדרכה‪ :‬דרך הנקודה ‪ F‬העבירו ישר ‪ AB‬כך ש‪ .AB ll EG -‬שימו לב‪ ,‬בשלב זה‬
‫‪F‬‬
‫לא ניתן לקבוע ש‪ AB -‬מקביל גם ל‪.HK -‬‬
‫‪α+β‬‬
‫‪α‬‬
‫‪K‬‬
‫א‪ .‬הביעו את מידת הזווית ‪ ∡EFB‬באמצעות ‪ ‬ו‪/‬או ‪.‬‬
‫‪H‬‬
‫באיזה משפט השתמשתם?‬
‫‪ ∡EFB = ‬על‪-‬פי המשפט אם ישרים הם מקבילים אז ישר שחותך אותם יוצר‬
‫‪G‬‬
‫‪β‬‬
‫זוויות מתחלפות שוות‪.‬‬
‫‪A‬‬
‫ב‪ .‬הביעו באמצעות ‪ ‬ו‪/‬או ‪ ‬את מידת הזווית ‪.∡BFH‬‬
‫‪E‬‬
‫‪F‬‬
‫‪α+β‬‬
‫‪B‬‬
‫‪α‬‬
‫‪∡BFH = ( + ) –  = ‬‬
‫‪K‬‬
‫‪H‬‬
‫ג‪ .‬איזו מסקנה ניתן להסיק לגבי הישרים ‪ AB‬ו‪?HK -‬‬
‫נמקו על‪-‬פי משפט מתאים‪.‬‬
‫הישרים מקבילים לפי המשפט‪ :‬אם חותך של שני ישרים יוצר זוויות מתחלפות שוות אז הישרים מקבילים‪.‬‬
‫בתרגיל זה השתמשנו בשני משפטים על זוויות מתחלפות‪ .‬בעמוד הבא מוצגת דרך נוספת לפתרון התרגיל‪.‬‬
‫בסעיף א היה נתון ששני ישרים מקבילים )‪ (AB ll EG‬והסקנו שזוויות מתחלפות שוות‪.‬‬
‫בסעיף ג ידענו שזוויות מתחלפות שוות והסקנו מסקנה שהישרים מקבילים )‪.(AB ll HK‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪125‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫ואפשר גם אחרת‪...‬‬
‫נאריך את ‪ EF‬מעבר ל‪ T .F -‬נקודת החיתוך של המשך ‪ EF‬עם ‪HK‬‬
‫‪E‬‬
‫‪G‬‬
‫‪β‬‬
‫ונראה כי ‪ ∡HKF = ‬על‪-‬פי המשפט על זווית חיצונית במשולש‪.‬‬
‫‪F‬‬
‫למרות שדרך זו פשוטה יותר‪ ,‬כיוונו לפתרון שבו מעבירים מקביל דרך ‪F‬‬
‫כדי לעשות שימוש דו כיווני במשפטים על זוויות מתחלפות‪.‬‬
‫‪α+β‬‬
‫‪α‬‬
‫‪T K‬‬
‫‪H‬‬
‫פעילות ‪ – 7‬בניית ישרים מקבילים – עמ' ‪259‬‬
‫מטרת פעילות ‪ 7‬היא ללמד לבנות‬
‫ישרים מקבילים באמצעות סרגל‬
‫ומחוגה‪ .‬בתכנון הבנייה נעזרנו‬
‫במשפט שישרים שמאונכים לאותו‬
‫ישר הם ישרים מקבילים‪ .‬ניתן‬
‫לזהות ישרים מקבילים גם‬
‫באמצעות זוויות מתאימות שוות‬
‫שאינן ישרות או זוויות מתחלפות‬
‫שוות שאינן ישרות‪ .‬אך בחרנו‬
‫להיעזר באנכים משיקולי נוחיות‪:‬‬
‫יותר קל לבנות אנך מאשר להעתיק‬
‫זווית‪.‬‬
‫למורים המעוניינים להציג את כל‬
‫שלושת הדרכים להעברת ישר‬
‫מקביל דרך נקודה‪ :‬באמצעות זוויות מתאימות שוות‪ ,‬באמצעות זוויות מתחלפות או באמצעות המשפט‪ ,‬הצענו פעילות‬
‫נוספת המופיעה בהמשך‪.‬‬
‫נציין כי בסביבות ממוחשבת יש לרוב כלי באמצעותו מסרטטים ישרים מקבילים‪.‬‬
‫הצעה להפעלה בכיתה‬
‫בעמוד הבא מצורף דף עבודה לתלמידים ובו הנחיות לבניית מקביל לישר נתון בשלוש דרכים שונות‪.‬‬
‫להלן כמה אפשרויות לעריכת הפעילות בכיתה‪:‬‬
‫א‪ .‬חלוקת הכיתה לשלשות‪ .‬כל תלמיד בשלשה בונה מקביל לישר נתון בדרך שונה‪ .‬התלמידים‪ ,‬בתום הבנייה‪,‬‬
‫מסבירים זה לזה מדוע הדרך בה בנו יוצרת ישרים המקבילים זה לזה‪ .‬הקבוצה תדון בשאלה‪ :‬האם כל התלמידים‬
‫בקבוצה קיבלו את אותו ישר? את תוצאות העבודה בקבוצה כדאי לסכם בדיון כיתתי משותף‪.‬‬
‫ב‪.‬‬
‫מתן דף העבודה כשיעורי בית‪ ,‬כהכנה לקראת הדיון הכיתתי בהצדקת כל אחת מדרכי הבנייה ודיון האם בכל‬
‫הדרכים מתקבל אותו ישר‪.‬‬
‫ג‪.‬‬
‫להסתפק בפעילות המופיעה בספר לתלמיד ולדון בכיתה ללא התנסות‪ ,‬אלו דרכים נוספות ייתכנו לבניית מקביל‬
‫לישר נתון‪ ,‬מדוע כל הדרכים נכונות ומדוע בכולן מתקבל אותו ישר‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪126‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫סיכום דף העבודה‬
‫הכרנו שלוש דרכים להעביר לישר ‪ m‬מקביל דרך הנקודה ‪. P‬‬
‫האם בנינו שלושה ישרים שונים שעוברים דרך ‪ P‬ומקבילים ל‪ ? m -‬התשובה כמובן שלילית!‬
‫דרך נקודה ניתן להעביר מקביל אחד לישר נתון‪ ,‬ולכן הישרים ‪ ,v ,m‬ו‪ t -‬שקיבלנו בדרכים השונות הם למעשה אותו ישר!‬
‫בסיפור ההיסטורי אנו מתייחסים לכך כי דרך נקודה מחוץ לישר עובר מקביל יחיד לישר נתון‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪127‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫דף עבודה – בניית מקביל לישר נתון דרך נקודה נתונה בשלוש דרכים‬
‫‪P‬‬
‫נתונים הישר ‪ m‬והנקודה ‪.P‬‬
‫כיצד נוכל להעביר דרך הנקודה ‪ P‬ישר מקביל לישר ‪? m‬‬
‫לפניכם שלוש דרכים לעשות זאת‪.‬‬
‫דרך א‪ :‬העברת מקביל באמצעות זוויות מתאימות שוות‬
‫‪m‬‬
‫‪R‬‬
‫‪P‬‬
‫‪Q‬‬
‫‪P‬‬
‫‪R‬‬
‫‪P‬‬
‫‪Q‬‬
‫‪C‬‬
‫‪C‬‬
‫‪C‬‬
‫‪B‬‬
‫‪B‬‬
‫‪m‬‬
‫שלב א‬
‫‪ ‬דרך הנקודה ‪ P‬נעביר ישר‬
‫‪ k‬החותך את הישר ‪.m‬‬
‫‪ ‬נסמן את נקודת החיתוך של‬
‫שני הישרים ב‪.A -‬‬
‫‪ ‬נחוג קשת שמרכזה ‪A‬‬
‫החותכת את שני הישרים‪.‬‬
‫‪ ‬נסמן ב‪ B -‬את נקודת‬
‫החיתוך של הקשת עם ‪m‬‬
‫‪ ‬וב‪ C -‬את נקודת החיתוך‬
‫שלה עם ‪.k‬‬
‫‪B‬‬
‫‪m‬‬
‫‪A‬‬
‫‪k‬‬
‫‪s‬‬
‫‪m‬‬
‫‪A‬‬
‫‪k‬‬
‫‪k‬‬
‫שלב ג‬
‫נעביר ישר דרך ‪ P‬ו‪Q -‬‬
‫ונסמנו ב‪.m -‬‬
‫שלב ב‬
‫‪ ‬נחוג קשת שמרכזה ‪P‬‬
‫ברדיוס ‪.AC‬‬
‫‪ ‬נסמן ב‪ R -‬את נקודת‬
‫החיתוך של הקשת עם ‪k‬‬
‫‪ ‬נחוג קשת שמרכזה ‪R‬‬
‫ברדיוס ‪.BC‬‬
‫‪ ‬נסמן ב‪ Q -‬את נקודת‬
‫החיתוך של שני הישרים‪.‬‬
‫הישר ‪ s‬העובר דרך‬
‫הנקודות ‪ P‬ו‪ Q -‬הוא‬
‫המקביל המבוקש‪.‬‬
‫‪R‬‬
‫א‪ .‬בצעו את כל צעדי הבנייה‪.‬‬
‫‪Q‬‬
‫‪P‬‬
‫ב‪ .‬הוסיפו לסרטוט את המשולשים ‪ ABC‬ו‪PQR -‬‬
‫שעוזרים להבין ולהצדיק את הבנייה‪.‬‬
‫‪s‬‬
‫‪C‬‬
‫ג‪ .‬הוכיחו‪.ABC  PQR :‬‬
‫‪B‬‬
‫ד‪ .‬הסבירו מדוע ‪.∡CAB = ∡RPQ‬‬
‫‪A‬‬
‫ה‪ .‬הסבירו מדוע הישרים ‪ s‬ו‪ k -‬מקבילים‪.‬‬
‫‪m‬‬
‫‪k‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪128‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫דרך ב‪ :‬העברת מקביל לישר באמצעות בניית זוויות מתחלפות שוות‬
‫האיורים הבאים מתארים בניה ששלביה דומים לשלבים של דרך א‪ .‬בניה זו מתבססת על יצירת זוויות מתחלפות‬
‫שוות בין שני ישרים וישר שלישי החותך אותם‪.‬‬
‫‪P‬‬
‫‪P‬‬
‫‪P‬‬
‫‪H‬‬
‫‪H‬‬
‫‪G‬‬
‫‪G‬‬
‫‪C‬‬
‫‪C‬‬
‫‪C‬‬
‫‪A‬‬
‫‪B‬‬
‫‪B‬‬
‫‪m‬‬
‫‪m‬‬
‫‪k‬‬
‫שלב א‬
‫‪v‬‬
‫‪B‬‬
‫‪m‬‬
‫‪A‬‬
‫‪k‬‬
‫שלב ב‬
‫‪k‬‬
‫שלב ג‬
‫באיור משמאל הוספנו את המשולשים ‪ ABC‬ו‪ PHG -‬שעוזרים להבין ולהצדיק את הבנייה‪.‬‬
‫א‪ .‬רשמו תיאור של שלבי הבנייה‪.‬‬
‫‪P‬‬
‫‪H‬‬
‫ב‪ .‬הוכיחו‪.ABC  PHG :‬‬
‫‪v‬‬
‫ג‪ .‬הסבירו מדוע ‪.∡CAB = ∡GPH‬‬
‫‪G‬‬
‫ד‪ .‬הסבירו מדוע הישרים ‪ m‬ו‪ v -‬מקבילים‪.‬‬
‫‪C‬‬
‫‪B‬‬
‫‪A‬‬
‫‪m‬‬
‫‪k‬‬
‫דרך ג‪ :‬העברת מקביל לישר על סמך המשפט‪ :‬שני ישרים שמאונכים לישר שלישי מקבילים זה לזה‪.‬‬
‫שלב א ‪ -‬הורידו מהנקודה ‪ P‬אנך לישר ‪ .m‬סמנו אותו ב‪.g -‬‬
‫שלב ב – העלו מהנקודה ‪ P‬אנך לישר ‪ .g‬סמנו אותו ב‪.t -‬‬
‫‪P‬‬
‫‪t‬‬
‫הסבירו מדוע הישרים ‪ m‬ו‪ t -‬מקבילים‪.‬‬
‫‪g‬‬
‫‪m‬‬
‫הכרנו שלוש דרכים להעביר לישר ‪ m‬מקביל דרך הנקודה ‪. P‬‬
‫האם בנינו שלושה ישרים שונים שעוברים דרך ‪ P‬ומקבילים ל‪? m -‬‬
‫תרגיל זה מתאים לתלמידים חזקים המחפשים אתגר וחשיבה יצירתית‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪129‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.19 260‬‬
‫למיטיבי לכת‪ :‬תרגילי אתגר‬
‫ב‪ .‬נתון‪.a ll b :‬‬
‫א‪ .‬נתון‪.EQ ll SR :‬‬
‫כל הזוויות המסומנות ב‪ α -‬שוות במידתן‪.‬‬
‫הוכיחו כי סכום הזוויות‬
‫מהו סכום הזוויות ‪? α+  +  +δ‬‬
‫‪ ∡1 + ∡3 + ∡5‬שווה לסכום הזוויות‬
‫‪. ∡2 + ∡4 + ∡6‬‬
‫‪a‬‬
‫‪α‬‬
‫‪‬‬
‫‪1‬‬
‫‪α‬‬
‫‪2‬‬
‫‪‬‬
‫‪δ‬‬
‫‪3‬‬
‫‪4‬‬
‫‪α‬‬
‫‪5‬‬
‫‪6‬‬
‫‪b‬‬
‫‪α‬‬
‫פתרון סעיף א‪. :‬‬
‫נאריך את ‪ EQ‬מעבר ל‪ Q -‬ונסמן את נקודת המפגש של המשך ‪ EQ‬עם ‪ RD‬ב‪.V -‬‬
‫‪ ∡QVD = ∡VRS‬כיוון שאלו זוויות מתאימות בין הישרים המקבילים ‪.EQ II SR‬‬
‫לכן נסמן גם אותה ב‪. -‬‬
‫דרך א‪ :‬המצולע ‪ EHZLNDV‬הוא משובע ולכן סכום זוויותיו‪:‬‬
‫‪180(7 – 2) = 900‬‬
‫לכן נרשום‪:‬‬
‫‪x +  + (360 – x) +  +(360 – x)+  + x = 900‬‬
‫ונקבל‪ +  +  +  = 180 :‬‬
‫דרכים נוספות‪:‬‬
‫ניתן לפתור את התרגיל בדרכים נוספות רבות אם מחלקים את המצולע‬
‫‪ EHZLNDV‬למרובעים ומשולשים על‪-‬ידי הארכת קטעים‪.‬‬
‫אחת האפשרויות מודגמת בסרטוט‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪130‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פתרון סעיף ב‪:‬‬
‫‪a‬‬
‫נעביר דרך ‪ ,M ,R ,A‬ו‪ E -‬ישרים מקבילים לישרים ‪ a‬ו‪ .b -‬נסמן זוויות מתחלפות‬
‫‪11‬‬
‫‪1‬‬
‫‪1‬‬
‫‪12‬‬
‫שוות באותו מספר (‪ 12 ,11‬וכן הלאה)‪.‬‬
‫ניתן לראות שסכום ‪ ∡1 + ∡3 + ∡5‬שווה לסכום הזוויות ‪∡2 + ∡4 + ∡6‬‬
‫‪12‬‬
‫‪1313‬‬
‫(ראו את סימון הזוויות במספרים ‪ 1-6‬בסרטוט למטה או בסרטוט המקור)‪.‬‬
‫‪14‬‬
‫‪14‬‬
‫‪15‬‬
‫‪15‬‬
‫‪b‬‬
‫דרך נוספת‪:‬‬
‫‪a‬‬
‫לסגור באמצעות הישר ‪ k‬למצולע כלשהו‪.‬‬
‫‪1‬‬
‫‪k‬‬
‫סכום הזוויות ‪7  8  1800‬‬
‫(חד‪-‬צדדיות בין ישרים מקבילים)‬
‫‪2‬‬
‫‪8‬‬
‫‪3‬‬
‫‪4‬‬
‫למצולע ‪ 8‬צלעות לכן‪:‬‬
‫‪5‬‬
‫‪6‬‬
‫‪180(8  2)  1  (360  2)  3  (360  4)  5  (180  6)  180‬‬
‫‪b‬‬
‫‪7‬‬
‫‪‬‬
‫‪180  6  1  3  5  2  4  6  3  360‬‬
‫‪‬‬
‫‪2  4  6  1 3  5‬‬
‫עמ' ‪.20 260‬‬
‫‪2‬‬
‫‪a‬‬
‫הישר ‪ PQ‬חותך זוג ישרים מקבילים ‪ a‬ו‪.b -‬‬
‫‪1‬‬
‫‪P‬‬
‫הראו שחוצי זוויות ‪ P‬ו‪ Q -‬מקבילים זה לזה‪.‬‬
‫‪2‬‬
‫עיקרי הפתרון‪:‬‬
‫‪ ∡P =∡Q‬זוויות מתאימות בין ישרים מקבילים‪ ,‬לכן חצאי הזוויות שווים ‪.∡P1 =∡Q1‬‬
‫‪b‬‬
‫‪1‬‬
‫‪Q‬‬
‫מצאנו זוויות מתאימות שוות ולכן הישרים מקבילים‬
‫תרגילים ‪22 - 21‬‬
‫חשוב לעסוק בתרגילים אלה כצמד לציין מה נתון ומה צריך להוכיח‪ ,‬ולשים לב לשימוש שנעשה בכל פעם במשפט אחר מתוך‬
‫ארבעה‪:‬‬
‫אם ישרים הם מקבילים אז ישר שחותך אותם יוצר זוויות מתחלפות שוות‪.‬‬
‫אם חותך של שני ישרים יוצר זוויות מתחלפות שוות אז הישרים מקבילים‪.‬‬
‫אם ישרים הם מקבילים אז ישר שחותך אותם יוצר זוויות מתאימות שוות‪.‬‬
‫אם חותך של שני ישרים יוצר זוויות מתאימות שוות אז הישרים מקבילים‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪131‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.21 260‬‬
‫המשולש ‪ ∆ABC‬הוא שווה‪-‬שוקיים‪.AC = BC ,‬‬
‫‪B‬‬
‫‪E‬‬
‫ממשיכים את הצלע ‪ AC‬עד לנקודה ‪.D‬‬
‫‪ CE‬חוצה את הזווית ‪.∡BCD‬‬
‫‪12‬‬
‫‪D‬‬
‫הוכיחו‪.AB ll CE :‬‬
‫‪A‬‬
‫‪C‬‬
‫שלבים עיקריים לפתרון‪:‬‬
‫‪B‬‬
‫‪‬‬
‫נסמן את זוויות הבסיס של המשולש שווה השוקיים ב‪. -‬‬
‫‪‬‬
‫‪ ∡BCD = 2‬לפי המשפט על זווית חיצונית למשולש‪.‬‬
‫‪‬‬
‫‪ ∡BCE = ∡ECD = ‬כיוון ש‪ CE -‬חוצה את הזווית ‪.∡BCE‬‬
‫‪‬‬
‫מכל אלה נוכל להסיק ‪.∡ABC = ∡BCE = ‬‬
‫‪‬‬
‫ומכאן ‪ AB II CE‬לפי המשפט‪ :‬אם חותך של שני ישרים יוצר זוויות מתחלפות שוות אז הישרים מקבילים‪.‬‬
‫‪.22‬‬
‫‪‬‬
‫‪E‬‬
‫‪‬‬
‫‪12‬‬
‫‪D‬‬
‫‪C‬‬
‫נתון משולש ‪.∆SUN‬‬
‫‪A‬‬
‫‪S‬‬
‫‪B‬‬
‫ממשיכים את הצלע ‪ UN‬עד לנקודה ‪.D‬‬
‫‪ BN‬חוצה את הזווית ‪.BN ll SU ,∡SND‬‬
‫‪12‬‬
‫‪D‬‬
‫הוכיחו‪ ∆SUN :‬הוא שווה‪-‬שוקיים‪.‬‬
‫‪U‬‬
‫‪N‬‬
‫רעיון הפתרון‪ :‬נגלה במשולש ‪ SUN‬שתי זוויות שכל אחת מהן שווה לאחד מחצאי הזווית ‪.∡SND‬‬
‫‪U‬‬
‫עמ' ‪.23 261‬‬
‫הקטעים ‪ NY‬ו‪ UK -‬מאונכים זה לזה וחוצים זה את זה‪.‬‬
‫א‪ .‬הוכיחו‪.UN ll YK :‬‬
‫רעיון הפתרון‪ :‬חפיפת משולשים ‪ ∆SKY  ∆SUN‬לפי צ‪.‬ז‪.‬צ‬
‫‪T‬‬
‫‪Y‬‬
‫‪S‬‬
‫‪N‬‬
‫‪R‬‬
‫ומתוך החפיפה זיהוי זוויות מתחלפות שוות‪.‬‬
‫‪K‬‬
‫‪ ,‬ו‪ TK -‬חוצה את‬
‫ב‪ UR .‬חוצה את הזווית ‪U‬‬
‫הזווית ‪ . K‬הוכיחו‪.UR ll KT :‬‬
‫רעיון הפתרון‪ :‬מסעיף א ידוע שזוויות ‪ ∡U‬ו‪ ∡K -‬שוות ולכן גם חצאי הזווית שווים‪.‬‬
‫הוכחנו זוויות מתחלפות שוות בין ישרים ולכן ניתן להשתמש במשפט ההפוך‪.‬‬
‫פעילות ‪ 8‬והתרגילים ‪ 25 - 24‬המופיעים בעקבותיה‪ ,‬מהווים מפגש חוזר עם דרך מוכרת לתלמידים להוכיח שישרים הם‬
‫מקבילים‪ :‬ישרים שיש להם אותו שיפוע הם ישרים מקבילים‪ ,‬ומציגה לה הסבר‪.‬‬
‫רעיון הפעילות הוא לקשר בין הנלמד באלגברה על פונ קציה קווית לבין הנלמד בגאומטריה בנושא ישרים מקבילים‪ .‬פעילויות‬
‫מסוג זה מהוות גם הכנה לגאומטריה אנליטית שתלמד בחטיבה העליונה‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪132‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫שיפוע של השינוי בערכי ‪y‬‬
‫=‬
‫ישר‬
‫השינוי בערכי ‪x‬‬
‫פעילות ‪ – 8‬על ישרים מקבילים במערכת צירים וזוויות מתאימות – עמ' ‪261‬‬
‫במערכת הצירים שלפניכם מסורטטים שני ישרים שיש להם אותו שיפוע‪.‬‬
‫‪y‬‬
‫למדנו שישרים שיש להם אותו שיפוע הם ישרים מקבילים‪.‬‬
‫אפשר להסביר זאת גם בעזרת זוויות מתאימות‪.‬‬
‫הישרים בסרטוט הם (‪.y = 2x – 6 )ii( y = 2x – 2 )i‬‬
‫‪‬‬
‫‪x‬‬
‫א‪ .‬זהו איזה ישר מתאים לכל אחת מן המשוואות‪.‬‬
‫‪‬‬
‫הקטע ‪ DF‬נמצא על הישר (‪ y = 2x – 6 )ii‬והקטע ‪ AB‬נמצא על הישר (‪.y = 2x – 2 )i‬‬
‫ב‪ .‬מה השיפוע של הישרים? השיפוע של שני הישרים הוא ‪.y = 2x – 6 )ii( y = 2x – 2 )i( .2‬‬
‫ג‪ .‬בנקודות החיתוך עם ציר ה‪ x -‬נסרטט מדרגה שהרוחב שלה הוא ‪.1‬‬
‫מהו גובה המדרגה? ‪ 2‬יחידות‪.‬‬
‫ד‪ .‬הסבירו מדוע ‪.ABC  FDE‬‬
‫חפיפה לפי משפט צ‪.‬ז‪.‬צ ‪ .‬יש זווית ישרה בשני המשולשים וגובה המדרגה ורוחבה יחידה זהים בשני המשולשים‪.‬‬
‫ה‪ .‬מהחפיפה נובע ש‪ , =  -‬מדוע? זווית שוות בהתאמה בין שני משולשים חופפים‪.‬‬
‫הישרים (‪ )i‬ו‪ ) ii(-‬הם שני ישרים הנחתכים על ידי ישר שלישי‪ .‬במקרה זה הישר החותך הוא ציר ה‪. x-‬‬
‫הזוויות ‪ ‬ו‪  -‬הן זוויות מתאימות שוות‪ .‬מכאן נובע ש‪.AB ll DF -‬‬
‫ראינו כי ישרים שיש להם אותו שיפוע הם ישרים מקבילים‪.‬‬
‫ישרים אלו יוצרים זוויות מתאימות שוות עם ציר ה‪ x -‬שחותך אותם‪.‬‬
‫תרגילים – עמ' ‪262 – 261‬‬
‫עמ' ‪.24 261‬‬
‫‪y‬‬
‫א‪ .‬חשבו את השיפועים של כל הישרים‬
‫בסרטוט (היעזרו במשבצות)‪.‬‬
‫‪0‬‬
‫‪0.5‬‬
‫השיפועים כתובים בכחול בצד הסרטוט‪.‬‬
‫‪-2‬‬
‫‪5‬‬
‫ב‪ .‬זהו זוגות של ישרים מקבילים‪.‬‬
‫‪5‬‬
‫ישרים מקבילים כאשר השיפועים שווים ולכן‪:‬‬
‫‪3‬‬
‫‪-4‬‬
‫‪0‬‬
‫‪0.5‬‬
‫‪k II c ; b II g ; h II a‬‬
‫שאר הישרים אינם מקבילים זה לזה‪.‬‬
‫‪x‬‬
‫‪3‬‬
‫‪-3‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪133‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪.25 262‬‬
‫לפניכם רשימה של ישרים‪.‬‬
‫‪)1‬‬
‫‪y = 2x + 5‬‬
‫‪)3‬‬
‫‪y = 0.5x + 5‬‬
‫‪)5‬‬
‫‪1‬‬
‫‪x+7‬‬
‫‪2‬‬
‫‪)2‬‬
‫‪y = –2x + 7‬‬
‫‪)4‬‬
‫‪y = 5x – 2‬‬
‫‪)6‬‬
‫‪y = 2x‬‬
‫=‪y‬‬
‫‪)7‬‬
‫‪y = 5 – 2x‬‬
‫‪)8‬‬
‫)‪y = 5(x – 3‬‬
‫א‪ .‬זהו ביניהם זוגות של ישרים מקבילים‪.‬‬
‫זוגות של ישרים מקבילים הם‪ )1( :‬ו‪ )2( ;)6(-‬ו‪;)7(-‬‬
‫(‪ )3‬ו‪ )4( ;)5( -‬ו‪)8( -‬‬
‫ב‪ .‬סרטטו את זוגות הישרים המקבילים שזיהיתם במערכת צירים‪.‬‬
‫בחרו צבע שונה עבור כל זוג ישרים מקבילים‪.‬‬
‫ג‪ .‬סמנו זוגות של זוויות מתאימות בסרטוט שלכם‪.‬‬
‫‪.26‬‬
‫לפניכם דגל נמיביה‪ .‬הדגל הוא בצורת מלבן שמורכב ממספר צורות גאומטריות‪.‬‬
‫(לצורך השאלה הניחו שהפסים הלבנים הינם ישרים חסרי עובי‪).‬‬
‫‪C‬‬
‫א‪ .‬רשמו את כל הצורות הגאומטריות שאתם מזהים בדגל‪.‬‬
‫‪N‬‬
‫‪B‬‬
‫‪A‬‬
‫עיגול‪ ,‬משולשים ישרי‪-‬זווית‪ ,‬משולשים שווי‪-‬שוקיים‪ ,‬משושה ומלבן‪.‬‬
‫‪H‬‬
‫ב‪ .‬כמה זוגות של צלעות מקבילות אתם מזהים במשושה?‬
‫‪E‬‬
‫‪F‬‬
‫רשמו אותם‪.‬‬
‫‪G‬‬
‫‪;BC II GF ;HG II CN‬‬
‫ג‪ .‬נמקו איך קבעתם שזוגות של צלעות מקבילות זו לזו‪ .‬לגבי איזה זוג של‬
‫צלעות אין לכם מספיק נתונים כדי לנמק שהן מקבילות?‬
‫‪ ;AC II GE , HG II CN‬הם קטעים על צלעות נגדיות במלבן מקבילות זו לזו‪.‬‬
‫‪ - BH , FN‬אין לנו מספיק נתונים‪.‬‬
‫‪C‬‬
‫ד‪ .‬ידוע גם כי ‪ .ABH  EFN‬האם זה מספיק כדי לקבוע ש‪?BH ll NF -‬‬
‫‪N‬‬
‫כן‪ .‬נעביר את הישר החותך ‪( BF‬את אותו תהליך ניתן לעשות גם עם ‪)HN‬‬
‫‪B‬‬
‫‪A‬‬
‫‪α‬‬
‫‪α‬‬
‫‪H‬‬
‫מהחפיפה ‪ .ABH  EFN‬ניתן להסיק כי ‪.∡NFE= ∡HBA‬‬
‫‪E‬‬
‫‪F‬‬
‫‪G‬‬
‫כמו כן ידוע ‪ AC II GE‬ולכן ‪( ∡BFE= ∡FBA‬זוויות מתחלפות בין ישרים מקבילים)‪.‬‬
‫מחיסור זוויות ‪ ∡BFE - ∡NFE= ∡FBA - ∡HBA = α‬נקבל זוויות מתחלפות שוות בין‬
‫ישרים ולכן‪.BH ll DF ,‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪134‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫‪A‬‬
‫‪B‬‬
‫עמ' ‪.27 262‬‬
‫הישרים ‪ EB‬ו‪ AF -‬נחתכים בנקודה ‪.D‬‬
‫‪D‬‬
‫נתון‪.∡EDF = 66 ;BD = DA ;ED = DF :‬‬
‫א‪ .‬הוכיחו כי ‪.EF ll AB‬‬
‫‪F‬‬
‫ב‪ .‬האם ניתן להוכיח כי ‪ EF ll AB‬גם מבלי לדעת את מידת הזווית ‪?∡EDF‬‬
‫‪E‬‬
‫ג‪ .‬קרש גיהוץ מתקפל בנוי כך שניתן לשנות את גובהו לנוחיות המשתמש על‪-‬ידי שינוי הזווית‬
‫שבין הרגלים התומכות‪ .‬הסבירו כיצד ניתן להבטיח שלוח הגיהוץ יקביל לרצפה‪ ,‬בלי קשר‬
‫למידת הזווית בין הרגלים התומכות של הקרש?‬
‫פתרון תרגיל ‪:27‬‬
‫ב‪ .‬נסמן ‪ ∡A = ‬ונקבל‪:‬‬
‫א‪ .‬נחשב את הזוויות על‪-‬פי הנתונים ונקבל‪:‬‬
‫‪B‬‬
‫‪57 57‬‬
‫‪66‬‬
‫‪A‬‬
‫‪B‬‬
‫‪A ‬‬
‫‪‬‬
‫‪D‬‬
‫‪180-2‬‬
‫‪D‬‬
‫‪180-2‬‬
‫‪66‬‬
‫‪F‬‬
‫‪57‬‬
‫‪57‬‬
‫‪ F‬‬
‫‪E‬‬
‫‪ EF II AB‬על‪-‬פי זוויות מתחלפות שוות‪.‬‬
‫‪E ‬‬
‫שוב‪ EF II AB ,‬על‪-‬פי זוויות מתחלפות שוות‪.‬‬
‫ג‪ .‬רגלי קרש הגיהוץ מחוברות כך ש‪ AD = BD -‬ו‪.ED = FD -‬‬
‫כמו בסעיף ב נוכל להראות כי ‪ EF II AB‬על‪-‬פי זוויות מתחלפות שוות‪.‬‬
‫‪A‬‬
‫‪B‬‬
‫‪D‬‬
‫‪F‬‬
‫‪E‬‬
‫אתנחתאות – עמ' ‪263‬‬
‫‪.1‬‬
‫אור ותום קיפלו רצועות נייר בעלות רוחב קבוע ובכל המקרים קיבלו משולש ישר‪-‬‬
‫זווית ושווה‪-‬שוקיים‪ ,‬שקו הקיפול הוא הבסיס שלו‪.‬‬
‫א‪ .‬האם זה מקרי שהתקבל משולש ישר‪-‬זווית? מקרי שהתקבל משולש ישר‪-‬זווית‪.‬‬
‫המשולש ‪ ABC‬נוצר באותה דרך ואינו ישר‪-‬זווית‪.‬‬
‫ב‪ .‬האם זה מקרי שהתקבל משולש שווה‪-‬שוקיים?‬
‫‪P‬‬
‫נסו לקפל רצועות נייר ולהסתכל במשולש שנוצר ליד קו הקיפול‪.‬‬
‫לא מקרי שהתקבל משולש שווה‪-‬שוקיים‪ .‬נוכיח זאת בסעיף ג‪.‬‬
‫‪C‬‬
‫ג‪ .‬הוכיחו שכאשר מקפלים רצועות נייר תמיד נוצר ליד קו הקיפול משולש שווה‪-‬שוקיים‪.‬‬
‫רמז‪ :‬האריכו את ‪ PA‬מעבר ל‪ A -‬והסבירו מדוע שלוש הזוויות המסומנות בנקודה‬
‫שוות זו לזו‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪135‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פתרון לסעיף ג‪:‬‬
‫אחרי הקיפול‬
‫לפני הקיפול‬
‫נתבונן ברצועת הנייר לפני ואחרי הקיפול‪ .‬קו הקיפול הוא‬
‫‪ .AB‬החלק הצבוע בירוק היה לפני הקיפול בהמשך רצועת‬
‫הנייר‪ .‬מכאן‪.∡A1 = ∡A2 :‬‬
‫‪ ∡A2‬היא זווית של המרובע הירוק במיקום שלפני קיפול‪.‬‬
‫‪ ∡A1‬היא אותה זווית של המרובע הירוק במיקום שאחרי הקיפול‪.‬‬
‫‪P‬‬
‫‪P‬‬
‫‪1 2‬‬
‫‪1‬‬
‫ההבחנה ש‪ ∡A1 = ∡A2 -‬היא המפתח לפתרון‪.‬‬
‫‪C‬‬
‫‪C‬‬
‫‪ ∡B1 = ∡A2‬כיוון שאלו זוויות מתחלפות בין ישרים מקבילים‪.‬‬
‫‪ ∡B1 = ∡A1‬שני גדלים השווים לגודל שלישי שווים ביניהם‪.‬‬
‫⇩‬
‫‪ AC = BC‬מ‪.‬ש‪.‬ל‬
‫‪ .2‬עליכם להשלים את ריבוע הקסם‪ ,‬כך שסכום המספרים בכל שורה‪,‬‬
‫‪10‬‬
‫בכל עמודה ובכל אלכסון יהיה זהה‪.‬‬
‫‪9‬‬
‫‪14‬‬
‫הפתרון וההסבר‪ :‬הסכום הקבוע (בכל שורה‪ ,‬בכל עמודה‪ ,‬ובכל אלכסון) הוא ‪.33‬‬
‫‪8‬‬
‫‪15‬‬
‫‪10‬‬
‫‪13‬‬
‫‪11‬‬
‫‪9‬‬
‫‪12‬‬
‫‪7‬‬
‫‪14‬‬
‫לכן‪ ,‬המספר במשבצת האמצעית חייב להיות שליש הסכום‪.‬‬
‫‪ .3‬במסיבה השתתפו ‪ 10‬בנות ו‪ 6-‬בנים‪.‬‬
‫הם חילקו ביניהם עוגה בצורת מלבן‪ ,‬באורך ‪ 40‬ס"מ וברוחב ‪ 20‬ס"מ‪.‬‬
‫מהעוגה חתכו שני חלקים זהים בצורת משולש‬
‫(ראו סרטוט) ואותם נתנו לבנים‪.‬‬
‫את החלק האמצעי אכלו הבנות‪.‬‬
‫כל הילדים אכלו חתיכת עוגה בגודל שווה‪.‬‬
‫מצאו את אורך הקטע ‪.AB‬‬
‫‪B‬‬
‫‪A‬‬
‫פתרון‪ 25 :‬ס"מ‪.‬‬
‫‪6‬‬
‫הסבר‪ :‬אם נצרף את שני המשולשים למלבן נראה שכל הבנים אכלו ביחד חלק מלבני שאורכו‬
‫‪16‬‬
‫מאורך העוגה‪,‬‬
‫כלומר‪ 15 ,‬ס"מ‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪136‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫טרפז‬
‫לצד הכרת הטרפז ותכונותיו המטרה של פרק הטרפז היא לחזק את המיומנויות הקשורות בזיהוי של ישרים מקבילים‬
‫ובתכונותיהם‪.‬‬
‫טרפז הוא מרובע שיש לו זוג אחד בלבד של צלעות נגדיות מקבילות‪ .‬הניסוח "זוג אחד בלבד של צלעות נגדיות מקבילות"‬
‫הוא ייחודי להגדרת הטרפז‪ ,‬והוא שו לל את האפשרות לראות במקבילית סוג של טרפז‪ .‬מקבילית‪ ,‬מרובע עם שני זוגות של‬
‫צלעות נגדיות מקבילות‪ ,‬אינה יכולה להיות טרפז כי אינה מקיימת את הגדרת הטרפז‪.‬‬
‫השיקולים לבחירת הגדרה זו קשורים בתכונות ייחודיות שיש לטרפז ואין למקבילית‪:‬‬
‫לו מקבילית היתה טרפז היא היתה טרפז שווה‪-‬שוקיים ולכן לא יכולנו לטעון שבטרפז שווה‪-‬שוקיים הזוויות ליד אותו בסיס‬
‫שוות זו‪ ,‬וגם לא יכולנו לטעון שבטרפז שווה‪-‬שוקיים האלכסונים שווים‪.‬‬
‫ישנם מקומות בעולם שבהם בהגדרת הטרפז לא דורשים קיום של זוג צלעות שאינן מקבילות‪ .‬במקומות אלה נאלצים להתאים‬
‫את המשפטים על טרפז שווה‪-‬שוקיים להגדרת הטרפז‪ .‬למשל‪ :‬בטרפז שווה‪-‬שוקיים שאינו מקבילית האלכסונים שווים זה‬
‫לזה‪.‬‬
‫בתוכנית הלימודים הישראלית מגדירים‪ ,‬כאמור‪ ,‬את הטרפז כמרובע עם זוג אחד בלבד של צלעות נגדיות מקבילות וחוסכים‬
‫את הסירבול בכתיבת התכונות של טרפז שווה‪-‬שוקיים הנהוג במקומות שאינם מגדירים כך‪.‬‬
‫גם היתרון של עיסוק בטרפז לפני העיסוק במקבילית נעוץ בכך שלטרפז יש זוג אחד של צלעות מקבילות וזוג אחד של צלעות‬
‫שאינן מקבילות‪ .‬לכן כדי להראות שמרובע הוא טרפז יש להשתמש גם בשיקולים המאפשרים לקבוע שישרים הם מקבילים‬
‫וגם בשיקולים המאפשרים לקבוע שישרים אינם מקבילים‪.‬‬
‫כאשר נתונים סרטוטים מורכבים שמכילים ישרים מקבילים וחותך‪ ,‬תלמידים לעתים מתקשים להבחין‪ ,‬או לא מרגישים צורך‬
‫להבחין‪ ,‬בין אלו ישרים זוויות הן מתחלפות‪ ,‬מתאימות‪ ,‬או חד‪-‬צדדיות‪ .‬כשעוסקים בטרפז חייבים לעשות את ההבחנות האלה‪.‬‬
‫בחרנו לחלק את פרק הטרפז לשני חלקים‪.‬‬
‫החלק הנוכחי שבא בסמוך לפרק המקבילית עוסק בטרפז כללי ובטרפז ישר‪-‬זווית מבלי לעסוק בטרפז שווה‪-‬שוקיים‪.‬‬
‫פרק נוסף על טרפז שווה‪-‬שוקיים יופיע בהמשך‪ ,‬אחרי פרק המקבילית‪ .‬הסיבה לכך היא שחלק מהתכונות של טרפז‬
‫שווה‪-‬שוקיים קל להוכיח באמצעות מקבילית‪ .‬נפרט יותר בנושא זה בפרק על טרפז שווה‪-‬שוקיים‪.‬‬
‫בהוראת הטרפז יש לבסס את התשתית למיומנויות היסודיות של היסק בנושא ישרים מקבילים‪:‬‬
‫א‪.‬‬
‫יש לזהות ישרים מקבילים על סמך שתי זוויות מתחלפות השוות זו לזו‪ ,‬או על סמך שתי זוויות מתאימות השוות זו‬
‫לזו או על סמך שתי זוויות חד‪-‬צדדיות שסכומן ‪( 180°‬אין חובה ללמד את המושג זוויות חד‪-‬צדדיות)‪ .‬יש לדעת לנמק‬
‫את הסיבה להקבלה‪.‬‬
‫אמנם אין חובה ללמד את המושג "זוויות חד‪-‬צדדיות" אך כדאי להביא בחשבון שזוויות חד‪-‬צדדיות הן זוויות של‬
‫הטרפז‪ .‬כדי להיעזר בזוויות מתאימות בדרך כלל יש להוסיף לסרטוט את המשכי הצלעות וכדי להשתמש בזוויות‬
‫מתחלפות יש להעביר אלכסון‪ .‬לכן השימוש בזוויות חד‪-‬צדדיות הוא לפעמים נוח במיוחד‪.‬‬
‫ב‪.‬‬
‫מכך ששני ישרים מקבילים זה לזה‪ ,‬יש לזהות שכל שתי זוויות מתחלפות שוות זו לזו‪ ,‬או שכל שתי זוויות מתאימות‬
‫שוות זו לזו או שסכום כל שתי זוויות חד‪-‬צדדיות הוא ‪ ,180°‬ויש לדעת לנמק זאת בהתאם‪.‬‬
‫חשוב לחזור על חישובי שטחים והיקפים בהוראת הפרק‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪137‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫דגשים בהוראת הטרפז‬
‫‪.1‬‬
‫במקרים שבהם הדבר אפשרי‪ ,‬יש להדגים דרכים שונות להוכיח אותו משפט‪.‬‬
‫‪.2‬‬
‫חשוב ללמד את התלמידים לכתוב נימוקים הקשורים להקבלה‪ ,‬ובפרט חשוב לציין את הישרים המקבילים שביניהן‬
‫הזוויות מתאימות מתחלפות או חד‪-‬צדדיות‪.‬‬
‫‪ .3‬במידת האפשר‪ ,‬מומלץ להציג לפני התלמידים יותר מדרך אחת לכתיבת הוכחה‪.‬‬
‫‪ .4‬יש להסתמך על הידע בבניות כדי להשתמש בבניות עזר בהוכחת משפטים‪ .‬הערה‪ :‬בטרפז שווה‪-‬שוקיים השימוש‬
‫בבניות עזר יהיה רב ומשמעותי יותר‪.‬‬
‫טרפז הוא מרובע שבו זוג אחד בלבד של צלעות מקבילות זו לזו‪.‬‬
‫‪B‬‬
‫הצלעות המקבילות נקראות‪ :‬בסיסי הטרפז‪.‬‬
‫בסיס‬
‫שוק‬
‫הצלעות שאינן מקבילות נקראות‪ :‬שוקי הטרפז‪.‬‬
‫‪C‬‬
‫‪A‬‬
‫שוק‬
‫בסיס‬
‫‪D‬‬
‫בסרטוט הבסיסים הם‪ AB :‬ו‪ ,CD -‬השוקיים הן‪ AD :‬ו‪.BC -‬‬
‫טרפז שווה‪-‬שוקיים הוא טרפז שהשוקיים שלו שוות זו לזו‪.‬‬
‫טרפז ישר‪-‬זווית הוא טרפז בעל זווית ישרה‪.‬‬
‫‪ ‬אם יש בטרפז זווית אחת ישרה‪ ,‬אז בהכרח יש לו שתי זוויות ישרות (אך לא יותר מזה)‪.‬‬
‫‪a‬‬
‫‪1‬‬
‫שטח של טרפז = (סכום הבסיסים) ∙ גובה ∙‬
‫‪2‬‬
‫‪(a  b)  h‬‬
‫‪S‬‬
‫‪2‬‬
‫‪h‬‬
‫שטח הטרפז שווה למחצית סכום הבסיסים כפול הגובה‪.‬‬
‫‪b‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪138‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫לאחר חזרה על הגדרת הטרפז וחלקיו חשוב לעסוק בתרגילי זיהוי‪ .‬תרגילי הזיהוי תפקידם לחדד את הגדרת הטרפז ואת‬
‫מושג ההגדרה ולכן חשוב לעסוק בהם גם כאשר אנו בטוחים שהתלמידים מכירים את הגדרת הטרפז‪.‬‬
‫פעילות ‪ – 1‬אילו מרובעים הם טרפזים? – עמ' ‪264‬‬
‫הישרים ‪ a‬ו‪ b -‬מקבילים זה לזה‪.‬‬
‫א‪ .‬על‪-‬פי הנתונים בסרטוט‪ ,‬זהו אלו מרובעים הם טרפזים‪.‬‬
‫הטרפזים הם ‪ KRMD ,RTZM , TEPZ‬ו‪.KDPE -‬‬
‫‪E‬‬
‫‪113‬‬
‫לארבעתם זוג צלעות שמונחות על הישרים המקבילים וזוג צלעות‬
‫שאינן מקבילות (לפי זוויות מתחלפות שאינן שוות)‪.‬‬
‫‪T‬‬
‫‪P‬‬
‫‪R‬‬
‫‪113‬‬
‫‪K‬‬
‫‪Z‬‬
‫ב‪ .‬זהו מרובע שאיננו טרפז‪ .‬נמקו מדוע קבעתם כך‪.‬‬
‫‪a‬‬
‫‪M‬‬
‫למשל‪ REPM ,‬אינו טרפז‪ .‬למרובע שני זוגות של צלעות‬
‫נגדיות מקבילות או ‪ KTZD‬הוא מלבן‪.‬‬
‫‪D‬‬
‫‪b‬‬
‫ג‪ .‬האם ניתן למצוא בסרטוט טרפז ישר‪-‬זווית? הסבירו‪.‬‬
‫כן‪ .‬למשל‪ KRMD ,‬טרפז ישר‪-‬זווית‪ .‬ידוע ש – ‪ aIIb‬וכן שזווית ‪ D‬הינה זווית ישרה‪ ,‬באמצעות חשבון זוויות‬
‫ניתן להסיק כי ‪ .KD ∦ RM‬ניתן גם להראות ש‪ KEPD -‬טרפז ישר‪-‬זווית‪ ,‬מנימוקים דומים או ‪.TZMR‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪139‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫פעילות ‪ – 2‬האם קיים טרפז שבסיסיו שווים באורכם? – עמ' ‪265‬‬
‫לפעילות ‪ 2‬שתי מטרות‪ .‬המטרה הראשונה היא לשים לב לעובדה שלא קיים טרפז עם בסיסים שווים‪ .‬המטרה השנייה היא‬
‫לתת בידי התלמידים כלי שמאפשר להבחין בקלות שמרובע אינו טרפז‪.‬‬
‫חשיבותה של הפעילות נובעת מהקדמת פרק הטרפז לפרק המקבילית‪.‬‬
‫ההוכחה שבפעילות ‪ 2‬למעשה מראה שמרובע שיש לו זוג צלעות שהן גם שוות וגם מקבילות הוא מקבילית‪ .‬כיוון שאין אנו‬
‫עוסקים במקבילית‪ ,‬אנחנו מסתפקים בכך שאנו מראים שבמקרה זה גם הצלעות האחרות מקבילות‪ ,‬ולכן לא מתקיימת‬
‫הגדרת הטרפז‪.‬‬
‫כדאי להעלות את השאלות "האם קיים טרפז שבסיסיו שווים באורכם?" ו"האם מרובע בעל זוג צלעות שהן גם שוות וגם‬
‫מקבילות יכול להיות טרפז?" עם ספרים סגורים‪ ,‬כי האיורים בפעילות מכוונים לתשובה‪ .‬כדאי גם לדון בקשר שבין השאלות‬
‫האלה‪.‬‬
‫את הפעילות מלווה יישומון דינמי ממנו ניתן לראות‪ ,‬שבכל פעם שאנו מצליחים לבנות מרובע שבו זוג צלעות שוות‪ ,‬הן גם‬
‫מקבילות‪ ,‬ניתן לראות על פי מידות הזוויות שגם הצלעות האחרות מקבילות‪.‬‬
‫אפשר לתת לתלמידים להתנסות בעבודה עם היישומון כשיעורי בית לקראת השיעור‪.‬‬
‫אפשר להשתמש ביישומון במליאת הכתה‪ ,‬להזמין תלמידים לנסות ליצור טרפז שבו הצלעות המקבילות גם שוות‪.‬‬
‫אפשר לצפות שתלמידים יחפשו הסבר לכך‪ ,‬שאינם מצליחים לבנות טרפז כזה ויגיעו בעצמם להוכחה שבפעילות‪.‬‬
‫פעילות ‪ – 2‬האם קיים טרפז שבסיסיו שווים באורכם?‬
‫א‪ .‬האם מרובע בעל זוג צלעות שהן גם שוות וגם מקבילות יכול להיות טרפז?‬
‫במרובע ‪ABCD‬‬
‫‪‬‬
‫לפעילות זו יישומון באתר‪.‬‬
‫‪B‬‬
‫‪A‬‬
‫נתון‪. AB = CD , AB II CD :‬‬
‫נראה שהמרובע ‪ ABCD‬לא יכול להיות טרפז‪.‬‬
‫‪C‬‬
‫לשם כך נסרטט במרובע אלכסון ‪ -‬את האלכסון ‪.BD‬‬
‫‪B‬‬
‫ב‪ .‬הוכיחו ש‪.∆ABD ≅ ∆CDB -‬‬
‫ההוכחה לפי משפט צ‪.‬ז‪.‬צ‪ ..‬במהלך ההוכחה משתמשים בכך שאם‬
‫‪D‬‬
‫‪A‬‬
‫ישר חותך זוג ישרים מקבילים‪ ,‬אז נוצרות זוויות מתחלפות שוות‪.‬‬
‫ג‪.‬‬
‫‪C‬‬
‫כיצד נוכל להסיק מהחפיפה ש‪? AD II BC -‬‬
‫‪D‬‬
‫מהחפיפה נסיק ‪ ,∢ADB = ∢CBD‬ומכאן נסיק ש‪.AD II BC -‬‬
‫הפעם השתמשנו בטענה ההפוכה לזו בה השתמשנו בסעיף הקודם‪ .‬אם ישר חותך זוג ישרים אחרים‪ ,‬כך‬
‫שנוצרות זוויות מתחלפות שוות‪ ,‬אז הישרים מקבילים‪.‬‬
‫ד‪ .‬מדוע ‪ ABCD‬לא יכול להיות טרפז?‬
‫מרובע עם שני זוגות של צלעות נגדיות מקבילות אינו טרפז‪ ,‬על‪-‬פי ההגדרה‪.‬‬
‫ה‪ .‬כמה זוויות ישרות יכולות להיות בטרפז? הוכיחו את תשובתכם‪.‬‬
‫או שיש שתי זוויות ישרות או שאין אף זווית ישרה‪ .‬אם יש זווית ישרה‪ ,‬אז הזווית השנייה הסמוכה לאותה שוק גם היא‬
‫ישרה (זוויות חד‪-‬צדדיות בין מקבילים)‪ .‬לו היתה זווית ישרה נוספת‪ ,‬אז היה מתקבל מלבן‪ .‬למלבן שני זוגות של צלעות‬
‫נגדיות שוות ועל כן אינו טרפז‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪140‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫בפעילות ‪ 2‬הראינו‪:‬‬
‫אם למרובע יש זוג צלעות שהן גם שוות וגם מקבילות אז גם הצלעות הנגדיות האחרות מקבילות‪.‬‬
‫טרפז הוא מרובע עם זוג אחד בלבד של צלעות מקבילות זו לזו‪.‬‬
‫לכן אורכי הבסיסים של הטרפז לא יכולים להיות שווים‪.‬‬
‫לכל טרפז יש בסיס גדול ובסיס קטן‪.‬‬
‫פעילות ‪ 3‬מחדדת את הדרכים להראות שמרובע הוא טרפז‪.‬‬
‫פעילות ‪ – 3‬איך נוכיח שמרובע הוא טרפז? – עמ' ‪265‬‬
‫במרובע ‪GEFH‬‬
‫‪E‬‬
‫נתון‪.∡E = 120º ,∡H = 70º ,∡G = 110º :‬‬
‫‪G‬‬
‫‪110‬‬
‫‪120‬‬
‫א‪ .‬הוכיחו ש‪ GEFH -‬הוא טרפז‪.‬‬
‫רעיון ההוכחה‪ :‬נראה שלמרובע ‪ GEFH‬יש זוג אחד של צלעות מקבילות‬
‫‪70‬‬
‫‪H‬‬
‫‪F‬‬
‫וזוג נוסף של צלעות נגדיות שאינן מקבילות‪.‬‬
‫הוכחה‪:‬‬
‫‪ GE ll HF‬כי החותך ‪ GH‬יוצר עם ‪ GE‬ו‪ HF -‬זוויות חד‪ -‬צדדיות שסכומן ‪.70 + 110 = 180‬‬
‫‪ GH ∦ EF‬כי החותך ‪ GE‬יוצר עם ‪ GH‬ו‪ EF -‬זוויות חד‪-‬צדדיות שסכומן ‪.110 + 120  180‬‬
‫מ‪.‬ש‪.‬ל‪.‬‬
‫המרובע ‪ GEFH‬הוא טרפז כי יש לו זוג אחד בלבד של צלעות מקבילות‪.‬‬
‫ב‪ .‬הפעם נתון ש‪ .∡E = 70 -‬האם גם במקרה זה המרובע ‪ GEFH‬הוא טרפז?‬
‫אם כן‪ ,‬הוכיחו‪ .‬אם לא‪ ,‬הסבירו מדוע‪ .‬הפעם המרובע מקבילית‪.‬‬
‫ג‪ .‬לפניכם בעיה דומה‪ .‬במרובע ‪ GEFH‬נתון‪.∡H = 50º ,∡G = 130º :‬‬
‫עבור אילו ערכים של הזווית ‪ ∡E‬המרובע ‪ GEFH‬הוא טרפז? נמקו‪.‬‬
‫‪)1‬‬
‫‪ ∡E = 150º‬‬
‫‪ ∡E = 50º )2‬‬
‫‪ ∡E = 130º )4‬‬
‫‪ ∡E = 45º )3‬‬
‫‪A‬‬
‫כדי להבטיח שמרובע יהיה טרפז עלינו לדרוש שני תנאים על צלעות המרובע‪:‬‬
‫‪AD ll BC‬‬
‫‪ )1‬זוג אחד של צלעות מקבילות‪.‬‬
‫‪)2‬‬
‫‪B‬‬
‫‪AB ∦ DC‬‬
‫זוג שני של צלעות שאינן מקבילות זו לזו‬
‫‪C‬‬
‫‪D‬‬
‫למרות שהתנאי השני מנוסח בשלילה‪ ,‬יש להוכיח אותו‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪141‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫ד‪ .‬אפשר גם אחרת! דרך נוספת להוכיח שמרובע הוא טרפז היא להראות שבסיסי הטרפז (הצלעות המקבילות) הם‬
‫בעלי אורך שונה‪ .‬הסבירו מדוע עובדה זו מבטיחה שהמרובע הוא טרפז‪.‬‬
‫כפי שראינו בפעילות ‪ ,2‬במרובע שבו יש זוג צלעות נגדיות שהן שוות וגם‬
‫היעזרו בפעילות ‪.2‬‬
‫מקבילות‪ ,‬יש זוג נוסף של צלעות נגדיות מקבילות ולכן אינו טרפז‪ .‬בכוונה‬
‫אין אנו משתמשים במילה "בסיסים" כי אם המרובע אינו טרפז אז‬
‫צלעותיו לא נקראות בסיסים‪.‬‬
‫ישנן דרכים אחדות להראות שזוג צלעות אינן מקבילות‪.‬‬
‫א‪ .‬לפעמים‪ ,‬כמו בפעילות ‪ 2‬נזהה שהצלעות אינן מקבילות באמצעות חישובי זוויות‪.‬‬
‫ב‪ .‬לפעמים נזהה שהצלעות אינן מקבילות כי הן מונחות על ישרים שיש להם נקודה משותפת‪.‬‬
‫תרגילים – עמ' ‪272 – 266‬‬
‫עמ' ‪ .1 266‬בכל אחד מהסרטוטים שלפניכם זהו אם המרובע טרפז‪.‬‬
‫אם המרובע הוא טרפז‪ ,‬ציינו מי הם הבסיסים ומי הן השוקיים‪.‬‬
‫א‬
‫ב‬
‫‪K‬‬
‫‪B‬‬
‫ג‬
‫‪117‬‬
‫‪L‬‬
‫‪F‬‬
‫‪E‬‬
‫‪48‬‬
‫‪36‬‬
‫‪A 106‬‬
‫‪108‬‬
‫‪117‬‬
‫‪T 63‬‬
‫‪C‬‬
‫‪34‬‬
‫‪72‬‬
‫‪G‬‬
‫‪D‬‬
‫‪M‬‬
‫לא‪ .‬המרובע מקבילית‬
‫כן‪ .‬הבסיסים ‪ AD‬ו‪.BC -‬‬
‫‪48‬‬
‫‪H‬‬
‫כן‪ .‬הבסיסים ‪ HG‬ו‪.EF -‬‬
‫‪Q‬‬
‫עמ' ‪ .2 267‬נתון שהמרובע ‪ PQRS‬טרפז ( ‪.)PQ II SR‬‬
‫‪P‬‬
‫לכל אחד מהשוויונות רשמו אם ניתן להסיק מהנתון שהוא‪:‬‬
‫(‪ )1‬בוודאות נכון (‪ )2‬בוודאות לא נכון (‪ )3‬אי‪-‬אפשר לדעת‪.‬‬
‫א‪∡QPR = ∡PRS .‬‬
‫בוודאות נכון‪ .‬זוויות‬
‫מתחלפות בין מקבילים‪.‬‬
‫ב‪∡SPR = ∡QRP .‬‬
‫בוודאות לא נכון‪ .‬לו היה‬
‫השוויון מתקיים היו למרובע‬
‫שני זוגות צלעות נגדיות‬
‫מקבילות‪.‬‬
‫‪R‬‬
‫ג‪∡ PQS = ∡ QSR .‬‬
‫‪S‬‬
‫ה‪∡ PQR = ∡ QPS .‬‬
‫בוודאות נכון‪ .‬זוויות‬
‫מתחלפות בין מקבילים‪.‬‬
‫אי אפשר לדעת‪.‬‬
‫ו‪∡PSQ = ∡SQR .‬‬
‫ד‪∡ PSR = ∡ QRS .‬‬
‫בוודאות לא נכון‪ .‬לו היה השוויון‬
‫מתקיים היו למרובע שני זוגות‬
‫צלעות נגדיות מקבילות‪.‬‬
‫אי אפשר לדעת‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪142‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪ ABCD .3 267‬טרפז ישר‪-‬זווית‪ .CD  AD ,‬נתון‪.AC  BC :‬‬
‫‪B‬‬
‫‪A‬‬
‫‪44‬‬
‫‪46‬‬
‫איזו טענה נובעת בוודאות מתוך הנתונים? נמקו את תשובתכם‪.‬‬
‫א‪ .AC = CB .‬הטענה לא נובעת מהנתונים‪ .‬אם למשל ‪ ∡BAC = 44‬אז הזוויות‬
‫‪46‬‬
‫‪44‬‬
‫כמסומן באיור והקטעים אינם שווים‪.‬‬
‫‪C‬‬
‫‪D‬‬
‫ב‪.‬‬
‫‪ .∡BAC = ∡DAC‬הטענה לא נובעת מהנתונים‪ .‬בדוגמה שבסעיף א לא מתקיים שוויון זה‪.‬‬
‫ג‪.‬‬
‫‪ .∡ABC = ∡DAC‬נובעת מהנתונים‪ .‬נוכיח ז את באמצעות זוויות מתחלפות בין ישרים מקבילים וסכום הזוויות בשני‬
‫המשולשים הישרי‪-‬זווית‪ .‬סעיף ד קל מסעיף ג‪ ,‬אך מופיע אחריו כדי לאפשר לתלמידים להתמודד עם משימה מעט‬
‫יותר מורכבת ובמידה ולא הצליחו לפתור‪ ,‬פתרון סעיף ד עשוי לרמז להם כיצד לפתור את סעיף ג‪.‬‬
‫ד‪.‬‬
‫‪ .∡BAC =∡DCA‬נובעת מהנתונים‪ .‬הזוויות מתחלפות בין מקבילים‪.‬‬
‫‪ .4‬בכל אחד מהסעיפים הבאים‪ ,‬קבעו אם ניתן לדעת בוודאות שהמרובע ‪ ABCD‬הוא טרפז‪.‬‬
‫הסבירו כיצד ניתן לדעת זאת על‪-‬פי הנתונים‪.‬‬
‫‪F‬‬
‫א‪.‬‬
‫‪B‬‬
‫‪A‬‬
‫ב‪.‬‬
‫‪46‬‬
‫‪D‬‬
‫‪C‬‬
‫‪M‬‬
‫‪A‬‬
‫‪75‬‬
‫‪B‬‬
‫נתון‪ ABMD :‬מקבילית‪.‬‬
‫‪59‬‬
‫הצעה א‪ ∡ABC + ∡BAD >180 :‬כי ‪.∡ABM + ∡BAD= 180‬‬
‫‪D‬‬
‫‪C‬‬
‫הצעה ב‪ AB II CD :‬כצלעות נגדיות של מקבילית‪ CB .‬לא מקביל‬
‫ל‪ AD -‬כי ‪ CB‬ו‪ CM -‬נחתכים‪ .‬אילו ‪ BC‬היה מקביל ל‪ AD -‬הוא היה‬
‫חשבון זוויות במשולש ‪ABF‬‬
‫מקביל גם ל‪ .BM -‬שיקולים מסוג "אילו היה מתקיים" הם חשובים כי‬
‫מראה ש‪ ∡FBA = 59 -‬ומכאן ‪.BA II CD‬‬
‫הם מפתחים מיומנויות שיהיו דרושות בהוכחות בדרך השלילה‪.‬‬
‫שתי הצלעות האחרות נפגשות ב‪.F -‬‬
‫ג‪.‬‬
‫ג‪.‬‬
‫‪K‬‬
‫‪A‬‬
‫‪K‬‬
‫‪B‬‬
‫‪83‬‬
‫ד‪.‬‬
‫‪118‬‬
‫‪M‬‬
‫‪D‬‬
‫‪D‬‬
‫‪A‬‬
‫‪J‬‬
‫‪C‬‬
‫‪B‬‬
‫נתון‪ΔDJM  Δ AKM :‬‬
‫‪C‬‬
‫נתון‪ AKDC :‬מלבן‪.‬‬
‫מהחפיפה נובע ‪ ∡DJM = ∡MKA‬ומכאן ‪AB II CD‬‬
‫גם כאן‪ ,‬אפשר להוכיח על פי חשבון זוויות‬
‫הצלעות האחרות אינן מקבילות ולכן ‪ ABCD‬טרפז‪.‬‬
‫ש‪ ,AD II BC -‬אבל אין כל מידע לגבי‬
‫הצלעות האחרות‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪143‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫תרגיל ‪ 5‬נועד לחזור ולחזק את המיומנות של קריאת שיפוע של ישר ישירות מתוך סרטוט‪ ,‬ללא חישובים‪ .‬מיומנות זו חשובה‬
‫במיוחד לקראת תחילת לימודי האנליזה בכתה י‪.‬‬
‫עמ' ‪ .5 268‬א‪ .‬מי מבין המרובעים שלפניכם הוא טרפז? הסבירו‪.‬‬
‫ב‪ .‬מי מבין הטרפזים הוא ישר‪-‬זווית?‬
‫מרובע א אינו טרפז (הוא מקבילית)‪ .‬יש לו שני זוגות של צלעות מקבילות‪.‬‬
‫‪45‬‬
‫‪45‬‬
‫‪‬‬
‫‪‬‬
‫מרובע ב טרפז – יש לו זוג צלעות עם שיפוע ‪ 0‬וזוג צלעות עם שיפועים שונים‪.‬‬
‫מרובע ג טרפז – יש לו זוג צלעות עם שיפוע ‪ 2‬וזוג צלעות עם שיפועים שונים‪.‬‬
‫ה‬
‫מרובע ד אינו טרפז‪ .‬אמנם יש זוג צלעות שנראות מקבילות אולם התבוננות בסריג‬
‫המשבצות מעלה שהשיפועים לא שווים‪.‬‬
‫מרובע ה הוא טרפז ישר‪-‬זווית‪ .‬הדרך להראות‪ ,‬בכלים של כתה ט‪ ,‬שהטרפז ישר‪-‬זווית‬
‫מתבססת על חלוקת הזווית הישרה לשתי זוויות והוכחה שכל אחת מהן בת ‪ .45‬ניתן‬
‫להסיק מקווי הסריג ששני המשולשים האפורים ישרי‪-‬זווית ושווי‪-‬שוקיים‪ ,‬ולכן מידות‬
‫הזוויות החדות שלהם הן ‪ .45‬לכן הטרפז ישר‪-‬זווית‪.‬‬
‫מרובע ו הוא טרפז ישר‪-‬זווית‪ .‬יש לו שתי צלעות עם שיפוע ‪ ,0‬צלע מאונכת להן‪ ,‬וצלע שאינה מאונכת להן‪.‬‬
‫מרובע ז טרפז – יש לו זוג צלעות על ישרים חסרי שיפוע וזוג צלעות עם שיפועים שונים‪.‬‬
‫מרובע ח אינו טרפז‪ .‬אין אף זוג של צלעות נגדיות מקבילות‪.‬‬
‫‪y‬‬
‫ב‪.‬‬
‫א‪.‬‬
‫ג‪.‬‬
‫טרפז‬
‫טרפז‬
‫ה‪.‬‬
‫ד‪.‬‬
‫ו‪.‬‬
‫‪x‬‬
‫‪10‬‬
‫ח‪.‬‬
‫טרפז‬
‫ישר‪-‬זווית‬
‫‪25‬‬
‫טרפז‬
‫ישר‪-‬זווית‬
‫ז‪.‬‬
‫‪20‬‬
‫‪15‬‬
‫‪5‬‬
‫טרפז‬
‫‪15‬‬
‫‪10‬‬
‫‪5‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪144‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫הדוגמה הפתורה עוסקת בתופעה שחוזרת בהקשרים רבים‪ :‬משולש שווה‪-‬שוקיים שיוצר חוצה זווית של זווית הנוצרת‬
‫כשישר חותך זוג ישרים מקבילים‪ .‬העיקרון מופיע בתרגילים ‪ 8‬ו‪.9-‬‬
‫דוגמה פתורה – עמ' ‪268‬‬
‫המרובע ‪ ABCD‬טרפז (‪ .)CD II AB‬האלכסון ‪ DB‬חוצה את הזווית ‪.∡D‬‬
‫הוכיחו כי ‪AB = AD‬‬
‫נתון ‪DC II AB )1( :‬‬
‫‪A‬‬
‫‪B‬‬
‫(‪.∡D1 = ∡D2 )2‬‬
‫‪1‬‬
‫צ"ל‪AB = AD :‬‬
‫הוכחה‬
‫טענה‬
‫נימוק‬
‫‪∡D1 = ∡D2‬‬
‫נתון‪.‬‬
‫‪∡B1 = ∡D2‬‬
‫זוויות מתחלפות בין הישרים המקבילים ‪ AB‬ו‪.DC -‬‬
‫‪∡B1 = ∡D1‬‬
‫כלל המעבר (זוויות ששוות לאותה זווית שוות זו לזו)‪.‬‬
‫‪AB = AD‬‬
‫‪1‬‬
‫‪2‬‬
‫‪C‬‬
‫‪D‬‬
‫מול זוויות שוות במשולש מונחות צלעות שוות‪.‬‬
‫‪A‬‬
‫עמ' ‪269‬‬
‫‪ .6‬בטרפז ‪ AD( ABCD‬מקביל ל‪ P , )BC -‬על השוק ‪ ,AB‬ו‪ Q-‬על השוק ‪CD‬‬
‫‪P‬‬
‫‪D‬‬
‫כך ש‪ PQ -‬מקביל לבסיס ‪.AD‬‬
‫הראו כי המרובע ‪ PBCQ‬הוא טרפז‪.‬‬
‫‪Q‬‬
‫‪ PQ‬מקביל ל‪ AD -‬ולכן גם ל‪ .BC -‬הצלעות האחרות אינן מקבילות כי הן נמצאות‬
‫‪B‬‬
‫‪C‬‬
‫על אותם ישרים כמו שוקי הטרפז הנתון שאינן מקבילות‪.‬‬
‫‪B‬‬
‫‪A‬‬
‫‪ .7‬בטרפז ‪ M )AD II BC( ABCD‬היא נקודת חיתוך האלכסונים‪.‬‬
‫א‪ .‬הוכיחו שמשולש ‪ ADM‬דומה למשולש ‪.CBM‬‬
‫‪M‬‬
‫בין המקבילים נוצרות זוויות מתחלפות שוות‪.‬‬
‫‪D‬‬
‫ב‪ .‬האם גם המשולשים ‪ ABM‬ו‪ CDM -‬בהכרח דומים? הסבירו‪.‬‬
‫המשולשים כמובן לא בהכרח דומים‪ .‬להלן דוגמה‪:‬‬
‫‪C‬‬
‫ג‪ .‬האם ייתכן שהמשולשים ‪ ABM‬ו‪ CDM -‬חופפים? הסבירו‪.‬‬
‫המשולשים יכולים להיות חופפים במקרה של משולש שווה‪-‬שוקיים (כדאי לציין‬
‫שמשולשים חופפים הם גם דומים‪ ).‬כיוון שעדין לא למדנו על טרפז שווה‪-‬שוקיים‬
‫אפשר לבנות את הדוגמה בדרך הבאה‪ :‬נבנה משולש שווה‪-‬שוקיים‪ .‬נאריך את השוקיים‬
‫מעבר לקדקוד כך שהתוספת לא תהיה שווה לשוק המשולש (כדי שלא נקבל זוג משולשים‬
‫חופפים‪ .‬נקבל עוד משולש שווה‪-‬שוקיים עם אותה זווית ראש‪ ,‬ולכן גם עם אותן זוויות בסיס‪.‬‬
‫לכן קיבלנו טרפז‪.‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪145‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪ .8 269‬המרובע ‪ HEGP‬הוא טרפז (‪.)HE II PG‬‬
‫‪H‬‬
‫‪E‬‬
‫‪.∡EPG = 33º ,PH = HE‬‬
‫‪33º‬‬
‫‪114º‬‬
‫א‪ .‬מצאו את מידת הזווית ‪ .114 .∡PHE‬חישובי הזוויות מתבססים על זוויות‬
‫‪33º‬‬
‫מתחלפות בין מקבילים ועל זוויות בסיס במשולש שווה‪-‬שוקיים‪.‬‬
‫‪G‬‬
‫‪z‬‬
‫‪33º‬‬
‫‪P‬‬
‫ב‪ .‬האם ניתן לדעת‪ ,‬על‪-‬פי הנתונים‪ ,‬את גודלה של הזווית ‪ ? ∡HEG‬הסבירו‪.‬‬
‫לא ניתן לדעת‪ :‬אין כל מידע על ‪ .EG‬אפשר להדגים זאת על ידי שינוי השוק ‪ EG‬שאינו משפיע על הנתונים האחרים‪.‬‬
‫ג‪ .‬הוכיחו‪ ,‬ללא קשר לנתונים המספריים‪ :‬אם ‪HE = HP‬‬
‫אז האלכסון ‪ PE‬חוצה את הזווית ‪.∡HPG‬‬
‫צעדי ההוכחה העיקריים בדומה לדוגמה הפתורה בעמ' ‪:268‬‬
‫‪ ∡HPE = ∡HEP‬זוויות בסיס במשולש שווה‪-‬שוקיים שוות‪.‬‬
‫‪ ∡GPE = ∡HEP‬זוויות מתחלפות בין מקבילים שוות‪.‬‬
‫‪ ∡HPE = ∡GPE‬על פי כלל המעבר‪.‬‬
‫‪ .9‬נתון טרפז ‪.)LE II FT( LEFT‬‬
‫‪E‬‬
‫‪ EK‬חוצה זווית ‪ FK ,∡E‬חוצה ‪.∡F‬‬
‫‪L‬‬
‫‪‬‬
‫‪.KM II TF‬‬
‫‪‬‬
‫‪‬‬
‫‪M‬‬
‫צריך להוכיח‪:‬‬
‫‪‬‬
‫א‪.MF = EM .‬‬
‫‪F‬‬
‫‪‬‬
‫‪K‬‬
‫‪‬‬
‫‪T‬‬
‫בדומה לדוגמה הפתורה בעמ' ‪:268‬‬
‫הזוויות השוות מסומנות באותו אופן‪ .‬מקבלים‪.MF = KM = EM :‬‬
‫ב‪KE  KF .‬‬
‫מחישוב זוויות במשולש ‪ KEF‬נקבל‪ + = 90  2 +2 = 180 :‬‬
‫עמ' ‪ .11 270‬בטרפז ‪ AD( ABCD‬מקביל ל‪ )BC -‬הנקודה ‪ E‬היא אמצע השוק ‪.DC‬‬
‫‪D‬‬
‫נסמן‪ a :‬הוא הבסיס ‪ b ,AD‬הוא הבסיס ‪ ,BC‬ו‪ h -‬הוא גובה הטרפז‪.‬‬
‫‪E‬‬
‫האריכו את הקטע ‪ AE‬עד לנקודת חיתוכו עם המשך הבסיס ‪.BC‬‬
‫‪ F‬היא נקודת החיתוך‪.‬‬
‫‪a‬‬
‫‪F‬‬
‫‪a‬‬
‫‪C‬‬
‫‪A‬‬
‫‪h‬‬
‫‪b‬‬
‫‪B‬‬
‫א‪ .‬הוכיחו‪ :‬משולש ‪ ∆ADE‬חופף למשולש ‪ .∆FCE‬לפי ז‪.‬צ‪.‬ז‬
‫ב‪ .‬בטאו באמצעות ‪ h ,b ,a‬את שטח המשולש ‪.∆ABF‬‬
‫‪(a  b)h‬‬
‫מהחפיפה מקבלים ‪ .CF = a‬לכן שטח המשולש‬
‫‪2‬‬
‫‪(a  b)h‬‬
‫ג‪ .‬מה היחס בין שטח המשולש לבין שטח הטרפז? שטח הטרפז הוא‬
‫‪2‬‬
‫ולכן יחס השטחים הוא ‪.1:1‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪146‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫בתרגילים ‪ 11‬ו‪ 12 -‬אנחנו מוסיפים בניות עזר שמאפשרות לבצע חישובים על פי משפט פיתגורס‪.‬‬
‫עמ' ‪270‬‬
‫‪ .11‬הגובה של טרפז הוא ‪ 12‬ס"מ‪ ,‬אורך הבסיס הקצר ‪ 7‬ס"מ‪ ,‬ואורכי שתי השוקיים ‪13‬‬
‫ס"מ ו‪ 15 -‬ס"מ‪.‬‬
‫מצאו את אורך הבסיס הארוך של הטרפז‪ 21 .‬ס"מ‬
‫באמצעות משפט פיתגורס נקבל את מידות הקטעים כמפורט באיור‪.‬‬
‫‪ .12‬המרובע ‪ ABCD‬הוא טרפז (‪,)CD II AB‬‬
‫‪B‬‬
‫‪ ABFE‬הוא ריבוע‪ .‬נתון כי השוק ‪ AD‬ארוכה פי ‪ 2‬מצלע הריבוע‪.‬‬
‫‪5‬‬
‫‪A‬‬
‫‪7.07‬‬
‫‪5‬‬
‫הנקודה ‪ F‬אמצע הקטע ‪ 5 .EC‬ס"מ = ‪.AB‬‬
‫מצאו את שטח הטרפז ואת היקפו‪.‬‬
‫‪C‬‬
‫היקף‪ 40.75 :‬ס"מ‪ .‬שטח ‪ 59.15‬סמ"ר‬
‫‪5‬‬
‫‪F‬‬
‫‪5‬‬
‫‪E‬‬
‫‪10‬‬
‫‪8.66‬‬
‫‪D‬‬
‫כל חישובי הצלעות מתבססים על משפט פיתגורס‪.‬‬
‫‪ .13‬במשולש ‪ ∆ABC‬העבירו ישר מקביל לצלע ‪ BC‬החותך את הצלע ‪AB‬‬
‫‪A‬‬
‫בנקודה ‪ D‬ואת הצלע ‪ AC‬בנקודה ‪.E‬‬
‫א‪ .‬הוכיחו כי המרובע ‪ DBCE‬הוא טרפז‪.‬‬
‫זוג אחד של צלעות נגדיות מקבילות וזוג שני של צלעות נגדיות על ישרים שנפגשים בנקודה ‪.A‬‬
‫‪E‬‬
‫‪D‬‬
‫ב‪ .‬נתון‪ :‬במשולש ‪ ∆ABC‬זווית ‪ ∡A‬בת ‪70‬‬
‫וזווית ‪ ∡B‬בת ‪ .40‬חשבו את מידת כל זוויות הטרפז‪.110 ,140 ,40 ,70 .‬‬
‫‪C‬‬
‫‪B‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪147‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫בתרגיל ‪ 14‬קיימות בכל סעיף שתי אפשרויות לקבוע מי הן הצלעות המקבילות‪ ,‬והנקודה ‪ D‬יכולה להיות בכל מקום על הישר‬
‫המקביל לצלע הנתונה‪ ,‬מלבד שתי נקודות שבהן נוצרת מקבילית (ראו סרטוטים והסבר בהמשך)‪ .‬שתי דוגמאות אפשריות‬
‫לפתרון‪ ,‬מסורטטות ‪ .‬מיקום הקדקוד הנוסף מסומן ב‪ D -‬או ב‪.D -‬‬
‫עמ' ‪ .14 270‬בכל אחד מהסעיפים העתיקו את הנקודות למחברת והוסיפו קדקוד ‪ D‬כך שיתקבל טרפז ‪.ABCD‬‬
‫פתרונות אפשריים‪:‬‬
‫‪D‬‬
‫‪C‬‬
‫‪A‬‬
‫‪A‬‬
‫‪B‬‬
‫‪B‬‬
‫‪D‬‬
‫‪D‬‬
‫‪B‬‬
‫‪A‬‬
‫‪C‬‬
‫‪C‬‬
‫‪D‬‬
‫א‬
‫‪D‬‬
‫ג‬
‫ב‬
‫‪D‬‬
‫הסרטוטים הבאים ממחישים בקו אדום מקוקו וסימון הנקודה ‪ E‬ובקו ירוק מקוקו וסימון הנקודה ‪ ,G‬את שני המקומות‬
‫היחידים על הישר המקביל לצלע הנתונה‪ ,‬בו לא ניתן למקם את הנקודה ‪ D‬כי מתקבלת מקבילית ולא טרפז כנדרש‪.‬‬
‫בכל סרטוט יש שני מקומות כאלה‪ .‬ניתן להדגים זאת גם לתלמידים הכיתה‪.‬‬
‫‪G‬‬
‫‪G‬‬
‫‪A‬‬
‫‪A‬‬
‫‪C‬‬
‫‪B‬‬
‫‪B‬‬
‫‪E‬‬
‫‪D‬‬
‫‪B‬‬
‫‪C‬‬
‫‪D‬‬
‫א‬
‫‪E‬‬
‫‪A‬‬
‫‪E‬‬
‫‪C‬‬
‫‪G‬‬
‫ב‬
‫‪D‬‬
‫ג‬
‫‪A‬‬
‫‪D‬‬
‫עמ' ‪ .15 271‬במשולש ‪ ∆ABC‬חוצה הזווית ‪ B‬חותך את הצלע ‪ AC‬בנקודה ‪.D‬‬
‫‪ E‬נקודה על הצלע ‪ AB‬המקיימת‪.EB=ED :‬‬
‫‪1‬‬
‫‪2‬‬
‫‪1‬‬
‫‪C‬‬
‫הוכיחו כי ‪ EBCD‬הוא טרפז‪.‬‬
‫‪E‬‬
‫‪B‬‬
‫כמו במספר תרגילים קודמים גם בתרגיל זה יש שילוב של זוויות שוות שיוצר חוצה זווית וזוויות בסיס של‬
‫משולש שווה‪-‬שוקיים‪ ,‬ממנו נובע ש‪ ∢B1=∢D1 -‬ומכאן ‪ .ED II BC‬המשכי הצלעות האחרות נפגשים בנקודה ‪.A‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪148‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫עמ' ‪271‬‬
‫‪ .16‬א‪ .‬בנו טרפז ישר‪-‬זווית באמצעות שני הבסיסים והשוק המאונכת לבסיסים‪.‬‬
‫ב‪ .‬כמה טרפזים שאינם חופפים ניתן לבנות באמצעות הנתונים?‬
‫בסיס‬
‫ג‪ .‬האם כל צירוף של נתונים מאפשר לבנות את הטרפז? הסבירו‪.‬‬
‫בסיס‬
‫ד‪ .‬בנו טרפז שאיננו ישר‪-‬זווית על‪-‬פי הנתונים‪ .‬כמה טרפזים תוכלו לבנות הפעם?‬
‫שוק‬
‫שלבי הבנייה‪:‬‬
‫נעתיק את הבסיס הגדול‪ .‬נעלה אנך בקצהו ונעתיק עליו את הגובה (השוק הנתונה)‪ .‬נעלה אנך בקצה הגובה ונסמו עליו‬
‫את הבסיס הקטן‪ .‬קיבלנו את ארבעת הקדקודים ונותר לסרטט את הצלע הרביעית‪.‬‬
‫‪ .17‬א‪ .‬בנו טרפז ישר‪-‬זווית באמצעות הבסיס הגדול ושתי השוקיים‪.‬‬
‫בסיס גדול‬
‫שלבי הבנייה‪:‬‬
‫נבנה את הבסיס הגדול‪.‬‬
‫שוק מאונכת לבסיס‬
‫נעלה אנך בקצהו ונעתיק עליו את הצלע המאונכת‪.‬‬
‫שוק נוספת‬
‫נעביר דרך קצה הצלע המאונכת מקביל לבסיס הגדול‪.‬‬
‫מהקצה השני של הבסיס הגדול נחוג מעגל ברדיוס השווה לשוק השנייה‪ .‬המעגל פוגש את המקביל בשתי נקודות‪.‬‬
‫רק אחת מהן מתאימה להיות הקדקוד הרביעי של הטרפז בהתאם לדרישה שהבסיס הנתון הוא הבסיס הגדול‪.‬‬
‫ב‪ .‬כמה טרפזים שאינם חופפים ניתן לבנות באמצעות הנתונים? אחד‬
‫ג‪ .‬האם כל צירוף של נתונים מאפשר לבנות את הטרפז? הסבירו‪ .‬השוק המאונכת לבסיס צריכה להיות קצרה מהשוק‬
‫השנייה‪.‬‬
‫ד‪ .‬האם יכולתם לדעת בעצמכם מי השוק המאונכת לבסיס? הסבירו‪ .‬יכולנו לדעת שהשוק הקצרה היא המאונכת‪.‬‬
‫האנך הוא הקטע הקצר ביותר בין שתי נקודות שעל ישרים מקבילים‪.‬‬
‫‪ .18‬המרובעים ‪ ABFE‬ו‪ EFCD -‬הם טרפזים‪.‬‬
‫‪B‬‬
‫האם נובע מכך שגם המרובע ‪ ABCD‬טרפז? לא‬
‫מהנתונים נובע ש‪ ,AB II DC -‬אולם לא נובע מהנתונים שאין למרובע צלעות‬
‫‪A‬‬
‫‪F‬‬
‫‪E‬‬
‫מקבילות נוספות‪ .‬מכאן שלא ניתן להסיק מהנתונים ש‪ ABCD -‬טרפז‪.‬‬
‫אם כן – הוכיחו‪.‬‬
‫‪D‬‬
‫‪C‬‬
‫אם לא – הוסיפו מידע ממנו ניתן להסיק בוודאות שהמרובע ‪ ABCD‬טרפז‪ .‬למשל‪,‬‬
‫‪.AB  DC‬‬
‫‪A‬‬
‫‪1‬‬
‫‪ .19‬המרובע ‪ ABCD‬הוא טרפז (‪ DT .) AD II BC‬אנך אמצעי לאלכסון ‪.AC‬‬
‫‪B‬‬
‫הוכיחו שהאלכסון ‪ AC‬חוצה את הזווית ‪.∡DCB‬‬
‫זהו תרגיל נוסף שבו מעורבים משולש שווה‪-‬שוקיים‪ ,‬ישרים מקבילים וחוצה זווית‪.‬‬
‫‪DC =AD‬‬
‫משולש שבו תיכון הוא גם גובה הוא שווה‪-‬שוקיים‪.‬‬
‫‪∢A1 = ∢C1‬‬
‫במשולש שווה‪-‬שוקיים זוויות הבסיס שוות‪.‬‬
‫‪∢A1 = ∢C2‬‬
‫זוויות מתחלפות בין ישרים מקבילים (‪ )AD II BC‬שוות‪.‬‬
‫‪∢C1 = ∢C2‬‬
‫כלל המעבר‪.‬‬
‫‪T‬‬
‫‪2‬‬
‫‪C‬‬
‫‪1‬‬
‫‪D‬‬
‫____________________________________________________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪149‬‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬
‫ארגז הכלים בספר מכיל את הנחות היסוד והמשפטים שעליהם אפשר להתבסס בתחילת כיתה ט‪ .‬הרעיון שהתלמידים יקבלו‬
‫העתק של עמוד זה בתחילת השנה וישתמשו במשפטים שנלמדו לפני כיתה ט ובכל פעם שילמדו משפט חדש יוסיפו אותו באופן‬
‫עצמאי לרשימה שלהם‪ .‬כך יבנה‪ ,‬באופן הדרגתי‪ ,‬ארגז כלים המכיל את המשפטים עליהם הם יכולים להתבסס בהוכחותיהם‬
‫בכל שלב בלמידה‪.‬‬
‫ארגז כלים‬
‫– עמ' ‪298‬‬
‫משפטים בגאומטריה – הנחות יסוד ומשפטים שלמדנו בכיתות ז ו‪ -‬ח‪.‬‬
‫‪‬‬
‫כלל המעבר (טרנס יטיביות)‪ :‬שני עצמים גאומטריים ששווים‪/‬חופפים לעצם שלישי שווים‪/‬חופפים ביניהם‪.‬‬
‫‪‬‬
‫כלל החיבור (לקטעים)‪ :‬שני קטעים‪ ,‬שכל אחד מהם מחולק לשני קטעים זרים‪ ,‬שווים אם הקטעים שמרכיבים אותם שווים‬
‫בהתאמה‪.‬‬
‫‪‬‬
‫כלל החיבור (לזוויות)‪ :‬שתי זוויות‪ ,‬שכל אחת מהן מחולקת לשתי זוויות זרות‪ ,‬שוות אם הזוויות המרכיבות אותן שוות‬
‫בהתאמה‪.‬‬
‫‪‬‬
‫בין כל שתי נקודות עובר קו ישר יחיד‪.‬‬
‫‪‬‬
‫סכום זוויות צמודות הוא ‪ 180‬מעלות‪.‬‬
‫‪‬‬
‫זוויות קודקודיות שוות זו לזו‪.‬‬
‫‪‬‬
‫משפט חפיפה צלע‪-‬זווית‪-‬צלע‪ :‬אם שני משולשים שווים בהתאמה בשתי צלעות ובזווית שביניהן‪ ,‬אז המשולשים חופפים‪.‬‬
‫‪‬‬
‫משפט חפיפה זווית‪-‬צלע‪-‬זווית‪ :‬אם שני משולשים שווים בהתאמה בשתי זוויות והצלע הכלואה ביניהן‪ ,‬אז המשולשים‬
‫חופפים‪.‬‬
‫‪‬‬
‫משפט חפיפה צלע‪ -‬צלע‪ -‬צלע‪ :‬אם שני משולשים שווים בהתאמה בשלוש צלעות‪ ,‬אז המשולשים חופפים‪.‬‬
‫‪‬‬
‫שני משולשים ישרי‪-‬זווית השווים בניצב ויתר חופפים‪.‬‬
‫‪‬‬
‫במשולש שווה‪-‬שוקיים חוצה זווית הראש‪ ,‬תיכון לבסיס‪ ,‬וגובה לבסיס מתלכדים‪.‬‬
‫‪‬‬
‫במשולש שווה‪-‬שוקיים זוויות הבסיס שוות זו לזו‪.‬‬
‫‪‬‬
‫אם שני קווים הם מקבילים‪ ,‬אז זוויות מתחלפות ביניהם שוות‪.‬‬
‫‪‬‬
‫סכום הזוויות במשולש הוא ‪ 180‬מעלות‪.‬‬
‫‪‬‬
‫סכום הזוויות הפנימיות במצולע קמור‪ ,‬בעל ‪ n‬צלעות‪ ,‬הוא ‪ (n-2)180‬מעלות‪.‬‬
‫‪‬‬
‫זווית חיצונית למשולש‪ ,‬שווה לסכום שתי הזוויות הפנימיות שאינן צמודות לה‪ ,‬ובפרט גדולה מכל זווית פנימית שאינה‬
‫צמודה לה‪.‬‬
‫‪‬‬
‫סכום אורכי שתי צלעות במשולש‪ ,‬גדול מאורך הצלע השלישית‪.‬‬
‫‪‬‬
‫משפט פיתגורס‪ :‬במשולש ישר‪-‬זווית סכום ריבועי הניצבים שווה לריבוע היתר‪.a + b = c :‬‬
‫‪‬‬
‫שני משולשים שכל זוויותיהם שוות בהתאמה הם דומים‪.‬‬
‫‪2‬‬
‫_______________________________________________________________________‬
‫© כל הזכויות שמורות "אפשר גם אחרת"‬
‫‪150‬‬
‫‪2‬‬
‫‪2‬‬
‫__________________________________‬
‫מדריך למורה לכיתה ט ‪ -‬ספר אפור‪ ,‬חלק א‬