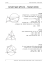זוויות משולשים קטעים מיוחדים זוויות בין ישרים משולשים חופפים

‫מונח‬
‫הגדרה ‪ /‬משפט‬
‫זוויות צמודות‬
‫שתי זוויות שלהן שוק אחת משותפת וקודקוד אחד משותף‪ ,‬ושתי השוקיים‬
‫האחרות נמצאות על ישר אחד‪.‬‬
‫זוויות‬
‫זוויות‬
‫קדקודיות‬
‫משפט‪ :‬סכום זוויות צמודות שווה ל‪.180 -‬‬
‫שני ישרים החותכים זאת את זה יוצרים ארבע זוויות‪ .‬כל שתי זוויות שאינן‬
‫צמודות נקראות זוויות קדקודיות‪.‬‬
‫בסרטוט הזוויות הקדקודיות הן‪ ∢α :‬ו‪ ∢γ ,∢β-‬ו‪.∢δ-‬‬
‫משפט‪ :‬זוויות קדקודיות שוות זו לזו‪.‬‬
‫משולשים‬
‫משולש שווה‬
‫שוקיים‬
‫משולש ששתיים מצלעותיו שוות‪.‬‬
‫הצלעות השוות נקראות שוקיים )‪(AB=AC‬‬
‫הצלע השלישית נקראת בסיס )‪(BC‬‬
‫משולש שווה צלעות הוא משולש שכל צלעותיו שוות‪.‬‬
‫קטע היוצא מקודקוד זווית המשולש ומחלק את הזווית לשתי זוויות שוות‪.‬‬
‫קטעים מיוחדים‬
‫חוצה זוויות‬
‫במשולש‬
‫‪ AD‬הוא חוצה זווית ‪∢A1=∢A2 .∢BAC‬‬
‫תיכון במשולש‬
‫קטע המחבר את קודקוד המשולש עם אמצע הצלע שמולו‪ AE :‬הוא תיכון‬
‫במשולש ‪.BE=EC .△ABC‬‬
‫גובה במשולש‬
‫קטע היוצא מקודקוד משולש ומאונך לצלע שממול )או להמשכה(‪.‬‬
‫‪ AD‬הוא גובה לצלע ‪ BC‬במשולש ‪ ,△ABC‬או‪90O=∢ADC :‬‬
‫סכום זוויות‬
‫במשולש‬
‫זוויות בין ישרים‬
‫זוויות‬
‫מתאימות‬
‫משפט‪ :‬סכום הזוויות במשולש שווה ל‪.180O-‬‬
‫‪180O=α+β+γ‬‬
‫שתי זוויות‪ ,‬הנמצאות באותו צד של הישר החותך ובאותו צד של הישרים‬
‫הנחתכים‪.‬‬
‫‪ ∢4‬ו‪ ∢3 ,∢8 -‬ו‪ ∢2 ,∢7 -‬ו‪ ∢1 ,∢6 -‬ו‪.∢5 -‬‬
‫משפט‪ :‬כל שתי זוויות מתאימות שוות‪.‬‬
‫זוויות‬
‫מתחלפות‬
‫שתי זוויות‪ ,‬הנמצאות בצדדים השונים של הישר החותך ובצדדים השונים של‬
‫הישרים הנחתכים‪.‬‬
‫‪ ∢3‬ו‪ ∢2 ,∢5 -‬ו‪ ∢4 ,∢8 -‬ו‪ ∢1 ,∢6 -‬ו‪.∢7 -‬‬
‫משפט‪ :‬כל שתי זוויות מתחלפות שוות‪.‬‬
‫משולשים חופפים‬
‫משולשים‬
‫חופפים‬
‫שני משולשים הם חופפים אם ניתן להניח משולש אחד על האחר באופן שיכסה‬
‫אותו בדיוק‪.‬‬
‫משפט צ‪.‬ז‪.‬צ‪ :‬אם שתי הצלעות והזווית ביניהן במשולש אחד שוות בהתאמה‬
‫לשתי הצלעות והזווית ביניהן במשולש אחר‪ ,‬אזי המשולשים חופפים‪.‬‬
‫משפט ז‪.‬צ‪.‬ז‪ :‬אם צלע ושתי הזוויות שלידה במשולש אחד שוות בהתאמה לצלע‬
‫ולשתי הזוויות שלידה במשולש אחר‪ ,‬אזי המשולשים חופפים‪.‬‬
‫משפט צ‪.‬צ‪.‬צ‪ :‬אם שלוש צלעות במשולש אחד שוות בהתאמה לשלוש הצלעות‬
‫במשולש אחר‪ ,‬אזי המשולשים חופפים‪.‬‬
‫שרטוט‬