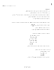בס``ד ריבוע נתון : ABCD אמצע BC E שווה לצלע הריבוע. :ל``צ CF הוכחה: צלע

‫בס''ד‬
‫נתון ‪ ABCD :‬ריבוע‬
‫‪ E‬אמצע ‪BC‬‬
‫צ''ל‪ CF :‬שווה לצלע הריבוע‪.‬‬
‫הוכחה‪:‬‬
‫‪ ‬נשתמש במה שהתחלת יפה ונמשיך את צלע ‪ AE‬עד שיפגוש את המשך צלע ‪DC‬‬
‫‪ ‬נסמן את נק' המפגש ב ‪G‬כמו שעשית ‪.‬‬
‫נסתכל כעת על המשולשים ‪ ∆ECG‬ו ‪∆EBA‬‬
‫∢ זוויות קודקודיות שוות‪.‬‬
‫∢‬
‫∢ משלימה ל ‪ 081‬את‬
‫∢‬
‫‪BE =CE‬‬
‫∆≅‬
‫∢ זווית ישרה בריבוע‬
‫∢ זוויות בעלות אותו הגודל הן שוות‪.‬‬
‫נתון כי ‪ E‬אמצע ‪BC‬‬
‫ולכן ‪ BA =CG‬צלעות מתאימות שוות במשולשים חופפים‪.‬‬
‫כלומר ‪CD=BA‬‬
‫ולכן ‪ CG =DC‬החלפת גדלים שווים בגדלים שווים‬
‫כעת נסתכל על משולש ‪ ∆ FDG‬זהו משולש ישר זווית לפי הנתון‬
‫ואנך לצלע יוצר זווית ישרה‪.‬‬
‫הנק' ‪C‬היא אמצע הצלע ‪ DG‬ולכן ‪FC‬הוא תיכון ליתר במשולש‬
‫קיבלנו כי ‪ DC =FC‬במשולש ישר זווית התיכון ליתר שווה למחצית היתר‪.‬‬
‫כלומר ‪CF‬שווה לצלע הריבוע‪.‬‬
‫מ‪.‬ש‪.‬ל‬
‫(ז)‬
‫(צ)‬
‫∆ לפי משפט חפיפה ז‪.‬צ‪.‬ז‬
‫נזכור כי מדובר בריבוע – על כן כל צלעותיו שוות‬
‫(ז)‬