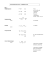ÅRSREGNSKAB 2013 FINANCIAL STATEMENTS FOR 2013 CVR

Formelsamling
Fra atomer og molekyler til materialer
Mikkel Bregnhøj
Oktober 2008
Indhold:
Forord og kildehenvisning..........................................................................................side 1
Molarmasser................................................................................................................. side 2
Antalsmidlet molarmasse............................................................................................side 2
Massemidlet molarmasse............................................................................................side 2
Polydispersitetsindeks................................................................................................ side 2
Eksempel.................................................................................................................... side 2
Osmose......................................................................................................................... side 3
Anden virialkoefficient............................................................................................... side 3
Eksempel.................................................................................................................... side 4
Polymerers længde og bevægelser............................................................................ side 5
Random walk..............................................................................................................side 5
Valence angle model................................................................................................... side 5
Restricted bond angle model...................................................................................... side 5
Gyrationsradius...........................................................................................................side 5
Eksempel.................................................................................................................... side 6
Elektromagnetisk tiltrækning og frastødning...........................................................side 7
Coulombs lov.............................................................................................................. side 7
Dipol-dipol vekselvirkning.........................................................................................side 7
Debyelængde.............................................................................................................. side 7
Eksempel.................................................................................................................... side 8
Generel rumgeometri.................................................................................................. side 9
Cirkler......................................................................................................................... side 9
Kugler......................................................................................................................... side 9
Cylindere.................................................................................................................... side 9
Mængdeberegning...................................................................................................... side 9
Micellers rumgeometri................................................................................................side 10
Pakningsparameter......................................................................................................side 10
Aggregeringstal...........................................................................................................side 10
Eksempel.................................................................................................................... side 11
Diverse..........................................................................................................................side 12
Konstanter...................................................................................................................side 12
Enheder....................................................................................................................... side 12
Omregningstabeller mellem enheder.......................................................................... side 12
Forord og kildehenvisning:
Nærværende formelsamling er et forsøg på at samle al den nødvendige viden for at kunne bestå
grundkurset ”Fra atomer og molekyler til materialer”, udbudt ved Kemisk Institut, Århus
Universitet. Formlerne i formelsamlingen er i det store hele magen til dem givet i ”Introduction to
Soft Matter” af Ian W. Hamley, Revised Edition, Wiley, 2007. Konstanter og tabelværdier er fra
”Kompendium i fysik”, udarbejdet af undervisningsministeriet, 1994, samt ”Databogen i fysik og
kemi” af Erik Strandgaard Andersen, Paul Jespersgaard og Ove Grønbæk Østergaard, 11. udgave,
2007. En speciel tak skal gives til professor Jan Skov Pedersen, Kemisk Institut, Århus Universitet,
for korrekturlæsning og god undervisning.
Mikkel Bregnhøj, Risskov, Oktober 2008.
1
Molarmasser:
Antalsmidlet molarmasse. Number-averaged molekular weight.
MN=
∑ ni⋅M i
∑ ni
MN=
∑ N i⋅M i
∑ Ni
ni er stofmængden af molekyler, der har molarmassen Mi. Ni er antallet af molekyler med
molarmassen Mi.
Massemidlet molarmasse. Weight-averaged molekular weight.
MW =
∑ wi⋅M i
∑ wi
MW =
∑ mi⋅M i
∑ mi
wi er vægtandelen af molekyler, der har molarmassen Mi. mi er massen af molekyler med
molarmassen Mi.
Polydispersitetsindeks PDI:
PDI =
MW
MN
Polydispersitetsindekset er et mål for hvor ens molekylerne i en opløsning er. Kun når molekylerne
er 100% monodisperse (samme kædelængde og molarmasse) er PDI = 1. Ellers er PDI altid større
end 1. Polydispersitetsindekset er dimensionsløst, dvs. uden enhed.
Eksempel:
I en opløsning er der 3 forskellige polymerer, kaldet 1, 2 og 3. De har hver især molarmasserne M1,
M2 og M3, og stofmængderne n1, n2 og n3. Find polydispersitetsindekset.
M1 = 10.000 g/mol
M2 = 15.000 g/mol
M3 = 20.000 g/mol
n1 = 2,00 mol
n2 = 1,00 mol
n3 = 0,50 mol
Den antalsmidlede molarmasse er:
∑ ni⋅M i n 1⋅M 1 n 2⋅M 2n3⋅M 3
MN=
=
∑ ni
n1n2n3
M N=
2,00 mol⋅10000 g / mol1,00 mol⋅15000 g /mol0,50 mol⋅20000 g /mol
g
=12857
2,00 mol1,00 mol0,50 mol
mol
og den massemidlede molarmasse er:
MW =
∑ mi⋅M i M 1⋅n1⋅M 1M 2⋅n2⋅M 2M 3⋅n 3⋅M 3
=
∑ mi
M 1⋅n 1M 2⋅n 2M 3⋅n3
MW =
2,00 mol⋅10000 g /mol 1,00 mol⋅15000 g /mol  0,50 mol⋅20000 g / mol
g
=13889
2,00 mol⋅10000 g / mol1,00 mol⋅15000 g /mol0,50 mol⋅20000 g /mol
mol
2
2
2
Og polydispersitetsindekset bliver:
MW
13889 g / mol
PDI =
=
= 1,080
MN
12857 g / mol
2
Osmose:
Når man opløser en polymer (eller andet stort molekyle) i et membran-osmometer, opstår der et
osmotisk tryk, som kan beskrives ved følgende ligning:
π
1
= R⋅T⋅
A 2⋅cA 3⋅c2 A 4⋅c3 ...
c
MN
π er det osmotiske tryk, c er koncentrationen af polymer i opløsningen. A2, A3, A4 osv. kaldes
virialkoefficienterne. Hvis polymeren opfører sig som en ideal gas er A2, A3, A4, ... = 0.
Virialkoefficienterne tager højde for at molekylerne påvirker hinanden. I praksis regner man med, at
A3 og højere er lig 0, hvorved ligningen kommer til at se således ud.
π
R⋅T
=
 R⋅T⋅A 2⋅c
c
MN
En lineær afbildning af π/c som funktion af c vil derfor give en ret linje med hældningskoefficienten
a = R·T·A2 og som skærer π/c-aksen i b = R·T/MN.
Anden virialkoefficient:
Den anden virialkoefficient A2, angiver om opløsningsmidlet er et godt, et dårligt eller theta-solvent.
Godt opløsningsmiddel
A2 > 0
Theta-solvent
A2 = 0
Dårligt opløsningsmiddel
A2 < 0
I et godt opløsningsmiddel tiltrækker solventmolekylerne og polymeren hinanden. Derfor forsøger
polymer-molekylerne at få så stor kontaktflade med opløsningsmidlet som muligt og de folder sig
ud til lange kæder. Tilsvarende er der stor frastødning mellem polymer og solvent i et dårligt
opløsningsmiddel og polymerene klumper sig sammen for at mindske overfladearealet. Man kan i
dette tilfælde regne på polymerene, som var de kugler. I et thetasolvent er der hverken frastødning
eller tiltrækning. Her vil polymeren opføre sig nogenlunde som en ideal gas.
3
Eksempel:
Ved et osmoseforsøg har man målt følgende ved 25 ºC:
Find den antalsmidlede molarmasse. Er opløsningsmidlet godt, dårligt eller theta?
π / Pa
71,5
148,5
237
368,5
504
660,5
8
12
16
20
24
28
8,9375
12,375
14,8125
18,425
21
23,589
c / kg/m3
π/c / kg/(m3·Pa)
Vi tegner da en graf over π/c som funktion af c og udfører lineær regression på datasættet:
Lineær regression:
Den bedste rette linie med ligningen
y = a·x + b er givet ved:
a = 0.734
b = 3.31
Der gælder da at:
J
J⋅m 3
a=R⋅T⋅A 2 = 8,314
⋅ 298 K⋅A 2=0,734
2
mol⋅K
kg
b =
R⋅T
=
MN
8,314
J
⋅ 298 K
mol⋅K
J
= 3,31
MN
kg
A 2 = 2,963⋅10
M N = 748,51
-4
mol⋅m 3
2
kg
kg
mol
OBS: Det er vigtigt at man holder styr på enhederne! a og b har også enheder!
Generelt gælder, at hvis c måles i kg/m3 eller i g/L og π måles i Pa eller N/m2, så får A2 enheden
(mol·m3)/kg2 og MN får enheden kg/mol. Det kan være praktisk at omregne til disse enheder før
man udfører lineær regression.
Som vi ser er A2 større end 0. Man kan derfor argumentere for at opløsningsmidlet er et godt
opløsningsmiddel. Samtidig ligger det så tæt på 0, at det også vil have nogle egenskaber som et
thetasolvent. Det er ikke en skarp overgang.
Som regel vil man kun blive bedt om at argumentere for hvilket af to opløsningsmidler, der er
bedst. Det er naturligvis det opløsningsmiddel, som har den højeste værdi af A2.
4
Polymeres længde og bevægelser:
Random walk:
Hvis atomerne i en polymerkæde kan bevæge sig frit i forhold til hinanden, (selvfølgelig med
samme afstand mellem atomerne) er den gennemsnitlige afstand mellem enderne i anden potens
(mean square end-to-end distance) givet ved:
< r ee2 > = n⋅l 2
n er antallet at bindinger i polymeren med længden l.
Valence angle model:
I denne model er der ikke fri bevægelighed, men hvert atom har en fast bindingsvinkel θ i forhold
til det næste atom i kæden (for C-C bindinger er θ = 109,5º). Der er dog stadig rotationsfrihed
omkring bindingsaksen. I denne model kommer formlen til at se således ud:

< r 2ee > = n⋅l 2⋅
1−cosθ
1cosθ

φ
Restricted bond angle model:
I denne model er der ikke længere fri rotation omkring en
binding. Atomerne foretrækker at sidde med en vis
rotationsvinkel φ i forhold til næste binding. For almindelige
carbonkæder er der tre vinkler af φ som foretrækkes, nemlig trans
(0º), gauche+ (120º) og gauche- (240º). Der kan imidlertid godt
findes enkelte bindinger med andre vinkler end de foretrukne,
derfor bruger man middelværdien af cos(φ) i formlen:

< r 2ee > = n⋅l 2⋅

1−cosθ 1〈 cosφ 〉
⋅
1cosθ 1−〈 cosφ 〉

θ
OBS: Det kun er muligt at finde den gennemsnitlige ende-til-ende
afstand i anden potens. Kvadratroden af dette tal er ikke
nødvendigvis lig med den gennemsnitlige ende-til-ende afstand,
men kun et hint til i hvilket område det ligger.
Gyrationsradius:
Gyrationsradius for en polymer er defineret som den gennemsnitlige afstand fra polymerens
massemidtpunkt til et vilkårligt punkt på kæden. Gyrationsradier fortæller altså noget om
molekylernes udbredelse i alle retninger fra massemidtpunktet, og kan udregnes som:
< G
2
r
> =
 <r
2
ee
>
6
Hvis den er tilgængelig bruges mean square end-to-end afstanden fra restricted bond angle
modellen. Ellers bruges afstanden fra valence angle modellen.
5
Eksempel:
Et givent polyethylen-molekyle indeholder 501 C-atomer (altså 500 C-C bindinger). Hver C-C
binding har en længde på 0,150 nm og og bindingsvinklen mellem to C-atomer er θ = 109,5º.
Desuden er <cos(φ)> = 0,65.
Hvad er mean square end-to-end distance ifølge hhv. random walk, valence angle og restricted
bond angle-modellerne? Hvad er gyrationsradius?
Random walk modellen giver os:
2
2
2
< r ee > = n⋅l = 500⋅0,150 nm = 11,25 nm
2
Valence angle model:
2
2

< r ee > = n⋅l ⋅



1−cosθ
2 1−cos 109,5 º
2
= 500⋅0,15 nm ⋅
= 22,52 nm
1cosθ
1cos 109,5 º
Restricted bond angle model:
2
2

< r ee > = n⋅l ⋅





1−cosθ 1〈 cosφ 〉
10,65
2 1−cos 109,5 º
2
⋅
= 500⋅0,15 nm ⋅
⋅
= 106,18 nm
1cosθ 1−〈 cosφ 〉
1cos 109,5 º 1−0,65
Som det ses bliver molekylet en del større, når der kommer begrænsninger på hvilke mulige
bindingskonformationer, det kan antage. Gyrationsradius er:
 < G2r > =
 <r
2
ee
6
>
=
106,18 nm2
6
= 4,21 nm
6
Elektromagnetisk tiltrækning og frastødning:
Coulombs lov:
To punktladninger frastøder eller tiltrækker hinanden
med kraft F, der er givet ved følgende:
F=
q 1⋅q 2
1
⋅ 2
4⋅π⋅ε 0⋅ε r r
Dette svarer til at de to punktladninger har en samlet
potentiel energi på V(r):
V r =
q ⋅q
1
⋅ 1 2
4⋅π⋅ε 0⋅ε r r
q1 og q2 er de to punktladningers ladning (incl. fortegn) og r er afstanden imellem dem. εr er er den
relative permitivitetsfaktor i forhold til permitiviteten i vacuum (kan for de fleste materialer slås op
i Databogen).
Hvis de to ladninger oplever yderligere afskærmning end den, der opstår på grund af opløsningsmediet, f.eks. ved tilsætning af salt eller andre ladede partikler, ganges en ekstra
afskærmningsfaktor på:
V r =
q ⋅q
1
⋅ 1 2 ⋅e -r/ R
4⋅π⋅ε 0⋅ε r r
D
RD kaldes for Debyelængden.
Dipol-dipol vekselvirkning:
To dipoler frastøder eller tiltrækker hinanden med følgende potentielle energi:
−q 1⋅q 2 2⋅l 2
V r =
⋅
4⋅π⋅ε 0⋅ε r r 3
V r =
eller
−μ 1⋅μ2 2
⋅
4⋅π⋅ε 0⋅ε r r 3
l er afstanden mellem de to ladninger i hver dipol, r er afstanden mellem dipolernes midtpunkter, og
q1 og q2 er de to dipolers ladning med fortegn. μ kaldes for dipolmomentet og er defineret som
dipolens ladning ganget med afstanden mellem polerne. Dvs: μ=q⋅l
l
l
r
Debyelængde:
Debyelængden RD for kolloidpartikler i en opløsning relaterer til den afstand hvor partiklerne
effektivt kan mærke den elektrostatiske påvirkning fra hinanden. Debyelængden er givet ved:

e 2⋅Σ ci⋅z 2i
RD=
ε 0⋅ε r⋅k b⋅T
-½

7
e er elementarladningen, ε0 er vacuumpermitiviteten, εr er er den relative permitivitet i forhold til
vacuum, kb er Boltzmanns konstant, T er kelvintemperaturen, ci er koncentrationen af molekyler
med ladningen zi. Husk at z regnes med fortegn.
OBS: Koncentrationen ci skal måles i antal per m3 (m-3). Ellers får debyelængden en tåbelig enhed.
Hvis man har en molær koncentration, skal denne ganges med 1000 L/m3 og med Avogadros tal, for
at få den om til m-3. Dvs. hvis c' måles i M, og c måles i m-3, så er sammenhængen:
c = c '⋅1000
L
L
⋅NA = 6,02⋅1026 3
⋅ c'
3
m
m ⋅mol
Eksempel:
Den relative permitivitet for vand er ε0 = 80,1 ved 20 ºC.
Udregn Debyelængden for 0,01 M NaCl ved 20 ºC . Hvad er vekselvirkningspotentialet for to
elektroner, som befinder sig med en afstand på 10 nm i en opløsning 0,01 M NaCl ved 20 ºC ?
I opløsning danner NaCl monovalente ioner med z=1 for Na+ og z=-1 for Cl-. Derfor får vi:

2
2
e ⋅Σ ci⋅z i
RD=
ε 0⋅ε r⋅k b⋅T
-½
 
1,602⋅10-19 C2⋅0,01 M⋅6,02⋅10 23 mol-1⋅1000 L/m 3⋅12−12 
=
8,85⋅10-12 C/ V⋅m⋅80,1⋅1,381⋅10-23 J / K⋅293 K

-½
-9
R D =3,0468⋅10 m=3,047 nm
Vekselvirkningspotentialet mellem to elektroner som befinder sig i denne opløsning med en
indbyrdes afstand på 10 nm bliver derfor:
V r =
1
-e⋅-e -r/ R
1
−1,602⋅10-19 C2 -10 nm/ 3,047 nm
⋅
⋅e
=
⋅
⋅e
4⋅π⋅ε 0⋅ε r r
4⋅π⋅8,85⋅10 -12 C/V⋅m ⋅80,1
10⋅10-9 m
D
V r =1,0817⋅10-23 J
8
Generel rumgeometri:
Cirkler:
Cirklers areal A:
A=π⋅r
2
r=
Cirklers omkreds O:
O = π⋅2⋅r

A
π
r=
O
2⋅π
r=

r
Kugler:
Kuglers volumen V:
4
V= ⋅π⋅r 3
3
3
3⋅V
4⋅π
r
Kuglers overfladeareal A:
A=4⋅π⋅r 2
r=
Cylindere:

A
4⋅π

V
l⋅π
Cylinderes volumen V:
V=π⋅r 2⋅l
r=
l=
r
V
r ⋅π
2
Cylinderes overfladeareal A:
l
A = 2⋅π⋅r⋅l2⋅π⋅r 2 = 2⋅π⋅r⋅lr 
God gammeldags mængdeberegning:
Skemaerne læses som følger: Det øverste felt i en trekant er lig de to nederste ganget sammen. F.eks
m = M · n. Et af de nederste felter er lig det øverste felt divideret med det andet af de nederste
felter. F.eks. M = m / n eller n = m / M
m
M
M = molarmasse
V = volumen
m
n
n
C
V
n = stofmængde
C = koncentration
ρ
V
m = masse
ρ = densitet (massefylde)
9
Micellers rumgeometri:
Pakningsparameter:
Formen af en micelle afhænger af formen på den surfactant, som den er dannet af.
Pakningsparameteren P, indikerer hvilken form micellen vil have, og givet ved følgende:
P=
Vhale
Ahoved⋅l hale
Vhale er volumen af surfactantens hydrofobe halegruppe, Ahoved er arealet af surfactantens hydrofile
hovedgruppe og lhale er længden af halen.
Sammenhængen mellem pakningsparameter, surfactantform og micelleform er som følger:
Pakningsparameter:
1
P 
3
1
1
 P 
3
2
1
 P  1
2
P ≈ 1
Surfactantform:
Micelleform:
Sfæriske (kuglerunde)
miceller
Cylindriske miceller
Vesicler (dobbeltlag)
Lamellare dobbeltlag
Inverse miceller
P ≫ 1
Aggregeringstal:
Aggregeringstallet for en micelle er ganske simpelt antallet af surfactant molekyler, som micellen
består af. Læg mærke til at man ikke kan finde aggregeringstal for lamellare dobbeltlag eller
cylindre, hvis de ikke har nogen endelig udstrækning. I så fald må man finde aggregeringstallet per
længde eller per volumen.
10
Eksempel:
En opløsning indeholder 0,50 mol af en surfactant med molarmassen 500 g/mol. Surfactanten har
en densitet på 0,79 g/cm3, og dens hovedgruppe har et overfladeareal på 0,5 nm2 og carbon-halen
har en længde på 8 nm. Surfactanten danner miceller med et volumen på 150 nm3.
Find pakningsparameteren. Hvilken form har de miceller som surfactanten danner? Hvor mange
surfactant-molekyler indeholder hver micelle? Hvor mange miceller er der i opløsningen?
Hver især vejer surfactant-molekylerne:
m surf. molekyle =
M
500 g/mol
=
= 8,305⋅10 -22 g
23
-1
N A 6,02⋅10 mol
Hvert surfactant-molekyle fylder da:
V surf. molekyle =
m surf. molekyle 8,305⋅10-22 g
=
= 1,051⋅10 -21 cm 3=1,051 nm 3
3
ρ
0,79 g /cm
Pakningsparameteren kan da udregnes:
P=
3
V surf.molekyle
1,051 nm
=
=0,263
Ahoved⋅l hale 0,5 nm 2⋅8 nm
Da dette ligger under 1/3 danner surfactanten kugleformede miceller.
En micelle består i dette tilfælde udelukkende af surfactant. Da vi ved, hvad hver surfactantmolekyle fylder og hvad hver micelle fylder, kan vi udregne aggregeringstallet:
V micelle
150 nm 3
N Agg. =
=
=142,72
V surf. molekyle 1,051 nm 3
De 0,50 mol surfactant vejer tilsammen:
m surf.i opl. = n⋅M = 0,50 mol⋅500 g/mol = 250 g
Dvs. at vi i alt har følgende antal surfactant-molekyler i opløsningen:
N surf.molekyle =
m surf.i opl.
250 g
=
=3,01⋅10 23
-22
m surf. molekyle 8,305⋅10 g
Da hver micelle indeholder 142,72 surfactant-molekyler må antallet af miceller i opløsningen være:
N micelle =
N surf. molekyle 3,01⋅1023
=
=2,109⋅1021
N Agg.
142,72
11
Konstanter:
Lysets fart i vacuum:
Boltzmanns konstant:
Plancks konstant:
Elementarladningen:
Avogadros tal
Vacuumpermitiviteten
Gaskonstanten
c
kb
h
e
NA
ε0
R
R
mp
mn
me
Protonens masse:
Neutronens masse:
Elektronens masse:
= 3,00 · 108 m/s
= 1,381 · 10-23 J/K
= 6,63 · 10-34 J/s
= 1,602 · 10-19 C
= 6,02 · 1023 mol-1
= 8,85 · 10-12 C/(V · m)
= 8,3145 J/(mol · K)
= 0,0831 (L · Bar)/(mol · K)
= 1,007276 u = 1,6726231 · 10-27 kg
= 1,008665 u = 1,674954 · 10-27 kg
= 5,49 · 10-4 u = 9,11 · 10-31 kg
Enheder:
Længde:
Masse:
Tid:
Stofmængde:
Strømstyrke:
Temperatur:
Meter
Kilogram
Sekunder
Mol
Ampere
Kelvin
m
kg
s
mol
A
K
Grundenhed
Grundenhed
Grundenhed
Grundenhed
Grundenhed
Grundenhed
Frekvens:
Kraft:
Tryk:
Energi:
Effekt:
Ladning:
Spænding:
Magn. fluxtæthed:
Kapacitans:
Resistans:
Radioaktivitet:
Hertz
Newton
Pascal
Joule
Watt
Coulomb
Volt
Tesla
Farad
Ohm
Becquerel
Hz
N
Pa
J
W
C
V
T
F
Ω
Bq
1 Hz
1N
1 Pa
1J
1W
1C
1V
1T
1F
1Ω
1 Bq
= 1 svingning per sekund (s-1)
= 1 kg · m/s2
= 1 N/m2
= 1 kg/(m · s2)
=1N·m
= 1 kg · m2/s2
= 1 J/s
= 1 kg · m2/s3
= 1A· s
= 1 J/C
= 1 (kg · m2)/(A · s3)
= 1 N/(A · m) = 1 (kg · m)/(s2 · A · m)
= 1 C/V
= 1 (kg · m2)/s2
= 1 V/A
= 1 (kg · m2)/(A2 · s3)
= 1 henfald per sekund (s-1)
Omregningstabeller (for dummies):
Hvis du har et skal det ganges for at få det i:
tal, der måles i:
med:
Hvis du har et skal det ganges for at få det i:
tal, der måles i:
med:
nm
10-7
cm
cm
107
nm
nm
10-9
m
m
109
nm
nm2
10-14
cm2
cm2
1014
nm2
nm2
10-18
m2
m2
1018
nm2
nm2
10-22
hektar
hektar
1022
nm2
nm3
10-21
cm3
cm3
1021
nm3
nm3
10-24
L
L
1024
nm3
nm3
10-27
m3
m3
1027
nm3
cm3
10-3
L
L
103
cm3
u
1,660 · 10-27
kg
kg
1,660 · 1027
u
s
3,156 · 10-7
år
år
3,156 · 107
s
12