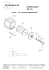Elektromekaniska energiomvandlare, speciellt

Transcription

Elektromekaniska
energiomvandlare, speciellt likströmsmaskinen
(relevanta delar av kap 7)
Inledning
• Elektromekanisk omvandlare
– en anordning som energimässigt förbinder ett elektriskt
och ett mekaniskt system.
– som regel roterande elektriska maskiner.
• Energitransporten kan ske i båda riktningar
– generatordrift då energi transporteras från det
mekaniska systemet till det elektriska.
– Omvänt betyder motordrift att energi flyttas från det
elektriska systemet till det mekaniska.
– Omvandlingsprocessen är i princip reversibel, vilket
innebär att alla motorer kan användas som generatorer
och vice versa.
Lunds universitet / Lunds tekniska högskola / Industriell Elektroteknik / PK
Magnetiskt eller elektriskt fält?
1. Kraft på en strömförande ledare i ett magnetiskt fält
2. Kraft mellan plattorna i en kondensator
Energitätheten per volymsenhet för de båda fälten
wmagn
1 1 2

B
2 0
1
wel    0 E 2
2
där den magnetiska flödestätheten B kan bli ca 1T och
den elektriska fältstyrkan E kan bli 3 106 V/m
wmagn
12
5
3


4

10
J
/
m
2  4 10 7
1
wel   8,85 10 12 9 1012  40 J / m 3
2
Den magnetiska energitätheten är suveränt störst.
Roterande och translatorisk rörelse (I)
Ur den stora flora av elektromekaniska energiomvandlare
som förekommer kan två grundläggande typer av mekanisk
rörelse hämtas, nämligen roterande respektive translatorisk
eller vibrerande, se figur 7.1.
Figur 7.1. Roterande rörelse (vänster) och
translatorisk eller vibrerande rörelse (höger).
Roterande och translatorisk rörelse (II)
• Roterande elektromekaniska energiomvandlare har nästan
alltid magnetiska fält som energibärare.
– Finns i effekter från bråkdelar av watt upp till de största
generatorerna på c:a 1 Gigawatt.
• Anordningar för translatorisk eller vibrerande rörelse t.ex
– elektromekaniska reläer,
– högtalare,
– mikrofoner,
– vissa typer av givare.
Mekanisk konstruktion (I)
Figur 7.2.
Figur 7.4.
Figur 7.3.
Figur 7.5.
Mekanisk konstruktion (II)
Figur 7.6. Illustration av magnetflödena i
en roterande maskin.
rotor
Figur 7.7. Rotorns uppbyggnad med
laminerade skivor.
Mekanisk konstruktion (III)
Statorhus
Lagersköld
Axel
Eventuella släpringar
eller kommutator
Lagersköld
Stator
Rotor
Lindningshärva
Figur 7.8. Motorns uppbyggnad.
Elektrisk konstruktion (I)
ROTOR
ROTOR
Luftgap
Figur 7.9. Varje faslindning blir nu
cylindrisk i ena ledden. Här visas en fas.
Elektrisk konstruktion (II)
B

I
A

B()

Figur 7.10. Geometri med homogen flödesfördelning .
För geometrin med homogent magnetiskt flöde (tv) gäller:
Magnetiskt flöde:   B  A  cos   L  I
Vridmoment:
d
T ( )  2  F   sin   F  d  sin  
2
 B  I  l  d  sin   B  I  A  sin 
Strömförande ledare i magnetfält
B
i
• Kraftverkan vill jämna ut fältfördelningen
–
–
–
–
Samverkande fält får mer plats
Ledaren rör sig mot motverkande fält – åt höger
Eller q vxB = F
Högerhandsregeln (I tumme, B pekfinger, F långfinger)
• Kraften på ledaren är F=Bil, där l är ledarens längd
Elektrisk konstruktion (III)
I verkligheten är det emellertid inte möjligt att uppnå idealt
sinusformigt utbredda lindningar bl.a beroende på att luftgapet
mellan stator och rotor måste hållas litet vilket inte ger plats
för lindningarna. I stället placeras lindningshärvorna i spår i
statorns och rotorns periferi, se figur 7.14.
Figur 7.14. Spår för lindningar.
Vridmoment!
• Det totala luftgapsflödet bildas av statorflöde och rotorflöde
i samverkan
• Statorflöde och rotorflöde ”vill” ligga i samma linje. Rotorn
rör sig när den påverkas av detta vridmoment
Vridmomentbildning (I)
• Elmaskinens uppgift i ett elektriskt drivsystem är oftast
att leverera ett önskat moment till axeln.
• Momentstyrningen är oftast den innersta och snabbaste
loopen i återkopplingen.
• För att kunna styra en elmaskins moment är det
naturligtvis viktigt att förstå hur maskinen bildar
vridmoment
Strömförande ledare i järn
Strömförande ledare, med ström in/ut ur papperets plan
Permanenta magneter,
magnetiserade uppåt/nedåt
i papperets plan
a)
Statisk
Statiskdel
del
c) S
+
Rörlig del
Rörlig del
R
• Kraftverkan vill jämna ut fältfördelningen
– Samverkande fält får mer plats – kraft på magnet åt vänster
– Ledaren vill flytta sig mot motverkande fält – kraft åt höger
– Endast magneter rörliga
• F=Bil på varje ledare
• Ström motsatt riktad  kraft motsatt riktad
Roterande rörelse från generisk
Permanentmagnetiserad (PM) DCmotor
• Magneter i statorn som i
likströmsmotor
• Ström i lindning i rotorn
• F=Bil
PM-stator: Skapa kraft och vridmoment
• F=Bil
• Kraft på ledarna upptill  (nedtill )
• Vridmoment på rotorn moturs
• Magneterna ger ett flöde riktat neråt
• Lindningarna ger ett flöde riktat åt vänster
• Maximalt vridmoment vid 90° vinkelskillnad
Ström ut ur bilden
Ström in i bilden
PM-stator: Maximera kraft och vridmoment
PM-stator: Låt rotorn rotera
• Rotorflödet ställer in sig i statorflödets riktning och vridmoment försvinner
• Om rotorflödet inte satt fast i rotorn utan kunde fortsätta vara riktat åt
vänster medan rotorn rör sig...
•  Byt strömriktning i ett ledarpar i taget
Kommutator
• En mekanisk växelriktare monterad på rotorn – kallad
kommutator kopplar om strömmarna i rotorn så att
riktningen på rotorflödet bibehålls
• Likström går bra: Det är en likströmsmotor!
Rotation (I)
- Resistanser, läckinduktanser och inducerad emk
Läckflöde: Bidrar inte till luftgapsflödet men däremot till det
totala statorflödet genom
   L  i
   Lm  i




Omagnetiserad rotor
Figur 7.20. Luftgapsflöde () och läckflöde ().
Rotation (II)
Läckinduktansen är konstant (förutsätter linjära magnetiska
förhållanden) vilket ger differentialekvationen arbetslindningen:
d a
dia
d a d
  a  La  ia  
 La 
 u a  Ra  ia
dt
dt
dt
dt
Rotation (VII)

T     ia

Rotation (III)
- Kommutatorlindning
Statorlindningen är enfasig och
fast monterad. Alltså ligger
statorns flödesbidrag fast i
rummet.
För maximalt moment
 
T     ia
ska flödesvektor och strömvektor
vara vinkelräta.
Alltså måste den i rummet
roterande rotorns strömvektor
också ligga fast i rummet.
Kommutatorn gör så att det blir
så!

Kompensationslindning
ir

Kommutator
ir
Stator
Rotor
is
Släpkontakt
is
Fältlindning
Figur 7.21. Maskin med
kommutatorlindning i rotorn

Rotation (IX)
- Kommutatorlindning

Inducerad emk:
ea   r  Lm  is   r     r 
Spänningsekvation för
ankarlindningen:
La 
dia
 u a  Ra  ia  ea 
dt
 u a  Ra  ia  r 
Kompensationslindning
ir

ir
Stator
Rotor
is
Momentekvationen:
Släpkontakt
is
T    ia
Kommutator
Fältlindning
Figur 7.21. Maskin med
kommutatorlindning i rotorn

Momentbildning och inducerad spänning
för likströmsmaskinen stationärt
• Vridmoment:
T   m  ia
• Inducerad spänning:
ea   m  
Figur 8.2. Principbild av genomskuren DC-motor.

Elektromekaniska energiomvandlare, speciellt

Transcription

Similar documents

Introduktion till Elektriska Drivsystem - IEA

Föreläsare Kerstin Vännman

Programmet för dagarna finns här.

STOFTSLUSS JM-20

Lagerbyte-fläktmotor

Ledning och styrning av projektbaserad

Den underhållsfria roterande borstlösa mataren