Document

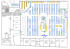
∆t
O K T O B E R
2 0 1 5
9.
U
T G A V E
HEI, DELTA!
Det er en glede å kunne presentere semesterets første ordinære utgave av ∆t. Som en del av dere kanskje
allerede har fått med dere, har jeg tatt over som redaktør, mens Joakim framover skal fungere som teknisk
ansvarlig. Med oss på laget har vi fått en super gjeng bestående av både initiativrike førsteklassinger og
etablerte tradisjonsbærere. Vi er stolte over at vi fortsatt kan skryte av å være den eneste linjeforeningen
ved NTNU som skriver sin avis i LATEX. Dette er noe vi ser på som en viktig del av avisas identitet, og målet
vårt er at du som matematikk- eller fysikkstudent vil sette pris på vårt noe “nerdete” særpreg. Samtidig
som vi på denne måten også i framtida vil ivareta etablerte tradisjoner, ønsker vi i redaksjonen også å
utvikle oss slik at vi kan gi dere en stadig bedre avis. For eksempel kan vi i denne utgaven for første gang
presentere en egen sitatspalte. Vi håper dere alle i tida som kommer vil holde ørene åpne og skriveblokken
klar, og sørge for å sende inn alle aktuelle gullkorn fra Deltas kloke sjeler.
Jeg er utrolig fornøyd med innsatsen og engasjementet redaksjonens medlemmer har lagt ned i forbindelse
med denne utgaven, og håper du som leser vil sette pris på resultatet.
– ANSVARLIG REDAKTØR, JOHANNE HAUGLAND
Utgave nr. 9
∆t - oktober 2015
LINJEFORENINGEN
DELTA
Org. nr: 996510352
ANERKJENNELSER
Redaktør
Teknisk ansvarlig
Baksideoppgave
Forsidebilde
Fotografering
JOHANNE HAUGLAND
JOAKIM FREMSTAD
ERLEND BØRVE
CAVALIERI FADDERGRUPPE
EIRIK DEGNES NEERLAND, TOMAS TAYLOR
HANNAH HOEM GRELLAND M.FL.
Bærplukketur og radioteater MICHELLE WAALER
Videohelg DIDRIK FOSSE
Send meg papirpost eller elektronisk post!
Ingen grunn til å være sjenert!
Kontakt:
[email protected]
Postkassen på Delta-kontoret
9. Utgave
INNLEDENDE
3
INNHOLD
Side
Forsiden . . . . . . . . . . . . . . . . . . . . . .
1
Kolofon . . . . . . . . . . . . . . . . . . . . . .
2
Innhold . . . . . . . . . . . . . . . . . . . . . . .
3
1 I Delta
Ord fra Deltas leder . . . . . . . . . . . . . . . .
Generalforsamling i Linjeforeningen Delta . . . .
Leserbrev . . . . . . . . . . . . . . . . . . . . .
2 Fadderukene og tiden derpå
Det var en gang ei fadderuke . . . . . .
Fadderbarncup 2015 . . . . . . . . . . .
Immatrikuleringsball 2015 . . . . . . .
Badekarpadlingen 2015 . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
4
5
6
7
7
11
12
14
3 Matematikk og fysikk
Midtsidegraf . . . . . . . . . . . . . . . . . . . .
Usikkerhetsprinsippet . . . . . . . . . . . . . . .
Om forståelse mellom deltagere, og dialekter i realfag
Teorem/Bevis . . . . . . . . . . . . . . . . . . .
16
16
20
22
24
4 Diverse
Anmeldelse: Dahls på hytta
vÅrgangsfest . . . . . . . .
Amazing Race . . . . . . .
Gobi - det nye Snapchat? .
Videohelg . . . . . . . . .
Utgavens postulater . . . .
.
.
.
.
.
.
26
26
28
30
32
33
34
Baksiden . . . . . . . . . . . . . . . . . . . . . .
36
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
I DELTA
4
∆t
I DELTA
ORD FRA DELTAS LEDER
Hei, Delta! Her kommer en liten hilsen fra deres
nye leder.
Først vil jeg si tusen takk for at dere valgte meg
som leder (selv om det ikke var noen andre som
stilte), og takk til Per-Dimitri som gjorde en så
fantastisk jobb før meg!
Deretter vil jeg komme med en oppfordring.
Til de som ikke har fått det med dere: På
generalforsamlingen som var bestemte vi at vi skal
ha en, og ikke to, generalforsamlinger i året, og den
skal være i november. Det betyr at vi allerede nå
snart skal ha en ny generalforsamling, og da skal det
velges et helt nytt styre.
Jeg vil gjerne oppfordre dere til å stille til styrevalg.
Det finnes utrolig mange kompetente mennesker i
Delta som kunne ha gjort en god jobb i styret, og
så mange som mulig av de som har lyst synes jeg
burde stille. Stiller mange, får vi konkurranse, og
da er vi sikre på at vi får de aller beste kandidatene.
Ikke minst er styrearbeid utrolig lærerikt og veldig
sosialt. Man blir kjent med styrene fra de andre
linjeforeningene og enda flere kule folk fra Delta.
Så still til styrevalg hvis du tenker at det høres ut
som noe for deg. Vet du om noen som kunne ha tenkt
seg å være med i styret, eller som du tror kunne ha
gjort en god jobb, få dem til å stille. Og finner du ut
at noen stiller imot, still likevel, og oppfordre den
andre kandidaten til å gjøre sitt beste mot deg!
Disse stillingene skal velges:
• Leder
• Nestleder
• Økonomiansvarlig
• Faddersjef
• Arrkomsjef
• Bedkomsjef
• Medkomsjef
• Komkomsjef
• Kvinnekomsjef
• Fagsjef
Du kan lese mer om hva stillingene innebærer
i statuttene på deltahouse, spørre de som sitter nå,
eller bare kontakte meg. Man kan velge å annonsere
sitt kandidatur på forhånd, eller man kan vente helt
til på generalforsamlingen.
Vi sees!
Hilsen Marte
I DELTA
9. Utgave
5
GENERALFORSAMLING I LINJEFORENINGEN DELTA
Av TARAN RUGE
Årsstudium i matematikk
Var du ikke én av de 47 deltagerne som oppholdt
seg i R7 til halv to natt til tirsdag 8. september? Frykt
ei, for her kommer et aldri så lite sammendrag av
generalforsamlingens begivenheter. Møtet startet kl.
17:15 og ble ledet av ordstyrer Yngve Hereide med
referent Kristian Hovd Sjøli. Etter å ha fått presentert
fjorårets regnskap og neste års budsjett gikk vi fort
over på votering av statuttendringer. Det var mange
små endringer som dere selv kan lese på Deltas
nettsider, men også noen ganske store endringer som
er verdt å få med seg som en alminnelig deltager.
DELTAGER
For å forenkle jobben til blant annet økonomiansvarlig og gjøre Delta til en mer oversiktlig forening,
foreslo styret å legge inn en endring i statuttene som
definerer en deltager. En deltager har stemmerett ved
generalforsamlinger og førsterett på arrangementer
i linjeforeningen. Alle som studerer eller har
studert matematikk eller fysikk, og som har betalt
medlemsavgiften på 150 kroner, er per definisjon en
deltager i tre år. Etter tre år vil deltagerskapet ende,
og man vil få et livsvarig medlemskap. Dette betyr
at fra nå av vil medlemsavgiften måtte betales hvert
tredje år1 .
betyr blant annet at neste års faddersjef skal velges
allerede om en måned!
FESTER
Nye statuttfestede fester er Den Store Bærplukketuren, arrangert på høsten for å plukke bær til
vÅrgangsfestvinen, og Pifest, arrangert så nært 14.
mars som mulig. Pifesten sammenfaller med jubileet
i primtallsår.
DELTAS FOND
En prosentandel av Deltas akkumulerte overskudd
skal settes i Deltas Fond. Fondet er kapital som er satt
til side for å finansiere spesielle begivenheter eller
innkjøp for Linjeforeningen Deltas medlemmer. For
å bli finansiert av Fondet må det skrives en søknad,
hvor kravene for Fondet må innfris og godkjennes
av Fondstyret. Fondstyret består i dag av Ingvild
Stautland, Håkon Pedersen, Bendik Deraas, PerDimitri Sønderland og Vegard Stenhjem Hagen.
NYTT STYRE
Hvem som ble valgt inn som nye styremedlemmer
kommer fram av tabellen på neste side.
ENDA EN GENERALFORSAMLING? Takk til noen som varmet pølser til hele
Kanskje har du allerede hørt nyheten om at det forsamlingen!
vil arrangeres enda en generalforsamling dette
semesteret og tenkt at det var en spøk. Det var
det ikke. Ved generalforsamlingen ble det vedtatt
å arrangere én generalforsamling i året, istedenfor de
to vi har hatt tidligere, der det blir holdt valg for alle
stillingene i Deltas styre. Denne generalforsamlingen
vil holde sted i slutten av oktober eller i begynnelsen
av november hvert år, og styret som blir valgt der
vil ta over for det sittende styret 1. januar. Dette
1 Alle aktive medlemmer som har medlemskap fra før 08.08.2015, får sin medlemskapsperiode satt fra 08.09.2015 til 08.09.2018.
I DELTA
6
∆Styremedlem
∆Leder
∆Nestleder
∆Leder av arrangementskomiteen
∆Leder av kvinnekomiteen
∆Leder av komitekomiteen
=
=
=
=
=
=
Styremedlem (NÅ)
Marte Stalsberg
Thale Lund Ness
Martine Andersen
Margrethe Skår
Patrick Jacobsen
Forandring i styret - ∆Styret
∆t
-
Styremedlem (DA)
Per-Dimitri B. Sønderland
Bendik Deraas
Thale Lund Ness
Kjerstin Skarpnes
Patrick Jacobsen
9. Utgave
FADDERUKENE OG TIDEN DERPÅ
7
FADDERUKENE OG TIDEN DERPÅ
DET VAR EN GANG EI FADDERUKE
Av HÅKON PEDERSEN
2. året bachelor i fysikk
Av OSCAR HANSEN FEDERL
Who knows?
Av JON KRISTIAN SLAPGAARD
1. året bachelor i fysikk
Oscar stirret tomt ut i lufta, mens Jon nippet
forsiktig til kaffen. Han var ny ved NTNU, så
smaksløkene hadde ikke vent seg til den mørke,
sterke kontordrinken riktig ennå. Håkon kikket i
gulvet. Stillheten var, i mangel på bedre ord, litt
klein. Jon var den første til å respondere på Oscars
utsagn. “Det går jo ikke an, vi hadde jo mange
dager der vi gjorde masse forskjellig! For eksempel
den dagen der vi. . . ja . . . ”. Gløden i øynene hans
sluknet litt. Han innså det samme som de to andre
hadde innsett et halvt minutt tidligere. Ingen var
sikre på hva som egentlig hadde foregått mellom 10.
og 23. august i dette herrens år 2015. Imellom all
vorsingen, festingen, hyggen og ikke minst lamboen
hadde minnet om hva som egentlig hadde foregått
under fadderukene gått tapt.
“Jeg husker noe om at vi gikk rundt mellom mange
barer i sentrum og gjorde masse tull, men jeg er
ganske usikker. Kan dette ha skjedd i fadderukene,
eller kan det bare ha vært en vanlig helg?” kom det
spørrende fra Jon. Etter noen sekunders stillhet kom
reaksjonen fra Håkon i form av et selvsikkert slag i
8
FADDERUKENE OG TIDEN DERPÅ
Delta-kontorets elskede Ikea-bord. “Ja, selvfølgelig!
Jeg er veldig sikker på at jeg satt på en bar med noen
folk i grønne skjorter og spilte kort, og så kom det
bare en masse fadderbarn inn, snakket med oss en
stund og dro igjen!”. Jon nikket kraftig. Han sluttet
med det da han fikk litt vondt i nakken. ”Ja, jeg tror
kanskje også at jeg har vage minner om opptaket til
Delta, men det er kun fordi jeg fant det som bare
kunne være fiskeskjell på klærne mine lenge etter
at fadderperioden var over”, sa han mens han tøyde
litt på nakkemusklene. Oscar klasket seg plutselig i
panna. “Herregud, jeg gikk i sentrum kun iført toga!”.
Jon satte en slurk kaffe i vranghalsen. Håkon lo ikke.
Dette var ikke noe å le av.
Stemninga var unektelig tung i rommet. Trioen
var enige i at det var på tide med en kontorøl for
å lette på trykket. Ved første slurk fosset minnene
på hos samtlige. “Jeg fikk skikkelig Déjà vu nå.
Gjorde vi ikke akkurat det samme for noen uker
siden?” spurte Håkon. Jon sperret opp øynene. “Nei,
ikke her! I en stappfull kjeller! En varm og svett
kjeller!”. Ikke alle delte hans entusiasme. “Kjeller?
Mener du Samfundet? Der er det jo ganske fullt, og
som oftest varmt og svett”, kom det fra Håkon. Jon
ristet på hodet. “Nei nei, faddergruppa gikk til en
kjeller! Det må ha vært ei real fyllekule, siden jeg
ikke husker hvem sin kjeller dette var, da.” Oscar og
Håkon kikket begge i veggen. Svart-hvitt-maleriet
av Per stirret ikke tilbake, men litt til siden. “Vi
skulle hatt færre av dem i fadderukene”, kom det fra
Håkon. “Færre hva?” Oscar rev blikket bort fra det
hypnotiske maleriet. Håkon pirket på Dahls-etiketten.
“Fyllekuler”, sa han lavt.
I det øyeblikket kom noen inn på kontoret og sank
ned i den smaragdgrønne sofaen. Vedkommende
ble ganske satt ut da han så at ølen til Jon var tom.
“Hva er greia med dere? Spesielt dere to, som har
vært faddere!”. Oscar var genuint forvirret. “Var...var
jeg fadder?” stotret han. “Tja, jeg husker ikke alle
fjesene, da”, sa noen. “Blåste ikke du opp en del
av av ballene på idrettsdagen? Nei, vent litt! Du
er ikke tilfeldigvis frimurer?” “Idrettsdag? Baller?
Hva er det du snakker om?” Oscar kunne ikke huske
oppblåsbare baller, ikke i sin tid i Delta.
“Hva jeg husker? Hva slags spørsmål er det?” Det
gikk sakte men sikkert opp for noen at minnet ikke
var i beste laget. “ Vel, jeg husker at jeg tok bussen
∆t
til Byåsen. Jeg var ganske kvalm etter hva enn jeg
hadde holdt på med tidligere på kvelden, og stirra på
ei dame for å ha noe å konsentrere meg om slik at
mageinnholdet holdt seg på plass. Jeg tror ikke hun
satte pris på det. Ja, og så hadde vi piratfest!”.
De tre tilhørerne skjønte ikke hvordan noen kunne
gjøre slikt, men trodde de skjønte hvorfor de
hadde funnet gulrøtter så og si overalt de siste
ukene, inkludert på seg selv. Allikevel nevnte ingen
gulrøttene for hverandre i frykt for å bli uglesett.
"Vel, jeg har i det minste blitt litt visere etter
fadderukene. Nå vet jeg at å drikke på tirsdager er
helt greit, og at det er lettere å få tak i macheter her
i byen enn man skulle trodd!". Nyttig viten til tross,
var ikke gruppa kommet noe nærmere et helhetlig
bilde av fadderukene. Håkon begynte å bli utålmodig,
og hentet nye øl til gjengen i sofaen. Delta Pi-en
kimet lystig idet transaksjonen ble utført. “Takker!
Du er en staut kar!” sa Oscar idet han fikk ølen
slengt i fanget. I det øyeblikket kviknet Jon til. “Kar?
Karsk! Vi hadde trønderfest!
9. Utgave
FADDERUKENE OG TIDEN DERPÅ
Så kom politiet!”. Rommet satte i et kollektivt,
bekreftende “Aaaah!”. “Det var jo ikke ordentlig
karsk der, da. Det var forsåvidt ikke mange ordentlig
skinnvester eller barter der heller. Jævla fake”, kom
det fra noen. Det var kanskje derfor politiet kom
innom", mumlet Jon litt bittert. Idet gjengen var på
nippet til å gi opp sin søken etter tapt hukommelse,
kom Cecilie inn på kontoret. Hun hadde tatt turen
innom med planer om å skrive litt på sin egen sak til
det respektable tidsskriftet ∆t, men begynte å tvile da
hun la øynene på den trasige kvartetten som befant
seg der inne fra før av. Hun tok det på seg å prøve å
lette litt på stemningen, og kastet et blikk over hele
rommet for å finne noe å snakke om. Avgjørelsen
falt på Delta-trofeet. ”Aah, fadderukene! Gode tider,
hva?” sa hun muntert mens hun slengte seg ned i
hjørnet av sofaen. Dette ble for mye for Oscar, som
ikke engang kunne huske å ha vært fadder. Han måtte
hvile hodet litt i hendene for å ta seg inn igjen. Noen
hadde sett seg lei på at det ikke fantes en dråpe kaffe
på kontoret, og gikk for å lage et par kanner. Håkon
var nå nesten fullstendig fraværende, og i full gang
med å rulle ut ledningen til en av Gamecube-spakene.
”Vi husker dessverre ikke så mye av fadderukene,
og vi begynner å få dårlig tid før vi må begynne å
få gjort andre ting. Kan du kjapt oppsummere det
viktigste som skjedde for oss?” Jon var kanskje den
eneste som fremdeles var ved godt mot. ”Vel, om
jeg skal oppsummere det kjapt, så vil jeg si det var
mye rølp. Noe utkledd rølp, noe idrettsrølp, noen
dager uten rølp i det hele tatt. Om jeg ikke husker
feil, auksjonerte vi bort mye rølp også!”
9
10
FADDERUKENE OG TIDEN DERPÅ
Jon kikket bort på pokalen for å se om det
kunne vekke en del latente minner, og fikk øye
på en bit gaffateip på stetten til trofeet. “Hvem
er ”Sagan”, egentlig?” spurte han undrende. Noen
stod i døråpningen med en kaffekanne i hver hånd.
Vedkommede hadde fått med seg spørsmålet, og
trakk på skuldrene til svar. Alle kikket på hverandre.
Det var tydelig at uansett hvem denne Sagan var, så
hadde hans prestasjoner vært ubetydelige i det lange
løp.
Mens noen helte kaffe i koppen, forsøkte Cecilie
en siste gang å dra gjengen ut av det mørke
tankesettet sitt. “Vel, om dere absolutt vil vite noe
av det beste ved fadderukene, så må det vel være alt
engasjementet! Fadderbarna gjorde alt de kunne for å
vinne heder og ære i konkurransene!”. Med ett hørtes
en røst fra døråpningen. “Ælt har sin pris, Cecilie.”
Alle dreide blikket mot Magnus. Han så heller ikke
ut som han var i god forfatning der han trasket inn,
helte seg en sjenerøs kopp kaffe og inntok godstolen
nærmest døra. Bilnøklene krampeholdt han mellom
tommelen og pekefingeren på høyre hånd. Hvordan
han klarte å helle kaffe var et mysterium. ”Je
har kjørt skytteltrafikk tæll legevakta mæ skada
fadderbarn under hele fadderperioden. Knækte armer
ætter tryning på skateboard, knækte tomler ætter
slurvete mottak av amerikanske fotballer, og det
rareste: hugguskader i funballs. Den siste skjønner je
itte åssen er fysisk mulig!” Mannen mente tydeligvis
alvor. Han hyllet innpå en imponerende slurk kaffe,
mens resten av kontoret bivånet det hele. Oscar ristet
på hodet. “I gamle dager kunne vi drikke ordentlig.
Det eneste de fadderbarna her kan er å knekke bein,
tydeligvis.” Magnus svelget ned kaffeslurken. Han
hadde mye mer på hjertet. “Men det stopper itte
der! Tenkj på stakkaren som vart verbalt angrepet
av Onkel P ætter å ha tala mæ kvinnfolket hass! Og
Hektor, som faen itte får ro når det sitt folk her hele
tia! Fadderbarna har virkelig vist si mørke side, og
da tenkjer je spesielt på dom sadista som pepra vinen
til uskyldige deltagere som bære ville drekke opp!”.
Magnus måtte ta en kort pust i bakken. Tiraden hadde
tappet han for krefter. Etter noen sekunder var han
på stasjon igjen, og kunne fullføre tanken. “Men,
ja, moro var det læll, sjøl gjennom blod, smerte, og
∆t
ændre usæle greier!”
Roen senket seg atter en gang på kontoret. Noen
hadde allerede dratt, resten valgte også å forlate
kontoret grunnet den tunge stemninga. Igjen satt
Oscar, Jon og Håkon, trioen som kanskje hadde
det største behovet for hjelp. “Jeg er ikke sikker på
om det hele henger på greip ennå”, sa Håkon. Han
hadde lagt seg på langsida av sofaen, tydelig preget.
Oscar holdt på å pakke datamaskinen i sekken. Jon
var heller ikke i godt humør. Konstellasjonen hadde
satt seg på kontoret i utgangspunktet for å få slengt
sammen en artikkel som oppsummerte fadderukene,
men de innså at de hadde tatt seg vann over hodet.
Utfordringen hadde vist seg vanskelig å takle. “Vi
kan vel trøste oss med at vi fikk litt info, da”, sa
Håkon til slutt. Jon lagde en liten grimase. Misnøyen
med å ikke få gjort noe som de hadde utsatt så lenge,
tæret på han. ”Joda, men det er ikke i nærheten av
å kunne fylle en lengre artikkel i ∆t med. Nå har
vi brukt hele ettermiddagen, og vi har ikke engang
skrevet så mye som en setning i LATEX-dokumentet.
Jeg skulle jo faktisk prøve å få gjort algdat i dag, men
det ser det ut til at jeg bare kan glemme, i likhet med
alt annet vi har glemt”, responderte Oscar og slengte
på seg jakken. Han hadde et poeng. Istedenfor å sitte
her kunne alle sammen helt sikkert ha klart å drukket
fire-fem øl, slått minst et par rundetider i Mario Kart
eller kanskje til og med kommet seg gjennom så
mye som en femtedel av en øving. “Er det ikke
bare å koke artikkelen da? Ligger sikkert noe på
Christians Kokebok som kan brukes”, sa Håkon. Jon
nikket ivrig. Han var åpen for alle muligheter akkurat
nå, det måtte han dersom han skulle bli ferdig med
linalgen til innleveringsfristen. Oscar sukket. ”Det
får bli løsningen. Stokk nå idet minste om litt på
ordene og skriv litt dårlig LATEX-kode slik at ingen
mistenker noe da”, sa han idet han spankulerte ut
døren.
(Red.anm: Grunnet betydelig bruk av LF i denne
artikkelen ble den i utgangspunktet forkastet, men
tatt med i siste liten da det viste seg at trykkeriet var
spandable med blekket. Vi ønsker likevel å advare
mot å lete etter en moral i denne fortellingen, og
heller opparbeide deg din egen gjennom årevis med
prøving og feiling.)
9. Utgave
FADDERUKENE OG TIDEN DERPÅ
11
FADDERBARNCUP 2015
Av MAGNUS RINGERUD
2. året bachelor i matematikk
Tidlig en lørdag i slutten av fadderuka dro en
gjeng slitne deltagere ned til Dødens dal for å
bedrive verdens beste idrett: fotball! Som i resten
av fadderperioden hadde vi værgudene med oss, og
med sol og blå himmel lå det an til en flott dag.
Tro til vårt motto, “Det viktigste er å delta”, var
vi den linjeforeningen som stilte med flest lag, hele
fire stykk. Tre mixlag: Det viktigste er å delta, ∇2 og
Delta Dynamite, samt et herrelag: Delta Youngboys.
Det var ingen krav til ferdigheter, her var det bare
om å gjøre å ha det gøy!
Ikke alle delte vår idrettsglede, og da heiaropet
“Kom igjen, det viktigste er å delta!” runget ut fra
tribunen, kom det skarpt: “Det er så løgn”, fra et
kvinnemenneske på idrettvitenskap.
Desto bedre gikk det for herrelaget, som kriget
seg helt frem til semifinalen. I en kamp som bare
var halvparten så lang som den skulle være, kjørte
Delta Youngboys over motstanderlaget fra marin,
men maktet ikke å score. Kampen måtte derfor
avgjøres på straffespark. Her trakk marin det lengste
strået, og vi måtte skuffet innse at eventyret var over
for denne gang.
Lagledere takker for oppmøtet, både fra spillere og
heiagjeng, og håper på tilsvarende interesse til neste
år!
Våre tre mixlag fikk det som ventet tøft i
gruppespillet, og selv om vi lenge klamret oss til
håpet om avansement for Det viktigste er å delta,
som med sitt ene tap og to walkover-seiere lenge
så ut til å kunne kapre beste gruppetoer, gikk det
desverre ikke vår vei, og alle tre røk ut.
Lyst til å spille fotball?
Lik Delta FK på facebook og møt opp på trening!
12
FADDERUKENE OG TIDEN DERPÅ
∆t
IMMATRIKULERINGSBALL 2015
Av CECILIE BJØRNSDOTTER RAUSTEIN
1. året bachelor i matematikk
Den 5. september 2015 var det duka for årets
Immatrikuleringsball, og for dei av oss som hugsar
heile eller deler av kvelden vart det ein minnerik
kveld. Eit siste vorspiel med faddergruppa fann stad
i forkant av sjølve ballet, før vi alle saman traska
av garde mot Royal Garden. Etter at ein hadde fått
levert frå seg jakker og liknande til ikkje-smilande
personale på hotellet var ballet endeleg i gong. Ei
stor samling spente deltagere sto og småprata før vi
fekk sleppe heilt inn, og for enkelte fann deira første
pins-bytter stad nettopp på dette teppet.
Så fekk vi endeleg kome inn og setje oss. Vil
påstå at vi sat ei stund og berre sikla på buffeten
før vi fekk forsyne oss, men det var absolutt verd
ventinga. Tallerkane var så fulle at det nærast kan
kallast eit under at det ikkje vart sølt meir mat på
veg frå buffeten til borda, og dei aller fleste forsynte
seg minst to gonger, i tillegg til dessert, sjølvsagt.
Det er trass alt ikkje kvar dag ein fattig student får
ete eit slikt herremåltid. Folk smilte, åt og skålte,
og stemninga steig i takt med promillen (på trass av
stive prisar i baren, men det bryr ein seg jo mindre
og mindre om for kvar Dahls ein drikk).
Vi veit likevel alle at det ikkje berre var maten
vi hadde å glede oss til, for på programmet sto
både talar, skålar og ikkje minst kåringar. Som
førsteklassing er det ikkje berre enkelt å lære seg Nu
klinger, men vi gjorde eit tappert forsøk på å henge
med. Eigentleg høyrdes songen ganske bra ut, heilt
til vi kom til adagioen. Denne vart så forferdeleg at
eg faktisk berre måtte nemne han her.
No over til talane. Eg skal ærleg innrømme at
nokon talar sit betre i minnet enn andre. Som
avtroppande leiar fortener Per-Dimitri at talen hans
vert nemnt. Han var nok ganske langt frå edru,
men han har ordet i si makt, og skapte både
latter og god stemning. Det er ikkje utenkjeleg at
det vart felt ei tåre då han prata om «Delta, den
mest sosialfremmede linjeforeningen». Moglegvis
ei lattertåre, men likevel... Det gjekk både ord om at
dette var første gong på mange år at leiaren faktisk
hadde hatt talen sin på immatrikuleringsballet, men
òg om at han vart kasta ut like etter talen sin. . .
Høgdepunktet for mange (kanskje spesielt dei som
faktisk vann) var nok kåringane. Å ramse opp alle
vert nok litt i overkant, så dette er heller eit forsøk
på å nemne dei viktigaste. I fadderperioden er det
sjølvsagt fadderbarna som står i sentrum, og her
hadde noen gjort seg fortent til tittelen som «Årets
fadderbarn». Vi går ei lys framtid i møte no som vi
har Lars til å gjere alt det som nokon burde gjere. . .
Ingen seier vel nei takk til vaflar og kaffi heller, så
med sin VaffKaffKom var Kristina like verdig då
ho tok imot tittelen saman med Lars. Likevel må
det seiast at vi fadderbarn hadde ikkje greidd å vere
like fantastiske om det ikkje hadde vore for våre
fantastiske fadderar! Årets fadderar vart Kristian og
Michelle, og denne tittelen har dei all grunn til å vere
stolte over!
Heilt til slutt kom vi endeleg til kåringa alle hadde
9. Utgave
FADDERUKENE OG TIDEN DERPÅ
venta på. Håpefulle fadderbarn sat på stolkanten
med vide auge då den beste faddergruppa skulle
lesast opp. Ein kunne likevel skimte ei lita gruppe
menneske som sat godt i stolane, avslappa og rolege.
Dei kunne ikkje heilt forstå kvifor alle var så spente
på denne kåringa. For dei var det nemleg ikkje
noko spørsmål. Med både «Årets fadder», «Årets
fyllesvin», «Årets ildsjel» OG «Årets tøs» på gruppa
var det sjølvsagt at Sagan kom til å vinne! Til heiarop
som «SAGAN SUGER!» og «FUCK SAGAN!»
gjekk årets beste faddergruppe opp for å ta imot
13
den store, lysegrøne deltaen. Frå gruppa si side kom
ein takketale med meir eller mindre velvalde ord, og
til slutt «SAGAN! SAGAN! SAGAN!» medan vi
vart bua ned frå scena. . . Vi vart kanskje hata, men
om Sagan sug, ja, då sug alle taparane endå meir!
Etter at vi omsider var ferdige på Royal
Garden, fortsatte kvelden på Bodegaen på Singsaker
Studenterhjem ut i dei seine nattetimar,
og snipp snapp snute, så var faddereventyret 2015
ute.
14
FADDERUKENE OG TIDEN DERPÅ
∆t
BADEKARPADLINGEN 2015
Av SEBASTIAN JOHANSEN
Byggmester ved badekarpadlingen
Av SIMON F. ØSTRAAT
Visebyggmester ved badekarpadlingen
Alt begynte med en stor, optimistisk gjeng med
unge deltagere. De trengte en leder og “noen” stilte
som eneste kandidat. Etter litt frem og tilbake
ble temaet statsledere, synet av Kim Jong-Un i et
badekar på Nidelva var litt for fristende. Kjapt etter
startskuddet ble Nablas badekar observert båret ned
i kjelleren.
badekar på litt over 70 kg. Rundt denne tiden ble
Lars oppringt av det såkalte “BadCom”. Det viste
seg å være medisin som lurte på hvor badekaret vårt
var, men takket være fjorårets lettlurte deltagere, var
vi klar over medisins utspekulerte planer (husk å
fjerne nummeret fra facebook neste gang, medisin).
Som de barmhjertige menneskene vi er, spilte vi med,
og sendte dem på villspor opp i Granåsen.
Engasjementet hadde vært stort rundt planleggingen og sabotasjen, men så kom showet, smiskingen
og pengeinnsamlingen... Vi var alle enig om at
dette måtte gjøres, så “noen” stilte opp. Lars gikk
til BadCom med is og en fantastisk stand-upfremføring. Etter anbefaling fra BadCom ble Lars
sitt enmannsshow Deltas bidrag til showkvelden. I
tillegg til vårt eget show er det verdt å nevne hva våre
gode venner, Nabla, stilte med. De gikk for det gode
gamle alternativet hvis du ikke har noe å fremføre:
dissing av andre linjeforeninger, x-files theme song
og et hardcore strippeshow (som måtte fremføres to
En liten gruppe med naive studenter, med litt ganger pga. tekniske problemer/dommernes ønske).
hjelp fra Per-Dimitri, fikk tak i nøklene til kjelleren, Av en eller annen grunn så vi ikke mer av
og dette skulle være begynnelsen på en lang rekke IllumiNabla under badekarpadlingen.
triumfer for Delta. Gruppen tok badekaret uten å ofre
en tanke på om det faktisk var badekaret Nabla skulle
bruke under padlingen, eller om det var badekaret de
nettopp hadde brukt under opptaket sitt. Badekaret
var allerede dekorert med nøyaktige beskrivelser som
“FysMat suger πkk”, og godtroende startet vi å lage
en sabotasjevideo, med Illuminati-inspirert tema. Det
viste seg i ettertid at det ikke var det riktige karet,
men det ble likevel en hyggelig kveld med pølser og
tennvæske. Vi vet fortsatt ikke med sikkerhet hvor
Nablas tema, IllumiNabla, kom fra, men vi har våre
mistanker.
Vi var litt trege med å få tak i et badekar, men
siden det viktigste er å delta, måtte vi få tak i et,
Endelig kom den store dagen. Folk var spente:
koste hva det koste ville. Vår kjære, suverene leder, Ville flåten få plass på vannet sammen med de
Lars Sæle, fikk etter hvert tak i et godt og solid andre linjeforeningene? Eller ville fjorårets fiasko
9. Utgave
FADDERUKENE OG TIDEN DERPÅ
gjentas? Da flåten skulle gå gjennom veltetesten,
var vi kun én person tilstede, ettersom de to andre
fortsatt var på jakt etter flytevester. Heldigvis fikk
vi låne tre hyggelige personer fra Volvox, slik at
vi ble fire på flåten. Til tross for Røde Kors sine
protester, ble flåten godkjent for tre, da det heldigvis
var brannvesenet som hadde det siste ordet. Med
vår såkalte doomed to fail-flåte, og Delta sin stolte
historie i badekarpadlingen, startet våre tilfeldig
valgte roere sin ferd over den majestetiske Nidelva.
Som en kan se på flåten vår, ble ikke temaet
statsledere veldig sentralt, men dette fikset vi ved å gi
padlerne våre masker. Vi startet bak showfinalistene
Medisin, Maskin og Volvox. Med en godt designet
flåte og fantastiske padlere padlet vi forbi Maskin.
Med denne heroiske innsatsen ble vi tredje flåte i
mål, med den raskeste totaltiden over elven (at det
eksisterer en mulighet for at vi hoppet over en post
under padlingen kan neglisjeres).
15
Av priser som ble utdelt senere på kvelden,
ble halvparten vunnet av, you guessed it, Maskin.
Delta vant desverre ingen priser direkte, men frykt
ikke. En fornøyd Lars Sæle kunne dra hjem med
entusiasmeprisen for hans engasjement og initiativ i
blant annet showet og pengeinnsamlingen.
Under dette årets badekarpadlingen har vi sabotert
feil kar, køddet med medisin, blitt traumatisert av
IllumiNabla og så vidt kommet oss på vannet, men
som dere vet; det viktigste er verken å være best eller
å være flest, men å Delta!
MATEMATIKK OG FYSIKK
16
∆t
MATEMATIKK OG FYSIKK
MIDTSIDEGRAF
Av FRODE BØRSETH
1. året master Fysikk
Det ble meg spurt, en dag for ikke lenge siden,
om det fortsatt var en mulighet for at ∆t kunne få
innsendt en aldri så liten midtsidegraf, til tross for
at jeg som graf-maker for øyeblikket ikke befinner
meg i nærheten av NTNU, Gløshaugen eller Deltakontoret. For som har blitt tradisjon i løpet av de
siste seks utgavene, må jo avisa ha en midtsidegraf.
Til det spørsmålet stormer altså frem svaret "Ja!",
i form av den mest omfattende grafen jeg hittil har
laget. I min avstand fra NTNU, og savnet som det
medfører, har jeg valgt å denne gang gjøre en graf
som symbol på det fraværet jeg kjenner aller sterkest.
s
δ (ξ , a, b) =
f1 (x) = 5.5 · δ (x, 17, 32.5)
f3 (x) = 6.8 · δ (x, 23.8, 24.8)
f4 (x) = 7.2 · δ (x, 23.8, 24.8)
f5 (x) = 8.2 · δ (x, 24.8, 25.0)
f6 (x) = 8.9 · δ (x, 24.8, 25.0)
f7 (x) = 9.3 · δ (x, 24.8, 25.0)
f8 (x) = 10.0 · δ (x, 23.6, 23.8)
f9 (x) = 10.3 · δ (x, 23.8, 24.8)
f10 (x) = 12.2 · δ (x, 23.8, 24.8)
f11 (x) = 12.85 · δ (x, 23.8, 24.8)
f12 (x) = 13.35 · δ (x, 23.8, 24.8)
f13 (x) = 13.6 · δ (x, 23.6, 23.8)
f14 (x) = 13.9 · δ (x, 24.5, 25.0)
f15 (x) = 14.1 · δ (x, 24.5, 25.0)
f16 (x) = 15.5 · δ (x, 23.0, 25.5)
f17 (x) = 16.0 · δ (x, 17, 32.5)
1 Ny
rekord!
(ξ − a)(b − ξ )
|(ξ − a)(b − ξ )|
6.7
· δ (x, 23.6, 23.8) · δ (x, 24.8, 25.0)
i
10.8
f19 (x) =
· δ (x, 23.8, 24.2) · δ (x, 24.4, 24.8)
i
11.1
f20 (x) =
· δ (x, 23.6, 23.8) · δ (x, 24.8, 25.0)
i
11.4
f21 (x) =
· δ (x, 23.6, 23.8) · δ (x, 24.8, 25.0)
i
11.7
f22 (x) =
· δ (x, 23.8, 24.2) · δ (x, 24.4, 24.8)
i
12.5
f23 (x) =
· δ (x, 23.6, 23.8) · δ (x, 24.8, 25.0)
i
12.7
f24 (x) =
· δ (x, 24.8, 25.0) · δ (x, 23.6, 23.8)
i
f25 (x) = − 0.376(x − 24.2) + 8.674 · δ (x, 23.6, 24.8)
f26 (x) = 0.541(x − 24.2) + 9.675 · δ (x, 23.6, 24.8)
f27 (x) = − 0.375(x − 24.4) + 8.85 · δ (x, 24.0, 24.3)
f28 (x) = − 0.3(x − 24.3) + 8.85 · δ (x, 24.5, 24.8)
f29 (x) = 0.625(x − 24.4) + 9.25 · δ (x, 24.0, 24.3)
f30 (x) = 0.5(x − 24.3) + 9.25 · δ (x, 24.5, 24.8)
f31 (x) = − 0.67(x − 24.65) + 13.799 · δ (x, 24.5, 24.8)
f32 (x) = − 0.99(x − 24.3)2 − 0.101(x − 24.3) + 7.897 · δ (x, 23.8, 24.8)
f33 (x) = − 1.31(x − 24.65)2 − 0.358(x − 24.65) + 14.985 · δ (x, 24.3, 25)
f18 (x) =
f2 (x) = 6 · δ (x, 23.0, 25.5)
Noen nyvinninger har måttet finne sted for at
dette portrettet skulle kunne lages. Tidligere har den
endelige ligningen (3.1) bare bestått av funksjoner
av x, altså fi (x), mens denne gang er ligningen mer
generell. Her består den endelige ligningen også av
funksjoner av y, nemlig g j (y).
Under defineres altså som før funksjonene f1 (x)
til f67 (x), men denne gang også g1 (y) til g50 (y). I
tillegg defineres aller først δ (ξ , a, b), som brukes
for å definere f -ene og g-ene. Til slutt legger vi
frem ligning (3.1) som midtsidegrafen oppfyller,
som bruker alle de 1171 funksjonene i sin definisjon.
f34 (x) = 1.28(x − 23.95)2 + 0.142(x − 23.95) + 14.092 · δ (x, 23.6, 24.3)
f35 (x) = 2.5(x − 24.7)2 + 1.0(x − 24.7) + 14.199 · δ (x, 24.5, 24.9)
f36 (x) = − 3.4(x − 23.85)2 + 1.33(x − 23.85) + 14.875 · δ (x, 23.7, 24.0)
f37 (x) = 0.0(x − 23.8) + 15.0 · δ (x, 23.6, 24.0)
f38 (x) = 2.19(x − 26.25)2 − 0.56(x − 26.25) + 9.599 · δ (x, 26, 26.5)
f39 (x) = − 1.5(x − 26.165) + 9.75 · δ (x, 26.08, 26.25)
f40 (x) = − 1.13(x − 26.25)2 + 0.04(x − 26.25) + 10.829 · δ (x, 26, 26.5)
f41 (x) = − 1.77(x − 26.3525)2 − 0.14(x − 26.3525) + 10.793 · δ (x, 26.08, 26.625)
f42 (x) = − 7.4(x − 26.625)2 − 2.09(x − 26.625) + 10.624 · δ (x, 26.5, 26.75)
f43 (x) = 4.0(x − 26.825)2 − 1.4(x − 26.825) + 10.87 · δ (x, 26.75, 26.9)
f44 (x) = − 0.41(x − 27.075) + 10.73 · δ (x, 26.9, 27.25)
f45 (x) = − 3.9(x − 27.375)2 − 1.05(x − 27.375) + 10.589 · δ (x, 27.25, 27.5)
f46 (x) = − 0.36(x − 27.1875) + 10.762 · δ (x, 26.875, 27.5)
f47 (x) = − 4.7(x − 26.425)2 − 0.21(x − 26.425) + 11.097 · δ (x, 26.3, 26.55)
f48 (x) = − 0.301(x − 26.875) + 11.312 · δ (x, 26.25, 27.5)
f49 (x) = − 0.7(x − 27.3125)2 − 0.61(x − 27.3125) + 11.035 · δ (x, 27.125, 27.5)
f50 (x) = − 0.315(x − 26.6875) + 11.262 · δ (x, 26.25, 27.125)
MATEMATIKK OG FYSIKK
9. Utgave
f51 (x) = − 0.034(x − 10.45)2 + 0.1463(x − 10.45) + 13.6427 · δ (x, 8.4, 12.5)
f52 (x) = 0.0339(x − 10.45)2 − 0.1464(x − 10.45) + 7.8572 · δ (x, 8.4, 12.5)
f53 (x) = 0.2884(x − 7.1) + 12.825 · δ (x, 5.8, 8.4)
f54 (x) = − 0.2885(x − 7.1) + 8.675 · δ (x, 5.8, 8.4)
f55 (x) = − 1.07(x − 4.25)2 + 0.555(x − 4.25) + 12.616 · δ (x, 3.8, 4.7)
f56 (x) = 1.06(x − 4.25)2 − 0.556(x − 4.25) + 8.883 · δ (x, 3.8, 4.7)
f57 (x) = − 0.307(x − 33.6)2 − 0.4546(x − 33.6) + 15.8713 · δ (x, 32.5, 34.7)
f58 (x) = 0.3069(x − 33.6)2 + 0.4545(x − 33.6) + 5.6286 · δ (x, 32.5, 34.7)
f59 (x) = − 8.8(x − 27.09)3 − 0.25(x − 27.09)2 + 0.78(x − 27.09) + 11.666 · δ (x, 26.83, 27.35)
f60 (x) = − 6.6(x − 27.175)3 − 1.03(x − 27.175)2 + 0.67(x − 27.175) + 11.777 · δ (x, 26.9, 27.45)
f61 (x) = − 6.7(x − 24.025)3 + 1.16(x − 24.025)2 + 1.5(x − 24.025) + 14.586 · δ (x, 23.75, 24.3)
f62 (x) = 0.079(x − 24.3)3 − 0.953(x − 24.3)2 − 0.111(x − 24.3) + 8.216 · δ (x, 23.6, 25.0)
f63 (x) = 0.3(x − 24.55)3 − 2.32(x − 24.55)2 + 0.78(x − 24.55) + 14.644 · δ (x, 24.3, 24.8)
f64 (x) = − 0.06381(x − 14.75)3 − 0.01512(x − 14.75)2 + 0.8118(x − 14.75) + 14.9765 · δ (x, 12.5, 17)
f65 (x) = 0.0638(x − 14.75)3 + 0.01511(x − 14.75)2 − 0.8119(x − 14.75) + 6.5234 · δ (x, 12.5, 17)
f66 (x) = − 2.68(x − 5.25)3 − 0.67(x − 5.25)2 + 0.81(x − 5.25) + 12.652 · δ (x, 4.7, 5.8)
f67 (x) = 2.67(x − 5.25)3 + 0.669(x − 5.25)2 − 0.811(x − 5.25) + 8.847 · δ (x, 4.7, 5.8)
g1 (y) = 3.8 · δ (y, 9.35, 12.15)
q
5.8
g27 (y) = 23 −
4.752 − (y − 10.75)2 · δ (y, 6.0, 15.5)
4.75
q
5.3
4.52 − (y − 10.75)2 · δ (y, 6.25, 15.25)
g28 (y) = 25.5 +
4.5
q
5.3
4.52 − (y − 10.75)2 · δ (y, 6.25, 15.25)
g29 (y) = 23 −
4.5
q
3.6
g30 (y) = 25.5 +
3.52 − (y − 10.75)2 · δ (y, 12.9, 14.25)
3.5
q
3.6
g31 (y) = 25.5 +
3.52 − (y − 10.75)2 · δ (y, 7.25, 8.56)
3.5
q
3.6
3.52 − (y − 10.75)2 · δ (y, 7.25, 14.25)
g32 (y) = 23 −
3.5
q
3.2
g33 (y) = 25.5 +
3.252 − (y − 10.75)2 · δ (y, 12.8, 14.0)
3.25
q
3.2
g34 (y) = 25.5 +
3.252 − (y − 10.75)2 · δ (y, 7.5, 8.7)
3.25
q
3.2
g35 (y) = 23 −
3.252 − (y − 10.75)2 · δ (y, 12.2, 14.01)
3.25
q
3.2
3.252 − (y − 10.75)2 · δ (y, 7.5, 9.31)
g36 (y) = 23 −
3.25
q
2.8
g37 (y) = 25.5 +
2.852 − (y − 10.75)2 · δ (y, 12.5, 13.6)
2.85
q
2.8
g38 (y) = 25.5 +
2.852 − (y − 10.75)2 · δ (y, 7.9, 9.0)
2.85
q
2.8
g39 (y) = 23 −
2.852 − (y − 10.75)2 · δ (y, 12.5, 13.6)
2.85
q
2.8
g40 (y) = 23 −
2.852 − (y − 10.75)2 · δ (y, 7.9, 9.0)
2.85
q
g41 (y) = 28.5 + 0.62 − (y − 12.25)2 · δ (y, 11.65, 12.85)
q
g42 (y) = 28.5 − 0.62 − (y − 12.25)2 · δ (y, 11.65, 12.85)
q
g43 (y) = 28.5 + 0.62 − (y − 9.25)2 · δ (y, 8.65, 9.85)
q
g44 (y) = 28.5 − 0.62 − (y − 9.25)2 · δ (y, 8.65, 9.85)
q
g45 (y) = 28.9 + 0.62 − (y − 11.5)2 · δ (y, 10.9, 12.07)
q
g46 (y) = 28.9 − 0.62 − (y − 11.5)2 · δ (y, 10.9, 11.66)
q
g47 (y) = 28.9 + 0.62 − (y − 10)2 · δ (y, 9.42, 10.6)
q
g48 (y) = 28.9 − 0.62 − (y − 10)2 · δ (y, 9.84, 10.6)
q
1.125
g49 (y) = 21.625 +
1.252 − (y − 10.75)2 · δ (y, 9.5, 12.0)
1.25
q
1.125
g50 (y) = 21.625 −
1.252 − (y − 10.75)2 · δ (y, 9.5, 12.0)
1.25
g2 (y) = 4.7 · δ (y, 8.85, 12.65)
g3 (y) = 22.1 · δ (y, 9.625, 11.9)
g4 (y) = 23.0 · δ (y, 6.0, 15.5)
g5 (y) = 24.2 · δ (y, 10.8, 11.7)
g6 (y) = 24.3 · δ (y, 8.9, 9.2)
g7 (y) = 24.4 · δ (y, 10.8, 11.7)
g8 (y) = 24.5 · δ (y, 8.8, 9.35)
g9 (y) = 25.5 · δ (y, 6.0, 15.5)
g10 (y) = 26.0 · δ (y, 9.875, 10.75)
g11 (y) = 26.08 · δ (y, 9.875, 10.7)
g12 (y) = 34.7 · δ (y, 6.5, 15.0)
g13 (y) =
17
23.6
· δ (y, 6.7, 7.8) · δ (y, 8.9, 9.35) · δ (y, 10.0, 11.1) · δ (y, 11.4, 12.5)×
i
× δ (y, 12.7, 13.6) · δ (y, 14.2, 15)
g14 (y) = 23.8i · δ (y, 6.7, 6.8) · δ (y, 7.2, 7.7) · δ (y, 10.0, 10.3) · δ (y, 10.8, 11.1)×
× δ (y, 11.4, 11.7) · δ (y, 12.2, 12.5) · δ (y, 12.7, 12.85) · δ (y, 13.3, 13.6)
g15 (y) = −24.8 · δ (y, 7.2, 7.6) · δ (y, 6.7, 6.8) · δ (y, 9.3, 9.5) · δ (y, 8.7, 8.9)×
× δ (y, 8.2, 8.45) · δ (y, 10.0, 10.3) · δ (y, 12.2, 12.5) · δ (y, 11.4, 11.7)×
× δ (y, 10.8, 11.1) · δ (y, 13.35, 13.7) · δ (y, 12.7, 12.85)
25
· δ (y, 6.7, 7.7) · δ (y, 8.2, 8.9) · δ (y, 9.3, 11.1) · δ (y, 11.4, 12.5)×
i
× δ (y, 12.7, 13.9) · δ (y, 14.1, 14.7)
g17 (y) = 4.5(y − 10.33375)2 − 0.64(y − 10.33375) + 26.204 · δ (y, 10.23, 10.4375)
g18 (y) = 0.2(y − 10.03)2 − 2.46(y − 10.03) + 26.801 · δ (y, 9.83, 10.23)
g19 (y) = − 1.67(y − 9.6375)2 − 0.36(y − 9.6375) + 27.508 · δ (y, 9.4, 9.875)
g20 (y) = 22.4(y − 10.0625)3 − 2.1(y − 10.0625)2 − 3.14(y − 10.0625) + 26.961 ×
g16 (y) =
× δ (y, 9.875, 10.25)
g21 (y) = 5.1(y − 11.575)2 − 0.72(y − 11.575) + 25.967 · δ (y, 11.4, 11.75)
g22 (y) = 5.0(y − 11.7375)2 + 0.09(y − 11.7375) + 26.766 · δ (y, 11.6, 11.875)
g23 (y) = − 4.2(y − 11.55)2 + 0.33(y − 11.55) + 27.393 · δ (y, 11.4, 11.7)
q
5.8
g24 (y) = 25.5 +
4.752 − (y − 10.75)2 · δ (y, 6.0, 10.4)
4.75
q
5.8
g25 (y) = 25.5 +
4.752 − (y − 10.75)2 · δ (y, 11.1, 15.5)
4.75
q
0.3
g26 (y) = 31.3 −
0.352 − (y − 10.75)2 · δ (y, 10.4, 11.1)
0.35
På neste side finner du grafen for alle reelle x og y verdier som
oppfyller ligning (3.1) med hensyn på de 67 fi (x) og 50 g j (y)
definert over.
67
∏
i=1
50 fi (x) − y × ∏ g j (y) − x = 0
j=1
(3.1)
20
MATEMATIKK OG FYSIKK
∆t
USIKKERHETSPRINSIPPET
Av MARIELL BREIVIK
1. året bachelor i fysikk
Sola skinner og du går langs Nidelva. Rundt deg
har du et eldorado av fysiske fenomener- fysiske
fenomener som er enkle å observere. Krefter som er
enkle å påvise. Virkninger som vi er totalt avhengige
av. Tenk bare for eksempel på friksjonskrafta!
Hvor enn irriterende den måtte være, kommer du
ikke særlig langt uten den. Men den klassiske og
målbare fysikken kan ikke forklare alt. Om vi
beveger oss ned på kvantenivå, begynner Newtons
lover og sammenhenger å sprike. Å vite nøyaktig
posisjon og fart samtidig blir ikke lenger mulig
- usikkerhetsprinsippet slår til med sin fulle kraft.
For våre daglige gjøremål kan usikkerhetsprinsippet
virke irrelevant, følgene er ikke direkte merkbare i
vår sansbare verden, men prinsippet er likevel helt
avgjørende for vår eksistens.
For å sette pris på usikkerhetsprinsippets slående
kraft, er det nødvendig med en viss forståelse.
Usikkerhetsprinsippet sier at produktet av usikkerhet
i posisjon og usikkerhet i fart må være større eller
lik h/4π. Det er altså ikke mulig å måle nøyaktig
fart og posisjon samtidig. Dette kan virke rart, for
å måle nøyaktig posisjon og fart er jo noe vi til
stadig gjør i hverdagen. Men da er det viktig å
huske på at vi opererer med store masser. Store
masser, som alle andre masser, har både partikkelog bølgeegenskaper. For store masser vil typisk
bølgelengden bli stor, og partikkelegenskapene blir
de mest dominante i vår sansbare verden. Om vi nå
velger en partikkel med liten masse, kan vi se på hva
som skjer om vi prøver å bestemme dens posisjon
og fart nøyaktig. Se for deg en liten partikkel.
Vi vet at denne partikkelen har bølgeegenskaper.
Bølgelengden forbundet med partikkelen gir at
partikkelen har momentum, p = m · v. Om vi klarer
å måle farten ganske nøyaktig, har vi også klart å
måle partikkelens momentum og bølgelengde ganske
nøyaktig. Vi kan da fremstille partikkelens posisjon
grafisk ved å bruke bølgefunksjonen til partikkelen,
som vist på den nederste grafen på figuren.
Bølgefunksjonen gir sannsynligheten for å finne
partikkelen i en gitt posisjon x. Om vi nå prøver å
bestemme posisjonen ved hjelp av bølgefunksjonen,
møter vi på et problem. Funksjonen er jo periodisk,
noe som gir at sannsynligheten er like stor i flere
punkter. Når vi leser grafen, vil det kunne se noe
slikt ut: partikkel, partikkel, partikkel, partikkel,
partikkel, partikkel, partikkel osv. Stor nøyaktighet i
momentum gir altså stor usikkerhet i posisjon.
For å minske usikkerheten i posisjon må vi klare
å uttrykke bølgefunksjonen til partikkelen med et
tydeligere toppunkt om en x-verdi. Vi vil med andre
ord prøve å få en graf som har et tydeligere toppunkt
og ikke gjentar seg periodisk. For å klare dette må
vi legge sammen flere bølgefunksjoner. Hver av
disse bølgefunksjonen svarer til partikkelen med
en viss bølgelengde, altså partikkelen med et visst
momentum og en viss fart. Partikkelen er den samme
- det eneste vi gjør er å øke usikkerheten i fart ved å
legge sammen flere bølgefunksjoner. Vi vil da få
en graf som har et tydeligere toppunkt samtidig
som avstanden mellom toppunktene blir større.
Den øverste grafen på figuren viser dette tilfellet.
Om vi leser grafen, vil det kunne se noe slikt ut:
partikkel, partikkel, partikkel, PARTIKKEL, partikkel,
partikkel,partikkel, partikkel, partikkel, PARTIKKEL,
partikkel, partikkel,partikkel osv. Voilà - vi har nå minsket
usikkerheten i posisjon akkurat som vi ønsket. Men
i iveren etter å minske usikkerheten i posisjon har vi
også økt usikkerheten i fart. Vi har altså ikke klart å
9. Utgave
MATEMATIKK OG FYSIKK
bestemme posisjon og fart nøyaktig. Større sikkerhet
i den ene medfører automatisk større usikkerhet i den
andre - akkurat som Heisenbergs usikkerhetsprinsipp
sier.
Men hva er så disse merkverdige følgene av
usikkerhetsprinsippet? Disse følgene som er helt
grunnleggende for vår eksistens? Vi beveger oss
tilbake til Nidelva. Tilbake til vår verden - som
du nå står og betrakter. Legg merke til sola. Sola
som sender ut store mengder energi i form av lys
og varmestråler. Denne energien blir frigjort når
hydrogenatomer fusjonerer til heliumatomer. Men
for at fusjonen skal skje må to positive kjerner
komme nær nok. Dette innebærer at den elektriske
frastøtningskraften må overvinnes, noe som krever
mye energi. På tross av solas høye temperatur,
21
er ikke varmeenergien nok for å overvinne denne
frastøtningskraften. Ifølge den klassiske mekanikken
skulle i prinsippet ikke fusjonen vært mulig - sola
skulle ikke skint. Om den klassiske mekanikken
hadde regjert, ville det vært nokså ille for alt
liv på jorda, men slik er det heldigvis ikke.
For fusjonsprosessen på sola er en merkverdig
konsekvens av usikkerhetsprinsippet. En grunnleggende usikkerhet i posisjonen til hydrogenatomene
gjør at hydrogenatomene kan befinne seg i dette
forbudte området som den klassiske fysikken
danner. Det er med andre ord en sannsynlighet,
dog veldig liten, for at hydrogenatomene er nær
nok til at fusjonsprosessen starter. Med flere
millioner hydrogenatomer resulterer denne lille
sannsynligheten i at sola skinner!
MATEMATIKK OG FYSIKK
22
∆t
OM FORSTÅELSE MELLOM DELTAGERE, OG DIALEKTER I
REALFAG
Av FRANCESCO POGLIANO
1. året master i fysikk
Som medlemmer i Delta holder dere sannsynligvis
på med en del matte og fysikk. Matematikk
er, som folk sier, realfagsspråket, altså måten
folk fra forskjellige vitenskapelige disipliner kan
kommunisere med og forstå hverandre. Problemet
her er at dette “folket” som regel er utenforstående
Dragvoll-samfunnsvitere som i beste fall måtte ha
S-matte for ren tvangs skyld. Som dere sikkert vet,
så kan notasjon endre seg drastisk mellom matte
og fysikk. Dette problemet finnes ikke bare mellom
disse to fagene, men også mellom kjemi og fysikk,
elektronikk og fysikk, eller fysikk og mer avansert
teoretisk fysikk.1 Forskjellen er i tillegg ikke bare
tverrfaglig, men tidsmessig. La oss ta multiplikasjon
som et eksempel. På barneskolen lærte dere kanskje
å uttrykke 3 ganger 4 som
VEKTORER
Dette er en av de første notasjonforskjellene dere
kommer til å møte i realfag. Alle disse er måter å si
“vektor a” på:
Fysikk og vgs ~a = (a1 , a2 , a3 , ..., an )
Vektor kalkulus (matte) a
Håndskrift, fysikk og matte a, a, ~a
T
Lineær algebra a1 a2 a3 ... an
eller
ikke transponert
Summasjon ∑ni=1 ai x̂i
Kvantemekanikk (Dirac) |a >
3 × 4 =?
ENHETSVEKTORER
eller mer generelt, når man innfører bokstaver og det
I “summasjon” har dere sett x̂, en måte å skrive
ukjente x:
enhetsvektoren langs x på. Her er det flere, med
a×b = x
et forsøk på å dele dem inn i de fagområdene de er
Dette endret seg etter hvert, og prikken tok plassen mest brukt i. For enkelhets skyld tar vi utgangspunkt
til ×. På videregående og universitet forsvinner til i de tre kartesiske enhetsvektorene som utspenner
og med prikken:
R3 .
ab = x
Matte i, j, k
Noe liknende skjer også med divisjon, hvor tegnet “:”
blir erstattet med “/”. Det meste er derimot forståelig Fysikk x̂1 , x̂2 , x̂3 x̂, ŷ, ẑ ~ax ,~ay ,~az
for alle. Tallene er de samme, + og - er ikke noe
ukjent for de fleste, og vanligvis er det kun noen Indeksnotasjon ~xi
små forskjeller man må huske på for å kunne forstå
En liten “false friend” mellom matematikere og
hverandre.
fysikere er de sfæriske koordinatene. I fysikken
Litt som dialektene i Norge, for eksempel. Det betegnes vinkelen i xy-planet med φ og vinkelen
er denne likheten som fikk meg til å ville skrive en til z-aksen med θ , mens i matte er disse byttet om.2
slags notasjonsordbok dere kan referere til når dere Fysikk ρ, φ , θ
har lyst å forstå hva som foregår i et dokument som
ikke handler om det som er deres hovedfag.
Matte ρ, θ , φ
1 Fysikere
2 Why?
er vitenskapens skotter. Jævla fysikere, dere ødela fysikken!
Just because.
MATEMATIKK OG FYSIKK
9. Utgave
23
INDREPRODUKT
Indreprodukt er det som vi kaller for prikkprodukt
for vanlige vektorer, men det er et litt bredere konsept
i algebra, og er brukt i forskjellige disipliner. Disse
har selvfølgelig utviklet sin særegne måte å uttrykke
det på.
Kalkulus og fysikk ~a ·~b
Algebra < a, b >
Kvantemekanikk (Dirac) < a|b >
DERIVERING
INDEKSNOTASJON
Om man driver med litt avansert vektorkalkulus i fysikk, er sannsynligheten stor for at man kommer borti
indeksnotasjon. Dette, utvidet med Kroeneker-delta
og Levi-Civita-symbol, tilbyr oss forskjellige måter å
uttrykke summer, prikkprodukter, kryssprodukter og
andre operatorer på. Mens indeksnotasjon begrenser
seg med å uttrykke kun den ene komponenten av
en vektor, tar Einsteins summasjonskonvensjon (ES)
det et skritt videre og sier at ved gjentatte indekser
mener man en sum. Her tas ES i parentes ved siden
av.
Derivasjon (spesielt med hensyn til tid) er veldig
mye brukt i fysikk, og når man må skrive dtd mange
Prikkprodukt ai x j δi j (ai xi )
ganger, skulle man ønske det var en kjappere måte å
gjøre det på.
Kryssprodukt a j bk εi jk (a j bk ε ijk~ei )
Newtons notasjon f˙(t)
Lagranges notasjon f 0 (t)
Eulers notasjon Dt ( f (t))
Gradient (∇ f )i =
∂
∂ xi
f ( ∂∂xi f~ei )
Mange vil nå mene at dette er unødvendig mange
PARTIELLDERIVERING
måter å uttrykke det samme på, og at man må bli
Den partiellderiverte ∂∂tf har også en kortere måte å enig om å nå en tverrfaglig standardisert notasjon.
bli uttrykt på, og det er ∂t f .
Dette er i min mening en overfladisk tankegang.
Hvor mange av dere ville vært villige til å gi opp
dialekten deres for å oppnå økt forståelse mellom
INTEGRERING
landsdelene? Hvor mange nynorskbrukere ville gått
Avhengig av om det er fysikk eller matte dere driver
med på å bytte om til bokmål, eller det motsatte?
med, kan integrasjon uttrykkes på to litt forskjellige
Selv om noen kanskje ville gjort det, vil eksemplet
måter:
fremvise at det ikke bare er forståelse mellom
R
Matte ...dx
studenter vi prater om, men også identitet og stolthet
R
av sine røtter og opphav. Eller fagområder. Så neste
Fysikk dx...
gang dere lurer på hvem i svarte det var som bestemte
at ting skulle skrives annerledes i de forskjellige
fagene, tenk litt på hvor unike og kule dere er
√
−1
for å ha deres egen fagdialekt. Dette er hvordan
√
i, eller −1, kan bli skrevet som j av de som driver dere gjør verden oppmerksom på at “JA, jeg er
med elektronikk, signalbehandling eller -analyse.
fysiker/matematiker, og er stolt av det!”
MATEMATIKK OG FYSIKK
24
∆t
TEOREM/BEVIS
Av GUNNAR ARVID SVEINSSON, ULRIK ENSTAD
2. året master i matematikk
La D være et positivt heltall som ikke er et
kvadrattall. Et sentralt område i tallteori er studiet av
Vi kommer
til å ta i bruk noe som kalles normen
√
delmengder av de komplekse tallene gitt på formen på Z[ D]. Den er gitt ved
√
√
√
Z[ D] := {a + b D : a, b ∈ Z}
N(a + b D)) = |a2 − Db2 |
En viktig egenskap ved disse mengdene er at de er
lukket under
Dersom
√ addisjon og multiplikasjon:
√
√
α = a + b D og β = c + d D er to tall i Z[ D],
ser vi at summen og produktet av disse tallene blir
nye tall på samme form:
√
α + β = (a + c) + (b + d) D
√
√
αβ = ac + ad D + bc D + bdD
√
= (ac + bdD) + (ad + bc) D
En enkel utregning viser at N er multiplikativ,
√ altså
at N(α · β ) = N(α) · N(β ) for alle α, β ∈ Z[ D].
Teorem 1. La D være et positivt heltall som ikke er
et kvadrat. Da har ligningen
x2 − Dy2 = 1
minst én heltallsløsning (x, y) 6= (±1, 0).
Før vi kommer til beviset for teoremet trenger vi et
lemma. Vi kommer også til å bruke skuffeprinsippet
√
På fagspråket kalles Z[ D] en underring1 av de flere ganger, som sier følgende: Hvis du skal plassere
komplekse tallene.
m gjenstander i n skuffer og m > n, så må du plassere
minst to gjenstander i minst én av skuffene.
Et viktig spørsmål er om man kan dele på disse Lemma. La r ∈ R være et reelt tall.
tallene og ende opp med et tall på samme form. √
Mer
1. For enhver positiv n ∈ N så eksisterer det
presist ønsker vi å finne
√ ut hvilke tall α ∈ Z[ D]
p, q ∈ N slik at 0 < q ≤ n og |qr − p| < 1/n.
som er slik at 1/α ∈ Z[ D]. Vi ser at
√
√
2. Hvis r er irrasjonal, finnes det uendelig mange
1
a−b D
a−b D
p, q ∈ N slik at |qr − p| < 1/q.
√ =
√
√ =
a + b D (a + b D)(a − b D) a2 − Db2
Bevis. Vi deler intervallet [0, 1) i underintervallene
1
1 2
n−1
2
2
Dersom vi da har at a − Db = 1, får vi det vi [0, n ), [ n , n ), · · · , [ n , 1). Se på tallene αk =
ønsket oss. Derfor er det ønskelig å kunne løse kr − bkrc for k = 0, . . . , n, hvor bxc generelt
betegner største heltall mindre enn eller lik x. Ved
likninger på formen
skuffeprinsippet må minst to av tallene, la oss
2
2
si αk1 , αk2 med k1 < k2 , være inneholdt i samme
x − Dy = 1
intervall. La q = k2 − k1 og p = bk2 rc − bk1 rc. Da
Denne ligningen kalles Pells ligning. Legg merke får vi at |p − qr| = |bk2 rc − bk1 rc − (k2 − k1 )r| =
til at (x, y) = (±1, 0) alltid er løsninger, de såkalte |αk2 − αk1 | < 1/n.
trivielle løsningene. Målet vårt her er å vise at
ligningen alltid har ikke-trivielle løsninger. Beviset
Beviset for del 2 går som følger: La r være
vi gjengir er originalt krevet av David Speyer på irrasjonal, og anta at |qr − p| < 1/q har kun endelig
nettstedet math.stackexchange.com.
mange løsninger. Siden r er irrasjonal, er alle
1 La
R være en ring (med enhet). En underring av R er en delmengde S av R som er lukket under addisjon, additive inverser og
multiplikasjon, og inneholder den multiplikative enheten i R. En underring av R kan betraktes som en ring i seg selv.
9. Utgave
MATEMATIKK OG FYSIKK
25
størrelsene |qr − p| strengt positive, så vi kan finne må være et heltall:
√
√
√
en N > 0 slik at 1/N < |qr − p| for hver løsning
p
+
q
D
(p
+
q
D)(p
−
q
D)
2
2
2
2
1
1
(p, q). Fra del 1 vet vi at det eksisterer et par ( p̃, q̃)
√ =
√
√
slik at 0 < q ≤ N og |q̃r − p̃| < 1/N ≤ 1/q̃. Men nå p1 + q1 D (p1 + q1 D)(p1 − q1 D)
√
ser vi at paret ( p̃, q̃) er en løsning på |qr − p| < 1/q,
(p1 p2 − Dq1 q2 ) + (p1 q2 − p2 q1 ) D
=
så vi må ha 1/N < |q̃r − p̃|, en selvmotsigelse.
p21 − Dq21
√
= P+Q D
Bevis
for
teoremet.
Siden
D
ikke
er
et
kvadrat,
må
√
D være irrasjonalt. Ved lemmaet finnes det da hvor
uendelig √
mange par (p, q) blant de naturlige tallene
p1 p2 − Dq1 q2
(p1 q2 − p2 q1 )
slik at |q D − p|≤ 1q . For ethvert slikt par kan vi
P=
og Q =
m
m
estimere |p2 − Dq2 | som følger:
Fra vårt valg av (p1 , q1 ) og (p2 , q2 ) har vi at
√ √ 2
2
|p − Dq | = p − Dq p + Dq
p1 p2 − Dq1 q2 ≡ p21 − Dq21 = m ≡ 0 (mod m) og
p1 q2 − p2 q1 ≡ p1 q1 − p1 q1 ≡ 0 (mod m). Dermed
√
√ 1 ≤ p − Dq + 2 Dq
er P og Q faktisk heltall. Ved å anvende funksjonen
q
N nevnt√innledningsvis
√ √ √ på begge sider
√ av likningen
1 ≤
p − Dq + 2 Dq
p2 + q2 D = (P + Q D)(p1 + q1 D) får vi
q
√
1
m = p22 − Dq22
≤ 2 +2 D
q
√
= (P2 − DQ2 )(p21 − Dq21 )
< 2 D+1
= (P22 − Dq22 )m
Merk at p2 − Dq2 er et heltall, og siden det√bare
er endelig
mange heltall i intervallet (−2 D −
√
1, 2 D + 1), gir skuffeprinsippet at ligningen
p2 − Dq2 = m har uendelig mange løsninger for
et passende heltall m 6= 0 i intervallet (hvorfor må
m 6= 0?)
Ved å kansellere m har vi funnet en løsning (P, Q) til
Pells ligning. Det overlates til leseren å vise at denne
ikke er triviell.
Noe man kan spørre seg om nå er hvor mange
ikke-trivielle løsninger ligningen har. Det viser seg
at svaret er uendelig mange, og nå som vi vet at
ikke-trivielle løsninger finnes, er det faktisk ikke
så vanskelig å vise at det finnes uendelig mange.
Den interesserte leser kan søke opp Brahmaguptas
identitet.
Tar vi alle de uendelig mange løsningene (p, q)
til p2 − Dq2 = m og reduserer dem modulo m,
dvs. beregner (p mod m, q mod m), så finnes det
kun m2 ulike “skuffer” de kan havne i. Igjen, ved
skuffeprinsippet, må minst to løsninger (p1 , q1 )
og (p2 , q2 ) havne i samme skuff, dvs. p1 ≡ p2 og
Alt i alt er kanskje bruken av skuffeprinsippet det
q1 ≡ q2 (mod m).
mest oppsiktsvekkende i beviset over. Skuffeprinsippet kan virke ganske uskyldig og opplagt, men gjør
√
√
Vi viser nå at brøken (p2 + q2 D)/(p1 + q1 D) undre i mange argumenter!
26
DIVERSE
∆t
DIVERSE
ANMELDELSE: DAHLS PÅ HYTTA
Av BRAGE SÆTH
Bragemedlem
Produksjonssted: E. C. Dahls her i Trondheim
Alkoholprosent: 4,6 %
Flaskestørrelse: 0,5 L
Pris: Mener det var i nærmeheten av 30,Farge: Uvisst, siden boksen ikke er gjennomsiktig.
Smak: Litt annerledes enn tidligere anmeldelser,
men fremdeles god.
TERNINGKAST: 6
Duft: Like frisk som fjelluften.
Smak: Kanskje mer metallisk en andre øl.
Farge: Gjetter at den er gyldenbrun.
Smak: Herlig å fukte ganen med en sen sommerdag.
Smak: Denne ølen hadde ekstra mye smak, nesten 2 desiliter ekstra.
Kommentar: Dersom en skal bære med seg øl på hytta, anbefaler jeg boks framfor flaske, ettersom panten
veier mindre.
9. Utgave
DIVERSE
27
DIVERSE
28
∆t
VÅRGANGSFEST
Av MARTIN MADSEN
2. året årsstudium i matematikk
For de av dere som er nye i år, så har dere kanskje
hørt de gamle hviske og tiske om vÅrgangsfesten,
og dere har sikkert et brennende ønske om å finne
ut hva som skjedde der i fjor. For de av dere som
faktisk var tilstede i fjor, så har sikkert dere også
samme brennende ønske. Derfor har ∆t tatt på seg
oppgaven med å få litt klarhet i kvelden.
Som et lite sidesprang vil jeg benytte denne
muligheten til å understreke hvor mye energi en
tekstforfatter bruker på å dra disse fuktige kveldene
frem fra glemmeboken. Etter å ha bedømt et ukjent
antall fester for Delta har jeg til slutt kommet fram til
en prosess basert på Edward Girden og Elmer Culler
sin forskning på tilstands-avhengig minne1 . Dette
kan til tider bli en ganske stor bauta, både mentalt
og fysisk.
Så hva er egentlig denne vÅrgangsfesten? Vel,
kort oppsummert så er dette de nødvendige
1 Tilstands-avhengig
ingrediensene: 140 glade og våryre deltagere, 256
liter konsumert hjemmebrygget vin på 13-15%,
havet i gangavstand, en håndfull tønnegriller varmere
enn Satans underbukser, samt et glimrende Deltaband. Hva kan gå galt? Tydeligvis ikke så alt for
mye, i hvert fall hvis man sammenligner med året
før. Så vidt jeg husker var ikke ambulansen tilstede,
redningsvesenet ble ikke innkalt, alle tønnegrillene
stod oppreist hele kvelden, og vinen var god. Ikke
mye å klage på for å være helt ærlig. ArrKom gjorde
en ypperlig jobb med å stelle i stand. Humøret var
også generelt bra, selv om jeg hørte rykter om litt
emosjonelle tilstander utover kvelden.
Enkelte danseglade deltagere har kanskje et ønske
om å vite nøyaktig hvilke sanger de danset til utover
kvelden. Så her kommer en liste med sangene Deltaband fremførte live i løpet av kvelden:
• Calvin Harris - Summer
minne benyttes i psykoterapi og baserer seg på idéen om at et minne vil bli klarere hvis man har samme
sinnstilstand som da minnet oppstod, les full. https://en.wikipedia.org/wiki/State-dependent_
memory
9. Utgave
DIVERSE
• Bruno Mars - Uptown Funk
• The Black Keys - Lonely boy
• BigBang - Girl in oslo
• Jets - Be my girl
• Elvis - A little less conversation
• Earth wind and fire - September
• Daft punkt - Get lucky
29
Det kan også nevnes at ved å bruke en promillekalkulator var promillen for en gjennomsnittlig
deltager på 2,8. Forfatter tar forbehold om at han
er lat og ikke gidder å opplyse tallverdier benyttet
i utregningen. Data publisert i denne artikkelen bør
tas med et trillebårlass med salt, og ikke under noen
omstendighet benyttes i videre arbeid.
Til slutt vil jeg innføre en rangeringskala for Delta
sine alkoholrelaterte fritidstilbud. Vårgangsfesten
vil få tildelt en Estimert Blackout koeffisient, EBK.
EBK’en vil gjøre det lett for leseren å fange
essensen av festen, og samtidig gjøre framtidig
sammenlikning av Delta sine festligheter trivielt.
• Queens of the stone ange - Make it wit chu
• EBK: 4,3
• White stripes - Seven nation army
• Rolling stones - Gimme shelter
• Beatles - Hey Jude
Entusiastiske ∆t-lesere får vente i spenning på
neste utgave, da jeg er for lat til å skrive en artikkel
om utledningen av EBK’en og dens funksjon på
nåværende tidspunkt.
30
DIVERSE
∆t
AMAZING RACE
Av PETER MARIUS FLYDAL
2. året bachelor i fysikk
Lørdag den 11. april inneværende år ble Deltas
eget rebusløp «Amazing Race» arrangert for aller
første gang, preget av både bred deltagelse og
fortreffelige værforhold. Med hele byen som
spillbrett og ArrKom i storform, var det duket for
et mesterskap uten sidestykke i linjeforeningens
historie, der oppfinnsomhet så vel som mot og
kondisjon var avgjørende for de åtte deltagende
gruppenes prestasjoner, og ingen påmeldte egentlig
visste hva det var de hadde latt seg lure med på.
Det hele gikk av stabelen tidlig på formiddagen1
midt på Torget, der Frelsesarmeens lokale korps
spilte opp til en storslagen åpningsseremoni. Da det
etterhvert viste seg at korpset overhodet ikke hadde
tenkt til å slutte å spille med det første, så arrangørene seg nødt til å flytte startstreken noen titalls meter
for å gjøre den allerede øredøvende opplevelsen litt
mindre intens mens instruksjonene ble lest opp, og
dagens første utfordring gjennomført.
1
Det begynte med en kort quiz som avgjorde hvilke
grupper som fikk starte først når det virkelige racet
begynte, og da rekkefølgen var bestemt gjallet
det historiske startskuddet gjennom gatene, tett
etterfulgt av de første gruppene, som ved hjelp
av utdelte kart forsøkte å finne frem til første
post og neste ledetråd. Alle deltagerne var på
forhånd fratatt sine mobiltelefoner og penger, men
utenom dette var det kun fantasien som satte grenser
for hjelpemiddelbruken. Det viste seg raskt at
transport mellom postene var like viktig som hurtig
gjennomføring av de forskjellige oppgavene, og både
sykler, biler og kollektivtransport ble tatt flittig i
bruk av forskjellige grupper. Likevel var det enkelte
hint og veibeskrivelser som – tolket på feil måte
– kunne lede en uheldig gruppe på fåfengt jakt
både høyt og lavt, og mange ble smertelig klare
over at høy hastighet er svært lite verdt hvis den
peker mot feil ende av byen. Trondheim var de
neste timene preget av seiershungrige deltagere
med konkurranseinnstinktet i høygir, og større eller
mindre forståelse av hvor de egentlig var på vei.
Hadde dette vært en skoledag, ville det fortsatt vært flere forelesninger igjen.
9. Utgave
DIVERSE
Av de mest interessante postene kan nevnes
hurtigspising av Egon-pizza, besøk i tre av byens
vakreste kirker, og den nådeløse klippeposten. På
sistnevnte ble deltagerne stilt overfor et valg om
enten å sitte 40 minutter og vente mens seieren glapp
sakte, men sikkert, ut av de stadig fastere knyttede
nevene deres, eller la én representant på gruppen
legge seg under saksen og frivillig motta en eller
annen heslig frisyre. For de gruppene som ankom
den provisoriske frisørsalongen samtidig, var dette
et godt eksempel på fangens dilemma, men som vi
alle vet er samarbeid vanskelig i slike situasjoner, og
da særlig når blodet koker og duften av seier river i
nesen. Resultatet ble null ventetid, én bolleklipp med
pannelugg, seks hanekammer og én munkesveis.2
2
31
Etter mange timer med iherdig innsats i denne
trekampen av utholdenhet, intelligens og vågemot,
som hadde tatt de forskjellige gruppene til både
Leangen og Hovedbygget– og enda lenger, hvis
du teller med dem som rotet seg bort – endte
maratonet i Byåsen, med Trine Ødegård Olsen,
Thomas Kallevik, Fride Skarland og Vegard Øverås
som endelige vinnere. Utover kvelden ramlet resten
av gruppene også i mål, og premieutdelingen ble
gjennomført foran den slukørede forsamlingen av
beseirede. Kvelden ble avsluttet med en såkalt
«Amazing Rave» på den etterhvert så velkjente Deltapuben Nattergalen, mens roen langsomt senket seg
over Trondheims hardt herjede gater. Arrangementet
hadde vært en stor suksess, og en ny tradisjon
var forhåpentligvis blitt født i vår ærverdige
linjeforening – og skulle staden noen gang glemme
at den er en studenterby, var det i alle fall ikke på
denne dagen.
Undertegnede undres fortsatt over denne frisyrefordelingen, og angrer ikke et sekund på å ha valgt bort hanekammen til
fordel for det noe mer elegante, og middelalderske, alternativet.
32
DIVERSE
∆t
GOBI - DET NYE SNAPCHAT?
Av ADRIAN RAMSVIK
1. året bachelor matematikk
Den
skandaleomsuste
Snapchat-brukeren
NTNUsnap fikk raskt over 4000 følgere på Snapchat,
der personer kunne sende snaps og dele det med alle
brukerens følgere. Etter sanksjoner fra både NTNU
og Snapchat måtte dessverre brukeren legges ned.
Fem studenter fra datateknologi på NTNU har nå
tatt ansvar og lansert bildedelingsappen Gobi, der
du kan opprette og delta på andres story-er - alt på
lovlig vis. Appen ble offisielt lansert 10. august i år,
dagen før immatrikuleringen, og flere tusen brukere
har lastet ned appen allerede.
Gobi er kalt opp etter et av grupperommene på
P15, et grupperom ofte brukt av datateknologistudentene ved NTNU. Gobi skulle først være et tilbud
for studenter i Trondheim ved NTNU, HiST og
BI, men utviklerene ser nå at studenter ved andre
utdanningsinstitusjoner kommer like etter. Egne
grupper for universiteter i USA har til og med blitt
opprettet.
Delta ligger ikke på latsiden, og har også laget en
egen story. De 37 personene som allerede har blitt
en del av storyen har delt bilder av Dahls, kjedelige
forelesere og fuktige nachspiel etter immballet. Vi
trenger å se flere fjes, med øl eller ikke, så her er
det bare å delta! Storyen heter linjeforeningdelta, og
passordet finner du på kontoret.
Gobi skiller seg ikke bare fra andre bildedelingstjenester ved at flere kan delta på storyen, men også at
du kan like bildene som blir lagt ut. Akkurat nå leder
nissetroll med 35 poeng, foran en delt andreplass
mellom sebastj og simonsolheim med 33 poeng. En
slik topplassering medfører ikke bare heder og ære,
men også en langt gjevere premie - en enhet drikke
på kontoret. Mediakomitéen vil med dette annonsere
Gobi-konkurransen 2015, der den personen som får
mest likes på Gobi i løpet av oktober, vinner en brus
eller en øl på MedKoms regning. Ta en selfie, tegn
kjole på foreleseren eller ta bilde av dobbelthaka på
sidemannen - i krig er alt lov, måtte den beste vinne!
9. Utgave
DIVERSE
33
VIDEOHELG
Har du noen gang ønsket å skape visuell magi?
Kanskje du drømmer om å bli filmstjerne? Eller bor
det en liten Spielberg eller Tarantino i deg? Da har
vi tilbudet for deg!
9.-11. oktober skal MedKom arrangere videomakingshelg. Det innebærer at dere, flotte
deltagere, skal planlegge, filme og redigere fram
kinematografiske mesterverk! Få med deres beste
venner, eller kanskje noen dere ikke kjenner ennå,
fyr opp engasjementet og la kreativiteten blomstre!
Alle er velkommen til å være med, og ingen
forkunnskaper nødvendig. Dere skal jobbe i grupper,
og det er i utgangspunktet ingen begrensning på
hvor få eller mange som får være på hver gruppe.
Opplegget er at dere skal lage en kort film fra bunnen
av i løpet av helgen. Det innebærer planlegging,
filming og redigering, og man burde ha en kreativ
idé til hva man vil lage. Etter at prosjektet er ferdig
vil vi låne et auditorium og vise alle filmene, slik at
hele Delta kan få se resultatet.
Noen forslag til idéer, for inspirasjon: Parodi
på klassiske scener fra kjente filmer, dokumentar
om livet på Dragvoll, stop-motion-animasjon,
musikkvideo, og mye mer. Det er kun fantasien som
setter grenser!
Dato: 9.-11. Oktober
Påmelding: Følg med på Linjeforeningen Delta
på Facebook, eller ta kontakt med Gert Kluge på
[email protected]
DIVERSE
34
∆t
UTGAVENS POSTULATER
“
“
“
“
“
“
“
“
“
Jeg skal aldri drikke mer!
Brage Sæth
Hvorfor blir det 2-jævla-fuckings-pi?!
Andreklassing BMAT
Det er ikke drikkepress,
det er bare Lambo!
Blondine, førsteklasse BMAT
Jeg ligger våken om nettene og tenker
på Michelle. . .
Betatt fadderbarn, BFY
Er Movember i november, eller er det i
oktober?
Mona-Lena
Det er øl til 29 kroner på Circus!
Simon om hvorfor han ikke kom på innut-møtet med styret
Skulle gjøre ting. Ble kontoret.
Haakon H.
Tallet går nesten opp i tre.
Tredjeklassing BMAT
Jeg har fått meg PT! Eller, det er bare
en tilfeldig student da. Han trener meg,
og jeg gjør øvingsopplegget i matte 1
for han.
Andreklasse BMAT
“
Hyttetur skal være litt sånn shady!
Mona-Lena om komitéhyttetur
”
”
”
”
”
”
”
”
”
”
“
“
“
“
Det finnes ikke bedre blandevann enn
vin.
Fadderbarn i Heisenberg
- Hvorfor jobber du ikke?
- Fordi du skriver av boka mi!
Samtale under øvingstime
... og takk til alle dere andre fordi dere
ikke klarte å slå oss!
Fra Sagans takketale under immballet
Hæ? Er det bare 36 kalorier i 100 gram
gulrot? Det er jo nesten ikke verdt
å spise, bruker jo flere kalorier på å
tygge!
Andreklassing, BMAT
“
Hva skal jeg med fjær?! Jeg sover på
fjær!
Fra forelesning om diffligninger
”
”
”
”
”
Send inn sitater til Cecilie Raustein (Facebook), eller andre du kjenner i redaksjonen.
BAKSIDEN
Start på det nederste punktet. I dette spillet flytter man seg på to forskjellige måter, og man skal
alternere mellom disse to. Først beveger man seg (i hvilken som helst retning) med antall steg
indikert ved nåværende posisjon. Fra neste punkt skal man dermed hoppe til et punkt som enten
har felles farge eller form. Repeter dette om og om igjen til du kommer til ∆.
4
∆
3
1
1
2
4
7
8
0
0
2
4
8
8
3
1
4
3
4
Har du funnet en løsning? Da kan du prøve å finne:
• Korteste løsning
• Korteste løsning slik at summen av alle tall du støter på blir et kvadrattall
• Korteste løsning slik at summen av alle tall du støter på blir et primtall
• Korteste løsning slik at summen av alle tall du støter på blir et fibonaccitall
Får du ikke sove?
• Finnes det løsninger med tilhørende sum på 10100 + 1?