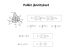Pitkä matematiikka (MAA), mallikoe, Peter Hästö
Transcription
Pitkä matematiikka (MAA), mallikoe, Peter Hästö
Pitkä matematiikka (MAA), mallikoe, Peter Hästö http://phasto.files.wordpress.com/2014/03/pitka_mallikoe_v0_4.pdf muokannut Terhi Raittila Osa A (ilman laskinta) Ratkaise kaikki tehtävät 1-4. 1. a) Laske lukujen 1 1 1 , ja keskiarvo. 2 3 4 b) Laske 43 42 40 . c) Ratkaise epäyhtälö 2 x 4 x 2 2. a) Sievennä a(a b) b(a b) . b) Supista x2 y y 2 x . x y c) Jaa tekijöihin 9 12a 4a 2 . 3. Päättele, pätevätkö seuraavat väittämät. Pelkkä vastaus (kyllä/ei) riittää. a) 5,3 > 12 b) 7,245 + 6 = 3,3 + 4,5 + 6,9 c) 146347 64367 < 146335 64467 d) 52 e) x3 6 x2 3x , kun x = 1 f) x 2 2 , kun x > 2 4. Määritä funktion f ( x) x3 6 x 2 suurin ja pienin arvo välillä [2,6] Osa B Ratkaise kolme (3) tehtävistä 5-9 5. Kahden kuution pinta-alojen suhde on 16:25. Laske kuutioiden tilavuuksien suhde. 6. Hajamielisellä professorilla on yksi luento jokaisena viitenä arkipäivänä, mutta hän muistaa pitää päivittäisen luentonsa vain 80 prosentin todennäköisyydellä. a) Millä todennäköisyydellä hän muistaa pitää viikon kaikki luennot? b) Millä todennäköisyydellä vain yksi viidestä luennosta jää pitämättä? c) Määritä viikossa pidettyjen luentojen lukumäärän odotusarvo. 7. Peter on ostanut uuden auton. Oletetaan, että auton arvo laskee vuosittain 15%. a) Kuinka monta prosenttia auton arvo on laskenut neljässä vuodessa? b) Muodosta funktio h(x), joka ilmoittaa auton hinnan, kun ostohetkestä on kulunut x vuotta. c) Kuinka monen vuoden kuluttua auton arvo on viidesosa alkuperäisestä? 8. Suorakulmion muotoisen ruohoalueen mitat ovat 25m x 11m. Aluetta kasvatetaan joka sivulta yhtä leveällä kaistaleella. Määritä kaistaleen leveys, kun alueen pinta-ala kaksinkertaistuu. 9. Ratkaise TOINEN kohdista i ja ii. Kumpikin on kuuden pisteen arvoinen. i. Konnektiivin W totuustaulu on A 1 1 0 0 B 1 0 1 0 AWB 0 1 0 0 Esitä lause A W(A W B) konnektiivien , ja avulla ii. Ratkaise yhtälö e x 3x Newtonin menetelmällä Osa C Ratkaise kolme (3) tehtävistä 10-13. 10. a) Määritä sellainen kerroin a, että ax 2 , kun x 1 f ( x) x 2 , kun x 1 1 x 2 on jatkuva kaikkialla. b) Määritä käyrän x y 5 ja koordinaattiakselien rajoittaman alueen pinta-ala. 11. Määritä ympyröiden 4 x2 4 y 2 16 x 16 y 7 0 ja 4 x2 4 y 2 16 x 8 y 205 0 yhteisten tangenttien yhtälöt. 12. Oheisen kuution särmän pituus on 2. Sen sisällä on vaaleanpunainen pallo, joka sivuaa jokaista kuution tahkoa. Kuution yhdessä kulmassa on pienempi sininen pallo, joka sivuaa suurta palloa ja kolmea kuution tahkoa kuvion mukaisesti. Laske sinisen pallon säteen tarkka arvo. 13. Sanomme, että kokonaisluku on kiva jos sen on kahden suurimman, eri suuren, aidon tekijänsä summa. Osoita, että mikään luku ei ole kiva.