Aufgaben zum Satz des Pythagoras und zum Kathetensatz
Transcription
Aufgaben zum Satz des Pythagoras und zum Kathetensatz
Aufgaben zum Satz des Pythagoras und zum Kathetensatz 1.) Zeichne die alles erklärende Skizze. (Das ist die Skizze, die jedem sofort vor Augen sein sollte, wenn er die Worte Kathetensatz oder Satz des Pythagoras hört. Tipp: Es geht um ein rechtwinkliges Dreieck, dessen Höhe und die Quadrate der Seiten.) 2.) Der Kathetensatz gilt in rechtwinkligen Dreiecken. Formuliere den Kathetensatz mit Hilfe der Bezeichnungen aus der alles erklärenden Skizze. (Hier sollen nicht nur zwei Formeln stehen! Die beiden Gleichungen müssen natürlich auch dahin, aber man soll verstehen können, was sie bedeuten.) 3.) Der Satz des Pythagoras ist allen in seiner kurzen From a2 + b2 = c2 bekannt. Bleibt die Frage, was das bedeutet. Fülle die Lücken im folgenden Text zur Erklärung. In einem Dreieck seien die drei Seiten wie folgt benannt: Die Hypotenuse (das ist die Seite, die ) heißt . Die beiden Katheten (das sind die Seiten, die ) heißen und . Dann gilt der Satz des Pythagoras, nämlich a2 + b2 = c2. Zusammengefasst bedeutet das: In einem Dreieck gilt: 4.) Berechne die übrigen Stücke in einem rechtwinkligen Dreieck mit Hypotenuse c und restlicher Beschriftung wie in der alles erklärenden Skizze. Trage die Ergebnisse in die Tabelle ein: a) a 8 cm b 6 cm b) c) 4 km c 3,5 mm p 0,7 mm 12 cm q h d) 2 cm 2,5 km 5.) Eine 4,2 m lange Leiter lehnt an einer Wand. Auf dem Fußboden beträgt ihr Wandabstand 1,5 m. Wie hoch reicht die Leiter? 6.) Ein Tapezierer will nachprüfen, ob die Zimmerdecke rechtwinklig ist. Er misst die Länge mit 5,10 m , die Breite mit 3,60 m und die Diagonale mit 6,24 m. Zu welchem Ergebnis kommt er? 7.) Berechne in diesem rechtwinkligen Dreieck die unbekannten Größen a, b und c. 8.) Berechne die Seitenhöhe s H und die Länge der Seitenkante s. 9.) Ein Quader besitzt die Maße 4 cm, 3 cm und 6 cm. Berechne die Länge der Raumdiagonalen d.




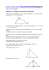





![Hans Walser, [20130522] Kathetensatz 1 Der - walser-h-m.ch Hans Walser, [20130522] Kathetensatz 1 Der - walser-h-m.ch](http://s1.doczz.net/store/data/006095448_1-fdbd48f6807b5923267b6746f8df262e-70x70.png)