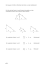Hans Walser, [20130522] Kathetensatz 1 Der - walser-h-m.ch

Hans Walser, [20130522]
Kathetensatz
1 Der Klassiker
Die Abbildung 1 illustriert die klassische Formulierung des Kathetensatzes.
Abb. 1: Kathetensatz
Die folgenden Abbildungen geben Varianten dazu.
2/14
Hans Walser: Kathetensatz
2
Varianten mit Quadraten
Abb.2
3/14
Hans Walser: Kathetensatz
Abb. 3
Abb.4
4/14
Hans Walser: Kathetensatz
Abb. 5
5/14
Hans Walser: Kathetensatz
3 Regelmäßige Vielecke
Wir lösen uns von den Quadraten.
Abb. 6
6/14
Hans Walser: Kathetensatz
Abb. 7: Obelix
7/14
Hans Walser: Kathetensatz
Abb. 8
8/14
Hans Walser: Kathetensatz
Die Abbildung 7 zeigt eine klassische Schulaufgabe.
Abb. 9
Abb. 10
9/14
Hans Walser: Kathetensatz
Das Siebeneck können wir zwar nicht konstruieren, aber für den Kathetensatz taugt es
allemal (Abb. 9).
Abb. 11
10/14
Hans Walser: Kathetensatz
Abb. 12
11/14
Hans Walser: Kathetensatz
4
Halbkreise
Abb. 13
Es braucht auch eine Viertelellipse.
5 Das Dreieck selber
Es geht auch mit dem Dreieck selber. Der Beweis des Kathetensatzes ist in diesem Fall
trivial.
Abb. 14
Abb. 15
12/14
Hans Walser: Kathetensatz
6 Puzzles
Und hier noch ein Puzzle in Varianten.
Im Puzzle der Abbildung 16 können alle Puzzle-Teile parallel verschoben werden.
Abb. 16: Puzzle
13/14
Hans Walser: Kathetensatz
Im Puzzle der Abbildung 17 müssen alle Puzzle-Teile zusätzlich vertikal gespiegelt
werden.
Abb. 17: Puzzle
14/14
Hans Walser: Kathetensatz
Und schließlich noch ein Turm.
Abb. 18: Turm