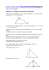Mathematik Geometrie Die Satzgruppe des Pythagoras Die

Mathematik
Geometrie
Die Satzgruppe des Pythagoras
Die Satzgruppe
des Pythagoras
Der Höhensatz des Euklid
h2 = pq
Der Kathetensatz des Euklid
a2 = cp und b2 = cq
Der Satz des Pythagoras
a2 + b2 = c2
Pythagoras von Samos
* um 570 v. Chr., † nach 510 v. Chr. war ein griechischer Philosoph
und Gründer einer religiös-philosophischen Bewegung
Was andere über Pythagoras sagten:
,,Er ist einer der bedeutendsten Menschen" - Bertrand Russell
,,Er ist der Anführer der Schwindler" – Heraklit
,,Der wise Pictagoras, der ein astronomierre was" - Wolfram von Eschenbach
,,Als er den Satz gefunden hatte, soll er den Göttern hundert Ochsen geopfert haben. Seitdem zittern alle
Ochsen, sooft eine neue Wahrheit entdeckt wird." - Ludwig Börne
Link zur Uni Erlangen: Verschiedene Beweise des Satzes des Pythagoras:
http://www.didmath.ewf.uni-erlangen.de/Verschie/Gut_Ref/Pythago/Pythagoras.html
Landesbildungsserver Baden-Württemberg: Weitere interessante Unterlagen zur
Satzgruppe des Pythagoras:
http://www.schule-bw.de/unterricht/faecher/mathematik/sek1/geometrie/pythgoras/einf_grundlagen
Mathematik / Geometrie
Die Satzgruppe des Pythagoras
B. Willimann
24.09.2006
Seite 1 / 2
Mathematik
Geometrie
Die Satzgruppe des Pythagoras
Beweis des Höhensatzes:
Die beiden Dreiecke sind ähnlich, da sie in allen drei Winkeln
Winkeln übereinstimmen (Winkelsumme im Dreieck)
Also lassen sie sich wie folgt anordnen:
Da nun die beiden grossen Dreiecke in beiden Abbildungen flächengleich sind, folgt sofort, dass
h2 = qp gilt.
q.e.d.
Beweis des Kathetensatzes:
1. BC und AF sind parallel – deshalb sind die Dreiecke
AFC und AFB flächengleich (gleiche Grundseite und
Höhe)
2. CD und AH sind parallel – deshalb sind die Dreiecke
AHD und AHC flächengleich (gleiche Grundseite und
Höhe)
3. Für die Dreiecke ABF und AHC gilt nun:
AB = AH = Hypothenu se c
AF = AC = Kathete c
∢BAF = ∢HAC = 900 + β
4. Nach dem Kongruenzsatz SWS sind die Dreiecke
Dreiecke AFB und AHC flächengleich.
Daraus folgt, dass auch die Dreiecke ACF und AHD
flächengleich sind – und damit:
2
2 ⋅ ∆ACF = b = 2 ⋅ ∆AHD = c ⋅ q
h.x.
Beweis des Satzes von Pythagoras:
Führt man den Beweis des Kathetensatzes auch für die andere Kathete durch, so erhält man
2
a = c ⋅p
also:
2
2
a +b = c ⋅p + c ⋅q
Mathematik / Geometrie
Die Satzgruppe des Pythagoras
2
2
a + b = c(p + q)
2
2
a +b = c
B. Willimann
24.09.2006
2
q.e.d.
Seite 2 / 2