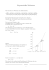Eine Aufgabe zu Kurvenscharen für die Klasse 11

Eine Aufgabe zu Kurvenscharen für die Klasse 11
Gegeben ist die Funktionenschar g t ( x ) = t x 3 − ( t + 1) x 2 mit t ∈ R \{0}
Diskutieren Sie zunächst diese Funktionenschar in Abhängigkeit vom Parameter t.
a) Bestimmen Sie alle Nullstellen und das Verhalten an den Grenzen des Definitionsbereichs.
b) Welche Punkte gehören zu jedem Graphen der Schar. Ermitteln Sie deren
Koordinaten.
c) Bestimmen Sie alle Hoch- und Tiefpunkte in Abhängigkeit von t .
d) Bestimmen Sie alle Wendepunkte in Abhängigkeit von t.
e) Skizzieren Sie die Graphen der Schar mit den Parametern -4, -1, -0.2, 0.5, 1 und 2.
(Verwenden Sie hierzu u.U. geeignete Software.)
Mit h t wird eine weitere Schar h t ( x ) = t x 3 − t 3 − t 2 ( mit t ∈ R \{0}) festgelegt.
f)
Zeigen Sie, dass sich für jedes t ≠ 0 und t ≠ -1 die Graphen von g t und h t
in zwei Punkten A t und B t mit den Koordinaten A t ( t / t 4 − t 3 − t 2 ) und
B t ( − t / − t 4 − t 3 − t 2 ) schneiden.
g) Auf welcher Ortskurve liegen die Punkte A t ?
Gibt es unter allen Punkten A t einen mit kleinster oder größter y-Koordinate?
Welches t gehört dazu?
Ergebnisse:
a) Doppelte Nullstelle x 1, 2 = 0 und einfache Nullstelle x 3 = 1 +
lim g t ( x ) = ± sgn(t ) ⋅∞
1
t
x→ ± ∞
b) P(0/0) und Q(1/-1) gehören zu jedem Graphen der Schar.
c) HOP(0/0) für t > -1
TP(0/0) für t = -1
TIP ( ≠ ) für t > -1
2 2
8 t 4 + 20 t 3 + 12 t 2 − 4 t − 4
HOP( +
/
) für t < -1
3 3t
27 t 3
d) WP (
1 1
t 4 + 2 t 3 − 2 t −1
+
/
) für t ≠ 0
3 3t
27 t 3
TIP(0/0) für t < -1
e)
f)
g t ( x) = h t ( x) ⇔ x 2 = t 2
falls t ≠ −1 ⇔
x 4 / 5 = ± t und A t = ( t / h t (t ) ) und B t = (− t / h t (t ) )
g) Ortskurve
a ( x ) = x4 − x3 − x2
mit x ≠ 0 und x ≠ − 1 .
Wegen lim a ( x ) = + ∞ gibt es keinen Punkt A t mit größter y-Koordinate.
x →±∞
Die Funktion a (x) hat zwei lokale Minima bei
41
8
41
≈ 1,175 liegt das absolute Minimum
8
− 299 − 41 41
=
≈ −1, 097
512
Bei x min =
y min
3+
3±
3+
41
≈ 1,175 gehört also der Punkt A t mit den
8
Koordinaten ( x min / y min ), der den kleinsten y-Wert hat.
Zu t
min
= x min =