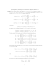Invertierbare Matrizen

Invertierbare Matrizen
Definition: Eine quadratische n × n−Matrix A heißt invertierbar, wenn es eine Matrix A−1 gibt,
mit
AA−1 = A−1 A = E
Beispiel: i) diag(λ1 , . . . , λn )−1 = diag( λ11 , . . . , λ1n ), speziell: En−1 = En
ii) Für Blockmatrizen passender Größe gilt:
−1 −1
−1
A 0
A
0
A
0
A 0
E 0
=
, denn
=
0 B
0 B
0 E
0
B −1
0
B −1
Satz: Inverse Matrizen sind , wenn es sie gibt, eindeutig.
Grund: Seien A−1 und A0 Inverse von A. Dann gilt: ( A0 A) A−1 = EA−1 = A−1 und A0 ( AA−1 ) =
A0 E = A0 .
Folgerung: Sind A und B invertierbare Matrizen, so ist auch AB invertierbar mit ( AB)−1 =
B −1 A −1
Grund: Es ist ( AB) B−1 A−1 = A( BB−1 ) A−1 = AEA−1 = AA−1 = E und B−1 A−1 ( AB) =
BB−1 = E. Die Behauptung folgt mit der Eindeutigkeit der Inversen.
−1
t
Satz: At
= A −1
t
Grund: At · A−1 = ( A−1 A)t = Ent = En
Bemerkung: Ist A−1 die Inverse von A, so hat das Gleichungssystem A~x = ~b für jedes ~b ∈ Rn
genau eine Lösung, denn:
A~x = ~b ⇔ ~x = A−1~b
Folgerung: Wenn A invertierbar ist, so hat das Gleichungssystem A~x = ~0 genau eine Lösung
(nämlich ~x = 0). Sind A = [~v1 , . . . , ~vn ] die Spaltenvektoren von A, so gilt:
A~x = x1~v1 + . . . + xn~vn = ~0 ⇔ ~x = ~0
In anderer Sprechweise: Die Spaltenvektoren von A bilden eine Basis des Rn .
Beispiel: i)
ii)
a b
c d
−1
1
=
ad − bc
d −b
−c a
 −1


a b c
ei − f h ch − bi b f − ce
 d e f  = 1  f g − di ai − cg cd − a f 
det A
g h i
dh − eg bg − ah ae − bd

allgemein gilt
A −1 =
1 t
Ãij
det A
wobei Ãij die Determinante der Matrix ist, die aus A durch Streichen der i −ten Zeile und j−ten
Spalte entsteht.
Grund: Nachrechnen
Bemerkung: Die Aussagen, daß A~x = ~b und A~x = ~0 eindeutige Lösungen haben, sind äquivalent. Sind nämlich ~x1 6= ~x2 zwei verschiedene Lösungen von A~x = ~b, so gilt A(~x1 − ~x2 ) = ~0,
also ist ~x1 − ~x2 eine Lösung von A~x = ~0, die selbst nicht der Nullvektor ist.
Definition: Für eine n × n−Matrix A = (~v1 , . . . , ~vn ) definieren wir


~v1


vec( A) :=  ... 
~vn
also den Vektor, der ensteht, wenn wir alle Spalten von A untereinander schreiben. Dieser Vektor hat dann n2 Einträge.
Satz: Rechtsinverse sind auch Linksinverse, d.h. aus AB = E folgt BA = E.
Grund: Die Menge der n × n−Matrizen mit der Matrizenaddition und der Multiplikation mit
Skalaren ist ein Vektorraum der Dimension n2 , eine Basis ist die Menge der Matrizen, die an
genau einer Stelle eine Eins und sonst überall Nullen haben.
2
Wir betrachten die Matrizen E, B, B2 , . . . , Bn . Wir haben gesehen, daß die Vektoren vec( E), vec( B), . . . , vec( B
linear abhängig sein müssen. Also gibt es a0 , . . . , an2 ∈ R (nicht alle gleich 0) mit
2
a0 vec( E) + a1 vec( B) + . . . + an2 vec( Bn ) = vec(0)
In Matrizenschreibweise:
2
a0 E + a1 B + . . . + an2 +1 Bn = 0 (∗)
Ist a0 = 0, so können wir diese Gleichung von links mit A multiplizieren und erhalten:
2
a1 AB + . . . + an2 ABn = a1 E + . . . + an2 Bn
2 −1
=0
Wir können also ohne Einschränkung annehmen, daß a0 6= 0 ist. Weiter dividieren wir die
Gleichung (*) durch a0 und erhalten:
2
E + b1 B + . . . + bn2 Bn = 0
Es gilt:
( BA − E) Bk = BABk − Bk = BBk−1 − Bk = 0
für k > 1.
Daher gilt:
2
2
0 = ( BA − E) · E + b1 B + . . . + bn2 +1 Bn +1 = BA − E + b1 ( BA − E) B + . . . + bn2 +1 ( BA − E) Bn +1
= BA − E
also: BA = E.
Zusammenfassung: Die folgenden Ausssagen sind äquivalent:
1) A ist invertierbar
2) Die Spalten von A bilden eine Basis des Rn
3) Aus A~x = ~0 folgt ~x = ~0
4) det( A) 6= 0
Grund:1 ⇒ 4: det( A) det( A−1 ) = det( AA−1 ) = det( E) = 1, also insbesondere det( A) 6= 0
4 ⇒ 3 : Cramersche Regel liefert ~x = 0
3 ⇒ 2 : Jede Linearkombination der n Spalten von A ist die triviale
2 ⇒ 1 : Jedes LGS A~xi = ~ei hat eine eindeutige Lösung. Die Matrix (. . . , ~xi , . . .) ist die Inverse:
A(. . . , ~xi , . . .) = (. . . , A~xi , . . .) = (. . . , ~ei , . . .). Also ist die Matrix (. . . , ~xi , . . .) Rechtsinverse von
A. Also nach obigem Satz auch Linksinverse, also Inverse.
Berechnung der Inversen: Wir hatten in den Übungen gesehen, daß die Multiplikation mit
Elementarmatrizen (von rechts oder links) enstprechende Zeilen- bzw. Spaltenumformung der
Matrix bedeuted. Alle diese Matrizen sind invertierbar (ihre Determinante ist nicht Null), falls
es sich nicht um eine Multiplikation einer Zeile oder Spalte mit Null handelt. Gibt es nun Elementarmatrizen J1 , . . . , Jm , mit
m
A · ∏ Ji = En
i =1
so ist
m
A=
∏ Jl
! −1
i =1
also
A −1 =
m
∏ Jm−−1 i
i =1
Wir betrachten die n × 2n Blockmatrix
A0 = ( A| En )
Dann gilt:
−1
−1
−1
−1
=
E
|
A
( A| En ) · ∏ Jm
=
A
·
J
|
E
·
J
n
n
∏ m −i
∏ m −i
−i
Anders gesagt: Läßt sich eine Matrix durch elementare Zeilenumformungen in die Einheitsmatrix überführen, so ist Sie invertierbar (und die Inverse kann wie oben beschrieben bestimmt
werden. Umgekehrt gilt: Geht das schief, so ist A nicht invertierbar.
Fakt: Jede n × n−Matrix ist Produkt von Elementarmatrizen. Elementarmatrizen spielen also
eine ähnliche Rolle für Matrizen, wie Primzahlen für die ganzen Zahlen.
Grund: Dies ist, auch ähnlich wie bei Primzahlen, technisch kompliziert, weswegen wir das
hier weglassen.
Definition: i) Zwei n × n−Matrizen heißen ähnlich, wenn wenn es eine invertierbare n × n−Matrix
P gibt, mit
A = P · B · P −1
Anwendung: Sind A und B ähnlich, so gilt:
An = PBP−1 · PBP−1 · . . . · PBP−1 = PBn P−1