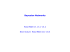Document 6590089

5'38
Chapter 14.
Probabilistic Reasoning
where the last step follows because a transition from x' is guaranteed to occur.
The transition probability q(x
x') defined by the sampling step in Glans-ASK is
actually a special case of the more general definition of Gibbs sampling, according to which
each variable is sampled conditionally on the current values of all the other variables. We
start by showing that this general definition of Gibbs sampling satisfies the detailed balance
equation with a stationary distribution equal to P(x I e), (the true posterior distribution on
the nonevidence variables). Then, we simply observe that, for Bayesian networks, sampling
conditionally on all variables is equivalent to sampling conditionally on the variable's Markov
blanket (see page 517).
To analyze the general Gibbs sampler, which samples each Xi in turn with a transition
probability (q i that conditions on all the other variables, we define X i to be these other variables (except the evidence variables); their values in the current state are K. If we sample a
new value x: fur Xi conditionally on all the other variables, including the evidence, we have
l
xi ) =
qi(x
C) = P(x i
e)
Now we show that the transition probability for each step of the Gibbs sampler is in detailed
balance with the true posterior:
7r(x)qi(x
= P(xi
x') = P(x e)P(Zi I
e)P(x% I e)P(x i.I
= P( i K,
= 91- ( x r )qi(x 1
3,7
' xi,
(x:
e)
e) = P( xi , xi I e)P(x ii I K., e)
e)
(using the chain rule on the first term)
(using the chain rule backward)
s x) .
We can think of the loop 'Tor each Z 1 in Z do" in Figure 14.16 as defining one large transition
probability q that is the sequential composition qi o 4 2 o • • • o qi, of the transition probabilities
for the individual variables. It is easy to show (Exercise 14.19) that if each of qi and qj has
r as its stationary distribution, then the sequential composition qi o qj does too; hence the
transition probability q for the whole loop has P(x e) as its stationary distribution. Finally,
unless the CPTs contain probabilities of 0 or 1—which can cause the state space to become
disconnected—it is easy to see that q is ergodic. Hence, the samples generated by Gibbs
sampling will eventually be drawn from the true posterior distribution
The final step is to show how to perform the general Gibbs sampling step—sampling
Xi from P(X i e) —in a Bayesian network. Recall from page 517 that a variable is independent of all other variables given its Markov blanket; hence,
P(x%
I
K, e) = P(x:
rrib(X i )) ,
where rrib(Xi ) denotes the values of the variables in X i 's Markov blanket, 114B(Xi ). As
shown in Exercise 14.7, the probability of a variable given its Markov blanket is proportional
to the probability of the variable given its parents times the probability of each child given its
respective parents:
P(x: I mb(X. i )) = cr P(ra parents(X 4 )) x
P(yj parents(Yj )) . (14.12)
E Chi idren(Xi)
Hence, to flip each variable Xi conditioned on its Markov blanket, the number of multiplications required is equal to the number of Xi's children.
Section 14.6.
Relational and First-Order Probability Models
539
Quail tri,B 1.)
Hun estqC 1 )
C;;;D
Qi
y(B )
Kindness(C 1 )
Kindness(C 1 )
Recommend nion(C
Rf
mlnencl irion(r ,f11 1 )
.)
Recommend col on(C
(u)
Remmmendwi on`,, C ) 430
(b)
Figure 14.17
(a) Bayes net for a single customer C1 recommending a single book B.
Honest (Ci) is Boolean, while the other variables have integer values from 1 to 5. (b) Hayes
net with two customers and Iwo books_
14.6 RELATIONAL AND FIRST-ORDER PROBABILITY MODELS
In Chapter 8, we explained the representational advantages possessed by first-order logic in
comparison to propositional logic. First-order logic commits to the existence of objects and
relations among them and can express facts about some or all of the objects in a domain. This
often results in representations that are vastly more concise than the equivalent propositional
descriptions. Now, Bayesian networks are essentially propositional: the set of random variables is fixed and finite, and each has a fixed domain of possible values This fact limits the
applicability of Bayesian networks. If we can ,find a way to combine probability theory with
the expressive power of first order representations, we expect to he able to increase draMall-
catty the range of problems that can be handled.
For example, suppose that an online book retailer would like to provide overall evaluations of products based on recommendations received from its customers. The evaluation
will take the form of a posterior distribution over the quality of the book, given the available evidence. The simplest solution to base the evaluation on the average recommendation,
perhaps with a variance determined by the number of recommendations, but this fails to take
into account the fact that some customers are kinder than others and some are less honest than
others. Kind customers tend to give high recommendations even to fairly mediocre books,
while dishonest customers give very high or very low recommendations for reasons other
than quality—for example, they might work for a publisher. 6
For a single customer C 1 , recommending a single book B1, the Bayes net might look
like the one shown in Figure 14.17(a). (Just as in Section 9.1, expressions with parentheses
such as Honest(C1) are just fancy symbols—in this case, fancy names for random variables.)
A game theorist would advise a dishonest customer to avoid detection by occasionally recommending a good
book from a competitor. See Chapter 17.
6