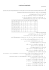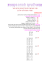פישוט ביטויים

‫ פישוט ביטויים‬- '‫'חיזוקית‬
a + 4x
(4)
y
a + 4 (3)
( x, y ≠ 0)
4 x ax
+
y
y
=?
x
y
x2
(2)
y2
x
(1)
y
.1
__________________________________________________________________________
(3 − x) ⋅ (3 + x) (4)
( x − 3) 2 (3)
( x ≠ 0)
 x 3
3x ⋅  −  = ?
3 x
( x − 3) ⋅ (3 + x) (2)
x 2 − 3 (1)
.2
__________________________________________________________________________
( a 2 ≠ 4)
a − 2 (4)
(a + 2)2
(3)
(a 2 + 4a + 4) ⋅ (a − 2)
=?
a2 −4
a + 2 (2)
.3
2 (1)
__________________________________________________________________________
(4b ≠ 6)
x 2 − 6 (4)
3 − 2b (3)
3 x 2 − 18 + 12b − 2 x 2 b
=?
6 − 4b
x2 − 3
(2)
2
.4
x2
− 3 (1)
2
__________________________________________________________________________
2 ⋅ (m − n) (4)
2 p (3)
( p ≠ 0, m ≠ n)
p
m−n = ?
−p
n−m
− 1 (2)
1 (1)
.5
__________________________________________________________________________
____________________________________________________________________
(a ≠ −1)
a −1
(4)
a +1
( x, y ≠ 0)
a2
(3)
a +1
x ⋅ (a − 1)
y
+
=?
x
(a + 1) ⋅ y
a 2 −1
(2)
xy
.6
xy
(1)
a +1
__________________________________________________________________________
2
(b, y ≠ 0)
x2 − a2
(4)
xb
2 ⋅ ( x + a)
(3)
by
2
a x  x a
 +  −  −  = ?
b y  y b
x−a
(2)
by
.7
4 xa
(1)
by
__________________________________________________________________________
(a ≠ −2)
5
(4)
6a + 12
− 5
(3)
a+2
5
5
−
=?
2 ⋅ ( a + 2) 3 ⋅ ( a + 2)
5
(2)
a+2
1
5 ⋅ (a + 2)
.8
(1)
__________________________________________________________________________
(3 x + 15) ⋅ (2 x + 10) = ?
(
6 ⋅ x + 15
)
2
.9
(1)
6 x + 90 (2)
( 6⋅x−
( 6⋅x+
)
150 )
150
2
2
(3)
(4)
_________________________________________________________________________
‫____________________________________________________________________‬
‫‪.10‬‬
‫? = ) ‪(x − y )−2 ⋅ (x 2 − 2 xy + y 2‬‬
‫)‪( x ≠ y‬‬
‫)‪x − y (3‬‬
‫)‪1 (2‬‬
‫)‪0 (1‬‬
‫)‪x + y (4‬‬
‫__________________________________________________________________________‬
‫‪.11‬‬
‫‪x 2 + 5x + 6‬‬
‫?=‬
‫‪x+3‬‬
‫)‪( x ≠ −3‬‬
‫)‪x + 1 (1‬‬
‫)‪x + 3 (3‬‬
‫)‪x + 2 (2‬‬
‫)‪x + 4 (4‬‬
‫__________________________________________________________________________‬
‫‪.12‬‬
‫?=‬
‫‪1 12 x + 2 12 y‬‬
‫) ‪(3 x ≠ −5 y‬‬
‫‪5 y + 3x‬‬
‫‪1‬‬
‫)‪(1‬‬
‫‪2‬‬
‫‪1‬‬
‫)‪(3‬‬
‫‪4‬‬
‫‪1‬‬
‫)‪(2‬‬
‫‪3‬‬
‫‪1‬‬
‫)‪(4‬‬
‫‪5‬‬
‫__________________________________________________________________________‬
‫‪.13‬‬
‫נתון ‪ a :‬ו‪ b -‬שלמים‪ ,‬חיוביים וגדולים מ‪.1 -‬‬
‫‪a + b +1‬‬
‫מה מהבאים נכון בוודאות לגבי ערכו של הביטוי‬
‫‪a+b‬‬
‫?‬
‫)‪ (1‬בין ‪ 0‬ל‪1-‬‬
‫)‪ (2‬ביו ‪ 1‬ל‪2 -‬‬
‫)‪ (3‬גדול מ‪2 -‬‬
‫)‪ (4‬לא ניתן לדעת מהנתונים‬
‫_________________________________________________________________________‬
‫‪.14‬‬
‫‪x 3 + 2x 2 − 4 x − 8‬‬
‫?=‬
‫‪x2 − 4‬‬
‫)‪x (1‬‬
‫)‪x − 2 (2‬‬
‫)‪( x ≠ 2,−2‬‬
‫)‪x + 2 (3‬‬
‫)‪x − 4 (4‬‬
‫__________________________________________________________________________‬
__________________________________________________________________________
1
a ⋅ (a + 1) = ?
a +1
a
a+
(a ≠ 0,−1)
1
(4)
a2
a 2 + 1 (3)
1
+ 1 (2)
a
.15
a + 1 (1)
__________________________________________________________________________
(23
44 (4)
33 (3)
11 (2)
2
) (
)
− 23 − 22 2 − 22 = ?
.16
1 (1)
__________________________________________________________________________
(a, b, c, d ≠ 0)
(a + b + c + d )2 + (a + b )2 − (c + d )2 = ?
.17
2 ⋅ (a + b) 2 (1)
2 ⋅ (a + b) ⋅ (c + d ) (2)
2 ⋅ (c + d ) 2 ⋅ (a + b + c + d ) (3)
2 ⋅ (a + b) ⋅ (a + b + c + d ) (4)
_________________________________________________________________________
‫הסברים ומפתח תשובות‬
‫שאלה‬
‫תשובה‬
‫שאלה‬
‫תשובה‬
‫‪1‬‬
‫‪2‬‬
‫‪3‬‬
‫‪4‬‬
‫‪5‬‬
‫‪6‬‬
‫‪7‬‬
‫‪8‬‬
‫‪9‬‬
‫‪3‬‬
‫‪2‬‬
‫‪2‬‬
‫‪1‬‬
‫‪1‬‬
‫‪3‬‬
‫‪1‬‬
‫‪4‬‬
‫‪4‬‬
‫‪10‬‬
‫‪11‬‬
‫‪12‬‬
‫‪13‬‬
‫‪14‬‬
‫‪15‬‬
‫‪16‬‬
‫‪17‬‬
‫‪2‬‬
‫‪2‬‬
‫‪1‬‬
‫‪2‬‬
‫‪3‬‬
‫‪3‬‬
‫‪4‬‬
‫‪4‬‬
‫הערה מקדימה ‪ :‬כמעט את כל השאלות בנושא 'פישוט ביטויים' ניתן לפתור גם באמצעות‬
‫טכניקת 'הצבה פוסלת'‪ ,‬בהסברים שלהלן נציג את דרך הפתרון הזו רק בחלק קטן מהמקרים‪,‬‬
‫אך יש לזכור כי היא רלוונטית כמעט תמיד‪.‬‬
‫‪.1‬‬
‫התשובה הנכונה היא )‪(3‬‬
‫‪4 x ax‬‬
‫‪+‬‬
‫‪y‬‬
‫‪y‬‬
‫שואלים‪= ? :‬‬
‫‪x‬‬
‫‪y‬‬
‫‪4 x ax 4 x + ax‬‬
‫‪+‬‬
‫‪y‬‬
‫‪y‬‬
‫‪y‬‬
‫) ‪(4 x + ax) ⋅ y 4 x + ax x ⋅ (4 + a‬‬
‫=‬
‫=‬
‫=‬
‫=‬
‫‪=4+a‬‬
‫‪x‬‬
‫‪x‬‬
‫‪yx‬‬
‫‪x‬‬
‫‪x‬‬
‫‪y‬‬
‫‪y‬‬
‫‪.2‬‬
‫התשובה הנכונה היא )‪(2‬‬
‫‪ x 3‬‬
‫שואלים‪3 x ⋅  −  = ? :‬‬
‫‪3 x‬‬
‫‪2‬‬
‫‪9x‬‬
‫‪ x 3  3x‬‬
‫= ‪3x ⋅  − ‬‬
‫‪−‬‬
‫‪3‬‬
‫‪x‬‬
‫‪3 x‬‬
‫נוכל לצמצם את השבר השמאלי ב‪ 3 -‬ואת הימני ב‪ , x -‬ונקבל‪. x 2 − 9 :‬‬
‫ביטוי זה הוא נוסחת הכפל המקוצר השלישית‪ ,‬ולכן‪:‬‬
‫)‪x 2 − 9 = ( x − 3) ⋅ ( x + 3) = ( x − 3) ⋅ (3 + x‬‬
‫‪.3‬‬
‫התשובה הנכונה היא )‪(2‬‬
‫)‪(a 2 + 4a + 4) ⋅ (a − 2‬‬
‫שואלים ‪= ? :‬‬
‫‪a2 −4‬‬
‫בטרם נתחיל לפתוח את הסוגריים שבמונה‪ ,‬כדאי להתבונן בביטוי‪ ,‬ולראות כי המכנה הוא נוסחת‬
‫הכפל המקוצר השלישית‪ . a 2 − 4 = ( a + 2) ⋅ ( a − 2) :‬ובמונה יש גם את נוסחת הכפל‬
‫המקוצר הראשונה‪ . a 2 + 4a + 4 = (a + 2) 2 :‬ולכן מרבית חלקי התרגיל יצטמצמו‪.‬‬
‫)‪(a 2 + 4a + 4) ⋅ (a − 2) (a + 2) 2 ⋅ (a − 2‬‬
‫=‬
‫אם כך‪= a + 2 ,‬‬
‫)‪(a + 2) ⋅ (a − 2‬‬
‫‪a2 − 4‬‬
‫‪.4‬‬
‫התשובה הנכונה היא )‪(1‬‬
‫‪3 x 2 − 18 + 12b − 2 x 2 b‬‬
‫שואלים ‪= ? :‬‬
‫‪6 − 4b‬‬
‫דרך א'‪' -‬הצבה פוסלת'‬
‫במבט חטוף בביטוי הנתון ניתן להתרשם כי תיתכן עבודה אלגברית רבה כדי לפשטו‪ ,‬ואולי בשל‬
‫כך כדאי לשקול בחיוב עבודה עם טכניקה 'הצבה פוסלת'‪.‬‬
‫נציב‪ x = 2 :‬ו‪. b = 3 -‬‬
‫‪3 x 2 − 18 + 12b − 2 x 2 b 3 ⋅ 2 2 − 18 + 12 ⋅ 3 − 2 ⋅ 2 2 ⋅ 3‬‬
‫=‬
‫ערכו של הביטוי הנתון‪= :‬‬
‫‪6 − 4b‬‬
‫‪6 − 4⋅3‬‬
‫‪3 ⋅ 4 − 18 + 36 − 2 ⋅ 4 ⋅ 3 12 − 18 + 36 − 24‬‬
‫‪6‬‬
‫=‬
‫=‬
‫‪= −1‬‬
‫‪6 − 12‬‬
‫‪−6‬‬
‫‪−6‬‬
‫=‬
‫עתה‪ ,‬נציב ‪ x = 2‬ו‪ b = 3 -‬בכל התשובות‪ ,‬ונפסול כל תשובה שערכה יצא שונה מ‪. (−1) -‬‬
‫‪x2‬‬
‫‪22‬‬
‫‪ ,‬תשובה לא נפסלת‪.‬‬
‫=‪−3‬‬
‫תשובה )‪− 3 = 2 − 3 = −1 :(1‬‬
‫‪2‬‬
‫‪2‬‬
‫‪x2 − 3 22 − 3 4 − 3 1‬‬
‫=‬
‫=‬
‫=‬
‫תשובה )‪:(2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪ ,‬תשובה נפסלת‪.‬‬
‫תשובה )‪ , 3 − 2b = 3 − 2 ⋅ 3 = 3 − 6 = −3 :(3‬תשובה נפסלת‪.‬‬
‫תשובה )‪ , x 2 − 6 = 2 2 − 6 = 4 − 6 = −2 :(4‬תשובה נפסלת‪.‬‬
‫עתה‪ ,‬נוכל לסמן בבטחה את תשובה )‪.(1‬‬
‫דרך ב'‪ -‬עקרונית – פישוט אלגברי‬
‫המכנֵה התפוגג )כלומר‪,‬‬
‫ָ‬
‫שימו לב‪ ,‬ממבט חטוף בתשובות ניתן להבחין כי בחצי מהתשובות‬
‫הצטמצם( ובחצי הוא משתנה‪ ,‬כלומר‪ ,‬יש לשאוף לצמצם או לשנות את המכנה‪.‬‬
‫אם כך‪ ,‬נשאף להוציא גורמים משותפים בכל חלקי הביטוי כדי להגדיל את הסיכויים לצמצום‪.‬‬
‫) ‪3 x 2 − 18 + 12b − 2 x 2 b 3 ⋅ ( x 2 − 6) + 2b ⋅ (6 − x 2‬‬
‫=‬
‫‪6 − 4b‬‬
‫)‪2 ⋅ (3 − 2b‬‬
‫תזכורת‪ :‬שינוי סדר מחוסרים ‪ :‬אם רוצים לשנות סדר מחוסרים ניתן לעשות זאת בתנאי‬
‫שמחליפים את הסימן שמחוץ לסוגריים‪ ,‬למשל‪m − n = −(n − m) :‬‬
‫ולכן‪ ,‬מאחר שהביטוי )‪ ( x 2 − 6‬והביטוי ) ‪ (6 − x 2‬דומים אך לא זהים‪ ,‬נוכל להפוך את הביטוי‬
‫) ‪ ( 6 − x 2‬ל ‪− ( x 2 − 6) :‬‬
‫)‪3 ⋅ ( x 2 − 6) + 2b ⋅ (6 − x 2 ) 3 ⋅ ( x 2 − 6) − 2b ⋅ ( x 2 − 6‬‬
‫=‬
‫כך נקבל‪:‬‬
‫)‪2 ⋅ (3 − 2b‬‬
‫)‪2 ⋅ (3 − 2b‬‬
‫עתה‪ ,‬נוכל להוציא במונה את הגורם המשותף )‪ , ( x 2 − 6‬ולקבל‪:‬‬
‫)‪3 ⋅ ( x 2 − 6) − 2b ⋅ ( x 2 − 6) ( x 2 − 6) ⋅ (3 − 2b‬‬
‫=‬
‫)‪2 ⋅ (3 − 2b‬‬
‫)‪2 ⋅ (3 − 2b‬‬
‫נצמצם מונה ומכנה בביטוי )‪ , (3 − 2b‬ונקבל‪:‬‬
‫‪( x 2 − 6) ⋅ (3 − 2b) x 2 − 6 x 2 6 x 2‬‬
‫=‬
‫=‬
‫= ‪−‬‬
‫‪−3‬‬
‫)‪2 ⋅ (3 − 2b‬‬
‫‪2‬‬
‫‪2 2 2‬‬
‫‪.5‬‬
‫התשובה הנכונה היא )‪(1‬‬
‫‪p‬‬
‫שואלים‪m − n = ? :‬‬
‫‪−p‬‬
‫‪n−m‬‬
‫‪p‬‬
‫‪m − n = p ⋅ (n − m) = pn − pm = 1‬‬
‫‪−p‬‬
‫‪− p ⋅ (m − n) − pm + pn‬‬
‫‪n−m‬‬
‫‪.6‬‬
‫התשובה הנכונה היא )‪(3‬‬
‫)‪x ⋅ (a − 1‬‬
‫‪y‬‬
‫‪+‬‬
‫שואלים ‪= ? :‬‬
‫‪x‬‬
‫‪(a + 1) ⋅ y‬‬
‫נוכל לצמצם את המונה והמכנה של השבר השמאלי ב‪ x -‬ואת המונה והמכנה של השבר הימני‬
‫‪1‬‬
‫ב‪ , y -‬ונקבל‪:‬‬
‫)‪(a + 1‬‬
‫‪(a − 1) +‬‬
‫נעשה מכנה משותף ‪ , (a + 1) :‬ונקבל‪:‬‬
‫‪1‬‬
‫)‪(a − 1) ⋅ (a + 1‬‬
‫‪1‬‬
‫‪a2 −1+1‬‬
‫‪a2‬‬
‫=‬
‫‪+‬‬
‫=‬
‫=‬
‫)‪(a + 1‬‬
‫)‪(a + 1‬‬
‫)‪(a + 1‬‬
‫‪a +1‬‬
‫‪a +1‬‬
‫‪.7‬‬
‫‪(a − 1) +‬‬
‫התשובה הנכונה היא )‪(1‬‬
‫‪2‬‬
‫‪2‬‬
‫‪a x  x a‬‬
‫שואלים ‪ +  −  −  = ? :‬‬
‫‪b y  y b‬‬
‫מאחר ששני החלקים שמהם מורכב הביטוי הם נוסחאות כפל מקוצר‪ ,‬והביטויים שבתוך שני‬
‫הסוגריים דומים מאוד‪ ,‬ככל הנראה כדאי לפתוח סוגריים ומרבית הביטויים יתבטלו‪.‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪a x  x a‬‬
‫‪a x  x    x ‬‬
‫‪x a a ‬‬
‫‪a‬‬
‫= ‪ +  −  −  =   + 2 ⋅ ⋅ +   −   − 2 ⋅ ⋅ +   ‬‬
‫‪b y  y   y ‬‬
‫‪y b b ‬‬
‫‪b‬‬
‫‪b y  y b‬‬
‫‪‬‬
‫‪‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2ax  x   x ‬‬
‫‪2 xa  a ‬‬
‫‪4ax‬‬
‫‪a‬‬
‫‪=  +‬‬
‫‪+   −   +‬‬
‫= ‪− ‬‬
‫‪by  y   y ‬‬
‫‪by  b ‬‬
‫‪by‬‬
‫‪b‬‬
‫‪.8‬‬
‫התשובה הנכונה היא )‪(4‬‬
‫‪5‬‬
‫‪5‬‬
‫‪−‬‬
‫שואלים‪= ? :‬‬
‫)‪2 ⋅ ( a + 2) 3 ⋅ ( a + 2‬‬
‫נעשה מכנה משותף‪ ,‬במקרה זה הוא‪ . 6 ⋅ (a + 2) :‬מאחר שאת המכנה של השבר השמאלי‬
‫הרחבנו פי ‪ , 3‬כך נעשה גם למונה שלו‪ .‬ומאחר שאת המכנה של השבר הימני הרחבנו פי ‪ 2‬כך‬
‫נעשה גם למונה שלו‪ ,‬ונקבל‪:‬‬
‫‪5‬‬
‫‪5‬‬
‫‪3 5‬‬
‫‪2 5‬‬
‫‪3 5−2 5‬‬
‫‪5‬‬
‫‪5‬‬
‫‪−‬‬
‫=‬
‫‪−‬‬
‫=‬
‫=‬
‫=‬
‫)‪2 ⋅ ( a + 2) 3 ⋅ ( a + 2) 6 ⋅ ( a + 2) 6 ⋅ ( a + 2‬‬
‫)‪6 ⋅ ( a + 2‬‬
‫‪6 ⋅ (a + 2) 6a + 12‬‬
‫‪.9‬‬
‫התשובה הנכונה היא )‪(4‬‬
‫השאלה שלפנינו היא למעשה "שאלה הפוכה"‪ ,‬כלומר‪ ,‬שאלה שבה הביטוי הנתון הוא פשוט יותר‬
‫מהתשובות‪ ,‬במקרה שכזה הגישה הטובה ביותר היא ככל הנראה‪' -‬בדיקת תשובות'‪.‬‬
‫נפתח סוגריים בביטוי הנתון‪:‬‬
‫‪(3 x + 15) ⋅ (2 x + 10) = 6 x 2 + 30 x + 30 x + 150 = 6 x 2 + 60 x + 150‬‬
‫כבר בשלב זה ניתן לפסול את תשובות )‪ (2‬ו‪ ,(3) -‬שכן תשובה )‪ (2‬מכילה רק שני גורמים‪ ,‬ותשובה‬
‫)‪ (3‬היא נוסחת הכפל המקוצר השנייה‪ ,‬שבה חייב להיות גם סימן שלילי‪.‬‬
‫תשובה )‪:(1‬‬
‫)‬
‫‪2‬‬
‫‪6 ⋅ x + 15‬‬
‫‪= 6 x 2 + 2 90 x + 15‬‬
‫(‬
‫; זוהי נוסחת הכפל המקוצר הראשונה‪.‬‬
‫) ‪( 15‬‬
‫‪2‬‬
‫‪+ 2 ⋅ 6 x ⋅ 15 +‬‬
‫)‪) = ( 6x‬‬
‫‪2‬‬
‫‪2‬‬
‫‪6 ⋅ x + 15‬‬
‫(‬
‫ניתן לעצור כבר בשלב זה‪ ,‬כיוון שבביטוי המקורי )לאחר פתיחת הסוגריים( יש את המספר‬
‫"החופשי" )כזה שלא קשור ל‪ , 150 ( x -‬ואילו בתשובה זו יש את המספר "החופשי" ‪. 15‬‬
‫אם כך‪ ,‬לאחר שפסלנו את תשובות )‪ (2) ,(1‬ו‪ ,(3) -‬נוכל לסמן בבטחה את תשובה )‪ (4‬אפילו מבלי‬
‫לבדוק אותה‪.‬‬
‫נסביר את תשובה )‪ (4‬לצורך לימוד‪:‬‬
‫תשובה )‪:(4‬‬
‫)‬
‫‪2‬‬
‫(‬
‫= ‪+ 2 ⋅ 6 x ⋅ 150 + 150 = 6 x 2 + 2 ⋅ 900 ⋅ x + 150‬‬
‫‪= 6 x 2 + 2 ⋅ 30 ⋅ x + 150 = 6 x 2 + 60 x + 150‬‬
‫)‪) = ( 6x‬‬
‫‪2‬‬
‫‪2‬‬
‫‪6 ⋅ x + 150‬‬
‫ביטוי זה הוא בדיוק מה שקיבלנו בעת שפתחו את הסוגריים של הביטוי הנתון‪ ,‬ולכן תשובה זו‬
‫נכונה‪.‬‬
‫‪.10‬‬
‫התשובה הנכונה היא )‪(2‬‬
‫שואלים‪(x − y )−2 ⋅ (x 2 − 2 xy + y 2 ) = ? :‬‬
‫‪1‬‬
‫‪(x − y)2‬‬
‫‪2‬‬
‫‪x‬‬
‫‪y‬‬
‫⋅‬
‫(‬
‫‪−‬‬
‫)‬
‫=‬
‫‪=1‬‬
‫‪( x − y) 2‬‬
‫‪(x − y)2‬‬
‫‪.11‬‬
‫= ) ‪(x − y )− 2 ⋅ (x 2 − 2 xy + y 2‬‬
‫התשובה הנכונה היא )‪(2‬‬
‫‪x 2 + 5x + 6‬‬
‫שואלים‪= ? :‬‬
‫‪x+3‬‬
‫מהתבוננות חטופה בתשובות‪ ,‬ניתן להבין כי המכנה של הביטוי המקורי אמור להצטמצם‪ ,‬שכן‬
‫באף תשובה אין מכנה‪ .‬כדי להשיג זאת‪ ,‬עלינו להפוך את המונה למכפלה שאחד ממרכיביה הוא‬
‫המכנה‪ ,‬כלומר )‪. ( x + 3‬‬
‫(‬
‫הביטוי שבמונה אינו נוסחת כפל מקוצר‪ ,‬ולכן האפשרות היחידה היא לעשות לו 'פירוק‬
‫טרינומי'‪ ,‬יתרה מזאת‪ ,‬יש לנו רמז עבה לגבי מרכיב אחד ב'פירוק הטרינומי' והוא הביטוי‬
‫)‪ ( x + 3‬שבמכנה‪ ,‬שכאמור אמור להצטמצם‪.‬‬
‫)‪x 2 + 5 x + 6 ( x + 3) ⋅ ( x + 2‬‬
‫=‬
‫‪= x+2‬‬
‫‪x+3‬‬
‫‪x+3‬‬
‫‪.12‬‬
‫התשובה הנכונה היא )‪(1‬‬
‫שואלים ‪= ? :‬‬
‫‪1 12 x + 2 12 y‬‬
‫‪5 y + 3x‬‬
‫מהתבוננות חטופה בתשובות ניתן להבין כי המשתנים אמורים להצטמצם‪ ,‬שכן באף תשובה הם‬
‫אינם נמצאים‪ ,‬כדי לגרום לצמצום עלינו להפוך את פעולת החיבור לפעולת כפל‪ ,‬ולשם כך נוכל‬
‫להוציא גורם משותף במונה )במכנה לא ניתן להוציא גורם משותף(‪.‬‬
‫‪3‬‬
‫‪5‬‬
‫‪1 12 x + 2 12 y 2 x + 2 y‬‬
‫=‬
‫‪5 y + 3x‬‬
‫‪5 y + 3x‬‬
‫‪5‬‬
‫‪1‬‬
‫‪3‬‬
‫‪1‬‬
‫‪1‬‬
‫הגורם המשותף היחיד שניתן לאתר במונה הוא ‪ ,‬שהרי ⋅ ‪ , = 3‬ו‪= 5 ⋅ -‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪.‬‬
‫‪3‬‬
‫‪5‬‬
‫‪1‬‬
‫‪x+ y‬‬
‫) ‪⋅ (3 x + 5 y‬‬
‫‪1‬‬
‫‪2‬‬
‫‪2 = 2‬‬
‫=‬
‫‪5 y + 3x‬‬
‫‪5 y + 3x‬‬
‫‪2‬‬
‫‪.13‬‬
‫התשובה הנכונה היא )‪(2‬‬
‫דרך א' – 'הצבה פוסלת'‬
‫אמנם יש לכאורה בעיה בשימוש בטכניקת 'הצבה פוסלת' בשאלה זו מכיוון שיש תשובה )‪(4‬‬
‫מתחכמת‪ ,‬אך בהחלט ייתכן שהצבה תסייע לנו להבין עקרונית את הסיטואציה‪.‬‬
‫נציב‪ a = 2 :‬ו‪. b = 5 -‬‬
‫‪a + b +1 2 + 5 +1 8‬‬
‫‪1‬‬
‫‪= =1‬‬
‫=‬
‫‪a+b‬‬
‫‪2+5‬‬
‫‪7‬‬
‫‪7‬‬
‫תוצאה זו למעשה פוסלת את תשובות )‪ (1‬ו‪ (3) -‬כיוון שהיא מוכיחה שהן לא נכונות בוודאות‪.‬‬
‫מאחר שלא הצלחנו לפסול ‪ 3‬תשובות נוכל להציב שוב‪.‬‬
‫הצבה שנייה‪ a = 5 :‬ו‪. b = 20 -‬‬
‫‪a + b + 1 5 + 20 + 1 26‬‬
‫‪1‬‬
‫=‬
‫=‬
‫‪=1‬‬
‫‪a+b‬‬
‫‪5 + 20‬‬
‫‪25‬‬
‫‪25‬‬
‫שוב קיבלנו תוצאה שהיא בין ‪ 1‬ל‪ , 2 -‬ולא פסלנו את תשובה )‪ ,(2‬במצב שכזה ככל הנראה ניתן‬
‫להניח שתשובה זו היא נכונה ולסמן אותה‪.‬‬
‫דרך ב'‪ -‬ניתוח עקרוני‬
‫‪a + b +1‬‬
‫הביטוי‬
‫‪a+b‬‬
‫הוא ביטוי שכל מרכיביו חיוביים וגדולים מ‪ , 1 -‬והמונה שלו גדול מהמכנה‬
‫שלו‪ ,‬כלומר מדובר במספר שערכו גדול בוודאות מ‪ , 1 -‬מה שפוסל את תשובה )‪.(1‬‬
‫עתה‪ ,‬נותרנו עם ההתלבטות בין תשובות )‪ (2‬ו‪.(3) -‬‬
‫כדי שתשובה )‪ (3‬תהייה נכונה המונה של הביטוי צריך להיות יותר מפי ‪ 2‬מהמכנה‪ ,‬ודבר זה אינו‬
‫אפשרי כאשר ההפרש ביניהם הוא ‪ 1‬ומדובר במספרים שלמים וחיוביים הגדולים מ‪ , 1-‬ולכן גם‬
‫תשובה )‪ (3‬נפסלת‪.‬‬
‫‪.14‬‬
‫התשובה הנכונה היא )‪(3‬‬
‫דרך א'‪ -‬עקרונית‬
‫מהתבוננות חטופה בתשובות ניתן להסיק כי המכנה מצטמצם )אין אף תשובה שיש בה מכנה(‪,‬‬
‫ולכן השאיפה שלנו היא ליצור במונה פעולת כפל שתאפשר צמצום‪ .‬נשים לב שבמכנה יש את‬
‫הביטוי ‪ x 2 − 4‬שהוא למעשה נוסחת הכפל המקוצר השלישית‪ ,‬ויכול להתפרק גם ל‪:‬‬
‫)‪. ( x + 2) ⋅ ( x − 2‬‬
‫מאחר שבמונה לא ניתן להוציא גורם משותף לכל מרכיבי הביטוי‪ ,‬ננסה להוציא גורם משותף‬
‫בחלקים‪ ,‬כלומר‪ ,‬להוציא גורם משותף לשני איברים ואז לשני האיברים האחרים‪.‬‬
‫)‪x 3 + 2 x 2 − 4 x − 8 x 2 ⋅ ( x + 2) − 4 ⋅ ( x + 2‬‬
‫=‬
‫‪x2 − 4‬‬
‫‪x2 − 4‬‬
‫עתה‪ ,‬נוכל לראות כי במונה יש גורם משותף ‪ , ( x + 2) :‬ולכן‪:‬‬
‫)‪x 2 ⋅ ( x + 2) − 4 ⋅ ( x + 2) ( x + 2) ⋅ ( x 2 − 4‬‬
‫=‬
‫‪= x+2‬‬
‫‪x2 − 4‬‬
‫‪x2 − 4‬‬
‫דרך ב'‪' -‬הצבה פוסלת'‬
‫כפי שנאמר בהערה שבתחילת ההסברים‪ ,‬את מרבית השאלות לא נפתור באמצעות 'הצבה פוסלת'‬
‫למרות שבהחלט ניתן לעשות כן‪ ,‬ולשם תזכורת נעשה זאת בשאלה זו‪.‬‬
‫כמו‪-‬כן‪ ,‬אולי 'הצבה פוסלת' יכולה להיות פתרון מצוין במקרה זה מכיוון שנדמה )לפחות במבט‬
‫ראשון( שלפנינו אלגברה מסובכת או ארוכה‪.‬‬
‫נציב ‪ . x = 0 :‬בסריקה זריזה של התשובות ניתן לראות כי עבור ‪ x = 0‬מתקבלות ‪ 4‬תוצאות‬
‫מספריות שונות‪ ,‬מה שאומר שלא נצטרך להציב פעם שנייה‪.‬‬
‫‪x3 + 2x 2 − 4 x − 8 03 + 2 ⋅ 0 2 − 4 ⋅ 0 − 8 − 8‬‬
‫=‬
‫=‬
‫‪=2‬‬
‫‪−4‬‬
‫‪x2 − 4‬‬
‫‪02 − 4‬‬
‫עתה‪ ,‬נעבור לתשובות ונציב בכולן ‪ , x = 0‬ונפסול כל תשובה שערכה יצא שונה מ‪. 2 -‬‬
‫תשובה )‪ , x = 0 ; x :(1‬תשובה נפסלת‪.‬‬
‫תשובה )‪ , x − 2 = 0 − 2 = −2 ; x − 2 :(2‬תשובה נפסלת‪.‬‬
‫תשובה )‪ , x + 2 = 0 + 2 = 2 ; x + 2 :(3‬תשובה לא נפסלת‪.‬‬
‫תשובה )‪ , x − 4 = 0 − 4 = −4 ; x − 4 :(4‬תשובה נפסלת‪.‬‬
‫עתה‪ ,‬נוכל לסמן בבטחה את תשובה )‪.(3‬‬
‫‪.15‬‬
‫התשובה הנכונה היא )‪(3‬‬
‫דרך א'‪' -‬הצבה פוסלת'‬
‫ממבט חטוף בביטוי הנתון ניתן להבחין כי הוא אמנם לא מערב אלגברה מורכבת‪ ,‬אך יהיה עלינו‬
‫לבצע הרבה פעולות פישוט ‪ :‬מכנים משותפים‪ ,‬חלוקת שבר בשבר וכו'‪ ,‬ולכן ככל הנראה הדרך‬
‫היעילה לגשת אליו היא 'הצבה פוסלת'‪.‬‬
‫נציב ‪ , a = 2 :‬ואם נסרוק את התשובות בזריזות נוכל לראות שעבור ‪ a = 2‬מתקבלות ‪4‬‬
‫תוצאות מספריות שונות‪ ,‬מה שמבטיח שלא ניאלץ לבצע הצבה שנייה‪.‬‬
‫‪5‬‬
‫‪2 ⋅3 = 5⋅ 2 ⋅3 = 5‬‬
‫‪3‬‬
‫‪2⋅3‬‬
‫‪2‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪2+‬‬
‫‪2‬‬
‫= )‪a ⋅ (a + 1‬‬
‫= ‪2 ⋅ (2 + 1) = 2 ⋅ 3‬‬
‫‪a +1‬‬
‫‪2 +1‬‬
‫‪3‬‬
‫‪a‬‬
‫‪2‬‬
‫‪2‬‬
‫‪a+‬‬
‫עתה‪ ,‬נעבור לתשובות ונציב בכל אחת מהן ‪ , a = 2‬ונפסול כל תשובה שערכה יצא שונה מ‪. 5 -‬‬
‫תשובה )‪ . a + 1 = 2 + 1 = 3 ; a + 1 :(1‬תשובה נפסלת‪.‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫תשובה )‪+ 1 = + 1 = 1 ; + 1 :(2‬‬
‫‪a‬‬
‫‪2‬‬
‫‪2‬‬
‫‪a‬‬
‫‪ .‬תשובה נפסלת‪.‬‬
‫תשובה )‪ . a 2 + 1 = 2 2 + 1 = 5 ; a 2 + 1 :(3‬תשובה לא נפסלת‪.‬‬
‫‪1‬‬
‫‪1 1‬‬
‫‪1‬‬
‫= ‪= 2‬‬
‫תשובה )‪; 2 :(4‬‬
‫‪2‬‬
‫‪4‬‬
‫‪a‬‬
‫‪2‬‬
‫‪a‬‬
‫‪ .‬תשובה נפסלת‪.‬‬
‫עתה‪ ,‬נוכל לסמן בבטחה את תשובה )‪.(3‬‬
‫דרך ב'‪ -‬עקרונית )פישוט אלגברי(‬
‫‪1‬‬
‫שואלים‪a ⋅ (a + 1) = ? :‬‬
‫‪a +1‬‬
‫‪a‬‬
‫‪a+‬‬
‫‪1‬‬
‫‪a‬‬
‫נוכל גם לכפול קודם את הביטוי )‪ (a + 1‬במונה ) ‪ ( a +‬כי כזכור‪ ,‬כאשר מספר או ביטוי‬
‫מוכפל בשבר המספר "נדבק למונה"‪ .‬אך הדרך המהירה יותר )אתם מוזמנים לבדוק ‪ ( . . .‬היא‬
‫קודם לעשות מכנה משותף בביטוי שבמונה‪ ,‬ואז להיפטר מקווי השבר באמצעות "שיטת האוזן"‬
‫ורק בסוף לכפול את התוצאה בביטוי )‪. (a + 1‬‬
‫‪1‬‬
‫‪a2 +1‬‬
‫‪2‬‬
‫‪2‬‬
‫‪a ⋅ (a + 1) = a ⋅ (a + 1) = (a + 1) ⋅ a ⋅ (a + 1) = (a + 1) ⋅ a ⋅ (a + 1) = a 2 + 1‬‬
‫‪a +1‬‬
‫‪a +1‬‬
‫)‪a ⋅ (a + 1‬‬
‫)‪a ⋅ (a + 1‬‬
‫‪a‬‬
‫‪a‬‬
‫‪a+‬‬
‫‪.16‬‬
‫התשובה הנכונה היא )‪(4‬‬
‫)‬
‫( )‬
‫שואלים‪− 23 − 22 2 − 22 = ? :‬‬
‫‪2‬‬
‫‪(23‬‬
‫כמובן שהדרך הלא נכונה והבלתי פסיכומטרית בעליל היא לחשב את הערך המספרי של הביטוי‬
‫המספרי הנתון‪.‬‬
‫תזכורת‪ :‬כאשר נתקלים בחישוב שהוא בלתי פסיכומטרי בעליל‪ ,‬כדאי לנהוג במספרים שבו‬
‫כאילו היו משתנים‪ ,‬ולבצע את פעולות הפישוט שהיינו מבצעים במשתנים‪.‬‬
‫אם היה לפנינו ביטוי אלגברי ‪ x 2 − x :‬הרי שפעולת הפישוט הראשונה שהייתה עולה בדעתנו‬
‫היא הוצאת גורם משותף‪ ,‬וכך נעשה גם במקרה לעיל‪.‬‬
‫)‬
‫( )‬
‫= ‪− 23 − 22 − 22 = 23 ⋅ (23 − 1) − 22 ⋅ (22 − 1) = 23 ⋅ 22 − 22 ⋅ 21‬‬
‫‪2‬‬
‫‪2‬‬
‫‪(23‬‬
‫‪= 22 ⋅ (23 − 21) = 22 ⋅ 2 = 44‬‬
‫‪.17‬‬
‫התשובה הנכונה היא )‪(4‬‬
‫דרך א'‪' -‬הצבה פוסלת'‬
‫ממבט חטוף בביטוי הנתון‪ ,‬ניתן לראות שתהייה לנו עבודת פישוט אלגברית ארוכה ואולי אף‬
‫מסובכת‪ ,‬ולכן ככל הנראה כדאי לבחור בגישה של 'הצבה פוסלת'‪.‬‬
‫שימו לב‪ ,‬מאחר שהתשובות מכילות ביטויים מורכבים לא נרצה להקדיש זמן ולבדוק‬
‫שהמספרים שאנו בוחרים מניבים ‪ 4‬תוצאות מספריות שונות )כדי להבטיח שלא תהייה הצבה‬
‫מפ ִתים"‪ ,‬כלומר לא נבחר ‪1‬‬
‫שנייה(‪ ,‬אולם כדי להקטין סיכון להצבה שנייה נבחר מספרים פחות " ָ‬
‫ו‪ , 0 -‬אלא ‪ c = 3 , b = 2 , a = 1 :‬ו‪. d = 4 -‬‬
‫= ‪(a + b + c + d )2 + (a + b )2 − (c + d )2 = (1 + 2 + 3 + 4) 2 + (1 + 2) 2 − (3 + 4) 2‬‬
‫‪= 10 2 + 3 2 − 7 2 = 100 + 9 − 49 = 60‬‬
‫עתה‪ ,‬נציב בכל אחת מהתשובות ‪ c = 3 , b = 2 , a = 1‬ו‪ , d = 4 -‬ונפסול כל תשובה שערכה‬
‫יצא שונה מ‪. 60 -‬‬
‫תשובה )‪ . 2 ⋅ ( a + b) 2 = 2 ⋅ (1 + 2) 2 = 2 ⋅ 3 2 = 18 :(1‬תשובה נפסלת‪.‬‬
‫תשובה )‪ . 2 ⋅ (a + b) ⋅ (c + d ) = 2 ⋅ (1 + 2) ⋅ (3 + 4) = 2 ⋅ 3 ⋅ 7 = 42 :(2‬תשובה נפסלת‪.‬‬
‫תשובה )‪. 2 ⋅ (c + d ) 2 ⋅ ( a + b + c + d ) = 2 ⋅ (3 + 4) 2 ⋅ (1 + 2 + 3 + 4) = : (3‬‬
‫‪ . = 2 ⋅ 7 2 ⋅ 10 = 2 ⋅ 49 ⋅ 10 = 980‬תשובה נפסלת‪.‬‬
‫תשובה )‪2 ⋅ (a + b) ⋅ (a + b + c + d ) = 2 ⋅ (1 + 2) ⋅ (1 + 2 + 3 + 4) = 2 ⋅ 3 ⋅ 10 = 60 :(4‬‬
‫תשובה לא נפסלת‪.‬‬
‫עתה‪ ,‬נוכל לסמן בבטחה את תשובה )‪.(4‬‬
‫דרך ב'‪ -‬עקרונית )פישוט אלגברי(‬
‫שימו לב‪ ,‬מאחר שהסוגריים הימניים ביותר מכילים סכום של ארבעה איברים שמועלה בריבוע‪,‬‬
‫עבודת פתיחת הסוגריים תהייה ארוכה מאוד ובשל כך גם עם סיכוני טעויות לא מבוטלים‪ ,‬ולכן‬
‫כדאי במצבים כאלו – להקטין את מספר המשתנים המעורבים בתרגיל על ידי "גישת הייצוג"‪,‬‬
‫כלומר‪ ,‬לייצג צירוף נעלמים )ביטוי כלשהו( באמצעות נעלם אחד‪ .‬ורק בשלב הפישוט הסופי‬
‫נחזיר את הערכים המקוריים‪.‬‬
‫אם כך‪ ,‬נייצג את הביטוי ‪ a + b‬בתור ‪ m‬ואת הביטוי ‪ c + d‬בתור ‪. n‬‬
‫‪ m = a + b‬ו‪. n = c + d -‬‬
‫= ‪= ( m + n) 2 + m 2 − n 2‬‬
‫‪(a + b + c + d )2 + (a + b )2 − (c + d )2‬‬
‫)‪= m 2 + 2mn + n 2 + m 2 − n 2 = 2m 2 + 2mn = 2m ⋅ (m + n‬‬
‫מע ֶבר לכך כבר לא נוכל לפשט‪ ,‬ועכשיו זה הזמן להחזיר את הערכים המקוריים של ‪ m‬ו‪. n -‬‬
‫ֶ‬
‫כזכור‪ m = a + b :‬ו‪. n = c + d -‬‬
‫ולכן‪2m ⋅ (m + n) = 2 ⋅ (a + b) ⋅ (a + b + c + d ) ,‬‬