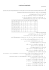תחשיב הפסוקים . כל משפט שהוא אמיתי או שיקרי אך לא שניהם - פסוק

‫תחשיב הפסוקים‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫פסוק‪ -‬כל משפט שהוא אמיתי או שיקרי אך לא שניהם‪.‬‬
‫קשרים לוגיים (לפי סדר קדימויות)‪-‬‬
‫‪ -~/ ‬לא (קשר חד מקומי)‬
‫‪ - ‬וגם (קשר דו מקומי)‬
‫‪ - ‬או (קשר דו מקומי)‬
‫‪ - ‬גרירה (קשר דו מקומי)‬
‫‪ - ‬גרירה דו כיוונית (קשר דו מקומי)‬
‫טבלת אמת‪ -‬טבלה שבה לכל הצבה לפסוקים היסודיים נתון ערך אמת או שקר‬
‫של הפסוק המורכב‪ .‬בטבלת האמת יש שורה לכל הצבה (אם בפסוק ‪ K‬פסוקים‬
‫𝑘‬
‫יסודיים אז יש ‪ 2‬הצבות‪ .‬כמו כן יש עמודה לכל משתנה פסוקי ועמודה לכל‬
‫קשר ביחס לפסוקים שעליהם הוא עובד‪).‬‬
‫טבלאות האמת של הקשרים הלוגיים‪-‬‬
‫‪p ‬‬
‫‪p p‬‬
‫‪F T‬‬
‫‪T F‬‬
‫‪pq ‬‬
‫‪pq ‬‬
‫‪pq ‬‬
‫‪q pq‬‬
‫‪T T‬‬
‫‪F F‬‬
‫‪T F‬‬
‫‪F F‬‬
‫‪p‬‬
‫‪T‬‬
‫‪T‬‬
‫‪F‬‬
‫‪F‬‬
‫‪q pq‬‬
‫‪T T‬‬
‫‪F T‬‬
‫‪T T‬‬
‫‪F F‬‬
‫‪q pq‬‬
‫‪T‬‬
‫‪T‬‬
‫‪F‬‬
‫‪F‬‬
‫‪T‬‬
‫‪T‬‬
‫‪F‬‬
‫‪T‬‬
‫‪p‬‬
‫‪T‬‬
‫‪T‬‬
‫‪F‬‬
‫‪F‬‬
‫‪p‬‬
‫‪T‬‬
‫‪T‬‬
‫‪F‬‬
‫‪F‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪))qp(  )pq((  pq ‬‬
‫‪p q pq‬‬
‫‪T T‬‬
‫‪T‬‬
‫‪T F‬‬
‫‪F‬‬
‫‪F T‬‬
‫‪F‬‬
‫‪F F‬‬
‫‪T‬‬
‫שקילות לוגית‪ -‬שני פסוקים ‪ ,‬נקראים שקולית לוגית אם יש להם אותה‬
‫טבלת אמת‪ .‬נסמן ‪ ‬או ‪‬‬
‫‪ ‬לכל הצבה לפסוקים היסודיים שני הפסוקים נותנים אותו ערך‪ .‬אחרת‬
‫יש הצבה שנותנת לשני הפסוקים ערכים שונים ואז נאמר שהפסוקים‬
‫אינם שקולים לוגית ונכתוב ‪.‬‬
‫דרכים להוכחת שקילות‪:‬‬
‫‪ ‬טבלת אמת‪.‬‬
‫‪ ‬שימוש בזהויות‪.‬‬
‫‪ ‬עץ שקר‪.‬‬
‫עץ אמת‪/‬שקר‪ -‬נבדוק מתי הפסוק מקבל אמת‪/‬שקר‪.‬‬
‫‪ ‬ברגע שיודעים מתי הפסוק הוא אמת‪/‬שקר אוטומטית יודעים מתי הוא‬
‫שקר‪/‬אמת (בכל ההצבות האחרות)‪( .‬מתחילים מההנחה שפסוק כלשהו‬
‫שיקרי ומראים שהפסוק השני גם שיקרי‪‬יש להראות שזה עובד לשני‬
‫הכיוונים)‪.‬‬
‫שקלויות לוגיות חשובות‪-‬‬
‫‪P(p) ‬‬
‫‪ ‬דה מורגן‪ pq((p)(q)) .1 :‬נובע משקלויות אלו שכל קשר ניתן‬
‫‪ pq((p)(q)) .2‬להציג בעזרת ‪,‬‬
‫‪pq(p )q ‬‬
‫‪pq (p ⋀q) ‬‬
‫‪ ‬אם הוכחנו כבר שקילות מסוימת אז השקילות נכונה לכל פסוק שנציב‬
‫בתוכה‪.‬‬
‫‪ ‬אם כל הפסוקים בדרך שקולים לוגית אז לכולם אותה טבלת אמת‪,‬‬
‫ובפרט הראשון והאחרון שקולים לוגית‪.‬‬
‫‪ ‬צורה חשבונית‪ -‬תרגום כל פסוק לתרגיל חשבוני כך שבהצבה של ‪ F/T‬לפסוקים‬
‫היסודיים שנותנת ‪ F/T‬לפסוק‪ .‬הצבה מתאימה ‪ 0/1‬בהתאמה‪ ,‬נקבל ‪0/1‬‬
‫בהתאמה‪.‬‬
‫פסוק צורה חשבונית‬
‫‪1-p‬‬
‫‪p‬‬
‫‪P*q pq‬‬
‫‪p+q-p*q pq‬‬
‫‪1-p+p*q pq‬‬
‫‪ ‬אם לשני פסוקים ‪ ,‬מתאים אותו תרגיל חשבוני אז ‪‬‬
‫‪ ‬הערה‪ -‬התרגילים לא חייבים להיות זהים אחד לאחד‪ ,‬הם צריכים להיות‬
‫זהים בהצבות של ‪(𝑝 1 − 𝑝 = 0, 𝑝 = 𝑝2 ( .1/0‬‬
‫‪ ‬תנאי הכרחי‪-‬אירוע שקיימו מתחייב לצורך האירוע העתידי‪ .‬תוצאה‪ ‬קיום‬
‫תנאי‪.‬‬
‫‪ ‬תנאי מספיק‪ -‬אירוע שאם הוא מתקיים תופיע בהכרח התוצאה‪ .‬קיום‬
‫התנאי ‪ ‬תוצאה‪.‬‬
‫‪ ‬טאוטולוגיות וסתירות‪-‬‬
‫‪ ‬פסוק ‪ ‬נקרא טאוטולוגיה אם לכל הצבה לפסוקים היסודיים הוא תמיד‬
‫אמת‪.‬‬
‫‪ ‬פסוק ‪ ‬נקרא סתירה אם לכל הצבה לפסוקים היסודיים הוא תמיד שקר‪.‬‬
‫‪ ‬סתירה מתקיימת רק אם אין אפשרות להימנע ממנה‪.‬‬
‫‪ ‬דרכים לבדיקת טאוטולוגיה‪/‬סתירה‪:‬‬
‫‪ ‬טבלת אמת‪ -‬אם בשורה אחת יוצא שקר אפשר לעצור‪.‬‬
‫‪ ‬עץ אמת‪/‬שקר‪ -‬כאשר אנחנו רוצים להוכיח טאוטולוגיה עדיף לעשות עץ‬
‫שקר ונצפה שתמיד לא יהיה פתרון (שלא יהיו שורשים)‪ .‬עץ שקר‪ -‬הוכחה‬
‫בשלילה‪.‬‬
‫‪ ‬כללים לשימוש בעץ שקר‪/‬אמת‪:‬‬
‫‪ ‬יש לאתר את הקשר המרכזי‪.‬‬
‫‪ ‬או‪ ,‬גרירה דורשים עץ שקר‪ ,‬וגם דורש עץ אמת‪ .‬בשלילה‬
‫ניתן להשתמש ב‪ 2-‬האפשרויות‪.‬‬
‫‪ ‬שימוש בשקילות‪ -‬אם יש טאוטולוגיה ואנחנו מוכיחים שיש פסוק שקול‬
‫אז הוא גם טאוטולוגיה‪.‬‬
‫‪ ‬תרגיל חשבוני‪ -‬אם מדובר בסתירה מצפים לקבל ‪ 0‬התרגיל החשבוני‪ .‬אם‬
‫מדובר בטאוטולוגיה מצפים לקבל ‪ 1‬בתרגיל החשבוני‪.‬‬
‫‪ ‬הערות‪:‬‬
‫‪ ‬אם ‪ ‬ו‪ -‬טאוטולוגיות אז ‪‬‬
‫‪ ‬אם ‪ ‬ו‪ -‬סתירות אז ‪‬‬
‫‪ ‬אם ‪ ‬טאוטולוגיה ו‪ -‬סתירה אז ‪‬‬
‫‪ ‬שלילה של טאוטולוגיה היא סתירה‬
‫‪ ‬שלילה של סתירה היא טאוטולוגיה‬
‫‪ ‬נביעה‪ /‬גרירה טאוטולוגית‪-‬‬
‫‪ ‬הגדרה‪ :‬נאמר שקבוצת פסוקים ‪ 1 ... n‬גוררת טאוטולוגית פסוק ‪ ‬אם‬
‫לכל הצבה שבה ‪ 1 ... n‬הם אמת מתקיים ‪ ‬אמת‪.‬‬
‫‪ ‬סימון‪ 1 ... n  -‬או ‪1 ... n  ‬‬
‫‪ ‬שלבים לבדיקת גרירה טאוטולוגית‪:‬‬
‫‪ ‬נמצא את כל ההצבות שבהן אגף שמאל אמת וכל אחת מהן בודקים‬
‫על אגף ימין‪.‬‬
‫‪ ‬בודקים מהם ההצבות שבהן אגף ימין שקר‪ .‬כל הצבה כזו נבדוק על‬
‫אגף שמאל‪ .‬אם יש הצבה כזו שבה כל הפסוקים משמאל הם אמת אז‬
‫אין גרירה ואחרת יש‪.‬‬
‫‪ ‬הערות‪ .1 -‬אם לא קיימת הצבה שבה כל ‪ 1 ... n‬הן אמת אז נאמר‬
‫ש‪1 ... n  -‬‬
‫‪ .2‬אם ‪ ‬הוא טאוטולוגיה בכל מקרה ‪1 ... n  ‬‬
‫‪ .3‬מצב שבו אין גרירה טאוטולוגית הוא מצב שבו הצבה‬
‫‪ 1 ... n‬כולם אמת ועבור אותה הצבה ‪ ‬הוא שקר‪.‬‬
‫‪ ‬דוגמאות לגרירה טאוטולוגית‪:‬‬
‫‪p,pqq :Modus ponens ‬‬
‫‪q,pqp :Modus tolens ‬‬
‫‪pq q p :Contraposition ‬‬
‫‪pq,pq ‬‬
‫‪ ‬טרנזיטיביות הגרירה‪pq,qrpr :‬‬
‫‪ ‬הערות‪:‬‬
‫‪  ‬אמ"ם ‪ ‬טאוטולוגיה‪.‬‬
‫‪ 1 ... n  ‬אמ"ם ‪ 1 ... n  ‬טאוטולוגיה‪.‬‬
‫‪ ‬הוכחה פורמאלית‪-‬‬
‫‪ ‬הגדרה‪ :‬הוכחה פורמאלית של מסקנה ‪ ‬מהנחות ‪ 1 ... n‬היא סדרה של‬
‫פסוקים שמתחילה בהנחות‪ ,‬מסתיימת במסקנה וכל פסוק בסדרה נובע‬
‫מהקודמים ע"פ כללים קבועים מראש‪.‬‬
‫‪ ‬בהוכחה פורמאלית מותר להשתמש רק בנתונים ובכללי ההיסק הנתונים‪.‬‬
‫‪ ‬אם בתרגיל נתונים כללים מסוים‪ ,‬ניתן להשתמש בהם לאותו תרגיל בלבד‪.‬‬
‫‪ ‬דרכים לגשת לפתרון‪ -‬א‪ .‬בוחנים את ההנחות ובודקים מה ניתן לדלות מהם‪.‬‬
‫ב‪ .‬הסתכלות על המסקנה וחיפושה כתוצאה של כלל היסק‪.‬‬
‫‪ ‬טעויות נפוצות‪:‬‬
‫‪ ‬שימוש בכללים שאנו חושבים (יודעים) שהם נכונים אבל לא‬
‫מופיעים ברשימת הכללים‪.‬‬
‫‪ ‬כאשר חלק מהפסוקים מורכבים לפעמים משתמשים בכללי‬
‫ההיסק על חלק מהפסוק וזאת טעות‪.‬‬
‫תחשיב הפרדיקטים‬
‫‪ ‬הבעיה היא ששפת תחשיב הפסוקים אינה מספיק עשירה כי‪:‬‬
‫‪ ‬לא ניתן לבטא את המילה "כל"‬
‫‪ ‬אי אפשר להציב אינסוף דברים‬
‫‪ ‬מרכיבי השפה‪:‬‬
‫‪ ‬שמות עצם‪:‬‬
‫‪ .1‬קבועים‪ -‬שמות (משה‪ ,‬סוקרטס)‪ ,‬מספרים‪.‬‬
‫מסומנים ע"י אותיות קטנות מהא"ב הלטיני‪ ,‬מראשיתו ‪a,b..‬‬‫‪ .2‬משתנים‪ -‬מסומנים ע"י אותיות קטנות מהא"ב הלטיני‪ ,‬מסופו ‪z,x….‬‬
‫‪ ‬לתוך המשתנים ניתן להציב בהמשך קבועים‪.‬‬
‫‪ ‬פרדיקטים‪:‬‬
‫‪ ‬פרדיקטים הם הפסוקים היסודיים שלנו בתחשיב הפסוקים‪.‬‬
‫‪ ‬טענות לגבי המשתנים‪ /‬הקבועים‪.‬‬
‫‪ ‬פרדיקט יכול להיות חד מקומי‪ -‬בכל פעם ניתן לבדוק אותו על‬
‫משתנה אחד‪.‬‬
‫‪ ‬פרדיקט יכול להיות דו מקומי‪ ,‬בכל פעם ניתן לבדוק אותו על ‪2‬‬
‫משתנים‪.‬‬
‫‪ ‬פרדיקט המופעל על קבוע תמיד ‪.F/T‬‬
‫‪ ‬פרדיקט המופעל על משתנה‪ F/T -‬תלוי במשתנה‪.‬‬
‫‪ ‬קשרים‪:‬‬
‫‪ ‬רק שבמקום להיות בין פסוקים יסודיים הם בין פרדיקטים‪.‬‬
‫‪ ‬כמתים‪:‬‬
‫‪ ‬לכל ‪ –x‬מייצג כולל אוניברסאלי ("וגם" אינסופי)‪.‬‬
‫‪ ‬קיים‪/‬יש ‪ –x‬לפחות אחד ("או" אינסופי)‪.‬‬
‫‪ ‬הכמתים מופיעים לפי הפסוק תמיד עם משתנה אחריהם‪.‬‬
‫‪ ‬המשתנה מגיע תמיד מתוך קבוצה מוגדרת מראש אבל לא כותבים אותה‬
‫בפסוק‪ .‬הקבוצה נובעת מתוך הפסוק עצמו‪.‬‬
‫‪ ‬משתנה הוא מכומת אם הוא מופיע עם כמת בתחילת הפסוק‪.‬‬
‫‪ ‬משתנה מכומת נקרא גם משתנה קשור‪.‬‬
‫‪ ‬משתנה שאינו מכומת נקרא משתנה חופשי‪.‬‬
‫‪ ‬פסוק שבו משתנה הוא מכומת אינו תלוי באותו משתנה‪.‬‬
‫‪ ‬פסוק שבו כל המשתנים מכומתים הוא ‪ T/F‬חד משמעית‪ ,‬ללא קשר‬
‫להצבה‪.‬‬
‫‪ ‬הוכחת ‪ F/T‬בתחשיב הפרדיקטים‪:‬‬
‫‪:x(P(x)) ‬‬
‫‪ ‬בשביל להוכיח ))‪ F = x(P(x‬עלינו למצוא הצבה אחת ‪ x=a‬עבורה‬
‫‪.p(a)=F‬‬
‫‪ ‬בשביל להוכיח ))‪ T = x(P(x‬עלינו להראות שעבור ‪ 𝑥0‬כללי (מעולם‬
‫הדיון) הפסוק ‪.p(𝑥0 )=T‬‬
‫‪:x(P(x)) ‬‬
‫‪ ‬בשביל להוכיח ))‪ T = x(P(x‬עלינו למצוא הצבה אחת ‪ x=a‬עבורה‬
‫‪.p(a)=T‬‬
‫‪ ‬בשביל להוכיח ))‪ F = x(P(x‬עלינו להראות שעבור ‪ 𝑥0‬כללי (מעולם‬
‫הדיון) הפסוק ‪.p(𝑥0 )=F‬‬
‫‪2‬‬
‫‪ ‬שלבים בהוכחה‪( :‬לדוגמא )‪(x y(y = x‬‬
‫‪ ‬נחליט האם הפסוק שיקרי או אמיתי (בדוגמא הנ"ל שיקרי)‪.‬‬
‫‪ ‬מכיוון שהכמת הראשון הוא ‪ ‬ורוצים להוכיח שקר עלינו למצוא הצבה‬
‫אחת שעבור הפסוק )‪ y(y 2 = x‬שקר‪ .‬לקחנו ‪ ,x=-2‬עלינו להראות‬
‫)‪ y(y 2 = -2‬שקר‪.‬‬
‫‪ ‬מכיוון שכעת הכמת הוא ‪ ‬ורוצים להוכיח שקר עלינו לקחת ‪ y‬כללי‪.‬‬
‫‪ ‬שלילת ביטויים‪:‬‬
‫השלילה‬
‫של‬
‫מצומצם‬
‫ביטוי‬
‫(ביטוי)‪‬‬
‫)‪P(x‬‬
‫)‪P(x‬‬
‫))‪(P(x)Q(x‬‬
‫)‪P(x)⋀ Q(x‬‬
‫))‪(P(x)⋀ Q(x‬‬
‫)‪P(x) Q(x‬‬
‫))‪(P(x)Q(x‬‬
‫)‪P(x)⋀ Q(x‬‬
‫))‪(xP(x‬‬
‫))‪x(P(x‬‬
‫))‪(xP(x‬‬
‫))‪x(P(x‬‬
‫‪ ‬הצרנת קיום ויחידות‪:‬‬
‫‪ ‬יחידות‪ :‬קיים איבר יחיד המקיים את תכונת )‪.P(x‬‬
‫)‪x y(P x P y x = y‬‬
‫‪ ‬שימו לב‪ :‬זה לא קיום‪ ,‬יכול להיות שאין אף אחד שמקיים את‬
‫התכונה והפסוק אמיתי כי אגף שמאל שיקרי‪.‬‬
‫‪ ‬סימון נוסף ליחידות‪ :‬‬
‫‪ ‬קיום‪.x(P(x)) :‬‬
‫‪ ‬קיים ויחיד‪(x(P(x)))( x y(P x P y x = y)) :‬‬
‫‪ ‬שקילויות בתחשיב הפקדיקטים‪:‬‬
‫‪ ‬פסוקים שקולים לוגית אם ‪(⋀‬‬
‫‪(xP(x))xP(x) ‬‬
‫‪xP(x)xP(x) ‬‬
‫‪x,y[_] = xy[_] = yx[_] ‬‬
‫‪x,y[_] = xy[_] = yx[_] ‬‬
‫‪ ‬אם יש ‪ 2‬כמתים שונים יש חשיבות לסדר ולכן לא ניתן להחליף סדר בין‬
‫כמתים שונים‪.‬‬
‫‪x(P(x)Q(x))xP(x)xQ(x) ‬‬
‫‪x(P(x)Q(x)) xP(x) xQ(x) ‬‬
‫‪x(P(x)Q(x))  xP(x)xQ(x) ‬‬
‫‪xP(x)xQ(x)  x(P(x)Q(x)) ‬‬
‫תורת הקבוצות‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫קשר בין קבוצה לסימנים לוגיים‪:‬‬
‫‪ ‬קבוצה=פסוק‬
‫‪ ‬איבר=מצב שבו הפסוק נותן אמת‬
‫‪ ‬הכלה=גרירה‬
‫הגדרה‪:‬קבוצה הינה אוסף של איברים לאו דווקא מאותו סוג בלי חשיבות‬
‫לסדר וללא חזרות‪.‬‬
‫סימונים‪:‬‬
‫‪ ‬קבוצות מסומנות באותיות לטיניות גדולות‪A,B,C… .‬‬
‫‪ ‬קבוצה מסומנת בסוגריים מסולסלות‪A={1,2,3} .‬‬
‫‪ ‬אם ‪ a‬איבר בקבוצה ‪ A‬נסמן‪aA :‬‬
‫‪ ‬אם ‪ a‬אינו איבר בקבוצה ‪ A‬נסמן‪aA( aA) :‬‬
‫הגדרות‪:‬‬
‫‪ ‬שייכות אינה טרנזיטיבית‪.‬‬
‫‪ ‬שתי קבוצות ‪ A‬ו‪ B-‬נקראות שוות ומסומנות ‪x(xA  xB) : B=A‬‬
‫‪ ‬כדי להוכיח שוויון בין קבוצות יש לקחת ‪ x0‬כללי ולהראות שהמשפט‬
‫נכון לגביו‪.‬‬
‫‪ ‬קבוצה ‪ A‬נקראת ריקה אם אין בה איברים‪x(xA )x (xA) :‬‬
‫‪ ‬אם ‪ A‬ו‪ B-‬קבוצות ריקות אז ‪.B=A‬‬
‫‪ ‬מכיוון שכל ‪ 2‬קבוצות ריקות שוות ‪ ‬יש קבוצה ריקה אחת‪ ,‬נקרא לה‬
‫הקבוצה הריקה ונסמנה‪ :‬‬
‫‪=x ‬סתירה תמיד!!! (בלי קשר ל‪.)x-‬‬
‫‪ ‬הכלה ממש‪ A :‬מוכל ממש ב‪ B-‬אמ"ם כל איבר של ‪ A‬נמצא ב‪ B-‬וגם קיים‬
‫איבר ב‪ B-‬כך שאינו ב‪( A-‬לתכונה הזו אין הקבלה בסימנים לוגיים)‪.‬‬
‫))‪A⊊Bx((xAxB)⋀b(bB⋀b∉A‬‬
‫‪ ‬נאמר שקבוצה ‪ A‬מוכלת בקבוצה ‪ B‬ונסמן ‪x(xA  xB) : AB‬‬
‫‪NZQR‬‬
‫‪ ‬הוכחת הכלה‪ :‬צריך להוכיח )‪T=x(xA  xB‬‬
‫‪ ‬בשביל להראות ‪ AB‬צריך להראות )‪ ,F=x(xA  xB‬כלומר‬
‫מוצאים ‪ x=a‬כך ש‪ F= xA  xB-‬כלומר‪aA = T, aB = F :‬‬
‫‪ ‬כל קבוצה ‪ A‬מקיימת ‪( AA‬כל קבוצה מוכלת בעצמה)‬
‫)‪x(xA  xA‬‬
‫‪ ‬לכל קבוצה ‪ A‬מתקיים ‪( A‬הקבוצה הריקה מוכלת בכל קבוצה)‬
‫)‪x(x  xA‬‬
‫‪ ‬שייכות והכלה הן ‪ 2‬תכונות שונות‪.‬‬
‫‪ ‬הכלה בודקת יחס בין איברים בקבוצות‪.‬‬
‫‪ ‬שייכות בודקת האם האיבר הבודד רשום בקבוצה‪.‬‬
‫‪ ‬שוויון שקול להכלה דו כיוונית‪A=B  ((AB)(BA)) :‬‬
‫‪ ‬הכלה היא טרנזיטיבית‪((AB)(BA))AC :‬‬
‫‪ ‬שייכות אינה טרנזיטיבית‪.‬‬
‫‪ ‬כשמוכיחים גרירה יש להתחיל מהנחות נכונות‪.‬‬
‫‪ ‬בבדיקת הכלה מתחילים מאיברי הקב' המוכלת‪.‬‬
‫‪  ‬היא הקבוצה היחידה אשר ניתן להתבונן עליה כאיבר וכקבוצה מבלי‬
‫לשנות אותה צורנית‪.‬‬
‫‪ ‬פעולות על ובין קבוצות‪:‬‬
‫‪ -U ‬קבוצה אוניברסלית שמכילה את כל הקבוצות האחרות‪ .‬ולכן‬
‫‪ x U‬אמת תמיד‪.‬‬
‫‪ ‬איחוד‪ AB -‬האיחוד של ‪ A‬עם ‪xAB  xA  xB :B‬‬
‫ ‪ AB  BA‬נכון תמיד!!!‬‫‪A‬‬
‫‪B‬‬
‫ ‪x(xA  (xA  xB)) -A AB‬‬‫ ‪x(xB  (xA  xB)) -B AB‬‬‫ ‪xA  xA  x  xA -A=A‬‬‫ ‪xA A  xA  x A  xA -A A =A‬‬‫ ‪xAU  xA  x U  x U - AU= U‬‬‫‪ ‬חיתוך‪ AB -‬החיתוך של ‪ A‬ו‪xAB  xA  xB :B-‬‬
‫ ‪ AB  BA‬נכון תמיד!!!‬‫‪A‬‬
‫‪B‬‬
‫ ‪x( (xA  xB)  xA ) - AB A‬‬‫‪x((xA  xB)  xB ) - AB B -‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫ ‪xA  xA  x  F  x :A=‬‬‫ ‪xA A  xA  x A  xA -A A =A‬‬‫ ‪xAU  xA  x U  xA - AU= A‬‬‫‪ ‬הפרש‪ A\B-‬ההפרש של ‪ A‬ו‪:B-‬‬
‫‪A‬‬
‫‪B‬‬
‫)‪xA\B  xA  x B  xA ( x B‬‬
‫ ‪A\BB\A‬‬‫ ‪A\A=‬‬‫‪ ‬הפרש סימטרי‪: AB -‬‬
‫‪B‬‬
‫)‪AB (A\B) (B\A) ( AB)\( AB‬‬
‫הפרש סימטרי הוא חלופי ‪AB BA‬‬‫ ‪AB BA‬‬‫‪ ‬המשלים‪ -‬לכל ‪ A‬מתקיים ‪ A U‬והמשלים של ‪ A‬יסומן 𝑐‪A‬‬
‫)‪xA𝑐  x U\ A x U ( x A) ( x A‬‬
‫ ‪AA𝑐  U‬‬‫ ‪AA𝑐  ‬‬‫אם יש פסוק ‪ xA  xB‬אז זה אומר ‪.A=B‬‬
‫בפסוק של גרירה בשביל להראות אמת מספיק להניח שאגף שמאל אמת‬
‫ולהראות שאגף ימין הוא אמת‪( .‬כלומר מה שאחרי האם נתון וצ"ל את מה‬
‫שאחרי האז)‪.‬‬
‫דרכים להוכחת זהויות בתורת הקבוצות‪:‬‬
‫‪ ‬באמצעות לוגיקה‪.‬‬
‫‪ ‬באמצעות דיאגרמת וואן (רק לאינטואיציה)‪.‬‬
‫‪ ‬באמצעות הכלה דו כיוונית‪.‬‬
‫‪ ‬באמצעות זהויות מתורת הקבוצות‪( .‬תמיד נבחר אגפים מסובכים‬
‫יותר‪ -‬כאלה שנוכל לפשט)‪.‬‬
‫מטרנזיטיביות ההכלה‪AB  AB  (AB) A( AB) :‬‬
‫‪ ‬אם ‪ A B‬אז‪(AB =B)  )AB= A (:‬‬
‫הגדרה‪ -‬שתי קבוצות ‪ A‬ו‪ B-‬נקראות זרות כאשר ‪AB=‬‬
‫חוק הפילוג‪A(BC) ( AB)  ( AC) -‬‬
‫)‪(AB) (CD) ( AC)  ( AB)  ( BC)  ( BD‬‬‫)‪(AB)  (CD) ( AC)  ( AB)  ( BC)  ( BD‬‬‫חוק הקיבוץ‪(AB)CA(BC) -‬‬
‫ )‪(AB) CA (BC‬‬‫ )‪(A\B)\CA\(B\C‬‬‫ )‪(AB)C  A(BC‬‬‫משפט‪A\B  AB 𝑐 -‬‬
‫כללי דה מורגן‪:‬‬
‫𝑐‬
‫‪AB A𝑐 B 𝑐 ‬‬
‫‪(AB)𝑐 A𝑐 B 𝑐 ‬‬
‫כללים אוניברסלים‪:‬‬
‫‪A‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪TP P ‬‬
‫‪FP F ‬‬
‫‪TP T ‬‬
‫‪FP P ‬‬
‫‪ ‬קבוצת החזקה‪:‬‬
‫‪ ‬קבוצת חזקה )‪ p(A‬היא קבוצת כל תתי הקבוצות של ‪.A‬‬
‫‪ ‬עבור קבוצה ‪ A‬קבוצת החזקה של ‪ A‬מסומנת )‪ p(A‬היא קבוצת כל‬
‫הקבוצות המוכלות ב‪x(x p(A) x A) .A-‬‬
‫‪ ‬ב‪ p(A)-‬האיברים הם קבוצות של איברים ב‪.A-‬‬
‫‪   p(A)  A ‬בקבוצת חזקה יש לפחות איבר אחד‬
‫(הקבוצה הריקה) ‪p(A)  ‬‬
‫‪.A  p(A)  A A ‬‬
‫‪ ‬בקבוצת החזקה )‪ p(A‬לפחות שני איברים (אלה אם כן ‪)A=‬‬
‫‪ ‬אם ‪ A‬קבוצה עם ‪ n‬איברים אז ב‪ 2𝑛 p(A)-‬איברים‪.‬‬
‫‪X A X B  X AB‬‬
‫)‪p(AB)p(A)  p(B‬‬
‫)‪p(A)  p(B)  p(AB‬‬
‫פארדוקס ראסל‪-‬‬
‫‪ ‬קבוצה לא שייכת לעצמה‪.‬‬
‫‪ ‬אוסף כל הקבוצות אינו קבוצה‪.‬‬
‫‪ -Imf‬קבוצת האיברים שיש להם מקור‪.‬‬
‫מכפלה קרטזית‪ :‬המכפלה הקרטזית של ‪ A‬ו‪ B-‬מסומנת ‪ .AB‬קבוצת הזוגות‬
‫הסדורים שמורכבת מאיבר ב‪ A-‬ואיבר ב‪.B-‬‬
‫}‪AB={(a,b)|aAbB‬‬
‫‪ ‬תכונות של מכפלה קרטזית‪:‬‬
‫‪ ‬אינה חילופית‪BA≠AB -‬‬
‫‪A= ‬‬
‫‪A = ‬‬
‫‪ ‬זוג סדור – בזוג סדור יש חשיבות לסדר‪ ,‬נסמנו )‪(a,b‬‬
‫‪ 2 ‬זוגות סדורים שווים כאשר )‪(b=d)  (a=c)  (a,b)=(c,d‬‬
‫‪(aA)  (bB)(a,b)  AB ‬‬
‫‪ ‬טענה‪A(BC) (AB)( AC) - :‬‬
‫ )‪A(BC) (AB)  ( AC‬‬‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫טענה‪ :‬אם ‪ AB=AC‬אז )‪(A=)(B=C‬‬
‫הוכחת פסוק או‪ :‬מניחים שאחד מהצדדים שקר ומראים שהשני חייב להיות‬
‫אמת‪.‬‬
‫‪( C≠B‬קיים איבר ב‪ B-‬שאינו ב‪(  )C-‬קיים איבר ב‪ C-‬שאינו ב‪) B-‬‬
‫‪BC=  C≠B‬‬
‫‪ ‬כללי התאמה‪ -‬כלל התאמה הוא שלשה סדורה )‪(A,B,‬‬
‫}‬
‫‪ - A‬התחום‬
‫‪ - B‬טווח‬
‫‪ -‬גרף ‪ AB -‬‬
‫‪ A,B‬הן קבוצות‬
‫‪ ‬ייתכן‪=- :‬‬
‫ ‪= AB‬‬‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫)‪(A=C)  (B=D)  (=T)  (A,B,) =(C,D,T‬‬
‫כאשר )‪ (A,B,‬ו‪ AB-‬נגיד ש‪ -‬תת גרף של ‪.AB‬‬
‫כדי לבדוק האם )‪ (A,B,‬כלל התאמה יש לבדוק האם ‪. AB‬‬
‫תכונות של כללי התאמה‪:‬‬
‫‪ ‬מלאות‪ -‬כלל התאמה נקרא מלא אם לכל איבר בתחום קיים איבר בטווח כך‬
‫שהזוג הסדור שלהם נמצא בגרף‪.aA(bB((a,b))) .‬‬
‫‪ ‬כדי להוכיח שכלל התאמה הוא מלא ניקח איבר כללי ונראה שהוא‬
‫מקיים את התנאי‪.‬‬
‫‪ ‬כדי להוכיח שכלל התאמה אינו מלא ניקח דוגמא נגדית‪.‬‬
‫‪ ‬מכל איבר ב‪ A-‬יוצא חץ אחד‪ ,‬כלומר ‪ x‬מופיע לפחות פעם אחת‪.‬‬
‫‪ ‬על‪ -‬כלל התאמה נקרא על אם ))‪bB (aA((a,b)‬‬
‫‪ ‬כדי להוכיח שכלל התאמה הוא על ניקח איבר כללי ונראה שהוא מקיים‬
‫את התנאי‪aA((a,b))) :‬‬
‫‪ ‬כדי להוכיח שכלל התאמה אינו על ניקח דוגמא נגדית‪.‬‬
‫‪ ‬כל איבר ב‪ B-‬מקבל חץ‪.‬‬
‫‪ ‬חד ערכיות‪ -‬לכל איבר בתחום יש לכל היותר איבר אחד בטווח כך שהזוג‬
‫הסדור שלהם בגרף‪(.‬מכל ‪ x‬ששייך ל‪ A-‬יש רק איבר אחד ב‪ B-‬כלומר ‪ x‬מופיע‬
‫לכל היותר פעם אחת ב‪.)B-‬‬
‫) ‪aA𝑏1 , 𝑏2 B ((a,𝑏1 ) (a, 𝑏2 ) 𝑏1 = 𝑏2‬‬
‫‪ ‬כדי להראות חד ערכיות עלינו להראות שבהנחה ש‪-‬‬
‫‪ (a, 𝑏2 )=T  (a, 𝑏1 ) =T‬אז ‪𝑏1 = 𝑏2‬‬
‫‪ ‬כדי להראות שכלל התאמה אינו חד ערכי עלינו למצוא ‪ aA‬ו‪𝑏1 , 𝑏2 B-‬‬
‫כך ש‪-(a, 𝑏1 ) -‬אמת וגם ‪-(a, 𝑏2 )‬אמת וגם ‪𝑏2 ≠𝑏1‬‬
‫‪ ‬חד חד ערכיות (חח"ע)‪ -‬לכל איבר בטווח יש לכל היותר איבר אחד בתחום‬
‫שהזוג הסדור ביניהם נכנס לגרף‪.‬‬
‫) ‪bB  𝑎1 , 𝑎2 A ((𝑎1 ,b) ( 𝑎2 ,b) 𝑎1 = 𝑎2‬‬
‫‪ ‬כדי להראות שכלל ההתאמה אינו חח"ע עלינו למצוא ‪ 𝑎1 , 𝑎2 A‬ו‪bB-‬‬
‫כך ש‪- (𝑎1 ,b)-‬אמת וגם ‪-(𝑎2 ,b)‬אמת וגם ‪. 𝑎2 ≠ 𝑎1‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪ Y ‬לכל היותר מופיע פעם אחת‪ ,‬אותו איבר לא יכול לקבל ‪ 2‬חצים‪.‬‬
‫הגדרת פונקציה‪ -‬פונקציה היא כלל התאמה מלא וחד ערכי ‪ ‬לכל איבר בתחום‬
‫קיים איבר יחיד בטווח כך שהזוג הסדור שלהם בגרף‪.‬‬
‫אם )‪ (A,B,‬כלל התאמה מלא וחד ערכי (פונקציה) נשתמש בסימונים הבאים‪:‬‬
‫‪ ‬פונקציות מסומנות באותיות …‪f,g,h‬‬
‫‪ f ‬היא פונקציה שתחומה ‪ A‬וטווחה ‪ B‬נכתוב‪ .f:AB :‬ובמקום לכתוב‬
‫‪ (x,y)‬נכתוב ‪.f(x)=y‬‬
‫‪ ‬קבוצת הפונקציות מ‪ A-‬ל‪ B-‬מסומנת ‪-B( B^A‬הטווח‪-A,‬התחום)‪.‬‬
‫עבור פונקציה ידוע שכלל ההתאמה הוא מלא וחד ערכי‪ ,‬נותר לבדוק האם‬
‫הפונקציה חח"ע והאם היא על‪.‬‬
‫כאשר מדובר בשתי קבוצות סופיות ושוות גודל‪ ,‬הפונקציה ביניהן תמיד תהיה‬
‫(חח"ע ועל) או (לא חח"ע ולא על)‪.‬‬
‫‪ ‬הגדרת חח"ע בפונקציות‪ 𝑎1 , 𝑎2 A (f(𝑎1 )=f(𝑎2 ) 𝑎1 = 𝑎2 ) :‬‬
‫‪ ‬הגדרת על בפונקציות‪bB (aA(f(a)=b)) :‬‬
‫‪ ‬הגדרת לא על בפונקציות‪bB (aA(f(a)b)) :‬‬
‫תכונות ושיטות לבדיקת קיום התכונה‪:‬‬
‫‪ ‬חד ערכיות‪ -‬האם הצבת ‪ x‬נותנת תשובה יחידה? כל ‪ x‬חייב לקיים דרישה זו‪.‬‬
‫‪ ‬מלאות‪ -‬האם הצבת ‪ x‬נותנת תשובה בטווח ‪ ?B‬כל ‪ x‬חייב לקיים דרישה זו‪.‬‬
‫‪ ‬חח"ע‪ -‬מניחים בשלילה ) ‪ 𝑥1 ≠ 𝑥2 ,𝑓(𝑥1 ) = 𝑓(𝑥2‬ומגיעים לסתירה –חח"ע‬
‫(או שלא מגיעים לסתירה ואז זה לא חח"ע)‪.‬‬
‫‪ ‬על‪ -‬מתחילים מ‪ y-‬כללי ומוצאים עבורו ‪.x‬‬
‫תמונת הפונקציה‪ :‬נגדיר את '‪ B‬כ‪ Im(f)-‬או כ"תמונה" באופן הבא‪:‬‬
‫‪ ,B'B‬נאמר כי )‪ y Im(f‬אם קיים ‪ xA‬כך ש‪.f(x)=y-‬‬
‫התמונה היא ת"ק של הטווח המכילה את היעדים המדוייקים של הפונקציה‪.‬‬
‫דוגמאות של פונקציות‪:‬‬
‫‪ ‬פונקציית הזהות‪ ,(A,A,{(x,x)|xA}) -‬פונקציית הזהות על ‪ A‬מסומנת ‪𝑖𝐴 :‬‬
‫‪𝑖𝐴 :AA‬‬
‫‪𝑖𝐴 : (x)=x‬‬
‫‪ ‬פונקציית הזהות היא חח"ע ועל‪.‬‬
‫‪ ‬פונקציה קבועה‪ -‬נבחר ‪ f:AB ,bB‬קבועה כך ש‪ f(a)=b-‬לכל ‪aA‬‬
‫‪ ‬פונקציה קבועה על ‪ ‬ב‪ B-‬יש רק איבר אחד‬
‫‪ ‬פונקציה קבועה חח"ע ‪ ‬ב‪ A-‬יש רק איבר אחד‬
‫‪ ‬פונקציה קבועה חח"ע ועל ‪ ‬ב‪ A-‬וב‪ B-‬יש רק איבר אחד‪.‬‬
‫‪ ‬בדר"כ פונקציה קבועה אינה חח"ע ואינה על‪.‬‬
‫‪ ‬פונקציה אופיינית של ‪ B‬ב‪ – A-‬נתונה ‪ B A‬הפונקציה האופיינית של ‪ B‬ב‪A-‬‬
‫מסומנת 𝐵‪ .‬פונקציה שתחומה ‪ A‬וטווחה {‪𝐵 : 𝐴 0,1 :}0,1‬‬
‫𝐵 ∈ 𝑎 ‪1,‬‬
‫= 𝑎 𝐵‪a∈ 𝐴 ‬‬
‫𝐵\𝐴 ∈ 𝑎 ‪0,‬‬
‫‪ ‬אם ‪ B=A‬אז ‪𝐵 𝑎 = 1‬‬
‫בשני המקרים האלה מדובר בפונ ' קבועה ואינה על‪.‬‬
‫‪ ‬אם ‪ B=‬אז ‪𝐵 𝑎 = 0‬‬
‫‪ 𝐵 ‬על ‪(B)(A\B) ‬‬
‫}‬
‫‪ 𝐵 ‬חח"ע ‪ ‬ב‪ B-‬לכל היותר איבר אחד וב‪ A\B-‬לכל היותר איבר אחד‪.‬‬
‫‪ 𝐵 ‬חח"ע ועל ‪ ‬ב‪ 2 A-‬איברים כאשר אחד מהם ב‪ B-‬והשני לא ב‪.B-‬‬
‫‪ ‬בפונקציות התחום והטווח תמיד אינם ריקים‪.‬‬
‫‪ ‬הרכבת פונקציות‪-‬‬
‫נתונות ‪ f:AB‬ו‪ g: BC-‬נגדיר פונקציה חדשה ‪ g( g৹f‬מורכבת על ‪(f‬‬
‫‪g৹f:AC‬‬
‫הטווח‬
‫של‬
‫החיצונית‬
‫התחום‬
‫של‬
‫הפנימית‬
‫‪g৹f (a)=g(f(a))C‬‬
‫חיצונית‬
‫פנימית‬
‫‪aA‬‬
‫‪ ‬בשביל שהרכבה תהיה מוגדרת‪ :‬הטווח של הפנימית = תחום של החיצונית‬
‫(בעיקרון מספיק הכלה)‪.‬‬
‫‪ ‬ייתכן ‪ g৹f‬מוגדר אבל ‪ 𝑓 ৹g‬לא מוגדר‪.‬‬
‫‪ ‬אם ‪ f‬ו‪ g-‬מלאות וחד ערכיות אז ‪ g৹f‬מלאה וחד ערכית‪.‬‬
‫‪ ‬בהרכבה אין חילוף!!!! (גם לא כאשר ‪ 2‬הצורות מוגדרות)‪.‬‬
‫‪ ‬תכונות של הרכבה‪:‬‬
‫‪ ‬קיבוץ‪( g৹(f৹h) = )g৹f)৹h -‬בהנחה שהכל מוגדר)‬
‫‪ ‬פונ' הזהות נייטרלית בהרכבה‪𝑖𝐵 ৹f=f ,f৹𝑖𝐴 =f -‬‬
‫‪ ‬משפטים על הרכבה‪:‬‬
‫‪ ‬אם ‪ 𝑓 ৹g‬חח"ע אז ‪ g‬חח"ע‪.‬‬
‫‪ ‬אם ‪ 𝑓 ৹g‬על אז ‪ f‬על‪.‬‬
‫‪ ‬אם ‪ 𝑓 ৹g‬חח"ע ‪ f ‬חח"ע‪.‬‬
‫‪ ‬אם ‪ g‬חח"ע ‪ 𝑓 ৹g ‬חח"ע‪.‬‬
‫‪ ‬אם ‪ g‬לא חח"ע ‪ 𝑓 ৹g ‬לא חח"ע‪.‬‬
‫‪ ‬אם ‪ f‬לא על ‪ 𝑓 ৹g ‬לא על‪.‬‬
‫‪ 𝑓 ৹g ‬על ‪ g ‬על‪.‬‬
‫‪ ‬הפיכות‪:‬‬
‫‪ ‬הגדרה‪f:AB :‬‬
‫‪ ‬נאמר ש‪ f-‬הפיכה מימין אם קיימת ‪ g:BA‬כך ש‪𝑓 ৹g=𝑖𝐵 -‬‬
‫𝑏= 𝑏‬
‫𝐵𝑖=)‪৹g(b‬‬
‫𝑓 ‪bB‬‬
‫‪ ‬נאמר ש‪ f-‬הפיכה משמאל אם קיימת ‪ g:BA‬כך ש‪g৹𝑓=𝑖𝐴 -‬‬
‫𝑎= 𝑎‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫𝐴𝑖=)‪৹𝑓(a‬‬
‫‪aA g‬‬
‫‪ ‬תנאים הכרחיים להפיכות (אם לא מתקיימים אז לא מתקיימת הפיכות‪ ,‬אם‬
‫מתקיימים לא יודעים כלום)‪.‬‬
‫‪ ‬אם ‪ f‬הפיכה מימין אז ‪ 𝑓 ৹g‬חח"ע ועל‪.‬‬
‫‪ ‬אם ‪ f‬הפיכה מימין אז ‪ f‬על‪.‬‬
‫‪ f ‬לא על ‪ f ‬לא הפיכה מימין‪.‬‬
‫‪ ‬אם ‪ f‬על יש לה הופכית ימנית (תיתכן יותר מהופכית ימנית אחת)‪.‬‬
‫‪ ‬תנאי הכרחי להפיכות מימין‪ f :‬על‪.‬‬
‫‪ f ‬על ‪ f ‬הפיכה מימין‪.‬‬
‫‪ ‬אם ‪ f‬הפיכה משמאל אז 𝑓‪ g৹‬חח"ע ועל‪.‬‬
‫‪ ‬אם ‪ f‬הפיכה משמאל אז ‪ f‬חח"ע‪.‬‬
‫‪ f ‬לא חח"ע ‪ f ‬לא הפיכה משמאל‪.‬‬
‫‪ ‬אם ‪ f‬חח"ע יש לה הופכית שמאלית (תיתכן יותר מהופכית ימנית אחת)‪.‬‬
‫‪ ‬תנאי הכרחי להפיכות משמאל‪ f :‬חח"ע‪.‬‬
‫‪ f ‬חח"ע ‪ f ‬הפיכה משמאל‪.‬‬
‫‪ ‬אם ‪ f‬חח"ע ולא על ‪ f ‬הפיכה משמאל ולא מימין‬
‫קיימת יותר מהופכית שמאלית אחת‪.‬‬
‫‪ ‬אם ‪ f‬על ולא חח"ע ‪ f ‬הפיכה מימין ולא משמאל‬
‫קיימת יותר מהופכית ימנית אחת‪.‬‬
‫‪ ‬אם ‪ f:AB‬חח"ע ועל אז‪:‬‬
‫‪ f o‬הפיכה מימין וההופכית הימנית יחידה‪.‬‬
‫‪ f o‬הפיכה משמאל וההופכית השמאלית יחידה‪.‬‬
‫‪−1‬‬
‫‪ o‬ההופכית הימנית = ההופכית השמאלית = 𝑓‬
‫‪ o‬נאמר ש‪ f-‬הפיכה‪.‬‬
‫‪ f ‬הפיכה ‪ f ‬חח"ע ועל ‪ f ‬הפיכה מימין ומשמאל‪.‬‬
‫‪𝑓 −1 ৹f=𝑖𝐴 ,f৹𝑓 −1 =𝑖𝐵 ‬‬
‫‪ ‬אם ‪ f‬ו‪ g-‬הפיכות מימין אז ‪ g৹f‬הפיכה מימין‪.‬‬
‫‪ ‬אם ‪ f‬ו‪ g-‬הפיכות משמאל אז ‪ g৹f‬הפיכה משמאל‪.‬‬
‫‪ ‬אם ‪ f‬ו‪ g-‬הפיכות אז ‪.g৹f‬‬
‫כאשר מדברים על תכונות של פונ' צריך "לקלף" מבחוץ פנימה‪.‬‬
‫אם ‪ A‬קבוצה סופית ו‪ f:AA-‬חח"ע ‪ f ‬על‪.‬‬
‫אם ‪ f:AB‬כאשר ‪ A‬ו‪ B-‬קבוצות סופיות ו‪ f-‬חח"ע ‪𝐴 ≤ 𝐵 ‬‬
‫לא עובד בקבוצות‬
‫אם ‪ f:AB‬כאשר ‪ A‬ו‪ B-‬קבוצות סופיות ו‪ f-‬על ‪𝐵 ≤ 𝐴 ‬‬
‫אינסופיות‬
‫בין שתי קבוצות סופיות ‪ B,A‬יש פונקציה חח"ע ועל ‪𝐵 = 𝐴 ‬‬
‫}‬
‫‪ ‬הוכחת על וחח"ע‪:‬‬
‫חח"ע‬
‫על‬
‫החוק הנדרש להוכחה‪:‬‬
‫) ‪ 𝑎1 , 𝑎2 A (f(𝑎1 )=f(𝑎2 ) 𝑎1 = 𝑎2‬‬
‫לכל ‪ y‬יש ‪x‬‬
‫הוכחת קיום לכל ‪y‬‬
‫מתחילים מ‪ y-‬כללי‪ ,‬מניחים ‪f(x)=y‬‬
‫ומבודדים את ‪x‬‬
‫מימוש‬
‫‪.1‬בניית הופכית שמאלית‬
‫‪ y.2‬הוא ייחודי לכל ‪x‬‬
‫‪.1‬בניית הופכית ימנית‬
‫‪ .2‬ניתן למצוא ‪ x‬מתאים‬
‫לכל ‪y‬‬
‫‪ ‬יחסים‬
‫‪ ‬הגדרה‪ :‬יחס הוא טענה על ‪ 2‬משתנים‪ ,‬הטענה יכולה להיות אמת או שקר‪.‬‬
‫‪ ‬ההגדרה הלוגית‪ :‬יחס הוא פרדיקט דו מקומי (המשתנים מגיעים מקבוצה ‪A‬‬
‫כלשהיא)‪.‬‬
‫‪ ‬הגדרה מתורת הקבוצות‪ :‬יחס ‪ R‬על ‪ A‬הוא ‪  R AA‬יחס ‪ R‬על קבוצה ‪A‬‬
‫הוא תת קבוצה של ‪ AA‬ונכתוב ‪(x,y)RxRy‬‬
‫‪ ‬היחס הריק‪    AA -‬יחס‪ .‬לכל ‪.(x,y)R x,yA‬‬
‫‪ ‬היחס המלא‪ R=AA -‬גם יחס ‪x,y(x,y)R‬‬
‫‪ ‬תכונות של יחסים‪:‬‬
‫‪ ‬רפלקסיביות‪ -‬זוגות זהים נמצאים ביחס‪ ,‬יחס ‪ R‬על ‪ A‬נקרא רפלקסיבי‬
‫)‪xA(xRx‬‬
‫‪ ‬לא רפלקסיבי‪xA(xRx) -‬‬
‫‪ ‬אנטי רפלקסיביות‪ -‬כל הזוגות הזהים לא ביחס‪ R ,‬הוא יחס אנטי רפלקסיבי‬
‫על ‪xA(xRx) A‬‬
‫‪ ‬היחסים שיכולים להיות אנטי רפלקסיביים הם אלה שהיו לא‬
‫רפלקסיביים‪ ,‬אבל זה לא בהכרח‪.‬‬
‫‪ ‬לא אנטי רפלקסיבי‪ -‬קיים איבר ב‪ A-‬שהזוג שלו עם עצמו בקבוצה‪.‬‬
‫)‪xA(xRx‬‬
‫‪ ‬רפלקסיבי ‪ ‬לא אנטי רפלקסיבי‪.‬‬
‫‪ ‬אנטי רפלקסיבי ‪ ‬לא רפלקסיבי‪.‬‬
‫‪ ‬סימטרי‪ -‬אין משמעות לסדר ביחס‪ ,‬יחס ‪ R‬על ‪ A‬נקרא סימטרי‬
‫)‪x,yA(xRyyRx‬‬
‫‪ ‬אם הזוג ‪ (x,y)R‬אז עלינו לבדוק ‪(y,x)R‬‬
‫‪ ‬לא סימטרי‪ -‬זוג ‪ x,y‬כך ש‪ (x,y)R-‬אבל ‪(y,x)R‬‬
‫‪ ‬אנטי סימטרי חלש‪ -‬יחס ‪ R‬על ‪ A‬נקרא אנטי סימטרי חלש אם‬
‫)‪x,y A(xRyyRxx=y‬‬
‫‪ ‬אין שום חובה להכניס זוגות לקבוצה אבל זוג שנכנס יכול להכניס את‬
‫שיקופו רק בתנאי שמדובר בזוג )‪.(x,x‬‬
‫‪ ‬סימטרי ‪‬אנטי סימטרי חלש ‪R{(x,x)|xA} ‬‬
‫‪ ‬סימטרי ‪‬אנטי סימטרי חלש‪ ‬רפלקסיבי‪R={(x,x)|xA} ‬‬
‫‪ ‬אנטי סימטרי חזק‪ -‬יחס ‪ R‬על ‪ A‬נקרא אנטי סימטרי חזק אם‬
‫)‪x,y A(xRyyRx‬‬
‫‪ ‬בפרט )‪(x,x)R  (xRxxRx‬‬
‫‪ ‬אנטי סימטרי חזק ‪ ‬אנטי רפלקסיבי‪.‬‬
‫‪ ‬תנאי הכרחי לאנטי סימטרי חזק הוא אנטי רפלקסיבי‪.‬‬
‫‪ ‬סימטרי ‪‬אנטי סימטרי חזק ‪x,y A(xRy) ‬‬
‫‪ ‬אנטי סימטרי חזק ‪ ‬אנטי רפלקסיבי ‪ ‬אנטי סימטרי חלש‬
‫)‪x,yA(xRyyRx) xA(xRx‬‬
‫‪ ‬אנטי סימטרי חזק ‪ ‬מכל זוג )‪ (x,y‬ניתן לבחור לכל היותר אחד וזוגות‬
‫)‪ (x,x‬אין בכלל‪.‬‬
‫‪ ‬טרנזיטיביות‪ -‬היחס נגרר מזוג לזוג‪ ,‬יחס ‪ R‬על ‪ A‬נקרא טרנזיטיבי ‪x,y,z‬‬
‫)‪A(xRyyRz xRz‬‬
‫‪ ‬לא טרנזיטיבי‪ -‬מוצאים ‪ x,y,z‬כך ש‪xRz , xRy,yRz-‬‬
‫‪ ‬טרנזיטיביות‪‬סימטריות‪ ‬על כל זוג שנמצא ביחס ‪(x,y)R‬‬
‫נמצא גם הזוג ‪(x,x)R‬‬
‫‪ ‬אם ‪ (x,y)R  R‬ואם הוא סימטרי וטרנזיטיבי ‪(x,x)R ‬‬
‫‪ ‬סוגי יחסים‪:‬‬
‫‪ ‬יחס שקילות‪ -‬יחס ‪ R‬על ‪ A‬נקרא יחס שקילות אם הוא רפלקסיבי‪,‬‬
‫סימטרי וטרנזיטיבי‪.‬‬
‫‪ ‬יחס שקילות מינימלי על קבוצה ‪( A‬המינימום הנדרש לשם שקילות)‪:‬‬
‫}‪R={(x,x)|xA‬‬
‫‪ ‬יחס שקילות מקסימלי‪R=AA :‬‬
‫‪ ‬שיוויון הוא אכן יחס שקילות והוא יחס השקילות המינימלי‬
‫האפשרי‪.‬‬
‫‪ ‬אם נצליח למצוא שיוויון ביחס יהיה יותר קל להוכיח שהוא יחס‬
‫שקילות‪.‬‬
‫‪ ‬יחסי סדר‪-‬‬
‫‪ R ‬הוא יחס סדר חלש מעל ‪ A‬אם ‪ R‬רפלקסיבי‪ ,‬אנטי סימטרי חלש‬
‫וטרנזיטיבי‪.‬‬
‫‪ R ‬הוא יחס סדר חזק מעל ‪A‬אם ‪ R‬אנטי רפלקסיבי‪ ,‬אנטי סימטרי‬
‫חזק וטרנזיטיבי‪.‬‬
‫‪ ‬כל יחס סדר חלש שנוציא ממנו את האיברים ששווים זה לזה יהיה‬
‫יחס סדר חזק‪.‬‬
‫‪ ‬כל יחס סדר חזק שנוסיף אליו את האיברים ששווים זה לזה יהיה‬
‫יחס סדר חלש‪.‬‬
‫‪ ‬איבר מינימלי‪ -‬יהי ‪ R‬יחס סדר מעל ‪ .A‬איבר ‪ xA‬נקרא מינימלי אם‬
‫‪( yyx yRx‬אין איבר שנמצא משמאל ל‪.)x-‬‬
‫‪ ‬איבר עוקב‪ -‬איבר ‪ yx‬נקרא עוקב של ‪ x‬ביחס ‪ R‬אם‬
‫)‪(xRy) ⋀ z A, z x,y (xRz⋀ zRy‬‬
‫‪ ‬יחס משווה‪ -‬יחס ‪ R‬מעל ‪ A‬נקרא משווה אם‬
‫)‪x,yA(xRy)(yRx) (x=y‬‬
‫‪ ‬מחלקת שקילות‪ -‬מחלקת שקילות של ‪ xA‬ביחס ‪( R‬שקילות)‬
‫‪𝑋 R ={yA|xRy} A‬‬
‫‪ ‬קבוצת איברי ‪ A‬שמקיימים את היחס ‪ R‬עם ‪.x‬‬
‫‪ ‬יחס שקילות מחלק את העולם לפי היחס ומחלקות השקילות מחלקות‬
‫את האיברים לפי התכונה השונה של האיברים‪.‬‬
‫‪ ‬אם ‪ R‬יחס שקילות אז אם ‪ xRy‬נאמר ‪ x‬שקול ל‪.y-‬‬
‫‪ ‬תכונות של מחלקת שקילות‪:‬‬
‫‪ 𝑋 R  ‬מכיוון ש‪ R-‬רפלקסיבי‪xRxx 𝑋 R :‬‬
‫‪ ‬כל ‪ 2‬מחלקות שקילות הן זרות‪.‬‬
‫‪ ‬איחוד כל המחלקות שווה לכל הקבוצה‪.‬‬
‫‪𝑥 R = 𝑦 R  xRy ‬‬
‫‪𝑥 R ⋂ 𝑦 R   xRy ‬‬
‫‪ ‬מסקנה‪𝑥 R = 𝑦 R  xRy -‬‬
‫‪ ‬אם מתחילים מנתון היפותטי (שיש בו גרירה) ורוצים להגיע למשהו בלי‬
‫גרירה צריך להכניס משהו שיבטל את הגרירה‪.‬‬
‫‪ ‬ביחס השוויון כל מחלקות השקילות זרות‪.‬‬
‫‪ ‬ביחס המלא כל מחלקות השקילות שוות‪.‬‬
‫‪ ‬קבוצת המנה‪ -‬יהי ‪ R‬יחס שקילות על ‪ A‬קבוצת המנה‪( :‬קבוצה שאיבריה‬
‫הם מחלקות שקילות (קבוצות)) )𝐴(𝑃‪𝐴 = 𝑅 = 𝑥 𝑥 ∈ 𝐴 ‬‬
‫𝑅‬
‫𝑅‬
‫𝐴‬
‫‪ ‬מחלקות השקילות נותנות חלוקה של הקבוצה ‪.A‬‬
‫‪ ‬חלוקה‪ -‬נאמר שאוסף קבוצות ‪(Ai‬אינסוף) הן חלוקה של ‪ A‬אם‪:‬‬
‫‪∀𝑖(𝐴𝑖  𝐴) .1‬‬
‫‪∀𝑖(𝐴𝑖 ≠ ∅) .2‬‬
‫‪𝐴𝑖 = 𝐴 .3‬‬
‫‪ .4‬כל ‪ 2‬קבוצות 𝑗𝐴 ‪ 𝐴𝑖 ,‬מקיימות ∅ = 𝑗𝐴⋂ 𝑖𝐴 ‪𝐴𝑖 = 𝐴𝑗 ‬‬
‫‪ ‬שקילות (יחס שקילות) בין קבוצות ושוויון עצמות‪:‬‬
‫‪ ‬הקבוצה ‪ ℕ‬היא הקבוצה האינסופית הקטנה ביותר‪.‬‬
‫קבוצה סופית‬
‫קבוצה אינסופית‬
‫לכל ‪ nℕ‬כך ש‪A~{1,…,n}-‬‬
‫קיים ‪ nℕ‬כך ש‪A~{1,…,n}-‬‬
‫קיימת ‪ B⊊A‬כך ש ‪B~A‬‬
‫לכל ‪ B⊊A‬מתקיים ‪B~A‬‬
‫קיימת ‪ ƒ:A->A‬חח"ע ולא על‬
‫לכל ‪ ƒ:A->A‬חח"ע היא גם על‬
‫(ולהיפך)‬
‫(ולהיפך)‬
‫קיימת ‪ BA‬כך ש‪B~ℕ -‬‬
‫לכל ‪ BA‬מתקיים ‪B~ℕ‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫עבור קבוצות ‪ A,B‬נגדיר ‪ ARBƒ:A->B‬כך ש‪ ƒ-‬חח"ע ועל‪.‬‬
‫מכיוון שהוכחנו יחס שקילות נוכל להגיד שאם ‪ ARB‬אז ‪ A‬שקולה ל‪B-‬‬
‫ונסמן זאת ב‪.A~B-‬‬
‫יש פונקציה חח"ע ועל בין קבוצות סופיות ‪ ‬יש להן אותו מספר‬
‫איברים‪.‬‬
‫אם ‪ A‬קבוצה סופית המקיימת ‪ |A|= n‬אז‪A R = 𝐵 𝐵 = 𝑛} :‬‬
‫בקבוצות סופיות‪|A| = |B| ARB A~B :‬‬
‫בקבוצות אינסופיות נקרא ל‪ |A| -‬עוצמת הקבוצה‪.‬‬
‫נאמר ש‪ A~B -‬אם ‪ A‬ו‪ B-‬שוות עוצמה‪.‬‬
‫יש לפחות ‪ 2‬עוצמות ∞‪.‬‬
‫עוצמת הטבעיים מסומנת ‪ ℵ0‬ונקראת עוצמה בת מנייה‪.‬‬
‫עוצמת הממשיים מסומנת ‪ ℵ‬או ‪ ℵ1‬ונקראת עוצמת הרצף‪.‬‬
‫‪ℝ~ℕ‬‬
‫‪ℕ~ℚ‬‬
‫‪ℤ~ℕ‬‬
‫‪ℕ ℕ ~ℕ‬‬
‫)‪ℝ= -,~(0,1‬‬
‫)‪ℕ ~(0,1‬‬
‫משפט‪ :‬אם ‪ A⋂B=‬ו‪ C⋂D=-‬ו‪ A~C-‬ו‪ B~D-‬אז ‪( A⋃B~C⋃D‬איחוד‬
‫זר)‬
‫סידרה‪ :‬קבוצה אינסופית שבה יש איבר ראשון ‪ ,a1‬לכל איבר יש עוקב‪,‬‬
‫לכל איבר חוץ מהראשון יש קודם‪.‬‬
‫כל קבוצה שניתן לסדר ככה נקראת מודל של הטבעיים והיא שקולה‬
‫לטבעיים‪.‬‬
‫משפט‪ :‬אם ‪ C~D,B~A‬אז ‪AC~BD‬‬
‫כל מספר טבעי≥‪ 2‬ניתן להצגה כמכפלה של חזקות טבעיות של ראשונים‪.‬‬
‫לכל מספר ממשי קיימת הצגה עשרונית‪:‬‬
‫‪ ‬הצגה עשרונית סופית‬
‫הצגות של מס' רציונליים‬
‫‪ ‬הצגה עשרונית אינסופית‪-:‬מחזורית‬
‫‪-‬לא מחזורית‬
‫הצגות של מס' אי רציונליים‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫לכל מס' ממשי קיימת הצגה עשרונית אינסופית (אם סופית נהפוך‬
‫לאינסופית)‪.‬‬
‫אם שני מס' ממשיים שונים‪ ‬ההצגות העשרוניות שלהם שונות‪( .‬קיים‬
‫מקום בהצגה העשרונית שבו הם שונים‪.‬‬
‫כל מספר ממשי הוא מבחינתנו רצף אינסופי של ספרות ‪9,...,0‬‬
‫משפט‪ :‬לכל קבוצה ‪ A‬מתקיים )‪ |P(P(ℕ()||P(ℕ( ||ℕ|  A~P(A‬וכך‬
‫הלאה‪ .‬כלומר‪ ,‬יש אינסוף עוצמות שונות של אינסוף‪.‬‬
‫משפט‪)ℵ0 <ℵ>ℵ2 >...( P( ℕ ~ℝ :‬‬
‫אם קיימת ‪ ƒ:A->B‬חח"ע ו‪ g:B->A-‬חח"ע אז ‪.A~B‬‬
‫‪ ‬אם קיימת ‪ ƒ:A->B‬חח"ע נכתוב |‪|B|=|A|  |B|≤|A| ⋀ |A|≤|B| |A|≤|B‬‬
‫‪ ‬אם קיימת ‪ g:B->A‬חח"ע נכתוב |‪|B|≤|A‬‬
‫אם ‪ |A|≤|B|  AB‬ולכן אם רוצים להראות ‪ A~B‬מספיק להראות‬
‫‪ ƒ:A->B‬על או לבנות ‪ g:B->A‬חח"ע‪.‬‬
‫חשבון עוצמות‪:‬‬
‫‪ ‬אינסופי*סופי=אינסופי‬
‫‪ ‬אינסופי‪+‬אינסופי = אינסופי‬
‫‪ ‬כל דרגה הופכת את הקודמת לזניחה‪.‬‬
‫סופי‬
‫אינסופי = אינסופי‬
‫‪‬‬
‫סופי‬
‫אינסופי = כל פעם משהו אחר‪=2ℵ ,ℵ=2ℵ0 ,‬רמה אחרת‬
‫‪‬‬