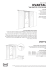פרק 2:

‫פרק ‪ :3‬משפט ההיכרויות ומשפט ‪Kőnig‬‬
‫מבוא לפרק‪:‬‬
‫בפרק זה ניעזר במונחים שפיתחנו עד כה‪ ,‬כדי להוכיח כמה משפטים‪.‬‬
‫נפתח במשפט שלפעמים מכונה "משפט לחיצת הידיים"‪ ,‬בעקבות הניסוח הבא‪:‬‬
‫משפט ‪3.1‬‬
‫בכל קבוצה של ‪ n  6‬אנשים‪ ,‬או שיש ביניהם שלשה אנשים שכל שניים מהם לחצו יד זה לזה ‪ ,‬או שיש‬
‫ביניהם שלשה אנשים שאף שנים מהם לא לחצו ידיים זה לזה ‪.‬‬
‫הערות‪:‬‬
‫‪ .1‬ייתכן ושתי האופציות מתקיימות בו זמנית‪ -‬הביאי דוגמה למצב כזה!‬
‫‪ .2‬ניסוחים חלופיים‪:‬‬
‫א‪ .‬בכל מפגש בין לפחות ‪ 6‬אנשים‪ ,‬לפחות אחת מבין ‪ 2‬האופציות הבאות מתקיימות ‪:‬‬
‫או שיש ביניהם ‪ 3‬אנשים‪ ,‬שכולם מכירים אחד את השני ‪ ,‬או שיש ביניהם ‪ 3‬אנשים ‪,‬כך שאף אחד מבין‬
‫השלושה לא מכיר אף אחד אחר בשלשה זו‪.‬‬
‫ניסוח א' הוא אותו ניסוח כפי שהבאנו אותו בפרק מבוא‪.‬‬
‫ב‪ .‬בכל גרף ‪ G‬מסדר לפחות ‪ ,6‬או ‪ G‬או ‪ G‬מכיל משולש‪.‬‬
‫במשולש בגרף‪ ,‬הכוונה (כצפוי?!) לשלשה קודקודים‪ ,‬שכל אחד מחובר לשניים האחרים על ידי צלע‪-‬‬
‫צורה זו של גרף מוכרת לכן כבר מפרק ‪ 2‬כ‪ C 3 -‬או ‪. K 3‬‬
‫ג‪ .‬בכל צבעיה של צלעות הגרף ‪ K 6‬בשני צבעים‪ ,‬קיים לפחות משולש אחד חד גוני ‪.‬‬
‫פרק ‪ - 3‬עמוד ‪1‬‬
‫תרגיל‪:‬‬
‫הוכיחי שקילות בין הניסוחים השונים!‬
‫הדרכה‪ :‬לשם כך‪ ,‬עלייך להראות‬
‫‪ .1‬שהניסוח במשפט הוא שקול לכל אחד מהגירסאות א' ו‪-‬ג'‪.‬‬
‫‪ .2‬שגירסה ב' ‪ ,‬שבה מדובר גם על גרפים מסדרים יותר גבוהים מ‪ ,6-‬גוררת אחריה את (אחת‬
‫מ)הגירסאות האחרות‪ ,‬וכן‪,‬‬
‫‪ .3‬אם בכל צבעיה של צלעות הגרף ‪ K 6‬בשני צבעים‪ ,‬קיים לפחות משולש אחד חד גוני‪ ,‬אזי‬
‫בכל גרף ‪ G‬מסדר לפחות ‪ ,6‬או ‪ G‬או ‪ G‬מכיל משולש‪.‬‬
‫הוכחת משפט ‪:3.1‬‬
‫נוכיח את גירסה ג'‪.‬‬
‫ראי גם המאמר מעשה בשש נקודות על ידי פרופסור עמוס אלטשולר המופיע באתר‬
‫תמצאי מספר וריאציות ויישומים שונים של המשפט ‪ .‬ההוכחה הבאה שוחזרה משם ‪.‬‬
‫אלף אפס שם‬
‫נתבונן ב‪ K 6 -‬שצלעותיו צבועות בשני צבעים (שחור וירוק )‪ ,‬ויהי ‪ x‬קדקוד בגרף זה ‪.‬מן הקדקוד ‪ x‬יוצאות‬
‫בדיוק חמש צלעות ‪ -‬אחת לכל אחד מחמשת הקדקודים האחרים ‪ .‬לפחות שלוש מתוך חמש צלעות אלה‬
‫צבועות באותו צבע ‪ ,‬שחור או ירוק (אילולא כן ‪ ,‬מספר הצלעות השחורות היוצאות מ ‪-x‬אינו עולה על ‪,2‬‬
‫ומספר הצלעות הירוקות היוצאות מ ‪-x‬אף הוא אינו עולה על ‪ ,2‬אך זה מסתכם בלכל היותר ארבע צלעות‬
‫הצבועות בשחור או בירוק ‪ ,‬בעוד שמספר הצלעות היוצאות מ ‪-x‬הוא חמש!)‬
‫בלי הגבלת הכלליות נוכל להניח אפוא שיוצאות מ ‪-x‬לפחות שלוש צלעות ירוקות ‪.‬נתבונן בשלוש צלעות‬
‫אלה ‪:‬‬
‫נסמנן ‪. xc,xb,xa‬עתה נתבונן בשלוש הצלעות ‪ . bc,ac,ab‬אם לפחות אחת מהן ירוקה (למשל ‪ (ab ,‬אזי‬
‫לפנינו משולש ירוק (הוא המשולש שקדקודיו ‪ .( x,a,b‬אם אף אחת מה ן לא ירוקה ‪ ,‬אזי שלושתן שחורות ‪,‬‬
‫ולפנינו משולש שחור (שקדקודיו ‪ .( c,b,a‬עד כאן הוכחת המשפט‪■ .‬‬
‫‪a‬‬
‫‪c‬‬
‫‪b‬‬
‫פרק ‪ - 3‬עמוד ‪2‬‬
‫שימי לב‪ :‬הביטוי "בלי הגבלת הכלליות"‪ ,‬פירושו‪ :‬מבין כמה אופציות‪ ,‬מותר לי להניח‬
‫שדבר מסוים קרה‪ ,‬שאם לא כן‪ ,‬ומשהו אחר קרה‪ ,‬השיקול הוא דומה לחלוטין‪.‬‬
‫תרגיל‪:‬‬
‫הוכיחי כי לא ניתן להחליף את המספר ‪ 6‬במשפט על ידי ‪ !5‬שאלה זו מופיעה בתרגיל ‪.3‬‬
‫מושגים של מרחק בגרף‪:‬‬
‫נוכחנו לראות שהמושג של מרחק אוקלידי אינו תופס מקום בנושא תורת הגרפים‪ .‬בכל זאת ‪ ,‬יש‬
‫משמעות למונח של "מרחק בין שני קודקודים בגרף"‪ ,‬והיא קשורה לאורך מסילה ביניהם‪ .‬הנה‬
‫ההגדרה המדויקת‪:‬‬
‫הגדרה‪:‬‬
‫‪‬‬
‫המרחק בין ‪ 2‬נקודות ‪ u, v‬בגרף ‪ G  V , E ‬מסומן על ידי ) ‪( d G (u , v‬או )‪) d (u, v‬‬
‫והוגדר להיות‪:‬‬
‫‪ ‬אורך המסילה הקצרה ביותר בין ‪ u‬ל ‪ v‬אם קיימת מסילה ביניהם ‪ ,‬ו‪-‬‬
‫‪  ‬אם ‪ u, v‬במרכיבי קשירות שונים ‪.‬‬
‫דוגמה‪:‬‬
‫‪‬‬
‫בגרף ‪ , d ( A, H )  5 ,2.1‬שכן המסילה הקצרה ביותר בין ‪ A‬ל‪ H-‬היא המסילה ‪,ABCFGH‬‬
‫‪‬‬
‫שהיא יותר קצרה מהמסילה ‪ ABCEDCFGH‬באורך ‪.8‬‬
‫בגרף ‪ d ( P, J )   ,2.2‬שכן הנקודות ‪,P‬ו‪ J-‬נמצאות במרכיבי קשירות שונים ‪.‬‬
‫מסילה בין ‪ u, v‬בעלת אורך הקצר ביותר נקראת מסילה גיאודזית‪.‬‬
‫כך נוכל להגדיר את המרחק בין ‪ 2‬קודקודים להיות אורך מסילה גיאודזית ביניהם‪.‬‬
‫פרק ‪ - 3‬עמוד ‪3‬‬
‫דוגמאות‪:‬‬
‫‪‬‬
‫בגרף ‪ ,2.1‬המסילה ‪ ABCFGH‬היא מסילה גיאודזית בין ‪ A‬ל‪ , H-‬בעוד שהמסילה‬
‫‪ ABCEDCFGH‬אינה גיאודזית‪.‬‬
‫‪‬‬
‫נחזור שוב לקובייה התלת מימדית ‪:‬‬
‫נחפש מסילות בין הקודקודים ‪.1,7‬‬
‫מסילות בין ‪ 2‬הקודקודים הללו הן‪:‬‬
‫‪ .  1,2,6,7  ,  1,4,8,7  ,  1,4,3,2,6,7  ,  1,2,6,5,8,7 ‬ויש עוד‪....‬‬
‫בדיקה קלה מראה שרק המסילות ‪  1,4,8,7 ‬ו ‪  1,5,8,7  ,  1,5,6,7  ,  1,2,6,7 ‬הן מסילות‬
‫גיאודזיות ‪,‬ולכן ‪. d (1,7)  3‬‬
‫מסתבר שההגדרה הזו של מרחק "מתקבלת על הדעת"‪ ,‬שכן יש לו תכונות דומות למרחק‬
‫האוקלידי‪ ,‬כפי שמשפט ‪ 3.2‬מראה‪.‬‬
‫פרק ‪ - 3‬עמוד ‪4‬‬
‫משפט ‪3.2‬‬
‫הפונקציה ) ‪ d G (u , v‬היא מטריקה‪ .‬כלומר‪:‬‬
‫א‪( .‬סימטריות)‪ :‬לכל שני קודקודים ‪d G (u, v)  d G (v, u ) , u, v  V‬‬
‫ב‪ .‬לכל שני קודקודים ‪, d G (u, v)  0 , u, v  V‬ובנוסף ‪. u  v  d G (u, v)  0‬‬
‫ג‪( .‬אי שיוויון המשולש )‪ :‬לכל ‪ u, v, w V‬מתקיים‪. d G (u, w)  d G (u, v)  d G (v, w) :‬‬
‫הוכחת משפט ‪3.2‬‬
‫הוכחות סעיפים א'ב' נובעות מההגדרה ומהעובדה שכל מסילה מ ‪ u‬ל ‪ v‬ניתנת להיפוך כדי ליצור מסילה‬
‫מ ‪ v‬ל‪. u‬‬
‫הוכחת ג' ‪:‬‬
‫מקרה ‪ . d G (u, w)   :1‬במקרה זה‪ u, w ,‬נמצאים באותו מרכיב קשירות ‪.‬‬
‫‪‬‬
‫תחילה נניח שגם ‪ v‬נמצא באותו מרכיב קשירות ‪.‬‬
‫תהא ‪ p uv‬מסילה גיאודזית מ ‪ u‬ל ‪ , v‬ותהא ‪ p vw‬מסילה גיאודזית מ ‪ v‬ל ‪ , w‬כמודגם באיור‪.‬‬
‫אזי צירוף המסילות ‪ p uv‬ולאחר מכן ‪ p vw‬היא מסילה (שנסמנה ‪ ) p uv p vw‬מ ‪ u‬ל ‪ , w‬ושימו לב שהיא‬
‫לא בהכרח גיאודזית (כי אולי קיימת מסילה קצרה יותר מ ‪ u‬ל ‪ .) w‬לכן ‪:‬‬
‫פרק ‪ - 3‬עמוד ‪5‬‬
‫(א) אורך המסילה ‪ p uv p vw‬גדול או שווה ל )‪. d G (u , w‬‬
‫(ב) אך אורך מסילה ‪ p uv p vw‬הוא סכום אורכי ‪ p uv‬ו ‪( , p vw‬שזה שווה )‪. (d G (u, v)  d G (v, w‬‬
‫כך מ(א) ומ(ב) נקבל את הדרוש‪. d G (u, w)  d G (u, v)  d G (v, w) :‬‬
‫‪‬‬
‫נניח ש ‪ v‬נמצא במרכיב קשירות אחר‪.‬‬
‫זה אומר ששני המרחקים )‪ d G (u, v), d G (v, w‬הם אינסופיים! בדקי שאז אי השיוויון מתקיים‬
‫אוטומטית‪.‬‬
‫מקרה ‪. d G (u, w)   :2‬‬
‫ש ‪ u, w‬במרכיבי קשירות שונים ‪.‬‬
‫על פי הגדרה‪ ,‬אם ‪ , d G (u, w)  ‬זה אומר ֶש‬
‫‪‬‬
‫אם ‪ v‬לא נמצא באף אחד מהמרכיבים האלה‪ ,‬המצב המצטייר הוא כמו באיור‪.‬‬
‫ולכן גם ‪ , d G (u, v)  d G (v, w)  ‬ואי השיוויון מתקיים ‪.‬‬
‫•‪u‬‬
‫•‪w‬‬
‫•‪v‬‬
‫פרק ‪ - 3‬עמוד ‪6‬‬
‫‪‬‬
‫אם ‪ v‬אכן נמצא באחד מהמרכיבים האלה‪ ,‬נניח בלי הגבלת הכלליות ‪ ,‬כי הוא באותו מרכיב כמו‬
‫‪ , u‬אזי ‪ , d G (u, v)  ‬אך ‪ , d G (v, w)  ‬כי ‪ v, w‬במרכיבי קשירות שונים ‪ ,‬כך ששוב אי‬
‫השיוויון מתקיים ‪.‬‬
‫•‪w‬‬
‫•‪U‬‬
‫•‪v‬‬
‫בכך הוכחנו את המשפט‪.‬‬
‫הקוטר‪:‬‬
‫בצורה אנלוגית להגדרת הקוטר במעגל‪ ,‬שהוא המרחק המקסימלי בין ‪ 2‬נקודות בו‪ ,‬ניתן להגדיר‬
‫קוטר של גרף‪:‬‬
‫הקוטר של גרף מודד את המרחק המקסימלי בין שתי נקודות כל שהן בגרף‪.‬‬
‫דוגמה‪:‬‬
‫‪‬‬
‫הקוטר של גרף ‪ 2.1‬שווה ‪ ,5‬כי המרחק המסימלי בין ‪ 2‬נקודות בגרף וא זה בין ‪,A‬ו‪,H-‬‬
‫שהוא ‪ ,5‬כפי שכבר גילינו‪.‬‬
‫הקוטר של גרף ‪( ,2.2‬או של כל גרף לא קשיר) הוא ‪. ‬‬
‫פרק ‪ - 3‬עמוד ‪7‬‬
‫הגדרה‪:‬‬
‫יהא ‪ G  V , E ‬גרף‪ .‬הקוטר של ‪ G‬מסומן על ידי ) ‪ d (G‬והוא אורך המסילה הגיאודזית הארוכה‬
‫ביותר‬
‫ב ‪ . G‬במילים אחרות‪. d (G)  max{ d G (u, v) | u, v  V } ,‬‬
‫דוגמאות נוספות‪:‬‬
‫‪‬‬
‫באיור לפניך גרף פשוט מסדר ‪ ,7‬ולידו טבלת המרחקים (המכונה שם בשם‬
‫”‪ ("Shimbel distance‬מכל קודקוד למשנהו ‪ .‬מהטבלה רואים שקוטר הגרף שווה ‪.4‬‬
‫שימו לב לכך ששתי התכונות הראשונות של מטריקה משתקפות מהטבלה‪ ,‬דהיינו לתכונות‬
‫המרחק‬
‫ה‪ 0-‬אך ורק בין נקודה לעצמו‪( ,‬תכונה א') וכן סימטריות של הטבלה ביחס לאלכסון הראשי‬
‫(תכונה ב')‪.‬‬
‫פרק ‪ - 3‬עמוד ‪8‬‬
‫‪‬‬
‫עבור גרף בעל יותר ממרכיב קשירות אחד‪,‬הקוטר הוא אינסופי ‪.‬‬
‫למעשה‪ ,‬לרוב‪ ,‬הקוטר יחושב רק עבור גרפים קשירים‪.‬‬
‫‪‬‬
‫‪d (C 7 )  4‬‬
‫‪‬‬
‫לפנייך גרף הנקרא "גרף פטרסן"‪,‬על שם ‪, Julius Petersen‬מתמטיקאי על שמו נקרא הגרף ‪.‬‬
‫בגרף זה שנעשה בה שימוש רב כדוגמה נגדית להפרכת השערות רבות בתורת הגרפים‪ .‬קל‬
‫לראות שגרף פטרסן הוא גרף רגולרי מערכיות ‪ 3‬ומסדר ‪ .10‬קוטרו הוא ‪.2‬‬
‫מעגלים בגרף‪:‬‬
‫נפנה עתה לאפיון של גרפים זוגיים (ראי פרק ‪ )2‬על ידי אי קיום של מעגלים מאורך מסוים‪:‬‬
‫המשפט הבא מכונה משפט ‪ Kőnig‬על שם המתמטיקאי ההונגרי בשם ‪: Dénes Kőnig‬‬
‫ראשית כל‪ ,‬נביא טענת עזר‪:‬‬
‫טענת עזר‪:‬‬
‫‪ G‬הוא גרף זוגי ‪ ‬ניתן לצבוע את קבוצת קודקודיו‪ ,‬כל קודקוד או בכחול או באדום ‪ ,‬כך שאין שני‬
‫שכנים בגרף צבועים באותו הצבע ‪.‬‬
‫פרק ‪ - 3‬עמוד ‪9‬‬
‫גרפים שניתן לצבוע אותם בשני צבעים בצורה זו נקראים גרפים בעלי מספר כרומטי ‪.2‬‬
‫הוכחת טענת העזר‪:‬‬
‫‪:‬‬
‫יהא ‪ G‬גרף זוגי‪ ,‬עם חלוקה ‪ . V  V1  V2‬צביעה של כל קודקודי ‪ V1‬באדום וכל קודקודי ‪ V2‬בכחול‬
‫היא צביעה כנדרש‪.‬‬
‫‪:‬‬
‫נניח שכל קודקודי הגרף צבועים או בכחול או באדום ‪ ,‬בצורה שאין שני שכנים בגרף צבועים באותו‬
‫הצבע‪ .‬נסמן את קבוצת הקודקודים האדומים על ידי ‪ , V1‬ואת קבוצת הקודקודים הכחולים על ידי ‪. V2‬‬
‫בדקי שהחלוקה ‪ V  V1  V2‬היא חלוקה המתאימה לזו של גרף זוגי‪.‬‬
‫משפט ‪-3.3‬משפט ‪Kőnig‬‬
‫גרף ‪ G‬הוא גרף זוגי ‪ ‬כל מעגליו בעלי אורך זוגי ‪.‬‬
‫דוגמאות‪:‬‬
‫‪‬‬
‫יישום של משפט קוניג מראה מיד שהגרף הימני הוא זוגי – הרי אין בו מעגלים! (מצד שני‪,‬‬
‫השתכנעי –מהי החלוקה?)‪ ,‬בעוד שהגרף ‪ C 7‬אינו זוגי‪.‬‬
‫הוכחת משפט ‪:3.3‬‬
‫‪:‬‬
‫פרק ‪ - 3‬עמוד ‪10‬‬
‫יהא ‪ G‬הוא גרף זוגי‪ ,‬עם חלוקה ‪ , V  V1  V2‬ויהי ‪  v1 , v2 ,.., vn , v1 ‬מעגל בו בעל אורך ‪, n‬‬
‫כאשר‪ ,‬בלי הגבלת הכלליות ‪ ,‬נניח ש ‪ . v1  V1‬עלינו להראות כי ‪ n‬מספר זוגי‪.‬‬
‫נביט במעגל ‪.  v1 , v2 ,.., vn , v1 ‬היות ו ‪ v 2 -‬שכן של ‪ , v1  V1‬ו‪ G -‬גרף זוגי‪ ,‬אנו מסיקים ש‪v2 V2 -‬‬
‫‪ .‬כמו כן‪ , v3  V1 ,‬בהיותו שכן של ‪ . v 2‬ממשיכים בדרך זו לאורך קודקודי המעגל ‪ ,‬אנו מסיקים‬
‫שקודקודים עוקבים שייכים לסירוגין לקבוצות ‪ V1‬ו‪ . V2 -‬היות ו"אחרי" ‪ n‬צלעות "חזרנו" לקודקוד‬
‫‪ , v1  V1‬אנו מסיקים כי ‪ n‬חייב להיות מספר זוגי‪.‬‬
‫‪:‬‬
‫נניח כי כל מעגלי ‪ G‬בעלי אורך זוגי‪ .‬עלינו להוכיח כי ‪ G‬הוא גרף זוגי‪ ,‬זאת אומרת שניתן לחלק את‬
‫קבוצת קודקודיו לחלוקה ‪ V  V1  V2‬מתאימה‪ ,‬כך שלכל הצלעות ב ‪ G‬קודקוד אחד מכל תת‬
‫קבוצה ‪.‬‬
‫‪‬‬
‫תחילה נניח כי ‪ G‬גרף קשיר‪.‬‬
‫לפי טענת העזר‪ ,‬מספיק להראות שניתן לצבוע את קודקודי ‪ G‬בצורה "חוקית" בשני צבעים‪.‬‬
‫תהליך זה נחלק לשני חלקים ‪:‬‬
‫א‪ .‬נכריז על כללי צביעת קודקודי ‪G‬‬
‫ב‪ .‬נוכיח שבצביעה זו‪ ,‬אין שני שכנים צבועים באותו הצבע ‪.‬‬
‫א‪ .‬כללי צביעת הקודקודים‬
‫נבחר קודקוד ‪ u V‬כל שהוא‪ ,‬ונצבע אותו בכחול‪ .‬לכל קודקוד אחר‪ , v  V ,‬תהא ‪ p uv‬מסילה כל‬
‫שהיא מ ‪ u‬ל ‪ . v‬נצבע את ‪ v‬בצורה הבאה‪:‬‬
‫‪ ‬נצבע אותו בכחול אם אורך המסילה ‪ p uv‬הוא מספר זוגי‪.‬‬
‫‪ ‬נצבע אותו באדום אם אורך המסילה ‪ p uv‬הוא מספר אי זוגי‪.‬‬
‫נשים לב שהצביעה לא תלויה במסילה הספציפית שבחרנו מ ‪ u‬ל ‪ . v‬שכן‪ ,‬תהא ‪ q uv‬מסילה אחרת‬
‫פרק ‪ - 3‬עמוד ‪11‬‬
‫מ ‪ u‬ל ‪ . v‬צירוף שתי המסילות הללו מהווה מעגל ב ‪ , G‬שאורכו סכום אורכי ‪ 2‬המסילות ‪ p uv‬ו ‪. q uv‬‬
‫היות ועל פי הנחה‪ ,‬אורך המעגל הוא זוגי ‪ ,‬חייב להיות שאורכי ‪ 2‬המסילות בעלי אותה זוגיות ‪ ,‬ולכן‬
‫שתי מסילות אלו היו נותנים אותו כלל צביעה ‪.‬‬
‫ב‪ .‬בצביעה זו‪ ,‬אין שני שכנים צבועים באותו הצבע ‪.‬‬
‫הוכחה‪ :‬תרגיל! (ראי תרגיל ‪)3‬‬
‫‪‬‬
‫נניח ש ‪ G‬אינו קשיר‪ .‬יהיו ‪ G1 , G 2 ,.....G k‬מרכיבי הקשירות של ‪ . G‬נסמן ‪ ,‬לכל ‪ , 1  i  k‬את‬
‫קבוצת קודקודי ‪ Gi‬על ידי ‪. V i‬‬
‫אם כן‪ ,‬כל אחד מהגרפים ‪ G1 , G 2 ,.....G k‬מהווה (תת) גרף קשיר! יתר על כן‪ ,‬מאחר וכל מעגלי ‪G‬‬
‫בעלי אורך זוגי‪ ,‬גם כל המעגלים בכל אחד מהגרפים הקשירים ‪ G1 , G 2 ,.....G k‬הם בעלי אורך זוגי‪.‬‬
‫לכן על פי נכונות המשפט עבור גרפים קשירים‪ ,‬נקבל שכל אחד מתת הגרפים ‪ G1 , G 2 ,.....G k‬הוא‬
‫גרף זוגי‪ .‬על פי הגדרה‪ ,‬זה אומר שלכל ‪ 1  i  k‬ניתן לחלק את ‪ Vi‬לחלוקה ‪. V i  V1i  V2i‬‬
‫‪k‬‬
‫‪k‬‬
‫‪i 1‬‬
‫‪i 1‬‬
‫כעת‪ ,‬נסמן ‪ , V1   V1i‬ו‪ . V2   V2i -‬החלוקה ‪ V  V1  V2‬נותנת חלוקה מתאימה של ‪, V‬‬
‫ולכן ‪ G‬גרף זוגי ■‪.‬‬
‫פרק ‪ - 3‬עמוד ‪12‬‬
‫דוגמה‪:‬‬
‫ראי למשל‪ ,‬באיור הבא‪- ,‬שם רואים שכל הצלעות בגרף מחברות בין אברי‬
‫‪ V1‬לאברי ‪. V2‬‬
‫} ‪V12  {C1 , C 2 , C3‬‬
‫} ‪V11  { A1 , A2 , A3 , A4 , A5‬‬
‫} ‪V2 2  {D1 , D2‬‬
‫} ‪V21  {B1 , B2, B3 , B4‬‬
‫‪V 2  V12  V22‬‬
‫‪V 1  V11  V21‬‬
‫‪G  G1  G2‬‬
‫‪V  V1  V2‬‬
‫סיכום מונחים מפרק ‪:3‬‬
‫‪‬‬
‫משפט לחיצת הידיים‬
‫‪‬‬
‫מרחק בגרף‬
‫‪‬‬
‫מרחק היא מטריקה‬
‫‪‬‬
‫קוטר‬
‫‪‬‬
‫איפיון גרף זוגי על ידי אורכי המעגלים בו‬
‫פרק ‪ - 3‬עמוד ‪13‬‬