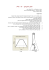מדידת מהירות הקול על פי הפרש – גלי קול מופע

‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫גלי קול – מדידת מהירות הקול על פי הפרש‬
‫מופע‬
‫‪Data Studio‬‬
‫שם קובץ הניסוי‪:‬‬
‫‪Sound Waves. ds‬‬
‫חוברת מס' ‪3‬‬
‫כרך‪ :‬גלים ואופטיקה‬
‫מאת‪ :‬משה גלבמן‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫גלי קול – מדידת מהירות הקול על פי הפרש‬
‫מופע‬
‫‪Data Studio‬‬
‫המטרה‬
‫נחקור את תלות זווית המופע במרחק ונמדוד את מהירות גלי הקול באוויר על פי הפרשי מופע‪.‬‬
‫השיטה‬
‫מתנד שמפיק אות שמע נקי )סינוסואידה( בתדרים שונים מפעיל רמקול‪ .‬מיקרופון )חישן קול(‬
‫קולט את גלי הקול במרחקים שונים מהרמקול‪ .‬מודדים את הפרש המופע בין המתח על הרמקול‬
‫והמתח שנקלט במיקרופון ומחשבים על פיו את מהירות התפשטות הקול‪.‬‬
‫תיאוריה‬
‫גלי הקול הם גלים אורכיים בחומר‪ .‬מתפשטים בחומר‪ :‬במוצקים בנוזלים ובגזים‪ .‬חלקיקי‬
‫החומר מעבירים את התנודות‪.‬‬
‫גלים אורכיים קיימים בתחום תדירויות רחב מאוד‪.‬‬
‫גלי הקול מאופיינים על‪-‬ידי תחום התדרים שאוזן האדם רגישה להם וגורמת תחושת שמע‪.‬‬
‫תחום התדירויות של גלי הקול – תחום השמע – הוא בין של ‪ 20‬תנודות‪/‬שנ' ל ‪ 20,000‬תנודות‪/‬שנ'‪.‬‬
‫גלים אורכיים קיימים גם בתדירויות תת‪-‬שמע ) ‪ ( infrasonic waves‬ועל‪-‬שמע‬
‫) ‪.( ultrasonic waves‬‬
‫רעידת אדמה היא דוגמה לגלים אורכיים בתדר תת‪-‬שמע‪.‬‬
‫תדירויות גבוהות מאוד של גלים אורכיים ) ‪ ( ultrasonic wave‬ניתן ליצור בגביש של קוורץ‪ .‬שדה‬
‫חשמלי מתחלף )מתנודד( גורם לתנודות של מולקולות הגביש‪ ,‬כאשר תדירות השדה החשמלי‬
‫שווה לאחת מהתדירויות העצמיות של הגביש )מצב תהודה(‪.‬‬
‫ניתן ליצור גלים אורכיים באוויר גם בתדר גבוה של כ‪ . 6 ⋅ 10 8 Hz -‬בתדר זה התנודות יוצרות‬
‫באוויר גלים עם אורך גל של כ ‪ , 5 ⋅ 10 −5 cm‬סדר גודל של אורך גלי האור!‬
‫בגלים אורכיים בתדירות על‪-‬שמע עושים שימוש רב ומגוון‪.‬‬
‫למשל‪:‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪44‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫במעבדה ‪ -‬עוקבים באמצעות גלי על‪-‬שמע אחר תנועה של גופים‪.‬‬
‫ברפואה ‪ -‬משתמשים בגלי על‪-‬שמע לאבחון )צילום דיגיטלי( וריפוי )ריסוק אבני כליה למשל(‪.‬‬
‫להלן נצטמצם לתדירויות שמע‪ ,‬ז"א לגלי קול‪.‬‬
‫רמקול שמוזן במתח מחולל אותות ) ‪ ( Signal Generator‬ממיר את תנודות המתח לגלי קול‪.‬‬
‫נבחר במתח שהתלות שלו בזמן היא סינוסית )פונקצית סינוס(‪.‬‬
‫התרשים הסכמתי למטה )תמונה ‪ (1‬מתאר מבנה של רמקול‪.‬‬
‫רמקול מכיל סליל חופשי לנוע סביב ליבת מגנט‪ .‬קצה אחד של הסליל מחובר לממברנה עדינה‪.‬‬
‫כאשר זורם זרם דרך הסליל פועל עליו כוח אלקטרומגטי שגורם למשיכה או דחיפה )לפי כיוון‬
‫הזרם( של הסליל‪ .‬תנודות הסליל מרעידות את הממברנה )הן התמרה מכנית של תנודות המתח(‬
‫ויוצרות גלי קול‪.‬‬
‫תמונה ‪ : 1‬תרשים סכמתי של רמקול‬
‫גלי הקול נקלטים במיקרופון קיבולי‪ .‬המיקרופון קולט את גלי הקול וממיר אותם לתנודות מתח‬
‫ניתנות למדידה‪ .‬להלן תרשים סכמתי למעגל של מיקרופון קיבולי )תמונה ‪.(2‬‬
‫תמונה ‪ :2‬תרשים סכמתי של מיקרופון קבל‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪45‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫קבל מחובר דרך נגד למקור מתח קבוע‪ .‬לוח אחד של הקבל עשוי מתכת דקה וגמישה )ממברנה(‬
‫שחשופה לגלי הקול‪ .‬גלי הקול מרעידים את הממברנה וגורמים לשינוי המרחק בין לוחות הקבל‬
‫ולכן לקיבול של הקבל‪ .‬כך נוצר במעגל זרם התלוי בזמן שתואם את השינוי בקיבול‪ .‬המתח שנופל‬
‫על הנגד‪ ,‬מתמיר לכן את תנודות הקול‪.‬‬
‫כיצד נוצרים גלי הקול?‬
‫כאמור‪ ,‬גלי קול מתקיימים רק בחומר‪ .‬כאשר מופעל כוח על שטח חתך ‪ A‬בזמן קצר ‪ Δt‬בתוך‬
‫רובד של החומר‪ ,‬תחול תזוזה של הרובד בכיוון שהכוח פועל‪.‬‬
‫על פי החוק השני של ניוטון – המתקף שווה לשינוי בתנע‪ .‬כיוון ההפרעה )שינוי במהירות‬
‫החלקיקים בסביבה( הוא כיוון התקדמותה )תמונה ‪.(3‬‬
‫תמונה ‪ :3‬גלי קול המתפשטים בצינור‪.‬‬
‫בתמונה ‪ 3‬התנודות נוצרות בגין תנועת הבוכנה )הלוך וחזור( בקצה הצינור‪ .‬הקווים המקבילים‬
‫מסמנים רבדים של החומר‪ ,‬למשל אוויר ‪ -‬קוים צפופים מסמנים לחץ גבוה ובמקומות שהמרווח‬
‫בין הקווים גדל‪ ,‬הלחץ נמוך‪ .‬למקומות שהמרווח בין הקווים קבוע‪ ,‬הגל עדיין לא הגיע‪.‬‬
‫סדרת התמונות בתרשים )תמונה ‪ (3‬מתארות את מצב התנודות בצינור‪ ,‬בזמנים שונים )הזמן עולה‬
‫מלמעלה למטה(‪.‬‬
‫חישוב מהירות גלי הקול‬
‫מהירות גלי הקול באוויר‬
‫ניוטון בחיבורו "עקרונות מתמטיים של הפילוסופיה של הטבע" בשנה ‪ ) 1687‬ספר שני‪ ,‬פרק‬
‫‪ , ( XVIII‬חישב את מהירות ההתפשטות של מתקף בסביבה אלסטית‪.‬‬
‫הפיתוח המובא להלן הוא גרסה מודרנית של החישוב הזה‪:‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪46‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫נתאר לעצמנו‪ ,‬גלי קול מתפשטים באוויר‪ :‬ז"א‪ ,‬שכבות של צפיפות‪-‬יתר וצפיפות‪-‬חסר מתקדמות‬
‫מהמקור החוצה‪) .‬תרשים א'(‪.‬‬
‫תרשים א'‬
‫למעשה‪ ,‬השינוי בצפיפות האוויר )מסה ליחידת נפח( הוא שנע מהמקור )במרכז( החוצה‪.‬‬
‫זה קורה‪ ,‬בגלל המתקף ‪ . f ⋅ dt‬במקום שפועל המתקף נוצר העתק קטן של אלמנט מסה ‪dm‬‬
‫וגורם לה לנוע במהירות ‪: v‬‬
‫‪(1).............. f ⋅ dt = dm ⋅ v‬‬
‫התרשים )תרשים ב'( מתאר "צינור" חומר ששטח החתך שלו ‪ A‬לפני ואחרי הפעלת המתקף‪.‬‬
‫תרשים ב'‬
‫‪ p‬הוא הלחץ העודף שנגרם בגלל פעולת הכוח ‪) f‬בכיוון מאונך(‪.‬‬
‫לכן‪:‬‬
‫‪f‬‬
‫‪A‬‬
‫=‬
‫‪p‬‬
‫או‪:‬‬
‫‪f = p⋅ A‬‬
‫‪.1‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪47‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫כידוע בתהליכים שבהם מתרחשת דפורמציה אלסטית ‪ ,‬הדפורמציה האלסטית היחסית‬
‫פרופורציונית לכוח על יחידת השטח )ללחץ(‪.‬‬
‫חוק הוק‪ , f = − kΔx :‬למשל הוא מקרה פרטי של הטענה הכללית הזאת‪.‬‬
‫)הדפורמציה היחסית‬
‫‪ε‬‬
‫‪dV‬‬
‫‪dl‬‬
‫‪ ,‬של הנפח היא‪:‬‬
‫של האורך היא‬
‫‪V‬‬
‫‪l‬‬
‫‪ ,‬של צפיפות היא‪:‬‬
‫‪dρ‬‬
‫‪ρ‬‬
‫וכו'(‬
‫למשל בדחיסה )דפורמציה של הנפח(‪ .‬אם שינוי לחץ בגודל ‪ p‬גורם לדפורמציה יחסית ‪ , ε‬אזי‪:‬‬
‫‪p = − B⋅ ε‬‬
‫‪ε = dV‬‬
‫‪V‬‬
‫‪ p‬הוא השינוי בלחץ )מסומן לעיתים ב ‪ ( dP‬שנגרם בגלל המתקף‪.‬‬
‫‪ B‬הוא קבוע הפרופורציה ונקרא "מודול יאנג"‪.‬‬
‫)מכאן שמודול יאנג הוא הלחץ שגורם לדפורמציה יחסית של הנפח בגודל ‪.( ε = 1‬‬
‫הערה‪ :‬הכנסנו סימן מינוס לפני ‪ B‬כי שינו חיובי בלחץ ) ‪ ( p > 0‬גורם לשינוי שלילי בנפח )דחיסה(‬
‫כאשר מציבים ‪ p ⋅ A‬עבור ‪ , f‬ו ‪ B ⋅ ε‬עבור ‪ , p‬מקבלים עבור המתקף‪:‬‬
‫‪(2)................ f ⋅ dt = − B⋅ ε⋅ A⋅ dt‬‬
‫‪.2‬‬
‫‪ A⋅ dx‬הוא השינוי בנפח האוויר )תרשים ב'( כאשר ‪ dx‬שווה להעתקה של שכבות האוויר )שהיא‬
‫למעשה העתקה של מסה ‪( dm‬‬
‫נרשום את ‪ dm‬כך‪:‬‬
‫‪dm = A ⋅ dx ⋅ dρ‬‬
‫כאשר ‪ - dρ‬הוא השינוי בצפיפות האוויר בגלל הדפורמציה היחסית של הנפח‪.‬‬
‫היות ומתקיים‪:‬‬
‫‪dρ‬‬
‫‪dV‬‬
‫‪=−‬‬
‫‪ρ‬‬
‫‪V‬‬
‫לכן‪:‬‬
‫‪dρ‬‬
‫‪ρ‬‬
‫‪dρ = − ε⋅ ρ‬‬
‫‪ε=−‬‬
‫נציב ונקבל‪:‬‬
‫‪dm = − A⋅ dx⋅ ε⋅ ρ‬‬
‫‪.3‬‬
‫אם ‪ v‬יסמן את מהירות ההתפשטות של הדפורמציה‪) ,‬את מהירות התקדמות המתקף(‪.‬‬
‫נקבל‪:‬‬
‫‪dx = v ⋅ dt‬‬
‫לכן‪ ,‬כשנציב בנוסחה ל ‪ , dm‬נקבל ‪:‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪48‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫‪(3)................. dm = − A⋅ v⋅ ε⋅ ρ⋅ dt‬‬
‫‪.4‬‬
‫נציב את )‪ (2‬ואת )‪ (3‬ב – )‪ (1‬ונקבל‪:‬‬
‫‪B ⋅ ε ⋅ A ⋅ dt = A ⋅ v 2 ⋅ ε ⋅ ρ ⋅ dt‬‬
‫נצמצם ונקבל‪:‬‬
‫‪B‬‬
‫‪ρ‬‬
‫=‪v‬‬
‫‪.5‬‬
‫תנועת גלים אורכיים בגז‪) ,‬באוויר למשל(‬
‫בתהליכים אדיאבטים )למשל במקרה שלנו‪ ,‬שבו הנפח משתנה במהירות גדולה מכדי להותיר זמן‬
‫לחילופי חום עם הסביבה( מתקיים הקשר הבא בין הנפח ללחץ‪:‬‬
‫‪γ‬‬
‫‪γ‬‬
‫‪P1V1 = P2V2‬‬
‫‪=C‬‬
‫‪γ‬‬
‫‪PV‬‬
‫‪ - γ‬היחס בין חום המולרי בלחץ קבוע לבין החום המולרי בנפח קבוע‪:‬‬
‫‪cP‬‬
‫‪cV‬‬
‫=‪γ‬‬
‫)חום מולרי שווה לכמות החום הדרושה להעלות את הטמפרטורה של מול‪-‬גרם של החומר במעלה‬
‫אחת צלסיוס‪(.‬‬
‫פיתוח לוגריתמי ייתן‪:‬‬
‫‪Ln P + γLnV = LnC‬‬
‫נגזור ונקבל‪:‬‬
‫‪dP‬‬
‫‪dV‬‬
‫‪+γ‬‬
‫‪=0‬‬
‫‪P‬‬
‫‪V‬‬
‫או‪:‬‬
‫‪− dP‬‬
‫‪= γ⋅ P‬‬
‫‪dV‬‬
‫‪V‬‬
‫אבל‬
‫‪p‬‬
‫‪p‬‬
‫=‬
‫‪dV‬‬
‫‪ε‬‬
‫‪V‬‬
‫וגם‪:‬‬
‫‪=−B‬‬
‫‪p‬‬
‫‪ε‬‬
‫)ראה ההגדרה של ‪ , B‬למעלה(‬
‫וגם רשמנו )בנוסחת הקשר בין נפח הגז ללחץ( ‪ dP‬בשביל השינוי בלחץ‪ ,‬במקום ‪ , p‬לכן‪:‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪49‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫‪B = γ⋅ P‬‬
‫נציב זאת בנוסחת המהירות ונקבל עבור מהירות התפשטות גלי קול בגז‪:‬‬
‫‪γP‬‬
‫‪ρ‬‬
‫=‪v‬‬
‫‪.6‬‬
‫את התלות בטמפרטורה נקבל ממשוואת המצב של הגזים )משוואת קלפיירון(‪:‬‬
‫‪m‬‬
‫‪RT‬‬
‫‪M‬‬
‫‪m RT‬‬
‫=‪P‬‬
‫‪V M‬‬
‫‪RT‬‬
‫‪P=ρ‬‬
‫‪M‬‬
‫= ‪PV‬‬
‫‪ – M‬מסה מולרית‬
‫‪ – R‬קבוע הגזים‬
‫‪R‬‬
‫‪ – T‬טמפרטורה מוחלטת‬
‫נציב בנוסחת המהירות ונקבל‪:‬‬
‫‪γRT‬‬
‫‪M‬‬
‫=‪v‬‬
‫נציב בנוסחה את הערכים הבאים‪:‬‬
‫המסה של מול‪-‬גרם אוויר‪:‬‬
‫‪M = 29 ⋅ 10 −3 kg‬‬
‫קבוע הגזים )האנרגיה הדרושה להעלות את הטמפרטורה של מול‪-‬גרם אחד של הגז במעלה אחת‬
‫צלסיוס(‪:‬‬
‫‪j‬‬
‫‪C‬‬
‫הטמפרטורה המוחלטת‪:‬‬
‫‪0‬‬
‫‪R = 8.31‬‬
‫] [ ] [‬
‫‪T o K = t o C + 273.16‬‬
‫‪ γ‬של אוויר‪:‬‬
‫‪γ = 1.40‬‬
‫ונקבל עבור מהירות גלי הקול באוויר‪ ,‬בטמפרטורה של ‪: 20 o C‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪50‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫‪1.4 ⋅ 8.31 ⋅ 293.16‬‬
‫‪m‬‬
‫‪= 342.94‬‬
‫‪−3‬‬
‫‪s‬‬
‫‪29 ⋅ 10‬‬
‫=‪v‬‬
‫תלות זווית המופע במרחק‬
‫נניח כי בנקודה ‪ x = 0‬מתקיימות תנודות המתוארות על‪-‬ידי המשוואה‪:‬‬
‫‪y = y max . sin ωt‬‬
‫‪ - ω‬התדירות הזוויתית‪:‬‬
‫‪ω=2πf‬‬
‫והתנודות יוצרות גל אורכי שמתקדם לאורך הציר ‪ x‬במהירות ‪. v‬‬
‫אם צורת הגל נשמרת בתנועה אזי בנקודה ‪ x = x1‬משוואת התנודות תהייה‪:‬‬
‫⎛ ⎡‬
‫⎤⎞ ‪x‬‬
‫⎥⎟ ‪y1 = y max . sin ⎢ω ⎜ t − 1‬‬
‫⎦⎠ ‪v‬‬
‫⎝ ⎣‬
‫‪x1‬‬
‫‪v‬‬
‫הארגומנט של הסינוס )הזווית שבסוגריים המלבניים( נקרא "זווית מופע"‪:‬‬
‫הוא הזמן שהיה דרוש לגל )המתקדם במהירות ‪ ( v‬לעבור את המרחק ‪. x1‬‬
‫⎞ ‪x‬‬
‫⎛‬
‫⎟ ‪Φ1 = ω ⋅ ⎜ t − 1‬‬
‫⎠‪v‬‬
‫⎝‬
‫באופן דומה‪ ,‬משוואת התנודות בנקודה ‪ x = x2‬תהיה‪:‬‬
‫⎛ ⎡‬
‫⎤⎞ ‪x‬‬
‫⎥⎟ ‪y 2 = y max . sin ⎢ω ⋅ ⎜ t − 2‬‬
‫⎦⎠ ‪v‬‬
‫⎝ ⎣‬
‫עם זווית מופע‪:‬‬
‫⎞ ‪x‬‬
‫⎛‬
‫⎟ ‪Φ2 =ω ⋅⎜t − 2‬‬
‫⎠ ‪v‬‬
‫⎝‬
‫הפרש המופעים בין התנודות במקום ‪ x = x1‬לבין המקום ‪ x = x2‬הוא קבוע ואינו תלוי בזמן‪:‬‬
‫‪ΔΦ = Φ1 − Φ 2‬‬
‫‪x1‬‬
‫‪x‬‬
‫] ‪−t + 2‬‬
‫‪v‬‬
‫‪v‬‬
‫‪x − x1‬‬
‫‪Δx‬‬
‫‪ΔΦ = ω ⋅ 2‬‬
‫⋅ ‪=ω‬‬
‫‪v‬‬
‫‪v‬‬
‫‪ΔΦ = ω ⋅ [t −‬‬
‫נציב‪ ω = 2πf :‬ו ‪ v = λf -‬נקבל‪:‬‬
‫‪Δx‬‬
‫‪λ‬‬
‫‪ΔΦ = 2π‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪51‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫או‪:‬‬
‫‪ΔΦ Δ x‬‬
‫=‬
‫‪λ‬‬
‫‪2π‬‬
‫בניסוח מילולי‪ :‬הפרש מופע מחולק ב ‪ 2π‬שווה להפרש המרחק מחולק באורך הגל‪.‬‬
‫מסך הסקופ למטה )תמונה ‪ (4‬מציג את התנודות של הרמקול‪ ,‬ושל מיקרופון המרוחק מממנו‬
‫מרחק ‪. x‬‬
‫תמונה ‪ : 4‬מסך הסקופ מתאר את תנודות המתח של הרמקול והמיקרופון‬
‫בשל המרחק בין הרמקול למיקרופון נמדד הפרש מופע בין שתי התנודות‪.‬‬
‫הערוץ ‪ Voltage, ChC‬מציג את תנודות המתח של הרמקול‪.‬‬
‫הערוץ ‪ Voltage, ChA‬מציג את תנודות המתח של המיקרופון‪.‬‬
‫מועד תחילת המדידות מסונכרן באמצעות הדק )‪ (Trigger‬לרגע שהמתח על הרמקול עולה מעל‬
‫מתח סף נבחר )ראה הסבר בהמשך‪" :‬תהליך המדידה"(‪.‬‬
‫)שים לב לקו הירוק‪ :‬הסינוס מתחיל תמיד בנקודה קבועה‪ ,‬קצת מעל ראשית הצירים( ‪.‬‬
‫כדי למדוד את זווית המופע של תנודות מתח המיקרופון‪ ,‬נעתיק את נתוני הגרף של המיקרופון אל‬
‫לוח התוצאות‪ ,‬נעביר קו מגמה‪ Sine Fit :‬דרך נקודות הגרף כדי לקבל‪:‬‬
‫‪y = Asin(Bx + 2 πC) + D‬‬
‫‪-A‬‬
‫משרעת התנודות‪.‬‬
‫‪-B‬‬
‫התדירות הזוויתית של התנודות‪.‬‬
‫‪-C‬‬
‫‪Φ‬‬
‫קשור לזווית מופע באופן‪:‬‬
‫‪2π‬‬
‫‪-D‬‬
‫הזזה )קטנה( של ציר הזמן ‪.‬‬
‫= ‪.C‬‬
‫להלן הגרף שהתקבל מאחת המדידות )תמונה ‪.(5‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪52‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫תמונה ‪ :5‬תלות מתח המיקרופון בזמן‬
‫מקדם המתאם ‪) Root MSE‬מדד סטטיסטי שמשתמשים בו לעיתים קרובות להערכת טיב‬
‫המתאם( מודד את פיזור נקודות המדידה סביב הקו‪ .‬ככל שערכו קטן יותר‪ ,‬כך קטן הפיזור‬
‫וגדולה ההתאמה בין נקודות המדידה לקו‪.‬‬
‫בגרף לעיל )תמונה ‪ (5‬ההתאמה טובה מאד‪. (Root MSE=0.0075 ) :‬‬
‫‪ΔΦ‬‬
‫מהמדידה נקבל )תמונה ‪= 0.80 :(5‬‬
‫‪2π‬‬
‫= ‪.C‬‬
‫‪ΔΦ‬‬
‫נרחיק את המיקרופון ונחזור ונמדוד את‬
‫‪2π‬‬
‫‪ΔΦ‬‬
‫נציג את הגרף של‬
‫‪2π‬‬
‫עבור מרחקים שונים‪.‬‬
‫לפי המרחק ‪ x‬של המיקרופון מהרמקול ‪.‬‬
‫כפי שהראנו מתקיים הקשר‪:‬‬
‫‪ΔΦ 1‬‬
‫‪= ⋅x‬‬
‫‪2π‬‬
‫‪λ‬‬
‫‪1‬‬
‫‪.‬‬
‫הערך המוחלט של שיפוע הגרף שווה ל‪-‬‬
‫‪λ‬‬
‫)הסימן של שיפוע הגרף תלוי בבחירת נקודת הייחוס(‪.‬‬
‫תהליך המדידה‬
‫רמקול משדר גלי קול בתדר שמע )ניתן לשליטה(‪.‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪53‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫מיקרופון שנמצא במרחק מדוד )באמצעות סרט מדידה מודדים את מרחק המיקרופון מהרמקול(‬
‫קולט את גלי הקול‪) .‬תמונה ‪.(6‬‬
‫מתחילים במרחק של כ – ‪ 35‬ס"מ‪ .‬מודדים את ‪ C‬ומקרבים את המיקרופון אל הרמקול‪ ,‬כל פעם‬
‫ב – ‪ 1‬ס"מ בדיוק ומודדים שוב ושוב‪.‬‬
‫תוצאת המדידה מתוארת בחלון‪) Scope :‬תמונה ‪.(4‬‬
‫הערה‪ :‬החלון ‪ Scope‬שומר בזיכרון רק הנתונים של המסך האחרון‪ ,‬וניתן לשלוח אותם לשמירה‬
‫והצגה בלוח תוצאות‪.‬‬
‫לאחר כל מדידה חדשה‪ ,‬שומרים את התוצאות של הגרף )הדגימה של המיקרופון בלבד(‪.‬‬
‫תמונה ‪ :6‬העמדת מערכת המדידה‬
‫המיקרופון )חישן קול( מחובר לכניסה האנלוגית ‪ A‬של הממשק‪.‬‬
‫הרמקול מחובר לנקודות ה‪ OUTPUT -‬של הממשק‪.‬‬
‫באמצעות חלון ה‪ Signal Generator -‬שולטים על משרעת המתח‪ ,‬על צורת הגל ועל התדר‪.‬‬
‫אל הנקודות ה‪ , OUTPUT -‬במקביל לרמקול‪ ,‬מחובר גם חישן מתח ששולח לממשק )דרך‬
‫הכניסה האנלוגית ‪ (C‬את מתח ההידוק ) ‪.( Triggering‬‬
‫המערכת מודדת ‪ 100,000‬מדידות לשנייה‪.‬‬
‫מודדים בתדר של ‪ 4000 Hz‬וחוזרים ומודדים בתדר של ‪. 4500 Hz‬‬
‫קול בתדרי שמע גבוהים כאלה יוצר תחושה בלתי נעימה‪ .‬לכן‪ ,‬כדי למנוע סבל מיותר‪ ,‬כל מדידה‬
‫נמשכת פרק זמן קצר של ‪ 0.5‬שנייה‪ .‬בזמן זה‪ ,‬המערכת מודדת ‪ 50,000‬מדידות ‪ -‬די והותר לקבלת‬
‫הגרפים‪ ,‬בצורה נאותה‪.‬‬
‫עבור תדר של ‪ , 4000 Hz‬זמן המחזור הוא ‪ . 2.5 ⋅ 10 −4 s‬במצב שהמערכת מודדת ‪ 105‬מדידות‬
‫בשנייה‪ ,‬נמדדות ‪ 25‬מדידות למחזור תנודות אחד‪ .‬זה מספיק כדי להפיק קו מגמה תואם בצורה‬
‫טובה את נקודות המדידה‪.‬‬
‫הערה‪ :‬היות והפרש המופע נמדד באמצעות קו המגמה‪ ,‬לכן חשוב מאוד שקו המגמה יחפוף היטב‬
‫את נקודות המדידה )תמונה ‪ .(5‬אם פיזור הנקודות סביב קו המגמה גדול יש לחזור על המדידה‪.‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪54‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫מייצבים את תמונת הגרפים בחלון ה‪ Scope -‬על‪-‬ידי הידוק )‪ ( Triggering‬מתח הרמקול לערך‬
‫סף קבוע ובמגמה קבועה )במגמת עליה למשל(‪ .‬אחרת כל תמונת מסך בחלון ה – ‪ scope‬תתחיל‬
‫בנקודה שונה‪.‬‬
‫במדידה הראשונה )ורק במדידה הראשונה!( ממקמים )מיקום התחלתי( את המיקרופון מיקום‬
‫התחלתי כך שהפרש המופע בין מתח הרמקול למתח המיקרופון יהיה קרוב לאפס‪ ,‬ככל הניתן‪.‬‬
‫)הפרמטר ‪ C‬של קו המגמה קרוב‪ ,‬ככל שניתן לאפס( בדרך זאת בכל מדידה נוספת הפרש המופעים‬
‫בעקבות שינוי המרחק בין הרמקול למיקרופון יהיה המופע של המיקרופון!‬
‫בכל מדידה חדשה‪ ,‬מקרבים את המיקרופון אל הרמקול ב ‪ 1‬ס"מ בדיוק ומודדים את הפרמטר ‪C‬‬
‫כנגד מרחק ההזזה )מהמיקום ההתחלתי(‪.‬‬
‫המדידה האחרונה ‪ -‬כאשר הפרמטר ‪ C‬של קו המגמה קרוב ל – ‪ 7) 1‬עד ‪ 8‬מדידות(‪.‬‬
‫)מודדים בתחום של אורך גל אחד בערך(‪.‬‬
‫הצבת מערכת הניסוי‬
‫נחבר את חישן הקול לכניסה האנלוגית ‪ A‬של הממשק )תמונה ‪.(7‬‬
‫נחבר את היציאה של חישן המתח לכניסה אנלוגית ‪ C‬של הממשק‪.‬‬
‫נחבר את הרמקול ואת הכניסה של חישן המתח למוצא ) ‪ ( output‬של הממשק )תמונה ‪.(7‬‬
‫תמונה ‪ :6‬חיבור החישנים והרמקול‬
‫חלון ה‪ Signal Generator -‬שולט על מתח המוצא )תמונה ‪.(7‬‬
‫בוחרים‬
‫גל‪Sin Wave Function :‬‬
‫תדר‪4000 Hz :‬‬
‫משרעת‪. 1.0 V :‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪55‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫תמונה ‪ :7‬השליטה על מקור מתח‬
‫הכנה לניסוי‬
‫העבודה עם חלון ה‪Scope -‬‬
‫כאשר הסמן נמצא בתוך מלבן הערוץ‪ ,‬למשל ‪ , Voltage, ChC‬הקשה על העכבר בוחרת את הגרף‪.‬‬
‫תמונה ‪ :8‬חלון הסקופ‬
‫במצב כזה‪ ,‬הכפתור ‪ Trigger‬מהדק את נקודת ההתחלה של הגרף הנבחר‪.‬‬
‫בעזרת הכפתור "שינוי נקודת הידוק" ניתן לכוון את נקודת ההידוק‪.‬‬
‫החצים כלפי מעלה ומטה )בתוך מלבן הערוץ( קובעים את המתח ליחידת חלוקה‪.‬‬
‫בתמונה ‪ :8‬יחידת חלוקה ב ‪ Ch C‬מודדת ‪ 1‬וולט ויחידת חלוקה ב ‪ CH A‬מודדת ‪ 0.5‬וולט‪.‬‬
‫החצים האופקים )מתחת לציר האופקי‪ ,‬באמצע החלון( שולטים בבסיס הזמן‪.‬‬
‫בתמונה ‪ 8‬בחרנו בסיס זמן של ‪ (0.0001s) 0.1ms‬ליחידת חלוקה‪.‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪56‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫תנודת מתח שלמה של ‪ ChC‬בתמונה ‪ 8‬נפרשת על ‪ 2.2‬יחידות חלוקה בערך לפיכך‪ ,‬זמן המחזור‬
‫שווה ל ‪ 0.00022‬שניות בערך‪) .‬התדר שווה ל ‪ 4545 Hz‬בערך(‬
‫תדר המתח שנבחרה מוצג בחלון הסקופ‪ .‬ערכו‪.( 4500H :‬‬
‫הקשה על הכפתור‪) Transfer Data :‬העבר נתונים( מעבירה את נתוני הגרף הנבחר )המסומן(‬
‫ללוח התוצאות‪.‬‬
‫קביעת נקודת ההידוק‬
‫∗ בחר‬
‫תדר‪4000 Hz :‬‬
‫משרעת מתח‪1.0 V :‬‬
‫∗ בחר את הערוץ‪Ch C :‬‬
‫∗ הפעל את המדידה על‪-‬ידי הקשה על ‪. Start‬‬
‫המדידה נעצרת אוטומטית אחרי ‪ 0.5‬שניות‪.‬‬
‫צריך למדוד שוב ושוב‪ ,‬עד שמקבלים כיוון אופטימלי עבור נקודת ההידוק )נקודת ההתחלה של‬
‫הגרף(‪.‬‬
‫∗ כוון את נקודת ההידוק‪ ,‬באמצעות הכפתור‪" :‬שינוי נקודת ההידוק"‪ ,‬קרוב ככל האפשר לנקודת‬
‫הראשית )תמונה ‪. (8‬‬
‫קליטת הנתונים‬
‫ניסוי א – תדר‪4000 Hz :‬‬
‫‪.1‬‬
‫מקם את המיקרופון‪) ,‬קרא את המרחק על הסרגל( בנקודה‪ 50 :‬ס"מ ואת הרמקול‪15 :‬‬
‫ס"מ‪.‬‬
‫‪.2‬‬
‫בחר את הערוץ ‪ Ch C‬של מתח הרמקול‪.‬‬
‫‪.3‬‬
‫מדוד ‪ -‬בהקשה על ‪. Start‬‬
‫‪.4‬‬
‫קרב את הרמקול אל המיקרופון ומדוד מחדש )להזכירך‪ :‬משך זמן המדידה ‪ 0.5‬שנייה(‪.‬‬
‫חזור על הפעולות עד שנקודת ההתחלה של גרף המתח בערוץ ‪) Ch A‬מוצא המיקרופון(‬
‫קרובה ככל שניתן לנקודת ההתחלה של המתח בערוץ ‪) Ch C‬מוצא הרמקול(‪.‬‬
‫יתכן ותצטרך לשנות את משרעת התנודות )תמונה ‪.(8‬‬
‫‪.5‬‬
‫לאחר שקבלת‪ ,‬על מסך הסקופ‪ ,‬את שתי תנודות המתח כך שהפרש המופע ההתחלתי ביניהם‬
‫קרוב לאפס‪ ,‬עבור וסמן את הערוץ ‪ ) Ch A‬מתח המיקרופון(‪.‬‬
‫‪.6‬‬
‫הקש על הכפתור‪ Transfer Data :‬להעברת הנתונים ללוח תוצאות‪.‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪57‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫‪.7‬‬
‫מופיע המילה ”‪ “Data‬בחלון ‪ Data‬מתחת הסימון ‪:‬‬
‫הדפס במקום המילה ”‪ ”Data‬את התדר ואת מיקום המיקרופון )תמונה ‪.(9‬‬
‫תמונה ‪ :9‬התצוגה של חלון ‪Data‬‬
‫‪.8‬‬
‫הצג חלון גרף‪ . Graph 1 :‬בחר את נתוני ההרצה הראשונה‪.‬‬
‫‪.9‬‬
‫הקש על הכפתור ‪ , Fit‬בשורת הבקרה של חלון הגרף ובחר באפשרות‪. Sine Fit :‬‬
‫הערה‪ :‬אם קו המגמה אינו חופף היטב את נקודות המדידה‪ ,‬מחק התוצאות וחזור על המדידה‪.‬‬
‫)גרף ‪.(1‬‬
‫גרף ‪ :1‬תלות מתח המיקרופון בזמן – הרצה ‪4‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪58‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫‪.10‬‬
‫הצג לוח תוצאות ‪) Table 1‬תמונה ‪.(10‬‬
‫תמונה ‪ :10‬לוח התוצאות לניסוי א'‬
‫הקש על סמל העפרון והקלד את המיקום של המיקרופון ואת הפרמטר ‪ . C‬הקטן את חלון הגרף‬
‫ואת חלון לוח התוצאות‪ .‬על המסך מוצג חלון הסקופ‪ .‬סמן את מלבן הערוץ ‪. Ch C‬‬
‫חזור ומדוד ‪ 6‬עד ‪ 7‬מדידות נוספות )סעיפים ‪ 2‬עד ‪ (8‬כאשר בכול מדידה חדשה אתה מקרב את‬
‫המיקרופון אל הרמקול ב – ‪ 1‬ס"מ בדיוק ‪.‬‬
‫התהליך מסתיים כאשר הפרמטר ‪ C‬קרוב ל ‪.1‬‬
‫הערה‪ :‬כדי לציין את סיום הקלדת הנתונים )לאחר הקלדת התוצאה האחרונה(‪ ,‬מקישים על‬
‫כפתור העיפרון )ולא על ‪.( Enter‬‬
‫ניסוי ב' – תדר‪4500 Hz :‬‬
‫∗ הצג את החלון‪) Signal Generator :‬תמונה ‪ (7‬ושנה את התדר ל – ‪. 4500 Hz‬‬
‫∗ חזור ומדוד )כמו בניסוי א'‪ ,‬סעיפים‪ 1 :‬עד ‪.(8‬‬
‫רשום את תוצאות המדידה של הניסוי ב' בחלון התוצאות‪. Table 2 :‬‬
‫עיבוד הנתונים‬
‫‪.1‬‬
‫הצג חלון הגרף‪. Graph 2 :‬‬
‫הגרף מציג את המדידות בניסוי א'‪.‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪59‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫בחר באפשרות‪ , Linear Fit :‬מהחלון ‪ Fit‬והדפס את הגרף )גרף ‪.(2‬‬
‫גרף ‪ :2‬תלות זווית המופע במיקום המיקרופון – ניסוי א'‬
‫‪.2‬‬
‫שאלה‪:‬‬
‫מהו אורך גל הקול – חשב באמצעות הפרמטרים של הגרף‪.‬‬
‫תשובה‪:‬‬
‫הגרף שקיבלנו בניסוי א' מציג את הפונקציה‪:‬‬
‫‪ΔΦ 1‬‬
‫‪= ⋅ Δx‬‬
‫‪2π‬‬
‫‪λ‬‬
‫זווית המופע ההתחלתי שנמדדה לגל מתח המיקרופון ‪ Φ‬שווה להפרש המופע ‪ ΔΦ‬בין מתח‬
‫הרמקול למתח המיקרופון‪.‬‬
‫אם ‪ - x1‬מיקום הרמקול‬
‫‪ - x 2‬מיקום המיקרופון‬
‫‪ Δx = x1 − x2‬הוא המרחק בין הרמקול למיקרופון‪.‬‬
‫הראנו ש‪:‬‬
‫‪Φ 1‬‬
‫‪= ⋅x‬‬
‫‪2π λ‬‬
‫‪Φ‬‬
‫‪2π‬‬
‫הוא הפרמטר ‪ C‬של קו המגמה‪.‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪60‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫‪Φ‬‬
‫‪2π‬‬
‫כפונקציה של ‪ x‬הוא ישר ששיפועו )בערך מוחלט( שווה להופכי של אורך גל‪:‬‬
‫‪1‬‬
‫‪λ‬‬
‫=‪m‬‬
‫הפרמטר ‪ m‬הוא השיפוע של קו המגמה‪.‬‬
‫מצאנו במדידה ש‪:‬‬
‫‪m = 0.117‬‬
‫‪= 0.117‬‬
‫‪1‬‬
‫‪λ‬‬
‫‪λ = 8.547cm‬‬
‫שאלה‪:‬‬
‫מדוע מתעלמים מהסימן של שיפוע הגרף?‬
‫תשובה‪:‬‬
‫הסימן של השיפוע תלוי בבחירת נקודת הייחוס‪ .‬במדידת שינוי מרחק המיקרופון מהרמקול‬
‫התעלמנו מהסימן של ‪ . Δx‬מסיבה זו יש להתעלם גם מהסימן של שיפוע הגרף‪.‬‬
‫שאלה‪:‬‬
‫מהי מהירות גלי הקול באוויר עלפי התוצאות של ניסוי א' ?‪.‬‬
‫תשובה‪:‬‬
‫מקבלים את מהירות הגל ממכפלת אורך הגל בתדר‪:‬‬
‫‪v = λ ⋅f‬‬
‫‪cm‬‬
‫‪sec‬‬
‫‪v = 8.547 ⋅ 4000 = 34,188‬‬
‫‪m‬‬
‫‪s‬‬
‫‪.3‬‬
‫‪v = 341.9‬‬
‫הצג חלון הגרף‪Graph 3 :‬‬
‫גרף ‪ :3‬תלות זווית המופע במיקום המיקרופון – ניסוי ב'‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪61‬‬
‫"שולמן" ציוד לימודי רח' מקווה‪-‬ישראל ‪ 10‬ת"ד ‪ 1039‬ת"א ‪61009‬‬
‫טל'‪ 03-5605536 :‬פקס‪www.shulman-sci.co.il 03-5660340 :‬‬
‫____________________________________‬
‫הגרף מציג את המדידות בניסוי ב'‪.‬‬
‫בחר באפשרות‪ , Linear Fit :‬מהחלון ‪ Fit‬והדפס את הגרף )גרף ‪.(3‬‬
‫תרגיל‪:‬‬
‫מדוד את אורך הגל וחשב את מהירות גלי הקול‪.‬‬
‫פתרון‪:‬‬
‫‪= 0.131‬‬
‫‪1‬‬
‫‪λ‬‬
‫‪λ = 7.633cm‬‬
‫‪cm‬‬
‫‪s‬‬
‫‪v = λ ⋅ f = 7.633 ⋅ 4500 = 34,348‬‬
‫‪m‬‬
‫‪s‬‬
‫‪v = 343.5‬‬
‫תרגיל‪:‬‬
‫הטמפרטורה בעת המדידות הייתה ‪. 20.0°C‬‬
‫קבל את מהירות גלי הקול מהנוסחה התיאורטית‪.‬‬
‫פתרון‪:‬‬
‫‪1.4 ⋅ 8.31 ⋅ 293.16‬‬
‫‪m‬‬
‫‪= 342.9‬‬
‫‪−3‬‬
‫‪s‬‬
‫‪29 ⋅ 10‬‬
‫=‪v‬‬
‫תרגיל‪:‬‬
‫חשב את המהירות הממוצעת של גלי הקול לפי התוצאות של ניסוי א' וניסוי ב'‪.‬‬
‫חשב את הטעות היחסית של המהירות הממוצעת ביחס למהירות התיאורטית‪.‬‬
‫פתרון‪:‬‬
‫‪343.5 + 341.9‬‬
‫‪m‬‬
‫‪= 342.7‬‬
‫‪2‬‬
‫‪s‬‬
‫_‬
‫=‪v‬‬
‫חישוב הטעות היחסית‪:‬‬
‫‪342.9 − 342.7‬‬
‫‪⋅ 100 = 0.06%‬‬
‫‪342.9‬‬
‫הערה‪ :‬טעות יחסית עד ‪ 3 %‬נחשבת מוסברת ע"י המגבלות בדיוק המדידה‪.‬‬
‫‪ – Sound Waves.doc‬חוברת מס' ‪ / 3‬גלים ואופטיקה‬
‫‪62‬‬
61009 ‫ ת"א‬1039 ‫ ת"ד‬10 ‫ישראל‬-‫"שולמן" ציוד לימודי רח' מקווה‬
www.shulman-sci.co.il 03-5660340 :‫ פקס‬03-5605536 :'‫טל‬
____________________________________
‫המכשירים הדרושים לביצוע התרגיל‬
1. Science Workshop 750 Interface
CI – 6450 Pasco
2. Sound Sensor
CI – 6506B Pasco
3. Voltage Sensor
CI – 6503 Pasco
4. Speaker
63
‫ גלים ואופטיקה‬/ 3 '‫ – חוברת מס‬Sound Waves.doc