FÖRÄNDRINGSHASTIGHET ( Tillämpningar av derivata) Uppgift 1

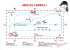
Armin Halilovic: EXTRA ÖVNINGAR
Förändringshastighet
FÖRÄNDRINGSHASTIGHET ( Tillämpningar av derivata)
Uppgift 1. En rak cirkulär kon med toppvinkeln 90o placeras med spetsen vänd nedåt.
Konen fylls med vatten med hastigheten 5 dm3/min.
Med vilken hastighet stiger vattenytan då vattendjupet är h=2 dm ?
Lösning:
Vi har
5 ;
vid h=2.
vi söker
Vattens volym är
3
där både r och h förändras med tiden t .
Toppvinkeln = 90o medför att
Eftersom vi söker
i konen.
eliminerar vi
, d v s substituerar
i (*) och får
3
Till slut deriverar vi (**) med avseende på t och använder kedjeregeln
( Kedjeregeln:
Vi substituerar
′
′
·
′
5
4
4
dm/min
1 av 3 ].
5 och h=2 i (***) och får
5
Svar:
·
eller
Armin Halilovic: EXTRA ÖVNINGAR
Förändringshastighet
Uppgift 2. En rät (rak) cirkulär kon placeras med spetsen vänd nedåt.
Basytans radie är R=6m. Höjden är H=8m.
Konen fylls med vatten med hastigheten 0.1 m3/min.
Med vilken hastighet stiger vattenytan då vattendjupet är h=4 m ?
Lösning:
Vi har
0.1 ;
vid h=4.
vi söker
Vattens volym är
3
där både r och h förändras med tiden t .
Från bilden ( likformiga trianglar) får vi följande samband mellan h och r 6
8
Eftersom vi söker
eliminerar vi
3
Till slut deriverar vi (**) med avseende på t :
′
′
·
′
3
, d v s substituerar
3
4
[Kedjeregeln:
3
. 4
·
eller
3
16
].
9
16
Vi substituerar
0.1 och h=4 i (***) och får
1
10
9 · 16
16
1
90
Svar: Vattenytan stiger med hastigheten
m/min
Uppgift 3. En kropp rör sig i planet längs kurvan ( hyperbel)
2 av 3 i (*), och får 4
Armin Halilovic: EXTRA ÖVNINGAR
Förändringshastighet
8,
längdenhet är meter
3, 1 är
Kroppens hastighet i x-led i punkten
2
/
a) Bestäm kroppens hastighet i y-led i samma punkt.
b) Beräkna kroppens fart
3, 1 .
c) Bestäm kurvans lutning (= tangentens lutning) i punkten
Lösning:
a) Vi har
2 i punkten
Vi söker
i samma punkt.
3, 1 .
Lägg märke till att både
och
är funktioner av tiden .
Vi deriverar ekvationen
8
på och får
2 ·
3,
I punkten P gäller
2 ·
1 och
2·3·2
0
2, som vi substituerar i (*) och får
2·1·
0
6
6m
Svar a) Kroppens hastighet i y-led i punkten P är
,
b) Kroppens fart [= längden av hastighets vektorn
2
är
Svar b)
6
√40
]
2√10
2√10 m/s
c) Vi deriverar implicit med avseende på x ekvationen
8
och får
2
2 ·
3
1
0
Svar c) Kurvans lutning (= tangentens lutning) i punkten
3 av 3 är
3
3.