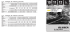Geometri - arbeidsplan.net

Geometri
Bruke og forklare Pythagoras' setning til beregninger og i praktisk arbeid
nu
te
po
Hy
s
c
5
Katet
4 a
b
90°
2
c  c = c = 25
3
Katet
2
a  a = a = 16
2
bb = b = 9
Π υ θ α γ ό ρ α ς = P y th a g o r a s (580 – 500 f.kr)
Pythagoras' læresetning :
"I en rettvinklet trekant er summen av kvadratene på katetene lik kvadratet på hypotenusen "
Gresk filosof, mystiker og matematiker
• I en rettvinklet trekant er en av vinklene 90°
• Hypotenus er en rettvinklet trekants lengste side
I en rettvinklet trekant der hypotenusen har lengden c og katetene har lengdene a og b har vi :
𝑐 2 = 𝑎2 + 𝑏 2
𝑐 = √𝑎2 + 𝑏 2

𝑐 2 = 𝑎2 + 𝑏 2

𝑎 = √𝑐 2 − 𝑏 2

𝑐 = √𝑎2 + 𝑏 2

𝑏 = √𝑐 2 − 𝑎2

Symbolet
𝟐
Symbolet √
eller 𝑎 = √𝑐 2 − 𝑏 2
52 = 42 + 32

4 = �52 − 32

5 = �42 + 32

3 = �52 − 42

leses som "opphøyd i andre "
• Katet kommer fra gresk kathetos som betyr loddlinje
eller 𝑏 = √𝑐 2 − 𝑎2
25 = 16 + 9
• Vinkelbein (katetene) er to rette linjer
som "stråler" ut fra ett felles punkt
• (I trekanter som ikke er rettvinklet benyttes cosinussetningen og sinussetningen)
Prøv ut
5 = √16 + 9

3 = √25 − 16

4 = √25 − 9
• Hypotenus kommer fra latin hypotenusa som igjen kommer
fra gresk hupoteinousa som betyr "strekker seg under"

5 = √25
52 = 25
3 = √9
32 = 9
42 = 16
4 = √16
𝟐
og √ på kalkulatoren med ulike tall . . .



√25 = 5
√16 = 4
√9 = 3
Nyttig bakgrunnsmateriale til læreplanmålet PYTHAGORAS :
Symbolet ° leses som "grader "
LIGNINGER AV FØRSTE GRAD (Tall og algebra)
POTENSLIGNINGER (Tall og algebra)
leses som "roten av "
FORHOLD (Tall og algebra)
AREAL – Trekant (Geometri)
EKSEMPLER
a) 
b) 
Hvilken av sidene i den rettvinklede trekanten er hypotenusen ?
—
Det er alltid den lengste siden som er hypotenusen.
Hvilke av sidene i den rettvinklede trekanten kalles katet ?
—
Vinkelbeinene til den rette vinkelen (90°) kalles kateter.
Det betyr at vi har to kateter i den rettvinklede trekanten.
c) 
d) 
Finn siden c (hypotenusen) i figuren ved beregning.
—
𝑐 = �𝑎2 + 𝑏 2 = �42 + 32 = √16 + 9 = √25 = 5
Finn siden b (den ene kateten) i figuren ved beregning.
—
𝑏 = �𝑐 2 − 𝑎2 = �52 − 42 = √25 − 16 = √9 = 3
© Geir Granberg JAN2015